Chapter 6 여러 개의 예측변수를 갖는 모형
여러 개의 예측변수를 갖는 모형의 ROC 곡선도 그릴 수 있다.
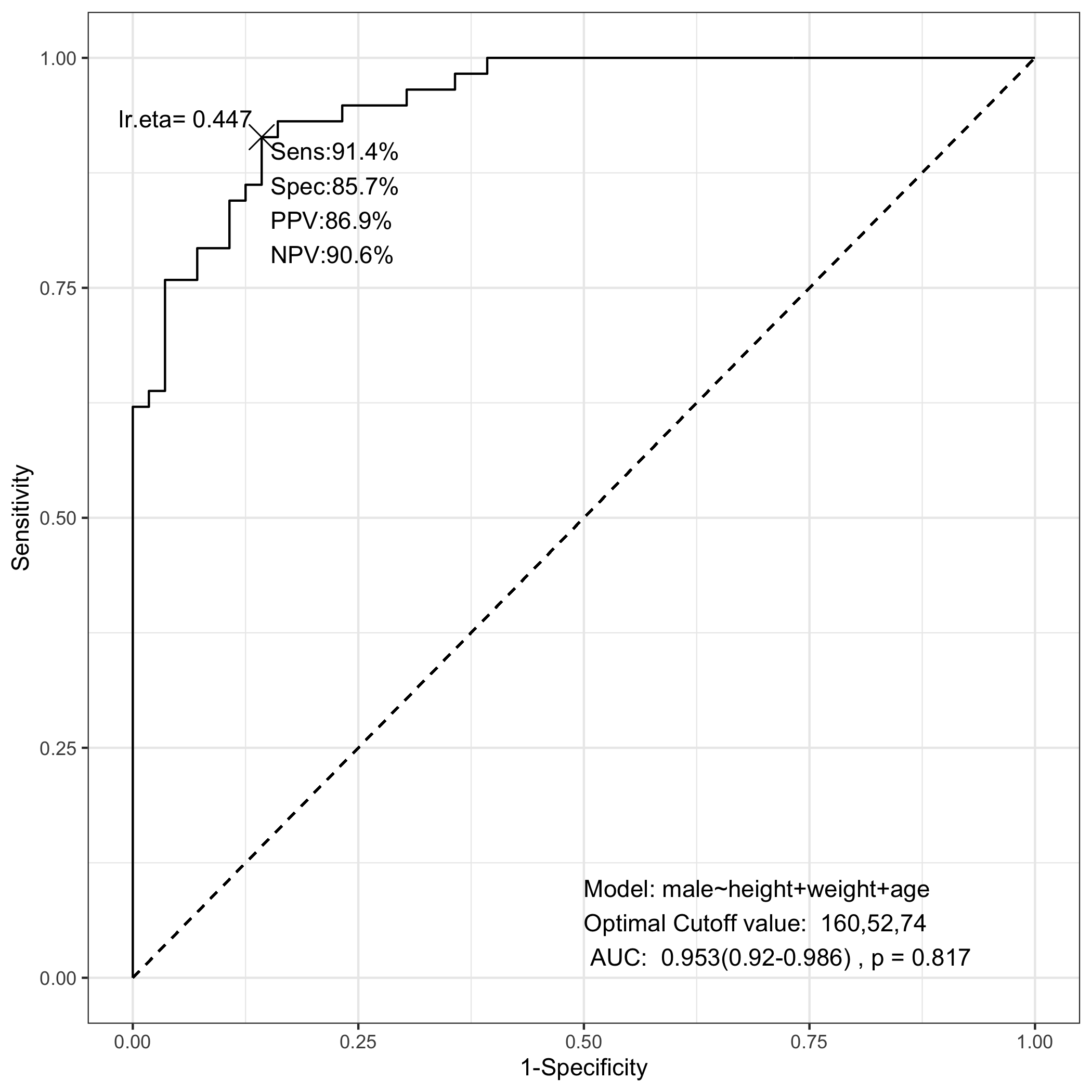
위의 ROC 곡선은 다음의 glm 객체를 통해 만들어진다.
6.1 자동화된 단계적 회귀
여러 개의 예측변수를 갖는 다중로지스틱회귀모형에서 step() 함수는 AIC 값을 기준으로 자동화된 후향적제거 과정을 통해 최종모형 선택을 도와준다.
Call:
glm(formula = male ~ height, family = binomial, data = radial)
Deviance Residuals:
Min 1Q Median 3Q Max
-2.15418 -0.30022 0.02699 0.25143 2.17328
Coefficients:
Estimate Std. Error z value Pr(>|z|)
(Intercept) -65.38126 12.72530 -5.138 2.78e-07 ***
height 0.40722 0.07918 5.143 2.71e-07 ***
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
(Dispersion parameter for binomial family taken to be 1)
Null deviance: 158.002 on 113 degrees of freedom
Residual deviance: 63.462 on 112 degrees of freedom
(1 observation deleted due to missingness)
AIC: 67.462
Number of Fisher Scoring iterations: 6이 경우 다음과 같이 초기모형과 최종모형을 비교할 수 있다.
Analysis of Deviance Table
Model 1: male ~ height
Model 2: male ~ height + weight + age
Resid. Df Resid. Dev Df Deviance Pr(>Chi)
1 112 63.462
2 110 63.352 2 0.11025 0.9464step_ROC함수는 위와 같은 단계적회귀를 통해 초기모형과 최종모형을 만들고 두 모형의 ROC 곡선을 그려주고 두 모형 의 AUC 값을 비교해준다.
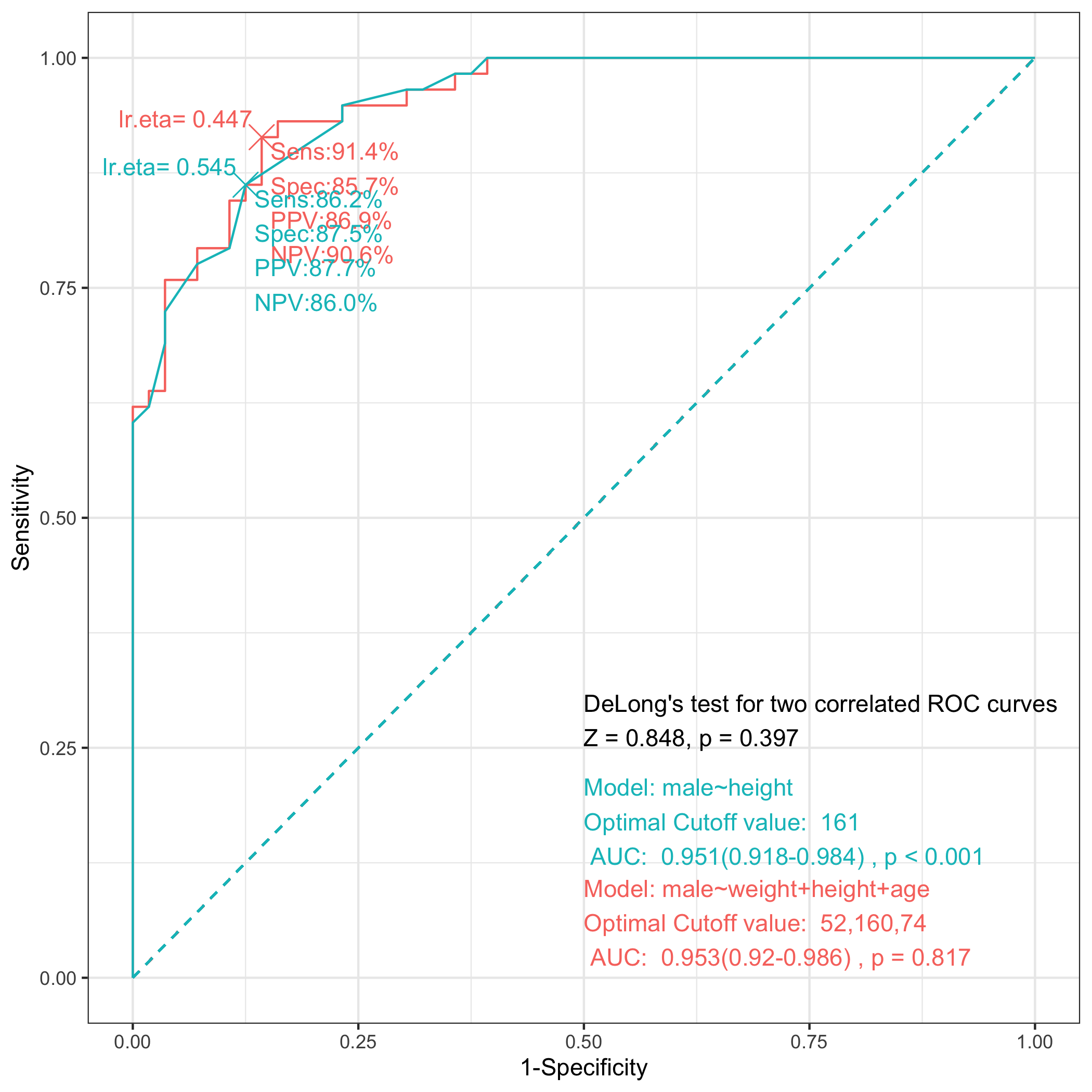
step_ROC함수의 plot인수를 FALSE로 설정하면 ANOVA 테이블을 출력해준다.
Analysis of Deviance Table
Model 1: male ~ height
Model 2: male ~ weight + height + age
Resid. Df Resid. Dev Df Deviance Pr(>Chi)
1 112 63.462
2 110 63.352 2 0.11025 0.9464