Chapter 2 첫번째 예제
2.1 키로 남녀 성별을 구별할수 있을까 ?
2.1.1 사용하는 패키지
에제 데이터로 moonBook 패키지의 radial 데이터를 사용하고 ROC 곡선을 그리기 위해 ggplot2 패키지를 사용한다. 또한 데이터의 조작을 위해 dplyr, tidyr, purrr 패키지를 사용한다.
2.1.2 최종결과 패키지
여기서 사용하는 R 코드를 모아 사용의 편의를 위해 R패키지를 만들어 github에 공개하였다. 다음 코드로 github에 있는 패키지를 설치하고 불러올 수 있다.
2.1.3 탐색적 분석
moonBook 패키지에 포함되어 있는 radial 데이터는 115명의 환자의 임상데이터로 여기에 기록되어있는 키(cm)로 남여 성별을 구별해보고자 한다. 먼저 탐색적 분석을 시작해본다.
theme_set(theme_bw())
data(radial,package="moonBook")
radial %>% group_by(sex) %>% numSummary(height)# A tibble: 2 x 13
# Groups: sex [2]
sex n mean sd median trimmed mad min max range skew
<fct> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl>
1 F 56 154. 6.01 153 154. 5.93 140 166 26 -0.0679
2 M 58 168. 5.84 169 167. 5.93 155 180 25 -0.00647
# … with 2 more variables: kurtosis <dbl>, se <dbl>탐색적 그래프를 그려 눈으로 확인해본다.
ggplot(data=radial)+geom_density(aes(x=height,fill=sex),alpha=0.5)
ggplot(data=radial)+geom_boxplot(aes(x=sex,y=height,fill=sex),alpha=0.5) 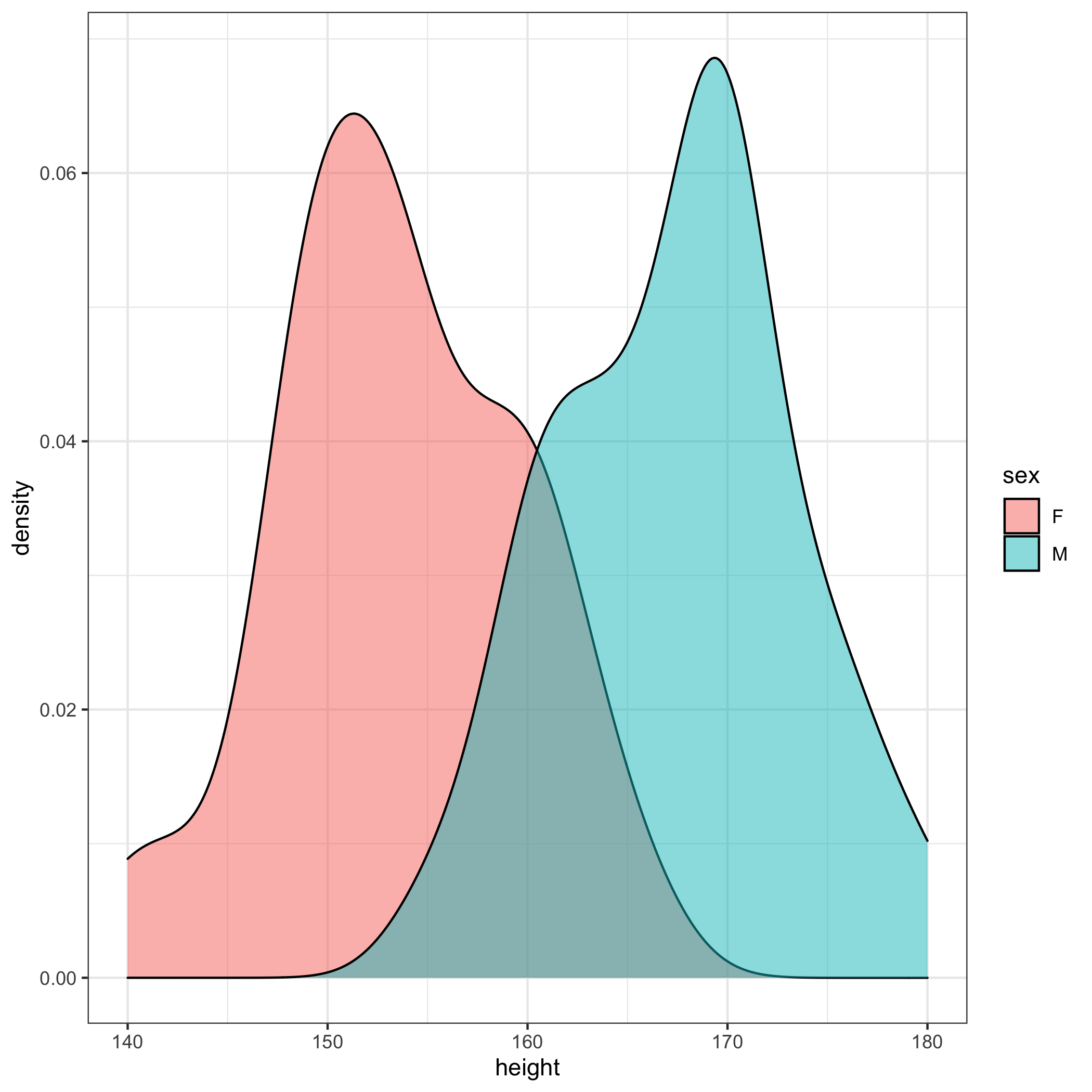
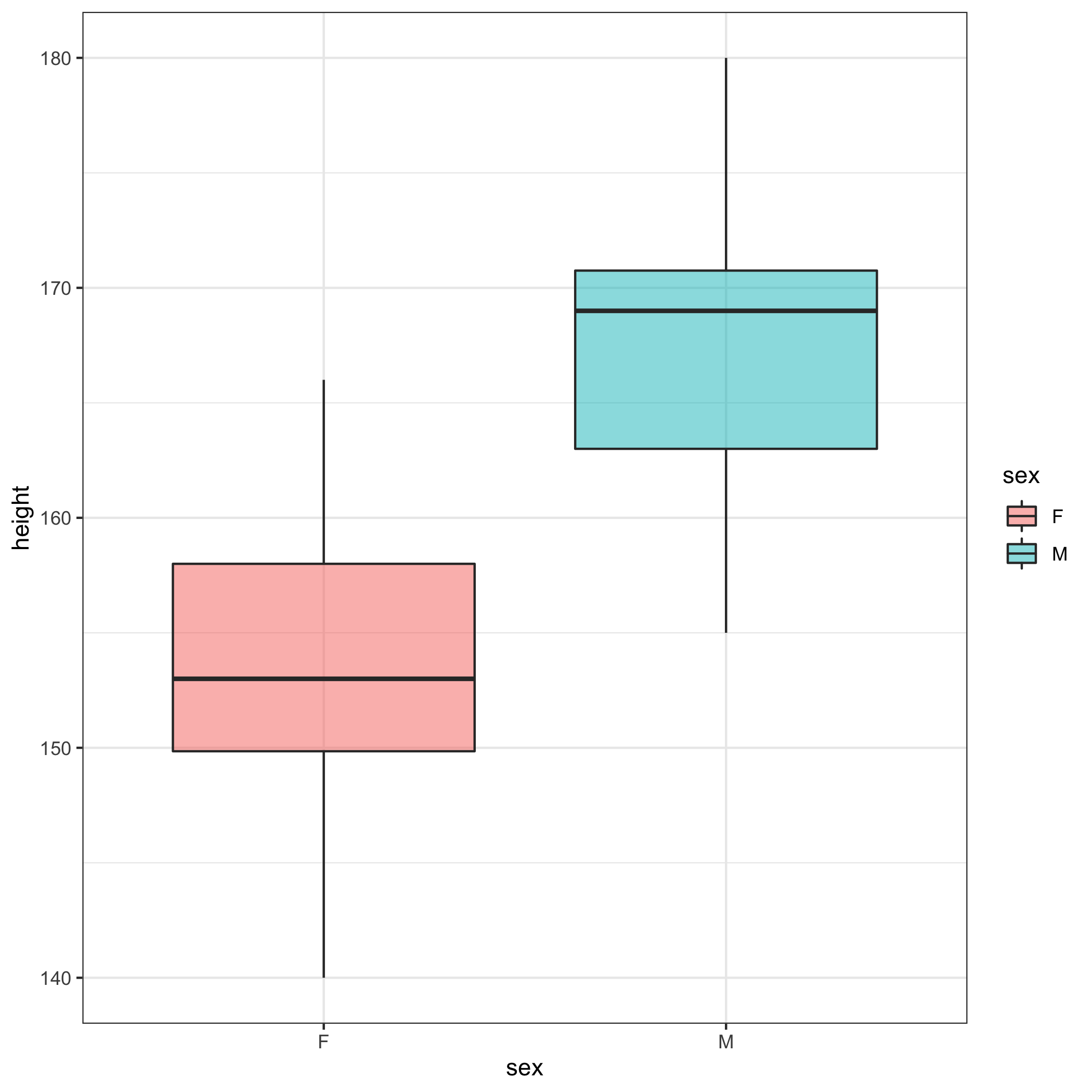
그래프에서 보는 바와 같이 남성환자가 어성환자에 비해 키가 큰 것을 알 수 있으나 최적의 절사점(optimal cutoff value)은 어떻게 정해야 할까?
2.2 첫번째 ROC 곡선 그리기
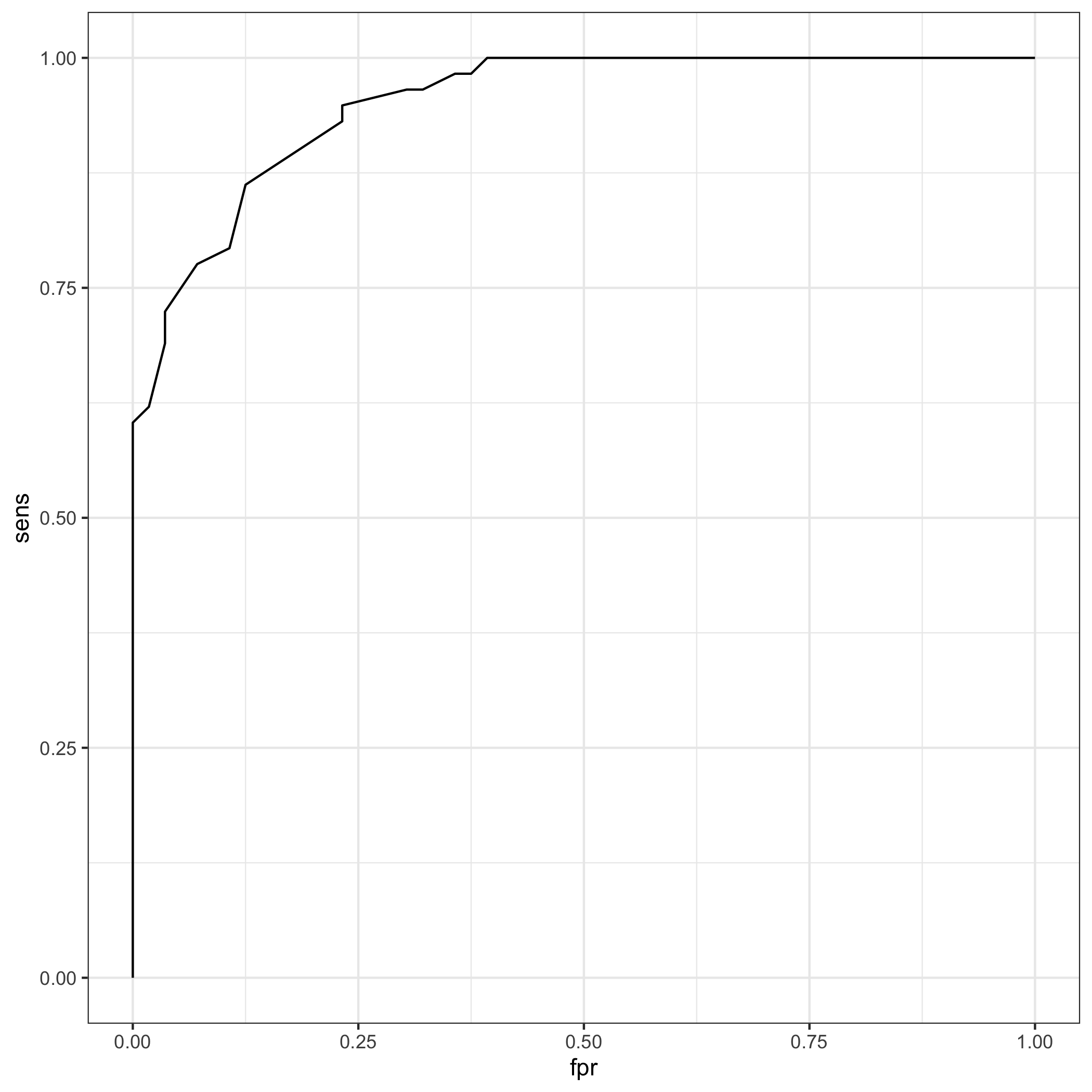
최적의 절사점(optimal cutoff value)을 결정할 수 있는 방법 중 하나는 ROC 곡선을 그려보는 것이다. 저자가 만든 multipleROC 패키지를 이용하여 다음 R코드로 ROC 곡선을 그릴 수 있다.
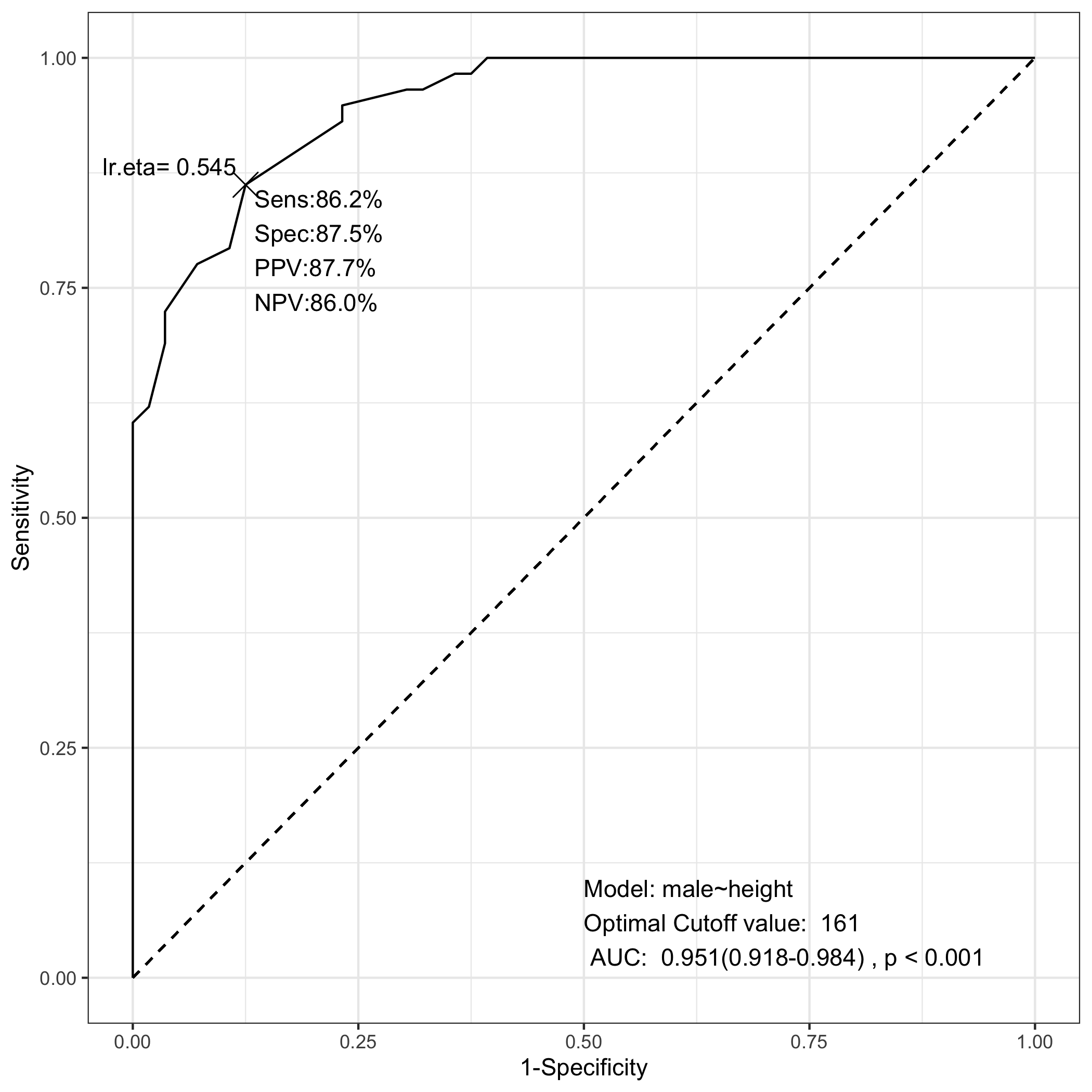
2.2.1 민감도(Sensitivity), 특이도(Specificity), 양성예측률(PPV) 그리고 음성예측률(NPV)
위의 그림에서 보면 민감도(sensitivity, Sens), 특이도(specificity, Spec), 양성예측률(Positive predictive value, PPV) 및 음성예측률(negative predictive value, NPV) 이 표시되어 있고 키의 최적절사점(optimal cutoff value)이 161cm로 나와 있다. 민감도 특이도 등은 161cm 를 기준으로 한 다음 표에서 구할 수 있다.
0 1
FALSE 49 8
TRUE 7 50키 \(\geq\) 161cm 이상을 기준으로 남여를 구별한다면 true positive(TP)는 114명중 50명, true negative(TN)는 49명, 위양성(false positive, FP)는 7명이고 위음성(false negative, FN)은 8명이다. 민감도, 특이도, 양성예측률, 음성예측률은 손으로 계산할 수 있다. 민감도는 실제로 양성인 사람들 중 검사에 양상을 나타나는 비율로 여기서는 남자들 중 키가 161cm이상인 사람들의 비율이다(참양성률이라고도 한다).
\[\begin{equation} Sensitivity=\frac{TP}{Male\, Patients}=\frac{TP}{FN+TP}=\frac{50}{8+50}=86.2 \% \end{equation}\]
특이도는 실제로 검사에 음성으로 나타난 사람들 중 실제로 음성인 비율로 여기서는 키가 161cm 미만인 사람들 중 여자의 비율이다(참음성률이라고도 한다. ).
\[\begin{equation} Specificity=\frac{TN}{Female\, Patients}=\frac{TN}{TN+FP}=\frac{49}{49+7}=87.5 \% \end{equation}\]
양성예측률은 검사에서 양성으로 나온 사람들 중 실제로 양성인 사람들의 비율로 다음과 같이 구할 수 있다.
\[\begin{equation} PPV=\frac{TP}{Pts\,with\, height \geq 161cm}=\frac{TP}{TP+FP}=\frac{50}{50+7}=87.7\% \end{equation}\]
음성예측률은 검사에서 음성으로 나온 사람들 중 실제로 음성인 사람들의 비율로 다음과 같이 구할 수 있다.
\[\begin{equation} NPV=\frac{TN}{Pts\,with\, height < 161cm}=\frac{TN}{TN+FN}=\frac{49}{49+8}= 85.9 \% \end{equation}\]
2.2.2 최적의 절사점
데이터 radial의 모든 키에 대해 민감도, 특이도 등을 구할 수 있다. 이 데이터는 모두 115명의 데이터이지만 한명의 키가 누락되어 있어 114명의 데이터이며 중복된 값이 있기 때문에 키의 유일한 값들은 모두 39개이다.
[1] 39손으로 이 값들을 모두 계산할 수 도 있지만 편의를 위해 multipleROC 패키지에 포함되어 있는 calSens()함수를 이용할 수 도 있다.
calSens=function(x,y){
newx=sort(c(unique(x),max(x,na.rm=TRUE)+1))
completeTable=function(res){
if(nrow(res)==1){
res1=matrix(c(0,0),nrow=1)
temp=setdiff(c("TRUE","FALSE"),attr(res,"dimnames")[[1]][1])
if(temp=="FALSE") res=rbind(res1,res)
else res=rbind(res,res1)
res
}
res
}
getSens=function(cut){
res=table(x>=cut,y)
res=completeTable(res)
sens=res[2,2]/sum(res[,2])
spec=res[1,1]/sum(res[,1])
ppv=res[2,2]/sum(res[2,])
npv=res[1,1]/sum(res[1,])
data.frame(x=cut,sens=sens,spec=spec,fpr=1-spec,ppv=ppv,npv=npv,sum=sens+spec)
}
map_dfr(newx,function(cut){getSens(cut)})
}다음은 calSens() 함수로 radial데이터의 모든 키에 대해 민감도, 특이도 등을 구한 결과이다. 이중 sum열에는 민감도와 특이도의 합이 기록되어 있다.
x sens spec fpr ppv npv sum
1 140.0 1.00000000 0.00000000 1.00000000 0.5087719 NaN 1.000000
2 142.0 1.00000000 0.03571429 0.96428571 0.5178571 1.0000000 1.035714
3 144.0 1.00000000 0.05357143 0.94642857 0.5225225 1.0000000 1.053571
4 147.0 1.00000000 0.07142857 0.92857143 0.5272727 1.0000000 1.071429
5 147.5 1.00000000 0.08928571 0.91071429 0.5321101 1.0000000 1.089286
6 148.0 1.00000000 0.10714286 0.89285714 0.5370370 1.0000000 1.107143
7 149.0 1.00000000 0.17857143 0.82142857 0.5576923 1.0000000 1.178571
8 149.4 1.00000000 0.23214286 0.76785714 0.5742574 1.0000000 1.232143
9 150.0 1.00000000 0.25000000 0.75000000 0.5800000 1.0000000 1.250000
10 151.0 1.00000000 0.35714286 0.64285714 0.6170213 1.0000000 1.357143
11 152.0 1.00000000 0.37500000 0.62500000 0.6236559 1.0000000 1.375000
12 153.0 1.00000000 0.42857143 0.57142857 0.6444444 1.0000000 1.428571
13 154.0 1.00000000 0.55357143 0.44642857 0.6987952 1.0000000 1.553571
14 155.0 1.00000000 0.60714286 0.39285714 0.7250000 1.0000000 1.607143
15 155.5 0.98275862 0.62500000 0.37500000 0.7307692 0.9722222 1.607759
16 156.0 0.98275862 0.64285714 0.35714286 0.7402597 0.9729730 1.625616
17 157.0 0.96551724 0.67857143 0.32142857 0.7567568 0.9500000 1.644089
18 158.0 0.96551724 0.69642857 0.30357143 0.7671233 0.9512195 1.661946
19 159.0 0.94827586 0.76785714 0.23214286 0.8088235 0.9347826 1.716133
20 160.0 0.93103448 0.76785714 0.23214286 0.8059701 0.9148936 1.698892
21 161.0 0.86206897 0.87500000 0.12500000 0.8771930 0.8596491 1.737069
22 162.0 0.79310345 0.89285714 0.10714286 0.8846154 0.8064516 1.685961
23 163.0 0.77586207 0.92857143 0.07142857 0.9183673 0.8000000 1.704433
24 164.0 0.72413793 0.96428571 0.03571429 0.9545455 0.7714286 1.688424
25 165.0 0.68965517 0.96428571 0.03571429 0.9523810 0.7500000 1.653941
26 166.0 0.62068966 0.98214286 0.01785714 0.9729730 0.7142857 1.602833
27 167.0 0.60344828 1.00000000 0.00000000 1.0000000 0.7088608 1.603448
28 168.0 0.55172414 1.00000000 0.00000000 1.0000000 0.6829268 1.551724
29 169.0 0.51724138 1.00000000 0.00000000 1.0000000 0.6666667 1.517241
30 170.0 0.39655172 1.00000000 0.00000000 1.0000000 0.6153846 1.396552
31 171.0 0.25862069 1.00000000 0.00000000 1.0000000 0.5656566 1.258621
32 172.0 0.22413793 1.00000000 0.00000000 1.0000000 0.5544554 1.224138
33 173.0 0.17241379 1.00000000 0.00000000 1.0000000 0.5384615 1.172414
34 174.0 0.15517241 1.00000000 0.00000000 1.0000000 0.5333333 1.155172
35 175.0 0.13793103 1.00000000 0.00000000 1.0000000 0.5283019 1.137931
36 176.0 0.08620690 1.00000000 0.00000000 1.0000000 0.5137615 1.086207
37 177.0 0.06896552 1.00000000 0.00000000 1.0000000 0.5090909 1.068966
38 180.0 0.03448276 1.00000000 0.00000000 1.0000000 0.5000000 1.034483
39 181.0 0.00000000 1.00000000 0.00000000 NaN 0.4912281 1.000000result 데이터중 마지막 x값인 181은 ROC 곡선이 c(0,0)에서 시작하게 하려고 인위적으로 만들어준 값이다. 민감도와 특이도의 관계를 알아보기 위해 다음과 같은 plot을 그려볼 수 있다. 먼저 데이터의 형태를 long form으로 바꾼 후 그림을 그린다.
longdf <- result %>% pivot_longer(cols=sens:spec,names_to = "rate")
ggplot(data=longdf,aes(x=x,y=value,color=rate))+geom_line()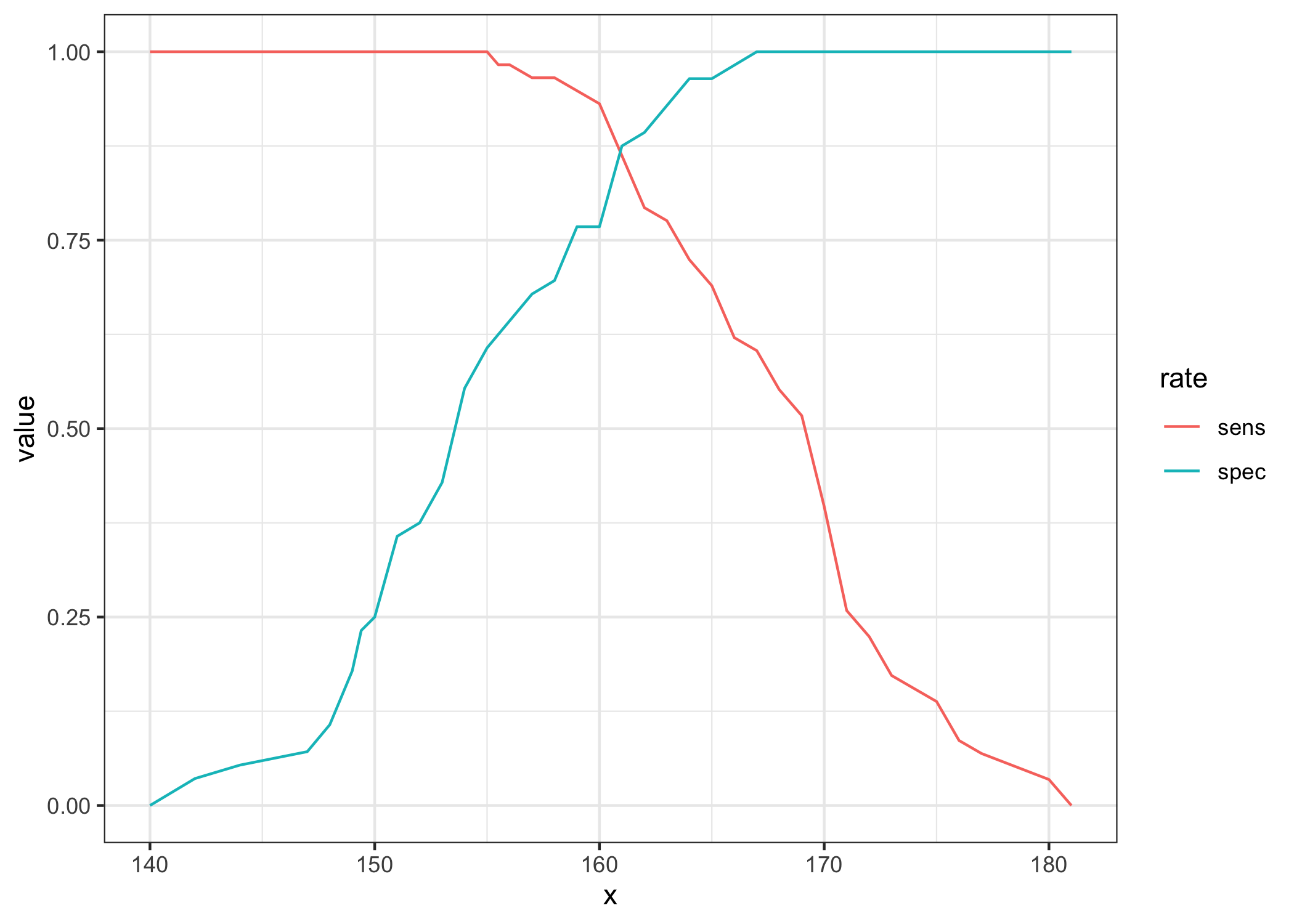
위의 그림에서 보는 바와 같이 민감도가 높아지면 특이도가 낮아지고 반대로 특이도가 높아지면 민감도가 낮아진다. 최적의 절사점은 민감도와 특이도의 합이 가장 높은 점이라고 할 수 있다.
x sens spec fpr ppv npv sum
21 161 0.862069 0.875 0.125 0.877193 0.8596491 1.737069여기서 보는 것처럼 키가 161cm일 경우 민감도와 특이도의 합이 가장 높으므로 최적의 절사점이라고 할 수 있다. 이 결과를 이용하여 ROC 곡선 그림을 그릴 수 있다.