Chapter 3 일반화회귀모형과 ROC
첫번째 ROC 곡선 그림을 다시 살펴보자.
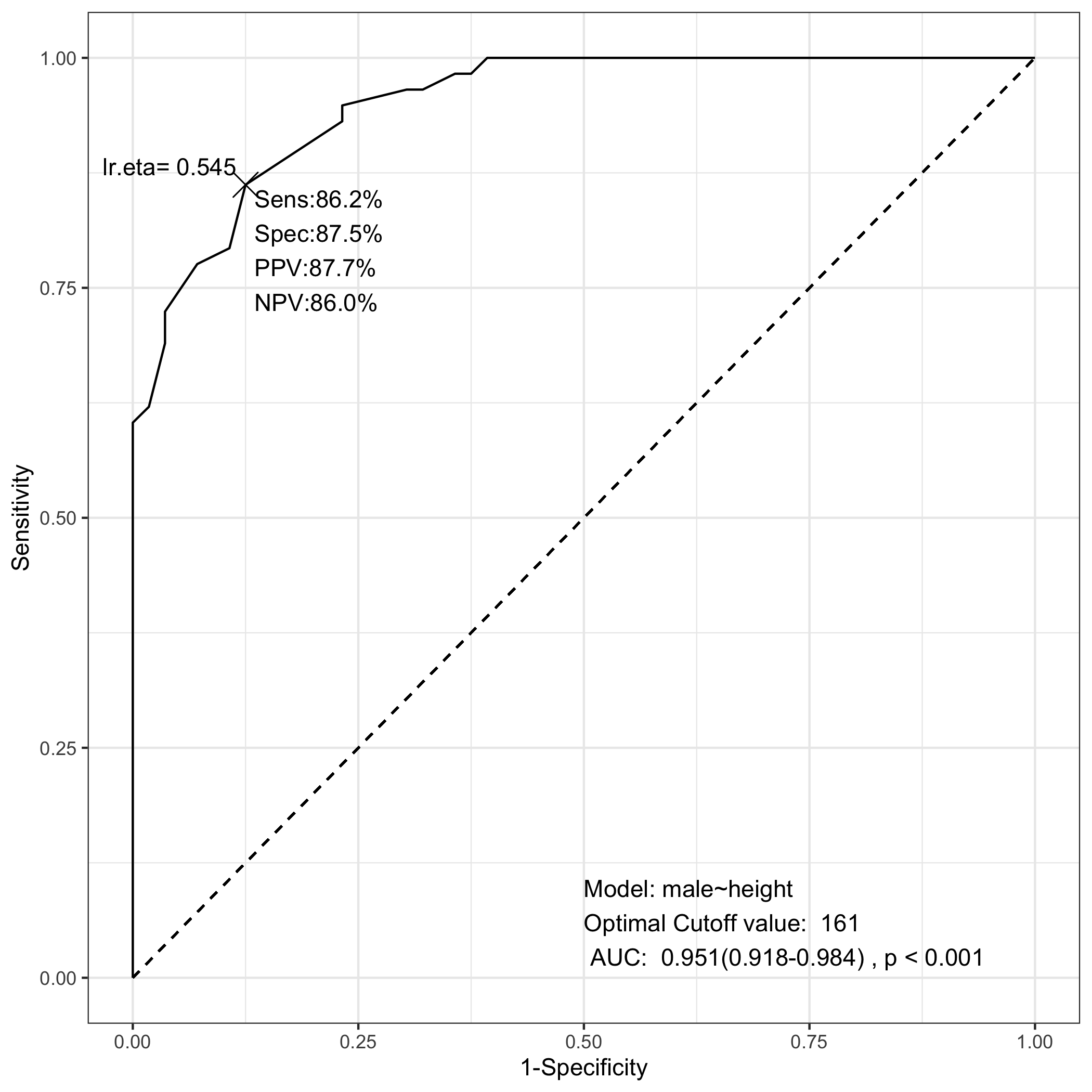
그림에서 최적의 절사점위에 lr.eta 값이 0.545로 표시되어 있다. 이 값은 어디에서 왔을까? 이 값은 다음의 일반화 회귀모형에서 나온 값이다.
1 2 3 4 5 6
0.0647799156 0.0089609908 0.5450612249 0.1902888834 0.7301078853 0.0134046841
7 8 9 10 11 12
0.8593140964 0.2609731323 0.9688855513 0.1131501263 0.8593140964 0.9972179420
13 14 15 16 17 18
0.0134046841 0.0059814642 0.9790755722 0.6428952491 0.9688855513 0.0089609908
19 20 21 22 23 24
0.9790755722 0.0059814642 0.0440658619 0.0039886420 0.9539663976 0.9859766507
25 26 27 28 29 30
0.0134046841 0.8593140964 0.4436202683 0.9906234843 0.9906234843 0.8593140964
31 32 33 34 35 36
0.9688855513 0.5450612249 0.9688855513 0.4436202683 0.9987659427 0.0440658619
37 38 39 40 41 42
0.9972179420 0.0059814642 0.5450612249 0.4436202683 0.4436202683 0.0440658619
43 44 45 46 47 48
0.3466721723 0.5450612249 0.4436202683 0.9323927854 0.0297645408 0.0297645408
49 50 51 52 53 54
0.9790755722 0.9790755722 0.7301078853 0.9688855513 0.7301078853 0.9937403001
55 56 57 58 59 60
0.9790755722 0.0011789400 0.1352457877 0.9539663976 0.7301078853 0.0059814642
61 62 63 64 65 66
0.7301078853 0.0134046841 0.9996359536 0.9790755722 0.6428952491 0.4436202683
67 68 69 70 71 72
0.1352457877 0.0942707968 0.0647799156 0.5450612249 0.9906234843 0.9017500029
73 74 75 76 77 78
0.9859766507 0.2609731323 0.9981468171 0.4436202683 0.6428952491 0.9996359536
79 80 81 82 83 84
0.0005224834 0.2609731323 0.4436202683 0.9688855513 0.4436202683 0.9017500029
85 86 87 88 89 90
0.0440658619 0.8593140964 0.9323927854 0.0002314699 0.9972179420 0.0297645408
91 92 93 94 95 96
0.8025624552 0.9958254317 0.0647799156 0.9790755722 0.0089609908 0.0048849508
97 98 99 100 102 103
0.0105295308 0.0134046841 0.0440658619 0.9688855513 0.0942707968 0.0200074872
104 105 106 107 108 109
0.0440658619 0.8025624552 0.9790755722 0.4436202683 0.9987659427 0.0440658619
110 111 112 113 114 115
0.0134046841 0.0002314699 0.1352457877 0.2609731323 0.2609731323 0.9323927854 이 모형의 결과 중 fitted.values는 로짓함수에 의해 변환된 값으로 이 값과 fit$y값을 이용해 민감도, 특이도를 구할 수 있다.
x sens spec fpr ppv npv sum
21 0.5450612 0.862069 0.875 0.125 0.877193 0.8596491 1.737069민감도와 특이도의 합이 가장 큰 최적의 절사점은 0.5451이다. 이 결과를 이용해 ROC곡선을 그릴 수 있다.
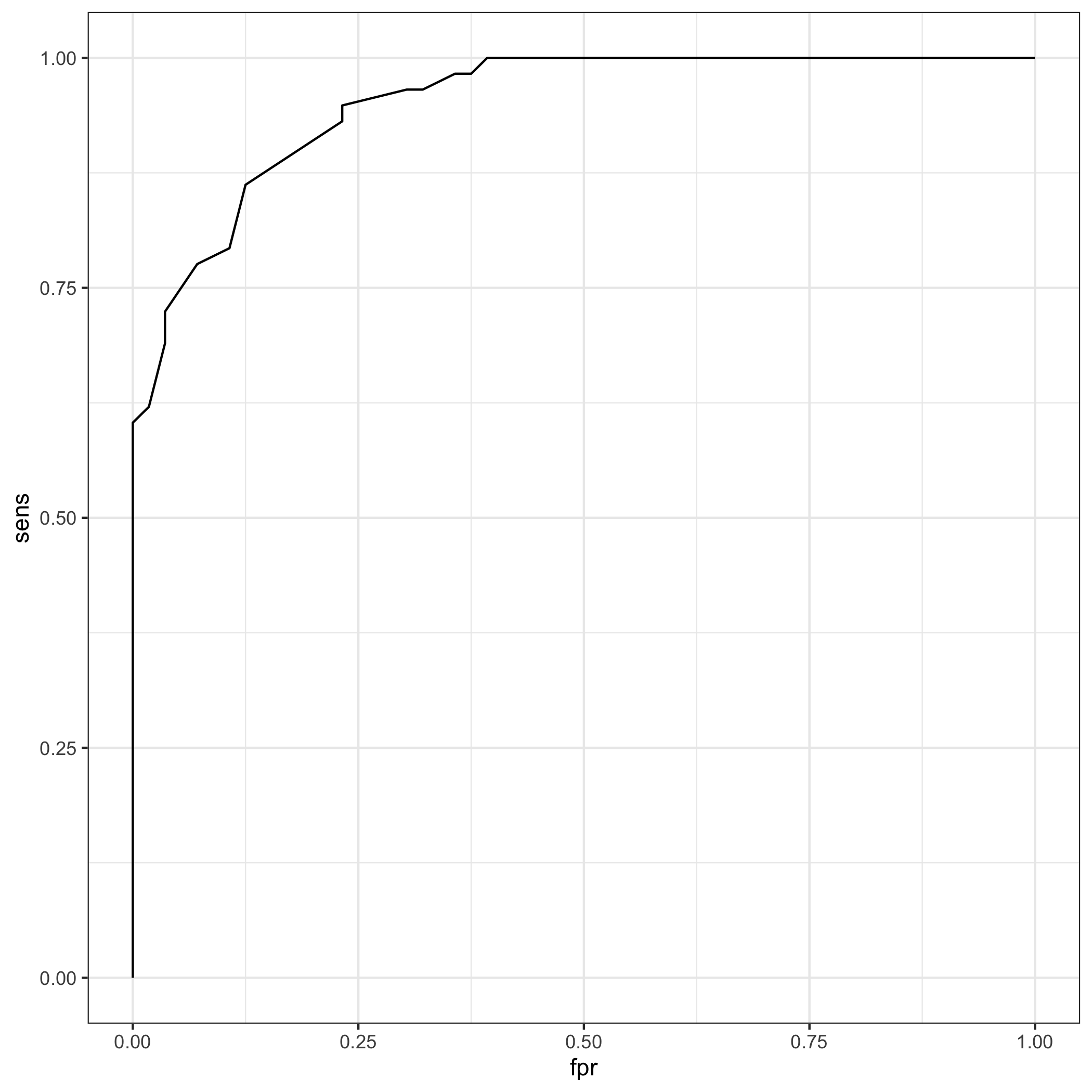
모형적합된 값 0.5451과 키 161cm는 어떤 관계가 있을까? 로지스틱 모형은 다음의 회귀식으로 표현할 수 있다.
\[\begin{equation} log(\frac{p}{1-p})=\beta_0+\beta_1*X \end{equation}\]
위의 식을 R코드로 표현하면 다음과 같다.
qlogis(x$cutpoint)=coef(x$fit)[1]+coef(x$fit)[2]*X여기서 모형적합된 값 0.5451에 해당하는 키의 값을 계산하면 다음과 같다.
[1] 161반대로 키 161cm에 해당되는 fitted value는 다음과 같이 구할 수 있다.
[1] 0.5450612