7 Yayım Yanlılığı Nedir?
Meta-analiz çalışmalarında yayım yanlılığı (publication bias), araştırma sonuçlarının literatürde sistematik biçimde dengesiz temsil edilmesi durumunu ifade eder. Genellikle anlamlı veya beklenen yönde sonuçlar rapor eden çalışmaların yayımlanma olasılığı, anlamsız ya da ters yönlü sonuçlara sahip çalışmalardan daha yüksektir (Rothstein, Sutton ve Borenstein, 2005). Bu durum, meta-analiz sonuçlarının gerçeği olduğundan daha güçlü ya da zayıf yansıtmasına neden olabilir.
Yayın yanlılığının değerlendirilmesi amacıyla çeşitli istatistiksel yöntemler geliştirilmiştir. Bu yayında en fazla tercih edilen Huni grafiği, Orwin güvenli N, Begg ve Mazumdar sıra korelasyonu ile Duval ve Tweedie’ nin kırp ve doldur yöntemleri kullanılarak uygulama yapılmıştır. Bu bölümdeki uygulamalar datayy isimli veri seti kullanılmıştır. Datayy’de 44 bireysel çalışmaya ilişkin korelasyon değerleri (r), örneklem büyüklüğü (n) ve korelasyon değerleri dönüştürülerek elde edilen Fisher z değerleri bulunmaktadır.
7.1 Huni Grafiği ve Örnek Uygulama
Huni grafiği (funnel plot), meta-analizlerde yayım yanlılığının görsel olarak değerlendirilmesini sağlayan en temel araçlardan biridir. Yatay eksende etki büyüklükleri, dikey eksende ise standart hatalar veya örneklem büyüklükleri yer alır. Simetrik bir dağılım, yayın yanlılığının düşük olduğunu; asimetrik bir görünüm ise küçük örneklemli çalışmaların eksikliğini veya belirli yönde yayın tercihlerini gösterebilir (Light ve Pillemer, 1984). Ancak huni grafiği yalnızca görsel bir ipucu sunduğu için yorumların istatistiksel testlerle desteklenmesi önerilmektedir (Sterne vd., 2011).
# Huni grafiği
library(metafor)
library(readxl)
# Veriyi yükle
data <- read_excel("datayy.xls", sheet = 1)
fisher_z <- data$`Fisher's Z`
std_err <- data$`Std Err (Z)`
# NA değerleri temizle
complete_cases <- complete.cases(fisher_z, std_err)
fisher_z <- fisher_z[complete_cases]
std_err <- std_err[complete_cases]
# Meta-analiz
meta_result <- rma(yi = fisher_z, sei = std_err)
# Huni grafiği
funnel(meta_result,
xlab = "Fisher's Z",
ylab = "Standart Hata",
main = "Huni Grafiği")
abline(v = 0, col = "red", lty = 2)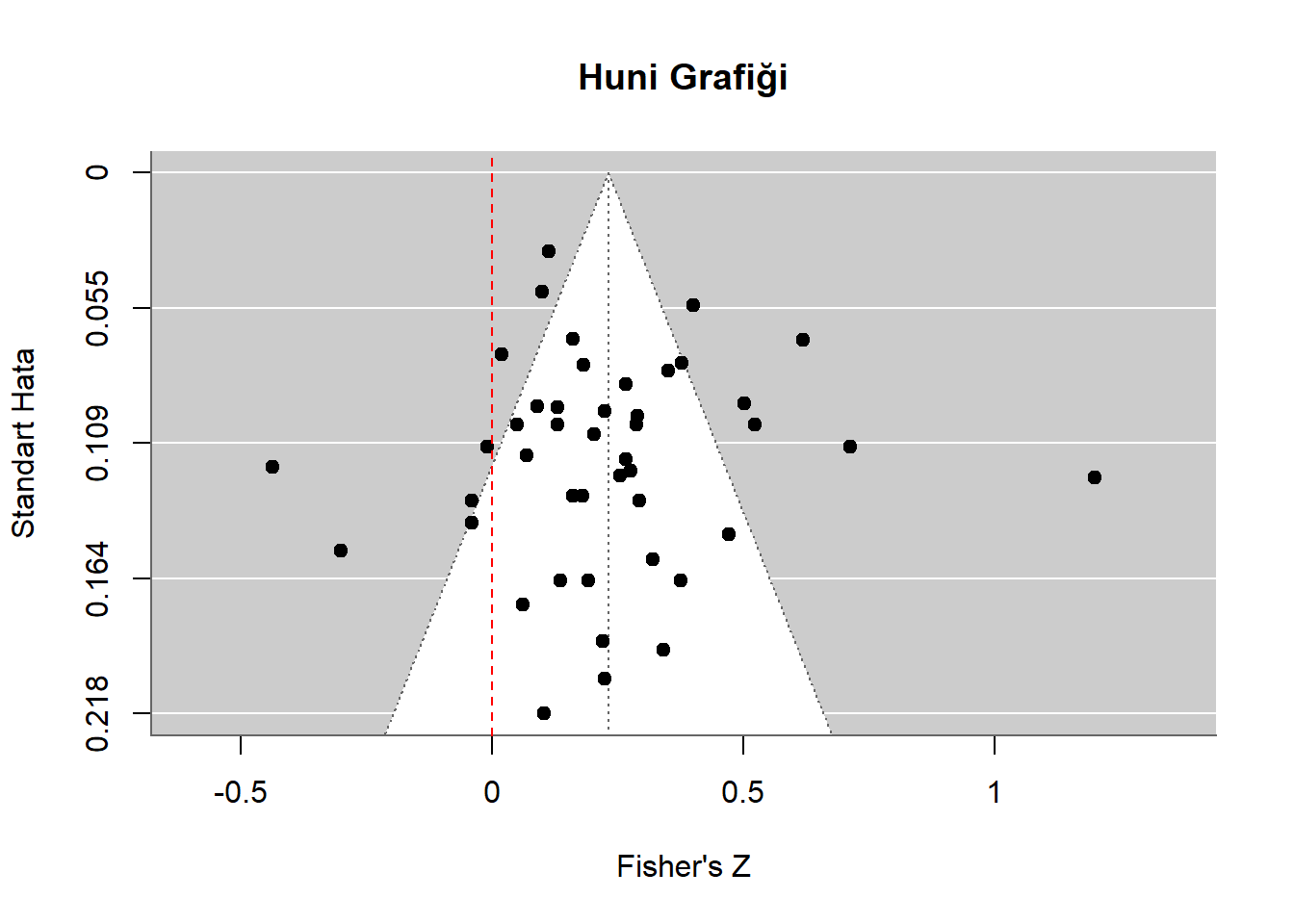
# Kontur ekleyen huni grafiği
funnel(meta_result,
level = c(90, 95, 99),
shade = c("darkgray", "gray", "lightgray"),
refline = 0,
main = "Konturlu Huni Grafiği")
legend("topright",
legend = c("p < 0.10", "p < 0.05", "p < 0.01"),
fill = c("darkgray", "gray", "lightgray"))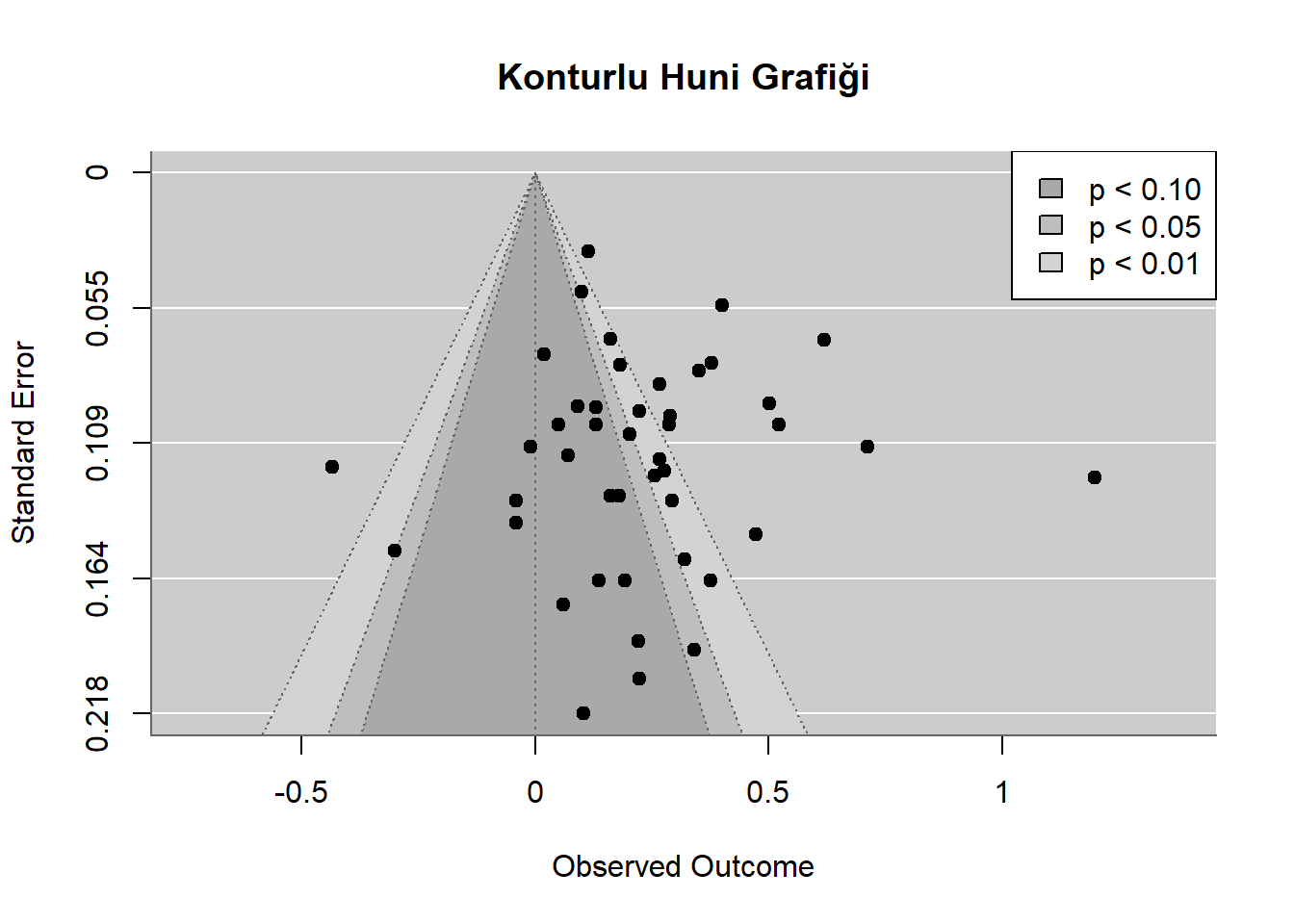
7.2 Orwin Güvenli N ve Örnek Uygulama
Orwin Güvenli N (Orwin’s Fail-Safe N), elde edilen genel etkinin anlamlılığını ortadan kaldırmak için literatüre kaç tane sıfır etki büyüklüğüne sahip çalışmanın eklenmesi gerektiğini hesaplayan bir ölçüttür. Bu yöntem, Rosenthal’in klasik güvenli N yaklaşımına göre daha esnektir; çünkü eklenen çalışmaların ortalama etkisinin sıfırdan farklı olabileceği varsayımına izin verir (Orwin, 1983). Yüksek bir Güvenli N değeri, meta-analiz sonuçlarının yayın yanlılığına karşı daha dayanıklı olduğunu gösterir (Rosenberg, 2005).
# Fisher's Z değerlerini al
fisher_z <- data$`Fisher's Z`
fisher_z <- fisher_z[!is.na(fisher_z)]
# Temel bilgiler
k <- length(fisher_z)
mean_observed <- mean(fisher_z)
criterion <- 0
mean_missing <- 0
# Orwin Güvenli N hesaplama
failsafe_N <- ((mean_observed - criterion) / (criterion - mean_missing)) * k
# Sonuçlar
cat("Gozlemlenen çalışma sayısı:", k, "\n")## Gozlemlenen çalışma sayısı: 44## Ortalama Fisher's Z: 0.2285## Kriter degeri: 0## Orwin Guvenli N: Inf7.3 Begg ve Mazumdar Sıra Korelasyonu ve Örnek Uygulama
Begg ve Mazumdar (1994) tarafından geliştirilen sıra korelasyonu testi, standart hata ile etki büyüklüğü arasındaki ilişkiyi inceleyerek yayın yanlılığına dair istatistiksel kanıt sunar. Bu test, küçük örneklemli çalışmalarda etki büyüklüklerinin sistematik biçimde farklılaşıp farklılaşmadığını belirler. Testin temel istatistiği olan Kendall’s tau, çalışmalar arasında negatif veya pozitif yönlü bir ilişki olup olmadığını değerlendirir. Anlamlı bir ilişki, yayın yanlılığının varlığına işaret eder (Begg ve Mazumdar, 1994; Sterne ve Egger, 2005).
# Fisher's Z ve SE (Z)
yi <- as.numeric(data$`Fisher's Z`)
sei <- as.numeric(data$`Std Err (Z)`)
# Meta-analiz modeli
res <- rma(yi = yi, sei = sei, method = "REML")
# Begg & Mazumdar testi
rank_out <- ranktest(res)
k <- length(yi)
# --- Hesaplamalar ---
tau <- as.numeric(rank_out$tau)
C <- choose(k, 2)
S <- tau * C
se_tau <- sqrt(2 * (2 * k + 5) / (9 * k * (k - 1)))
# Without continuity correction
z_no_cc <- abs(tau / se_tau) # mutlak değer eklendi
p2_no_cc <- 2 * (1 - pnorm(z_no_cc))
p1_no_cc <- p2_no_cc / 2
# With continuity correction
varS <- k * (k - 1) * (2 * k + 5) / 18
z_cc <- abs(if (S > 0) (S - 1) / sqrt(varS) else if (S < 0) (S + 1) / sqrt(varS) else 0)
p2_cc <- 2 * (1 - pnorm(z_cc))
p1_cc <- p2_cc / 2
# --- Sonuçlar ---
cat("Kendall's S (P - Q):", round(S, 4), "\n\n")## Kendall's S (P - Q): -14.0896cat("Without continuity correction:\n",
"tau =", round(tau, 4),
" | z =", round(z_no_cc, 4),
" | p(1-tailed) =", signif(p1_no_cc, 4),
" | p(2-tailed) =", signif(p2_no_cc, 4), "\n\n")## Without continuity correction:
## tau = -0.0149 | z = 0.1425 | p(1-tailed) = 0.4433 | p(2-tailed) = 0.8867cat("With continuity correction:\n",
"tau =", round(tau, 4),
" | z =", round(z_cc, 4),
" | p(1-tailed) =", signif(p1_cc, 4),
" | p(2-tailed) =", signif(p2_cc, 4), "\n")## With continuity correction:
## tau = -0.0149 | z = 0.1324 | p(1-tailed) = 0.4473 | p(2-tailed) = 0.89477.4 Duwal ve Tweedie’ nin Kırp ve Doldur Yöntemi ve Örnek Uygulama
Duval ve Tweedie’nin (2000) kırp ve doldur (trim and fill) yöntemi, hem yayım yanlılığının görselleştirilmesini hem de düzeltilmesini sağlayan bir yaklaşımdır. Bu yöntem, asimetrik huni grafiğinde yer alan çalışmaları kırparak ve eksik çalışmaları doldurarak simetriyi yeniden oluşturur. Doldurulan çalışmaların etkileri hesaba katıldığında, düzeltilmiş (adjusted) etki büyüklüğü elde edilir. Böylece yayın yanlılığının genel meta-analiz sonucuna ne kadar etki ettiği sayısal olarak da ortaya konulmaktadır (Duval ve Tweedie, 2000).
# Fisher's Z ve varyans değerleri
yi <- data$`Fisher's Z`
vi <- data$`Std Err (Z)`^2
# FIXED EFFECTS MODEL
fe_model <- rma(yi, vi, method = "FE")
# RANDOM EFFECTS MODEL
re_model <- rma(yi, vi, method = "DL")
# FIXED EFFECTS MODEL - Trim and Fill (to left)
ta_fe_left <- trimfill(fe_model, side = "left")
# RANDOM EFFECTS MODEL - Trim and Fill (to left)
ta_re_left <- trimfill(re_model, side = "left")
# Sonuçları görüntüleme fonksiyonu
print_trimfill_results <- function(original_model, trimfill_model, model_name) {
cat("\n", "==================================================", "\n")
cat(model_name, "MODEL - TRIM AND FILL RESULTS\n")
cat("==================================================", "\n")
cat("OBSERVED VALUES (before trim and fill):\n")
cat("Number of studies (observed):", original_model$k, "\n")
cat("Point estimate (observed):", original_model$beta[1], "\n")
cat("CI lower (observed):", original_model$ci.lb, "\n")
cat("CI upper (observed):", original_model$ci.ub, "\n")
cat("Q value (observed):", original_model$QE, "\n")
cat("p-value for Q (observed):", original_model$QEp, "\n\n")
cat("ADJUSTED VALUES (after trim and fill):\n")
cat("Number of studies (adjusted):", trimfill_model$k, "\n")
cat("Number of imputed studies:", trimfill_model$k0, "\n")
cat("Point estimate (adjusted):", trimfill_model$beta[1], "\n")
cat("CI lower (adjusted):", trimfill_model$ci.lb, "\n")
cat("CI upper (adjusted):", trimfill_model$ci.ub, "\n")
cat("Q value (adjusted):", trimfill_model$QE, "\n")
cat("p-value for Q (adjusted):", trimfill_model$QEp, "\n")
}
# Fixed effects model sonuçları
print_trimfill_results(fe_model, ta_fe_left, "FIXED EFFECTS")##
## ==================================================
## FIXED EFFECTS MODEL - TRIM AND FILL RESULTS
## ==================================================
## OBSERVED VALUES (before trim and fill):
## Number of studies (observed): 44
## Point estimate (observed): 0.2222503
## CI lower (observed): 0.1953787
## CI upper (observed): 0.2491218
## Q value (observed): 250.2971
## p-value for Q (observed): 4.766018e-31
##
## ADJUSTED VALUES (after trim and fill):
## Number of studies (adjusted): 44
## Number of imputed studies: 0
## Point estimate (adjusted): 0.2222503
## CI lower (adjusted): 0.1953787
## CI upper (adjusted): 0.2491218
## Q value (adjusted): 250.2971
## p-value for Q (adjusted): 4.766018e-31##
## ==================================================
## RANDOM EFFECTS MODEL - TRIM AND FILL RESULTS
## ==================================================
## OBSERVED VALUES (before trim and fill):
## Number of studies (observed): 44
## Point estimate (observed): 0.2324238
## CI lower (observed): 0.1629097
## CI upper (observed): 0.3019379
## Q value (observed): 250.2971
## p-value for Q (observed): 4.766018e-31
##
## ADJUSTED VALUES (after trim and fill):
## Number of studies (adjusted): 44
## Number of imputed studies: 0
## Point estimate (adjusted): 0.2324238
## CI lower (adjusted): 0.1629097
## CI upper (adjusted): 0.3019379
## Q value (adjusted): 250.2971
## p-value for Q (adjusted): 4.766018e-31##
##
## DETAILED IMPUTED STUDIES INFORMATION:## FIXED EFFECTS - Imputed studies: 0if (ta_fe_left$k0 > 0) {
imputed_indices_fe <- (length(ta_fe_left$yi) - ta_fe_left$k0 + 1):length(ta_fe_left$yi)
imputed_yi_fe <- ta_fe_left$yi[imputed_indices_fe]
imputed_vi_fe <- ta_fe_left$vi[imputed_indices_fe]
cat("Imputed Fisher's Z values:", round(imputed_yi_fe, 4), "\n")
cat("Imputed variances:", round(imputed_vi_fe, 4), "\n")
} else {
cat("No studies imputed in fixed effects model\n")
}## No studies imputed in fixed effects model##
## RANDOM EFFECTS - Imputed studies: 0if (ta_re_left$k0 > 0) {
imputed_indices_re <- (length(ta_re_left$yi) - ta_re_left$k0 + 1):length(ta_re_left$yi)
imputed_yi_re <- ta_re_left$yi[imputed_indices_re]
imputed_vi_re <- ta_re_left$vi[imputed_indices_re]
cat("Imputed Fisher's Z values:", round(imputed_yi_re, 4), "\n")
cat("Imputed variances:", round(imputed_vi_re, 4), "\n")
} else {
cat("No studies imputed in random effects model\n")
}## No studies imputed in random effects model# Özet tablo oluşturma
results_summary <- data.frame(
Model = c("Fixed Effects - Observed", "Fixed Effects - Adjusted",
"Random Effects - Observed", "Random Effects - Adjusted"),
k = c(fe_model$k, ta_fe_left$k, re_model$k, ta_re_left$k),
k0 = c(0, ta_fe_left$k0, 0, ta_re_left$k0),
Estimate = round(c(fe_model$beta[1], ta_fe_left$beta[1],
re_model$beta[1], ta_re_left$beta[1]), 4),
CI_Lower = round(c(fe_model$ci.lb, ta_fe_left$ci.lb,
re_model$ci.lb, ta_re_left$ci.lb), 4),
CI_Upper = round(c(fe_model$ci.ub, ta_fe_left$ci.ub,
re_model$ci.ub, ta_re_left$ci.ub), 4),
Q_Value = round(c(fe_model$QE, ta_fe_left$QE,
re_model$QE, ta_re_left$QE), 4),
Q_p_value = round(c(fe_model$QEp, ta_fe_left$QEp,
re_model$QEp, ta_re_left$QEp), 4)
)
cat("\n\nSUMMARY RESULTS TABLE:\n")##
##
## SUMMARY RESULTS TABLE:## Model k k0 Estimate CI_Lower CI_Upper Q_Value Q_p_value
## 1 Fixed Effects - Observed 44 0 0.2223 0.1954 0.2491 250.2971 0
## 2 Fixed Effects - Adjusted 44 0 0.2223 0.1954 0.2491 250.2971 0
## 3 Random Effects - Observed 44 0 0.2324 0.1629 0.3019 250.2971 0
## 4 Random Effects - Adjusted 44 0 0.2324 0.1629 0.3019 250.2971 0