4 Dati categorici
4.1 Tabelle di contingenza
Esercizio 4.1
Consideriamo i dati di un medico su 159 pazienti depressi. La seguente tabella riporta il livello depressivo osservato rispetto allo stato civile:
| stato civile | ||||
|---|---|---|---|---|
| livello depressivo | sposato | celibe | vedovo | Totale |
| grave | 22 | 16 | 19 | 57 |
| medio | 33 | 29 | 14 | 76 |
| leggero | 14 | 9 | 3 | 26 |
| Totale | 69 | 54 | 36 | 159 |
Di che tipo di variabili si tratta?
Determinare la distribuzione marginale di frequenza dello stato civile.
Quale é la moda per il carattere livello depressivo?
Quale è la percentuale di pazienti che risultano vedovi e con un livello depressivo grave?
Quale è la percentuale di vedovi con livello depressivo grave?
Quale è la percentuale di pazienti con livello depressivo almeno pari a un livello ‘medio’?
Determinare la distribuzione condizionata, di frequenze assolute e di frequenze percentuali, del livello depressivo allo stato civile vedovo.
Determinare la distribuzione marginale del livello depressivo e confrontarla con la distribuzione condizionata ricavata al punto precedente. Cosa si può dire sull’associazione tra i due caratteri?
Soluzione
Il livello depressivo è un carattere qualitativo ordinato, lo stato civile è un carattere qualitativo sconnesso.
La distribuzione marginale dello stato civile è la seguente:
sposato celibe vedovo Totale 69 54 36 159 La moda è il livello depressivo ‘medio’ ovvero la modalità del carattere alla quale è associata la massima frequenza.
La percentuale di pazienti che sono simultaneamente vedovi e con livello depressivo grave è data da: \[\frac{19}{159} 100 = 11.9\%\]
La percentuale di vedovi che presentano un livello depressivo grave è data da \[\frac{19}{36} 100 = 52.8\%\]
Il numero di pazienti con un livello depressivo pari almeno ad un livello medio è dato dalla somma tra il numero di pazienti con livello depressivo medio e quello con livello depressivo grave, \(76+57 = 133\). La percentuale richiesta è quindi: \[\frac{133}{159} 100 = 84\%\]
la distribuzione condizionata è riportata nella seguente tabella:
stato civile\(=\)vedovo livello depressivo freq. assolute freq.percentuali grave 19 \(19/ 36 \cdot 100 = 52.8\%\) medio 14 \(14/36\cdot 100 = 38.9\%\) leggero 3 \(3/36\cdot 100 = 8.3\%\) Totale 36 100 La distribuzione marginale del livello depressivo è la seguente:
livello depressivo freq. assolute freq.percentuali grave 57 \(57/ 159 \cdot 100 = 35.8\%\) medio 76 \(76/159\cdot 100 = 47.8\%\) leggero 26 \(26/159\cdot 100 = 16.4\%\) Totale 159 100 Analizzando la distribuzione condizionata allo stato civile vedovo, possiamo notare che la proporzione di vedovi con livello depressivo grave è superiore rispetto a quella calcolata sul totale. Dal confronto tra distribuzione condizionata e distribuzione marginale si può notare che le frequenze percentuali sono diverse, il che indica la presenza di un’associazione tra i due caratteri.
Esercizio 4.2
(dal libro di testo OpenIntro Statistics di Diez et al., es. 1.51)
Il rosiglitazone è il principio attivo presente nella medicina per il diabete di tipo 2 Avandia ed è stato considerato causa dell’insorgenza di seri problemi cardiovascolari come infarto, insufficienza cardiaca e morte. Un trattamento alternativo è il pioglitazone, principio attivo presente in un’altra medicina per il diabete, Actos. Nella seguente tabella sono riportati i dati relativi ad uno studio osservazionale retrospettivo su 22,571 beneficiari di assistenza pubblica di età pari a 65 anni o più.
| Problemi cardiovascolari | |||
|---|---|---|---|
| Trattamento | Si | No | Totale |
| Rosiglitazone | 2,593 | 65,000 | 67,593 |
| Pioglitazone | 5,386 | 154,592 | 159,978 |
| Totale | 7,979 | 219,592 | 227,571 |
Determinare se ciascuna delle seguenti affermazioni è vera o falsa. Se falsa, spiegare perché. Attenzione: il ragionamento può essere sbagliato anche se la conclusione dell’affermazione è corretta. I questi casi, l’affermazione dovrebbe essere considerata falsa.
Poiché più pazienti con trattamento pioglitazone hanno avuto problemi cardiovascolari (5,386 vs. 2,593), possiamo concludere che il tasso di problemi cardiovascolari per quelli a cui è stato somministrato questo trattamento è più alto.
I dati suggeriscono che i pazienti diabetici a cui è stato somministrato rosiglitazone sono più inclini ad avere problemi cardiovascolari poiché il tasso di incidenza è (\(2,593 / 67,593 = 0.038\)) \(3.8\%\) per pazienti con questo trattamento, mentre solo (\(5,386 / 159,978 = 0.034\)) \(3.4\%\) per pazienti a cui è stato somministrato l’altro trattamento (pioglitazone).
Il fatto che il tasso di incidenza sia più alto per il gruppo rosiglitazone dimostra che il rosiglitazone causa seri problemi cardiovascolari.
Sulla base delle informazioni a disposizione, non possiamo dire se la differenza tra i tassi di incidenza è dovuta alla relazione tra le due variabili o al caso.
Soluzione
Falso. Invece di confrontare le frequenze assolute, bisognerebbe confrontare le percentuali.
Vero.
Falso. Non possiamo dedurre una relazione causale da una associazione in uno studio osservazionale. Comunque, possiamo dire che il trattamento a cui uno è sottoposto ha un impatto sul rischio in questo caso, perché il paziente ha scelto quel trattamento e la sua scelta può essere associata ad altre variabili, che è il motivo per cui il punto b. è vero. La differenza in queste affermazioni è sottile ma importante.
Vero.
4.2 Inferenza su una singola proporzione
Esercizio 4.3
Su un campione casuale di 100 studenti di un’università, 82 hanno
dichiarato di non essere fumatori. Sulla base di questo, costruisci un
intervallo di confidenza a livello \(1-\alpha = 0.99\) per \(p\), la
proporzione di tutti gli studenti dell’università che non fumano.
Soluzione
Dobbiamo costruire un intervallo di confidenza per la proporzione \(p\) di tutti gli studenti dell’università che non fumano. Tale intervallo di confidenza ha la seguente forma \[\left[\hat{p}-z^{*}\sqrt{\frac{\hat{p}(1-\hat{p})}{n}}, \hat{p}+z^{*}\sqrt{\frac{\hat{p}(1-\hat{p})}{n}}\right]\] dove
\(\hat{p}\) è la proporzione di non fumatori nel campione osservato: \(\hat{p}=\frac{82}{100}=0.82\);
\(z^{*}\) è il quantile a livello \(\alpha/2=(1-0.99)/2=0.005\) di una distribuzione Normale standard; dalla tavola C (oppure dalla tavola della distribuzione Normale standard) si ha \(z^{*}=2.576\);
\(n = 100\) è la numerosità campionaria.
Sostituendo questi valori, si ottiene il seguente intervallo di confidenza: \[[0.721,0.919]\]
Esercizio 4.4
Un’indagine Gallup studia periodicamente un campione casuale di 1500 americani. La percentuale di individui nel campione che è a favore della legalizzazione del possesso di marijuana è scesa dal 52% nel 1980 al 46% nel 1985.
Si costruisca un intervallo di confidenza al 95% per la percentuale della popolazione a favore della legalizzazione nel 1980;
Si costruisca un intervallo di confidenza al 95% per la percentuale della popolazione a favore della legalizzazione nel 1985.
Soluzione
Dobbiamo costruire un intervallo di confidenza per una proporzione: \[\left[\hat{p}-z^{*}\sqrt{\frac{\hat{p}(1-\hat{p})}{n}} ; \hat{p}+z^{*}\sqrt{\frac{\hat{p}(1-\hat{p})}{n}} \right]\] Quindi per ciascun anno si ha:
Per l’anno 1980: \[\left[0.52 - 1.96 \sqrt{\frac{0.52(1-0.52)}{1500}} ; 0.52 + 1.96 \sqrt{\frac{0.52(1-0.52)}{1500}}\right] = [0.495; 0.545]\]
Per l’anno 1985: \[\left[0.46 - 1.96 \sqrt{\frac{0.46(1-0.46)}{1500}} ; 0.46 + 1.96 \sqrt{\frac{0.46(1-0.46)}{1500}}\right] = [0.435; 0.485]\]
Esercizio 4.5
(dal libro di testo OpenIntro Statistics di Diez et al., es. 1.53)
Nell’Esercizio 4.2 è stato introdotto uno studio in cui vengono confrontati i tassi di incidenza di alcune gravi patologie cardiovascolari per pazienti affetti da diabete, trattati con rosiglitazone e pioglitazone. La seguente tabella rappresenta i dati raccolti:
| Problemi cardiovascolari | |||
|---|---|---|---|
| Trattamento | Si | No | Totale |
| Rosiglitazone | 2,593 | 65,000 | 67,593 |
| Pioglitazone | 5,386 | 154,592 | 159,978 |
| Totale | 7,979 | 219,592 | 227,571 |
Quale è la proporzione di pazienti sul totale che hanno avuto problemi cardiovascolari?
Se il tipo di trattamento e l’insorgenza di problemi cardiovascolari fossero indipendenti, quanti pazienti con problemi cardiovascolari ci dovremmo aspettare nel gruppo rosiglitazone?
La relazione tra trattamento e outcome in questo studio può essere analizzata adottando una tecnica di randomizzazione. L’istogramma seguente rappresenta la simulazione dei conteggi degli eventi cardiovascolari nel gruppo rosiglitazione assumendo il modello di indipendenza. (i) Quali sono le ipotesi sottoposte a verifica? (ii) Rispetto al numero calcolato al punto b., fornirebbe maggiore supporto all’ipotesi alternativa un numero maggiore o un numero minore di pazienti con problemi cardiovascolari nel gruppo rosiglitazione? (iii) Cosa suggeriscono i risultati della simulazione rispetto alla relazione tra il trattamento rosiglitazione e l’insorgenza di problemi cardiovascolari nei pazienti diabetici?
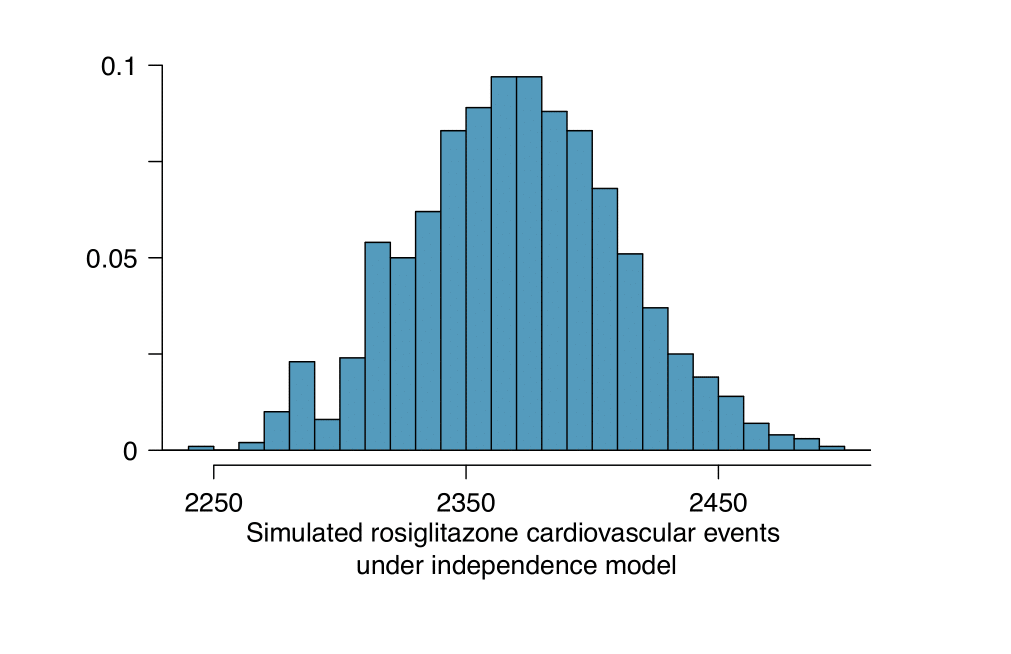
Soluzione
La proporzione di pazienti che hanno avuto problemi cardiovascolari è pari a \(\frac{7979}{227571} \approx 0.035\).
Il numero atteso di problemi cardivascolari nel gruppo rosiglitazione sotto l’ipotesi di indipendenza, può essere calcolato moltiplicando il numero di pazienti di quel gruppo per il tasso complessivo di problemi cardiovascolari osservato nello studio, ovvero: \(67593 \cdot \frac{7979}{227571} = 2730\)
(i) L’ipotesi nulla \(H_0\) corrisponde al modello di indipendenza: il trattamento e l’insorgenza di problemi cardiovascolari sono indipendenti, ovvero non c’è relazione tra loro, quindi la differenza riscontrata nei tassi di incidenza nei due gruppi di trattamento è dovuta al caso. L’ipotesi alternativa \(H_A\) corrisponde invece alla negazione del modello di indipendenza: il trattamento e l’insorgenza di problemi cardiovascolari non sono indipendenti, ovvero la differenza riscontrata nei tassi di incidenza nei due gruppi di trattamento non è dovuta al caso, ma il rosiglitazione è associato con un maggior rischio di sviluppare problemi cardiovascolari. (ii) Un numero di pazienti con problemi cardiovascolari nel gruppo rosiglitazione piú elevato rispetto a quello atteso sotto l’ipotesi di indipendenza fornirebbe un maggiore supporto all’ipotesi alternativa. Questo suggerirebbe che il rosiglitazione comporta un incremento del rischio di problemi cardiovascolari. (iii) In questo studio sono stati effettivamente osservati 2593 eventi cardiovascolari nel gruppo rosiglitazione. Nelle 1000 simulazioni effettuate sotto il modello di indipendenza sono stati osservati praticamente sempre meno di 2593 eventi, il che induce a concludere che i dati osservati non siano compatibili con il modello di indipendenza. In altre parole, l’analisi fornisce forte evidenza contro l’ipotesi nulla ovvero a supporto dell’ipotesi che il rosiglitazione sia associato significativamente con un maggiore rischio di problemi cardiovascolari.
Esercizio 4.6
(dal libro di testo OpenIntro Statistics di Diez et al., es. 6.1)
Supponendo che l’ \(8\%\) degli studenti siano vegetariani, determinare se le seguenti affermazioni sono vere o false, fornendo motivazioni appropriate.
La distribuzione della proporzione campionaria di vegetariani in un campione casuale di dimensione 60 è approssimativamente normale dal momento che \(n \geq 30\).
La distribuzione della proporzione campionaria di vegetariani in un campione casuale di dimensione 50 è asimmetrica a destra.
Un campione casuale di 125 studenti di cui il \(12\%\) sono vegetariani può essere considerato anomalo.
Un campione casuale di 250 studenti di cui il \(12\%\) sono vegetariani può essere considerato anomalo.
L’errore standard si dimezzerebbe se la dimensione campionaria aumentasse da 125 a 250.
Soluzione
Falso. Infatti non è soddisfatta la condizione: \(np \geq 10\) e \(n(1 - p) \geq 10\).
Vero. Infatti non è soddisfatta la condizione: \(np \geq 10\) e \(n(1 - p) \geq 10\). Inoltre, nella maggior parte dei campioni ci si può aspettare che \(\hat{p}\) sia vicina a 0.08 che rappresenta la proporzione vera di vegetariani nella popolazione. Mentre \(\hat{p}\) può assumere valori anche di molto superiori a 0.08, sarà certamente limitata dal valore 0; ciò implica che la forma della distribuzione tenderà ad essere asimmetrica a destra.
Falso. L’errore standard è pari a \(SE_{\hat{p}} = \sqrt{\frac{p(1-p)}{n}} = 0.0243\) e \(\hat{p} = 0.12\) è distante soltanto \(\frac{0.12-0.08}{0.0243} = 1.65 SE\) dalla media, cosa che non può essere considerata anomala.
Vero. L’errore standard è pari a \(SE_{\hat{p}} = \sqrt{\frac{p(1-p)}{n}} = 0.0172\) e \(\hat{p} = 0.12\) è distante soltanto \(\frac{0.12-0.08}{0.0172} = 2.32 SE\) dalla media e rappresenta quindi un valore anomalo.
Falso. L’errore standard si ridurrebbe di un fattore \(\frac{1}{\sqrt{2}}\).
Esercizio 4.7
(dal libro di testo OpenIntro Statistics di Diez et al., es. 6.3)
Supponendo che il \(90\%\) dei gatti rossi tigrati sia maschio, determinare se le seguenti affermazioni sono vere o false, fornendo motivazioni appropriate.
La distribuzione della proporzione campionaria di un campione casuale di dimensione 30 è asimmetrica a sinistra.
Adottando una dimensione campionaria 4 volte maggiore, lo standard error della proporzione campionaria si dimezza.
La distribuzione della proporzione campionaria di un campione casuale di dimensione 140 è approssimativamente normale.
La distribuzione della proporzione campionaria di un campione casuale di dimensione 280 è approssimativamente normale.
Soluzione
Vero. Infatti non è soddisfatta la condizione: \(np \geq 10\) e \(n(1 - p) \geq 10\). Inoltre, nella maggior parte dei campioni ci si può aspettare che \(\hat{p}\) sia vicina a 0.90 che rappresenta la proporzione vera di maschi nella popolazione. Mentre \(\hat{p}\) può assumere valori anche di molto inferiori a 0.90, sarà certamente limitata dal valore 1; ciò implica che la forma della distribuzione tenderà ad essere asimmetrica a sinistra.
Vero. Nella formula dell’errore standard compare infatti la radice quadrata della numerosità campionaria.
Vero. Sono rispettate sia la condizione di indipendenza sia la condizione: \(np \geq 10\) e \(n(1 - p) \geq 10\).
Vero. Sono rispettate sia la condizione di indipendenza sia la condizione: \(np \geq 10\) e \(n(1 - p) \geq 10\).
Esercizio 4.8
(dal libro di testo OpenIntro Statistics di Diez et al., es. 6.5)
In un’indagine condotta da Survey USA nel 2010, il \(70\%\) dei \(119\) rispondenti di età compresa tra i 18 e i 34 anni ha affermato che avrebbe votato a favore della cosiddetta Prop 19, un provvedimento per legalizzare la marjiuana in California modificando la legge vigente e adottando una opportuna regolamentazione e tassazione. Ad un livello di confidenza del \(95\%\), il margine di errore per questo campione è pari all’\(8\%\). Sulla base di queste informazioni, determinare se le seguenti affermazioni sono vere o false, fornendo motivazioni appropriate.
Si può essere fiduciosi, con un livello di confidenza del \(95\%\), che una percentuale di elettori compresa tra il \(62\%\) e il \(78\%\) in questo campione voterà a favore della Prop 19.
Si può essere fiduciosi, con un livello di confidenza del \(95\%\), che tra gli elettori di età tra i 18 e i 34 anni, una percentuale compresa tra il \(62\%\) e il \(78\%\) voterà a favore della Prop 19.
Se si considerassero molti campioni casuali di 119 elettori di età tra i 18 e i 34 anni, e si calcolassero i corrispondenti intervalli di confidenza, il \(95\%\) di essi includerebbe il valore vero della proporzione di elettori favorevoli alla Prop 19 nella popolazione.
Per ridurre il margine di errore al \(4\%\), è necessario moltiplicare la dimensione campionaria per 4.
In base a questo intervallo di confidenza, c’è evidenza sufficiente per concludere che la maggioranza degli elettori Californiani di età tra i 18 e i 34 anni, supportano la Prop 19.
Soluzione
Falso. Un intervallo di confidenza viene costruito per stimare la proporzione nella popolazione, non nel campione.
Vero. L’intervallo di confidenza al \(95\%\) è \(70\% \pm 8\%\).
Vero, per la definizione di intervallo di confidenza.
Vero. Moltiplicando la dimensione campionaria per 4, l’errore standard e il margine di errore si riducono di un fattore \(\frac{1}{\sqrt{4}}\).
Vero. L’intervallo di confidenza al \(95\%\) è tutto al di sopra del \(50\%\).
Esercizio 4.9
(dal libro di testo OpenIntro Statistics di Diez et al., es. 6.7)
Alla fine di Giugno 2012, Survey USA ha pubblicato i risultati di un’indagine in cui si diceva che il \(56\%\) di 600 residenti del Kansas scelti in modo casuale aveva programmato di fare i fuochi d’artificio il 4 Luglio. Determinare il margine di errore per la stima puntuale per un livello di confidenza del \(95\%\).
Soluzione
Dal momento che il campione considerato è inferiore al 10\(\%\) della popolazione, la condizione di indipendenza è soddisfatta. Anche la condizione \(np \geq 10\) e \(n(1 - p) \geq 10\) è verificata. Il margine di errore è dunque: \(ME = z^* \sqrt{\frac{\hat{p}(1-\hat{p})}{n}} = 1.96 \sqrt{\frac{0.56 \cdot 0.44}{600}} = 0.0397 = 4\%\).
Esercizio 4.10
(dal libro di testo OpenIntro Statistics di Diez et al., es. 6.9)
L’obiettivo di questa indagine è stimare la proporzione di laureati in una classe di piú di 4500 studenti che hanno trovato un lavoro entro un anno dalla laurea. Supponendo che 348 su 400 studenti estratti casualmente abbiano dichiarato di avere un lavoro, rispondere ai seguenti quesiti.
Descrivere il parametro di interesse della popolazione. Quale è la stima puntuale di questo parametro?
Controllare se le condizioni per la costruzione di un intervallo di confidenza sono soddisfatte dai dati a disposizione.
Calcolare un intervallo di confidenza al \(95\%\) per la proporzione di laureati che ha trovato lavoro entro un anno dalla laurea e fornire una sua interpretazione.
Cosa significa confidenza al \(95\%\)?
Calcolare ora un intervallo di confidenza al \(99\%\) per la proporzione di laureati che ha trovato lavoro entro un anno dalla laurea e fornire una sua interpretazione.
Confrontare le ampiezze dei due intervalli al livello \(95\%\) e \(99\%\). Quale è piú ampio? Spiegare il perché.
Soluzione
Il parametro di interesse della popolazione è la proporzione di laureati che ha trovato lavoro a un anno dalla laurea. La stima puntuale è \(\hat{p} = 348/400 = 0.87\).
Il campione considerato è inferiore al 10\(\%\) della popolazione, quindi la condizione di indipendenza è soddisfatta. Anche la condizione \(np \geq 10\) e \(n(1 - p) \geq 10\) è verificata.
L’intervallo è: \((0.8371,0.9029)\). Si può essere fiduciosi al \(95\%\) che approssimativamente una percentuale compresa tra l’\(84\%\) e il \(90\%\) dei laureati abbia trovato lavoro entro un anno dalla laurea.
Significa che estraendo un gran numero di campioni e calcolando gli intervalli corrispondenti, si otterrebbe nel \(95\%\) dei casi un intervallo contenente il valore vero del parametro.
L’intervallo è \((0.8267, 0.9133)\). Si può essere fiduciosi al \(99\%\) che approssimativamente una percentuale compresa tra l’\(83\%\) e il \(91\%\) dei laureati abbia trovato lavoro entro un anno dalla laurea.
L’intervallo a livello \(99\%\) è piú ampio, perché richiede un livello di fiducia maggiore che la proporzione vera sia contenuta all’interno dell’intervallo e quindi deve coprire un range maggiore.
Esercizio 4.11
(dal libro di testo OpenIntro Statistics di Diez et al., es. 6.11)
Un’indagine su 1509 studenti liceali che hanno compilato un questionario online non obbligatorio tra il 25 e il 30 aprile 2007 mostra che il 55\(\%\) degli intervistati è piuttosto sicuro che in seguito parteciperà ad un programma di studio all’estero.
Questo campione è rappresentativo della popolazione di tutti i liceali degli Stati Uniti? Spiegare il perché.
Supponendo che le condizioni per fare inferenza siano soddisfatte, anche se la risposta al punto a. indicasse che questo approccio non è affidabile, questa analisi potrebbe essere ancora interessante. Costruire un intervallo di confidenza al \(90\%\) per la proporzione di studenti che è piuttosto sicura che in seguito parteciperà ad un programma di studio all’estero e fornire una sua interpretazione.
Cosa significa confidenza al \(90\%\)?
In base a questo intervallo, sarebbe corretto affermare che la maggior parte degli studenti è piuttosto sicura che in seguito parteciperà ad un programma di studio all’estero?
Soluzione
No. Si tratta di un campione di volontari, quindi un campione non casuale.
\((0.5289, 0.5711)\). Si può essere fiduciosi al \(90\%\) che una percentuale di studenti compresa tra il \(53\%\) e il \(57\%\) sia piuttosto sicura che in seguito parteciperà ad un programma di studio all’estero.
Significa che estraendo un gran numero di campioni e calcolando gli intervalli corrispondenti, si otterrebbe nel \(90\%\) dei casi un intervallo contenente il valore vero del parametro.
Si perché l’intervallo cade al di sopra del valore 0.5.
Esercizio 4.12
(dal libro di testo OpenIntro Statistics di Diez et al., es. 6.13)
Un articolo del Washington Post del 2009 ha riportato che 7 democratici su 10 sostengono la riforma della sanità, mentre quasi 9 su 10 repubblicani sono contrari a questa riforma. Il 52\(\%\) degli indipendenti sono contro e il 42\(\%\) a favore (il \(6\%\) rispondono ‘altro’). Complessivamente erano stati intervistati 819 democratici, 566 repubblicani e 783 indipendenti.
Una trasmissione televisiva riportando questa notizia, ha affermato che la maggior parte degli Indipendenti è contraria alla riforma. Questi dati forniscono una forte evidenza a supporto di questa affermazione?
Ci si può aspettare che un intervallo di confidenza per la proporzione di indipendenti contrari alla riforma includa il valore \(0.5\)? Motivare la risposta.
Soluzione
In questo caso si può impostare il seguente sistema di ipotesi: \(H_0: p = 0.50 \text{ vs } H_A: p > 0.50\). Le due condizioni (indipendenza e \(np \geq 10\) e \(n(1 - p) \geq 10\)) sono entrambe verificate. In questo caso si ottiene un valore osservato della statistica test \(z = 1.12\) che corrisponde ad un p-value pari a \(0.1314\). Dal momento che il p-value supera la soglia \(0.05\), non è possibile rifiutare \(H_0\), ovvero i dati non forniscono forte evidenza a favore dell’affermazione di interesse.
Si, da quanto affermato al punto precedente segue che l’intervallo conterrà il valore \(0.5\).
Esercizio 4.13
(dal libro di testo OpenIntro Statistics di Diez et al., es. 6.15)
Un’indagine del 2012 su 2254 americani adulti ha mostrato che il \(17\%\) di coloro che possiedono un telefono cellulare naviga su internet utilizzando il suo dispositivo mobile anziché un personal computer.
Secondo un articolo pubblicato online, una ricerca condotta da una compagnia telefonica ha mostrato che il \(38\%\) degli utenti Cinesi accede a internet solo attraverso i cellulari. Verificare mediante un test di ipotesi se questi dati supportano l’ipotesi che la proporzione di Americani che utilizza il telefono cellulare per navigare su internet è differente dalla medesima proporzione nella popolazione cinese.
Interpretare il p-value ottenuto al punto a.
Calcolare un intervallo al \(95\%\) per la proporzione di americani che utilizza il telefono cellulare per navigare su internet e fornire un’interpretazione.
Soluzione
In questo caso si può impostare il seguente sistema di ipotesi: \(H_0: p = 0.38 \text{ vs } H_A: p \neq 0.38\). Le due condizioni (indipendenza e \(np \geq 10\) e \(n(1 - p) \geq 10\)) sono entrambe verificate. Il valore osservato della statistica test è \(z = 20.5\) e il corrispondente p-value \(\approx 0\), Dal momento che il p-value è trascurabile si può rifiutare l’ipotesi nulla, quindi i dati forniscono forte evidenza che la proporzione di Americani che utilizza il telefono cellulare per navigare su internet è diversa dalla (in particolare, inferiore alla) proporzione corrispondente nella popolazione Cinese.
Se il \(38\%\) degli americani usasse il cellulare come mezzo per accedere a internet, la probabilità di ottenere un campione casuale di 2254 americani in cui una percentuale inferiore o uguale al \(17\%\) o superiore o uguale al \(59\%\) di utenti di internet via cellulare sarebbe pressoché trascurabile.
L’intervallo è \((0.1545, 0.1855)\). Si può avere fiducia a livello \(95\%\) che approssimativamente una percentuale compresa tra il \(15\%\) e il \(18.6\%\) degli americani utilizza il proprio cellulare per navigare su internet.
Esercizio 4.14
(dal libro di testo OpenIntro Statistics di Diez et al., es. 6.17)
Alcune persone sostengono di poter individuare la differenza tra una bevanda dietetica e una normale al primo sorso. Un ricercatore volendo sottoporre a verifica questa affermazione, ha estratto un campione casuale tra queste persone di numerosità pari a 80. Ha poi predisposto 40 bicchieri della bevanda dietetica e 40 di quella normale in modo casuale e infine ha chiesto a ciascun assaggiatore di provare le bevande e classificarle come dietetiche o regolari. 53 partecipanti hanno classificato correttamente le bevande.
Questi dati forniscono forte evidenza del fatto che queste persone sono capaci di individuare la differenza tra la bevanda dietetica e quella normale? In altre parole, i risultati sono significativamente migliori rispetto a un’assegnazione casuale alle due tipologie?
Interpretare il p-value ottenuto al punto a.
Soluzione
In questo caso si può impostare il seguente sistema di ipotesi: \(H_0: p = 0.5 \text{ vs } H_A: p > 0.5\). Le due condizioni (indipendenza e \(np \geq 10\) e \(n(1 - p) \geq 10\)) sono entrambe verificate. Il valore osservato della statistica test è \(z = 2.91\) e il corrispondente p-value è pari a \(0.0018\). Poiché il p-value è inferiore a 0.05, rifiutiamo l’ipotesi nulla. I dati forniscono forte evidenza che il tasso di corretta identificazione della tipologia di bevanda di queste persone è significativamente migliore rispetto a un’assegnazione casuale.
Se le persone assegnassero casualmente la tipologia di bevanda, la probabilità di ottenere una campione casuale in cui 53 persone su 80 identificassero correttamente la bevanda sarebbe pari a \(0.0018\).
Esercizio 4.15
(dal libro di testo OpenIntro Statistics di Diez et al., es. 6.19)
Si vuole stimare la proporzione di studenti universitari fumatori. In un campione casuale di 200 studenti universitari, 40 sono fumatori.
Calcolare un intervallo di confidenza al \(95\%\) per la proporzione di studenti universitari fumatori, e fornire un’interpretazione dell’intervallo.
Se si volesse un margine di errore non superiore al \(2\%\) per l’intervallo di confidenza al \(95\%\), quale dovrebbe essere la dimensione campionaria?
Soluzione
Le due condizioni (indipendenza e \(np \geq 10\) e \(n(1 - p) \geq 10\)) sono entrambe verificate. L’intervallo di confidenza a livello \(95\%\) risulta essere \((0.145,0.255)\). Si può avere un livello di fiducia del \(95\%\) che una percentuale compresa tra il \(14\%\) e il \(25.5\%\) degli studenti universitari fumi.
\(z^* SE\) non deve eccedere il valore 0.02. Dato che \(z^* = 1.96\), sostituendo la stima puntuale di p, \(\hat{p} = 0.2\) nella formula dell’errore standard si ha \(1.96 \sqrt{0.2(1-0.2)/n} \leq 0.02\), da cui segue che la numerosità campionaria dovrà essere almeno pari a 1537.
Esercizio 4.16
(dal libro di testo OpenIntro Statistics di Diez et al., es. 6.21)
Nell’Esercizio 4.12 si è detto che il \(52\%\) degli Indipendenti intervistati a proposito della riforma del sistema sanitario, si è dichiarato contrario alla riforma stessa. Se volessimo stimare questo numero con un margine di errore dell’\(1\%\) con un livello di confidenza del \(90\%\), quale dimensione campionaria risulterebbe adeguata a tale obiettivo?
Soluzione
Il margine di errore \(z^* SE\) deve essere minore di \(0.01\). Poiché vogliamo un livello di confidenza del \(90\%\) avremo \(z^* = 1.65\) e sostituiremo la stima puntuale \(\hat{p} = 0.52\) nella formula \(1.96 \sqrt{0.52(1-0.52)/n} \leq 0.01\), ottenendo una numerosità campionaria maggiore o uguale a 6796.
Esercizio 4.17
In un campione di 400 proprietari di negozi e piccole imprese, che hanno dichiarato fallimento, 88 non hanno alcuna esperienza professionale precedente.
Sottoporre a test l’ipotesi nulla che il 25% di coloro che vanno in fallimento non hanno esperienze precedenti al livello di significatività del 5% contro l’ipotesi alternativa che la percentuale sia inferiore;
Definire il \(p-value\) del test e calcolarlo;
Se il livello di significatività fosse stato il 10% l’ipotesi nulla sarebbe stata respinta?
Soluzione
È un test sulla proporzione di successi. Qui il successo è “il proprietario ha dichiarato fallimento”. La proporzione stimata è \(\hat{p}=88/400=0.22\). Useremo l’approssimazione normale della statistica test, avendo cura di sostituire la deviazione standard con l’errore standard. Le ipotesi sono: \[H_0:\: p=p_0=0.25; \qquad H_1:\: p < 0.25\] Determiniamo il \(p-value\): \[p-value = P(Z<z)\] La statistica test Z si distribuisce come una normale standard. Il valore \(z\) è il valore della statistica test osservato nel campione \[z= \frac{\hat{p} - p_0}{\sqrt{\frac{p_0 (1-p_0)}{n}}} = \frac{0.22 -0.25}{ \sqrt{\frac{0.25 \cdot (1-0.25)}{400}}} = -1.39\] Il \(p-value\) risulta quindi \[p-value = P(Z<z)=0.0823\] Non possiamo rifiutare l’ipotesi \(H_0\) a livello di significatività \(\alpha = 0.05\) perché ovviamente il \(p-value\) è \(>\) 0.05.
Se consideriamo invece un livello di significatività \(\alpha = 0.1\), poiché \(p-value < \alpha\), possiamo rifiutare l’ipotesi nulla.
Esercizio 4.18
Un famoso educatore dichiara che piú della metà della popolazione adulta
degli USA è preoccupata dalla carenza di programmi educativi in
televisione. Per raccogliere dati sulla questione, nell’ambito di un
sondaggio nazionale vengono scelti e intervistati 920 individui. Se 478
(52%) degli intervistati dichiarano di essere preoccupati, abbiamo
dimostrato la dichiarazione dell’educatore?
Soluzione
Dobbiamo valutare il seguente sistema di ipotesi per la proporzione \(p\) di popolazione americana preoccupata per la carenza di programmi educativi in televisione: \[H_{0}: p = 0.50 \hspace{2cm} H_{1}:p>0.50\] Si tratta di un test per proporzioni; in questo caso la statistica test, \(Z\), è definita come \[Z=\frac{\hat{p}-p_0}{\sqrt{\frac{p_0(1-p_0)}{n}}}\] dove
\(\hat{p}\) è la proporzione di individui preoccupati nel campione osservato (\(\hat{p}=0.52\));
\(n\) è la numerosità campionaria (\(n=920\)).
Si dimostra che sotto l’ipotesi nulla \(H_{0}\), questa statistica test ha
distribuzione Normale standardizzata, ossia \[Z \sim N(0,1)\] Al fine di
valutare questo sistema di ipotesi possiamo calcolare il p-value
corrispondente, ossia dobbiamo valutare \(Pr(Z>z)\) dove
\(z=\frac{\hat{p}-p_{0}}{\sqrt{\frac{p_{0}(1-p_{0})}{n}}}\) con \(p_{0}\)
valore della proporzione assunta sotto l’ipotesi nulla (\(p_{0}=0.5\)).
Possiamo quindi calcolare il \(p-value\) come segue: \[\begin{aligned}
p-value=Pr(Z > z) &= Pr\left(Z>\frac{\hat{p}-p_{0}}{\sqrt{\frac{p_{0}(1-p_{0})}{n}}}\right)=\\
&= Pr\left(Z> \frac{0.52-0.50}{\sqrt{\frac{0.50(1-0.50)}{920}}}\right)=\\
&= Pr(Z> 1.21)=1-Pr(Z \leq 1.21) = 1-0.887=0.113\end{aligned}\] dove il
valore 0.877 è stato controllato sulle tavole della distribuzione
Normale standardizzata.
Concludendo, poiché il \(p-value=0.113\), possiamo rifiutare l’ipotesi
nulla e quindi validiamo l’ipotesi dell’educatore, solo se consideriamo
un livello di significatività \(\alpha>0.113\) (con \(\alpha=0.05\) o
\(\alpha=0.10\) l’ipotesi nulla non viene rifiutata).
Esercizio 4.19
Un professore ritiene che la percentuale di ricercatori che, nel suo settore scientifico disciplinare, pubblicano su riviste internazionali è pari al 70%. In un campione di 160 ricercatori, 108 hanno pubblicazioni internazionali. Verificare il seguente sistema di ipotesi: \[H_{0}: p = 0.7 \ \ H_{1}: p <0.7\]
Soluzione
Anche in questo caso possiamo procedere come fatto nel precedente esercizio calcolando il p-value come segue (\(\hat{p}=\frac{108}{160}=0.675\)): \[\begin{aligned} p-value&=Pr(Z<z)=Pr\left(Z<\frac{\hat{p}-p_{0}}{\sqrt{\frac{p_{0}(1-p_{0})}{n}}}\right)=\\ &= Pr \left(Z< \frac{0.675-0.70}{\sqrt{\frac{0.70(1-0.70)}{160}}}\right)= Pr(Z < -0.69) = 0.2451\end{aligned}\] Pertanto, il valore minimo di \(\alpha\) per rifiutare l’ipotesi nulla è 0.25.
Esercizio 4.20
(dal libro di testo OpenIntro Statistics di Diez et al., es. 6.47)
In un’indagine campionaria USA del 2012 i residenti in Florida sono stati interrogati su quanto grande fosse secondo loro il problema del bullismo nelle scuole locali. 9 su 191 tra i 18 e i 34 anni hanno risposto che il bullismo non è affatto un problema. Usando questi dati, è possibile costruire un intervallo di confidenza utilizzando la formula \(\widehat{p}\pm z^* \sqrt{\widehat{p} (1-\widehat{p})/n}\) per la proporzione vera di residenti in Florida di età 18-34 che pensano che il bullismo non sia per niente un problema? Se si ritiene appropriato, costruire l’intervallo di confidenza, altrimenti, spiegare il perché.
4.3 Inferenza sulla differenza tra due proporzioni
Esercizio 4.21
(dal libro di testo OpenIntro Statistics di Diez et al., es. 6.23)
Un esperimento sociologico condotto da un programma televisivo ha analizzato il comportamento di alcune persone quando assistono a un litigio di coppia in cui la donna viene palesemente offesa dall’uomo, in due differenti occasioni allo stesso ristorante. Nel primo caso la donna è vestita in modo provocante e nell’altro caso è invece abbligliata in modo castigato. La seguente tabella riassume i dati raccolti su quante persone hanno deciso di intervenire o meno:
| Provocante | Castigato | Totale | |
|---|---|---|---|
| Intervenuti | 5 | 15 | 20 |
| Non intervenuti | 15 | 10 | 25 |
| Totale | 20 | 25 | 45 |
Spiegare perché la distribuzione campionaria della differenza tra le proporzioni di intervento sotto i due scenari non segue una distribuzione approssimativamente normale.
Soluzione
Si tratta di un esperimento non randomizzato e non è chiaro se le persone possono essere influenzato dal comportamento degli altri avventori del ristorante. In questo caso non è quindi possibile assumere l’indipendenza. In piú ci sono solo 5 persone intervenute nel caso dello scenario ‘Provocante’, quindi non vale neanche la condizione \(np \geq 10\) e \(n(1 - p) \geq 10\). Anche se considerassimo un test di ipotesi basato su una media delle proporzioni, tale condizione non potrebbe essere soddisfatta. Per questi motivi non è possibile assumere che la distribuzione campionaria della differenza delle proporzioni sia approssimativamente normale.
Esercizio 4.22
(dal libro di testo OpenIntro Statistics di Diez et al., es. 6.25)
In uno studio del 2001, 1924 maschi e 3666 femmine tra gli studenti del college sono stati intervestati in merito al loro colore preferito. Un intervallo al \(95\%\) per la differenza tra le proporzioni di maschi e femmine il cui colore preferito è il nero \((p_{male}-p_{female})\) è risultato essere \((0.02,0.06)\). Sulla base di questa informazione, determinare se le seguenti affermazioni sono vere o false, motivando la risposta.
Si può essere fiduciosi al \(95\%\) che la proporzione vera di maschi il cui colore preferito è nero sia il \(2\%\) inferiore e il \(6\%\) superiore rispetto alla proporzione vera di femmine.
Si può essere fiduciosi al \(95\%\) che la proporzione vera di maschi il cui colore preferito è nero sia tra il \(2\%\) e il \(6\%\) superiore rispetto alla proporzione vera di femmine.
Il \(95\%\) dei campioni casuali produrrà intervalli di confidenza che includono la differenza vera tra le proporzioni di maschi e femmine il cui colore preferito è nero.
Possiamo concludere che c’è una differenza significativa tra le proporzioni di maschi e femmine il cui colore preferito è nero e che la grandezza della differenza tra le due proporzioni campionarie sia plausibilmente imputabile al caso.
L’intervallo di confidenza al \(95\%\) per \((p_{female}-p_{male})\) non può essere calcolato sulla base delle informazioni disponibili in questo esercizio
Esercizio 4.23
(dal libro di testo OpenIntro Statistics di Diez et al., es. 6.51)
Nell’esercizio 4.21 è stato introdotto un esperimento sociologico condotto da un programma televisivo in cui è stato analizzato il comportamento di alcune persone quando assistono a un litigio di coppia in cui la donna viene palesemente offesa dall’uomo, in due differenti occasioni allo stesso ristorante. Nel primo caso la donna è vestita in modo provocante e nell’altro caso è invece in modo castigato. La seguente tabella riassume i dati raccolti su quante persone hanno deciso di intervenire o meno:
| Provocante | Castigato | Totale | |
|---|---|---|---|
| Intervenuti | 5 | 15 | 20 |
| Non intervenuti | 15 | 10 | 25 |
| Totale | 20 | 25 | 45 |
Una simulazione è stata effettuata per verificare se le persone reagiscono in maniera diversa nelle due situazioni. 10000 differenze simulate sono state generate per costruire la distribuzione sotto l’ipotesi nulla. Il valore \(\widehat{p}_{pr,sim}\) rappresenta la proporzione di clienti che è intervenuta nella simulazione per difendere una donna vestita in modo provocante e \(\widehat{p}_{con,sim}\) la proporzione che è intervenuta per una donna vestita in modo castigato.
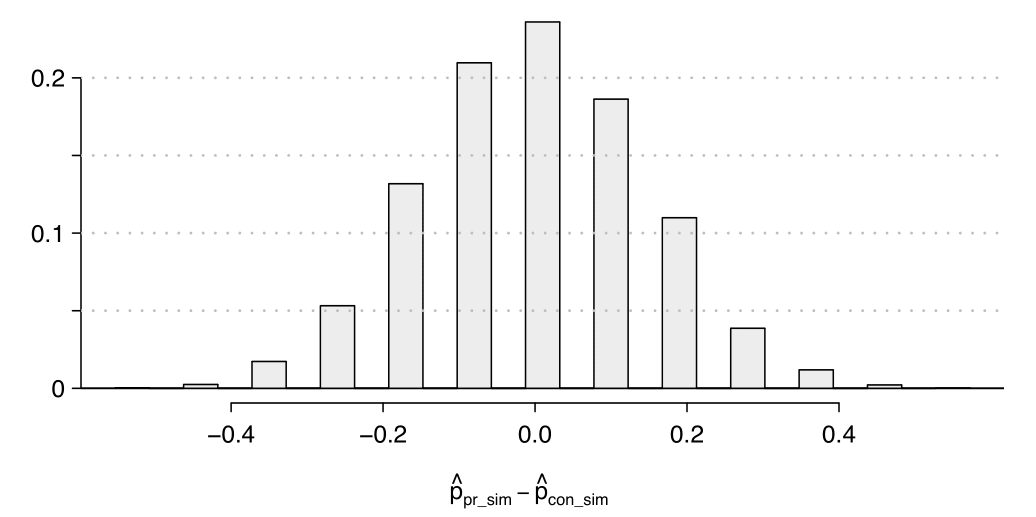
Quali sono le ipotesi? Per gli scopi di questo esercizio, si può assumere che ogni persona osservata al ristorante si comporti in modo indipendente, anche se tale assunzione dovrebbe essere verificata in modo rigoroso se volessimo riportare ufficialmente i risultati dei questo esperimento.
Calcolare la differenza osservata tra i tassi di intervento nelle due situazioni: \(p_{pr}-p_{con}\).
Stimare il \(p\)-value usando il grafico riportato sopra. Cosa si può dedurre?
Soluzione
Il suffisso \({}_{pr}\) corrisponde a provocante e \({}_{con}\) a castigato.
\(H_0\): \(p_{pr}=p_{con}\). \(H_A\): \(p_{pr}\neq p_{con}\).
-0.35.
La coda sinistra per il \(p\)-value è calcolata sommando \(0.005\) e \(0.015\). Raddoppiando tale valore (\(0.02\)) si ottiene che il \(p\)-value è pari a 0.04. (Gli studenti possono ottenere risultati approssimati, e un piccolo numero di studenti può ottenere un \(p\)-value pari a 0.05.) Poiché il \(p\)-value è piccolo, rifiutiamo \(H_0\). I dati forniscono una forte evidenza empirica che le persone reagiscono in modo diverso nelle due situazioni.
Esercizio 4.24
(dal libro di testo OpenIntro Statistics di Diez et al., es. 6.27)
L’esercizio 4.12 presenta i risultati di un sondaggio per valutare il sostegno alla riforma del sistema sanitario nel 2009. Il \(70\%\) dei democratici e il \(42\%\) degli indipendenti supporta tale riforma.
Costruire l’intervallo di confidenza al \(95\%\) per la differenza tra \(p_D\) e \(p_I\), (\(p_D - p_I\)), e commentare i risultati. Già sono state verificate le condizioni.
Vero o falso: se estraiamo casualmente un democratico e un indipendente, contemporaneamente, dal campione preso in esame, è più probabile che un democratico sostenga la riforma del sistema sanitario piuttosto che un indipendente.
Esercizio 4.25
(dal libro di testo OpenIntro Statistics di Diez et al., es. 6.29)
Un’indagine del 2010 ha chiesto a 827 elettori scelti casualmente in California "Sei a favore o contro la trivellazione per estrarre petrolio e gas naturale al largo delle coste della California? Oppure non ne sai abbastanza per esprimerti?" Di seguito è riportata la distribuzione delle risposte, in cui gli elettori sono stati divisi tra laureati e non laureati.
| Laureati | Non laureati | |
| Favorevoli | 154 | 132 |
| Contrari | 180 | 126 |
| Non sanno | 104 | 131 |
| Totale | 438 | 389 |
Qual è la percentuale di laureati e quale la percentuale di non laureati in questo campione che non ne sa abbastanza per avere un’opinione sull’estrazione di petrolio e gas naturale al largo delle coste della California?
Usare un test d’ipotesi per determinare se vi è una forte evidenza empirica per cui la proporzione di laureati che non ha un’opinione sull’argomento è diversa dalla proporzione di non laureati.
Soluzione
Laureati: \(23,7\%\). Non laureati: \(33,7\%\).
Siano \(p_{L}\) e \(p_{NL}\), rispettivamente, la proporzione di laureati e la proporzione di non laureati che hanno risposto “non so”. \(H_0: p_{L}=p_{NL}\) e \(H_A: p_{L}\neq p_{NL}\). Le due condizioni (indipendenza e \(np \geq 10\) e \(n(1 - p) \geq 10\)) sono entrambe verificate. Per la seconda condizione si usa la proporzione empirica/stimata (\(\widehat{p}=235/827=0,284\)). \(Z=-3.18 \rightarrow\) \(p\)-value\(=0.0014\). Poiché il \(p\)-value è molto piccolo, si rifiuta \(H_0\). C’è abbastanza evidenza sperimentale per poter rifiutare l’ipotesi nulla, in altre parole la differenza tra laureati e non laureati che non hanno un’opinione sull’argomento è statisticamente significativa. I dati indicano anche che meno laureati che non laureati hanno risposto “non so” (cioè i dati indicano la direzione dopo il rifiuto di \(H_0\)).
Esercizio 4.26
(dal libro di testo OpenIntro Statistics di Diez et al., es. 6.31)
I risultati di un’indagine sulla trivellazione per l’estrazione di petrolio e gas naturale al largo della costa della California sono stati introdotti nell’Esercizio 4.25.
Qual è la percentuale di laureati e quale la percentuale di non laureati in questo campione che è a favore dell’estrazione di petrolio e gas naturale al largo delle coste della California?
Usare un test d’ipotesi per determinare se vi è una forte evidenza empirica per cui la proporzione di laureati che è favorevole è diversa dalla proporzione di non laureati.
Soluzione
Laureati: \(35,2\%\). Non laureati: \(33,9\%\).
Siano \(p_{L}\) e \(p_{NL}\), rispettivamente, la proporzione di laureati e la proporzione di non laureati che sono favorevoli. \(H_0: p_{L}=p_{NL}\) e \(H_A: p_{L}\neq p_{NL}\). Le due condizioni (indipendenza e \(np \geq 10\) e \(n(1 - p) \geq 10\)) sono entrambe verificate. Per la seconda si usa la proporzione empirica/stimata (\(\widehat{p}=286/827=0.346\)). \(Z=0.39 \rightarrow\) \(p\)-value\(=0.6966\). Poiché il \(p\)-value è maggiore di \(\alpha\) (0.05), non si può rifiutare \(H_0\). Non c’è abbastanza evidenza sperimentale per poter rifiutare l’ipotesi nulla, in altre parole la differenza tra laureati e non laureati che sono favorevoli alla trivellazione in California non è statisticamente significativa.
Esercizio 4.27
(dal libro di testo OpenIntro Statistics di Diez et al., es. 6.33)
La Fondazione del sonno statunitense ha condotto un’indagine sulle abitudini di un campione aleatorio di lavoratori dei trasporti e un campione controllo di persone che non lavorano nel mondo dei trasporti. I risultati dell’indagine sono riportati sotto.
| Lavoratori dei Trasporti | |||||
| Operatori | Autisti | ||||
| Ore di sonno | Controllo | Piloti | Camionisti | treno | bus/taxi/limo |
| \(<6\) | 35 | 19 | 35 | 29 | 21 |
| \([6, 8]\) | 193 | 132 | 117 | 119 | 131 |
| \(>8\) | 64 | 51 | 51 | 32 | 58 |
| Totale | 292 | 202 | 203 | 180 | 210 |
Usare un test d’ipotesi per valutare se i dati forniscono una forte evidenza sulla significatività della differenza tra la proporzione di camionisti e il gruppo controllo che dormono meno di 6 ore al giorno, cioè che sono considerati carenti di sonno.
Soluzione
Indichiamo con \(NT\) il gruppo controllo e con \(C\) i camionisti. \(H_0: p_{NT}=p_{C}\) e \(H_A: p_{NT}\neq p_{C}\). Le due condizioni (indipendenza e \(np \geq 10\) e \(n(1 - p) \geq 10\)) sono entrambe verificate. Per la seconda si usa la proporzione empirica/stimata (\(\widehat{p}=70/495=0,141\)). \(Z=-1,58 \rightarrow\) \(p\)-value\(=0,1164\). Poiché il \(p\)-value è maggiore di \(\alpha\) (0,05), non si può rifiutare \(H_0\). Non c’è una forte evidenza sperimentale per poter rifiutare l’ipotesi nulla. La differenza tra i tassi di carenza di sonno del gruppo controllo e il gruppo dei camionisti non è statisticamente significativa.
Esercizio 4.28
(dal libro di testo OpenIntro Statistics di Diez et al., es. 6.35)
A luglio 2008 gli istituti nazionali statunitensi di sanità hanno annunciato che era stato interrotto uno studio clinico a causa di risultati inaspettati. La popolazione oggetto di studio era formata da donne dell’Africa sub-Sahariana a cui era stata somministrata una singola dose di Nevaripine (un trattamento per l’HIV) durante il parto, per prevenire la trasmissione dell’HIV al neonato. Con questo studio ci si chiedeva se proseguire il trattamento dopo il parto con Nevaripine oppure con il trattamento alternativo Lopinavir. Allo studio hanno partecipato 240 donne; 120, aleatoriamente scelte, per ogni trattamento. Ventiquattro settimane dopo aver iniziato lo studio sul trattamento, ogni donna è stata analizzata per vedere se la situazione era peggiorata (un risultato chiamato fallimento virologico). Un fallimento virologico è stato riscontrato su 26 delle 120 donne trattate con Nevaripine e 10 delle 120 donne a cui era stato somministrato l’altro trattamento.
Costruire una tabella a due vie in cui vengono riportati i risultati dello studio.
Definire un appropriato test d’ipotesi per verificare l’indipendenza tra trattamento e fallimento virologico.
Analizzare i risultati del test d’ipotesi e trarre le conclusioni. (N.B: verificare tutte le condizioni necessarie per il test.)
Soluzione
- Sintesi dello studio
| Fallimento Virale | |||
|---|---|---|---|
| Si | No | Totale | |
| Nevaripine | 26 | 94 | 120 |
| Lopinavir | 10 | 110 | 120 |
| Totale | 36 | 204 | 240 |
\(H_0: p_N=p_L\). Non c’è differenza tra i tassi di fallimento virologico nei due gruppi (Nevaripine e Lopinavir). \(H_A: p_N \neq p_L\). C’è differenza tra i tassi di fallimento virologico nei due gruppi.
È stata usata un’assegnazione aleatoria, quindi, le osservazioni in ciascun gruppo sono indipendenti. Se i pazienti in uno studio sono rappresentativi di quelli dell’intera popolazione (impossibile da verificare con le informazioni a disposizione), allora possiamo anche generalizzare i risultati alla popolazione. La condizione \(np \geq 10\) e \(n(1 - p) \geq 10\), che si verifica usando la proporzione campionaria (\(\widehat{p}=36/240=0.15\)), è soddisfatta. \(Z=3.04 \rightarrow\) \(p\)-value\(=0.0024\). Poiché il \(p\)-value è piccolo, si può rifiutare \(H_0\). C’è una forte evidenza sperimentale per poter rifiutare l’ipotesi nulla. La differenza tra i tassi di fallimento virologico del gruppo Nevaripine e del gruppo Lopinavir è statisticamente significativa.
4.4 Verifica della bontà di adattamento
Esercizio 4.29
(dal libro di testo OpenIntro Statistics di Diez et al., es. 6.37)
Indicare se le seguenti affermazioni sono vere o false. Per ogni affermazione falsa, suggerire un modo alternativo di scriverla per renderla vera.
La distribuzione \(\chi^2\), così come la distribuzione Normale, ha due parametri, la media e la deviazione standard.
La distribuzione \(\chi^2\) è sempre asimmetrica a destra, qualsiasi sia il valore del parametro “gradi di libertà”.
La statistica Chi quadrato (\(X^2\)) è sempre positiva.
All’aumentare dei gradi di libertà, la forma della distribuzione \(\chi^2\) diventa più asimmetrica.
Esercizio 4.30
(dal libro di testo OpenIntro Statistics di Diez et al., es. 6.39)
Un professore che usa un libro di introduzione alla statistica open-source prevede che il \(60\%\) degli studenti comprerà una copia cartacea del libro, il \(25\%\) stamperà il libro dal web e il \(15\%\) lo leggerà online. Alla fine del semestre chiede ai suoi studenti di rispondere a un questionario dove dovranno indicare qual è il formato del libro che hanno usato. Dei \(126\) studenti, \(71\) hanno detto di aver comprato una copia cartacea del libro, \(30\) lo hanno stampato dal web e \(25\) lo hanno letto online.
Definire le ipotesi per verificare se le previsioni del professore erano accurate.
Quanti studenti il professore si aspettava che comprassero il libro, lo stampassero e lo leggessero esclusivamente online?
Si tratta di una situazione appropriata per usare un test Chi quadrato. Elencare le condizioni richieste per tale test e verificare che siano soddisfatte.
Calcolare la statistica Chi quadrato, i gradi di libertà associati e il \(p\)-value.
Sulla base del \(p\)-value calcolato, cosa possiamo concludere? Commentare i risultati ottenuti
Soluzione
\(H_0:\) La distribuzione del formato del libro usato dagli studenti è quella prevista dal professore. \(H_A:\) La distribuzione del formato del libro usato dagli studenti non è quella prevista dal professore
\(E_{\textit{copia cartacea}}=126 \times 0.60=75.6\). \(E_{\textit{stampa}}=126 \times 0.25=31.5\). \(E_{\textit{online}}=126 \times 0.15=18.9\)
Indipendenza: il campione non è aleatorio. Comunque, se il professore ritiene che le proporzioni siano stabili da un periodo (semestre) al successivo e che le abitudini degli studenti non siano influenzate da quelle degli altri, allora l’indipendenza è probabilmente ragionevole.
\(X^2=2.32\), i gradi di libertà sono 2 e il \(p\)-value è maggiore di \(0.3\).
Poiché il \(p\)-value è grande, non possiamo rifiutare \(H_0\). I dati non forniscono una forte evidenza che indichi che le previsioni del professore siano statisticamente non significative.
4.5 Test di indipendenza
Esercizio 4.31
Torniamo a considerare i dati relativi all’Esercizio 4.1. La seguente tabella riporta il livello depressivo osservato rispetto allo stato civile:
| stato civile | ||||
|---|---|---|---|---|
| livello depressivo | sposato | celibe | vedovo | Totale |
| grave | 22 | 16 | 19 | 57 |
| medio | 33 | 29 | 14 | 76 |
| leggero | 14 | 9 | 3 | 26 |
| Totale | 69 | 54 | 36 | 159 |
Determinare la distribuzione marginale e la distribuzione condizionata del livello depressivo allo stato civile vedovo e confrontarle. Cosa si può dire sull’associazione tra i due caratteri?
Verificare con un opportuno test l’ipotesi che ci sia associazione tra i due caratteri fissando il livello di significatività a 0.05.
Soluzione
- La distribuzione marginale del livello depressivo è la seguente:
| livello depressivo | freq. assolute | freq.percentuali |
| grave | 57 | \(57/ 159 \cdot 100 = 35.8\%\) |
| medio | 76 | \(76/159\cdot 100 = 47.8\%\) |
| leggero | 26 | \(26/159\cdot 100 = 16.3\%\) |
| Totale | 159 | 100 |
La distribuzione condizionata del livello depressivo allo stato civile vedovo è riportata nella seguente tabella:
| stato civile\(=\)vedovo | ||
|---|---|---|
| livello depressivo | freq. assolute | freq.percentuali |
| grave | 19 | \(19/ 36 \cdot 100 = 52.8\%\) |
| medio | 14 | \(14/36\cdot 100 = 38.9\%\) |
| leggero | 3 | \(3/36\cdot 100 = 8.3\%\) |
| Totale | 36 | 100 |
Analizzando la distribuzione condizionata allo stato civile vedovo, possiamo notare che la proporzione di vedovi con livello depressivo grave è superiore rispetto a quella calcolata sul totale. Dal confronto tra distribuzione condizionata e distribuzione marginale si può notare che le frequenze percentuali sono diverse, il che indica la presenza di un’associazione tra i due caratteri. Non possiamo dire però se questa associazione sia significativa o no.
- Il test Chi quadrato ci consente di verificare il seguente test di ipotesi:
\(H_0:\) il livello depressivo non è associato allo stato civile
\(H_A:\) c’è un’associazione significativa tra livello depressivo e stato civile
La statistica test \[X^2 = \sum_i \sum_j \frac{\left(n_{ij}-\frac{n_{i0} n_{0j}}{n}\right)^2}{\frac{n_{i0} n_{0j}}{n}} = n \left( \sum_i \sum_j \frac{n^2_{ij}}{n_{i0}n_{0j}}-1\right)\] si distribuisce, sotto l’ipotesi nulla come una v.a. Chi quadrato con \((r-1)(c-1) = 4\) gradi di libertà (dove \(r\) e \(c\) indicano rispettivamente il numero di righe e il numero di colonne della tabella di contingenza).
Calcoliamo innanzi tutto il valore osservato della statistica test Chi-quadrato che esprime una misura della distanza tra frequenze osservate e frequenze teoriche. Si noti che le due formule sono equivalenti, ma la seconda ci consente di abbreviare i calcoli, ottenendo:
\[\chi^2 = 159 \left( \frac{22^2}{57 \cdot 69}+\frac{16^2}{57 \cdot 54} +\frac{19^2}{57 \cdot 36}+\frac{33^2}{76 \cdot 69} + \right.\] \[\left. +\frac{29^2}{76 \cdot 54}+\frac{14^2}{76 \cdot 36}+\frac{14^2}{26 \cdot 69}+\frac{9^2}{54 \cdot 26}+\frac{3^2}{36 \cdot 26} -1 \right) = 6.828\]
Possiamo ora calcolare il p-value, ovvero la probabilità di osservare un valore della statistica test Chi-quadrato piú estremo di quello effettivamente osservato:
\[P\left(X^2_{(r-1)(c-1)} > \chi^2\right) = P\left(X^2_{4} > 6.828 \right) = 0.14\]
Poiché il p-value è pari a \(0.14 > 0.05 = \alpha\), possiamo concludere che non c’è abbastanza evidenza sperimentale per poter rifiutare l’ipotesi nulla, in altre parole l’associazione tra livello depressivo e stato civile non è statisticamente significativa.
Esercizio 4.32
(dal libro di testo OpenIntro Statistics di Diez et al., es. 6.41)
Far parte di un gruppo di sostegno influenza la capacità delle persone di smettere di fumare? Il ministero della salute ha coinvolto 400 fumatori in un esperimento aleatorio. 150 partecipanti hanno usato un cerotto alla nicotina e hanno incontrato settimanalmente un gruppo di sostegno.; gli altri 150 hanno usato il cerotto ma non hanno incontrato il gruppo di sostegno. Alla fine dell’esperimento, 40 partecipanti del primo gruppo ha smesso di fumare mentre solo 30 fumatori del secondo gruppo ha smesso di fumare.
Creare una tabella a doppia entrata riportando i risultati di questo studio.
Rispondere a ciascuna delle seguenti domande sotto l’ipotesi nulla che essere parte di un gruppo di sostegno non influenza la capacità di smettere di fumare, ed indicare se i valori attesi sono più alti o più bassi di quelli osservati.
- Quanti soggetti del primo gruppo ti aspetti che smettano di fumare?
- Quanti soggetti del secondo gruppo ti aspetti che smettano di fumare?
Soluzione
- La tabella a doppia entrata è la seguente
| Smettere di fumare | ||||
| Trattamento | Si | No | Totale | |
| Cerotto + gruppo di sostegno | 40 | 110 | 150 | |
| Solo cerotto | 30 | 120 | 150 | |
| Totale | 70 | 230 | 300 |
b-i. \(E_{\textit{rig1, col1}}=\dfrac{(\textit{totale riga 1}) \times(\textit{totale colonna 1})}{\textit{totale tabella}}=\dfrac{150 \times 70}{300}=35\). Questo valore è più piccolo di quello osservato.
b-ii. \(E_{\textit{rig2, col2}}=\dfrac{(\textit{totale riga 2}) \times(\textit{totale colonna 2})}{\textit{totale tabella}}=\dfrac{150 \times 230}{300}=115\). Questo valore è più piccolo di quello osservato.
Esercizio 4.33
(dal libro di testo OpenIntro Statistics di Diez et al., es. 6.43)
La tabella sotto sintetizza il dataset analizzato nell’Esercizio 4.25 dove sono riportate le risposte di un campione aleatorio di laureati e non laureati sul tema della trivellazione. Usare un test Chi quadrato per verificare se c’è una differenza statisticamente significativa tra le risposte dei laureati e quelle dei non laureati.
| Laureati | Non laureati | |
|---|---|---|
| Favorevoli | 154 | 132 |
| Contrari | 180 | 126 |
| Non sanno | 104 | 131 |
| Totale | 438 | 389 |
Soluzione
\(H_0\): L’opinione dei laureati e dei non laureati è differente sul tema della trivellazione per estrarre petrolio e gas naturale al largo delle coste della California. \(H_A\): L’opinione riguardante la trivellazione per estrarre petrolio e gas naturale al largo delle coste della California ha un’associazione con l’essere laureati oppure no.
\[E_{\textit{rig1, col1}}=151.5 \qquad E_{\textit{rig1, col2}}=134.5\] \[E_{\textit{rig2, col1}}=162.1 \qquad E_{\textit{rig2, col2}}=143.9\] \[E_{\textit{rig3, col1}}=124.5 \qquad E_{\textit{rig3, col2}}=110.5\]
Indipendenza: i campioni sono entrambi aleatori, non collegati ed estratti da meno del \(10\%\) della popolazione, perciò l’ipotesi di indipendenza tra le osservazioni è ragionevole. Campione: tutti le frequenze osservate sono almeno pari a 5. Gradi di libertà: \((R-1) \times (C-1)=(3-1) \times (2-1)=2\), che è più grande di 1. \(X^2=11.47\) e \(p\)-value compreso tra 0.001 e 0.005. Quindi c’è una forte evidenza empirica sull’associazione tra supportare la trivellazione e l’essere laureati.
Esercizio 4.34
(dal libro di testo OpenIntro Statistics di Diez et al., es. 6.45)
In un’indagine del 2011 806 utenti Facebook adulti, scelti aleatoriamente, sono stati interrogati sulle loro impostazioni sulla privacy di Facebook. Una delle domande era “Sai come cambiare le impostazioni riguardanti privacy di Facebook per controllare le persone che possono e non possono vederti?”. Le risposte sono riportate nella seguente tabella divise per genere.
| Genere | |||
|---|---|---|---|
| Maschile | Femminile | Totale | |
| Si | 288 | 378 | 666 |
| No | 61 | 62 | 123 |
| Non so | 10 | 7 | 17 |
| Totale | 359 | 447 | 806 |
Definire un test d’ipotesi per verificare l’indipendenza tra genere e la capacità degli utenti di Facebook di modificare le impostazioni sulla privacy.
Verificare tutte le condizioni necessarie per il test e determinare se è possibile utilizzare un test Chi quadrato.
Soluzione
\(H_0\): Non c’è relazione tra genere e la capacità degli utenti di Facebook di modificare le impostazioni sulla privacy. \(H_A\): C’è una relazione tra genere e la capacità degli utenti di Facebook di modificare le impostazioni sulla privacy.
I valori attesi sono:
\[E_{\textit{rig1, col1}}=296.6 \qquad E_{\textit{rig1, col2}}=369.3\] \[E_{\textit{rig2, col1}}=54.8 \qquad E_{\textit{rig2, col2}}=68.2\] \[E_{\textit{rig3, col1}}=7.6 \qquad E_{\textit{rig3, col2}}=9.4\]
Il campione è aleatorio, tutti i valori attesi sono più grandi di 5 e i gradi di libertà sono pari a \((3-1) \times (2-1)=2 >1\), quindi è possibile effettuare il test.