Chapter 3 Homelessness

3.1 Introduction

The 2020 point-in-time count of people experiencing homelessness for Seattle/King County was 11,751. This represents a 5% increase over the 2019 count and reflects similar trend across many counties in the western U.S.. A step towards addressing homelessness is improving our understanding of the relationship between local housing market factors and homelessness.

The U.S. Department of Housing and Urban Development (HUD) produced a report in 2019 Market Predictors of Homelessness that describes a model-based approach to understanding of the relationship between local housing market factors and homelessness. Our project is motivated by the goals of the HUD study:

“To continue progressing toward the goals of ending and preventing homelessness, we must further our knowledge of the basic community-level determinants of homelessness. The primary objectives of this study are to (1) identify market factors that have established effects on homelessness, (2) construct and evaluate empirical models of community-level homelessness..”

We will investigate whether there are alternative modeling approaches that outperform the models described in the HUD report.

3.2 Data Collection

The data for this project are described in HUD’s report Market Predictors of Homelessness in the section titled DATA.

I will refer you to this section of the HUD report for a detailed description of the sources of the data and how they were processed.

3.2.1 Load necessary packages

#skimr provides a nice summary of a data set
library(skimr)
#leaps will be used for model selection
library(leaps)
#readxl lets us read Excel files
library(readxl)
#GGally has a nice pairs plotting function
library(GGally)
#corrplot has nice plots for correlation matrices
library(corrplot)
#gridExtra
library(gridExtra)
#glmnet is used to fit glm's. It will be used for lasso and ridge regression models.
library(glmnet)
#tidymodels has a nice workflow for many models. We will use it for XGBoost
library(tidymodels)
#xgboost lets us fit XGBoost models
library(xgboost)
#vip is used to visualize the importance of predicts in XGBoost models
library(vip)
#tidyverse contains packages we will use for processing and plotting data
library(tidyverse)

#Set the plotting theme
theme_set(theme_bw())

3.2.2 Examine the data dictionary

The data dictionary HUD TO3 - 05b Analysis File - Data Dictionary.xlsx contains descriptions of all variables in the data set.

\(\rightarrow\) Load the data dictionary (call it dictionary) and view its contents using the function View.

Show Coding Hint

Use the function read_xlsx

Show Answer 
dictionary <- read_xlsx("HUD TO3 - 05b Analysis File - Data Dictionary.xlsx")
View(dictionary)

3.2.2.1 What are the sources of data?

\(\rightarrow\) Use the dictionary to find the unique sources of data that are not derived from other variables. We will assume that derived variables are either have Derived equal to No or Source or Root Variable starts with the string See.

Show Coding Hint

You can use the str_detect function to determine whether a string includes particular string as a component.

Show Answer 
dictionary %>% 
  filter(Derived == "No" & str_detect(`Source or Root Variable`, "See") == FALSE) %>%  
  select(`Source or Root Variable`) %>% 
  unique()
## # A tibble: 26 × 1
##    `Source or Root Variable`                    
##    <chr>                                        
##  1 HUD                                          
##  2 HUD PIT                                      
##  3 HUD System Performance Measures              
##  4 HUD CoC Funding Reports                      
##  5 HUD HIC                                      
##  6 Census Intercensal Population Estimates      
##  7 Census ACS 5-Year Estimates                  
##  8 Federal Housing Finance Agency               
##  9 BLS Local Area Unemployment Statistics (LAUS)
## 10 Census (County Area in Sq. Miles)            
## # … with 16 more rows


What are the sources of most of the data?

\(\rightarrow\) Make a bar graph of the counts of different data sources described in Source or Root Variable. Your graph should have the following features:

  1. Order the bars in descending order based on the count.
  2. Only include the 10 most common data sources.
  3. Orient the plot so that it is easy to read the labels.
Show Coding Hint

Use the fct_reorder to reorder the bars. Use head to limit the number of bars shown.

Show Answer 
dictionary %>% 
  count(`Source or Root Variable`) %>% 
  mutate(`Source or Root Variable` = fct_reorder(`Source or Root Variable`, n)) %>% 
  head(10) %>% 
  ggplot(aes(x = `Source or Root Variable`, y = n)) +
  labs(x = "Source or Root Variable", y = "Count") +
  geom_col() +
  coord_flip()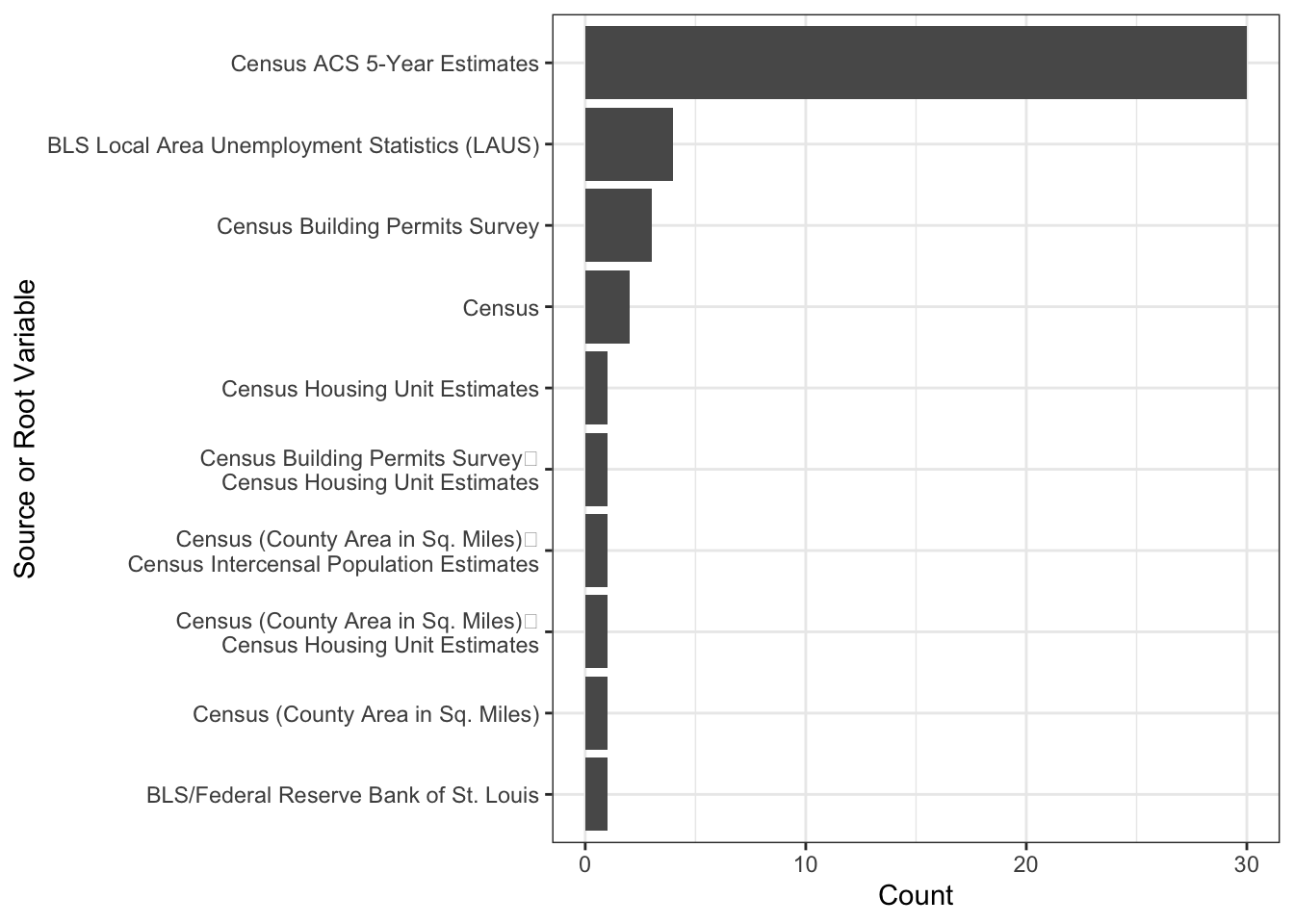

The most common source of data is the Census.


\(\rightarrow\) What are the different Associated Domains of the variables?

Show Answer 
dictionary %>% 
  count(`Associated Domain`) %>% 
  mutate(`Associated Domain` = fct_reorder(`Associated Domain`, n)) %>% 
  ggplot(aes(x = `Associated Domain`, y = n/sum(n))) +
  geom_col() +
  scale_y_continuous(labels = scales::percent) +
  labs(x = "Associated Domain", y = "Percentage") +
  coord_flip()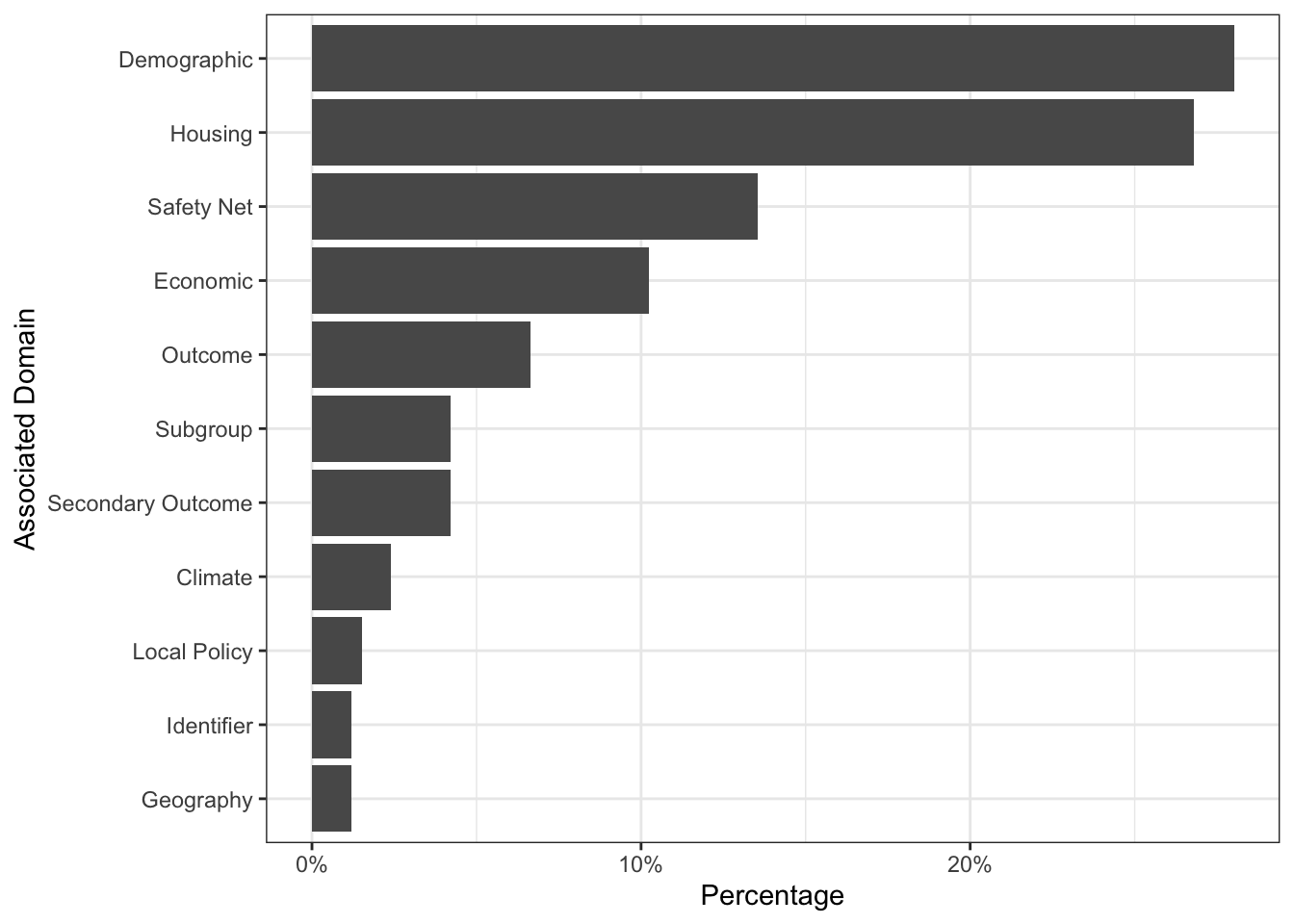

We see that there are 10 types of variables, plus an identifier. We also see that there are many demographic, housing, safety net, and economic variables. Demographic and housing variables make up more than 50% of the variables.


A big part of this project will be figuring out what variables to include in the analysis.

3.2.3 Data ethics

3.2.3.1 Data Science Ethics Checklist

Deon badge

A. Problem Formulation

  • A.1 Well-Posed Problem: Is it possible to answer our question with data? Is the problem well-posed?

B. Data Collection

  • B.1 Informed consent: If there are human subjects, have they given informed consent, where subjects affirmatively opt-in and have a clear understanding of the data uses to which they consent?
  • B.2 Collection bias: Have we considered sources of bias that could be introduced during data collection and survey design and taken steps to mitigate those?
  • B.3 Limit PII exposure: Have we considered ways to minimize exposure of personally identifiable information (PII) for example through anonymization or not collecting information that isn’t relevant for analysis?
  • B.4 Downstream bias mitigation: Have we considered ways to enable testing downstream results for biased outcomes (e.g., collecting data on protected group status like race or gender)?

C. Data Storage

  • C.1 Data security: Do we have a plan to protect and secure data (e.g., encryption at rest and in transit, access controls on internal users and third parties, access logs, and up-to-date software)?
  • C.2 Right to be forgotten: Do we have a mechanism through which an individual can request their personal information be removed?
  • C.3 Data retention plan: Is there a schedule or plan to delete the data after it is no longer needed?

D. Analysis

  • D.1 Missing perspectives: Have we sought to address blindspots in the analysis through engagement with relevant stakeholders (e.g., checking assumptions and discussing implications with affected communities and subject matter experts)?
  • D.2 Dataset bias: Have we examined the data for possible sources of bias and taken steps to mitigate or address these biases (e.g., stereotype perpetuation, confirmation bias, imbalanced classes, or omitted confounding variables)?
  • D.3 Honest representation: Are our visualizations, summary statistics, and reports designed to honestly represent the underlying data?
  • D.4 Privacy in analysis: Have we ensured that data with PII are not used or displayed unless necessary for the analysis?
  • D.5 Auditability: Is the process of generating the analysis well documented and reproducible if we discover issues in the future?

E. Modeling

  • E.1 Proxy discrimination: Have we ensured that the model does not rely on variables or proxies for variables that are unfairly discriminatory?
  • E.2 Fairness across groups: Have we tested model results for fairness with respect to different affected groups (e.g., tested for disparate error rates)?
  • E.3 Metric selection: Have we considered the effects of optimizing for our defined metrics and considered additional metrics?
  • E.4 Explainability: Can we explain in understandable terms a decision the model made in cases where a justification is needed?
  • E.5 Communicate bias: Have we communicated the shortcomings, limitations, and biases of the model to relevant stakeholders in ways that can be generally understood?

F. Deployment

  • F.1 Redress: Have we discussed with our organization a plan for response if users are harmed by the results (e.g., how does the data science team evaluate these cases and update analysis and models to prevent future harm)?
  • F.2 Roll back: Is there a way to turn off or roll back the model in production if necessary?
  • F.3 Concept drift: Do we test and monitor for concept drift to ensure the model remains fair over time?
  • F.4 Unintended use: Have we taken steps to identify and prevent unintended uses and abuse of the model and do we have a plan to monitor these once the model is deployed?

Data Science Ethics Checklist generated with deon.

We will discuss these issues in class.

3.3 Data Preparation

3.3.1 Load the data

The HUD data set is contained in the file 05b_analysis_file_update.csv.

\(\rightarrow\) Load the data set contained in the file 05b_analysis_file_update.csv and name the data frame df.

Show Coding Hint

Use read_csv

Show Answer 
df <- read_csv("05b_analysis_file_update.csv")
## Rows: 3008 Columns: 332
## ── Column specification ─────────────────────────────────────────────────────────────────────────────────────
## Delimiter: ","
## chr   (2): cocnumber, state_abr
## dbl (329): year, pit_tot_shelt_pit_hud, pit_tot_unshelt_pit_hud, pit_tot_hless_pit_hud, pit_ind_shelt_pit...
## lgl   (1): dem_health_ins_acs5yr_2012
## 
## ℹ Use `spec()` to retrieve the full column specification for this data.
## ℹ Specify the column types or set `show_col_types = FALSE` to quiet this message.

Note that we used read_csv, rather than read.csv because read_csv loads the data as a tibble.


3.3.2 Explore the contents of the data set

\(\rightarrow\) Look at the first few rows of the data frame.

Show Coding Hint

You can use the functions head or glimpse to see the head of the data frame or the function skim to get a nice summary.

Show Answer 
head(df)
## # A tibble: 6 × 332
##    year cocnumber pit_tot_shelt_pit_hud pit_tot_unshelt_p… pit_tot_hless_p… pit_ind_shelt_p… pit_ind_unshelt…
##   <dbl> <chr>                     <dbl>              <dbl>            <dbl>            <dbl>            <dbl>
## 1  2010 AK-500                     1113                118             1231              633              107
## 2  2011 AK-500                     1082                141             1223              677              117
## 3  2012 AK-500                     1097                 50             1147              756               35
## 4  2013 AK-500                     1070                 52             1122              792               52
## 5  2014 AK-500                      970                 53             1023              688               48
## 6  2015 AK-500                     1029                179             1208              679              158
## # … with 325 more variables: pit_ind_hless_pit_hud <dbl>, pit_perfam_shelt_pit_hud <dbl>,
## #   pit_perfam_unshelt_pit_hud <dbl>, pit_perfam_hless_pit_hud <dbl>, pit_ind_chronic_hless_pit_hud <dbl>,
## #   pit_perfam_chronic_hless_pit_hud <dbl>, pit_vet_hless_pit_hud <dbl>, econ_urb_urbanicity <dbl>,
## #   coctag <dbl>, panelvar <dbl>, hou_pol_totalind_hud <dbl>, hou_pol_totalday_hud <dbl>,
## #   hou_pol_totalexit_hud <dbl>, hou_pol_numret6mos_hud <dbl>, hou_pol_numret12mos_hud <dbl>,
## #   hou_pol_fedfundcoc <dbl>, hou_pol_fund_project <dbl>, hou_pol_bed_es_hic_hud <dbl>,
## #   hou_pol_bed_oph_hic_hud <dbl>, hou_pol_bed_psh_hic_hud <dbl>, hou_pol_bed_rrh_hic_hud <dbl>, …

We see that there are many columns in the data frame (332!), so it will not be easy to make sense of the data set without the data dictionary.

Refer to the data dictionary and the HUD report to understand what variables are present.

3.3.2.1 Explore the columns

What are the variables?

What variable(s) do we want to predict?

What variables seem useful as predictors?

What predictor variables are redundant?

It will take a significant amount of work to understand the contents of the data set. We will discuss this in class.

3.3.2.2 Select a subset of columns

Below are suggested variables to keep in the analysis. You may include other variables that might be useful as predictors. Provide an explanation for why you kept the variables.

\(\rightarrow\) Construct the list variable_names that we will keep for the analysis.

#Search through data dictionary to find other variables to include


variable_names <- c("year", "cocnumber",
  
  "pit_tot_hless_pit_hud", "pit_tot_shelt_pit_hud", "pit_tot_unshelt_pit_hud","dem_pop_pop_census",
  
  "fhfa_hpi_2009", "ln_hou_mkt_medrent_xt", "hou_mkt_utility_xt", "hou_mkt_burden_own_acs5yr_2017", "hou_mkt_burden_sev_rent_acs_2017", "hou_mkt_rentshare_acs5yr_2017", "hou_mkt_rentvacancy_xt", "hou_mkt_density_dummy", "hou_mkt_evict_count", "hou_mkt_ovrcrowd_acs5yr_2017", "major_city", "suburban",
           
           "econ_labor_unemp_rate_BLS", "econ_labor_incineq_acs5yr_2017", "econ_labor_pov_pop_census_share",
           
           "hou_pol_hudunit_psh_hud_share", "hou_pol_occhudunit_psh_hud", "hou_mkt_homeage1940_xt",
           
           "dem_soc_black_census", "dem_soc_hispanic_census", "dem_soc_asian_census", "dem_soc_pacific_census", "dem_pop_child_census", "dem_pop_senior_census", "dem_pop_female_census", "dem_pop_mig_census", "d_dem_pop_mig_census_share", "dem_soc_singadult_xt", "dem_soc_singparent_xt", "dem_soc_vet_xt", "dem_soc_ed_lessbach_xt", "dem_health_cost_dart",
           "dem_health_excesdrink_chr",
           
           "env_wea_avgtemp_noaa", "env_wea_avgtemp_summer_noaa", "env_wea_precip_noaa", "env_wea_precip_annual_noaa")

\(\rightarrow\) Select this subset of variables from the full data set. Call the new data frame df_small.

Coding Hint

Use the select function and your variable_names list. You should use all_of(variable_names). See https://tidyselect.r-lib.org/reference/faq-external-vector.html for an explanation of why we use all_of().

Show Answer 
df_small <- df %>% 
  select(all_of(variable_names))

#See https://tidyselect.r-lib.org/reference/faq-external-vector.html for an explanation of
#why we use all_of()


\(\rightarrow\) Examine the head of the new, smaller data frame.

Show Answer 
head(df_small)
## # A tibble: 6 × 43
##    year cocnumber pit_tot_hless_pit_hud pit_tot_shelt_pit_hud pit_tot_unshelt… dem_pop_pop_cen… fhfa_hpi_2009
##   <dbl> <chr>                     <dbl>                 <dbl>            <dbl>            <dbl>         <dbl>
## 1  2010 AK-500                     1231                  1113              118           285194       0      
## 2  2011 AK-500                     1223                  1082              141           293370       0.00936
## 3  2012 AK-500                     1147                  1097               50           296291      -0.0491 
## 4  2013 AK-500                     1122                  1070               52           298520      -0.255  
## 5  2014 AK-500                     1023                   970               53           301081       3.17   
## 6  2015 AK-500                     1208                  1029              179           300296       7.33   
## # … with 36 more variables: ln_hou_mkt_medrent_xt <dbl>, hou_mkt_utility_xt <dbl>,
## #   hou_mkt_burden_own_acs5yr_2017 <dbl>, hou_mkt_burden_sev_rent_acs_2017 <dbl>,
## #   hou_mkt_rentshare_acs5yr_2017 <dbl>, hou_mkt_rentvacancy_xt <dbl>, hou_mkt_density_dummy <dbl>,
## #   hou_mkt_evict_count <dbl>, hou_mkt_ovrcrowd_acs5yr_2017 <dbl>, major_city <dbl>, suburban <dbl>,
## #   econ_labor_unemp_rate_BLS <dbl>, econ_labor_incineq_acs5yr_2017 <dbl>,
## #   econ_labor_pov_pop_census_share <dbl>, hou_pol_hudunit_psh_hud_share <dbl>,
## #   hou_pol_occhudunit_psh_hud <dbl>, hou_mkt_homeage1940_xt <dbl>, dem_soc_black_census <dbl>, …


\(\rightarrow\) Create a new dictionary for this subset of variables and use View to examine the contents.

Coding Hint

Use the filter function.

Show Answer 
#Create the smaller data dictionary
dictionary_small <- dictionary %>% 
  filter(Variable %in% variable_names) 
#View it
dictionary_small %>% 
  View()


How many variables of each Associated Domain are in the smaller data set?

\(\rightarrow\) Make a bar graph of the counts of different Associated Domain. Your graph should have the following features:

  1. Order the bars in descending order based on the count.
  2. Orient the plot so that it is easy to read the labels.
Show Answer 
dictionary_small %>% 
  count(`Associated Domain`) %>% 
  mutate(`Associated Domain` = fct_reorder(`Associated Domain`,n)) %>% 
  ggplot(aes(x = `Associated Domain`, y = n)) +
  geom_col() +
  labs(x = "Associated Domain", y = "Count") +
  coord_flip()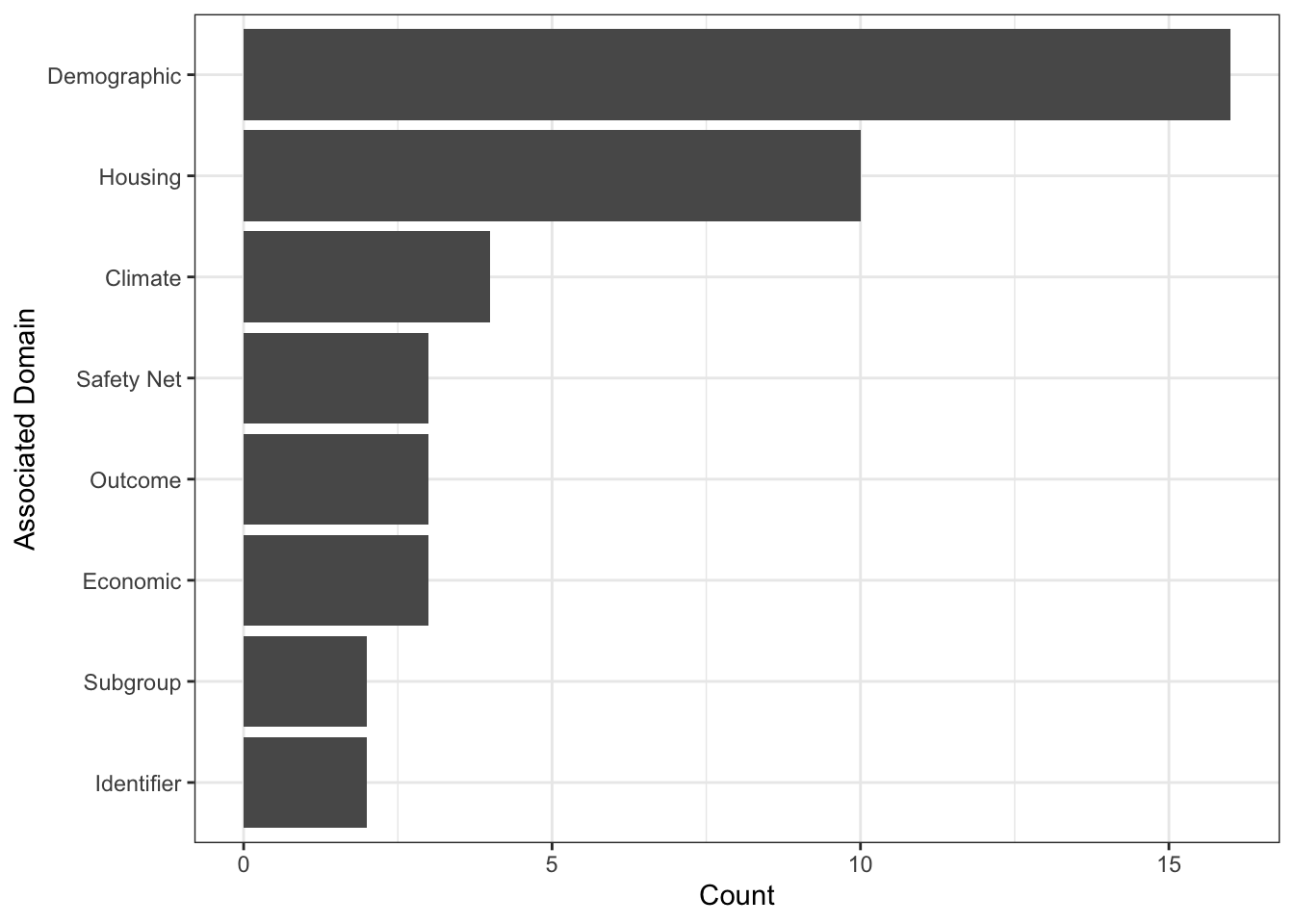

There are now 7 domains and an identifier. As with the full data frame, we have mostly demographic and housing variables.


3.3.3 Further exploration of basic properties

3.3.3.1 Check for a tidy data frame

In a tidy data set, each column is a variable or id and each row is an observation. It will take some work to determine whether the data set is tidy.

It was difficult to assess whether the full data frame was tidy because of the large number of columns with confusing names. We will do the analysis on the smaller data frame.

Show Answer

Each column is a variable or id and each row is an observation, so the data frame is tidy. We are benefiting from some of the pre-processing that HUD did with the data.


\(\rightarrow\) How many observations are in the data set?

Show Answer 
nrow(df_small)
## [1] 3008

There are 3008 observations.


3.3.4 Data cleaning

3.3.4.1 Rename variables

I used the data dictionary to create more readable names for the minimal set of variables. You should add in new names for the additional variables you included in the data set.

The data frame with renamed columns is called df_hud.

#Add your new names to this list. If you add variable names, the order of the variables in the dictionay_small will change and you will need to reassign the numbers.

df_hud <- df_small %>% 
  rename(coc_number = dictionary_small$Variable[2],
    total_sheltered = dictionary_small$Variable[3],
total_unsheltered = dictionary_small$Variable[4],
total_homeless = dictionary_small$Variable[5],
total_population = dictionary_small$Variable[6],
total_female_population = dictionary_small$Variable[7],
total_population_0_19 = dictionary_small$Variable[8],
total_population_65_plus = dictionary_small$Variable[9],
total_black = dictionary_small$Variable[10],
total_asian = dictionary_small$Variable[11],
total_pacific_islander = dictionary_small$Variable[12],
total_latino_hispanic = dictionary_small$Variable[13],
house_price_index_2009 = dictionary_small$Variable[14],
rate_unemployment = dictionary_small$Variable[15],
net_migration = dictionary_small$Variable[16],
HUD_unit_occupancy_rate = dictionary_small$Variable[17],
number_eviction = dictionary_small$Variable[18],
percentage_excessive_drinking = dictionary_small$Variable[19],
medicare_reimbursements_per_enrollee = dictionary_small$Variable[20],
average_summer_temperature = dictionary_small$Variable[21],
total_annual_precipitation = dictionary_small$Variable[22],
average_Jan_temperature = dictionary_small$Variable[23],
total_Jan_precipitation = dictionary_small$Variable[24],
gini_coefficient_2016 = dictionary_small$Variable[25],
poverty_rate = dictionary_small$Variable[26],
share_renters_2016 = dictionary_small$Variable[27],
share_overcrowded_units_2016 = dictionary_small$Variable[28],
percentage_owners_cost_burden_2016 = dictionary_small$Variable[29],
percentage_renters_severe_cost_burden_2016 = dictionary_small$Variable[30],
share_HUD_units = dictionary_small$Variable[31],
high_housing_density = dictionary_small$Variable[32],
share_built_before_1940  = dictionary_small$Variable[33],
utility_costs  = dictionary_small$Variable[34],
rental_vacancy_rate = dictionary_small$Variable[35],
proportion_one_person_households  = dictionary_small$Variable[36],
share_under_18_with_single_parent = dictionary_small$Variable[37],
share_veteran_status = dictionary_small$Variable[38],
log_median_rent = dictionary_small$Variable[39],
migration_4_year_change  = dictionary_small$Variable[40],
share_no_bachelors = dictionary_small$Variable[41],
city_or_urban = dictionary_small$Variable[42],
suburban = dictionary_small$Variable[43]
)

\(\rightarrow\) Examine the head of the new data frame with the updated names:

Show Answer 
head(df_hud)
## # A tibble: 6 × 43
##    year coc_number total_homeless total_sheltered total_unsheltered total_population house_price_index_2009
##   <dbl> <chr>               <dbl>           <dbl>             <dbl>            <dbl>                  <dbl>
## 1  2010 AK-500               1231            1113               118           285194                0      
## 2  2011 AK-500               1223            1082               141           293370                0.00936
## 3  2012 AK-500               1147            1097                50           296291               -0.0491 
## 4  2013 AK-500               1122            1070                52           298520               -0.255  
## 5  2014 AK-500               1023             970                53           301081                3.17   
## 6  2015 AK-500               1208            1029               179           300296                7.33   
## # … with 36 more variables: log_median_rent <dbl>, utility_costs <dbl>,
## #   percentage_owners_cost_burden_2016 <dbl>, percentage_renters_severe_cost_burden_2016 <dbl>,
## #   share_renters_2016 <dbl>, rental_vacancy_rate <dbl>, high_housing_density <dbl>, number_eviction <dbl>,
## #   share_overcrowded_units_2016 <dbl>, city_or_urban <dbl>, suburban <dbl>, rate_unemployment <dbl>,
## #   gini_coefficient_2016 <dbl>, poverty_rate <dbl>, share_HUD_units <dbl>, HUD_unit_occupancy_rate <dbl>,
## #   share_built_before_1940 <dbl>, total_black <dbl>, total_latino_hispanic <dbl>, total_asian <dbl>,
## #   total_pacific_islander <dbl>, total_population_0_19 <dbl>, total_population_65_plus <dbl>, …


\(\rightarrow\) Display the names of the columns of the new data frame:

Show Answer 
names(df_hud)
##  [1] "year"                                       "coc_number"                                
##  [3] "total_homeless"                             "total_sheltered"                           
##  [5] "total_unsheltered"                          "total_population"                          
##  [7] "house_price_index_2009"                     "log_median_rent"                           
##  [9] "utility_costs"                              "percentage_owners_cost_burden_2016"        
## [11] "percentage_renters_severe_cost_burden_2016" "share_renters_2016"                        
## [13] "rental_vacancy_rate"                        "high_housing_density"                      
## [15] "number_eviction"                            "share_overcrowded_units_2016"              
## [17] "city_or_urban"                              "suburban"                                  
## [19] "rate_unemployment"                          "gini_coefficient_2016"                     
## [21] "poverty_rate"                               "share_HUD_units"                           
## [23] "HUD_unit_occupancy_rate"                    "share_built_before_1940"                   
## [25] "total_black"                                "total_latino_hispanic"                     
## [27] "total_asian"                                "total_pacific_islander"                    
## [29] "total_population_0_19"                      "total_population_65_plus"                  
## [31] "total_female_population"                    "net_migration"                             
## [33] "migration_4_year_change"                    "proportion_one_person_households"          
## [35] "share_under_18_with_single_parent"          "share_veteran_status"                      
## [37] "share_no_bachelors"                         "medicare_reimbursements_per_enrollee"      
## [39] "percentage_excessive_drinking"              "average_Jan_temperature"                   
## [41] "average_summer_temperature"                 "total_Jan_precipitation"                   
## [43] "total_annual_precipitation"

Renaming the variables is a huge pain, but I find that it helps me to understand what the variables represent. This is useful for projects where you will spend a significant amount of time with the data.


3.3.5 Identify and deal with missing values

\(\rightarrow\) How many missing values are there in each column? Give the number of missing values and the percent of values in each column that are missing.

Show Coding Hing

The skim function shows the number of missing values and the completion rate for each column. You can also use skim_without_charts to get the same information without the graphs.

Show Answer

Recall that missing values may be coded with NA, or they may be empty. We want to convert empty cells to NA, so that we can use the function is.na to find all missing values. The function read_csv that we used to read in the data does this automatically, so we do not need to take further action to deal with empty cells. Note that the default argument in read_csv that controls this is na = c("", "NA"), which means that empty cells or NA values are treated as NA.

skim_without_charts(df_hud)
Table 3.1: Data summary
Name df_hud
Number of rows 3008
Number of columns 43
_______________________
Column type frequency:
character 1
numeric 42
________________________
Group variables None

Variable type: character

skim_variable n_missing complete_rate min max empty n_unique whitespace
coc_number 0 1 6 7 0 376 0

Variable type: numeric

skim_variable n_missing complete_rate mean sd p0 p25 p50 p75 p100
year 0 1.00 2013.50 2.29 2010.00 2011.75 2013.50 2015.25 2017.00
total_homeless 14 1.00 1560.43 4313.39 7.00 320.25 679.00 1468.00 76501.00
total_sheltered 14 1.00 1033.85 3445.81 3.00 224.00 445.50 961.50 72565.00
total_unsheltered 14 1.00 526.58 1742.31 0.00 36.25 114.00 418.25 42828.00
total_population 0 1.00 837457.01 1217309.59 29344.00 266710.75 481798.50 896909.25 11058958.00
house_price_index_2009 0 1.00 -2.74 10.14 -26.50 -8.61 -3.28 0.00 63.86
log_median_rent 1504 0.50 1.97 0.31 1.24 1.73 1.94 2.16 2.87
utility_costs 1504 0.50 14.66 3.10 5.60 12.60 14.80 16.90 22.60
percentage_owners_cost_burden_2016 0 1.00 14.87 3.04 8.07 12.48 14.39 17.08 22.96
percentage_renters_severe_cost_burden_2016 0 1.00 25.54 3.86 16.38 22.86 25.00 27.76 37.65
share_renters_2016 0 1.00 34.55 8.23 15.10 28.64 33.52 39.66 69.22
rental_vacancy_rate 1504 0.50 7.15 2.98 1.92 5.20 6.60 8.40 24.63
high_housing_density 0 1.00 0.25 0.43 0.00 0.00 0.00 0.25 1.00
number_eviction 0 1.00 2501.98 4314.93 0.00 96.75 935.50 2693.00 37105.00
share_overcrowded_units_2016 0 1.00 2.70 1.95 0.66 1.51 2.04 3.04 12.26
city_or_urban 0 1.00 0.28 0.45 0.00 0.00 0.00 1.00 1.00
suburban 0 1.00 0.43 0.49 0.00 0.00 0.00 1.00 1.00
rate_unemployment 0 1.00 7.48 2.70 2.51 5.51 7.18 8.94 28.86
gini_coefficient_2016 0 1.00 45.52 2.85 37.56 43.70 45.40 46.99 54.78
poverty_rate 0 1.00 14.42 4.46 3.35 11.45 14.32 17.31 35.79
share_HUD_units 0 1.00 3.65 1.92 0.09 2.32 3.30 4.69 13.96
HUD_unit_occupancy_rate 0 1.00 92.60 3.99 69.44 90.77 93.01 95.15 100.00
share_built_before_1940 1504 0.50 13.46 10.78 0.22 4.88 10.11 20.13 56.88
total_black 0 1.00 103606.65 202325.49 152.00 10567.00 36742.00 109931.25 1956449.00
total_latino_hispanic 0 1.00 142104.15 407635.29 224.00 14898.50 35744.50 92569.50 4924272.00
total_asian 0 1.00 42375.38 117157.23 80.00 4291.75 11239.50 30542.50 1474987.00
total_pacific_islander 0 1.00 1388.47 5558.70 1.00 117.00 259.00 642.25 89016.00
total_population_0_19 0 1.00 219436.13 329651.86 6194.00 67781.25 124462.00 234535.00 3204024.00
total_population_65_plus 0 1.00 117131.31 161665.55 4781.00 38146.75 66976.00 124377.25 1525916.00
total_female_population 0 1.00 425237.98 618118.92 14816.00 135979.25 244430.50 461586.00 5542088.00
net_migration 0 1.00 2458.73 8426.78 -41321.00 -719.00 492.50 3207.75 101369.00
migration_4_year_change 2632 0.12 0.07 0.68 -3.45 -0.26 0.02 0.36 2.60
proportion_one_person_households 1504 0.50 27.73 4.15 12.48 25.40 27.82 30.10 46.71
share_under_18_with_single_parent 1504 0.50 25.58 6.94 9.44 20.94 24.61 29.21 55.63
share_veteran_status 1504 0.50 10.89 3.05 2.80 8.96 10.78 12.66 23.88
share_no_bachelors 1504 0.50 69.69 10.30 23.69 64.34 71.09 77.36 88.64
medicare_reimbursements_per_enrollee 0 1.00 9.36 1.25 6.03 8.44 9.22 10.08 17.95
percentage_excessive_drinking 2632 0.12 0.19 0.03 0.11 0.17 0.19 0.21 0.29
average_Jan_temperature 0 1.00 35.36 12.85 -3.24 26.32 33.71 44.11 74.70
average_summer_temperature 2 1.00 74.05 6.17 55.80 69.54 73.90 78.74 93.25
total_Jan_precipitation 0 1.00 2.94 2.51 0.00 1.33 2.53 3.59 25.32
total_annual_precipitation 0 1.00 41.03 15.36 1.25 33.52 42.03 49.96 105.19

Most variables are not missing any values, but there are many variables that are missing half or more of the values.


We are interested in predicting the number of people experiencing homelessness. So, we will remove the rows where those numbers are missing.

\(\rightarrow\) Remove the rows where total_homeless is NA.

Show Coding Hint

Use the filter function.

Show Answer 
df_hud <- df_hud %>% 
  filter(is.na(total_homeless) == FALSE)
skim_without_charts(df_hud)
Table 3.2: Data summary
Name df_hud
Number of rows 2994
Number of columns 43
_______________________
Column type frequency:
character 1
numeric 42
________________________
Group variables None

Variable type: character

skim_variable n_missing complete_rate min max empty n_unique whitespace
coc_number 0 1 6 7 0 376 0

Variable type: numeric

skim_variable n_missing complete_rate mean sd p0 p25 p50 p75 p100
year 0 1.00 2013.50 2.29 2010.00 2012.00 2013.00 2015.00 2017.00
total_homeless 0 1.00 1560.43 4313.39 7.00 320.25 679.00 1468.00 76501.00
total_sheltered 0 1.00 1033.85 3445.81 3.00 224.00 445.50 961.50 72565.00
total_unsheltered 0 1.00 526.58 1742.31 0.00 36.25 114.00 418.25 42828.00
total_population 0 1.00 840371.32 1219259.79 29344.00 267388.75 484041.50 900588.25 11058958.00
house_price_index_2009 0 1.00 -2.72 10.15 -26.50 -8.60 -3.25 0.00 63.86
log_median_rent 1495 0.50 1.97 0.31 1.24 1.73 1.94 2.16 2.87
utility_costs 1495 0.50 14.65 3.11 5.60 12.60 14.80 16.90 22.60
percentage_owners_cost_burden_2016 0 1.00 14.87 3.04 8.07 12.48 14.39 17.07 22.96
percentage_renters_severe_cost_burden_2016 0 1.00 25.56 3.84 16.38 22.86 25.00 27.85 37.65
share_renters_2016 0 1.00 34.55 8.25 15.10 28.55 33.53 39.73 69.22
rental_vacancy_rate 1495 0.50 7.14 2.98 1.92 5.20 6.59 8.40 24.63
high_housing_density 0 1.00 0.25 0.43 0.00 0.00 0.00 1.00 1.00
number_eviction 0 1.00 2513.26 4321.83 0.00 107.50 941.50 2722.00 37105.00
share_overcrowded_units_2016 0 1.00 2.71 1.95 0.66 1.51 2.05 3.06 12.26
city_or_urban 0 1.00 0.28 0.45 0.00 0.00 0.00 1.00 1.00
suburban 0 1.00 0.43 0.49 0.00 0.00 0.00 1.00 1.00
rate_unemployment 0 1.00 7.48 2.71 2.51 5.50 7.18 8.94 28.86
gini_coefficient_2016 0 1.00 45.53 2.85 37.56 43.70 45.42 47.01 54.78
poverty_rate 0 1.00 14.42 4.47 3.35 11.43 14.32 17.31 35.79
share_HUD_units 0 1.00 3.66 1.91 0.09 2.32 3.29 4.70 13.96
HUD_unit_occupancy_rate 0 1.00 92.60 3.99 69.44 90.77 93.01 95.15 100.00
share_built_before_1940 1495 0.50 13.44 10.76 0.22 4.88 10.13 20.12 56.88
total_black 0 1.00 104005.74 202698.30 168.00 10750.00 36833.00 110397.25 1956449.00
total_latino_hispanic 0 1.00 142706.42 408490.87 224.00 15101.25 36013.00 93348.75 4924272.00
total_asian 0 1.00 42564.47 117398.02 80.00 4369.00 11316.50 30792.50 1474987.00
total_pacific_islander 0 1.00 1394.53 5570.97 1.00 117.00 259.50 646.50 89016.00
total_population_0_19 0 1.00 220205.33 330188.04 6194.00 67984.75 124752.50 235074.50 3204024.00
total_population_65_plus 0 1.00 117515.06 161921.65 5132.00 38351.75 67198.50 124875.25 1525916.00
total_female_population 0 1.00 426719.90 619107.26 14816.00 136479.75 246606.00 464249.50 5542088.00
net_migration 0 1.00 2470.68 8444.32 -41321.00 -720.50 501.50 3211.50 101369.00
migration_4_year_change 2620 0.12 0.07 0.68 -3.45 -0.26 0.02 0.36 2.60
proportion_one_person_households 1495 0.50 27.72 4.15 12.48 25.40 27.81 30.10 46.71
share_under_18_with_single_parent 1495 0.50 25.58 6.95 9.44 20.93 24.61 29.21 55.63
share_veteran_status 1495 0.50 10.89 3.06 2.80 8.96 10.78 12.68 23.88
share_no_bachelors 1495 0.50 69.66 10.30 23.69 64.25 71.08 77.35 88.64
medicare_reimbursements_per_enrollee 0 1.00 9.37 1.25 6.03 8.45 9.22 10.08 17.95
percentage_excessive_drinking 2620 0.12 0.19 0.03 0.11 0.17 0.19 0.21 0.29
average_Jan_temperature 0 1.00 35.37 12.87 -3.24 26.32 33.71 44.17 74.70
average_summer_temperature 2 1.00 74.06 6.18 55.80 69.54 73.92 78.74 93.25
total_Jan_precipitation 0 1.00 2.94 2.51 0.00 1.33 2.54 3.59 25.32
total_annual_precipitation 0 1.00 41.06 15.33 1.25 33.56 42.03 49.99 105.19


There are some variables that are missing many of their values.

\(\rightarrow\) Produce scatter plots of the variables that are missing many values vs. time to see if data are missing from particular years.

Show Answer

This is one example:

df_hud %>% 
  ggplot(aes(x = year, y = migration_4_year_change)) +
  geom_point()
## Warning: Removed 2620 rows containing missing values (geom_point).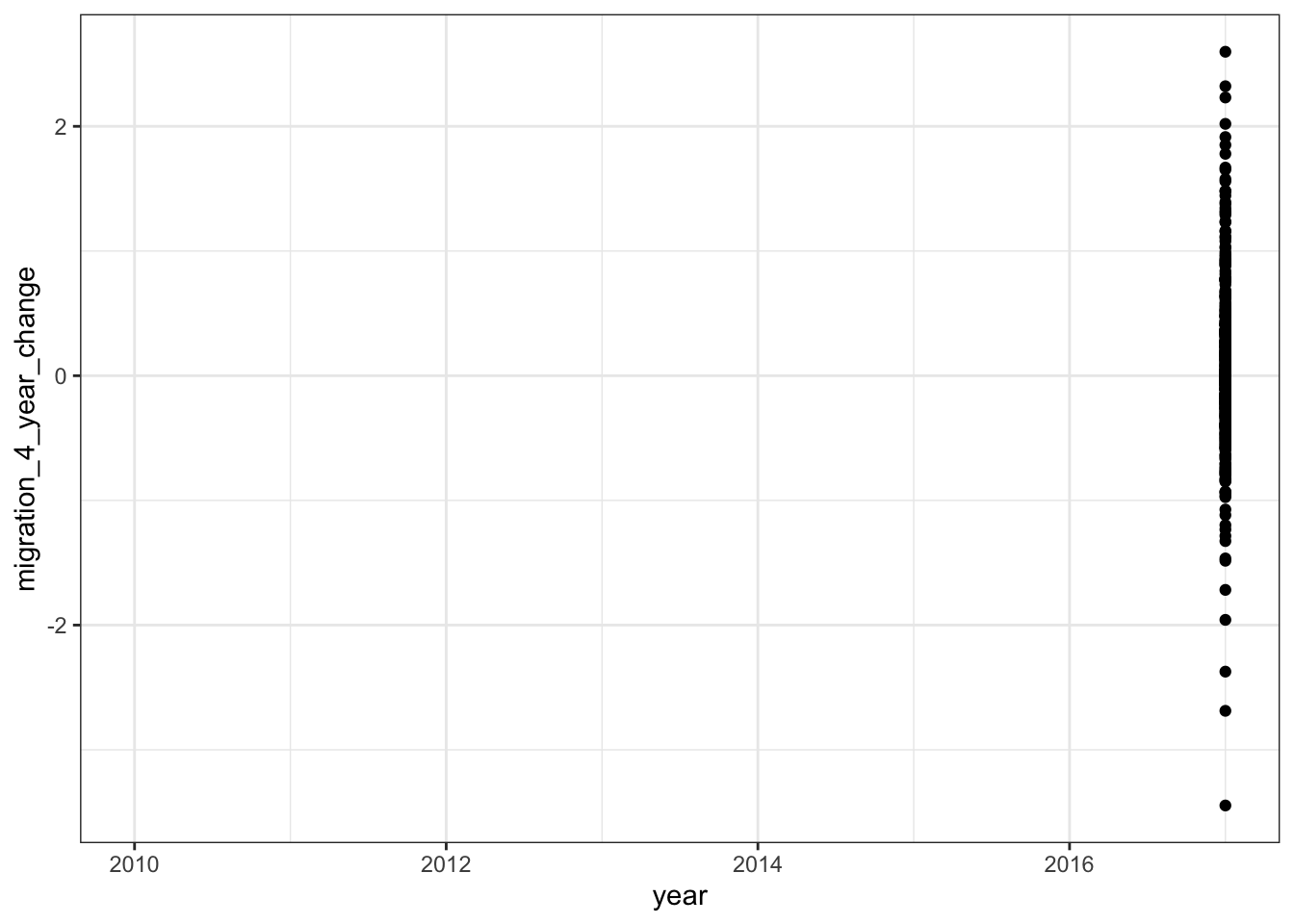

percentage_excessive_drinking and migration_4_year_change only have data from 2017. Following the analysis in the HUD report, we will focus on data from 2017.


\(\rightarrow\) Produce a data frame with data only from 2017. Call it df_2017.

Show Answer 
df_2017 <- df_hud %>% 
  filter(year == 2017)


\(\rightarrow\) Check for missing values in the 2017 data.

Show Answer 
skim_without_charts(df_2017)
Table 3.3: Data summary
Name df_2017
Number of rows 374
Number of columns 43
_______________________
Column type frequency:
character 1
numeric 42
________________________
Group variables None

Variable type: character

skim_variable n_missing complete_rate min max empty n_unique whitespace
coc_number 0 1 6 7 0 374 0

Variable type: numeric

skim_variable n_missing complete_rate mean sd p0 p25 p50 p75 p100
year 0 1 2017.00 0.00 2017.00 2017.00 2017.00 2017.00 2017.00
total_homeless 0 1 1466.07 5114.12 10.00 282.75 567.50 1203.00 76501.00
total_sheltered 0 1 961.68 3921.31 5.00 189.00 373.00 850.75 72565.00
total_unsheltered 0 1 504.39 2334.30 0.00 37.00 109.50 384.00 42828.00
total_population 0 1 862794.07 1257003.13 29344.00 271652.75 498140.50 924319.75 11058958.00
house_price_index_2009 0 1 6.90 14.68 -17.53 -2.61 3.12 13.51 63.86
log_median_rent 0 1 2.02 0.31 1.36 1.80 1.98 2.20 2.87
utility_costs 0 1 14.84 2.97 5.90 12.95 14.97 17.16 22.60
percentage_owners_cost_burden_2016 0 1 14.88 3.04 8.07 12.49 14.40 17.09 22.96
percentage_renters_severe_cost_burden_2016 0 1 25.55 3.87 16.38 22.89 25.00 27.82 37.65
share_renters_2016 0 1 34.57 8.26 15.10 28.58 33.53 39.71 69.22
rental_vacancy_rate 0 1 6.47 2.73 1.92 4.78 6.24 7.61 21.05
high_housing_density 0 1 0.25 0.44 0.00 0.00 0.00 1.00 1.00
number_eviction 0 1 2402.04 4297.43 0.00 75.75 854.50 2441.00 36357.00
share_overcrowded_units_2016 0 1 2.71 1.96 0.66 1.51 2.04 3.05 12.26
city_or_urban 0 1 0.28 0.45 0.00 0.00 0.00 1.00 1.00
suburban 0 1 0.43 0.50 0.00 0.00 0.00 1.00 1.00
rate_unemployment 0 1 5.00 1.57 2.51 4.14 4.90 5.57 23.64
gini_coefficient_2016 0 1 45.53 2.86 37.56 43.71 45.40 47.00 54.78
poverty_rate 0 1 13.41 4.14 3.50 10.50 13.23 16.08 25.56
share_HUD_units 0 1 3.53 1.84 0.09 2.24 3.22 4.57 11.86
HUD_unit_occupancy_rate 0 1 92.42 4.08 73.00 90.13 93.00 95.00 100.00
share_built_before_1940 0 1 13.04 10.52 0.26 4.58 9.91 19.21 56.01
total_black 0 1 107580.71 207495.53 244.00 11811.25 37467.50 113661.50 1909362.00
total_latino_hispanic 0 1 154259.52 431612.58 344.00 17374.50 39273.00 100622.25 4924272.00
total_asian 0 1 47716.18 128225.20 106.00 5367.00 12655.50 34762.75 1474987.00
total_pacific_islander 0 1 1512.28 5793.14 1.00 130.00 290.50 697.25 88323.00
total_population_0_19 0 1 219133.87 329833.51 6194.00 67203.00 125673.00 236132.50 3204024.00
total_population_65_plus 0 1 131381.43 180215.56 6218.00 42612.75 75493.50 138750.00 1525916.00
total_female_population 0 1 437977.63 638095.05 14823.00 137737.75 252411.00 473421.25 5542088.00
net_migration 0 1 3030.79 10140.42 -41321.00 -990.25 442.00 3645.50 91270.00
migration_4_year_change 0 1 0.07 0.68 -3.45 -0.26 0.02 0.36 2.60
proportion_one_person_households 0 1 28.00 4.17 12.48 25.54 28.18 30.34 44.69
share_under_18_with_single_parent 0 1 25.76 6.89 9.77 21.02 24.81 29.44 54.47
share_veteran_status 0 1 9.94 2.86 2.80 8.16 10.07 11.28 22.27
share_no_bachelors 0 1 68.89 10.45 23.69 63.02 70.41 76.62 88.37
medicare_reimbursements_per_enrollee 0 1 9.91 1.21 6.79 9.02 9.70 10.61 14.31
percentage_excessive_drinking 0 1 0.19 0.03 0.11 0.17 0.19 0.21 0.29
average_Jan_temperature 0 1 39.10 12.07 10.98 30.30 37.48 46.48 73.50
average_summer_temperature 0 1 75.16 5.87 59.55 71.27 75.23 79.67 93.25
total_Jan_precipitation 0 1 4.39 3.68 0.21 2.47 3.39 4.70 25.32
total_annual_precipitation 0 1 39.43 13.69 3.06 33.84 38.58 45.04 96.34

There are no missing values! We will do our analysis on the 2017 data set.


3.4 Exploratory data analysis

We have two main goals when doing exploratory data analysis. The first is that we want to understand the data set more completely. The second goal is to explore relationships between the variables to help guide the modeling process to answer our specific question.

3.4.1 Graphical summaries

3.4.1.1 Look at the distributions of the homeless counts

\(\rightarrow\) Make a histogram of the total number of homeless in 2017.

Show Answer 
df_2017 %>% 
  ggplot(aes(x = total_homeless)) +
  geom_histogram(boundary = 0) +
  labs(x = "Total homeless", y = "Count")
## `stat_bin()` using `bins = 30`. Pick better value with `binwidth`.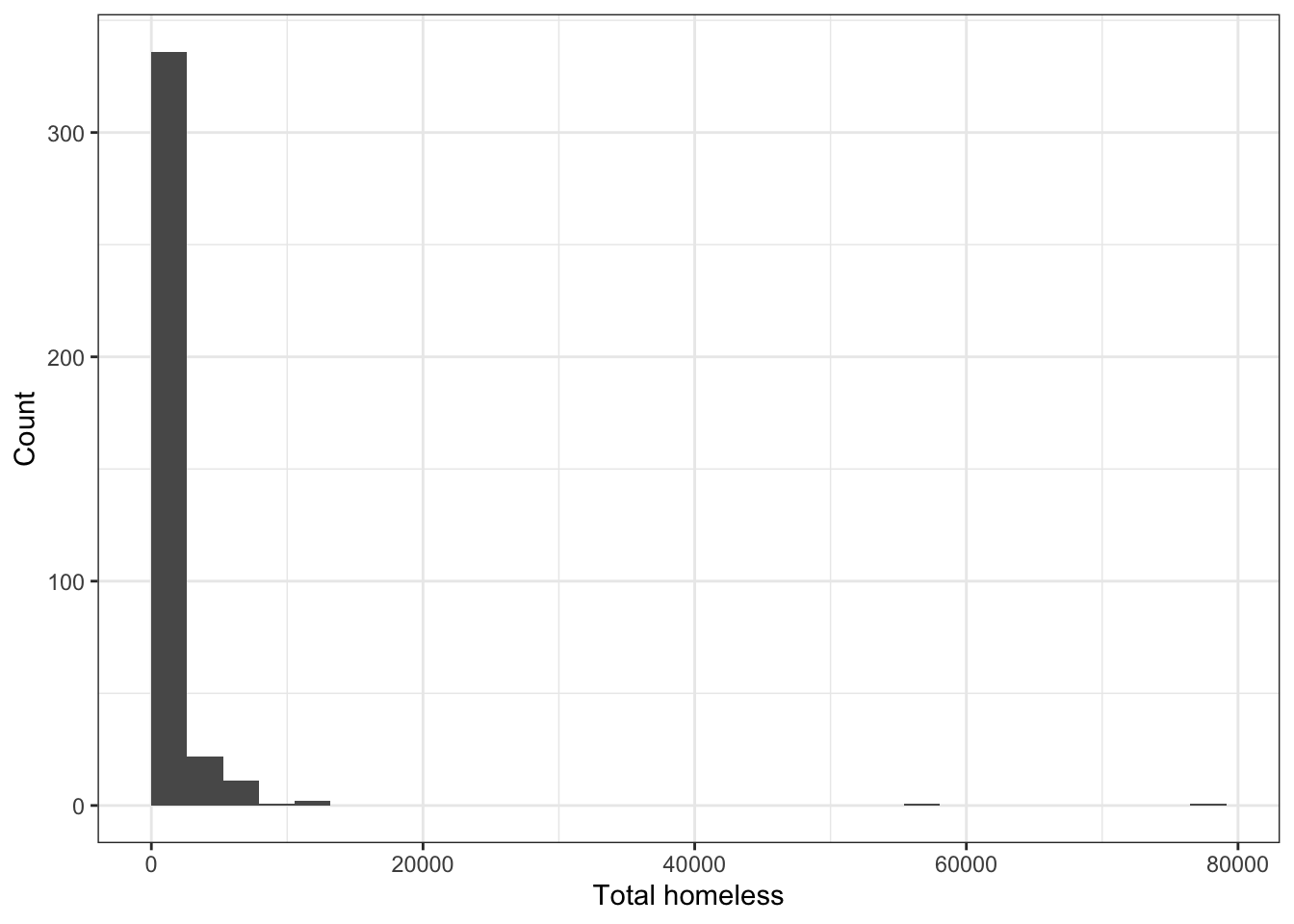

It appears that there are some outliers, but it can be hard to see because of the limits of the y-axis. We can limit the y-axis values to get a better view of the small bars.

df_2017 %>% 
  ggplot(aes(x = total_homeless)) +
  geom_histogram(boundary = 0) +
  labs(x = "Total homeless", y = "Count") +
  coord_cartesian(ylim = c(0, 15)) 
## `stat_bin()` using `bins = 30`. Pick better value with `binwidth`.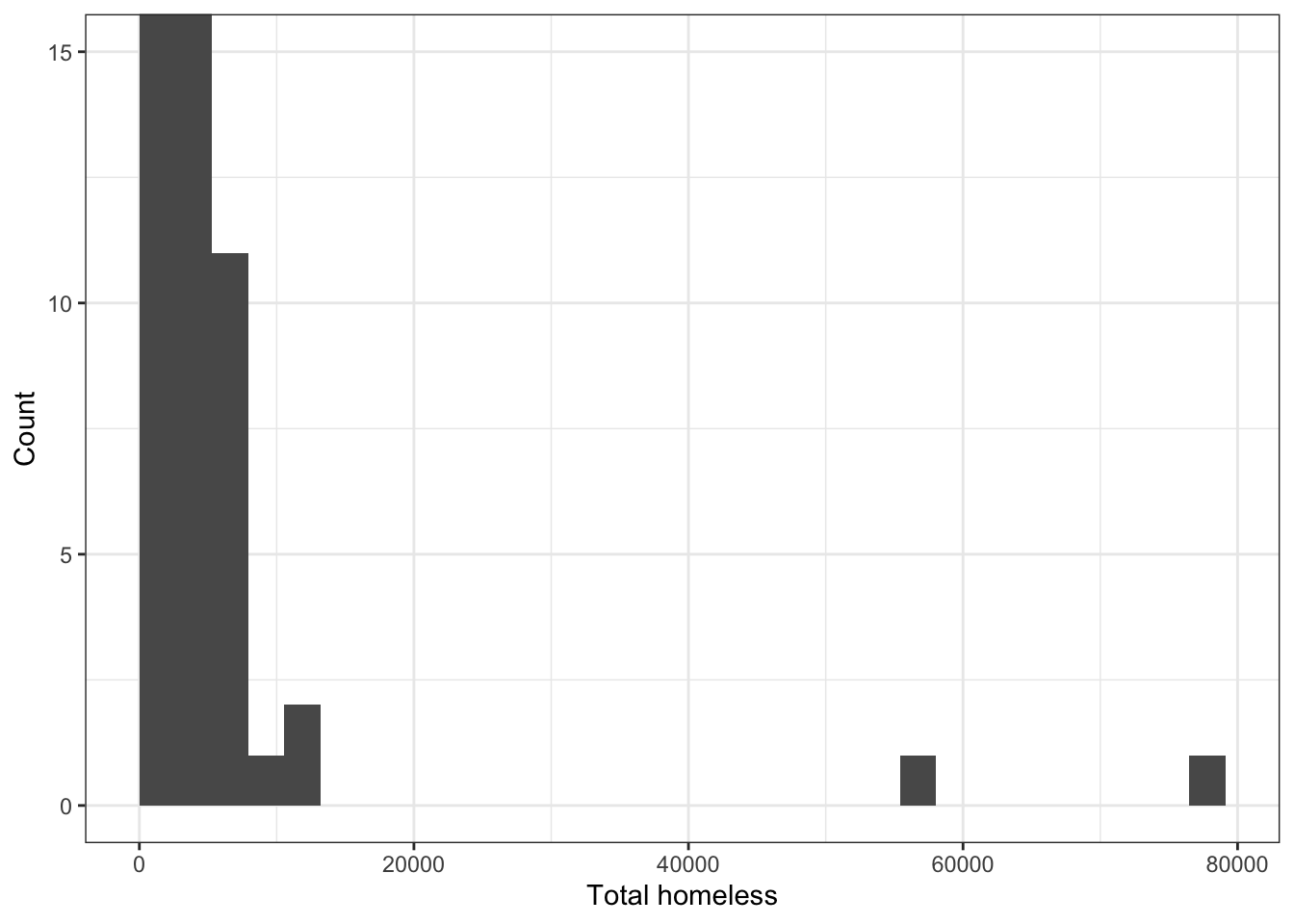

There are some large outliers because there is a wide range of populations among the areas represented in the data set. We can see this by making a histogram of total_population.

df_2017 %>% 
  ggplot(aes(x = total_population)) +
  geom_histogram(boundary = 0) +
  labs(x = "Total population", y = "Count")
## `stat_bin()` using `bins = 30`. Pick better value with `binwidth`.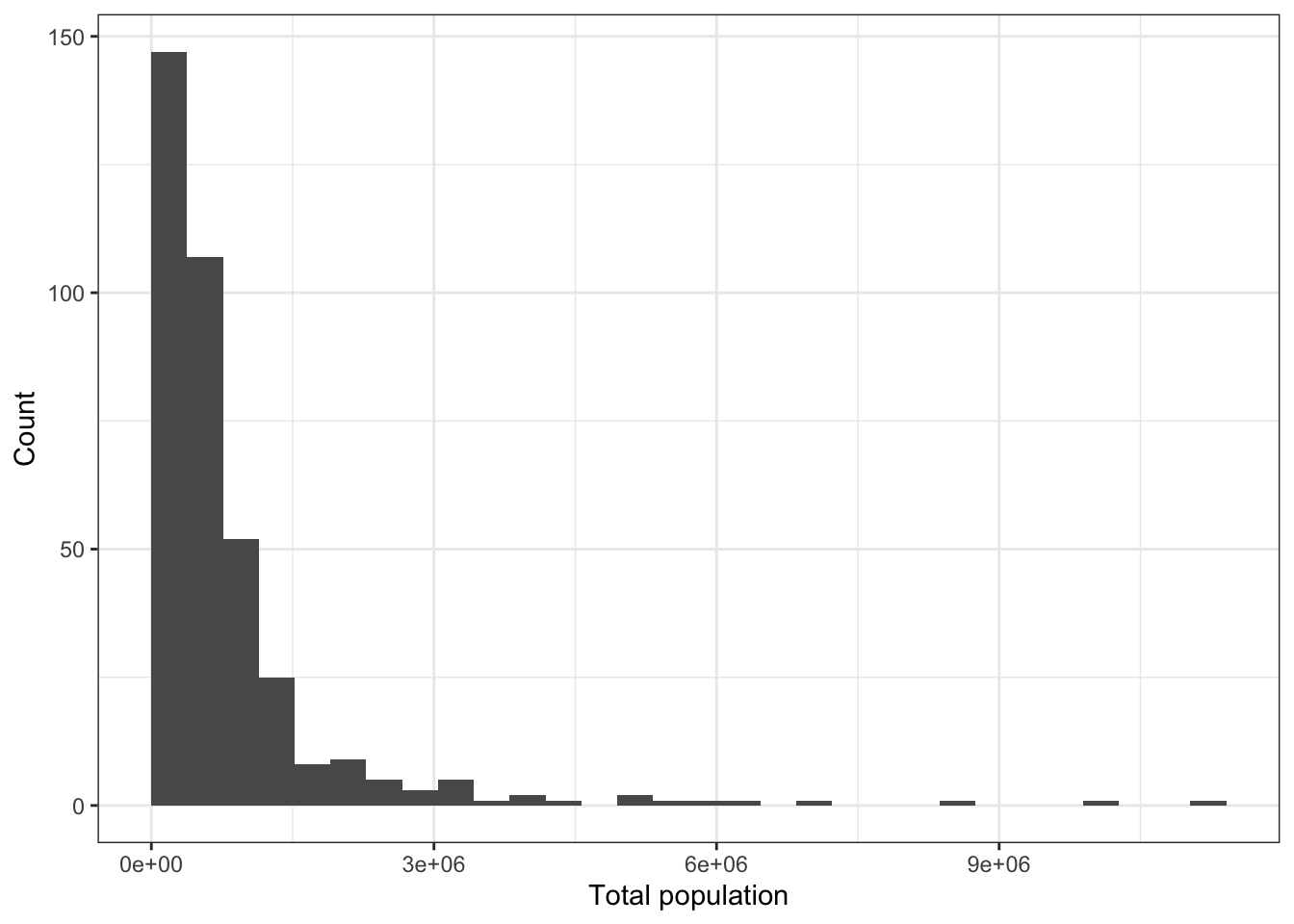


\(\rightarrow\) Make a histogram of the number of sheltered homeless in 2017.

Show Answer 
df_2017 %>% 
  ggplot(aes(x = total_sheltered)) +
  geom_histogram(boundary = 0) +
  labs(x = "Sheltered homeless", y = "Count") 
## `stat_bin()` using `bins = 30`. Pick better value with `binwidth`.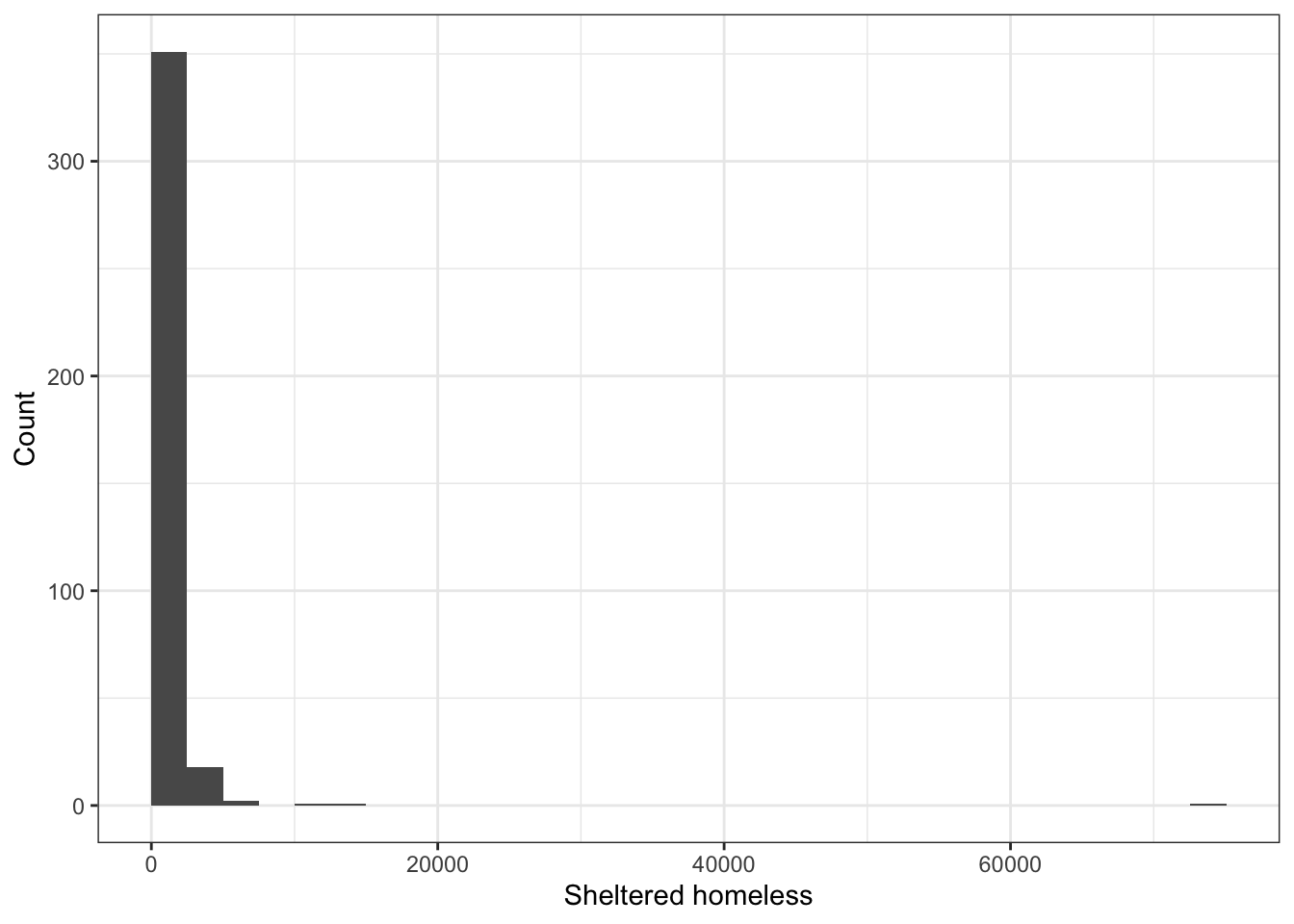


\(\rightarrow\) Make a histogram of the number of unsheltered homeless in 2017.

Show Answer 
df_2017 %>% 
  ggplot(aes(x = total_unsheltered)) +
  geom_histogram(boundary = 0) +
  labs(x = "Unsheltered homeless", y = "Count") 
## `stat_bin()` using `bins = 30`. Pick better value with `binwidth`.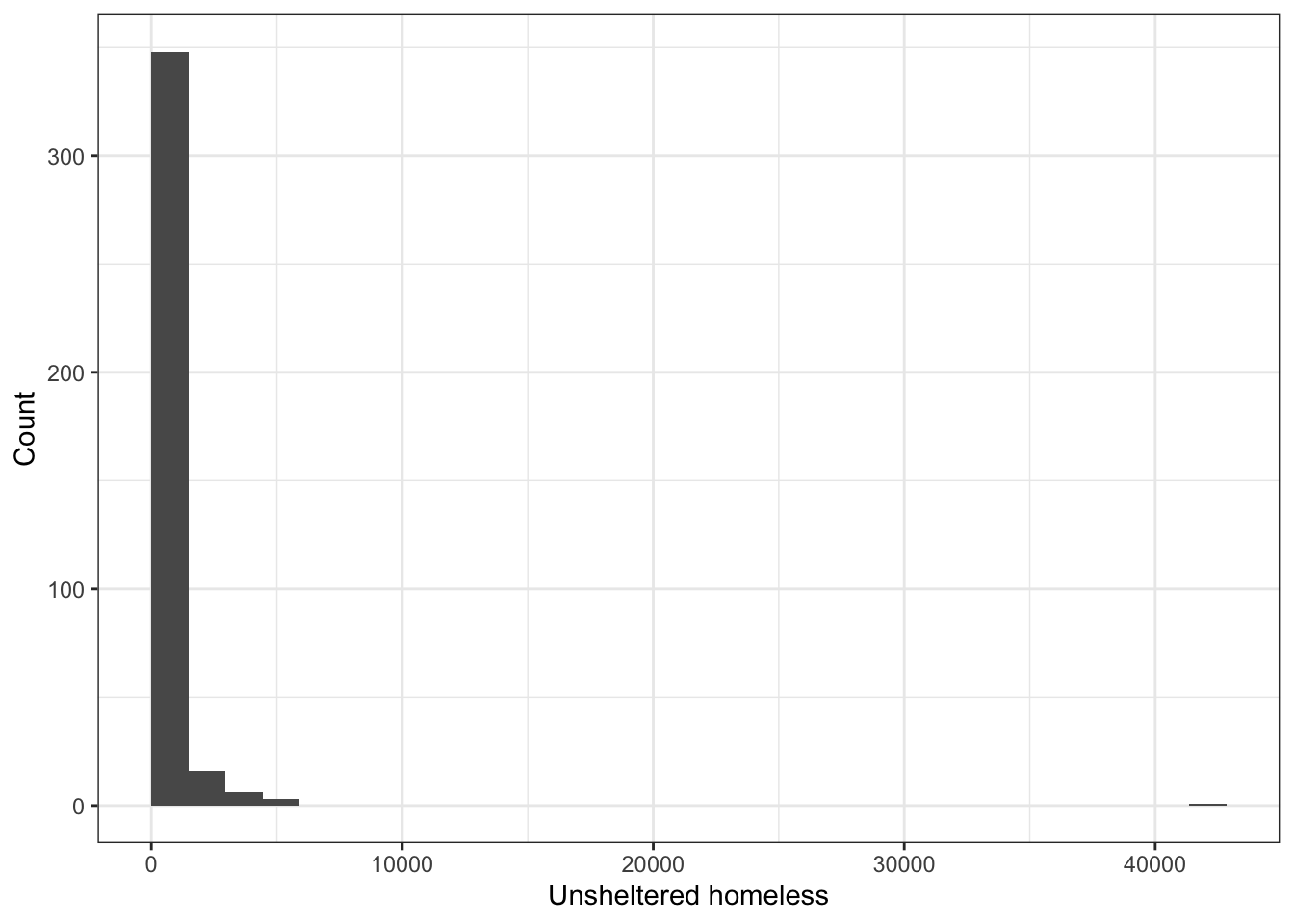


Converting the total counts to rates relative to population size should remove extreme outliers.

\(\rightarrow\) Use the mutate function to create a new variable rate_homeless that is the total number of homeless per 10,000 people in the population and make a histogram of rate_homeless.

Show Answer 
df_2017 %>% 
  mutate(rate_homeless = total_homeless/(total_population/10000)) %>% 
  ggplot(aes(x = rate_homeless)) +
  geom_histogram(boundary = 0) +
  labs(x = "Homeless rate per 10,000", y = "Count") 
## `stat_bin()` using `bins = 30`. Pick better value with `binwidth`.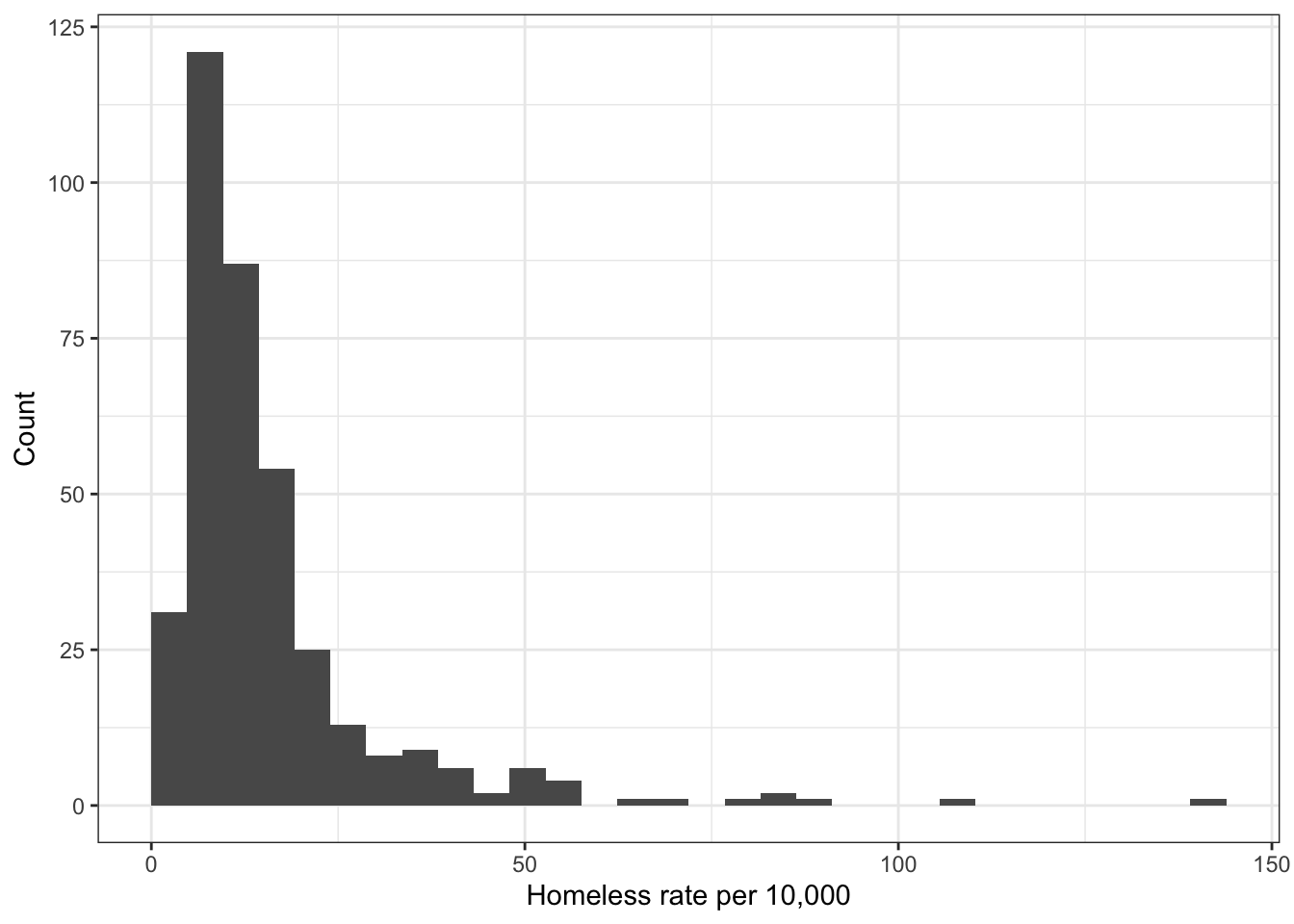


\(\rightarrow\) Compare boxplots of rate_homeless and total_homeless to visually assess whether outliers are less extreme in rate_homeless than in total_homeless.

Show Answer 
#Boxplot of rate_homeless
p1 <- df_2017 %>% 
  mutate(rate_homeless = total_homeless/(total_population/10000)) %>% 
  ggplot() +
  geom_boxplot(aes(y = rate_homeless))

#Boxplot of total_homeless
p2 <- df_2017 %>% 
  ggplot() +
  geom_boxplot(aes(y = total_homeless))

#Display as two panels in one graph
grid.arrange(p1, p2, nrow = 1)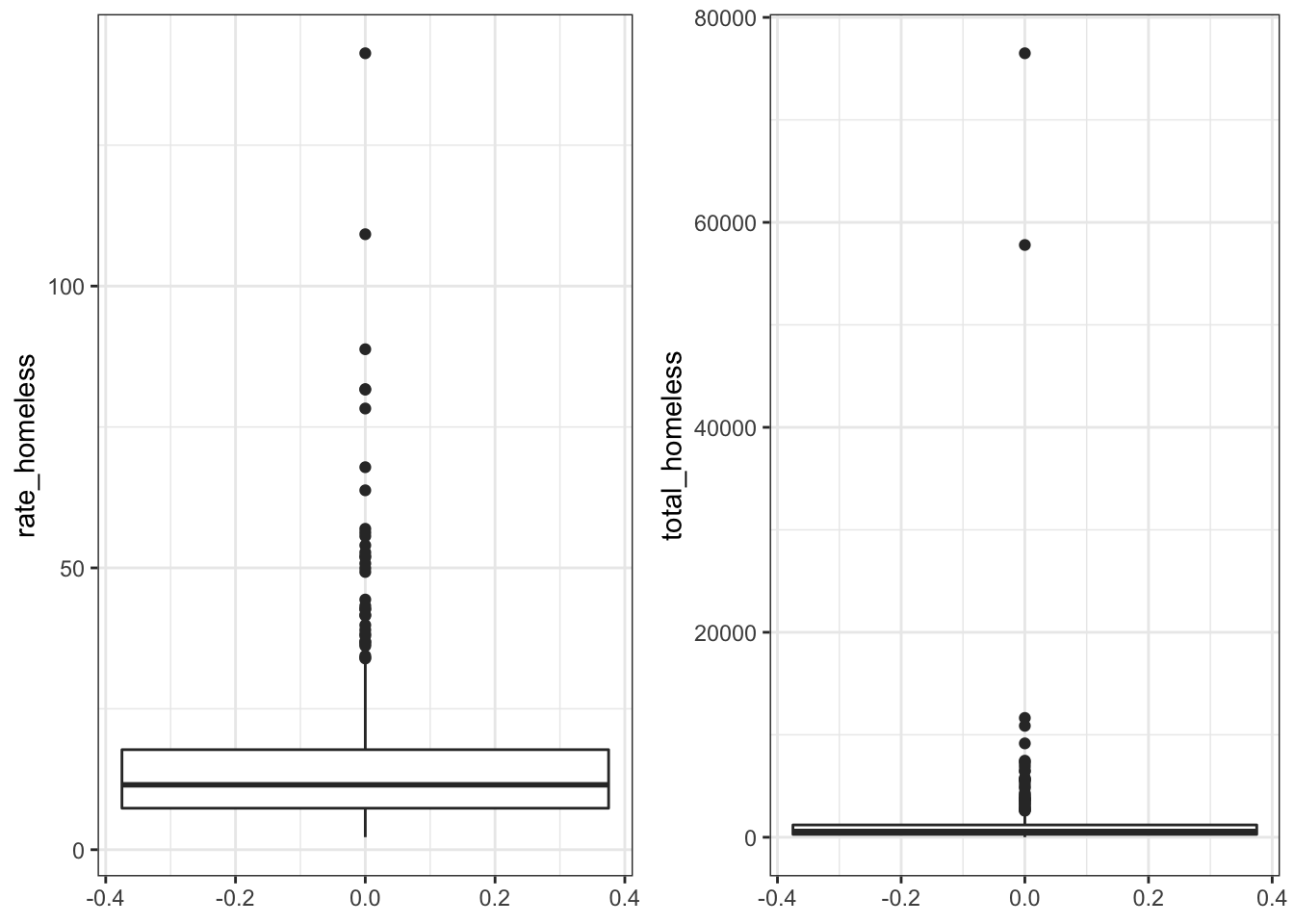

There are still points that are outliers in the rates, but they are not as extreme as in the totals.


3.4.1.2 Data processing

We will add rates to the data frame. Following the HUD report, we will produce rates per 10,000 people.

\(\rightarrow\) Use the mutate function to create new variables rate_homeless, rate_sheltered, and rate_unsheltered in the data frame df_2017 that are the counts per 10,000 people in the population.

Show Answer 
df_2017 <- df_2017 %>% 
  mutate(rate_sheltered = total_sheltered/(total_population/10000),
         rate_unsheltered = total_unsheltered/(total_population/10000),
         rate_homeless = total_homeless/(total_population/10000))


We should note that the demographic variables (race, gender, age) are given as total counts. We will also convert these totals to percentages.

\(\rightarrow\) Use the mutate function to create new demographics variables in the data frame df_2017 that are percentages of the total population.

Show Answer 
df_2017 <- df_2017 %>% 
  mutate(percent_black = total_black/total_population, 
  percent_latino_hispanic = total_latino_hispanic/total_population, 
  percent_asian = total_asian/total_population, 
  percent_pacific_islander = total_pacific_islander/total_population, 
  percent_population_0_19 = total_population_0_19/total_population, 
  percent_population_65_plus = total_population_65_plus/total_population,
  percent_female_population = total_female_population/total_population)


3.4.1.3 Basic summary

\(\rightarrow\) How many people were experiencing homelessness in 2017? How many were sheltered and how many were unsheltered?

Show Answer 
df_2017 %>% 
  select(total_homeless, total_unsheltered, total_sheltered) %>% 
  colSums()
##    total_homeless total_unsheltered   total_sheltered 
##            548312            188643            359669


\(\rightarrow\) What are the minimum, maximum, mean, and median number of total, sheltered, and unsheltered homeless in 2017?

Show Answer 
df_2017 %>% 
  select(total_homeless, total_unsheltered, total_sheltered) %>% 
  pivot_longer(cols = c(total_homeless, total_unsheltered, total_sheltered), names_to = "variable", values_to = "count") %>% 
  group_by(variable) %>% 
  summarize(min = min(count), max = max(count), mean = round(mean(count),1), median = median(count)) 
## # A tibble: 3 × 5
##   variable            min   max  mean median
##   <chr>             <dbl> <dbl> <dbl>  <dbl>
## 1 total_homeless       10 76501 1466.   568.
## 2 total_sheltered       5 72565  962.   373 
## 3 total_unsheltered     0 42828  504.   110.


3.4.2 Correlations between numerical variables

\(\rightarrow\) Plot the correlation coefficients between all pairs of numerical variables using the corrplot function.

Show Answer

Try this first with no optional arguments in corrplot and notice the problems.

df_2017%>% 
  select_if(is.numeric) %>%  
  cor(use = "pairwise.complete.obs") %>% 
  corrplot()
## Warning in cor(., use = "pairwise.complete.obs"): the standard deviation is zero

There are two problems. First, year is only equal to 2017, so it doesn’t make sense to compute a correlation coefficient with this variable. So, year should be removed. Also, the labels are huge, so we can’t read the plot.

Try this:

df_2017 %>% 
  select_if(is.numeric) %>% 
  select(-"year") %>% 
  cor(use = "pairwise.complete.obs") %>% 
  corrplot(tl.cex = 0.5, type = "lower")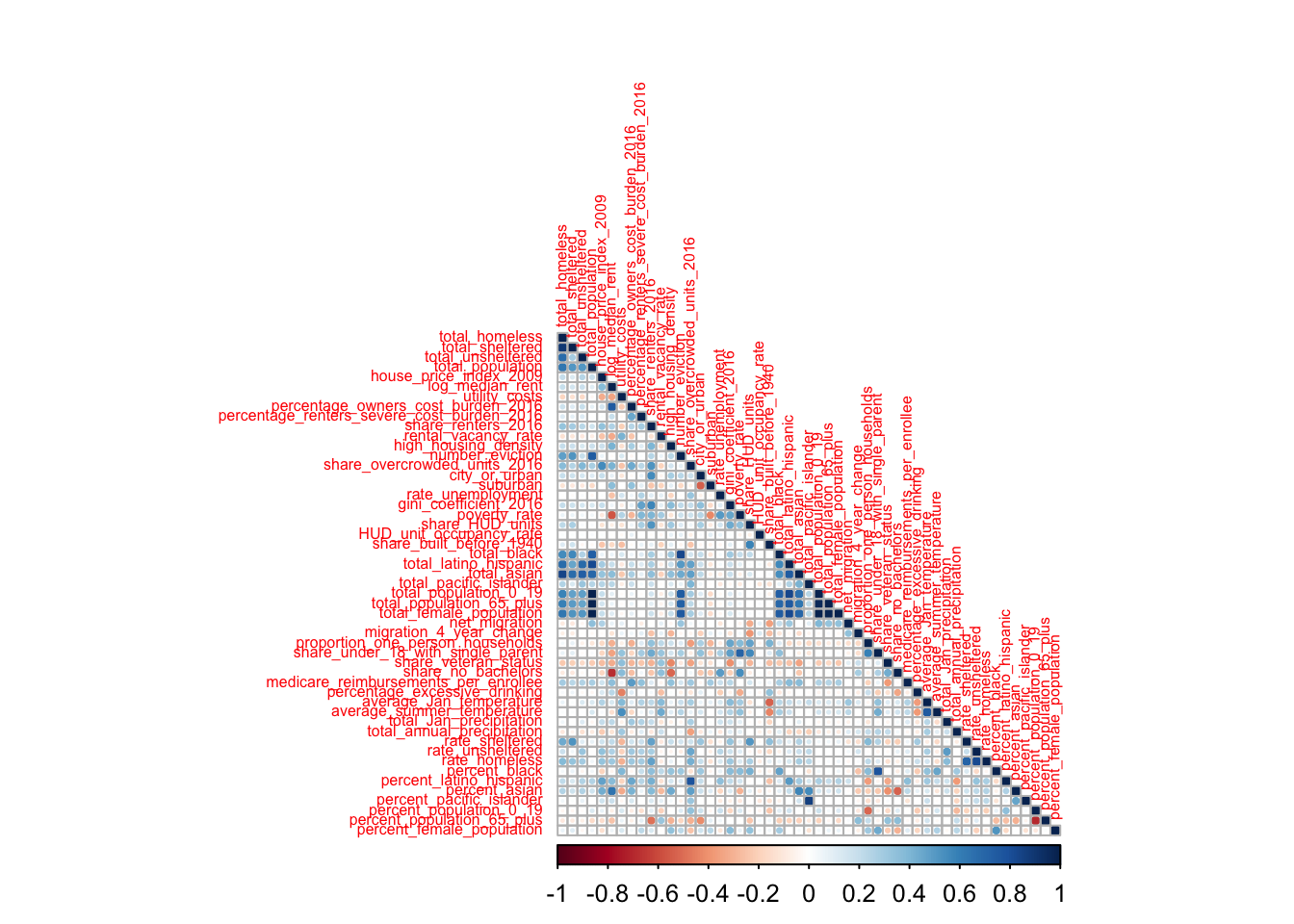


There are some variables that are highly correlated with the rate of homeless. Some are obvious, such as the rate of sheltered homeless. Other correlations show the existence of environmental variables, such as the share of overcrowded units, that are correlated with the rate of homeless.

Note the high correlation among subsets of the input variables. We will want to remove redundant variables or make a transformation of the input variables to deal with the correlation before constructing a model.

Next, we will find the variables with the highest correlation with rate_homeless. First, create the correlation matrix. Then examine the row with rate_homeless to find its correlation with the other variables.

M <- df_2017 %>% 
  select_if(is.numeric) %>% 
  cor(use = "pairwise.complete.obs")
## Warning in cor(., use = "pairwise.complete.obs"): the standard deviation is zero
round(M["rate_homeless",],2)
##                                       year                             total_homeless 
##                                         NA                                       0.39 
##                            total_sheltered                          total_unsheltered 
##                                       0.33                                       0.29 
##                           total_population                     house_price_index_2009 
##                                       0.05                                       0.34 
##                            log_median_rent                              utility_costs 
##                                       0.31                                      -0.31 
##         percentage_owners_cost_burden_2016 percentage_renters_severe_cost_burden_2016 
##                                       0.32                                       0.30 
##                         share_renters_2016                        rental_vacancy_rate 
##                                       0.48                                      -0.08 
##                       high_housing_density                            number_eviction 
##                                       0.08                                       0.03 
##               share_overcrowded_units_2016                              city_or_urban 
##                                       0.42                                       0.19 
##                                   suburban                          rate_unemployment 
##                                      -0.12                                       0.13 
##                      gini_coefficient_2016                               poverty_rate 
##                                       0.31                                       0.13 
##                            share_HUD_units                    HUD_unit_occupancy_rate 
##                                       0.27                                      -0.08 
##                    share_built_before_1940                                total_black 
##                                       0.09                                       0.07 
##                      total_latino_hispanic                                total_asian 
##                                       0.14                                       0.28 
##                     total_pacific_islander                      total_population_0_19 
##                                       0.23                                       0.02 
##                   total_population_65_plus                    total_female_population 
##                                       0.03                                       0.05 
##                              net_migration                    migration_4_year_change 
##                                      -0.04                                       0.03 
##           proportion_one_person_households          share_under_18_with_single_parent 
##                                       0.21                                       0.11 
##                       share_veteran_status                         share_no_bachelors 
##                                      -0.13                                      -0.07 
##       medicare_reimbursements_per_enrollee              percentage_excessive_drinking 
##                                       0.11                                       0.19 
##                    average_Jan_temperature                 average_summer_temperature 
##                                       0.15                                      -0.14 
##                    total_Jan_precipitation                 total_annual_precipitation 
##                                       0.37                                      -0.03 
##                             rate_sheltered                           rate_unsheltered 
##                                       0.72                                       0.83 
##                              rate_homeless                              percent_black 
##                                       1.00                                      -0.04 
##                    percent_latino_hispanic                              percent_asian 
##                                       0.28                                       0.25 
##                   percent_pacific_islander                    percent_population_0_19 
##                                       0.22                                      -0.20 
##                 percent_population_65_plus                  percent_female_population 
##                                       0.00                                      -0.08

Find the variables where the absolute value of the correlation with rate_homeless is greater than 0.3.

M["rate_homeless",abs(M["rate_homeless",]) > 0.3 & is.na(M["rate_homeless",]) == FALSE] %>% 
  abs() %>%
  round(2) %>% 
  sort(decreasing = T)
##                      rate_homeless                   rate_unsheltered                     rate_sheltered 
##                               1.00                               0.83                               0.72 
##                 share_renters_2016       share_overcrowded_units_2016                     total_homeless 
##                               0.48                               0.42                               0.39 
##            total_Jan_precipitation             house_price_index_2009                    total_sheltered 
##                               0.37                               0.34                               0.33 
## percentage_owners_cost_burden_2016                    log_median_rent                      utility_costs 
##                               0.32                               0.31                               0.31 
##              gini_coefficient_2016 
##                               0.31

\(\rightarrow\) Make a pairs plot with a subset of the variables with the highest magnitude correlations. Select a small enough group so that you can see the panels. Do not include variables that you will not use as predictors (e.g. rate_unsheltered, any demographic totals)

Show Answer 
df_2017 %>% 
  select("rate_homeless", "share_renters_2016", "share_overcrowded_units_2016", "total_Jan_precipitation", "house_price_index_2009", "percentage_owners_cost_burden_2016", "log_median_rent", "utility_costs", "gini_coefficient_2016") %>% 
  filter("coc_number" != "CA-613") %>% 
  ggpairs(progress = FALSE, lower = list(continuous = "cor"), upper = list(continuous = "points"))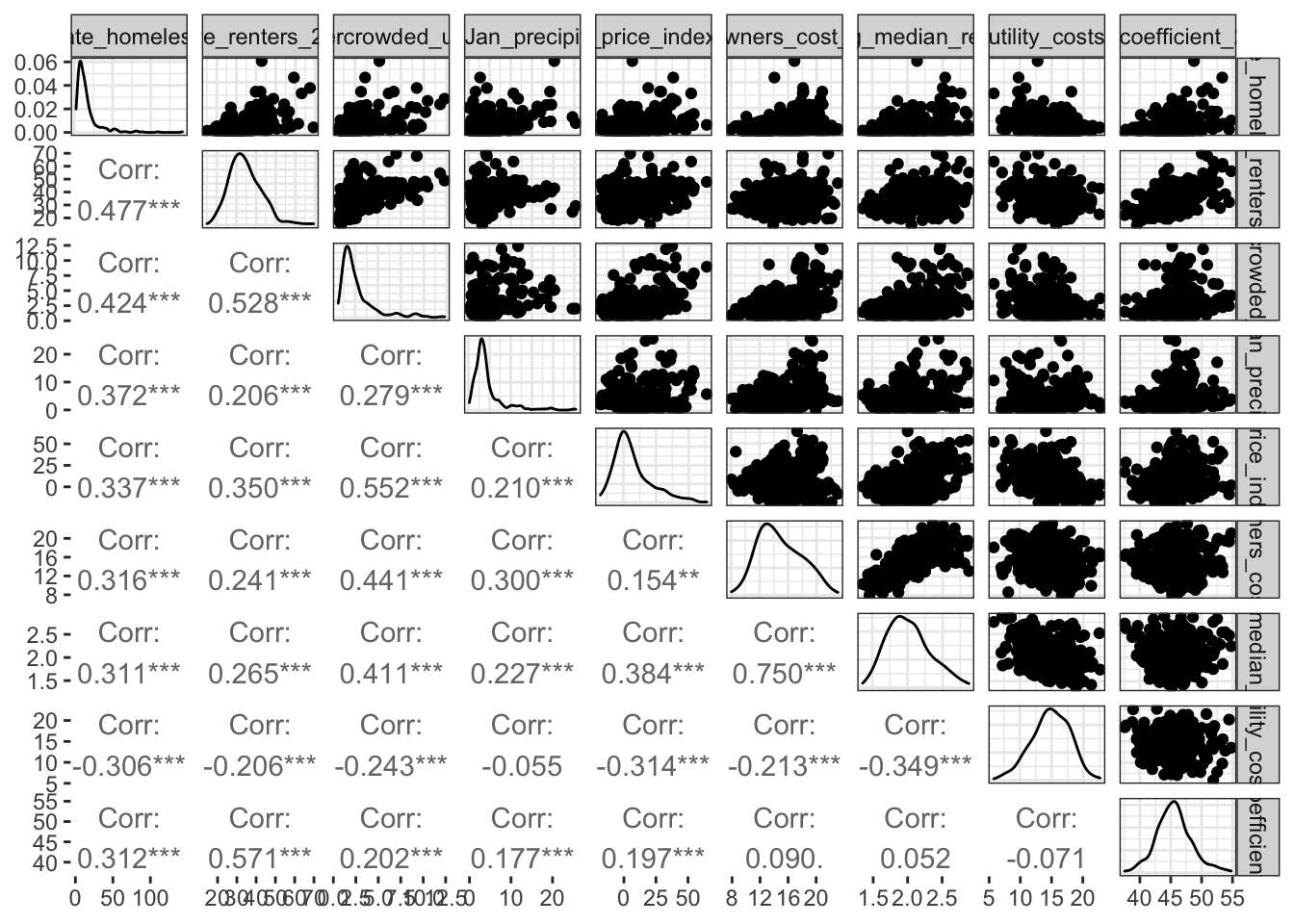


\(\rightarrow\) Create additional plots to further understand the data set. Describe your findings.

3.5 Model

We will multiple approaches to construct models that predict rate_homeless:

  1. Use statistical significance to create a multiple linear regression model.
  2. Best subset selection for a multiple linear regression model.
  3. Lasso
  4. Ridge regression
  5. XGBoost

To compare the different approaches, we will use a training and testing split of the data set.

3.5.1 Set up the data set for training and testing

3.5.1.1 Remove some variables

There are several variables that we do not want to include as predictors. We want to remove demographic totals, the year, the CoC number, and the other homeless rates that we are not predicting. You may have additional variables to remove to create the data set that contains only the response variable and the predictors that you want to use.

variable_remove = c("total_homeless", "total_sheltered", "total_unsheltered", "total_black", "total_latino_hispanic", "total_asian", "total_pacific_islander", "total_population_0_19", "total_population_65_plus", "total_female_population", "year", "coc_number", "total_population", "rate_unsheltered", "rate_sheltered")

df_model <- df_2017 %>% 
  select(-all_of(variable_remove))

names(df_model)
##  [1] "house_price_index_2009"                     "log_median_rent"                           
##  [3] "utility_costs"                              "percentage_owners_cost_burden_2016"        
##  [5] "percentage_renters_severe_cost_burden_2016" "share_renters_2016"                        
##  [7] "rental_vacancy_rate"                        "high_housing_density"                      
##  [9] "number_eviction"                            "share_overcrowded_units_2016"              
## [11] "city_or_urban"                              "suburban"                                  
## [13] "rate_unemployment"                          "gini_coefficient_2016"                     
## [15] "poverty_rate"                               "share_HUD_units"                           
## [17] "HUD_unit_occupancy_rate"                    "share_built_before_1940"                   
## [19] "net_migration"                              "migration_4_year_change"                   
## [21] "proportion_one_person_households"           "share_under_18_with_single_parent"         
## [23] "share_veteran_status"                       "share_no_bachelors"                        
## [25] "medicare_reimbursements_per_enrollee"       "percentage_excessive_drinking"             
## [27] "average_Jan_temperature"                    "average_summer_temperature"                
## [29] "total_Jan_precipitation"                    "total_annual_precipitation"                
## [31] "rate_homeless"                              "percent_black"                             
## [33] "percent_latino_hispanic"                    "percent_asian"                             
## [35] "percent_pacific_islander"                   "percent_population_0_19"                   
## [37] "percent_population_65_plus"                 "percent_female_population"

\(\rightarrow\) How many input variables remain in the data set that you can use as predictors?

Show Answer 
ncol(df_model) - 1
## [1] 37

There are 37 input variables.


3.5.1.2 Get train and test splits

We will split the data into training and testing sets, with 85% of the data kept for training.

#Do the split. Keep 85% for training. Use stratified sampling based on rate_homeless
set.seed(20)
split <- initial_split(df_model, prop = 0.85, strata = rate_homeless)

#Extract the training and testing splits
df_train <- training(split)
df_test <- testing(split)

\(\rightarrow\) Check the sizes of the training and testing splits

Show Answer 
dim(df_train)
## [1] 316  38
dim(df_test)
## [1] 58 38


3.5.2 Full regression model

3.5.2.1 Fit the model on the training data

\(\rightarrow\) Use the training data to fit a multiple linear regression model to predict rate_homeless using all possible predictor variables.

Show Coding Hint

Use the lm function:

fit <- lm()
Show Answer 
fit <- lm(rate_homeless ~ ., df_train)


\(\rightarrow\) Examine the summary of the fit. Which predictors have statistically significant coefficients? Do the signs of the coefficients make sense?

Show Answer 
summary(fit)
## 
## Call:
## lm(formula = rate_homeless ~ ., data = df_train)
## 
## Residuals:
##     Min      1Q  Median      3Q     Max 
## -34.128  -5.250  -0.639   4.658  77.227 
## 
## Coefficients:
##                                              Estimate Std. Error t value Pr(>|t|)    
## (Intercept)                                -8.630e+01  7.408e+01  -1.165 0.245058    
## house_price_index_2009                      8.148e-02  6.847e-02   1.190 0.235077    
## log_median_rent                             3.066e+01  7.959e+00   3.852 0.000146 ***
## utility_costs                              -1.534e-01  3.674e-01  -0.418 0.676600    
## percentage_owners_cost_burden_2016         -1.980e-01  5.030e-01  -0.394 0.694100    
## percentage_renters_severe_cost_burden_2016 -7.813e-02  2.803e-01  -0.279 0.780661    
## share_renters_2016                          1.313e-01  2.302e-01   0.570 0.568882    
## rental_vacancy_rate                         1.027e-01  3.422e-01   0.300 0.764296    
## high_housing_density                       -3.113e+00  2.257e+00  -1.379 0.168943    
## number_eviction                             1.765e-04  1.695e-04   1.041 0.298659    
## share_overcrowded_units_2016                1.961e+00  8.910e-01   2.201 0.028584 *  
## city_or_urban                              -1.319e+00  2.481e+00  -0.532 0.595463    
## suburban                                   -4.344e+00  2.259e+00  -1.923 0.055511 .  
## rate_unemployment                          -7.330e-01  7.791e-01  -0.941 0.347614    
## gini_coefficient_2016                       1.638e-01  4.853e-01   0.338 0.735922    
## poverty_rate                               -2.161e-01  5.039e-01  -0.429 0.668308    
## share_HUD_units                             2.040e+00  7.314e-01   2.789 0.005655 ** 
## HUD_unit_occupancy_rate                    -9.037e-02  1.700e-01  -0.532 0.595347    
## share_built_before_1940                     4.870e-02  1.192e-01   0.409 0.683136    
## net_migration                              -1.186e-04  7.745e-05  -1.532 0.126764    
## migration_4_year_change                     4.159e+00  1.218e+00   3.414 0.000736 ***
## proportion_one_person_households            1.394e+00  4.198e-01   3.319 0.001022 ** 
## share_under_18_with_single_parent           4.269e-01  3.274e-01   1.304 0.193394    
## share_veteran_status                        3.439e-02  4.078e-01   0.084 0.932852    
## share_no_bachelors                          2.719e-01  2.172e-01   1.252 0.211522    
## medicare_reimbursements_per_enrollee       -5.274e-02  8.654e-01  -0.061 0.951451    
## percentage_excessive_drinking               3.351e+01  3.440e+01   0.974 0.330951    
## average_Jan_temperature                     1.973e-01  1.740e-01   1.134 0.257909    
## average_summer_temperature                 -2.084e-01  3.013e-01  -0.692 0.489812    
## total_Jan_precipitation                     9.512e-01  2.519e-01   3.777 0.000194 ***
## total_annual_precipitation                  7.055e-02  6.875e-02   1.026 0.305695    
## percent_black                              -3.948e+01  1.482e+01  -2.665 0.008158 ** 
## percent_latino_hispanic                    -1.515e+01  1.227e+01  -1.235 0.218042    
## percent_asian                              -4.096e+01  2.356e+01  -1.739 0.083220 .  
## percent_pacific_islander                    2.220e+02  1.278e+02   1.737 0.083571 .  
## percent_population_0_19                     4.381e+01  6.449e+01   0.679 0.497519    
## percent_population_65_plus                 -2.935e+00  5.118e+01  -0.057 0.954303    
## percent_female_population                  -7.396e+01  1.107e+02  -0.668 0.504533    
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## Residual standard error: 10.93 on 278 degrees of freedom
## Multiple R-squared:  0.5973, Adjusted R-squared:  0.5437 
## F-statistic: 11.15 on 37 and 278 DF,  p-value: < 2.2e-16

Isolate the predictors that have statistically significant coefficients.

#Name the summary
s <- summary(fit)

#Use logical indexing on the matrix of coefficients to find coefficients where the p-value < 0.05
s$coefficients[s$coefficients[,4] < 0.05,1] %>% 
  round(2) %>%     #Round because we don't need to look at a million decimal places
  data.frame()     #Create a data frame because it produces a nicer display
##                                       .
## log_median_rent                   30.66
## share_overcrowded_units_2016       1.96
## share_HUD_units                    2.04
## migration_4_year_change            4.16
## proportion_one_person_households   1.39
## total_Jan_precipitation            0.95
## percent_black                    -39.48


We should also do a qualitative assessment of the fit to the training data.

\(\rightarrow\) Plot the residuals to look for systematic patterns of residuals that might suggest a new model.

Show Answer 
plot(fit,1)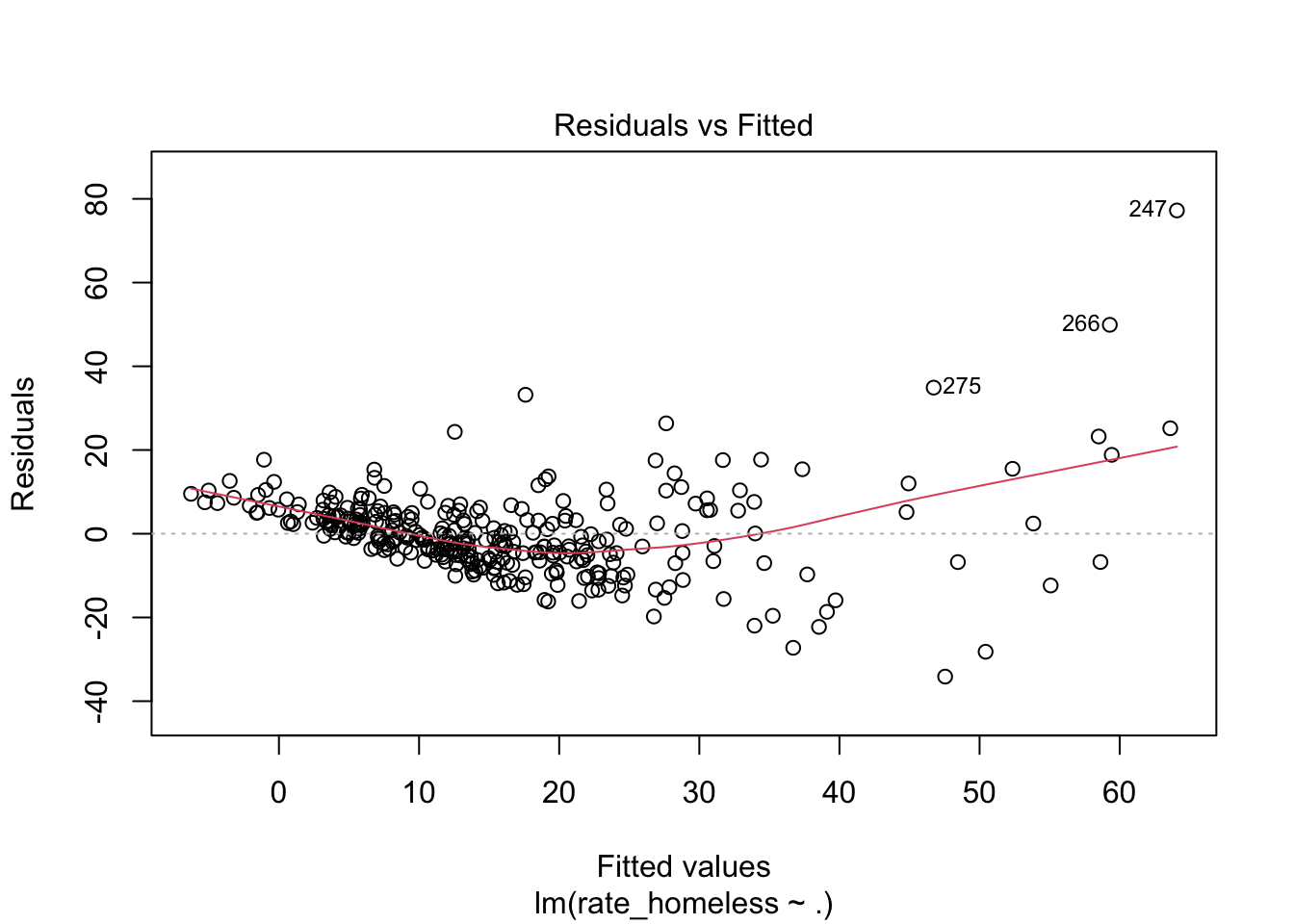

The residual plot has a systematic pattern. How might you use this to alter the model? This is something to explore in the Additional Step.


3.5.2.2 Assess the model on the testing data

\(\rightarrow\) Use the model to predict the homeless rate in the testing data.
Coding Hint

Use the function predict to make the predictions.

Show Answer 
lm_pred <- predict(fit, df_test)


\(\rightarrow\) Make a scatter plot to compare the actual value and the predicted value of rate_homeless.

Show Answer 
plot(df_test$rate_homeless, lm_pred, xlab = "Measured homeless rate", ylab = "Predicted homeless rate", pch = 20)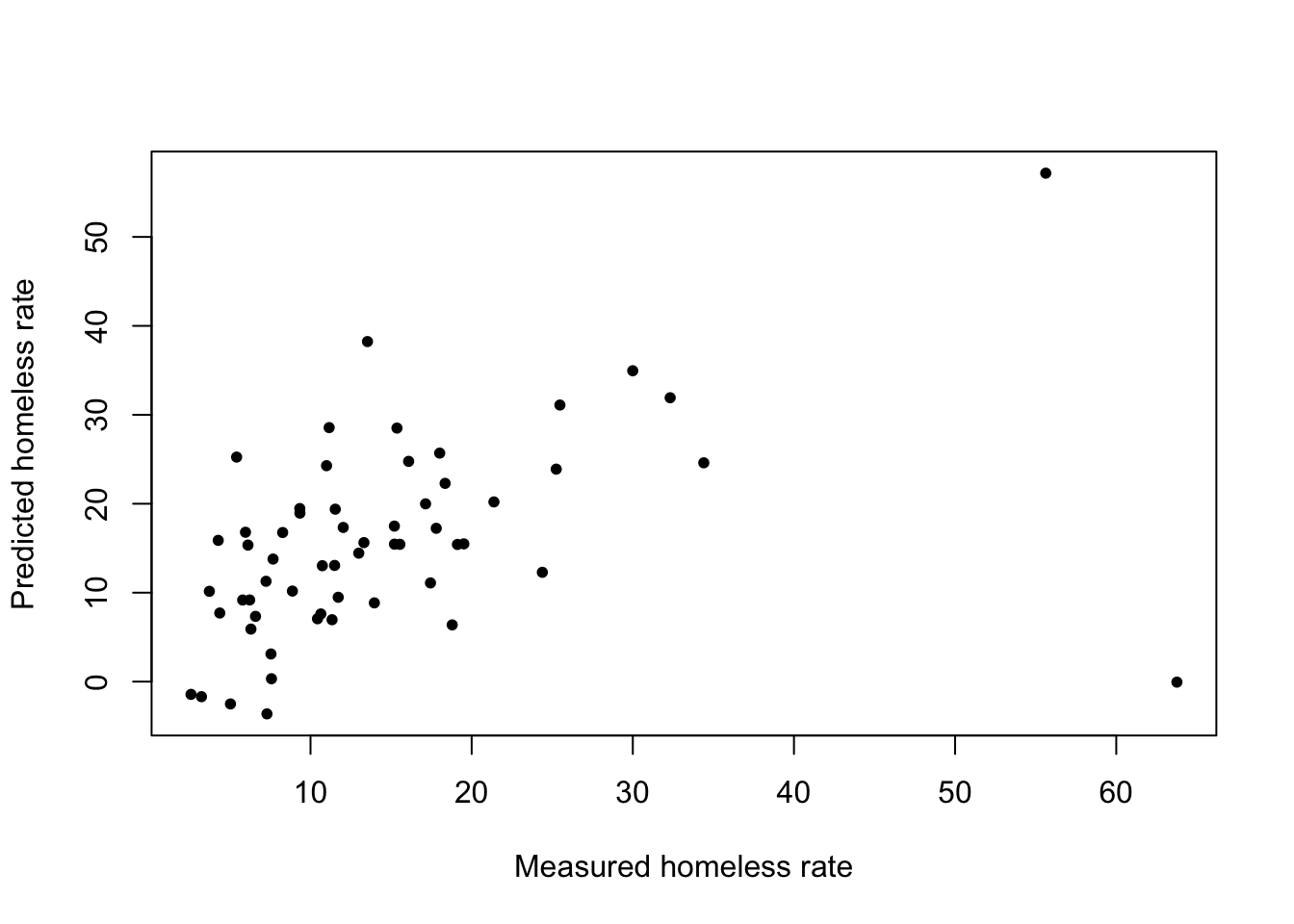


\(\rightarrow\) Compute the RMSE

Show Answer 
lm_rmse <- sqrt(mean((df_test$rate_homeless- lm_pred)^2))

lm_rmse
## [1] 11.46046

Or, use pipes if you prefer:

lm_rmse <- (df_test$rate_homeless- lm_pred)^2 %>% 
  mean() %>% 
  sqrt()

lm_rmse
## [1] 11.46046


\(\rightarrow\) Repeat the regression analysis, but using a different random seed before the train-test split. Does the train-test split affect the significance of the coefficients and their values?

3.5.3 Subset selection

The full model contains too many predictors, so we will use subset selection on the training data to find a smaller number of predictors.

\(\rightarrow\) Get the number of variables in the data set that will be used as predictors. This will be used to set the subset size.

Show Answer 
num_var <- ncol(df_train) - 1


\(\rightarrow\) Do best subset selection on the training data. Set the maximum number of variables to equal the number of predictor variables in the data set.

Show Answer 
regfit_full <- regsubsets(rate_homeless ~ . , data = df_train, nvmax = num_var)


\(\rightarrow\) Get the summary. We will use this after performing cross validation to determine the best model.

Show Answer 
reg_summary <- summary(regfit_full)


3.5.3.1 Cross validation

\(\rightarrow\) Use 10-fold cross validation on the training data to determine the best subset of predictors in the model.

Show Answer 
#Number of observations
n <- nrow(df_train)

#number of folds
k <- 10

#folds
set.seed(1)
#Each observation is randomly assigned to a fold 1, 2, .. k
folds <- sample(1:k,n,replace = TRUE)

#Initialize error for testing data
cv_errors <- matrix(NA,k,num_var,dimnames = list(NULL,paste(1:num_var)))

#For each testing fold
for (j in 1:k){
  #Best subsets on training folds
  reg_fit_best <- regsubsets(rate_homeless ~ ., data = df_train[folds !=j,], nvmax = num_var)
  
  #test matrix with test fold
  test_mat <- model.matrix(rate_homeless ~ .,data = df_train[folds == j,])

    #Compare errors across models with different numbers of variables  
    for (i in 1:num_var){
    #get coefficients of best model with i variables
    coefi <- coef(reg_fit_best,id = i)
    #make predictions using test data
    pred <- test_mat[,names(coefi)] %*% coefi
    #compute test MSE
    cv_errors[j,i] <- mean((df_train$rate_homeless[folds == j] - pred)^2)
  }
}

#Average error over folds
cv_errors_mean <- apply(cv_errors,2,mean)


\(\rightarrow\) Plot the assessment measures vs. the number of predictors

Show Answer 
par(mfrow = c(2,2))

ind_cp = which.min(reg_summary$cp)
plot(reg_summary$cp,type = "b",xlab = "Number of variables",ylab = "Cp", main = toString(ind_cp))
points(ind_cp, reg_summary$cp[ind_cp],col = "red",pch = 20)

ind_bic = which.min(reg_summary$bic)
plot(reg_summary$bic,type = "b",xlab = "Number of variables",ylab = "BIC", main = toString(ind_bic))
points(ind_bic, reg_summary$bic[ind_bic],col = "red",pch = 20)

ind_adjr2 = which.max(reg_summary$adjr2)
plot(reg_summary$adjr2,type = "b",xlab = "Number of variables",ylab = "Adjusted R2", main = toString(ind_adjr2))
points(ind_adjr2, reg_summary$adjr2[ind_adjr2],col = "red",pch = 20)

ind_cv <- which.min(cv_errors_mean)
plot(cv_errors_mean,type = "b",xlab = "Number of variables",ylab = "Cross validation", main = toString(ind_cv))
points(ind_cv, cv_errors_mean[ind_cv],col = "red",pch = 20)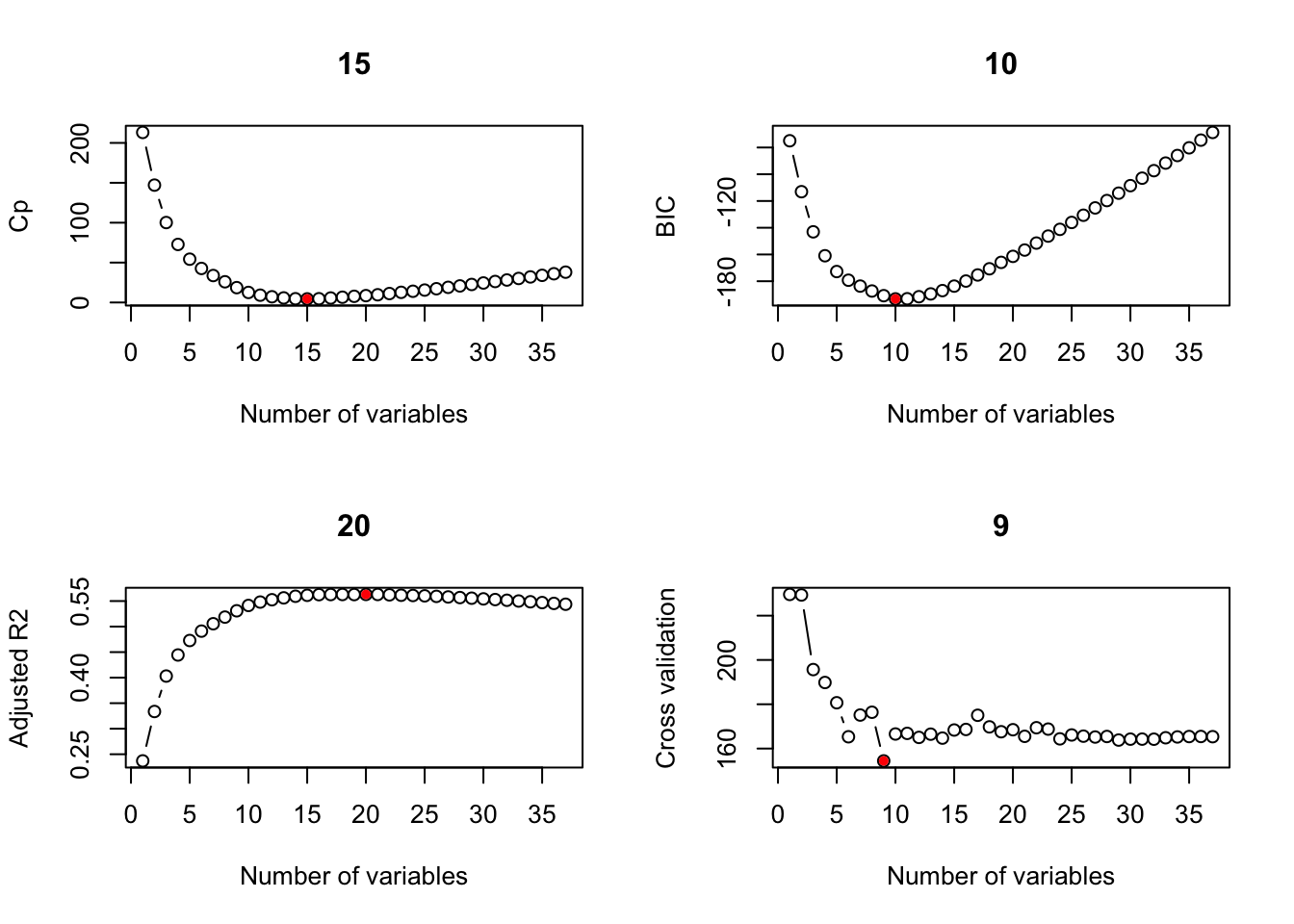


\(\rightarrow\) What are the coefficients of the best model according to different measures?

Show Answer

Try each of: ind_cp, ind_bic, ind_adjr2, ind_cv

coef(regfit_full,ind_cp) %>% 
  round(2) %>% 
  data.frame()
##                                          .
## (Intercept)                        -140.81
## log_median_rent                      31.22
## percentage_owners_cost_burden_2016   -0.56
## high_housing_density                 -4.08
## share_overcrowded_units_2016          2.29
## suburban                             -3.51
## rate_unemployment                    -1.08
## share_HUD_units                       2.36
## migration_4_year_change               3.55
## proportion_one_person_households      1.73
## share_no_bachelors                    0.44
## percentage_excessive_drinking        52.57
## total_Jan_precipitation               1.09
## total_annual_precipitation            0.11
## percent_black                       -21.39
## percent_pacific_islander            211.57
coef(regfit_full,ind_bic) %>% 
  round(2) %>% 
  data.frame()
##                                        .
## (Intercept)                      -123.86
## log_median_rent                    26.78
## share_overcrowded_units_2016        1.49
## suburban                           -4.31
## share_HUD_units                     2.04
## migration_4_year_change             3.79
## proportion_one_person_households    1.80
## share_no_bachelors                  0.34
## total_Jan_precipitation             1.12
## percent_black                     -27.04
## percent_pacific_islander          247.62


3.5.3.2 Assess the performance of the model on the testing data

Use the model to predict the homeless rate in the testing data. We will use the best BIC model as an example, but you should compare the performance of all models.

\(\rightarrow\) Select the variables that are indicated by the best subset selection criterion that you choose (Cp, BIC, Adjusted R-squared, or CV) and produce a new, smaller data frame.

Show Answer 
df_bic <- df_train %>% 
  select(all_of(names(coef(regfit_full,ind_bic))[2:length(coef(regfit_full,ind_bic))]), "rate_homeless")

head(df_bic)
## # A tibble: 6 × 11
##   log_median_rent share_overcrowded_units_2016 suburban share_HUD_units migration_4_year_ch… proportion_one_…
##             <dbl>                        <dbl>    <dbl>           <dbl>                <dbl>            <dbl>
## 1            1.36                         1.54        0            4.34                0.232             28.3
## 2            1.44                         1.87        0            3.65                0.191             27.3
## 3            1.45                         1.98        0            3.75               -0.206             29.2
## 4            1.42                         2.49        0            4.71                0.179             30.5
## 5            1.50                         2.01        0            2.56                0.630             28.7
## 6            1.89                         2.47        0            2.38                0.642             23.6
## # … with 5 more variables: share_no_bachelors <dbl>, total_Jan_precipitation <dbl>, percent_black <dbl>,
## #   percent_pacific_islander <dbl>, rate_homeless <dbl>


\(\rightarrow\) Fit the model using this subset. The lm object will help us to make predictions easily.

Show Answer 
fit_bic <- lm(rate_homeless ~., data = df_bic)

summary(fit_bic)
## 
## Call:
## lm(formula = rate_homeless ~ ., data = df_bic)
## 
## Residuals:
##     Min      1Q  Median      3Q     Max 
## -36.546  -4.824  -1.366   4.441  79.701 
## 
## Coefficients:
##                                   Estimate Std. Error t value Pr(>|t|)    
## (Intercept)                      -123.8573    15.5886  -7.945 3.77e-14 ***
## log_median_rent                    26.7838     3.9648   6.755 7.22e-11 ***
## share_overcrowded_units_2016        1.4937     0.4581   3.261 0.001238 ** 
## suburban                           -4.3119     1.4781  -2.917 0.003793 ** 
## share_HUD_units                     2.0380     0.4553   4.477 1.07e-05 ***
## migration_4_year_change             3.7909     1.0552   3.593 0.000381 ***
## proportion_one_person_households    1.8011     0.2065   8.721  < 2e-16 ***
## share_no_bachelors                  0.3420     0.1015   3.370 0.000848 ***
## total_Jan_precipitation             1.1238     0.1894   5.934 8.04e-09 ***
## percent_black                     -27.0435     5.9002  -4.584 6.68e-06 ***
## percent_pacific_islander          247.6198    82.7792   2.991 0.003004 ** 
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## Residual standard error: 10.96 on 305 degrees of freedom
## Multiple R-squared:  0.5559, Adjusted R-squared:  0.5414 
## F-statistic: 38.18 on 10 and 305 DF,  p-value: < 2.2e-16

Are all of the coefficients statistically significant?


\(\rightarrow\) Generate predictions of the ACT score in the testing data.

Show Answer 
bic_pred <- predict(fit_bic, df_test)


\(\rightarrow\) Make a scatter plot to compare the actual value and the predicted value of rate_homeless.

Show Answer 
plot(df_test$rate_homeless, bic_pred, xlab = "Measured homeless rate", ylab = "Predicted homeless rate", pch = 20)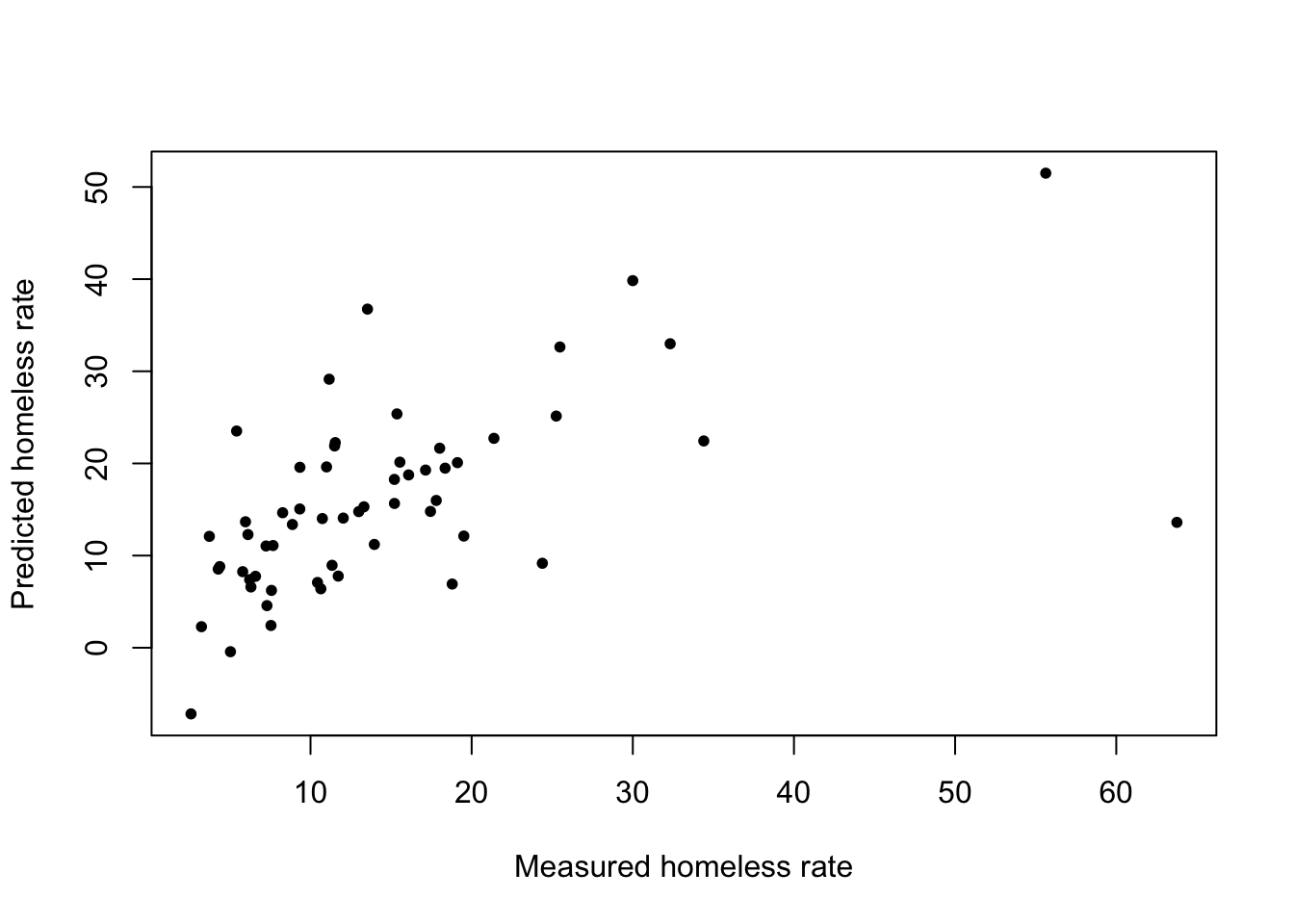


\(\rightarrow\) Compute the RMSE. How does the RMSE compare to the error for the full model?

Show Answer 
bic_rmse <- sqrt(mean((df_test$rate_homeless- bic_pred)^2))

bic_rmse
## [1] 9.817378


3.5.4 Lasso

The lasso is another approach to producing a linear regression model with a subset of the available predictors. The lasso works by finding coefficients \(\boldsymbol{\beta}\) that minimize the cost function:

\[C(\boldsymbol{\beta}) = \sum_{i=1}^n(y_i - \beta_{0} - \sum_{j=1}^p\beta_{j}x_{ij})^2 + \lambda \sum_{j=1}^p|\beta_{j}| = \text{RSS} + \lambda \sum_{j=1}^p|\beta_{j}|\]

where \(\lambda \geq 0\) is a tuning parameter (or hyperparameter).

\(\rightarrow\) Prepare the data by creating a model matrix x_train from the training data. Create the model matrix using model.matrix so that it includes the training data for all predictors, but does not include a column for the intercept. Also create the training response data y_train.

Show Answer 
x_train <- model.matrix(rate_homeless ~ ., df_train)[,-1] #Remove the intercept
y_train <- df_train$rate_homeless


\(\rightarrow\) Use cross-validation to find the best hyperparameter \(\lambda\)

Show Answer 
#alpha = 1 says that we will use the lasso
cv_lasso <- cv.glmnet(x_train, y_train, alpha = 1)


\(\rightarrow\) Show error as a function of the hyperparameter \(\lambda\) and its best value.

Show Answer 
plot(cv_lasso)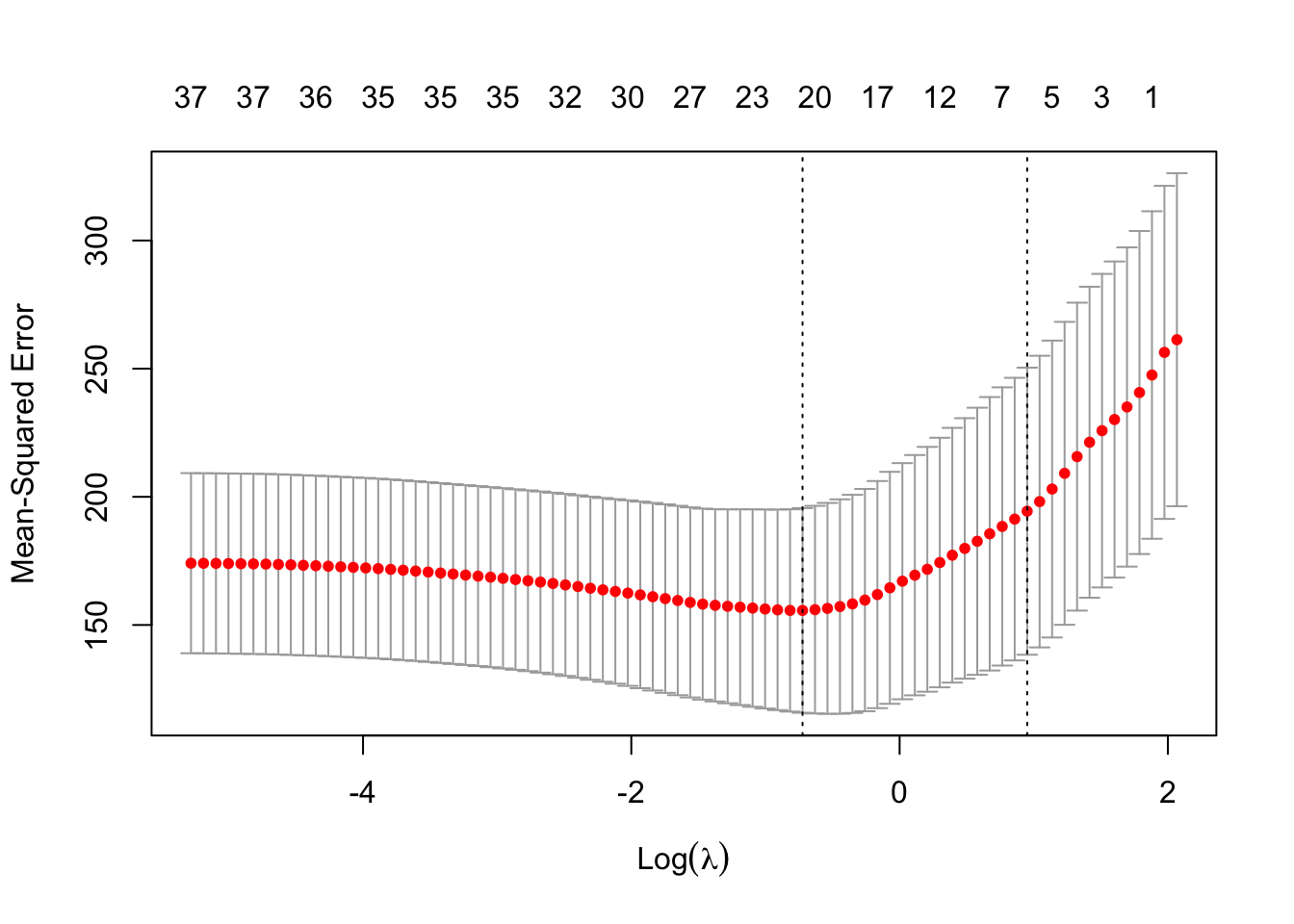

best_lam <- cv_lasso$lambda.min
best_lam
## [1] 0.4849755


\(\rightarrow\) Fit the lasso with the best \(\lambda\) using the function glmnet.

Show Answer 
lasso_mod <- glmnet(x_train, y_train, alpha = 1, lambda = best_lam)


\(\rightarrow\) Examine the coefficients. Which variables have non-zero coefficients?

Show Answer 
round(coef(lasso_mod),3)
## 38 x 1 sparse Matrix of class "dgCMatrix"
##                                                 s0
## (Intercept)                                -41.161
## house_price_index_2009                       0.057
## log_median_rent                             13.326
## utility_costs                               -0.061
## percentage_owners_cost_burden_2016           .    
## percentage_renters_severe_cost_burden_2016   .    
## share_renters_2016                           0.106
## rental_vacancy_rate                          .    
## high_housing_density                        -2.443
## number_eviction                              .    
## share_overcrowded_units_2016                 1.929
## city_or_urban                                .    
## suburban                                    -1.970
## rate_unemployment                            .    
## gini_coefficient_2016                        .    
## poverty_rate                                 .    
## share_HUD_units                              1.652
## HUD_unit_occupancy_rate                      .    
## share_built_before_1940                      .    
## net_migration                                .    
## migration_4_year_change                      2.854
## proportion_one_person_households             1.147
## share_under_18_with_single_parent            .    
## share_veteran_status                         0.102
## share_no_bachelors                           0.065
## medicare_reimbursements_per_enrollee         .    
## percentage_excessive_drinking               40.582
## average_Jan_temperature                      .    
## average_summer_temperature                  -0.005
## total_Jan_precipitation                      1.024
## total_annual_precipitation                   0.027
## percent_black                               -9.311
## percent_latino_hispanic                      .    
## percent_asian                                .    
## percent_pacific_islander                   208.525
## percent_population_0_19                    -40.775
## percent_population_65_plus                   .    
## percent_female_population                  -43.891


3.5.4.1 Look at prediction error

\(\rightarrow\) Use the model to predict the homeless rate in the testing data.

Show Answer

First create a model matrix with the testing data

x_test <- model.matrix(rate_homeless ~ .,df_test)[,-1] #Remove the intercept

Use the predict function to make the prediction of the testing ACT data.

lasso_pred <- predict(lasso_mod, s = best_lam, newx = x_test)


\(\rightarrow\) Make a scatter plot to compare the actual value and the predicted value of rate_homeless.

Show Answer 
plot(df_test$rate_homeless, lasso_pred, xlab = "Measured homeless rate", ylab = "Predicted homeless rate", pch = 20)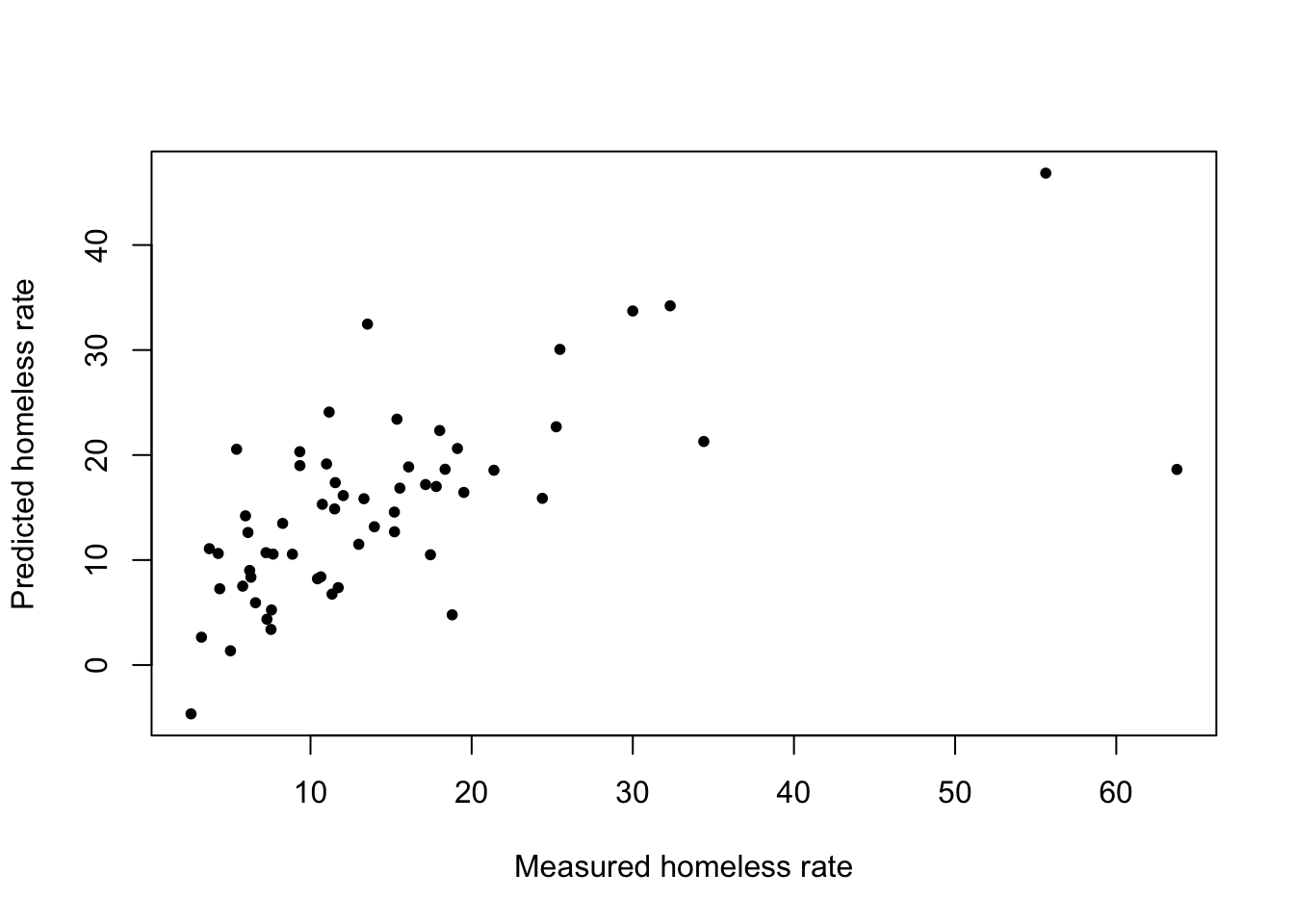


\(\rightarrow\) Compute the RMSE. How does it compare to the other models?

Show Answer 
lasso_rmse <- sqrt(mean((df_test$rate_homeless - lasso_pred)^2))
lasso_rmse
## [1] 8.63238


3.5.5 Ridge regression

Ridge regression is another approach to model building

Ridge regression works by finding coefficients \(\boldsymbol{\beta}\) that minimize the cost function:

\[C(\boldsymbol{\beta}) = \sum_{i=1}^n(y_i - \beta_{0} - \sum_{j=1}^p\beta_{j}x_{ij})^2 + \lambda \sum_{j=1}^p\beta_{j}^2 = \text{RSS} + \lambda \sum_{j=1}^p\beta_{j}^2\]

In contrast to the lasso, ridge regression will not reduce the number of non-zero coefficients in the model. Ridge regression will shrink the coefficients, which helps to prevent overfitting of the training data.

The fitting procedure for the ridge regression model mirrors the lasso approach, only changing the parameter \(\alpha\) to 0 in the cv.glmnet and glmnet functions.

\(\rightarrow\) Fit and assess a ridge regression model. How does it compare to the other models?

Show Answer

First, do cross validation to find the best value of the \(\lambda\)

cv_ridge <- cv.glmnet(x_train,y_train,alpha = 0)

best_lam <- cv_ridge$lambda.min

Fit the model with the best value of the \(\lambda\)

ridge_mod <- glmnet(x_train, y_train, alpha = 0, lambda = best_lam)

Predict the ACT scores in the test data

ridge_pred <- predict(ridge_mod, s = best_lam, newx = x_test)

Compute the RMSE

ridge_rmse <- sqrt(mean((df_test$rate_homeless - ridge_pred)^2))
ridge_rmse
## [1] 9.47263


3.5.6 XGBoost

XGBoost is short for eXtreme Gradient Boosting.

We are going to use the tidymodels package to fit the XGBoost model.

3.5.6.1 Set up the model

The model will be a boosted tree model, so we start by specifying the features of a boost_tree model. Theboost_tree creates a specification of a model, but does not fit the model.

xgb_spec <- boost_tree(
  mode = "regression",  #We are solving a regression problem
  trees = 1000, 
  tree_depth = tune(),  # tune() says that we will specify this parameter later
  min_n = tune(), 
  loss_reduction = tune(),                     
  sample_size = tune(), 
  mtry = tune(),         
  learn_rate = tune(),                         
  ) %>% 
  set_engine("xgboost", objective = "reg:squarederror") ## We will use xgboost to fit the model and try to minimize the squared error

xgb_spec
## Boosted Tree Model Specification (regression)
## 
## Main Arguments:
##   mtry = tune()
##   trees = 1000
##   min_n = tune()
##   tree_depth = tune()
##   learn_rate = tune()
##   loss_reduction = tune()
##   sample_size = tune()
## 
## Engine-Specific Arguments:
##   objective = reg:squarederror
## 
## Computational engine: xgboost

Create a workflow that specifies the model formula and the model type. We are still setting up the model; this does not fit the model.

xgb_wf <- workflow() %>%
  add_formula(rate_homeless ~ .) %>%
  add_model(xgb_spec)

xgb_wf
## ══ Workflow ═════════════════════════════════════════════════════════════════════════════════════════════════
## Preprocessor: Formula
## Model: boost_tree()
## 
## ── Preprocessor ─────────────────────────────────────────────────────────────────────────────────────────────
## rate_homeless ~ .
## 
## ── Model ────────────────────────────────────────────────────────────────────────────────────────────────────
## Boosted Tree Model Specification (regression)
## 
## Main Arguments:
##   mtry = tune()
##   trees = 1000
##   min_n = tune()
##   tree_depth = tune()
##   learn_rate = tune()
##   loss_reduction = tune()
##   sample_size = tune()
## 
## Engine-Specific Arguments:
##   objective = reg:squarederror
## 
## Computational engine: xgboost

3.5.6.2 Fit the model

We need to fit all of the parameters that we specified as tune(). We will specify the parameter grid using the functions grid_latin_hypercube:

xgb_grid <- grid_latin_hypercube(
  tree_depth(),
  min_n(),
  loss_reduction(),
  sample_size = sample_prop(),
  finalize(mtry(), df_train),
  learn_rate(),
  size = 30  #Create 30 sets of the 6 parameters
)

Create folds for cross-validation.

#folds <- vfold_cv(df_train, strata = rate_homeless)

folds <- vfold_cv(df_train)

Do the parameter fitting. This will take some time.

xgb_res <- tune_grid(
  xgb_wf,              #The workflow
  resamples = folds,   #The training data split into folds
  grid = xgb_grid,     #The grid of parameters to fit
  control = control_grid(save_pred = TRUE)
)
## ! Fold01: internal: A correlation computation is required, but `estimate` is constant and has 0 standard deviat...
## ! Fold02: internal: A correlation computation is required, but `estimate` is constant and has 0 standard deviat...
## ! Fold03: internal: A correlation computation is required, but `estimate` is constant and has 0 standard deviat...
## ! Fold04: internal: A correlation computation is required, but `estimate` is constant and has 0 standard deviat...
## ! Fold05: internal: A correlation computation is required, but `estimate` is constant and has 0 standard deviat...
## ! Fold06: internal: A correlation computation is required, but `estimate` is constant and has 0 standard deviat...
## ! Fold07: internal: A correlation computation is required, but `estimate` is constant and has 0 standard deviat...
## ! Fold08: internal: A correlation computation is required, but `estimate` is constant and has 0 standard deviat...
## ! Fold09: internal: A correlation computation is required, but `estimate` is constant and has 0 standard deviat...
## ! Fold10: internal: A correlation computation is required, but `estimate` is constant and has 0 standard deviat...
xgb_res
## Warning: This tuning result has notes. Example notes on model fitting include:
## internal: A correlation computation is required, but `estimate` is constant and has 0 standard deviation, resulting in a divide by 0 error. `NA` will be returned.
## internal: A correlation computation is required, but `estimate` is constant and has 0 standard deviation, resulting in a divide by 0 error. `NA` will be returned.
## internal: A correlation computation is required, but `estimate` is constant and has 0 standard deviation, resulting in a divide by 0 error. `NA` will be returned.
## # Tuning results
## # 10-fold cross-validation 
## # A tibble: 10 × 5
##    splits           id     .metrics           .notes           .predictions       
##    <list>           <chr>  <list>             <list>           <list>             
##  1 <split [284/32]> Fold01 <tibble [60 × 10]> <tibble [1 × 1]> <tibble [960 × 10]>
##  2 <split [284/32]> Fold02 <tibble [60 × 10]> <tibble [1 × 1]> <tibble [960 × 10]>
##  3 <split [284/32]> Fold03 <tibble [60 × 10]> <tibble [1 × 1]> <tibble [960 × 10]>
##  4 <split [284/32]> Fold04 <tibble [60 × 10]> <tibble [1 × 1]> <tibble [960 × 10]>
##  5 <split [284/32]> Fold05 <tibble [60 × 10]> <tibble [1 × 1]> <tibble [960 × 10]>
##  6 <split [284/32]> Fold06 <tibble [60 × 10]> <tibble [1 × 1]> <tibble [960 × 10]>
##  7 <split [285/31]> Fold07 <tibble [60 × 10]> <tibble [1 × 1]> <tibble [930 × 10]>
##  8 <split [285/31]> Fold08 <tibble [60 × 10]> <tibble [1 × 1]> <tibble [930 × 10]>
##  9 <split [285/31]> Fold09 <tibble [60 × 10]> <tibble [1 × 1]> <tibble [930 × 10]>
## 10 <split [285/31]> Fold10 <tibble [60 × 10]> <tibble [1 × 1]> <tibble [930 × 10]>

Set up the final workflow with the best model parameters.

#Get the best model, according to RMSE
best_rmse <- select_best(xgb_res, "rmse")

#Update the workflow with the best parameters
final_xgb <- finalize_workflow(
  xgb_wf,
  best_rmse
)

final_xgb
## ══ Workflow ═════════════════════════════════════════════════════════════════════════════════════════════════
## Preprocessor: Formula
## Model: boost_tree()
## 
## ── Preprocessor ─────────────────────────────────────────────────────────────────────────────────────────────
## rate_homeless ~ .
## 
## ── Model ────────────────────────────────────────────────────────────────────────────────────────────────────
## Boosted Tree Model Specification (regression)
## 
## Main Arguments:
##   mtry = 7
##   trees = 1000
##   min_n = 3
##   tree_depth = 4
##   learn_rate = 0.0107153006007263
##   loss_reduction = 0.00168670164001662
##   sample_size = 0.60449863047339
## 
## Engine-Specific Arguments:
##   objective = reg:squarederror
## 
## Computational engine: xgboost

3.5.6.3 Prediction

Fit the final model to the training data.

xgb_fit <- final_xgb %>% 
  fit(df_train)

Generate predictions and bind them together with the true values from the test data.

predictions_xgb <- xgb_fit %>%
  predict(new_data = df_test) %>% 
  bind_cols(df_test %>% select(rate_homeless))

Show the RMSE. Compare the result to the test RMSE for the other models.

predictions_xgb %>%
  metrics(rate_homeless, .pred) 
## # A tibble: 3 × 3
##   .metric .estimator .estimate
##   <chr>   <chr>          <dbl>
## 1 rmse    standard       9.11 
## 2 rsq     standard       0.417
## 3 mae     standard       5.77

Plot the ACT scores and the prediction

plot(df_test$rate_homeless, predictions_xgb$.pred, pch = 20, xlab = "Homeless rate", ylab = "Predicted homeless rate")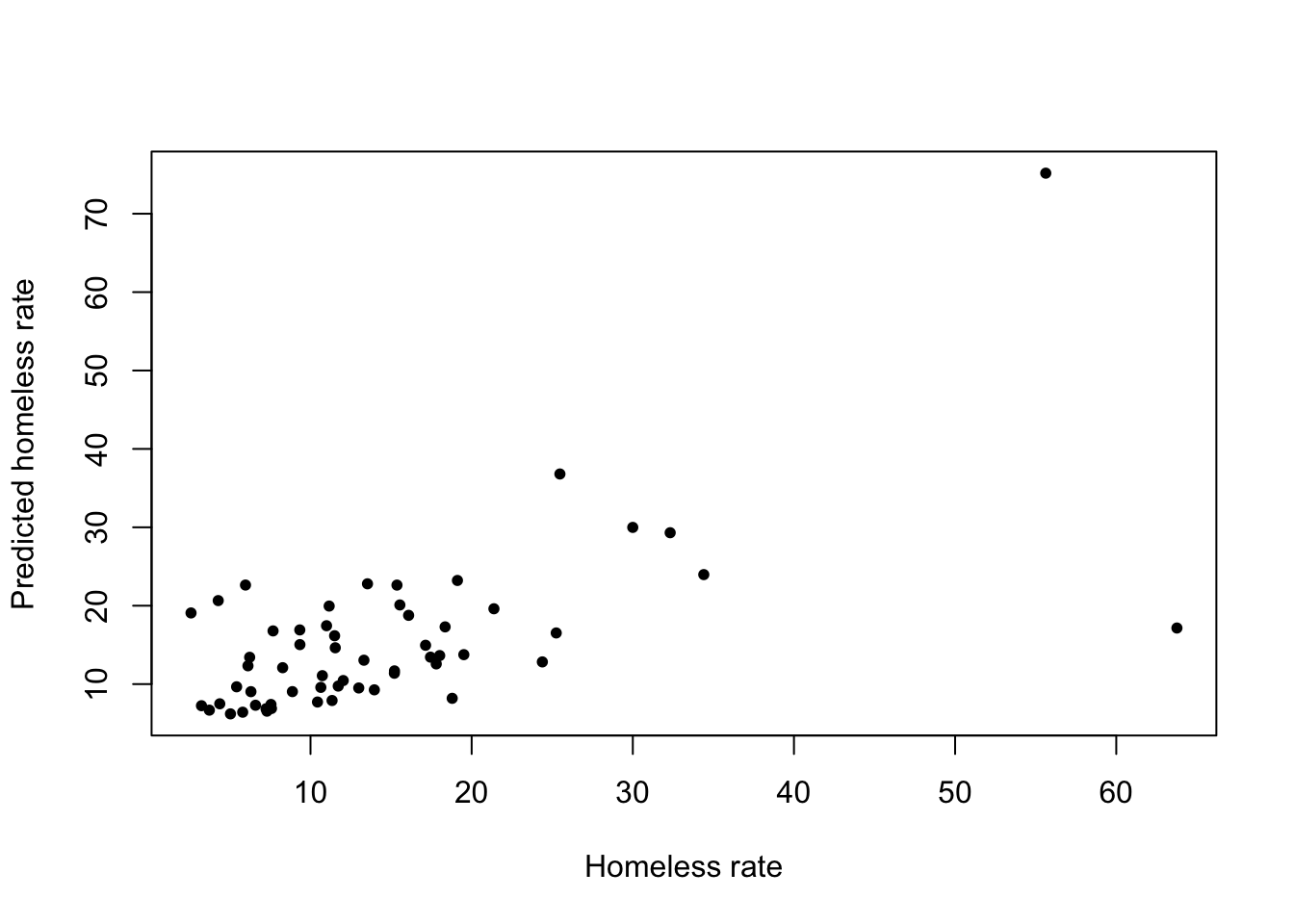

3.5.6.4 Relative importance of predictors

Look at which predictors are most important in the model

xgb_fit %>%
  pull_workflow_fit() %>%
  vip(geom = "col")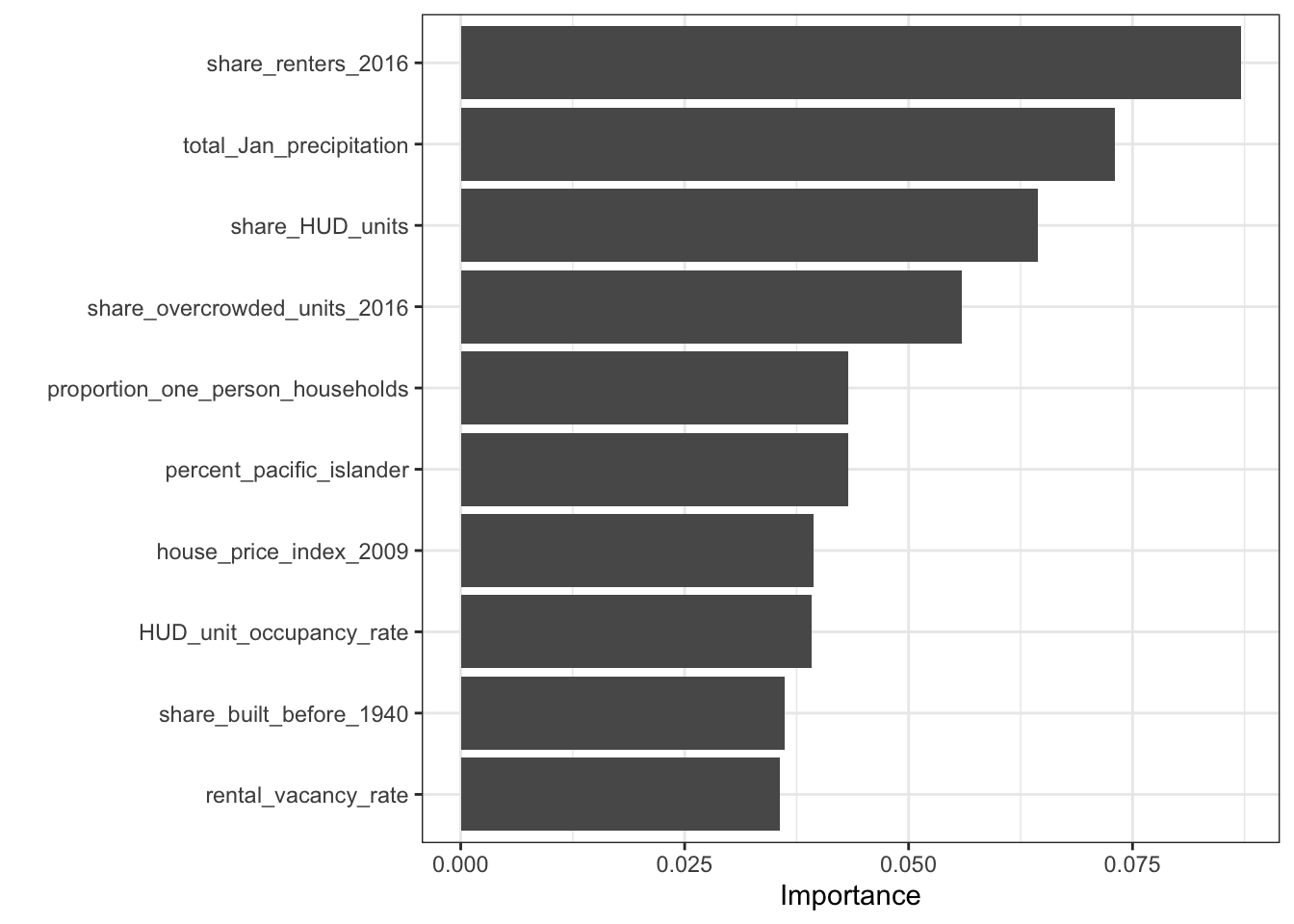

3.5.7 Compare models

You used several methods to construct a model

  1. Use statistical significance to create a multiple linear regression model.
  2. Best subset selection for a multiple linear regression model.
  3. Lasso
  4. Ridge regression
  5. XGBoost

Compare the performance of the models.

3.6 Additional step

In addition to completing the above analyses, you should perform any revisions to the models that you think might improve their performance. Consult Canvas for further directions.

3.7 Conclusion

After completing your analyses, you will make your conclusions and communicate your results. Consult Canvas for further directions.