Chapter 2 Education inequality

2.1 Introduction

This project addresses inequality of educational opportunity in U.S. high schools. Here we will focus on average student performance on the ACT or SAT exams that students take as part of the college application process.

We expect a range of school performance on these exams, but is school performance predicted by socioeconomic factors?

2.2 Data Collection

This project utilizes two data sets. The primary data set is the EdGap data set from EdGap.org. This data set from 2016 includes information about average ACT or SAT scores for schools and several socioeconomic characteristics of the school district. The secondary data set is basic information about each school from the National Center for Education Statistics.

2.2.1 EdGap data

All socioeconomic data (household income, unemployment, adult educational attainment, and family structure) are from the Census Bureau’s American Community Survey.

EdGap.org report that ACT and SAT score data is from each state’s department of education or some other public data release. The nature of the other public data release is not known.

The quality of the census data and the department of education data can be assumed to be reasonably high.

EdGap.org do not indicate that they processed the data in any way. The data were assembled by the EdGap.org team, so there is always the possibility for human error. Given the public nature of the data, we would be able to consult the original data sources to check the quality of the data if we had any questions.

2.2.2 School information data

The school information data is from the National Center for Education Statistics. This data set consists of basic identifying information about schools and can be assumed to be of reasonably high quality. As for the EdGap.org data, the school information data is public, so we would be able to consult the original data sources to check the quality of the data if we had any questions.

2.2.3 Data ethics

2.2.3.1 Data Science Ethics Checklist

Deon badge

A. Problem Formulation

  • A.1 Well-Posed Problem: Is it possible to answer our question with data? Is the problem well-posed?

B. Data Collection

  • B.1 Informed consent: If there are human subjects, have they given informed consent, where subjects affirmatively opt-in and have a clear understanding of the data uses to which they consent?
  • B.2 Collection bias: Have we considered sources of bias that could be introduced during data collection and survey design and taken steps to mitigate those?
  • B.3 Limit PII exposure: Have we considered ways to minimize exposure of personally identifiable information (PII) for example through anonymization or not collecting information that isn’t relevant for analysis?
  • B.4 Downstream bias mitigation: Have we considered ways to enable testing downstream results for biased outcomes (e.g., collecting data on protected group status like race or gender)?

C. Data Storage

  • C.1 Data security: Do we have a plan to protect and secure data (e.g., encryption at rest and in transit, access controls on internal users and third parties, access logs, and up-to-date software)?
  • C.2 Right to be forgotten: Do we have a mechanism through which an individual can request their personal information be removed?
  • C.3 Data retention plan: Is there a schedule or plan to delete the data after it is no longer needed?

D. Analysis

  • D.1 Missing perspectives: Have we sought to address blindspots in the analysis through engagement with relevant stakeholders (e.g., checking assumptions and discussing implications with affected communities and subject matter experts)?
  • D.2 Dataset bias: Have we examined the data for possible sources of bias and taken steps to mitigate or address these biases (e.g., stereotype perpetuation, confirmation bias, imbalanced classes, or omitted confounding variables)?
  • D.3 Honest representation: Are our visualizations, summary statistics, and reports designed to honestly represent the underlying data?
  • D.4 Privacy in analysis: Have we ensured that data with PII are not used or displayed unless necessary for the analysis?
  • D.5 Auditability: Is the process of generating the analysis well documented and reproducible if we discover issues in the future?

E. Modeling

  • E.1 Proxy discrimination: Have we ensured that the model does not rely on variables or proxies for variables that are unfairly discriminatory?
  • E.2 Fairness across groups: Have we tested model results for fairness with respect to different affected groups (e.g., tested for disparate error rates)?
  • E.3 Metric selection: Have we considered the effects of optimizing for our defined metrics and considered additional metrics?
  • E.4 Explainability: Can we explain in understandable terms a decision the model made in cases where a justification is needed?
  • E.5 Communicate bias: Have we communicated the shortcomings, limitations, and biases of the model to relevant stakeholders in ways that can be generally understood?

F. Deployment

  • F.1 Redress: Have we discussed with our organization a plan for response if users are harmed by the results (e.g., how does the data science team evaluate these cases and update analysis and models to prevent future harm)?
  • F.2 Roll back: Is there a way to turn off or roll back the model in production if necessary?
  • F.3 Concept drift: Do we test and monitor for concept drift to ensure the model remains fair over time?
  • F.4 Unintended use: Have we taken steps to identify and prevent unintended uses and abuse of the model and do we have a plan to monitor these once the model is deployed?

Data Science Ethics Checklist generated with deon.

We will discuss these issues in class.

2.3 Data Preparation

2.3.1 Load necessary packages

#readxl lets us read Excel files
library(readxl)
#GGally has a nice pairs plotting function
library(GGally)
#skimr provides a nice summary of a data set
library(skimr)
#leaps will be used for model selection
library(leaps)
#kableExtra will be used to make tables in the html document
library(kableExtra)
#latex2exp lets us use LaTex in ggplot
library(latex2exp)
#tidyverse contains packages we will use for processing and plotting data
library(tidyverse)

2.3.2 Load the data

2.3.2.1 Load the EdGap set

\(\rightarrow\) Load the data set contained in the file EdGap_data.xlsx and name the data frame edgap.

Show Coding Hint

Use the function read_excel from the package readxl to load the data.


Show Answer 
edgap <- read_excel("EdGap_data.xlsx")


2.3.3 Explore the contents of the data set

\(\rightarrow\) Look at the first few rows of the data frame.

Show Coding Hint

You can use the function head to see the head of the data frame.


Show Answer 
head(edgap, n = 5)
## # A tibble: 5 × 7
##   `NCESSCH School ID` `CT Unemployment …` `CT Pct Adults…` `CT Pct Childr…` `CT Median Hou…` `School ACT av…`
##                 <dbl>               <dbl>            <dbl>            <dbl>            <dbl>            <dbl>
## 1        100001600143              0.118             0.445            0.346            42820             20.4
## 2        100008000024              0.0640            0.663            0.768            89320             19.5
## 3        100008000225              0.0565            0.702            0.713            84140             19.6
## 4        100017000029              0.0447            0.692            0.641            56500             17.7
## 5        100018000040              0.0770            0.640            0.834            54015             18.2
## # … with 1 more variable: `School Pct Free and Reduced Lunch` <dbl>
We used the option n = 5 to show the first 5 rows.


Use the View function to explore the full data set.

View(edgap)

2.3.3.1 Load school information data

\(\rightarrow\) Load the data set contained in the file ccd_sch_029_1617_w_1a_11212017.csv and name the data frame school_info.

Show Answer 
school_info <- read_csv("ccd_sch_029_1617_w_1a_11212017.csv")
## Warning: One or more parsing issues, see `problems()` for details
## Rows: 102181 Columns: 65
## ── Column specification ─────────────────────────────────────────────────────────────────────────────────────
## Delimiter: ","
## chr (60): SCHOOL_YEAR, FIPST, STATENAME, ST, SCH_NAME, LEA_NAME, STATE_AGENCY_NO, UNION, ST_LEAID, LEAID,...
## dbl  (3): SY_STATUS, UPDATED_STATUS, SCH_TYPE
## lgl  (2): MSTREET3, LSTREET3
## 
## ℹ Use `spec()` to retrieve the full column specification for this data.
## ℹ Specify the column types or set `show_col_types = FALSE` to quiet this message.


\(\rightarrow\) Look at the first few rows of the data frame.

Show Answer 
head(school_info)
## # A tibble: 6 × 65
##   SCHOOL_YEAR FIPST STATENAME ST    SCH_NAME   LEA_NAME STATE_AGENCY_NO UNION ST_LEAID LEAID ST_SCHID NCESSCH
##   <chr>       <chr> <chr>     <chr> <chr>      <chr>    <chr>           <chr> <chr>    <chr> <chr>    <chr>  
## 1 2016-2017   01    ALABAMA   AL    Sequoyah … Alabama… 01              <NA>  AL-210   0100… AL-210-… 010000…
## 2 2016-2017   01    ALABAMA   AL    Camps      Alabama… 01              <NA>  AL-210   0100… AL-210-… 010000…
## 3 2016-2017   01    ALABAMA   AL    Det Ctr    Alabama… 01              <NA>  AL-210   0100… AL-210-… 010000…
## 4 2016-2017   01    ALABAMA   AL    Wallace S… Alabama… 01              <NA>  AL-210   0100… AL-210-… 010000…
## 5 2016-2017   01    ALABAMA   AL    McNeel Sc… Alabama… 01              <NA>  AL-210   0100… AL-210-… 010000…
## 6 2016-2017   01    ALABAMA   AL    Alabama Y… Alabama… 01              <NA>  AL-210   0100… AL-210-… 010000…
## # … with 53 more variables: SCHID <chr>, MSTREET1 <chr>, MSTREET2 <chr>, MSTREET3 <lgl>, MCITY <chr>,
## #   MSTATE <chr>, MZIP <chr>, MZIP4 <chr>, LSTREET1 <chr>, LSTREET2 <chr>, LSTREET3 <lgl>, LCITY <chr>,
## #   LSTATE <chr>, LZIP <chr>, LZIP4 <chr>, PHONE <chr>, WEBSITE <chr>, SY_STATUS <dbl>,
## #   SY_STATUS_TEXT <chr>, UPDATED_STATUS <dbl>, UPDATED_STATUS_TEXT <chr>, EFFECTIVE_DATE <chr>,
## #   SCH_TYPE_TEXT <chr>, SCH_TYPE <dbl>, RECON_STATUS <chr>, OUT_OF_STATE_FLAG <chr>, CHARTER_TEXT <chr>,
## #   CHARTAUTH1 <chr>, CHARTAUTHN1 <chr>, CHARTAUTH2 <chr>, CHARTAUTHN2 <chr>, NOGRADES <chr>,
## #   G_PK_OFFERED <chr>, G_KG_OFFERED <chr>, G_1_OFFERED <chr>, G_2_OFFERED <chr>, G_3_OFFERED <chr>, …


2.3.4 Check for a tidy data frame

In a tidy data set, each column is a variable or id and each row is an observation. We again start by looking at the head of the data frame to determine if the data frame is tidy.

2.3.4.1 EdGap data

head(edgap)
## # A tibble: 6 × 7
##   `NCESSCH School ID` `CT Unemployment …` `CT Pct Adults…` `CT Pct Childr…` `CT Median Hou…` `School ACT av…`
##                 <dbl>               <dbl>            <dbl>            <dbl>            <dbl>            <dbl>
## 1        100001600143              0.118             0.445            0.346            42820             20.4
## 2        100008000024              0.0640            0.663            0.768            89320             19.5
## 3        100008000225              0.0565            0.702            0.713            84140             19.6
## 4        100017000029              0.0447            0.692            0.641            56500             17.7
## 5        100018000040              0.0770            0.640            0.834            54015             18.2
## 6        100019000050              0.0801            0.673            0.483            50649             17.0
## # … with 1 more variable: `School Pct Free and Reduced Lunch` <dbl>

The units of observation are the schools. Each school occupies one row of the data frame, which is what we want for the rows.


\(\rightarrow\) What variables are present? What types of variables are present?

Show Coding Hint

There are several ways to get this information:

  1. The head of the data frame shows the names of the variables and how they are represented.

  2. The functions skim or skim_without_charts from the library skimr produces a detailed summary of the data.

  3. The functions glimpse and str produce a summary of the data frame that is similar to the head.

You should explore multiple approaches as you learn what each function can do, but you do not need to use all of the approaches each time you explore a data set.

Show Answer 
skim(edgap)
Table 2.1: Data summary
Name edgap
Number of rows 7986
Number of columns 7
_______________________
Column type frequency:
numeric 7
________________________
Group variables None

Variable type: numeric

skim_variable n_missing complete_rate mean sd p0 p25 p50 p75 p100 hist
NCESSCH School ID 0 1 3.321869e+11 1.323638e+11 1.000016e+11 2.105340e+11 3.600085e+11 4.226678e+11 5.60583e+11 ▇▆▆▅▇
CT Unemployment Rate 14 1 1.000000e-01 6.000000e-02 0.000000e+00 6.000000e-02 9.000000e-02 1.200000e-01 5.90000e-01 ▇▃▁▁▁
CT Pct Adults with College Degree 13 1 5.700000e-01 1.700000e-01 9.000000e-02 4.500000e-01 5.500000e-01 6.800000e-01 1.00000e+00 ▁▅▇▅▂
CT Pct Childre In Married Couple Family 25 1 6.300000e-01 2.000000e-01 0.000000e+00 5.200000e-01 6.700000e-01 7.800000e-01 1.00000e+00 ▁▂▅▇▃
CT Median Household Income 20 1 5.202691e+04 2.422806e+04 3.589000e+03 3.659725e+04 4.683350e+04 6.136925e+04 2.26181e+05 ▇▆▁▁▁
School ACT average (or equivalent if SAT score) 0 1 2.018000e+01 2.600000e+00 -3.070000e+00 1.860000e+01 2.040000e+01 2.191000e+01 3.23600e+01 ▁▁▂▇▁
School Pct Free and Reduced Lunch 0 1 4.200000e-01 2.400000e-01 -5.000000e-02 2.400000e-01 3.800000e-01 5.800000e-01 1.00000e+00 ▃▇▆▃▂

We have 7 columns, but the first column is a school ID, not a variable measured for the school. It is also important to note that each column is a unique variable; we do not have values for one variable that are separated over multiple columns. So, there are 6 variables present.

Each column contains numeric values. We should be careful to note that this does not mean that each column is a numerical variable. For example, NCESSCH School ID is an identifier, so even though it is coded as a numeric value, it is a categorical variable. We may make transformations of such variables to factors to help with analyses.

Here we provide a more readable description of each variable.

Data dictionary

name description
NCESSCH School ID NCES school ID
CT Unemployment Rate unemployment rate
CT Pct Adults with College Degree percent of adults with a college degree
CT Pct Childre In Married Couple Family percent of children in a married couple family
CT Median Household Income median household income
School ACT average (or equivalent if SAT score) average school ACT or equivalent if SAT score
School Pct Free and Reduced Lunch percent of students at the school who receive free or reduced price lunch


\(\rightarrow\) Is the edgap data frame tidy?

Show Answer

Yes, each column is a variable or id and each row is an observation, so the data frame is tidy.

2.3.4.2 School information data

We again start by looking at the head of the data frame to determine if the data frame is tidy.

head(school_info)
## # A tibble: 6 × 65
##   SCHOOL_YEAR FIPST STATENAME ST    SCH_NAME   LEA_NAME STATE_AGENCY_NO UNION ST_LEAID LEAID ST_SCHID NCESSCH
##   <chr>       <chr> <chr>     <chr> <chr>      <chr>    <chr>           <chr> <chr>    <chr> <chr>    <chr>  
## 1 2016-2017   01    ALABAMA   AL    Sequoyah … Alabama… 01              <NA>  AL-210   0100… AL-210-… 010000…
## 2 2016-2017   01    ALABAMA   AL    Camps      Alabama… 01              <NA>  AL-210   0100… AL-210-… 010000…
## 3 2016-2017   01    ALABAMA   AL    Det Ctr    Alabama… 01              <NA>  AL-210   0100… AL-210-… 010000…
## 4 2016-2017   01    ALABAMA   AL    Wallace S… Alabama… 01              <NA>  AL-210   0100… AL-210-… 010000…
## 5 2016-2017   01    ALABAMA   AL    McNeel Sc… Alabama… 01              <NA>  AL-210   0100… AL-210-… 010000…
## 6 2016-2017   01    ALABAMA   AL    Alabama Y… Alabama… 01              <NA>  AL-210   0100… AL-210-… 010000…
## # … with 53 more variables: SCHID <chr>, MSTREET1 <chr>, MSTREET2 <chr>, MSTREET3 <lgl>, MCITY <chr>,
## #   MSTATE <chr>, MZIP <chr>, MZIP4 <chr>, LSTREET1 <chr>, LSTREET2 <chr>, LSTREET3 <lgl>, LCITY <chr>,
## #   LSTATE <chr>, LZIP <chr>, LZIP4 <chr>, PHONE <chr>, WEBSITE <chr>, SY_STATUS <dbl>,
## #   SY_STATUS_TEXT <chr>, UPDATED_STATUS <dbl>, UPDATED_STATUS_TEXT <chr>, EFFECTIVE_DATE <chr>,
## #   SCH_TYPE_TEXT <chr>, SCH_TYPE <dbl>, RECON_STATUS <chr>, OUT_OF_STATE_FLAG <chr>, CHARTER_TEXT <chr>,
## #   CHARTAUTH1 <chr>, CHARTAUTHN1 <chr>, CHARTAUTH2 <chr>, CHARTAUTHN2 <chr>, NOGRADES <chr>,
## #   G_PK_OFFERED <chr>, G_KG_OFFERED <chr>, G_1_OFFERED <chr>, G_2_OFFERED <chr>, G_3_OFFERED <chr>, …

It is more difficult to assess whether this data frame is tidy because of the large number of columns with confusing names.

We have 65 columns, but many of the columns are identifying features of the school and are irrelevant for the analysis. We will select a subset of columns and do the analysis on the subset.

2.3.4.3 Select a subset of columns

We want to select the following variables:

name description
NCESSCH NCES School ID
MSTATE State name
MZIP Zip code
SCH_TYPE_TEXT School type
LEVEL LEVEL


\(\rightarrow\) Use the select function to select these columns from the data frame.

Show Answer 
#We redefine the data frame to be the smaller version
school_info <- school_info %>% 
  select(NCESSCH,MSTATE,MZIP,SCH_TYPE_TEXT,LEVEL)

\(\rightarrow\) Examine the head of the new, smaller data frame

Show Answer 
head(school_info)
## # A tibble: 6 × 5
##   NCESSCH      MSTATE MZIP  SCH_TYPE_TEXT      LEVEL         
##   <chr>        <chr>  <chr> <chr>              <chr>         
## 1 010000200277 AL     35220 Alternative School High          
## 2 010000201667 AL     36057 Alternative School High          
## 3 010000201670 AL     36057 Alternative School High          
## 4 010000201705 AL     36057 Alternative School High          
## 5 010000201706 AL     35206 Alternative School High          
## 6 010000201876 AL     35080 Regular School     Not applicable

\(\rightarrow\) Is the data frame tidy?

Show Answer

Yes, each column is a variable or id and each row is an observation, so the data frame is tidy.

2.3.5 Further exploration of basic properties

2.3.5.1 EdGap data

\(\rightarrow\) How many observations are in the EdGap data set?

Show Algorithmic Hint

The number of observations is equal to the number of rows in the data frame.

Show Coding Hint

The number of rows in a data frame is one of the outputs of the skim function.

The number of rows in a data frame can be found using the function nrow.

You can also use the function dim to get the number of rows and columns in a data frame.

Show Answer 
nrow(edgap)
## [1] 7986
There are 7986 rows, so there are 7986 observations in the data set.

2.3.5.2 School information data

\(\rightarrow\) How many observations are in the school information data set?

Show Answer 
nrow(school_info)
## [1] 102181
There are 102,181 rows, so there are 102,181 observations in the data set. The EdGap data clearly is a subset of all schools.

2.3.6 Data cleaning

2.3.6.1 Rename variables

In any analysis, we might rename the variables in the data frame to make them easier to work with. We have seen that the variable names in the edgap data frame allow us to understand them, but they can be improved. In contrast, many of the variables in the school_info data frame have confusing names.

Importantly, we should be thinking ahead to joining the two data frames based on the school ID. To facilitate this join, we should give the school ID column the same name in each data frame.

2.3.6.2 EdGap data

\(\rightarrow\) View the column names for the EdGap data
Show Answer 
names(edgap)
## [1] "NCESSCH School ID"                               "CT Unemployment Rate"                           
## [3] "CT Pct Adults with College Degree"               "CT Pct Childre In Married Couple Family"        
## [5] "CT Median Household Income"                      "School ACT average (or equivalent if SAT score)"
## [7] "School Pct Free and Reduced Lunch"


To follow best practices, we should

  1. Use all lowercase letters in variable names.
  2. Use underscores _ between words in a variable name. Do not use blank spaces, as they have done.
  3. Do not use abbreviations, e.g. Pct, that can easily be written out.
  4. Be consistent with naming structure across variables. For example, the descriptions rate, percent, median, and average should all either be at the beginning or end of the name.

We will use the rename function from the dplyr package to rename the columns.

#The new name for the column is on the left of the =

edgap <- edgap %>% 
  rename(id = "NCESSCH School ID",
         rate_unemployment = "CT Unemployment Rate",
         percent_college = "CT Pct Adults with College Degree",
         percent_married = "CT Pct Childre In Married Couple Family",
         median_income = "CT Median Household Income",
         average_act = "School ACT average (or equivalent if SAT score)",
         percent_lunch = "School Pct Free and Reduced Lunch"
        )

\(\rightarrow\) Use the names function to see that the names have changed

Show Answer 
names(edgap)
## [1] "id"                "rate_unemployment" "percent_college"   "percent_married"   "median_income"    
## [6] "average_act"       "percent_lunch"

2.3.6.3 School information data

\(\rightarrow\) View the column names for the school information data

Show Answer 
names(school_info)
## [1] "NCESSCH"       "MSTATE"        "MZIP"          "SCH_TYPE_TEXT" "LEVEL"


The names can be improved for readability. We also have the constraint that we rename ncessch to id to be consistent with the edgap data.

Rename the columns of the school information data frame.

school_info <- school_info %>% 
  rename(id = "NCESSCH",
         state = "MSTATE",
         zip_code = "MZIP",
         school_type = "SCH_TYPE_TEXT",
         school_level = "LEVEL"
         )

#Print the names to see the change
names(school_info)
## [1] "id"           "state"        "zip_code"     "school_type"  "school_level"

2.3.6.4 Join

We will join the edgap and school_info data frames based on the school ID. We should first note that the id is coded differently in the two data frames:

typeof(edgap$id)
## [1] "double"
typeof(school_info$id)
## [1] "character"

While id is a number, it is a categorical variable and should be represented as a character variable in R.

Convert id in edgap id to a character variable:

We will use the mutate function from the dplyr package to convert id in edgap id to a character variable:

edgap <- edgap %>% 
  mutate(id = as.character(id))

#Check that the type has been converted to character
typeof(edgap$id)
## [1] "character"

We will now join the data frames. We want to perform a left join based on the school ID id so that we incorporate all of the school information into the edgap data frame.

edgap <- edgap %>% 
  left_join(school_info, by = "id")

Examine the head of the new data frame:

head(edgap)
## # A tibble: 6 × 11
##   id           rate_unemployme… percent_college percent_married median_income average_act percent_lunch state
##   <chr>                   <dbl>           <dbl>           <dbl>         <dbl>       <dbl>         <dbl> <chr>
## 1 100001600143           0.118            0.445           0.346         42820        20.4        0.0669 DE   
## 2 100008000024           0.0640           0.663           0.768         89320        19.5        0.112  DE   
## 3 100008000225           0.0565           0.702           0.713         84140        19.6        0.0968 DE   
## 4 100017000029           0.0447           0.692           0.641         56500        17.7        0.297  DE   
## 5 100018000040           0.0770           0.640           0.834         54015        18.2        0.263  DE   
## 6 100019000050           0.0801           0.673           0.483         50649        17.0        0.425  DE   
## # … with 3 more variables: zip_code <chr>, school_type <chr>, school_level <chr>

2.3.6.5 Identify and deal with missing values

\(\rightarrow\) How many missing values are there in each column? Give the number of missing values and the percent of values in each column that are missing.

Recall that missing values are coded in R with NA, or they may be empty. We want to convert empty cells to NA, so that we can use the function is.na to find all missing values. The function read_excel that we used to read in the data does this automatically, so we do not need to take further action to deal with empty cells.

Show Coding Hint

This is easiest using the skim function. This function count the number of NAs in each column, gives the percentage of complete results, and provides the 5-number summary, mean, and standard deviation of each column.

The function is.na produces a set of logical TRUE and FALSE values the same dimension as the data that indicates whether a value is NA or not.

The functions map_df and sum, or the function colSums can be used together with is.na to count the number of NAs in each column.

Show Answer

Solution using map_df

edgap %>% 
  map_df(~sum(is.na(.)))
## # A tibble: 1 × 11
##      id rate_unemployment percent_college percent_married median_income average_act percent_lunch state
##   <int>             <int>           <int>           <int>         <int>       <int>         <int> <int>
## 1     0                14              13              25            20           0             0    88
## # … with 3 more variables: zip_code <int>, school_type <int>, school_level <int>

Show the results as a percent of the number of observations:

edgap %>% 
  map_df(~sum(is.na(.)))/nrow(edgap)*100 
##   id rate_unemployment percent_college percent_married median_income average_act percent_lunch    state
## 1  0         0.1753068       0.1627849       0.3130478     0.2504383           0             0 1.101928
##   zip_code school_type school_level
## 1 1.101928    1.101928     1.101928

Solution using colSums

#Using pipes 
edgap %>% 
  is.na() %>% 
  colSums()
##                id rate_unemployment   percent_college   percent_married     median_income       average_act 
##                 0                14                13                25                20                 0 
##     percent_lunch             state          zip_code       school_type      school_level 
##                 0                88                88                88                88
#alternatively without using the pipe operator:
#colSums(is.na(edgap))

Show the results as a percent of the number of observations:

edgap %>% 
  is.na() %>% 
  colSums()/nrow(edgap)*100 
##                id rate_unemployment   percent_college   percent_married     median_income       average_act 
##         0.0000000         0.1753068         0.1627849         0.3130478         0.2504383         0.0000000 
##     percent_lunch             state          zip_code       school_type      school_level 
##         0.0000000         1.1019284         1.1019284         1.1019284         1.1019284

Solution using skim

skim(edgap)
Table 2.2: Data summary
Name edgap
Number of rows 7986
Number of columns 11
_______________________
Column type frequency:
character 5
numeric 6
________________________
Group variables None

Variable type: character

skim_variable n_missing complete_rate min max empty n_unique whitespace
id 0 1.00 12 12 0 7986 0
state 88 0.99 2 2 0 20 0
zip_code 88 0.99 5 5 0 6519 0
school_type 88 0.99 14 27 0 4 0
school_level 88 0.99 4 12 0 4 0

Variable type: numeric

skim_variable n_missing complete_rate mean sd p0 p25 p50 p75 p100 hist
rate_unemployment 14 1 0.10 0.06 0.00 0.06 0.09 0.12 0.59 ▇▃▁▁▁
percent_college 13 1 0.57 0.17 0.09 0.45 0.55 0.68 1.00 ▁▅▇▅▂
percent_married 25 1 0.63 0.20 0.00 0.52 0.67 0.78 1.00 ▁▂▅▇▃
median_income 20 1 52026.91 24228.06 3589.00 36597.25 46833.50 61369.25 226181.00 ▇▆▁▁▁
average_act 0 1 20.18 2.60 -3.07 18.60 20.40 21.91 32.36 ▁▁▂▇▁
percent_lunch 0 1 0.42 0.24 -0.05 0.24 0.38 0.58 1.00 ▃▇▆▃▂

We do not have any missing school IDs because this information is available for any school.

The columns average_act and percent_lunch do not have missing values. This is understandable because this is information on the students in the school.

The four columns that describe socioeconomic properties of the adults in the community do have missing values. However, less than half of one percent of the values are missing for each variable.

There are 88 schools where we do not have the basic school information.


\(\rightarrow\) Find the rows where the missing value occurs in each column.

Show Coding Hint

is.na(edgap) is a set of logical TRUE and FALSE values the same dimension as the data frame that indicates whether a value is NA or not.

The function which gives the location where is.an(edgap) is TRUE within each column if we apply the which function along the 2nd dimension.

Show Answer 
#is.na(edgap) is a set of logical TRUE and FALSE values the same dimension as the data frame that indicates whether a value is NA or not.
#the function `which` gives the location where is.an(edgap) is TRUE within each column because we apply the which function along the 2nd dimension.

apply(is.na(edgap),2,which)
## $id
## integer(0)
## 
## $rate_unemployment
##  [1]  142  143  205  364 1056 1074 2067 2176 2717 2758 2931 3973 4150 6103
## 
## $percent_college
##  [1]  142  205  364 1056 1074 2067 2176 2717 2758 2931 3973 4150 6103
## 
## $percent_married
##  [1]    7  142  143  205  364  465 1056 1074 2067 2176 2313 2419 2593 2717 2758 2774 2931 3905 3973 4150 4772
## [22] 5879 6103 6626 7248
## 
## $median_income
##  [1]  142  143  205  364  465 1056 1074 2067 2176 2419 2593 2717 2758 2931 3973 4150 5879 6103 6626 7248
## 
## $average_act
## integer(0)
## 
## $percent_lunch
## integer(0)
## 
## $state
##  [1]  482  483  485  486  487  488  490  507 1088 1428 1444 1458 1468 1575 1649 2028 2029 2042 2046 2047 2105
## [22] 2107 2575 2580 2589 2592 2617 2635 2688 2767 2771 2772 2773 2774 2775 2776 2777 2778 2779 2780 2781 2782
## [43] 2783 2784 2785 2786 2787 2788 2932 3001 3127 3487 3544 3830 4397 4660 4662 4665 4737 4766 4776 5096 5421
## [64] 5453 5454 5496 5568 5764 6006 6007 6025 6027 6029 6032 6034 6043 6044 6350 6354 6356 6357 6359 6379 6834
## [85] 6901 7564 7568 7961
## 
## $zip_code
##  [1]  482  483  485  486  487  488  490  507 1088 1428 1444 1458 1468 1575 1649 2028 2029 2042 2046 2047 2105
## [22] 2107 2575 2580 2589 2592 2617 2635 2688 2767 2771 2772 2773 2774 2775 2776 2777 2778 2779 2780 2781 2782
## [43] 2783 2784 2785 2786 2787 2788 2932 3001 3127 3487 3544 3830 4397 4660 4662 4665 4737 4766 4776 5096 5421
## [64] 5453 5454 5496 5568 5764 6006 6007 6025 6027 6029 6032 6034 6043 6044 6350 6354 6356 6357 6359 6379 6834
## [85] 6901 7564 7568 7961
## 
## $school_type
##  [1]  482  483  485  486  487  488  490  507 1088 1428 1444 1458 1468 1575 1649 2028 2029 2042 2046 2047 2105
## [22] 2107 2575 2580 2589 2592 2617 2635 2688 2767 2771 2772 2773 2774 2775 2776 2777 2778 2779 2780 2781 2782
## [43] 2783 2784 2785 2786 2787 2788 2932 3001 3127 3487 3544 3830 4397 4660 4662 4665 4737 4766 4776 5096 5421
## [64] 5453 5454 5496 5568 5764 6006 6007 6025 6027 6029 6032 6034 6043 6044 6350 6354 6356 6357 6359 6379 6834
## [85] 6901 7564 7568 7961
## 
## $school_level
##  [1]  482  483  485  486  487  488  490  507 1088 1428 1444 1458 1468 1575 1649 2028 2029 2042 2046 2047 2105
## [22] 2107 2575 2580 2589 2592 2617 2635 2688 2767 2771 2772 2773 2774 2775 2776 2777 2778 2779 2780 2781 2782
## [43] 2783 2784 2785 2786 2787 2788 2932 3001 3127 3487 3544 3830 4397 4660 4662 4665 4737 4766 4776 5096 5421
## [64] 5453 5454 5496 5568 5764 6006 6007 6025 6027 6029 6032 6034 6043 6044 6350 6354 6356 6357 6359 6379 6834
## [85] 6901 7564 7568 7961

Now we need to decide how to deal with the NAs. We have a few decisions to make:

  1. Do we drop rows that have NAs?
  2. Do we replace NAs with something like the mean of the variable?
  3. Do we replace NAs with estimates based on the other variable values?

There are some schools that are missing all four of the socioeconomic variables, e.g. at rows 142 and 205. However, many of the schools are missing only a subset of the variables. If we drop rows that have NAs, then we will negatively affect our analysis using the variables where data were present. So, we will not drop the rows in this data set that are missing the socioeconomic variables. We have so few missing values from each value that we will not worry about replacing NAs with some other value. We will selectively omit the NAs when working with those columns.

There are, however, 88 schools where we do not have the school information. This raises the possibility that the information is unreliable. Because we are not able to check from the source, we will omit these rows from the data set.

\(\rightarrow\) Use the filter function to drop only those rows where the state information is missing.

Show Answer 
edgap <- edgap %>% 
  filter(is.na(state) == FALSE)


Recheck for missing values:

skim(edgap)
Table 2.3: Data summary
Name edgap
Number of rows 7898
Number of columns 11
_______________________
Column type frequency:
character 5
numeric 6
________________________
Group variables None

Variable type: character

skim_variable n_missing complete_rate min max empty n_unique whitespace
id 0 1 12 12 0 7898 0
state 0 1 2 2 0 20 0
zip_code 0 1 5 5 0 6519 0
school_type 0 1 14 27 0 4 0
school_level 0 1 4 12 0 4 0

Variable type: numeric

skim_variable n_missing complete_rate mean sd p0 p25 p50 p75 p100 hist
rate_unemployment 14 1 0.10 0.06 0.00 0.06 0.09 0.12 0.59 ▇▃▁▁▁
percent_college 13 1 0.57 0.17 0.09 0.45 0.56 0.68 1.00 ▁▅▇▅▂
percent_married 24 1 0.64 0.20 0.00 0.53 0.67 0.78 1.00 ▁▂▅▇▃
median_income 20 1 52167.27 24173.80 3589.00 36786.75 47000.00 61516.75 226181.00 ▇▆▁▁▁
average_act 0 1 20.21 2.57 -3.07 18.64 20.40 21.94 32.36 ▁▁▂▇▁
percent_lunch 0 1 0.42 0.24 -0.05 0.24 0.38 0.57 1.00 ▃▇▆▃▂

2.3.7 Are there data points that look like errors?

We will do some quality control for the data set.

We can check the range of each variable to see that the values fall in the expected ranges.

summary(edgap)
##       id            rate_unemployment percent_college   percent_married  median_income     average_act    
##  Length:7898        Min.   :0.00000   Min.   :0.09149   Min.   :0.0000   Min.   :  3589   Min.   :-3.071  
##  Class :character   1st Qu.:0.05854   1st Qu.:0.45120   1st Qu.:0.5261   1st Qu.: 36787   1st Qu.:18.639  
##  Mode  :character   Median :0.08523   Median :0.55572   Median :0.6686   Median : 47000   Median :20.400  
##                     Mean   :0.09806   Mean   :0.56938   Mean   :0.6354   Mean   : 52167   Mean   :20.211  
##                     3rd Qu.:0.12272   3rd Qu.:0.67719   3rd Qu.:0.7778   3rd Qu.: 61517   3rd Qu.:21.935  
##                     Max.   :0.59028   Max.   :1.00000   Max.   :1.0000   Max.   :226181   Max.   :32.363  
##                     NA's   :14        NA's   :13        NA's   :24       NA's   :20                       
##  percent_lunch         state             zip_code         school_type        school_level      
##  Min.   :-0.05455   Length:7898        Length:7898        Length:7898        Length:7898       
##  1st Qu.: 0.23772   Class :character   Class :character   Class :character   Class :character  
##  Median : 0.37904   Mode  :character   Mode  :character   Mode  :character   Mode  :character  
##  Mean   : 0.41824                                                                              
##  3rd Qu.: 0.57060                                                                              
##  Max.   : 0.99873                                                                              
##

There are a few suspicious values. The minimum average_act is -3.071, but ACT scores must be non-negative. Similarly, the minimum percent_lunch is -0.05455, but a percent must be non-negative. These are out-of-range values. We do not have access to information about how these particular data points were generated, so we will remove them from the data set by converting them to NA.

#Number of NA ACT scores before conversion
sum(is.na(edgap$average_act))
## [1] 0
#Convert negative scores to NA
edgap[edgap$average_act < 0,"average_act"] = NA

#Number of NA ACT scores after conversion
sum(is.na(edgap$average_act))
## [1] 3

There were 3 schools with negative ACT scores, where the values were omitted from the data set.

#Number of NA percent_lunch values before conversion
sum(is.na(edgap$percent_lunch))
## [1] 0
#Convert negative values to NA
edgap[edgap$percent_lunch < 0,"percent_lunch"] = NA

#Number of NA percent_lunch values after conversion
sum(is.na(edgap$percent_lunch))
## [1] 20

There were 20 schools with negative percent free or reduced lunch, where the values were omitted from the data set.

\(\rightarrow\) What school levels are present in the data set and with what frequency? Present the results as a table and as a bar graph.

Show Answer

As a table:

edgap %>% 
  count(school_level) %>% 
  mutate(proportion = round(n/sum(n),3))
## # A tibble: 4 × 3
##   school_level     n proportion
##   <chr>        <int>      <dbl>
## 1 Elementary       2      0    
## 2 High          7230      0.915
## 3 Not reported    35      0.004
## 4 Other          631      0.08

As a graph:

edgap %>% 
  count(school_level) %>%
  mutate(school_level = fct_reorder(school_level, n)) %>% 
  ggplot(aes(x = school_level, y = n)) +
  geom_col() +
  coord_flip() +
  labs(x = "School level", y = "Count") +
  theme_bw()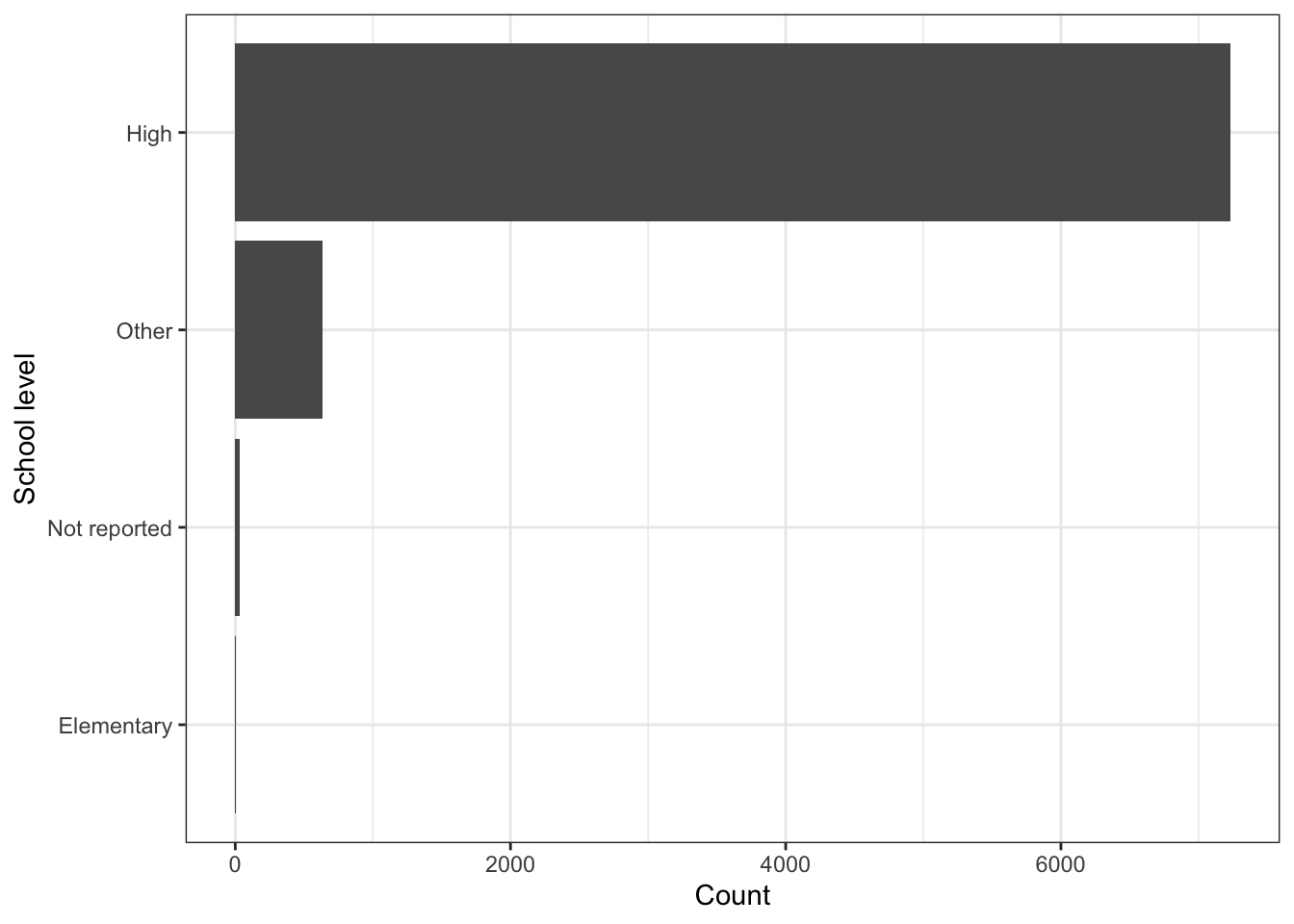

Most of the schools are high schools, but there are some schools listed as Other and Not reported.

It is strange that students in an elementary school are taking the ACT or SAT. We will limit our analysis to high schools.

\(\rightarrow\) Modify the edgap data frame to include only the schools that are high schools.

Show Answer 
edgap <- edgap %>% 
  filter(school_level == 'High')
edgap %>% 
  count(school_level) %>% 
  mutate(proportion = round(n/sum(n),3))
## # A tibble: 1 × 3
##   school_level     n proportion
##   <chr>        <int>      <dbl>
## 1 High          7230          1


2.4 Exploratory data analysis

We have two main goals when doing exploratory data analysis. The first is that we want to understand the data set more completely. The second goal is to explore relationships between the variables to help guide the modeling process to answer our specific question.

2.4.1 Graphical summaries

Make a pairs plot of the ACT scores and the socioeconomic variables. We will use the ggpairs function from the GGally package.

#It may take a few seconds to produce the plot

edgap %>% 
  select(-c(id,state,zip_code,school_type,school_level)) %>% 
  ggpairs(lower = list(continuous=wrap("smooth"))) +
  theme_bw()
## plot: [1,1] [=>-----------------------------------------------------------------------------] 3% est: 0s
## plot: [1,2] [===>---------------------------------------------------------------------------] 6% est: 2s
## plot: [1,3] [======>------------------------------------------------------------------------] 8% est: 2s
## plot: [1,4] [========>----------------------------------------------------------------------] 11% est: 3s
## plot: [1,5] [==========>--------------------------------------------------------------------] 14% est: 3s
## plot: [1,6] [============>------------------------------------------------------------------] 17% est: 2s
## plot: [2,1] [==============>----------------------------------------------------------------] 19% est: 2s
## plot: [2,2] [=================>-------------------------------------------------------------] 22% est: 2s
## plot: [2,3] [===================>-----------------------------------------------------------] 25% est: 2s
## plot: [2,4] [=====================>---------------------------------------------------------] 28% est: 2s
## plot: [2,5] [=======================>-------------------------------------------------------] 31% est: 2s
## plot: [2,6] [=========================>-----------------------------------------------------] 33% est: 2s
## plot: [3,1] [============================>--------------------------------------------------] 36% est: 2s
## plot: [3,2] [==============================>------------------------------------------------] 39% est: 2s
## plot: [3,3] [================================>----------------------------------------------] 42% est: 2s
## plot: [3,4] [==================================>--------------------------------------------] 44% est: 2s
## plot: [3,5] [====================================>------------------------------------------] 47% est: 1s
## plot: [3,6] [=======================================>---------------------------------------] 50% est: 1s
## plot: [4,1] [=========================================>-------------------------------------] 53% est: 1s
## plot: [4,2] [===========================================>-----------------------------------] 56% est: 1s
## plot: [4,3] [=============================================>---------------------------------] 58% est: 1s
## plot: [4,4] [===============================================>-------------------------------] 61% est: 1s
## plot: [4,5] [=================================================>-----------------------------] 64% est: 1s
## plot: [4,6] [====================================================>--------------------------] 67% est: 1s
## plot: [5,1] [======================================================>------------------------] 69% est: 1s
## plot: [5,2] [========================================================>----------------------] 72% est: 1s
## plot: [5,3] [==========================================================>--------------------] 75% est: 1s
## plot: [5,4] [============================================================>------------------] 78% est: 1s
## plot: [5,5] [===============================================================>---------------] 81% est: 1s
## plot: [5,6] [=================================================================>-------------] 83% est: 1s
## plot: [6,1] [===================================================================>-----------] 86% est: 0s
## plot: [6,2] [=====================================================================>---------] 89% est: 0s
## plot: [6,3] [=======================================================================>-------] 92% est: 0s
## plot: [6,4] [==========================================================================>----] 94% est: 0s
## plot: [6,5] [============================================================================>--] 97% est: 0s
## plot: [6,6] [===============================================================================]100% est: 0s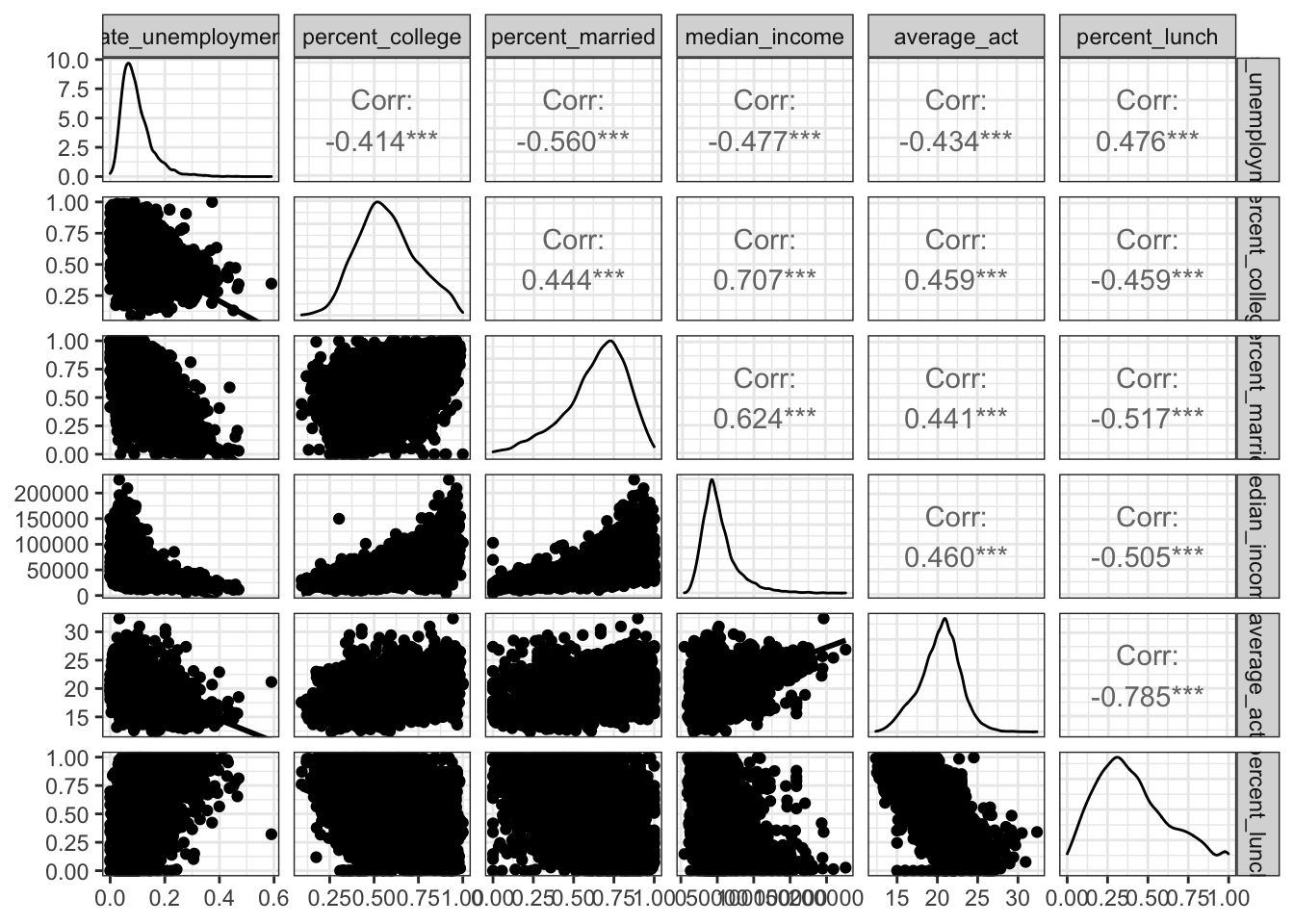

2.4.1.1 Distributions of individual numerical variables

\(\rightarrow\) Describe the shape of the distribution of each variable.

Show Answer

We examine the density plots along the main diagonal of the pairs plots.

All distributions appear to be unimodal.

rate_unemployment has a positively skewed distribution. The values near 0.6 may be outliers.

percent_college has a roughly symmetric distribution.

percent_married has a negatively skewed distribution.

average_act has an approximately normal distribution. This is not surprising for a distribution of averages.

median_income has a positively skewed distribution, which is what you expect for income distributions.

percent_lunch has a slightly positively skewed distribution.

2.4.1.2 Categorical variables

What states are present in the data set and with what frequency?

\(\rightarrow\) First find the states present.
Show Answer 
edgap %>% 
  select(state) %>% 
  unique()
## # A tibble: 20 × 1
##    state
##    <chr>
##  1 DE   
##  2 FL   
##  3 GA   
##  4 IL   
##  5 IN   
##  6 KY   
##  7 LA   
##  8 MA   
##  9 MI   
## 10 MO   
## 11 NJ   
## 12 NY   
## 13 NC   
## 14 OH   
## 15 PA   
## 16 TN   
## 17 TX   
## 18 WA   
## 19 WI   
## 20 WY
There are 20 states represented in the data set.


\(\rightarrow\) Now count the observations by state. Display the results as a bar graph.

Show Answer 
edgap %>% 
  count(state) %>% 
  ggplot(aes(x = state, y = n)) +
  geom_col() +
  coord_flip() +
  labs(x = "State", y = "Count") +
  theme_bw()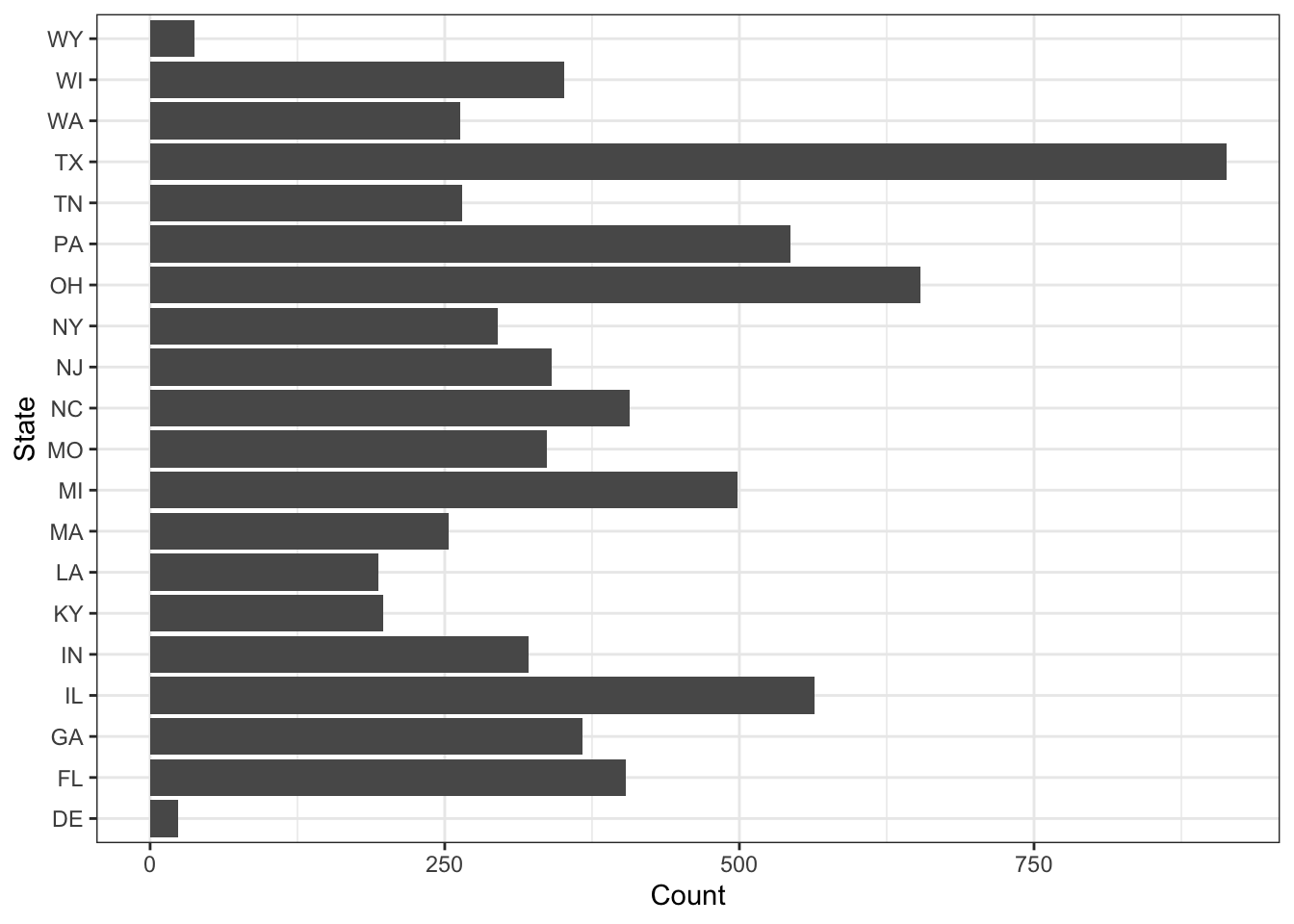


\(\rightarrow\) Reorder the states by count using fct_reorder

Show Answer 
edgap %>% 
  count(state) %>%
  mutate(state = fct_reorder(state, n)) %>% 
  ggplot(aes(x = state, y = n)) +
  geom_col() +
  coord_flip() +
  labs(x = "State", y = "Count") +
  theme_bw()

There is not an equal number of schools from the represented states.


\(\rightarrow\) What school types are present in the data set and with what frequency? Present the results as a table and as a bar graph.

Show Answer 
edgap %>% 
  count(school_type) %>% 
  mutate(proportion = round(n/sum(n),3))
## # A tibble: 4 × 3
##   school_type                     n proportion
##   <chr>                       <int>      <dbl>
## 1 Alternative School              9      0.001
## 2 Career and Technical School     1      0    
## 3 Regular School               7218      0.998
## 4 Special Education School        2      0

The vast majority (99.8%) are regular schools, but there are a few other types of schools.

We can also present the information as a graph:

edgap %>% 
  count(school_type) %>%
  mutate(school_type = fct_reorder(school_type, n)) %>% 
  ggplot(aes(x = school_type, y = n)) +
  geom_col() +
  coord_flip() +
  labs(x = "School type", y = "Count") +
  theme_bw()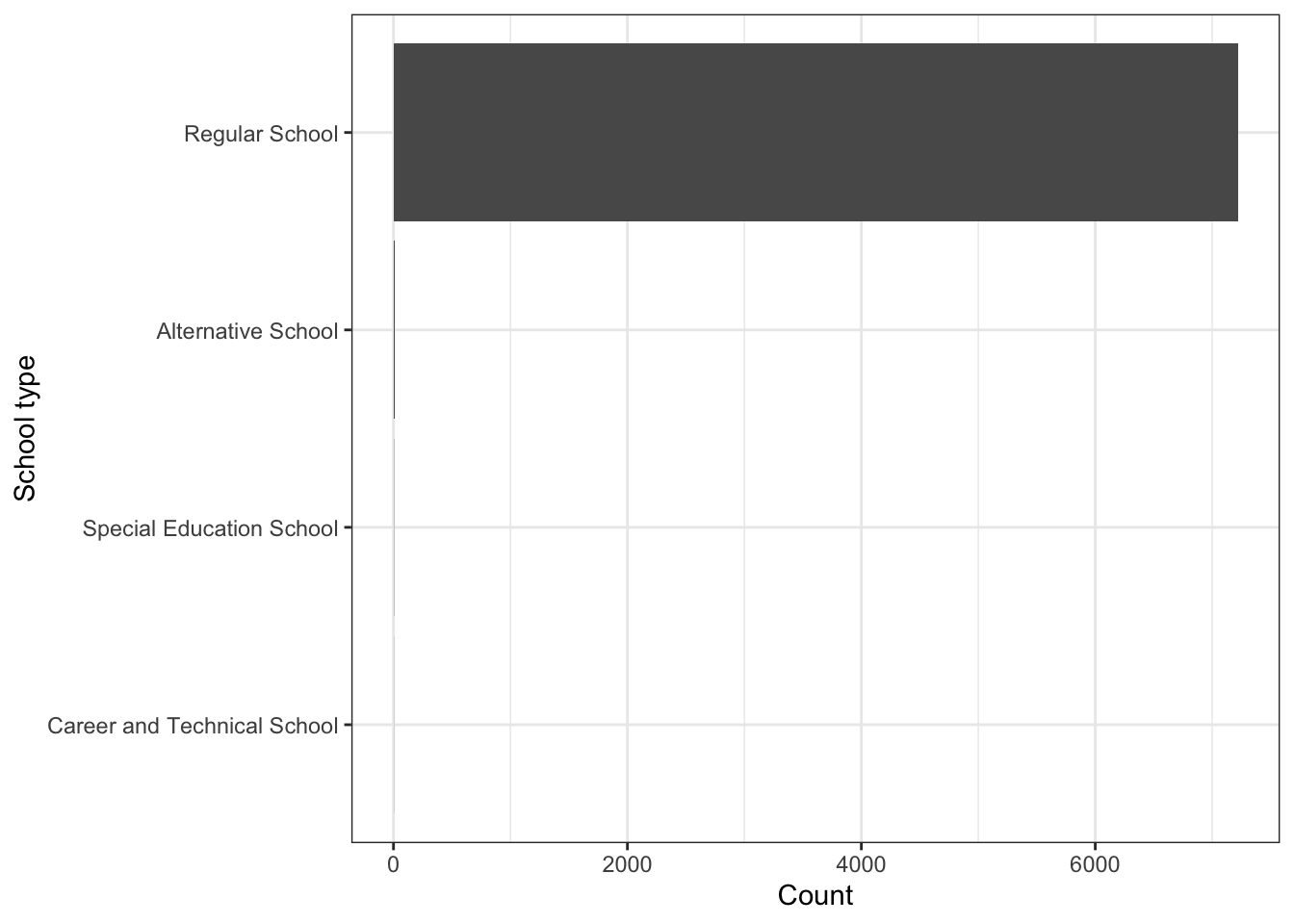
but the graph can be misleading because of the large number of regular schools and the few schools of the other types.


2.4.1.3 Focus on relationships with average_act

Our primary goal is to determine whether there is a relationship between the socioeconomic variables and average_act, so we will make plots to focus on those relationships.

The largest correlation coefficient between a socioeconomic variable and average_act is for percent_lunch, so we will start there.

\(\rightarrow\) Make a scatter plot of percent_lunch and average_act

Show Answer 
ggplot(edgap, aes(x = percent_lunch, y = average_act)) +
  geom_point() +
  labs(x = 'Percent reduced or free lunch', y = 'Average school ACT or equivalent if SAT') +
  theme_bw()
## Warning: Removed 23 rows containing missing values (geom_point).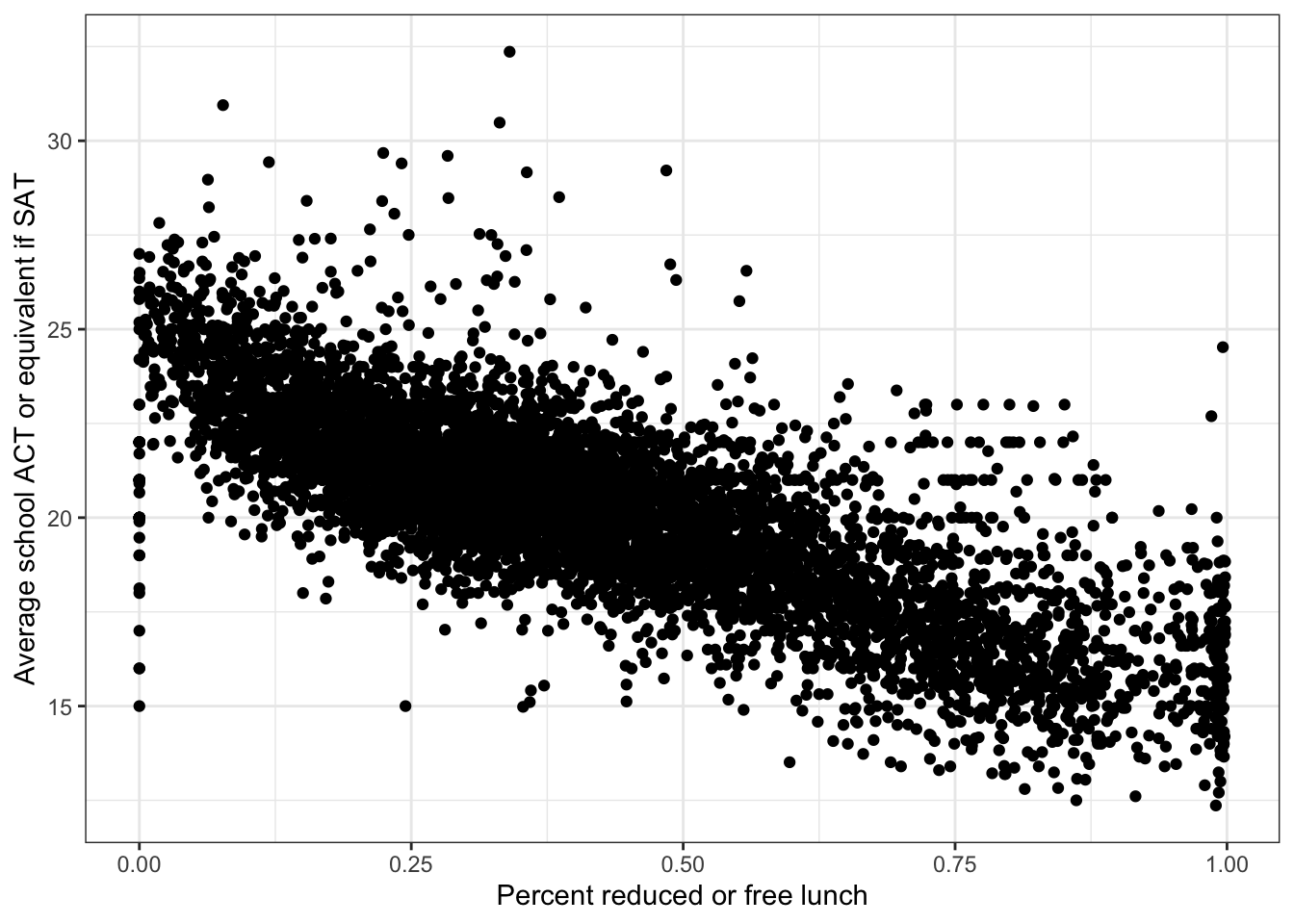

There is a clear negative linear association between percent_lunch and average_act.

Why is there a wide range of ACT scores at percent_lunch = 0? It may be the case that some schools have no students receiving free or reduced lunch because the program does not exist, not because there are no families that would qualify under typical standards. This would require further research into the availability of the free or reduced price lunch program.


\(\rightarrow\) Make a scatter plot of median_income and average_act

Show Answer 
ggplot(edgap, aes(x = median_income, y = average_act)) +
  geom_point() +
  labs(x = 'Median income ($)', y = 'Average school ACT or equivalent if SAT' ) +
  theme_bw()
## Warning: Removed 19 rows containing missing values (geom_point).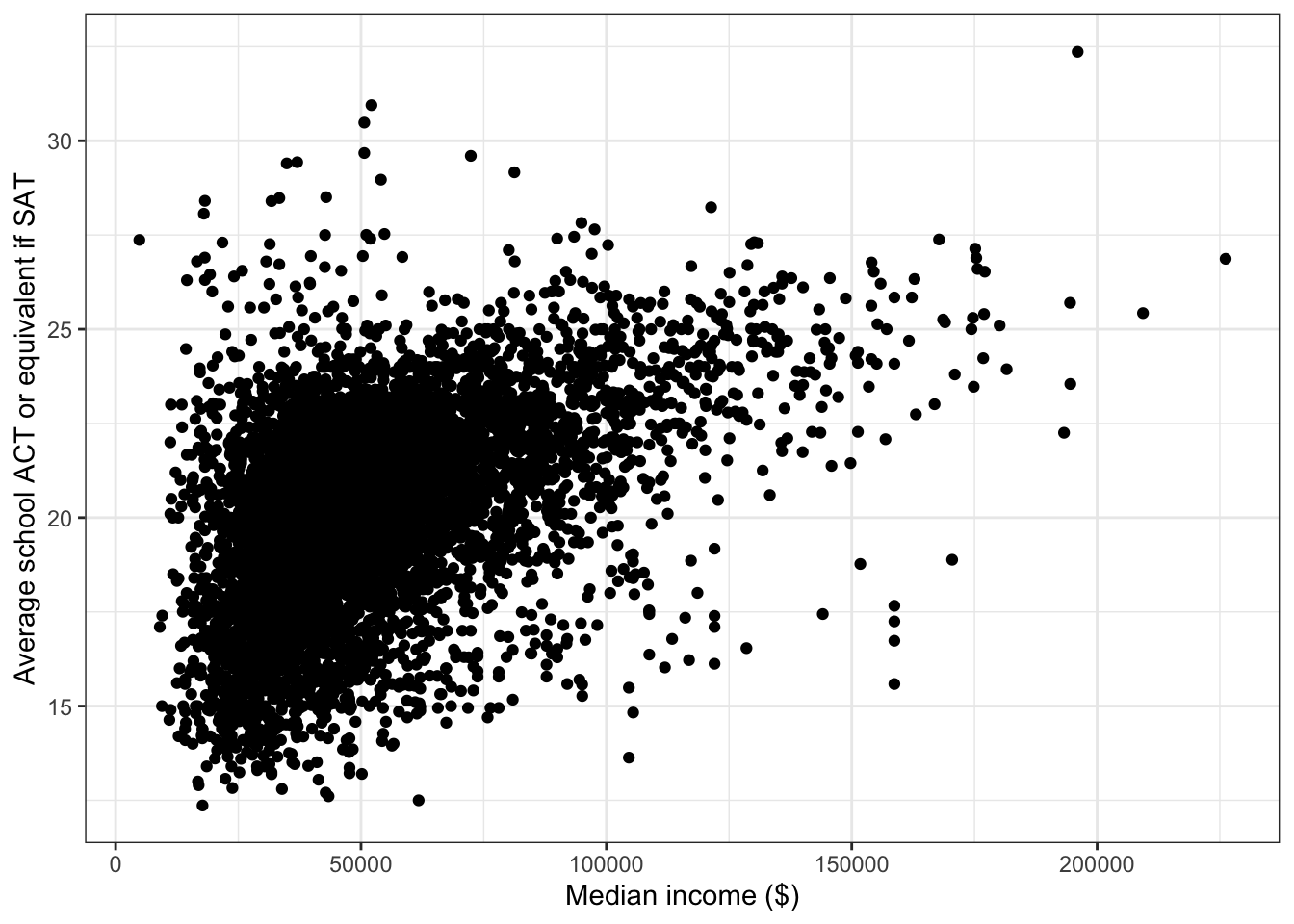

There is a positive association between median_income and average_act. The form of the association appears to be nonlinear.


\(\rightarrow\) median_income has a skewed distribution, so make a scatter plot with median_income plotted on a log scale.

Show Answer 
ggplot(edgap, aes(x = median_income, y = average_act)) +
  geom_point() +
  scale_x_log10() +
  labs(x = 'Median income ($)', y = 'Average school ACT or equivalent if SAT' ) +
  theme_bw()
## Warning: Removed 19 rows containing missing values (geom_point).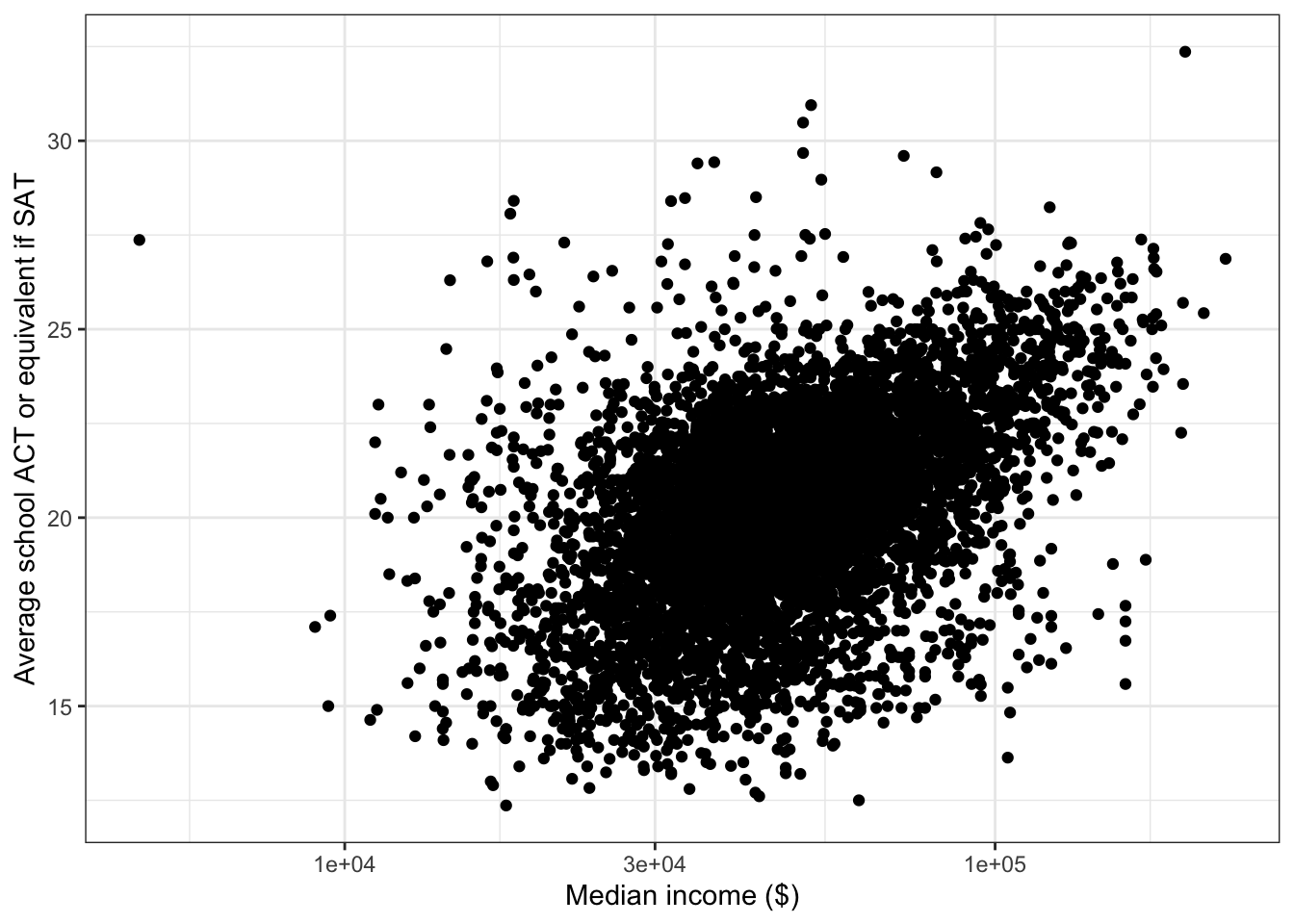

There is a positive linear associate between the log of median_income and average_act. Note also that the typical regression assumption of equal variance of errors is closer to being satisfied after the log transformation.


\(\rightarrow\) Make a scatter plot of percent_college and average_act

Show Answer 
ggplot(edgap, aes(x = percent_college, y = average_act)) +
  geom_point() +
  labs(x = 'Percent college', y = 'Average school ACT or equivalent if SAT') +
  theme_bw()
## Warning: Removed 14 rows containing missing values (geom_point).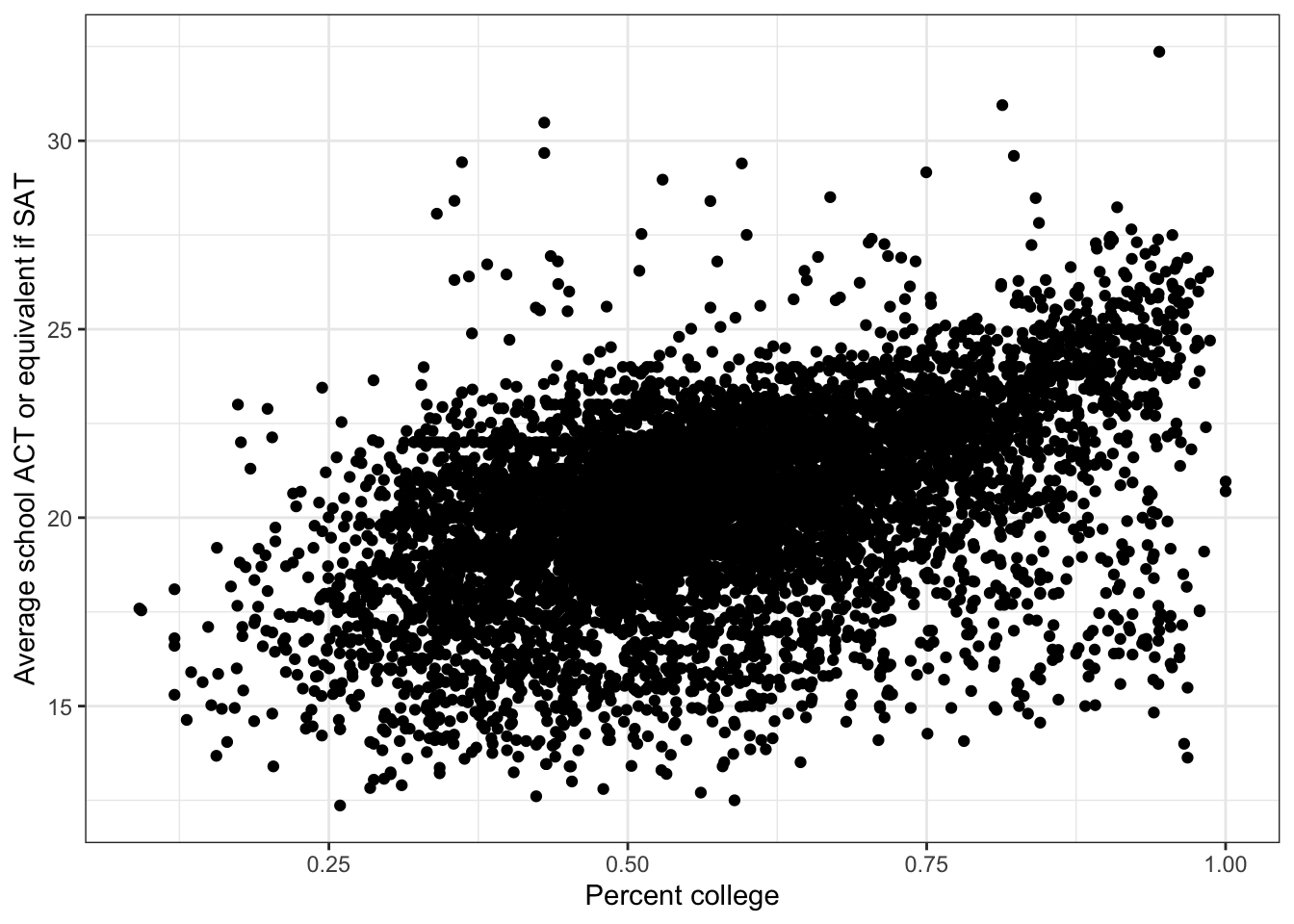

There is a positive association between percent_college and average_act. There may be a nonlinear component to the association, but it is difficult to assess visually from the scatter plot.


\(\rightarrow\) Make a scatter plot of percent_married and average_act

Show Answer 
ggplot(edgap, aes(x = percent_married, y = average_act)) +
  geom_point() +
  labs(x = 'Percent college', y = 'Average school ACT or equivalent if SAT') +
  theme_bw()
## Warning: Removed 23 rows containing missing values (geom_point).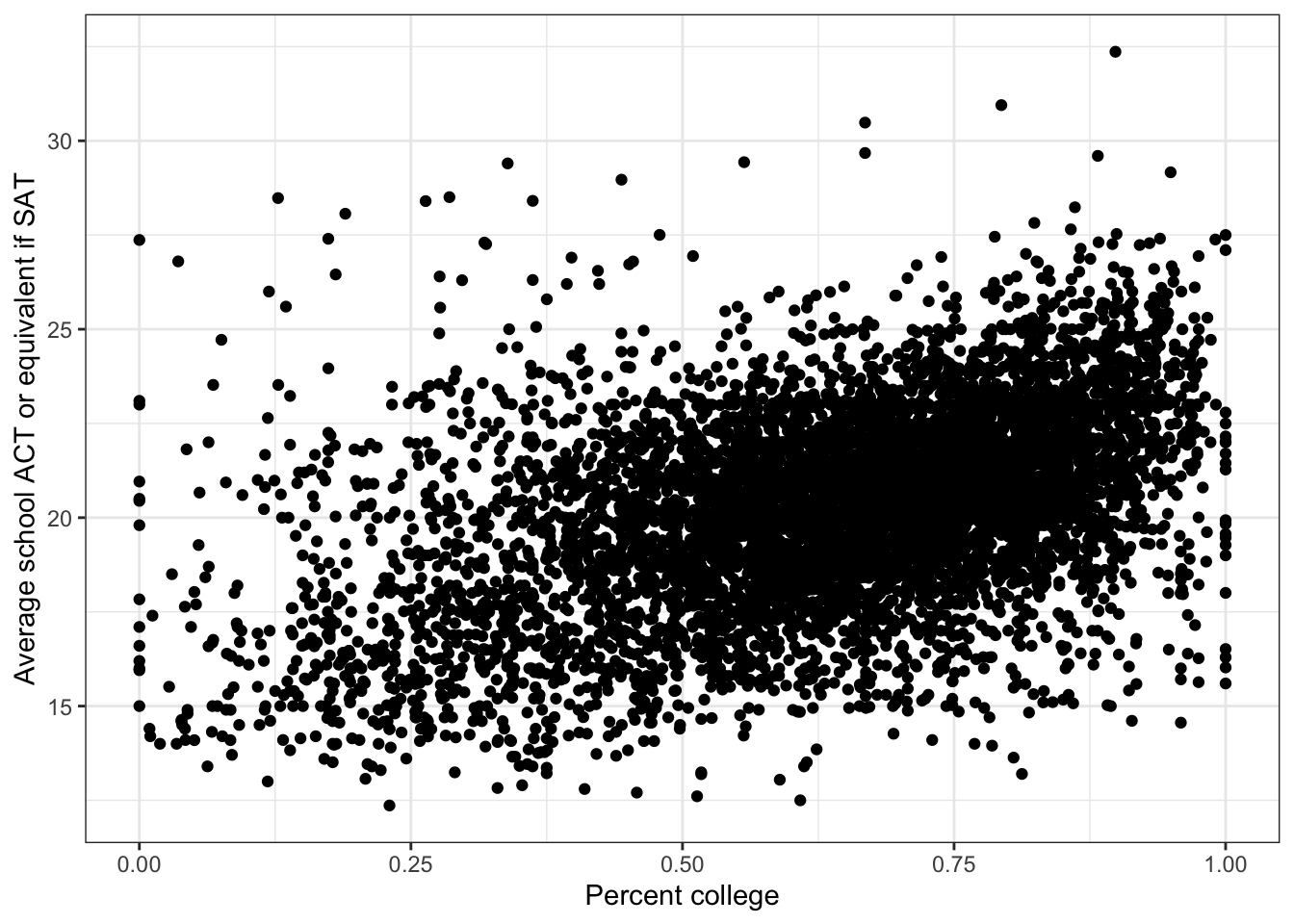

There is a positive association between percent_married and average_act.


\(\rightarrow\) Make a scatter plot of rate_unemployment and average_act

Show Answer 
ggplot(edgap, aes(x = rate_unemployment, y = average_act)) +
  geom_point() +
  labs(x = 'Rate of unemployment', y = 'Average school ACT or equivalent if SAT') +
  theme_bw()
## Warning: Removed 15 rows containing missing values (geom_point).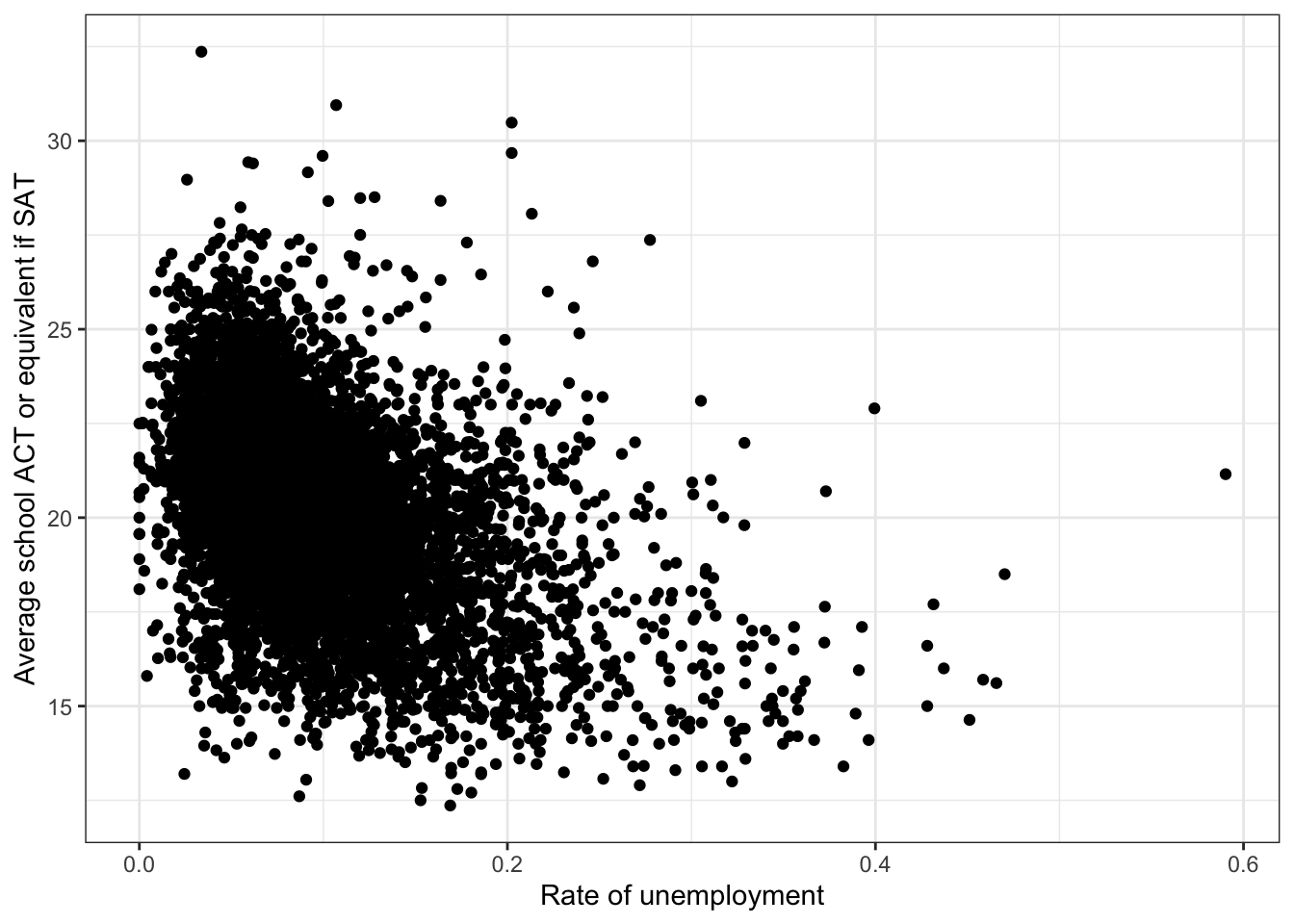

There is a negative association between rate_unemployment and average_act.


rate_unemployment has a positively skewed distribution, so we should make a scatter plot on a transformed scale. There are values of rate_unemployment that are equal to zero,

min(edgap$rate_unemployment, na.rm = TRUE)
## [1] 0

so we will use a square root transformation, rather than a log transformation.

library(latex2exp) #This library is used for LaTex in the axis labels

edgap %>% 
  ggplot(aes(x = sqrt(rate_unemployment), y = average_act)) +
  geom_point() +
  labs(x = TeX('$\\sqrt{$Rate of unemployment$}$'), y = 'Average school ACT or equivalent if SAT') +
  theme_bw()
## Warning: Removed 15 rows containing missing values (geom_point).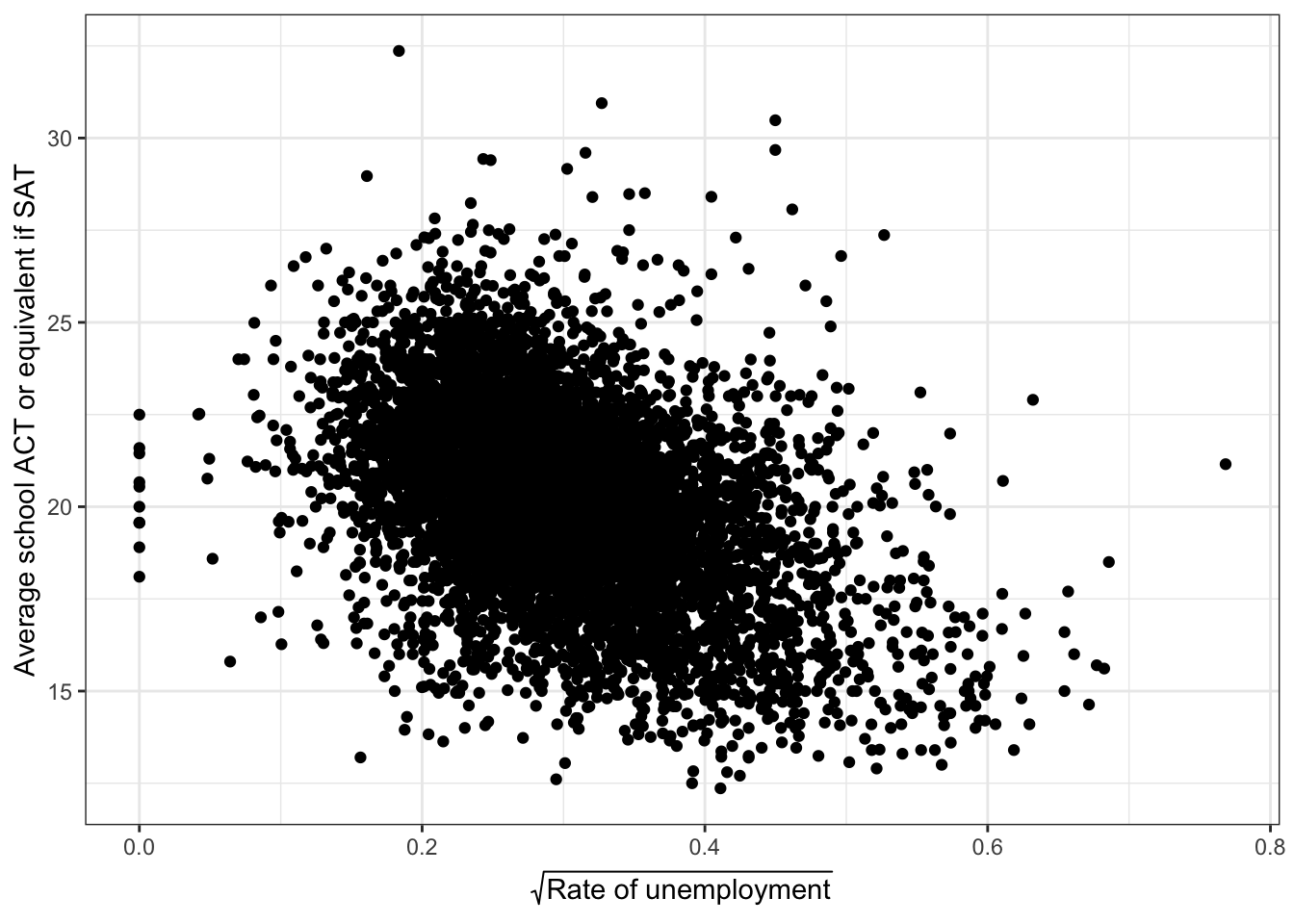

2.4.1.4 Numerical summaries

\(\rightarrow\) Use the skim function to examine the basic numerical summaries for each variable.

Show Answer 
edgap %>% select(-id) %>% skim()
Table 2.4: Data summary
Name Piped data
Number of rows 7230
Number of columns 10
_______________________
Column type frequency:
character 4
numeric 6
________________________
Group variables None

Variable type: character

skim_variable n_missing complete_rate min max empty n_unique whitespace
state 0 1 2 2 0 20 0
zip_code 0 1 5 5 0 6128 0
school_type 0 1 14 27 0 4 0
school_level 0 1 4 4 0 1 0

Variable type: numeric

skim_variable n_missing complete_rate mean sd p0 p25 p50 p75 p100 hist
rate_unemployment 12 1 0.10 0.06 0.00 0.06 0.08 0.12 0.59 ▇▂▁▁▁
percent_college 11 1 0.57 0.17 0.09 0.45 0.56 0.68 1.00 ▁▅▇▅▂
percent_married 20 1 0.64 0.19 0.00 0.53 0.67 0.78 1.00 ▁▂▅▇▃
median_income 16 1 52760.47 24365.51 4833.00 37106.00 47404.00 62106.00 226181.00 ▇▆▁▁▁
average_act 3 1 20.30 2.51 12.36 18.80 20.50 22.00 32.36 ▁▇▇▁▁
percent_lunch 20 1 0.41 0.23 0.00 0.23 0.37 0.56 1.00 ▅▇▆▃▂

2.5 Model

Our exploratory data analysis has led to the following observations that will help guide the modeling process:

  1. Each of the socioeconomic variables is associated with the ACT score and is worthwhile to consider as a predictor.
  2. Some of the socioeconomic variables may have a nonlinear relationship with the ACT score, so nonlinear models should be explored.
  3. The socioeconomic variables are correlated with each other, so the best prediction of ACT score might not include all socioeconomic variables.

2.5.1 Simple linear regression with each socioeconomic predictor

In this project, we are very concerned with understanding the relationships in the data set; we are not only concerned with building a model with the highest prediction accuracy. Therefore, we will start by looking at simple linear regression models using each socioeconomic predictor.

2.5.1.1 Percent free or reduced lunch

Fit a model

We want to fit the simple linear regression model

average_act \(\approx \beta_0 + \beta_1\) percent_lunch

Use the function lm to fit a simple linear regression model.

fit_pl <- lm(average_act ~ percent_lunch, data = edgap)

Use the summary function to

  1. Interpret the coefficients in the model.
  2. Assess the statistical significance of the coefficient on the predictor variable.
summary(fit_pl)$coefficients
##                Estimate Std. Error  t value Pr(>|t|)
## (Intercept)   23.744781 0.03693874  642.815        0
## percent_lunch -8.393695 0.07814631 -107.410        0

The intercept is 23.7 and the slope is -8.39. The intercept is interpreted as the best estimate for the mean ACT score when percent_lunch is zero. The slope can be interpreted as saying that a percent_lunch increase of 0.1 is associated with a decrease in the estimated mean ACT score of -0.839 points.

The slope is highly statistically significant, as the p-values are reported as zero. So, there is a statistically significant relationship between percent_lunch and the average ACT score in a school.

Plot the regression line together with the scatter plot

#geom_smooth(method = "lm",formula = y ~ x) adds the regression line to the scatter plot

ggplot(edgap, aes(x = percent_lunch, y = average_act)) + 
  geom_point() + 
  geom_smooth(method = "lm",formula = y ~ x) +
  labs(x = "Percent free or reduced lunch", y = "School ACT average (or equivalent if SAT score)") +
  theme_bw()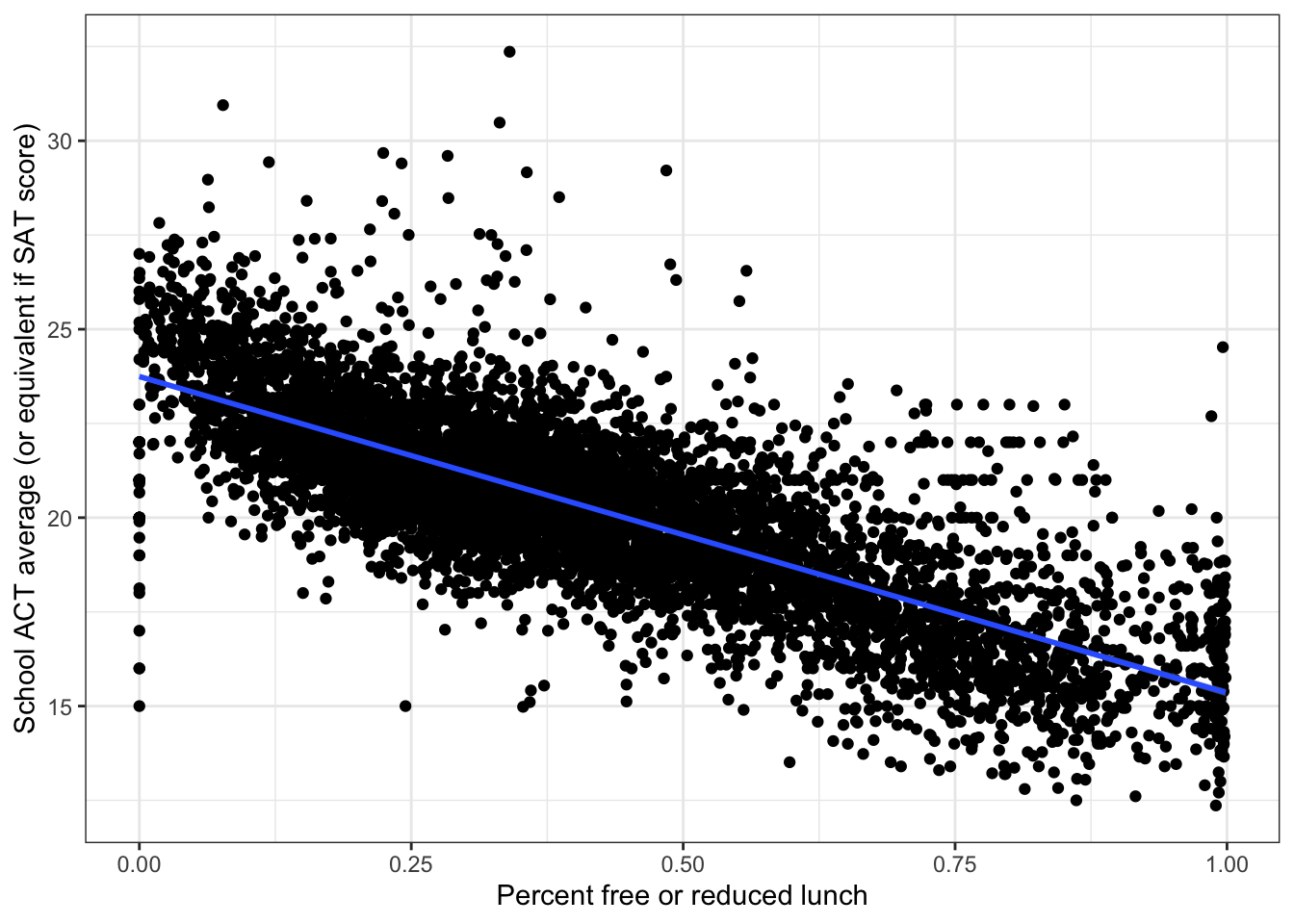

Assess the accuracy of the fit

Examine the \(R^2\) and the residual standard error

summary(fit_pl)$r.squared
## [1] 0.6155674

The simple linear regression model using percent free or reduced lunch as a predictor can explain 61.6% in the variance of the ACT score.

summary(fit_pl)$sigma
## [1] 1.55522

The residual standard error is 1.56 points. This means that the model is off by about 1.56 points, on average.

Together, these results show that we can make a good prediction of the average ACT score in a school only by knowing the percent of students receiving free or reduced lunch.

Note that, in this example, we called different components from the summary output individually. We took this approach to walk through each step of the analysis, but you can simply look at the output of summary(fit_pl) to see all of the information at once.

Residual plot

Examine a residual plot to see if we can improve the model through a transformation of the percent_lunch variable.

#We will use ggplot2 to make the residual plot. You can also use plot(fit_pl) 
ggplot(fit_pl,aes(x=percent_lunch, y=.resid)) + 
  geom_point() +
  geom_smooth(method = "loess", formula = y ~ x) +
  labs(x = "Percent free or reduced lunch", y = "Residuals") +
  theme_bw()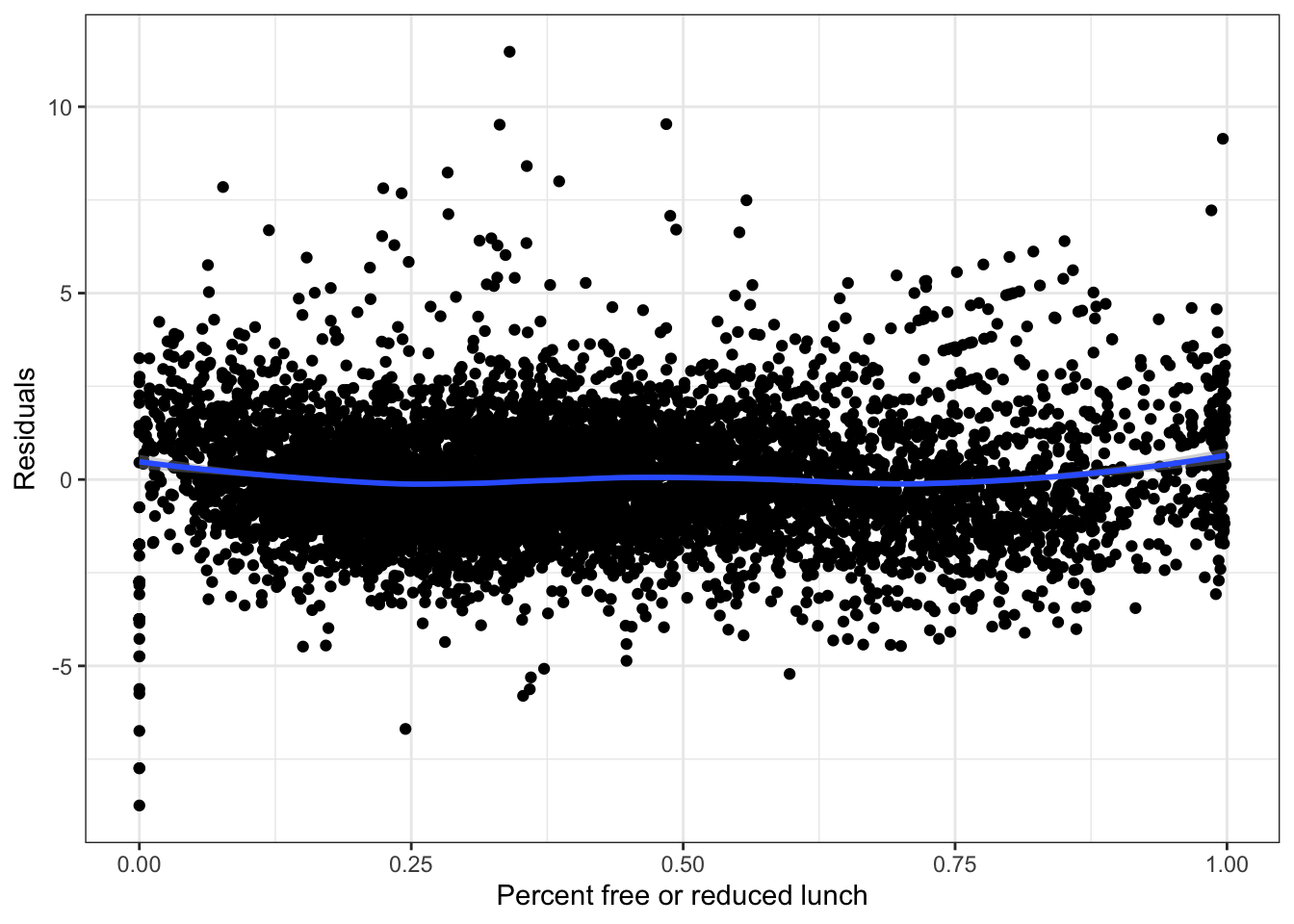

The residual plot does not have much systematic structure, so we have used percent_lunch as well as we can as a predictor. We do not need to consider a more complicated model that only uses percent_lunch as an input variable.

2.5.1.2 Median income

Fit a model

We want to fit the simple linear regression model

average_act \(\approx \beta_0 + \beta_1\) median_income

\(\rightarrow\) Use the function lm to fit a simple linear regression model.

Show Answer 
fit_mi <- lm(average_act ~ median_income, data = edgap)


\(\rightarrow\) Use the summary function to:

  1. Interpret the coefficients in the model.
  2. Assess the statistical significance of the coefficient on the predictor variable.
Show Answer 
summary(fit_mi)$coefficients
##                   Estimate   Std. Error   t value Pr(>|t|)
## (Intercept)   1.780119e+01 6.253060e-02 284.67963        0
## median_income 4.733825e-05 1.075819e-06  44.00205        0

The intercept is 17.8 and the slope is \(4.7 \times 10^{-5}\).

The intercept is interpreted as the best estimate for the mean ACT score when median_income is zero. The median income is never equal to zero, so the intercept does not have a clear interpretation in this model.

The slope can be interpreted as saying that a difference of $1 in median_income is associated with a difference in the estimated mean ACT score of \(4.7 \times 10^{-5}\) points. This value of the slope is not intuitive because the median income is in dollars, but differences in annual income of several dollars is not meaningful. It would be helpful to represent median income in tens of thousands of dollars to make a one-unit change more meaningful.

We will use the mutate function to add a new variable to the data frame called median_income_10k that represents median income in tens of thousands of dollars.

edgap <- edgap %>% 
  mutate(median_income_10k = median_income/1e4)

We can refit the model

fit_mi <- lm(average_act ~ median_income_10k, data = edgap)

summary(fit_mi)$coefficients
##                     Estimate Std. Error   t value Pr(>|t|)
## (Intercept)       17.8011868 0.06253060 284.67963        0
## median_income_10k  0.4733825 0.01075819  44.00205        0

The intercept remains 17.8, but the slope is now 0.47, corresponding to the scaling of the median income units.

The slope can be interpreted as saying that a difference of $10,000 in median income is associated with a difference in the estimated mean ACT score of 0.47 points.

The slope is highly statistically significant. So, there is a statistically significant relationship between median income and the average ACT score in a school.


\(\rightarrow\) Plot the regression line together with the scatter plot

Show Answer 
ggplot(edgap, aes(x = median_income_10k, y = average_act)) + 
  geom_point() + 
  geom_smooth(method = "lm",formula = y ~ x) +
  labs(x = "Median Household Income (ten thousand $)", y = "School ACT average (or equivalent if SAT score)") +
  theme_bw()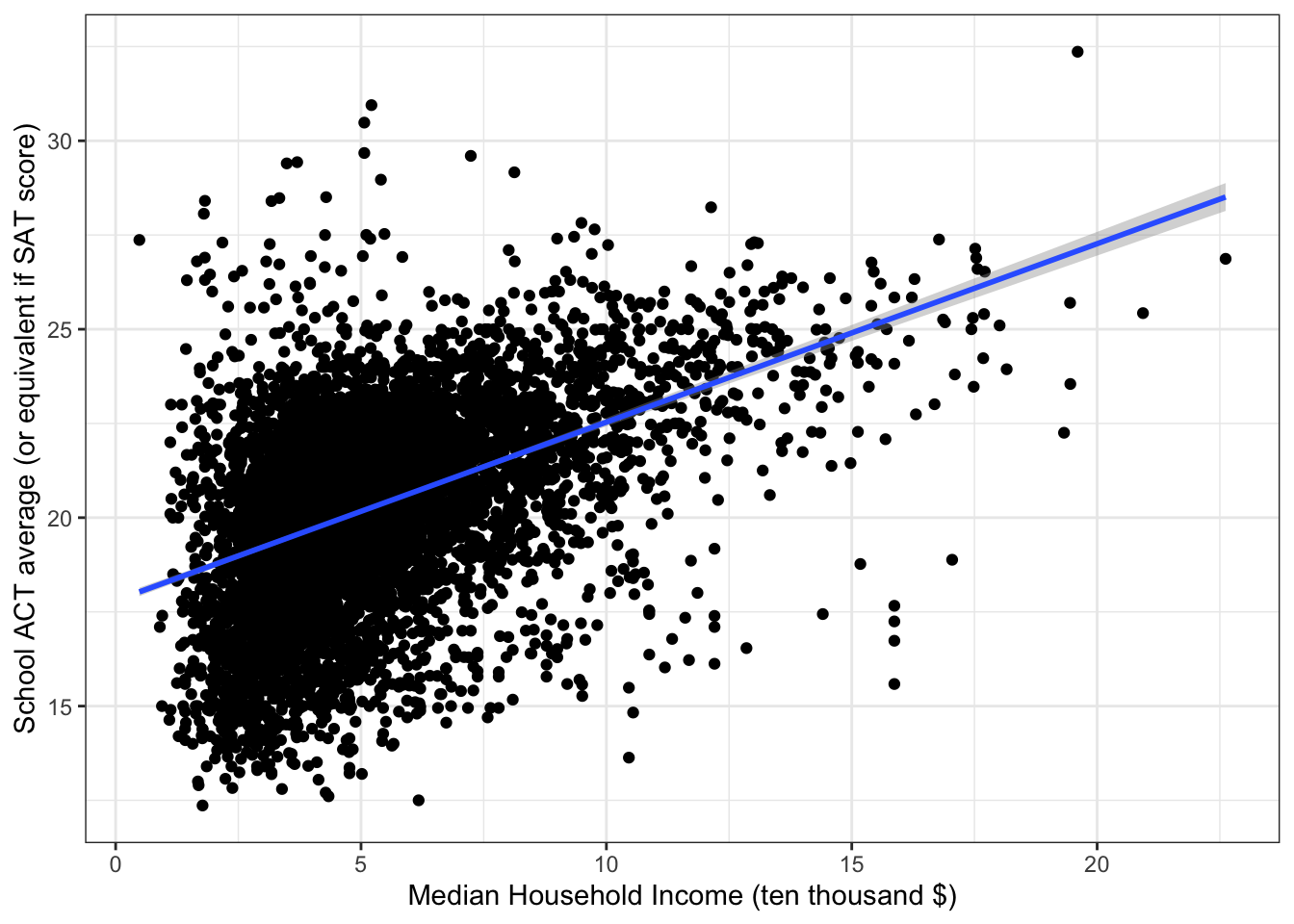


Assess the accuracy of the fit

\(\rightarrow\) Examine the \(R^2\) and the residual standard error

Show Answer 
summary(fit_mi)$r.squared
## [1] 0.2117159

The simple linear regression model using median income as a predictor explains 21.2% in the variance of the ACT score.

summary(fit_mi)$sigma
## [1] 2.225708

The residual standard error is 2.26 points. This means that the model is off by about 2.26 points, on average.

Together, these results show that we can do some moderate prediction of the average ACT score in a school only by knowing the median income.


Residual plot

\(\rightarrow\) Examine a residual plot to see if we can improve the model through a transformation of the median_income_10 variable.

Show Answer 
ggplot(fit_mi,aes(x=median_income_10k, y=.resid)) + 
  geom_point() +
  geom_smooth(method = "loess", formula = y ~ x) +
  labs(x = "Median Household Income (ten thousand $)", y = "Residuals") +
  theme_bw()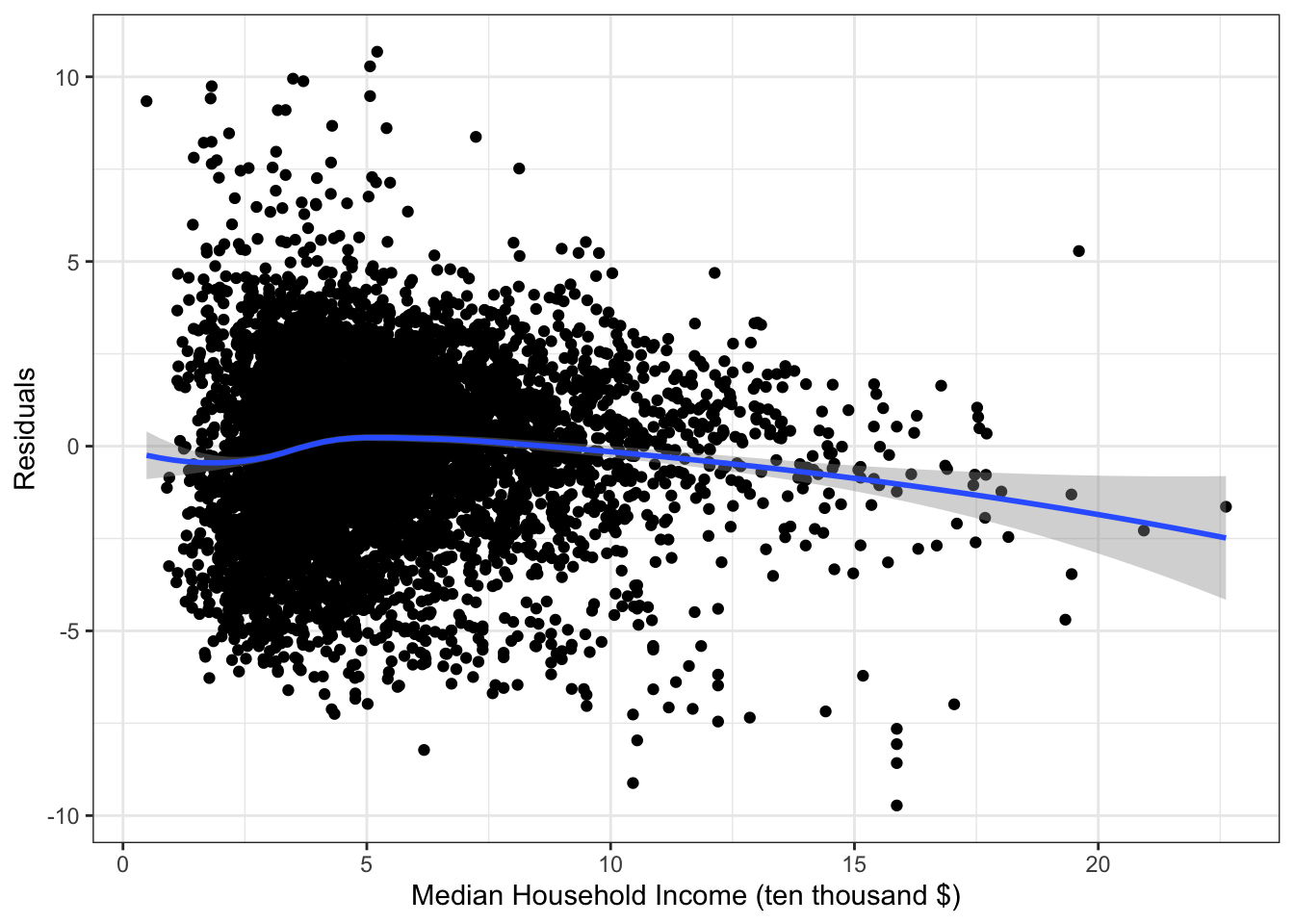

The residual plot suggests that a nonlinear model may improve the fit.

We will try a log transformation.


Log transformation

Fit the model

\(\rightarrow\) Fit a linear regression model using the log of median_income_10 as the predictor.

Show Answer 
fit_mi_log <- lm(average_act ~ log10(median_income_10k), data = edgap)


\(\rightarrow\) Use the summary function to:

  1. Interpret the coefficients in the model.
  2. Assess the statistical significance of the coefficient on the predictor variable.
Show Answer 
summary(fit_mi_log)$coefficients
##                           Estimate Std. Error   t value Pr(>|t|)
## (Intercept)              16.040603 0.09908011 161.89529        0
## log10(median_income_10k)  6.245003 0.14014512  44.56097        0

The intercept is 16.0. The intercept is interpreted as the prediction of the average ACT score when the predictor is zero, which means that the median income is $10,000.

The slope is 6.3. Because we used a base 10 log, the slope is interpreted as saying that a median income ten times greater than another is associated with an average ACT score that is 6.3 points higher.

The slope is highly statistically significant.


\(\rightarrow\) Plot the regression line together with the scatter plot

Show Answer 
ggplot(edgap, aes(x = log10(median_income_10k), y = average_act)) + 
  geom_point() + 
  geom_smooth(method = "lm",formula = y ~ x) +
  labs(x = "Log of median Household Income", y = "School ACT average (or equivalent if SAT score)") +
  theme_bw()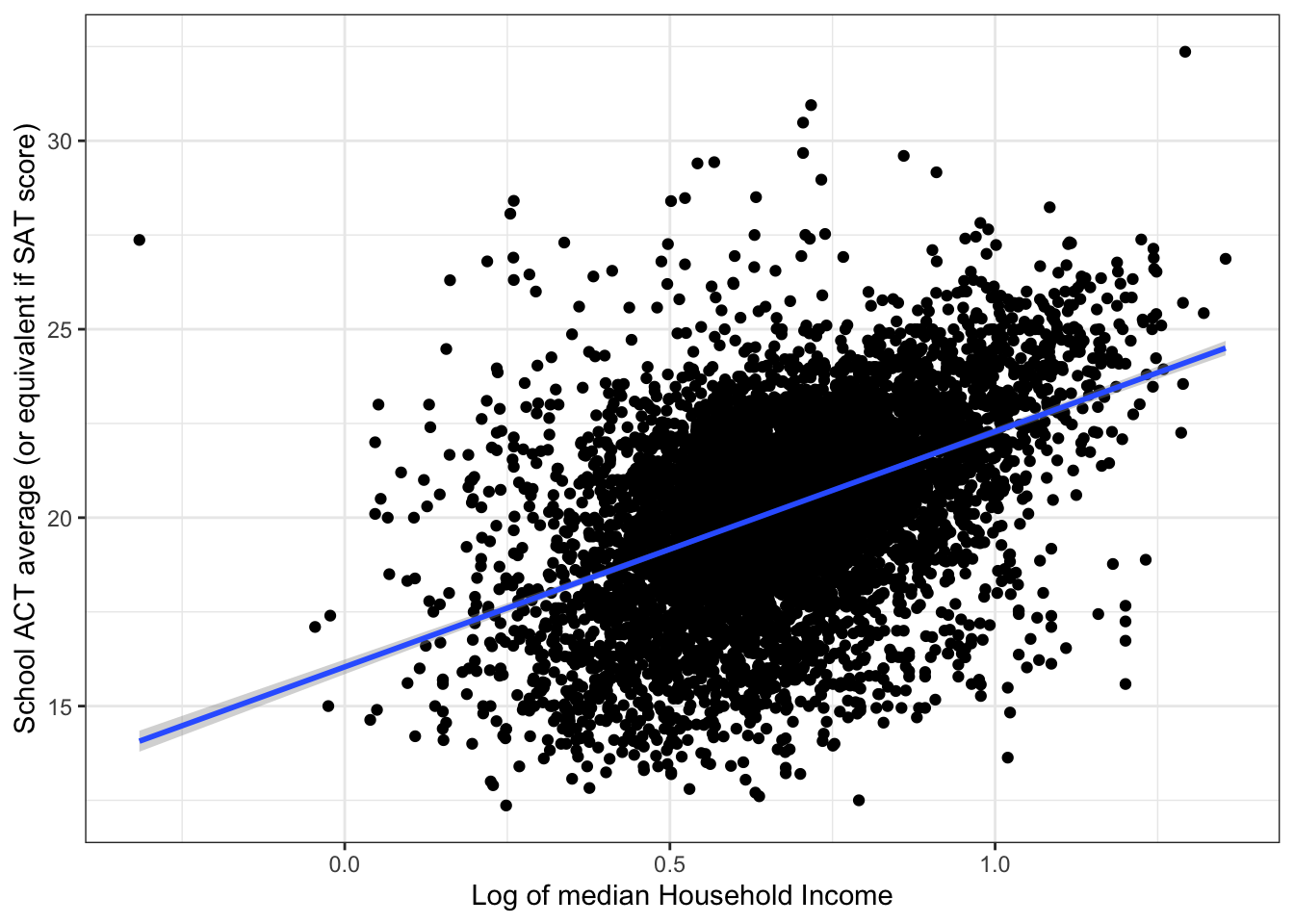


Assess the accuracy of the fit

\(\rightarrow\) Examine the \(R^2\) and the residual standard error

Show Answer 
summary(fit_mi_log)$r.squared
## [1] 0.2159597

The simple linear regression model using median income as a predictor can explain 21.6% in the variance of the ACT score.

summary(fit_mi_log)$sigma
## [1] 2.219709

The residual standard error is 2.22 points. This means that the model is off by about 2.22 points, on average.

Together, these results show that we can do some moderate prediction of the average ACT score in a school only by knowing the median income.


Residual plot

\(\rightarrow\) Examine a residual plot to see if we can improve the model through a transformation of the input.

Show Answer 
ggplot(fit_mi_log, aes(x=.fitted, y=.resid)) + 
  geom_point() +
  geom_smooth(method = "loess", formula = y ~ x) +
  labs(x = "Log Median Household Income", y = "Residuals") +
  theme_bw()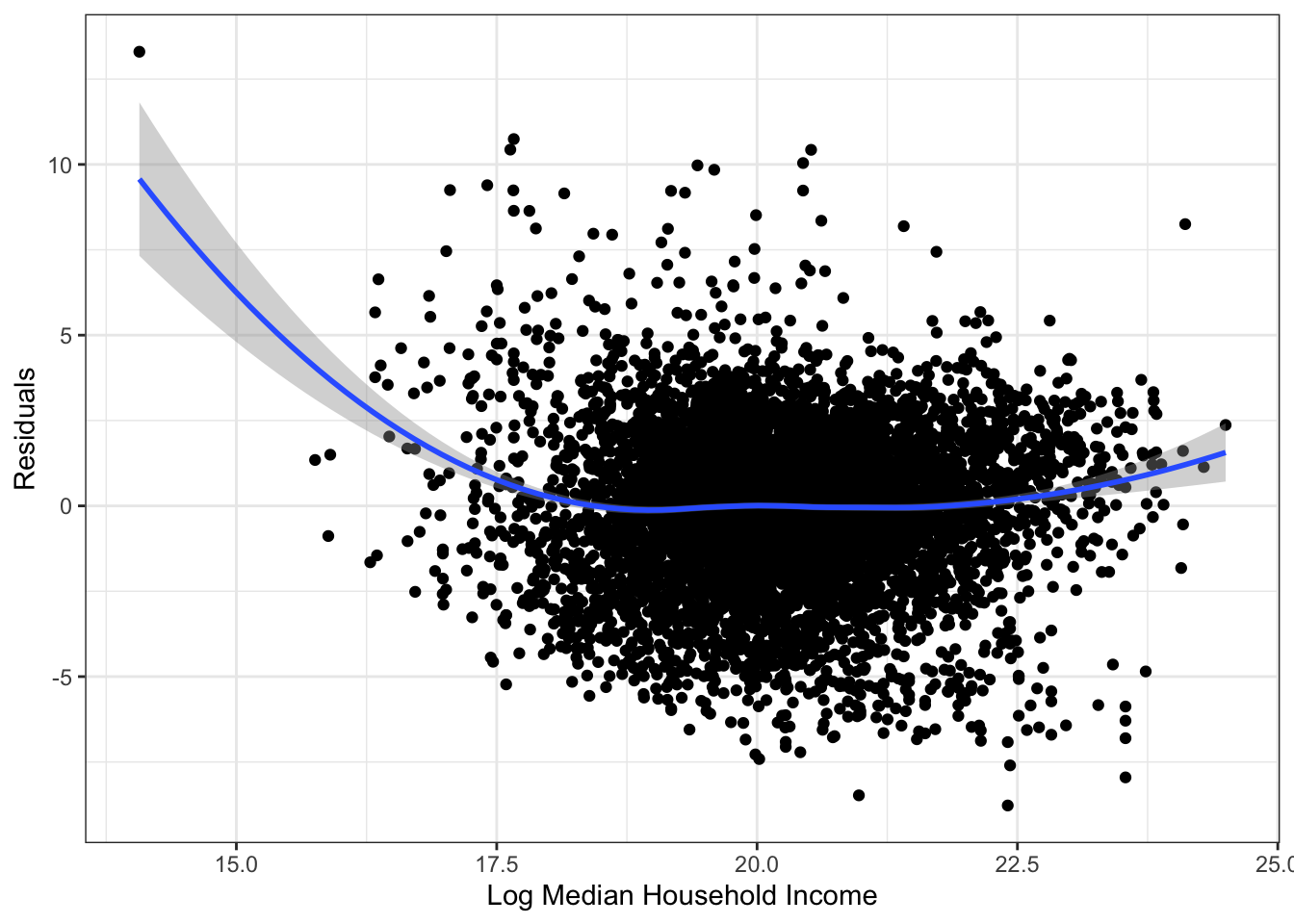

The structure in the residual plot appears to be due to the points near 14. Therefore, we will not consider further transformations.

2.5.1.3 Percent college

Fit a model

We want to fit the simple linear regression model

average_act \(\approx \beta_0 + \beta_1\) percent_college

\(\rightarrow\) Use the function lm to fit a simple linear regression model.

Show Answer 
fit_pc <- lm(average_act ~ percent_college, data = edgap)


\(\rightarrow\) Use the summary function to

  1. Interpret the coefficients in the model.
  2. Assess the statistical significance of the coefficient on the predictor variable.
Show Answer 
summary(fit_pc)$coefficients
##                  Estimate Std. Error   t value Pr(>|t|)
## (Intercept)     16.307759 0.09476034 172.09477        0
## percent_college  6.966002 0.15889860  43.83929        0

The slope is highly statistically significant. So, there is a statistically significant relationship between percent college and the average ACT score in a school.


\(\rightarrow\) Plot the regression line together with the scatter plot

Show Answer 
ggplot(edgap, aes(x = percent_college, y = average_act)) + 
  geom_point() + 
  geom_smooth(method = "lm",formula = y ~ x) +
  labs(x = "Percent college", y = "School ACT average (or equivalent if SAT score)") +
  theme_bw()
## Warning: Removed 14 rows containing non-finite values (stat_smooth).
## Warning: Removed 14 rows containing missing values (geom_point).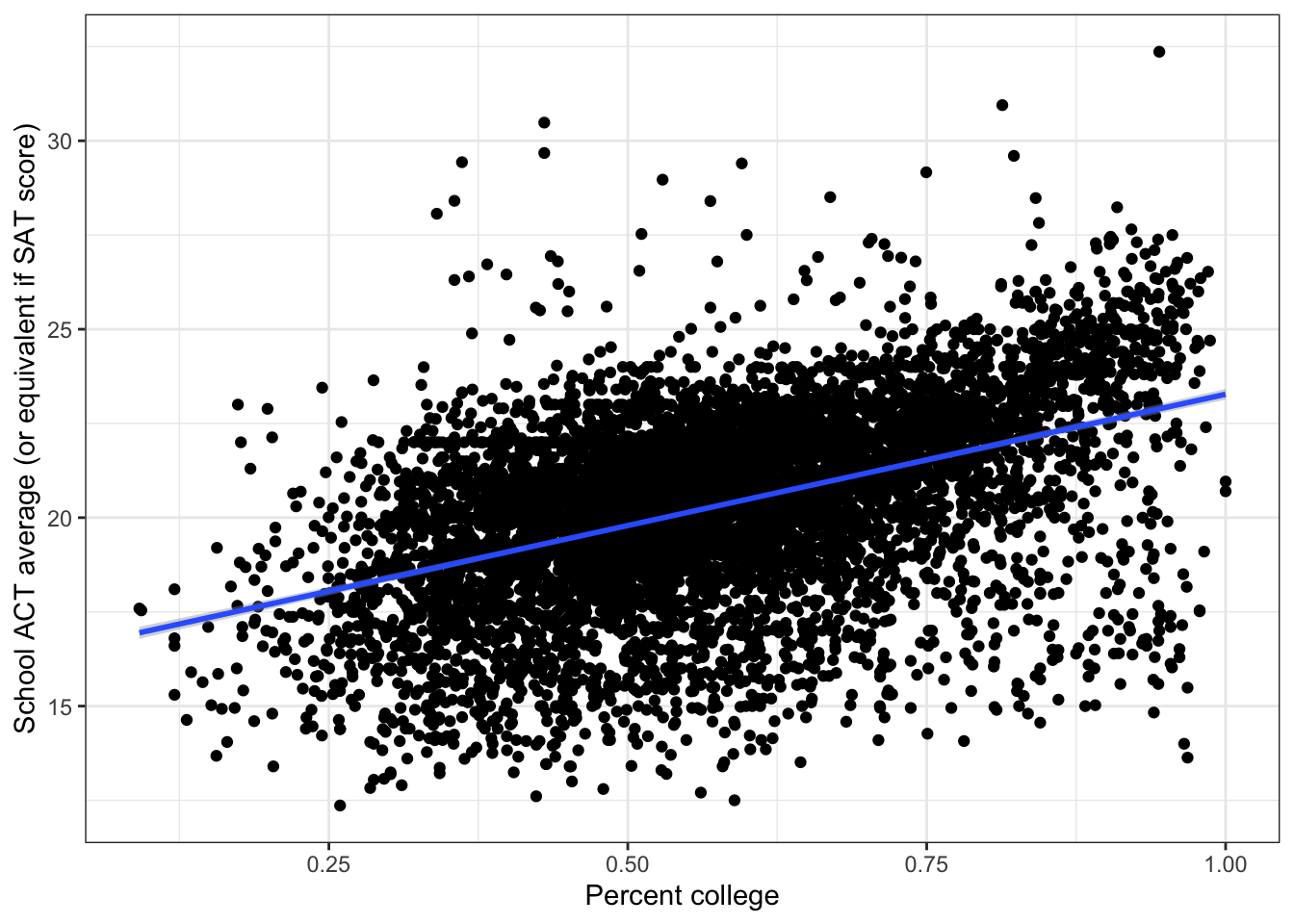


Assess the accuracy of the fit

\(\rightarrow\) Examine the \(R^2\) and the residual standard error

Show Answer 
summary(fit_pc)$r.squared
## [1] 0.2103665

The simple linear regression model using median income as a predictor can explain 21.0% in the variance of the ACT score.

summary(fit_pc)$sigma
## [1] 2.227256

The residual standard error is 2.23 points. This means that the model is off by about 2.23 points, on average.

Together, these results show that we can do some moderate prediction of the average ACT score in a school only by knowing the percent of college graduates among adults.


Residual plot

\(\rightarrow\) Examine a residual plot to see if we can improve the model through a transformation of the input variable.

Show Answer 
ggplot(fit_pc, aes(x=percent_college, y=.resid)) + 
  geom_point() +
  geom_smooth(method = "loess", formula = y ~ x) +
  labs(x = "Percent college", y = "Residuals") +
  theme_bw()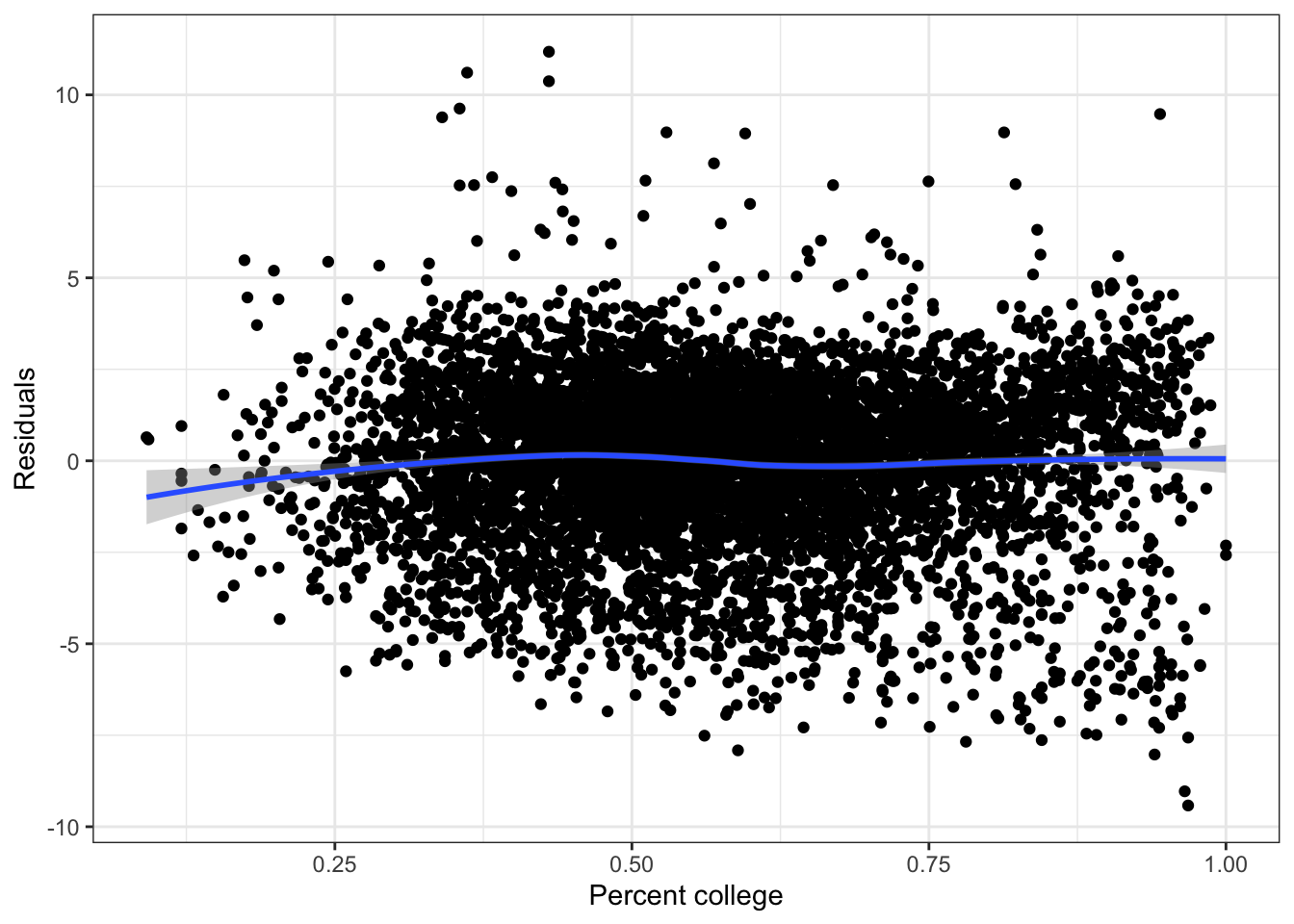

The residual plot has a small suggestion that a quadratic model might be useful.


\(\rightarrow\) Fit and assess a quadratic model

Show Answer 
fit_pc_quad <- lm(average_act ~ poly(percent_college,2, raw = T), data = edgap)
summary(fit_pc_quad)
## 
## Call:
## lm(formula = average_act ~ poly(percent_college, 2, raw = T), 
##     data = edgap)
## 
## Residuals:
##     Min      1Q  Median      3Q     Max 
## -9.3502 -1.2283  0.2854  1.4668 11.1775 
## 
## Coefficients:
##                                    Estimate Std. Error t value Pr(>|t|)    
## (Intercept)                         16.1091     0.2686  59.980   <2e-16 ***
## poly(percent_college, 2, raw = T)1   7.6930     0.9333   8.242   <2e-16 ***
## poly(percent_college, 2, raw = T)2  -0.6129     0.7754  -0.790    0.429    
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## Residual standard error: 2.227 on 7213 degrees of freedom
##   (14 observations deleted due to missingness)
## Multiple R-squared:  0.2104, Adjusted R-squared:  0.2102 
## F-statistic: 961.2 on 2 and 7213 DF,  p-value: < 2.2e-16

The coefficient on the squared term is not significant, so the quadratic model does not provide an improvement over the linear model.


2.5.1.4 Rate of unemployment

Fit a model

We want to fit the simple linear regression model

average_act \(\approx \beta_0 + \beta_1\) rate_unemployment

\(\rightarrow\) Use the function lm to fit a simple linear regression model.

Show Answer 
fit_ru <- lm(average_act ~ rate_unemployment, data = edgap)


\(\rightarrow\) Use the summary function to:

  1. Interpret the coefficients in the model.
  2. Assess the statistical significance of the coefficient on the predictor variable.
Show Answer 
summary(fit_ru)$coefficients
##                    Estimate Std. Error   t value Pr(>|t|)
## (Intercept)        22.15006 0.05252349 421.71719        0
## rate_unemployment -19.19084 0.46971479 -40.85636        0
The slope is highly statistically significant. So, there is a statistically significant relationship between unemployment rate and the average ACT score in a school.


\(\rightarrow\) Plot the regression line together with the scatter plot

Show Answer 
ggplot(edgap, aes(x = rate_unemployment, y = average_act)) + 
  geom_point() + 
  geom_smooth(method = "lm",formula = y ~ x) +
  labs(x = "Unemployment rate", y = "School ACT average (or equivalent if SAT score)") +
  theme_bw()
## Warning: Removed 15 rows containing non-finite values (stat_smooth).
## Warning: Removed 15 rows containing missing values (geom_point).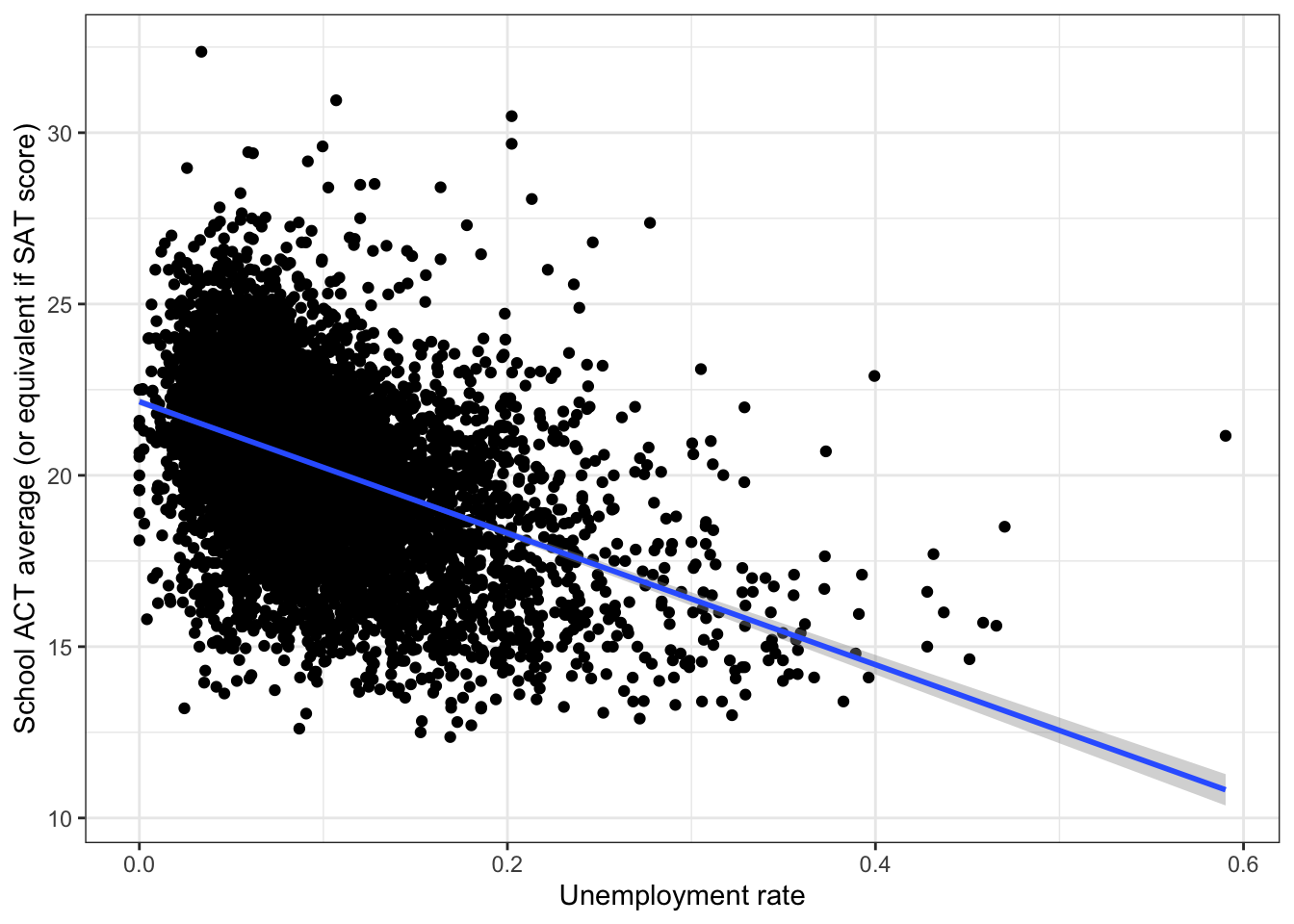


Assess the accuracy of the fit

\(\rightarrow\) Examine the \(R^2\) and the residual standard error

Show Answer 
summary(fit_ru)$r.squared
## [1] 0.1879303

The simple linear regression model using unemployment rate as a predictor can explain 18.8% in the variance of the ACT score.

summary(fit_ru)$sigma
## [1] 2.258699

The residual standard error is 2.26 points. This means that the model is off by about 2.26 points, on average.

Together, these results show that we can do some moderate prediction of the average ACT score in a school only by knowing the unemployment rate.


Residual plot

\(\rightarrow\) Examine a residual plot to see if we can improve the model.

Show Answer 
ggplot(fit_ru,aes(x=rate_unemployment, y=.resid)) + 
  geom_point() +
  geom_smooth(method = "loess", formula = y ~ x) +
  labs(x = "Unemployment rate", y = "Residuals") +
  theme_bw()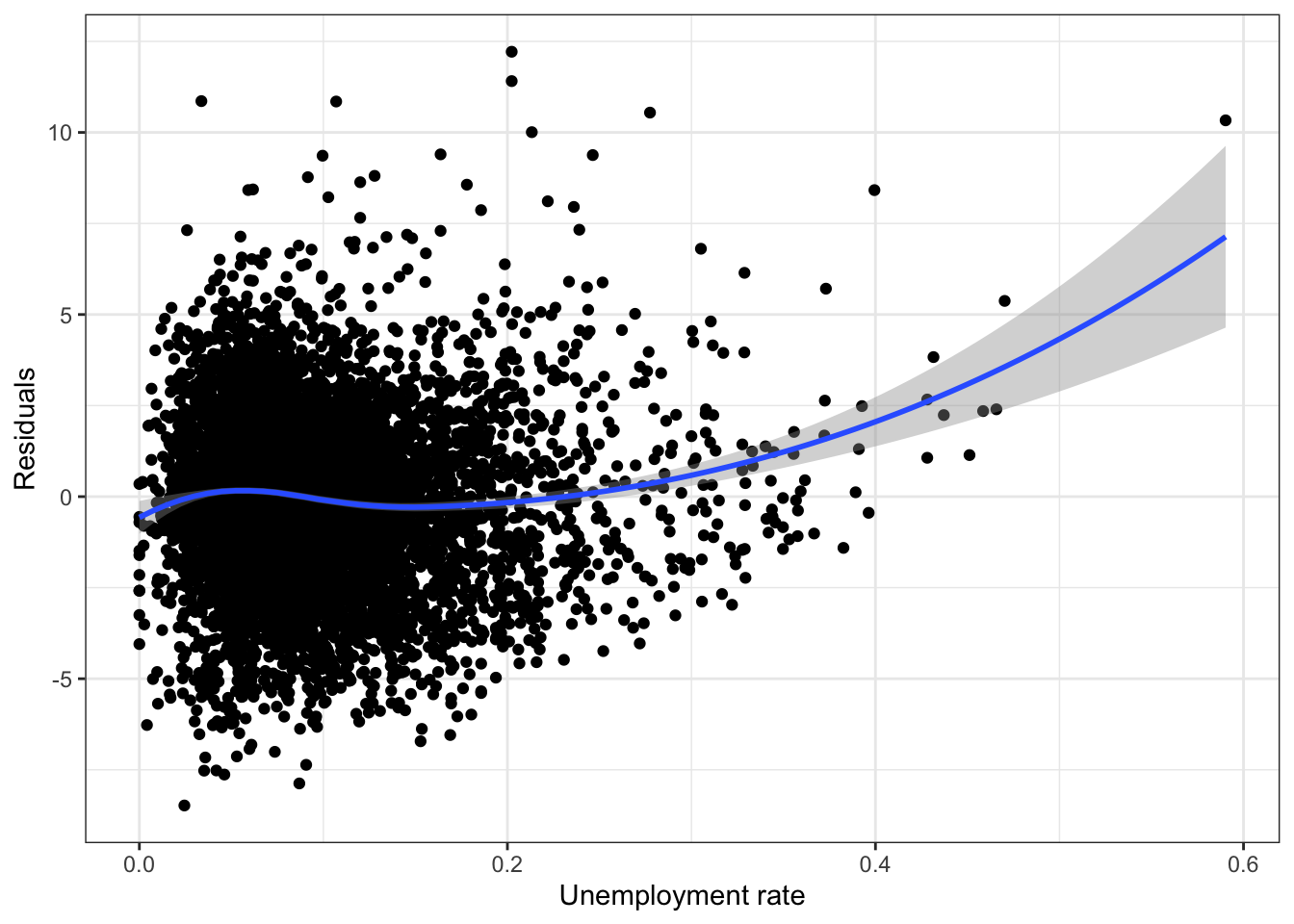


Try a square root transformation of rate_unemployment

Show Answer 
fit_ru_sqrt <- lm(average_act ~ sqrt(rate_unemployment), data = edgap)
summary(fit_ru_sqrt)
## 
## Call:
## lm(formula = average_act ~ sqrt(rate_unemployment), data = edgap)
## 
## Residuals:
##     Min      1Q  Median      3Q     Max 
## -8.9088 -1.3999  0.0888  1.4304 12.1059 
## 
## Coefficients:
##                          Estimate Std. Error t value Pr(>|t|)    
## (Intercept)              24.09827    0.09705   248.3   <2e-16 ***
## sqrt(rate_unemployment) -12.72070    0.31252   -40.7   <2e-16 ***
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## Residual standard error: 2.26 on 7213 degrees of freedom
##   (15 observations deleted due to missingness)
## Multiple R-squared:  0.1868, Adjusted R-squared:  0.1867 
## F-statistic:  1657 on 1 and 7213 DF,  p-value: < 2.2e-16

The square root transformation provides a small improvement over the linear model.

ggplot(edgap, aes(x = rate_unemployment, y = average_act)) + 
  geom_point() + 
  geom_smooth(method = "lm", formula = y ~ x) +
  geom_smooth(method = "lm", formula = y ~ sqrt(x),color = 'red') +
  labs(x = "Unemployment rate", y = "School ACT average (or equivalent if SAT score)") +
  theme_bw()
## Warning: Removed 15 rows containing non-finite values (stat_smooth).
## Removed 15 rows containing non-finite values (stat_smooth).
## Warning: Removed 15 rows containing missing values (geom_point).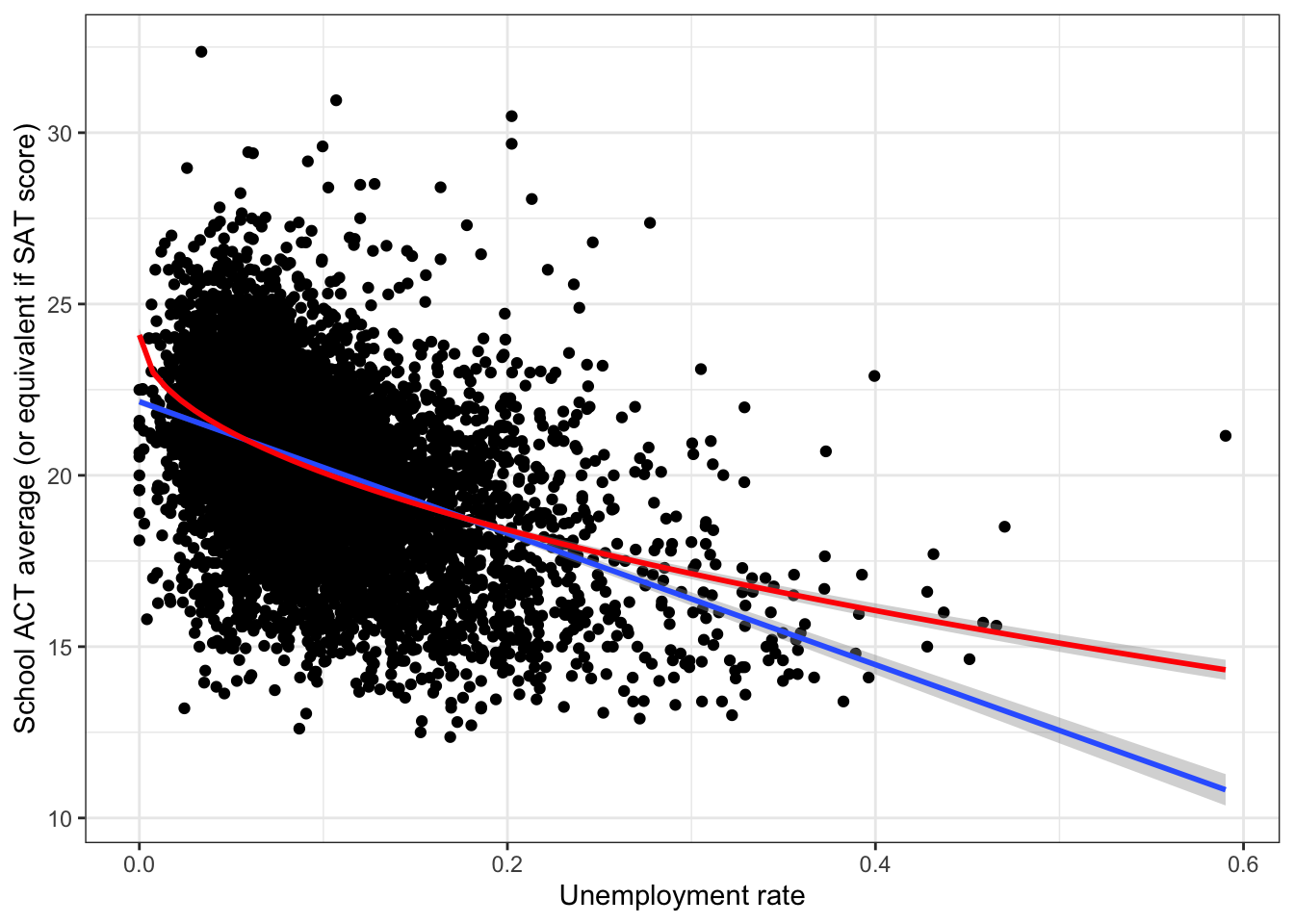

The models are very similar for most of the data, but differ a lot for high unemployment rates. There are few data points with high unemployment rates, so the numerical measures of accuracy are very similar.

ggplot(fit_ru_sqrt,aes(x=.fitted, y=.resid)) + 
  geom_point() +
  geom_smooth(method = "loess", formula = y ~ x) +
  labs(x = "Square root of unemployment rate", y = "Residuals") +
  theme_bw()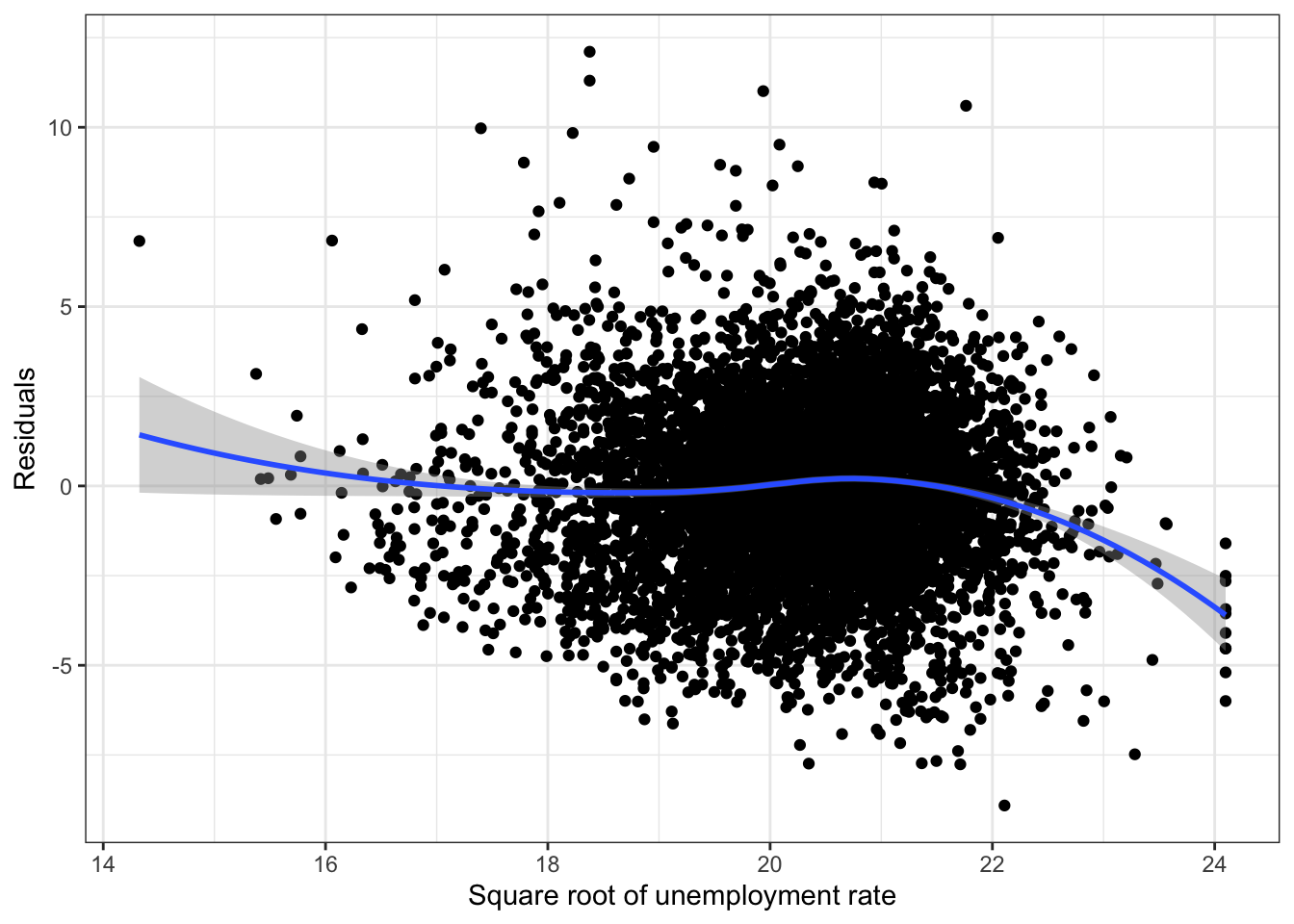


2.5.1.5 Percent married

Fit a model

We want to fit the simple linear regression model

average_act \(\approx \beta_0 + \beta_1\) percent_married

\(\rightarrow\) Use the function lm to fit a simple linear regression model.

Show Answer 
fit_pm <- lm(average_act ~ percent_married, data = edgap)


\(\rightarrow\) Use the summary function to:

  1. Interpret the coefficients in the model.
  2. Assess the statistical significance of the coefficient on the predictor variable.
Show Answer 
summary(fit_pm)$coefficients
##                  Estimate Std. Error   t value Pr(>|t|)
## (Intercept)     16.599927 0.09268168 179.10690        0
## percent_married  5.774247 0.13862735  41.65301        0
The slope is highly statistically significant. So, there is a statistically significant relationship between percent married and the average ACT score in a school.


\(\rightarrow\) Plot the regression line together with the scatter plot

Show Answer 
ggplot(edgap, aes(x = percent_married, y = average_act)) + 
  geom_point() + 
  geom_smooth(method = "lm",formula = y ~ x) +
  labs(x = "Percent married", y = "School ACT average (or equivalent if SAT score)") +
  theme_bw()
## Warning: Removed 23 rows containing non-finite values (stat_smooth).
## Warning: Removed 23 rows containing missing values (geom_point).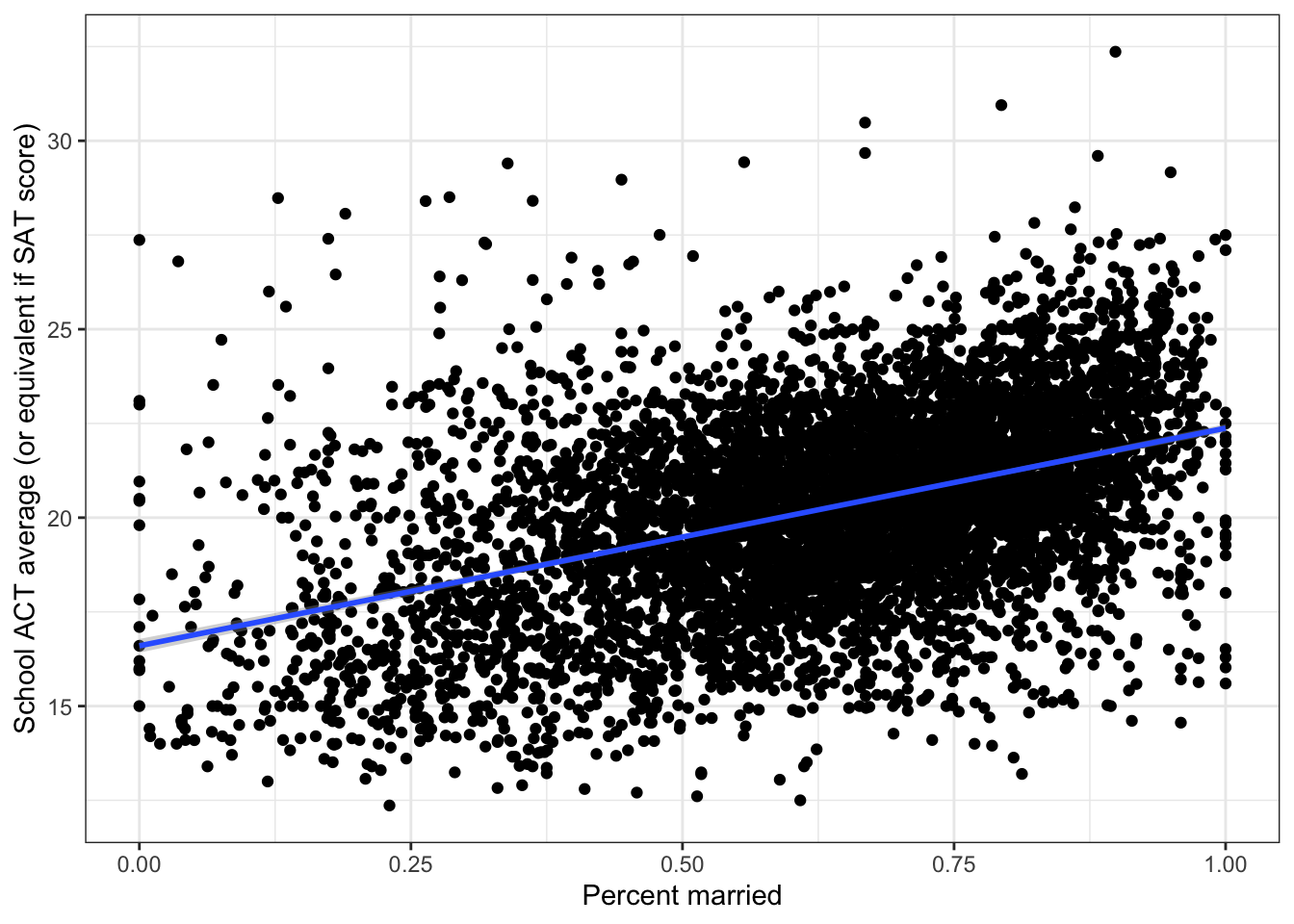


Assess the accuracy of the fit

\(\rightarrow\) Examine the \(R^2\) and the residual standard error

Show Answer 
summary(fit_pm)$r.squared
## [1] 0.1940692

The simple linear regression model using percent married as a predictor can explain 19.4% in the variance of the ACT score.

summary(fit_pm)$sigma
## [1] 2.250251

The residual standard error is 2.25 points. This means that the model is off by about 2.25 points, on average.

Together, these results show that we can do some moderate prediction of the average ACT score in a school only by knowing the median income.


Residual plot

\(\rightarrow\) Examine a residual plot to see if we can improve the model.

Show Answer 
ggplot(fit_pm,aes(x=percent_married, y=.resid)) + 
  geom_point() +
  geom_smooth(method = "loess", formula = y ~ x) +
  labs(x = "Percent married", y = "Residuals") +
  theme_bw()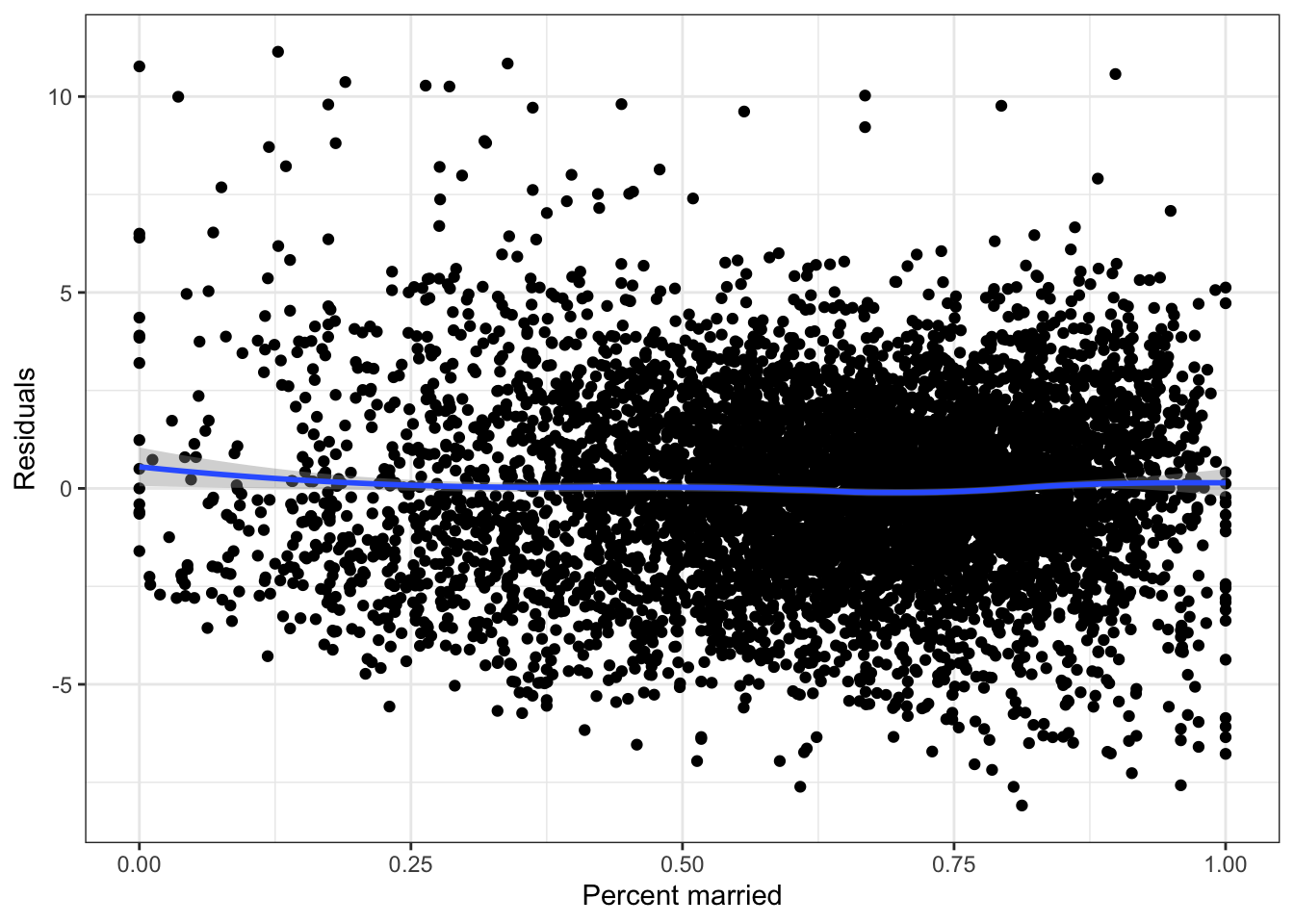

The residual plot suggests a quadratic model may be useful.

fit_pm_quad <- lm(average_act ~ poly(percent_married, 2, raw = T), data = edgap)
summary(fit_pm_quad)
## 
## Call:
## lm(formula = average_act ~ poly(percent_married, 2, raw = T), 
##     data = edgap)
## 
## Residuals:
##     Min      1Q  Median      3Q     Max 
## -8.1179 -1.4156  0.0554  1.3895 10.9173 
## 
## Coefficients:
##                                    Estimate Std. Error t value Pr(>|t|)    
## (Intercept)                         17.0161     0.1808  94.093  < 2e-16 ***
## poly(percent_married, 2, raw = T)1   4.0920     0.6430   6.364 2.08e-10 ***
## poly(percent_married, 2, raw = T)2   1.4801     0.5524   2.679  0.00739 ** 
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## Residual standard error: 2.249 on 7204 degrees of freedom
##   (23 observations deleted due to missingness)
## Multiple R-squared:  0.1949, Adjusted R-squared:  0.1946 
## F-statistic: 871.8 on 2 and 7204 DF,  p-value: < 2.2e-16

The quadratic term is statistically significant, even though the improvement in accuracy is not large.

ggplot(edgap, aes(x = percent_married, y = average_act)) + 
  geom_point() + 
  geom_smooth(method = "lm",formula = y ~ x) +
  geom_smooth(method = "lm",formula = y ~ poly(x,2), color = "red") +
  labs(x = "Percent married", y = "School ACT average (or equivalent if SAT score)") +
  theme_bw()
## Warning: Removed 23 rows containing non-finite values (stat_smooth).
## Removed 23 rows containing non-finite values (stat_smooth).
## Warning: Removed 23 rows containing missing values (geom_point).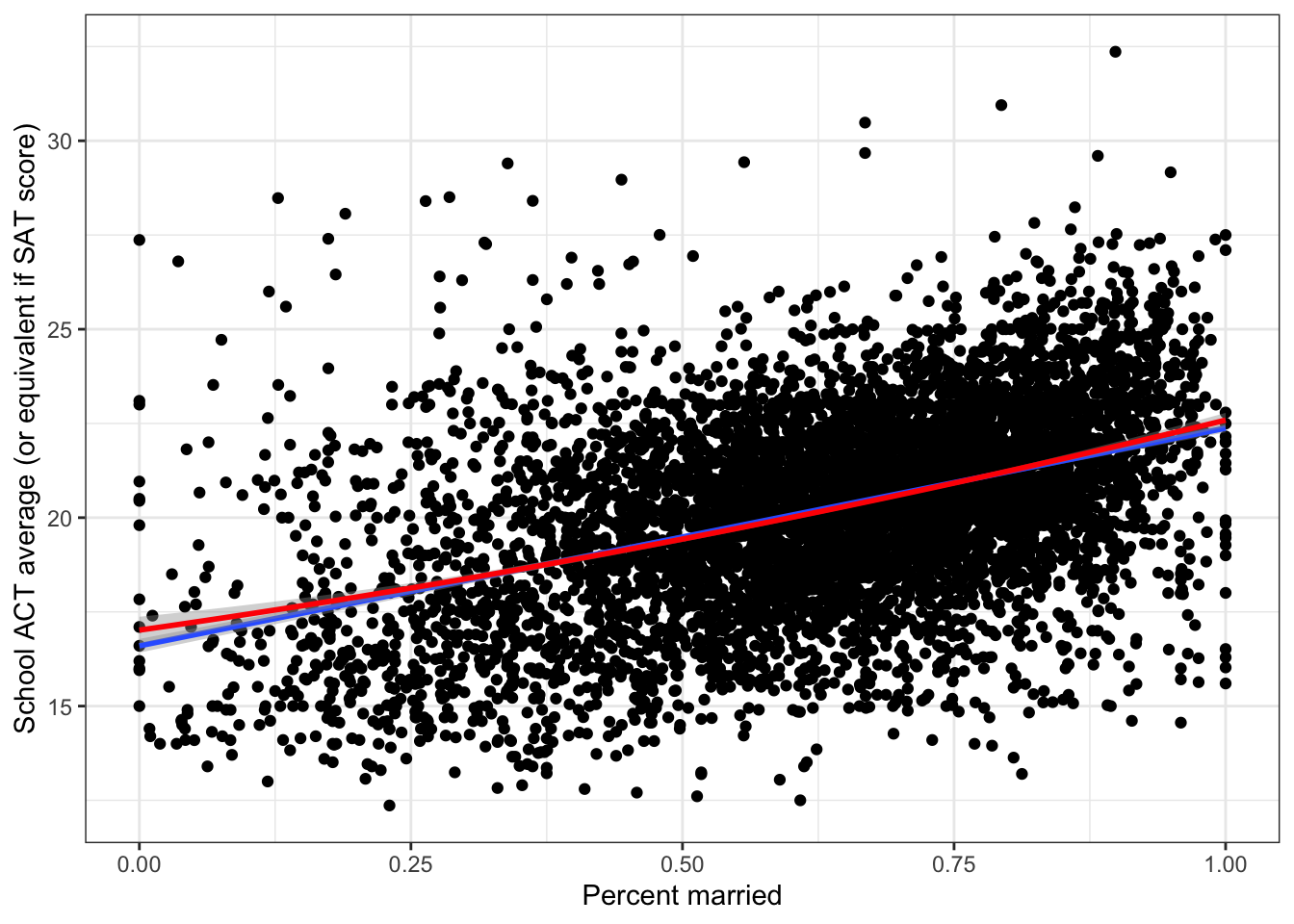

The graph shows that the models are nearly identical.


2.5.2 Model selection

Now that understand how each variable is individually related to the ACT score, we want to know how to best use all of the socioeconomic variables to predict the ACT score.

We do not have many input variables, so we can examine the full model.

fit_full <- lm(average_act ~ percent_lunch + median_income + rate_unemployment + percent_college + percent_married, data = edgap)

Examine the summary of the fit

summary(fit_full)
## 
## Call:
## lm(formula = average_act ~ percent_lunch + median_income + rate_unemployment + 
##     percent_college + percent_married, data = edgap)
## 
## Residuals:
##     Min      1Q  Median      3Q     Max 
## -8.5334 -0.9347 -0.0858  0.8578 10.7692 
## 
## Coefficients:
##                     Estimate Std. Error t value Pr(>|t|)    
## (Intercept)        2.269e+01  1.371e-01 165.492  < 2e-16 ***
## percent_lunch     -7.604e+00  9.650e-02 -78.801  < 2e-16 ***
## median_income     -1.081e-07  1.205e-06  -0.090    0.929    
## rate_unemployment -2.324e+00  4.065e-01  -5.717 1.13e-08 ***
## percent_college    1.754e+00  1.570e-01  11.171  < 2e-16 ***
## percent_married   -7.501e-02  1.332e-01  -0.563    0.573    
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## Residual standard error: 1.522 on 7181 degrees of freedom
##   (43 observations deleted due to missingness)
## Multiple R-squared:  0.6316, Adjusted R-squared:  0.6314 
## F-statistic:  2463 on 5 and 7181 DF,  p-value: < 2.2e-16

The coefficients for median_income and percent_married are not statistically significant. Additionally, the sign of the coefficients for median_income and percent_married do not make sense. These results support removing median_income and percent_married from the model.

2.5.2.1 Do best subset selection

Use the regsubsets function from the leaps package to perform best subset selection in order to choose the best model to predict average_act from the socioeconomic predictors.

#perform best subset selection
regfit_full <- regsubsets(average_act ~ percent_lunch + median_income + rate_unemployment + percent_college + percent_married, data = edgap)

Get the summary of the best subset selection analysis

reg_summary <- summary(regfit_full)

What is the best model obtained according to Cp, BIC, and adjusted \(R^2\)? Make a plot of Cp, BIC, and adjusted \(R^2\) vs. the number of variables in the model.

#Set up a three panel plot
par(mfrow = c(1,3))

#Plot Cp
plot(reg_summary$cp,type = "b",xlab = "Number of variables",ylab = "Cp")
#Identify the minimum Cp
ind_cp = which.min(reg_summary$cp)
points(ind_cp, reg_summary$cp[ind_cp],col = "red",pch = 20)

#Plot BIC
plot(reg_summary$bic,type = "b",xlab = "Number of variables",ylab = "BIC")
#Identify the minimum BIC
ind_bic = which.min(reg_summary$bic)
points(ind_bic, reg_summary$bic[ind_bic],col = "red",pch = 20)

#Plot adjusted R^2
plot(reg_summary$adjr2,type = "b",xlab = "Number of variables",ylab = TeX('Adjusted $R^2$'),ylim = c(0,1))

#Identify the maximum adjusted R^2
ind_adjr2 = which.max(reg_summary$adjr2)
points(ind_adjr2, reg_summary$adjr2[ind_adjr2],col = "red",pch = 20)

The three measures agree that the best model has three variables.

Show the best model for each possible number of variables. Focus on the three variable model.

reg_summary$outmat
##          percent_lunch median_income rate_unemployment percent_college percent_married
## 1  ( 1 ) "*"           " "           " "               " "             " "            
## 2  ( 1 ) "*"           " "           " "               "*"             " "            
## 3  ( 1 ) "*"           " "           "*"               "*"             " "            
## 4  ( 1 ) "*"           " "           "*"               "*"             "*"            
## 5  ( 1 ) "*"           "*"           "*"               "*"             "*"

The best model uses the predictors percent_lunch, rate_unemployment and percent_college.

Fit the best model and examine the results

fit_best <- lm(average_act ~ percent_lunch + rate_unemployment + percent_college, data = edgap)
summary(fit_best)
## 
## Call:
## lm(formula = average_act ~ percent_lunch + rate_unemployment + 
##     percent_college, data = edgap)
## 
## Residuals:
##     Min      1Q  Median      3Q     Max 
## -8.4923 -0.9363 -0.0886  0.8611 10.7536 
## 
## Coefficients:
##                   Estimate Std. Error t value Pr(>|t|)    
## (Intercept)       22.62497    0.10206 221.688  < 2e-16 ***
## percent_lunch     -7.59143    0.09212 -82.405  < 2e-16 ***
## rate_unemployment -2.13118    0.37252  -5.721  1.1e-08 ***
## percent_college    1.73653    0.12637  13.741  < 2e-16 ***
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## Residual standard error: 1.522 on 7191 degrees of freedom
##   (35 observations deleted due to missingness)
## Multiple R-squared:  0.6311, Adjusted R-squared:  0.631 
## F-statistic:  4101 on 3 and 7191 DF,  p-value: < 2.2e-16

2.5.2.2 Relative importance of predictors

To compare the magnitude of the coefficients, we should first normalize the predictors. Each of the predictors percent_lunch, rate_unemployment and percent_college is limited to the interval (0,1), but they occupy different parts of the interval. We can normalize each variable through a z-score transformation:

scale_z <- function(x, na.rm = TRUE) (x - mean(x, na.rm = na.rm)) / sd(x, na.rm)

edgap_z <- edgap %>% 
  mutate_at(c("percent_lunch","rate_unemployment","percent_college"),scale_z)

\(\rightarrow\) Fit the model using the transformed variables and examine the coefficients

Show Answer 
fit_z <- lm(average_act ~ percent_lunch + rate_unemployment + percent_college, data = edgap_z)

summary(fit_z)
## 
## Call:
## lm(formula = average_act ~ percent_lunch + rate_unemployment + 
##     percent_college, data = edgap_z)
## 
## Residuals:
##     Min      1Q  Median      3Q     Max 
## -8.4923 -0.9363 -0.0886  0.8611 10.7536 
## 
## Coefficients:
##                   Estimate Std. Error  t value Pr(>|t|)    
## (Intercept)       20.29713    0.01795 1130.931  < 2e-16 ***
## percent_lunch     -1.78055    0.02161  -82.405  < 2e-16 ***
## rate_unemployment -0.12065    0.02109   -5.721  1.1e-08 ***
## percent_college    0.28665    0.02086   13.741  < 2e-16 ***
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## Residual standard error: 1.522 on 7191 degrees of freedom
##   (35 observations deleted due to missingness)
## Multiple R-squared:  0.6311, Adjusted R-squared:  0.631 
## F-statistic:  4101 on 3 and 7191 DF,  p-value: < 2.2e-16

The coefficient on percent_lunch is an order of magnitude larger than the other coefficients. This supports the conclusion that percent_lunch is the most important predictor.

Additionally, the performance of the single predictor model using percent_lunch is very close to the performance of the best model.

2.6 Additional step

In addition to completing the above analyses, you should ask and answer one question about the data set. Consult Canvas for further directions.

2.7 Conclusion

After completing your analyses, you will make your conclusions and communicate your results. Consult Canvas for further directions.