16 單變數迴歸

本章為 Ismay and Kim (2019) 第 5 章內容。

需要的套件

library(tidyverse)
library(moderndive)
library(skimr)
library(gapminder)

其中，moderndive 使用 tidyverse style 編寫，可以從事基本的線性迴歸；skimr 則可以幫助我們快速地計算敘述統計。

16.1 解釋變數為連續變數

以下，我們想了解的是老師的外貌與其教學評鑑的分數有關係嗎？是什麼關係？因此，解釋變數（explanatory variable） \(x\) 為老師的外貌分數，而結果變數（outcome variable）為老師的教學評鑑分數。

16.1.1 探索性資料分析

在 moderdive 中，有一 data frame 為 eval，其包含了 UT Austin 的 463 門課程。我們使用 select() 選取我們接下來將要使用的變數，包括 ID、score 與 bty_avg，並且存在名為 evals_ch5 裡頭。

evals_ch5 <- evals %>%
  select(ID, score, bty_avg)

回憶第 7 章所提及的，當我們拿到資料要分析或建模之前，第一件事情就是進行探索性資料分析，即 EDA。EDA 讓我們了解個別變數的分配、變數之間是否有潛在的關係與是否有 outliers 或缺漏值。EDA 常見的三個步驟：⁵

觀察原始資料的值。
計算概括的統計量，如平均數、中位數或四分位距等。
資料視覺化。

16.1.1.1 EDA：觀察原始資料的值

我們可以使用 tibble 中的 glimpse() 查看資料，如：

glimpse(evals_ch5)

## Rows: 463
## Columns: 3
## $ ID      <int> 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18,…
## $ score   <dbl> 4.7, 4.1, 3.9, 4.8, 4.6, 4.3, 2.8, 4.1, 3.4, 4.5, 3.8, 4.5, 4.…
## $ bty_avg <dbl> 5.000, 5.000, 5.000, 5.000, 3.000, 3.000, 3.000, 3.333, 3.333,…

也能使用 dplyr 中的 sample_n() 函數，隨機挑選給定數量的觀察值，如：

evals_ch5 %>%
  sample_n(size = 5)

## # A tibble: 5 × 3
##      ID score bty_avg
##   <int> <dbl>   <dbl>
## 1   183   3      4.33
## 2    25   4.6    5.5 
## 3   307   4.6    3.33
## 4   124   3.5    4.83
## 5   273   4.5    5.67

由上，我們可知有 463 個觀察值。其中，各個變數分別代表：

ID：在這份資料中用以編號觀察值的變數。
score：連續變數；老師的平均教學評鑑分數；最高 5 分，最低 1 分；為我們所關切的結果變數 \(y\)。
bty_avg：連續變數；老師的平均外貌分數，最高 10 分，最低 1 分；為我們所關切的解釋變數 \(x\)。

16.1.1.2 EDA：簡單的敘述統計

既然 score 與 bty_avg 是連續的數值變數，那我們可以計算他們的平均值與中位數，如：

evals_ch5 %>%
  summarise(mean_score = mean(score),
            mean_bty_avg = mean(bty_avg),
            median_score = median(score),
            median_bty_avg = median(bty_avg))

## # A tibble: 1 × 4
##   mean_score mean_bty_avg median_score median_bty_avg
##        <dbl>        <dbl>        <dbl>          <dbl>
## 1       4.17         4.42          4.3           4.33

不過，如果要使用 summarize 來計算標準差、極值與分量的話，並非不可，只是比較麻煩。我們可以使用套件 skimr 中的 skim() 函數。把 data frame 丟入這個函數，將會回傳常用的敘述統計量，如：

evals_ch5 %>% select(score, bty_avg) %>% skim()

── Data Summary ────────────────────────
                           Values    
Name                       Piped data
Number of rows             463       
Number of columns          2         
_______________________              
Column type frequency:               
  numeric                  2         
________________________             
Group variables            None      

── Variable type: numeric ───────────────────────────────────────────────────────────────────
  skim_variable n_missing complete_rate  mean    sd    p0   p25   p50   p75  p100 hist 
1 score                 0             1  4.17 0.544  2.3   3.8   4.3    4.6  5    ▁▁▅▇▇
2 bty_avg               0             1  4.42 1.53   1.67  3.17  4.33   5.5  8.17 ▃▇▇▃▂

其中，回傳的有：

missing：缺漏值的數量。
complete：非缺漏值的數量。
n：所有值變數值的數量。
mean：平均值。
sd：標準差（standard deviation）。
p0：0th 分量，即最小值。
p25：25th 分量。
p50：50th 分量。
p75：75th 分量。
p100：100th 分量，即最大值。

不過，skim() 回傳的這些都是所謂的 univariate summary statistics。但我們還會想知道 binary summary statistics。例如，如果兩個變數都是數值變數，那我們可以計算相關係數（correlation coefficients） 。

想要計算相關係數的話，我們有兩種方式。

使用 moderndive 中的 get_correlation() 函數，使用 formula ~，把解釋變數放在 ~ 右邊，結果變數放在 ~ 左邊，如：

evals_ch5 %>%
  get_correlation(formula = score ~ bty_avg)

## # A tibble: 1 × 1
##     cor
##   <dbl>
## 1 0.187

使用 summarize() 中的 cor 函數，如：

evals_ch5 %>%
  summarise(correlation = cor(score, bty_avg))

## # A tibble: 1 × 1
##   correlation
##         <dbl>
## 1       0.187

16.1.1.3 EDA：視覺化

加上 position = "jitter"（或者不用 geom_point()，改用 hgeom_jitter()）如同第 5 章所說的，是為了避免 overplotting 的情況。

evals_ch5 %>%
  ggplot(aes(x = bty_avg, y = score)) +
  geom_point(position = "jitter") +
  labs(x = "Beauty Score",
       y = "Teaching Score",
       title = "Scatterplot of realtionship of traching and beauty scores")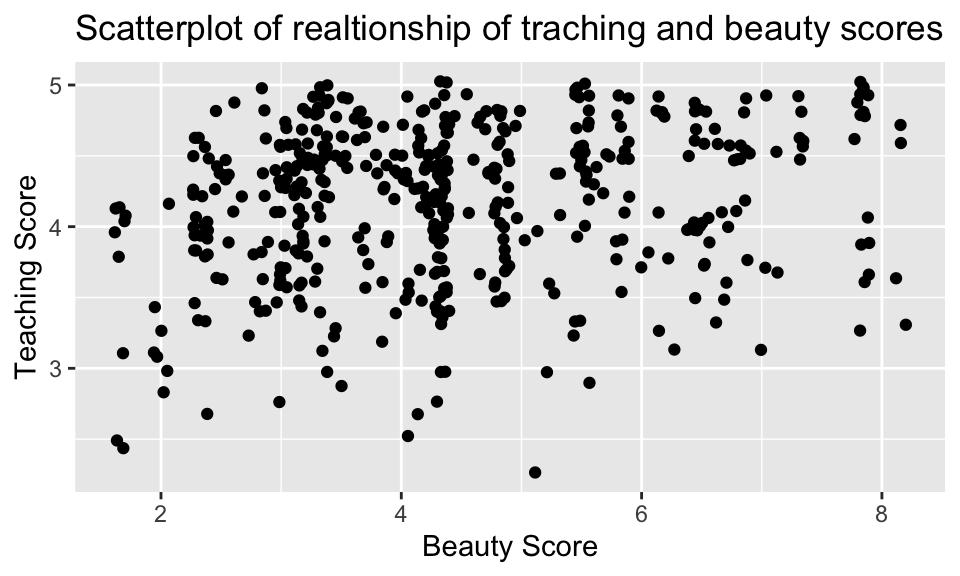

我們也可以使用 geom_smooth(method = "lm")，就能以最小平方法來適配模型，並畫出迴歸線（regression line），如：

evals_ch5 %>%
  ggplot(aes(x = bty_avg, y = score)) +
  geom_jitter() +
  geom_smooth(method = "lm", se = FALSE, formula = 'y ~ x') +
  labs(x = "Beauty Score",
       y = "Teaching Score",
       title = "Relationship between teaching and beauty scores")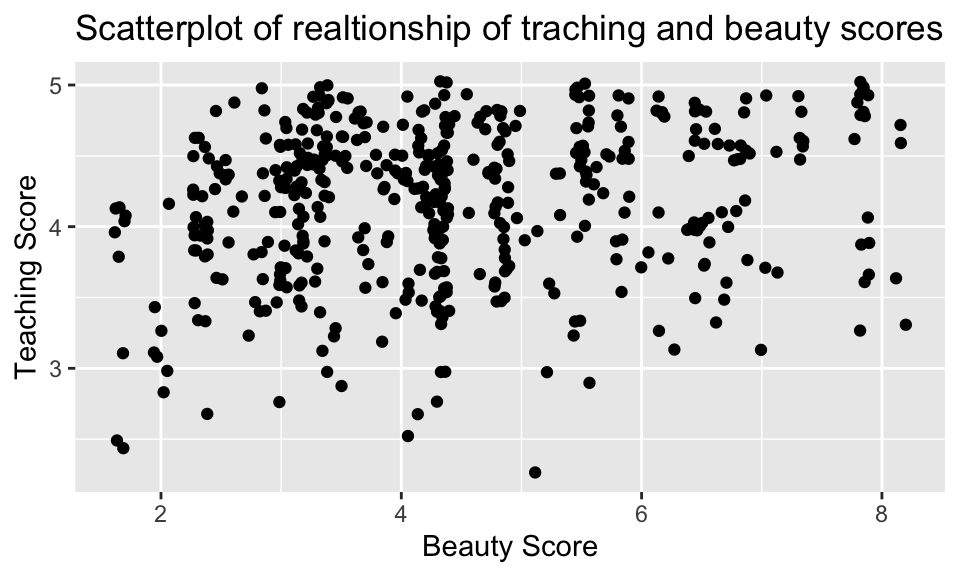

事實上，藍色線段的斜率恰等於上節所算出的相關係數 0.0187。不過，雖然相關係數與迴歸線的斜率的正負號通常相同，但其值通常不同。

16.1.2 簡單線性迴歸

如何進行簡單線性回歸？定義一迴歸線 \(\hat{y} = \hat{b}_0 + \hat{b}_1\cdot x\)，我們可以：

使用 lm() 函數適配迴歸模型，然後存在 score_model 中。
把 score_model 丟到套件 moderndive 中的 get_regression_table() 函數得到 regression table。

score_model <- lm(score ~ bty_avg, data = evals_ch5)
get_regression_table(score_model)

## # A tibble: 2 × 7
##   term      estimate std_error statistic p_value lower_ci upper_ci
##   <chr>        <dbl>     <dbl>     <dbl>   <dbl>    <dbl>    <dbl>
## 1 intercept    3.88      0.076     51.0        0    3.73     4.03 
## 2 bty_avg      0.067     0.016      4.09       0    0.035    0.099

簡而言之，我們適配出的迴歸模型即 \[ \begin{aligned} \hat{y} &= \hat{b}_0 +\hat{b}_1 \cdot x\\ \widehat{\rm score} &= 3.88 + 0.067 \cdot {\rm bty\_avg} \end{aligned} \] 這說明了，當 bty_avg 每增加 1 單位，score 平均會增加 0.067 單位。不過要注意的是，這是相關，而不是因果；即這是 associated increase，而非 causal increase。

16.1.3 Observed/fitted values and residuals

如果我們想看個別的點的預測值與殘差呢？我們可以 get_regression_points() 來完成這件事，如：

regression_points <- get_regression_points(score_model)
head(regression_points)

## # A tibble: 6 × 5
##      ID score bty_avg score_hat residual
##   <int> <dbl>   <dbl>     <dbl>    <dbl>
## 1     1   4.7       5      4.21    0.486
## 2     2   4.1       5      4.21   -0.114
## 3     3   3.9       5      4.21   -0.314
## 4     4   4.8       5      4.21    0.586
## 5     5   4.6       3      4.08    0.52 
## 6     6   4.3       3      4.08    0.22

16.2 解釋變數為類別變數

世界上各國的預期壽命有什麼差異？各個大陸的人的預期壽命之間有何差異？同個大陸之間，預期壽命的分佈又是如何呢？

我們可以使用套件 gapminder 中的 gapminder 這個 data frame 來嘗試回答這個問題。其中，結果變數 \(y\) 是國家的預期壽命，一個連續變數；解釋變數 \(x\) 是國家屬於哪大洲，一個類別變數。資料詳情可以參照套件說明。

16.2.1 探索性資料分析

首先載入資料。我們觀察的焦點放在 2007 年的狀況，並且我們需要 country、lifeExp、continent 的資料。

library(gapminder)
gapminder2007 <- gapminder %>%
  filter(year == 2007) %>%
  select(continent, country, lifeExp)

16.2.1.1 EDA：觀察原始資料

glimpse(gapminder2007)

## Rows: 142
## Columns: 3
## $ continent <fct> Asia, Europe, Africa, Africa, Americas, Oceania, Europe, Asi…
## $ country   <fct> "Afghanistan", "Albania", "Algeria", "Angola", "Argentina", …
## $ lifeExp   <dbl> 43.828, 76.423, 72.301, 42.731, 75.320, 81.235, 79.829, 75.6…

gapminder2007 %>% sample_n(size = 5)

## # A tibble: 5 × 3
##   continent country                  lifeExp
##   <fct>     <fct>                      <dbl>
## 1 Europe    Finland                     79.3
## 2 Africa    Central African Republic    44.7
## 3 Africa    Angola                      42.7
## 4 Africa    Tunisia                     73.9
## 5 Africa    Cameroon                    50.4

16.2.1.2 EDA：簡單的敘述統計

gapminder2007 %>%
  select(lifeExp, continent) %>%
  skim()

── Data Summary ────────────────────────
                           Values    
Name                       Piped data
Number of rows             142       
Number of columns          2         
_______________________              
Column type frequency:               
  factor                   1         
  numeric                  1         
________________________             
Group variables            None      

── Variable type: factor ───────────────────────────────────────────────────────────────────
  skim_variable n_missing complete_rate ordered n_unique top_counts                        
1 continent             0             1 FALSE          5 Afr: 52, Asi: 33, Eur: 30, Ame: 25

── Variable type: numeric ──────────────────────────────────────────────────────────────────
  skim_variable n_missing complete_rate  mean    sd    p0   p25   p50   p75  p100 hist 
1 lifeExp               0             1  67.0  12.1  39.6  57.2  71.9  76.4  82.6 ▂▃▃▆▇

16.2.2 線性迴歸

16.2.3 Observed/fitted values and residuals

15 以 magrittr 使用 Pipes

17 多變數迴歸