2 Les modèles linéaires généralisés

Les modèles linéaires généralisés sont une généralisation du modèle linéaire Gaussien, obtenu en autorisant d’autres lois (conditionnelles) que la loi Gaussienne. Les lois possibles doivent appartenir à la famille exponentielle, c’est à dire dont la densité (ou mesure de probabilité dans le cas discret) s’écrit :

\[f(y|\theta,\phi) = \exp\bigg(\frac{y\theta-b(\theta)}{\phi}+c(y,\phi) \bigg)\]

La fonction lien est la fonction qui permet de lier les variables explicatives \(X\) à la prédiction \(\mu\), alors que la loi apparaît via la fonction variance, sur la forme de l’hétéroscédasticité et l’incertitude associée à la prédiction.

La cellule de code suivante permet d’entraîner 3 régressions GLM différentes puis de les comparer.

library(dplyr)
dataglm = database[,c("SumSINAPS","SEX","STATUT","ZONE","CSP","USAGE","AGECOND")]
set.seed(1234)
echantillon = sample(1:length(SumSINAPS))[1:(length(SumSINAPS)%/%4)]
datatrain = dataglm[-echantillon,]
datatest = dataglm[echantillon,]
#GLMs
# Gaussian identity
regNId  <- glm(SumSINAPS~.,family=gaussian(link="identity"),data = datatrain)
# Poisson identity
regPId  <- glm(SumSINAPS~.,family=poisson(link="identity"),data = datatrain)
# Poisson log
regPlog <- glm(SumSINAPS~.,family=poisson(link="log"),data = datatrain)
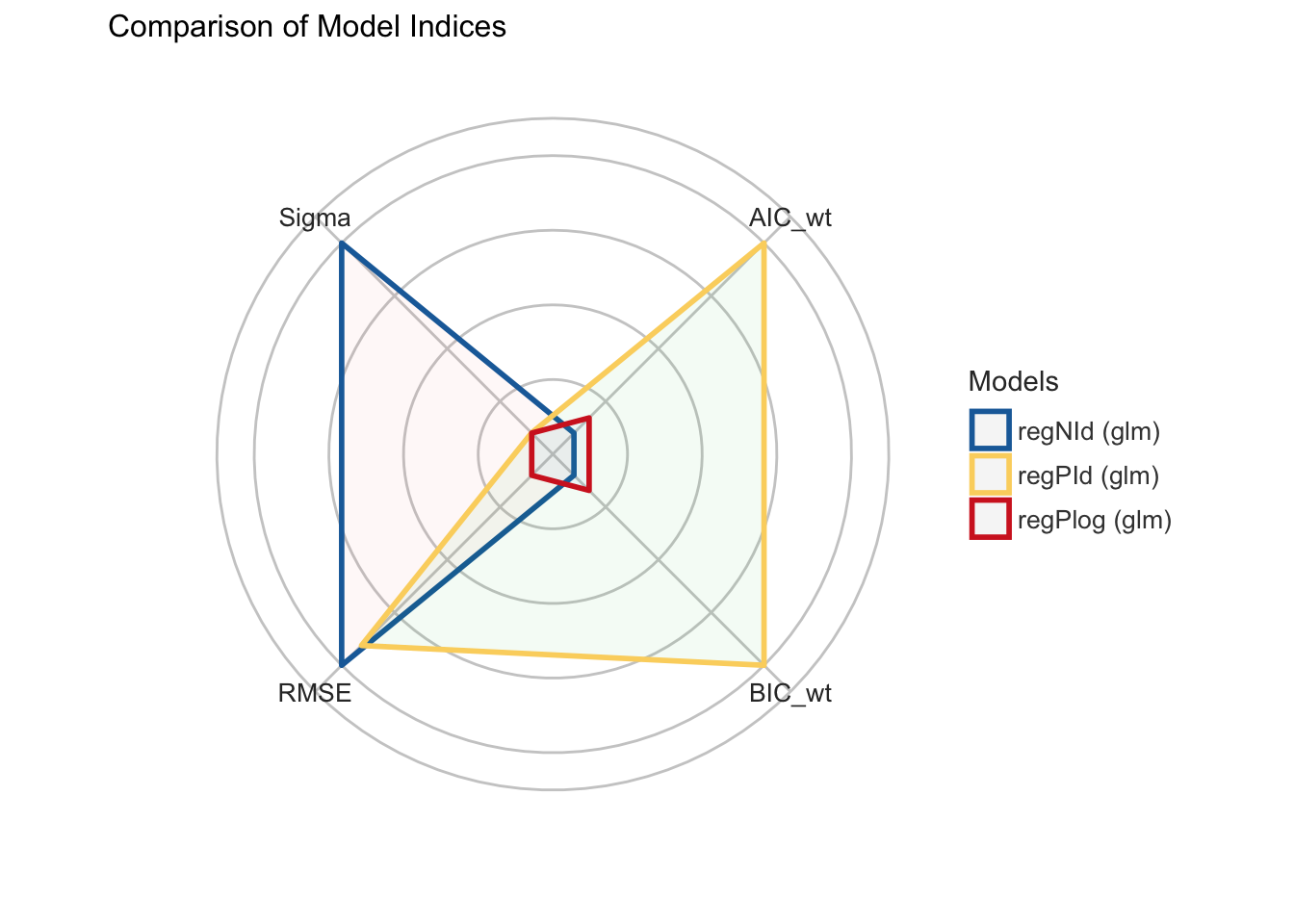
comparemodel <-  performance::compare_performance(regNId,regPId,regPlog)
comparemodel[,c("Name","AIC","AIC_wt","BIC")]

## # Comparison of Model Performance Indices
## 
## Name    |       AIC | AIC weights |       BIC
## ---------------------------------------------
## regNId  | 24500.744 |     < 0.001 | 24559.927
## regPId  | 12971.160 |       0.926 | 13022.944
## regPlog | 12976.219 |       0.074 | 13028.004

Sous le critère de l’AIC et du BIC on peut choisir le modèle regPlog c’est à dire celui qui a pour fonction de lien logpoisson.

Régression logistique ou probit

On peut modéliser l’éxistance d’un sinistre pour un client. Pour cela il va falloire créer une nouvelle colonne Indicatrice dans notre database qui prend 0 si SumSINAPS est nul et 1 sinon.

database$Indicatrice <- ifelse(SumSINAPS>0,1,0)

Passons maintenant La régression logistique !

dataglm = database[,c("Indicatrice","AGECOND")]
datatrain = dataglm[-echantillon,]
datatest = dataglm[echantillon,]
logistic <- glm(Indicatrice~.,data = datatrain,family = binomial(link = 'logit'))
Probit <- glm(Indicatrice~.,data = datatrain,family = binomial(link = 'probit'))

La cellule suivante permet de faire des prédictions pour chaque modèle :

predLogistic <- predict(logistic,datatest[,-1],type = "response")
predProbit <- predict(Probit,datatest[,-1],type = "response")