4 Semana IV
4.1 Inferencia sobre dos poblaciones independientes
Uno de los parámetros que puede ser de nuestro interés es la diferencia de las medias poblacionales de dos poblaciones que son independientes. Suponga que \(x_1,x_2,\cdots,x_{n_1}\) y \(y_1,y_2,\cdots,y_{n_2}\) son dos muestras aleatorias de dos poblaciones independientes, denotemos por \(\mu_x\) y \(\mu_y\) las medias poblacionales de las poblaciones 1 y 2 respectivamente, vamos a estar interesados en probar las hipótesis:
Bilaterales \[\begin{eqnarray} H_0: \mu_x=\mu_y &\Rightarrow& \mu_x-\mu_y=0\\ & vrs &\\ H_1: \mu_x \neq \mu_y &\Rightarrow& \mu_x-\mu_y \neq 0 \end{eqnarray}\]
Unilaterales \[\begin{eqnarray} H_0: \mu_x \leq \mu_y &\Rightarrow& \mu_x-\mu_y\leq 0\\ & vrs &\\ H_1: \mu_x > \mu_y &\Rightarrow& \mu_x-\mu_y > 0 \end{eqnarray}\]
o
\[\begin{eqnarray} H_0: \mu_x \geq \mu_y &\Rightarrow& \mu_x-\mu_y\geq 0\\ & vrs &\\ H_1: \mu_x < \mu_y &\Rightarrow& \mu_x-\mu_y < 0 \end{eqnarray}\]
Recordemos que solo conocemos las muestras aleatorias de nuestras poblaciones, para realizar un test con poblaciones independientes necesitamos asumir uno de estos dos casos
- Varianzas poblacionales iguales
- Varianzas poblacionales diferentes
La función t.test() de r nos sirve para contrastar esta hipótesis, consideremos un ejemplo
Example 4.1 El AZT fue el primer fármaco antirretroviral aprobado por la FDA que se usó en el cuidado de personas infectadas por el VIH. La dosis habitual es de 300 mg dos veces al día. Las dosis más altas provocan más efectos secundarios. Pero, ¿son más efectivos? Un estudio realizado en 1990 comparó dosis de 300 mg, 600 mg y 1500 mg (fuente http://www.aids.org). El estudio encontró una mayor toxicidad con dosis más altas y, lo que es más importante, que la dosis más baja puede ser igualmente efectiva.
El antígeno p24 puede estimular las respuestas inmunitarias. La medición de los niveles de p24 para los grupos de 300 mg y 600 mg se muestra en la siguiente tabla. Realice una prueba t para determinar si hay una diferencia en las medias, asumiendo que la dosis no cambia la varianza.
| dosis | Nivel de p24 | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| 300 mg | 284 | 279 | 289 | 292 | 287 | 295 | 285 | 279 | 306 | 298 |
| 600 mg | 298 | 307 | 297 | 279 | 291 | 335 | 299 | 300 | 306 | 291 |
Definamos nuestras poblaciones:
- Población 1: Dosis de 300 mg
- Población 2: Dosis de 600 mg
Estamos interesados en saber si existe o no diferencia entre los niveles de p24 entre las dosis de 300 mg y 600 mg, es decir que nuestras hipótesis a conrastar serán:
\(H_0\): No hay diferencia entre los niveles de p24 en ambas poblaciones.
\(H_1:\) Existe diferencia entre los niveles de p24 en ambas poblaciones.
Lo que es equivalente
\[\begin{eqnarray} H_0: \mu_x=\mu_y &\Rightarrow& \mu_x-\mu_y=0\\ & vrs &\\ H_1: \mu_x \neq \mu_y &\Rightarrow& \mu_x-\mu_y \neq 0 \end{eqnarray}\]
Antes de realizar el test comprobemos las hipótesis de normalidad, realizando algunos gráficos
d300 <- c(284, 279, 289, 292, 287, 295, 285, 279, 306, 298)
d600 <- c(298, 307, 297, 279, 291, 335, 299, 300, 306, 291)
plot(density(d300), col="coral3",
xlab="Niveles de p24")
lines(density(d600), col="deepskyblue3")
legend("topright", lty = 1,
legend = c("300 mg", "600 mg"),
col=c("coral3","deepskyblue3"))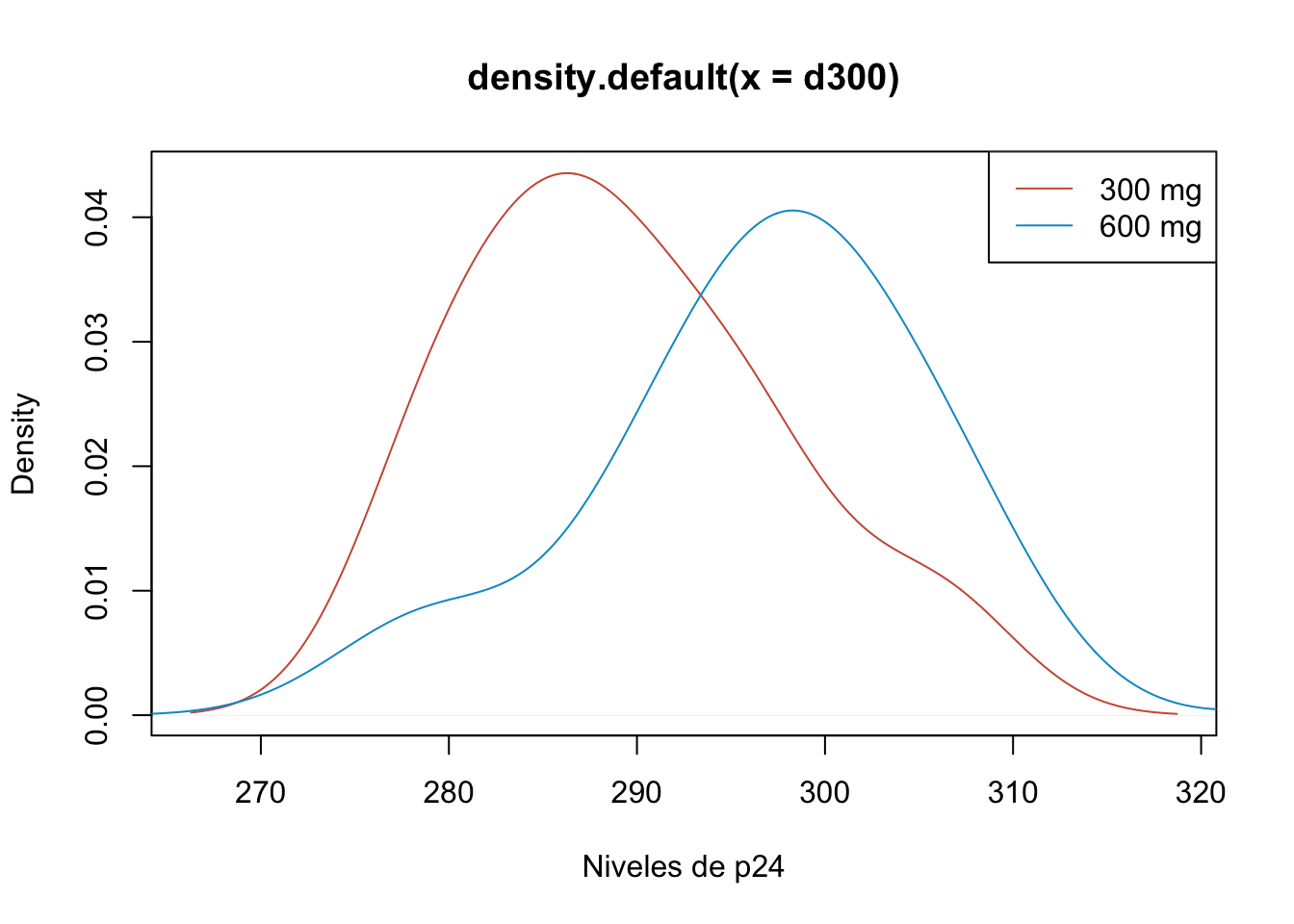
par(mfrow=c(1,2))
qqnorm(d300, col="coral3", main="300 mg")
qqline(d300)
qqnorm(d600, col="deepskyblue3", main = "600 mg")
qqline(d600)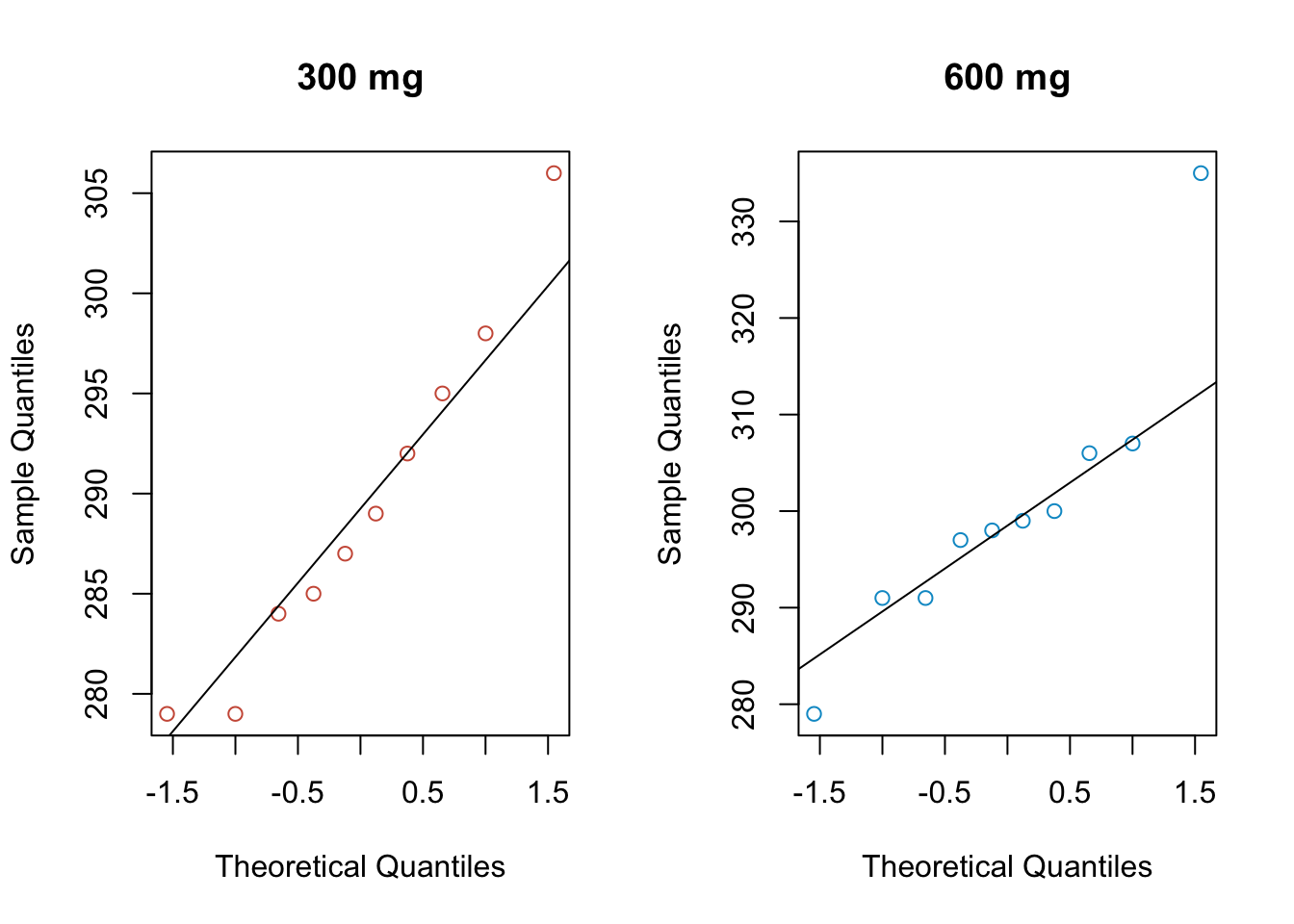
par(mfrow=c(1,1))y también algunas pruebas
shapiro.test(d300)##
## Shapiro-Wilk normality test
##
## data: d300
## W = 0.95218, p-value = 0.6943shapiro.test(d600)##
## Shapiro-Wilk normality test
##
## data: d600
## W = 0.8734, p-value = 0.1095De estos resultados anteriores podriamos aceptar la hipótesis de normalidad, además de las graficas de las densidades podríamos notar que la varianza en ambas poblaciones es similiar.
Una vez comprobado esto procedemos a realizar el test en R.
t.test(d300, d600, var.equal=TRUE)##
## Two Sample t-test
##
## data: d300 and d600
## t = -2.034, df = 18, p-value = 0.05696
## alternative hypothesis: true difference in means is not equal to 0
## 95 percent confidence interval:
## -22.1584072 0.3584072
## sample estimates:
## mean of x mean of y
## 289.4 300.34.2 Comparaciones por parejas
Hay ocasiones en las que dos muestras dependen una de la otra de alguna manera, por ejemplo, muestras de estudios de gemelos, donde los gemelos idénticos o fraternos se utilizan como pares, de modo que se pueden controlar los factores genéticos o ambientales. Para ello, no se aplica la prueba t habitual de dos muestras.
Suponga que \(x_1,\cdots,x_n\) y \(y_1,\cdots, y_n\) son dos muestras dependientes, consideremos las observaciones \(d_i = x_i - y_i\) \(i=1,\cdots,n\), vamos a considerar a las observaciones \(d_1,\cdots , d_n\) como una muestra aleatoria y procedemos a realizar el test como en el caso de una media poblacional. Tomando en cuenta que si \(\mu_d \neq 0\), la media poblacional de las diferencias es distinta de cero, esto significa que hay diferencia en los tratamientos.
| Prueba | Puntuación | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Previa | 77 | 56 | 64 | 60 | 57 | 53 | 72 | 62 | 65 | 66 |
| Posterior | 88 | 74 | 83 | 68 | 58 | 50 | 67 | 64 | 74 | 60 |
Podemos construir un boxplot para visualizar la dispersión de las dos poblaciones y darnos una idea de lo que podría estar sucediendo
pre <- c(77, 56, 64, 60, 57, 53, 72, 62, 65, 66)
post <- c(88, 74, 83, 68, 58, 50, 67, 64, 74, 60)
boxplot(pre, post, col="firebrick3",
names=c("Previa","Posterior"))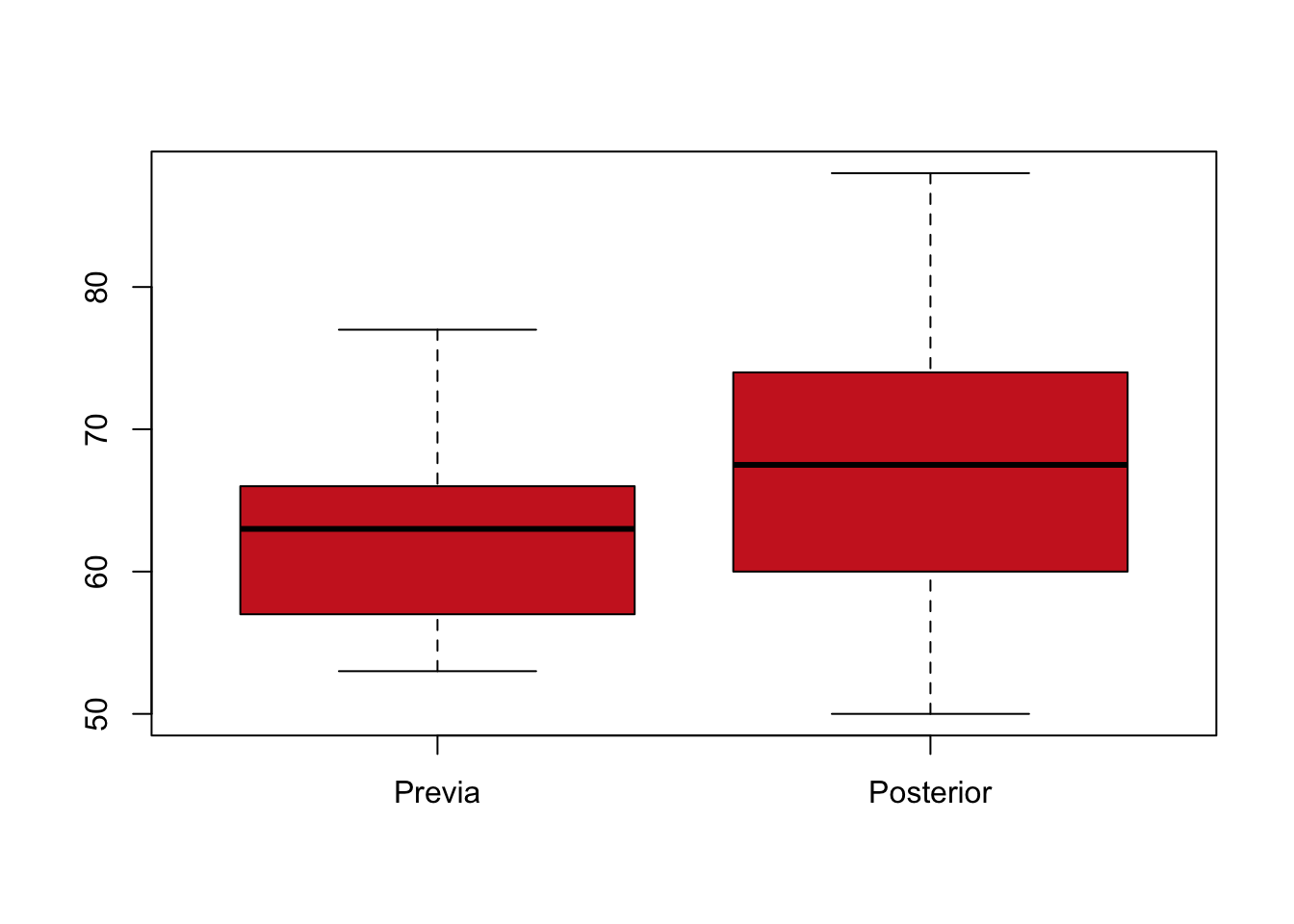
En el gráfico observamos que las puntuaciones posteriores parecen acumularse un poco más arriba de las puntuaciones previas, ahora podemos plantear las hipótesis
\(H_0:\) El curso universitario no está funcionando
\(H_1:\) El curso universitario está funcionando
Equivalente a
\(H_0:\mu_d \geq 0\)
\(H_1:\mu_d<0\)
t.test(pre, post, paired=TRUE, alternative="less")##
## Paired t-test
##
## data: pre and post
## t = -1.8904, df = 9, p-value = 0.04564
## alternative hypothesis: true difference in means is less than 0
## 95 percent confidence interval:
## -Inf -0.1635821
## sample estimates:
## mean of the differences
## -5.4Notemos que el valor p es menor qu el nivel de significancia de 0.05, por lo que rechazamos \(H_0\) y concluimos que el curso universitario está funcionando. (la media de las puntuaciones previas son menores que las posteriores).
4.3 Potencia del test
La potencia de una prueba estadística o el poder estadístico es la probabilidad de que la hipótesis alternativa sea aceptada cuando la hipótesis alternativa es verdadera (es decir, la probabilidad de no cometer un error del tipo II). La potencia es en general una función de las distribuciones posibles, a menudo determinada por un parámetro, bajo la hipótesis alternativa. A medida que aumenta la potencia, las posibilidades de que se presente un error del tipo II disminuyen.
\[\begin{eqnarray} Potencia & = & P(\text{Rechazar }H_0\vert H_0\text{ es falsa})\\\\ & = & 1-\beta \end{eqnarray}\]
El análisis de potencia se puede utilizar para calcular el tamaño mínimo de la muestra necesario para que uno pueda detectar razonablemente un efecto de un determinado tamaño. El análisis de poder también se puede utilizar para calcular el tamaño del efecto mínimo que es probable que se detecte en un estudio usando un tamaño de muestra dado.
La potencia de la prueba la podemos calcular para un valor especifico bajo \(H_1\), la hipótesis alternativa.
Dados el nivel de significacia \(\alpha\) de un test, la desviación típica de la variable cuyo parámetro se contrasta, el tipo de test (una muestra, dos muestras independientes o dos muestras emparejadas) y la hipótesis alternativa (unilateral o bilateral), la función power.t.test() permite:
Calcular la potencia del t-test para detectar una diferencia delta con un tamaño de muestra n prefijados.
Calcular el tamaño de la muestra necesario para detectar una diferencia delta con una potencia prefijada.
Calcular la diferencia máxima delta que es posible detectar con un tamaño de muestra n para una potencia específica.
Example 4.3 Una empresa vende sus productos por internet y cree que un cambio en el diseño de su página web, aumentando el número y la calidad de las fotos de los productos que exhibe, conseguirá incrementar sus ventas.
El volumen medio de ventas diarias, utilizando el diseño de la página actual, es de 9300$.
Antes de tomar una decisión, decide hacer una prueba durante 30 dias presentando sus productos con el nuevo diseño de página web.
El volumen medio de ventas de esos 30 días, en los que se utiliza el nuevo diseño de página, ha sido 9700$, y la desviación típica de las cifras de ventas ha sido de 1570$.
Determinar la potencia del test para detectar un incremento medio de las ventas por dia de 500$ e interpretar este resultado.El test que se pretende realizar en este experimento es:
\(H_0:\mu\leq9300\$\)
\(H_1: \mu > 9300\$\)
power.t.test(n=30, delta= 500, sd=1570,
alternative = "one.sided",
type = "one.sample")##
## One-sample t test power calculation
##
## n = 30
## delta = 500
## sd = 1570
## sig.level = 0.05
## power = 0.5233641
## alternative = one.sidedNotemos que la pontecia del test nos da 0.52, esto significa que, si el nuevo diseño de página incrementase las ventas medias diarias en una cantidad igual a 500, la probabilidad de que el test propuesto detecte esta situación (rechazando correctamente \(H_0:\mu=9300\$\)) sería igual a 0.52. Podriamos decir que el test es poco potente para detectar este incremento en las ventas.
Ahora nos podemos preguntar: ¿Cuál deberia ser el tamaño de muestra para que esta diferencia sea detectada con una probabilidad de 0.8?
power.t.test(power=0.8, delta= 500, sd=1570,
alternative = "one.sided",
type = "one.sample")##
## One-sample t test power calculation
##
## n = 62.33288
## delta = 500
## sd = 1570
## sig.level = 0.05
## power = 0.8
## alternative = one.sided4.4 Regresión Lineal simple
En regresión lineal simple, intentamos modelar la relación entre dos variables, por ejemplo, ingreso y número de años de educación, altura y peso de las personas, largo y ancho de los sobres, temperatura y producción de un proceso industrial, altitud y punto de ebullición del agua o dosis de un fármaco y respuesta. Para una relación lineal, podemos usar un modelo de la forma
\[ y=\beta_0 + \beta_1x + \epsilon \]
donde y es la variable dependiente o de respuesta, x es la variable independiente o predictora. La variable aleatoria \(\epsilon\) es el término de error en el modelo. En este contexto, error no significa error, sino un término estadístico que representa fluctuaciones aleatorias, errores de medición o el efecto de factores fuera de nuestro control.
El modelo de regresión lineal simple para n observaciones puede escribirse de la forma \(y_i=\beta_0 + \beta_1x_i + \epsilon_i\), \(i=1,\cdots,n\).
El modelo debe cumplir los siguietes supuestos:
\(E(\epsilon_i)=0\) \(\forall i=1,\cdots,n\), o equivalente \(E(y_i)=\beta_0 + \beta_1x_i\)
\(Var(\epsilon_i)=\sigma^2\) \(\forall i=1,\cdots,n\), o equivalente \(Var(y_i)=\sigma^2\) (Homocedasticidad, varianza constante o varianza homogénea)
\(Cov(\epsilon_i, \epsilon_j)=0\) \(\forall i=1,\cdots,n\) o equivalente \(Cov(y_i,y_j)=0\)
Nuestro objetivo es estimar los parámetros \(\beta_0\) y \(\beta_1\) para poder hacer predicciones del modelo.
Example 4.4 Los estudiantes de la clase de estadística afirmaron que hacer la tarea no los había ayudado a prepararse para el examen de mitad de período. El puntaje del examen y y el puntaje de la tarea x (promediado hasta el momento de la mitad del período) para los 18 estudiantes de la clase fueron los siguientes:
| prueba | 96 | 77 | 0 | 0 | 78 | 64 |
| examen | 95 | 80 | 0 | 0 | 79 | 77 |
| prueba | 89 | 47 | 90 | 93 | 18 | 86 |
| examen | 72 | 66 | 98 | 90 | 0 | 95 |
| prueba | 0 | 30 | 59 | 77 | 74 | 67 |
| examen | 35 | 50 | 72 | 55 | 75 | 66 |
Quremos estudiar si existe una relación lineal entre la calificación del examen y la prueba, o en otras palabras, será que podemos predecir la calificación de la prueba mediante la calificación del examen \[ examen=\beta_0 +\beta_1prueba + \epsilon \]
primero veamos la correlación de las variables con cor()
prueba <- c(96, 77, 0, 0, 78, 64,
89, 47, 90, 93, 18, 86,
0 , 30, 59, 77, 74, 67)
examen <- c(95, 80, 0, 0, 79, 77,
72, 66, 98, 90, 0, 95,
35, 50, 72, 55, 75, 66)
cor(prueba,examen)## [1] 0.91041el coeficiente de correlación nos da 0.91041, eso indica una alta correlación y que además es positiva, esto quiere decir que entre más alta es la calificación de la prueba, más alta será la calificación del examen.
Podemos ver la correlación de las dos variables cosntruyendo un diagrama de dispersión con plot()
plot(prueba,examen, pch=20,
col="coral4")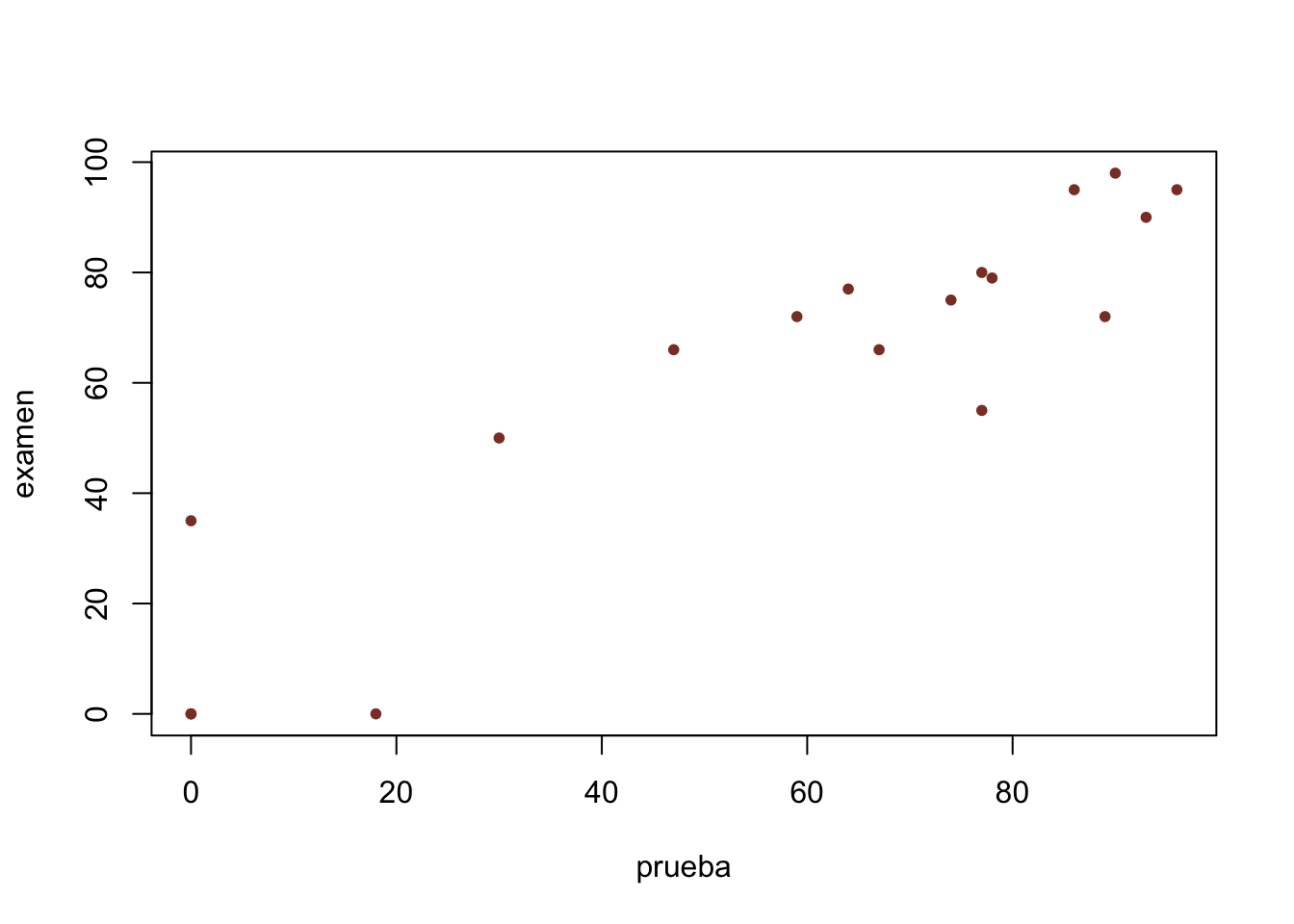
En el grafíco notamos más claro la relación lineal entre las dos variables, ahora podemos hacer la estimación de los parámetros \(\beta_0\) y \(\beta_1\), para esto usamos la función lm() indicando un objeto de tipo fórmula como parámetro.
modelo <- lm(examen~prueba)
summary(modelo)##
## Call:
## lm(formula = examen ~ prueba)
##
## Residuals:
## Min 1Q Median 3Q Max
## -26.4345 -8.8437 0.3528 9.6466 24.2731
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) 10.72691 6.61733 1.621 0.125
## prueba 0.87265 0.09914 8.802 1.57e-07 ***
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 13.85 on 16 degrees of freedom
## Multiple R-squared: 0.8288, Adjusted R-squared: 0.8181
## F-statistic: 77.48 on 1 and 16 DF, p-value: 1.571e-07Vamos a analizar este resultado, vamos a llamar modelo saturado al modelo que incluya todos los parámetros, en este caso \(\beta_0\) y \(\beta_1\), nuestro objetivo es encontrar el modelo que haga las mejores predicciones utilizando la menor cantidad de parámetros. Podemos hacer pruebas de hipótesis para los parámetros \(\beta_i\) de la forma:
\(H_0: \beta_i=0\)
\(H_1: \beta_i\neq0\)
cuando hacemos summary() podemos ver el valor p asociado a la estimación de cada parámetro
summary(modelo)##
## Call:
## lm(formula = examen ~ prueba)
##
## Residuals:
## Min 1Q Median 3Q Max
## -26.4345 -8.8437 0.3528 9.6466 24.2731
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) 10.72691 6.61733 1.621 0.125
## prueba 0.87265 0.09914 8.802 1.57e-07 ***
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 13.85 on 16 degrees of freedom
## Multiple R-squared: 0.8288, Adjusted R-squared: 0.8181
## F-statistic: 77.48 on 1 and 16 DF, p-value: 1.571e-07En este caso no podemos rechazar que \(\beta_0=0\), es decir, la recta de regresión pasa por el origen, volvemos a correr el modelo, esta vez sin considerar el coeficiente para el intercepto.
modelo_sin_intercepto <- lm(examen ~ 0 + prueba)
summary(modelo_sin_intercepto)##
## Call:
## lm(formula = examen ~ 0 + prueba)
##
## Residuals:
## Min 1Q Median 3Q Max
## -22.956 -2.102 0.056 11.137 35.000
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## prueba 1.01242 0.05121 19.77 3.62e-13 ***
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 14.5 on 17 degrees of freedom
## Multiple R-squared: 0.9583, Adjusted R-squared: 0.9559
## F-statistic: 390.8 on 1 and 17 DF, p-value: 3.617e-13Un criterio para elegir que modelo es mejor, es analizar el coeficiente de determinación \(R^2\) ajustado, que se define como el porcentaje de la variación en la variable de respuesta que es explicado por el modelo lineal. Entre más grande mejor.
plot(prueba,examen, pch=20,
col="coral4")
abline(a=0,b=modelo_sin_intercepto$coefficients[1],
col="deepskyblue2")
pre <- predict(modelo_sin_intercepto)
segments(prueba,examen, prueba,pre)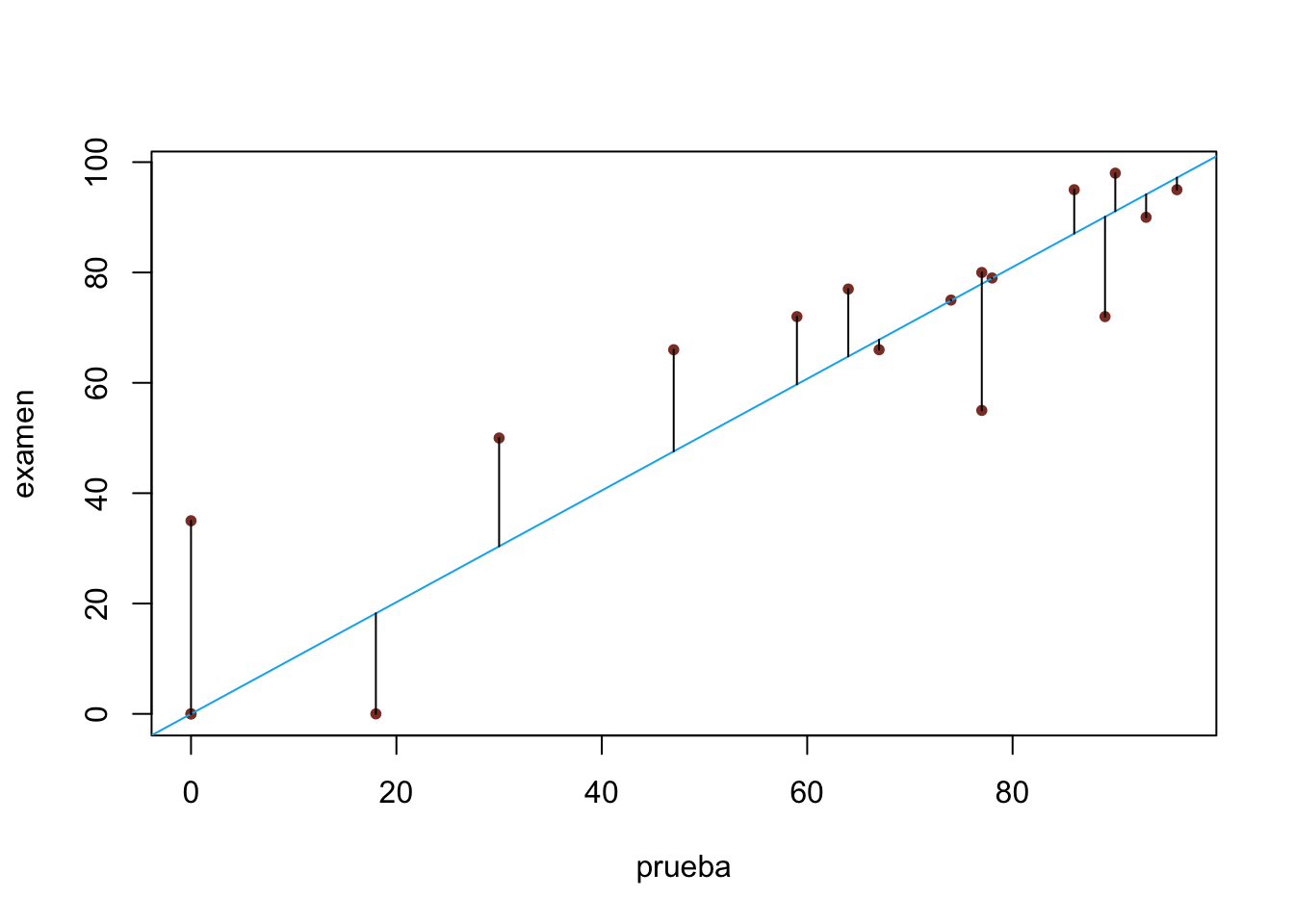
También podemos construir intervalos de confianza para los parámetros estimados
confint(modelo_sin_intercepto)## 2.5 % 97.5 %
## prueba 0.9043723 1.120466Que pasa si queremos hacer una predicción, ¿Qué calificación esperaría obtener un estudiante que tiene como nota de prueba 50 puntos?
prueba_pre <- data.frame(prueba=50)
predict.lm(modelo_sin_intercepto, prueba_pre, interval = "confidence")## fit lwr upr
## 1 50.62096 45.21862 56.023294.4.1 Diagnostico del modelo
Vamos ahora a verificar los supuestos del modelo de regresión simple, como ya vimos previamente podemos verficar los supuestos del modelo mediante los errores o mediante la variable respuesta.
4.4.1.1 Residuos
Vamos a llamar residuos a los valores \(\epsilon_i=y_i-\hat{y}_i\), para estos residuos o errore debemos verificar.
El supuesto de normalidad puede verificarse con los métodos que ya hemos estudiado antes
- qqplot
- Densidades o histogramas
- Test de shapiro-wilks o kolmogorov-smirnov
residuos <- modelo_sin_intercepto$residuals
qqnorm(residuos, col="firebrick4")
qqline(residuos)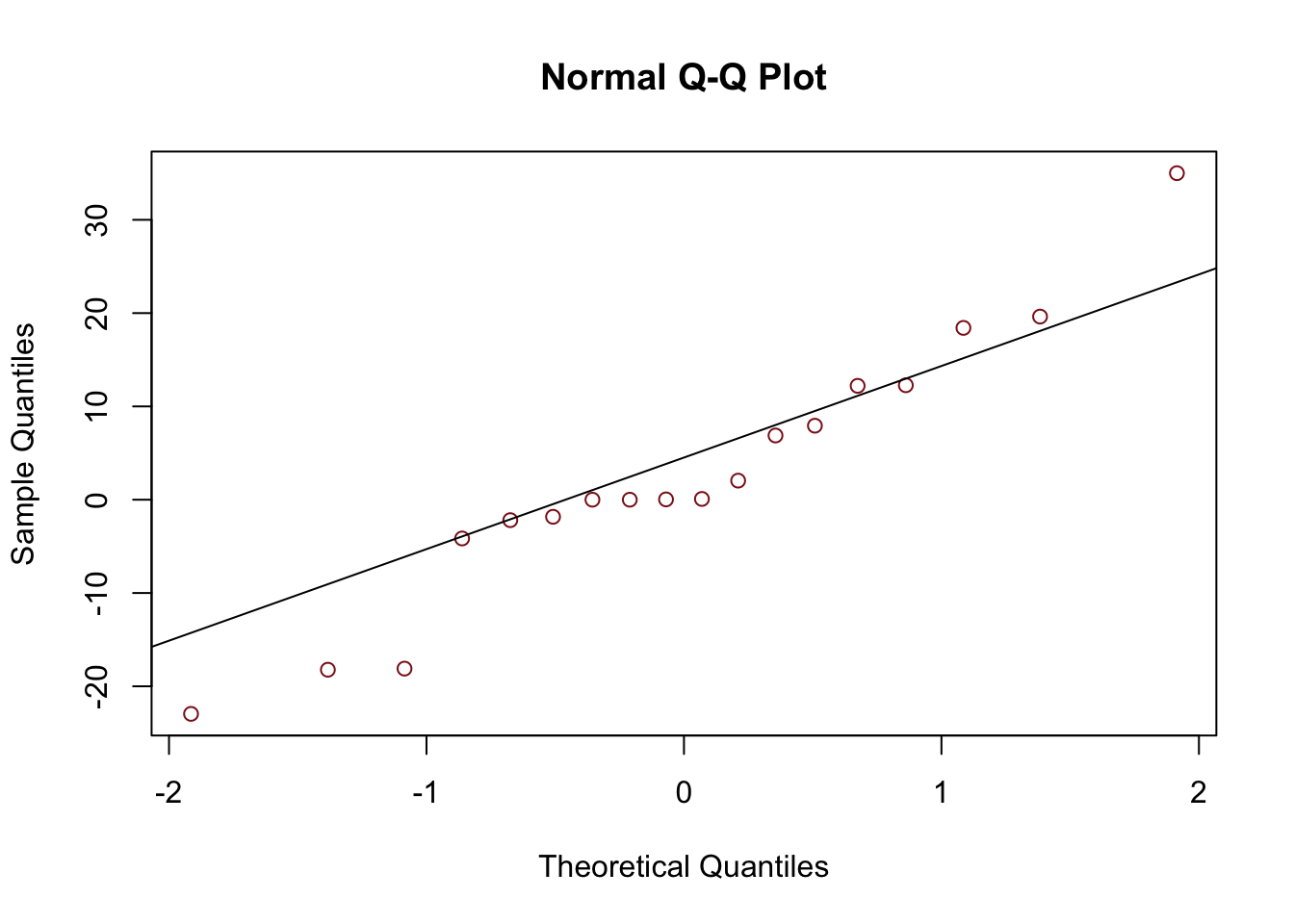
shapiro.test(residuos)##
## Shapiro-Wilk normality test
##
## data: residuos
## W = 0.95436, p-value = 0.4975Pra verificar los supuestos de homocedasticidad, podemos gráficar los valores ajustados contra los residuos, esperamos no encontrar patrones, en r, si hacemos un plot de el modelo podemos ver los gráficos que ayudan a verificar los supuestos.
par(mfrow=c(2,2))
plot(modelo_sin_intercepto)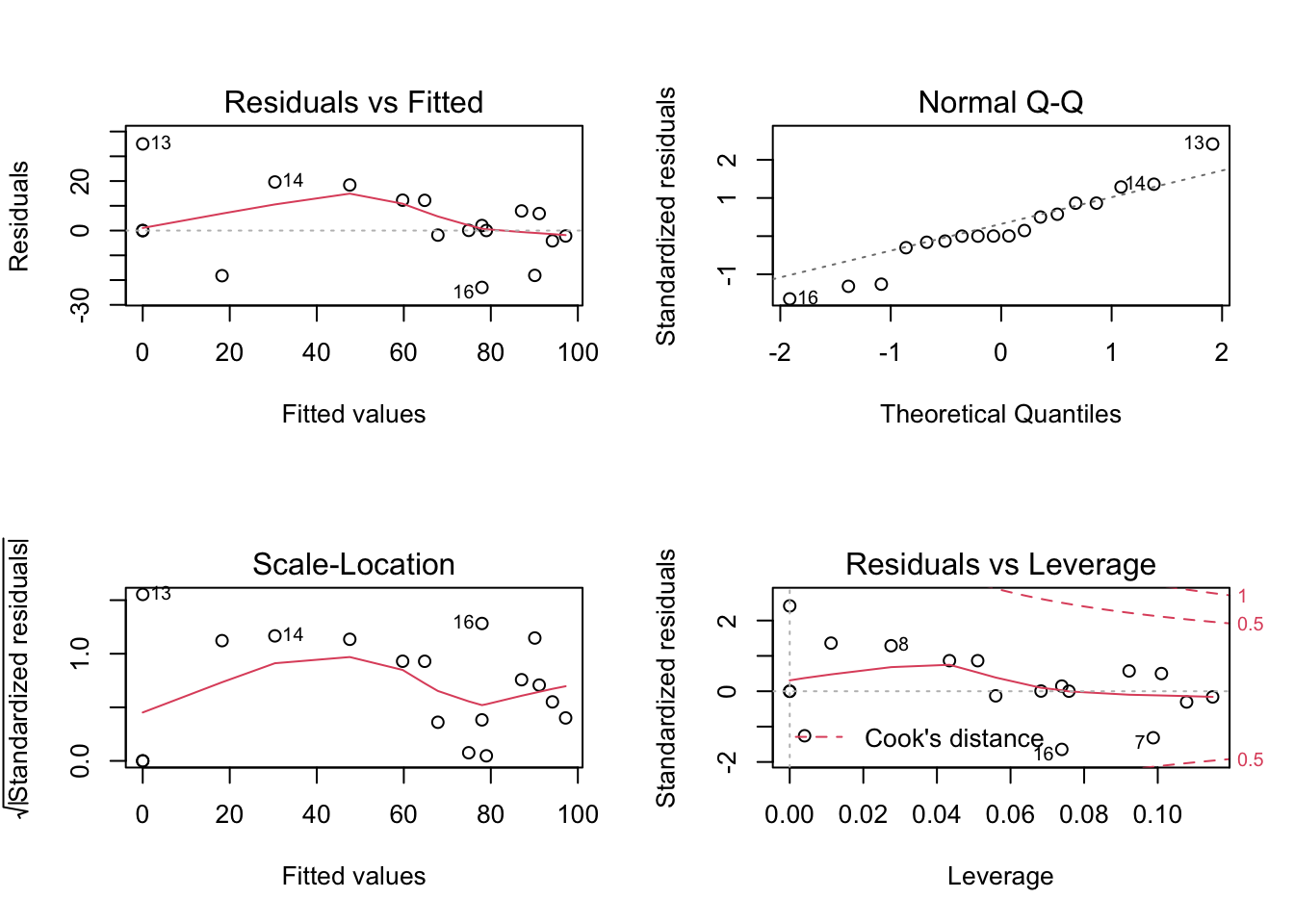
par(mfrow=c(1,1))4.5 Regresión Lineal Múltiple
El modelo de regresión lineal múltiple puede ser expresado de la forma:
\[ y=\beta_0 + \beta_1x_1+\cdots+\beta_kx_k +\epsilon \]
Para estimar los \(\beta's\), utilizaremos una muestra de n observaciones de y e x, y el modelo para la i-esima observación tiene la forma: \[ y_i=\beta_0 + \beta_1x_{i1}+\cdots+\beta_kx_{ik} +\epsilon_i \]
y los supuestos del modelo se siguen manteniendo similares al modelo de regresión lineal simple. Veamos un ejemplo
autompg este conjunto de datos contiene una variable de respuesta mpg que almacena la eficiencia de combustible de la ciudad de los automóviles, así como varias variables predictoras para los atributos de los vehículos.
Podemos hacer un diagrama de dispersión para visualizar la correlación entre todas las variables y también construir una matiz de corelación
autompg <- read.csv("autompg.csv")
plot(autompg)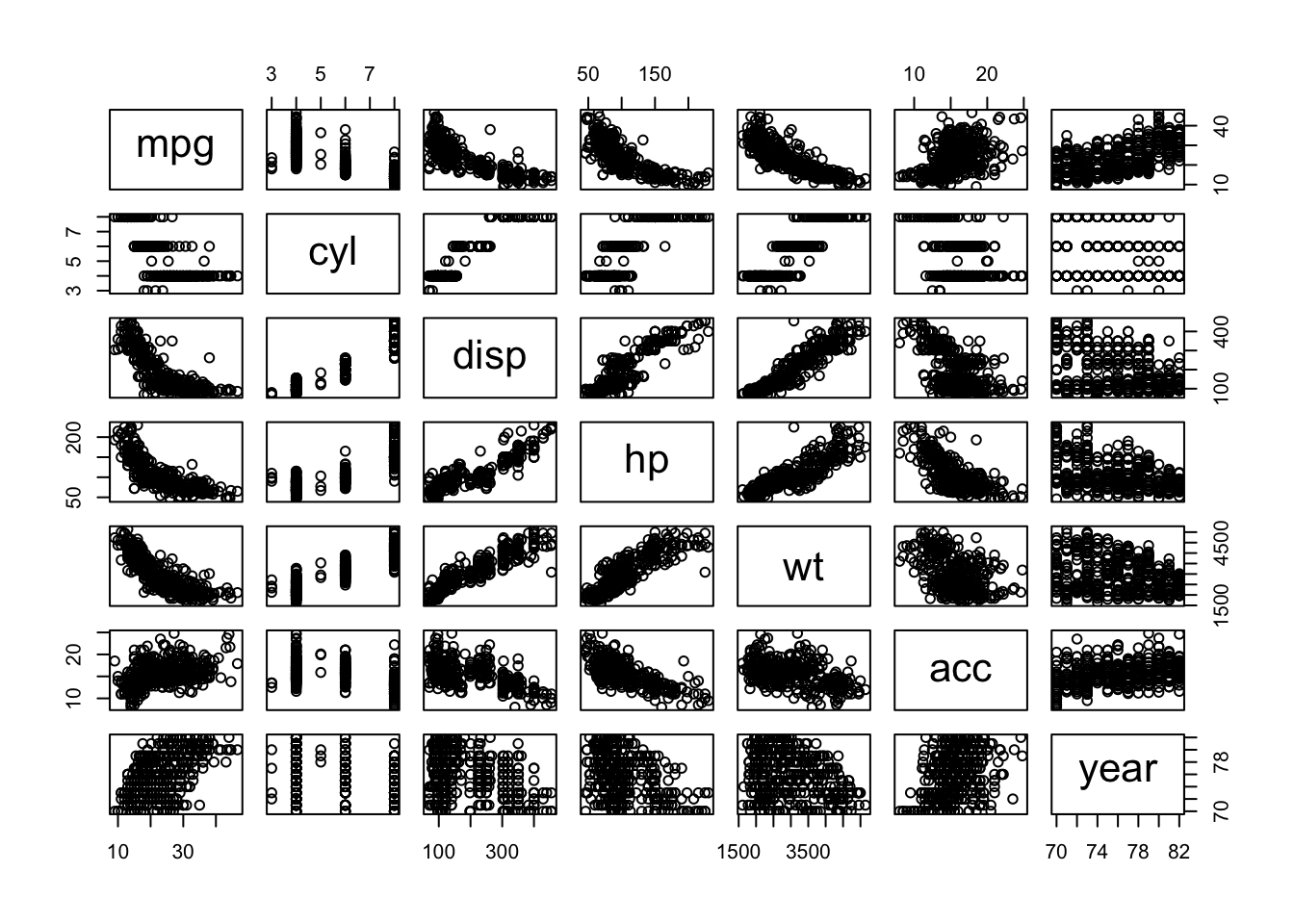
m_correlacion <- cor(autompg)
m_correlacion## mpg cyl disp hp wt acc
## mpg 1.0000000 -0.7771106 -0.8048348 -0.7781234 -0.8319025 0.4263374
## cyl -0.7771106 1.0000000 0.9509132 0.8428507 0.8973659 -0.5082518
## disp -0.8048348 0.9509132 1.0000000 0.8971003 0.9328901 -0.5462105
## hp -0.7781234 0.8428507 0.8971003 1.0000000 0.8643344 -0.6917443
## wt -0.8319025 0.8973659 0.9328901 0.8643344 1.0000000 -0.4194050
## acc 0.4263374 -0.5082518 -0.5462105 -0.6917443 -0.4194050 1.0000000
## year 0.5793812 -0.3418894 -0.3679416 -0.4149214 -0.3064515 0.2952284
## year
## mpg 0.5793812
## cyl -0.3418894
## disp -0.3679416
## hp -0.4149214
## wt -0.3064515
## acc 0.2952284
## year 1.0000000corrplot(m_correlacion, type = "upper")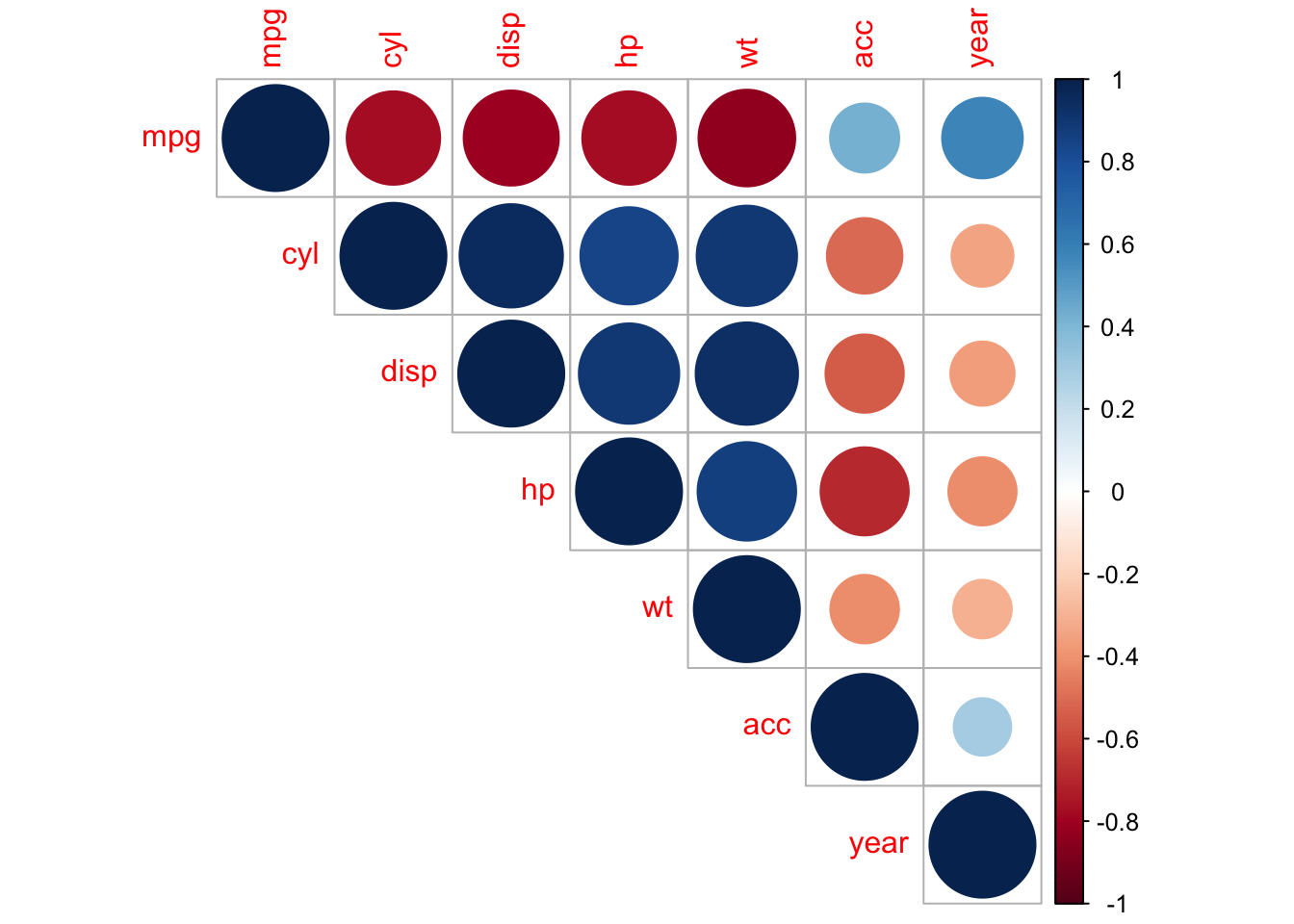
Por ahora nos centraremos en utilizar dos variables, peso wt y año year, como variables predictoras. Es decir, nos gustaría modelar la eficiencia de combustible mpg de un automóvil en función de su peso wt y año del modelo year.
Definamos el modelo
\[ y_i=\beta_0 + \beta_1x_{i1} + \beta_2x_{i2} + \epsilon_i \]
\(x_{i1}\) es el peso del i-esimo automovil
\(x_{i2}\) es el año del modelo del i-esimo automovil
En este caso aun podriamos visualizar la correlación de las variables, ya que estamos en \(\mathbb{R}^3\). Para hacer una mejor visualización de lo que está pasando vamos a usar el paquete plotly
plot_ly(autompg,
x=~wt,
y=~year,
z=~mpg,
type="scatter3d",
mode="markers")Queremos encontrar el plano de regresión que mejor se ajuste a esta nube de puntos
modelo <- lm(mpg ~ wt + year, data = autompg)Visualicemos el plano de regresión
x <- seq(from=5000, to=2000, length=20)
y <- seq(from=70, to=82,length=20)
plano <- outer(x, y, function(a, b){modelo$coef[1] +
modelo$coef[2]*a + modelo$coef[3]*b})
plot_ly(autompg,
x=~wt,
y=~year,
z=~mpg,
type="scatter3d",
mode="markers") %>%
add_surface(x=~x,
y=~y,
z=~plano,
showscale=F,
showlegend=F)4.6 Regresión Logistica
En algunas situaciones de regresión, la variable de respuesta y tiene solo dos resultados posibles, por ejemplo, presión arterial alta o presión arterial baja, desarrollar cáncer de esófago o no desarrollarlo, si un crimen se resolverá o no, y si un espécimen de abeja es una abeja “asesina” (africanizada) o una abeja doméstica. En tales casos, el resultado y puede codificarse como 0 o 1 y deseamos predecir el resultado (o la probabilidad del resultado) sobre la base de una o más x. El modelo tendría la forma:
\(y_i=\beta_0 + \beta_1x_i +\epsilon_i\) , \(y_i=0,1\); \(i=1,\cdots,n\)
Como \(y_i\) son solo 1 o 0, la esperanza \(E(y_i)\) para cada \(x_i\) es la proporción de observaciones de \(x_i\) para el cual \(y_i=1\)
\[\begin{eqnarray} E(y_i) &=&P(y_i=1)=p_i\\\\ 1-E(y_i) &=&P(y_i=0)=1-p_i \end{eqnarray}\]
Luego el modelo se puede escribir como \[ E(y_i)=p_i=\beta_0+\beta_1x_i \] Un modelo para \(E(y_i)\) que esté acotado entre 0 y 1 y llegue a 0 y 1 asintóticamente (en lugar de linealmente) sería más adecuado. Una opción popular es el modelo de regresión logística.
\[ p_i=E(y_i)=\frac{e^{\beta_0 + \beta_1x_i}}{1+ e^{\beta_0 + \beta_1x_i}}=\frac{1}{1+e^{-\beta_0-\beta_1x_i}} \]
Este modelo puede ser linealizado por la transformación logit \[ \ln\left( \frac{p_i}{1-p_i}\right)=\beta_0 + \beta_1x_i \]
WAIS, un valor de senilidad=1 representa la presencia de senilidad y 0 la ausencia.
WAIS <- read_excel("WAIS.xls")Si hacemos un plot de las puntuaciones contra la senilidad vamos a notar algo como lo siguiente
plot(WAIS)
modelo_log <- glm(senilidad ~ wais, data = WAIS, family = "binomial")
summary(modelo_log)##
## Call:
## glm(formula = senilidad ~ wais, family = "binomial", data = WAIS)
##
## Deviance Residuals:
## Min 1Q Median 3Q Max
## -1.6702 -0.7402 -0.4749 0.5200 2.1157
##
## Coefficients:
## Estimate Std. Error z value Pr(>|z|)
## (Intercept) 2.4040 1.1918 2.017 0.04369 *
## wais -0.3235 0.1140 -2.838 0.00453 **
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## (Dispersion parameter for binomial family taken to be 1)
##
## Null deviance: 61.806 on 53 degrees of freedom
## Residual deviance: 51.017 on 52 degrees of freedom
## AIC: 55.017
##
## Number of Fisher Scoring iterations: 5Significa que, con este resultado, podemos modelar la probabilidad de padecer senilidad en función de las puntuaciones de WAIS, como
\[ p_i=\frac{1}{1+e^{-2.40+0.32x_i}} \]
Visualicemos la regresión logistica
beta_0_est <- modelo_log$coefficients[1]
beta_1_est <- modelo_log$coefficients[2]
plot(WAIS, col="coral3",pch=20)
curve(1/(1+ exp(-beta_0_est - beta_1_est *x)),
add = TRUE, col="deepskyblue3")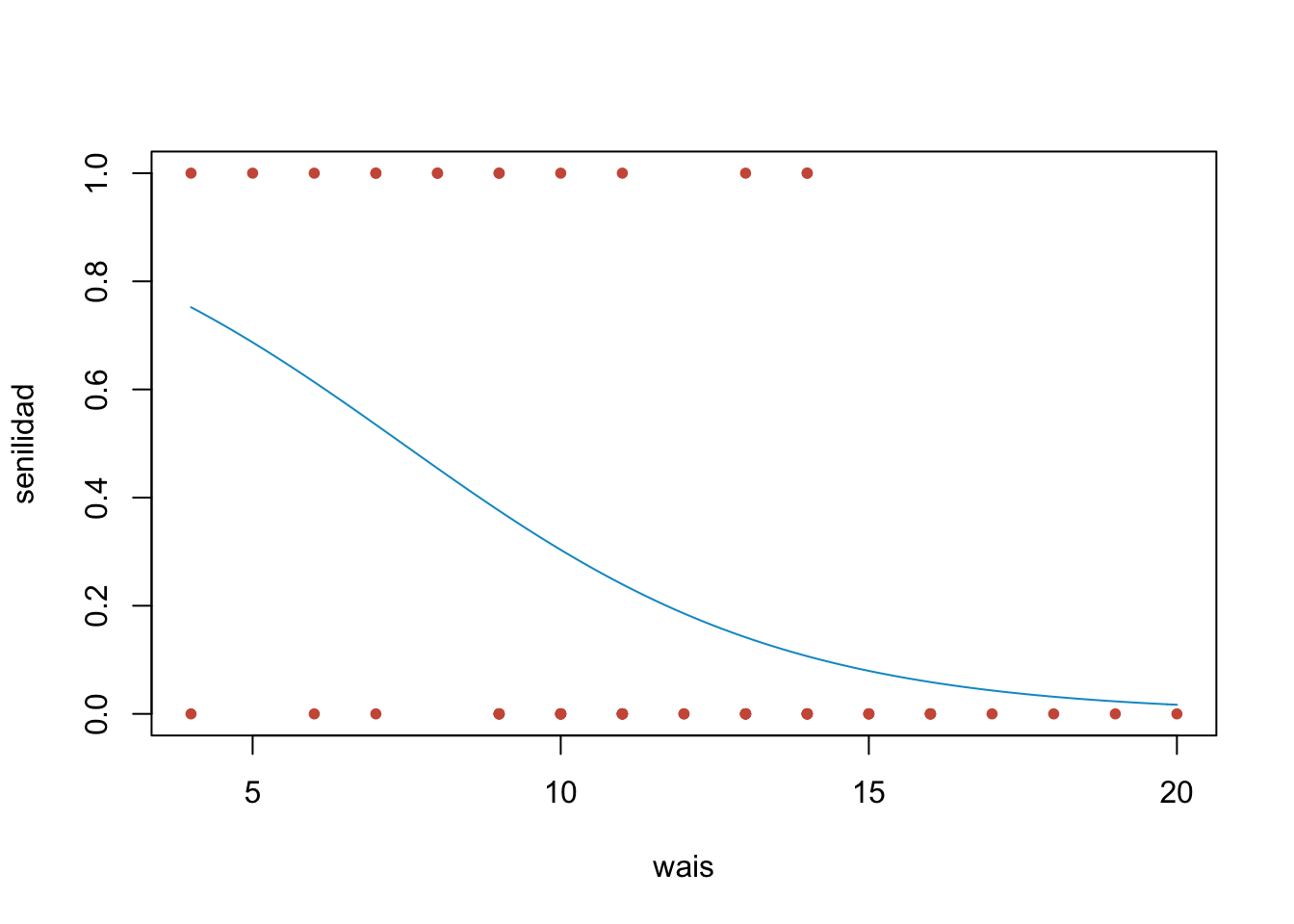
Y podemos hacer predicciones
nuevos_datos <- data.frame(wais=c(4:20))
senilidad_pred <- predict.glm(modelo_log, newdata =nuevos_datos,
type="response")
nuevos_datos<- data.frame(nuevos_datos,senilidad_pred)
nuevos_datos## wais senilidad_pred
## 1 4 0.75211453
## 2 5 0.68705597
## 3 6 0.61369267
## 4 7 0.53477641
## 5 8 0.45407982
## 6 9 0.37572578
## 7 10 0.30337860
## 8 11 0.23961509
## 9 12 0.18568111
## 10 13 0.14162581
## 11 14 0.10665418
## 12 15 0.07951811
## 13 16 0.05883161
## 14 17 0.04327366
## 15 18 0.03169146
## 16 19 0.02313427
## 17 20 0.016847464.7 Ejercicios
- Se estudian los hábitos de alimentación de dos especies de arañas. Estas especies, Dinopis y Menneus, coexisten en Australia oriental. Una variable de interés es el tamaño de las presas de cada especie. La araña Menneus adulta tiene aproximadamente el mismo tamaño que la araña Dinopis joven. Se sabe que existe una diferencia entre el tamaño de las presas en Dinopis adulta y joven a causa de la diferencia entre sus tamaños. ¿Hay una diferencia en el tamaño medio de las presas entre Dinopis adulta y Menneus adulta? Si es así, ¿cuál es la causa? Para responder a estas preguntas, se obtuvieron las siguientes observaciones sobre el tamaño, en milímetros, de las presas de las dos especies:
| Dinopis adulta | 12.9 | 11.9 | 10.2 | 7.1 | 7.4 | 9.9 | 7.0 | 14.4 | 10.5 | 11.3 |
| Menneus adulta | 10.2 | 5.3 | 6.9 | 7.5 | 10.9 | 10.3 | 11.0 | 9.2 | 10.1 | 8.8 |
Explore la función
var.test()para contrastar la hipótesis de igualdad de varianzasVerifique la hipótesis de normalidad para ambas poblaciones de especies de arañas.
Haga una prueba de hipótesis para comprobar si realmente existe una diferencia entre el tamaño de las presas de las dos especies adultas.
- Supongamos que un ensayo clínico patrocinado por la industria “demostró” que Finasteride inhibe la caída del cabello de patrón masculino. El enfoque utilizado incluyó dos grupos de tratamiento: uno recibió un tratamiento con finasteride y el otro, un placebo. Se realizó un estudio aleatorizado. Para el estudio, se toman fotografías de cada cabeza. Se evalúan utilizando una metodología estándar. Esto da como resultado una puntuación entre 1 y 7: 1 que indica una gran disminución del crecimiento del cabello y 7 un gran aumento. Los datos se muestran en la siguiente tabla
| Grupo | |
| Finasteride | 5 | 3 | 5 | 7 | 4 | 4 | 7 | 4 | 3 |
| Placebo | 2 | 3 | 2 | 4 | 2 | 2 | 3 | 4 | 2 |
Compruebe si realmente el medícamento es efectivo para evitar la caida del cabello.
- Suponga que deseamos probar la hipótesis
\[\begin{eqnarray} H_0: \mu& \leq &68\text{ Kilogramos}\\\\ H_1: \mu & > & 68\text{ Kilogramos} \end{eqnarray}\] Para los pesos de estudiantes de cierta universidad, usando un nivel de significancia \(\alpha = 0.05\). Cuando se sabe que la población sigue una distribución normal con \(\sigma=5\). Calcule el tamaño muestral que se requiere si la potencia de nuestra prueba debe ser 0.95 cuando la media real es de 69 Kilogramos.
(Entrega) Considere los datos
SleepStudydel paqueteLock5Data, la variableAverageSleepcontiene las horas de sueño de cada estudiante y la variableGendercontiene el género, queremos saber si existen diferencias en el promedio de horas de sueño diarias entre hombres y mujeres.Elabore un test de varianzas para comprobar la hipótesis de igualdad de varianzas.
Compruebe las hipótesis de normalidad para ambas poblaciones.
Elabore el test de hipótesis para verificar si existen diferencias entre el promedo de horas de sueño.
Construya un boxplot de las horas de sueño para cada género, ¿ Concuerda la información de los boxplot con la decisión que tomó en el inciso anterior?
(Entrega) Considere los datos
QuizPulse10del paqueteLock5Data, contiene una muestra de 10 estudiantes a los cuales se les midio el número de pulsaciones del corazón por minuto durante un examenQuizy durante una clase normalLecture. Estamos interesado en probar si existe un cambio en el número de pulsaciones durante el examen y durante la clase normal.
Realice un test adecuado para comprobar la hipótesis del problema
¿Cuál es la potencia alcanzada en el test anterior en que aceptamos que la diferencia observada de 2.7 pulsaciones por minuto no era significativa? (la desviación estándar debe calcularse de las diferencias)
¿De qué tamaño debería ser la muestra si queremos alcanzar una potencia del 85% para detectar una diferencia de 8 pulsaciones por minuto a favor de una de las dos condiciones experimentales?
- El conjunto de datos
prostatedel paquetefarawayproviene de un estudio en 97 hombres con cáncer de próstata que debían someterse a una prostatectomía radical. Queremos ajustar un modelo conlpsacomo respuesta ylcavolcomo predictor.
Encuentre el coeficiente de correlación entre las dos variables y analice si estas dos variables son una buena elección para el modelo de regresión lineal.
Grafique el diagrama de dispersión entre las dos variables.
Ajuste el modelo pedido, realice un breve diagnostico del modelo.
Superponga la recta de regresión sobre la nube de puntos.
Suponga que un nuevo paciente presenta un valor de
lcavolde 1.44692, realice una predicción paralpsajunto con un IC del 95%.
- El archivo
admision.csvse trata de información sobre la admisión a programas de posgrado universitario en una universidad de Estados Unidos tenemos cuatro variables.
admit: 0 = no admitido, 1 admitidogre: nota en el examen GRE. Puede tomar valores de 200 a 800gpa: promedio crédito acumulado de pregrado. Puede tomar valores de 0 a 4.rank: Ranking de la universidad de pregrado, hay 4 categorias de mayor calidad (1) a menor calidad (4).
Estamos interesados en la probabilidad de que un individuo sea admitido en la universidad.
Consideremos un modelo de regresión logistica simple con la variable
gpacon variable predictora y admit como variable respuesta, grafique ambas variables, luego ajuste el modelo con los datos.Considere ahora un modelo de regresión logistica múltple, incluyendo las variables
gpaygrecomo predictoras paraadmit.
- (Entrega) Se analizaron treinta muestras de queso cheddar para determinar su contenido de ácido acético
Acetic, sulfuro de hidrógenoH2Sy ácido lácticoLactic. Cada muestra fue catada y calificada por un panel de jueces y se obtuvo el puntaje promedio de sabortaste. Utilice los datos decheddardel paquetefarawaypara responder lo siguiente:
Ajuste un modelo de regresión con
tastecomo respuesta y los tres contenidos químicos como predictores. Informe los valores de los coeficientes de regresión. ¿Són estos significativos?Ajuste de nuevo el modelo retirando el coeficiente del intercepto.
Compare el \(R^2\) de los dos modelos para indicar cual es el mejor modelo.
Cuál deberia ser la puntuación del sabor para un queso con contenido de ácido acetico de 5, sulfuro de hidrógeno de 4.5 y ácido láctico de 2.