3 Semana III

3.1 Variables aleatorias

Algunos fenomenos pueden ser representados mediante algún modelo o ley aleatoria, en esta sección vamos a estudiar las variables aleatorias y sus funciones de probabilidad. Antes repasemos algúnos conceptos básicos.

Definition 3.1 Vamos a llamar variable aleatoria a una función X tal que \[ X: \Omega \rightarrow \mathbb{R} \] Es decir, X toma un valor en el espacio muestral y le asigna un número real

Dependiendo del número que asigne la función X, las variables aleatorias pueden clasificarse en:

• Discretas: Toman valores en un conjunto finito o infinito númerable.

• Continuas: Toman valores en un intervalo de los número reales

Definition 3.2 Vamos a llamar función de distribución a la función \[ F_X(x)=P[X\leq x] \]

La distribución de probabilidad de una v.a. describe teóricamente la forma en que varían los resultados de un experimento aleatorio. Intuitivamente se trataría de una lista de los resultados posibles de un experimento con las probabilidades que se esperarían ver asociadas con cada resultado.

Definition 3.3 Sea X una variable aleatoria discreta, llamamos función de probabilidad o función de masa de probabilidad a la función

\[ P_X(x)= P[X=x] \]

Definition 3.4 Sea X una variable aleatoria continua, llamamos función de densidad a la función

\[ f_X(x)= \frac{d F(x)}{dx} \]

La fdp se utiliza con el propósito de conocer cómo se distribuyen las probabilidades de un suceso o evento, en relación al resultado del suceso.

la función de distribución es la integral de la función de densidad \[ F_X(x)=\int_{-\infty}^x f_X(x)dx \]

En r nosotros podemos calcular probabilidades, encontrar cuantiles, generar muestras aleatorias para las distribuciones continuas y discretas más conocidas, la sintaxis para indentificar estas funciones se diferencia anteponiendo una letra al nombre de la distribución, algunas distribuciones que podemos encontrar son:

• exp: Distribución exponencial
• norm: Distribución normal
• t: Distribución t student
• chisq: Distribución Chi- cuadrado
• `gamma : Distribución gamma
• unif: Distribución uniorme
• binom: Distribución binomial

A lo largo del curso iremos conociendo algunas otras, a estos nombres podemos colocarle antes las letras q, p, r o d dependiendo de lo que queremos, por ejemplo si tomamos la distribución normal

• qnorm(p): Encuentra el cuantil p de la distribución normal, es decir el valor \(x_0\) tal que \(P[X \leq x_0]=p\)

• pnorm(q): Nos da la función de distribución, es decir \(P[X \leq q]\)

• dnorm(x): Nos da el valor de la función de densidad o función de probabilidad evaluada en x, es decir \(f_X(x)\)

• rnorm(n): Nos genera una muestra de tamaño n de una distribución normal.

Exploremos un poco la distribución normal, vamos usar curve para gráficar su fución de densidad

curve(dnorm(x,mean = 0, sd = 1), from = -6 , to = 6,
      col = "firebrick", ylim=c(0,0.6),
      ylab = "Densidad")

curve(dnorm(x,mean = 0, sd = 2), from = -6 , to = 6 ,
      add = T, col="deepskyblue4")

curve(dnorm(x,mean = 0, sd = 0.7), from = -6 , to = 6 ,
      add = T, col="darkolivegreen4")

curve(dnorm(x,mean = 2, sd = 1), from = -6 , to = 6 ,
      add = T, col="darkorange2")


curve(dnorm(x,mean = -2, sd = 1), from = -6 , to = 6 ,
      add = T, col="darkorchid4")

legend("topright",
       legend = c("N(0,1)","N(0,4)","N(0,49)","N(2,1)","N(-2,1)"),
       col=c("firebrick","deepskyblue4","darkolivegreen4","darkorange2","darkorchid4"), 
       lwd=1)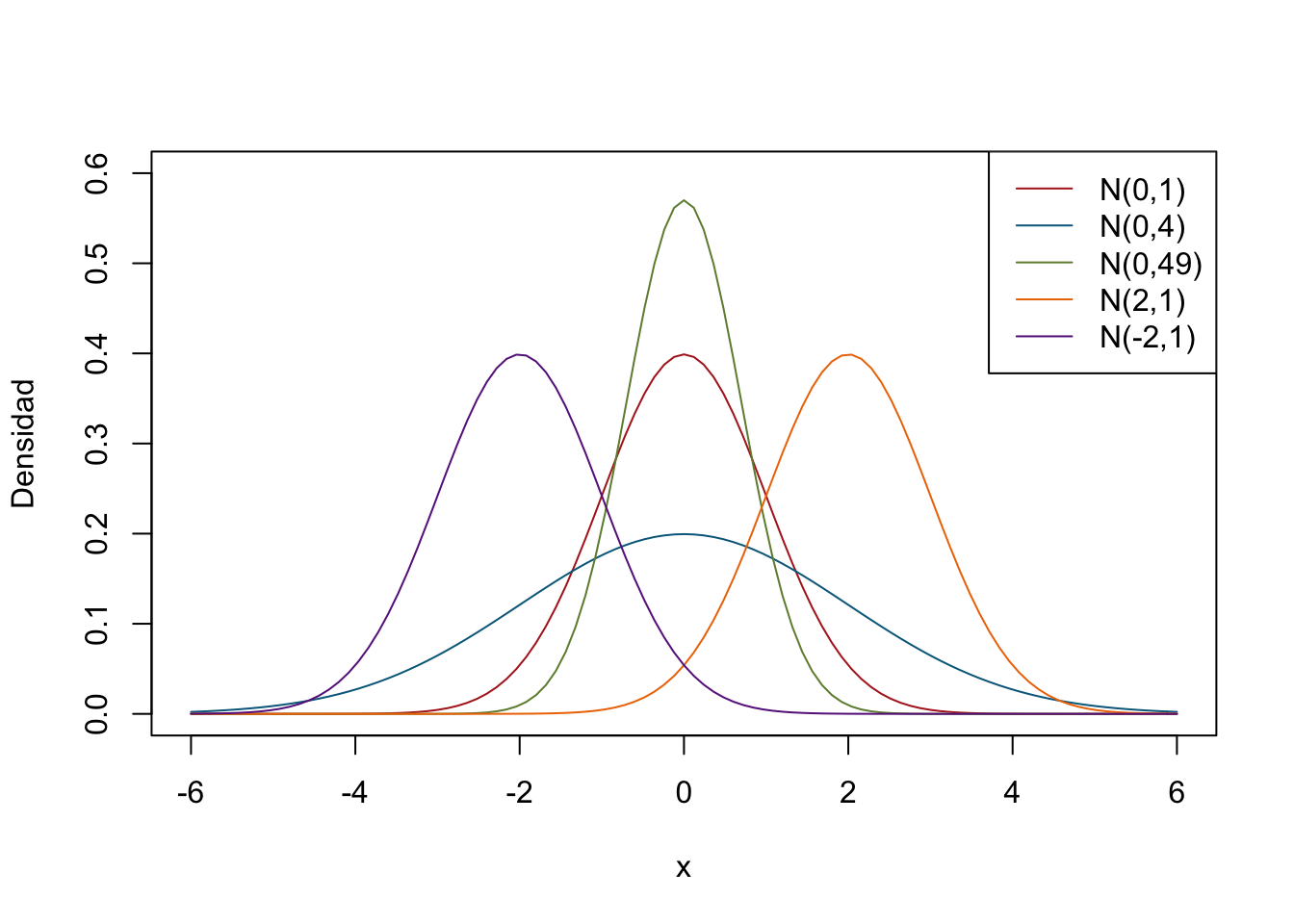

Example 3.1 Los promedios de calificaciones (GPA, por sus siglas en inglés) de una gran población de estudiantes universitarios están normalmente distribuidos en forma aproximada, con media de 2.4 y desviación estándar 0.8.

# Sea X: Los promedios de calificaciones de los estudiantes
curve( dnorm(x, mean= 2.4, sd=0.8),from = -2, to = 6,
       col="firebrick", xlab = "GPA",ylab = "Densidad")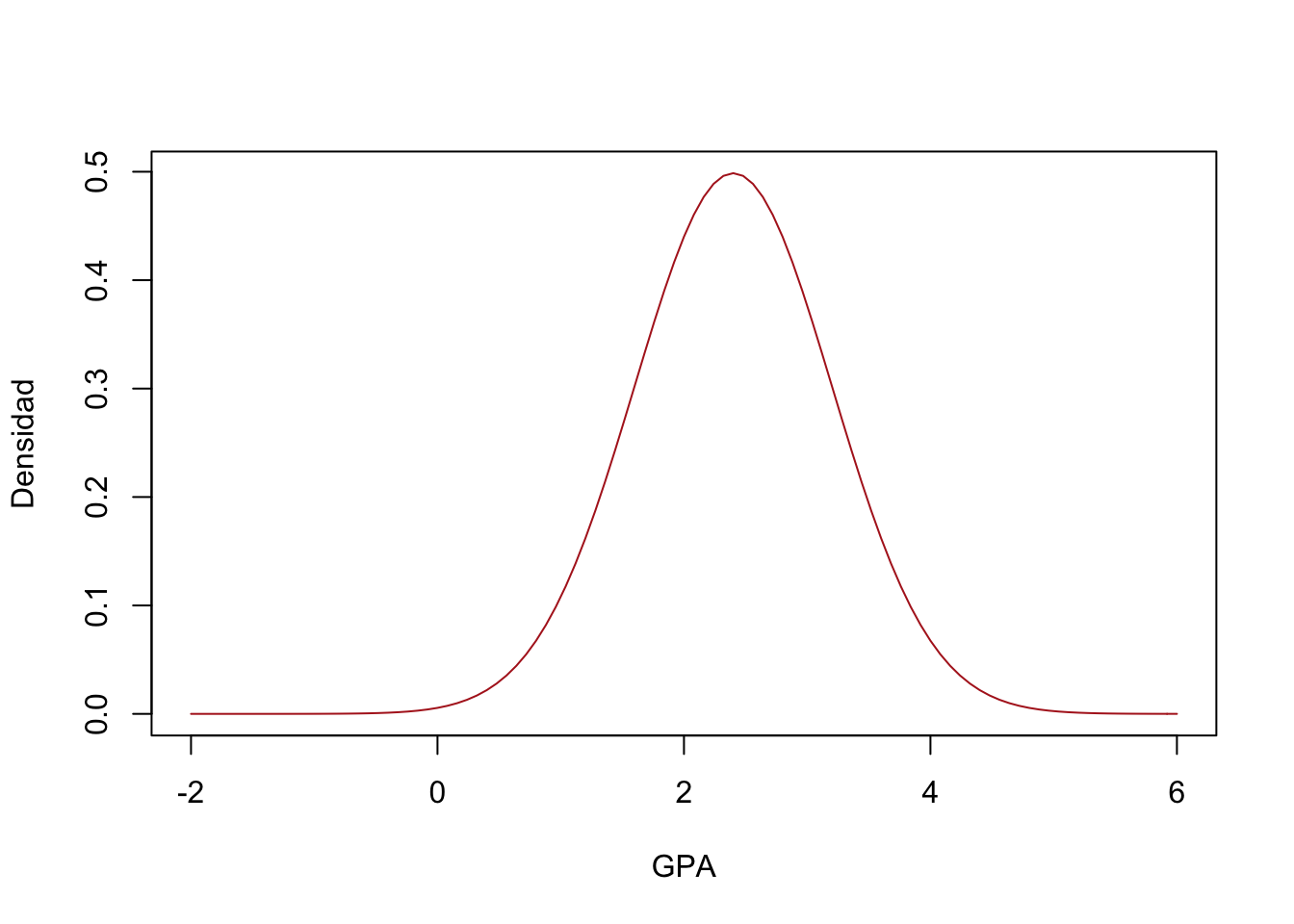

1. Si los estudiantes que alcancen un GPA menor que 1.9 serán suspendidos de la universidad, ¿qué porcentaje de los estudiantes será suspendido?

# a) P(X < 1.9)
pnorm(1.9, mean=2.4, sd = 0.8)

## [1] 0.2659855

curve( dnorm(x, mean= 2.4, sd=0.8),from = -2, to = 6,
       col="firebrick", xlab = "GPA",ylab = "Densidad")

Shade(dnorm(x, mean = 2.4, sd=0.8), breaks = c(-2,1.9),
      density = 500, col="firebrick")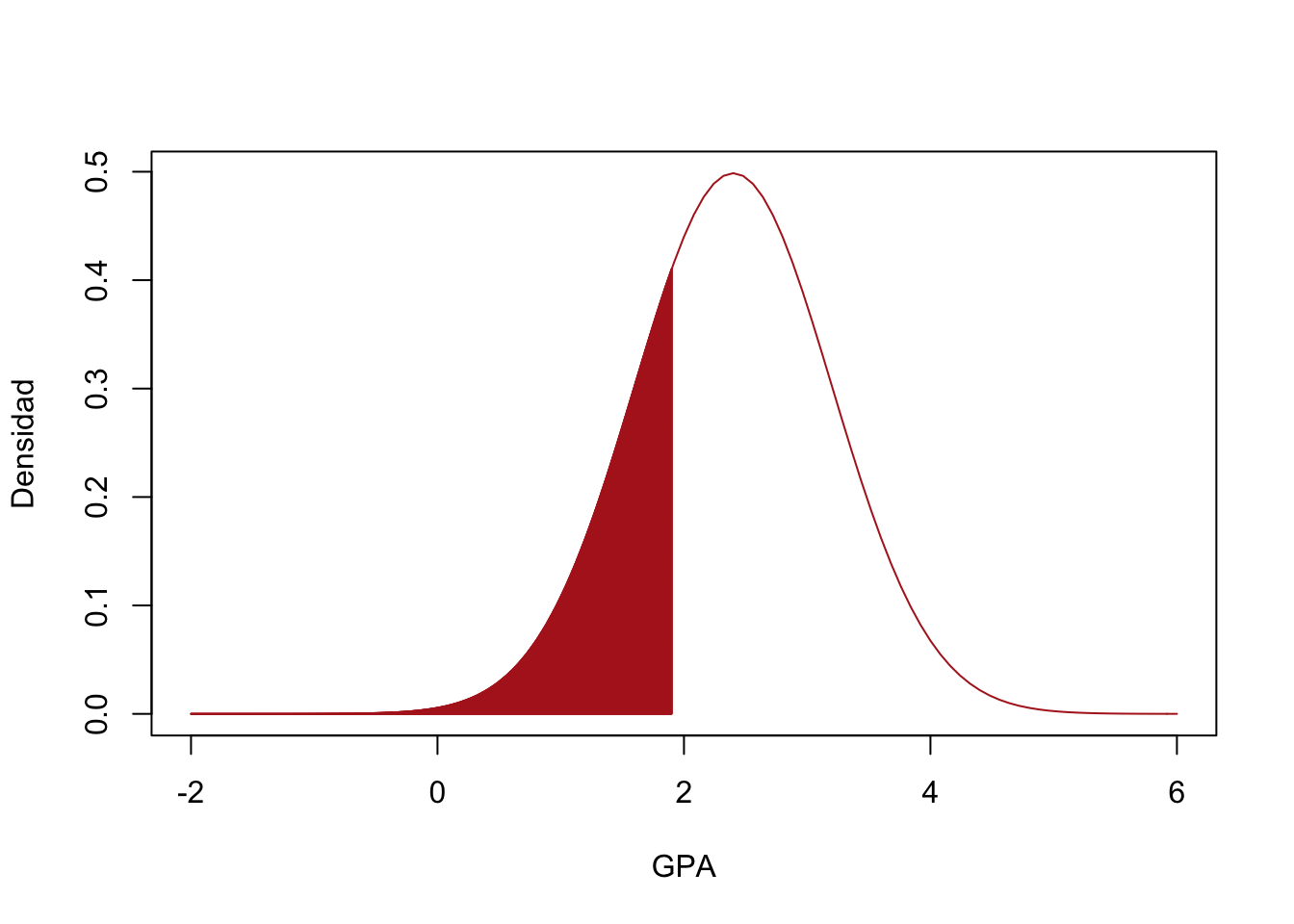

2. Se pretende otorgarles un incentivo a los estudiantes que obtengan el 25% más alto de los porcentajes, a partir de que valor se empezaran a otorgar los incentivos?

# b) P(X > x ) = 0.25
# P (X <= x) = 0.75

x <- qnorm(0.75, mean=2.4, sd=0.8)

curve( dnorm(x, mean= 2.4, sd=0.8),from = -2, to = 6,
       col="firebrick", xlab = "GPA",ylab = "Densidad")
Shade(dnorm(x, mean = 2.4, sd=0.8), breaks = c(x,6),
      density = 500, col="firebrick")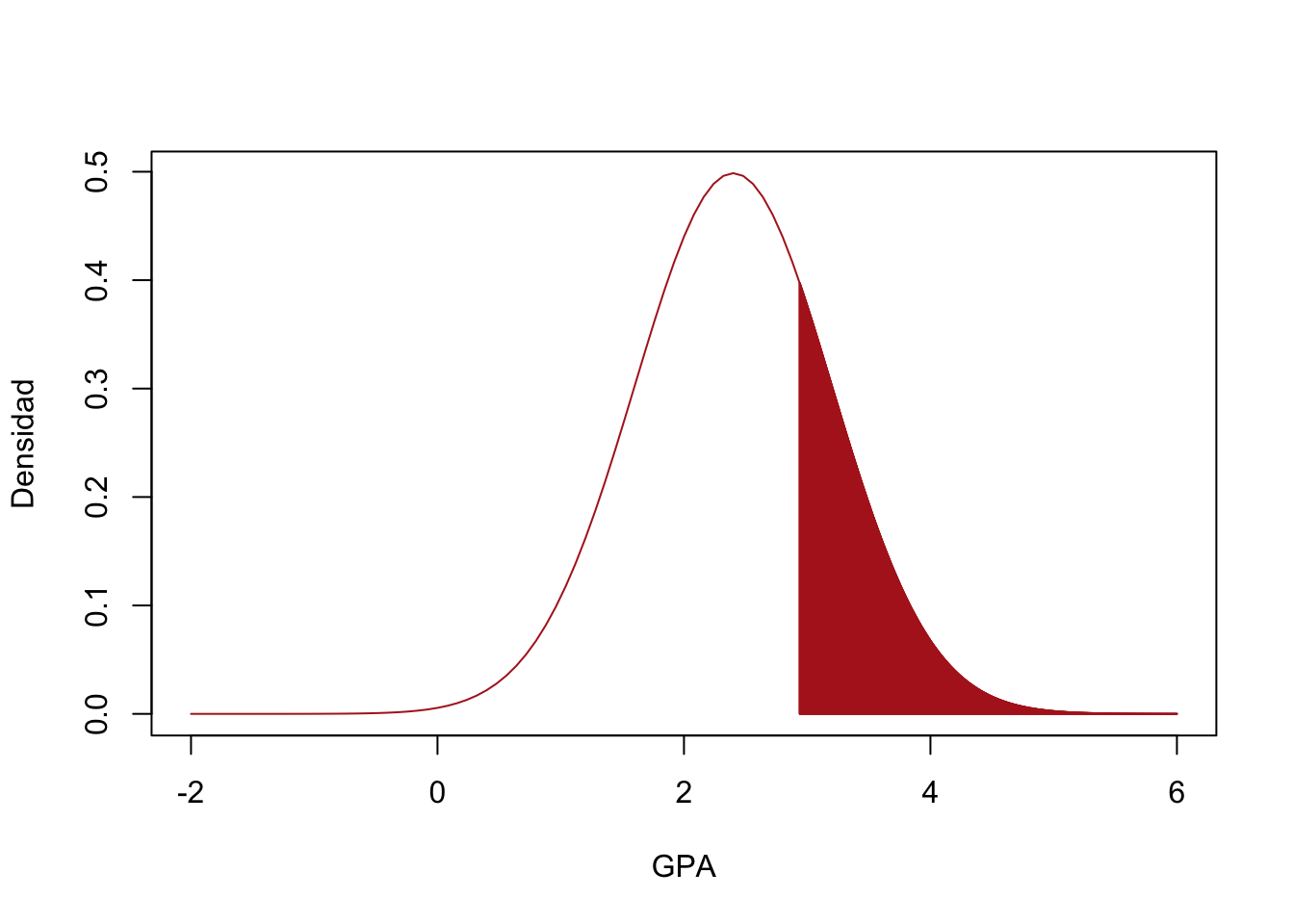

3. Simule una muestra aleatoria de la distribución definida en el problema, encuentre la cantidad de estudiantes que recibiran el incentivo en esta muestra, ¿Qué porcentaje de la muestra obtendran ese incentivo?

#c) 

muestra <- rnorm(1000, mean = 2.4, sd=0.8)

plot(density(muestra), col="darkolivegreen4",
     ylim=c(0,0.5),xlab="GPA")

curve( dnorm(x, mean= 2.4, sd = 0.8),from = -2, to = 6,
       add = T, col="coral1")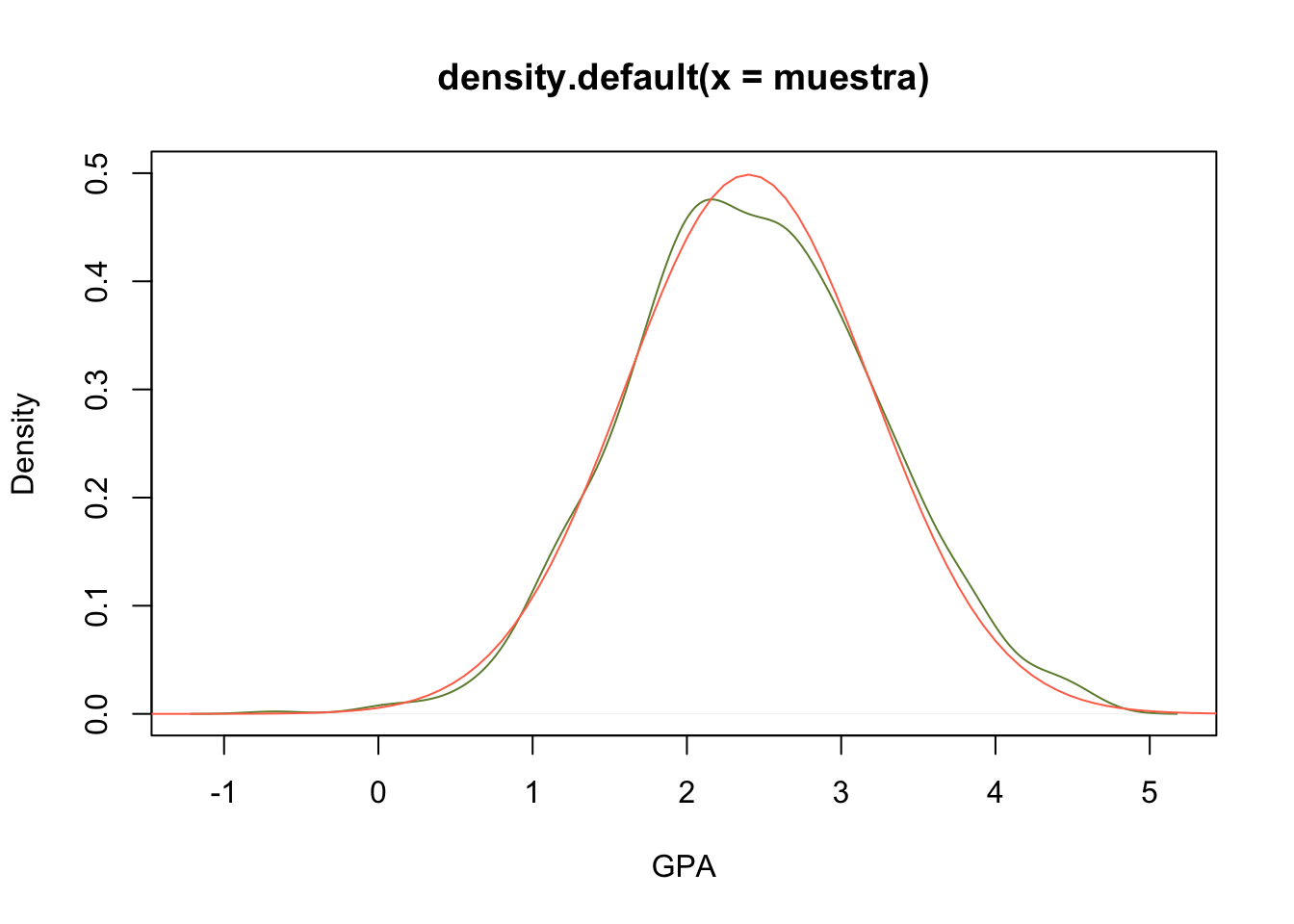

mean(muestra > x)

## [1] 0.264

Example 3.2 Algunos fenómenos pueden modelarse mediante distribuciones conocidas, considere los datos de las longitudes de los rios rivers, exploremos la función fitdist del paquete MASS para modelar estos datos usando

rios <- rivers

plot(density(rios), col="darkorchid4",xlab="Longitud en millas")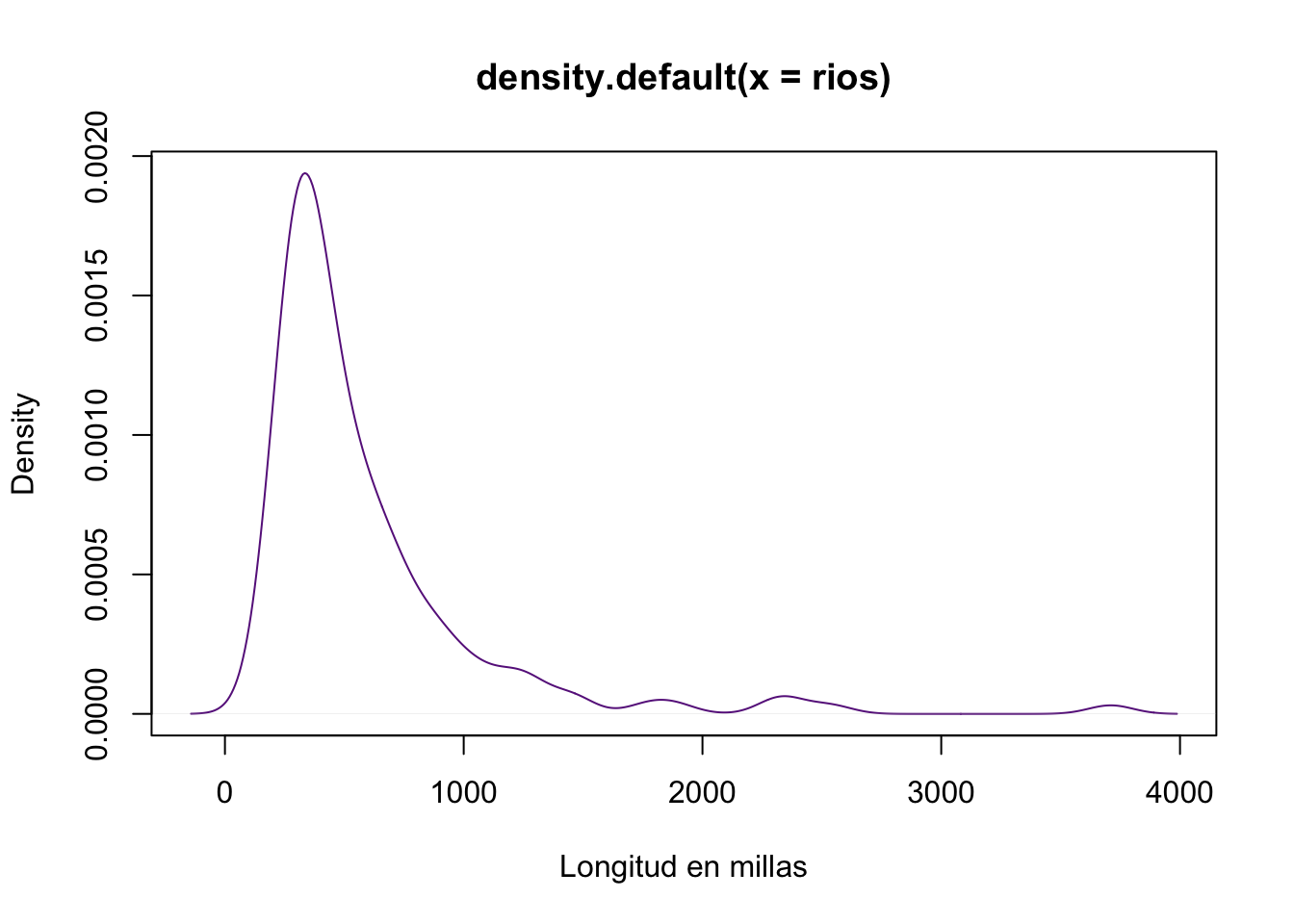

1. Una distribución gamma

estimacion <- fitdistr(rios, densfun = "gamma")
shape_est <- estimacion$estimate[1]
rate_est <- estimacion$estimate[2]
plot(density(rios), col="darkorchid4",xlab="Longitud en millas")
curve(dgamma(x, shape = shape_est, rate = rate_est),
      add = T, col="coral")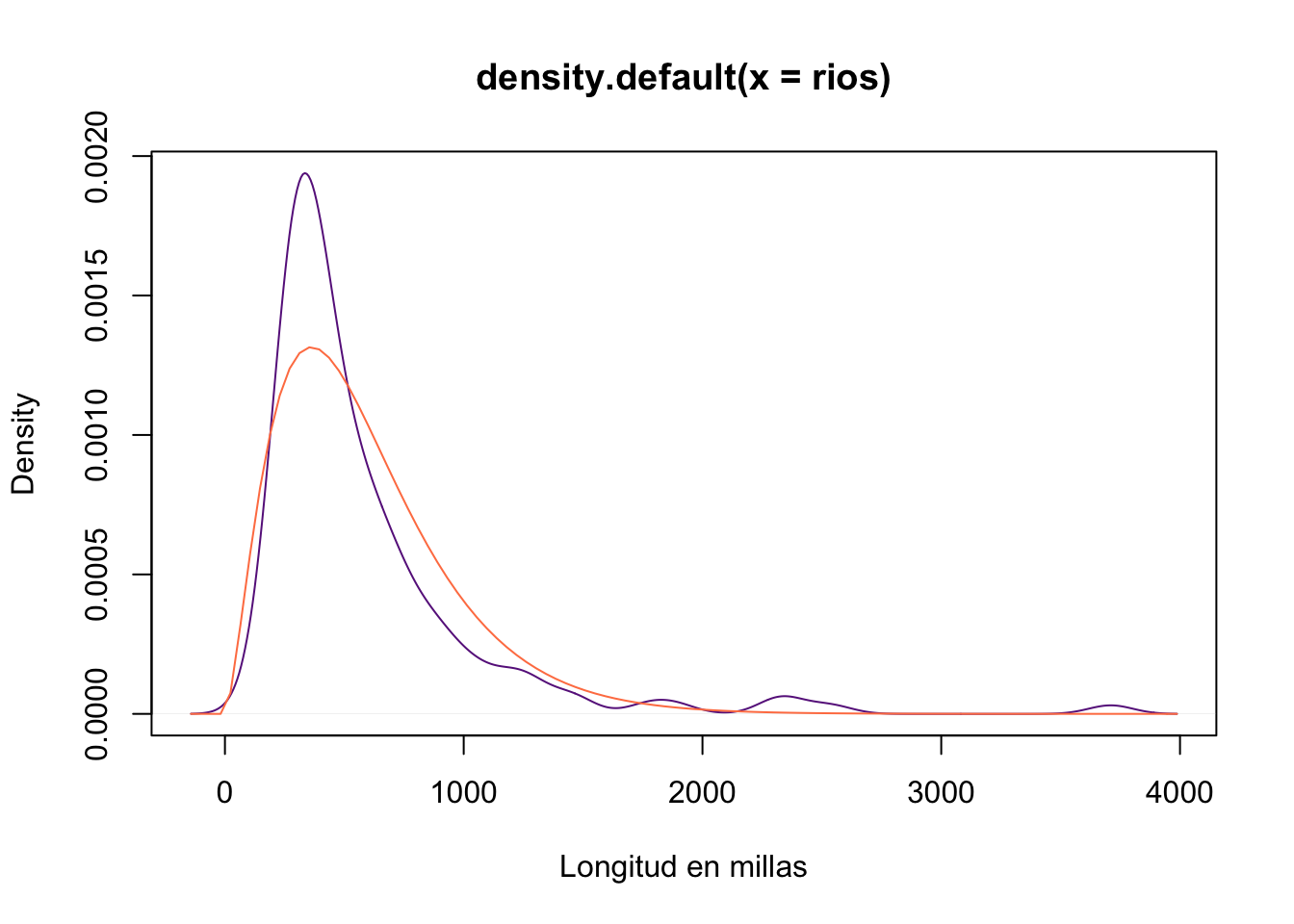

2. Una distribución lognormal

estimacion <- fitdistr(rios, densfun = "lognormal")
meanlog_est <- estimacion$estimate[1]
sdlog_est <- estimacion$estimate[2]

plot(density(rios), col="darkorchid4",xlab="Longitud en millas")
curve(dgamma(x, shape = shape_est, rate = rate_est),
      add = T, col="coral")

curve(dlnorm(x, meanlog = meanlog_est, sdlog = sdlog_est),
      add = T, col="darkolivegreen4")

legend("topright",
       legend=c("Datos","Gamma","Log-Normal"),
       col=c("darkorchid4","coral","darkolivegreen4"),
       lwd=1)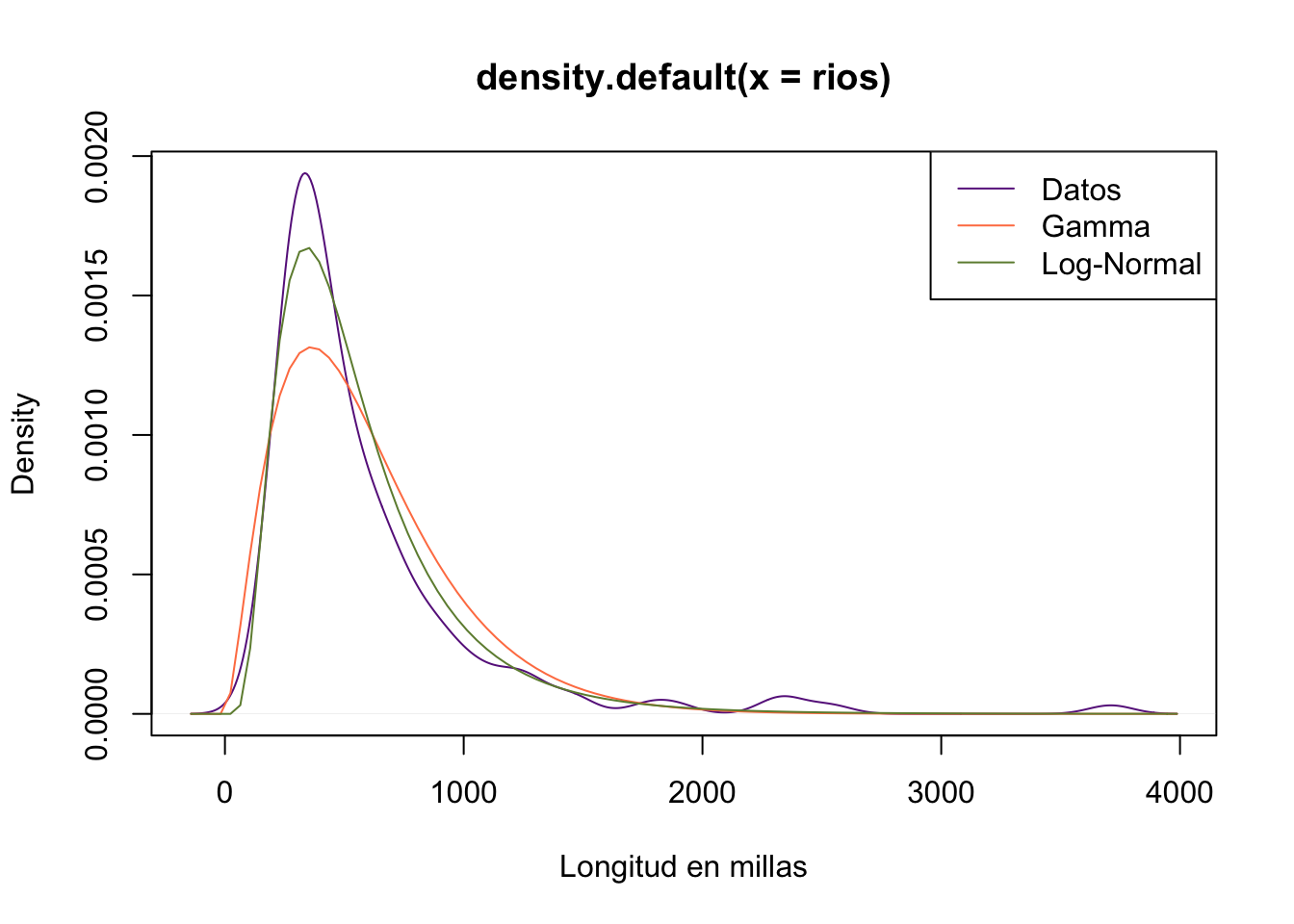

3. Encuenre la probabilidad de que un rio tenga una longitud menor a 1000 millas usando: los datos, el ajuste gamma y el ajuste log-normal

# con los datos
mean(rios < 1000)

## [1] 0.8794326

# con la distribución gamma
pgamma(1000, shape = shape_est, rate = rate_est)

## [1] 0.8697051

# con la distrbución log-normal
plnorm(1000,meanlog = meanlog_est, sdlog = sdlog_est)

## [1] 0.8928388

3.2 Teorema Central del Límite

Ahora vamos a enunciar quiza el resultado más importante de la estadística, vamos a enunciar una versión bastante fácil de entender, tomada del libro Bioestadística de Wayne Daniel

Theorem 3.1 Dada una población con cualquier forma funcional no normal con media \(\mu\) y varianza finita \(\sigma^2\), la distribución muestral de \(\bar{X}\), calculada a partir de muestras de tamaño n de esta población, tendrá media \(\mu\) y varianza \(\frac{\sigma^2}{n}\) y tendrá una distribución aproximadamente normal con estos parámetros

\[ \bar{X} \sim N\left( \mu, \frac{\sigma^2}{n} \right) \]

Veamos un ejemplo, considere \(X_1, X_2, \cdots , X_n\) una muestra aleatoria de una población con distribución Binomial(10, 0.4).

Para una distribución binomial sabemos que \[ \mu = E(X_i)=mp \]

\[ \sigma^2 =Var(X_i)=mp(1-p) \]

Para el ejemplo tenemos que \(\mu = 10(0.4)=4\) y \(\sigma^2=10(0.4)(0.6)=2.4\), entonces

\[ \bar{X}\sim N\left(4,\frac{2.4}{n} \right) \]

Para poder visualizar este resultado podemos simular varias muestas de una distribución binomial con estos parámetros y luego construir histogramas con las observaciones y superponer la distribución normal en cada histograma.

set.seed(2021)
par(mfrow=c(1,2))
Nrep <- 100

n <- c(5,20,30,100)

est1 <- replicate(Nrep, mean(mean(rbinom(n[1], size = 10, prob = 0.4))))
est2 <- replicate(Nrep, mean(mean(rbinom(n[2], size = 10, prob = 0.4))))
est3 <- replicate(Nrep, mean(mean(rbinom(n[3], size = 10, prob = 0.4))))
est4 <- replicate(Nrep, mean(mean(rbinom(n[4], size = 10, prob = 0.4))))


hist(est1,freq = F, col="deepskyblue", main= "n=5")
curve(dnorm(x, mean =4, sd=sqrt(2.4/n[1]) ),
      add = T,col="firebrick")


hist(est2,freq = F, col="deepskyblue",main= "n=20")
curve(dnorm(x, mean =4, sd=sqrt(2.4/n[2]) ),
      add = T,col="firebrick")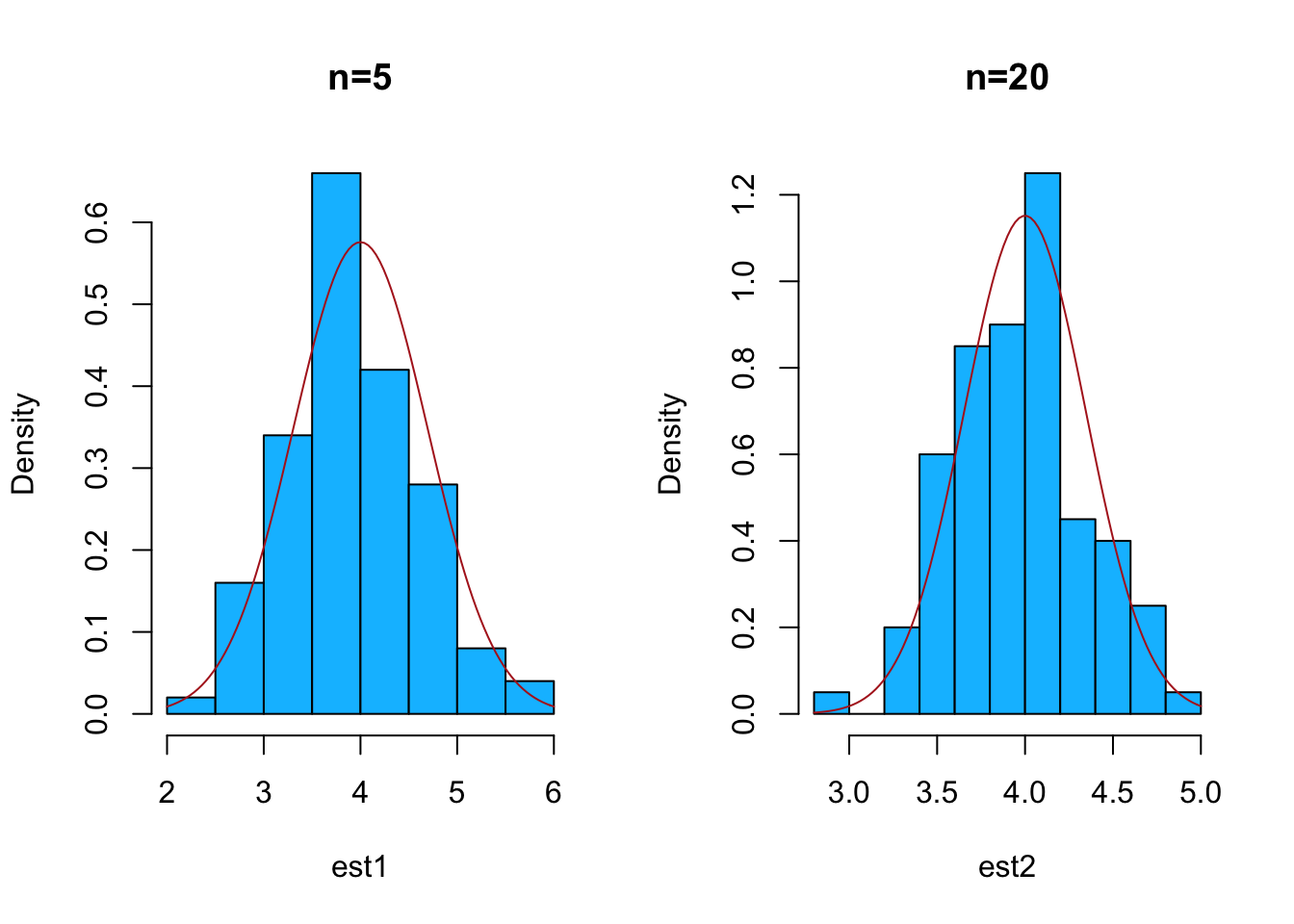

hist(est3,freq = F, col="deepskyblue",main= "n=30")
curve(dnorm(x, mean =4, sd=sqrt(2.4/n[3]) ),
      add = T,col="firebrick")

hist(est4,freq = F, col="deepskyblue",main= "n=100",
     ylim = c(0,2.5))
curve(dnorm(x, mean =4, sd=sqrt(2.4/n[4]) ),
      add = T,col="firebrick")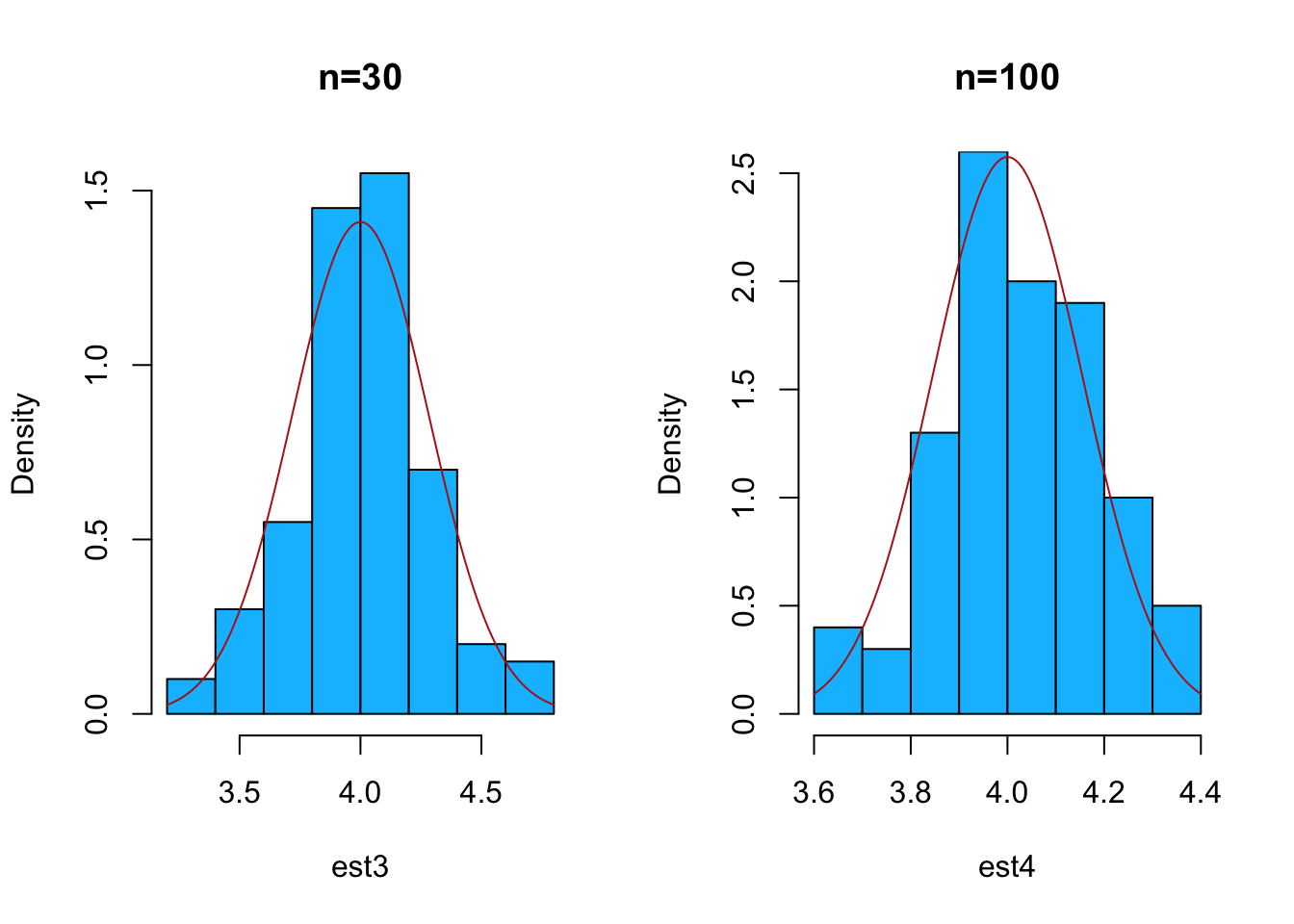

par(mfrow=c(1,1))

3.2.1 Estudiando la normalidad de los datos

Para estudiar si una muestra aleatoria proviene de una población con distribución normal se disponen de tres herramientas.

• Histogramas y/o densidad
• Gráfico cuantil cuantil (qqplot)
• Pruebas de normalidad

Como ya hemos hablado algo sobre los histogramas y densidades vamos a concentrarnos el las pruebas de normalidad

• Prueba Shapiro-Wilk con la función shapiro.test.
• Prueba Anderson-Darling con la función ad.test del paquete nortest.
• Prueba Cramer-von Mises con la función cvm.test del paquete nortest.
• Prueba Lilliefors (Kolmogorov-Smirnov) con la función lillie.test del paquete nortest.
• Prueba Pearson chi-square con la función pearson.test del paquete nortest.
• Prueba Shapiro-Francia con la función sf.test del paquete nortest).

Las hipótesis que contrastan estas pruebas son:

\(H_0\): La muestra viene de una población normal

\(H_1\): La muestra no viene de una población normal

El test de Kolmogorov-Smirnov se utiliza para contrastar si un conjunto de datos se ajustan o no a una distribución normal. Es similar en este caso al test de Shapiro Wilk, pero la principal diferencia con éste radica en el número de muestras. Mientras que el test de Shapiro Wilk se puede utilizar con hasta 50 datos, el test de Kolmogorov Smirnov es recomendable utilizarlo con más de 50 observaciones.

Veamos un ejemplo con datos simulados, vamos a simular una muestra aleatoria de una población con distribución \(N(5, 4)\) luego vamos a contrastar con una distribución \(N(0,4)\) y con la distribución correcta. Veamos el primer caso, las hipótesis a contrastar son:

\(H_0\): La muestra viene de una población con distribución \(N(0,4)\)

\(H_1\): La muestra no viene de una población con distribución \(N(0,4)\)

set.seed(10)
x <- rnorm(100, mean=5, sd=2)
ks.test(x, "pnorm", mean=0, sd=2)

## 
##  One-sample Kolmogorov-Smirnov test
## 
## data:  x
## D = 0.78377, p-value < 2.2e-16
## alternative hypothesis: two-sided

Como podemos observar el resultado me lleva al rechazo de la hipótesis nula, ahora probemos las hipótesis

\(H_0\): La muestra viene de una población con distribución \(N(5,4)\)

\(H_1\): La muestra no viene de una población con distribución \(N(5,4)\)

ks.test(x, "pnorm", mean=5, sd=2)

## 
##  One-sample Kolmogorov-Smirnov test
## 
## data:  x
## D = 0.093092, p-value = 0.3515
## alternative hypothesis: two-sided

La prueba de Kolmogorov-Smirnov para un conjunto de datos univariados funciona cuando la distribución en la hipótesis nula está completamente especificada antes de mirar los datos. En particular, las suposiciones sobre los valores de los parámetros no deben depender de los datos, ya que esto puede cambiar la distribución del muestreo.

Una consecuencia es que no podemos usar la prueba de Kolmogorov-Smirnov para probar la normalidad de un conjunto de datos a menos que conozcamos los parámetros de la distribución subyacente. La prueba de Shapiro-Wilk nos permite realizar ese análisis. Esta estadística de prueba se basa en las ideas detrás de la gráfica de cuantiles-cuantiles, que hemos utilizado para medir la normalidad. Su definición es un poco complicada, pero su uso en R no lo es.

Exploremos la variable sat.m del data frame stud.recs del paquete UsingR

shapiro.test(stud.recs$sat.m)

## 
##  Shapiro-Wilk normality test
## 
## data:  stud.recs$sat.m
## W = 0.98983, p-value = 0.3055

y ahora podemos notar que nos lleva al no rechazo de la hipótesis de normalidad. Como podemos asumir normalidad podriamos usar fitdistr para estimar los parámetros de esa distribución.

plot(density(stud.recs$sat.m), col="darkolivegreen4",
     ylim=c(0,0.006))

estimacion <- fitdistr(stud.recs$sat.m,densfun = "normal")
estimacion

##       mean          sd    
##   485.937500    68.913867 
##  (  5.448120) (  3.852402)

media <- estimacion$estimate[1]
s <- estimacion$estimate[2]

curve(dnorm(x, mean=media, sd=s),add = T,
      col="firebrick4")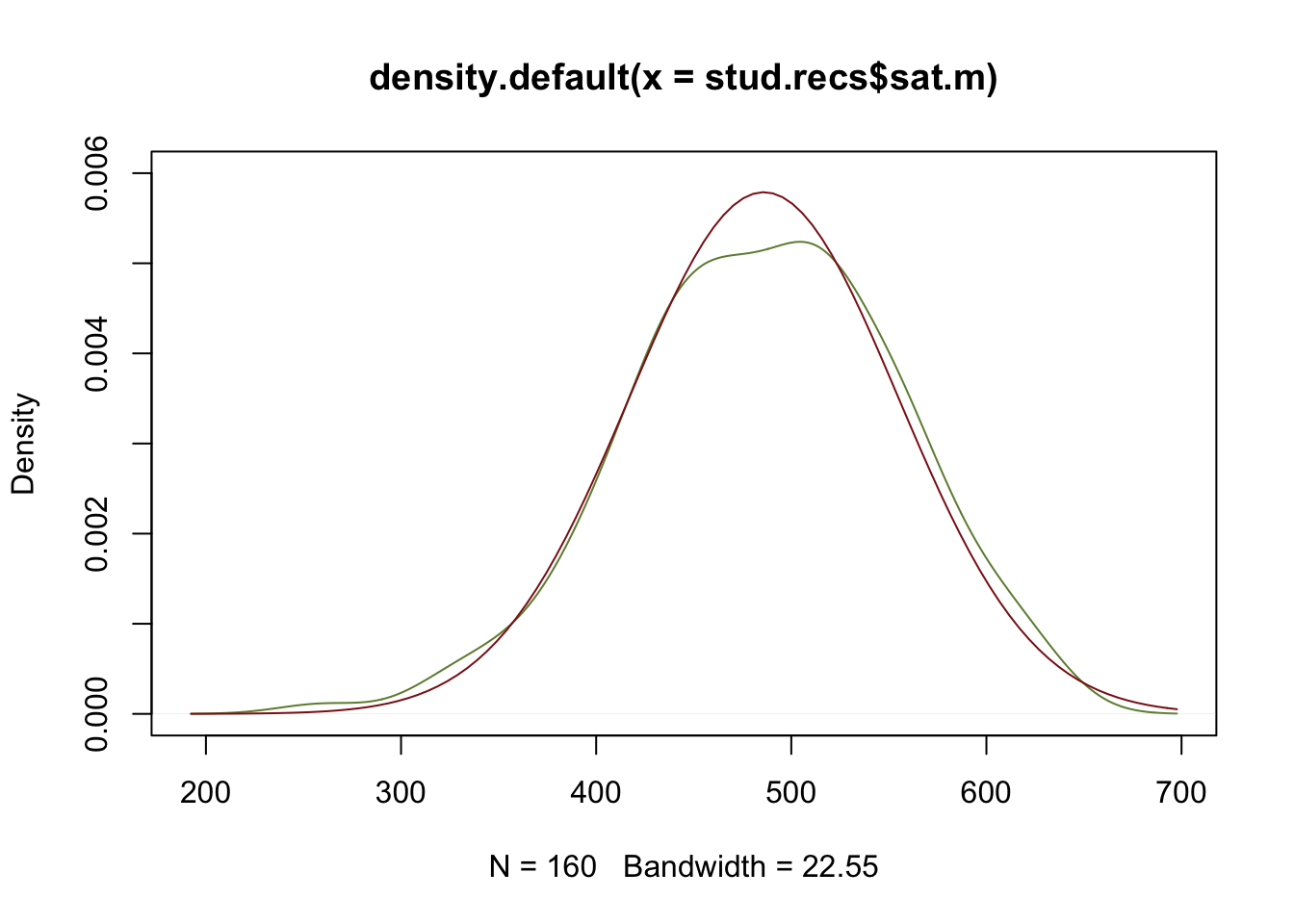

Otra forma gráfica de verificar la normalidad es construyendo un qqplot

qqnorm(stud.recs$sat.m, col="deepskyblue")
qqline(stud.recs$sat.m)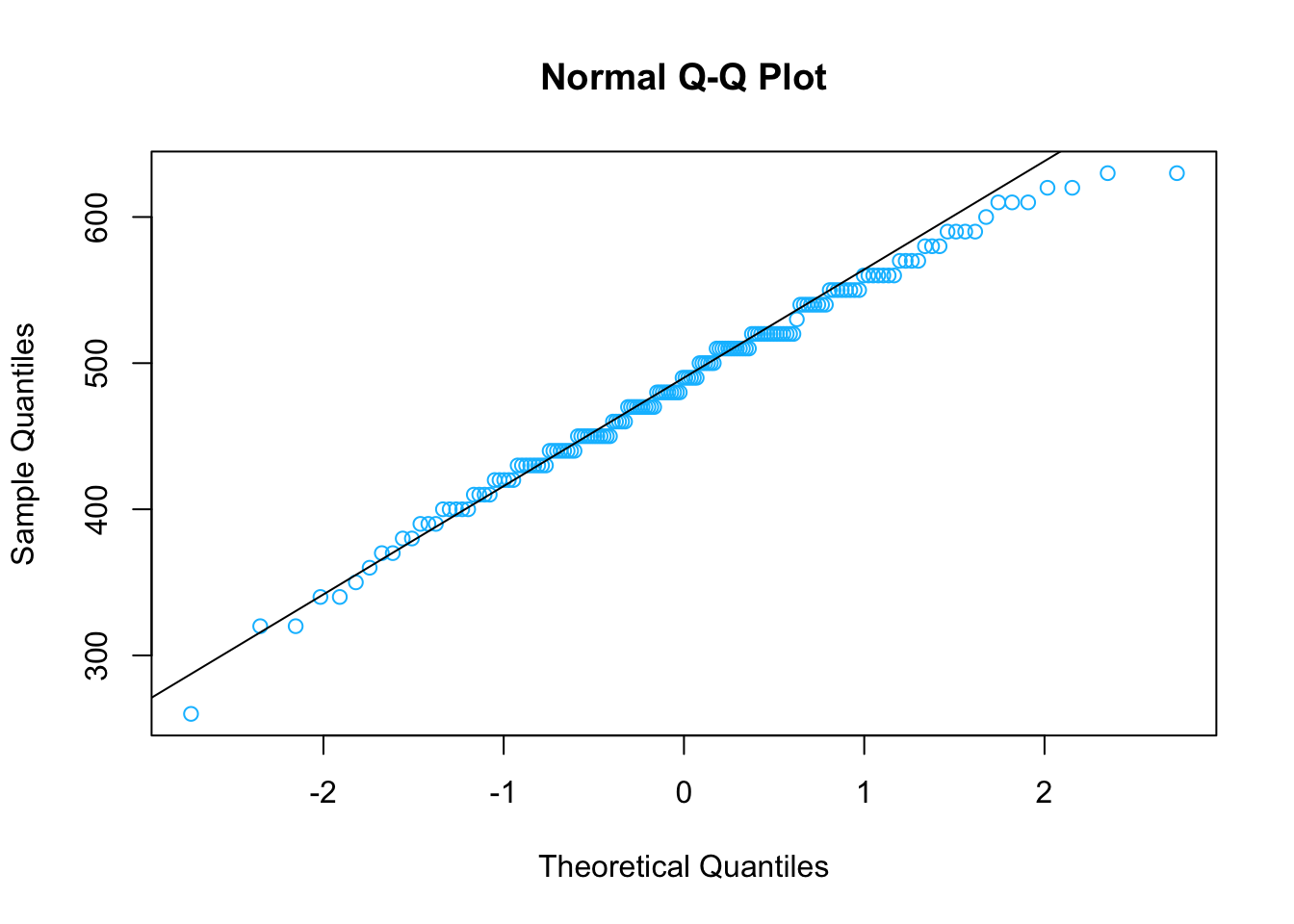

Ya antes vimos la data rivers, ya descubirmos que su comportamiento no es normal, veamos que pasa con los qqplot

\(H_0\): La muestra viene de una población con distribución normal

\(H_1\): La muestra no viene de una población con distribución normal

shapiro.test(rivers)

## 
##  Shapiro-Wilk normality test
## 
## data:  rivers
## W = 0.66662, p-value < 2.2e-16

Concluimos que la muestra no viene de una distribución normal, como era de esperarse, veamos como se ve el qqnorm

qqnorm(rivers,col="firebrick3")
qqline(rivers)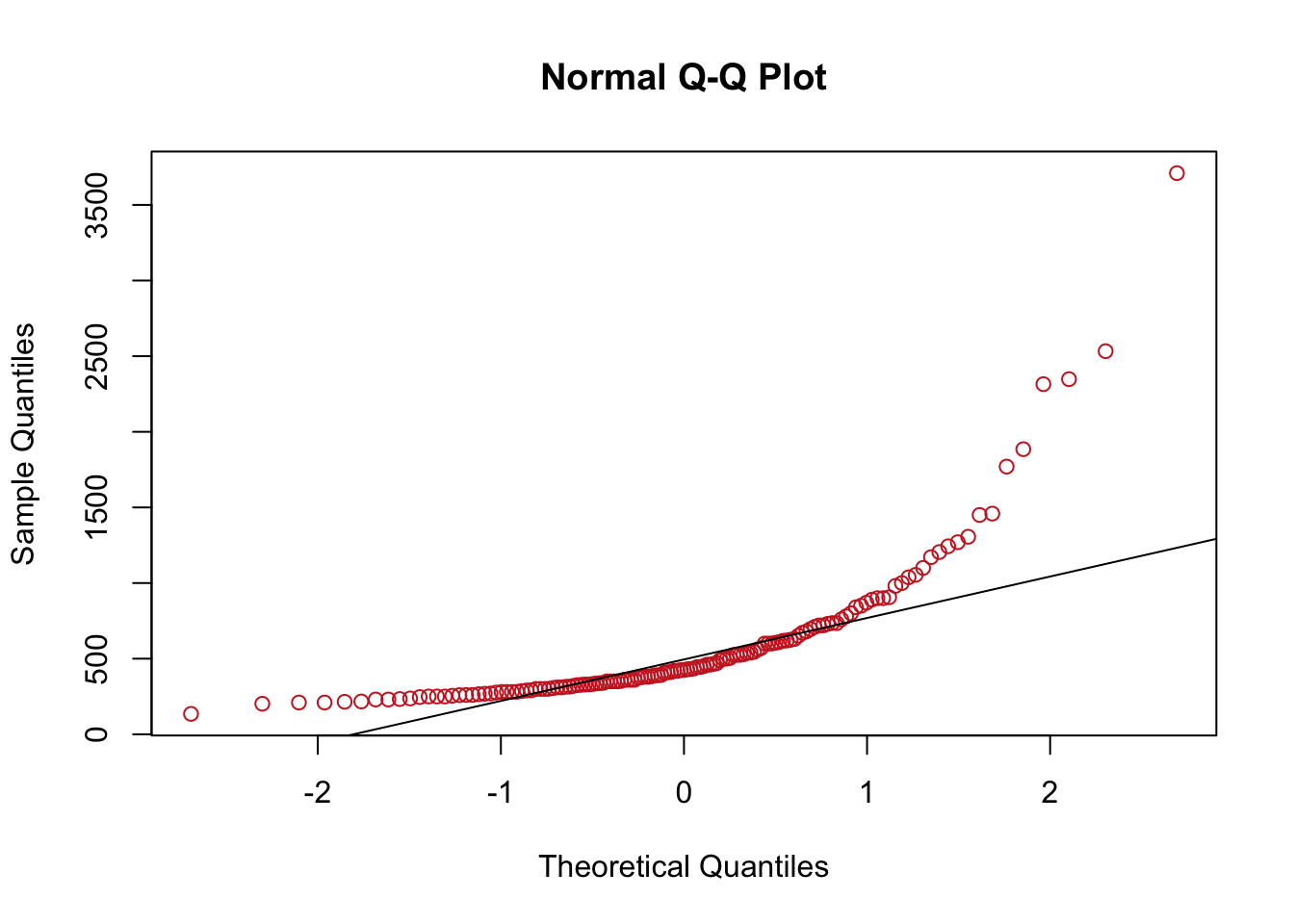

3.3 Inferencia

La inferencia es la parte de la estadística que nos permite realizar una toma de decisiones o establecer conclusiones respecto a algún parámetro de la población basandonos en la información que nos porporciona una muestra.

En general hay dos formas de hacer inferencia

• Estimación
  • Puntual
  • Por intervalos
• Pruebas de Hipótesis

La estimación puntual consiste en encotrar un valor que estime el parámetro de estudio, una media, una porporción o una diferencia de proporciones o medias, entre otros. Por otro lado, una estimación por intervalos es encontrar un rango de valores en los cuales, con cierto nivel de confianza, queremos que se encuentre el verdadero valor del parámetro.

Ejemplo: Si la verdadera media poblacional es \(\mu = 5\), entonces \(\bar{x}=4.8\) es un estimador puntual para \(\mu\) y \([4.7, 5.2 ]\) es una estimación por intervalos para \(\mu\).

Las hipótesis estadísticas son afirmaciones sobre el valor de un parámetro, o valores de varios parámetros. Queremos decidir entre dos hipótesis excpluyentes que compiten.

Vamos a estudiar de forma simultanea estos dos métodos de estimación

3.3.1 IC y Test de Hipótesis

Antes de realizar el proceso en R vamos a repasar algunos conceptos importantes:

• Hipótesis Nula, \(H_0\): Usualmente el status quo
• Hipótesis alternativa, \(H_1\): Usualmente lo que queremos probar o afirmar

Ejemplos de \(H_0\): La hipótesis nula muchas veces codifica el ‘status quo’

1. La vacuna no genera un aumento en los anticuerpos
2. La moneda que estamos testeando es balanceada
3. El paciente está enfermo

Ejemplos de \(H_1\): En estos casos, hipótesis alternativa codifica un descubrimiento informalmente, que encontramos algo nuevo que no sabiamos antes.

1. La vacuna genera un aumento en los anticuerpos
2. La moneda ques estamos testeando favorece a la cara
3. El paciente está sano

Observaciones:

• La hipótesis nula y alternativa tienen roles distintos en el test de hipótesis y no son intercambiables.

• La carga de la prueba cae sobre la hipótesis alternativa \(H_1\).

• Hablaremos de rechazar o no rechazar \(H_0\). Cuando no podemos rechazar la nula, no es que aceptamos que esta vale, simplemente decimos que no hay evidencia para rechazarla.

Cuando tomamos una decisión en una prueba de hipótesis podemos estar tomando la decisión correcta o comentiendo algún error.

• Error tipo I \(\alpha\) = P(rechazar \(H_0\) | \(H_0\) es verdadera)
• Error tipo II \(\beta\) = P(no rechazar \(H_0\) | \(H_0\) es falsa)

Al error tipo I también lo conocemos como nivel de confianza y al complementeo de error tipo II lo llamamos potencia del test.

Queremos nivel bajo y potencia alta.

Observación: Siempre existe un intercambio entre potencia y nivel. Si disminuyó el nivel del test baja la potencia. Si aumentó la potencia aumenta el nivel.

Tipos de test

• Test bilaterales

  • \(H_0:\theta=\theta_0\)
  • \(H_1:\theta \neq \theta_0\)

• Test unilateral

  • \(H_0: \theta \leq \theta_0\)
  • \(H_1: \theta > \theta_0\)

  ó

  • \(H_0: \theta \geq \theta_0\)
  • \(H_1: \theta < \theta_0\)

En R la función que se encarga de realizar un test de hipótesis cuando tenemos muestras pequeñas es t.test(), algúnos parámetros de esta función son:

• x: Vector numérico con los datos
• alternative: Tipo de hipótesis alternativa
• mu: Valor supuesto de la media bajo la hipótesis nula.
• conf.level: nivel de confianza \(1-\alpha\)

Veamos ahora como aplicar esta función para varios casos.

3.3.2 Pruebas de hipótesis para una población

Example 3.3 El data.frame SleepStudy del paquete Lock5Data contiene datos de un estudio de patrones de sueño para estudiantes universitarios, en estos datos tenemos las variables:

• Gender: Género del estudiante
• AverageSleep: Horas de sueño por dia.

Se dice que una persona debe dormir 8 horas al día para mantenerse saludable. ¿ Ofrecen estos datos información suficiente como para suponer que los estudiantes no duermen el número adecuado de horas ?, use $= 0.05 $

Primero contrastemos la hipótesis de normalidad

\(H_0\): La muestra viene de una población con distribución normal

\(H_1\): La muestra no viene de una población con distribución normal

library(Lock5Data)
suenho <- SleepStudy
shapiro.test(suenho$AverageSleep)

## 
##  Shapiro-Wilk normality test
## 
## data:  suenho$AverageSleep
## W = 0.99044, p-value = 0.0959

par(mfrow=c(1,2))
qqnorm(suenho$AverageSleep, col="coral2")
qqline(suenho$AverageSleep)
hist(suenho$AverageSleep, col="coral2",
     xlab="Promedio de horas de sueño diarias", 
     main="Estudio del sueño en \n estudiantes universitarios")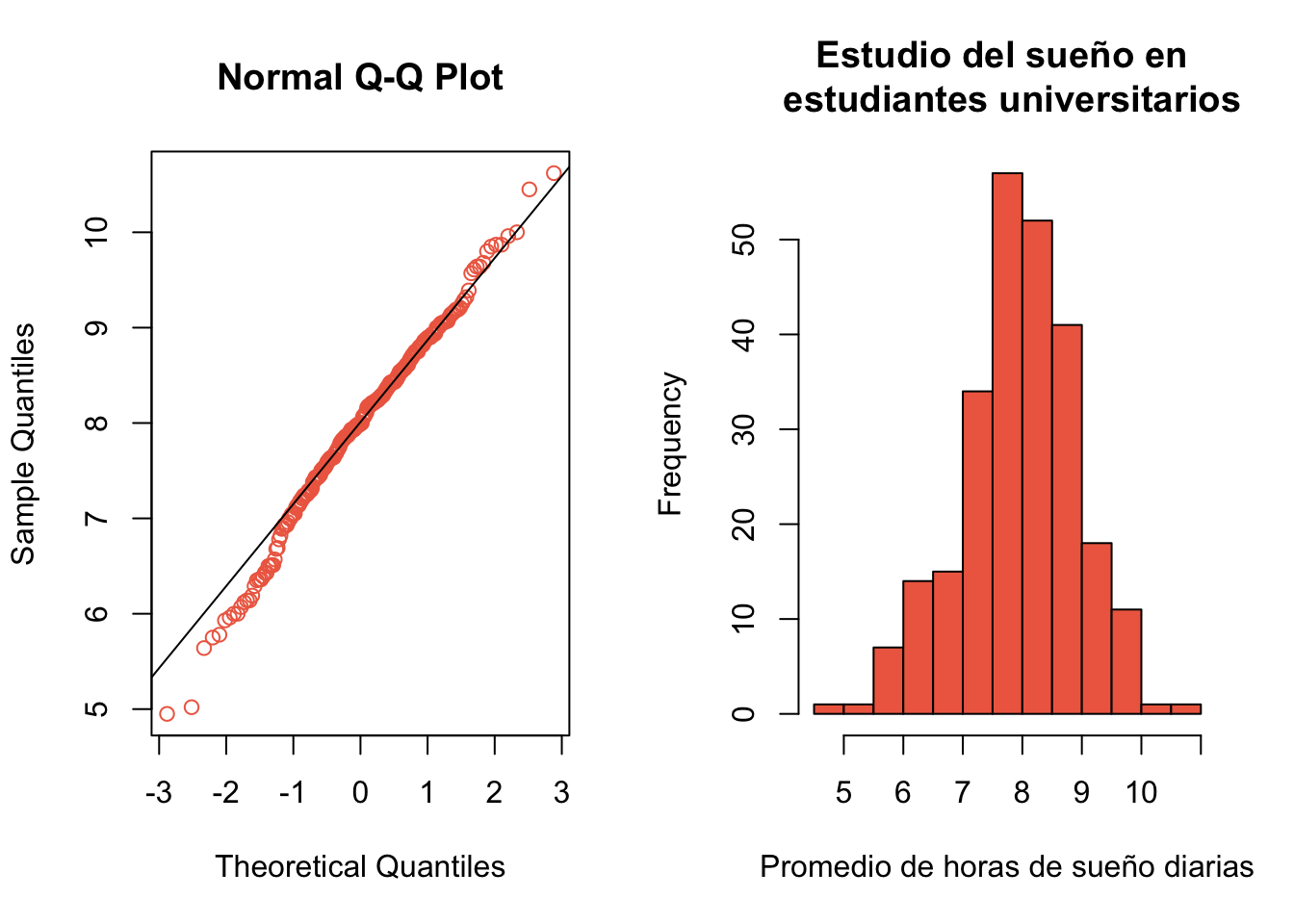  

par(mfrow=c(1,1))

Una vez comprobada la hipótesis de normalidad podemos proceder a realizar el test

\(H_0:\mu = 8\)

\(H_1:\mu \neq 8\)

t.test(suenho$AverageSleep, mu=8)

## 
##  One Sample t-test
## 
## data:  suenho$AverageSleep
## t = -0.56168, df = 252, p-value = 0.5748
## alternative hypothesis: true mean is not equal to 8
## 95 percent confidence interval:
##  7.846466 8.085392
## sample estimates:
## mean of x 
##  7.965929

Notemos que el valor p > 0.05, por lo tanto no podemos rechazar \(H_0\) y decimos que las evidencias no son suficientes para afirmar que el los estudiantes no está durmiendo el número adecuado de horas. Por otro lado notemos que el intervalo de confianza del 95% para el número promedio de horas es

\[ [7.846466, 8.085392] \]

Esto significa que el 95% de las veces que repitamos este experimento el verdadero promedio de horas de sueño está entre 7.846466 y 8.085392.

Ahora nos preguntamos, ¿ Será que los estudiantes están durmiendo más de 7 horas?, es decir, que ahora debemos probar las hipótesis:

\(H_0:\mu \leq 7\)

\(H_1:\mu > 7\)

t.test(suenho$AverageSleep,  mu=7, alternative="greater")

## 
##  One Sample t-test
## 
## data:  suenho$AverageSleep
## t = 15.924, df = 252, p-value < 2.2e-16
## alternative hypothesis: true mean is greater than 7
## 95 percent confidence interval:
##  7.865786      Inf
## sample estimates:
## mean of x 
##  7.965929

Ahora notemos que el valor p es menor que 0.05 por lo tanto si podriamos rechazar la hipótesis nula y concluir que los estudiantes si están durmiendo en promedio mas de 7 horas.

3.4 Ejercicios

1. Un nuevo procedimiento quirurgico es exitoso con una probabilidad p. Suponga que la operación se realizó cinco veces y los resultados son independientes entre sí, ¿Cuál es la probabilidad de que :

   1. Todas las operaciones sean exitosas si p = 0.8

   2. exactamente cuatro sean exitosas si p = 0.6

   3. menos de dos sean exitosas si p = 0.3

   4. Grafique las funciones de probabilidad que describen los incisos a, b y c

2. (Entrega) El conjunto de datos babyboom del paquete UsingR contiene la hora de nacimiento, el sexo y el peso al nacer de 44 bebés nacidos en un período de 24 horas en un hospital de Brisbane, Australia. La variable running.time, registra la hora del día de cada nacimiento (medida en minutos después de la media noche). Consideremos las diferencias de tiempo entre nacimientos sucesivos, a estas diferencias se le llaman tiempos entre llegadas.

   1. Explore la función diff para calcular los tiempos entre llegadas.

   2. Haga una estimación de la densidad de los tiempos entre llegadas, ¿ Que distribución propone que pueda modelar estos datos?

   3. Estime los parámetros de una gamma y luego superponga la densidad de la con los parámetros estimados en la densidad estimada en b.

   4. Encuentre la probabilidad de que el tiempo entre llegadas sea menor a 60 minutos, usando los datos y luego con el modelo gamma ajustado.

3. Se supone que las calificaciones de un examen están normalmente distribuidas con media de 78 y varianza de 36

   1. ¿Cuál es la probabilidad de que una persona que haga el examen alcance calificaciones mayores de 72?

   2. Suponga que los estudiantes que alcancen el 10% más alto de esta distribución reciben una calificación de A. ¿Cuál es la calificación mínima que un estudiante debe recibir para ganar la calificación de A?

   3. ¿Cuál debe ser la nota minima para pasar el examen si el examinador desea pasar sólo al 28.1% más alto de todas las calificaciones?

4. (Entrega) Considere la variable fheight del data frame father.son del paquete UsingR. Este data frame contiene una muestra de alturas de padres en hijos en pulgadas, fheight es la altura del padre.

   1. Realice una estimación no paramétrica de la densidad de fheight con el comando density

   2. Si podemos asumir una distribución normal para modelar estos datos, estime los parámetros \mu y sigma y luego grafique sobre la densidad estimada la distribución normal con los parámetros encontrados, use colores diferentes para indicar cada gráfico.

   3. Use los datos para encontrar cual es la probabilidad de que un padre tenga una altura menor a 70 pulgadas, luego estime esta probabilidad usando el modelo normal con los parámetros estimados en b.

   4. Encuentre que estatura deja el 75% de los valores menores o iguales que ella, compare esto con el cuantil 75 de la distribución normal con los parámetros estimados en b.

5. La eficiencia (en lúmenes por watt) de los focos de cierto tipo tiene una media poblacional de 9.5 y desviación estándar de .5, de acuerdo con especificaciones de producción. Las especificaciones para un cuarto en el que ocho de estos focos se han de instalar exigen que el promedio de eficiencia de los mismos sea mayor que 10.

   1. Encuentre la probabilidad de que se satisfaga esta especificación para el cuarto, suponiendo que las mediciones de eficiencia están distribuidas normalmente.

   2. ¿ Cuál debe ser la eficiencia media por foco si debe satisfacerse la especifi- cación para el cuarto con una probabilidad de aproximadamente .80 ? (Suponga que la varianza de las mediciones de eficiencia continúa en .5.)

6. La variable temperature en el conjunto de datos normtemp del paquete UsingR contiene mediciones de temperatura corporal normal para 130 individuos sanos seleccionados al azar. Pruebe la suposición de que los datos muestrales de temperatura corporal normal provienen de una distribución normal.

7. Use los datos del ejercicio anterior para realizar una prueba t para ver si el valor comunmente asumido de 98.5 grados F es correcto. (los estudios han sugerido que 98.2 grados F es en realidad más preciso), construya un intervalo de confianza del 95% para la temperatura corporal promedio.

8. Cuando estamos seguros que la población de la que viene la muestra sigue una distribución normal, y además conocemos la varianza de la población, entonces podemos asegurar que \[ \frac{\bar{X}-\mu}{\frac{\sigma}{\sqrt{n}}}\sim N(0,1) \]

Este resultado puede utilizarse para construir intervalos de confianza de nivel \(1-\alpha\). Para construir el intervalo de confianza se siguen los siguienes pasos:

• Calcular la media muestral de los datos como estimador puntual de la media poblacional

• Encontrar el error estándar de la media muestral \(\frac{\sigma}{\sqrt{n}}\)

• Determinar el cuantil \(1-\alpha/2\) de la distribución normal estándar.

• Construir el intervalo :

\[ \left[\bar{x}-z_{1-\alpha/2}\frac{\sigma}{\sqrt{n}} , \bar{x} + z_{1-\alpha/2}\frac{\sigma}{\sqrt{n}} \right] \]

Utilice estos pasos para respoder el siguiente problema:

Se trata de medir el período de un péndulo y se tiene un cronómetro de precisión conocida (es decir, se conoce la varianza del error). Si las obserbaciones vienen de una población con una distribución \(N(\mu, \frac{1}{4})\) y son independientes. Los datos obtenidos son:

Utilice esta información para construir un intervalo de confianza del 95% para la media poblacional.

9.(Entrega) Para verificar si el proceso de llenado de bolsas de café con 500 gramos está operando correctamente se toman aleatoriamente muestras de tamaño 10 cada cuatro horas. Una muestra de bolsas está compuesta por las siguientes observaciones: 510, 492, 494, 498, 492,496, 502, 491, 507, 496.

1. ¿ Está el proceso llenando bolsas conforme dice la envoltura ? Use nivel de significancia del 5%.

2. Construya un intervalo de confianza del 95% para el promedio del peso lleno de las bolsas de café.