2 Semana II

2.1 Estadística Descriptiva

Como una primera aproximación al análisis de un conjunto de datos, nos va a interesar realizar una descripción del mismo ya sea de fórma gráfica o numérica.

2.1.1 Medidas de tendencia central

En primer lugar vamos a analizar las medidas de tendencia central, estas las podemos encontrar con las funciones:

  • mean() Para la media
  • median() Para la mediana
  • mfv() del paquete modeest Para la moda

Ejemplo: La prevención es la mejor manera de combatir la enfermedad cardíaca coronaria. Los factores potenciales que influyen en su desarrollo son una combinación que incluye (pero no es exclusiva) factores biológicos, hereditarios y elecciones de estilo de vida. Los siguientes datos corresponden a un estudio sobre dicha enfermedad y analizaremos la relación entre el desarrollo de la enfermedad y las variables presente.

Las variables medidas son:

  • sbp: presión arterial sistólica
  • tabaco: tabaco acumulativo (kg)
  • ldl: colesterol de baja densidad
  • adiposidad: índice de adiposidad coporal
  • famhist: antecedentes familiares de enfermedad cardíaca. Variable categórica con dos niveles: Ausente, Presente.
  • tipoA: personalidad y comportamiento tipo A
  • obesidad: ındice de masa corporal
  • alcohol: consumo actual de alcohol
  • edad: edad al inicio del estudio
  • chd: enfermedad cardíaca conoraria sí, no codificada por los números 1, 0

Esta información está en el archivo heart.csv

Hagamos un análisis descriptivo para la variable obesidad

corazon<-read.csv("heart.csv")
mean(corazon$obesidad)
## [1] 26.04411
median(corazon$obesidad)
## [1] 25.805
mfv(corazon$obesidad)
## [1] 24.86 26.09

Algunas veces vamos a querer calcular estadísticas descriptivas por grupo, por ejemplo, si queremos encontrar el promedio de la variable obesidad agrupada por antecedentes familiares de enfermedad cardíaca, para esto podemos usar la función tapply(variable_de_analisis, variable_de_agrupacion, estadistica_de_interes)

tapply(corazon$obesidad, corazon$famhist, mean)
##  Ausente Presente 
## 25.63381 26.62109
tapply(corazon$obesidad, corazon$famhist, median)
##  Ausente Presente 
##   25.365   26.205
tapply(corazon$obesidad, corazon$famhist, mfv)
##  Ausente Presente 
##    26.09    25.99

Si queremos hacer algo parecido a lo anterior con tidyverse vamos a usar las funciones group_by() y summarise combiandas, exploremos primero summarise

summarise(corazon, media=mean(obesidad), mediana=median(obesidad)
          , moda=mfv(obesidad))
##      media mediana  moda
## 1 26.04411  25.805 24.86
## 2 26.04411  25.805 26.09

Ahora combinemos con group_by

corazon %>% 
  group_by(famhist) %>% 
  summarise( media=mean(obesidad), mediana=median(obesidad), moda=mfv(obesidad))
## # A tibble: 2 × 4
##   famhist  media mediana  moda
##   <chr>    <dbl>   <dbl> <dbl>
## 1 Ausente   25.6    25.4  26.1
## 2 Presente  26.6    26.2  26.0

2.1.2 Medidas de dispersión y posición

Una vez analizamos la centralidad de los datos vamos a querer ver la dispersión, las medidas de dispersión conocidas las calculamos con:

  • range() para el rango
  • var() para la varianza
  • sd() para la desviación estándar
  • quantile() para los cuantiles

Ejemplo: Ahora calculemos la varianza y el rango para el ejemplo anterior

tapply(corazon$obesidad, corazon$famhist, var)
##  Ausente Presente 
## 17.70116 17.35141
tapply(corazon$obesidad, corazon$famhist, range)
## $Ausente
## [1] 17.81 46.58
## 
## $Presente
## [1] 14.70 41.76
corazon %>% 
  group_by(famhist) %>% 
  summarise( varianza=var(obesidad), rango=range(obesidad))
## `summarise()` has grouped output by 'famhist'. You can override using the
## `.groups` argument.
## # A tibble: 4 × 3
## # Groups:   famhist [2]
##   famhist  varianza rango
##   <chr>       <dbl> <dbl>
## 1 Ausente      17.7  17.8
## 2 Ausente      17.7  46.6
## 3 Presente     17.4  14.7
## 4 Presente     17.4  41.8
quantile(corazon$obesidad)
##      0%     25%     50%     75%    100% 
## 14.7000 22.9850 25.8050 28.4975 46.5800

Veamos un poco mas sobre los cuantiles, una fórma muy práctica de analizar la dispersión de un conjunto de datos gráficamente es haciendo un boxplot, en R esto lo hacemos con la función boxplot(), veamos para la obesidad

boxplot(corazon$obesidad)

Con boxplot() estamos haciendo un primer acercamiento a los gráficos en R, esta función gráfica puede recibir más parámetros

  • main título principal del gráfico
  • xlab y ylab etiquetas del eje x e y respectivamente
  • `col color del gráfico
  • horizontal orientación del gráfico, horizontal=T si lo queresmos de forma horizontal

Podemos entonces modificar el gráfico sencillo anterior

boxplot(corazon$obesidad,ylab="índice de masa corporal",
        main="Gráfico de dispersión para el indice de masa corporal",
        col="darkred")

Veamos como interpretar un box plot, estos gráficos tienen una caja y dos bigotes:

  • Las dimensiones de la caja está determinada por la distancia del rango intercuartílico, que es la diferencia entre el primer y tercer cuartil, en la caja se encuentra el 50% de las observaciones

  • El segmento que divide la caja en dos partes es la mediana, que facilitará la comprensión de si la distribución es simétrica o asimétrica.

    • Si la mediana se sitúa en el centro de la caja entonces la distribución es simétrica y tanto la media, mediana y moda coinciden.

    • Si la mediana corta la caja en dos lados desiguales se tiene:

      • Asimetría positiva o segada a la derecha si la parte más larga de la caja es la parte superior a la mediana. Los datos se concentran en la parte inferior de la distribución. La media suele ser mayor que la mediana.

      • Asimetría negativa o sesgada a la izquierda si la parte más larga es la inferior a la mediana. Los datos se concentran en la parte superior de la distribución. La media suele ser menor que la mediana.

  • La continuación de dos segmentos en la caja se denominan bigotes que determina el límite para la detección de valores atípicos.

Los bigotes deben tener una longitud máxima. Dicha longitud no debe ser superior al 150% del rango intercuartílico.

Habrá un límite superior, que no podrá superar el 1,5 veces el RIC, si el máximo no supera ese valor, la longitud del bigote será desde el tercer cuartil hasta el máximo.

Habrá un límite inferior, que no podrá superar el 1,5 veces el RIC, si el mínimo no supera ese valor, la longitud del bigote será desde el primer cuartil hasta el mínimo.

Todos aquellos valores que estén mas alla de los limites inferiores o superiores de los bigotes se consideran valores atipicos

Ahora, que pasa si queremos ver los boxplot organizados por grupos, estudiemos las formulas en r:

Las fórmulas se utilizan para expresar relaciones entre variables para muchas funciones diferentes, y la interpretación de una fórmula puede variar según su uso. La forma básica de una fórmula modelo es respuesta(s) ~ predictor(es)

boxplot(obesidad ~ famhist, data=corazon )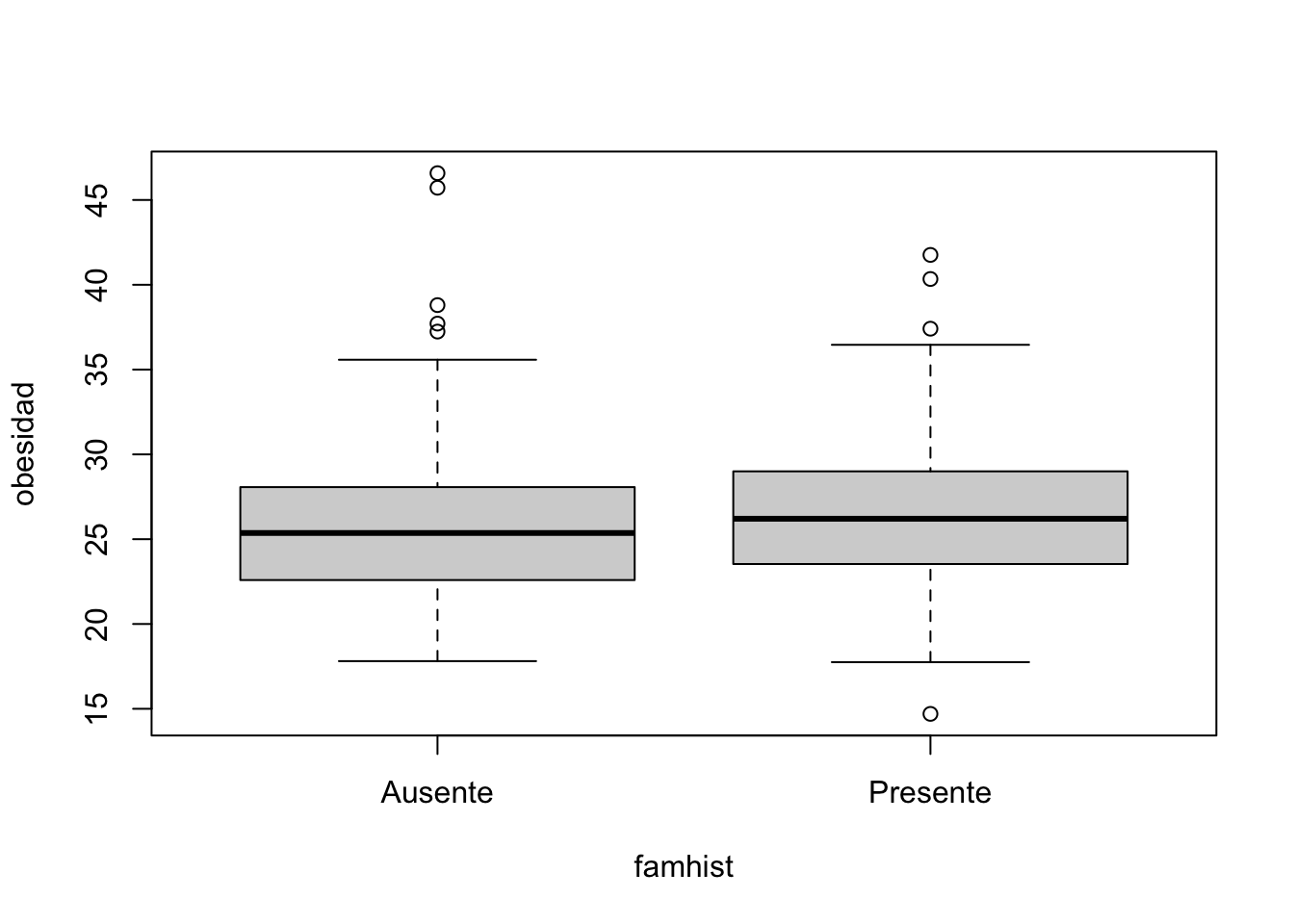

2.1.3 Gráficos

Como parte de la estadística descriptiva esta la representación gráfica de nuestros datos, ya sea de variables cualitativas como cuantitativas, vamos a explorar las funciones básicas de graficos de R y las del paquete ggplot2(). Vamos a explorar los gráficos para variables cualitativas primero.

2.1.3.1 Gráficos para variables cualitativas

En primer lugar debemos tener organizados nuestros datos en una tabla, volvamos al ejemplo del titanic, exploremos la variable embarked que daba la información sobre el lugar donde embarcaron los pasajeros, queremos construir una tabla de frecuencias, la función que hace esto en el r básico es table()

titanic<-read.csv("titanic.csv",na.strings = "")
table(titanic$embarked)
## 
##   C   Q   S 
## 270 123 914

Si queremos construir una tabla de frecuencias relativas usamos la función prop.table() esta función debemos aplicarla a una tabla.

prop.table(table(titanic$embarked))
## 
##          C          Q          S 
## 0.20657995 0.09410865 0.69931140

Estas funciones podemos aplicarlas para elaborar tablas cruzadas, veamos cuantas personas embarcaron de cada género por lugar de embarque.

table(titanic$embarked,titanic$sex)
##    
##     female male
##   C    113  157
##   Q     60   63
##   S    291  623
prop.table(table(titanic$embarked,titanic$sex))
##    
##         female       male
##   C 0.08645754 0.12012242
##   Q 0.04590666 0.04820199
##   S 0.22264728 0.47666412

La función addmargins() me permite encontrar los totales por filas y columnas

addmargins(table(titanic$embarked,titanic$sex))
##      
##       female male  Sum
##   C      113  157  270
##   Q       60   63  123
##   S      291  623  914
##   Sum    464  843 1307
addmargins(prop.table(table(titanic$embarked,titanic$sex)))
##      
##           female       male        Sum
##   C   0.08645754 0.12012242 0.20657995
##   Q   0.04590666 0.04820199 0.09410865
##   S   0.22264728 0.47666412 0.69931140
##   Sum 0.35501148 0.64498852 1.00000000

Ahora vamos a tomar estas tablas de frecuencia y las vamos a convertir en gráficos, uno de los gráficos mas sencillos para representar variables cualitativas es el de pastel, este lo podemos obtener aplicando a una tabla la función pie() veamos el más básico:

t<-table(titanic$embarked)
pie(t)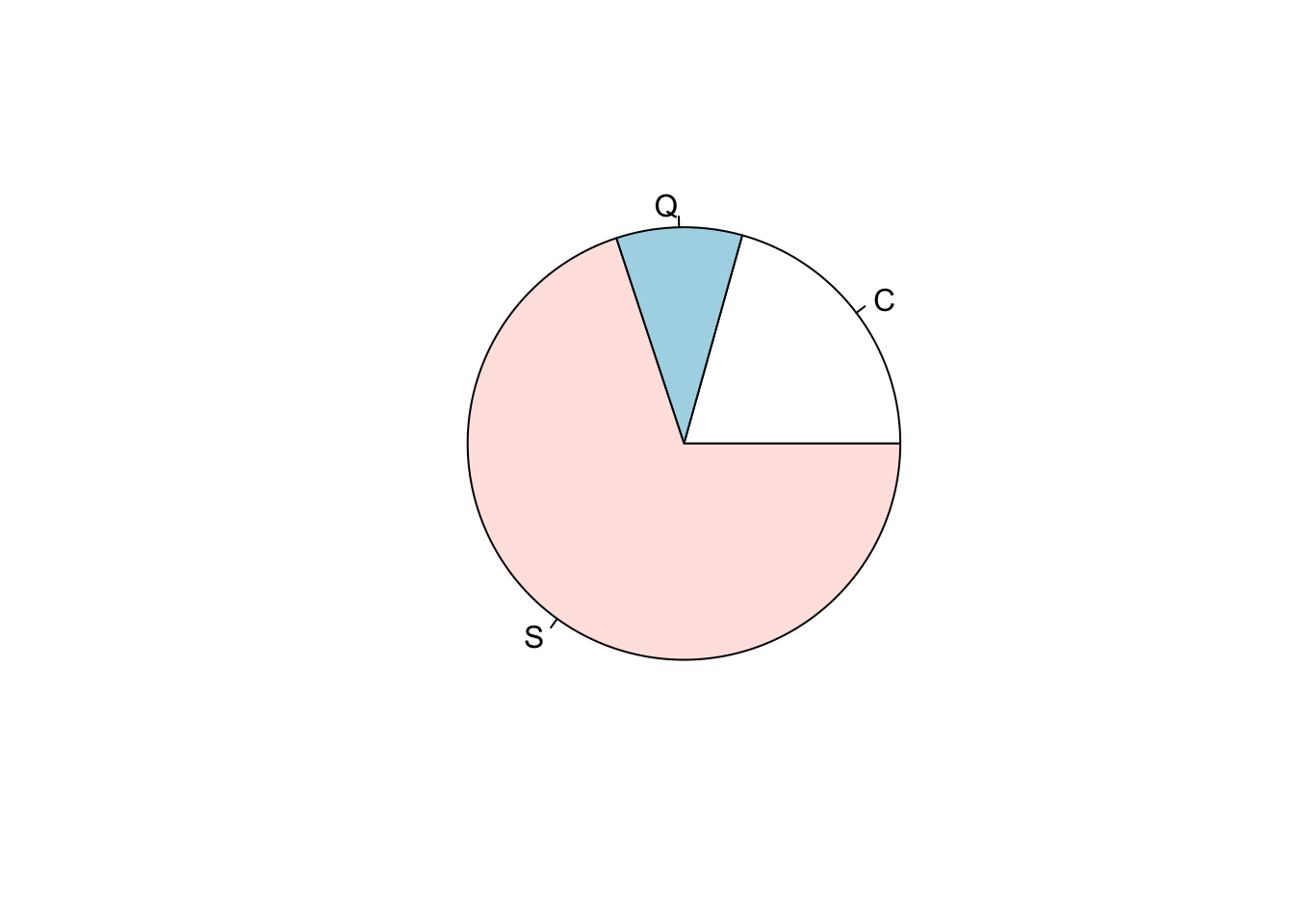

Ahora mejoremos esteticamente este gráfico, los parámetros que vimos en los boxplot() también los podemos aplicar aquí

pie(t,main="Lugar de embarcación",xlab="Etiqueta de eje x",
    ylab="etiqueta de eje y",col=c("red","green","blue"))

Podemos agregar una leyenda a nuestro gráfico con legend()

porce<-round(prop.table(table(titanic$embarked)),1)*100
porce
## 
##  C  Q  S 
## 20 10 70
pie(t,main="Lugar de embarcación",xlab="Etiqueta de eje x",
    ylab="etiqueta de eje y",col=c("red","green","blue"),
    labels=porce)

legend("topright",title="Lugar de embarcación",
       legend = c("Cherbourg","Queenstown","Southampton"),
       fill=c("red","green","blue"),cex=0.7)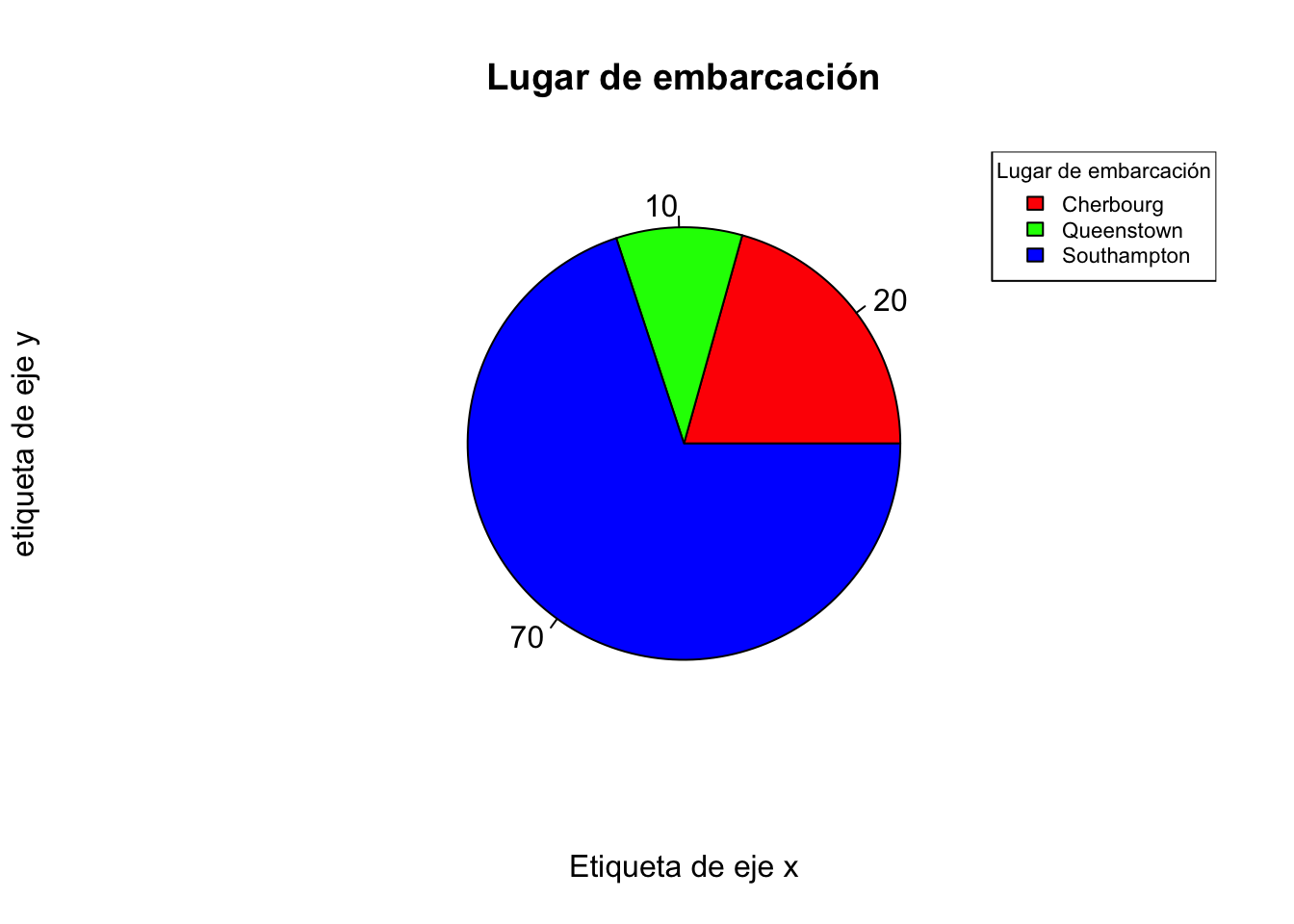

Cuando las variables tienen muchas categorias no es muy estetico mostrarlo en un gráfico de pastel, en estos casos podemos usar los gráficos de barra con la función barplot(). Consideremos el archivo kc_house.csv este conjunto de datos consta de los precios de las viviendas del condado de King, un área en el estado de Washington de los EE. UU. la variable condition nos indica la condición de la vivienda (de 1 a 5)

casas<-read.csv("kc_house.csv")

t<-table(casas$condition)
pie(t)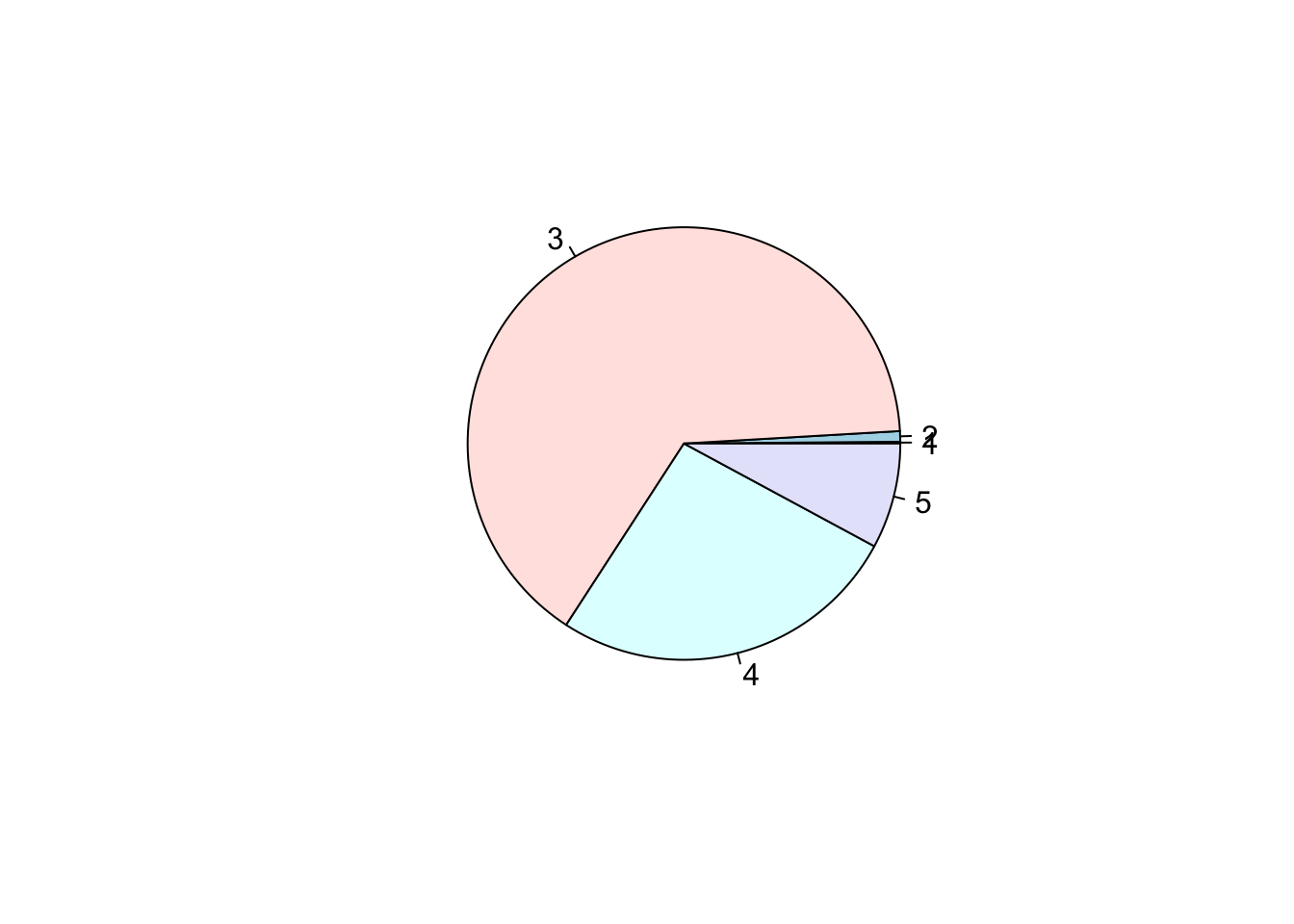

barplot(t)

barplot(t,main="Condición de las casas en el condado King",
        xlab = "Condición de la vivienda",ylab = "Número de viviendas",
        col=topo.colors(5))

legend("topright", title="Condición",
       legend = c("Muy Mala","Mala","Intermedia","Aceptable","Perfecta"),
       fill=topo.colors(5), cex=0.7)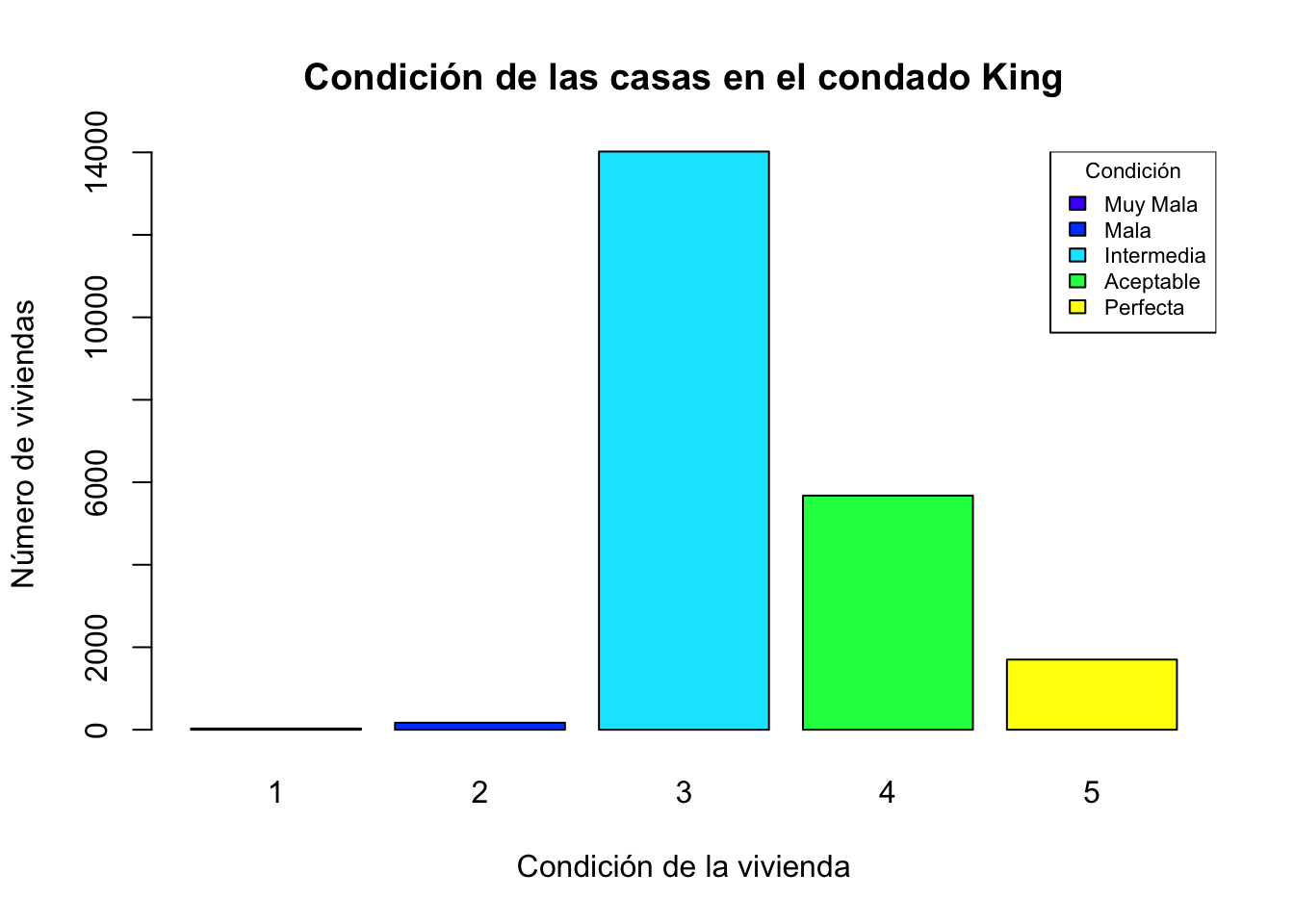

La función par() me permite estableces algunos parámetros generales repecto a los gráficos, por ejemplo, me permite graficar varios elementos en un solo espacio con mfrow

par(mfrow = c(1,2) )
t<-table(casas$condition)
barplot(t,main="Condición de las casas en el condado King",
        xlab = "Condición de la vivienda",ylab = "Número de viviendas",
        col=topo.colors(5))

legend("topright", title="Condición",
       legend = c("Muy Mala","Mala","Intermedia","Aceptable","Perfecta"),
       fill=topo.colors(5), cex=0.7)

t <- table(titanic$embarked)
pie( t , main = "Lugar de embarcación" , col=terrain.colors(3),
     labels =porce)

legend("topright", title="Lugar de embarcación",
       legend = c("Cherbourg","Queenstown","Southampton"),
       fill=terrain.colors(3), cex=0.7)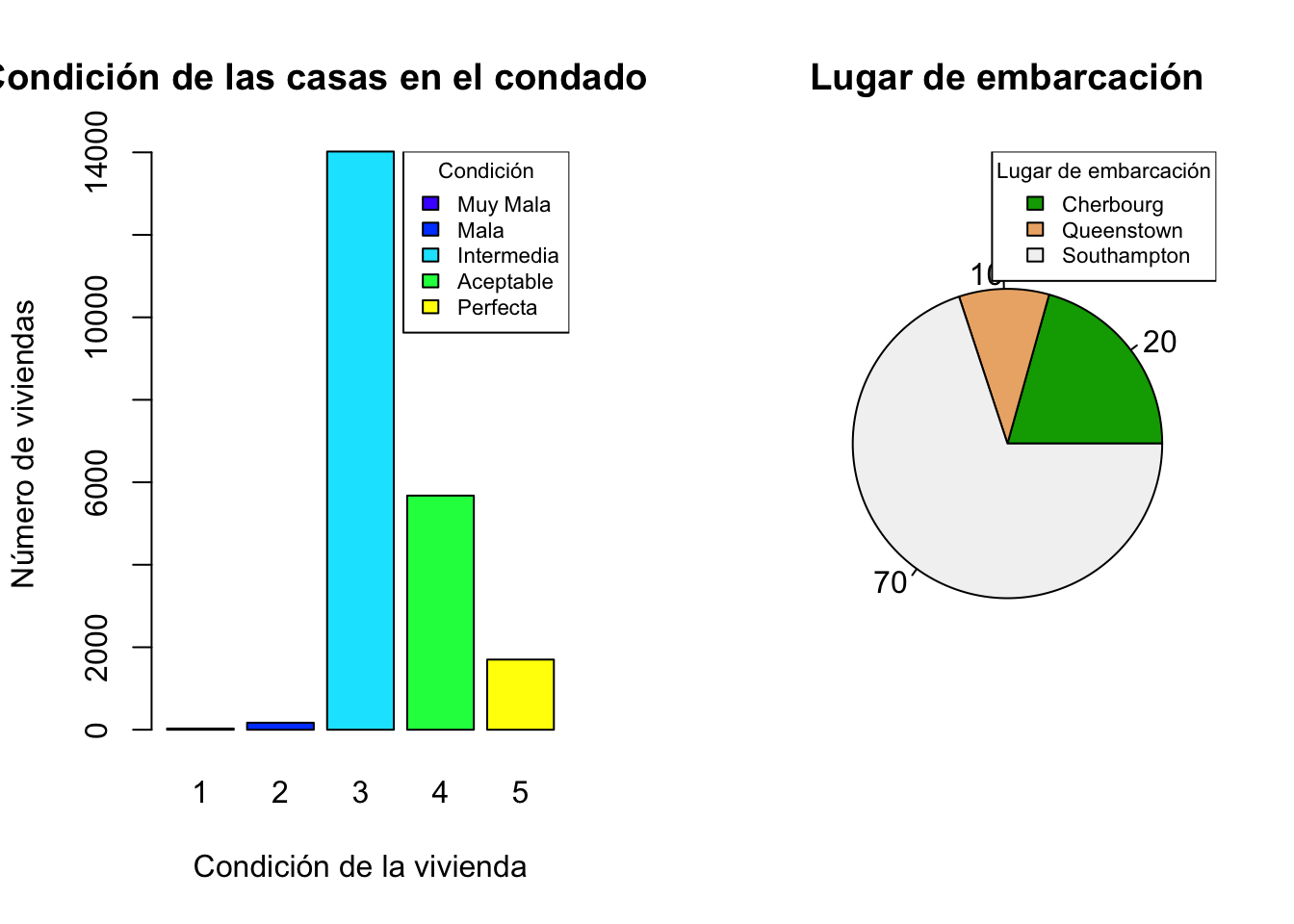

par(mfrow = c(1,1))

2.1.3.2 El paquete ggplot2

Un gráfico ggplot2 se construye combinando una serie de elementos básicos y comunes a muchos tipos de gráficos distintos mediante una sintaxis sencilla.

  • Datos: Uno de los elementos más importantes de un gráfico son los datos que se quieren representar. ggplot solo acepta objetos del tipo data.frame

  • Esteticas: En un gráfico hay, en la terminología de ggplot2 estéticas, estéticas son, por ejemplo, la distancia horizontal o vertical, el color, la forma (de un punto), el tamaño (de un punto o el grosor de una línea), etc.

  • Capas: Las capas o geoms indican que hacer con los datos y las esticas elegidas, como representarlos en un lienzo

Retomemos los datos de los pasajeros del titanic y construyamos un gráfico de barra usando ggplot2

titanic<-na.omit(titanic)
p<-ggplot(data=titanic)

El código anterior crea un objeto, p que viene a ser un protográfico, contiene los datos que vamos a utilizar, los del conjunto de datos titanic. Obviamente, el código anterior es insuficiente para crear un gráfico, aún no hemos indicado qué queremos hacer con titanic.

ggplot(titanic, aes(x = embarked)) + geom_bar()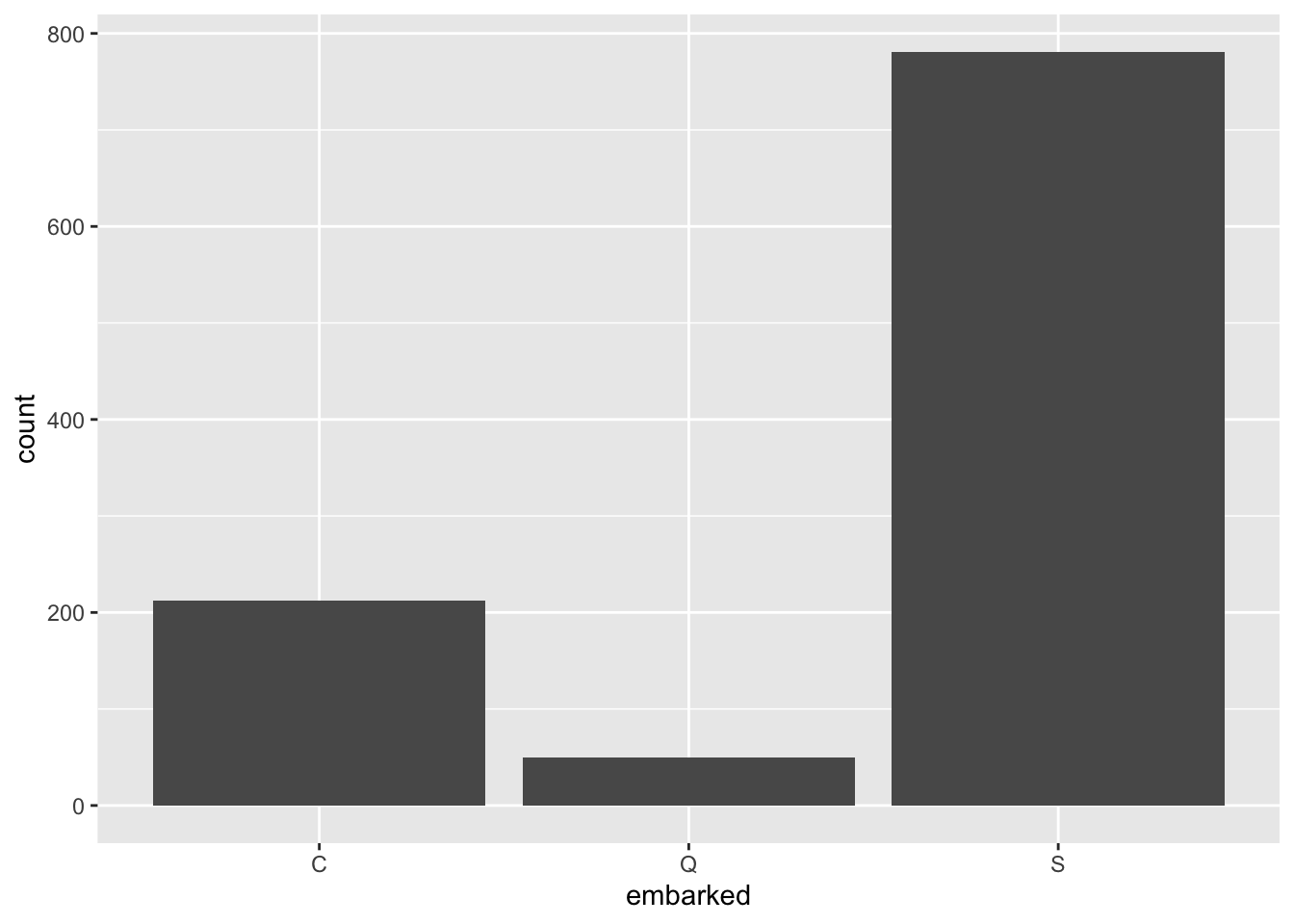

Ahora mediante geom_bar() le estamos indicando el objeto que deseamos graficar, agreguemos algunas capas mas a nuestro gráfico

ggplot(titanic, aes(x = embarked, fill=embarked )) + 
  geom_bar()+
  ggtitle("Lugar de embarque de los pasajeros del Titanic")+
  xlab("Lugar de embarque") + ylab("Número de pasajeros")+
  scale_fill_discrete(labels=c("Cherbourg", "Queenstown", "Southampton"),
                      name=c("Lugar de embarque")) +
  theme_bw()

Ahora construyamos gráficos compartivos, veamos primero con el paquete gráfico básico

t<-table( titanic$embarked , titanic$sex )

barplot(t)

barplot(t,beside = T)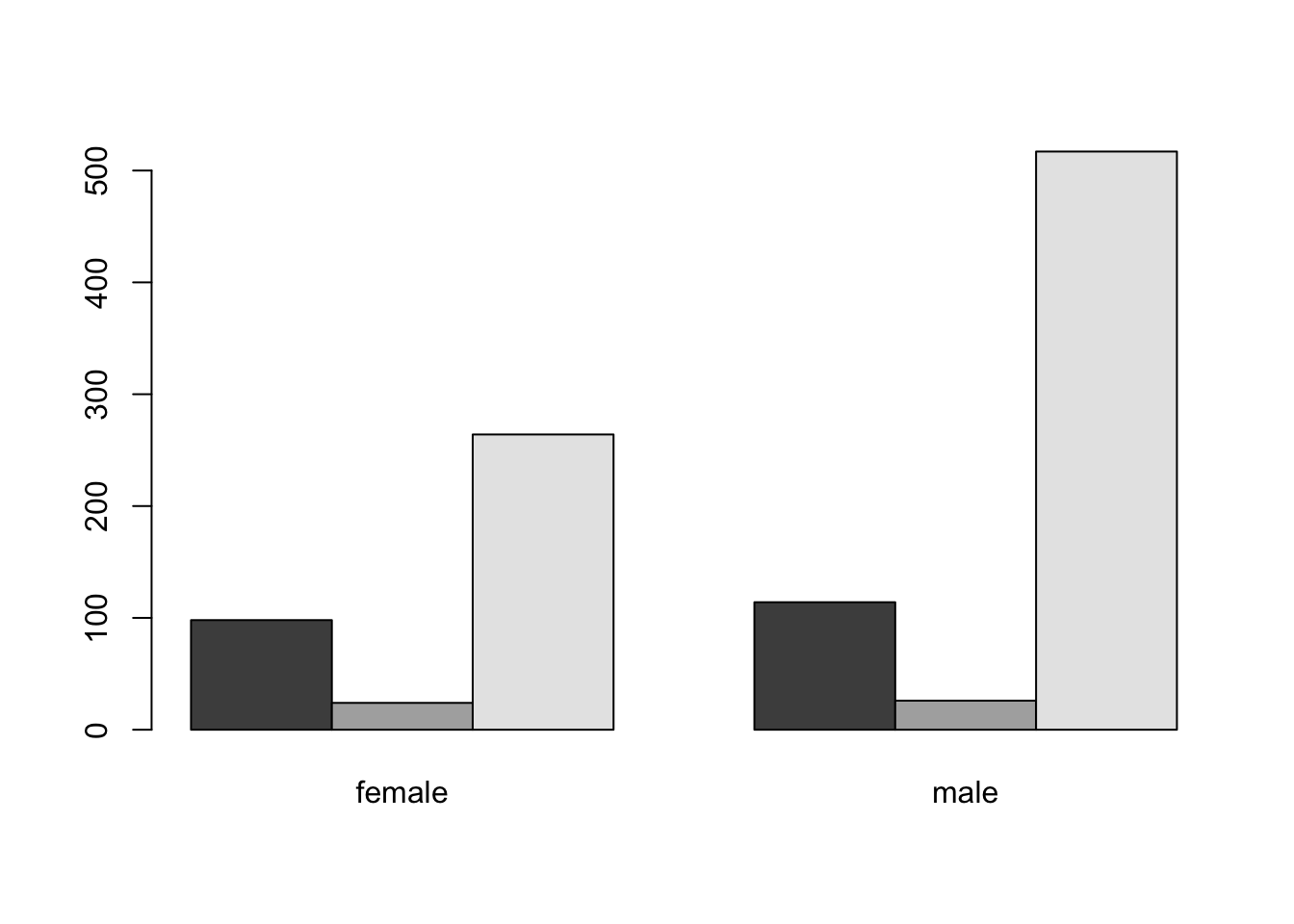

Luego podemos jugar con los demás parámetros esteticos para mejorar nuestro gráfico, veamos ahora con ggplot2

ggplot(titanic,aes(x=embarked, fill=sex)) + geom_bar(position="dodge")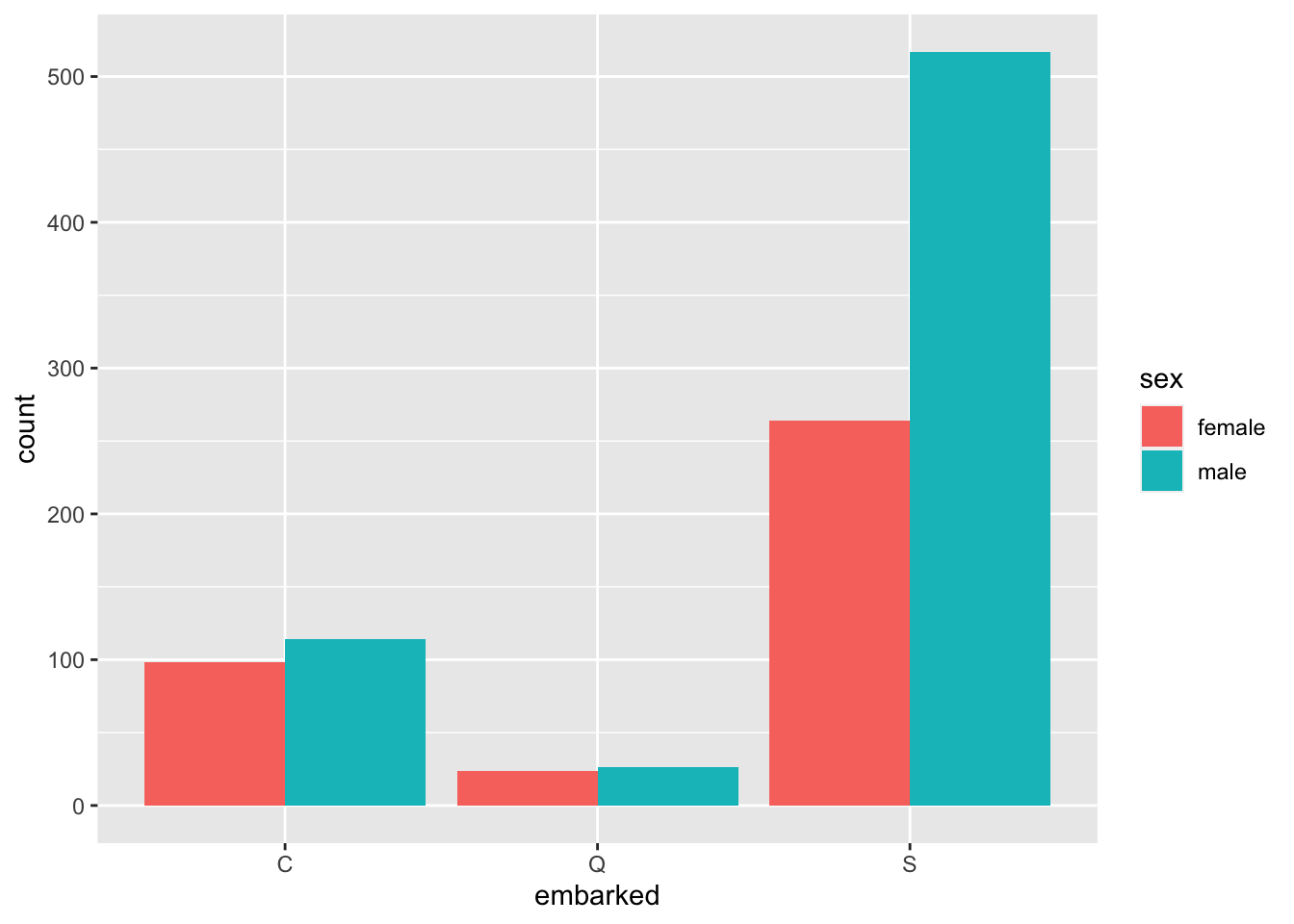

Con ggplot podemos usar facets, estos son gráficos generados por categorias de otra variable

MiGrafico<-ggplot(titanic, aes(x = embarked, fill=embarked )) + 
  geom_bar()+
  ggtitle("Lugar de embarque de los pasajeros del Titanic")+
  xlab("Lugar de embarque") + ylab("Número de pasajeros")+
  scale_fill_discrete(labels=c("Cherbourg", "Queenstown", "Southampton"),
                      name=c("Lugar de embarque")) +
  theme_bw()

MiGrafico + facet_grid(sex ~.)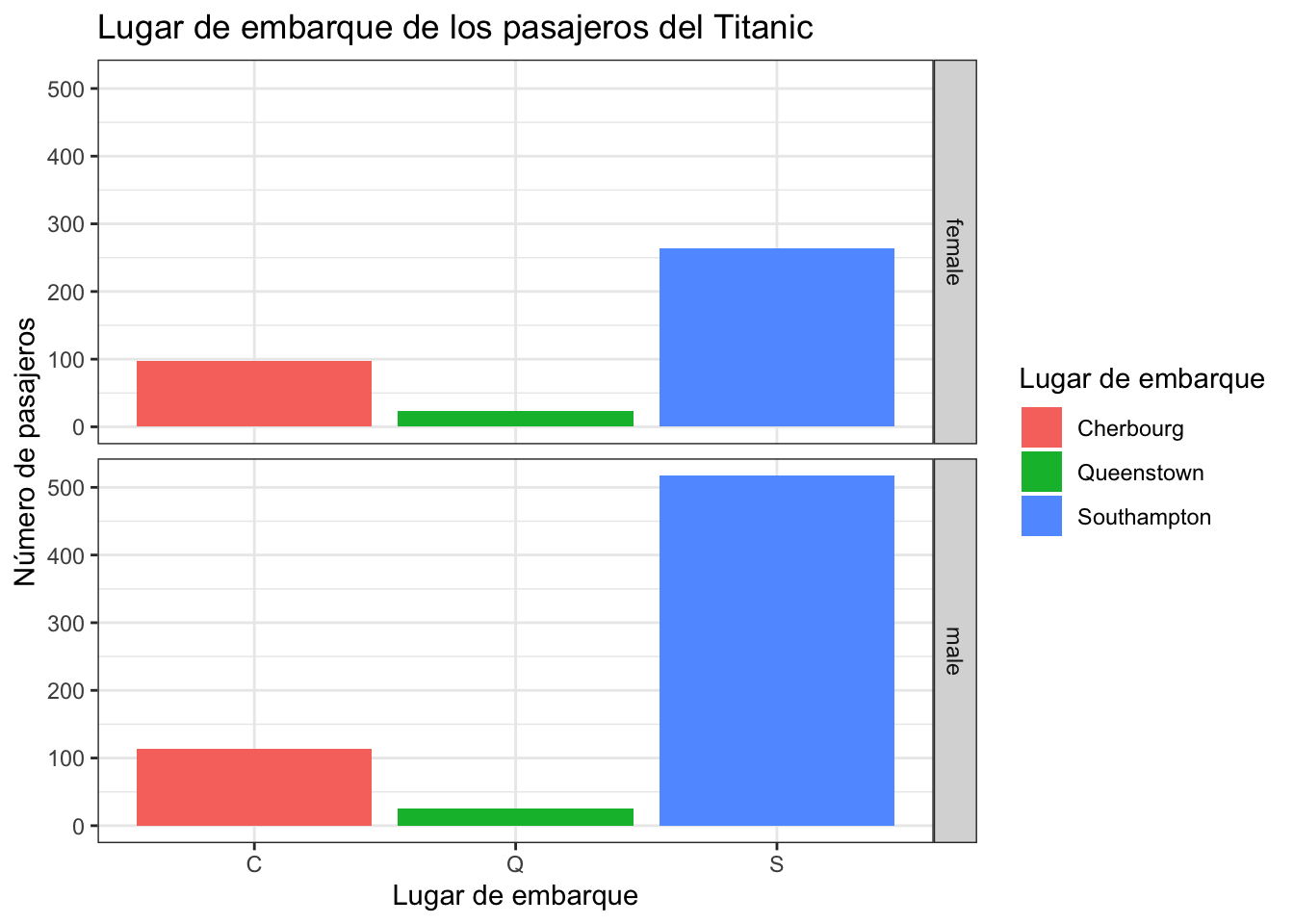

MiGrafico + facet_grid(.~sex)

casas %>%
  filter(waterfront==1) %>% 
  ggplot(aes(x=condition))+
  geom_bar()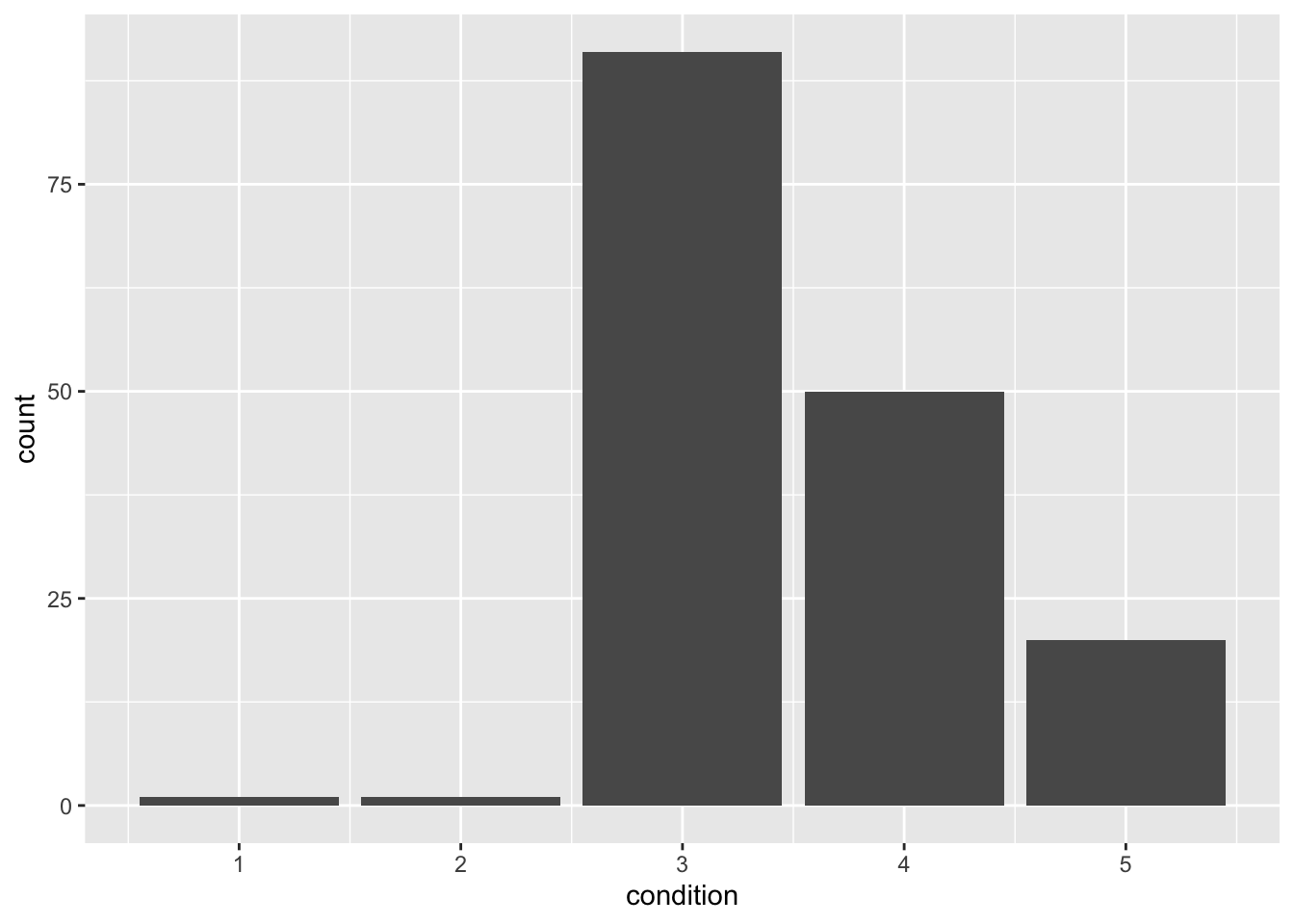

2.1.3.3 Gráficos para variables cuantitativas

Exploremos ahora algunas opciones de representación gráfica para un conjunto de datos continuo. Es de mucha importancia conocer la forma funcional de nuestros datos, para esto podemos construir histogramas, la función que construye hitogramas en R se llama hist(). Tomemos el conjunto de datos heart.csv y constuyamos un histograma para la variable tabaco acumulativo.

corazon<-read.csv("heart.csv")
hist(corazon$tabaco,
     main="Histograma del tabaco acumulativo",
     xlab="tabaco acumulativo",
     col="deepskyblue")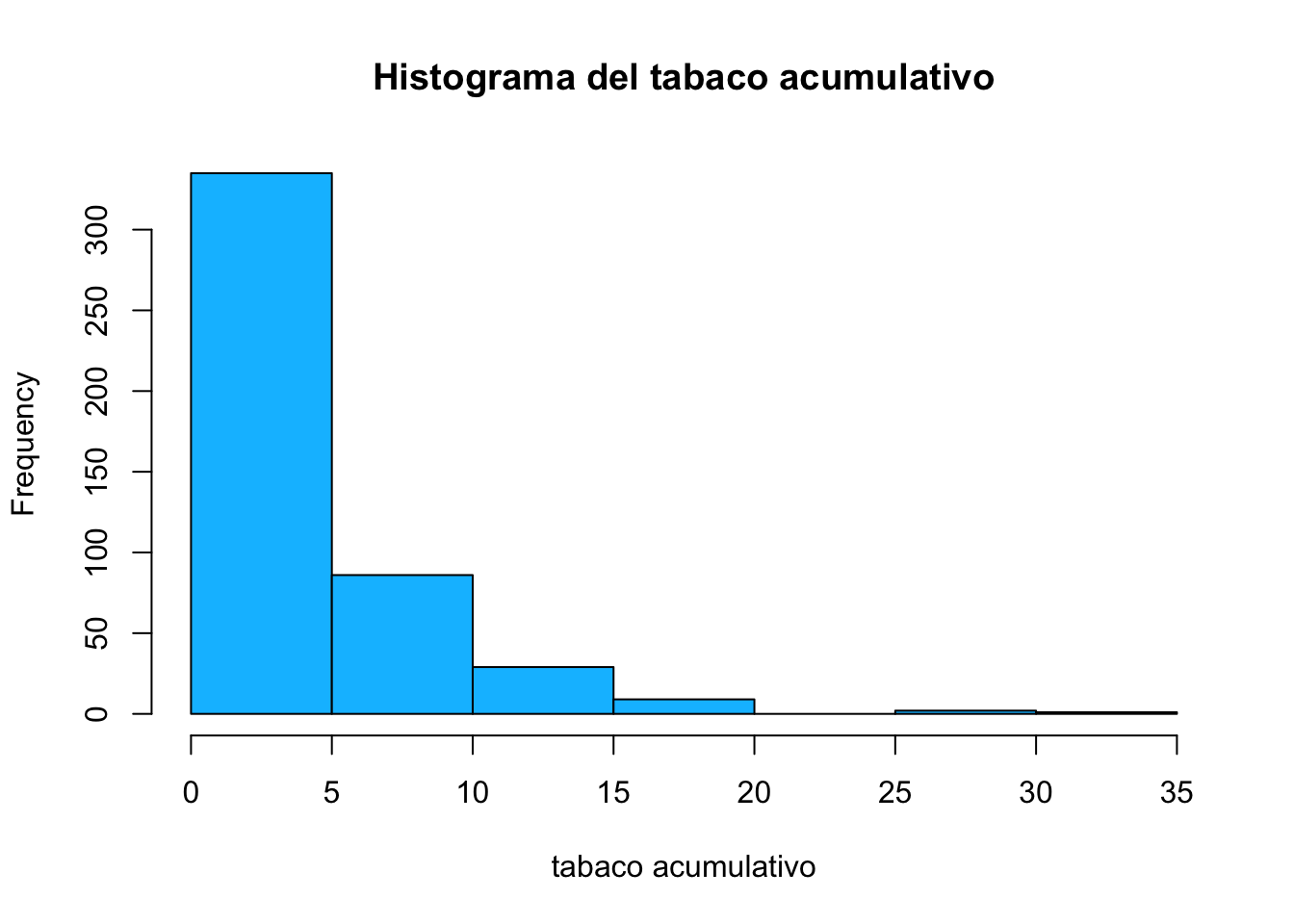

Con el parámetro breaks puedo indicar de distintas formas el número de barras posibles que lleve el histograma. Podemos indicarle un método (Struges, Scott,Freedman-Diaconis)

par(mfrow=c(1,2))
hist(corazon$tabaco, breaks  ="Scott",
     main="Histograma del tabaco acumulativo",
     xlab="tabaco acumulativo",
     col="deepskyblue")
hist(corazon$tabaco, breaks  ="FD",
     main="Histograma del tabaco acumulativo",
     xlab="tabaco acumulativo",
     col="deepskyblue")

par(mfrow=c(1,1))

Otra forma es indicando un vector que determine los puntos que limitan cada barra

breaks<-seq(from=min(corazon$tabaco), to=max(corazon$tabaco),
            length=5)
breaks
## [1]  0.0  7.8 15.6 23.4 31.2
hist(corazon$tabaco, breaks  = breaks,
     main="Histograma del tabaco acumulativo",
     xlab="tabaco acumulativo",
     col="deepskyblue")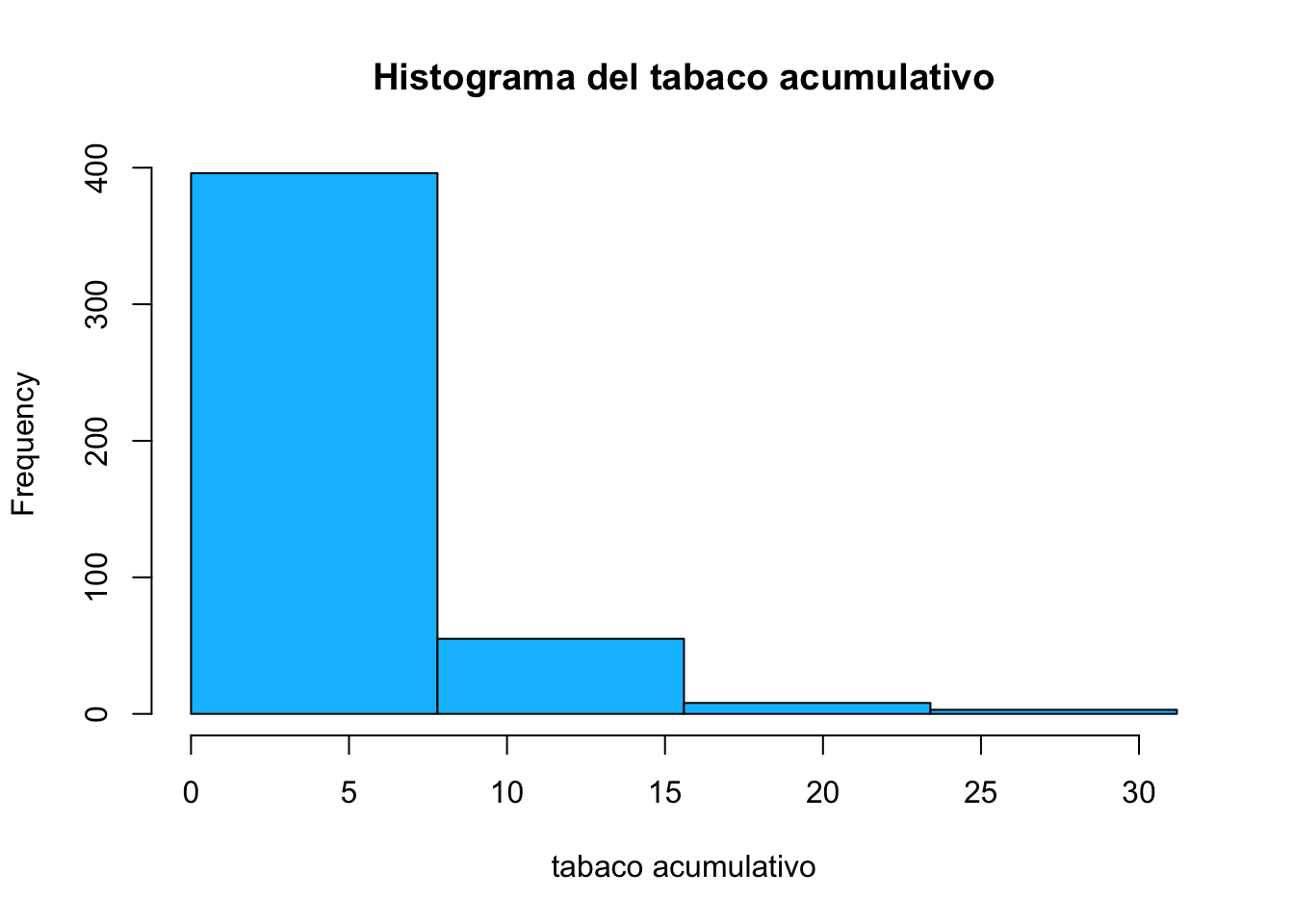

Exploremos la estructura de un objeto que me devuelve la función hist

histograma <- hist(corazon$tabaco,
     main="Histograma del tabaco acumulativo",
     xlab="tabaco acumulativo",
     col="deepskyblue")

str(histograma)
## List of 6
##  $ breaks  : num [1:8] 0 5 10 15 20 25 30 35
##  $ counts  : int [1:7] 335 86 29 9 0 2 1
##  $ density : num [1:7] 0.145 0.0372 0.0126 0.0039 0 ...
##  $ mids    : num [1:7] 2.5 7.5 12.5 17.5 22.5 27.5 32.5
##  $ xname   : chr "corazon$tabaco"
##  $ equidist: logi TRUE
##  - attr(*, "class")= chr "histogram"

Ahora como lo hacemos con ggplot

ggplot(corazon, aes(x=tabaco)) + geom_histogram(bins = 5,
                                                fill="deepskyblue",
                                                col="black")

Si los quremos colocar en un misma pantalla podemos usar la función grid.arrange() del paquete gridExtra

install.packages("gridExtra")
library(gridExtra)
grafico1 <- corazon %>%
  filter(famhist=="Ausente")%>%
  ggplot(aes(x=tabaco))+geom_histogram(bins=10,
                                       fill="darkolivegreen",
                                       col="black")

grafico2 <- corazon %>%
  filter(famhist=="Presente")%>%
  ggplot(aes(x=tabaco))+geom_histogram(bins=10,
                                       fill="chocolate",
                                       col="black")

grid.arrange(grafico1, grafico2, ncol=2)

Otra forma de explorar una variable continua es construyendo un gráfico estimado de su densidad, para estimar la densidad usarmos density() luego aplicamos plot() al objeto retornado por density().

densidad <- density(corazon$tabaco)
plot(densidad)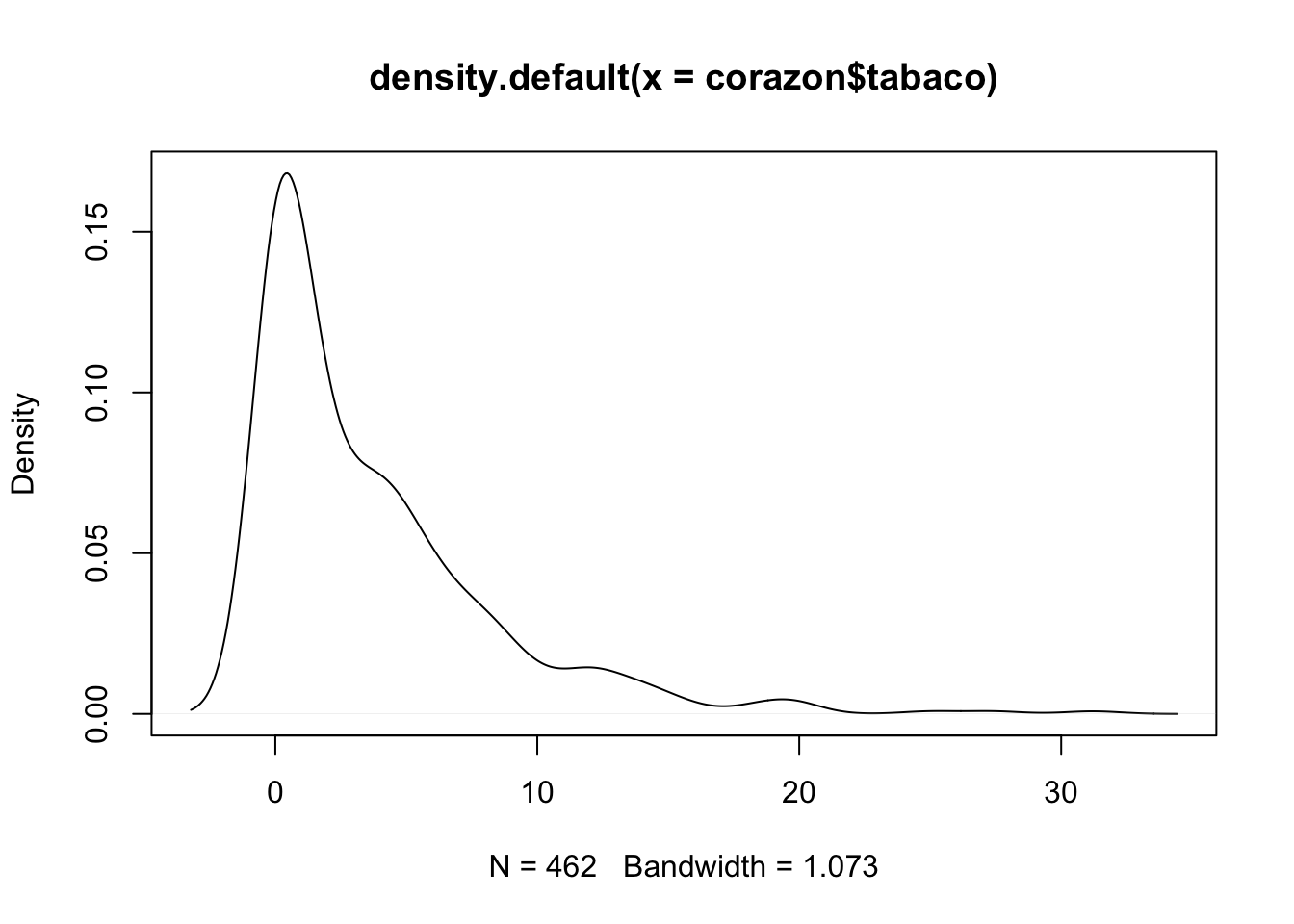

Podemos superponer este gráfico sobre el histograma usando lines en lugar de plot luego de hacer el histograma

hist(corazon$tabaco, breaks  ="Scott",freq = F,
     main="Histograma del tabaco acumulativo",
     xlab="tabaco acumulativo",
     col="deepskyblue")

lines(densidad, col="firebrick")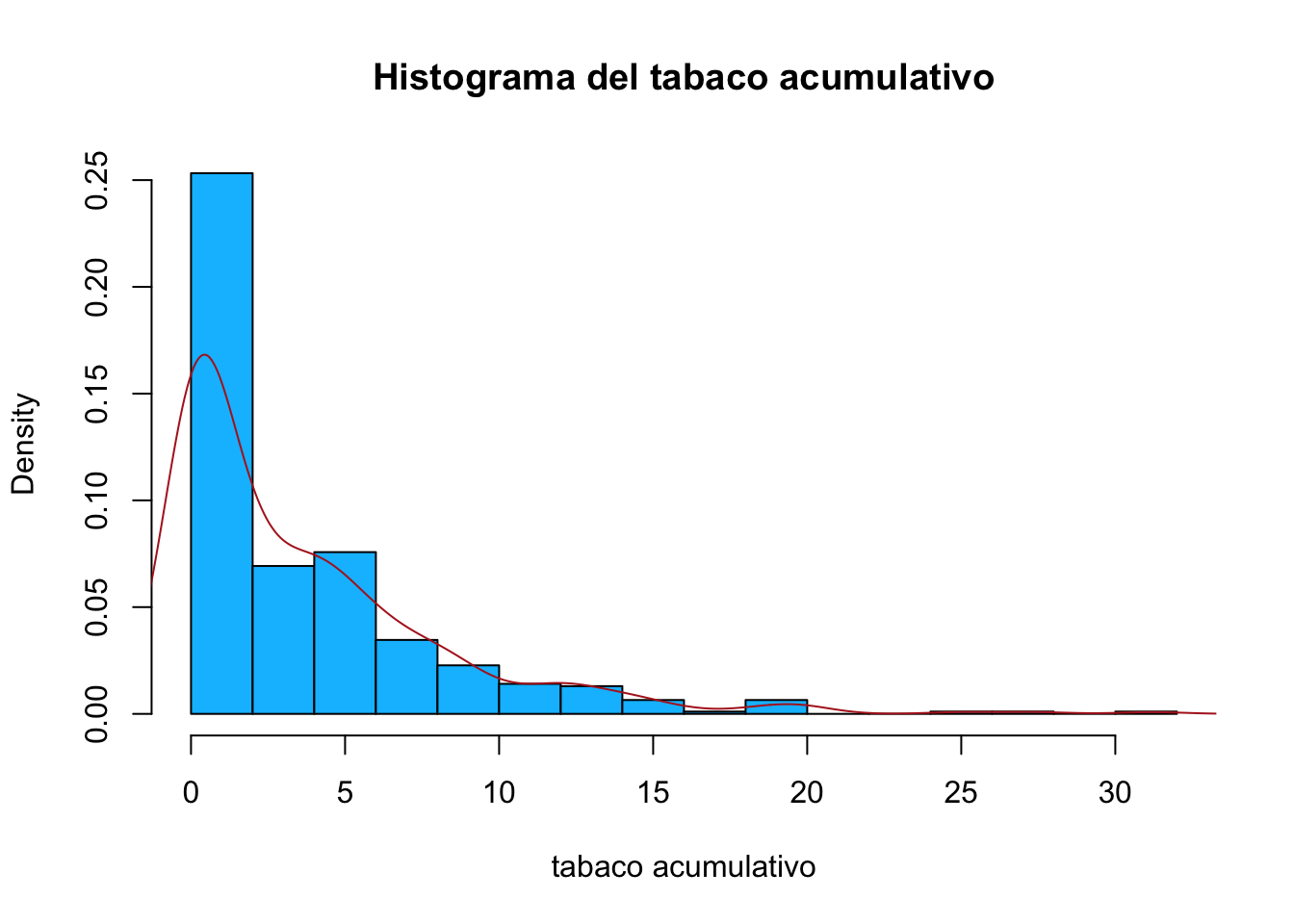

Otro gráfico que puede ser de nuestro interes son los diagramas de dispersión, es un grafico para dos variables continuas que me da información sobre la correlación que podrian tener estas variables.

Ejemplo: El archivo alturas_n_500.csv contiene una muestra de 500 personas donde se les registra su altura, la altura de su madre y la contextura de su madre, nos preguntamos si existe alguna relación entre la altura de una persona con la altura de su madre.

alturas<-read.csv("alturas_n_500.csv")

plot(alturas$altura_madre,alturas$altura)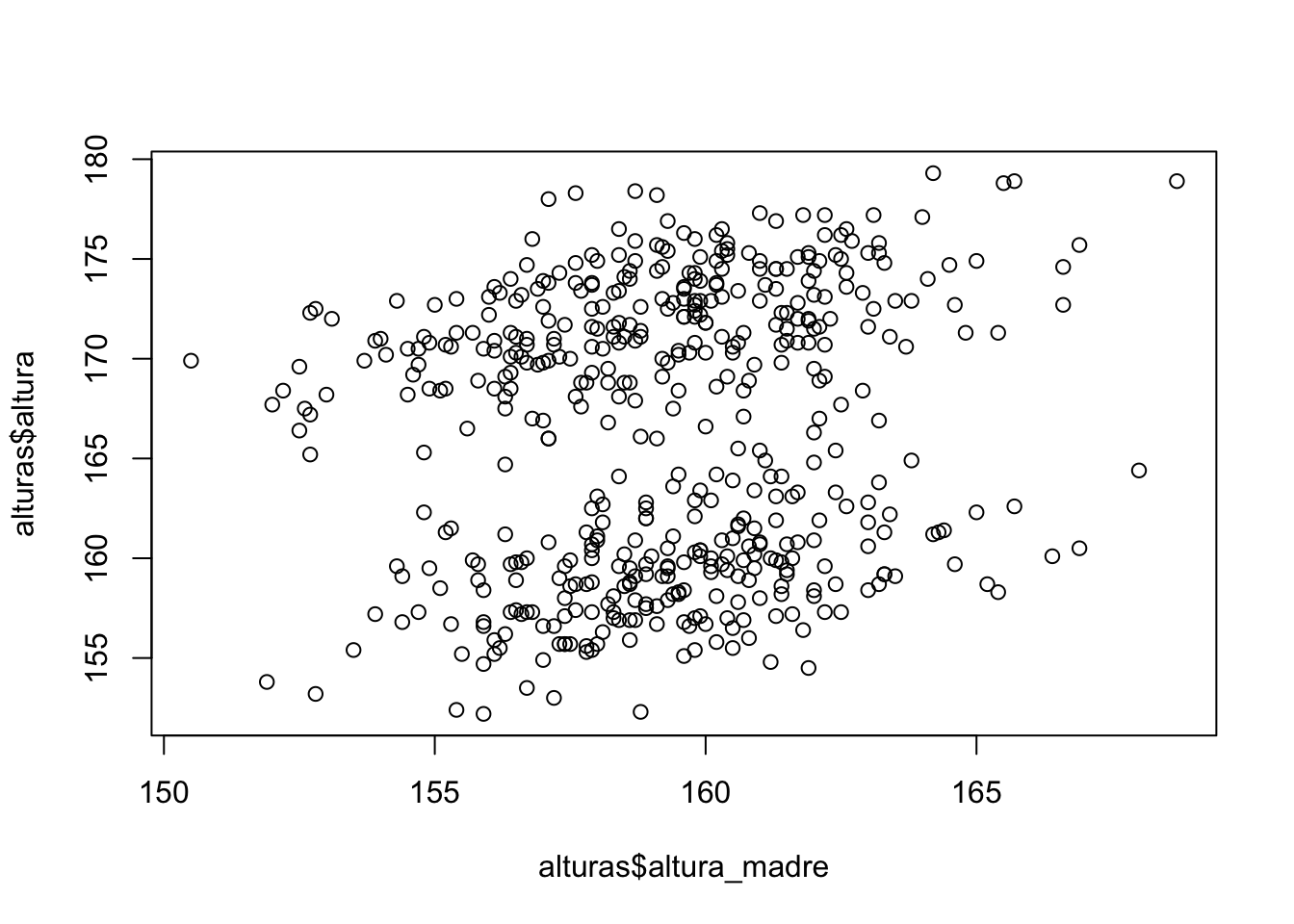

Podemos mejorar esteticamente este gráfico

plot(alturas$altura_madre,alturas$altura,
     xlab="altura de la madre", ylab="altura del hijo",
     pch=19,col="firebrick1")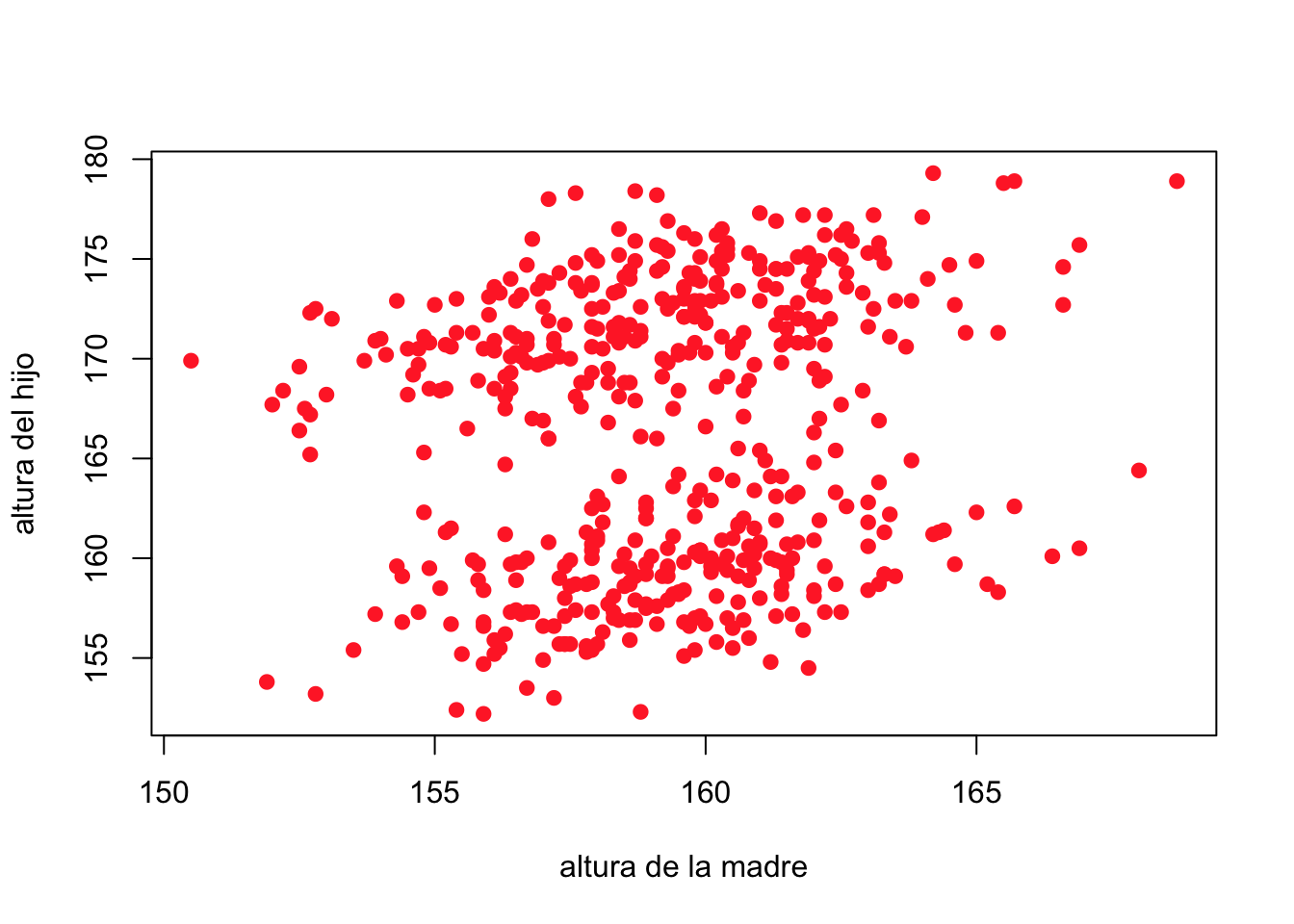

plot(alturas$altura_madre,alturas$altura,
     xlab="altura de la madre", ylab="altura del hijo",
     pch=19,col=as.factor(alturas$genero))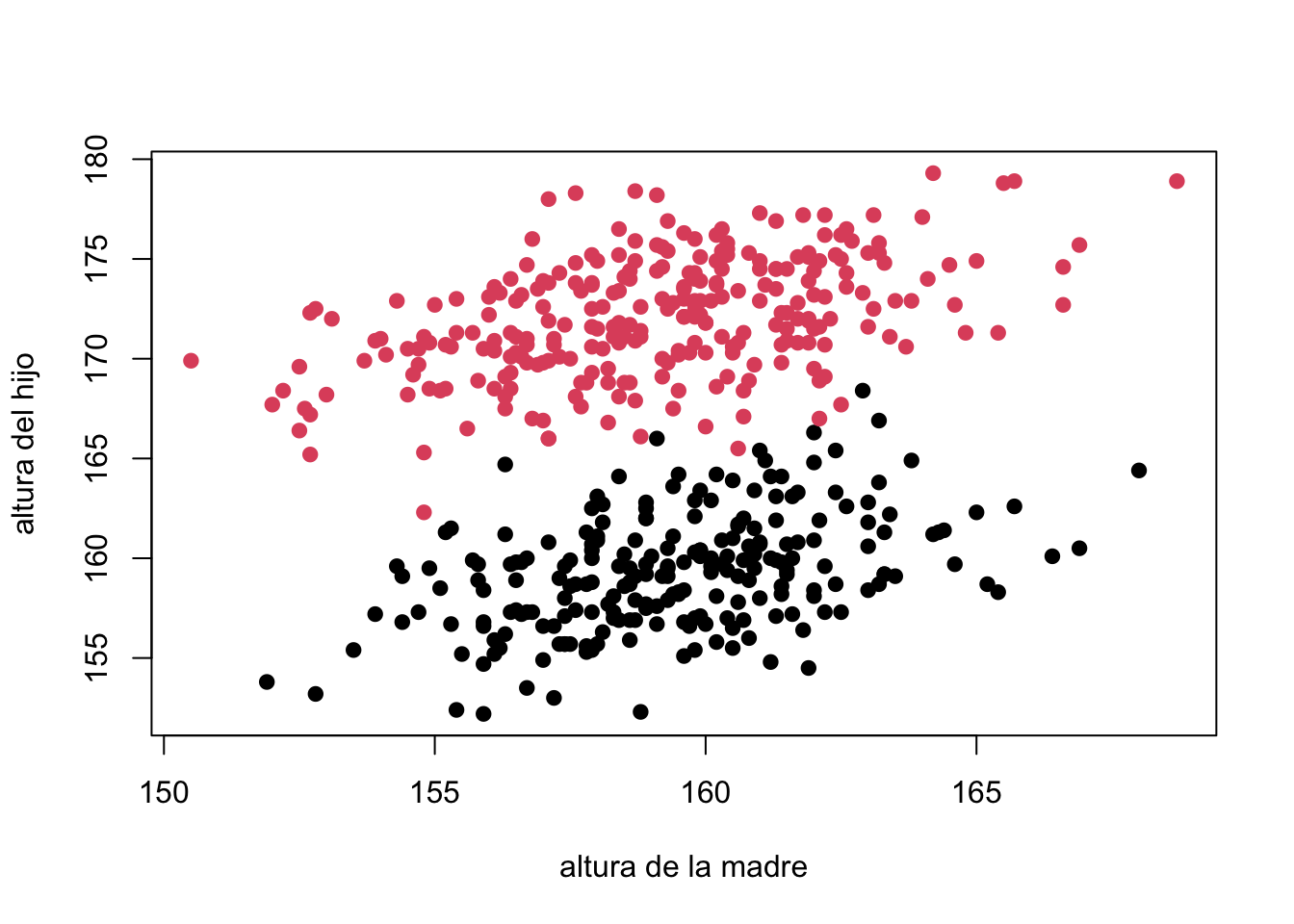

2.2 Ejercicios

  1. El data set rivers contiene la longitud en millas de 141 de los rios mas grandes de Norte America

    1. ¿Qué proporción de esos rios tiene una longitud menor a 500 millas?

    2. ¿Qué proporción son menores que el promedio?

    3. Encuentre el tercer cuartil

    4. ¿Qué valor de longitud deja el 20% de los rios a la izquierda?

    5. ¿Que se puede decir de la forma de la distribución de la longitud de los rios?, compare la media y la mediana.

    6. Construya un boxplot para los datos, que puede observar, explore las siguientes transformaciones y luego construya boxplot para la nueva data

      • \(log(x_i)\)
      • \(\frac{x_i-\bar{x}}{s}\)

2.(Entrega) Una empresa que elabora trampas para insectos se pregunta ¿ El color de nuestras trampas tendra algún efecto en la eficiencia de las mismas? para contestar esta pregunta colocan trampas de diferentes colores se dejan un tiempo y luego se regresa y cuenta la cantidad de insectos capturadas por trampa obteniendo los siguientes resultados

Color Cantidad de insectos capturados
Azul 16, 11, 20, 21, 14, 7
Verde 37, 32, 15, 25, 39, 41
Blanco 21, 12, 14, 17, 13, 17
Amarillo 45, 59, 48, 46, 38, 47

  1. Encuentre el promedio de insectos capturados por color de trampa

  2. Determine si realmente el color de la trampa tiene efecto en la eficiencia de estas, solo utilizando algún gráfico adecuado.

  1. Para evaluar el índice de alfabetización de cuatro municipios de un determinado departamento, se ha pasado un test a varios habitantes de cada uno de ellos con los siguientes resultados:
Pueblo 1 Pueblo 2 Pueblo 3 Pueblo 4
78 52 82 57
85 48 91 61
90 60 85 45
77 35 74 46
69 51 70
47

  1. Encuentre las calificaciones promedio de cada uno de los Pueblos

  2. Se requiere hacer una inversión para un programa de alfabetización, pero el presupuesto es limitado y solo ajusta para uno de los municipios, basandose en la dispersión de las calificaciones y en las estadísticas descriptivas ¿Cuál pueblo elegiria para aplicar el programa?

  1. El data frame nym.2002 del paquete UsingR contiene una muestra aleatoria simple del 1000 finalistas del maraton de New York del año 2002. Las variables son:

  • place Lugar en la carrera

  • gender Género del corredor

  • age Edad en dias del corredor

  • home indicador de ciudad de origen o nacionalidad

  • time Tiempo en minutos para terminar la carrera

    1. Calcule la media y la varianza del tiempo para terminar la carrera por género del corredor.

  1. Almacene en una variable la media y la varianza del tiempo para terminar la carrera por el género del corredor, use estas variables para calcular el coeficiente de variación \(CV=\frac{s}{\bar{x}}\)

  2. la variable place indica el lugar en el que terminó el corredor, Usando esta información ¿A quienes les fue mejor en la carrera hombres o mujeres?

  3. ¿Qué porcentaje terminaron la carrera en menos de 3 horas?

  1. (Entrega) El archivo syc.csv contiene algunas variables seleccionadas de la encuensta de jovenes en custodia Fuente: Consorcio Interuniversitario de Investigación Política y Social, NCJ-130915 (Departamento de Justicia de EE. UU., 1989). entre las variables que se encuentra en el archivo estan:

  • age: Edad del residente

  • ``race```: Raza del residente (1: Blanco, 2: Negro, 3: Asiatico, 4: Indio americano, aleuta o esquimal, 5: Otra, 9: Valor perdido)

  • ethnicty: Etnia del residente (1: Hispano, 0: No hispano, 9:Valor perdido)

  • sex: Sexo del residente

  • initwt: Peso inicial del residente

  • finalwt: Peso final del residente

    1. Lea los datos considerando los caracteres que indican valores perdidos

    2. Construya un gráfico circular donde se indique la cantidad de residentes por su Etnia

    3. Construya un gráfico de barra donde se indique la raza del residente

    4. Construya un gráfico de barra comparativa donde se indique los residentes por su raza y sexo.

  1. (Entrega) Considere el archivo alturas_n_500.csv

    1. Construya histogramas para la variable altura por sexo de cada hijo, sobre el mismo eje.

    2. Use ggplot() para graficar un boxplot de la variable altura

  2. Considere el conjunto de datos iris, elabore los siguientes gráficos usando ggplot

    1. Construya boxplots para la variable Sepal.Length (Longitud del sepalo) separados por Species (Especie de la flor).

    2. Grafique la densidad para la variable Sepal.Length para cada una de las especies, en el mismo gráfico.

    3. Coloque los gráficos de a y b uno al lado del otro.

    4. Grafique los valores de la variable Sepal.Length contra los valores de la variable Petal.Length, identifique con un color diferente los puntos para cada especie.

    5. Construya un gráfico de barra para cada especie.

  3. Considere la función \[\rho_k(x)= \left\{ \begin{array}{lcc} x^2 & si & \vert x\vert \leq k \\ \\ 2k\vert x\vert-k^2 & si & \vert x\vert> k \end{array} \right.\] Queremos gráficar esta función en el intervalo cerrado de -10 a 10

    1. Genere una secuencia de valores de -10 hasta 10 con saltos de 0.01, guarde su secuencia en el vector x.

    2. Calcule en un vector y los valores de la función \(\rho_k(x)\) para \(k=5\)

    3. Use la función plot() para graficar \(\rho_k(x)\).

  4. Siga los pasos del ejercicio anterior para gráficar la función \[f(x)= \left\{ \begin{array}{lcc} x+1 & si & x \leq 1 \\ \\ x^2-2x & si & x> 1 \end{array} \right.\] En el intervalo de -4 a 4.