A Mathematical conversions of quantities and units, scientific notation
A.1 Quantities, Units, and Dimensions
International System of Units (SI units) are used so basic and derived quantities are standardized and defined in terms of grams, meters, and seconds. Common SI units include:
- Mass (M): kg
- Length (L): m
- Time (t): s
- Temperature (T): K
Basic quantities can be derived into more complex quantities, dimensions, and units. For example, Area (L2): m2 and Volume (L3): m3.
A.2 Scientific Notation
Scientific notation: a way of writing very large or small numbers; written in standard decimal notation with power of 10. It is used as follows:
where:
- \(N\) = number between 1 and 10
- \(n\) = exponent that is a positive or negative integer (whole number).
There are specific rules that accompany the use of scientific notation:
- Anything raised to the zero power is 1:
2.Power rule; to raise a power to a power you need to multiply the exponents:
- A negative exponent indicates the inverse of a value:
- When multiplying, add the exponents:
- When dividing, subtract the exponents:
Example:
Area of the Earth = 510,100,000 km2. In scientific notation = 5.101 × 108 km2 Scientific notation should be used to SIMPLIFY really big or really small numbers. How big or small? Rule of thumb: 0.01 > # > 10 000
A.3 Prefixes of SI Units
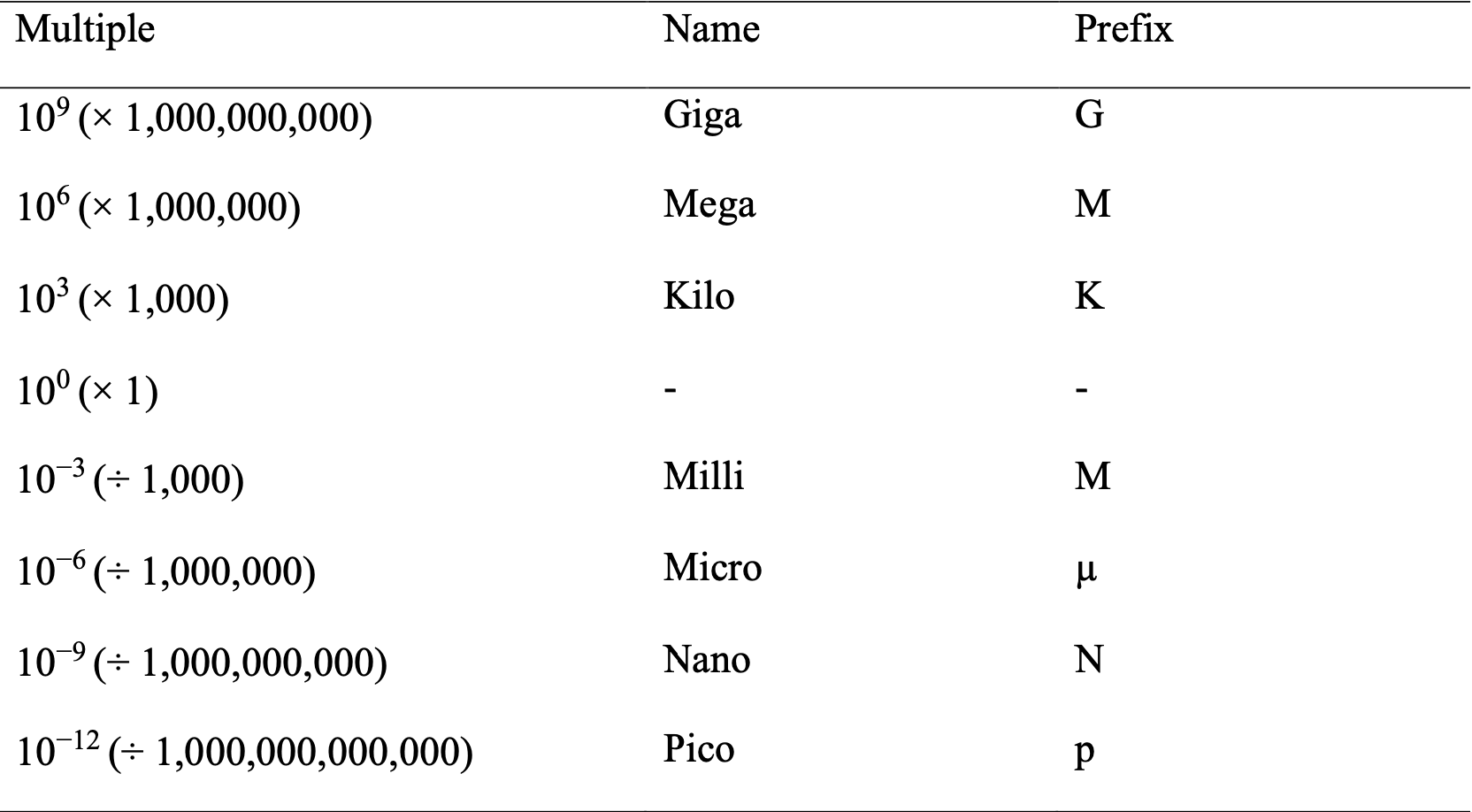
A.4 Precision and Accuracy
Accuracy: how close the measurement is to the true/real value.
Precision: a measure of how closely individual measurements are to one another. For example, constantly getting the same value is considered very precise.
A.5 Significant Figures
Definition: all digits of a measured quantity, including the uncertain ones, are related to precision–the measurement is limited by the least precise measuring instrument. What do we mean by “uncertain”?
- You measure the weight of a dime to be 2.2405 ± 0.0001 g
- The notation (±) expresses the magnitude of uncertainty of your measurement
- Uncertainty is okay because there will always be some uncertainty in the last digit reported for any measured quantity. Precision of quantitative data is expressed through the use of significant figures, defined by the following rules:
- The leftmost non-zero digits is the most significant figure:
- 25.3 cm
- 5200.021 km
- 0.0669 m
- 561,000 kg
- 0.0052 g
- 0.0001162 m2
- When not followed by a decimal point, the rightmost non-zero digit is the least significant figure. However, if there is a decimal point, the rightmost figure is the least significant figure, even if it is a zero:
- 1508 kg
- 9500 g
- 0.000568 m
- 0.0030 cm
- All figures between the least and most significant figures are also counted as significant figures:
- 6.5980 cm (5 significant digits)
- 521,000.00 m (8 significant digits)
- 0.00998 g (3 significant digits)
- 665,000 kg (3 significant digits)
- 1300 m2 (2 significant digits)
- Figures before the power of 10 (scientific notation) are significant:
- 9.3 × 105 km2 (2 significant figures)
A.5.1 Significant Figures for Zeros
Any non-zero figure is significant. 8339832
Zeros between non-zero figures are significant. 1005
Zeros to the left of the first non-zero figure are NOT significant. Their purpose is to indicate the placement of the decimal point. 0.02 (one significant figure)
For numbers that do not contain decimal points, the zeros after the last non-zero number may or may not be significant, we cannot know without more information. By using scientific notation, however, we can avoid this ambiguity (usually we assume the minimum number of significant figures). 3,240,000 most likely only has 3 significant figures.
If a number is greater than 1, then all zeros written to the right of the decimal point count as significant figures. If a number is less than 1, then only the zeros that are at the end of the number and the zeros between the non-zero figures are significant. 89939.0000 or 0.438000219
A.5.2 Adding and Subtracting
The result has the same number of decimal places as the measurement with the fewest decimal places: 0.39 + 0.0039 = 0.39, not 0.3939
With whole numbers, consider the number of significant digits in the largest value: 3900 + 0.39 = 3900, since 3900 contains no decimals (so has the fewest). 400 − 1 = 400 (not 399, since 400 has one significant digit). With the whole number subtraction issue, be mindful of the number with the fewest number of significant digits. To make this clear, imagine a situation where you are measuring 400cm using a stick that could only measure in 1m denominations (it’s a bad measuring stick). You then have another measurement using something that could get down to cm and measure have a measurement of 1cm. If you then calculated 400 cm (using bad stick) – 1 cm (using better implement), can you really say you have 399cm? There is uncertainty based on the fact that the 400 cm was only good to one digit.
Multiplying and Dividing: The result contains the same number of significant figures as the measurement with the fewest significant figures. 41 × 2.13 = 87.33 = 87 (since 41 has two significant digits; 5963 ÷ 39 = 150 (rounded down from 152.8).
Exact/constant numbers (e.g. conversion values) are considered to have an infinity number of significant figures–meaning that constants do not factor into your significant digits.
A.5.3 Carrying Over an Extra Digit
When completing multiple calculation steps, carry over one extra digit in your intermediate calculations but exclude it from the final answer.
The extra precaution will help you to avoid rounding errors.
A.5.4 Rounding Off
Rule: look at the leftmost figure to be removed:
If the leftmost figure removed is less than 5, the preceding number is not changed. 7.248 rounded to two significant figures is 7.2.
If the leftmost figure removed is 5 or greater, the preceding number is increased by 1. 4.735 rounded to three significant figures is 4.74.