3 La régression linéaire simple

3.1 Introduction

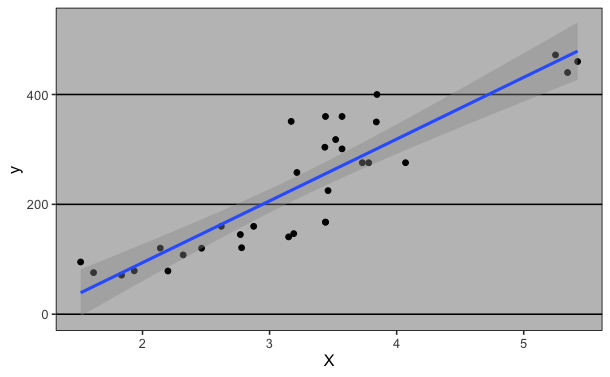Console La régression linéaire simple est une méthode statistique permettant de trouver une relation linéaire entre une variable explicative $X$ et une variable à expliquer $y$. Ce modèle consiste à considérer $y$ comme une fonction affine de $X$. En d’autre terme, la régression linéaire a pour but de trouver une droite ajustée au nuage de points de $y$ en fonction de $X$.
Dans ce chapitres nous allons voir en détail le modèle linéaire simple ainsi que son application avec R. Nous utiliserons les données de income disponible sur github. Vous pouvez télécharger le jeux de données avec la fonction read_csv() disponible dans le package readr comme suit :

library(readr)
income = read_csv("https://github.com/AODiakite/r4econometrics/blob/master/Data/income.data.csv")

Table 3.1: Données pour la régression linéaire simple : income( niveau de revenu par 10 000 dollars ), happiness(score du bonheur entre 0 et 10), nombre d’observations(498)
income	happiness
3.862647	2.314489
4.979381	3.433490
4.923957	4.599373
3.214372	2.791114
7.196409	5.596398
3.729643	2.458556
4.674517	3.192992
4.498104	1.907137
3.121631	2.942450
4.639914	3.737942

3.2 Modélisation mathématique

L’ajustement affine de $y$ par $X$ stipule que $y$ peut s’écrire comme équation d’une droite :

\[\begin{equation} y = \beta_0 + \beta_1 X \tag{3.1} \end{equation}\]

$y(y_1,y_2,\dots,y_n)$ : variable à expliquer, variable dépendante, variable endogène, variable réponse
$X(x_1,x_2,\dots,x_n)$ : variable explicative,variable exogène, Variable régresseur
$\beta_0$ : l’ordonnée à l’origine, coefficient inconnu
$\beta_1$ : la pente de la droite, coefficient inconnu

En réalité sauf dans le cas d’un modèle parfait, la liaison linéaire (3.1) entre y et X est perturbée par un bruit $\epsilon$. l’équation du modèle devient alors :

\[\begin{equation} y = \beta_0 + \beta_1 X +\epsilon \tag{3.2} \end{equation}\]

La variable aléatoire $\epsilon$ est indépendante de $X$ et est supposée suivre une loi normale de moyenne $0$ et d’écart type $\sigma$ :

\[ (\epsilon_1,\epsilon_2,\dots,\epsilon_n)= \epsilon \sim \mathcal{N}(0,\,\sigma^{2})\]

Pour le jeu de données income nous allons prendre comme variable exogène $X$ les revenus des individus(income) et le niveau de bonheur(happiness) comme variable endogène $y$. Ce choix n’est pas hasardeux, car dans la régression linéaire, la variable indépendante doit être déterministe c’est à un dire ne comportant pas de caractère aléatoire alors que la variable dépendante comporte quant à elle un bruit aléatoire $\epsilon$.
Du fait que la moyenne de $\epsilon$ soit nulle, l’équation (3.2) revient juste à une estimation d’une moyenne conditionnelle :

\[\begin{equation} \mathbb{E}(y_i|X_i) = \beta_0 + \beta_1 X_i \tag{3.3} \end{equation}\]

La première étape lors d’une régression linéaire c’est la représentation graphique du nuage de points. En effet si le nuage ne s’apparente pas à une droite, la régression linéaire ne sera pas le meilleur modèle pour notre jeu de données. Dans cet ouvrage nous utiliserons le package ggplot2³ pour nos représentations graphiques.

library(ggplot2) #Chargement du package
fig1 = ggplot(data = income,aes(x =income, y = happiness)) +
               geom_point()
fig1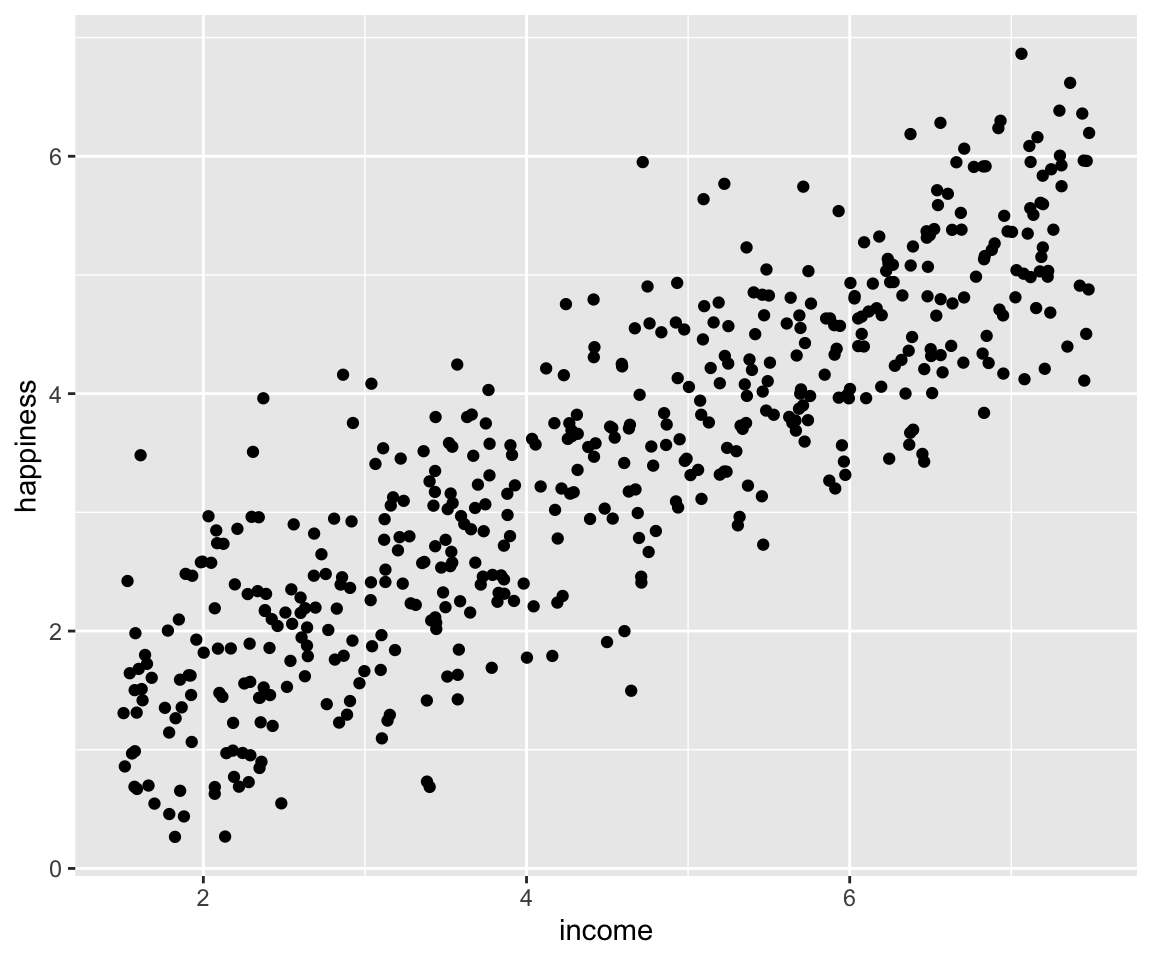

Figure 3.1: A première vue, ce nuage admet bien une tendance linéaire.

3.3 Estimateurs des moindres carrés ordinaires ($MCO$)

La problématique du modèle(3.2), c’est de trouver les coefficients $\beta_i$ qui donnent un meilleur ajustement linéaire de $y$. Pour cela on a recours aux estimateurs des moindres carrés. Cette méthode consiste à trouver les coefficients qui minimise la quantité :

\[\begin{equation} (\beta_0,\beta_1) = \sum\limits^{n}_{i=1}(y_i -\beta_0-\beta_1 x_i)^2=\sum\limits^{n}_{i=1}\epsilon_i^2 \tag{3.4} \end{equation}\]

Les estimateurs $\hat{\beta}_i$ s’écrivent donc de la forme :

\[(\hat\beta_0,\hat\beta_1) =\operatorname*{argmin}_{(\beta_0,\beta_1)\in \mathbb{R}\times\mathbb{R}}S(\beta_0,\beta_1)\]

La fonction $S$ est strictement convexe donc si elle admet un point singulier, celui-ci correspondra à l’unique minimum. Les estimateurs des moindres carrés sont obtenus en résolvant le système d’équation qui annule les dérivées partielles de $S$ aux points $\beta_i$. Le résultat de ce système est :

\[\hat{\beta}_1 = \frac{\sum(x_i – \bar{x}) (y_i – \bar{y})} {\sum(x_i – \bar{x})^2} = \frac{Cov(X,y)}{Var(X)}\] \[\hat{\beta}_0 = \bar{y} – \hat{\beta}_1 \bar{x}\] \[avec\; :\; \bar{y} = \frac{1}{n}\sum\limits_{i=1}^n y_i\; et\; \bar{x} = \frac{1}{n}\sum\limits_{i=1}^n x_i \]

La fonction lm() permet d’entrainer un modèle linéaire sur R. Dans notre exemple, on procède ainsi :

lm_simple <- lm(formula = happiness~income, data = income)

summary(lm_simple)
#> 
#> Call:
#> lm(formula = happiness ~ income, data = income)
#> 
#> Residuals:
#>      Min       1Q   Median       3Q      Max 
#> -2.02479 -0.48526  0.04078  0.45898  2.37805 
#> 
#> Coefficients:
#>             Estimate Std. Error t value Pr(>|t|)    
#> (Intercept)  0.20427    0.08884   2.299   0.0219 *  
#> income       0.71383    0.01854  38.505   <2e-16 ***
#> ---
#> Signif. codes:  
#> 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
#> 
#> Residual standard error: 0.7181 on 496 degrees of freedom
#> Multiple R-squared:  0.7493, Adjusted R-squared:  0.7488 
#> F-statistic:  1483 on 1 and 496 DF,  p-value: < 2.2e-16

La sortie précédente indique une matrice (Coefficients) de 5 colonnes.

Estimate : les estimations des paramètres. Dans notre exemple, $\beta_0 = 0.20427$ et $\beta_1 = 0.71383$.
Std. Error : les écarts-types estimés des coefficients.
t value : La valeur observée de la statistique de test d’hypothèses $\begin{cases} H_0: \beta_i = 0 \\ H_1: \beta_i \neq 0 \end{cases}$
Pr(>|t|) : la probabilité critique (ou « p-value ») qui est la probabilité, pour la statistique de test sous $H_0$, de dépasser la valeur estimée.
La dernière colonne est une indication sur le résultat des tests. Si elle est vide cela signifie qu’on ne peut pas rejeter l’hypothèse $H_0$. Par contre si elle n’est pas vide ce qu’on rejette l’hypothèse $H_0$ au seuil significatif correspondant au symbole (***: 0.001, **: 0.01, *: 0.05, .: 0.1)

Les « p-value » de notre exemple sont toutes inferieures à $\alpha = 5\%$, on peut donc rejeter l’hypothèse nulle pour un niveau de confiance de $95\%$.
En plus des informations sur les coefficients, la sortie de la fonction summary modèle renseigne aussi sur :

Residual standard error : l’estimation de $\sigma$ de $\epsilon$ qui vaut $0.7181$
Degrees of freedom : le nombre de degré de liberté associe ($n-2 = 496$)

3.4 Le coefficient de détermination ($R^2$)

La qualité d’un modèle dépend de combien les $\hat{y}_i$ estimés sont proches des $y$ observés. Le coefficient de détermination est la quantité :

\[R^2 = \frac{SCT}{SCE}\] avec :
\[ \underbrace{\sum\limits_{i=1}^{n}(y_{i}-\overline{y})^2}_{SCT}=\underbrace{\sum\limits_{i=1}^{n}(\hat{y}_{i}-\overline{y})^2}_{SCE}+\underbrace{\sum\limits_{j=1}^n (y_i-\hat{y_i})^2}_{SCR} \]

où $SCT$(somme des carrés totaux), $SCR$( somme des carrés résiduels) et $SCE$(somme des carrés expliqués).

Ce coefficient correspond à Multiple R-squared dans la sortie de la fonction summary(lm_simple).
La qualité du modèle dépend donc de combien $R^2$ est proche de $1$. Plus $R^2$ est proche de $1$ plus notre modèle est bon.
Dans notre exemple le coefficient de détermination est de $0.7493$. Sachant qu’un bon coefficient est de l’ordre de $0.85$, le nôtre est assez faible dans ce cas.

3.5 Représentations graphiques

3.5.1 La droite de régression

Avec ggplot2, il est très simple de représenter la droite de régression avec la fonction geom_smooth(). Nous allons l’ajouter à notre objet fig1 3.1 en spécifiant la methode = "lm".

fig1 = ggplot(data = income,aes(x =income, y = happiness)) +
               geom_point() + geom_smooth(method = "lm")
fig1
#> `geom_smooth()` using formula = 'y ~ x'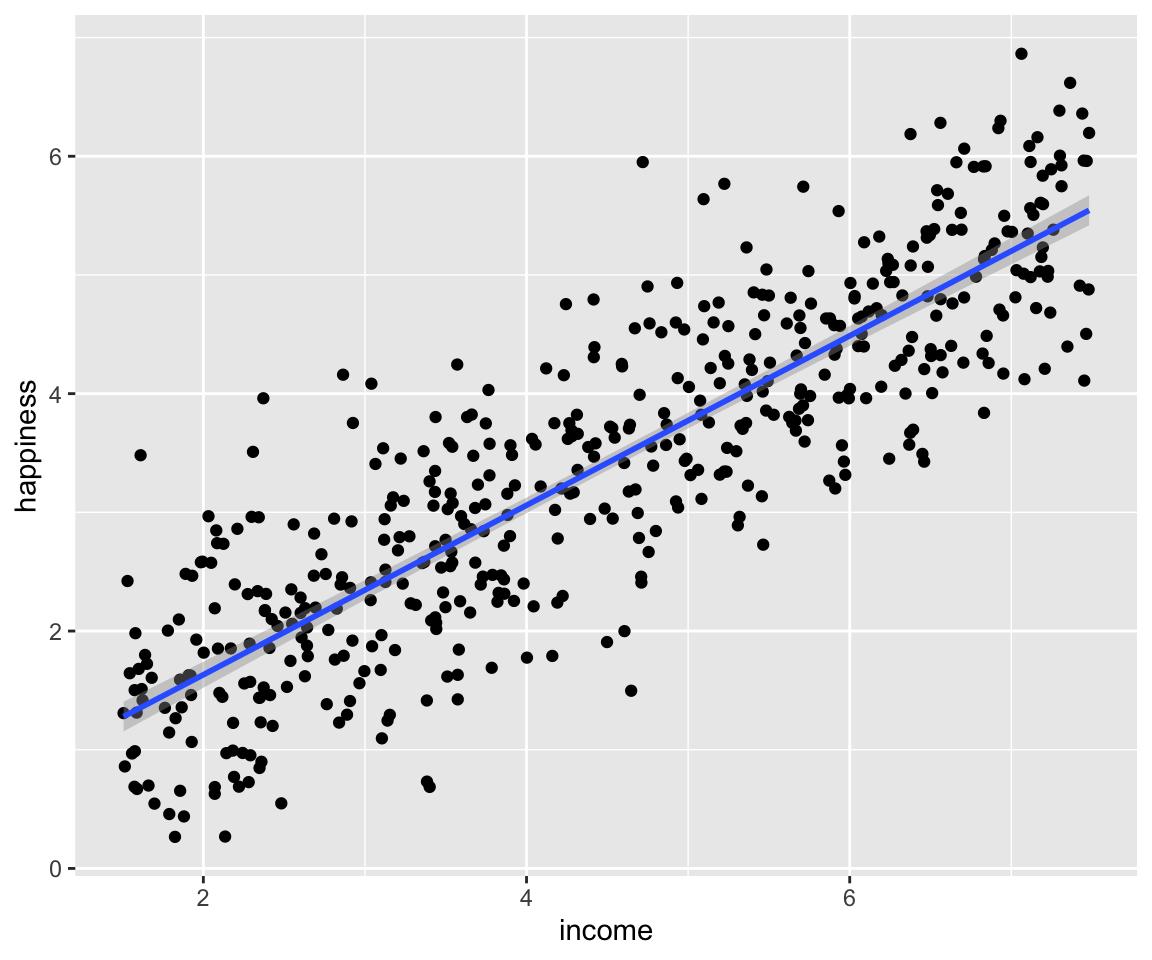

Figure 3.2: La droite de régression

3.5.2 Graphes des résidus

On peut visualiser les résidus $\hat\epsilon_i = y_i -\hat y_i$ afin de voir leur dispersion autour de la moyenne $0$. Les résidus peuvent être obtenu dans le modèle entrainé lm_simple, on y accède par $residuals.

X = income$income
residuals_ = lm_simple$residuals
ggplot(data = NULL) + geom_point(aes(x = X,y =residuals_)) +
  geom_abline(slope = 0, intercept = 0, color = 'red',size = 1)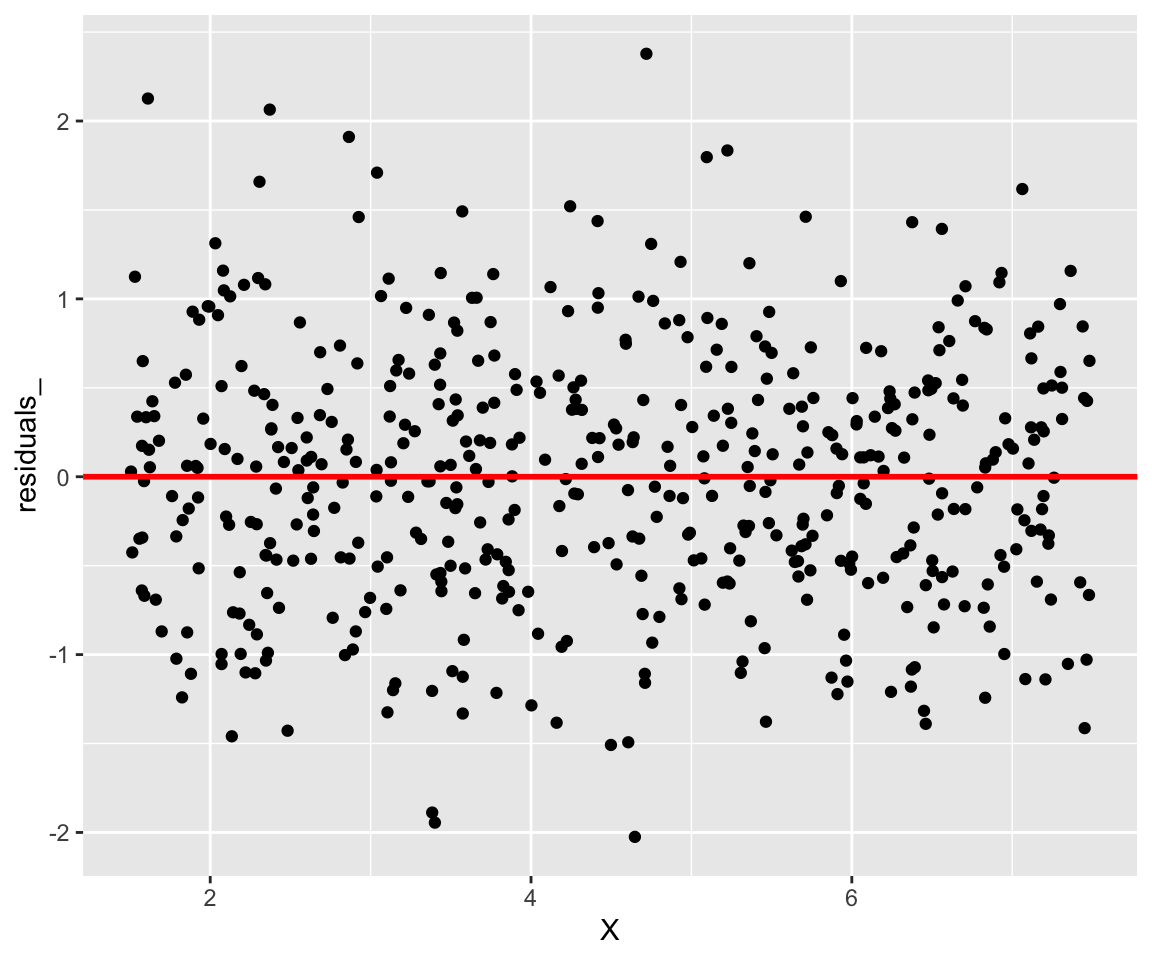

Figure 3.3: On voit bien que nos résidus se disperse de part et d’autre de 0

On peut aussi ajouter des sagements dans la figure 3.2 pour visualiser les résidus. Nous allons choisir juste un échantillon de 50 observations.

# Les indices choisis au hasard
echantillon = sample(1:498)[1:50]
# Echantillon des revenu
X_residuals = X[echantillon]
# echention du niveau de bonheur
y = income$happiness[echantillon]
# les y estimes correspondants a l'echantillon
y_hat = lm_simple$fitted.values[echantillon]

# Representation de l'echantillon 
ggplot()+ 
  # nuage de points
  geom_point(data = income,aes(x =income, y = happiness),alpha =0.4) +
  # droite de regression
  geom_smooth(data = income,aes(x =income, y = happiness), method = 'lm') +
  # echantillon de y
  geom_point(aes( x= X_residuals, y = y), color ='red', size = 2,) +
  #les erreurs
  geom_segment(aes(x = X_residuals, y = y_hat, xend = X_residuals, yend = y),color = 'red')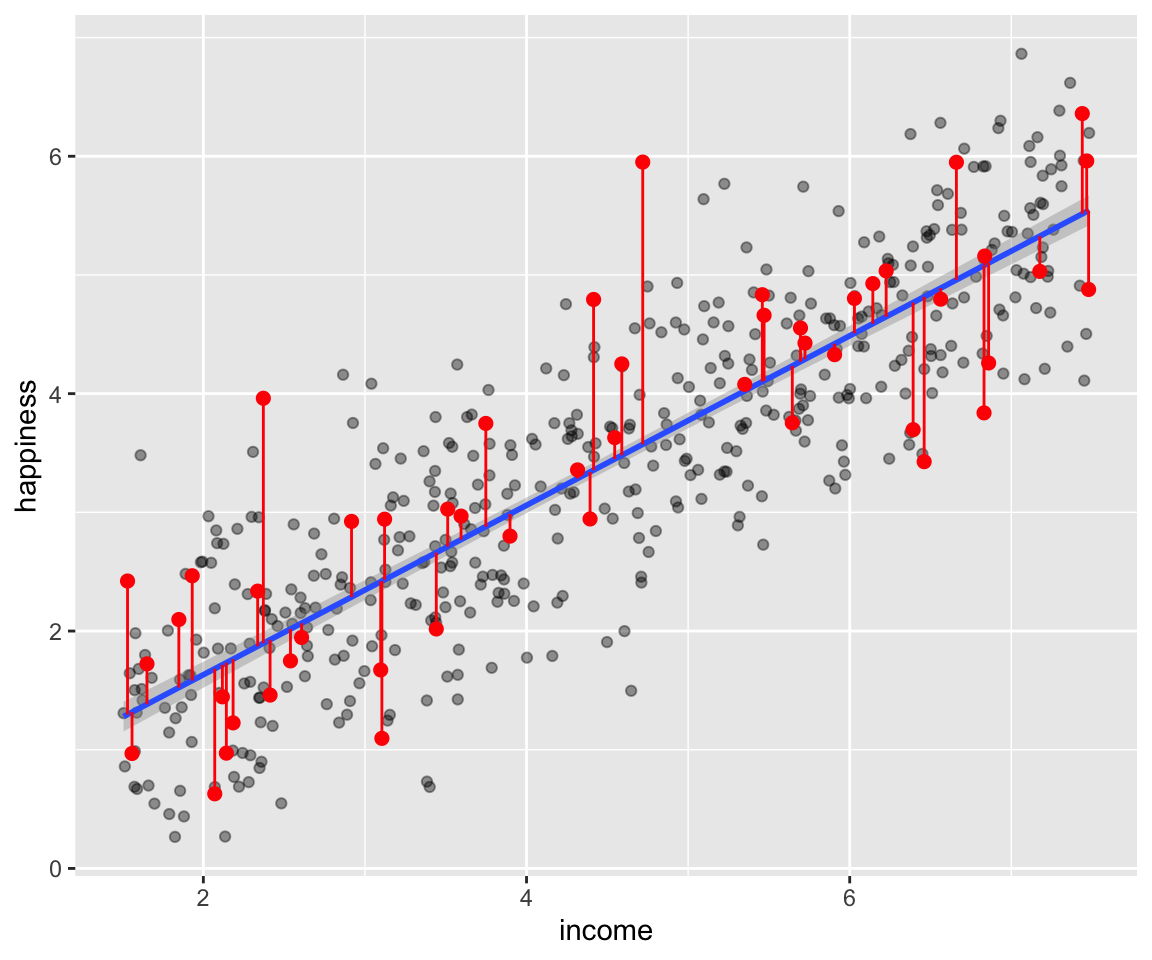

Figure 3.4: Les segments en rouges repressentent l’écart entre les valeurs estimées et les valeurs mesurées du niveau de bonheur (happiness)

3.6 Prédiction

Le but final d’une régression c’est de prédire des variables à expliquées sans avoir à faire des mesures. Pour une nouvelle valeur de $X$ nous cherchons quel serait le $y$ à partir de notre modèle. Cette prédiction peut se faire sur R avec la fonction predict().
On va reprendre notre modèle lm_simple sauf que cette fois-ci, nous n’allons pas entrainer un échantillon de $100$ observations qui représentent $20\%$ de notre jeu de données income.

set.seed(1234) # pour fixer une racine a la fonction sample
echantillon = sample(1:498)[1:100] # indices de nos echantillons
data_train = income[-echantillon,] # data a entrainer
data_test = income[echantillon,] # data non entrainé
lm_simple = lm(data = data_train, formula = happiness~income) # entrainement du modele

# prediction des y correspondants a notre echantillon de X
y_predict = predict(object = lm_simple, newdata = data_test[,1])
y_predict[1:10] # Affichage des 10 premiers elements 
#>        1        2        3        4        5        6 
#> 1.577312 5.114610 4.689354 4.817752 1.968143 1.504369 
#>        7        8        9       10 
#> 1.324728 3.422421 4.913247 3.493572

On peut visualiser la qualité de notre prédiction en représentant en abscisse les y_test et en ordonnée les y_predict. Pour un modèle parfait, le nuage de point doit être sur la première bissectrice⁴.

y_test = data_test$happiness
ggplot() +
  geom_point(aes(x = y_test, y = y_predict)) +
  geom_abline(slope = 1, color ='darkred')  # première bissectrice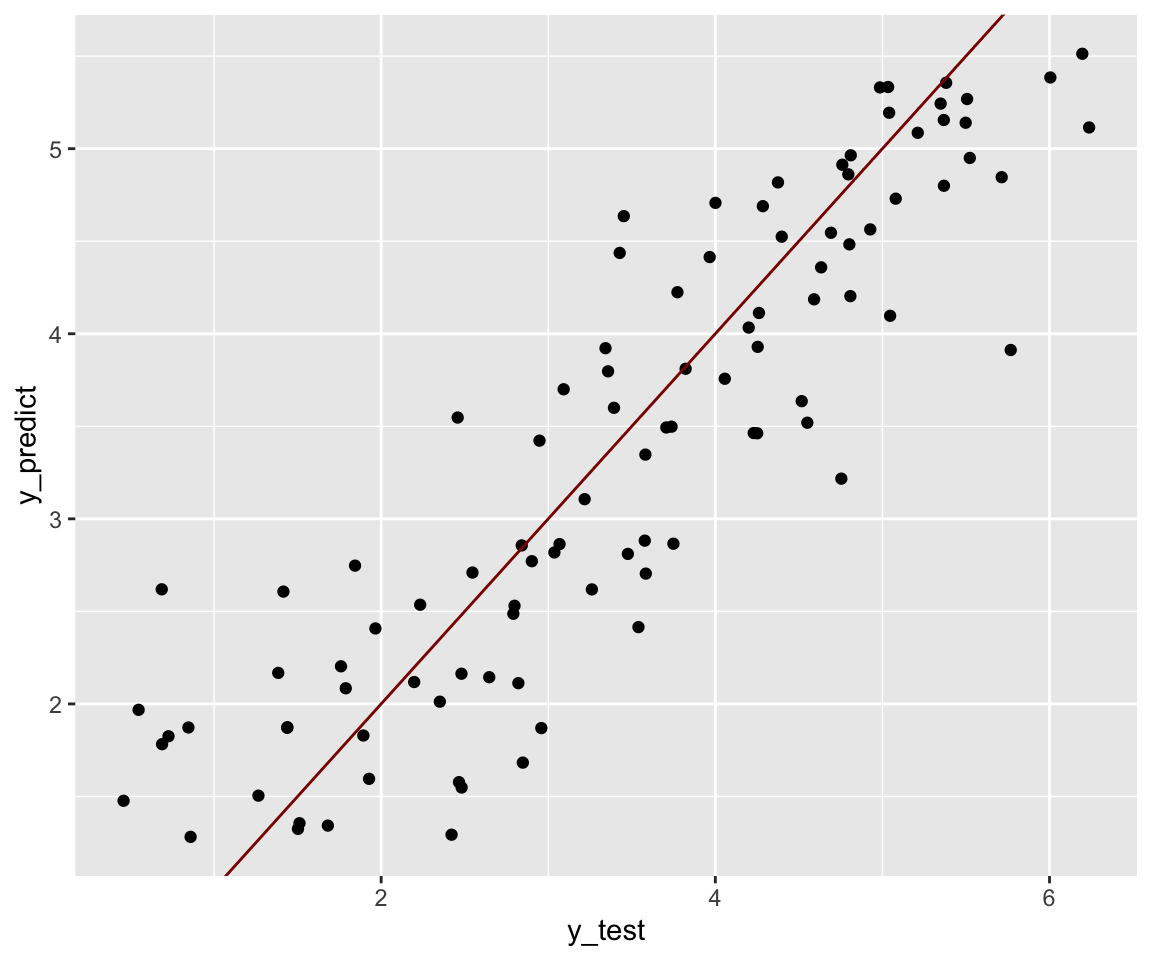

Figure 3.5: Représentations des y prédits en fonctions des y observés

Comme dans la figure3.4, nous pouvons représenter les écarts entre les y prédits et les y observés sous forme de segments.

x_test = data_test$income
ggplot() +
  geom_point(data =data_test,aes(income,happiness),color = 'green') +
  geom_point(aes(x = x_test, y =y_predict), color ='blue') +
  geom_segment(aes(x =x_test , 
                   y = y_test, xend = x_test, yend = y_predict),color = 'red')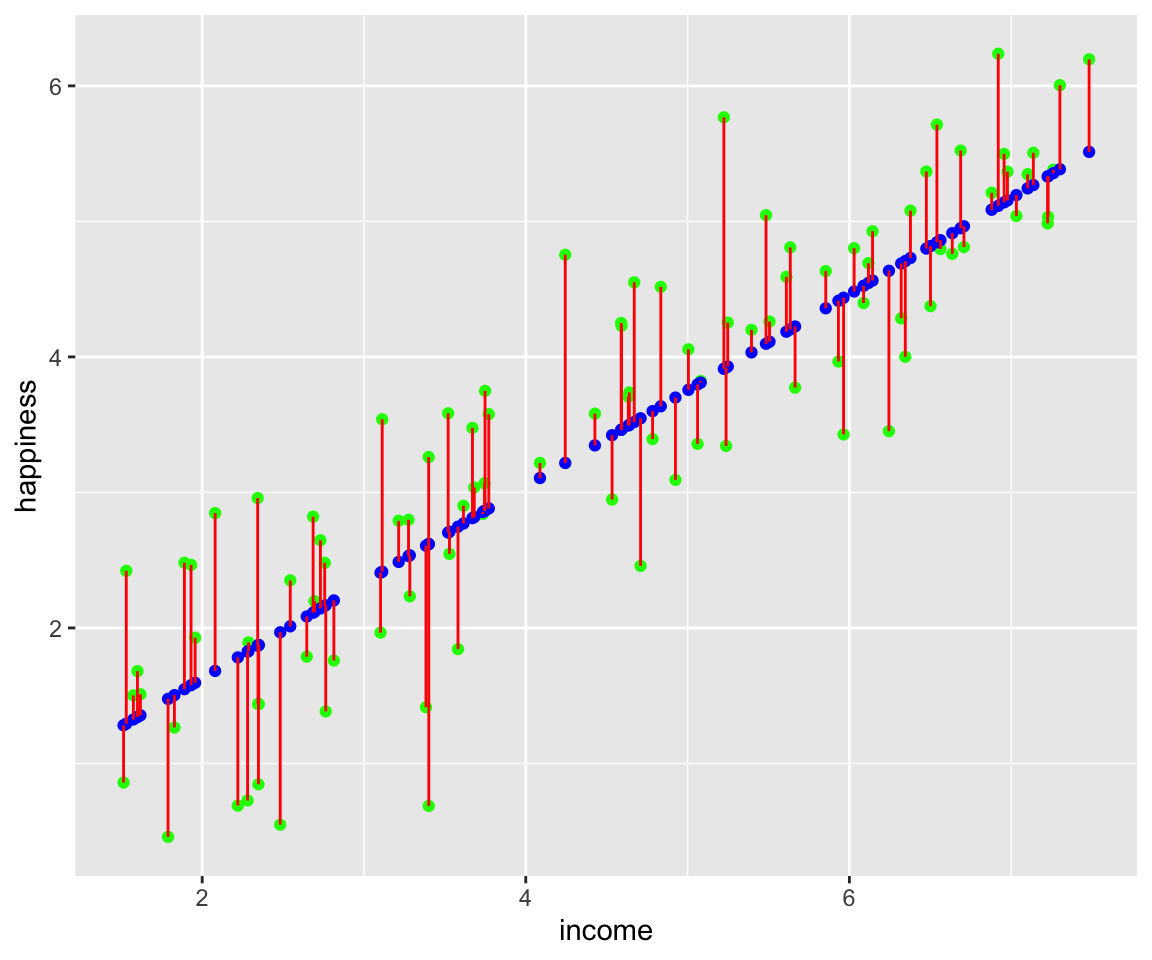

Les segments en rouges représentent les résidus, les points verts les y non entrainés qui ont servi au test et les points rouges représentent les y prédits à partir de notre modèle.

Figure 3.6: Les segments en rouges représentent les résidus, les points verts les y non entrainés qui ont servi au test et les points rouges représentent les y prédits à partir de notre modèle.

Référence

Pierre-André Cornillon et Éric Matzner-Løber⁵

2 les bases

4 La régression linéaire multiple

R pour l’économétrie