4 La régression linéaire multiple

Dans le chapitre précédent, nous avons cherché à expliquer une variable $y$ par une seule variable quantitative $X$ grâce à une fonction affine. Le modèle linéaire multiple est une généralisation du cas simple, en effet au lieu d’avoir une seule variable explicative nous en aurons plusieurs en nombre fini bien sûr, d’où le nom de régression lineaire multiple. Les jeu de données heart_data utilisé dans ce chapitre vient d’une enquête sur 498 villes, on a recueilli les données dans chaque ville en pourcentage de personnes atteintes de maladies cardiaques (heart.disease), qui fument(smoking) et qui se rendent au travail en vélo(biking). On cherche les facteurs qui pourraient avoir une influence sur les maladies cardiaques.

# Load data
heart_data <- read.csv("Data/heart.data.csv",
                       header = T,sep = ",")

4.1 Modélisation mathématique

La relation affine dans le cas de la régression linéaire multiple est de la forme suivante :

\[\begin{equation} y_i = \beta_0 + \beta_1x_{i1} + \beta_2x_{i2} +\dots+\beta_px_{ip}+\epsilon_{i}\;\; avec\;i\in\{1,2,3\dots,n\} \end{equation}\]

$y_i$ représentent la $i$ème valeur de la variable dépendantes $y$.
$x_{ij}$ représente la mesure de la $i$ème observation de la variable explicative $X_j$
les $\beta_j$ sont les paramètres inconnus du modèle à estimer
$\epsilon_i$ représente le bruit associé à la $i$ème observation

L’équation précédente peut être écrite sous une forme matricielle de cette manière :

\[\begin{equation} y = X\beta +\epsilon \tag{4.1} \end{equation}\]

avec : \[\begin{equation} y = \begin{pmatrix}y_1\\y_2\\\vdots\\y_n \end{pmatrix} \hspace{0.2cm} X = \begin{pmatrix} 1 & x_{11} & x_{12} & \dots &x_{1p}\\ 1 & x_{21} & x_{22} & \dots &x_{2p}\\ \vdots &\vdots&\vdots & &\vdots\\ 1 & x_{n1} & x_{n2} & \dots &x_{np} \end{pmatrix} \hspace{0.2cm} \beta = \begin{pmatrix}\beta_0\\ \beta_1\\ \vdots\\ \beta_n \end{pmatrix} \hspace{0.2cm} \epsilon = \begin{pmatrix} \epsilon_1\\ \epsilon_2\\ \vdots\\ \epsilon_n \end{pmatrix} \hspace{0.2cm} \end{equation}\]

Dans notre jeu de données heart_data, $y$ représente le pourcentage de personnes atteintes de maladies cardiaques (heart.disease), $X_1$ le pourcentage de personnes qui se rendent au travail en vélo(biking) et $X_2$ le pourcentage de personnes qui fument(smoking).

4.2 Estimateurs des moindres carrés ordinaires ($MCO$)

Comme dans la régression linéaire simple, l’estimateur $\hat\beta$ des moindres carrés de $\beta$ est la quantité :

La solution de cette équation est la suivante : \[ \hat\beta = (X'X)^{-1}(X'y) \]
Une section entière dédiée au calcul de cet estimateur se trouve dans l’ouvrage Éric Matzner-Løber⁶.

4.3 Application du modèle linéaire multiple avec R

Le langage R permet d’entraîner le modèle linéaire multiple grâce à la fonction lm(). Pour indiquer à la fonction que nous sommes dans le cas d’une régression multiple, l’argument formula doit recevoir y~X1+X2+...+XP et pour notre exemple heart.disease~biking+smoking. Lors qu’on précise l’argument data de la fonction lm et que les données ne contiennent que les variables à étudier, l’argument formel peut dans ce cas recevoir juste y~.. En Pratique, pour notre jeu de données heart_data, ces deux écritures sont équivalentes :

lm_multiple <- lm(formula = heart.disease~biking+smoking, data = heart_data)
lm_multiple <- lm(formula = heart.disease~., data = heart_data)

On peut afficher le résumé de l’entraînement de notre modèle avec la fonction summary(). Nous avons déjà appris la signification des éléments de la sortie de cette fonction dans la section3.3 du chapitre 3.

# Resume du model
summary(lm_multiple)
#> 
#> Call:
#> lm(formula = heart.disease ~ ., data = heart_data)
#> 
#> Residuals:
#>     Min      1Q  Median      3Q     Max 
#> -2.1789 -0.4463  0.0362  0.4422  1.9331 
#> 
#> Coefficients:
#>              Estimate Std. Error t value Pr(>|t|)    
#> (Intercept) 14.984658   0.080137  186.99   <2e-16 ***
#> biking      -0.200133   0.001366 -146.53   <2e-16 ***
#> smoking      0.178334   0.003539   50.39   <2e-16 ***
#> ---
#> Signif. codes:  
#> 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
#> 
#> Residual standard error: 0.654 on 495 degrees of freedom
#> Multiple R-squared:  0.9796, Adjusted R-squared:  0.9795 
#> F-statistic: 1.19e+04 on 2 and 495 DF,  p-value: < 2.2e-16

On constate que pour toutes les variables y compris l’Intercept, les p-values sonts très inférieures à $5\%$, on rejette alors l’hypothèse $H_0$ insinuant que $\beta_j$ est nulle avec un niveau de confiance de $95\%$.
De plus, le coefficient d’ajustement $R^2$ est de $0.9796$, soit un score de $97,96\%$ pour notre modèle ce qui est un très bon résultat.

Lors de la régression multiple, on peut s’intéresser à l’effet de l’interaction entre les variables explicatives sur la variable $y$. L’étude de cette interaction peut se faire dans notre exemple par la formula heart.disease~biking+smoking+biking:smoking où la troisième composante biking:smoking représente l’interaction entre le pourcentage de personnes qui se rendent au travail en vélo et le pourcentage de personnes qui fument. Cette écriture peut prendre une forme plus simple telle que heart.disease~biking*smoking. lm_multiple devient alors :

lm_multiple <- lm(formula = heart.disease~biking*smoking, data = heart_data)
summary(lm_multiple)
#> 
#> Call:
#> lm(formula = heart.disease ~ biking * smoking, data = heart_data)
#> 
#> Residuals:
#>      Min       1Q   Median       3Q      Max 
#> -2.20619 -0.44862  0.02892  0.44099  1.94142 
#> 
#> Coefficients:
#>                  Estimate Std. Error t value Pr(>|t|)    
#> (Intercept)    15.0527397  0.1248112 120.604   <2e-16 ***
#> biking         -0.2019916  0.0029472 -68.536   <2e-16 ***
#> smoking         0.1740065  0.0070359  24.731   <2e-16 ***
#> biking:smoking  0.0001177  0.0001653   0.712    0.477    
#> ---
#> Signif. codes:  
#> 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
#> 
#> Residual standard error: 0.6544 on 494 degrees of freedom
#> Multiple R-squared:  0.9796, Adjusted R-squared:  0.9795 
#> F-statistic:  7922 on 3 and 494 DF,  p-value: < 2.2e-16

Dans la nouvelle sortie on peut voir une nouvelle variable biking:smoking dont la p-value est très proche de $5\%$ donc par prudence, on ne peut rejeter l’hypothèse nulle $H_0$ associée au $\beta_j$ de cette variable. Autrement dit, on peut se passer de l’interaction entre biking($X_1$) et smoking($X_2$) dans l’explication de heart.disease($y$).

4.4 Représentations graphiques

Lorsque le nombre de variables explicatives dépasse 2, il est impossible de représenter sur un même graphes le nuage de point formé par y, en effet la dimension physique maximale est de 3. Il existe plusieurs packages qui donnes des représentations assez significatives en deux dimensions du modèle lineair multiple tel que car⁷.

4.4.1 Nuage de points 3D

Pour notre exemple nous pouvons faire une représentation interactive en 3 dimensions de nos variable avec la fonction plot_ly() du package plotly.

library(plotly)
figure <- plot_ly(heart_data, x = ~biking, y = ~smoking, z = ~heart.disease, 
   color =~heart.disease
  ) %>%
  add_markers() %>%
  layout(
    scene = list(xaxis = list(title = 'biking'),
        yaxis = list(title = 'smoking'),
        zaxis = list(title = 'heart.disease'))
        )
figure

Figure 4.1: Nuage de points en 3D

Une représentation 3 dimensions plus simple peut être faite avec la fonction scatterplot3d() du package de même nom.

library(scatterplot3d)
scatterplot3d(x =heart_data[,"biking"],
                         y = heart_data[,"smoking"],
                         z= heart_data[,"heart.disease"], type="p",pch=16,box=FALSE,
                         xlab="biking",ylab="smoking",zlab="heart.disease")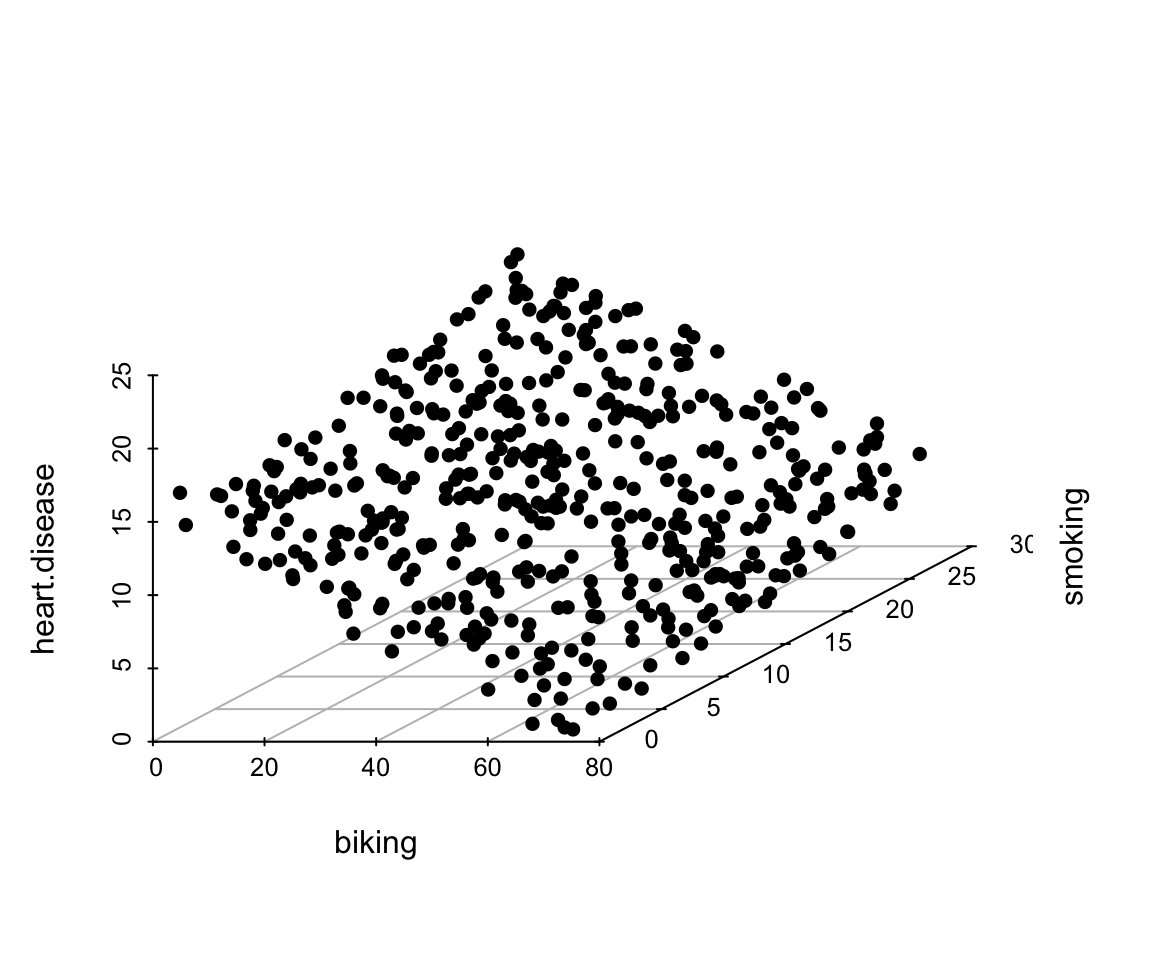

4.4.2 Droite de régression

La représentation de la droite de régression peut se faire sur chaque dimension des variables explicative grâce à la fonction avPlots() de la libraire car

library(car)
avPlots(lm_multiple)

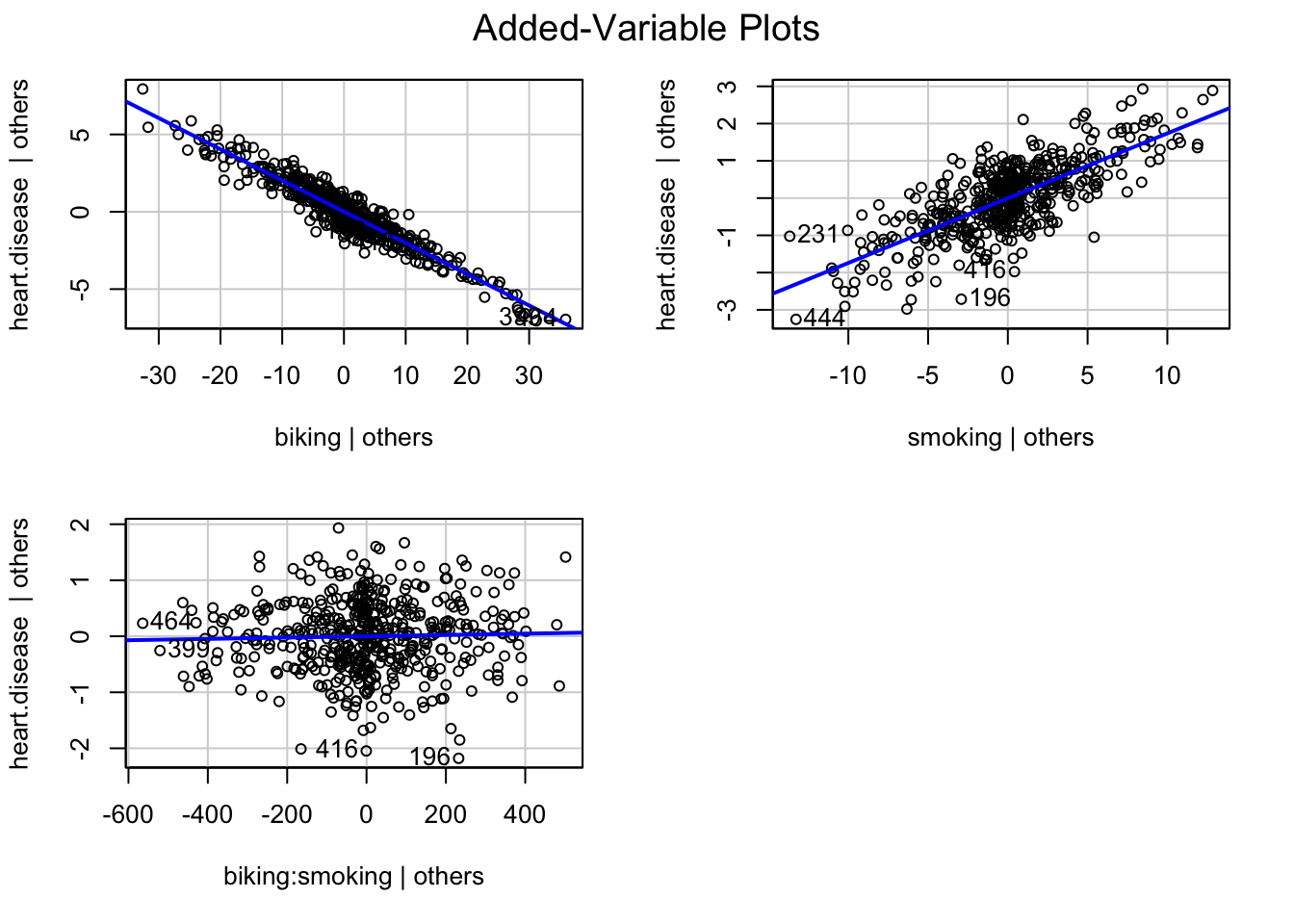
Cette représentation confirme notre interprétation. On voit clairement une corrélation entre les variables explicatives et $y$ mais pas entre l’interaction de ces variable et $y$

(#fig:lm_multiple)Cette représentation confirme notre interprétation. On voit clairement une corrélation entre les variables explicatives et $y$ mais pas entre l’interaction de ces variable et $y$

4.5 Prédiction

La prédiction dans le modèle linéaire multiple se fait aussi avec la fonction predict() comme dans le cas simple. On peut reprendre l’entraînement de notre modèle avec $80\%$ de nos données soient 400 observations et utiliser les $20\%$ pour effectuer une prédiction. Cela peut nous permettre de voir les résidus entre les valeurs prédites et les valeurs réelles de $y$.

set.seed(2345)
echantillon = sample(1:498)[1:100]
data_train <- heart_data[-echantillon,]
data_test <- heart_data[echantillon,]
model <- lm(heart.disease~.,data = data_test)
# Prediction
y_predict <- predict(model,data_test[,-3])
y_predict[1:10]
#>       483       494       359       211       418       335 
#> 10.222660 10.432554 13.843535 16.974577  6.824394 12.325991 
#>       204       475        67        66 
#>  5.947508 12.011159 12.926691 18.413173

On peut visualiser les résidus entre les variables $y_i$ observés et les $y_i$ prédites :

library(ggplot2)
y_test = data_test$heart.disease
ggplot() +
  geom_point(aes(x = y_test, y = y_predict)) +
  geom_abline(slope = 1, color ='darkred') +
  geom_segment(aes(x =y_test , 
                   y = y_test, xend = y_test, yend = y_predict),
               color = 'red') +
  ylab("Predicted heart disease")+xlab("Heart disease")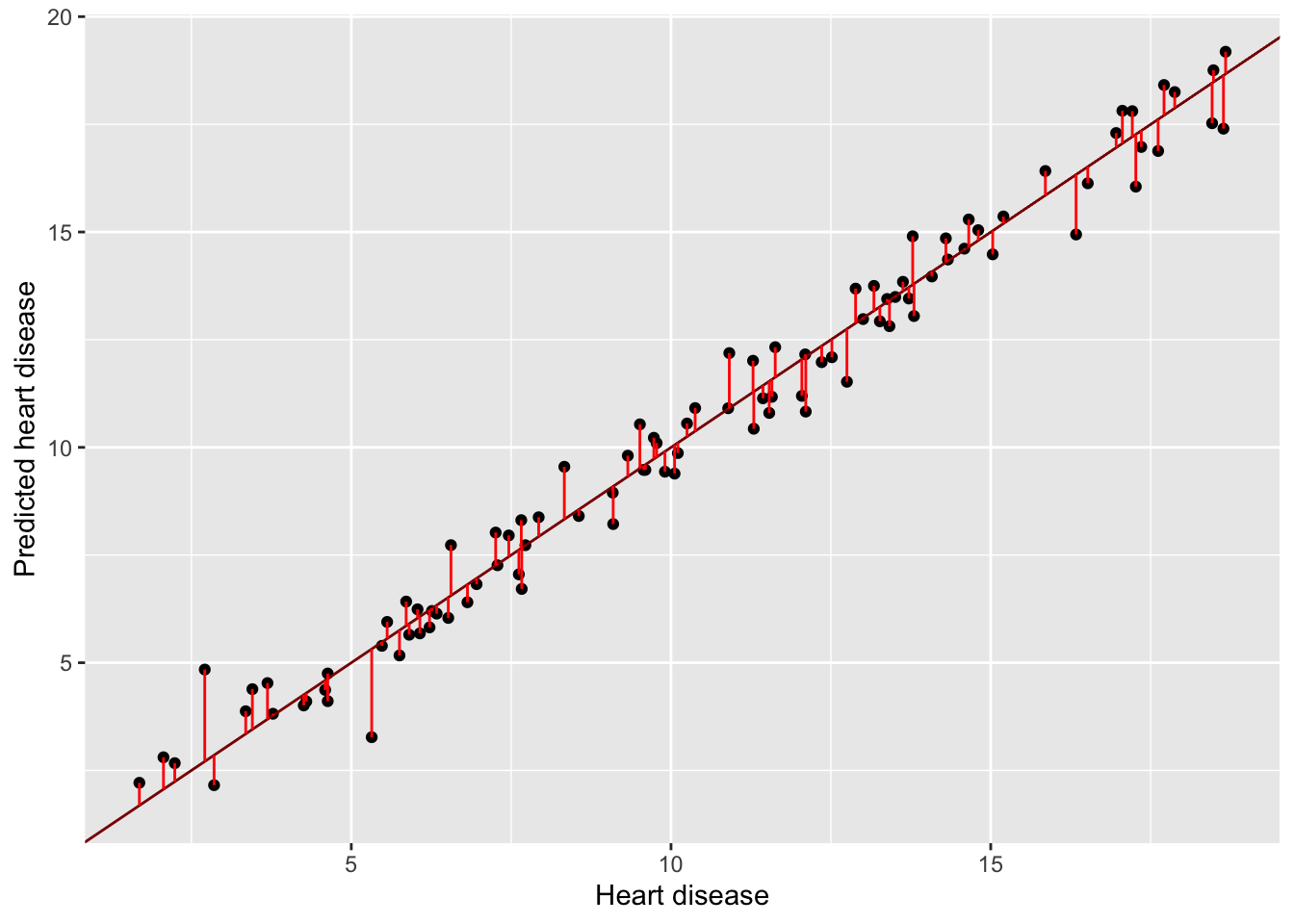

Figure 4.2: Les résidus sont très proches de 0 cela qui reflète la bonne qualité du modèle.

3 La régression linéaire simple

5 Le modèle linéaire généralisé

R pour l’économétrie