图 7.1 展示美国怀俄明州黄石国家公园老忠实间歇泉喷发规律，横轴表示喷发持续时间（以分钟计），纵轴表示等待时间（以分钟计），点的亮暗程度（白到黑）代表附近点密度的高低，亮度值通过二维核密度估计方法得到，具体实现借助了 KernSmooth (Wand 和 Jones 1995) 包提供的 bkde2D() 函数，设置了喷发时间的窗宽为 0.7 分钟，等待时间的窗宽为 7分钟。不难看出，每等待 55 分钟左右间歇泉喷发约 2 分钟，或者每等待 80 分钟左右间歇泉喷发 4.5 约分钟，非常守时，表现得很老实，故而得名。说实话，二维核密度估计在这里有点大材小用了，因为数据点比较少，肉眼也能分辨出来哪里聚集的点多，哪里聚集的点少。
# faithful 添加二维核密度估计 density 列
library(KernSmooth)
den <- bkde2D(x = faithful, bandwidth = c(0.7, 7), gridsize = c(51L, 51L))
faithful2d <- expand.grid(eruptions = den$x1, waiting = den$x2) |>
transform(density = as.vector(den$fhat))
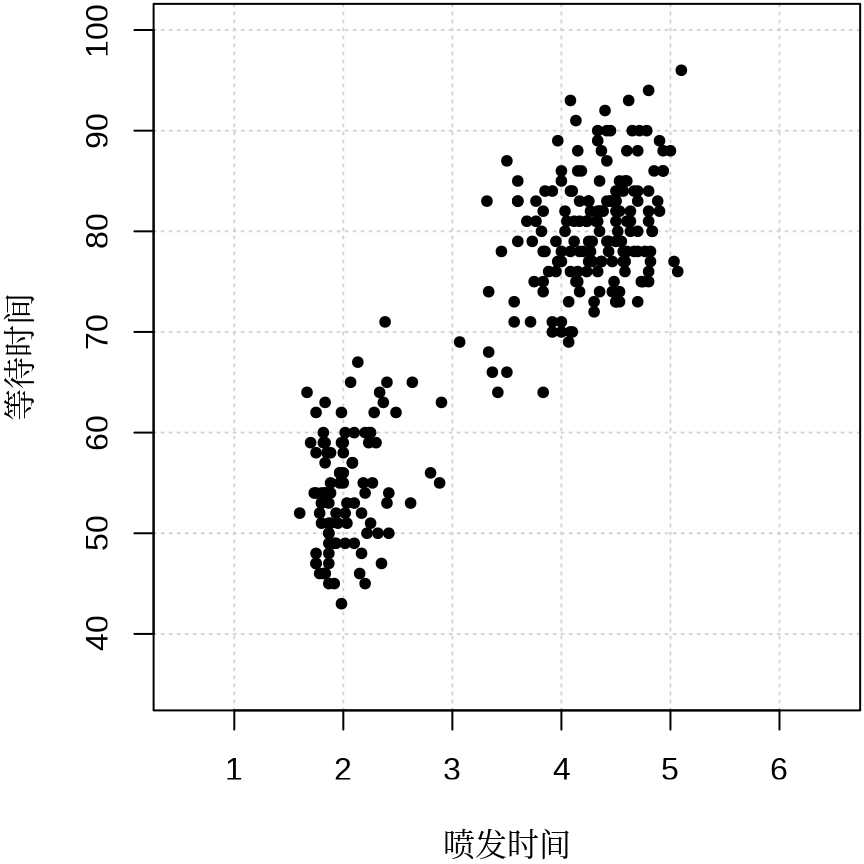
plot(faithful,
pch = 20, panel.first = grid(), cex = 1, ann = FALSE,
xlim = c(0.5, 6.5),
ylim = c(35, 100)
)
title(xlab = "喷发时间", ylab = "等待时间", family = "Noto Serif CJK SC")
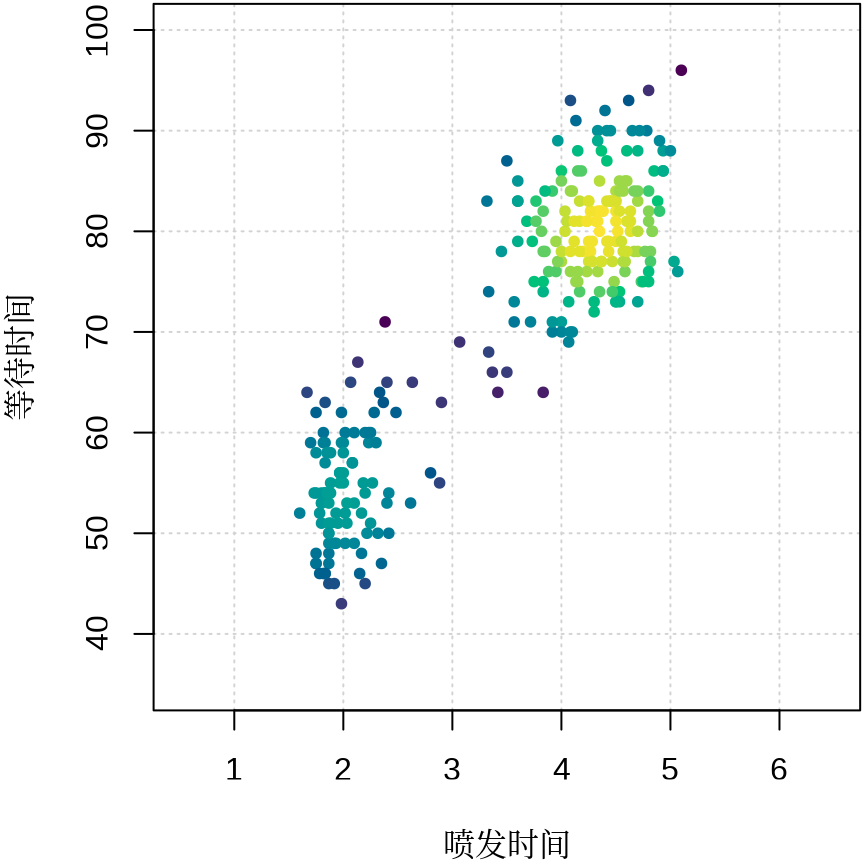
plot(faithful,
pch = 20, panel.first = grid(), cex = 1, ann = FALSE,
xlim = c(0.5, 6.5),
ylim = c(35, 100),
col = densCols(faithful,
bandwidth = c(0.7, 7),
nbin = c(51L, 51L), colramp = hcl.colors
)
)
title(xlab = "喷发时间", ylab = "等待时间", family = "Noto Serif CJK SC")
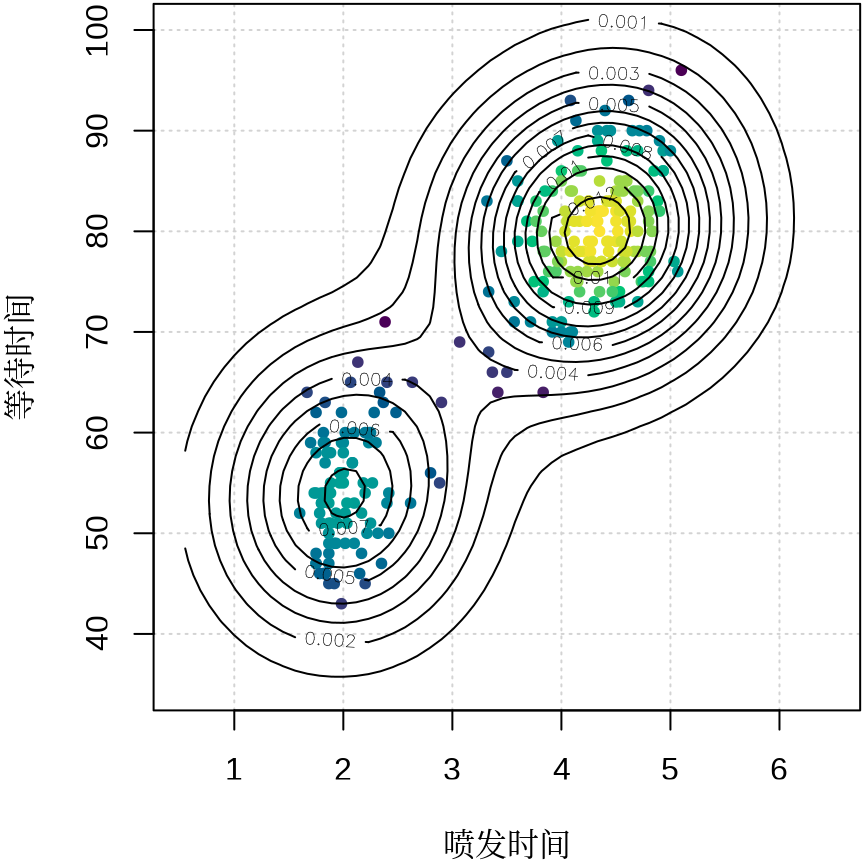
plot(faithful,
pch = 20, panel.first = grid(), cex = 1, ann = FALSE,
xlim = c(0.5, 6.5),
ylim = c(35, 100),
col = densCols(faithful,
bandwidth = c(0.7, 7),
nbin = c(51L, 51L), colramp = hcl.colors
)
)
contour(den$x1, den$x2, den$fhat, nlevels = 10, add = TRUE, family = "sans")
title(xlab = "喷发时间", ylab = "等待时间", family = "Noto Serif CJK SC")
# 散点添加颜色
mkBreaks <- function(u) u - diff(range(u)) / (length(u) - 1) / 2
# faithful 划入网格内
xbin <- cut(faithful[, 1], mkBreaks(den$x1), labels = FALSE)
ybin <- cut(faithful[, 2], mkBreaks(den$x2), labels = FALSE)
# 网格对应的核密度估计值即为 faithful 对应的核密度估计值
faithful$dens <- den$fhat[cbind(xbin, ybin)]
# 若是 faithful 数据点没有划分，则置为 0
faithful$dens[is.na(faithful$dens)] <- 0
library(ggplot2)
library(ggnewscale)
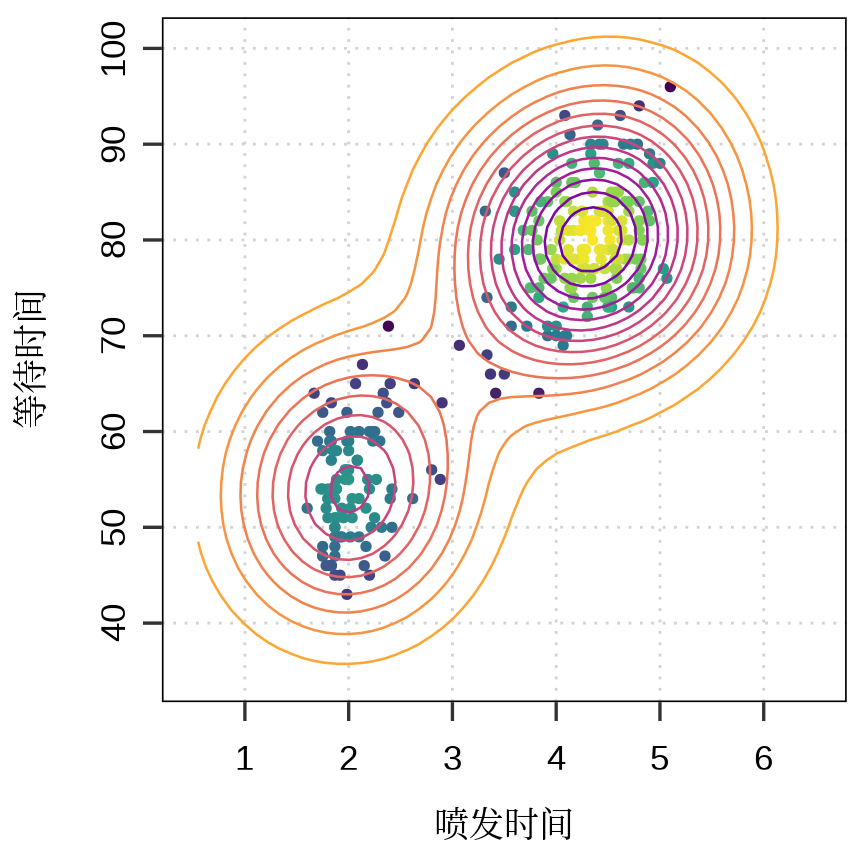
ggplot() +
geom_point(
data = faithful, aes(x = eruptions, y = waiting, color = dens),
shape = 20, size = 2, show.legend = FALSE
) +
scale_colour_viridis_c(option = "D") +
new_scale_color() +
geom_contour(data = faithful2d, aes(
x = eruptions, y = waiting,
z = density, colour = after_stat(level)
), bins = 14, linewidth = 0.45, show.legend = FALSE) +
scale_colour_viridis_c(option = "C", direction = -1, begin = 0.2, end = 0.8) +
# colorspace::scale_color_continuous_sequential(palette = "Grays") +
scale_x_continuous(breaks = 1:6) +
scale_y_continuous(breaks = 10 * 4:10) +
coord_cartesian(xlim = c(0.5, 6.5), ylim = c(35, 100)) +
labs(x = "喷发时间", y = "等待时间", colour = "密度") +
theme_bw(base_size = 13) +
theme(
legend.title = element_text(family = "Noto Serif CJK SC"),
axis.title = element_text(family = "Noto Serif CJK SC"),
axis.title.x = element_text(
margin = margin(b = 0, l = 0, t = 20, r = 0)
),
axis.title.y = element_text(
margin = margin(b = 0, l = 0, t = 0, r = 20)
),
panel.border = element_rect(color = "black"),
panel.grid = element_blank(),
panel.grid.major = element_line(
color = "lightgray",
linetype = 3, linewidth = 0.5
),
axis.ticks.length = unit(0.25, "cm"),
axis.text.x = element_text(
family = "sans", color = "black",
vjust = -1.5, size = rel(1.25)
),
axis.text.y = element_text(
family = "sans", color = "black",
angle = 90, vjust = 1.5, hjust = 0.5,
size = rel(1.25)
)
)
函数 bkde2D() 实现二维带窗宽的核密度估计（2D Binned Kernel Density Estimate），R 语言存在多个版本，grDevices 包的函数 densCols() 直接调用 KernSmooth 包的函数 bkde2D()，graphics 包的函数 smoothScatter() 与函数 densCols() 一样，内部也是调用 bkde2D() 函数，ggplot2 包的图层 geom_density_2d() 采用 MASS 包的函数 kde2d()，在算法实现上，MASS::kde2d() 与 KernSmooth::bkde2D() 不同，前者是二维核密度估计（Two-Dimensional Kernel Density Estimation）。Tarn Duong 的著作 《Multivariate Kernel Smoothing and Its Applications 》 (José. Chacón 2018) 对多元核平滑方法及其应用作了专门的论述，相关实现见书籍配套的 ks 包。
图 7.2 (a) 展示 2020 年中国各省、自治区和直辖市分城市、镇和乡村的性别比数据。数据来自中国国家统计局发布的 2021 年统计年鉴，在数据量不太大的情况下，尽可能展示原始数据，可以捕捉到更加细致的差异。社会经济相关的数据常常显示有马太效应，对原始数据适当做一些变换有利于比较和展示数据，图 7.2 (b) 展示对数变换后的性别比数据的分布。大部分地区的性别比数据都在 100:100 左右，流动人口的性别比波动大很多。
china_household_sex <- readRDS(file = "data/china-household-sex-2020.rds")
ggplot(data = china_household_sex, aes(x = `户口登记状况`, y = `男性` / `女性`)) +
geom_jitter(aes(color = `区域`), width = 0.3) +
theme_classic()
ggplot(data = china_household_sex, aes(x = `户口登记状况`, y = `男性` / `女性`)) +
geom_jitter(aes(color = `区域`), width = 0.3) +
scale_y_continuous(trans = "log10") +
theme_classic()
图 7.3 展示美国 1933-2020 年男性分年龄的死亡率数据1。图分上下两部分，上半部分展示死亡率原值随年龄的变化情况，以 ggplot2 默认的调色板给各个年份配色，下半部分展示死亡率对数变换后随年龄的变化情况，并以红、橙、黄、绿、青、蓝、紫构造彩虹式的调色板给各个年份配色。作图过程中，使用对数变换和调用彩虹式的调色板，帮助我们观察到更多的细节、层次。对数变换后，更加清晰地展示死亡率的变化，尤其是 0-20 岁之间的死亡率起伏变化。调用彩虹式的调色板后，约 20 年为一个阶段，每个阶段内呈现梯度变化，多个阶段体现层次性，更加清晰地展示死亡率曲线的变动趋势。透过层次看到 80 多年来，美国在医疗和公共卫生方面取得的显著改善。
usa_mortality <- readRDS(file = "data/usa-mortality-2020.rds")
library(patchwork)
p1 <- ggplot(data = usa_mortality, aes(x = Age, y = Male, group = Year)) +
geom_vline(xintercept = "100", colour = "gray", lty = 2) +
geom_line(aes(color = Year), linewidth = 0.25) +
scale_x_discrete(
breaks = as.character(20 * 0:5),
labels = as.character(20 * 0:5)
) +
theme_classic()
p2 <- p1 +
labs(x = "年龄", y = "死亡率", color = "年份")
p3 <- p1 +
scale_y_log10(labels = scales::label_log()) +
scale_colour_gradientn(colors = RColorBrewer::brewer.pal(name = "Spectral", n = 11)) +
labs(x = "年龄", y = "死亡率（对数尺度）", color = "年份")
p2 / p3
图 7.3 也展示了很多基础信息，出生时有很高的死亡率，出生后死亡率迅速下降，一直到10岁，死亡率才又开始回升，直到 20 岁，死亡率才回到出生时的水平。之后，在青年阶段死亡率缓慢增加，直至老年阶段达到很高的死亡率水平。相比于老年阶段，医疗水平的改善作用主要体现在婴儿、儿童、青少年阶段。
图 7.3 还展示了一个潜在的数据质量问题，在 100 岁之后，死亡率波动程度明显在变大，这是因为高龄人数变得很少，即死亡率的分母变得很小，分子的细小波动会被放大，也因为同样的原因，100 岁以上的死亡率主要依赖模型估计，甚至出现死亡率大于 1 的罕见情况。因此，就对比医疗和公共卫生水平的变化而言，从数据的实际情况出发，100 岁以上的情况可以不参与比较。
图 7.4 以年份为横轴，以年龄为纵轴绘制网格，网格内部根据男性死亡率数据填充颜色制作热力图，死亡率数据是对数尺度，颜色的变化和死亡率的变化关系同前，采用了相同的调色板。更加深入的分析和建模，详见 Marron 和 Dryden (2022) 的第一章。
ggplot(data = usa_mortality, aes(x = Year, y = Age, fill = Male)) +
scale_fill_gradientn(
colors = RColorBrewer::brewer.pal(name = "Spectral", n = 11),
trans = "log10", labels = scales::percent_format()
) +
geom_tile(linewidth = 0.4) +
scale_y_discrete(
breaks = as.character(10 * 0:10),
labels = as.character(10 * 0:10),
expand = c(0, 0)
) +
scale_x_continuous(
breaks = 1940 + 10 * 0:8,
labels = 1940 + 10 * 0:8,
expand = c(0, 0)
) +
theme_classic() +
labs(x = "年份", y = "年龄", fill = "死亡率")
VADeaths 数据来自 Base R 内置的 datasets 包，记录 1940 年美国弗吉尼亚州死亡率，如下表。
| 农村男 | 农村女 | 城市男 | 城市女 | |
|---|---|---|---|---|
| 50-54 | 11.7 | 8.7 | 15.4 | 8.4 |
| 55-59 | 18.1 | 11.7 | 24.3 | 13.6 |
| 60-64 | 26.9 | 20.3 | 37.0 | 19.3 |
| 65-69 | 41.0 | 30.9 | 54.6 | 35.1 |
| 70-74 | 66.0 | 54.3 | 71.1 | 50.0 |
死亡率数据是按年龄段、城乡、性别分组统计的，这是一个三因素交叉统计表，表格中第1行第1列的数据表示 50-54 岁乡村男性的死亡率为 11.7 ‰ ，即在 50-54 岁乡村男性群体中，1000 个人中死亡 11.7 个，这是抽样调查出来的数字。下图分年龄段、城乡、性别展示弗吉尼亚州死亡率数据，从图例来看，突出的是各年龄段的对比，图主要传递的信息是各年龄段的死亡率差异。无论城市还是乡村，也无论男性还是女性，年龄越大死亡率越高，这完全是一个符合生物规律的客观事实，这是众人皆知的，算不上洞见。
dat <- transform(expand.grid(
site = c("乡村", "城镇"), sex = c("男", "女"),
age = ordered(c("50-54", "55-59", "60-64", "65-69", "70-74"))
), deaths = as.vector(t(VADeaths)) / 1000)
library(ggplot2)
# (\u2030) 表示千分号
ggplot(data = dat, aes(x = sex, y = deaths, fill = age)) +
geom_col(position = "dodge2") +
scale_y_continuous(labels = scales::label_percent(scale = 1000, suffix = "\u2030")) +
scale_fill_brewer(palette = "Spectral") +
facet_wrap(~site, ncol = 1) +
theme_bw(base_size = 13) +
labs(x = "性别", y = "死亡率", fill = "年龄")
将对比对象从年龄段转变为城乡，描述城乡差距在死亡率上的体现，是不是一下子更深刻了呢？城市降低各个年龄段的死亡率，暗示着城市的居住条件、医疗水平比乡村好，提高城市化率增加全民的寿命。严格来说，就这个粗糙的数据集不能如此快地下这个结论，但是，它暗示这个信息，同样也符合人们的常识。
ggplot(data = dat, aes(x = age, y = deaths, fill = site)) +
geom_col(position = "dodge2") +
scale_y_continuous(labels = scales::label_percent(scale = 1000, suffix = "\u2030")) +
scale_fill_brewer(palette = "Spectral") +
facet_wrap(~sex, ncol = 1) +
theme_bw(base_size = 13) +
labs(x = "年龄", y = "死亡率", fill = "城乡")
不失一般性，考虑连续随机变量的条件分布和累积分布。不妨设随机变量 \(x\) 的概率分布函数和概率密度函数分别是 \(F(x)\) 和 \(f(x)\) 。已知概率分布函数和概率密度函数之间有如下关系。
\[ F(x) = \int_{-\infty}^{x} f(t) \mathrm{dt} \]
diamonds 数据来自 ggplot2 包，记录了约 54000 颗钻石的价格、重量、切工、颜色、纯净度、尺寸等属性信息。图 7.7 展示这批不同切工的钻石随价格的分布，在这个示例中，如何表达累积分布？概率分布的密度曲线是根据直方图估计得来的，根据不同价格区间内钻石的数量占总钻石的比例估计概率。固定窗宽，即在同一价格区间内累积不同切工的钻石数量，得到累积概率，最后获得累积概率密度曲线，更多理论细节见数据可视化陷阱 (Pu 和 Kay 2020) 。
library(ggplot2)
library(patchwork)
p1 <- ggplot(diamonds, aes(x = price, y = after_stat(density), fill = cut)) +
geom_density(position = "stack", colour = "white") +
scale_fill_brewer(palette = "Spectral") +
scale_y_continuous(
labels = expression(0, 5~"·"~10^-4, 10 ~ "·" ~ 10^-4, 15 ~ "·" ~ 10^-4),
breaks = c(0, 5, 10, 15) * 10^(-4)
) +
theme_bw(base_family = "Noto Serif CJK SC") +
labs(x = "价格", y = "概率密度", fill = "切工", tag = "坏") +
theme(
axis.text.x = element_text(family = "sans", color = "black"),
axis.text.y = element_text(
family = "sans", color = "black",
angle = 90, vjust = 1.5, hjust = 0.5
),
legend.text = element_text(family = "sans"),
plot.tag = element_text(family = "Noto Serif CJK SC", color = "red"),
plot.tag.position = "topright"
)
p2 <- ggplot(diamonds, aes(x = price, y = after_stat(density * n), fill = cut)) +
geom_density(position = "stack", colour = "white") +
scale_fill_brewer(palette = "Spectral") +
theme_bw(base_family = "Noto Serif CJK SC") +
labs(x = "价格", y = "概率质量", fill = "切工", tag = "好") +
theme(
axis.text.x = element_text(family = "sans", color = "black"),
axis.text.y = element_text(
family = "sans", color = "black",
angle = 90, vjust = 1.5, hjust = 0.5
),
legend.text = element_text(family = "sans"),
plot.tag = element_text(family = "Noto Serif CJK SC", color = "black"),
plot.tag.position = "topright"
)
p1 / p2
0 和 1 是世界的原点，蕴含大道真意，从 0-1 分布也叫伯努利分布，独立同 0-1分布之和可以衍生出二项分布。在一定条件下，可以用泊松分布近似二项分布。根据中心极限定理，独立同二项分布的极限和与正态分布可以发生关系。在二项分布、正态分布的基础上，可以衍生出超几何分布、贝塔分布等等。本书多个地方以二项分布为例介绍基本统计概念和模型。
在给定置信水平为 0.95，即 \(\alpha = 0.05\)，固定样本量 \(n = 10\)，观测到的成功次数 \(x\) 可能为 \(0,1,\cdots,10\)。对于给定的 \(p\)，不同 \(x\) 值出现的机率 \(P(X = x)\) 由 \((p + q)^{10}\) 二项展开式的项给出，这里 \(q = 1-p\)，即：
\[ P(X = x) = \binom{n}{x}p^x(1-p)^{n-x} \tag{7.1}\]
在给定 \(p = 0.1\) 的情况下，求二项分布的上 \(\alpha/2 = 0.025\) 分位点，尾项之和不应超过 \(\alpha/2\)，最大的 \(x\) 值可有如下方程给出：
\[ \sum_{r = x}^{n}\binom{n}{x}p^x(1-p)^{n-x} = \frac{\alpha}{2} \tag{7.2}\]
在 R 语言中，函数 qbinom() 可以计算上述二项分布的上分位点 \(x = 3\)，即
qbinom(0.025, size = 10, prob = 0.1, lower.tail = F)
#> [1] 3反过来，若已知上分位点为 \(x = 3\)，则概率为
\[ P(X > 3) = \sum_{x > 3}^{10}\binom{10}{x}0.1^x*(1-0.1)^{10-x} \tag{7.3}\]
在 R 语言中，函数 pbinom() 可以计算上述二项分布的上分位点对应的概率为 \(0.0127952\)。
pbinom(q = 3, size = 10, prob = 0.1, lower.tail = F)
#> [1] 0.0127952首先简单回顾一下置信区间，在学校和教科书里，有两种说法如下：
为什么要采纳第一种说法而不是第二种呢？这其实涉及到置信区间的定义问题，历史上 E. S. Pearson 和 R. A. Fisher 曾有过争论。和大多数以正态分布为例介绍参数的置信估计不同，下面以二项分布为例展开介绍。我们知道二项分布是 N 个伯努利分布的卷积，而伯努利分布又称为 0-1 分布，最形象的例子要数抛硬币了，反复投掷硬币，将正面朝上记为 1，反面朝上记为 0，记录正反面出现的次数，正面朝上的总次数又叫成功次数。
1934 年 C. J. Clopper 和 E. S. Pearson 在给定置信水平 \(1- \alpha = 0.95\) 和样本量 \(n = 10\) 的情况下，给出二项分布 \(B(n, p)\) 参数 \(p\) 的区间估计（即所谓的 Clopper-Pearson 精确区间估计）和置信带 (Clopper 和 Pearson 1934)，如 图 7.8 所示，横坐标为观测到的成功次数，纵坐标为参数 \(p\) 的置信限。具体来说，固定样本量为 10，假定观测到的成功次数为 2，在置信水平为 0.95 的情况下，Base R 内置的二项精确检验函数 binom.test()，可以获得参数 \(p\) 的精确区间估计为 \((p_1, p_2) = (0.025, 0.556)\)，即：
# 精确二项检验 p = 0.2
binom.test(x = 2, n = 10, p = 0.2)
#>
#> Exact binomial test
#>
#> data: 2 and 10
#> number of successes = 2, number of trials = 10, p-value = 1
#> alternative hypothesis: true probability of success is not equal to 0.2
#> 95 percent confidence interval:
#> 0.02521073 0.55609546
#> sample estimates:
#> probability of success
#> 0.2值得注意，这个估计的区间与函数 binom.test() 中参数 p 的取值无关，也就是说，当 \(p = 0.4\)，区间估计结果是一样的，如下：
# 精确二项检验 p = 0.4
binom.test(x = 2, n = 10, p = 0.4)
#>
#> Exact binomial test
#>
#> data: 2 and 10
#> number of successes = 2, number of trials = 10, p-value =
#> 0.3335
#> alternative hypothesis: true probability of success is not equal to 0.4
#> 95 percent confidence interval:
#> 0.02521073 0.55609546
#> sample estimates:
#> probability of success
#> 0.2由此，也可以看出区间估计与假设检验的一些关系。
library(rootSolve) # uniroot.all
options(digits = 4)
# r 为上分位点
p_fun <- function(p, r = 9) qbinom(0.025, size = 10, prob = p, lower.tail = F) - r # 上分位点
l_fun <- function(p, r = 9) qbinom(0.025, size = 10, prob = p, lower.tail = T) - r # 下分位点
# 计算每个分位点对应的最小的概率 p
p <- sapply(0:10, function(x) min(uniroot.all(p_fun, lower = 0, upper = 1, r = x)))
# 计算每个分位点对应的最大的概率 l
l <- sapply(0:10, function(x) max(uniroot.all(l_fun, lower = 0, upper = 1, r = x)))
plot(
x = seq(from = 0, to = 10, length.out = 11),
y = seq(from = 0, to = 1, length.out = 11),
type = "n", ann = FALSE, family = "sans", panel.first = grid()
)
title(xlab = "成功次数", ylab = "置信限", family = "Noto Serif CJK SC")
lines(x = 0:10, y = p, type = "s") # 朝下的阶梯线
lines(x = 0:10, y = p, type = "l") # 折线
# points(x = 0:10, y = p, pch = 16, cex = .8) # 散点
# abline(a = 0, b = 0.1, col = "gray", lwd = 2, lty = 2) # 添加对称线
text(x = 5, y = 0.5, label = "置信带", cex = 1.5, srt = 45, family = "Noto Serif CJK SC")
# points(x = 5, y = 0.5, col = "black", pch = 16) # 中心对称点
# points(x = 5, y = 0.5, col = "black", pch = 3) # 中心对称点
lines(x = 0:10, y = l, type = "S") # 朝上的阶梯线
lines(x = 0:10, y = l, type = "l") # 折线
# points(x = 0:10, y = l, pch = 16, cex = .8) # 散点
points(x = c(2, 2), y = c(0.03, 0.55), pch = 8, col = "black")
text(x = 2, y = 0.55, labels = expression(p[2]), pos = 1)
text(x = 2, y = 0.03, labels = expression(p[1]), pos = 3)
统计图形很重要的一个作用是解释统计概念，这就要求不拘泥于抽象的严格数学表达，借助数值模拟，可视化等手段帮助读者发散思维，加深理解复杂的逻辑概念，建立统计直觉，正如顾恺之所言「以形写神，形神兼备」。下面仅以二项分布为例讲讲区间估计及其覆盖概率。众所周知，在置信水平为 \(1 - \alpha\) 的情况下，二项分布 \(\mathrm{Bin}(n,p)\) 的参数 \(p\) （也叫成功概率）的 Wald 区间估计为
\[ (\hat{p} - Z_{1-\alpha/2} \sqrt{\hat{p}*(1-\hat{p})/n}, \hat{p} + Z_{1-\alpha/2} \sqrt{\hat{p}*(1-\hat{p})/n}) \tag{7.4}\]
其中，\(n\) 为样本量，\(Z_{1-\alpha/2}\) 为标准正态分布 \(\mathcal{N}(0,1)\) 在 \(1-\alpha/2\) 处的分位点。 \(\alpha\) 一般取 0.05，进而 \(Z_{1-\alpha/2} \approx 1.96\)。用通俗的话说，有 \(1 - \alpha\) 的把握确定参数真值 \(p\) 在该估计区间内。可见区间估计的意义是解决点估计可靠性问题，但是可靠性和精度往往不能兼得。统计上，通常的做法是先给定可靠性，去尽可能提升精度，即给定置信水平，使估计区间的长度尽可能短，这就涉及到区间估计的方法问题。
下面通过数值模拟的方式辅助说明 Wald 和 Agresti-Coull 两种区间估计方法，现固定样本量 \(n = 10\) 或 \(n = 100\)，重复抽样 1000 次，将参数 \(p\) 以 0.01 的间隔离散化，从 0.01 取值到 0.99。已知给定参数 \(p\)，每次抽样都可以得到参数 \(p\) 的估计值 \(\hat{p}\) 及其置信区间，1000 次的重复抽样可以计算出来 1000 个置信区间，每个区间要么覆盖真值，要么没有覆盖真值，覆盖的比例可以近似为覆盖概率。
如 图 7.9 所示，从上往下分别代表 Wald、 Agresti-Coull、 Wilson 和 Clopper-Pearson 区间估计，纵坐标是覆盖概率，横坐标是参数 \(p\) 的真值，图中黑虚线表示置信水平 \(1-\alpha=0.95\)，红、蓝点线分别表示样本量 \(n=10\) 和 \(n=100\) 的模拟情况。不难看出，Wald 区间估计方法在小样本情况下表现很差，覆盖概率很少能达到置信水平的，而 Agresti-Coull 区间估计在 Wald 基础上添加了修正后，情况得到显著改善。更多区间估计方法的详细比较见文献 Blyth 和 Hutchinson (1960);Brown, Cai, 和 DasGupta (2001);Geyer 和 Meeden (2005) 。
# 计算覆盖概率
# Wald 覆盖
coverage_wald <- function(p = 0.1, n = 10, nsim = 1000) {
phats <- rbinom(nsim, prob = p, size = n) / n
ll <- phats - qnorm(1 - 0.05 / 2) * sqrt(phats * (1 - phats) / n)
ul <- phats + qnorm(1 - 0.05 / 2) * sqrt(phats * (1 - phats) / n)
mean(ll < p & ul > p)
}
# Agresti-Coull 覆盖
coverage_agresti <- function(p = 0.1, n = 10, nsim = 1000) {
phats <- (rbinom(nsim, prob = p, size = n) + 2) / (n + 4)
ll <- phats - qnorm(1 - 0.05 / 2) * sqrt(phats * (1 - phats) / n)
ul <- phats + qnorm(1 - 0.05 / 2) * sqrt(phats * (1 - phats) / n)
mean(ll < p & ul > p)
}
# Clopper and Pearson (1934)
# 与 binom.test() 计算结果一致
coverage_clopper <- function(p = 0.1, n = 10, nsim = 1000) {
nd <- rbinom(nsim, prob = p, size = n)
ll <- qbeta(p = 0.05 / 2, shape1 = nd, shape2 = n - nd + 1)
ul <- qbeta(p = 1 - 0.05 / 2, shape1 = nd + 1, shape2 = n - nd)
mean(ll < p & ul > p)
}
# Wilson (1927)
# 与 prop.test(correct = FALSE) 计算结果一致
coverage_wilson <- function(p = 0.1, n = 10, nsim = 1000) {
phats <- rbinom(nsim, prob = p, size = n) / n
lambda <- qnorm(1 - 0.05 / 2)
ll <- phats + lambda^2 / (2 * n) - lambda * sqrt(phats * (1 - phats) / n + lambda^2 / (4 * n^2))
ul <- phats + lambda^2 / (2 * n) + lambda * sqrt(phats * (1 - phats) / n + lambda^2 / (4 * n^2))
mean(ll / (1 + lambda^2 / n) < p & ul / (1 + lambda^2 / n) > p)
}
sim_dat <- transform(expand.grid(
p = seq(0.01, 0.99, by = 0.01),
n = c(10, 100),
nsim = 1000,
methods = c("Wald", "Agresti-Coull", "Wilson", "Clopper-Pearson")
), prob = ifelse(methods == "Wald",
Vectorize(coverage_wald)(p = p, n = n, nsim = nsim),
ifelse(methods == "Agresti-Coull",
Vectorize(coverage_agresti)(p = p, n = n, nsim = nsim),
ifelse(methods == "Wilson",
Vectorize(coverage_wilson)(p = p, n = n, nsim = nsim),
Vectorize(coverage_clopper)(p = p, n = n, nsim = nsim)
)
)
), nsample = ifelse(n == 10, "n=10", "n=100"))
ggplot(data = sim_dat, aes(x = p, y = prob, color = nsample)) +
geom_hline(yintercept = 0.95, linetype = 2,
linewidth = 1, color = "gray60") +
geom_point() +
geom_path() +
# annotate(geom = "text", x = 0, y = 0.95, label = "0.950",
# fontface = "bold", hjust = 2, size = 3.5) +
# scale_color_grey() +
scale_color_brewer(palette = "Set1") +
facet_wrap(facets = ~methods, ncol = 1, scales = "free_y") +
labs(x = "成功概率", y = "覆盖概率", color = "样本量") +
theme_bw(base_size = 13, base_family = "sans") +
theme(title = element_text(family = "Noto Serif CJK SC")) +
coord_cartesian(clip = 'off')
通过 图 7.9 一看就明白了几种区间估计方法的优劣，以及为什么软件普遍默认采用 Wilson 估计方法？因为它又稳定又准确。 Wilson 区间估计用的更加广泛的，Base R 内置的比例检验函数 prop.test() 在不启用 Yates 修正时，就是用该方法获得比例 \(p\) 的区间估计 (Wilson 1927)。Clopper-Pearson 区间估计特别适合小样本情形，它是精确区间估计方法，Base R 内置的二项比例检验函数 binom.test() 就是用该方法获得比例 \(p\) 的区间估计(Clopper 和 Pearson 1934)。
请读者再思考两个问题： 图 7.9 为什么呈现对称的形式，泊松分布会和二项分布有类似的现象吗？如果有的话，连续分布，如正态分布和指数分布也会有吗？
1888 年，瑞士开始进入一个人口转变的阶段，从发展中国家的高出生率开始下滑。分析生育率和经济指标的关系。数据集 swiss 记录了 1888 年瑞士 47 个说法语的省份的生育率和社会经济指标数据。Fertility（生育率，采用常见的标准生育率统计口径）、Agriculture（男性从事农业生产的比例）、Examination（应征者在军队考试中获得最高等级的比例）、Education（应征者有小学以上教育水平的比例）、Catholic（信仰天主教的比例）、Infant.Mortality（婴儿死亡率，仅考虑出生一年内死亡），各个指标都统一标准化为百分比的形式。其中，Examination 和 Education 是 1887 年、1888 年和 1889 年的平均值。瑞士 182 个地区 1888 年及其它年份的数据可从网站获得。
数据来自德国马克斯普朗克人口研究所、美国加州大学伯克利分校、法国人口研究所共同建立的人类死亡率数据库 (https://www.mortality.org/)。↩︎