3  统计图形

3.1 描述分布

数据来自中国国家统计局发布的2021年统计年鉴，各省、直辖市和自治区分区域的性别比数据（部分）情况见 表格 3.1 。

表格 3.1: 各省、直辖市和自治区分区域的性别比数据（部分）
地区 人口数/男 人口数/女 性别比（女=100） 区域
北京 8937161 8814520 101.39 城市
天津 5610161 5322931 105.40 城市
河北 11010407 11119188 99.02 城市
山西 6588788 6608849 99.70 城市
内蒙古 4714495 4731924 99.63 城市
辽宁 12626419 12946058 97.53 城市

3.1.1 箱线图

library(ggplot2)
ggplot(data = province_sex_ratio, aes(x = `区域`, y = `性别比（女=100）`)) +
  geom_boxplot() +
  theme_classic()
ggplot(data = province_sex_ratio, aes(x = `区域`, y = `性别比（女=100）`)) +
  geom_boxplot(outlier.colour = "red") +
  theme_classic()
library(lvplot)
ggplot(data = province_sex_ratio, aes(x = `区域`, y = `性别比（女=100）`)) +
  geom_lv() +
  theme_classic()
boxplot(`性别比（女=100）` ~ `区域` , data = province_sex_ratio)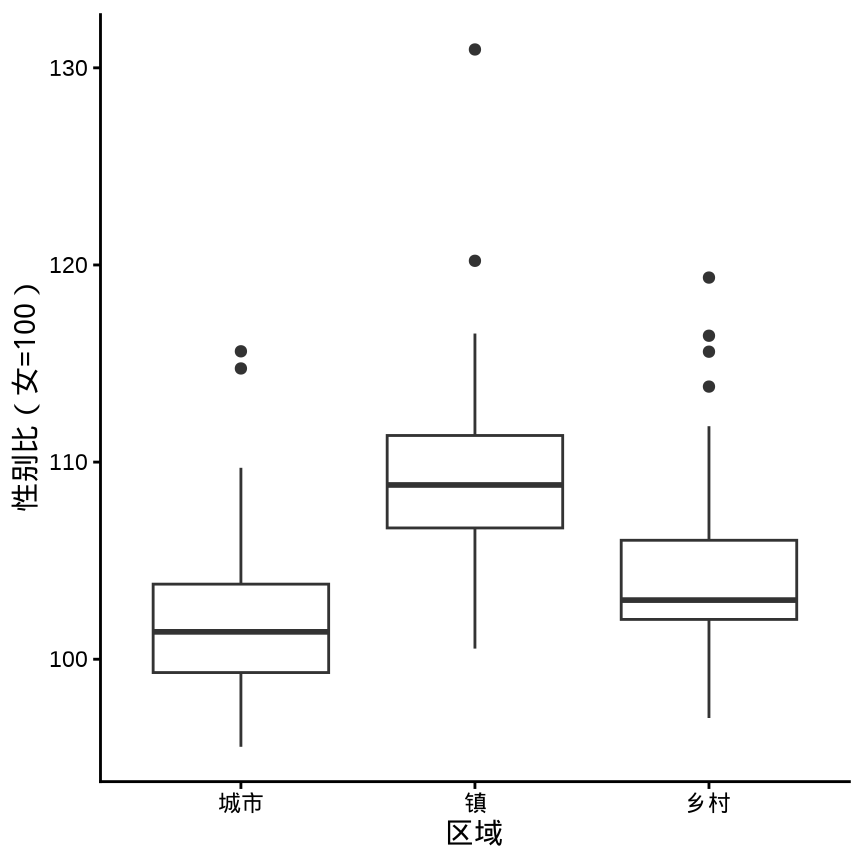
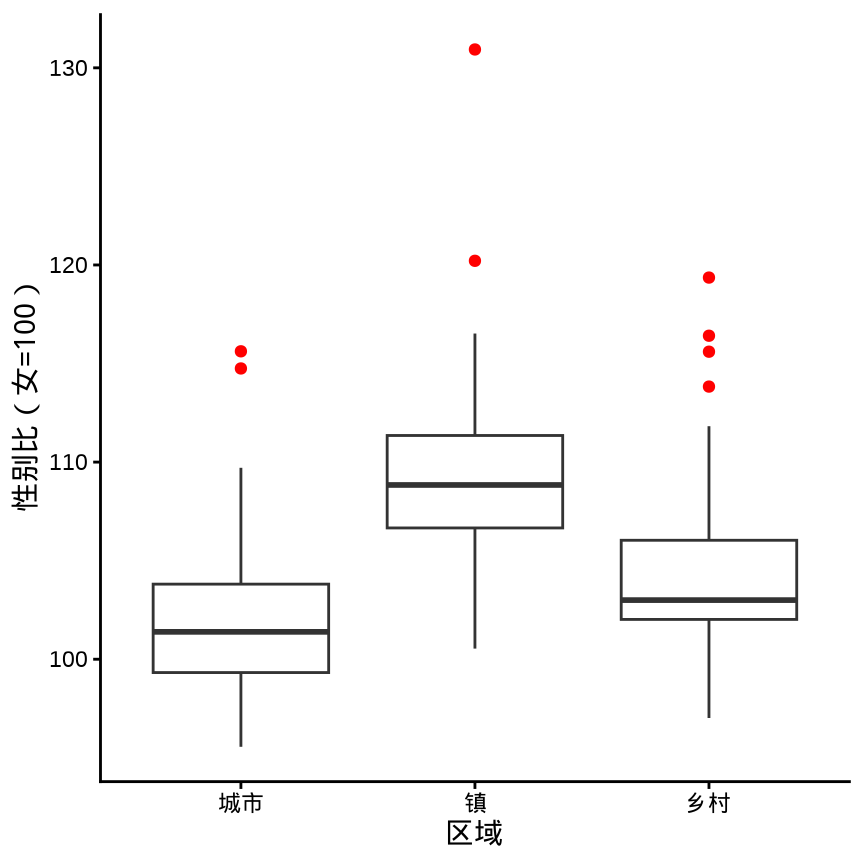
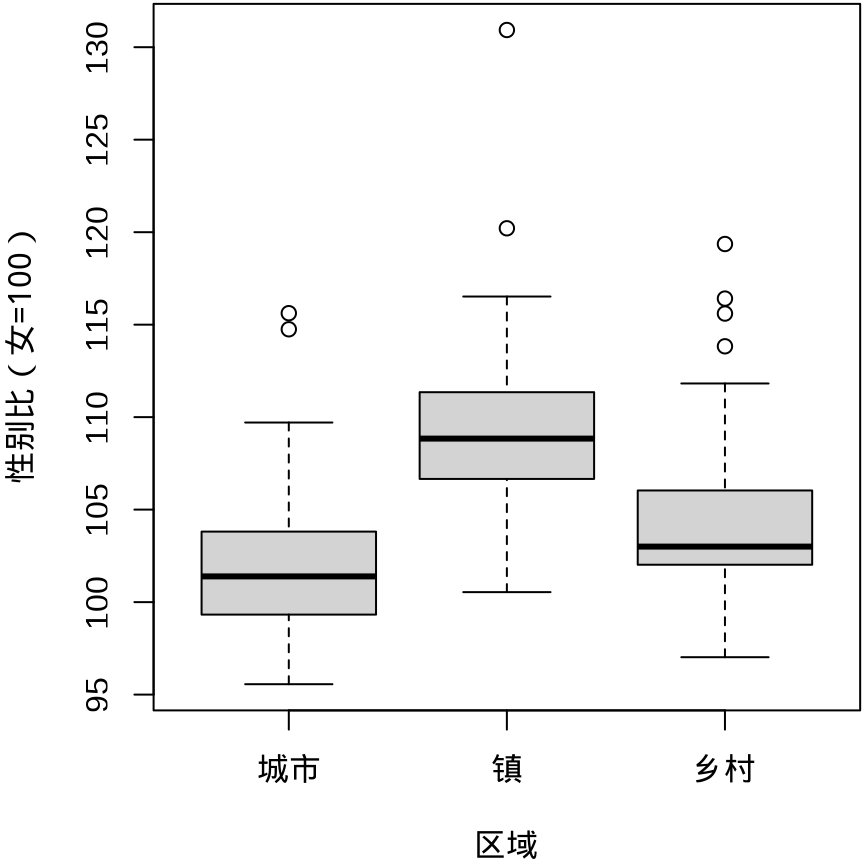
(a) ggplot2 包
(b) ggplot2 包（高亮离群值）
(c) lvplot 包
(d) Base R 包
图 3.1: 箱线图的几种绘制形式

箱线图的历史有 50 多年了，它的变体也有很多，除了 ggplot2 包，lvplot 包也可以绘制箱线图的变体 (McGill 和 Larsen 1978)。更多详情见 Hadley Wickham 和 Lisa Stryjewski 的文章 40 years of boxplots。

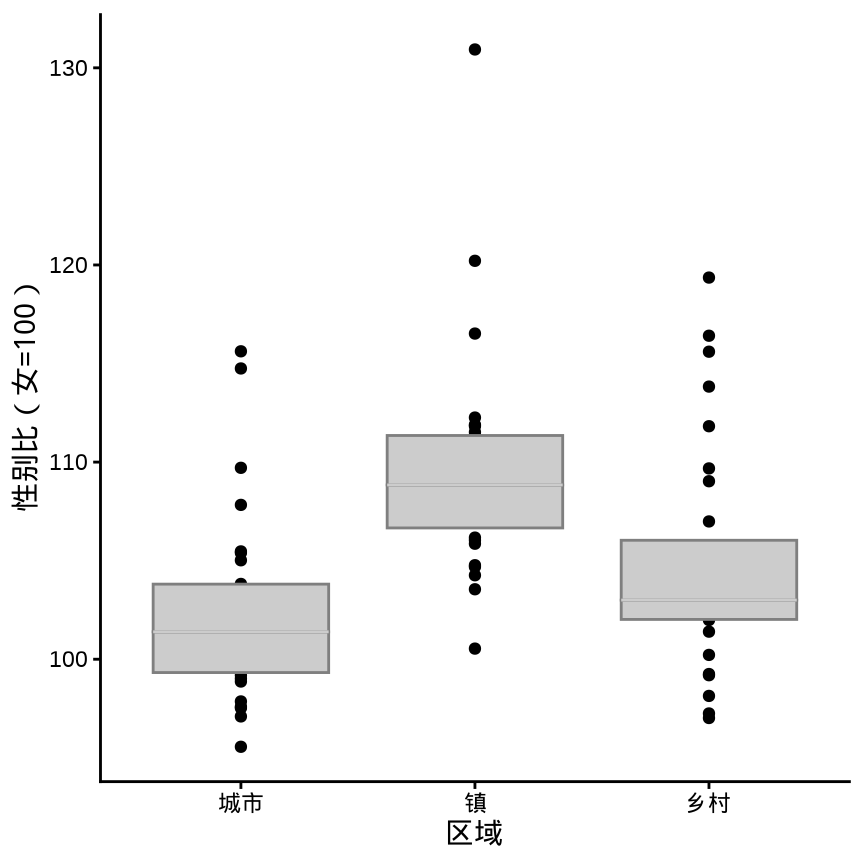
3.1.2 提琴图

ggplot(data = province_sex_ratio, aes(x = `区域`, y = `性别比（女=100）`)) +
  geom_violin(fill = "lightgray") +
  theme_classic()
ggplot(data = province_sex_ratio, aes(x = `区域`, y = `性别比（女=100）`)) +
  geom_violin(fill = "lightgray", draw_quantiles = c(0.25, 0.5, 0.75)) +
  theme_classic()
vioplot::vioplot(`性别比（女=100）` ~ `区域`,
  data = province_sex_ratio, col = "lightgray")
beanplot::beanplot(`性别比（女=100）` ~ `区域`,
  data = province_sex_ratio, col = "lightgray", log = "",
  xlab = "区域", ylab = "性别比（女=100）")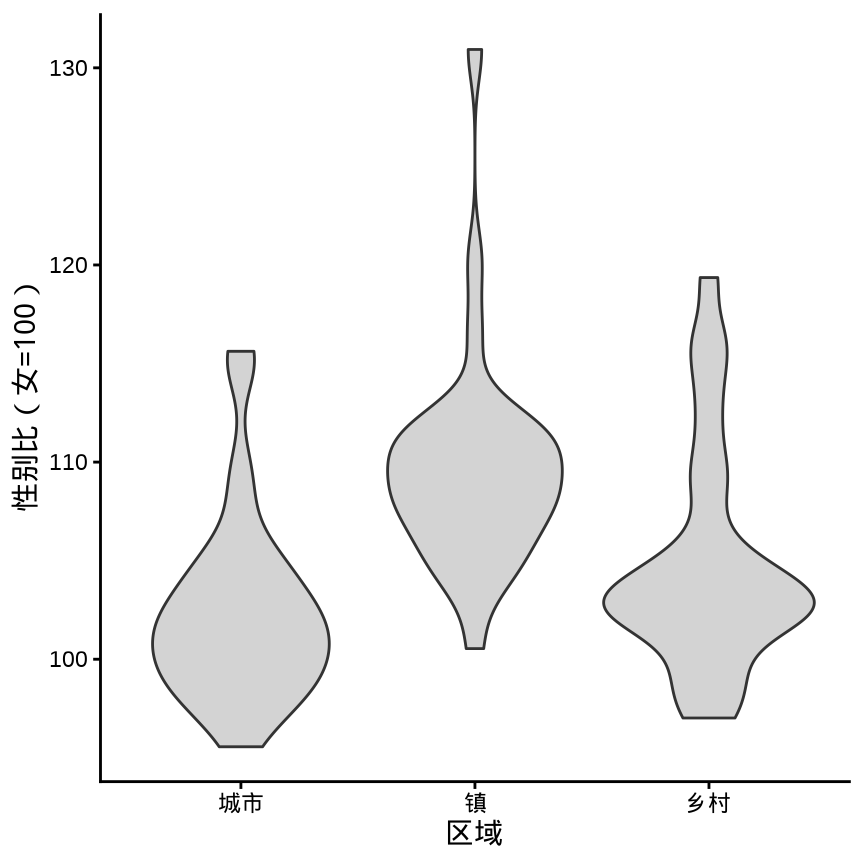
(a) 函数 geom_violin()
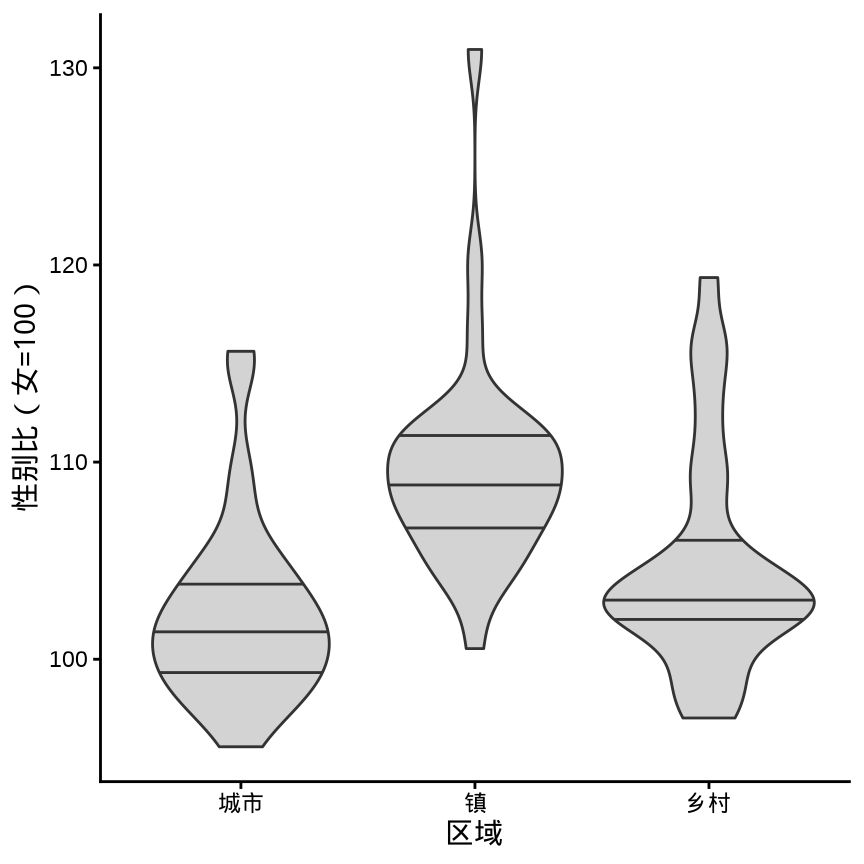
(b) 函数 geom_violin() 标记分位点
(c) vioplot 包
(d) beanplot 包
图 3.2: 提琴图

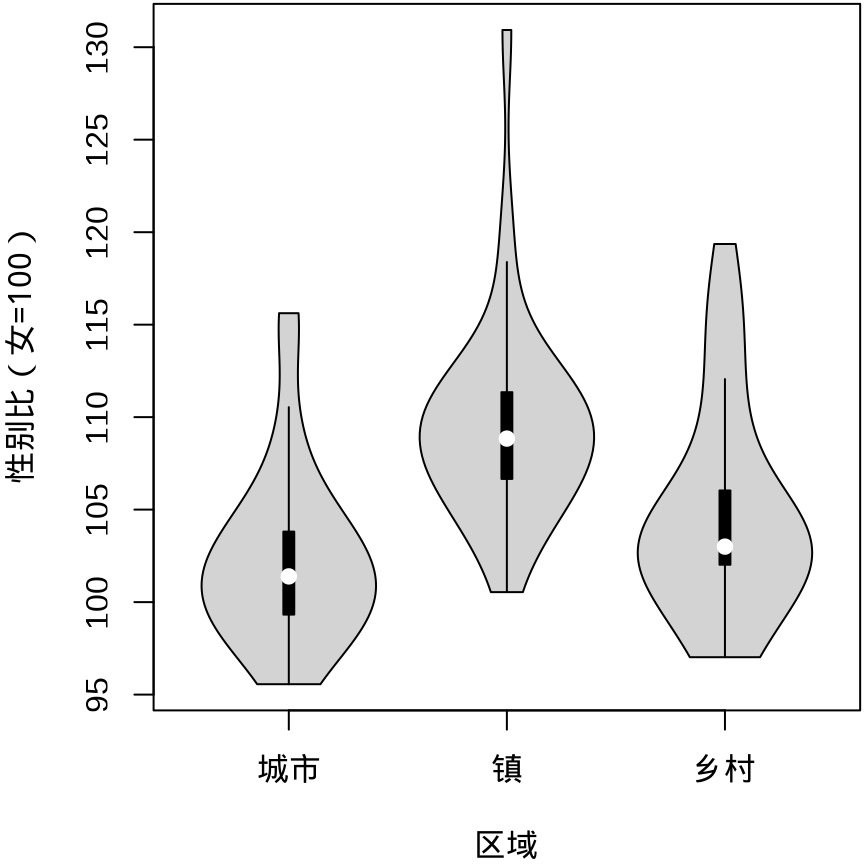
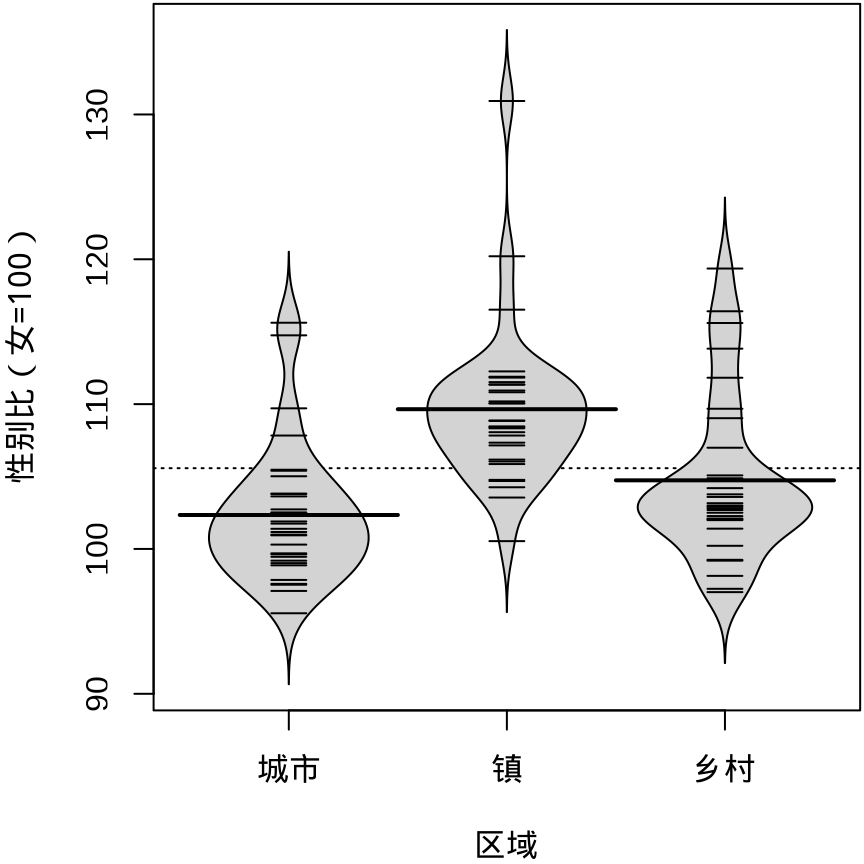
beanplot 包的名字是根据图形的外观取的，bean 即是豌豆，rug 用须线表示数据。

3.1.3 直方图

ggplot2 包绘制直方图的函数是 geom_histogram() ，而与之相关的函数 geom_freqpoly() 是绘制折线图，将直方图中每个柱子的顶点连接起来。

ggplot(data = province_sex_ratio, aes(x = `性别比（女=100）`, fill = `区域`)) +
  geom_histogram(binwidth = 5, color = "white", position = "stack") +
  scale_fill_grey() +
  theme_classic() +
  theme(legend.position = "inside", legend.position.inside = c(0.9, 0.8)) +
  labs(y = "频数")
ggplot(data = province_sex_ratio, aes(x = `性别比（女=100）`, color = `区域`)) +
  geom_freqpoly(binwidth = 5, stat = "bin", position = "stack") +
  scale_color_grey() +
  theme_classic() +
  theme(legend.position = "inside", legend.position.inside = c(0.9, 0.8))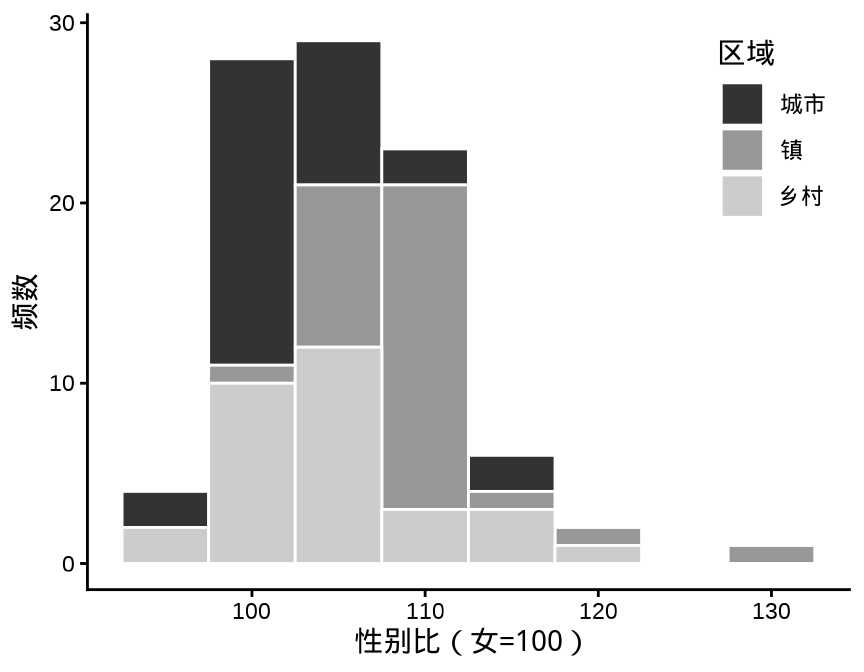
(a) 函数 geom_histogram()
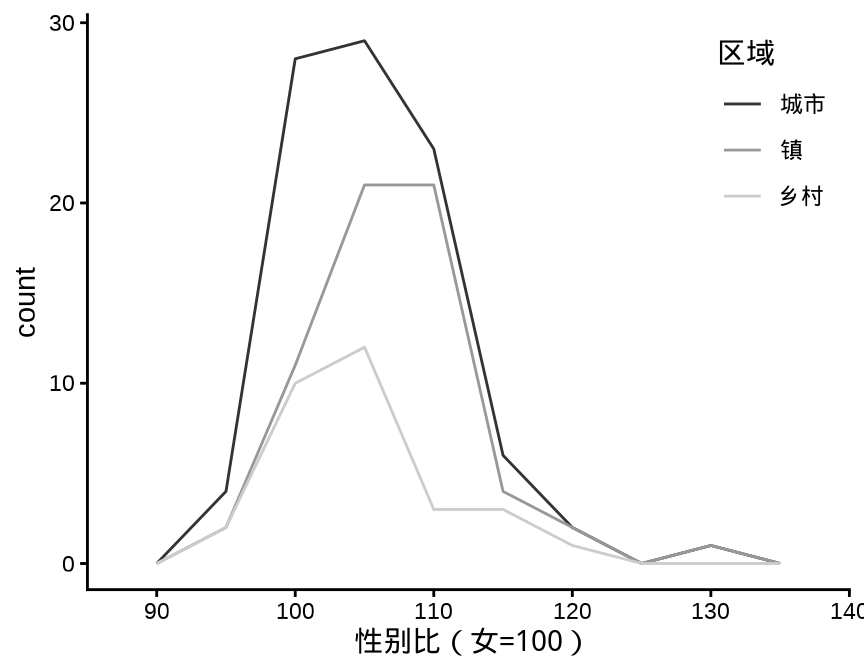
(b) 函数 geom_freqpoly()
图 3.3: 直方图

3.1.4 密度图

ggplot2 包绘制密度图的函数是 geom_density()， 图 3.4 展示分组密度曲线图

ggplot(data = province_sex_ratio, aes(x = `性别比（女=100）`)) +
  geom_density(aes(fill = `区域`), alpha = 0.75) +
  scale_fill_grey() +
  theme_classic()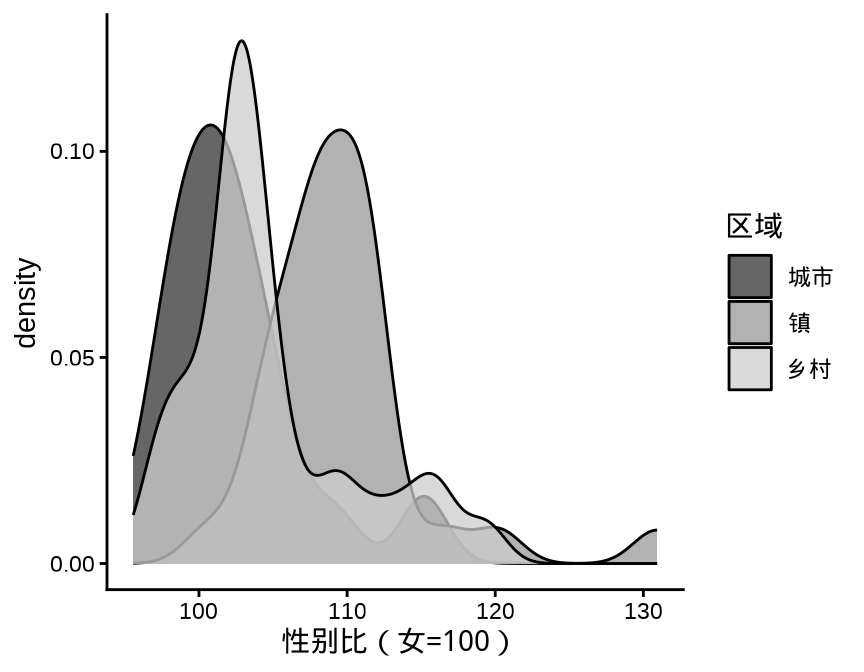
图 3.4: 密度图

3.1.4.1 堆积（条件）密度图

注意

Stacked density plots: if you want to create a stacked density plot, you probably want to ‘count’ (density * n) variable instead of the default density

堆积密度图正确的绘制方式是保护边际密度。

ggplot(data = province_sex_ratio, aes(x = `性别比（女=100）`, y = after_stat(density))) +
  geom_density(aes(fill = `区域`), position = "stack", alpha = 0.5) +
  scale_fill_grey() +
  theme_classic() +
  theme(legend.position = "inside", legend.position.inside = c(0.9, 0.8))
ggplot(data = province_sex_ratio, aes(x = `性别比（女=100）`, y = after_stat(density * n))) +
  geom_density(aes(fill = `区域`), position = "stack", alpha = 0.5) +
  scale_fill_grey() +
  theme_classic() +
  theme(legend.position = "inside", legend.position.inside = c(0.9, 0.8))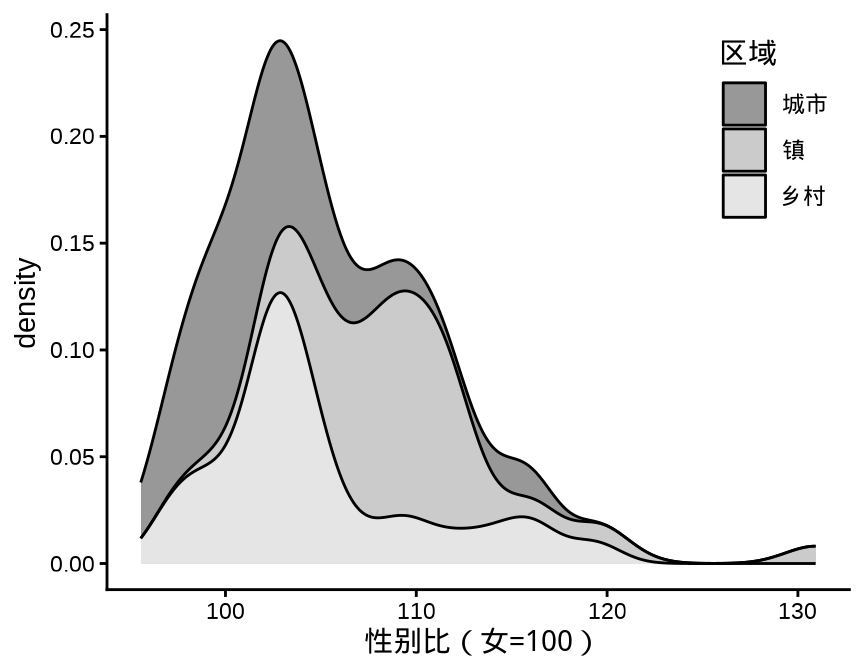
(a) 堆积密度图 after_stat(density)
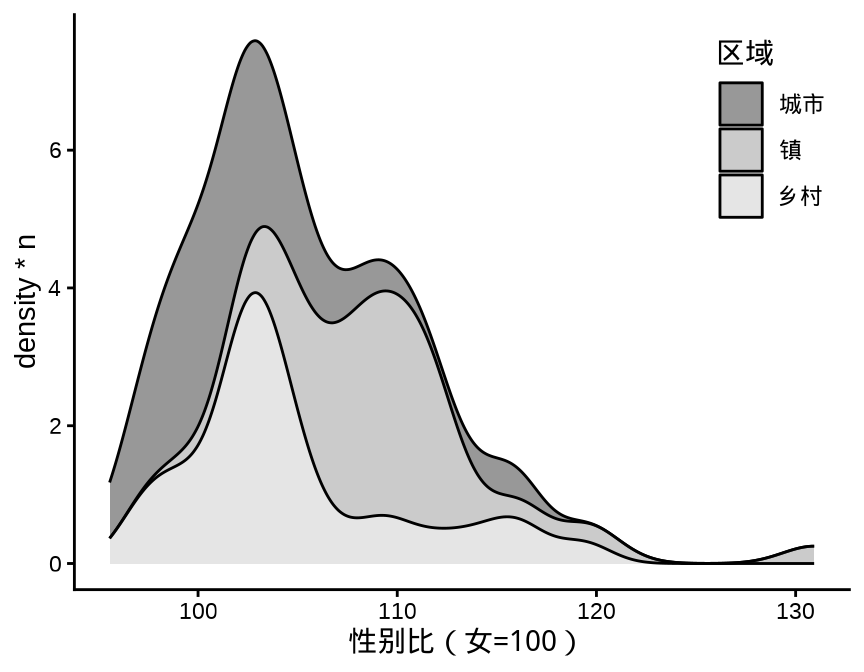
(b) 堆积密度图 after_stat(density * n)
图 3.5: 累积分布密度图

什么原因导致 图 3.5 中两个子图看起来没什么差别呢？而换一组数据，就可以看出明显的差别。

ggplot(diamonds, aes(x = carat, y = after_stat(density), fill = cut)) +
  geom_density(position = "stack") +
  scale_fill_grey() +
  theme_classic() +
  theme(legend.position = "inside", legend.position.inside = c(0.8, 0.7)) +
  labs(x = "克拉", y = "频数", fill = "切工")
ggplot(diamonds, aes(x = carat, y = after_stat(density * n), fill = cut)) +
  geom_density(position = "stack") +
  scale_fill_grey() +
  scale_y_continuous(
    breaks = c(25000, 50000, 75000), 
    labels = c("25K", "50K", "75K")) +
  theme_classic() +
  theme(legend.position = "inside", legend.position.inside = c(0.8, 0.7)) +
  labs(x = "克拉", y = "频数", fill = "切工")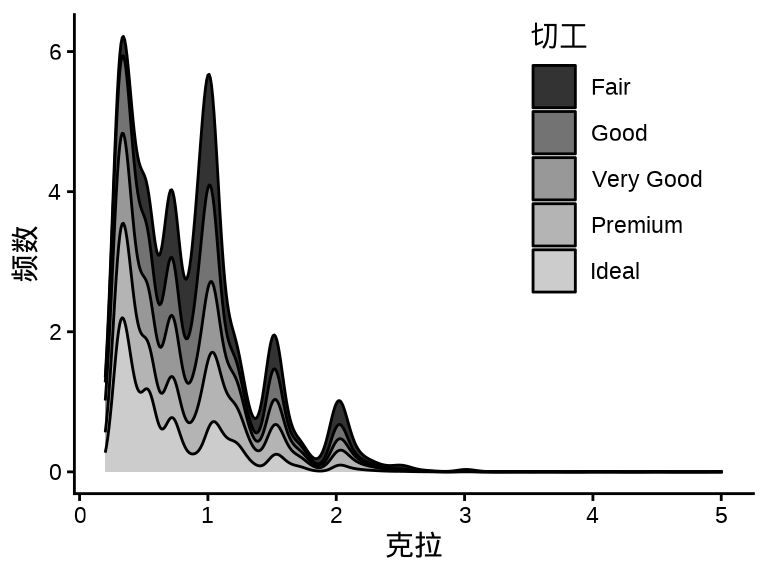
(a) 函数 after_stat(density)
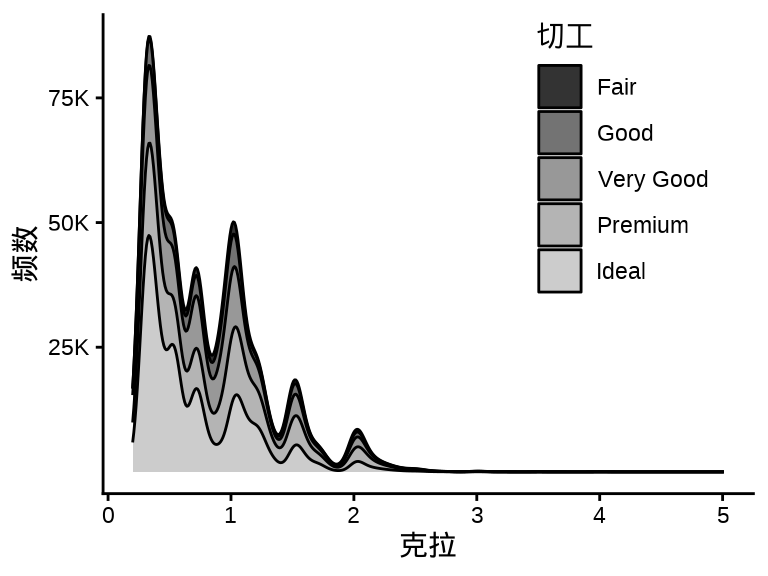
(b) 函数 after_stat(density * n)
图 3.6: 堆积密度图

3.1.4.2 联合密度图

state_x77 <- data.frame(state.x77, state_name = rownames(state.x77),
  state_region = state.region, check.names = FALSE)
p1 <- ggplot(data = state_x77, aes(x = Income, y = `Life Exp`)) +
  geom_point() +
  geom_density_2d(
    aes(color = after_stat(level), alpha = after_stat(level)), show.legend = F
  ) +
  scale_color_distiller(palette = "Greys") +
  labs(
    x = "人均收入（美元）", y = "预期寿命（年）",
    title = "1977 年各州预期寿命与人均收入的关系",
    caption = "数据源：美国人口调查局"
  ) +
  theme_classic()
p1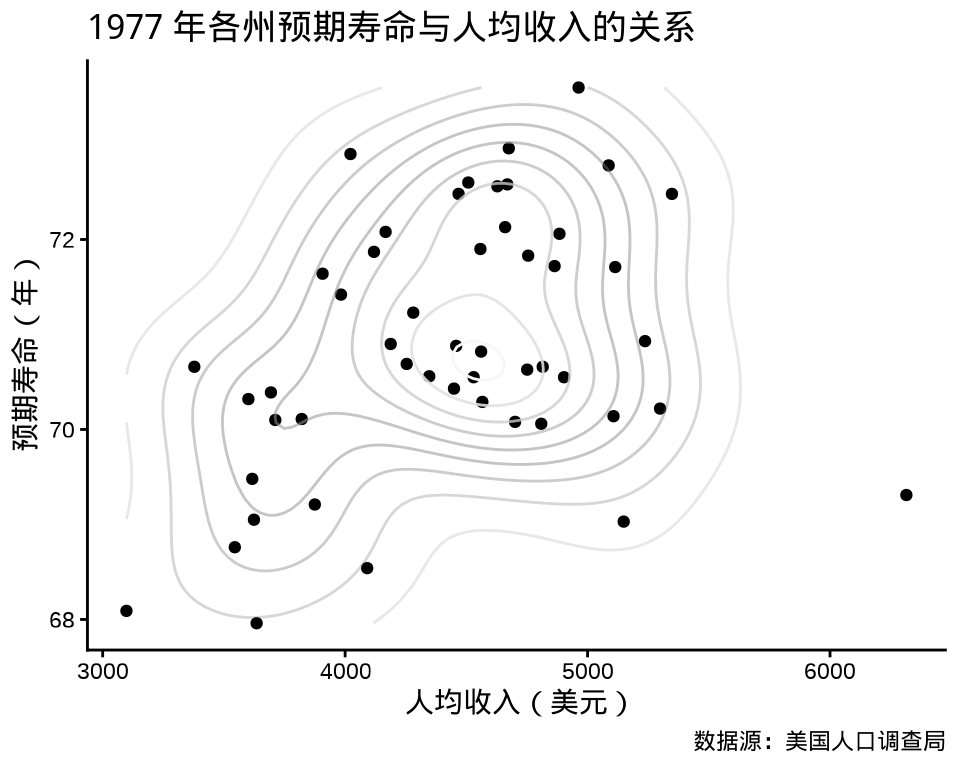
图 3.7: 二维联合密度图

3.1.4.3 边际密度图

ggExtra 包(Attali 和 Baker 2022) 添加边际密度曲线和边际直方图。

library(ggExtra)
ggMarginal(p1, type = "density")
ggMarginal(p1, type = "histogram")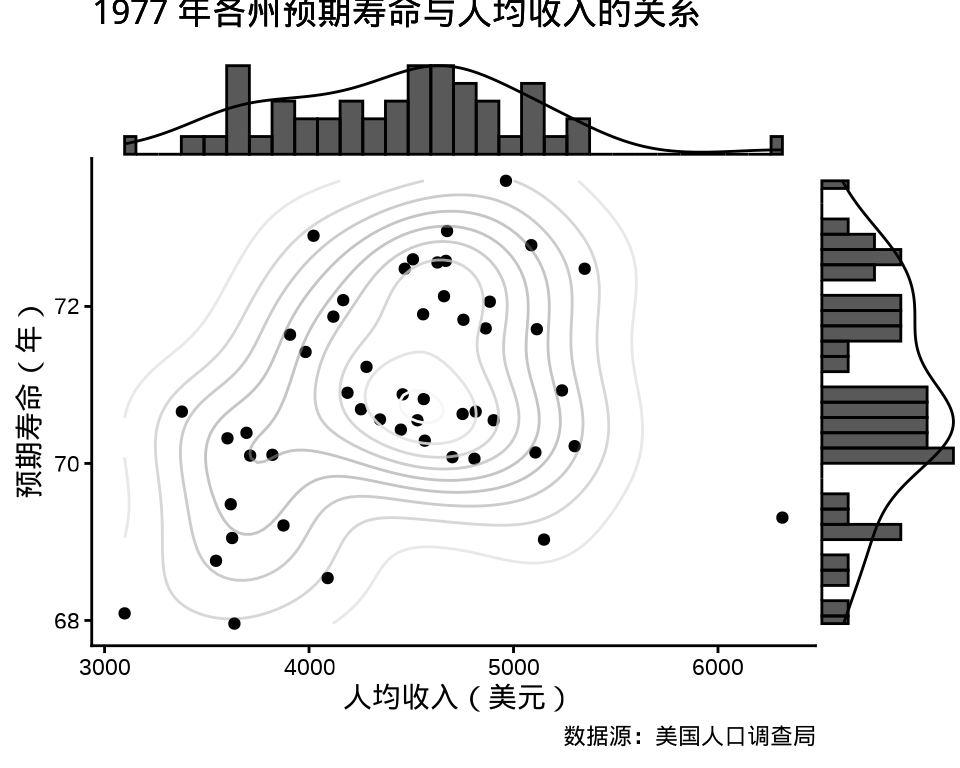
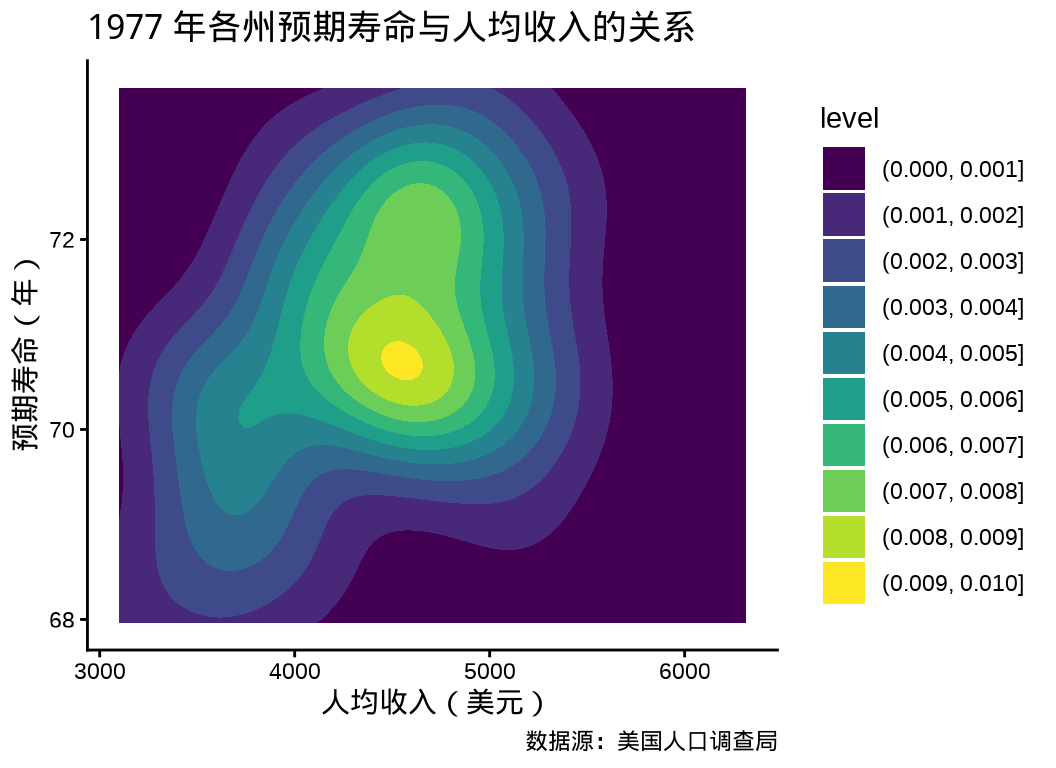
图 3.8: 描述边际分布

3.1.4.4 填充密度图

ggplot2 包提供二维密度图层 geom_density_2d_filled() 绘制热力图， ggdist (Kay 2022) 进行了一些扩展。

ggplot(data = state_x77, aes(x = Income, y = `Life Exp`)) +
  geom_density_2d_filled(contour_var = "count") +
  theme_classic() +
  labs(
    x = "人均收入（美元）", y = "预期寿命（年）",
    title = "1977 年各州预期寿命与人均收入的关系",
    caption = "数据源：美国人口调查局"
  )
图 3.9: ggplot2 包绘制二维填充密度图

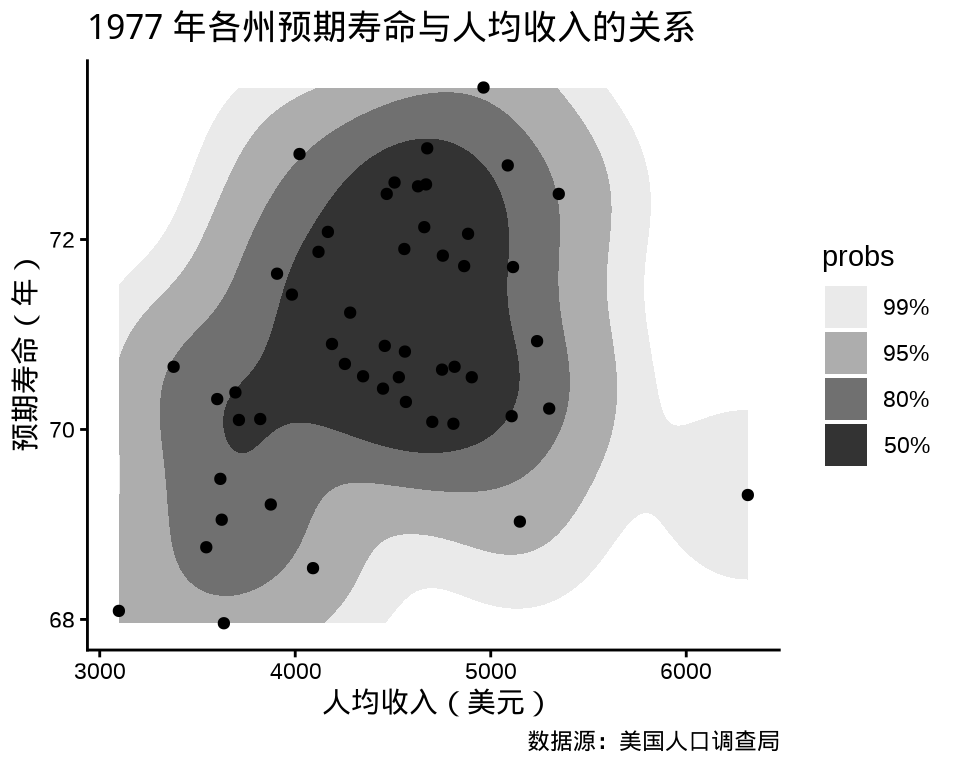
相比于 ggplot2 内置的二维核密度估计，ggdensity (Otto 和 Kahle 2023) 有一些优势，根据数据密度将目标区域划分，更加突出层次和边界。gghdr 包与 ggdensity 类似，展示 highest density regions (HDR)

library(ggdensity)
ggplot(data = state_x77, aes(x = Income, y = `Life Exp`)) +
  geom_hdr() +
  geom_point() +
  theme_classic() +
  labs(
    x = "人均收入（美元）", y = "预期寿命（年）",
    title = "1977 年各州预期寿命与人均收入的关系",
    caption = "数据源：美国人口调查局"
  )
图 3.10: ggdensity 包绘制二维填充密度图

3.1.5 岭线图

叠嶂图，还有些其它名字，如峰峦图、岭线图等，详情参考统计之都主站《叠嶂图的前世今生》，主要用来描述数据的分布情况，在展示分布的对比上效果非常好。

图 3.11 设置窗宽为 1.5 个百分点

(a) 岭线图
(b) 岭线图和抖动图组合
(c) 岭线图和轴须图组合
图 3.11: 描述数据分布
提示

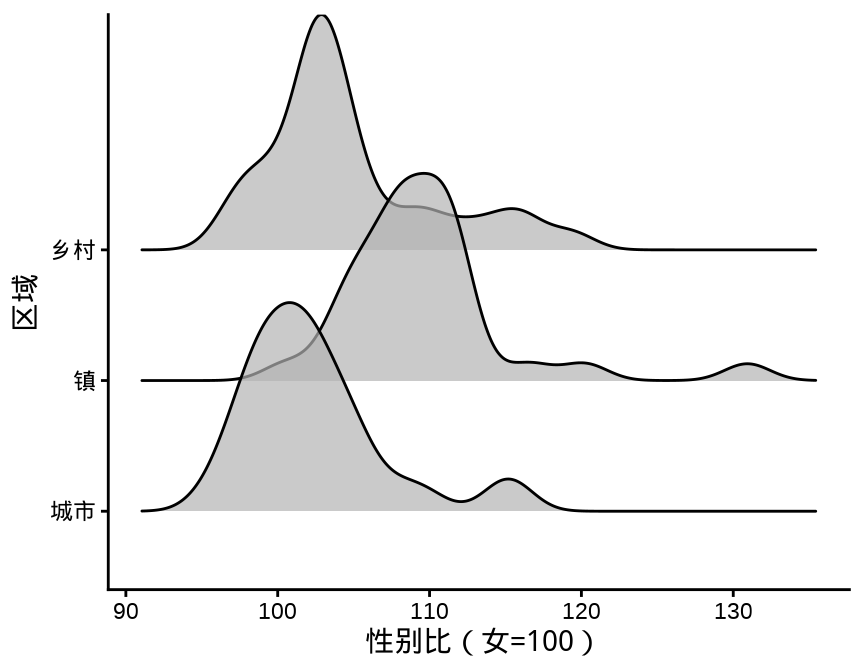
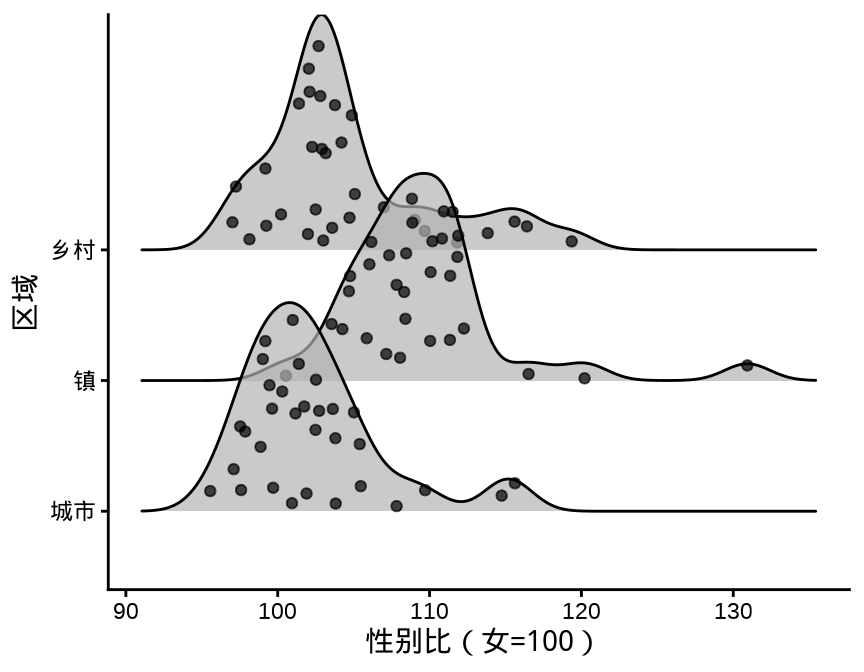
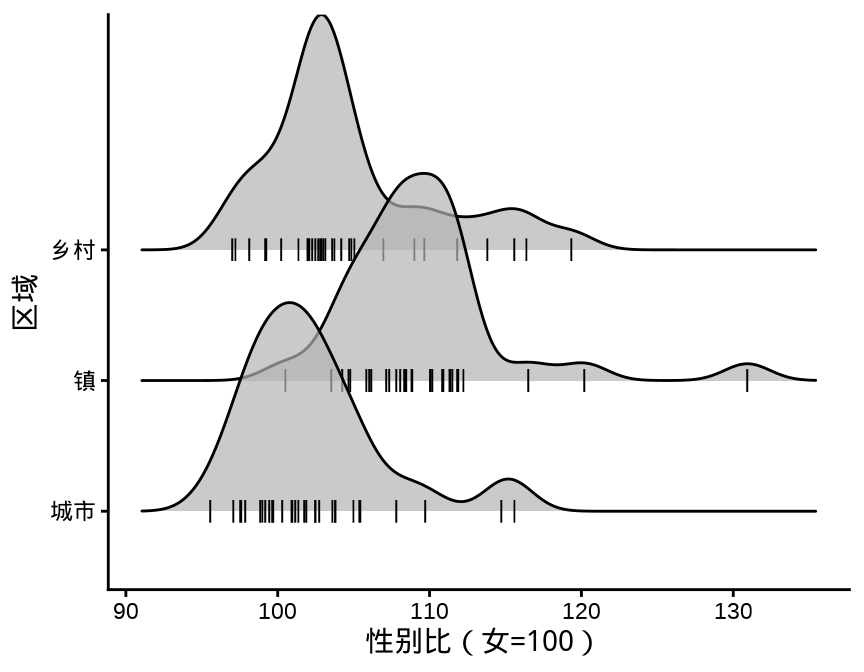
除了中国国家统计年鉴，各省、自治区、直辖市及各级统计局每年都会发布一些统计年鉴、公告等数据，读者可以在此基础上继续收集更多数据，来分析诸多有意思的问题：

  1. 城市、镇和乡村男女性别比呈现差异化分布的成因。
  2. 城市、镇和乡村男女年龄构成。
  3. 将上述问题从省级下钻到市、县级来分析。

3.1.6 抖动图

下面先用函数 geom_point() 绘制散点图展示原始数据，通过点的疏密程度暗示数据的分布。Base R 函数 stripchart() 可以实现类似的效果。当数据量比较大时，点相互覆盖比较严重，此时，抖动图比较适合用来展示原始数据。函数 geom_beeswarm() 提供了另一种散点的组织方式，按一定的规则，而不是近似随机的方式组织。

ggplot(data = province_sex_ratio, aes(x = `区域`, y = `性别比（女=100）`)) +
  geom_point() +
  theme_classic()
stripchart(
  `性别比（女=100）` ~ `区域`, vertical = TRUE, pch = 1,
  data = province_sex_ratio, xlab = "区域")
ggplot(data = province_sex_ratio, aes(x = `区域`, y = `性别比（女=100）`)) +
  geom_jitter(width = 0.25) +
  theme_classic()
library(ggbeeswarm)
ggplot(data = province_sex_ratio, aes(x = `区域`, y = `性别比（女=100）`)) +
  geom_beeswarm() +
  theme_classic()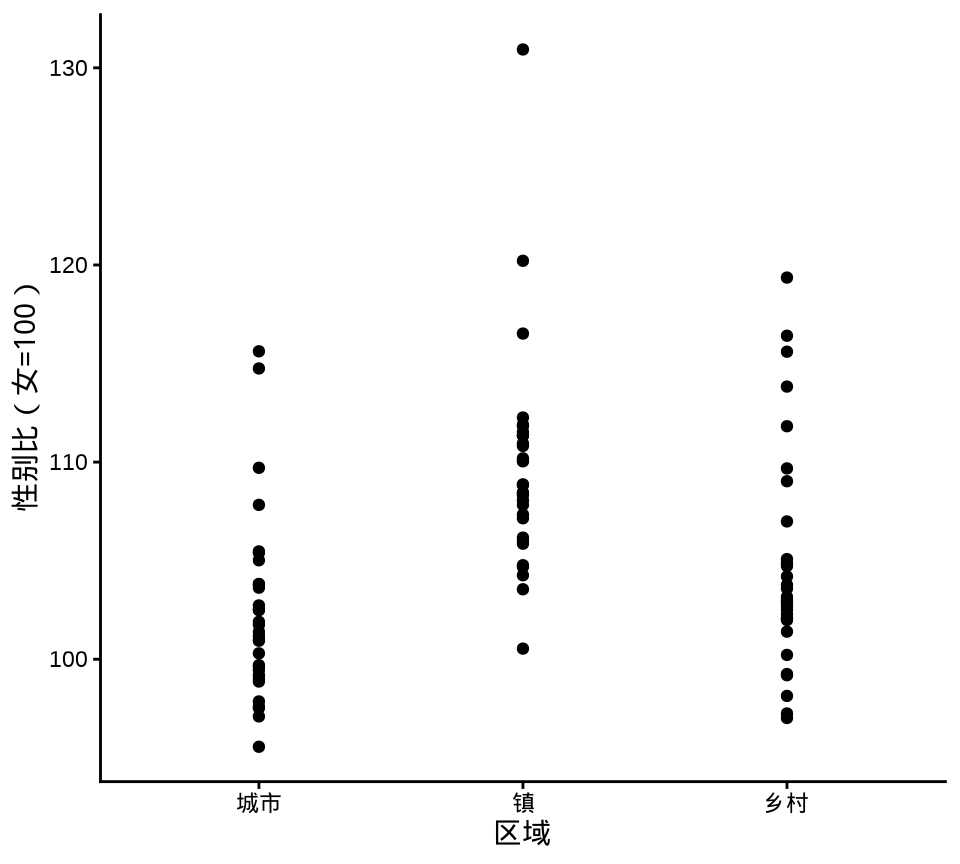
(a) 函数 geom_point()
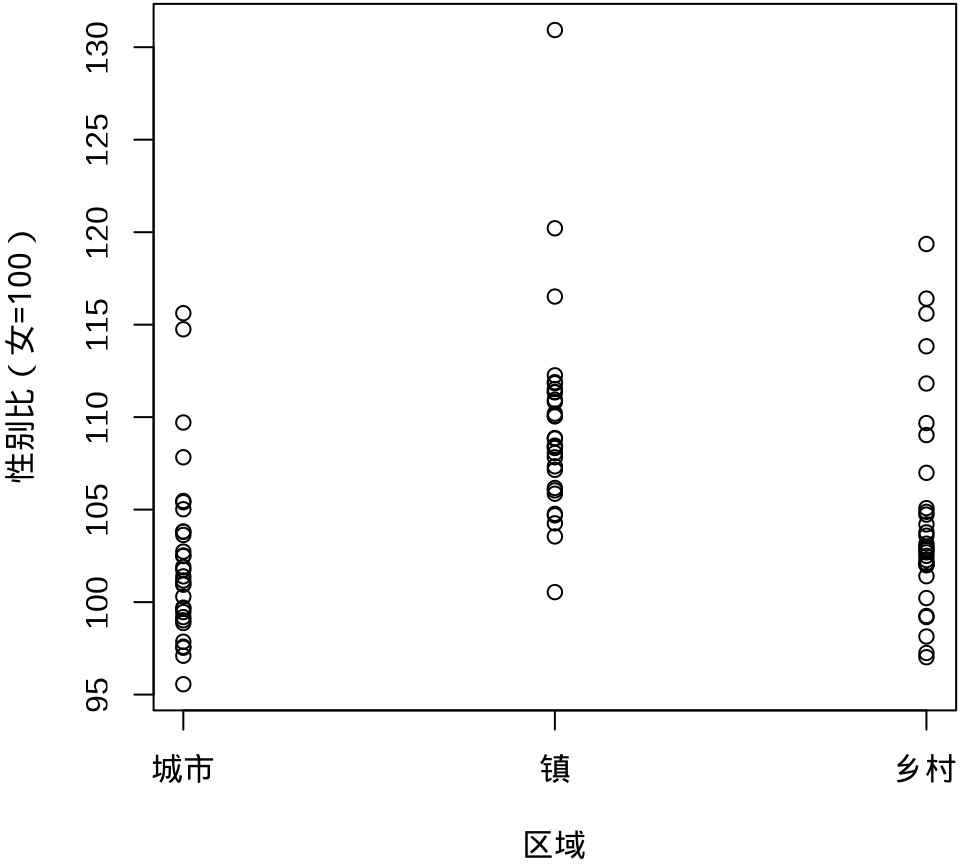
(b) 函数 stripchart()
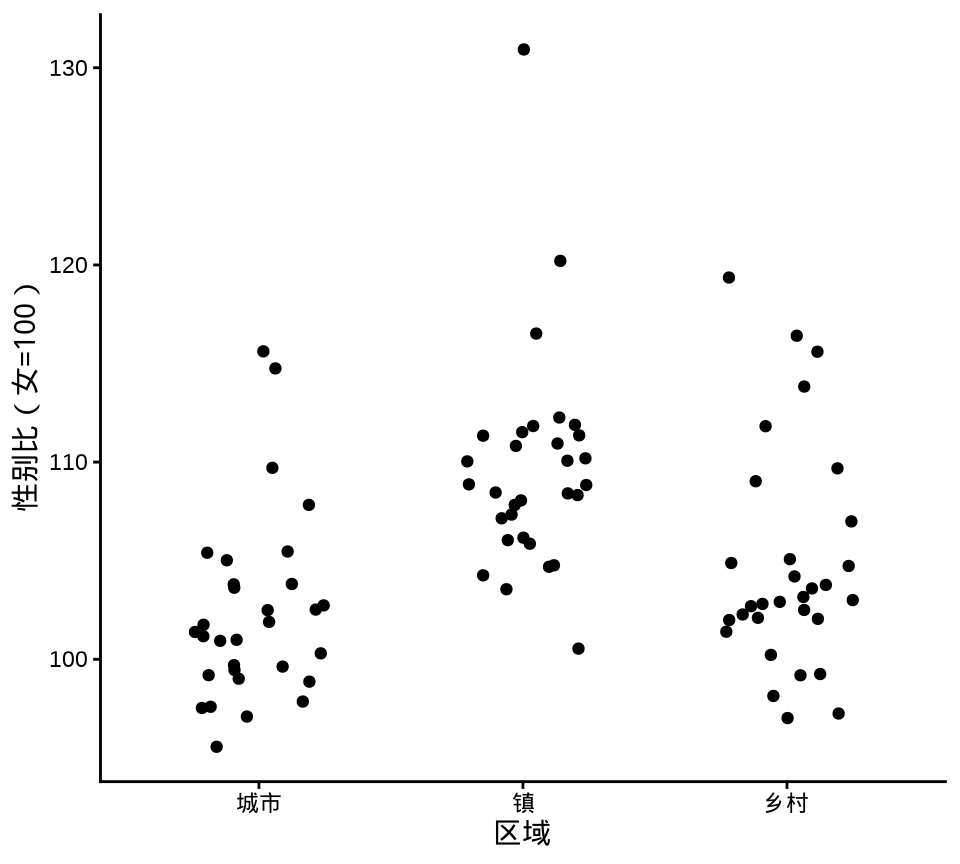
(c) 函数 geom_jitter()
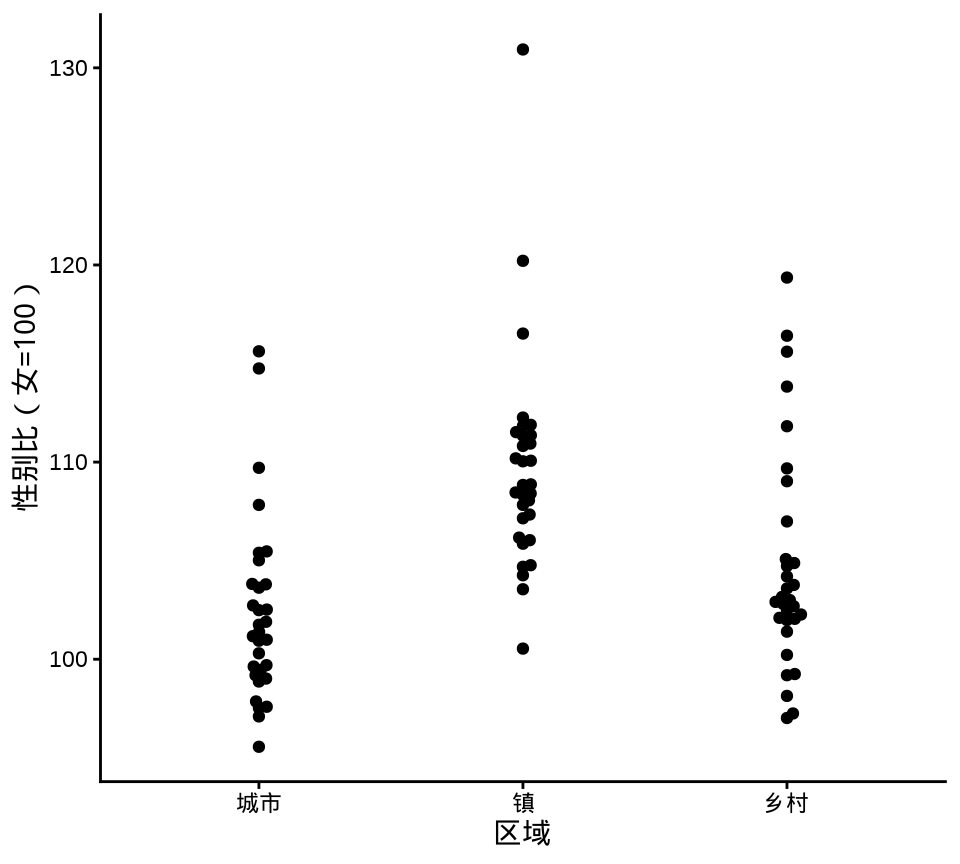
(d) 函数 geom_beeswarm()
图 3.12: 散点图

Sidiropoulos 等 (2018) 提出一种新的方式描述数据的分布，集合抖动图和小提琴图的功能，在给定的分布界限内抖动。数据点受 violin 的曲线限制，蜂群图也是某种形式的抖动图，添加 violin 作为参考边界，与 sina 图是非常类似的。

library(ggforce)
ggplot(data = province_sex_ratio, aes(x = `区域`, y = `性别比（女=100）`)) +
  geom_sina() +
  theme_classic()
ggplot(data = province_sex_ratio, aes(x = `区域`, y = `性别比（女=100）`)) +
  geom_violin() +
  geom_sina() +
  theme_classic()
library(ggbeeswarm)
ggplot(data = province_sex_ratio, aes(x = `区域`, y = `性别比（女=100）`)) +
  geom_quasirandom() +
  theme_classic()
ggplot(data = province_sex_ratio, aes(x = `区域`, y = `性别比（女=100）`)) +
  geom_violin() +
  geom_quasirandom() +
  theme_classic()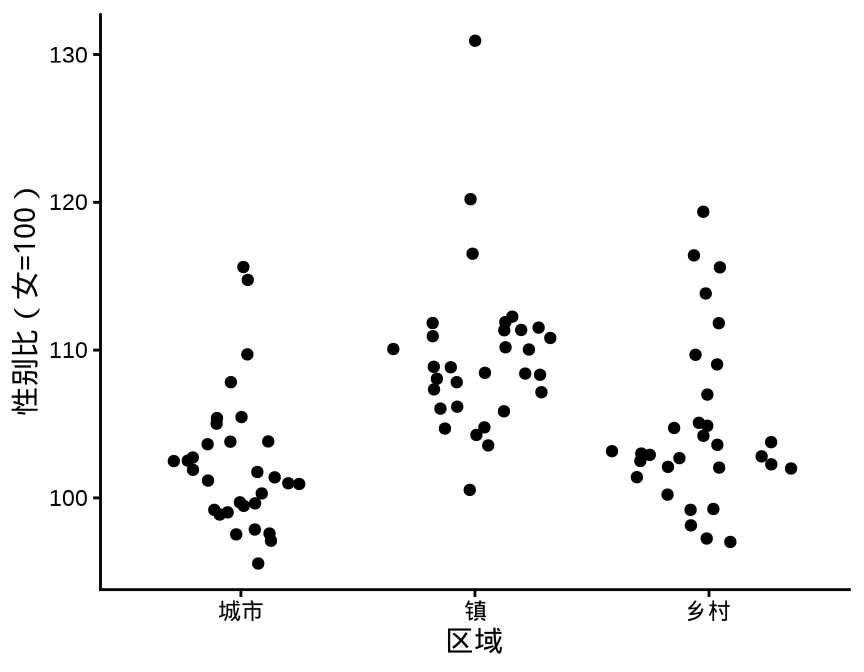
(a) ggforce 包的函数 geom_sina()
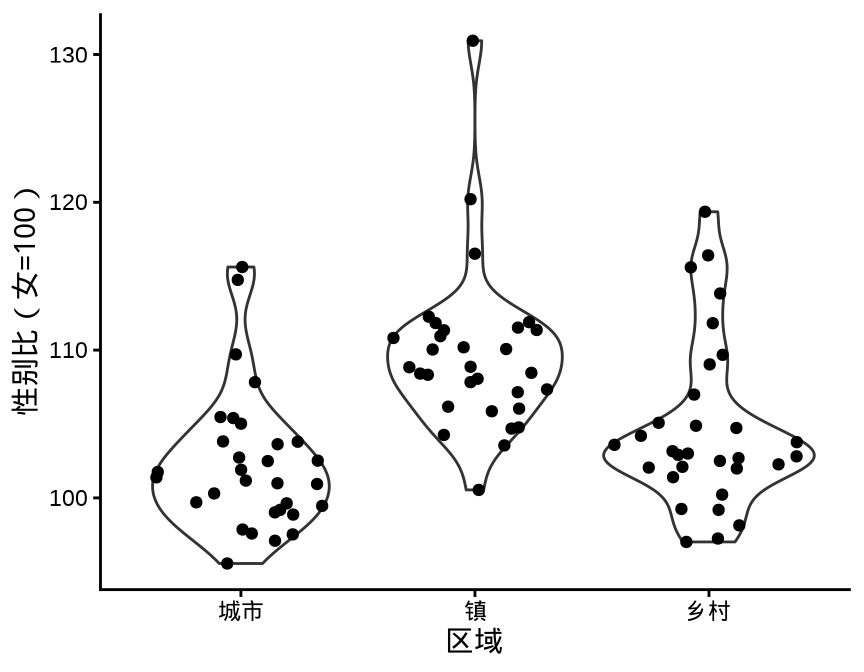
(b) 函数 geom_sina() 叠加函数 geom_violin()
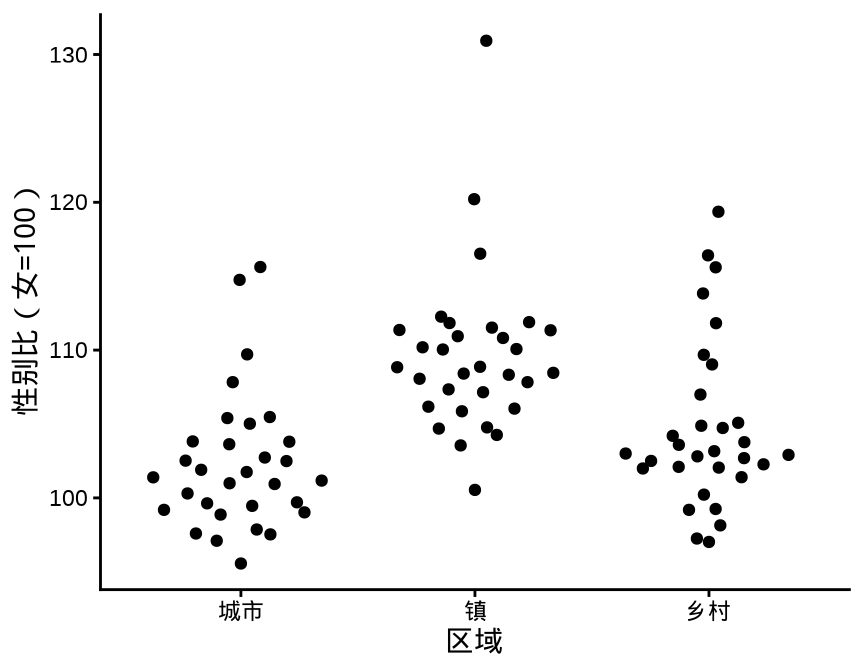
(c) ggbeeswarm 包的函数 geom_quasirandom()
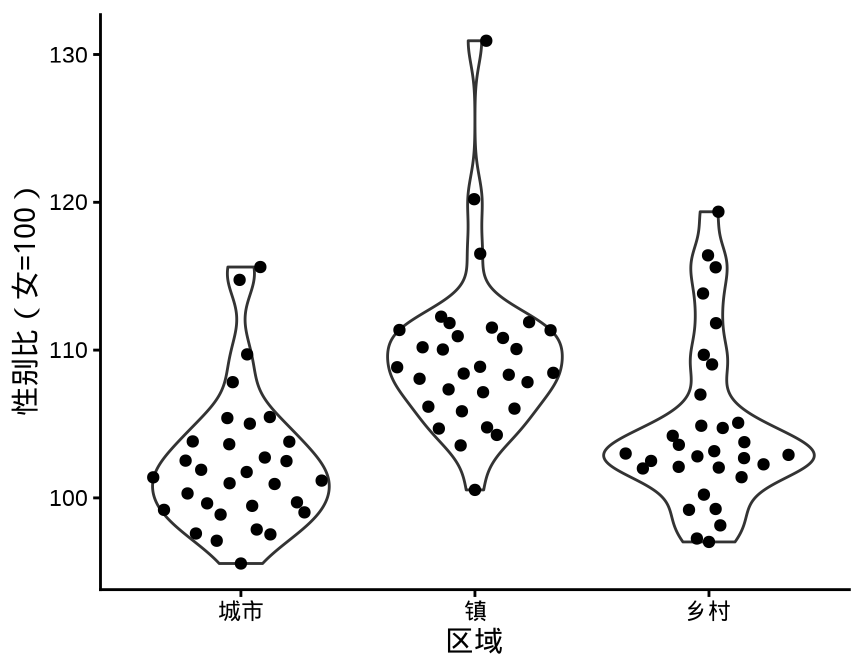
(d) 函数 geom_quasirandom() 叠加函数 geom_violin()
图 3.13: 加强版的抖动图

3.2 描述关系

3.2.1 散点图

散点图用以描述变量之间的关系，展示原始的数据，点的形态、大小、颜色等都可以随更多变量变化。

中国国家统计局 2021 年发布的统计年鉴，2020 年 31 个省、直辖市、自治区的抚养比、文盲率、人口数的关系。

表格 3.2: 2020 年各省、直辖市、自治区，总抚养比和文盲率相关数据（部分）
地区 人口数 15-64岁 抚养比 15岁及以上人口 文盲人口 文盲率
广东 126012510 91449628 37.79 102262628 1826344 1.79
山东 101527453 67100737 51.31 62464815 3308280 4.01
河南 99365519 62974661 57.79 76376565 2228594 2.92
江苏 84748016 58129537 45.79 71856068 2211291 3.08
四川 83674866 56036154 49.32 70203754 3330733 4.74
河北 74610235 49133330 51.85 59521267 1128423 1.90

其中，文盲人口是指15岁及以上不识字及识字很少人口，文盲率 = 文盲人口 / 15岁及以上人口，抚养比 = (0-14岁 + 65岁及以上) / 15-64岁人口数。

library(ggplot2)
ggplot(data = china_raise_illiteracy) +
  geom_point(aes(x = `总抚养比`, y = `文盲人口占15岁及以上人口的比重`)) +
  theme_classic() +
  labs(x = "抚养比（%）", y = "文盲率（%）")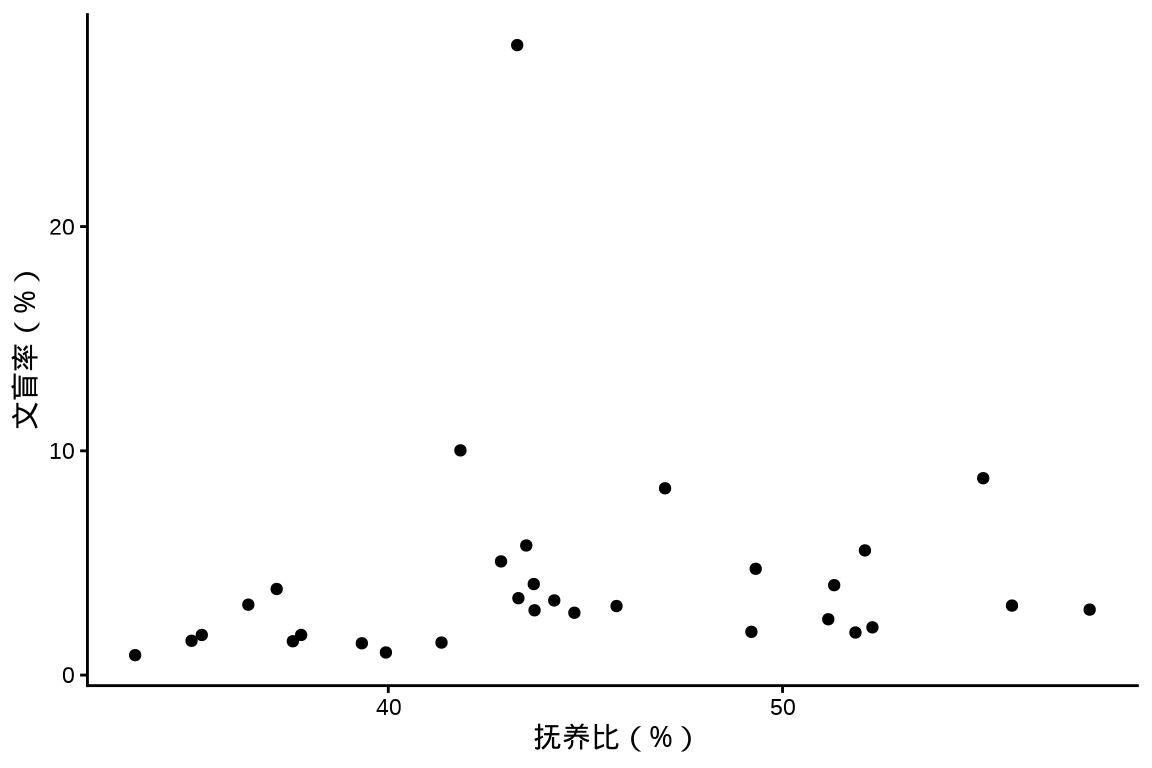
图 3.14: 文盲率与抚养比的关系

3.2.2 气泡图

气泡图在散点图的基础上，添加了散点大小的视觉维度，可以在图上多展示一列数据，下 图 3.15 新增了人口数变量。此外，在气泡旁边添加地区名称，将气泡填充的颜色也映射给了人口数变量。

library(ggrepel)
library(scales)
ggplot(
  data = china_raise_illiteracy,
  aes(x = `总抚养比`, y = `文盲人口占15岁及以上人口的比重`)
) +
  geom_point(aes(size = `人口数`, color = `人口数`),
    alpha = 0.85, pch = 16,
    show.legend = c(color = FALSE, size = TRUE)
  ) +
  scale_size(labels = label_number(scale_cut = cut_short_scale())) +
  scale_color_viridis_c(option = "C") +
  geom_text_repel(
    aes(label = `地区`), size = 3, max.overlaps = 50,
    segment.colour = "gray", seed = 2022, show.legend = FALSE
  ) +
  coord_cartesian(xlim = c(30, 60), ylim = c(0, 10.5), expand = FALSE) +
  theme_classic() +
  labs(x = "抚养比（%）", y = "文盲率（%）")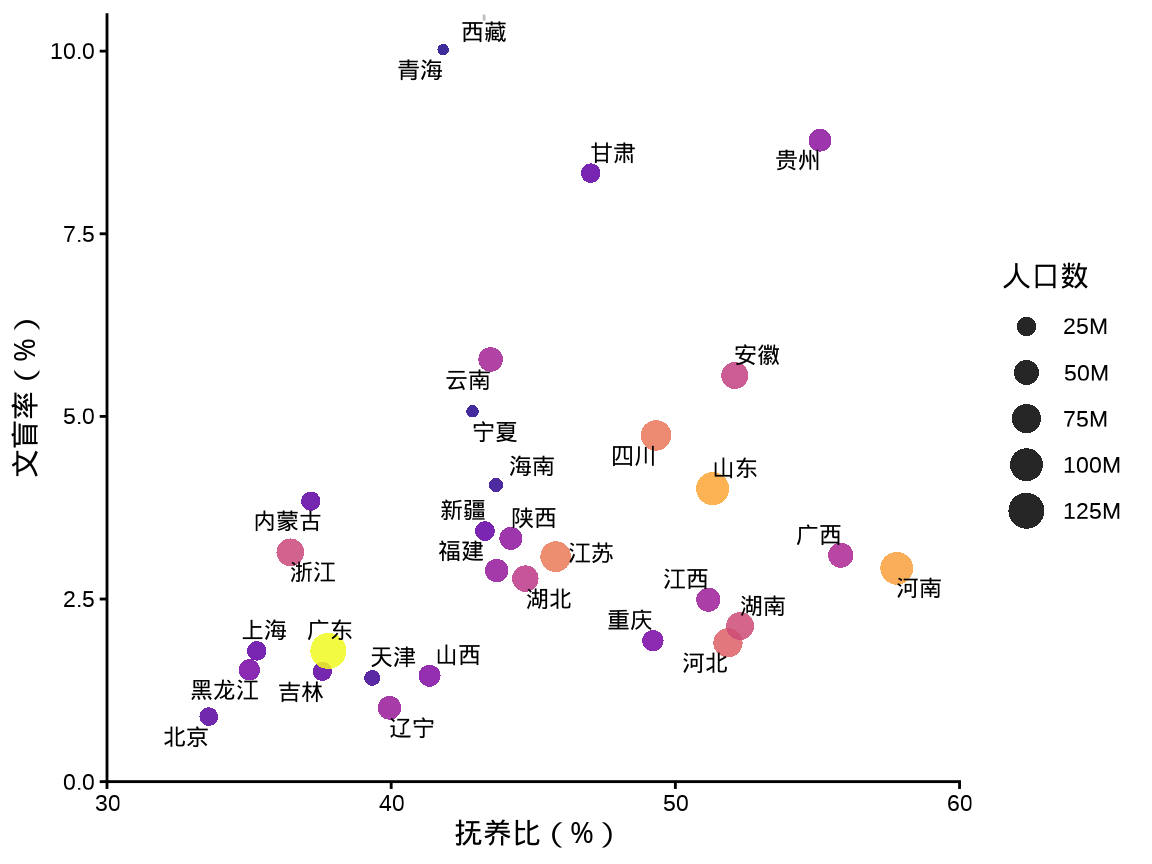
图 3.15: 文盲率和抚养比数据

3.2.3 凹凸图

凹凸图描述位置排序关系随时间的变化，比如前年、去年和今年各省的 GDP 排序变化，春节各旅游景点的人流量变化。ggbump 包专门用来绘制凹凸图，如 图 3.16 所示，展示

library(ggbump)
# 位置排序变化
df <- data.frame(
  country = c(
    "印度", "印度", "印度", "瑞典",
    "瑞典", "瑞典", "德国", "德国",
    "德国", "芬兰", "芬兰", "芬兰"
  ),
  year = c(
    2018, 2019, 2020, 2018, 2019, 2020,
    2018, 2019, 2020, 2018, 2019, 2020
  ),
  value = c(
    492, 246, 246, 369, 123, 492,
    246, 369, 123, 123, 492, 369
  )
)

library(data.table)
df <- as.data.table(df)
df[, rank := rank(value, ties.method = "random"), by = "year"]

ggplot(df, aes(year, rank, color = country)) +
  geom_point(size = 7) +
  geom_text(data = df[df$year == min(df$year), ],
            aes(x = year - .1, label = country), size = 5, hjust = 1) +
  geom_text(data = df[df$year == max(df$year), ],
            aes(x = year + .1, label = country), size = 5, hjust = 0) +
  geom_bump(linewidth = 2, smooth = 8) +
  scale_x_continuous(limits = c(2017.6, 2020.4), breaks = seq(2018, 2020, 1)) +
  theme_minimal(base_size = 14) +
  theme(legend.position = "none", panel.grid.major = element_blank()) +
  labs(x = NULL, y = "排名") +
  scale_y_reverse() +
  coord_fixed(ratio = 0.5)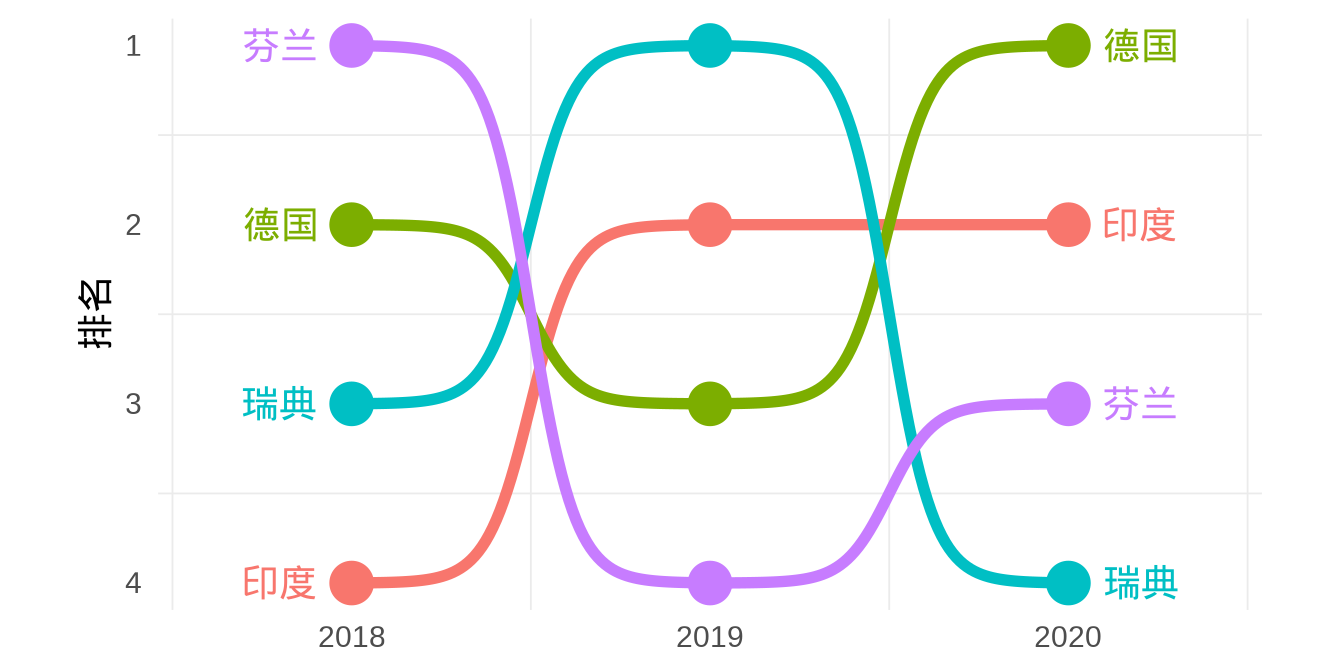
图 3.16: 凹凸图

3.2.4 韦恩图

韦恩图描述集合、群体的交叉关系，整体和部分的包含关系，ggVennDiagram 包展示 A、B、C 三个集合的交叉关系，如 图 3.17 所示

x <- list(A = 1:5, B = 2:7, C = 5:10)
ggVennDiagram::ggVennDiagram(x) +
  scale_fill_gradient(low = "#F4FAFE", high = "#4981BF")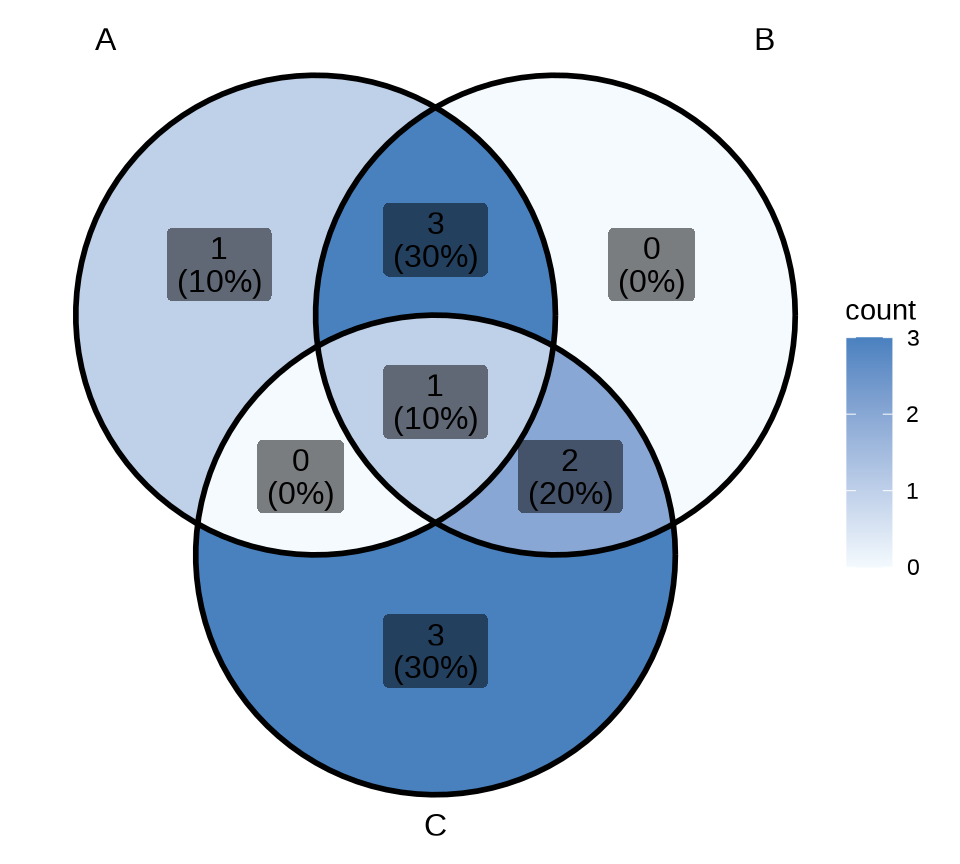
图 3.17: A、B、C 三个集合的交叉关系

3.2.5 网络图

tidygraph 包基于 igraph 包操作图数据，计算网络图中节点重要性，ggraph包基于 ggplot2 包可视化网络关系。

library(ggraph)
data("highschool")
str(highschool)
#> 'data.frame':    506 obs. of  3 variables:
#>  $ from: num  1 1 1 1 1 2 2 3 3 4 ...
#>  $ to  : num  14 15 21 54 55 21 22 9 15 5 ...
#>  $ year: num  1957 1957 1957 1957 1957 ...

highschool 是一个数据框类型的数据，记录了1957 年和 1958 年一些高中男生之间的关系，在数据集中，这些男生被编码成数字 1-71。

highschool[highschool$from == 1, ]
#>     from to year
#> 1      1 14 1957
#> 2      1 15 1957
#> 3      1 21 1957
#> 4      1 54 1957
#> 5      1 55 1957
#> 244    1 15 1958
#> 245    1 21 1958
#> 246    1 22 1958

1 号男生在 1957 年与 14、15、21、54、55 男生关系密切，到了 1958 年，他与 15、21、22 关系比较密切。tidygraph 包在 igraph 的基础上，可以对图数据进行操作，下面先将数据框转化为图，然后计算中心度，作为高中生的受欢迎程度。

graph <- tidygraph::as_tbl_graph(highschool, directed = TRUE) |> 
  dplyr::mutate(Popularity = tidygraph::centrality_degree(mode = 'in'))
graph
#> # A tbl_graph: 70 nodes and 506 edges
#> #
#> # A directed multigraph with 1 component
#> #
#> # Node Data: 70 × 1 (active)
#>    Popularity
#>         <dbl>
#>  1          2
#>  2          0
#>  3          0
#>  4          4
#>  5          5
#>  6          2
#>  7          2
#>  8          3
#>  9          4
#> 10          4
#> # ℹ 60 more rows
#> #
#> # Edge Data: 506 × 3
#>    from    to  year
#>   <int> <int> <dbl>
#> 1     1    13  1957
#> 2     1    14  1957
#> 3     1    20  1957
#> # ℹ 503 more rows
ggraph(graph, layout = "kk") +
  geom_edge_fan(aes(alpha = after_stat(index)), show.legend = FALSE) +
  geom_node_point(aes(size = Popularity)) +
  facet_edges(~year) +
  theme_graph(base_family = "sans", foreground = "steelblue", fg_text_colour = "white")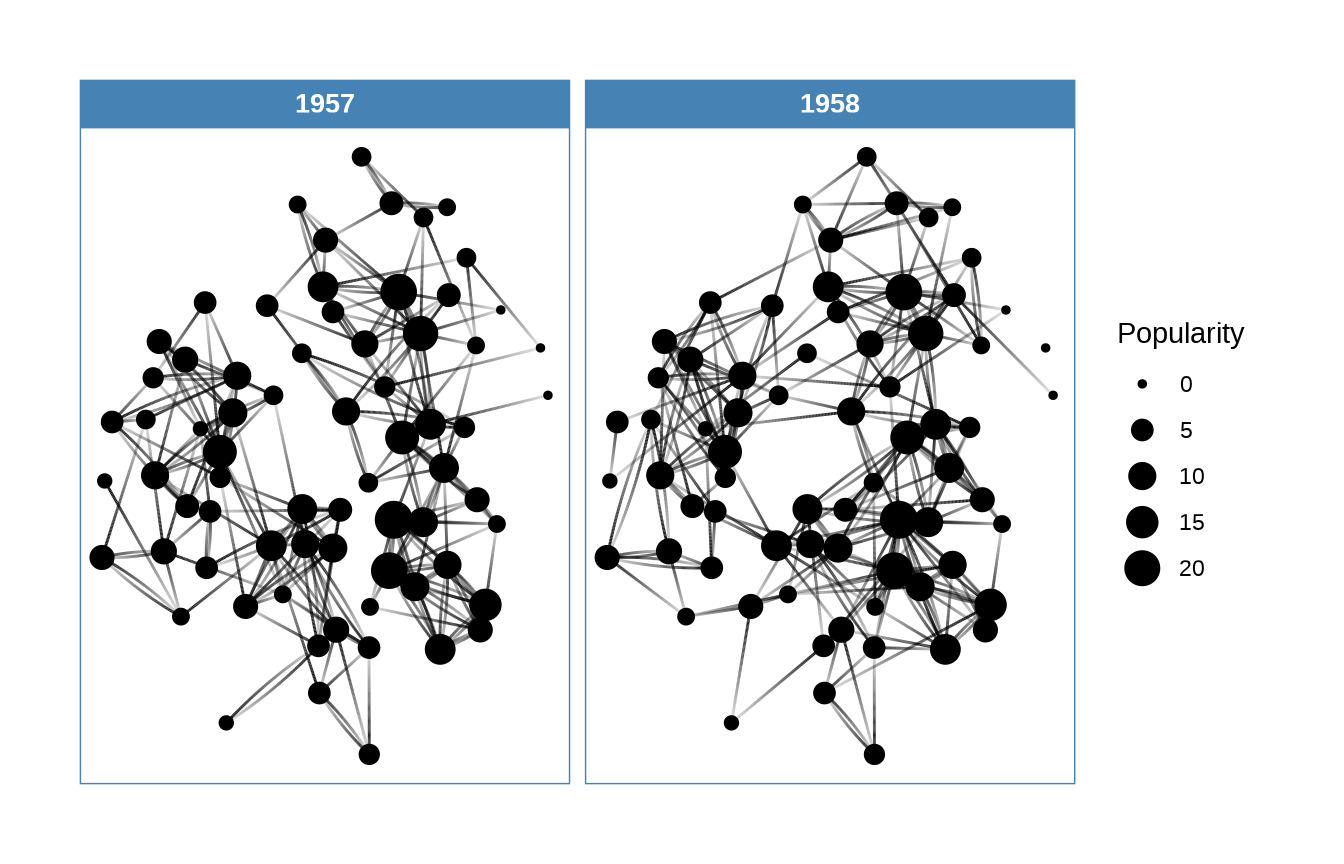
图 3.18: 高中男生间关系的变化

3.3 描述不确定性

统计是一门研究不确定性的学科，由不确定性引出许多的基本概念，比如用置信区间描述点估计的不确定性，用覆盖概率描述区间估计方法的优劣。下面以二项分布参数的点估计与区间估计为例，通过可视化图形介绍这一系列统计概念。就点估计来说，描述不确定性可以用标准差、置信区间。

ggdist 包可视化分布和不确定性 (Kay 2022)

3.3.1 置信区间

表格 3.3: 二项分布的分布列
0 1 2 \(\cdots\) n
\(p_0\) \(p_1\) \(p_2\) \(\cdots\) \(p_n\)

二项分布 \(\mathrm{Binomial}(n,p)\) 的参数 \(p\) 的精确区间估计如下：

\[ \big(\mathrm{Beta}(\frac{\alpha}{2}; x, n-x+1), \mathrm{Beta}(1-\frac{\alpha}{2}; x+1, n-x)\big) \tag{3.1}\]

其中， \(x\) 表示成功次数，\(n\) 表示实验次数，\(\mathrm{Beta}(p;v,w)\) 表示形状参数为 \(v\) 和 \(w\) 的 Beta 贝塔分布的 \(p\) 分位数，参数 \(p\) 的置信区间的上下限 \(P_L,P_U\) 满足

\[ \begin{aligned} \frac{\Gamma(n+1)}{\Gamma(x)\Gamma(n-x+1)}\int_{0}^{P_L}t^{x-1}(1-t)^{n-x}\mathrm{dt} &= \frac{\alpha}{2} \\ \frac{\Gamma(n+1)}{\Gamma(x+1)\Gamma(n-x)}\int_{0}^{P_U}t^{x}(1-t)^{n-x-1}\mathrm{dt} &= 1-\frac{\alpha}{2} \end{aligned} \]

\(p_x\) 表示二项分布 \(\mathrm{Binomial}(n,p)\) 第 \(x\) 项的概率，\(x\) 的取值为 \(0,1,\cdots,n\)

\[p_x = \binom{n}{x}p^x(1-p)^{n-x}, \quad x = 0,1,\cdots,n\]

二项分布的累积分布函数和 \(S_k\) 表示前 \(k\) 项概率之和

\[S_k = \sum_{x=0}^{k} p_x\]

\(S_k\) 服从形状参数为 \(n-k,k+1\) 的贝塔分布 \(I_x(a,b)\)，对应于 R 函数 pbeta(x,a,b)。 \(S_k\) 看作贝塔分布的随机变量 \(X\)

\[ \begin{aligned} B_x(a,b) &=\int_{0}^{x}t^{a-1}(1-t)^{b-1}\mathrm{dt} \\ I_x(a,b) &= \frac{B_x(a,b)}{B(a,b)}, \quad B(a,b) = B_1(a,b) \end{aligned} \]

考虑二项总体的参数 \(p=0.7\)，重复模拟 50 次，每次模拟获得的比例 \(\hat{p}\) 及其置信区间，区间估计方法来自 (Clopper 和 Pearson 1934) ，函数 binom.test() 也是采用此方法，二者计算结果相同。如 图 3.19 所示，置信区间覆盖真值的情况用不同颜色表示，覆盖用灰色表示，没有覆盖用黑色表示。

clopper_pearson <- function(p = 0.1, n = 10, nsim = 100) {
  set.seed(2022)
  nd <- rbinom(nsim, prob = p, size = n)
  ll <- qbeta(p = 0.05 / 2, shape1 = nd, shape2 = n - nd + 1)
  ul <- qbeta(p = 1 - 0.05 / 2, shape1 = nd + 1, shape2 = n - nd)
  data.frame(nd = nd, ll = ll, ul = ul, cover = ul > p & ll < p)
}
# 二项分布的参数 p = 0.7
dat <- clopper_pearson(p = 0.7, n = 10, nsim = 50)
# 二项分布的参数的置信区间覆盖真值的情况
ggplot(data = dat, aes(x = 1:50, y = nd / 10, colour = cover)) +
  geom_hline(yintercept = 0.7, lty = 2, linewidth = 1.2, color = "gray") +
  geom_pointrange(aes(ymin = ll, ymax = ul)) +
  scale_color_grey(labels = c(`TRUE` = "是", `FALSE` = "否")) +
  theme_classic() +
  labs(x = "n", y = "p", color = "覆盖")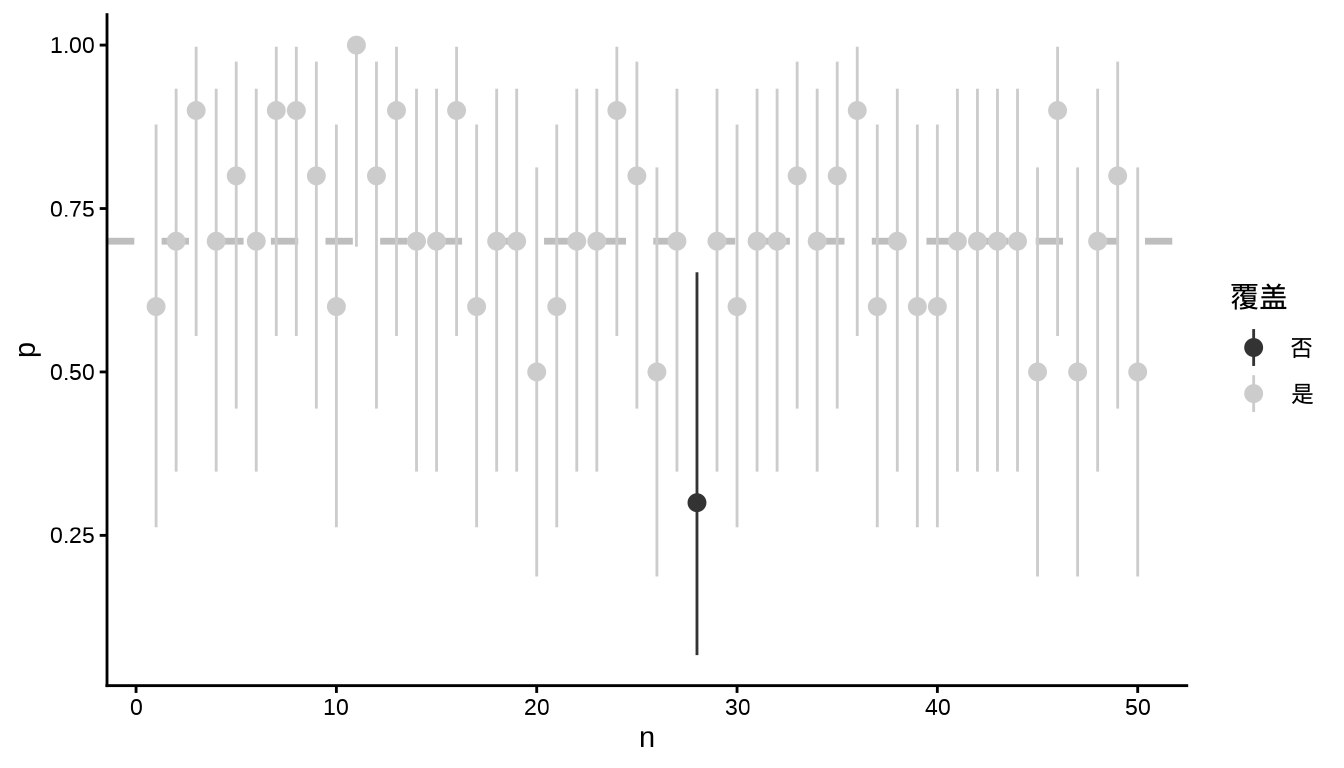
图 3.19: Clopper-Pearson 置信区间

图中，横坐标表示模拟次数 \(n\) ，纵坐标表示对应的成功概率 \(p\) ，线段端点表示置信区间上下限。

3.3.2 假设检验

假设检验的目的是做决策，决策是有风险的，是可能发生错误的，为了控制犯第一类错误的可能性，我们用 P 值描述检验统计假设的不确定性，用功效描述检验方法的优劣。对同一个统计假设，同一组数据，不同的检验方法有不同的 P 值，本质是检验方法的功效不同。

ggpval 在图上添加检验的 P 值结果，ggsignif (Constantin 和 Patil 2021) 在图上添加显著性注释。ggstatsplot (Patil 2021) 可视化统计检验、模型的结果，描述功效变化。ggpubr 制作出版级统计图形，两样本均值的比较。

with(
  aggregate(
    data = PlantGrowth, weight ~ group,
    FUN = function(x) c(dist_mean = mean(x), dist_sd = sd(x))
  ),
  cbind.data.frame(weight, group)
) |>
  ggplot(aes(x = group, y = dist_mean)) +
  geom_col(
    position = position_dodge(0.4), width = 0.4, fill = "gray"
  ) +
  geom_errorbar(aes(ymin = dist_mean - dist_sd, ymax = dist_mean + dist_sd),
    position = position_dodge(0.4), width = 0.2) +
  theme_classic() +
  labs(x = "组别", y = "植物干重")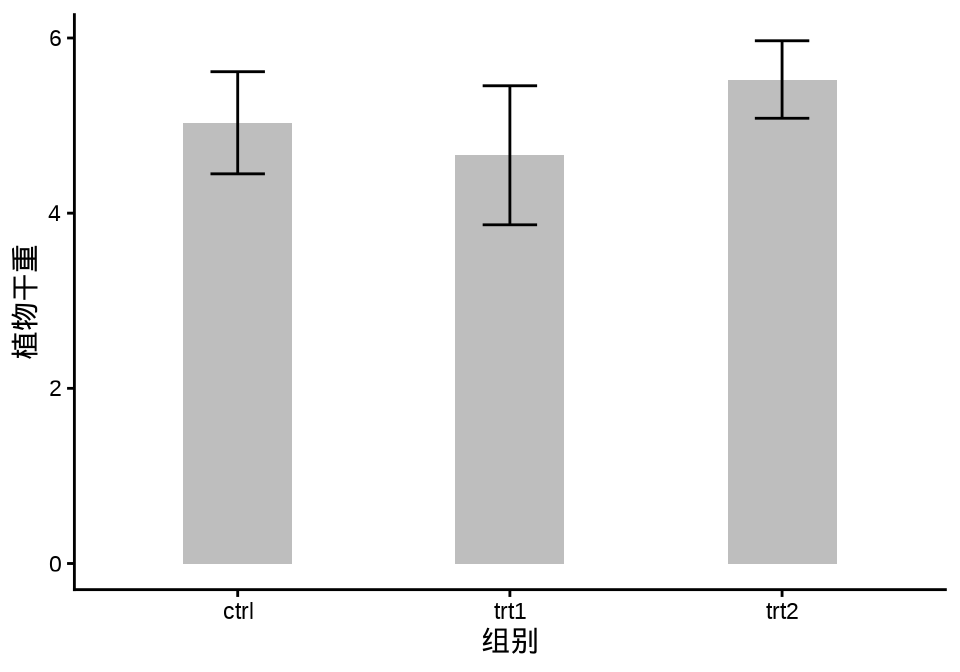
图 3.20: 植物生长
注释

R 3.5.0 以后，函数 aggregate() 的参数 drop 默认值为 TRUE， 表示扔掉未用来分组的变量，聚合返回的是一个矩阵类型的数据对象。

单因素方差分析 oneway.test() 检验各组的方差是否相等。

oneway.test(data = PlantGrowth, weight ~ group)
#> 
#>  One-way analysis of means (not assuming equal variances)
#> 
#> data:  weight and group
#> F = 5.181, num df = 2.000, denom df = 17.128, p-value =
#> 0.01739

结果显示方差不全部相等，因此，采用函数 t.test(var.equal = FALSE) 来检验数据。图 3.21 展示假设检验的结果，分别标记了 ctrl 与 trt1、trt1 与 trt2 两组 t 检验的结果。

library(ggsignif)
ggplot(data = PlantGrowth, aes(x = group, y = weight)) +
  geom_boxplot(width = 0.25) +
  geom_jitter(width = 0.15) +
  geom_signif(comparisons = list(c("ctrl", "trt1"), c("trt1", "trt2")), 
              map_signif_level = function(p) sprintf("p = %.2g", p), 
              textsize = 6, test = "t.test") +
  theme_classic() +
  coord_cartesian(clip = "off")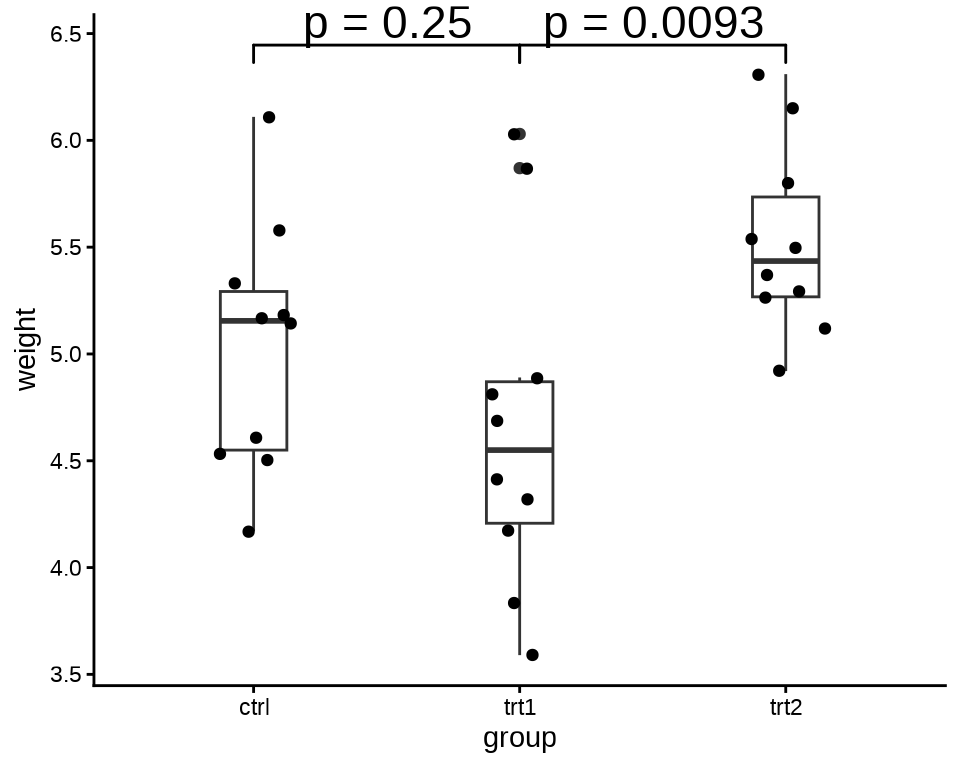
图 3.21: 展示假设检验的结果

为了了解其中的原理，下面分别使用函数 t.test() 检验数据，结果给出的 P 值与上 图 3.21 完全一样。

t.test(data = PlantGrowth, weight ~ group, subset = group %in% c("ctrl", "trt1"))
#> 
#>  Welch Two Sample t-test
#> 
#> data:  weight by group
#> t = 1.1913, df = 16.524, p-value = 0.2504
#> alternative hypothesis: true difference in means between group ctrl and group trt1 is not equal to 0
#> 95 percent confidence interval:
#>  -0.2875162  1.0295162
#> sample estimates:
#> mean in group ctrl mean in group trt1 
#>              5.032              4.661
t.test(data = PlantGrowth, weight ~ group, subset = group %in% c("trt1", "trt2"))
#> 
#>  Welch Two Sample t-test
#> 
#> data:  weight by group
#> t = -3.0101, df = 14.104, p-value = 0.009298
#> alternative hypothesis: true difference in means between group trt1 and group trt2 is not equal to 0
#> 95 percent confidence interval:
#>  -1.4809144 -0.2490856
#> sample estimates:
#> mean in group trt1 mean in group trt2 
#>              4.661              5.526

3.3.3 模型预测

描述模型预测的不确定性，预测的方差、预测区间。线性回归来说，回归线及置信带。代码提交量的趋势拟合

svn_trunk_log <- readRDS(file = "data/svn-trunk-log-2022.rds")
svn_trunk_log$year <- as.integer(format(svn_trunk_log$stamp, "%Y"))
trunk_year <- aggregate(data = svn_trunk_log, revision ~ year, FUN = length)
ggplot(data = trunk_year[trunk_year$year != 1997,], aes(x = year, y = revision)) +
  geom_point() +
  geom_smooth(aes(color = "LOESS", fill = "LOESS"),
    method = "loess", formula = "y~x",
    method.args = list(
      span = 0.75, degree = 2, family = "symmetric",
      control = loess.control(surface = "direct", iterations = 4)
    )) +
  geom_smooth(aes(color = "GAM", fill = "GAM"),
    formula = y ~ s(x, k = 12), method = "gam", se = TRUE) +
  geom_smooth(aes(color = "Cubic Spline", fill = "Cubic Spline"),
                method = "lm", formula = y ~ splines::bs(x, 3), se = T) +
  scale_color_brewer(name = "模型", palette = "Set1") +
  scale_fill_brewer(name = "模型", palette = "Set1") +
  theme_classic() +
  theme(panel.grid.major.y = element_line(colour = "gray90")) +
  labs(x = "年份", y = "提交量")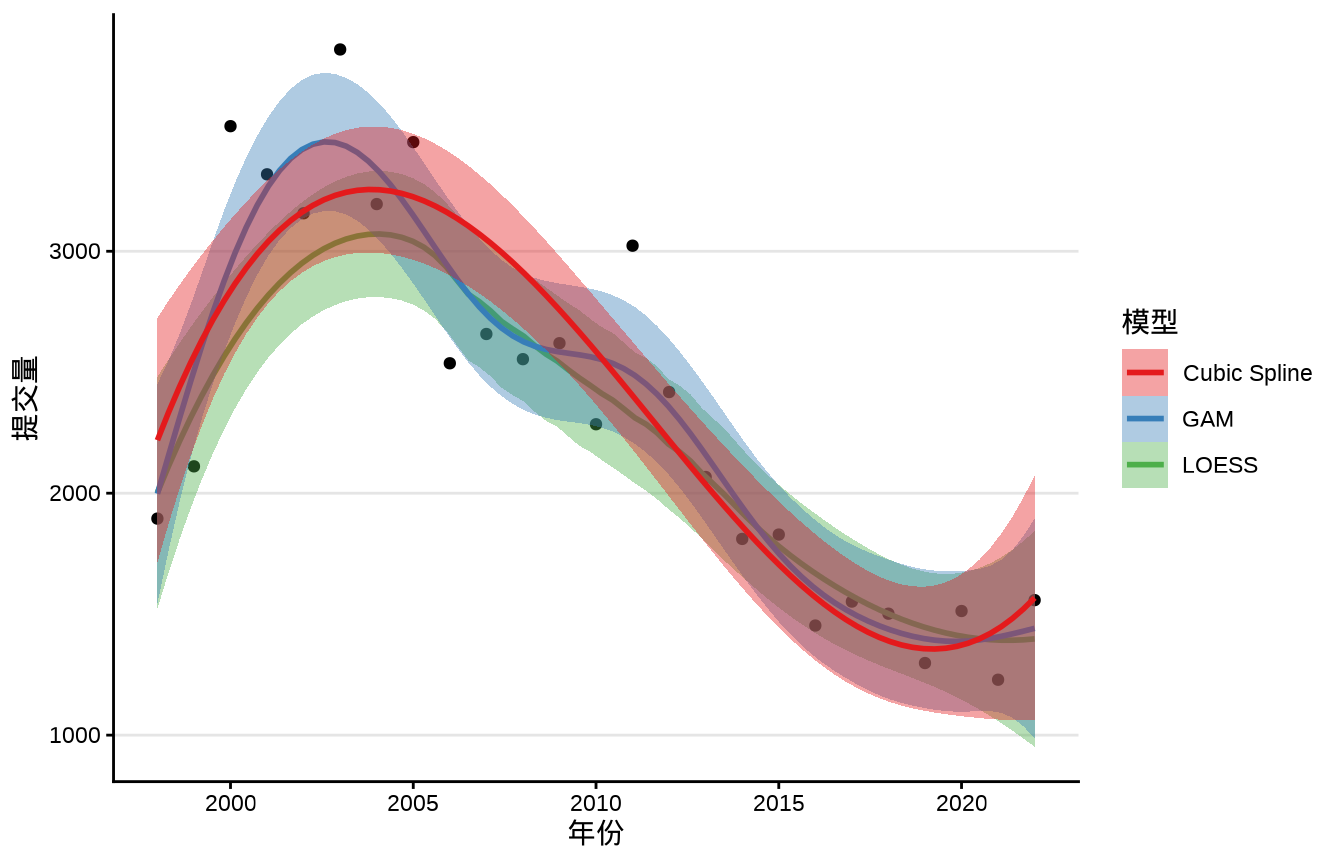
图 3.22: 趋势拟合、预测和推断

3.3.4 模型诊断

所有模型都是错误的，但有些是有用的。

— 乔治·博克斯

描述模型的敏感性，数据中存在的离群值，变量之间的多重共线性等。引入 Cook 距离、杠杆值、VIF 等来诊断模型。

# 准备数据
state_x77 <- data.frame(state.x77,
  state_name = rownames(state.x77), state_region = state.region,
  state_abb = state.abb, check.names = FALSE
)
# 线性模型拟合
fit <- lm(`Life Exp` ~ Income + Murder, data = state_x77)
# 模型诊断图
library(ggfortify)
autoplot(fit, which = 1:6, label.size = 3)
图 3.23: 线性模型的诊断图

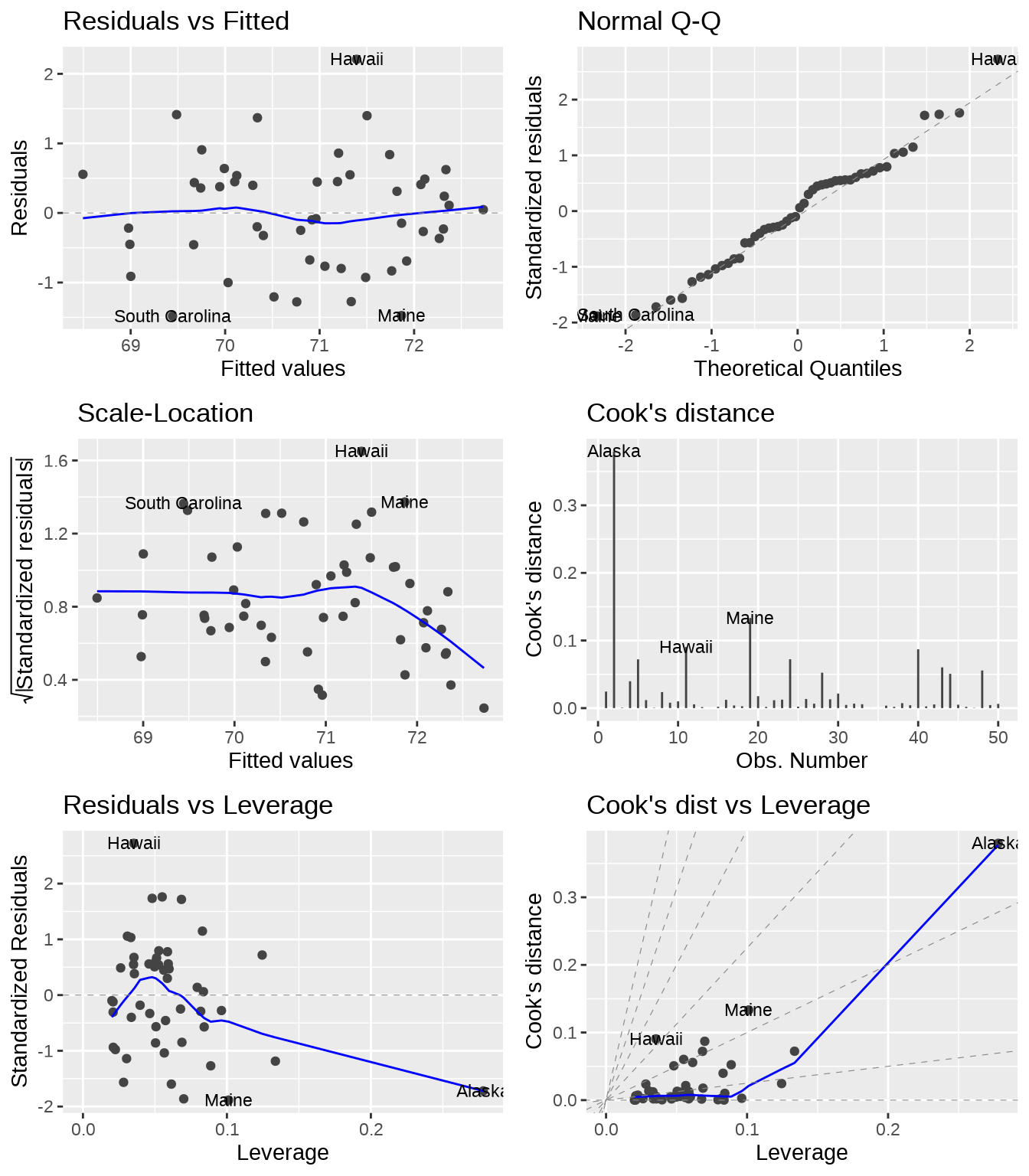
对于复杂的统计模型，比如混合效应模型的诊断，ggPMX 包。

3.3.5 边际效应

继续 state_x77 数据集，以预期寿命（1969-1971 年统计）为因变量，Income 人均收入（1974 年）和 Murder 谋杀和非过失杀人率（单位：十万分之一，1976 年统计）为自变量，建立线性模型如下：

\[ \text{Life Exp} = \alpha + \beta_1 \text{Income} + \beta_2 \text{Murder} + \epsilon \tag{3.2}\]

在 R 语言中，可以用函数 lm() 拟合上述模型，

fit <- lm(`Life Exp` ~ Income + Murder, data = state_x77)

模型拟合结果输出如下：

summary(fit)
#> 
#> Call:
#> lm(formula = `Life Exp` ~ Income + Murder, data = state_x77)
#> 
#> Residuals:
#>      Min       1Q   Median       3Q      Max 
#> -1.48301 -0.62099 -0.01714  0.47768  2.20831 
#> 
#> Coefficients:
#>               Estimate Std. Error t value Pr(>|t|)    
#> (Intercept) 71.2255815  0.9673952  73.626  < 2e-16 ***
#> Income       0.0003705  0.0001973   1.878   0.0666 .  
#> Murder      -0.2697594  0.0328408  -8.214 1.22e-10 ***
#> ---
#> Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
#> 
#> Residual standard error: 0.8259 on 47 degrees of freedom
#> Multiple R-squared:  0.637,  Adjusted R-squared:  0.6215 
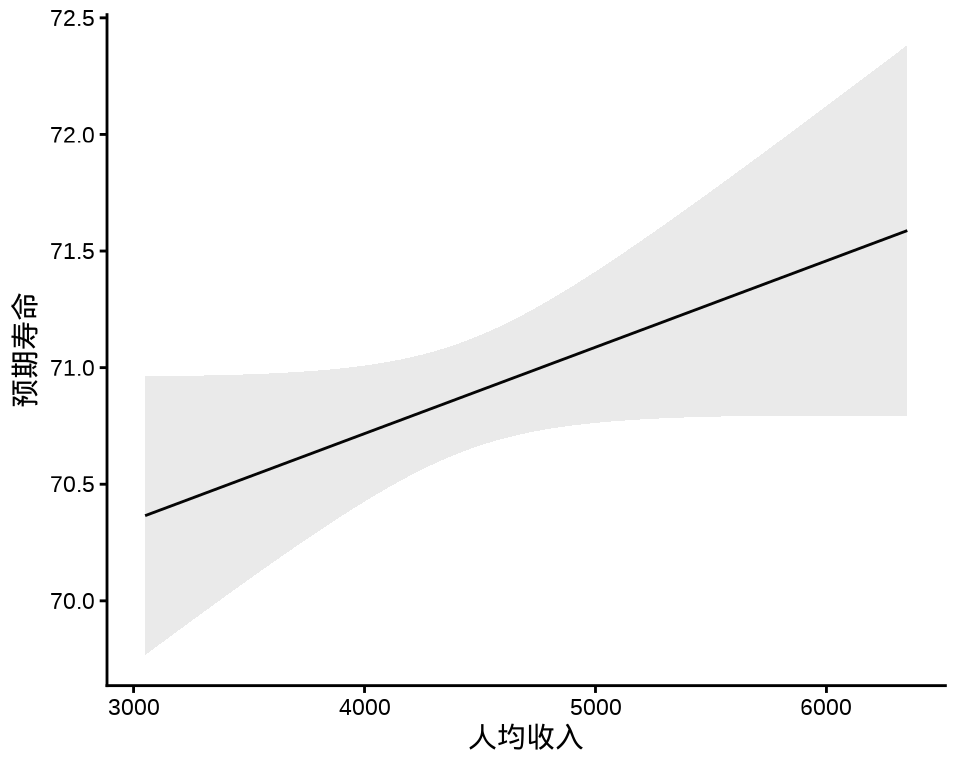
#> F-statistic: 41.23 on 2 and 47 DF,  p-value: 4.561e-11

ggeffects 描述单个自变量的作用，人均收入对预期寿命的边际效应

library(ggeffects)
income_pred <- ggpredict(fit, terms = "Income")
ggplot(income_pred, aes(x, predicted)) +
  geom_line() +
  geom_ribbon(aes(ymin = conf.low, ymax = conf.high), alpha = 0.1) +
  theme_classic() +
  labs(x = "人均收入", y = "预期寿命")
图 3.24: 边际效应