Chapter 3 Sampling the imaginary

3.0.1 Probabilities vs. Frequency counts

Vampires in the population Probabilities There is a blood test that can correctly identify a vampire 95% of the time. Or mathematically, Pr(positive|vampire) = 0.95. 1% of the time the test gives a false positive or Pr(positive|mortal) = 0.01. Also, vampires are rare in the population only making up 0.1% of the population so, Pr(vampire) = 0.001
If someone tests poisitve, what is the probability that they are actually a vampire?

Using Bayes’ theorem, Pr(vampire|positive) can be inverted as:

\[\begin{equation} \text{Pr(vampire|positive)} = \frac{\text{Pr(positive|vampire)} \times \text{Pr(vampire)} {\text{Pr(positive)}} \end{equation}\]

Here, Pr(positive) is the average probability of a positive test result or:

\begin{eqaution} = + (1 - ) \end{equation}

Pr_Positive_Vampire <- 0.95
Pr_Positive_Mortal <- 0.01
Pr_Vampire <- 0.001

Pr_Positive <- Pr_Positive_Vampire * Pr_Vampire + Pr_Positive_Mortal * (1 - Pr_Vampire)

(Pr_Vampire_Positive <- Pr_Positive_Vampire * Pr_Vampire / Pr_Positive)

## [1] 0.08683729

There is an 8.7% chance that a positive test result is actually a vampire.

Frequency counts

In 100,000 people, 100 are vampires
of the 100 vampires, 95 will test positive
of the 99,900 mortals, 999 will test positive

Pr_Positive_Vampire <- 95 / 100
Pr_Positive_Mortal <- 999 / 99900
Pr_Vampire <- 100 / 100000

Pr_Positive <- 95 + 999

(Pr_Vampire_Positive <- Pr_Positive_Vampire * 100 / Pr_Positive)

## [1] 0.08683729

OR:

Pr_Positive_Vampire <- 95 #positive results from vampires
Pr_Positive <- 95 + 999 #all positive results

(Pr_Vampire_Positive <- Pr_Positive_Vampire / Pr_Positive)

## [1] 0.08683729

3.1 Sampling from a grid-approximate posterior

Let’s recreate the grid approximation for the globe tossing example:

p_grid <- seq(from = 0, to = 1, length.out = 1000) #create 1000 values between 0 and 1
prob_p <- rep(1, 1000) #the uniform prior of 1
prob_data <- dbinom(6, size = 9, prob = p_grid) #The observed tosses (data)
posterior <-prob_data*prob_p #calculate the posterior
posterior <-posterior/sum(posterior) #standardize by dividing by the sum

Let’s pull some samples from our posterior (n = 10000)

samples <- sample(p_grid, prob = posterior, size = 1e4, replace = TRUE) #notice replace set to true as there are only 1000 values in p_grid

#find the mode of your samples
getmode <- function(x) {
   uniqv <- unique(x)
   uniqv[which.max(tabulate(match(x, uniqv)))]
}
samples_mode <- getmode(samples)

And plot them

plot(samples) #left panel of figure 3.1
abline(h = samples_mode, col = 'red')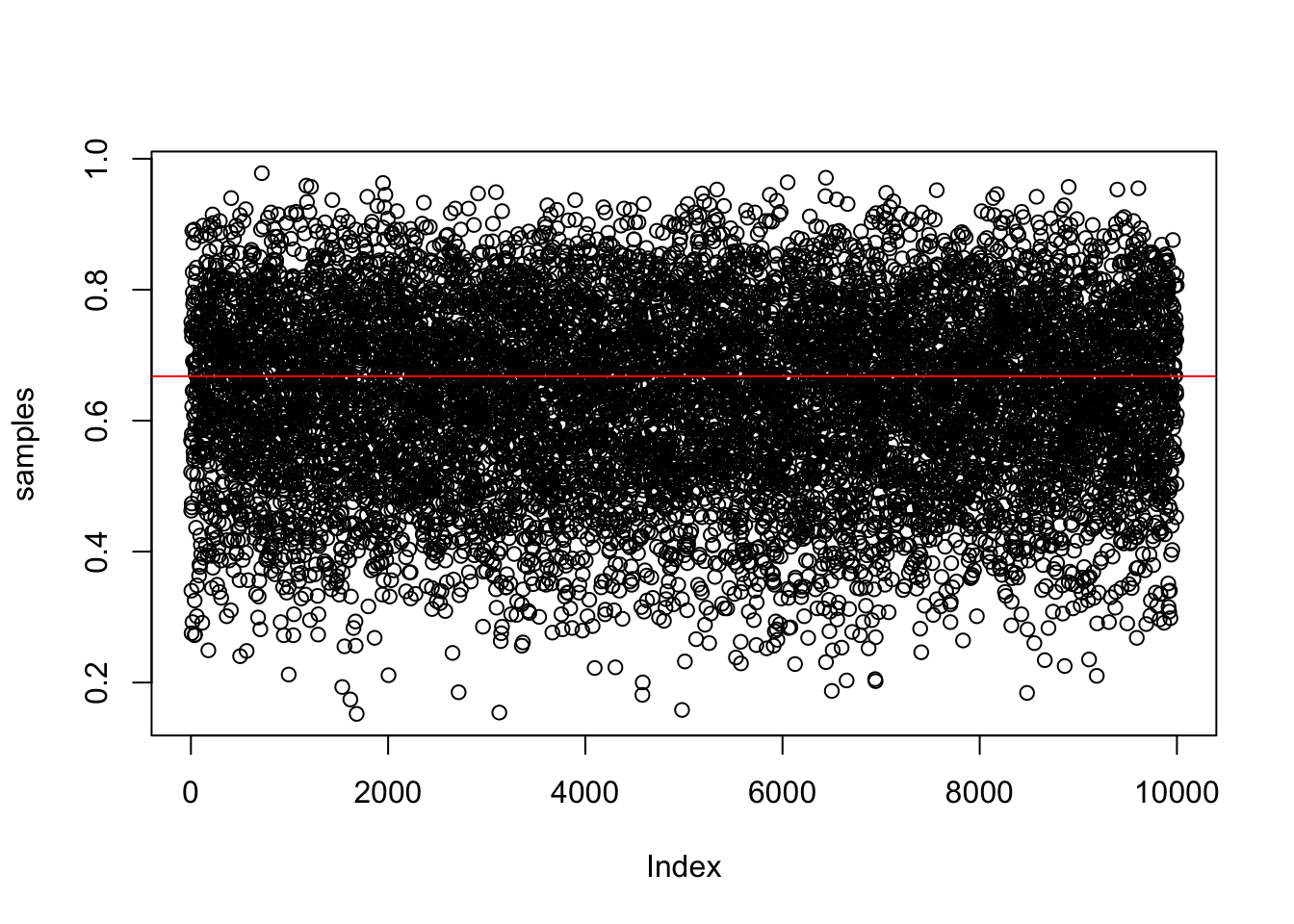

View the samples as a density

plot(density(samples), main = "Density of samples from posterior")
polygon(density(samples), col = 'black', border = 'blue')
abline(v = samples_mode, col = 'red')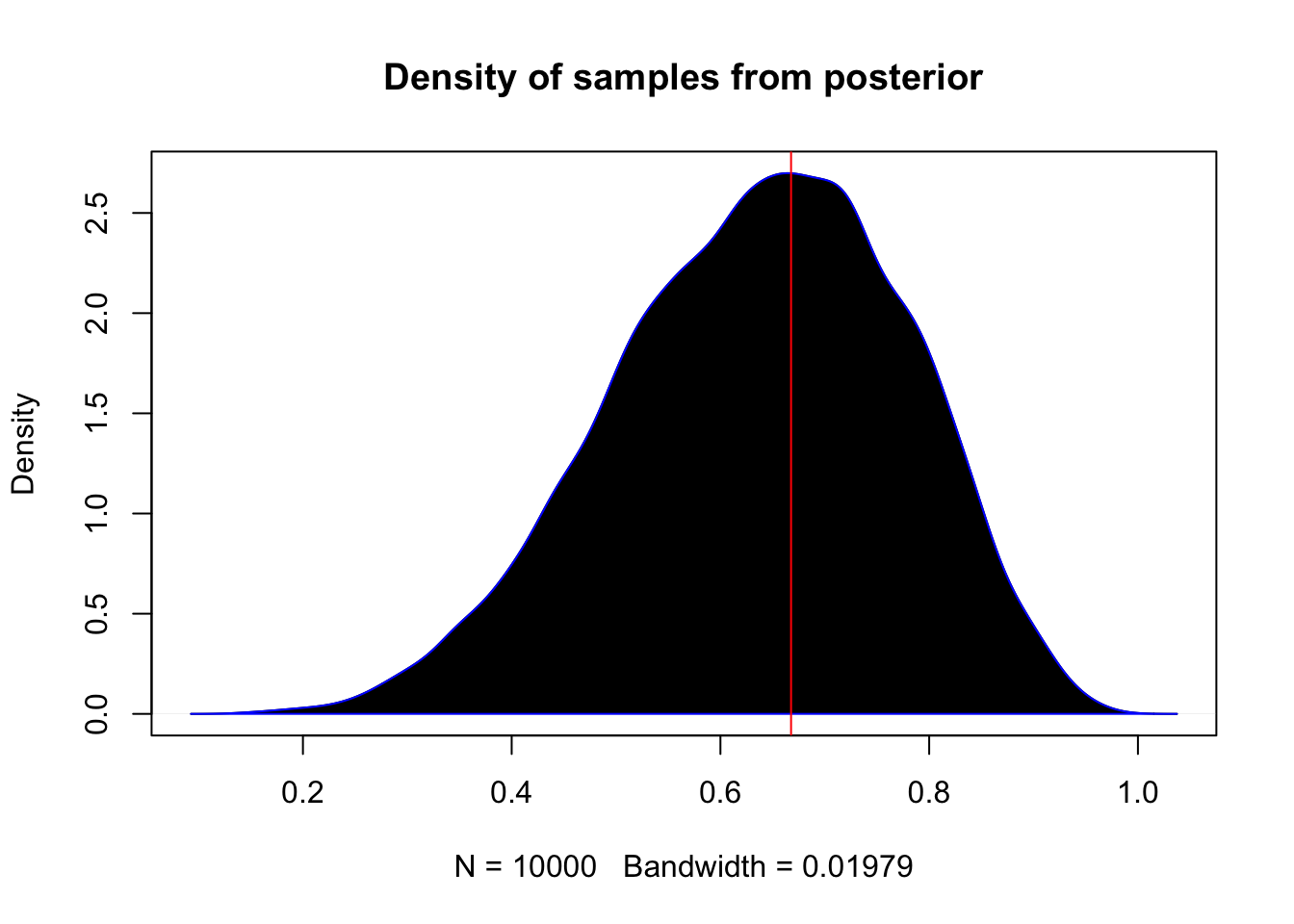

#library(rethinking)
#dens(samples)

3.2 Sampling to summarize

Common questions about your posterior: 1. intervals of defined boundaries 2. intervals of defined probability mass 3. point estimates

3.2.1 Intervals of defined boundaries

What is the posterior probability that the proportion of water is >0.5?

sum(posterior[p_grid < 0.5])

## [1] 0.1718746

about 17%

Doing the same using the samples from the posterior

sum(samples < 0.5) / 1e4 #divide by the number of samples you gathered

## [1] 0.1729

what about between 0.5 and 0.75?

sum(samples > 0.5 & samples < 0.75) / 1e4

## [1] 0.6065

Recreating figure 3.2 (upper left panel)

library(ggplot2)
library(dplyr)

df <- tibble(p_grid, posterior)

df %>% ggplot(aes(x = p_grid)) +
  geom_line(aes(y = posterior)) +
  geom_ribbon(data = df %>% filter(p_grid < 0.5),
              aes(ymin = 0, ymax = posterior)) +
  labs(x = "proportion of water (p)",
       y = "density") +
  theme_bw()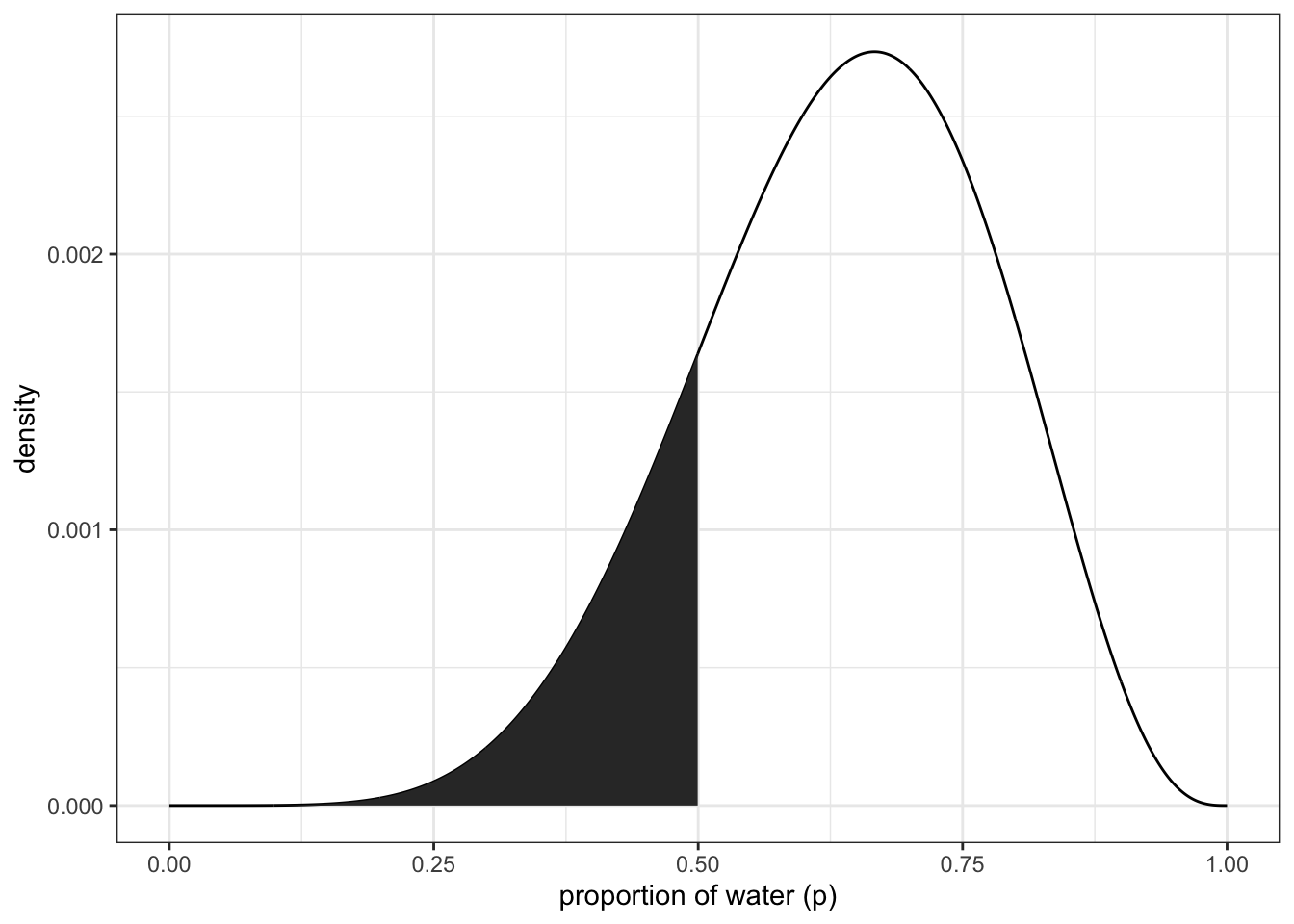

upper right panel

df %>% ggplot(aes(x = p_grid)) +
  geom_line(aes(y = posterior)) +
  geom_ribbon(data = df %>% filter(p_grid < 0.75 & p_grid > 0.5),
              aes(ymin = 0, ymax = posterior)) +
  labs(x = "proportion of water (p)",
       y = "density") +
  theme_bw()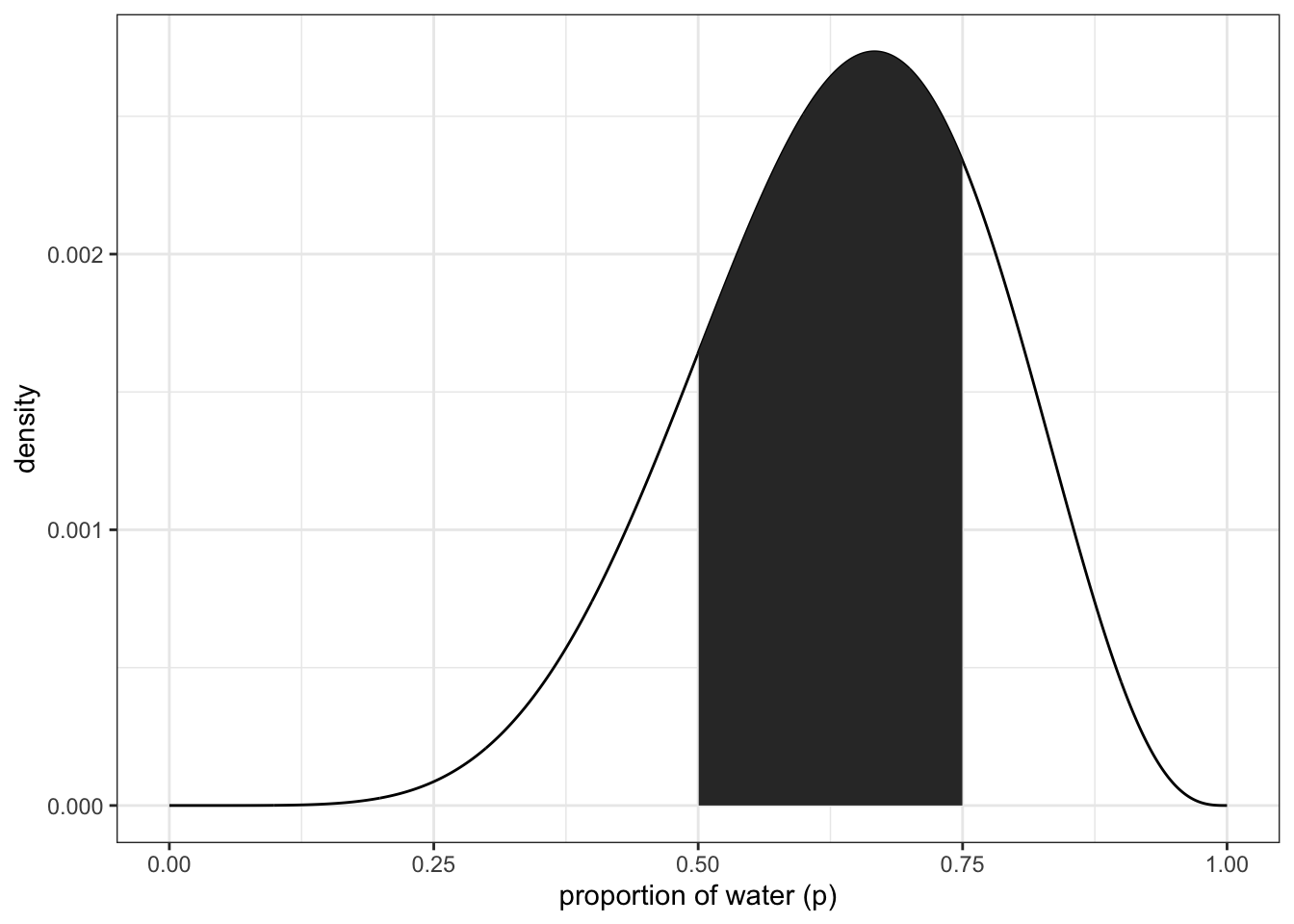

3.2.2 intervals of defined mass

finding the lower 80% of the probability mass using samples

(q_80 <- quantile(samples, 0.8))

##       80% 
## 0.7607608

finding the middle 80% (10-90%)

(q_10_90 <- quantile(samples, c(0.1, 0.9)))

##       10%       90% 
## 0.4474474 0.8108108

Bottom panels to figure 3.2 lower left:

df %>% ggplot(aes(x = p_grid)) +
  geom_line(aes(y = posterior)) +
  geom_ribbon(data = df %>% filter(p_grid < q_80),
              aes(ymin = 0, ymax = posterior)) +
  annotate(geom = 'text', x = 0.25, y = 0.0025,
           label = 'lower 80%') +
  labs(x = "proportion of water (p)",
       y = "density") +
  theme_bw()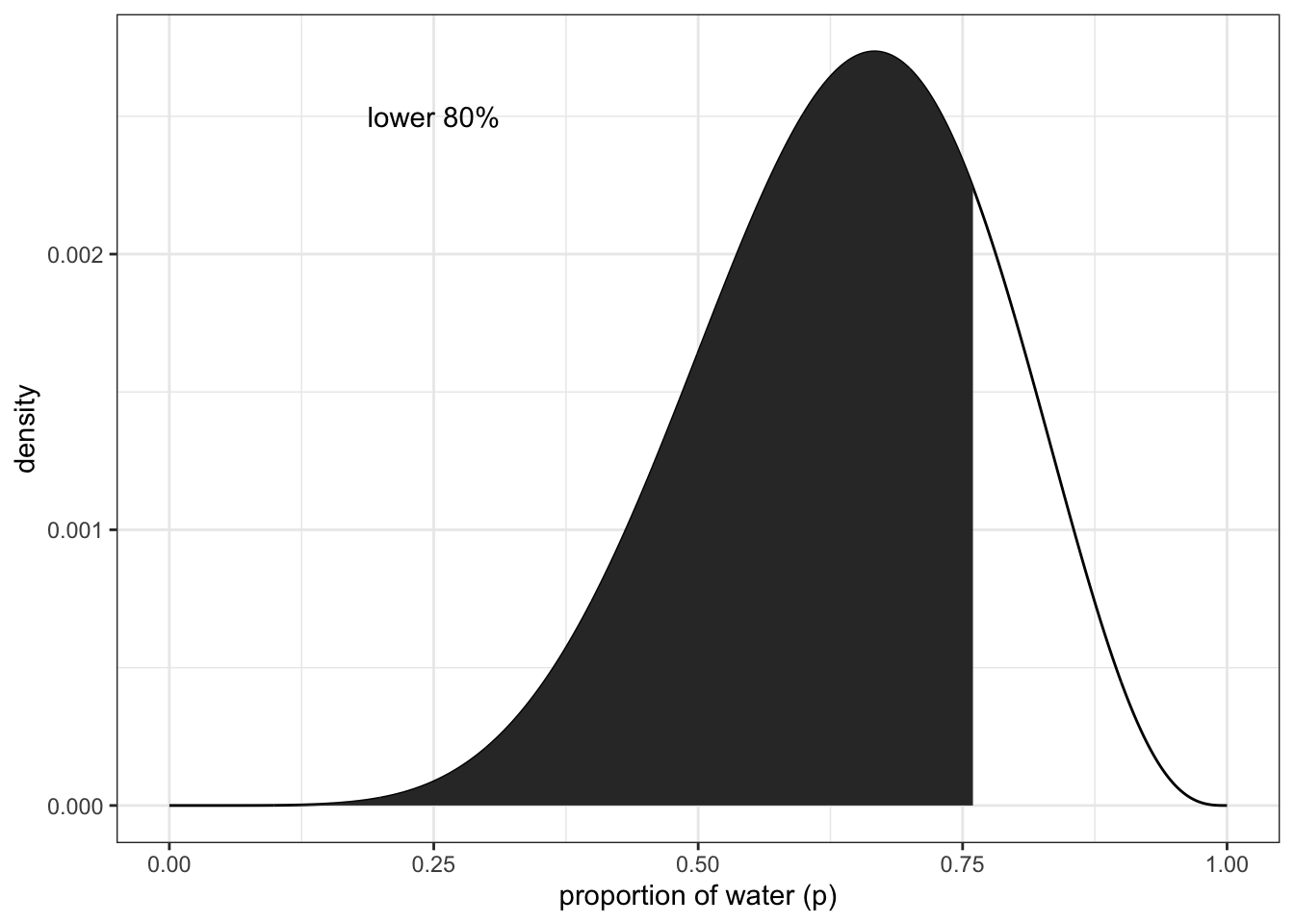

df %>% ggplot(aes(x = p_grid)) +
  geom_line(aes(y = posterior)) +
  geom_ribbon(data = df %>% filter(p_grid > q_10_90[1] & p_grid < q_10_90[2]),
              aes(ymin = 0, ymax = posterior)) +
  annotate(geom = 'text', x = 0.25, y = 0.0025,
           label = 'middle 80%') +
  labs(x = "proportion of water (p)",
       y = "density") +
  theme_bw()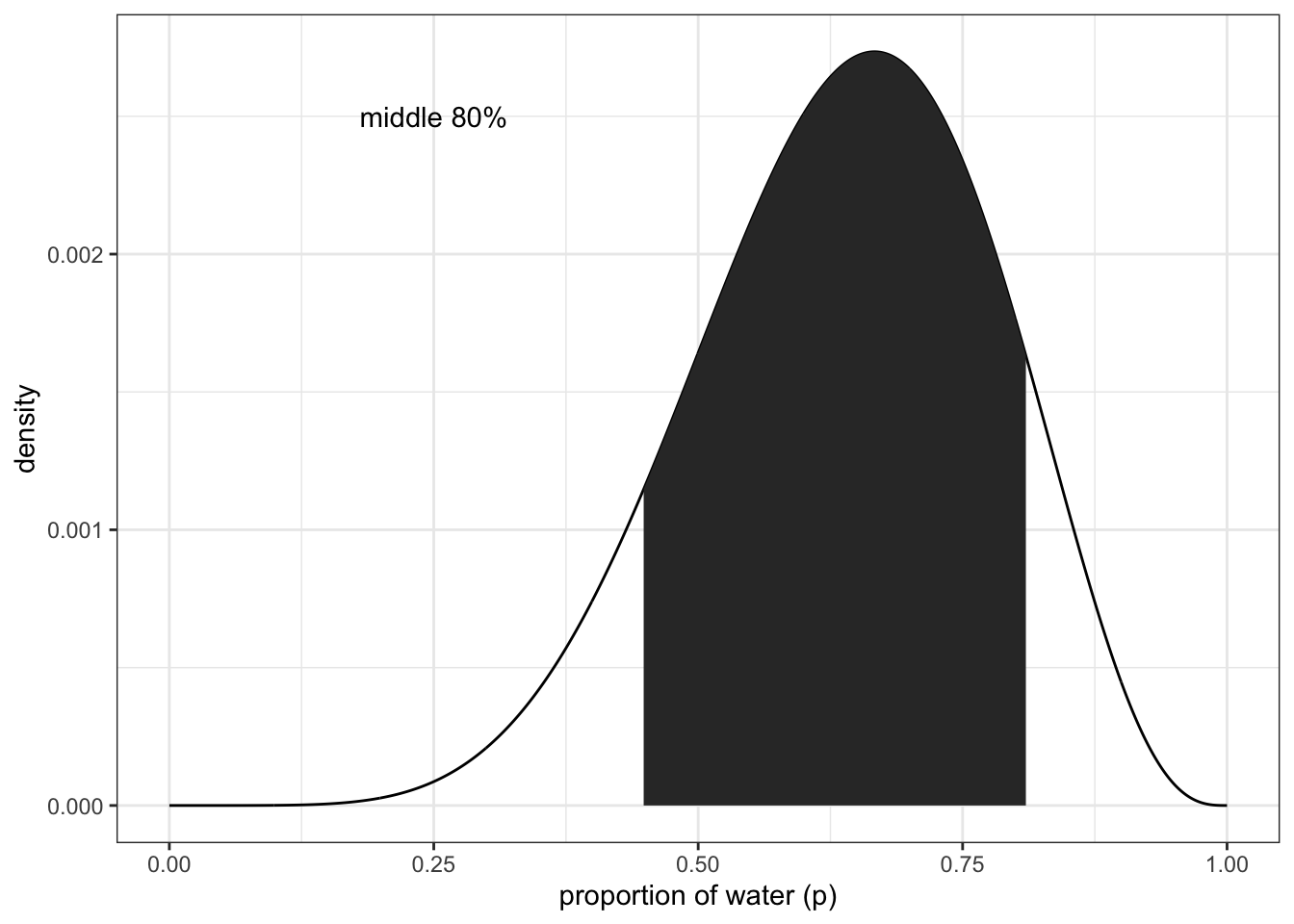

example of three tosses and three water observations:

p_grid <- seq(from = 0, to = 1, length.out = 1000)
prior <- rep(1, 1000)
likelihood <- dbinom(3, size = 3, prob = p_grid)
posterior <- likelihood * prior
posterior <- posterior / sum(posterior)
samples <- sample(p_grid, size = 1e4, replace = TRUE, prob = posterior)

Getting the 50% interval

quantile(samples, c(0.25, 0.75))

##       25%       75% 
## 0.7057057 0.9299299

#PI(samples, prob = 0.5) #rethinking package

Tidybayes package:

library(tidybayes)

## Warning: package 'tidybayes' was built under R version 4.1.2

## 
## Attaching package: 'tidybayes'

## The following objects are masked from 'package:brms':
## 
##     dstudent_t, pstudent_t, qstudent_t, rstudent_t

median_qi(samples, .width = 0.5)

##           y      ymin      ymax .width .point .interval
## 1 0.8418418 0.7057057 0.9299299    0.5 median        qi

Notice that all methods above give us the same interval from ~70 - ~93 With tidybayes, you can also look for multiple intervals at once:

median_qi(samples, .width = c(0.5, 0.8, 0.99))

##           y      ymin      ymax .width .point .interval
## 1 0.8418418 0.7057057 0.9299299   0.50 median        qi
## 2 0.8418418 0.5685686 0.9749750   0.80 median        qi
## 3 0.8418418 0.2792743 0.9989990   0.99 median        qi

Finding the Highest Posterior Density Interval (HPDI)

#HPDI(samples, prob = 0.5) #rethinking

mode_hdi(samples, .width = 0.5) #tidybayes

##           y      ymin ymax .width .point .interval
## 1 0.9565123 0.8418418    1    0.5   mode       hdi

Note: you can get just the points of refernce by using qi() for quantiles and hdi() for highest density intervals. Useful for plotting

recreate figure 3.3 left panel

df <- tibble(p_grid, posterior)

df %>% 
  ggplot(aes(x = p_grid)) +
  geom_ribbon(data = df %>% filter(p_grid > qi(samples, .width = 0.5)[1] & 
                                     p_grid < qi(samples, .width = 0.5)[2]),
              aes(ymin = 0, ymax = posterior)) +
  geom_line(aes(y = posterior)) +
  labs(subtitle = '50% Percentile interval',
       x = 'proportion of water (p)',
       y = 'density')+
  theme_bw()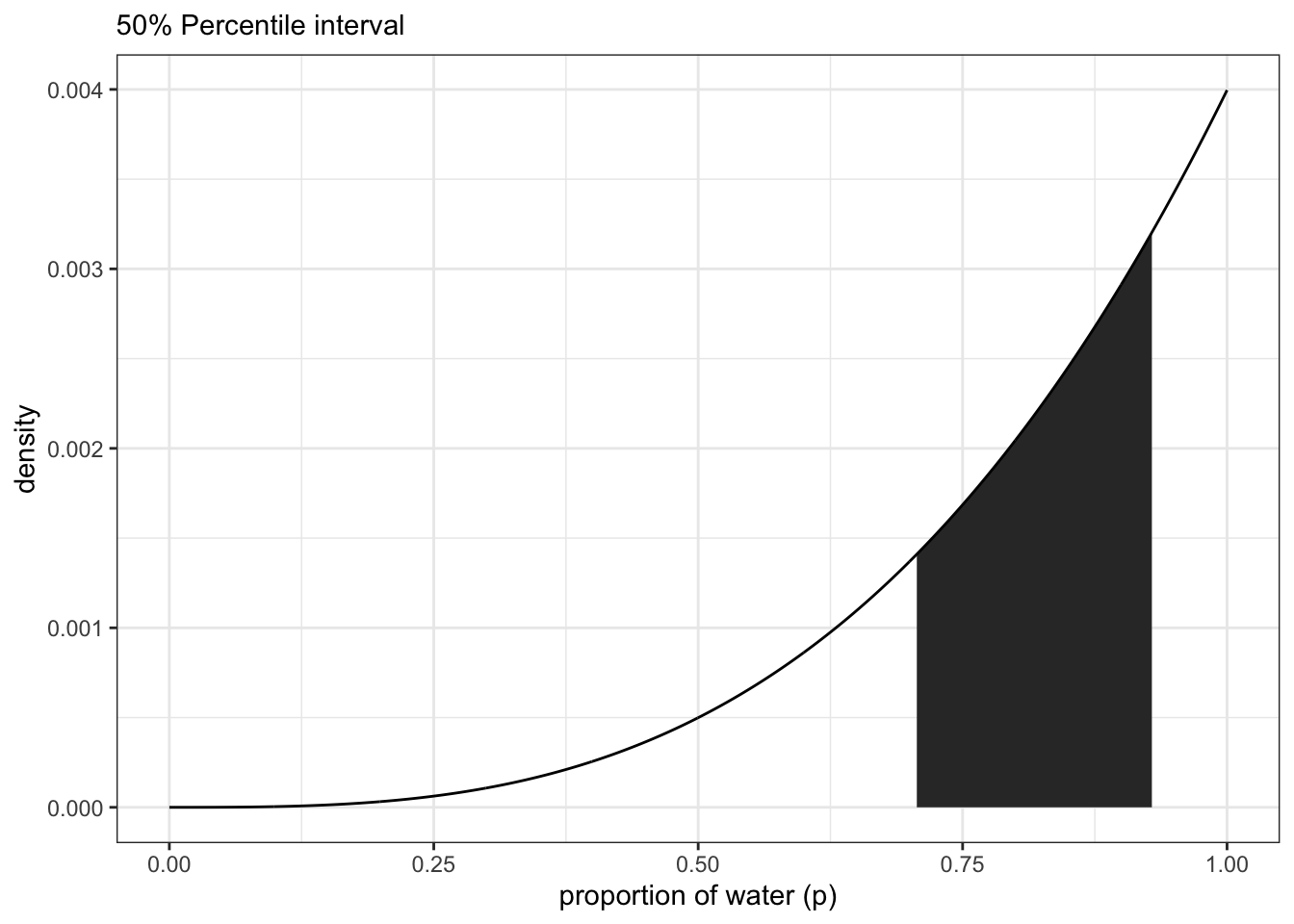

right panel

df %>% 
  ggplot(aes(x = p_grid)) +
  geom_ribbon(data = df %>% filter(p_grid > hdi(samples, .width = 0.5)[1] & 
                                     p_grid < hdi(samples, .width = 0.5)[2]),
              aes(ymin = 0, ymax = posterior)) +
  geom_line(aes(y = posterior)) +
  labs(subtitle = '50% HPDI',
       x = 'proportion of water (p)',
       y = 'density')+
  theme_bw()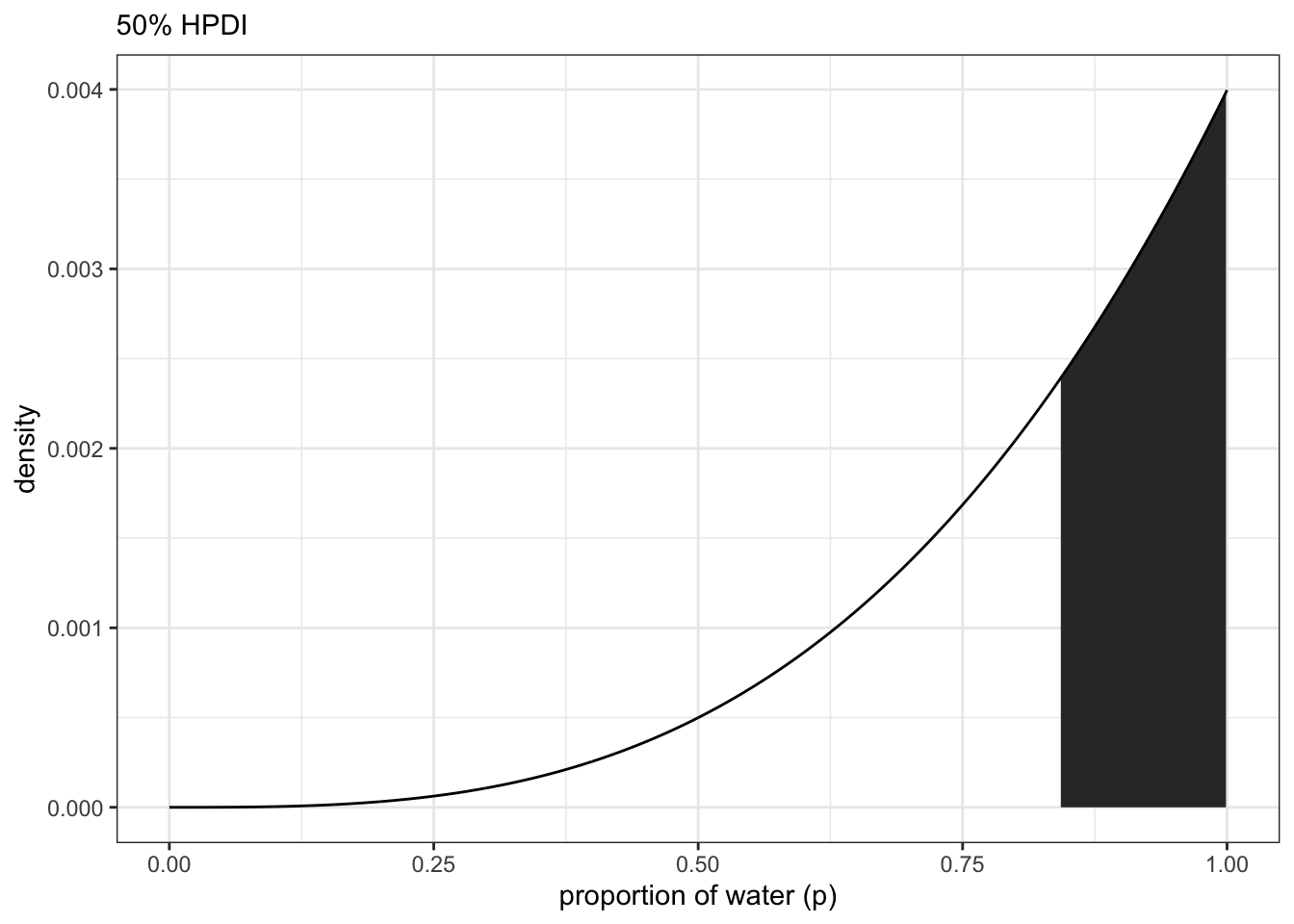

3.2.3 Point estimates

How to get a single useful (?) point estimate for your parameter. First option is the maximum a posteriori (MAP).

p_grid[which.max(posterior)]

## [1] 1

With samples:

Mode(samples) #tidybayes

## [1] 0.9565123

#chainmode(samples, adj = 0.01) #rethinking

what about mean or median?

mean(samples)

## [1] 0.801547

median(samples)

## [1] 0.8418418

Visualize the mean, median, and mode (figure 3.4)

create a small data frame

(
point_estimates <- 
  bind_rows(
    mean_qi(samples),
    median_qi(samples),
    mode_qi(samples)
  ) %>% 
  select(y, .point) %>% 
  mutate(x = y + c(-0.03, 0.03, -0.03),
         z = c(0.001, 0.0015, 0.0025))
)

##           y .point         x      z
## 1 0.8015470   mean 0.7715470 0.0010
## 2 0.8418418 median 0.8718418 0.0015
## 3 0.9565123   mode 0.9265123 0.0025

plot

df %>% 
  ggplot(aes(x = p_grid)) +
  geom_ribbon(aes(ymin = 0, ymax = posterior),
              fill = "grey75") +
  geom_vline(xintercept = point_estimates$y) +
  geom_text(data = point_estimates, 
            aes(x = x, y = z, label = .point),
            angle = 90) +
  labs(x = "proportion of water (p)",
       y = "density") +
  theme(panel.grid = element_blank())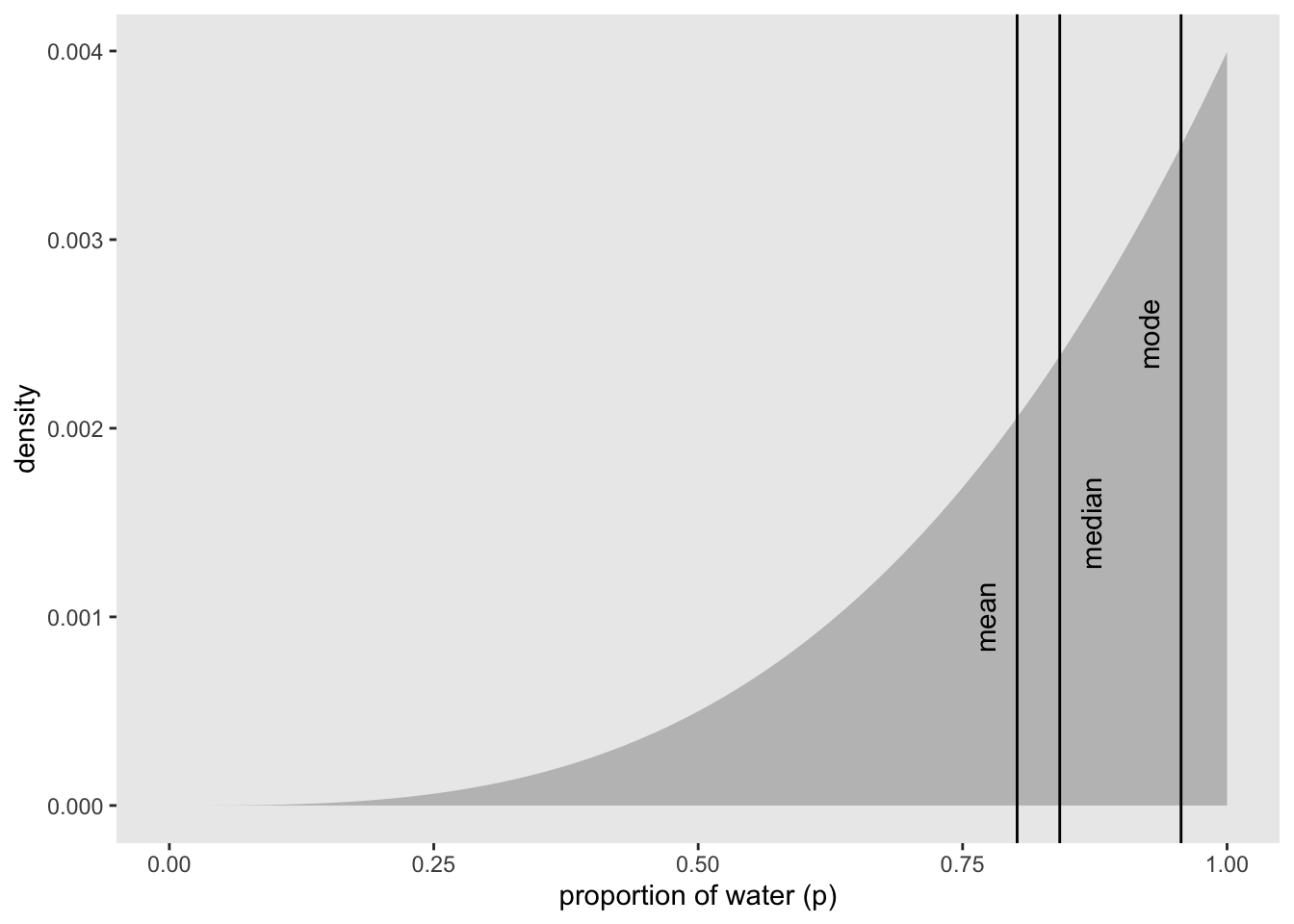

How do we choose between the point estimates? Loss functions

If we assume that p = 0.5 then the expected loss would be:

sum(posterior * abs(0.5 - p_grid))

## [1] 0.3128752

applying this method to all values of p_grid:

loss <- sapply(p_grid, function(d) sum(posterior * abs(d - p_grid)))

Now find the p value with the lowest loss

p_grid[which.min(loss)]

## [1] 0.8408408

Visualize the loss function

min_loss_x <- p_grid[which.min(loss)]
min_loss_y <- loss[which.min(loss)]

df <- tibble(p_grid, loss)

df %>% 
  ggplot(aes(x = p_grid)) +
  geom_ribbon(aes(ymin = 0, ymax = loss), fill = 'grey75') +
  geom_point(aes(x = min_loss_x, y = min_loss_y), size = 3, shape = 21, color = 'blue') +
  labs(x = 'decision',
       y = 'expected proportional loss') +
  theme(panel.grid = element_blank())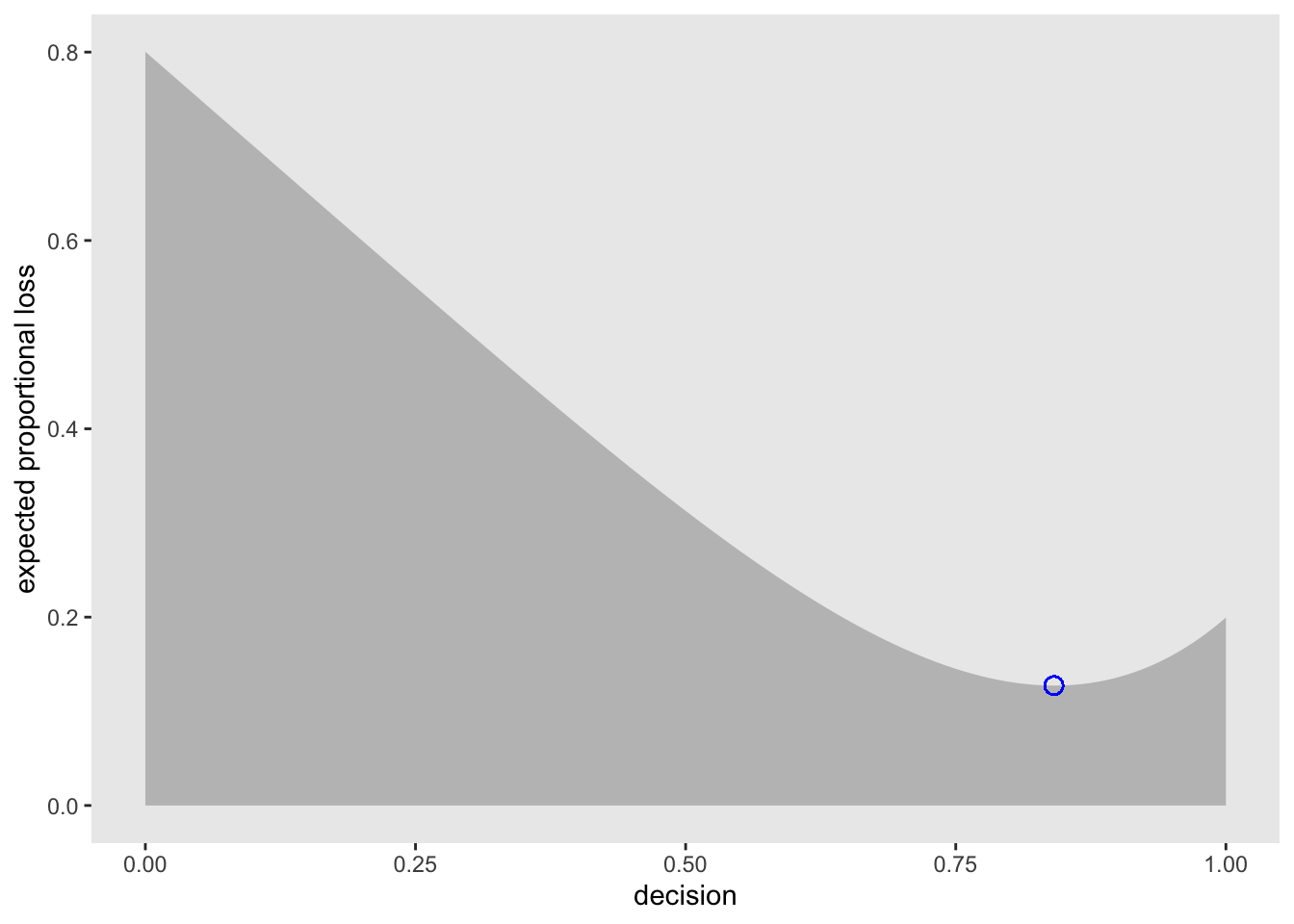

3.3 Sampling to simulate prediction

McElreath’s 5 reasons for posterior simulation: 1. Model design - We can sample from both the posterior and the priors to see how the model behaves
2. Model checking - simulating implied observations to check the model fit
3. Software validation - To double check that the software is running as expected, it helps to simulate observations for a known model and try to recover the parameter values
4. Research design - you can test observations from your hypothesis to test your design. similar to power analysis
5. Forecasting - Estimates can be used to simulate new predictions, for new cases and future observations

3.3.1 Dummy data

From the globe tossing example we can use the likelihood function to create dummy data

\[\begin{equation} \text{Pr}(W|N,p) = \frac{N!}{ W!(N-W)!}p^W\left(1-p\right)^{N-W} \end{equation}\]

If we had two tosses (N = 2), there are 3 possibilities: 0 W, 1W, 2W. So we can compute the probabilities of each with the p value set to 0.7

dbinom(0:2, size = 2, prob = 0.7)

## [1] 0.09 0.42 0.49

So we see a 9% chance for 0 W, 42% chance of 1 W, and 49% 2 W. So we can sample from the binomial distribution. For example:

rbinom(1 , size = 2, prob = 0.7)

## [1] 2

This is a single random draw from the described distribution. You can also sample multiples:

rbinom(10, size = 2, prob = 0.7)

##  [1] 1 1 2 2 1 2 2 2 2 0

So we can create a large selection of random draws as dummy data and see if the 0s, 1s, and 2s appear in the same proportions as the probabilities above (9%, 42%, and 49%)

dummy_w <- rbinom(1e5, size = 2, prob = 0.7)
table(dummy_w) / 1e5

## dummy_w
##       0       1       2 
## 0.08972 0.41847 0.49181

Now, let’s update the tosses to match all the previous examples (N = 9).

dummy_w <- rbinom(1e5, size = 9, prob = 0.7)
n <- c(1:1e5)
df_w <- tibble(n, dummy_w) 

df_w %>% ggplot(aes(x = dummy_w)) +
  geom_histogram(binwidth = 1) +
  scale_x_continuous("dummy water count", breaks = seq(from = 0, to = 9, by = 2)) +
  ylab("frequency") +
  theme(panel.grid = element_blank())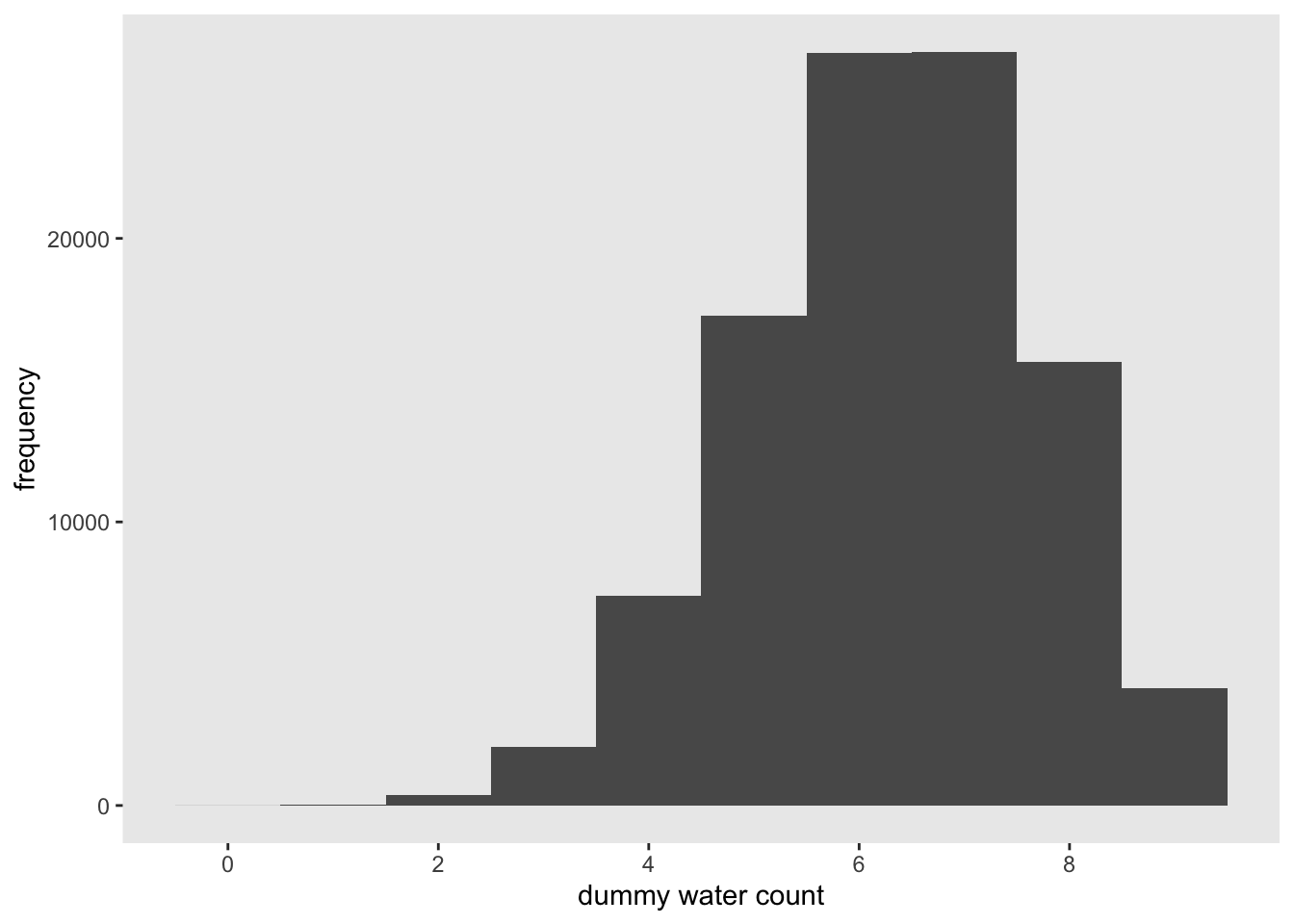

#simplehist(dummy_w, xlab = 'dummy water count') #rethinking

3.3.2 Model checking

3.3.2.1 Did the software work?

There actually is no way to check if the software is working correctly. You just have to set yourself an acceptable amount of correspondence between the observations (data) and implied predictions.

3.3.2.2 Is the model adequate?

We need to incorporate the model’s posterior distribution (and its uncertainty) with the implied predictions (and their uncertainty) to create a Posterior Predictive Distribution. To visulize this, we can recreate McElreath’s figure 3.6 below.

# number of grid point in p_grid
n <- 1001
# number of W in 9 tosses
n_w <- 6
# number of tosses
n_t <- 9

# make a table that contains the p_grid, prior, and posterior
df <- tibble(
  p_grid = seq(from = 0, to = 1, length.out = n),
  #prior is still flat
  prior = 1) %>% 
  mutate(likelihood = dbinom(n_w, size = n_t, prob = p_grid)) %>% 
  mutate(posterior = (likelihood * prior)/sum(likelihood*prior))

#visualize the posterior distribution with 9 p values to sample from
df %>% 
  ggplot(aes(x = p_grid)) +
  geom_ribbon(aes(ymin = 0, ymax = posterior),
              color = 'grey70', fill = 'grey70') +
  geom_segment(data = . %>% 
                 filter(p_grid %in% c(seq(from = 0.1, to = 0.9, by = 0.1), 3 / 10)),
               aes(xend = p_grid, y = 0, yend = posterior, size = posterior),
               color = 'grey35', show.legend = FALSE) +
  geom_point(data = . %>% 
               filter(p_grid %in% c(seq(from = 0.1, to = 0.9, by = 0.1), 3 / 10)),
             aes(y = posterior)) +
  annotate(geom = 'text', x = 0.08, y = 0.0025, label = 'Posterior probability') +
  scale_size_continuous(range = c(0,1)) +
  scale_x_continuous('probability of water', breaks = c(0:10) / 10) +
  scale_y_continuous(NULL, breaks = NULL) +
  theme(panel.grid = element_blank())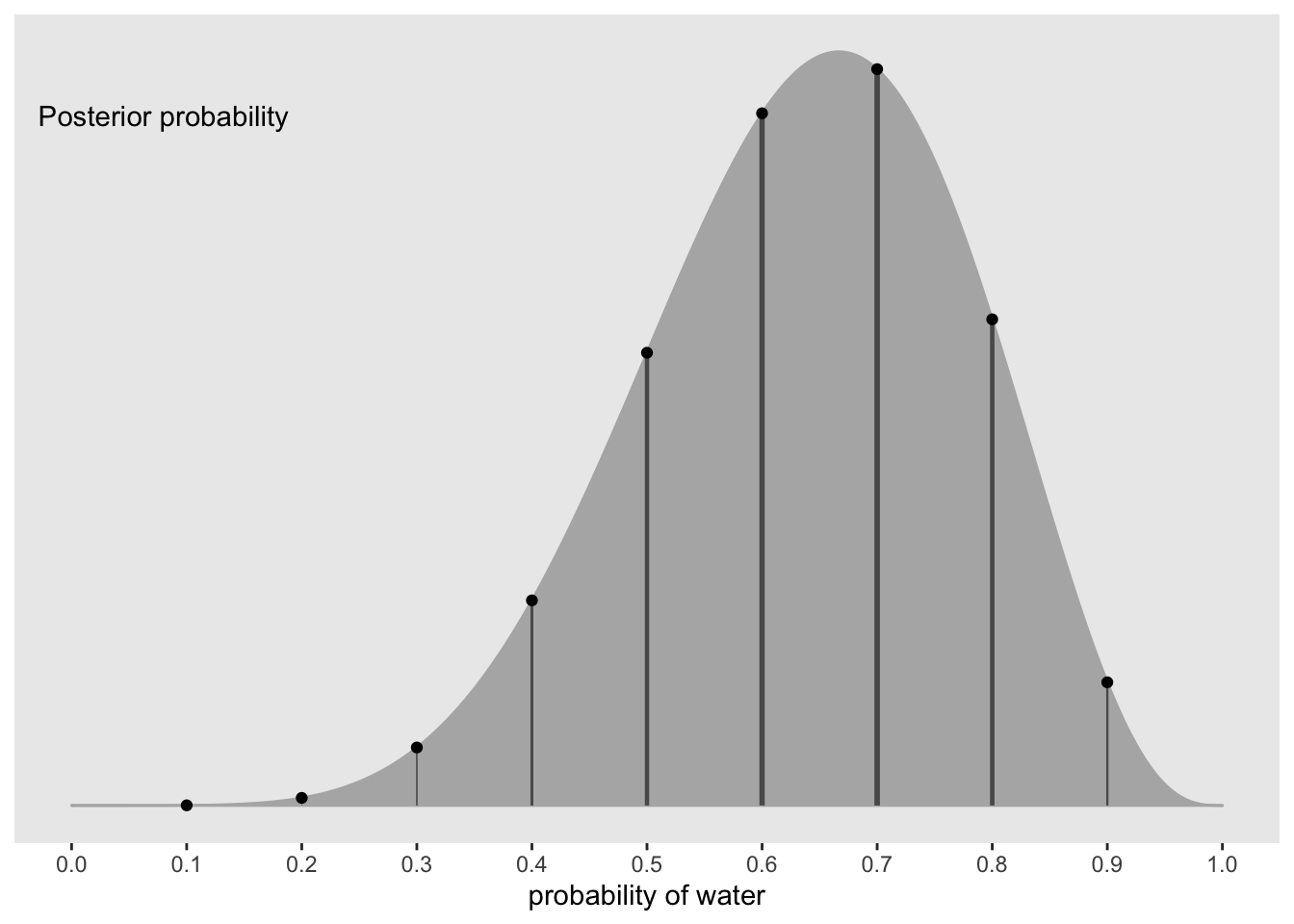

#show the sampling distributions for each p value above
library(tidyr)

## 
## Attaching package: 'tidyr'

## The following object is masked from 'package:rstan':
## 
##     extract

#number of simulated draws
n_draws <- 1e5

#simulation function
simulate_binom <- function(probability){
  set.seed(11) #reproducible
  rbinom(n_draws, size = 9, prob = probability)
}

# make a table of simulated draws for each probability
df_small <- 
  tibble(probability = seq(from = 0.1, to = 0.9, by = 0.1)) %>% 
  mutate(draws = purrr::map(probability, simulate_binom)) %>% 
  unnest(draws) %>% 
  mutate(label = str_c("p = ", probability))

#create a histogram for each simulated p value
df_small %>% 
  ggplot(aes(x = draws)) +
  geom_histogram(binwidth = 1, center = 0, color = 'grey90', size = 1/10) +
  scale_x_continuous(NULL, breaks = seq(from = 0, to = 9, by = 3)) +
  scale_y_continuous(NULL, breaks = NULL) +
  labs(subtitle = 'Sampling distributions') +
  #coord_cartesian(xlim = 0:9) +
  theme(panel.grid = element_blank()) +
  facet_wrap(~ label, ncol = 9)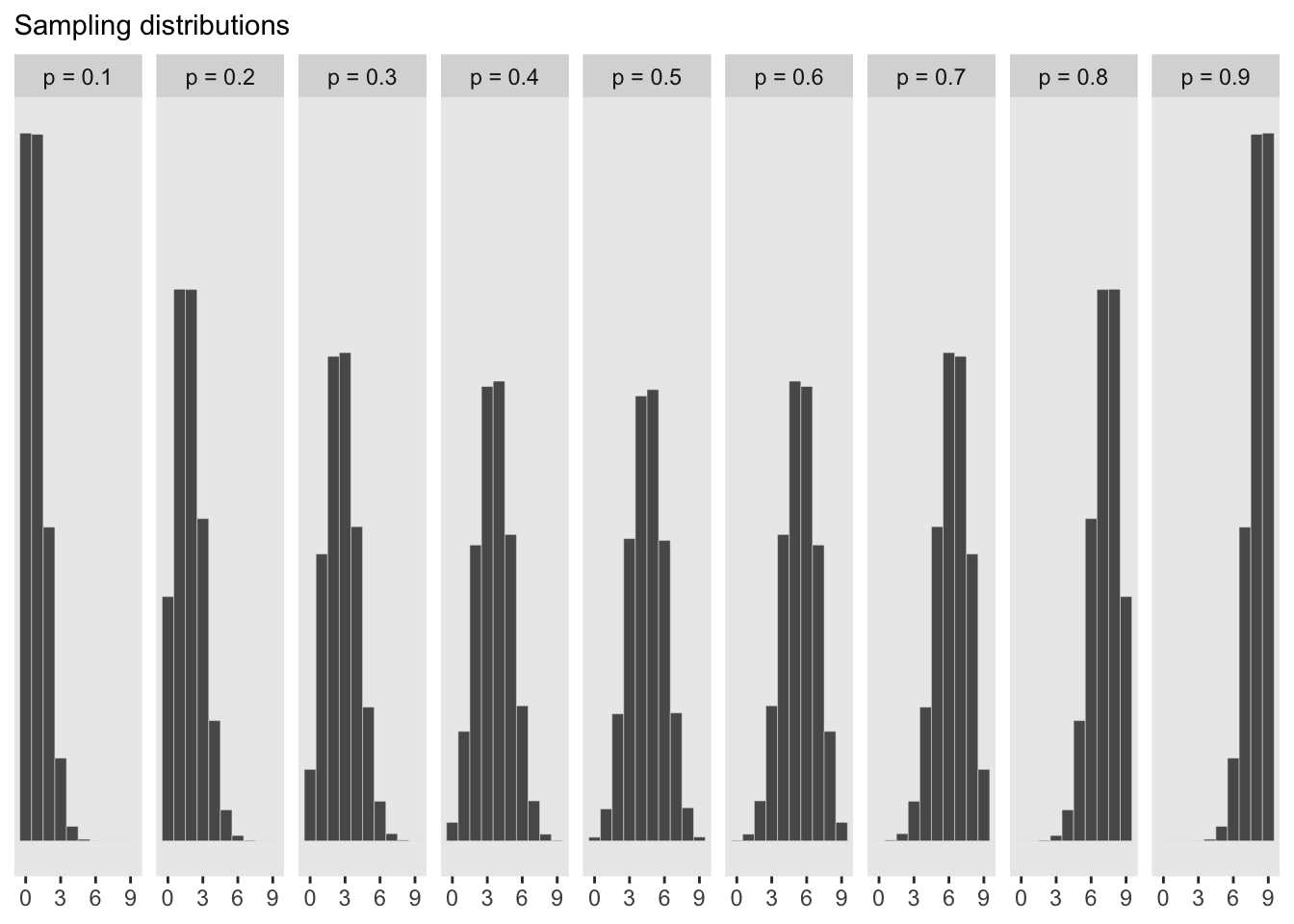

#show the newly calculated PPD

#number of samples
n_samples <- 1e4

#make sure it can be replicated
set.seed(11)
# sample rows of the original dataframe and calculate a W value for each p_grid value
samples <- df %>% 
  sample_n(size = n_samples, weight = posterior, replace = TRUE) %>% 
  mutate(w = purrr::map_dbl(p_grid, rbinom, n = 1, size = 9))

#plot the newly created PPD
samples %>% 
  ggplot(aes(x = w)) +
  geom_histogram(binwidth = 1, center = 0, color = 'grey90', size = 1/10) +
  scale_x_continuous('number of water samples', breaks = seq(from = 0, to = 9, by = 3)) +
  scale_y_continuous(NULL, breaks = NULL) +
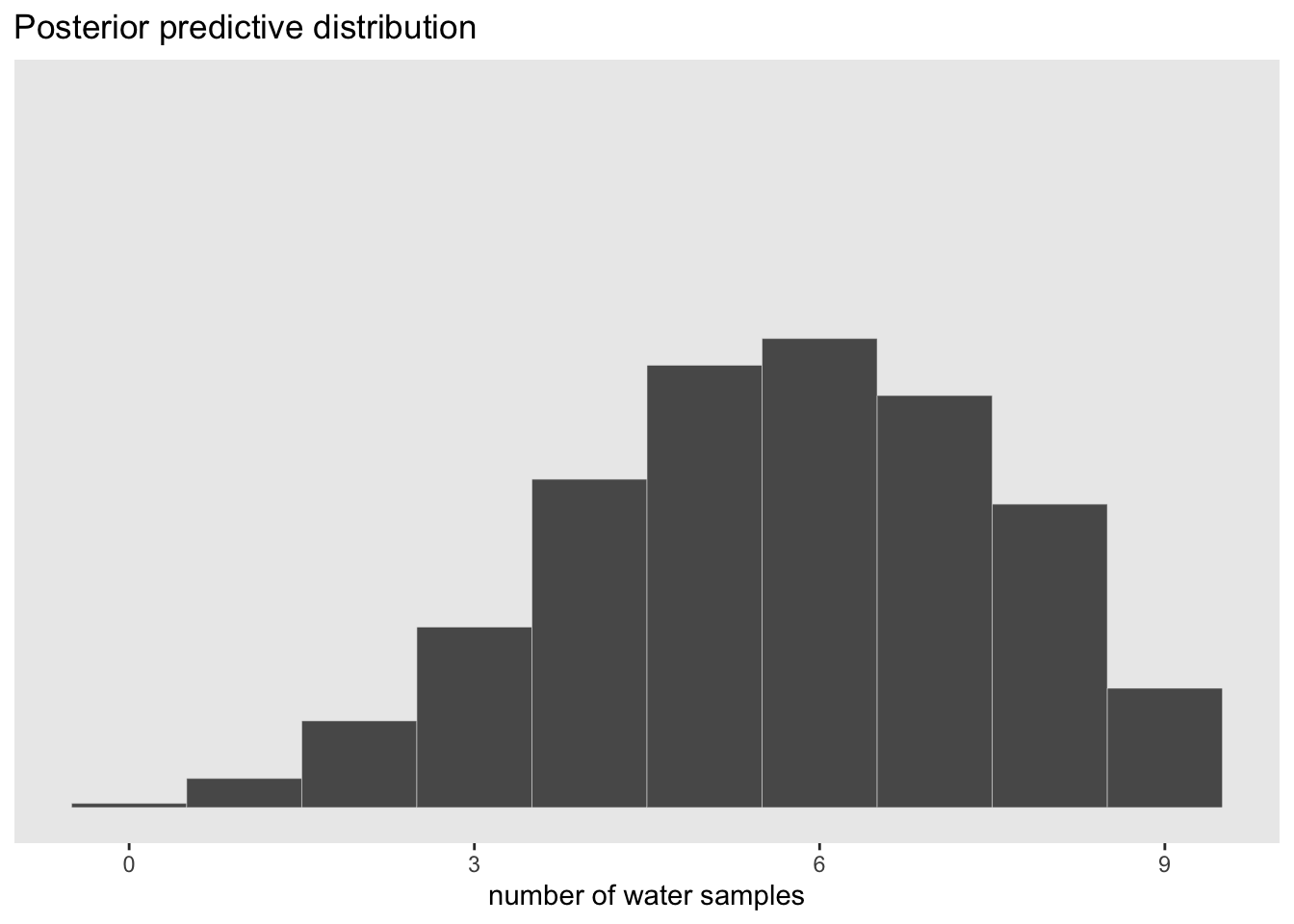
  ggtitle('Posterior predictive distribution') +
  #coord_cartesian(xlim = 0:9, ylim = 0:3000) +
  theme(panel.grid = element_blank())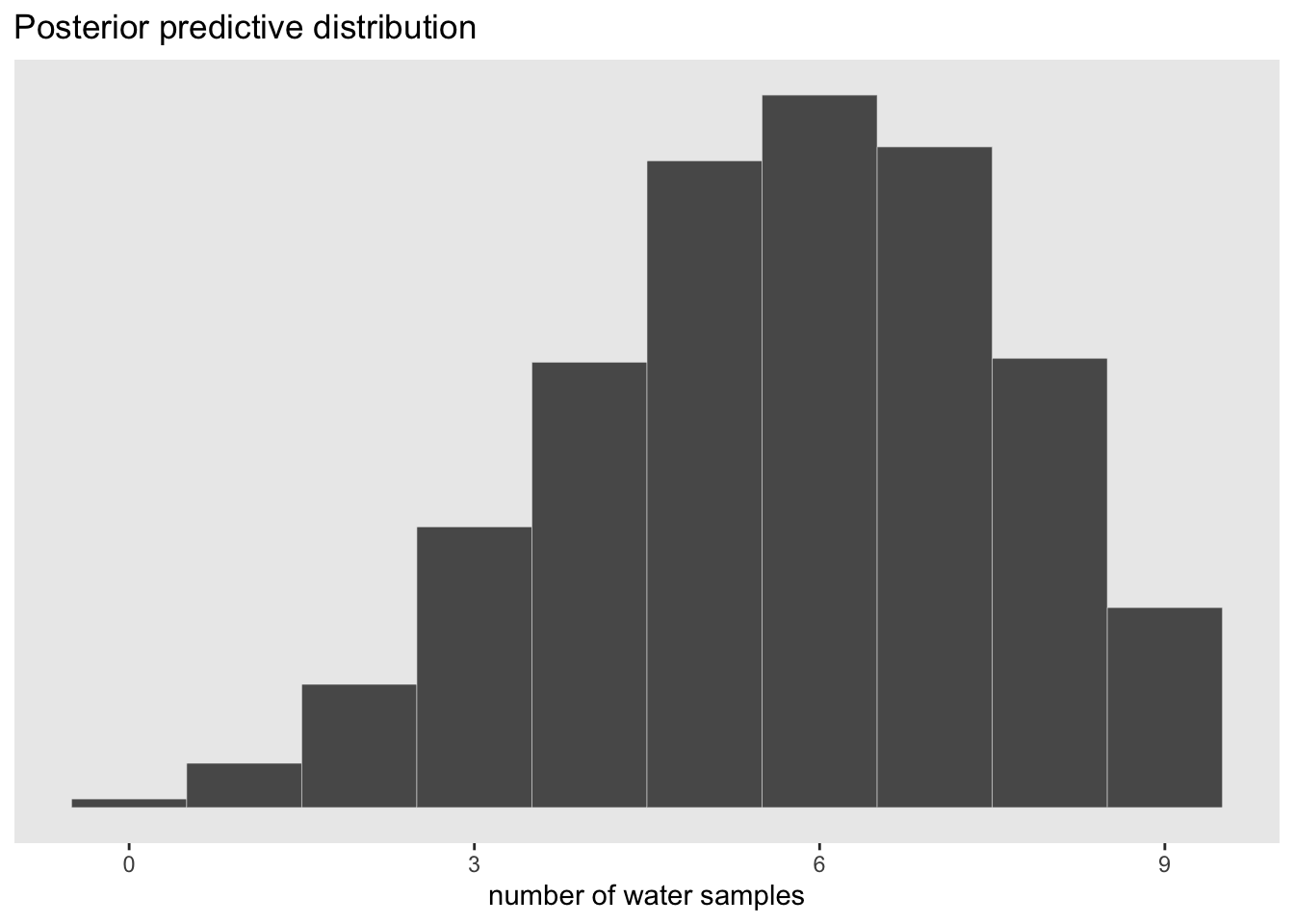

The advantage here is that the predictive distribution is still quite spread out compared to the observed data (w = 6). This is much more informative than if we were to just pick out the mode of the posterior and make implied predictions from that value. This would look like the sampling distribution of p = 0.6 above which would be overconfident.

3.3.3 Practice with brms

Let’s create a PPD with brms

Load the package

library(brms)

brms_3 <- brm(data = list(w = 6),
              family = binomial(link = 'identity'),
              w | trials(9) ~ 1,
              prior(beta(1, 1), class = Intercept),
              seed = 11,
              control = list(adapt_delta = 0.999))

## Compiling Stan program...

## recompiling to avoid crashing R session

## Start sampling

## 
## SAMPLING FOR MODEL '32a7f51a2d1717ef80875b648bc79f41' NOW (CHAIN 1).
## Chain 1: Rejecting initial value:
## Chain 1:   Error evaluating the log probability at the initial value.
## Chain 1: Exception: binomial_lpmf: Probability parameter[1] is -0.232403, but must be in the interval [0, 1]  (in 'modeld712023842a_32a7f51a2d1717ef80875b648bc79f41' at line 22)
## 
## Chain 1: 
## Chain 1: Gradient evaluation took 2.1e-05 seconds
## Chain 1: 1000 transitions using 10 leapfrog steps per transition would take 0.21 seconds.
## Chain 1: Adjust your expectations accordingly!
## Chain 1: 
## Chain 1: 
## Chain 1: Iteration:    1 / 2000 [  0%]  (Warmup)
## Chain 1: Iteration:  200 / 2000 [ 10%]  (Warmup)
## Chain 1: Iteration:  400 / 2000 [ 20%]  (Warmup)
## Chain 1: Iteration:  600 / 2000 [ 30%]  (Warmup)
## Chain 1: Iteration:  800 / 2000 [ 40%]  (Warmup)
## Chain 1: Iteration: 1000 / 2000 [ 50%]  (Warmup)
## Chain 1: Iteration: 1001 / 2000 [ 50%]  (Sampling)
## Chain 1: Iteration: 1200 / 2000 [ 60%]  (Sampling)
## Chain 1: Iteration: 1400 / 2000 [ 70%]  (Sampling)
## Chain 1: Iteration: 1600 / 2000 [ 80%]  (Sampling)
## Chain 1: Iteration: 1800 / 2000 [ 90%]  (Sampling)
## Chain 1: Iteration: 2000 / 2000 [100%]  (Sampling)
## Chain 1: 
## Chain 1:  Elapsed Time: 0.037163 seconds (Warm-up)
## Chain 1:                0.048304 seconds (Sampling)
## Chain 1:                0.085467 seconds (Total)
## Chain 1: 
## 
## SAMPLING FOR MODEL '32a7f51a2d1717ef80875b648bc79f41' NOW (CHAIN 2).
## Chain 2: 
## Chain 2: Gradient evaluation took 1.8e-05 seconds
## Chain 2: 1000 transitions using 10 leapfrog steps per transition would take 0.18 seconds.
## Chain 2: Adjust your expectations accordingly!
## Chain 2: 
## Chain 2: 
## Chain 2: Iteration:    1 / 2000 [  0%]  (Warmup)
## Chain 2: Iteration:  200 / 2000 [ 10%]  (Warmup)
## Chain 2: Iteration:  400 / 2000 [ 20%]  (Warmup)
## Chain 2: Iteration:  600 / 2000 [ 30%]  (Warmup)
## Chain 2: Iteration:  800 / 2000 [ 40%]  (Warmup)
## Chain 2: Iteration: 1000 / 2000 [ 50%]  (Warmup)
## Chain 2: Iteration: 1001 / 2000 [ 50%]  (Sampling)
## Chain 2: Iteration: 1200 / 2000 [ 60%]  (Sampling)
## Chain 2: Iteration: 1400 / 2000 [ 70%]  (Sampling)
## Chain 2: Iteration: 1600 / 2000 [ 80%]  (Sampling)
## Chain 2: Iteration: 1800 / 2000 [ 90%]  (Sampling)
## Chain 2: Iteration: 2000 / 2000 [100%]  (Sampling)
## Chain 2: 
## Chain 2:  Elapsed Time: 0.039711 seconds (Warm-up)
## Chain 2:                0.061793 seconds (Sampling)
## Chain 2:                0.101504 seconds (Total)
## Chain 2: 
## 
## SAMPLING FOR MODEL '32a7f51a2d1717ef80875b648bc79f41' NOW (CHAIN 3).
## Chain 3: Rejecting initial value:
## Chain 3:   Error evaluating the log probability at the initial value.
## Chain 3: Exception: binomial_lpmf: Probability parameter[1] is -0.794659, but must be in the interval [0, 1]  (in 'modeld712023842a_32a7f51a2d1717ef80875b648bc79f41' at line 22)
## 
## Chain 3: 
## Chain 3: Gradient evaluation took 1e-05 seconds
## Chain 3: 1000 transitions using 10 leapfrog steps per transition would take 0.1 seconds.
## Chain 3: Adjust your expectations accordingly!
## Chain 3: 
## Chain 3: 
## Chain 3: Iteration:    1 / 2000 [  0%]  (Warmup)
## Chain 3: Iteration:  200 / 2000 [ 10%]  (Warmup)
## Chain 3: Iteration:  400 / 2000 [ 20%]  (Warmup)
## Chain 3: Iteration:  600 / 2000 [ 30%]  (Warmup)
## Chain 3: Iteration:  800 / 2000 [ 40%]  (Warmup)
## Chain 3: Iteration: 1000 / 2000 [ 50%]  (Warmup)
## Chain 3: Iteration: 1001 / 2000 [ 50%]  (Sampling)
## Chain 3: Iteration: 1200 / 2000 [ 60%]  (Sampling)
## Chain 3: Iteration: 1400 / 2000 [ 70%]  (Sampling)
## Chain 3: Iteration: 1600 / 2000 [ 80%]  (Sampling)
## Chain 3: Iteration: 1800 / 2000 [ 90%]  (Sampling)
## Chain 3: Iteration: 2000 / 2000 [100%]  (Sampling)
## Chain 3: 
## Chain 3:  Elapsed Time: 0.039656 seconds (Warm-up)
## Chain 3:                0.035382 seconds (Sampling)
## Chain 3:                0.075038 seconds (Total)
## Chain 3: 
## 
## SAMPLING FOR MODEL '32a7f51a2d1717ef80875b648bc79f41' NOW (CHAIN 4).
## Chain 4: Rejecting initial value:
## Chain 4:   Error evaluating the log probability at the initial value.
## Chain 4: Exception: binomial_lpmf: Probability parameter[1] is -0.0368002, but must be in the interval [0, 1]  (in 'modeld712023842a_32a7f51a2d1717ef80875b648bc79f41' at line 22)
## 
## Chain 4: Rejecting initial value:
## Chain 4:   Error evaluating the log probability at the initial value.
## Chain 4: Exception: binomial_lpmf: Probability parameter[1] is 1.49284, but must be in the interval [0, 1]  (in 'modeld712023842a_32a7f51a2d1717ef80875b648bc79f41' at line 22)
## 
## Chain 4: 
## Chain 4: Gradient evaluation took 1.2e-05 seconds
## Chain 4: 1000 transitions using 10 leapfrog steps per transition would take 0.12 seconds.
## Chain 4: Adjust your expectations accordingly!
## Chain 4: 
## Chain 4: 
## Chain 4: Iteration:    1 / 2000 [  0%]  (Warmup)
## Chain 4: Iteration:  200 / 2000 [ 10%]  (Warmup)
## Chain 4: Iteration:  400 / 2000 [ 20%]  (Warmup)
## Chain 4: Iteration:  600 / 2000 [ 30%]  (Warmup)
## Chain 4: Iteration:  800 / 2000 [ 40%]  (Warmup)
## Chain 4: Iteration: 1000 / 2000 [ 50%]  (Warmup)
## Chain 4: Iteration: 1001 / 2000 [ 50%]  (Sampling)
## Chain 4: Iteration: 1200 / 2000 [ 60%]  (Sampling)
## Chain 4: Iteration: 1400 / 2000 [ 70%]  (Sampling)
## Chain 4: Iteration: 1600 / 2000 [ 80%]  (Sampling)
## Chain 4: Iteration: 1800 / 2000 [ 90%]  (Sampling)
## Chain 4: Iteration: 2000 / 2000 [100%]  (Sampling)
## Chain 4: 
## Chain 4:  Elapsed Time: 0.039805 seconds (Warm-up)
## Chain 4:                0.027747 seconds (Sampling)
## Chain 4:                0.067552 seconds (Total)
## Chain 4:

Posterior summary of the probability of w

posterior_summary(brms_3)['b_Intercept', ] %>% 
  round(digits = 2)

##  Estimate Est.Error      Q2.5     Q97.5 
##      0.63      0.14      0.34      0.88

Now we can sample draws with fitted() in the brms package from the posterior

library(purrr)

## 
## Attaching package: 'purrr'

## The following object is masked from 'package:rethinking':
## 
##     map

f <- fitted(brms_3, summary = FALSE, scale = 'linear') %>% 
  as_tibble() %>% 
  set_names('p')

## Warning: The `x` argument of `as_tibble.matrix()` must have unique column names if `.name_repair` is omitted as of tibble 2.0.0.
## Using compatibility `.name_repair`.

glimpse(f)

## Rows: 4,000
## Columns: 1
## $ p <dbl> 0.6109911, 0.5994330, 0.6465488, 0.6851288, 0.5909901, 0.6042266, 0.…

As a density:

f %>% 
  ggplot(aes(x = p)) +
  geom_density(fill = 'grey50', color = 'grey50') +
  annotate(geom = 'text', x = 0.08, y = 2.5, label = 'Posterior probability') +
  scale_x_continuous('probability of water', breaks = c(0, 0.5, 1), limits = 0:1) +
  scale_y_continuous(NULL, breaks = NULL) +
  theme(panel.grid = element_blank())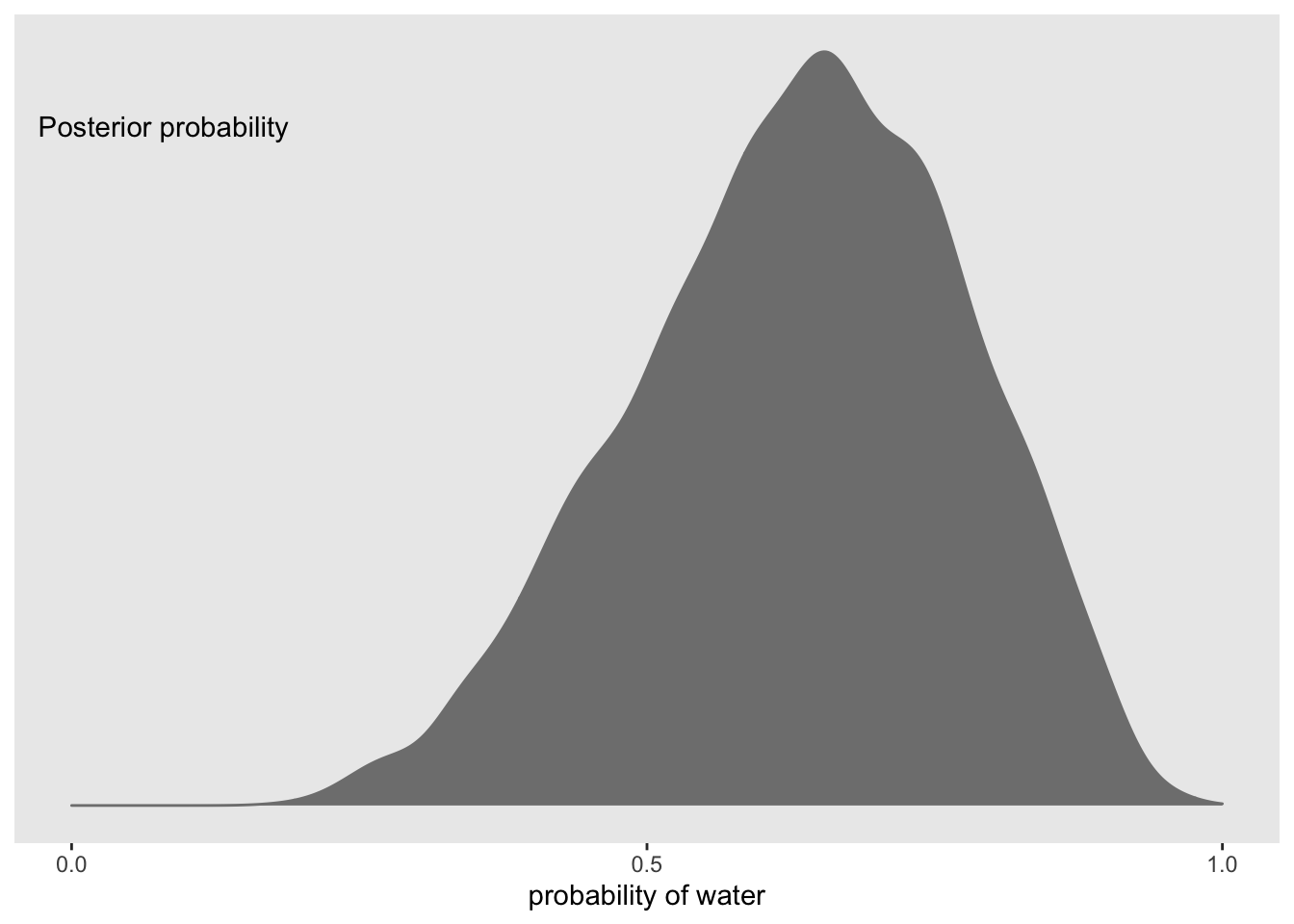

Now we can use this distribution to simulate samples

#make reproducible
set.seed(11)

#simulate samples
f <- f %>% 
  mutate(w = rbinom(n(), size = n_t, prob = p))

#plot PPD
f %>% 
  ggplot(aes(x = w)) +
  geom_histogram(binwidth = 1, center = 0, color = 'grey90',
                 size = 1/10) +
  scale_x_continuous('number of water samples', breaks = seq(from = 0, to = 9, by =3)) +
  scale_y_continuous(NULL, breaks = NULL, limits = c(0, 1200)) +
  ggtitle('Posterior predictive distribution') +
  theme(panel.grid = element_blank())