3.METODOS
3.1APLICANDO CLUSTER JERARQUICO
AGRUPAMIENTO DE INDIVIDUOS
library(readxl)
datosc <- read_excel("data_media.xlsx")Estructura: Tenemos 24 variables de formato numerico y 1 variable en formato character(meses)
str(datosc)## tibble [12 x 25] (S3: tbl_df/tbl/data.frame)
## $ meses: chr [1:12] "Ene" "Feb" "Mar" "Abr" ...
## $ Caud : num [1:12] 40.6 56 71.9 47.6 26.3 23.1 23.5 21.7 22.8 22.4 ...
## $ Temp : num [1:12] 19.2 20.2 20.2 20.1 18.5 17.2 16.6 15.7 16.5 18.6 ...
## $ pH : num [1:12] 7.7 7.8 7 7 8 7 7.8 7 7 8 ...
## $ Turb : num [1:12] 47.2 301.9 391.7 100.4 12.5 ...
## $ CE : num [1:12] 488 440 402 426 595 ...
## $ OD : num [1:12] 8.7 8.84 8.94 8.51 8.55 8.64 9 8.76 8.7 8.64 ...
## $ SD : num [1:12] 338 308 278 284 380 ...
## $ Akal : num [1:12] 95.6 91 81.6 91.3 120.4 ...
## $ DI : num [1:12] 211 189 165 176 255 ...
## $ Cls : num [1:12] 14.3 12.8 12.8 11.9 21.8 24.8 18.8 19.3 19.9 17.8 ...
## $ so : num [1:12] 138.6 116.5 97.5 114.6 146.7 ...
## $ N03 : num [1:12] 2.98 2.78 2.54 2.41 3.38 3.64 3.83 3.58 3.61 3.38 ...
## $ N02 : num [1:12] 0.2 0.13 0.08 0.1 0.21 0.3 0.23 0.28 0.18 0.24 ...
## $ PO : num [1:12] 0.2 0.14 0.09 0.18 0.23 0.28 0.32 0.38 0.36 0.34 ...
## $ Cu : num [1:12] 0.04 0.065 0.077 0.038 0.03 0.027 0.022 0.025 0.028 0.023 ...
## $ Al : num [1:12] 1.707 7.207 10.89 3.644 0.408 ...
## $ Fe : num [1:12] 2.176 7.595 11.37 4.471 0.434 ...
## $ Mu : num [1:12] 0.118 0.324 0.342 0.173 0.111 0.089 0.074 0.064 0.049 0.045 ...
## $ Pb : num [1:12] 0.024 0.081 0.079 0.056 0.015 0.02 0.013 0.015 0.022 0.012 ...
## $ Cd : num [1:12] 0.002 0.005 0.003 0.002 0.003 0.002 0.002 0.002 0.002 0.001 ...
## $ Zn : num [1:12] 0.372 0.611 0.641 0.343 0.468 0.323 0.273 0.28 0.28 0.171 ...
## $ As : num [1:12] 0.029 0.126 0.088 0.074 0.024 0.023 0.022 0.019 0.022 0.022 ...
## $ Colo : num [1:12] 178600 247014 208035 174967 160299 ...
## $ Cole : num [1:12] 74326 95332 90325 58096 63802 ...Convirtiendo en un dataframe:
datosc=as.data.frame(datosc)rownames(datosc)<- datosc$mesesEliminanos la variable meses(cualitativa)
datosc$meses=NULL
head(datosc,3)## Caud Temp pH Turb CE OD SD Akal DI Cls so N03 N02 PO
## Ene 40.6 19.2 7.7 47.2 487.71 8.70 337.86 95.6 211.4 14.3 138.6 2.98 0.20 0.20
## Feb 56.0 20.2 7.8 301.9 440.00 8.84 307.96 91.0 189.1 12.8 116.5 2.78 0.13 0.14
## Mar 71.9 20.2 7.0 391.7 401.96 8.94 278.04 81.6 164.6 12.8 97.5 2.54 0.08 0.09
## Cu Al Fe Mu Pb Cd Zn As Colo Cole
## Ene 0.040 1.707 2.176 0.118 0.024 0.002 0.372 0.029 178600 74326
## Feb 0.065 7.207 7.595 0.324 0.081 0.005 0.611 0.126 247014 95332
## Mar 0.077 10.890 11.370 0.342 0.079 0.003 0.641 0.088 208035 90325ANALISIS EXPLORATORIO
#Verificando si hay valores faltantes:
#Detectando y graficando los % de datos perdidos
#No hay valores perdidos en ninguna variable
library(DataExplorer)
library(ggplot2)
plot_missing(datosc,ggtheme=theme_minimal())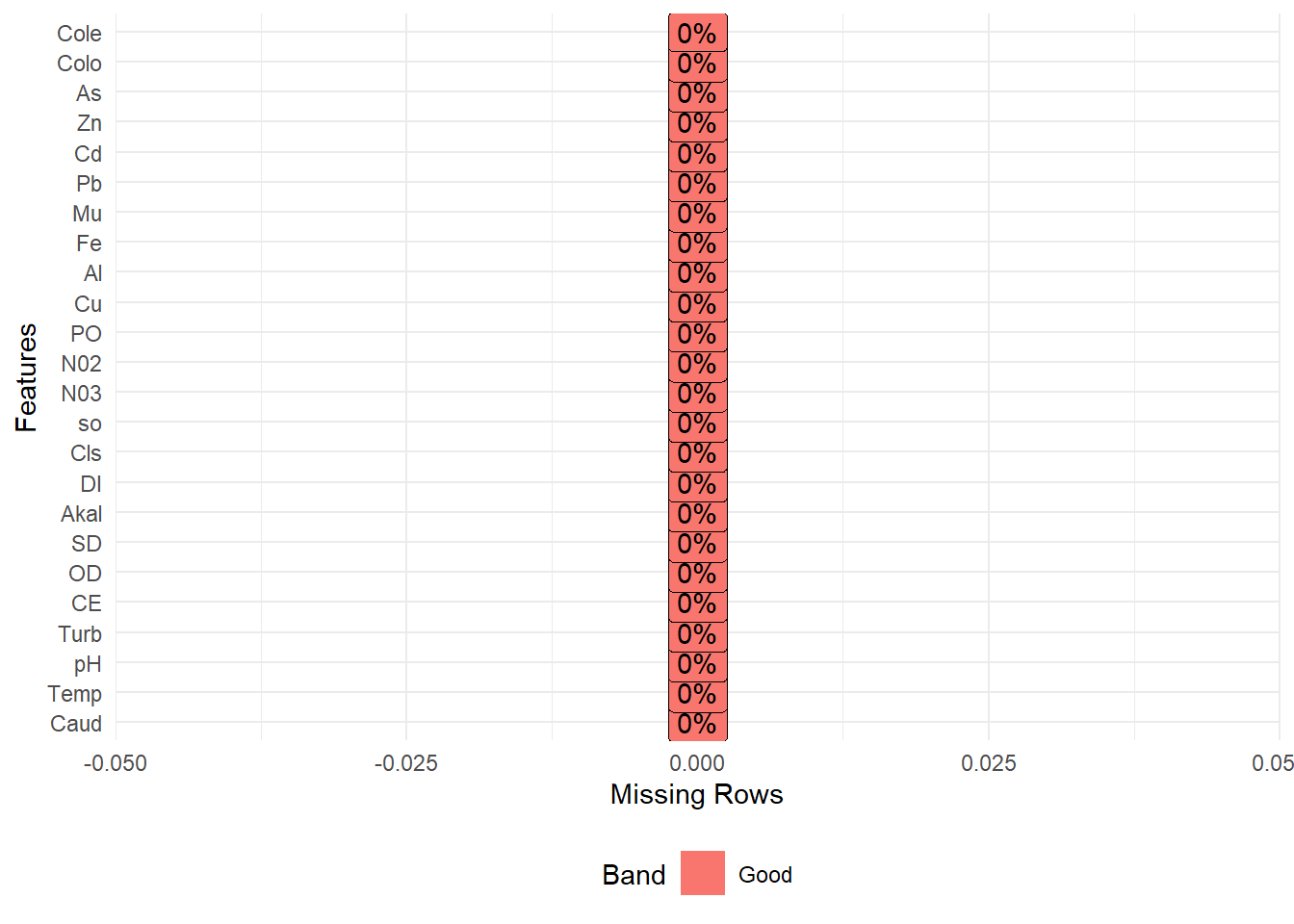
#estandarizamos los datos porque las variables se encuentran en diferentes escalas
datosc <- as.data.frame(scale(datosc))CLUSTER JERARQUICO AGLOMERATIVO
Distancia euclidiana y metodo de enlace Ward.D2
#-----------------------------------
#calculando la matriz de disimilaridad
d <- dist(datosc, method = "euclidean")
#el metodo ward.d2 ,para reconstruir la matriz distancia
res.hc <- hclust(d, method = "ward.D2" ) res.hc$merge## [,1] [,2]
## [1,] -10 -11
## [2,] -8 -9
## [3,] -1 -12
## [4,] -6 2
## [5,] -7 4
## [6,] -5 1
## [7,] -2 -3
## [8,] 3 6
## [9,] -4 7
## [10,] 5 8
## [11,] 9 10#formacion de "n" cluster hasta 1 cluster
#observamos que son 11 etapas:
#En la etapa 1
#el individuo 10 y el individuo 11 forman un cluster
#En la entapa 2
#el individuo 8 y el individuo 9 forman un cluster
#y asi sucesivamente hasta llegar a la etapa 11 donde se
#forma un solo cluster#estructura:
str(res.hc)## List of 7
## $ merge : int [1:11, 1:2] -10 -8 -1 -6 -7 -5 -2 3 -4 5 ...
## $ height : num [1:11] 1.55 1.9 2.54 3.36 3.95 ...
## $ order : int [1:12] 4 2 3 7 6 8 9 1 12 5 ...
## $ labels : chr [1:12] "Ene" "Feb" "Mar" "Abr" ...
## $ method : chr "ward.D2"
## $ call : language hclust(d = d, method = "ward.D2")
## $ dist.method: chr "euclidean"
## - attr(*, "class")= chr "hclust"options(scipen = 999)#sin notacion cientifica#distancia
res.hc$height## [1] 1.554549 1.904331 2.540561 3.359679 3.950460 4.065524 4.075132
## [8] 4.573464 7.031689 7.392952 18.178469EL NUMERO DE CLUSTER
#Hemos considerado que un cambio brusco seria de la etapa 9
#a la etapa 10,entonces el numero de cluster es 3
library(ggplot2)
alturas <- data.frame(etapa=1:11,distancia=res.hc$height)#distancia
alturas## etapa distancia
## 1 1 1.554549
## 2 2 1.904331
## 3 3 2.540561
## 4 4 3.359679
## 5 5 3.950460
## 6 6 4.065524
## 7 7 4.075132
## 8 8 4.573464
## 9 9 7.031689
## 10 10 7.392952
## 11 11 18.178469#screeplot con las distancias
ggplot(alturas) + aes(x=etapa,y=distancia) +
geom_point() + geom_line() +
scale_x_continuous(breaks=seq(1,15)) +
geom_vline(xintercept = 9,col="red",lty=2) +
theme_bw() 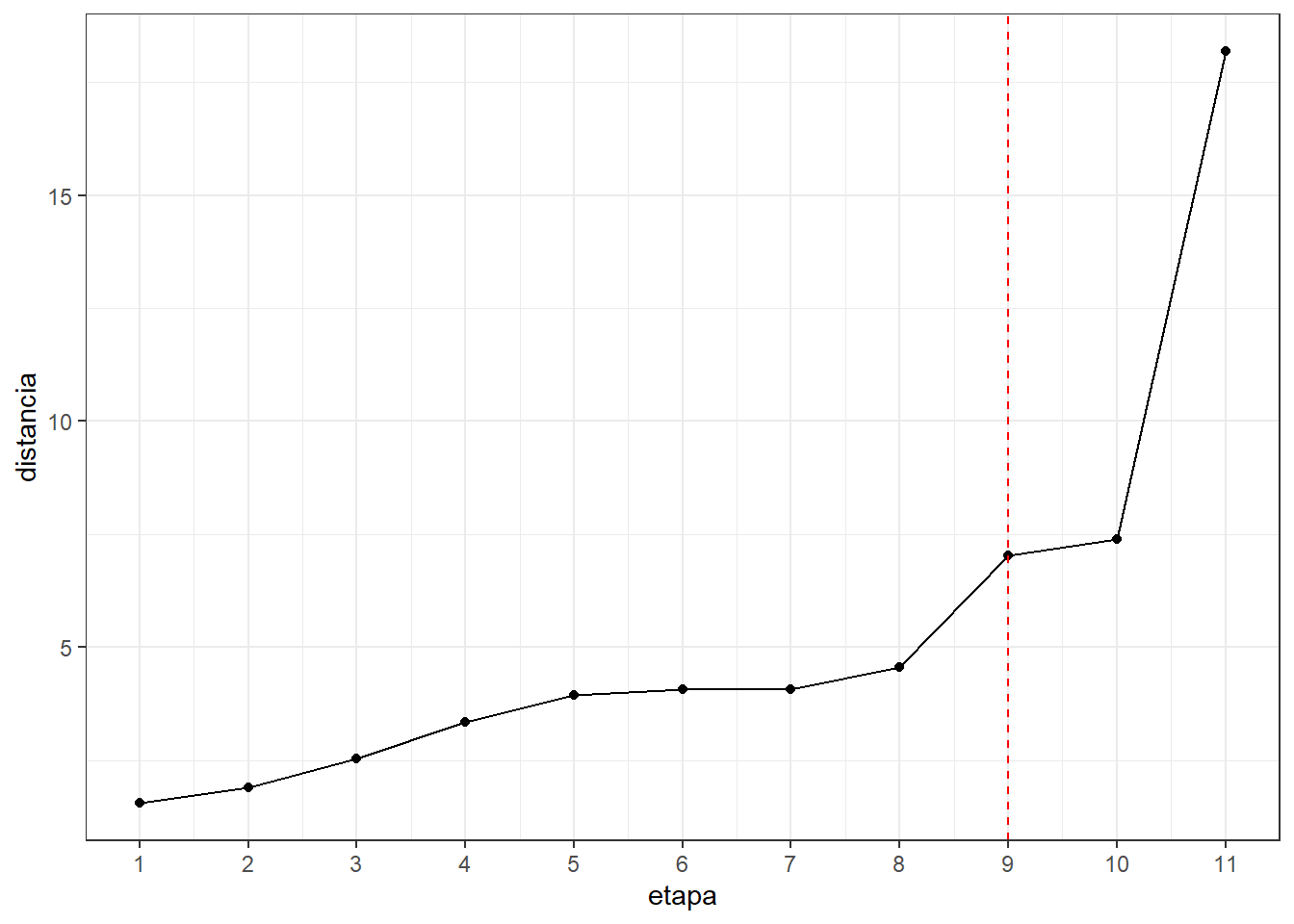
# Dividir en 3 clusters
#La asignacion de cada elemento(mes) a cada cluster
grp <- cutree(res.hc, k = 3)
grp ## Ene Feb Mar Abr May Jun Ju! Ago Set Oct Nov Dic.
## 1 2 2 2 1 3 3 3 3 1 1 1#cluster1:
#enero,mayo,octubre,noviembre y diciembre
#cluster2:
#febrero,marzo,abril
#cluster3:
#junio,julio,agosto,setiembreDEDONGRAMA
visualizacion de los 3 cluster:
library(factoextra)## Welcome! Want to learn more? See two factoextra-related books at https://goo.gl/ve3WBafviz_dend(res.hc, k=3, cex = 0.5,
k_colors = rainbow(3), # Colores del arco iris
color_labels_by_k = TRUE,
rect=T)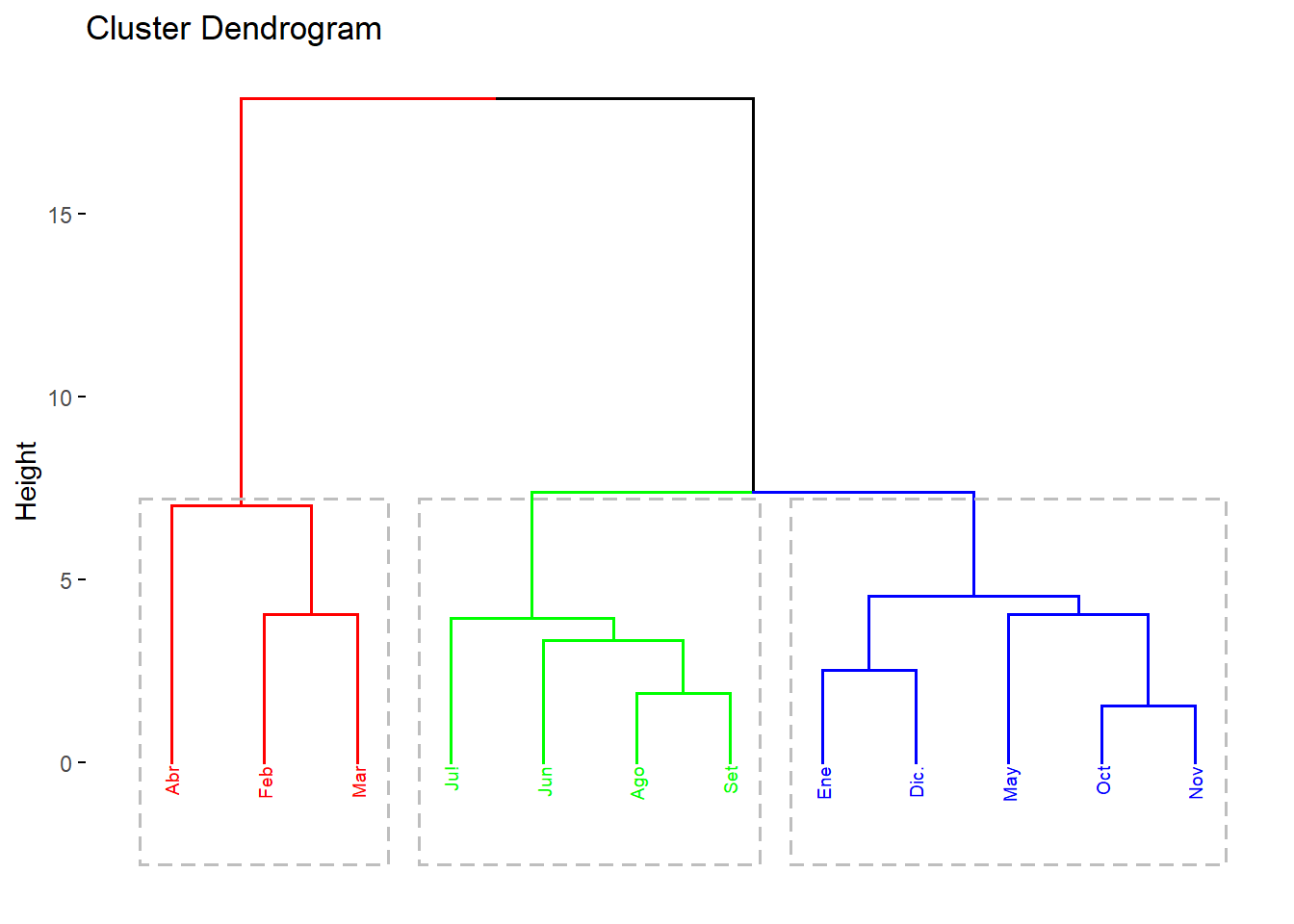
CONCLUSION DEL DENDOGRAMA:
estiage(fujo bajo del rio):
junio,julio,agosto y setiembre
transicion(incremento o disminucion del flujo del rio):
octubre, noviembre , diciembre , enero y mayo
avenida(flujo alto de rio):
febrero, marzo y abril.
En nuestro dendograma concluimos que los meses de transicion son octubre, noviembre , diciembre , enero y mayo son meses que esta en un ritmo de cambio o bien sube el nivel del agua del rio o bien baja el nivel del agua del rio,es decir para que el nivel del agua del rio sea de flujo alto(avenida),en los meses previos como enero,diciembre,noviembre,octubre tuvo que aumentar de poco a poco el nivel del agua hasta que febrero,marzo y abril (periodo flujo del rio es alto),luego llegando al mes de mayo comienza a disminuir el nivel del agua de rio rimac este es el mes transicion, despues en los meses posteriores junio,julio,agosto y setiembre el nivel flujo del rio es bajo.
#conclusion del tesista:
#estiaje:
#mayo,junio,julio, agosto, setiembre y octubre
#transicion(generan cambios inesperados o esperados):
#noviembre, diciembre y enero
#avenida:
#febrero, marzo y abril.GRAFICA#ACP con CLUSTER
GRAFICO 1
#Se puede apreciar que con 2 componentes retenemos 83.8% de la inercia total
library(factoextra)
fviz_cluster(list(data = datosc, cluster = grp),
palette =c("#DB1515", "#3722BF", "#D41AC4") ,
ellipse.type = "convex", # Concentration ellipse
repel = T, # Avoid label overplotting (slow)
show.clust.cent = FALSE, ggtheme = theme_bw())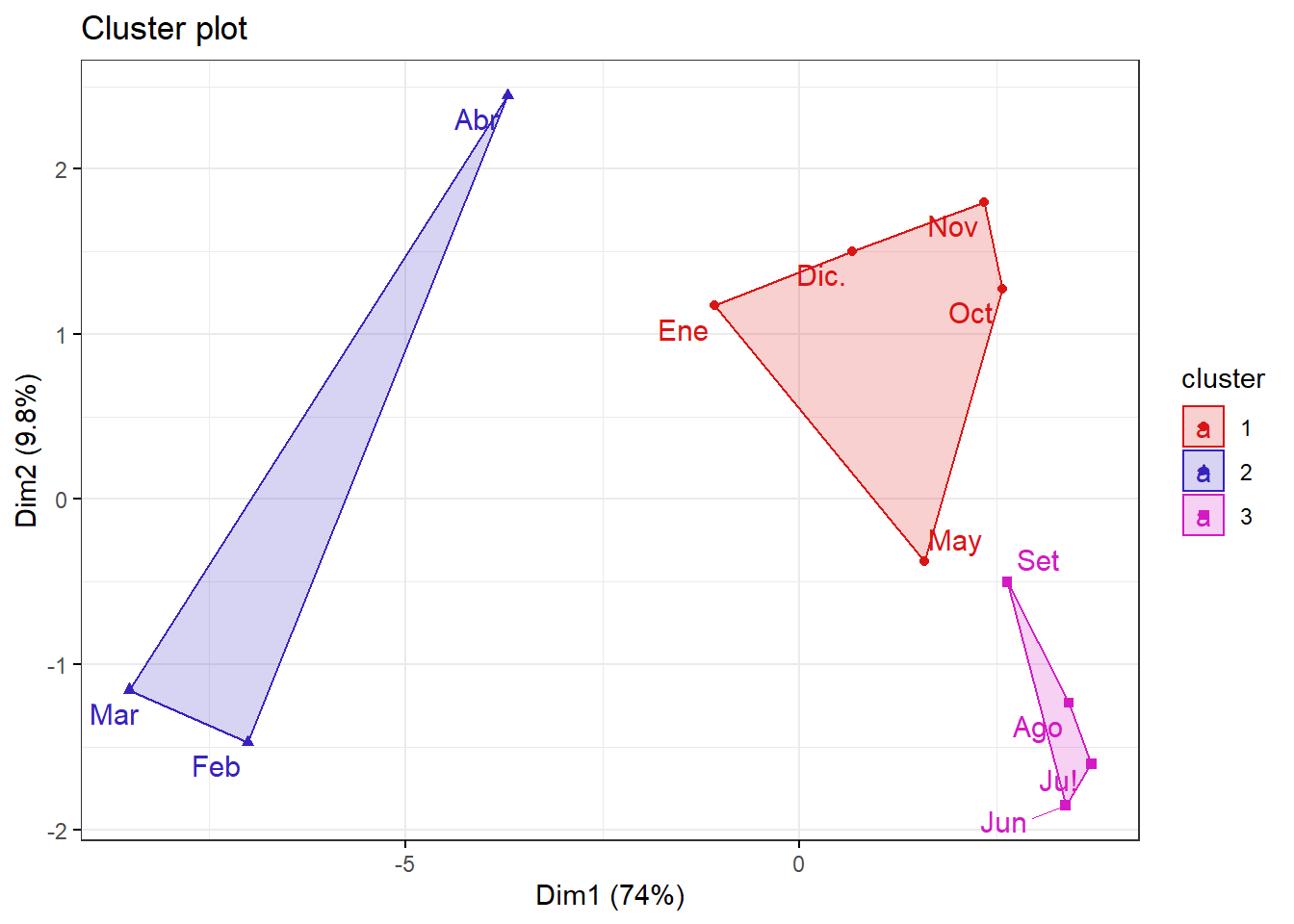
Insumo para un modelo predictivo como regresion lineal
# Juntando el archivo de "datos" con la columna de "cluster"
datos.j <- cbind(datosc,grp)#convirtiendo en factor la varaible "grp"
datos.j$grp <- factor(datos.j$grp)
#Si deseamos exportar :
# write.csv(datos.j,"Compras con Jerarquico Aglomerativo.csv")Analisis de componenentes principales:
En las variables(24)
ANALISIS EXPLORATORIO :
library(GGally)## Registered S3 method overwritten by 'GGally':
## method from
## +.gg ggplot2ggcorr(datosc)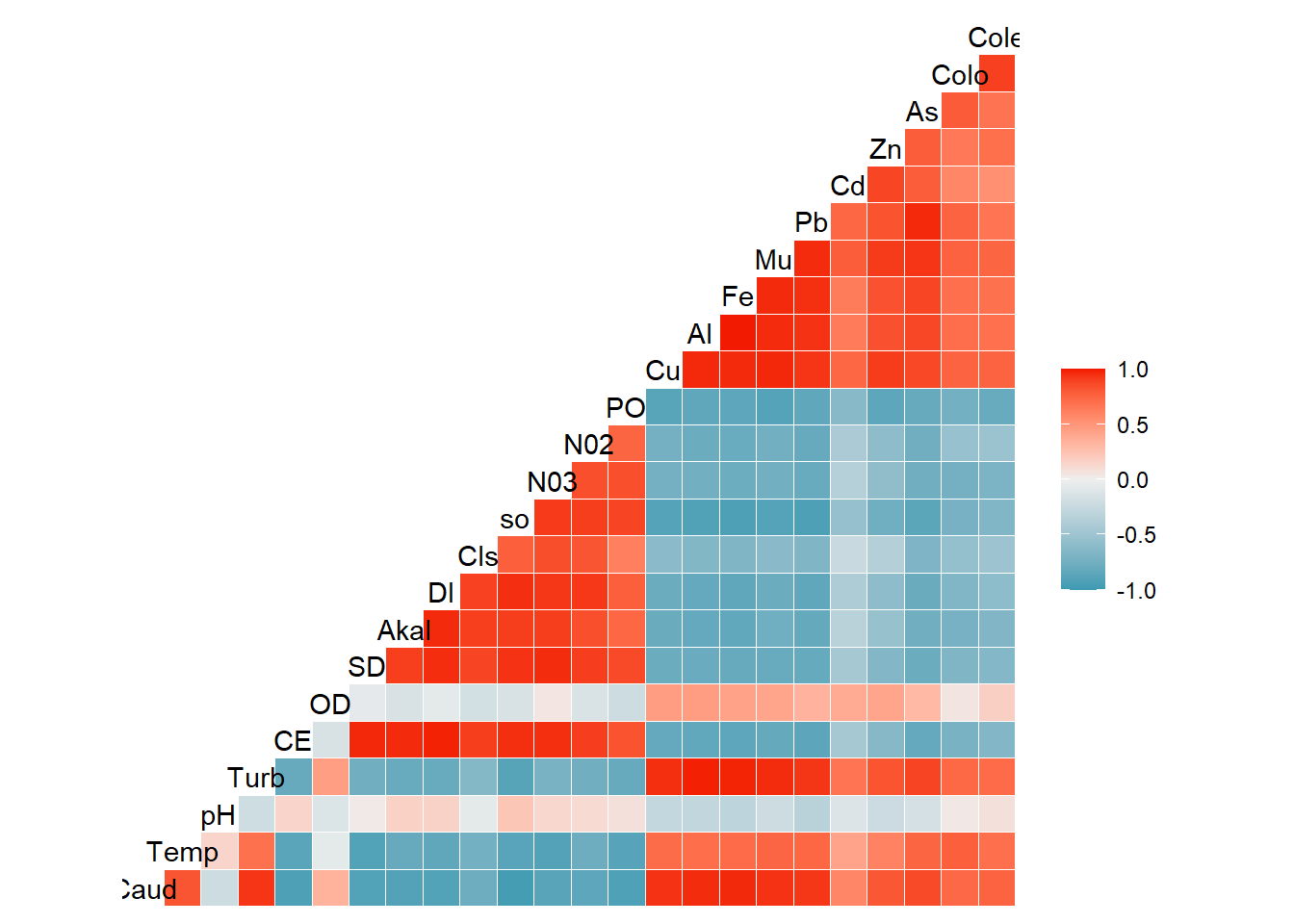
#Se puede observar que entre las 24 variables,
#hay correlaciones muy altas , correlaciones altas y correlaciones medias.
#esto podria traer problemas de multicolinealidad.Prueba de Esfericidad de Bartlett
library(psych)##
## Attaching package: 'psych'## The following objects are masked from 'package:ggplot2':
##
## %+%, alphacorrelaciones<- corr.test(datosc) # se crea la matriz de correlaciones
#correlaciones$r # existe correlaciones entre las variables
library(rela)
r<-as.matrix(correlaciones$r)
options(scipen=999)
n<-dim(datosc) ;n## [1] 12 24cortest.bartlett(r,nrow(datosc))## Warning in log(detR): Se han producido NaNs## $chisq
## [1] NaN
##
## $p.value
## [1] NaN
##
## $df
## [1] 276#¿Por que sucede esto?
#Puede ser que nuestras variables estan altamente correlacionadas,
#verficamos la determinante de la matriz correlacion de las variables.
det(correlaciones$r)## [1] -0.000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000001650829#si la determinante de la matriz correlacion es muy
#pequeña pero no es cero indica que mis variables
#estan altamente intercorrelaciones.
#https://www.uv.es/ceaces/multivari/factorial/matriz.htm
# Prueba de Esfericidad de Bartlett
#Prueba de Esfericidad de Bartlett
#Ho: |Rp|=1 (las correlaciones teóricas entre cada par de variables es nulo)
#H1: |Rp|≠1 (las correlaciones teóricas entre cada par de variables NO es nulo)
#conclusion:
#p-valor < 0.05 ,
#se rechaza la H0, se puede afirmar que las las correlaciones
#teóricas entre cada par de variables NO es nulo.
#en otras palabras nuestra matriz correlacion es diferente
# a la matriz identidad podemos realizar analisis de componentes principales.Indicador Kaiser-Meyer-Olkinn KMO y MSA
library(psych)
KMO(datosc) ## Error in solve.default(r) :
## sistema es computacionalmente singular: número de condición recíproco = 2.02895e-19## matrix is not invertible, image not found## Kaiser-Meyer-Olkin factor adequacy
## Call: KMO(r = datosc)
## Overall MSA = 0.5
## MSA for each item =
## Caud Temp pH Turb CE OD SD Akal DI Cls so N03 N02 PO Cu Al
## 0.5 0.5 0.5 0.5 0.5 0.5 0.5 0.5 0.5 0.5 0.5 0.5 0.5 0.5 0.5 0.5
## Fe Mu Pb Cd Zn As Colo Cole
## 0.5 0.5 0.5 0.5 0.5 0.5 0.5 0.5#la advetencia que sale significa que mis variables
#estan altamente correlacionadas
#Por otro lado el indicador "kmo" es superior igual 0.5
#que indica que puedo trabajar con todas
#las 24 variables3.2Análisis de Componentes Principales con el paquete ade4
CORROBORANDO LA GRAFICA 1
¿se podra explicar con 2 componentes todas las 24 variables ?
vamos a comprobar:
En el Grafico 1, se podia apreciar que
con 2 componentes(retiene 83.8% de la inercia total)
se podria explicar todas las 24 variables.
¿Cuantos componentes?
library(ade4)
acp <- dudi.pca(datosc,scannf=FALSE,nf=ncol(datosc))
summary(acp) ## Class: pca dudi
## Call: dudi.pca(df = datosc, scannf = FALSE, nf = ncol(datosc))
##
## Total inertia: 24
##
## Eigenvalues:
## Ax1 Ax2 Ax3 Ax4 Ax5
## 17.7541 2.3548 1.3683 0.9189 0.5800
##
## Projected inertia (%):
## Ax1 Ax2 Ax3 Ax4 Ax5
## 73.976 9.812 5.701 3.829 2.417
##
## Cumulative projected inertia (%):
## Ax1 Ax1:2 Ax1:3 Ax1:4 Ax1:5
## 73.98 83.79 89.49 93.32 95.73
##
## (Only 5 dimensions (out of 11) are shown)Podemos observar que con 2 componenetes retenemos 83.79 % de la inercia total
Podemos observar que con 3 componenetes retenemos 89.49 % de la inercia total
Podemos observar que con 4 componenetes retenemos 93.32 % de la inercia total
Podemos observar que con 5 componenetes retenemos 95.73 % de la inercia total
CRITERIO DE LA MEDIA
# Valores propios
#el criterio de la media:
acp$eig ## [1] 17.75412281 2.35476144 1.36828719 0.91885927 0.58004727 0.40691705
## [7] 0.24251967 0.16344726 0.11008407 0.06970343 0.03125052#estamos trabajando con la matriz correlacion cada variable deberia retener
#1% de la inercia total , nos podemos quedar hasta con 3 componenetes(89.49% inercia total)
#pero tambien con 2 componentes se retiene 83.79% (inercia total)# Grafica de Valores propios - ScreePlot
#El primer componente retiene 74% de la inercia total
#El segundo componete retiene 9.8% de la inercia total
#El tercer componente retiene 5.7% de la inercia total
fviz_eig(acp, addlabels=TRUE, hjust = -0.3,
barfill="white", barcolor ="darkblue",
linecolor ="red") + ylim(0,80) + theme_minimal() 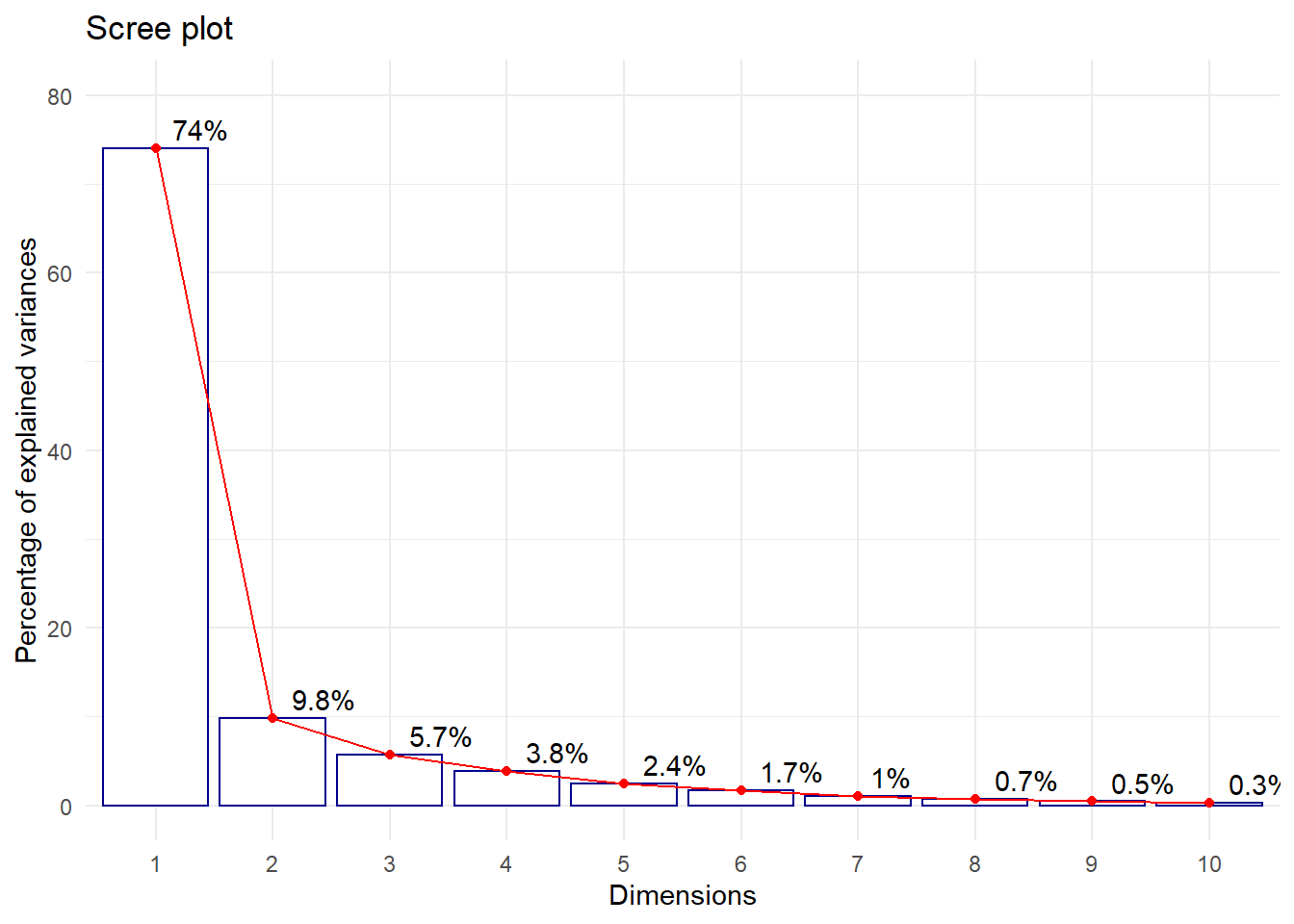
Conclusion:
Con 2 componentes podemos explicar todas las 24 variables reteniendo 83.79% % de la inercia total
#Por eso que en la GRAFICA 1 , la agrupacion de los meses en 3 cluster
#se explica 83.79% (inercia total).
inertia.dudi(acp)## Inertia information:
## Call: inertia.dudi(x = acp)
##
## Decomposition of total inertia:
## inertia cum cum(%)
## Ax1 17.75412 17.75 73.98
## Ax2 2.35476 20.11 83.79
## Ax3 1.36829 21.48 89.49
## Ax4 0.91886 22.40 93.32
## Ax5 0.58005 22.98 95.73
## Ax6 0.40692 23.38 97.43
## Ax7 0.24252 23.63 98.44
## Ax8 0.16345 23.79 99.12
## Ax9 0.11008 23.90 99.58
## Ax10 0.06970 23.97 99.87
## Ax11 0.03125 24.00 100.00ANALISIS DE COMPONENTES PRINCIPALES
Con 2 componentes principales
acp <- dudi.pca(datosc,scannf=FALSE,nf=2)
summary(acp) ## Class: pca dudi
## Call: dudi.pca(df = datosc, scannf = FALSE, nf = 2)
##
## Total inertia: 24
##
## Eigenvalues:
## Ax1 Ax2 Ax3 Ax4 Ax5
## 17.7541 2.3548 1.3683 0.9189 0.5800
##
## Projected inertia (%):
## Ax1 Ax2 Ax3 Ax4 Ax5
## 73.976 9.812 5.701 3.829 2.417
##
## Cumulative projected inertia (%):
## Ax1 Ax1:2 Ax1:3 Ax1:4 Ax1:5
## 73.98 83.79 89.49 93.32 95.73
##
## (Only 5 dimensions (out of 11) are shown)¿Como estan agrupadas las variables?
Nos basamos del criterio de las correlaciones
# Correlaciones entre las variables y los componentes
#acp$c1 vectores propios
acp$co[c(1,2)] ## Comp1 Comp2
## Caud -0.9856905 -0.01901796
## Temp -0.8575730 0.34464942
## pH 0.1718367 0.32044552
## Turb -0.9346113 -0.23625366
## CE 0.9441237 -0.27906809
## OD -0.2805474 -0.66047211
## SD 0.9217281 -0.33148387
## Akal 0.9013802 -0.30784486
## DI 0.9190383 -0.32601318
## Cls 0.7834060 -0.44555826
## so 0.9720223 -0.12524082
## N03 0.8933136 -0.39175400
## N02 0.8656142 -0.26140158
## PO 0.9171172 0.02090579
## Cu -0.9478302 -0.27917688
## Al -0.9482153 -0.21768133
## Fe -0.9559193 -0.19131422
## Mu -0.9553130 -0.27329191
## Pb -0.9570670 -0.17625217
## Cd -0.6493169 -0.55943616
## Zn -0.8225078 -0.45618080
## As -0.9213033 -0.15271183
## Colo -0.8002671 0.02046972
## Cole -0.7701392 -0.05606211componente1:#FACTORES DE NO AIREACION
caudal temp Turb CE SD Akal Di Cls so NO3 NO2 PO Cu Al Fe Mu Pb Cd Zn As Colo Cole
componente2:# FACTORES DE AIREACION
OD pH
Un análisis realizados en los tanques de aireación para asegurar condiciones ideales, los dos parámetros más importantes son el pH y el oxígeno disuelto (OD) El pH en tanques de aireación debe estar entre 6.5 a 8.5 para evitar el estrés en las colonias microbianas, y permitirles una actividad
https://www.hannacolombia.com/aqua/blog/item/midiendo-ph-y-od-en-tanques-de-aireacion-de-aguas-residuales#:~:text=Adem%C#3%A1s%20de%20una%20variedad%20de,microbianas%2C%20y%20permitirles%20una%20actividad
GRAFICA 2
library(factoextra)
fviz_pca_var(acp, col.var="steelblue")+theme_minimal()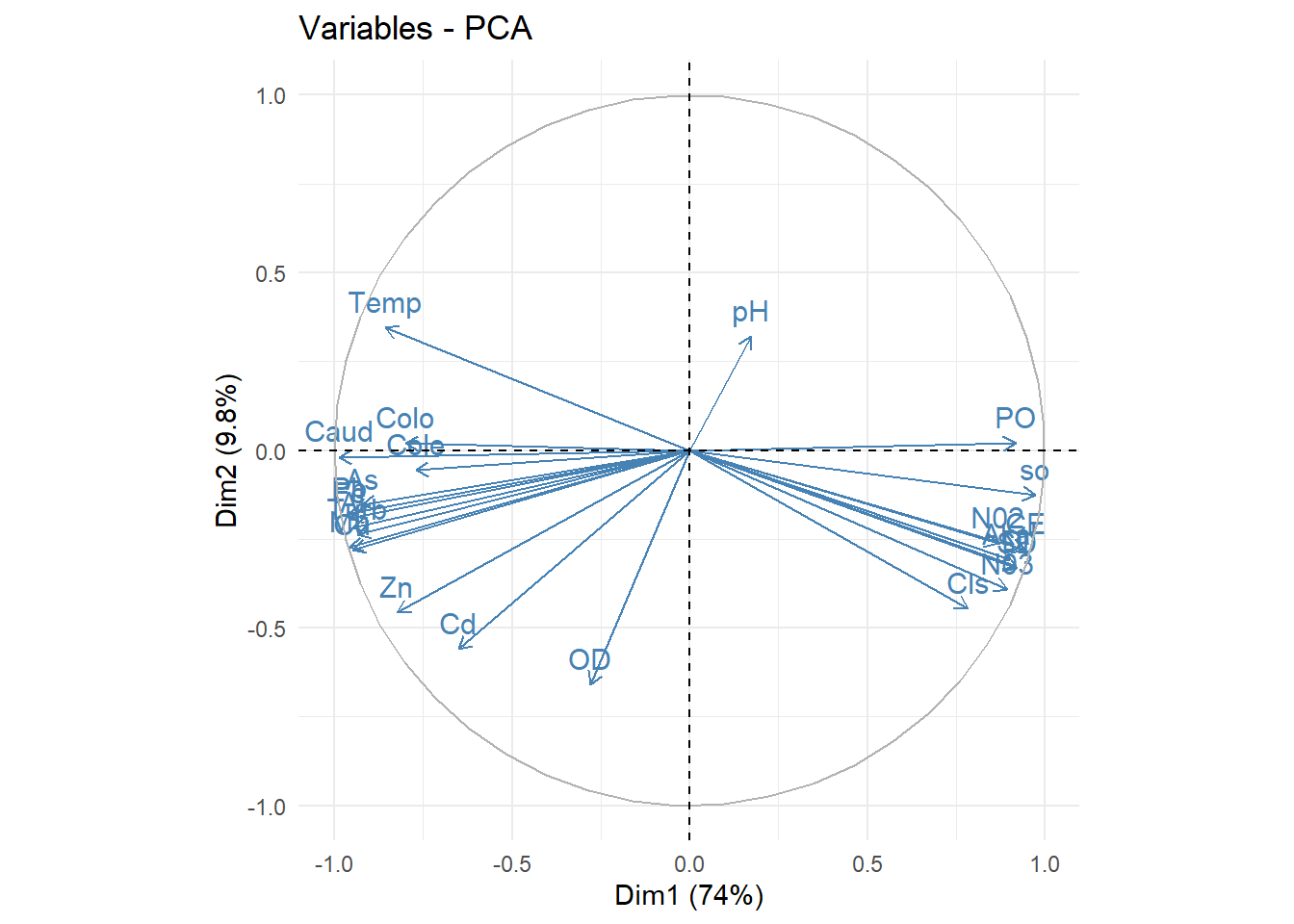
#podemos observar que todos las variables estan asociados mas a la dimension1(componente1),
#excepto las variables "pH" y "OD" que pertenecen a la dimension2(componente2) pero
#con la matriz de correlacion ya determinamos la variable "pH" y "OD" pertenece a la dimension2.VARIABLES DE AIRIACION (PH Y OD ),a medida que aumenta la variable “PH” de manera inversamente proporcional la variable “OD” disminuye (estan muy relacionados).
VARIABLES DE NO AIRIACION, a medida que aumentan las variables(caudal,temperatura(temp),turbidez(Turb), cobre(Cu),aluminio(Al),Hierro(Fe),Manganeso(Mn),Plomo(Pb),cadmio(Cd),Zinc(Zn),Arsenico(As), Coliformes totales(CoTo),Coliformes termotolerables(Cote) de forma inversamente proporcional disminuye las variables(Coductividad electrica(CE),Solidos Disuelto(SD),Alcalinidad(Akal),Dureza total(DI),cloruros(cls) ,sulfatos(so),nitratos(NO3),nitritos(NO2),fosfatos(PO))
Por ejemplo con la variable “Alcalinidad(Akal)”
Una alta alcalinidad(Akal)
por ejemplo a una alta alcalinidad(Akal) tambien afectara de manera directa a las variables (Coductividad electrica(CE),Solidos Disuelto(SD) ,Dureza total(DI),cloruros(cls),sulfatos(so),nitratos(NO3),nitritos(NO2),fosfatos(PO)) y tambien afectara de manera inversamente inversamente proporcional a las variables (caudal,temperatura(temp),turbidez(Turb),cobre(Cu),aluminio(Al),Hierro(Fe),Manganeso(Mn), Plomo(Pb),cadmio(Cd),Zinc(Zn),Arsenico(As),Coliformes totales(CoTo),Coliformes termotolerables(Cote) .
¿Si aumenta la cantidad de plomo(Pb) en el rio rimac ,afectara sobre en la Alcalinidad(AKal) ?
Si aumenta la concentracion de plomo(Pb) afectara a la Alcalinidad(Akal) de manera negativa es decir disminuye la concentracion de alcalinidad.
#biplot
library(factoextra)
fviz_pca_biplot(acp, repel = F,
col.var = "steelblue",
col.ind = "black" )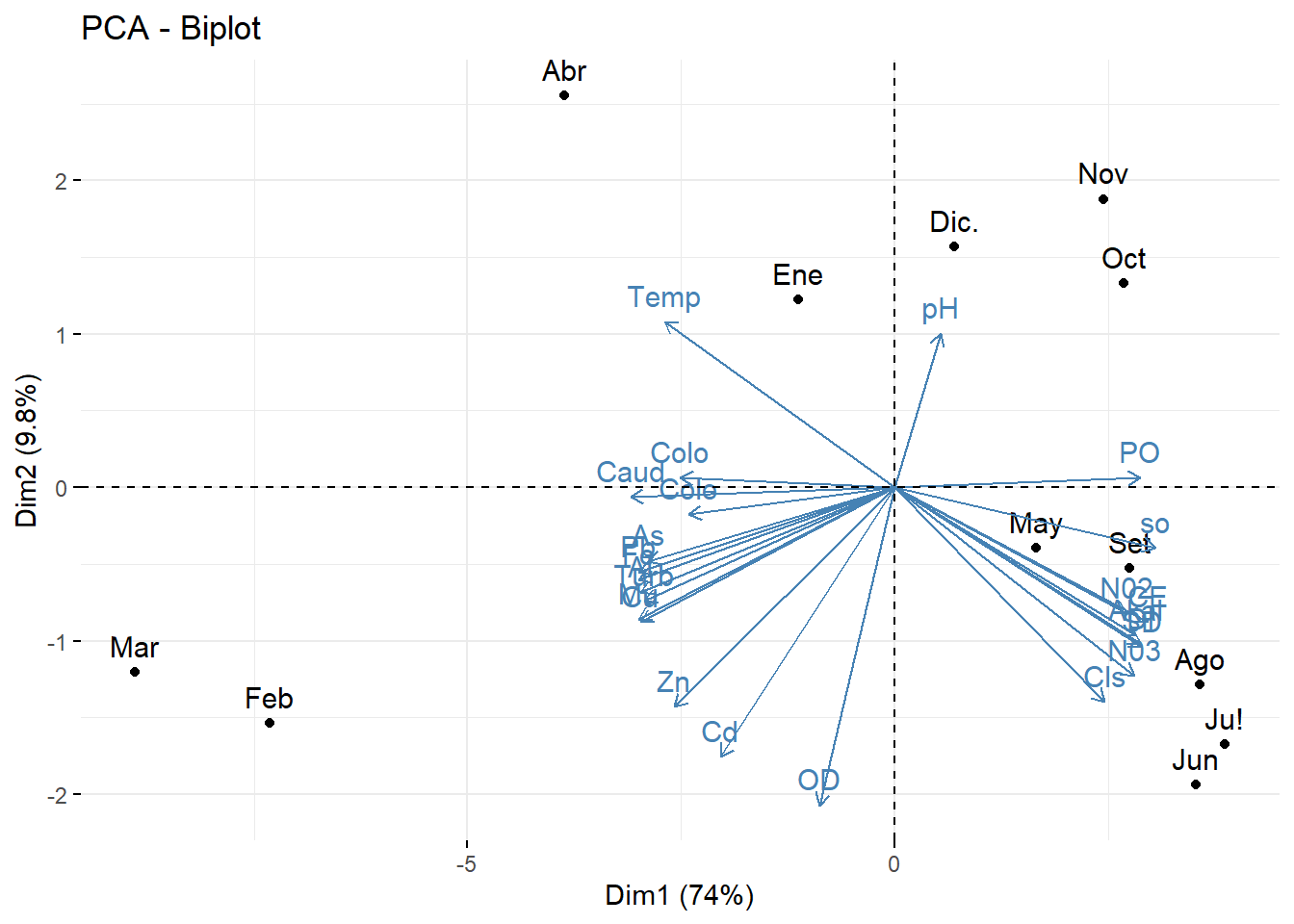
###indicadoresEn los meses de Marzo y febrero esta asociado
SCORES
Insumo para modelos predictivos como regresion lineal
# Scores o Puntuaciones de cada individuo
#10 primeros
acp$li[1:10,]## Axis1 Axis2
## Ene -1.127415 1.2241429
## Feb -7.321424 -1.5374149
## Mar -8.892270 -1.2061457
## Abr -3.864966 2.5559978
## May 1.653208 -0.3952227
## Jun 3.526615 -1.9367091
## Ju! 3.869064 -1.6735475
## Ago 3.572872 -1.2874593
## Set 2.750543 -0.5237799
## Oct 2.683794 1.3317449