Chapitre1 Exactitude d’une méthode de mesure normalisée

Dans ce chapitre on présente l’approche d’évaluation de la fidélité d’une méthode de mesure normalisée par le biais des essais inter-laboratoires.

1.1 Introduction

La maîtrise du processus de mesure est devenu un véritable enjeu économique, commercial et réglementaire. En effet, c’est un outil de la qualité indispensable à la prise de décision (déclaration de conformité ou de non-conformité d’un produit manufacturé, diagnostic à la suite d’une analyse médicale, respect ou non de la législation en matière de sécurité, d’environnement…). Les laboratoires qui sont reconnus comme compétents, c’est-à-dire ayant la réputation de produire des données de qualité, ont bien évidement plus de chances d’être compétitifs sur le marché. Les tests d’aptitude sont des essais organisés par des organismes officiels (par exemple organismes d’accréditation). Les résultats des essais sont évalués statistiquement et des points sont attribués aux laboratoires. Ces tests sont destinés à évaluer la compétence d’un groupe de laboratoires pour des analyses spécifiques ou pour juger la compétence de laboratoires dans un domaine d’analyses.

Dans ce contexte, les laboratoires doivent être en mesure d’évaluer et de démontrer leur compétence par des moyens internes (audits internes, utilisation des matériaux de référence certifiés) et externes (comparaison avec d’autres laboratoires). Des études entre laboratoires travaillant dans le même domaine sont fréquemment organisées pour évaluer les performances d’une ou plusieurs méthodes analytiques appliquées par plusieurs laboratoires.

Une expérience d’exactitude peut souvent être considérée comme un essai pratique de l’adéquation de la méthode de mesure normalisée. La validation d’une méthode analytique est un procédé qui permet de démontrer que les résultats obtenus par cette méthode sont fiables, reproductibles et que la méthode est adaptée à l’application prévue.

Afin que les mesures soient faites de la même façon, il est nécessaire que la méthode de mesure ait été normalisée. Toutes les mesures devront alors avoir été effectuées selon la norme correspondante. Cela signifie qu’il doit exister un document écrit, sans ambiguïté et complet, décrivant en détail comment la mesure doit être effectuée, comportant de préférence une description de la façon dont il convient d’obtenir et de préparer le spécimen de mesure. Il convient de spécifier avec précision la façon de calculer ou d’exprimer le résultat d’essai, y compris le nombre de chiffres significatifs à donner. Une telle méthode doit être robuste, c’est-à-dire que des petites variations dans la procédure ne produisent pas de façon imprévue de grandes modifications dans les résultats.

Les données obtenues par une expérience d’exactitude révèleront l’efficacité avec laquelle ce but aura été atteint. Des différences prononcées dans les résultats des laboratoires peuvent indiquer que la méthode de mesure normalisée n’est pas encore suffisamment détaillée et peut être améliorée. S’il en est ainsi, il convient de faire un rapport à l’organisme de normalisation avec une demande d’approfondissement de l’étude.

La validation des méthodes implique donc que toutes les sources éventuelles d’erreurs soient détectées et résolues, et qu’un système de contrôle de qualité soit mis en place pour détecter l’introduction de telles erreurs. La validation des méthodes joue un rôle crucial pour obtenir et assurer la qualité des résultats analytiques. Les activités de contrôle de qualité interne et externe doivent être considérées dans ce contexte. Les études de validation d’une méthode sont réalisées pour évaluer sa capacité à remplir une tache spécifique. Elles n’ont pas pour but d’évaluer la performance d’un laboratoire. De nombreux laboratoires perdent de vue ce fait lorsqu’ils participent à des essais de validation de méthodes.

1.2 Modèle statistique

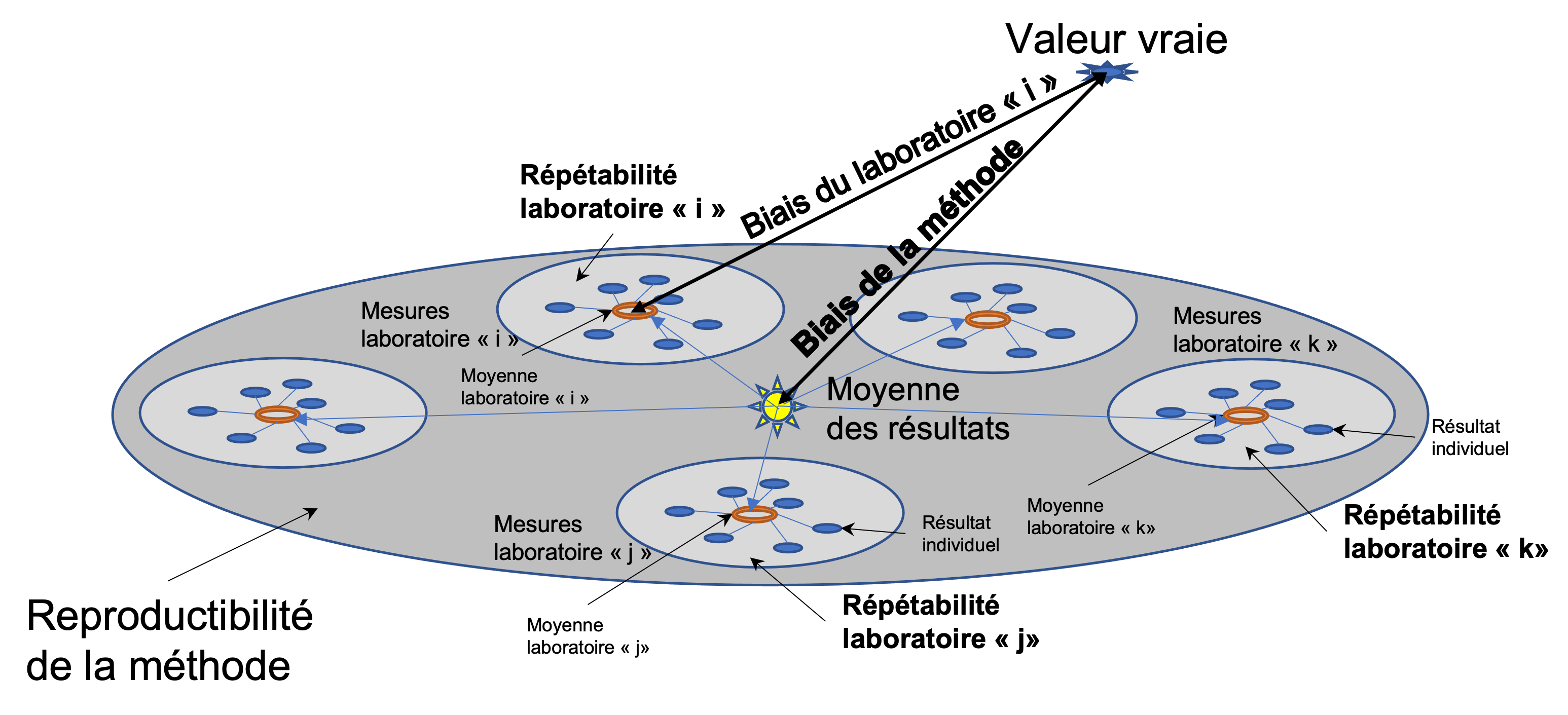
Pour l’estimation de l’exactitude (c.à.d. la justesse et la fidélité) d’une méthode de mesure, il est utile de supposer que chaque résultat d’essai (\(y\)) est la somme de trois composantes (voir aussi la figure 1):

\[\begin{equation} \tag{1.1} y=m+B+e \end{equation}\]

où: \(m\) - est la moyenne générale; \(B\) - est la composante laboratoire du biais; \(e\) - est l’erreur aléatoire survenant dans chaque mesure (sous conditions de répétabilité).

Les conditions de répétabilité sont les conditions où les résultats d’essai indépendants sont obtenus par la même méthode sur des individus d’essai identiques dans le même laboratoire, par le même opérateur, utilisant le même équipement et pendant un court intervalle de temps.

Figure 1 - Caractéristiques d'exactitude d'une méthode de mesure

La moyenne générale (\(m\)) est aussi appelée niveau de l’essai (par exemple, les spécimens de puretés différentes d’un matériau chimique correspondront à différents niveaux). Dans de nombreuses situations techniques, le niveau de l’essai est exclusivement défini par la méthode de mesure et la notion d’une valeur vraie indépendante ne s’applique pas.

Le biais du laboratoire est la différence entre l’espérance mathématique des résultats d’essai d’un laboratoire particulier et une valeur de référence acceptée (voir figure 1).

Le biais de la méthode de mesure est la différence entre l’espérance mathématique des résultats d’essai obtenus à partir de tous les laboratoires utilisant cette méthode et une valeur de référence acceptée.

La composante laboratoire du biais (\(B\)) est la différence entre le biais du laboratoire et le biais de la méthode de mesure (voir figure 1). Elle est spécifique à un laboratoire donné et aux conditions de mesure dans ce laboratoire, et peut également être différente à différents niveaux de l’essai. Elle est relative au résultat de la moyenne générale et non à la valeur vraie ou de référence. La variance de la composante laboratoire du biais est appelée la variance inter-laboratoire et inclut les variabilités entre les opérateurs et entre les équipements.

Le terme d’erreur (\(e\)) représente une erreur aléatoire survenant pour chaque résultat d’essai. Les erreurs aléatoires sont liés à des facteurs qui influencent la valeur ou la quantité mesurée mais qui sont incontrôlables par la personne effectuant l’analyse (exemple: bruit de fond électronique d’un appareil; effets thermaux, etc.). En général on suppose que la distribution de cette variable est normale. A l’intérieur d’un laboratoire individuel, sa variance, sous des conditions de répétabilité est appelée variance intra-laboratoire.

On pourrait s’attendre à ce que la variance inter-laboratoires ait différentes valeurs d’un laboratoire à l’autre. Toutefois, il est supposé que dans le cas d’une méthode de mesure normalisée, de telles différences entre les laboratoires devraient être petites. Par conséquent, il est justifié d’établir une valeur commune de variance intra-laboratoire pour tous les laboratoires utilisant la méthode de mesure. Cette valeur commune, estimée par la moyenne arithmétique de toutes les variances intra-laboratoires est appelée la variance de répétabilité.

1.3 Fidélité d’une méthode de mesure

Pour l’estimation de la Fidélité d’une méthode de mesure normalisée, il est nécessaire d’évaluer deux grandeurs:

• La répétabilité (\(r\)) des résultats de mesure - définie comme étant l’étroitesse de l’accord entre les résultats des mesurages successifs du même mesurande, mesurages effectués dans la totalité des mêmes conditions de mesure. Les conditions de répétabilité comprennent: le même mode opératoire, le même opérateur, le même instrument de mesure utilisé dans les mêmes conditions, le même lieu et une répétition de mesures réalisée durant une courte période de temps. La répétabilité peut s’exprimer quantitativement à l’aide de caractéristiques de dispersion des résultats (écart-type de répétabilité). Ainsi, supposant que l’on dispose de \(p\) laboratoires participant à l’étude de la fidélité d’une méthode de mesure normalisée, pour calculer l’écart-type de répétabilité on procède comme suit:

  1. on calcule la variance de répétabilité du laboratoire \(i\):

\[\begin{equation} \tag{1.2} e_i=\frac{1}{n_i-1}\sum_{j=1}^{n_i}(y_j^i-\bar{y^i})^2 \end{equation}\]

où: \(n_i\) représente le nombre de mesures réalisées dans le laboratoire \(i\); \(y_j^i\) représente la \(j^{ème}\) mesure du laboratoire \(i\); \(\bar{y^i}=\frac{1}{n_i}\sum_{j=1}^{n_i}y_j^i\) représente la moyenne des mesures du laboratoire \(i\).

2. on calcule la variance de répétabilité moyenne pour tous les laboratoires ayant participé à l’étude:

\[\begin{equation} \tag{1.3} e=\frac{1}{p}\sum_{i=1}^{p} e_i \end{equation}\]

3. on calcule l’écart-type de répétabilité:

\[\begin{equation} \tag{1.4} \sigma_r=\sqrt{e} \end{equation}\]

• La reproductibilité (\(R\)) des résultats de mesure - définie comme étant l’étroitesse de l’accord entre les résultats des mesurages d’un même mesurande, mesurages effectués en faisant varier les conditions de mesure qui peuvent comprendre: le principe de mesure, la méthode de mesure, l’opérateur, l’instrument de mesure, l’étalon de référence, le lieu, les conditions d’utilisation et le temps. Tout comme la répétabilité, la reproductibilité peut s’exprimer quantitativement à l’aide de caractéristiques de dispersion des résultats (écart-type de reproductibilité)

\[\begin{equation} \tag{1.5} \sigma_R=\sqrt{\sigma_L^2+\sigma_r^2} \end{equation}\]

où: \(\sigma_L\) est l’écart-type inter-laboratoires.

L’estimation de la Fidélité d’une méthode de mesure normalisée est un processus qui se déroule en trois étapes:

1. Examen critique des données afin d’identifier et traiter les valeurs aberrantes ou autres irrégularités et de tester l’adéquation du modèle.
2. Calcul des valeurs préliminaires de fidélité et des moyennes séparément pour chaque niveau.
3. Établissement des valeurs finales de fidélité et des moyennes, y compris l’établissement de la relation entre la fidélité et les moyennes par niveaux lorsque l’analyse indique qu’une telle relation peut exister.

1.4 Examen critique des données

Les données recueillies afin d’estimer la fidélité d’une méthode de mesure peuvent être regroupées dans un tableau comme celui présenté dans la figure 2.

Figure 2 - Tableau de données brutes utilisé pour recueillir les résultats de mesures des laboratoires ayant participé à une étude de fidélité

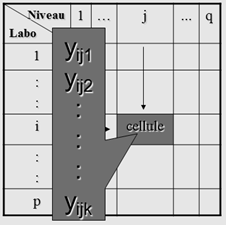
On note par : \(y_{ijk}\) - le \(k^{ème}\) résultat de mesure (\(k = 1, 2, ..., n_{ij}\)) de la cellule ij (laboratoire \(i\) et niveau \(j\)) du tableau de données brutes; \(n_{ij}\) est le nombre de résultats d’essai dans la cellule ij; \(p_j\) est le nombre de laboratoires rapportant au moins un résultat d’essai pour le niveau \(j\).

A partir de ce tableau de données brutes, on calcule les moyennes des cellules:

\[\begin{equation} \tag{1.6} \bar{y}_{ij}=\frac{1}{n_{ij}}\sum_{k=1}^{n_{ij}}y_{ijk} \end{equation}\]

et les variances des cellules:

\[\begin{equation} \tag{1.7} s_{ij}^2=\frac{1}{n_{ij-1}}\sum_{k=1}^{n_{ij}}(y_{ijk}-\bar{y}_{ij})^2 \end{equation}\]

1.4.1 Examen de la cohérence des résultats

Avant d’estimer la fidélité d’une méthode il est utile de vérifier si les résultats fournis par les laboratoires sont cohérents. Pour cela, on utilise une approche statistique proposée par Mandel qui consiste à vérifier la cohérence des résultats inter-laboratoires (c.à.d. entre les laboratoires) et respectivement intra-laboratoires (c.à.d. à l’intérieur des laboratoires).

1.4.1.1 Cohérence des résultats inter-laboratoires

On calcule la statistique de cohérence inter-laboratoires (\(h\)) avec la formule suivante:

\[\begin{equation} \tag{1.8} h_{ij}=\frac{\bar{y}_{ij}-\bar{\bar{y}}_j}{\sqrt{\frac{1}{p_j-1}\sum_{j=1}^{p_j}(\bar{y}_{ij}-\bar{\bar{y}}_j)^2}} \ \forall i \in \{1,...,p\}, \ j \in \{1,...,q\} \end{equation}\]

où: \(\bar{\bar{y}}_j=\frac{\sum_{j=1}^{p_j}n_{ij}\bar{y}_{ij}}{\sum_{j=1}^{p_j}n_{ij}}\) est la moyenne du niveau \(j\); \(p_j\) est le nombre de laboratoires ayant fourni des résultats au niveau \(j\).

1.4.1.2 Cohérence des résultats intra-laboratoires

On calcule la statistique de cohérence intra-laboratoires (\(k\)) avec la formule suivante:

\[\begin{equation} \tag{1.9} k_{ij}=\frac{s_{ij}}{\sqrt{\frac{1}{p_j}\sum_{j=1}^{p_j}s_{ij}^2}} \ \forall i \in \{1,...,p\}, \ j \in \{1,...,q\} \end{equation}\]

où: \(s_{ij}^2\) est la variance de la cellule \(ij\) du tableau de données brutes (voir l’équation (1.7)).

1.4.1.3 Interprétation des statistiques \(h\) et \(k\) de Mandel

L’examen des statistiques \(h_{ij}\) et \(k_{ij}\) peut peut montrer que certains laboratoires fournissent des résultats substantiellement différents des autres.

En effet, les statistiques \(h\) et \(k\) de Mandel sont tabulées et des valeurs critiques (quantiles) peuvent être extraites de la table pour chacune d’elles. Ces valeurs serviront ensuite de référence pour la détection des laboratoires présentant des résultats non-cohérents avec les autres laboratoires (c.à.d. ayant des statistiques \(h_{ij}\) ou \(k_{ij}\) significativement plus grandes ou plus petites que les autres laboratoires au même niveau).

Étant donné que dans cet ouvrage on utilise le logiciel R pour les calculs effectués dans le cadre des applications abordées, on ne présentera pas la table de Mandel mais les fonctions qmandelh et qmandelk du package metRology qui permettent de déduire les valeurs critiques (quantiles) pour les statistiques \(h\) et \(k\) de Mandel. Les syntaxes de ces fonctions sont les suivantes:

qmandelh(p, g) - pour le calcul des quantiles de la statistique \(h\) de Mandel. qmandelk(p, g, n) - pour le calcul des quantiles de la statistique \(k\) de Mandel.

où: p est la probabilité; g est le nombre de laboratoires ayant participé à l’étude; n est le nombre de résultats de mesure dans chaque cellule du tableau de données brutes.

Pour faciliter la comparaison des statistiques \(h\) de Mandel, on peut les afficher graphiquement sous la forme d’un diagramme en battons (plot) ou sous la forme de diagrammes de type boîte à moustaches (boxplot). Différentes situations peuvent apparaître lorsque l’on examine les graphiques des statistiques \(h_{ij}\) et \(k_{ij}\):

• Tous les laboratoires peuvent avoir à la fois des valeurs positives et négatives des statistiques \(h\) à différents niveaux de l’expérience.

• Certains laboratoires ne donnent que des valeurs positives ou des valeurs négatives des statistiques \(h\), et le nombre de laboratoires donnant des valeurs négatives est approximativement égal aux nombre de laboratoires donnant des valeurs positives.

Aucune de ces situations n’est inhabituelle ou ne nécessite d’investigation, bien que la seconde puisse suggérer qu’il existe une source commune de biais de laboratoire.

D’un autre côté, si toutes les valeurs des statistiques \(h\) pour un laboratoire sont d’un signe et que les valeurs des statistiques \(h\) pour les autres laboratoires sont toutes de signe contraire, il faut alors en rechercher la raison.

De même, si les valeurs des statistiques \(h\) pour un laboratoire sont extrêmes et paraissent dépendre du niveau expérimental de façon systématique, il faut alors en rechercher la raison.

Si un laboratoire apparaît sur le graphique des statistiques \(k\) comme ayant de fortes valeurs, il faut alors en rechercher la raison : cela indique qu’il a une plus faible répétabilité que les autres laboratoires. Un laboratoire pourrait présenter des valeurs très petites des statistiques \(k\) en raison d’un arrondi excessif de ses données ou d’une échelle de mesure non adaptée.

Lorsque l’examen d’un graphique de la statistique \(h\) ou \(k\) de Mandel regroupée par laboratoire suggère qu’un laboratoire possède plusieurs valeurs de la statistique \(h\) et/ou \(k\) proches de la valeur critique, il faut examiner le graphique correspondant regroupé par niveau. Souvent une valeur qui paraît forte dans un graphique regroupé par laboratoire semblera être raisonnablement cohérente par rapport aux autres laboratoires pour le même niveau. Si elle se révèle fortement différente des valeurs des autres laboratoires, il faut alors en chercher la raison.

1.4.2 Recherche des valeurs atypiques

La présence des valeurs atypiques (aberrantes ou isolées) peut fausser l’estimation de la fidélité de la méthode de mesure. Ce pour cette raison qu’il est indiqué de détecter la présence de telles valeurs et de les écarter de l’étude.

Dans la suite, on présentera deux tests pour la détection des valeurs atypiques: le test de Grubbs et le test de Cochran.

1.4.2.1 Test simple de Grubbs

Il s’agit d’un test d’hypothèse pour statuer si la plus petite ou la plus grande valeur d’un ensemble de valeurs \(\{y_1, y_2, ..., y_p\}\) est atypique. Par conséquent, on formule les hypothèses suivantes:

\[\begin{equation*} \left\{ \begin{aligned} & H_0: y_{min} \ ou \ y_{max} \ n'est \ pas \ atypique\\ & H_1: y_{min} \ ou \ y_{max} \ est \ atypique \end{aligned} \right. \end{equation*}\]

La construction du test repose sur le calcul des deux statistiques de test suivantes:

\[\begin{equation*} \left\{ \begin{aligned} & G_{min}=\frac{\bar{y}-y_{min}}{s}\\ & G_{max}=\frac{y_{max}-\bar{y}}{s} \end{aligned} \right. \tag{1.10} \end{equation*}\]

où: \(s=\sqrt{\frac{1}{p-1}\sum_{i=1}^p (y_i-\bar{y})^2}\) et \(\bar{y}=\frac{1}{p}\sum_{i=1}^py_i\) sont l’écart-type et respectivement la moyenne de l’ensemble de valeurs \(\{y_1, y_2, ..., y_p\}\).

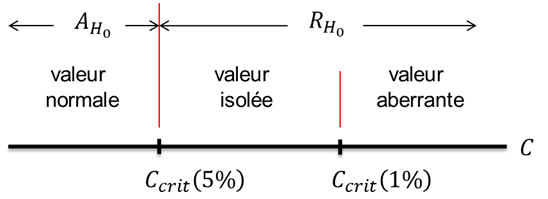
On adopte la règle de décision suivante (voir figure 3):

Figure 3 - Prise de décision dans le cadre du test simple de Grubbs

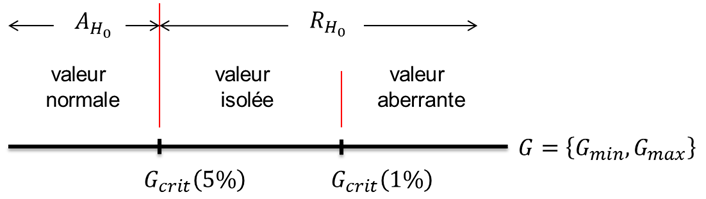
Les valeurs critiques du test simple de Grubbs (\(G_{crit(5\%)}\) et \(G_{crit(1\%)}\)) se trouvent dans la table de Grubbs en fonction du nombre de laboratoires ayant participé à l’étude (\(p\)). Pour la même raison que dans le cas des statistiques de Mandel, on préfère donner les fonctions R qui permettent de déduire les valeurs critiques au lieu de présenter la table de Grubbs:

qgrubbs(p,n,type)

où: p est la probabilité; n est le nombre de laboratoires ayant participé à l’étude; type est le type de test: type = 10 pour le test simple de Grubbs; type = 20 pour le test double de Grubbs (voir le paragraphe 1.4.2.2).

1.4.2.2 Test double de Grubbs

Il s’agit d’un test d’hypothèse pour statuer si les deux plus petites ou les deux plus grandes valeurs d’un ensemble de valeurs \(\{y_1, y_2, ..., y_p\}\) sont atypiques. Par conséquent, on formule les hypothèses suivantes:

\[\begin{equation*} \left\{ \begin{aligned} & H_0: \{y_{(1)}, y_{(2)}\} \ ou \ \{y_{(p-1)}, y_{(p)}\} \ ne \ sont \ pas \ atypiques\\ & H_1: \{y_{(1)}, y_{(2)}\} \ ou \ \{y_{(p-1)}, y_{(p)}\} \ sont \ atypiques \end{aligned} \right. \end{equation*}\]

où: \(y_{(1)} \leq y_{(2)} \leq ... \leq y_{(p-1)} \leq y_{(p)}\) sont les valeurs \(\{y_1, y_2, ..., y_p\}\) rangées en ordre croissant (c.à.d. que \(y_{(1)}=min(y_1, y_2, ..., y_p)\) et \(y_{(p)}=max(y_1, y_2, ..., y_p)\)).

La construction du test repose sur le calcul des deux statistiques de test suivantes:

\[\begin{equation*} \left\{ \begin{aligned} & G_{2min}=\frac{SCE_{(p-2)}^{min}}{SCE_{(p)}}\\ & G_{2max}=\frac{SCE_{(p-2)}^{max}}{SCE_{(p)}} \end{aligned} \right. \tag{1.11} \end{equation*}\]

où:

\[\begin{equation} \tag{1.12} SCE_{(p)} = \sum_{i=1}^{p} (y_{(i)}-\bar{y}_p)^2 \end{equation}\] \[\begin{equation} \tag{1.13} \bar{y}_p = \frac{1}{p}\sum_{i=1}^py_{(i)} \end{equation}\] \[\begin{equation} \tag{1.14} SCE_{(p-2)}^{min}=\sum_{i=3}^{p} (y_{(i)}-\bar{y}_{(p-2)}^{min})^2 \end{equation}\] \[\begin{equation} \tag{1.15} \bar{y}_{(p-2)}^{min}=\frac{1}{p-2}\sum_{i=3}^py_{(i)} \end{equation}\] \[\begin{equation} \tag{1.16} SCE_{(p-2)}^{max}=\sum_{i=1}^{p-2}(y_{(i)}-\bar{y}_{(p-2)}^{max})^2 \end{equation}\] \[\begin{equation} \tag{1.17} \bar{y}_{(p-2)}^{max}=\frac{1}{p-2}\sum_{i=1}^{p-2}y_{(i)} \end{equation}\]

On adopte la règle de décision suivante (voir figure 4):

Figure 4 - Prise de décision dans le cadre du test double de Grubbs

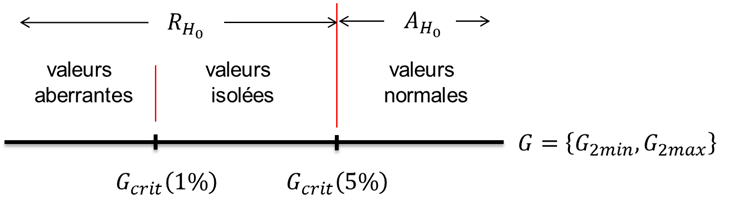
Remarque: La règle de décision pour le test double de Grubbs est inversée par rapport à la règle de décison du test simple de Grubbs.

La fonction R grubbs.test(x,type) du package outliers permet de faire le test de Grubbs. Les paramètres de cette fonctions sont: x - le vecteur de valeurs testé; type - désigne le type de test réalisé (type = 10 pour le test simple de Grubbs; type = 20 pour le test double de Grubbs).

Les logiciels statistiques affichent plutôt les p-values à la place des valeurs critiques. On rappelle que la p-value est la probabilité d’avoir une valeur de test plus extrême que celle que l’on a obtenu sur la base de l’ensemble de valeurs analysé. On peut trancher entre les deux hypothèses en examinant la p-value du test et en la comparant aux seuils critiques de 1% et 5%. Ainsi, si la p-value est :

• supérieure à 5%, alors on accepte l’hypothèse nulle (\(H_0\)) et on considère que la/les valeur(s) testée(s) est/sont normale(s).

• entre 1% et 5%, alors on rejette l’hypothèse nulle (\(H_0\)) et on considère que la/les valeur(s) testée(s) est/sont isolée(s).

• inférieure à 1%, alors on rejette l’hypothèse nulle (\(H_0\)) et on considère que la/les valeur(s) testée(s) est/sont aberrante(s).

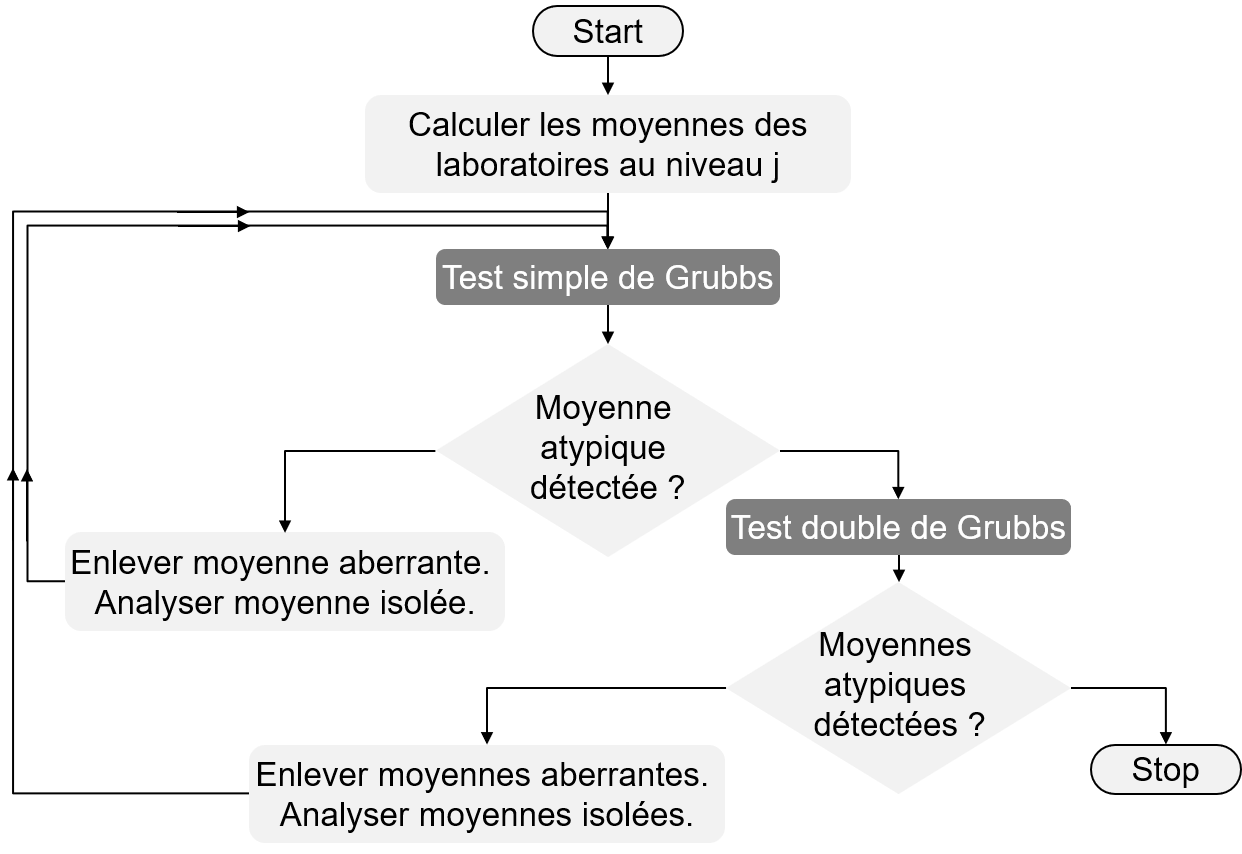
Pour détecter des valeurs atypiques à l’aide du test de Grubbs on procède comme indiqué dans la figure 5:

1. On applique dans un premier temps le test simple de Grubbs; si l’on détecte une valeur aberrante, on l’exclue de l’ensemble de données et on répète le test simple de Grubbs jusqu’à ce que l’on ne détecte plus de valeur aberrante.

2. On applique alors le test double de Grubbs; si le test double de Grubbs détecte des valeurs aberrantes on les enlève du jeu de données et on revient au point 1, sinon on arrête les tests.

Figure 5 - Schéma de détection des valeurs atypiques à l'aide du test de Grubbs

Remarques:

1. Lors de l’évaluation de la Fidélité d’une méthode de mesure normalisée, le test de Grubbs (simple et/ou double) s’applique aux moyennes des cellules du tableau de données brutes.

2. Le test de Grubbs peut expliquer certaines incohérences constatées lors de la réalisation du test \(h\) de Mandel.

1.4.2.3 Test de Cochran

Il s’agit d’un test d’hypothèse pour statuer si la plus grande variance d’un ensemble de variances \(\{s_1^2, s_2^2, ..., s_p^2\}\) est atypique. Par conséquent, on formule les hypothèses suivantes:

\[\begin{equation*} \left\{ \begin{aligned} & H_0: s_{max}^2 \ n'est \ pas \ atypique\\ & H_1: s_{max}^2 \ est \ atypique \end{aligned} \right. \end{equation*}\]

où: \(s_{max}^2=max\{s_1^2, s_2^2, ..., s_p^2\}\)

La statistique de test utilisée pour trancher entre les deux hypothèses formulées ci-dessus est:

\[\begin{equation} \tag{1.18} C=\frac{s_{max}^2}{\sum_{i=1}^{p}s_{i}^2} \end{equation}\]

On adopte la règle de décision suivante (voir figure 6):

Figure 6 - Prise de décision dans le cadre du test de Cochran

Les valeurs critiques du test de Cochran (\(C_{crit(5\%)}\) et \(C_{crit(1\%)}\)) se trouvent dans la table de Cochran en fonction du nombre de laboratoires ayant participé à l’étude (\(p\)). Pour la même raison que dans le cas des statistiques de Mandel, on préfère donner la fonction R qui permet de déduire ces valeurs critiques au lieu de présenter la table de Cochran:

qcochran(p,n,k)

où: p est la probabilité; k est le nombre de laboratoires ayant participé à l’étude; n est le nombre de résultats de mesure dans chaque cellule du tableau de données brutes.

La fonction R cochran.test(object, data) du package outliers permet de faire le test de Cochran Les paramètres de cette fonctions sont: object - vecteur de variances testées; data - vecteur qui indique le nombre de valeurs à partir duquel chaque variance a été calculée.

Remarque: le test de Cochran s’applique pour des écarts-types calculés sur le même nombre de valeurs.

1.5 Estimation de la fidélité d’une méthode de mesure

Les calculs suivants sont nécessaires afin d’évaluer la fidélité d’une méthode de mesure normalisée:

• Calcul des moyennes par niveaux:

\[\begin{equation} \tag{1.19} \hat{m}_j=\bar{\bar{y}}_j=\frac{\sum_{j=1}^{p_j}n_{ij}\bar{y}_{ij}}{\sum_{j=1}^{p_j}n_{ij}} \end{equation}\]

où: \(n_{ij}\) et \(\bar{y}_{ij}\) sont le nombre de résultats de mesure et respectivement la moyenne de la cellule \(ij\) après l’élimination des éventuelles valeurs aberrantes/isolées; \(p_j\) est le nombre de laboratoires ayant fourni des mesures au niveau \(j\).

Remarques:

1. La formule de calcul de la moyenne par niveau est une moyenne pondérée selon le nombre de mesures de chaque laboratoire au niveau respectif.

2. Si le nombre de mesures de chaque laboratoire à un niveau donné est le même (\(n_{ij}=const.\)), alors la formule de calcul de la moyenne par niveau (équation (1.19)) devient une simple moyenne arithmétique des moyennes des laboratoires au niveau respectif:

\[\begin{equation} \tag{1.20} \hat{m}_j=\bar{\bar{y}}_j=\frac{1}{p_j}\sum_{j=1}^{p_j}\bar{y}_{ij} \end{equation}\]

• Calcul de la variance de répétabilité:

\[\begin{equation} \tag{1.21} s_{rj}^2=\frac{\sum_{i=1}^{p_j}(n_{ij}-1)s_{ij}^2}{\sum_{i=1}^{p_j}(n_{ij}-1)} \end{equation}\]

où: \(s_{ij}^2\) est la variance de la cellule \(ij\) (voir l’équation (1.7)).

Remarque: Si le nombre de mesures de chaque laboratoire à un niveau donné est le même (\(n_{ij}=const.\)), alors la formule de calcul de la variance de répétabilité par niveau (équation (1.21)) devient une simple moyenne arithmétique des variances des laboratoires au niveau respectif:

\[\begin{equation} \tag{1.22} s_{rj}^2=\frac{1}{p_j}\sum_{i=1}^{p_j}s_{ij}^2 \end{equation}\]

• Calcul de la variance inter-laboratoire:

\[\begin{equation} \tag{1.23} s_{Lj}^2=\frac{s_{dj}^2 - s_{rj}^2}{\bar{\bar{n}}_j} \end{equation}\]

où:

\[\begin{equation} \tag{1.24} s_{dj}^2=\frac{1}{p_j-1}\sum_{i=1}^{p_j} n_{ij}(\bar{y}_{ij}-\bar{\bar{y}}_j)^2 \end{equation}\] \[\begin{equation} \tag{1.25} \bar{\bar{n}}_j=\frac{1}{p_j-1}\left[\sum_{i=1}^{p_j} n_{ij}-\frac{\sum_{i=1}^{p_j} n_{ij}^2}{\sum_{i=1}^{p_j} n_{ij}}\right] \end{equation}\]

Remarque: Si le nombre de mesures de chaque laboratoire à un niveau donné est le même (\(n_{ij}=n\)), alors la formule de \(\bar{\bar{n}}_j\) devient:

\[\begin{equation} \tag{1.26} \bar{\bar{n}}_j= n \end{equation}\]

• Calcul de la variance de reproductibilité:

\[\begin{equation} \tag{1.27} s_{Rj}^2=s_{rj}^2+s_{Lj}^2 \end{equation}\]

1.6 Rrelation fonctionnelle entre les écarts-types de répétabilité/reproductibilité et les moyennes par niveaux

Il convient de rechercher si les valeurs de fidélité dépendent de \(\hat{m}_j\) et s’il en est ainsi, il convient de déterminer la relation fonctionnelle. Cela permettrait de déterminer plus aisément les valeurs de fidélité pour d’autres niveaux qui n’ont pas été pris en compte dans le cadre du protocole d’essais inter-laboratoires.

Seuls trois types de relations sont prises en compte :

1. Une droite passant par l’origine:

\[\begin{equation} \tag{1.28} s_j=b\times \hat{m}_j \ \forall j \in \{1,2,...,q\} \end{equation}\]

où: \(s_j\) représente l’écart-type de répétabilité ou reproductibilité au niveau \(j\); \(b\) est le coefficient directeur de la droite (à estimer sur la base de données disponibles); \(\hat{m}_j\) est l’estimation de la moyenne au niveau \(j\).

2. Une droite qui ne passe pas par l’origine:

\[\begin{equation} \tag{1.29} s_j=a+b\times \hat{m}_j \ \forall j \in \{1,2,...,q\} \end{equation}\]

où: \(a\) est l’ordonnée à l’origine (à estimer sur la base de données disponibles).

3. Une relation exponentielle:

\[\begin{equation} \tag{1.30} log(s_j)=a+b\times log(\hat{m}_j) \ \forall j \in \{1,2,...,q\} \end{equation}\]

où: \(a\) et \(b\) sont respectivement l’ordonnée à l’origine et le coefficient directeur de la droite après la transformation logarithmique (à estimer sur la base de données disponibles).

1.7 Synthèse de l’approche d’évaluation de la fidélité d’une méthode de mesure normalisée

Un récapitulatif des étapes majeures dans l’estimation de la fidélité d’une méthode de mesure normalisée est donné ci-dessous:

1. Rassembler tous les résultats d’essai disponibles dans un même formulaire. Il est recommandé que ce tableau soit présenté avec \(p\) lignes (représentant les \(p\) laboratoires ayant fourni des données), et \(q\) colonnes (représentant les \(q\) niveaux dans un ordre croissant).

2. Calculer les moyennes et les écarts-type des cellules dans le tableau de données.

3. Examiner la cohérence des résultats (statistiques \(h\) et \(k\) de Mendel).

4. Rechercher des valeurs atypiques (tests de Cochran et Grubbs). S’il n’y a pas de valeurs isolées/aberrantes, ignorer les étapes 5-7 et passer directement à l’étape 8.

5. Rechercher des explications techniques à la présence des valeurs isolées et/ou aberrantes. Corriger (ou éliminer) les valeurs isolées et/ou aberrantes pour lesquelles une explication satisfaisante à été trouvée. Corriger les moyennes et les écarts-type calculés à l’étape 2.

6. S’il existe une raison suffisamment forte de suspecter aberrants certains laboratoires, éliminer alors les données en question et en faire un rapport à la commission.

7. S’il subsiste des valeurs isolées et/ou aberrantes qui ne sont ni expliquées ni attribuées à un laboratoire aberrant, éliminer les valeurs aberrantes, mais conserver les valeurs isolées.

8. A partir des données validées calculer: la moyenne de chaque niveau (\(\hat{m}_j\)) et les écarts-type de répétabilité (\(s_{rj}\)) et reproductibilité (\(s_{Rj}\)).

9. Si un seul niveau a été utilisé pour l’expérience, ou s’il a été décidé qu’il convient de donner séparément pour chaque niveau les écarts-types de répétabilité et de reproductibilité, ignorer les étapes 10 à 12 et passer directement à l’étape 13.

10. Tracer graphiquement \(s_{rj}=f(\hat{m}_j)\) et \(s_{Rj}=f(\hat{m}_j)\). Si l’on juge qu’il y a une relation fonctionnelle linéaire ou exponentielle, alors ignorer l’étape 11 et passer à l’étape 12.

11. Utiliser comme valeur finale de l’écart-type de répétabilité/reproductibilité:

\[\begin{equation*} \left\{ \begin{aligned} & s_r=\frac{1}{q}\sum_{j=1}^q s_{rj}\\ & s_R=\frac{1}{q}\sum_{j=1}^q s_{Rj} \end{aligned} \right. \tag{1.11} \end{equation*}\]

Ignorer l’étape 12 et passer directement à l’étape 13.

12. Si une relation satisfaisante a été établie (linéaire ou exponentielle) alors les valeurs finales de \(s_r\) et \(s_R\) sont les valeurs lissées obtenues à partir de cette relation.

13. Préparer un rapport exposant les données de base et les résultats et conclusions de l’analyse statistique, et présenter celui-ci à la commission.

1.8 Exemple applicatif

Une campagne de comparaisons inter-laboratoires a été menée afin d’évaluer la fidélité d’une méthode de mesure normalisée. Dix laboratoires ont participé à cette campagne et ont mesuré des échantillons provenant de six niveaux différents. Lors du transport des échantillons d’un laboratoire à l’autre, certains échantillons ont subi des dégradations, ce qui fait que tous les laboratoires n’ont pas fait le même nombre de mesures.

On illustrera ci-après l’approche d’estimation de la fidélité en utilisant le logiciel R pour la partie calculatoire. Dans cet exemple, l’accent est mis sur l’interprétation des résultats, motif pour lequel le code R utilisé n’apparaît pas de manière explicite.

Dans les tableaux 1.1, 1.2, 1.3, on résume le nombre de répétitions par laboratoire, les moyennes et les écarts-type des laboratoires par niveau.

Tableau 1.1: Nombre de répétitions par laboratoire

	Niv1	Niv2	Niv3	Niv4	Niv5	Niv6
1	4	4	4	4	4	4
2	3	3	3	3	3	3
3	5	5	5	5	5	5
4	4	4	4	4	4	4
5	5	5	5	5	5	5
6	4	4	4	4	4	4
7	4	4	4	4	4	4
8	4	4	4	4	4	4
9	4	4	4	4	4	4
10	3	3	3	3	3	3

Tableau 1.2: Moyennes des laboratoires

	Niv1	Niv2	Niv3	Niv4	Niv5	Niv6
1	9.995000	49.9950	89.99250	130.0675	170.1050	210.1675
2	9.990000	49.9500	90.08667	129.9500	169.9633	210.1233
3	9.998000	50.0000	89.94400	129.0060	169.8880	210.1320
4	10.002500	50.0150	90.99000	130.0475	169.9525	209.8875
5	10.002000	49.9860	90.02800	129.9820	170.0480	210.1020
6	9.987500	50.0425	90.00500	130.0125	169.8950	210.1850
7	10.002500	49.9600	89.98500	130.0575	170.0025	209.8675
8	10.002500	49.8650	89.96250	130.0150	169.9050	210.1525
9	10.000000	50.0000	89.94250	129.9800	170.0000	209.8475
10	9.996667	50.0100	89.96667	129.9633	170.0133	209.8933

Tableau 1.3: Ecarts-type des laboratoires

	Niv1	Niv2	Niv3	Niv4	Niv5	Niv6
1	0.0057735	0.0191485	0.0665207	0.0953502	0.1709776	0.0694622
2	0.0916515	0.0435890	0.3523256	0.1513275	0.1814754	0.0611010
3	0.0044721	0.0689202	0.0763544	0.0151658	0.2298260	0.1883348
4	0.0050000	0.0613732	0.0787401	0.0602080	0.0708872	0.2396351
5	0.0130384	0.0415933	0.1035374	0.1154123	0.0973139	0.2179908
6	0.0150000	0.0590903	0.0519615	0.0411299	0.1244990	0.1729162
7	0.0125831	0.0391578	0.1528616	0.1276388	0.0793200	0.1795132
8	0.0095743	0.1984103	0.0457347	0.1668333	0.2223361	0.1705628
9	0.0000000	0.0294392	0.0537742	0.1197219	0.1174734	0.1936276
10	0.0115470	0.0346410	0.0461880	0.1026320	0.1096966	0.2804164

On vérifie la cohérence des résultats des laboratoires via les tests de Mandel.

On affiche les valeurs critiques de la statistique h de Mandel dans le tableau 1.4.

Tableau 1.4: Valeurs critiques pour la statistique h de Mandel

	5%	1%
	1.79841	2.176068

Les statistiques h de Mandel sont affichées dans le tableau 1.5.

Tableau 1.5: Statistiques h de Mandel

	Niv1	Niv2	Niv3	Niv4	Niv5	Niv6
1	-0.4917455	0.2584443	-0.3064804	0.4988036	1.8157329	0.9296071
2	-1.4137682	-0.6609229	-0.0113356	0.1310390	-0.1980627	0.6178164
3	0.0614682	0.3605962	-0.4584931	-2.8235979	-1.2689282	0.6789979
4	0.8912887	0.6670520	2.8199648	0.4362054	-0.3520589	-1.0470287
5	0.7990864	0.0745709	-0.1952135	0.2311962	1.0054763	0.4672155
6	-1.8747796	1.2288875	-0.2673019	0.3266585	-1.1694230	1.0531469
7	0.8912887	-0.4566190	-0.3299875	0.4675045	0.3586925	-1.1882170
8	0.8912887	-2.3975053	-0.4005089	0.3344833	-1.0272727	0.8237159
9	0.4302773	0.3605962	-0.4631945	0.2249363	0.3231550	-1.3294052
10	-0.1844045	0.5649001	-0.3874494	0.1727711	0.5126887	-1.0058488

Comparer les statistiques h de Mandel (tableau 1.5) avec les valeurs critiques apparaissant (tableau 1.4), c’est assez fastidieux car cela nécessite un effort de concentration soutenu dans le temps. Pour faciliter l’interprétation des résultats, il est bien plus confortable de les afficher graphiquement (voir figure 1).

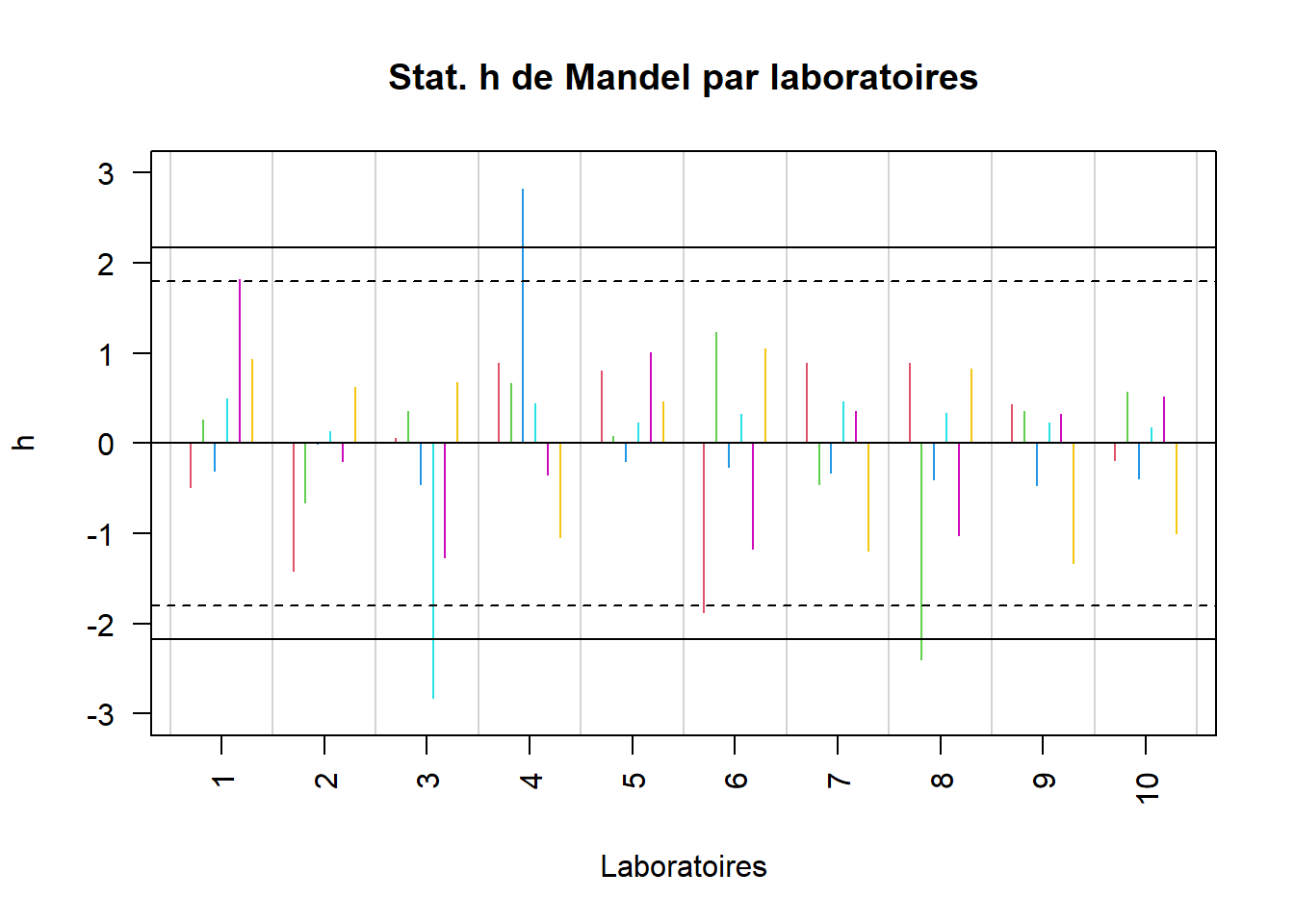Figure 1 - Statistiques h de Mandel par laboratoires

En effet, les valeurs apparaissant sur l’axe des abscisses sont les indexes des dix laboratoires ayant participé à cette étude. Sur l’axe des ordonnées on a les valeurs des statistiques h de Mandel (tableau 1.5) sous la forme d’un diagramme en battons.Chaque niveau est représenté par une couleur différente. Le trait horizontal continu représente la valeur critique à 1% pour la statistique h de Mandel (2.176 - voir le tableau 1.4). Le trait horizontal en pointillé marque la valeur critique à 5% pour la statistique h de Mandel (1.798 - voir le tableau 1.4).

Remarques: On remarque certaines incohérences au niveau des moyennes des laboratoires:

• Le laboratoire 3 au niveau 4 présente une moyenne beaucoup plus basse que celle des autres laboratoires au même niveau.

• Le laboratoire 4 au niveau 3 présente une moyenne beaucoup plus élevée que celle des autres laboratoires au même niveau.

• Le laboratoire 8 au niveau 2 présente une moyenne beaucoup plus basse que celle des autres laboratoires au même niveau.

Les statistiques h de Mandel peuvent aussi être comparées niveau par niveau à l’aide des boîtes à moustache (voir figure 2). Les points qui apparaissent en exergue (numérotés dans la figure 2), représentent les laboratoires qui présentent des statistiques h atypiques par rapport aux statistiques h des autres laboratoires au même niveau. Les conclusions sont les mêmes que présentées ci-dessus.

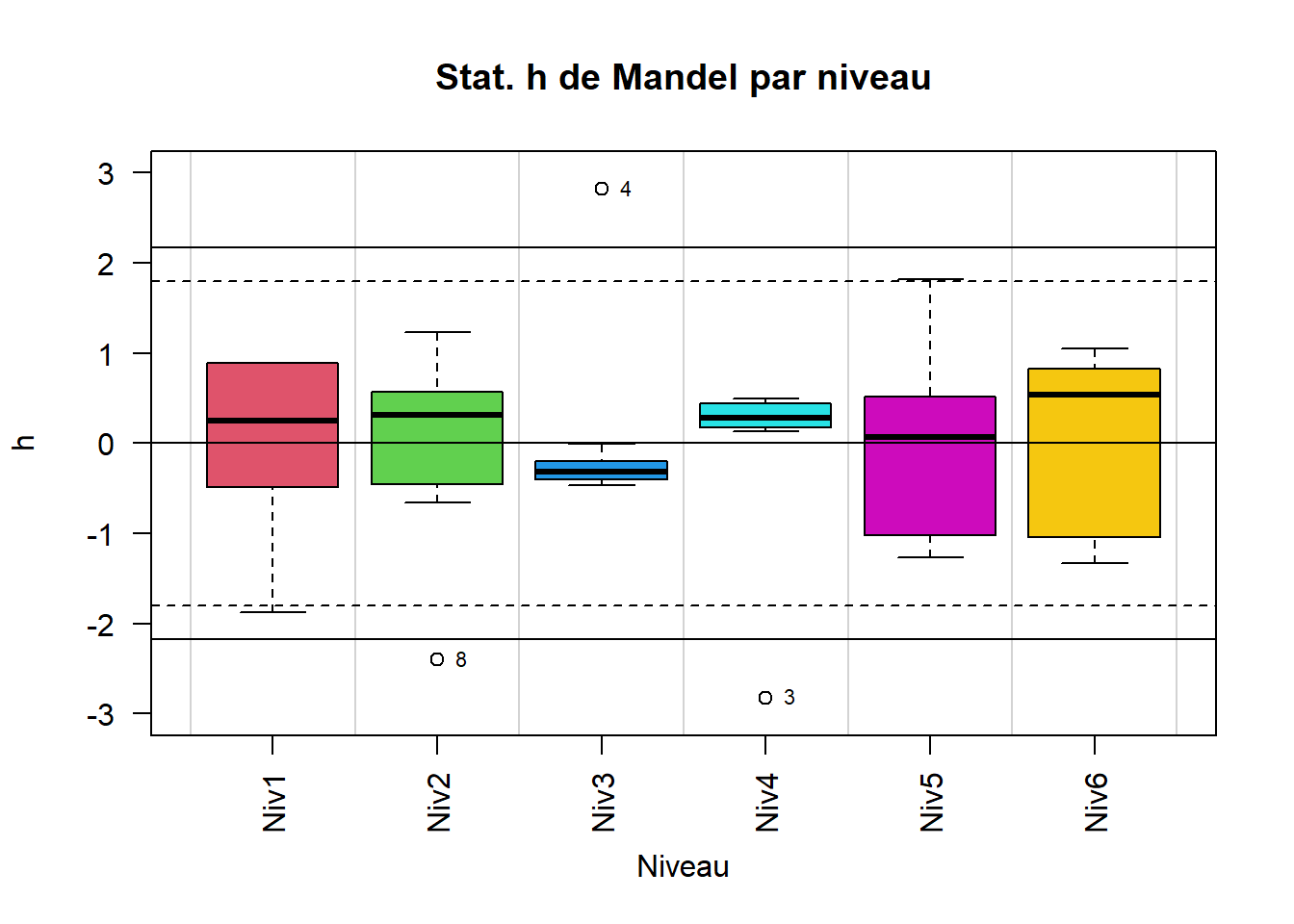Figure 2 - Statistiques h de Mandel par niveaux

On affiche les valeurs critiques de la statistique k de Mandel dans le tableau 1.6.

Tableau 1.6: Valeurs critiques pour la statistique k de Mandel

	5%	1%
Nombre de repetitions = 3	1.682643	2.001289
Nombre de répétitions = 4	1.573257	1.839237
Nombre de répétitions = 5	1.504574	1.737242

Les statistiques k de Mandel sont affichées dans le tableau 1.7.

Tableau 1.7: Statistiques k de Mandel

	Niv1	Niv2	Niv3	Niv4	Niv5	Niv6
1	0.1897632	0.2493527	0.4897430	0.8709691	1.1359696	0.3679863
2	3.0123979	0.5676166	2.5939155	1.3822886	1.2057170	0.3236915
3	0.1469900	0.8974807	0.5621418	0.1385303	1.5269568	0.9977312
4	0.1643398	0.7992026	0.5797056	0.5499649	0.4709725	1.2695022
5	0.4285457	0.5416283	0.7622703	1.0542245	0.6465506	1.1548383
6	0.4930193	0.7694753	0.3825547	0.3756976	0.8271674	0.9160487
7	0.4135794	0.5099136	1.1254080	1.1659065	0.5269997	0.9509976
8	0.3146867	2.5837032	0.3367114	1.5239250	1.4771939	0.9035813
9	0.0000000	0.3833578	0.3959002	1.0935901	0.7804896	1.0257708
10	0.3795265	0.4510959	0.3400486	0.9374841	0.7288204	1.4855466

Pour les mêmes raisons que celles qui ont été évoquées lorsque l’on a interprété les statistiques h de Mandel, dans le cas des statistiques k de Mandel aussi l’affichage graphique est bien plus utile pour l’identification des éventuelles incohérences au niveau des variances des laboratoires (voir les figures 3 et 4).

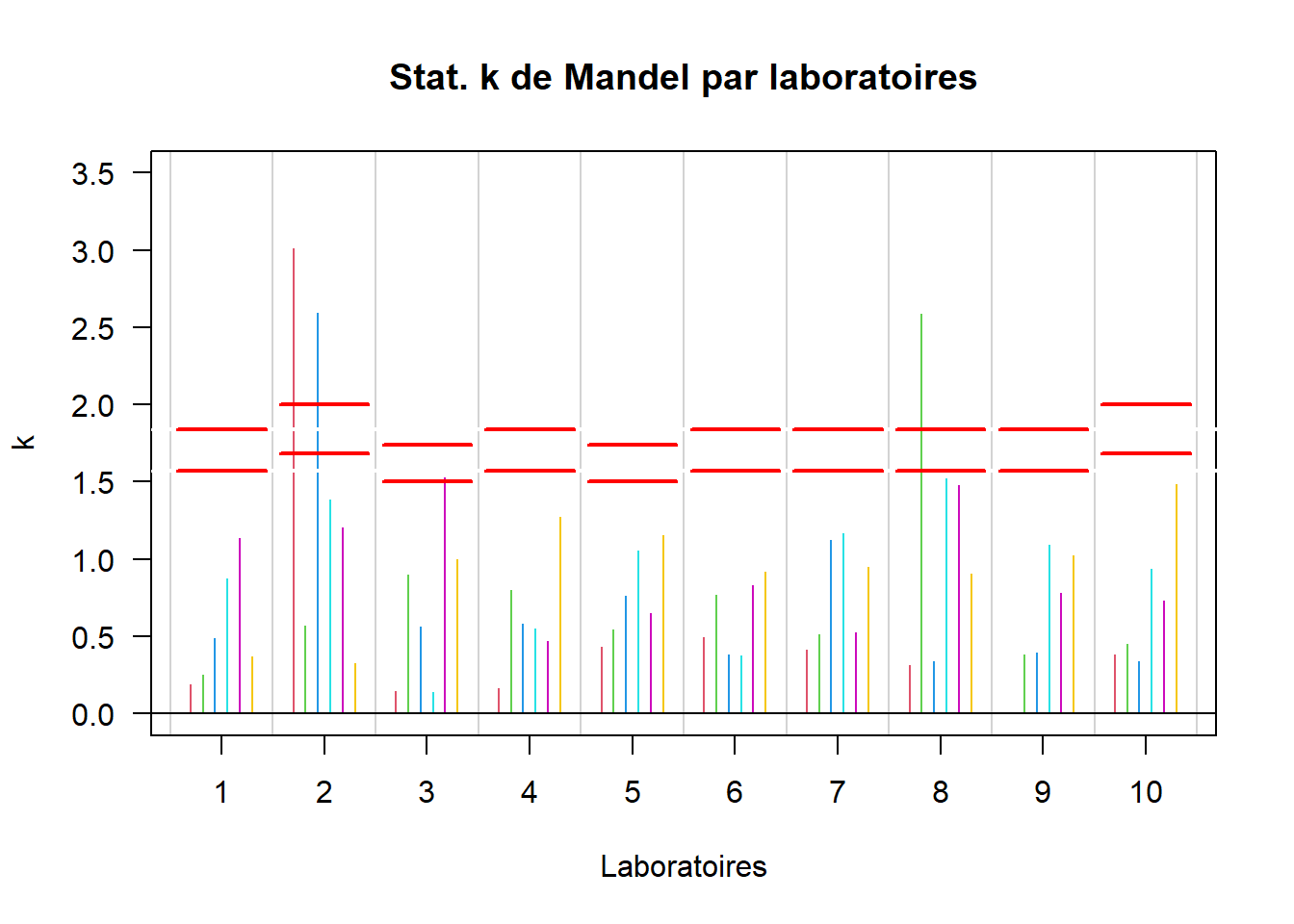Figure 3 - Statistiques k de Mandel par laboratoires

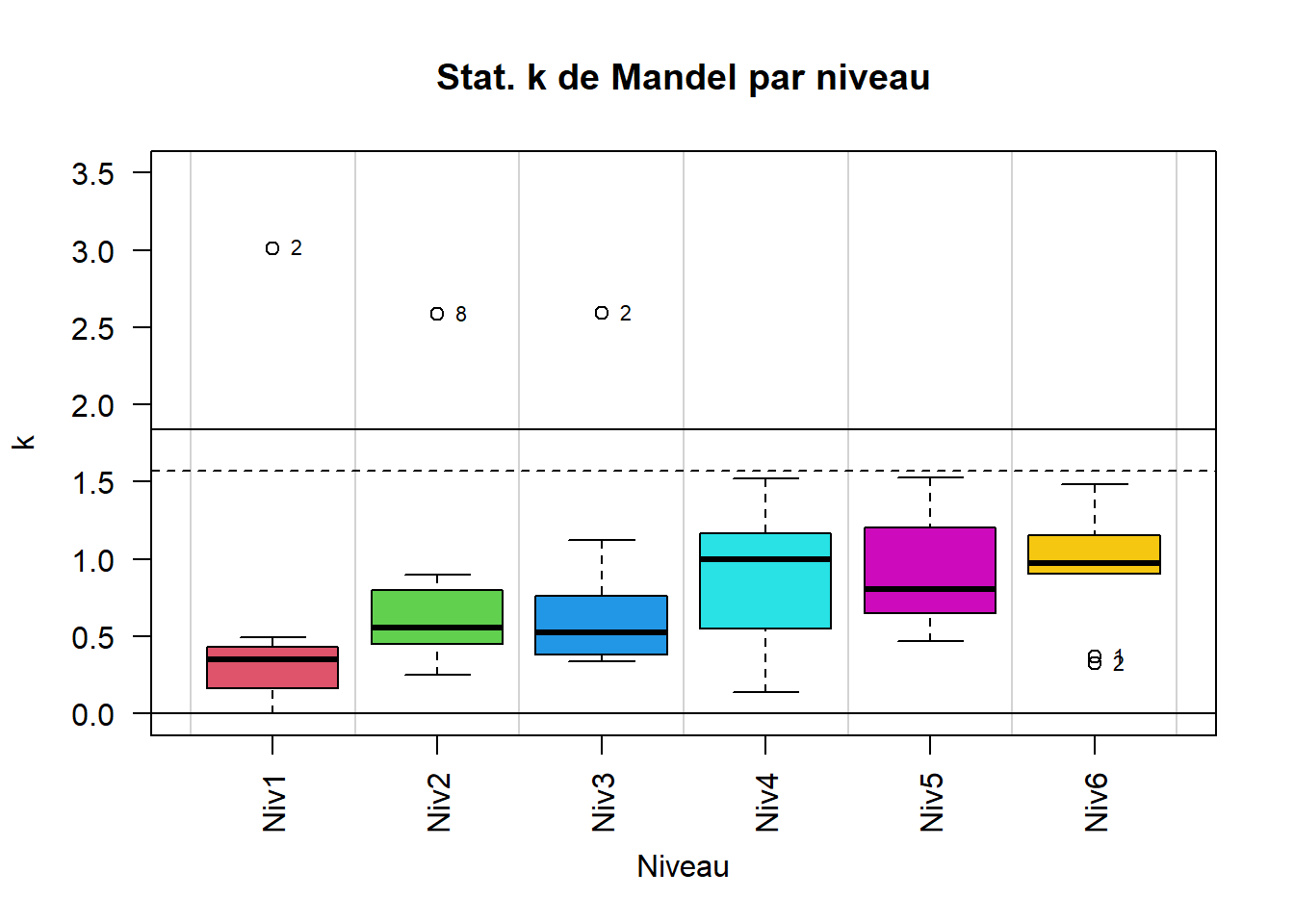Figure 4 - Statistiques k de Mandel par niveaux

On peut remarquer dans la figure 3 et dans le tableau 1.6 que les limites critiques varient en fonction du nombre de répétitions par laboratoire.

Remarques: On remarque certaines incohérences au niveau des variances des laboratoires:

• Le laboratoire 2 aux niveaux 1 et 3 présente une variance beaucoup plus élevée que celle des autres laboratoires au même niveau.

• Le laboratoire 8 au niveau 2 présente une variance beaucoup plus élevée que celle des autres laboratoires au même niveau.

• Les laboratoires 1 et 2 au niveau 6 présentent une variance bien plus faible que celle des autres autres laboratoires au même niveau

On vérifie s’il y a des valeurs atypiques parmi les résultats des laboratoires.

On fait tout d’abord le test de Cochran. Les valeurs critiques pour ce test sont données dans le tableau 1.8.

Tableau 1.8: Valeurs critiques pour le test de Cochran

	5%	1%
Nombre de repetitions = 3	0.4449527	0.5358411
Nombre de répétitions = 4	0.3733082	0.4468861
Nombre de répétitions = 5	0.3311121	0.3933764

Le tableau 1.9 résume de manière synthétique les résultats de l’application répétitive du test de Cochran niveau par niveau.

Tableau 1.9: Résultats des tests de Cochran par niveau

	Niv1	Niv2	Niv3	Niv4	Niv5	Niv6
Statistique	0.907454087144404	0.667552214340219	0.672839784994803	0.232234737866772	0.233159706895037	0.220684880887229
p.value	4.52526904837214e-13	1.2364794705233e-05	9.99382944710803e-06	0.639838619497893	0.630477243336268	0.767551174906533
Hypothèse H1	Group 2 has outlying variance	Group 8 has outlying variance	Group 2 has outlying variance	Group 8 has outlying variance	Group 3 has outlying variance	Group 10 has outlying variance
Variance testée	0.00839999999999996	0.0393666666666668	0.124133333333335	0.0278333333333325	0.0528200000000019	0.0786333333333332

Il y a deux manières équivalentes d’interpréter les résultats et de trancher entre les deux hypothèses:

• On compare la statistique de test avec les valeurs critiques : par exemple, au niveau 1 la plus grande variance enregistrée est celle du laboratoire 2 (voir l’hypothèse H1: “Group 2 has outlying variance”); ce laboratoire a fait 3 répétitions à ce niveau (voir le tableau 1.1); la statistique de test (0.907) est supérieure à la valeur critique à 1% (0.535) affichée dans le tableau 1.8; par conséquent, on rejette l’hypothèse H0 et l’on conclue qu’au niveau de significativité de 1% la variance du laboratoire 2 au niveau 1 est aberrante.

• On constate que la p.value du test au niveau 1 (4.525e-13) est inférieure à 1%, par conséquent l’on conclue qu’au niveau de significativité de 1% la variance du laboratoire 2 au niveau 1 est aberrante.

Remarques: On constate la présence des variances atypiques au niveau des laboratoires:

• Niveau 1: la variance du laboratoire 2 est aberrante.

• Niveau 2: la variance du laboratoire 8 est aberrante.

• Niveau 3: la variance du laboratoire 2 est aberrante.

Selon les spécifications de la norme ISO 5725 on ne peut utiliser ces valeurs pour le calcul des caractéristiques de fidélité de la méthode. Un travail d’investigation devrait être réalisé pour identifier les causes qui ont conduit à ces variances trop élevées au niveau de ces laboratoires. On décide donc de supprimer les valeurs de ces laboratoires au niveaux précisés ci-dessus et on vérifie à nouveau si le test de Cochran détecte des valeurs atypiques.

Tableau 1.10: Résultats des tests de Cochran par niveau

	Niv1	Niv2	Niv3	Niv4	Niv5	Niv6
Statistique	0.262645914396887	0.242285131344052	0.387132403700126	0.232234737866772	0.233159706895037	0.220684880887229
p.value	0.505144731640473	0.709507683054082	0.0601856998229792	0.639838619497893	0.630477243336268	0.767551174906533
Hypothèse H1	6 has outlying variance	3 has outlying variance	7 has outlying variance	Group 8 has outlying variance	Group 3 has outlying variance	Group 10 has outlying variance
Variance testée	0.00022499999999999	0.00475000000000017	0.0233666666666675	0.0278333333333325	0.0528200000000019	0.0786333333333332

Remarque: On constate dans le tableau 1.10 que toutes les p.values sont supérieures à 5%, ce qui ne permet pas de rejeter l’hypothèse H0. Par conséquent, on peut considérer qu’il n’y a plus de variance atypique au niveau des laboratoires.

On continue par la réalisation du test de Grubbs. On commence par le test simple de Grubbs. Le tableau 1.11 donne les valeurs critiques des tests simple et double de Grubbs.

Tableau 1.11: Valeurs critiques pour le test de Grubbs

	5%	1%
Test simple	2.176068	2.409725
Test double (2 valeurs de même côté)	0.721000	0.787000
Test double (2 valeurs de côtés opposés)	3.684965	3.874880

Remarque: Au niveau du test double de Grubbs, il y a deux possibilités: les deux valeurs testé sont dites “de même côté” lorsqu’elles sont soit les deux plus petites soit les deux plus grandes; elles sont dites “de côtés opposés” lorsque l’on teste la plus petite et la plus grande.

Le tableau 1.12 résume de manière synthétique les résultats du test simple de Grubbs réalisé de manière répétitive niveau par niveau.

Tableau 1.12: Synthèse du test simple de Grubbs par niveaux

	Niv1	Niv2	Niv3	Niv4	Niv5	Niv6
Statistique	2.20724904949534	1.68403201043879	2.65752190520293	2.82359794738668	1.81573290919383	1.32940524850856
p.value	0.0264551585740294	0.306542812867347	3.48749419343264e-08	8.39221891979491e-08	0.235845145380134	0.867398110669074
Hypothèse H1	lowest value 9.9875 is an outlier	highest value 50.0425 is an outlier	highest value 90.99 is an outlier	lowest value 129.006 is an outlier	highest value 170.105 is an outlier	lowest value 209.8475 is an outlier

Comme dans le cas du test de Cochran, dans le cas du test simple de Grubbs aussi il y a deux manières équivalentes d’interpréter les résultats et de trancher entre les deux hypothèses:

• On compare la statistique de test avec les valeurs critiques : par exemple, au niveau 1 la statistique de test (2.207) est entre la valeur critique à 5% (2.176) et la valeur critique à 1% (2.409); par conséquent, la plus petite moyenne au niveau 1 (9.9875 - voir l’hypothèse H1 dans le tableau 1.12) qui appartient au laboratoire 6 (voir le tableau 1.2) peut être considérée comme une valeur isolée.

• On constate que la p.value du test au niveau 1 (0.0264) est comprise entre 1% et 5%. Par conséquent, on conclue la moyenne du laboratoire 6 au niveau 1 est une valeur isolée.

Remarques: On constate la présence des moyennes atypiques au niveau des laboratoires:

• Niveau 1: la moyenne du laboratoire 6 est isolée.

• Niveau 3: la plus grande moyenne (90.99 - voir l’hypothèse H1 “highest value 90.99 is an outlier” dans le tableau 1.12) qui appartient au laboratoire 4 (voir le tableau 1.2) est une valeur aberrante (p.value = 3.487e-08 < 1%).

• Niveau 4: la plus petite moyenne (129.006 - voir l’hypothèse H1 “lowest value 129.006 is an outlier” dans le tableau 1.12) qui appartient au laboratoire 3 (voir le tableau 1.2) est une valeur aberrante (p.value = 8.392e-08 < 1%).

En accord avec les spécifications de la normme ISO 5725, on supprime les valeurs aberrantes et on décide de garder les valeurs isolées. Après la suppression des valeurs des laboratoires 4 et 3 au niveaux 3 et respectivement 4, on refait le test simple de Grubbs. Le tableau 1.13 résume la deuxième itération de ce test.

Tableau 1.13: Synthèse du test simple de Grubbs par niveaux

	Niv1	Niv2	Niv3	Niv4	Niv5	Niv6
Statistique	2.20724904949534	1.68403201043879	1.66125438511478	1.39186941029896	1.81573290919383	1.32940524850856
p.value	0.0264551585740294	0.306542812867347	0.273461808188968	0.672674680915585	0.235845145380134	0.867398110669074
Hypothèse H1	lowest value 9.9875 is an outlier	highest value 50.0425 is an outlier	highest value 90.028 is an outlier	highest value 130.0675 is an outlier	highest value 170.105 is an outlier	lowest value 209.8475 is an outlier

Remarque: Après la deuxième itération du test simple de Grubbs on constate qu’il n’y a plus de moyenne aberrante au niveau des laboratoires.

On poursuit donc les tests en appliquant le test double de Grubbs (2 valeurs de même côté). Le tableau 1.14 synthétise les résultats de l’application répétitive niveau par niveau de ce test.

Tableau 1.14: Synthèse du test double de Grubbs (2 valeurs de même côté) par niveaux

	Niv1	Niv2	Niv3	Niv4	Niv5	Niv6
Statistique	0.177474432924067	0.48249652668622	0.336519770245928	0.474692216582999	0.410803188966813	0.558724377434981
p.value	0.0407866993031125	0.543105053106867	0.319110926627548	0.524965330858769	0.30149317756384	0.654067333223059
Hypothèse H1	lowest values 9.9875 , 9.995 are outliers	highest values 50.015 , 50.0425 are outliers	highest values 90.005 , 90.028 are outliers	highest values 130.0575 , 130.0675 are outliers	highest values 170.048 , 170.105 are outliers	lowest values 209.8475 , 209.8675 are outliers

Remarque: On constate que les deux plus petites moyennes au niveau 1 sont isolées (“lowest values 9.9875 , 9.995 are outliers”) car la p.value du test (0.0407) est inférieure à 5%; ces valeurs appartiennent aux laboratoires 6 et 1 (voir le tableau 1.2); selon les spécification de la norme ISO 5725 on peut les garder pour le calcul de la fidélité de la méthode.

On poursuit donc les tests en appliquant le test double de Grubbs (2 valeurs de côtés opposés). Le tableau 1.15 synthétise les résultats de l’application répétitive niveau par niveau de ce test.

Tableau 1.15: Synthèse du test double de Grubbs (2 valeurs de côtés opposés) par niveaux

	Niv1	Niv2	Niv3	Niv4	Niv5	Niv6
Statistique	3.00482643712829	3.30650152993026	2.85621616946462	2.7658663978535	3.0846610748566	2.38255210923949
p.value	0.70677199370329	0.216154318581779	0.770831445869767	1	0.773834463605043	1
Hypothèse H1	9.9875 and 10.0025 are outliers	49.95 and 50.0425 are outliers	89.9425 and 90.028 are outliers	129.95 and 130.0675 are outliers	169.888 and 170.105 are outliers	209.8475 and 210.185 are outliers

Remarque: Selon le test double de Grubbs (2 valeurs de côtés opposés), il n’y a pas de valeur atypique.

Comme les tests simple et double de Grubbs ne détectent plus de valeur atypique, on peut arrêter la procédure de test et considérer que le jeu de données restant est approprié pour évaluer les paramètres de fidélité de la méthode de mesure normalisée. Le tableau 1.16 résume ces paramètres pour chaque niveau de l’étude.

Tableau 1.16: Paramètres de fidélité de la méthode

	Niv1	Niv2	Niv3	Niv4	Niv5	Niv6
m	9.9986486	49.9961111	89.9790909	130.0105714	169.9762500	210.0412500
sr	0.0096855	0.0479950	0.0841170	0.1141434	0.1524186	0.1888181
sR	0.0096324	0.0486146	0.0788958	0.1057743	0.1488674	0.2108671

On vérifie si une relation fonctionnelle entre ces paramètres et les valeurs moyennes par niveau peut être établie (voir figure 5).

#> `geom_smooth()` using formula = 'y ~ x'
#> `geom_smooth()` using formula = 'y ~ x'
#> `geom_smooth()` using formula = 'y ~ x'
#> `geom_smooth()` using formula = 'y ~ x'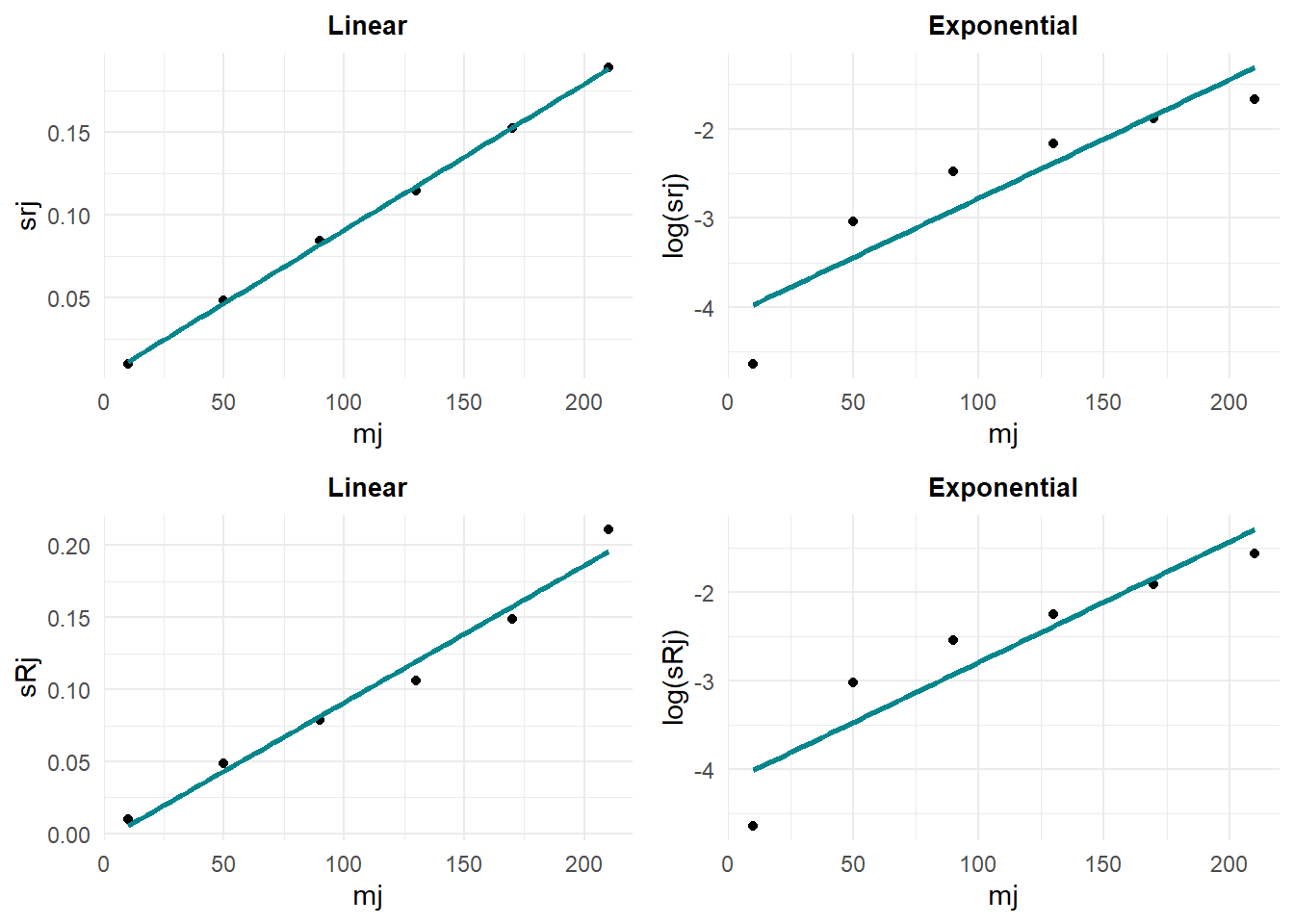

Remarque: On constate qu’une relation linéaire caractérise assez bien la dépendance entre les écarts-type de répétabilité et de reproductibilité par rapport aux valeurs moyennes par niveaux. Par conséquent, on en déduit les équations de régression caractérisant ces droites.

#> 
#> Call:
#> lm(formula = srj ~ mj)
#> 
#> Residuals:
#>       Niv1       Niv2       Niv3       Niv4       Niv5 
#> -0.0013573  0.0015603  0.0023032 -0.0030923 -0.0001808 
#>       Niv6 
#>  0.0007670 
#> 
#> Coefficients:
#>              Estimate Std. Error t value Pr(>|t|)    
#> (Intercept) 2.195e-03  1.720e-03   1.276    0.271    
#> mj          8.848e-04  1.328e-05  66.618 3.04e-07 ***
#> ---
#> Signif. codes:  
#> 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
#> 
#> Residual standard error: 0.002223 on 4 degrees of freedom
#> Multiple R-squared:  0.9991, Adjusted R-squared:  0.9989 
#> F-statistic:  4438 on 1 and 4 DF,  p-value: 3.042e-07

Remarque: On constate que le modèle de régression linéaire est pertinent pour modéliser la dépendance entre l’écart-type de répétabilité et les valeurs des moyennes par niveau. On note que le coefficient directeur de la droite de régression est significativement différent de zéro et que l’ordonnée à l’origine ne l’est pas (cela veut dire que la droite de régression passe par l’origine).

#> 
#> Call:
#> lm(formula = sRj ~ mj)
#> 
#> Residuals:
#>      Niv1      Niv2      Niv3      Niv4      Niv5      Niv6 
#>  0.004454  0.005334 -0.002473 -0.013730 -0.008709  0.015124 
#> 
#> Coefficients:
#>               Estimate Std. Error t value Pr(>|t|)    
#> (Intercept) -4.347e-03  9.052e-03   -0.48 0.656186    
#> mj           9.526e-04  6.991e-05   13.63 0.000168 ***
#> ---
#> Signif. codes:  
#> 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
#> 
#> Residual standard error: 0.0117 on 4 degrees of freedom
#> Multiple R-squared:  0.9789, Adjusted R-squared:  0.9736 
#> F-statistic: 185.7 on 1 and 4 DF,  p-value: 0.0001679

Remarque: Même commentaire que dans le cas de l’écart-type de répétabilité.

Puisque les écarts-types de répétabilité et de reproductibilité dépendent linéairement des valeurs moyennes par niveau, on peut utiliser les équations des deux modèles de régression pour en déduire quels seront les paramètres de fidélité de la méthode pour d’autres niveaux moyens qui n’ont pas été étudiés dans cette étude. Par exemple, supposons que l’on veuille estimer les écarts-types de répétabilité/reproductibilité pour la valeur de 100 qui représente une valeur entre celle caractérisant le niveau 3 et celle caractérisant le niveau 4. En plus, admettons que l’on veuille donner les intervalles de confiance à 95% pour ces estimations.

Tableau 1.17: Predictions des paramètres de fidélité pour le niveau de 100 accompagnées des intervalles de confiance à 95%

	fit	lwr	upr
sr	0.0906808	0.0840044	0.0973572
sR	0.0909154	0.0557766	0.1260543

Remarques:

• On estime que l’écart-type de répétabilité au niveau de 100 serait de 0.0906; l’intervalle de confiance à 95% pour cette estimation est [0.0840044 - 0.0973572].

• On estime que l’écart-type de reproductibilité au niveau de 100 serait de 0.0909; l’intervalle de confiance à 95% pour cette estimation est [0.0557766 - 0.1260543].