Chapitre2 Capabilité des systèmes de mesure
Dans le cadre d’un processus, chaque mesure effectuée par un système de mesure intègre deux sources de variation : la variation inhérente au processus mesuré et la variation caractéristique du système de mesure (voir la figure 1).
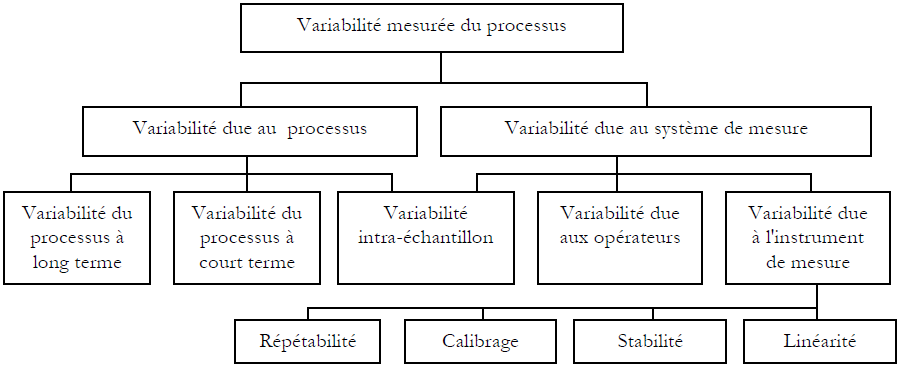
L’étude de Répétabilité et de Reproductibilité (R&R) permet d’estimer les variations des résultats de mesure engendrées par l’instrument de mesure (Répétabilité) et par les opérateurs (Reproductibilité). La répétabilité est la variabilité observée quand un opérateur mesure plusieurs fois la même pièce avec le même instrument de mesure. La reproductibilité est la variation additionnelle observée quand plusieurs opérateurs mesurent la même pièce avec le même instrument de mesure. L’addition de ces deux sources de variation donne une dispersion que nous allons appeler variation de R&R (ou variation du système de mesure):
\[\begin{equation} \tag{2.1} \sigma_{R \& R}^2=\sigma_{Répétabilité}^2 + \sigma_{Reproductibilité}^2 \end{equation}\]Par conséquent, la variabilité totale mesurée (voir la figure 2) peut s’exprimer comme étant :
\[\begin{equation} \tag{2.2} \sigma_{T}^2=\sigma_{Processus}^2 + \sigma_{R \& R}^2 \end{equation}\]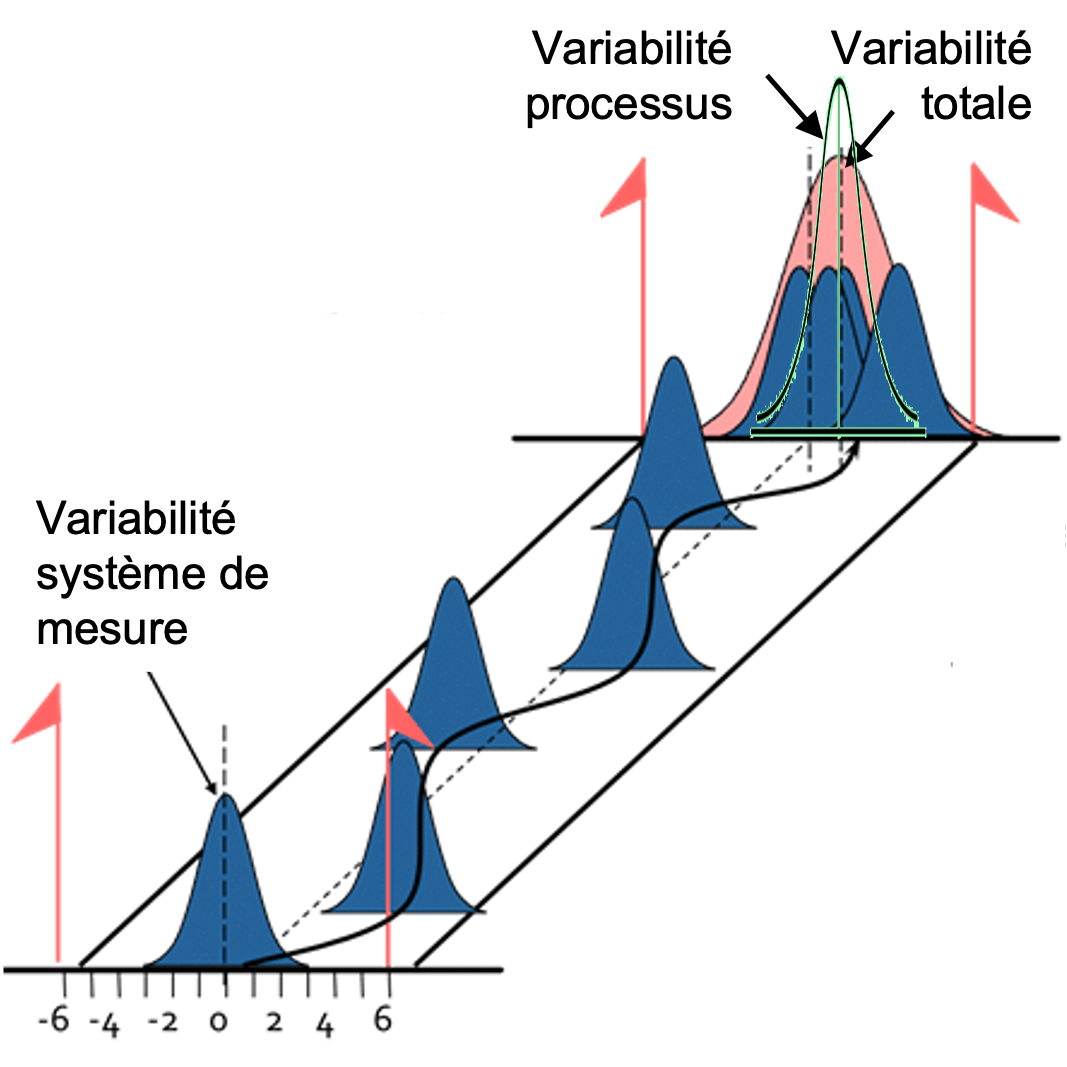
Dans le cadre des études R&R on considère comme négligeables les autres sources de variation potentielles. Cela ne veut pas dire que le calibrage, la stabilité ou la linéarité sont moins importantes, mais que leur impact sur les résultats obtenus est considéré comme étant plus réduit. Toutefois, quand on ne peut pas faire abstraction de ces sources de variation additionnelles, les études de R&R doivent être complétées par une vérification du calibrage, une évaluation de la variation intra-échantillon, etc.… La prise en compte de la variation intra-échantillon, par exemple, donne des informations concernant la manière dont on peut améliorer la capabilité du processus. Aussi, une attention particulière doit être accordée à l’influence de l’environnement sur les résultats de mesures. Cette influence peut être étudiée par la méthode des plans d’expériences, par exemple. Dans les études de R&R il est nécessaire d’accomplir des efforts afin de réduire ou d’éliminer si possible ces sources de variations environnementales.
2.1 Etapes dans le cadre d’une étude R&R
La procédure standard de mise en œuvre d’une étude de R&R a été proposée par General Motors. Cette méthode permet de calculer séparément les deux composantes de la variabilité du système de mesure : la variabilité de répétabilité et la variabilité de reproductibilité. Les autres sources de variation (le calibrage, la stabilité, la linéarité et la variation intra-échantillon) ne sont pas prises en compte par cette méthodologie.
Cette approche définit la variation de R&R comme un intervalle contenant 99 % de la distribution théorique des résultats de mesure (c.à.d. \(5.15 \times \sigma\)). Certaines entreprises utilisent un intervalle contenant 99.7% des valeurs (c.à.d. \(6 \times \sigma\)) et d’autres préfèrent utiliser un intervalle 95 % (c.à.d. \(4 \times \sigma\)) pour définir la variation de R&R. Pour éviter toute confusion il faut clairement spécifier, dès le départ, quel type d’intervalle on utilise dans le cadre de l’étude de R&R.
Les étapes pour la mise en œuvre de l’approche R&R sont:
S’assurer que l’instrument de mesure est calibré (si nécessaire, effectuer le calibrage de l’instrument).
Faire mesurer, en ordre aléatoire, tous les échantillons par le premier opérateur.
Faire mesurer, en ordre aléatoire, tous les échantillons par le deuxième opérateur.
Continuer, de cette manière, jusqu’à ce que tous les opérateurs aient effectué les mesures.
Répéter les étapes de 2 à 4, en effectuant des nouvelles séries de mesures (essais) sur l’ensemble d’échantillons (les précédents résultats de mesure ne doivent plus être accessibles aux opérateurs). Noter les résultats sur la feuille de relevé donnée dans la figure 3.

-
Calculer:
pour chaque échantillon l’étendue de chaque opérateur.
l’étendue moyenne de chaque opérateur (\(\bar{R}_A, \bar{R}_B, ...\)) et l’étendue moyenne globale (\(\bar{R}\)).
la limite de contrôle sur la carte de contrôle des étendues. (Remarque: Les étendues qui dépassent la limite de contrôle supérieure doivent être éliminés et ensuite les calculs refaits; il faut, bien évidemment, chercher les causes de ces éventuels dépassements).
la moyenne des résultats de chaque opérateur et l’étendue de ces moyennes (\(\bar{X}_{DIFF}\)).
-
Calculer:
- La répétabilité, appelée aussi « Equipment Variation » (EV). Dans le cas où nb. opérateurs × nb. échantillons < 16, les valeurs du coefficient K1 utilisé pour le calcul de la répétabilité sont données dans le tableau 1.
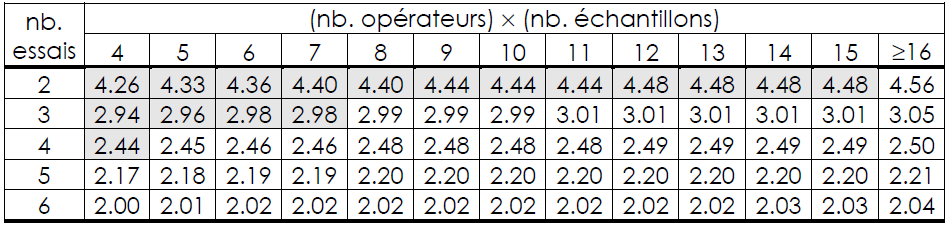
La reproductibilité, appelée aussi « Appraiser Variation » (AV).
La répétabilité et la reproductibilité, appelée aussi « Repeatability and reproducibility » (R&R).
Les estimateurs pour les écarts-type de répétabilité, de reproductibilité et de R&R: \(\sigma_{EV}\); \(\sigma_{AV}\); \(\sigma_{R \& R}\).
Calculer le coefficient de capabilité du système de mesure. Exprimer la variation de R&R comme un pourcentage de l’Intervalle de Tolérance (IT). Une meilleure solution c’est d’exprimer cette variation comme un pourcentage de la variabilité du processus. Cette dernière solution a l’avantage de permettre une certaine indépendance vis-à-vis de la limite de tolérance qui peut être parfois assez arbitraire.
Analyser les résultats et effectuer si besoin les actions correctives nécessaires.
2.2 Coefficients de capabilité
L’objectif d’une étude de R&R est de déterminer si le système de mesure est apte à effectuer les mesures. Pour répondre à cette question, il est nécessaire de calculer le coefficient de capabilité du système de mesure (\(C_{IM}\)). Habituellement, les critères retenus pour juger l’aptitude d’un système de mesure à effectuer les mesures sont illustrés dans le tableau 2:

2.2.1 Coefficient de capabilité \(C_{IM(1)}\)
Le coefficient de capabilité \(C_{IM(1)}\) exprime la variation du système de mesure comme une proportion de la variation totale mesurée (voir la figure 4):
\[\begin{equation} \tag{2.3} C_{IM(1)}= \frac{\sigma_{R \& R}}{\sigma_{T}} \end{equation}\]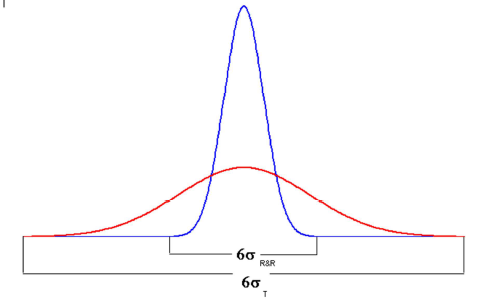
Remarque: Lorsque l’on ne dispose pas d’une estimation de l’écart-type total (\(\sigma_{T}\)) à partir de l’historique du processus, on peut utiliser en dernière instance les données de l’étude R&R pour cela. Ainsi, une estimation de l’écart-type total serait:
\[\begin{equation} \tag{2.4} \sigma_{T} = \frac{\bar{R}}{d_2} \end{equation}\]Pourtant, cette solution n’est pas tout à fait recommandable au vu du nombre réduit d’échantillons utilisés dans le cadre de l’étude R&R.
2.2.2 Coefficient de capabilité \(C_{IM(2)}\)
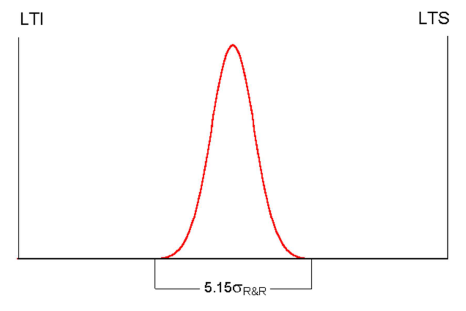
Le coefficient de capabilité \(C_{IM(2)}\) exprime la variation du système de mesure comme une proportion de l’intervalle de tolérance (voir la figure 5):
\[\begin{equation} \tag{2.5} C_{IM(2)}= \frac{5.15 \times \sigma_{R \& R}}{LTS-LTI}=\frac{5.15 \times \sigma_{R \& R}}{IT} \end{equation}\]où: \(LTS\) et \(LTI\) sont respectivement la limite supérieure et inférieure de l’intervalle de tolérance (\(IT\)).
Remarques:
La modification de l’intervalle de tolérance (réalisée lors d’une dérogation demandée par le client par exemple), conduit au changement de l’indicateur de capabilité (\(C_{IM(2)}\)) - voir l’équation (2.5). Ainsi, un système de mesure jugé non-capable, pourrait par l’élargissement de l’intervalle de tolérance devenir capable sans avoir pour autant enregistré une amélioration quelconque. Ceci représente un inconvénient majeur de cet indicateur.
L’indicateur de capabilité \(C_{IM(2)}\) s’avère très pratique lorsque l’on est confronté au problème de prise de décision concernant l’acceptabilité ou pas d’une certaine caractéristique mesurée (voir la figure 6).
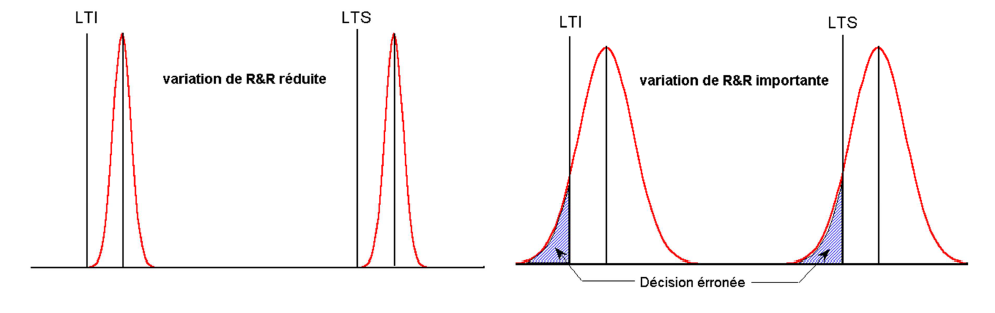
On peut constater que plus grande est la variabilité de R&R et plus grand est le risque de commettre une erreur décisionnelle.
2.3 Effet de la variation de R&R sur l’estimation de la capabilité du processus
La capabilité observée du processus est définie en comparant l’intervalle de dispersion d’un processus statistiquement stable avec l’intervalle de tolérance. Le coefficient de capabilité observée du processus (noté \(C_{p_o}\)) est donné par:
\[\begin{equation} \tag{2.6} C_{p_O}= \frac{IT}{6 \times \sigma_{T}} \end{equation}\]Évidemment, toute réduction de la variation de R&R conduit à la réduction de la variation totale (voir l’équation (2.2)) et donc implicitement à l’augmentation du coefficient de capabilité observée du processus (voir l’équation (2.6)). Toutefois, la capabilité réelle du processus est:
\[\begin{equation} \tag{2.7} C_{p_R}= \frac{IT}{6 \times \sigma_{Processus}} \end{equation}\]On en déduit que:
\[\begin{align} \frac{C_{p_O}}{C_{p_R}} & = \frac{\sigma_{Processus}}{\sigma_{T}} = \frac{\sqrt{\sigma_{T}^2-\sigma_{R \& R}^2}}{\sigma_{T}} = \\ & = \sqrt{1-\left(\frac{\sigma_{R \& R}}{\sigma_{T}} \right)^2} = \sqrt{1 - C_{IM(1)}^2} \tag{2.8} \end{align}\]La figure 7, traduit cette dépendance entre la capabilité réelle et observée d’un processus selon les valeurs de \(C_{IM(1)}\).
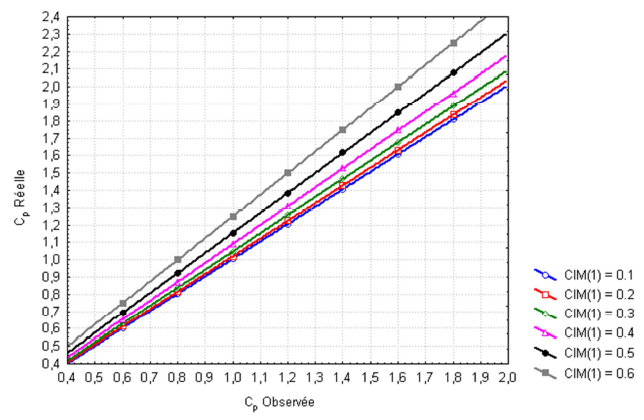
De la même manière, on peut écrire :
\[\begin{align} \frac{C_{p_O}}{C_{p_R}} & = \sqrt{1-\left(\frac{\sigma_{R \& R}}{\sigma_{T}} \right)^2} = \\ & = \sqrt{1-\left( \frac{5.15 \times \sigma_{R \& R}}{IT} \right)^2 \times \left( \frac{{IT}}{5.15 \times \sigma_{T}} \right)^2} = \\ & = \sqrt{1-C_{IM(2)}^2 C_{p_O}^2 \left( \frac{6}{5.15} \right)^2} \tag{2.9} \end{align}\]La figure 8, traduit cette dépendance entre la capabilité réelle et observée d’un processus selon les valeurs de \(C_{IM(2)}\).
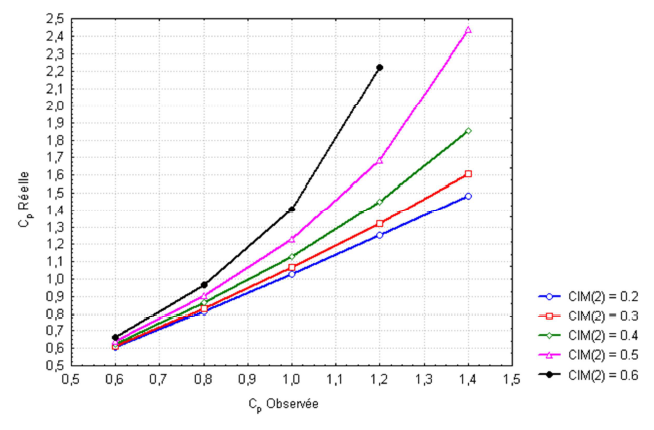
En comparant les figures 7 et 8 on constate que :
L’influence de la variation de R&R sur l’estimation de la capabilité réelle du processus est réduite si le coefficient de capabilité du système de mesure est inférieure à 30 %.
Le coefficient de capabilité \(C_{IM(1)}\) est plus robuste que le coefficient de capabilité \(C_{IM(2)}\).
A première vue, il peut paraître surprenant que l’influence de la variation de R&R est plus réduite pour les processus ayant des faibles capabilités. Cela nous indique que le point le plus important dans ce cas est d’améliorer le processus plutôt que d’agir sur le système de mesure.
La variabilité de R&R devient plus dérangeante quand on est en présence d’un processus de bonne capabilité.
2.4 Relations entre les coefficients de capabilité
Les coefficients de capabilité \(C_{IM(1)}\), \(C_{IM(2)}\) et \(C_{p_o}\) ne sont pas indépendants. Il suffit de connaître deux parmi eux pour en déterminer le troisième.
Ainsi, par exemple, si l’on suppose connus les coefficients de capabilité du système de mesure (\(C_{IM(1)}\) et \(C_{IM(2)}\)), alors on peut déduire le coefficient de capabilité observé du processus comme suit:
à partir de l’équation (2.3) on déduit que : \(\sigma_{T} = \frac{\sigma_{R \& R}}{C_{IM(1)}}\)
à partir de l’équation (2.5) on déduit que: \(IT = \frac{5.15 \times \sigma_{R \& R}}{C_{IM(2)}}\)
en remplacant \(\sigma_{T}\) et \(IT\) dans l’équation (2.6), on obtient:
2.5 Comment planifier une étude R&R ?
La planification d’une étude R&R doit tenir compte des aspects suivants:
-
Comment et quand un instrument de mesure doit être calibré ? Idéalement, un instrument de mesure doit être soumis au calibrage avant le démarrage de l’étude et par la suite non recalibré jusqu’à la fin de l’étude. Si ceci n’est pas possible, des variations dues au calibrage peuvent être rajoutées aux autres sources de variations. Chaque opérateur doit bien connaître et appliquer la procédure de calibrage. Toute indication de la présence d’une importante variation due au calibrage doit être impérativement accompagnée des actions correctives. Il faut savoir que :
S’il faut calibrer l’instrument de mesure après chaque mesure effectuée, alors la variabilité due au calibrage et la variabilité due à la répétabilité vont s’ajouter.
Si chaque opérateur doit calibrer l’instrument de mesure avant d’effectuer une série de mesures, alors la variation de répétabilité et la variation due au calibrage vont s’ajouter.
Parfois, la planification des opérateurs est telle que chaque opérateur doit exécuter successivement ses séries de mesures (ainsi l’opérateur A, par exemple, effectue la première série des mesures dans un ordre aléatoire, ensuite il aborde, toujours dans un ordre aléatoire, la deuxième série des mesures, et ainsi de suite). Dans cette situation, si chaque opérateur effectue le calibrage de l’instrument de mesure avant de commencer les mesures, la variation due au calibrage va s’ajouter à la variation de reproductibilité.
Combien d’opérateurs doivent participer à l’étude ? Une attention particulière doit être accordée au nombre d’opérateurs employés dans l’étude. Certains instruments de mesure ne nécessitent pas la présence d’un opérateur (les instruments de mesure automatiques, par exemple). Il est recommandable de considérer pour l’étude de R&R de ce type d’instruments, qu’un seul opérateur a été utilisé. Dans le cas où un seul opérateur effectue les mesures, il est impossible de déterminer quelle est son influence dans l’opération de mesure. Néanmoins, il est souhaitable d’utiliser au moins deux opérateurs. Pour améliorer d’avantage la précision des estimations, il est bien de faire appel à trois ou quatre opérateurs (un nombre plus important d’opérateurs complique sensiblement l’interprétation des résultats). Le groupe d’opérateurs participant à l’étude R&R doit être représentatif pour l’ensemble d’opérateurs de l’entreprise. Ces opérateurs doivent être des professionnels et avoir le même niveau des connaissances techniques. Il ne faut jamais mettre dans le même groupe, des opérateurs ayant une formation insatisfaisante avec des opérateurs expérimentés.
Combien d’échantillons doivent être mesurés ? Le nombre d’échantillons le plus courant en pratique est 10. En tout cas, il faut choisir un nombre d’échantillons suffisant pour que : (nb. échantillons) × (nb. opérateurs) > 15. Si cette condition ne peut pas être respectée, il faut augmenter le nombre des essais exécutées par chaque opérateur.
Comment choisir les échantillons ? Les échantillons doivent être représentatifs pour l’ensemble d’opérations de mesure effectuées usuellement. Il faut rester conscient que le nombre réduit d’échantillons ne peut pas nous donner une image claire du processus de production et, par conséquent, ils vont servir uniquement pour la représentation de l’étendue de mesure.
Combien d’essais doivent être exécutées par chaque opérateur ? Le nombre d’échantillons et d’opérateurs retenus pour l’étude de R&R vont déterminer le nombre d’essais nécessaires. Le plus souvent deux essais sont suffisants.
Faut-il utiliser des mesures individuelles ou des moyennes ? Il faut effectuer les mesures de la même manière qu’elles sont réalisées pour la procédure standard d’évaluation du produit. Si une seule mesure est utilisée pour vérifier le produit alors il va falloir utiliser une seule mesure aussi pour l’étude R&R. Si plusieurs mesures sont réalisées et ensuite leur moyenne est calculée, il faut faire de même pour l’étude R&R. En tout cas, même si les moyennes sont utilisées, il faut enregistrer quand même les valeurs individuelles. Ces valeurs individuelles peuvent s’avérer très utiles pour le diagnostic.
-
Qu’est-ce qu’il faut faire quand on a une seule limite de tolérance ? Certaines grandeurs physiques ne présentent pas deux limites de tolérance. Par conséquent, il n’est plus possible d’utiliser le coefficient de capabilité \(C_{IM(2)}\). Deux alternatives se présentent :
Utiliser le coefficient de capabilité \(C_{IM(1)}\).
Utiliser une deuxième limite de tolérance artificielle pour déterminer un intervalle de tolérance. Dans ce cas, il faut éviter de considérer que la limite de tolérance inférieure (LTI) est égale à zéro, seulement parce que la caractéristique mesurée ne présente qu’une limite de tolérance supérieure. Il faut noter que « l’absence de spécification » et « spécification nulle » c’est n’est pas tout à fait la même chose.
-
Comment peut-on savoir si la discrimination des résultats de mesure est inadéquate ? La discrimination des résultats de mesure est l’habilité de l’instrument utilisé de faire la distinction entre deux valeurs proches et ceci d’une manière fiable. Quelques règles très simples nous permettent de savoir s’il y a des problèmes au niveau de la discrimination des résultats de mesure. Nous présentons ici seulement deux :
Moins de trois étendues (calculées sur la feuille R&R) ont des valeurs inférieures à la limite de contrôle supérieure.
Plus que 25 % des étendues sont nuls.
-
Qu’est-ce qu’il faut faire dans le cas où la discrimination des résultats de mesure n’est pas adéquate ? Seulement trois solutions sont possibles :
Effectuer les mesures et enregistrer les résultats avec autant de décimales que l’instrument de mesure affiche. Utiliser, par contre, au niveau des calculs seulement la première décimale.
Utiliser des instruments de mesure plus performants qui peuvent mesurer des écarts plus réduits.
Si aucune solution n’est pas envisageable à court terme, il faut vivre avec. Il faut quand même signaler la situation et en tenir compte. L’impact de cette situation dépend de la capabilité du processus pour la caractéristique mesurée.
Peut-on analyser par une étude R&R plusieurs instruments de mesure ? En mode normal, chaque étude R&R est menée pour un seul instrument de mesure. Certains instruments de mesure, comme les micromètres par exemple, peuvent être étudiés à plusieurs par une seule étude R&R.
Comment peut-on éviter des influences indésirables pendant le déroulement de l’étude de R&R ? En prenant soin de noter tous les détails et les circonstances de l’étude. Un journal de bord est très indiqué.
2.6 Que faire dans le cas des mauvais résultats ?
Si les résultats de l’étude R&R ne sont pas satisfaisants (mauvaise capabilité du système de mesure), il est nécessaire de savoir quelle est la cause/les causes responsable(s) de la situation. Est-ce que c’est l’instrument de mesure (c.à.d. la répétabilité) la source de la variabilité excessive ? Est-ce que c’est l’opérateur (c.à.d. la reproductibilité) le responsable ? C’est la combinaison de deux ? Connaître la réponse à ces questions nous donne la possibilité de savoir comment faut-il réagir.
Des mauvais résultats ont à l’origine soit l’instrument de mesure, soit l’opérateur soit les deux.
Des détails offerts par le constructeur de l’instrument de mesure peuvent conduire à la conclusion que celui-ci ne peut être amélioré aucunement. Dans ce cas, il faut passer à l’étape 3 (voir ci-dessus).
Si la plupart de la variation est due à la répétabilité, un moyen d’augmenter la précision de l’instrument de mesure est d’utiliser la moyenne de plusieurs résultats pour la même caractéristique mesurée. Travailler avec les moyennes, réduit la proportion de la répétabilité dans la variation de R&R par la racine carrée du nombre des valeurs utilisées pour le calcul de la moyenne. Pourtant, il faut faire attention, car cette procédure ne doit pas être utilisée si elle n’est pas aussi employée habituellement lors de la réalisation des mesures.
Quand les opérateurs (c.à.d. la reproductibilité) sont la cause de la grande variabilité observée, il faut le former d’avantage.
Les tolérances peuvent être trop sévères.
Avons-nous des éléments pour suspecter une variabilité additionnelle due au manque de calibrage ou à une variabilité intra-échantillon élevée ? Si oui, il faut être capable de déterminer si les mauvais résultats ne sont pas dus à ces facteurs. Il est nécessaire d’entreprendre des études supplémentaires afin de les isoler.
Si la capabilité du processus est adéquate (> 1.33), la mauvaise variabilité de R&R n’est pas un inconvénient majeur ni une priorité immédiate. Si la capabilité du processus est à la limite d’acceptabilité (entre 1 et 1.33), la variation indésirable du système de mesure peut faire la différence entre le cas où le processus est jugé capable et le cas où il est jugé inacceptable. Si la capabilité du processus est mauvaise (< 1), il faut envisager d’améliorer le processus et la système de mesure en même temps (avec la priorité accordée au système de mesure).
Il est toujours souhaitable d’utiliser plusieurs indicateurs de capabilité pour bien comprendre la situation et pour déceler les futures priorités.
2.7 Conclusion
L’approche de l’amélioration continue est fondamentale dans le cadre de la mesure. En même temps c’est un cadre où il n’y a pas de solution standard universelle. Chaque dispositif de mesure doit être analysé séparément avec beaucoup d’attention et la meilleure solution doit être adoptée.
Les études R&R donnent la possibilité d’améliorer les processus. L’utilisation d’un coefficient qui quantifie les performances du système et d’un critère d’acceptation ne signifie pourtant qu’il faut tolérer des situations qui peuvent être corrigées. Même si, suite à une étude R&R, le système de mesure ne s’avère pas une priorité immédiate, la démarche d’amélioration continue stipule que des actions correctives doivent être programmées et exécutées dans le temps.
Dans la démarche exposée dans ce cours, on a ignoré (considéré comme négligeables) certaines composantes de la variation totale mesurée (elles ont été intégrés dans la variation du processus). Pour compléter l’étude R&R il est important également d’évaluer l’impact du calibrage, de la stabilité et de la linéarité du système de mesure sur la qualité des résultats obtenus.
2.8 Exemple applicatif : Poinçons d’acier
On veut réaliser une étude R&R pour évaluer l’aptitude d’un micromètre à mesurer les hauteurs des poinçons d’acier. Trois opérateurs ont mesuré trois fois chacun dix poinçons sélectionnés au hasard de la fabrication. Les résultats (en \(10^{-3}\) pouces) sont disponibles dans le fichier RR_micro.xlsx (voir la section Base de données dans Moodle). L’intervalle de tolérance spécifié pour les mesures est de \(\pm 2 \times 10^{-3}\) pouces.
Remarque: Il est conseillé de mettre le fichier de données et les fichier de code R (.r) dans le même répertoire (pour éviter de préciser tout le chemin d’accès vers le fichier de données lors de son ouverture).
Le code R ci-dessous permet d’importer les données de cet exemple et d’afficher les 10 premières lignes du fichier:
# Importation de données
# ======================
library(readxl)
dataset <- read_excel("RR_micro.xlsx")
attach(dataset)
# Affichage de l'entête de données
# ================================
library(kableExtra)
head(dataset,n=10L) %>% # 10 premières lignes affichées
kbl(align = "c") %>%
kable_classic_2(full_width = F)| Operateur | Piece | Essai | Hauteur |
|---|---|---|---|
| 1 | 1 | 1 | 496 |
| 2 | 1 | 1 | 497 |
| 3 | 1 | 1 | 497 |
| 1 | 2 | 1 | 498 |
| 2 | 2 | 1 | 498 |
| 3 | 2 | 1 | 497 |
| 1 | 3 | 1 | 498 |
| 2 | 3 | 1 | 497 |
| 3 | 3 | 1 | 496 |
| 1 | 4 | 1 | 497 |
Tableau n°1 - Entête de données (10 premières lignes)
Remarque: Par rapport à la feuille standard R&R (voir la figure 3), on constate que le tableau de données ci-dessus est structuré de manière différente: la colonne Operateur (désigne l’opérateur qui fait la mesure) est composée des valeurs dans l’ensemble {1,2,3} (car 3 opérateurs dans cette étude); la colonne Piece (désigne la pièce mesurée) est composée des valeurs dans l’ensemble {1,…,10} (car 10 opérateurs dans cette étude); la colonne Essai (désigne la répétition de la mesure effectué par l’opérateur sur la même pièce) est composée des valeurs dans l’ensemble {1,2,3} (car 3 répétitions pour chaque opérateur dans cette étude); enfin, la colonne Hauteur (désigne la mesure effectué) donne la hauteur mesurée du poinçon (en \(10^{-3}\) pouces). Cette structuration des données est nécessaire lorsque l’on veut utiliser le logiciel R pour faire les calculs.
On utilise la fonction ss.rr du package SixSigma pour les calculs (pour plus de détails voir l’aide de cette fonction):
library(SixSigma)
resRR<-ss.rr(
var=Hauteur, #variable qui contient les résultats
part=Piece, #variable qui contient l'index des pièces
appr=Operateur, #variable qui contient l'index des opérateurs
sigma = 5.15, #pour des intervalles de 99%
#(sigma = 6 si l'on veut des intervalles de 99.73%)
tolerance = 4, #intervalle de tolérance +/-2
data=dataset, #nom du jeu de données dans R
main = "Etude R&R micromètre", #titre pour la sortie graphique
sub = "", #sous-titre éventuel pour la sortie graphique
alphaLim = 0.05, #limite pour la prise en compte d'une interaction
errorTerm = "repeatability", #variance considérée comme résiduelle dans le modèle avec
#interaction Opérateur:Pièce
digits = 4, #nombre de décimales pour les résultats
method = "crossed", #type d'analyse
print_plot = TRUE, #affichage des graphiques
signifstars = TRUE
)#> Complete model (with interaction):
#>
#> Df Sum Sq Mean Sq F value Pr(>F)
#> Piece 9 122.40 13.600 9.344 1.04e-08 ***
#> Operateur 2 2.49 1.244 0.855 0.430
#> Piece:Operateur 18 16.40 0.911 0.626 0.865
#> Repeatability 60 87.33 1.456
#> Total 89 228.62
#> ---
#> Signif. codes:
#> 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
#>
#> alpha for removing interaction: 0.05
#>
#>
#> Reduced model (without interaction):
#>
#> Df Sum Sq Mean Sq F value Pr(>F)
#> Piece 9 122.40 13.600 10.226 3.08e-10 ***
#> Operateur 2 2.49 1.244 0.936 0.397
#> Repeatability 78 103.73 1.330
#> Total 89 228.62
#> ---
#> Signif. codes:
#> 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
#>
#> Gage R&R
#>
#> VarComp %Contrib
#> Total Gage R&R 1.329915 49.38
#> Repeatability 1.329915 49.38
#> Reproducibility 0.000000 0.00
#> Operateur 0.000000 0.00
#> Part-To-Part 1.363343 50.62
#> Total Variation 2.693257 100.00
#>
#> VarComp StdDev StudyVar %StudyVar
#> Total Gage R&R 1.329915 1.153219 5.939079 70.27
#> Repeatability 1.329915 1.153219 5.939079 70.27
#> Reproducibility 0.000000 0.000000 0.000000 0.00
#> Operateur 0.000000 0.000000 0.000000 0.00
#> Part-To-Part 1.363343 1.167623 6.013257 71.15
#> Total Variation 2.693257 1.641115 8.451741 100.00
#> %Tolerance
#> Total Gage R&R 148.48
#> Repeatability 148.48
#> Reproducibility 0.00
#> Operateur 0.00
#> Part-To-Part 150.33
#> Total Variation 211.29
#>
#> Number of Distinct Categories = 1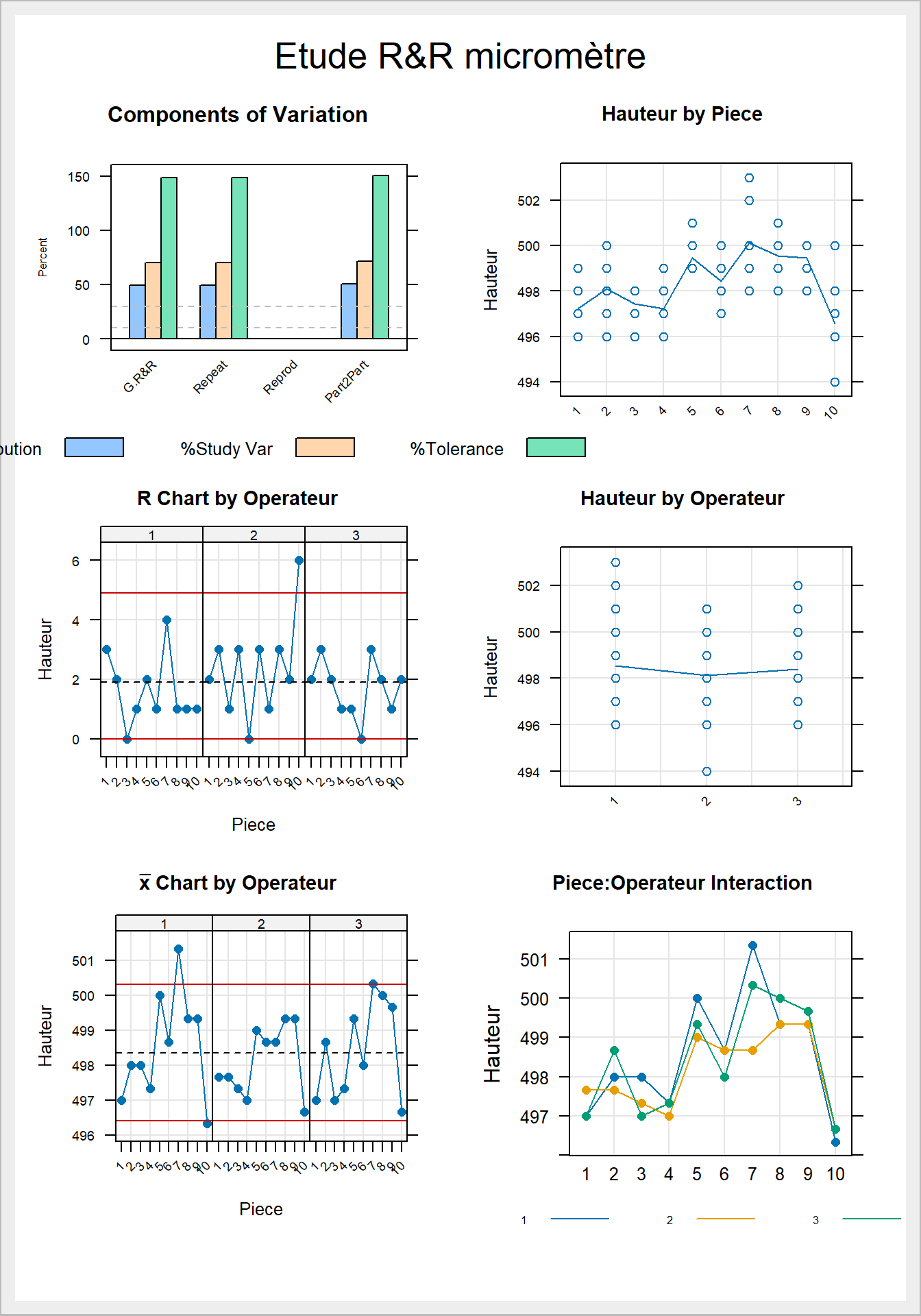
Figure 1: Résultats graphiques pour l’étude R&R
Analyse des résultats:
On constate tout d’abord que le système de mesure n’est pas capable (\(CIM_{(2)}=148.48\% > 30\%\)).
Remarques:
1. Si la tolérance avait été de \(\pm 5 \times 10^{-3}\) pouces, alors on aurait obtenu un coefficient de capabilité \(CIM_{(2)}=59.39\%\) (en choisissant tolerance = 10 dans la fonction ss.rr()). On voit bien ici, que sans apporter aucun changement au système de mesure, sa capabilité s’est amélioré sensiblement uniquement parce-que l’on a élargi l’intervalle de tolérance! Ceci, est l’inconvénient majeur de ce coefficient de capabilité.
2. On ne peut pas calculer le coefficient de capabilité \(CIM_{(1)}\) faute d’avoir \(\sigma_T\); une estimation de la variance totale apparaît dans le tableau Gage R&R (Total variation = 2.693257) mais il ne faut pas oublier que cet estimateur est très faible car calculé uniquement sur les 10 pièces utilisées dans cette étude; si toutefois on utilisait cet estimateur pour en déduire le coefficient de capabilité \(CIM_1=100\times\frac{\sigma_{R\&R}}{\sigma_T}\) on obtiendrait le résultat suivant:
(CIM1=100*(sqrt(resRR$varComp[which(rownames(resRR$varComp)=="Total Gage R&R"), which(colnames(resRR$varCom)=="VarComp")])/sqrt(resRR$varComp[which(rownames(resRR$varComp)=="Total Variation"), which(colnames(resRR$varCom)=="VarComp")])))#> [1] 70.27048et on peut constater que selon ce coefficient de capabilité aussi le système de mesure est inapte à l’utilisation que l’on veut lui donner (\(CIM_{(1)}\)=70.27048% > 30%).
3. Dans certaines études de cas, le processus analysé a fait l’objet d’une démarche d’amélioration de la qualité de type MSP (Maîtrise Statistique de Processus) et on dispose d’un coefficient de capabilité du processus. Cette information suplémentaire peut être expoloitée pour en déduire une valeur plus fiable de l’estimateur de l’écart-type total, car on sait que: $\(C_{p_o}=\frac{IT}{6\sigma_T}\). Par example, si on sait que la capabilité du processus est de 1.33, alors on déduit que \(\sigma_T=\frac{IT}{6C_{p_o}}=\frac{4}{6\times 1.33}=0.501253\). Par la suite, on déduit que \(CIM_{(1)}=100\times\frac{\sigma_{R\&R}}{\sigma_T}=100\times\frac{\sqrt{1.329915}}{0.501253}=230.07\%\).
Par conséquent, une analyse plus détaillée est nécessaire afin d’identifier les causes de la mauvaise capabilité constatée.
Dans un premier temps, on constate que le système de mesure représente 49.38% de la variabilité totale enregistrée dans les résultats (voir la colonne %Contrib pour Total Gage R&R dans le tableau Gage R&R). Cette variabilité est trop grande pour être acceptable. Lorsque l’on regarde de plus près, on voit que la variabilité de répétabilité est intégrallement responsable de ce mauvais résultat (voir la colonne %Contrib pour Repeatability dans le tableau Gage R&R). Le même constat peut être fait visuellement en regardant le graphique Components of Variation dans la figure 1. Par conséquent, on en déduit que le principal problème vient de l’instrument de mesure et non des opérateurs. On est renforcé dans cette conclusion en analysant le tableau ANAVAR (Complete model (with interaction)) où l’on peut remarquer que l’opérateur et l’interaction opérateur:pièce ne sont pas significatives statistiquement au seuil de significativité de 10% (p-values de 0.280 et respectivement de 0.865). Par conséquent, la variabilité due aux opérateurs peut être considérée comme négligeable par rapport à la variabilité due à l’instrument de mesure (Repeatability) qui est prise ici comme étant la variabilité résiduelle. La même conclusion reste valable aussi dans le cas du tableau ANAVAR Reduced model (without interaction) où l’on a supprimé l’interaction operateur:pièce (car non-significative) et attribué aux résidus la variabilité correspondante. Le fait que cette intéraction est non-significative est illustré dans le graphique Piece:Operateur Interaction de la figure 1. En effet, on peut voir que les traces des hauteurs moyennes pour les trois opérateurs ont à peu près le même profile, ce qui laisse sous-entendre que les opérateurs n’ont pas eu des difficultés à mesurer les pièces de la même manière. Par contre, on constate qu’il y a une variabilité qui est hautement significative (p-value = 1.23e-06): la variabilité de pièce à pièce (Piece). Ceci, signifie qu’il y a des variations d’une pièce à l’autre qui sont bien plus grandes que la variabilité de répétabilité enregistrée et qui ne peuvent pas être négligées (voir aussi le graphique Hauteur by piece dans la figure 1). Toutefois, dans les études R&R on ne se propose pas d’améliorer le procédé de fabrication de ces pièces, ceci étant l’objectif d’autres approches comme: l’optimisation par les plans d’expériences, la maîtrise statistique de processus, les plans de contrôle en réception, etc. N’oublions pas qu’ici on se concentre uniquement sur le système de mesure et les améliorations que l’on veut apporter concernent uniquement celui-ci. Le graphique Hauteur by Operateur montre aussi que les opérateurs ne sont pas à l’origine de la mauvaise capabilité constatée, car les dispersions de trois opérateurs semblent très similaires et leurs moyennes ne different pas substantiellement (l’opérateur 2 ayant une moyenne légèrement plus basse que les deux autres opérateurs). Le graphique des étendues R chart by Operateur montre que les opérateurs n’ont pas enregistré une dispersion trop élevée pour les mesures répétées sur les même pièces (un seul point dépasse la limite supérieure de contrôle - pour l’opérateur 2 lors de la mesure de la pièce 10 - ce qui peut être considéré comme une situation accidentelle). Par contre, la carte de contrôle de moyennes (\(\bar{X}\) Chart by Operator) montre que la plupart de points sont situés entre les deux limites de contrôle, ce qui signifie que l’instrument de mesure n’est pas capable de bien saisir les différence entre les pièces (c.à.d. que la dispersion de l’instrument de mesure est trop grande par rapport à la dispersion de pièce à pièce). Attention: n’oublions pas que les limites de contrôle de la carte de moyennes pour les études R&R sont calculées à l’aide de \(\bar{R}\) qui représente l’étendu moyen des mesures répétées sur la même pièce (traduisant la variabilité de l’instrument de mesure), alors que dans la Maîtrise Statistique de Processus (MSP), \(\bar{R}\) représente l’étendu moyen du processus (donc qui traduit la variabilité de pièce à pièce).
Conclusion: Après l’analyse effectuée ci-dessus, en corroborant tous les constats, on en déduit que si l’on veut améliorer la capabilité du système de mesure, on doit concentrer les efforts sur l’instrument de mesure utilisé (le micromètre). Remplacer le micromètre par un instrument de mesure plus précis, serait la solution la plus simple, mais on peut également envisager de changer la procédure de mesure actuellement en place: par exemple, des mesures répétées sur la même pièce et l’utilisation de la moyenne à la place des valeurs individuelles, permettrait d’améliorer la situation (car les moyennes sont moins dispersées que les valeurs individuelles).