추가 Random Effect

앞에서 랜덤 절편을 살펴보았지만, 클러스터마다 어떤 관측값이나 낮은 레벨의 covariate 효과도 변하게 할 수 있다. 이는 효과가 다른 관측값의 수준/값에 따라 변하도록 하는 interaction(교호작용) 개념과 동일하다.

적용

GPA 데이터에 돌아가서, 앞선 시각화를 상기해 보자. 학생들 사이의 차이를 강조하기 위해 애니메이션으로 표현해 보았다. 시간에 따라 일반적으로 증가하지만, 어떤 학생은 상대적으로 평평하거나 일직선이 아니다. 이러한 현상을 어떻게 포착할 수 있을까?

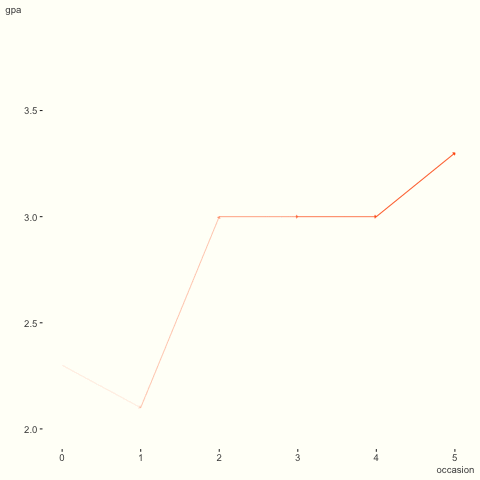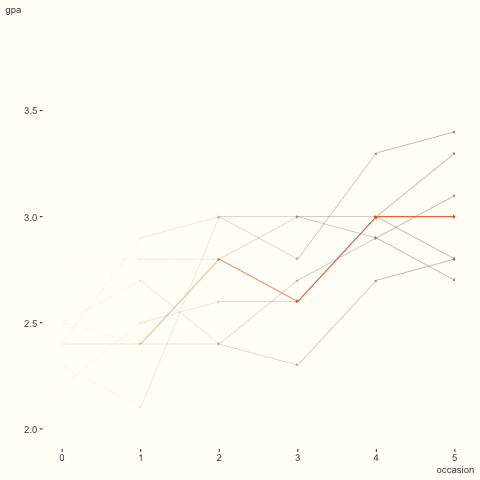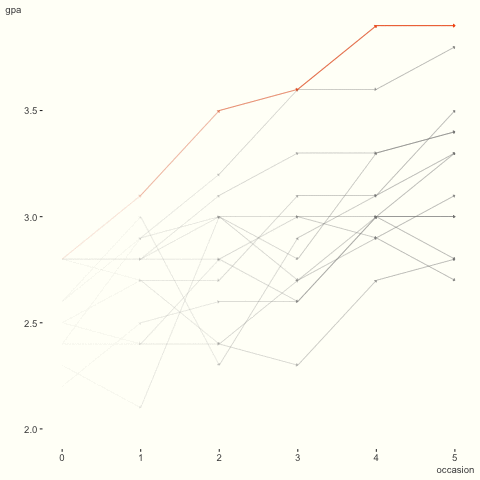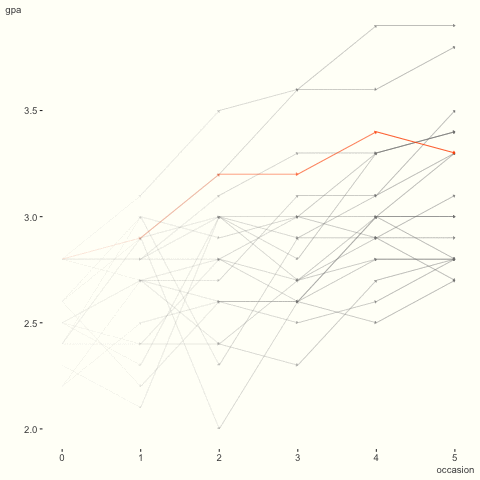
이 문제를 해결하기 위해, 절편뿐만 아니라 시간에 따른 변화도 학생에 따라 변할 수 있다고 가정해 보자. lme4 를 사용하면 바로할 수 있다.

gpa_mixed =  lmer(gpa ~ occasion + (1 + occasion | student), data = gpa)
summary(gpa_mixed)

꽤 쉽지 않은가? 괄호 안에서, 바 | 왼편에 대부분 모델링 함수¹²에서 하는 것처럼 모델 공식을 위치시키는 것이다. 결과를 보자.

term	value	se	lower_2.5	upper_97.5
Intercept	2.599	0.018	2.563	2.635
occasion	0.106	0.006	0.095	0.118

group	effect	variance	sd	var_prop
student	Intercept	0.045	0.213	0.491
student	occasion	0.005	0.067	0.049
Residual		0.042	0.206	0.460

이전에서처럼, 0 을 첫 학기로 하고 있으므로, 절편은 첫 학기의 평균 학점을 의미하게 된다. 이전과 같이 학기 계수는 한 학기의 학점변화량을 의미한다. 모형의 fixed effect 부분에 변화가 없으므로, 값은 전과 같게 된다.

절편 분산은 시작학기의 평점이 학생마다 얼마나 차이가 나는지를 의미한다. 학기 효과의 분산은 비교할 것이 없는 것 같지만, 기울기는 절편보다 더 스케일에 큰 차이가 있다. 학기에 대한 평균 기울기, 즉 fixed 효과는 0.11 이지만, 학생마다 절반 정도 차이가 난다. 따라서 대부분의 학생들이 0 을 가지는 flat effect 에서 population 평균의 두배 이상의 값 사이의 한 값을 가지리라 예상할 수 있다¹³.

절편과 기울기의 correlation 은 다른 흥미로운 포인트이다. 우리 경우는 -0.1 이다. 꽤 작은 편이지만 다른 correlation 과 해석은 비슷하다. 이 경우 절편값이 작을수록 기울기가 커지게 된다. 일반적으로 사람들 성적이 좋아지고 잘 못하는 사람은 개선될 여지가 더 많을 것이라는 것은 직관적이다. 하지만, 매우 약하고, 실제로는 여기에 큰 비중을 둘 필요가 없다.

개별 회귀모델과 비교

이러한 결과를 각 학생에 대해 분리된 회귀를 실행했을 때의 결과와 비교해보자. 다음에서 모든 학생들에 대한 절편과 기울기 계수의 분포를 볼 수 있다. occansion x student interaction¹⁴이 있는 fixed 효과모델에서 추정한 것과 같다는 것을 주목하라.

여기에서 우리는 mixed model 절편이 일반적으로 극단적이지 않음을 볼 수 있다, 즉, 분포 꼬리가 전체 효과쪽으로 당겨졌다. 기울기들도 마찬가지이다. 두 경우다 mixed model 은 by-group 추정치를 감소시켰는데, 다르게 취급했다면 이러한 시나리오에서 과적합되었을 것이다. 이러한 regularizing 효과는 mixed model¹⁵을 사용할 때 얻을 수 있는 또다른 보너스이다. 그룹마다 관측값이 많지 않고, 랜덤이팩트의 추정 분산이 작을 때 이러한 일이 일어난다. 다른 말로 하면, 그룹마다 정보가 적거나, 관측값 분산에 비해 그룹레벨 분산이 상대적으로 작으면, mixed model 은 group-specific effect 가 전체 population effect 에 가까운 값으로 제공할 것이다. 이러한 맥락에서 mixed model group 계수들은 우리가 모른다는 것을 더 잘 반영한다. 반대로, with more pronounced group effec, 전체 효과에 대한 우리의 불확실성은 증가한다.

다음은 앞서 보았던 GPA 모델의 결과에 기반한 시뮬레이션 데이터의 다양한 세팅 아래에서 비슷한 데이터에 어떤 일들이 일어나는 지를 보여준다. 맨 왼쪽은 현재 데이터 세팅을 바로 보여준다. 그 다음, 원 결과를 따라 네가지 세팅이 있다. 처음은 학생마다 훨씬 많은 측정값이 있다면 어떤 일이 일어나는지를 보여준다. 다음은, 절편과 기울기 분산을 증가하고 잔차분산을 감소시키지만 샘플 사이즈를 원 데이터와 같게 유지한다. 두 경우 다 mixed model 의 regulizaing effect 가 더 작다. 랜덤 계수들은 개별 회귀 결과와 매우 유사하다. 그리고, 데이터를 동일하게 유지하지만, 학생당 4 관측값만 있을 때, 학생당 결과에서 변동성이 더 커서 mixed model 에서 shrinkage 가 상대적으로 덜 일어난다. 마지막으로 학생당 occasions 숫자를 더하지만 (10), 시간이 흐르면서 유실도 있어서 대략 데이터 양은 비슷하지만, 불균형이다. 이 주제에 대한 더 보고 싶으면, 내 게시글을 여기 에서 보라.

효과 시각화

우리 예측값들을 시각적으로 비교해보자. 첫번째로 선형 회귀 적합이 있다. 시작점과 기울기가 모든 사람에게 있어 같다고 가정하자. 우리가 mixed model 에 subject specific 효과가 있는 조건부 예측을 더한다면, subject specific 예측을 할 수 있어서 모델의 실용성을 크게 증가시킨다.

반면에 그룹별 접근법은 모든 사람을 독립적으로 다루기 때문에 더 노이지하다. 학생이 더 많으면 mixed model 대비 기울기가 아래를 향하거나 평평해질 것이다. 하지만, mixed model 은 3 개의 기울기만 음수로 추정이 된다.

요약

이러한 것들을 왜 richly parameterized linear models 로 불리는지 감을 잡았을 것이다. 표준 회귀에 비해 모델의 불확실성 소스에 대한 우리의 이해에 더해지는 추가 분산 파라미터를 얻고, subject specific 효과와 correlation 을 얻고, 이 정보를 이용하여 훨씬 좋은 예측값을 얻을 수 있다. 좋아하지 않을 이유가 없다.

Exercises for Random Slopes

Sleep revisited

Run the sleep study model with random coefficient for the Days effect, and interpret the results. What is the correlation between the intercept and Days random effects? Use the ranef and coef functions on the model you’ve created to inspect the individual-specific effects. What do you see?

library(lme4)
data("sleepstudy")

In the following, replace model with the name of your model object. Run each line, inspecting the result of each as you go along.

re = ranef(model)$Subject
fe = fixef(model)

apply(re, 1, function(x) x + fe) %>% t()

The above code adds the fixed effects to each row of the random effects (the t just transposes the result). What is the result compared to what you saw before?

Simulation revisited

The following shows a simplified way to simulate some random slopes, but otherwise is the same as the simulation before. Go ahead and run the code.

set.seed(1234)  # this will allow you to exactly duplicate your result
Ngroups = 50
NperGroup = 3
N = Ngroups * NperGroup
groups = factor(rep(1:Ngroups, each = NperGroup))
re_int = rnorm(Ngroups, sd = .75)
re_slope = rnorm(Ngroups, sd = .25)
e = rnorm(N, sd = .25)
x = rnorm(N)
y = (2 + re_int[groups]) + (.5 + re_slope[groups]) * x + e

d = data.frame(x, y, groups)

This next bit of code shows a way to run a mixed model while specifying that there is no correlation between intercepts and slopes. There is generally no reason to do this unless the study design warrants it¹⁶, but you could do it as a step in the model-building process, such that you fit a model with no correlation, then one with it.

model_ints_only = lmer(y ~ x + (1|groups), data = d)

model_with_slopes = lmer(y ~ x + (1|groups) + (0 + x|groups), data = d)

summary(model_with_slopes)

confint(model_with_slopes)

library(ggplot2)

ggplot(aes(x, y), data = d) +
  geom_point()

Compare model fit using the AIC function, e.g. AIC(model). The model with the lower AIC is the better model, so which would you choose?

---

12. Technically the intercept is assumed but you should keep it for clarity.↩︎

13. In case it’s not clear, I’m using the fact that we assume a normal distribution for the random effect of occasion. A quick rule of thumb for a normal distribution is that 95% falls between \(\pm\) 2 standard deviations of the mean.↩︎

14. This is just one issue with a fixed effects approach. You would have to estimate 400 parameters, but without anything (inherently) to guard against overfitting. The so-called fixed effects model from the econometrics perspective gets around this by demeaning variables that vary within groups, i.e. subtracting the per group mean. This is also equivalent to a model adding a dummy variable for the groups, though it’s a computationally more viable model to fit, as one no longer includes the grouping variable in the model (not really a concern with data FE models are actually applied to and it being what year it is). But while it controls for group level effects, we still cannot estimate them. Traditional approaches to fixed effects models also do not have any way to incorporate group-specific slopes, except perhaps by way of an interaction of a covariate with the cluster, which brings you back to square one of having to estimate a lot of parameters. For more about FE models and their issues, see my document on clustered data approaches, and Bell et al. (2016). Fixed and Random effects: making an informed choice.↩︎

15. This phenomenon is also sometimes referred to as partial pooling. This idea of pooling is as in ‘pooling resources’ or borrowing strength. You have complete pooling, which would be the standard regression model case of ignoring the clusters, i.e. all cluster effects are assumed to be the same. With no pooling, we assumes the clusters have nothing in common, i.e. the separate regressions approach. Partial pooling is seen in the mixed model scenario, where the similarity among the clusters is estimated in some fashion, and data for all observations informs the estimates for each cluster. I’ve never really liked the ‘pooling’ terminology, as regularization/shrinkage is a more broad concept that applies beyond mixed models, and I’d prefer to stick to that. In any case, if interested in more, see practically anything Andrew Gelman has written on it, and the pool-no-pool document here.↩︎

16. I personally have not come across a situation where I’d do this in practice. Even if the simpler model with no correlation was a slightly better fit, there isn’t much to be gained by it.↩︎