베이지언 방법
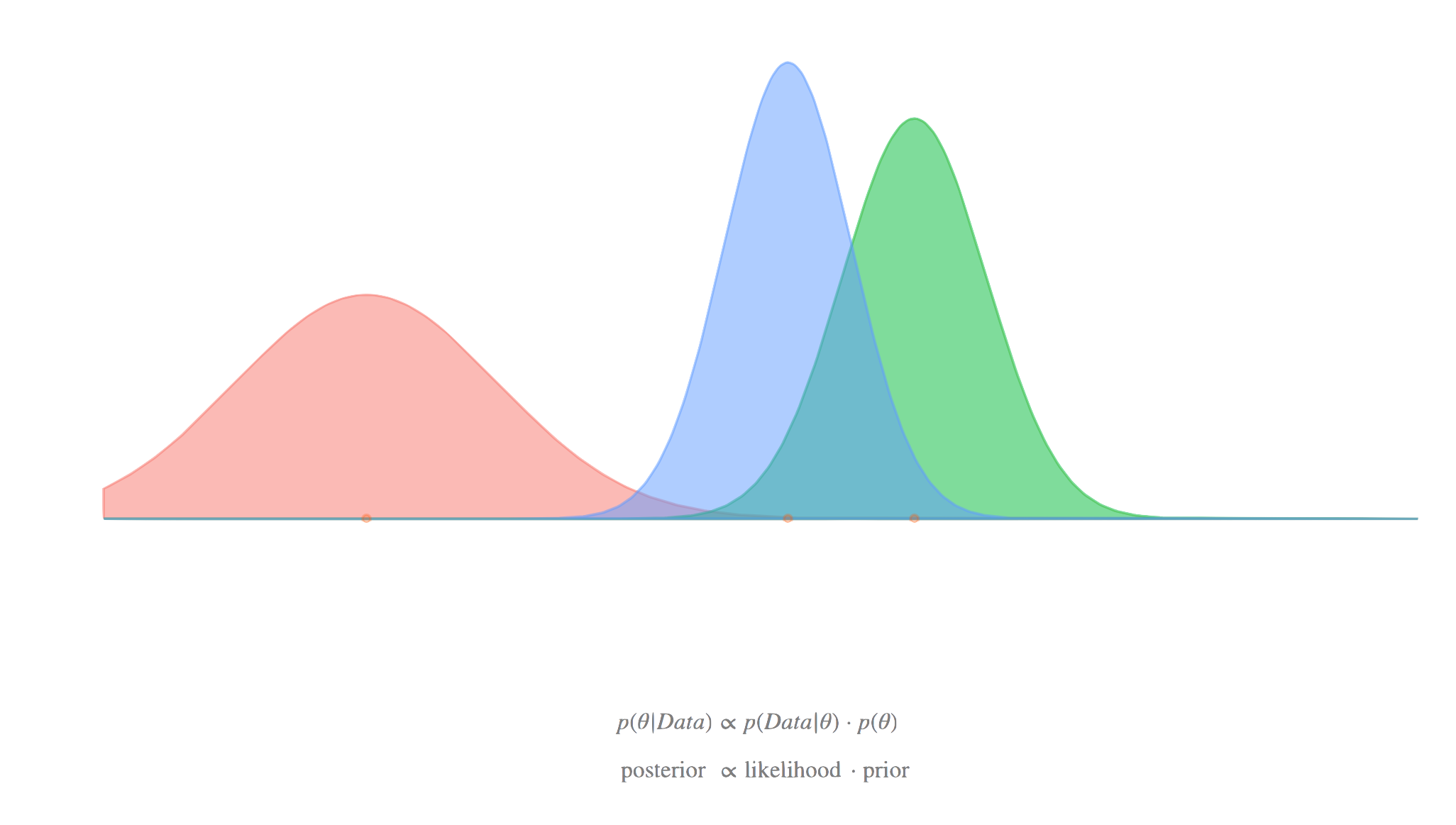
mixed model 에서는 계수들이 분포에서 온 것으로 가정한다. Mixed model 에는 ‘fixed’ 효과도 있지만, 랜덤 컴포넌트가 있다는 것이 큰 특징이다. 이제 표준 회귀모델, 즉, 클러스터링 없는 모델을 고려하자. 이 모델로도 같은 것을 할 수 있다, 즉, 계수가 고정되지 않고 랜덤이다. 목표는 분포의 요약, 예를 들어 평균이 아니라 분포를 이해하고 이에 집중하는 것이다. 이 분포의 평균 (혹은 다른 central tendancy)에 대해서, 표준 모델에서 fixed 효과에 대해 하는 것과 같이 취급할 수 있다.
따라서 mixed model 에서 랜덤효과에 관해 생각한 바를 베이지언 방법론에 관한 자연스러운 변환버전처럼 사용할 수 있다. 베이지언 방법에서 모든 파라미터는 분포에서 랜덤 추출한다. 가장 좋아하는 모델의 베이지언 버전을 사용하는 것은 표준모델의 문법 이외의 노력이 필요하지 않다. 다음은 brms 패키지에서 표준선형회귀와 mixed model 이지만, rstanarm 에서와 같다.
brms::brm(gpa ~ occasion, data = gpa)
brms::brm(Reaction ~ Days + (1 + Days | Subject), data = sleepstudy)
rstanarm::stan_lm(gpa ~ occasion, data = gpa)
rstanarm::stan_lmer(Reaction ~ Days + (1 + Days | Subject), data = sleepstudy)베이지언 모델을 실행하는 것은 쉬울 뿐 아니라 문법적으로 동일하다! mixed model 을 사용하면 데이터를 더 깊이 이해할 수 있듯이, 베이지언 모델도 이러한 잠재력이 있다. 이 모델에서 산출되는 확률과 구간은 더 의미가 있다. rstanarm 과 brms 을 사용하면, 확률적 프로그래밍 언어인 Stan 으로 모델코딩하는 법을 배우지 않고도 표준 mixed model 패키지보다 복잡한 모델링을 할 수 있다. 모델링 확률은 상상에 의해서만 제약을 받는다.
MCMC 방법 뿐만 아니라, 새로운 추론 프레임워크를 배워야 할 것이다. 하지만, 기초사항이 생각보다 훨씬 쉽다는 것을 알면 놀랄 것이다. brms 과 관련된 도구들을 사용하면 베이지언 데이터 분석으로 깊이 들어가는 것보다 훨씬 쉽게 될 것이고, mixed model 과 같은 유사한 것을 보았다. 따라서, 언제 한번 시도해 보길 바란다.
introduction to Baysian analysis with Stan 에서 소개를 볼 수 있고, 이 문서 에서 베이지언 방법론과 mixed model 에 관해 조금 더 볼 수 있다.
Priors
Priors 에 관한 다음 정보는 베이지언 분석, 특별히 회귀모델에 관한 배경지식을 가정한다. Stan 개발 그룹은 여기 에 추천을 제공하기 때문에 자주 살펴보길 바란다. Stan 은 conjugacy 를 필요로 하지 않는다는 점이 BUGS/JAGS 같은 도구와 대비된다. 알맞은 다른 prior 분포를 사용할 수 있다. 하지만, 일반적으로 fixed 효과에 대한 정규 분포와 variance components 에 관한 패키지 defaults 를 사용하는 것은 우리가 논의한 표준 모델에 관해 충분할 것이다.
Fixed 효과
Fixed 효과 회귀계수에 관해, 정규 그리고 student t 분포는 가장 보편적인 prior 분포이지만, default brms (와 rstanarm) 구현은 아무 것도 명시하지 않기 때문에, 좋은 선택이 아닌 uniform/improper prior 를 기본값으로 한다. 모델에 이를 설정해야 할 것이다. 여기에서 수치형 설명변수를 스케일링하면 lme4 에서와 같이 이점이 있고 prior 를 명시하기 쉬워지기도 한다.
Variance components
베이지언 선형 mixed model 에서, 랜덤효과는 fixed 효과와 같이 추정되는 파라미터이다 (따라서 BLUPs 가 아닙니다). 이것의 장점은 구간 추정하는 것이나 이를 이용한 예측값을 얻는 것이 다른 것과 같이 쉽다는 것이다. 일반적으로 variance component 에 관한 prior 는 half-t 인데, 값들이 양수만 될 수 있기 때문이다. 이 밖에도, 예를 들어, 절편과 기울기 상관계수 등에 관해서는 패키지 기본값을 사용하면 된다.
더 명시적으로 하면, 랜덤 절편과 기울기 분산이 각각 1 과 .1 이고 상관계수가 .3 인 경우를 가정해 보자. 랜덤 효과, 예를 들어 10 클러스터는 다음과 같이 다변량 분포로부터 올 수 있다.
re_cov = matrix(c(1, .3, .3, .1), ncol = 2)
re_cov [,1] [,2]
[1,] 1.0 0.3
[2,] 0.3 0.1mvtnorm::rmvnorm(10, mean = c(0, 0), sigma = re_cov) [,1] [,2]
[1,] -1.2221063 -0.19934740
[2,] 0.5511788 0.14630128
[3,] 1.0696280 0.51653368
[4,] -0.4822097 -0.11822515
[5,] 1.3431782 0.37536983
[6,] -0.2609433 -0.16101335
[7,] -0.8579271 -0.24116103
[8,] 0.3269719 0.05641921
[9,] -0.4339689 0.12164433
[10,] -0.7510034 -0.22716122모델의 prior 는 상관 행렬과 추정을 regard 하고 추정된 랜덤 효과가 앞 에서 본 것 같이 선형 설명변수에 추가된다.
Demonstration
GPA 모델로 돌아가봅시다. fixed 효과 prior 를 추가하고 체인을 병렬화하여 계산을 빠르게 하는 옵션을 추가할 것이다.
library(brms)
pr = prior(normal(0, 1), class = 'b')
bayesian_mixed = brm(
gpa ~ occasion + (1 + occasion | student),
data = gpa,
prior = pr,
cores = 4
)summary(bayesian_mixed) Family: gaussian
Links: mu = identity; sigma = identity
Formula: gpa ~ occasion + (1 + occasion | student)
Data: gpa (Number of observations: 1200)
Draws: 4 chains, each with iter = 2000; warmup = 1000; thin = 1;
total post-warmup draws = 4000
Group-Level Effects:
~student (Number of levels: 200)
Estimate Est.Error l-95% CI u-95% CI Rhat Bulk_ESS Tail_ESS
sd(Intercept) 0.21 0.02 0.18 0.25 1.00 2060 3217
sd(occasion) 0.07 0.01 0.06 0.08 1.00 1536 2398
cor(Intercept,occasion) -0.08 0.11 -0.29 0.15 1.00 977 1697
Population-Level Effects:
Estimate Est.Error l-95% CI u-95% CI Rhat Bulk_ESS Tail_ESS
Intercept 2.60 0.02 2.56 2.64 1.00 3423 3086
occasion 0.11 0.01 0.10 0.12 1.00 2760 3008
Family Specific Parameters:
Estimate Est.Error l-95% CI u-95% CI Rhat Bulk_ESS Tail_ESS
sigma 0.21 0.01 0.20 0.22 1.00 2562 3088
Draws were sampled using sampling(NUTS). For each parameter, Bulk_ESS
and Tail_ESS are effective sample size measures, and Rhat is the potential
scale reduction factor on split chains (at convergence, Rhat = 1).이전의 결과와 비교해 보라.
summary(gpa_mixed, cor = F)Linear mixed model fit by REML ['lmerMod']
Formula: gpa ~ occasion + (1 + occasion | student)
Data: gpa
REML criterion at convergence: 261
Scaled residuals:
Min 1Q Median 3Q Max
-3.2695 -0.5377 -0.0128 0.5326 3.1939
Random effects:
Groups Name Variance Std.Dev. Corr
student (Intercept) 0.045193 0.21259
occasion 0.004504 0.06711 -0.10
Residual 0.042388 0.20588
Number of obs: 1200, groups: student, 200
Fixed effects:
Estimate Std. Error t value
(Intercept) 2.599214 0.018357 141.59
occasion 0.106314 0.005885 18.07베이지언 결과는 근본적으로 같지만, 추가적으로 진단 정보를 주는 것 외에도 이제 모델을 탐색할 수 있다. brms 패키지는 가능한 한 lme4 와 같은 함수 이름을 사용하려고 하기 때문에 ranef, fixef, VarCorr 등을 사용할 수 있다. 하지만, 표준모델에 관한 내 함수를 사용할 수 있는데, 이는 타이디한 데이터프레임을 반환한다.
# examine random effects with the usual functions, not too tidy
# ranef(bayesian_mixed)
mixedup::extract_random_effects(bayesian_mixed)# A tibble: 400 × 7
group_var effect group value se lower_2.5 upper_97.5
<chr> <chr> <chr> <dbl> <dbl> <dbl> <dbl>
1 student Intercept 1 -0.199 0.116 -0.43 0.02
2 student Intercept 2 -0.208 0.112 -0.429 0.01
3 student Intercept 3 -0.006 0.109 -0.223 0.204
4 student Intercept 4 -0.095 0.114 -0.319 0.125
5 student Intercept 5 0.083 0.116 -0.151 0.311
6 student Intercept 6 -0.204 0.112 -0.424 0.019
7 student Intercept 7 -0.15 0.11 -0.37 0.064
8 student Intercept 8 0.149 0.117 -0.079 0.383
9 student Intercept 9 0.039 0.113 -0.183 0.254
10 student Intercept 10 0.1 0.113 -0.125 0.321
# … with 390 more rows하지만, 좋은 플롯팅 함수도 있다. 여기 학기효과 뿐만 아니라 모델에서 추정된 예측값 vs. 관측한 GPA 값을 플롯한다.
conditional_effects(bayesian_mixed)pp_check(bayesian_mixed)곧 보겠지만 훨씬 많은 모델링을 여기서 할 수 있지만, 기초적인 것을 더 쉽게 할 수 있다는 것을 아는 것이 더 중요한다.
예제 모델
이제 brms 에서 사용할 수 있는 다양한 (mixed) 모델을 보겠다. 모델링 함수 brm 을 볼 것이데, 문법은 lme4와 비슷하다.
특별한 bf 함수를 사용하는데, 복잡한 공식을 별개의 객체로 만들어 최종 모델링 함수에서 사용하는 것이 가능하다. 예를 들어,
brm(y ~ x, data = mydata, family = gaussian)
f = bf(y ~ x)
brm(f, ...)표준 mixed model
랜덤 절편.
brm(y ~ x + z + (1 | g))랜덤 절편 및 x 에 대한 랜덤 계수.
brm(y ~ x + z + (1 + x | g))다중 그룹화 구조/랜덤 효과.
brm(y ~ x + z + (1 | g1) + (1 | g2))
brm(y ~ x + z + (1 | g1 + g2)) # 같음
brm(y ~ x + z + (1 | g1) + (1 | g1:g2))기타 분포 패밀리
범주형 특수 효과를 포함하는 ‘일반화’ 혹은 ‘변화하는 계수’ 모델을 포함하는 다양한 유형의 일반 모델.
brm(y ~ x + z + (1 | g), family = cumulative)
# x has category specific effects
brm(y ~ cs(x) + z + (1 | g), family = acat)
# for ordered predictors, see the mo() function.Multinomial. 표준적인 다범주 타겟을 위한 범주형 분포를 사용.
brm(y ~ x + z + (1 | g), family = categorical)Zero-inflated 및 허들모델.
brm(
y ~ x + z + (1 | g),
zi ~ x + z,
family = zero_inflated_negbinomial(link = 'log')
)
brm(y ~ x + z + (1 | g), family = hurdle_lognormal)weibull, 스튜던트 t, 베타, 치우친 정규분포, von mises, 등등을 포함하여 다수.
잔차 구조와 이종분산
시간적, 공간적 잔차 구조를 모델링하기 위해 다양한 함수들이 존재합니다.
brm(y ~ time + (1 + time | g) + ar(time, person, p = 2))분산을 다른 것과 같이 모델할 수 있다.
brm(y ~ x + z + (1 | g),
sigma ~ x + (1 | g))분산성분 자체가 그룹에 따라 변하도록 할 수 있습니다. 다음에서, 남자와 여자에 대해 분산이 분리합니다.
brm(count ~ Sex + (1|gr(g, by = Sex)))각 개인이 하나 이상의 클러스터에 속할 수 있는 멀티멤버십 모델도 사용할 수 있습니다.
다음에서, g1 과 g2 가 개념적으로 동일하지만, 어떤 관측값들에 대해 다른 값을 가질 수 있습니다.
brm(y ~ 1 + (1 | mm(g1, g2))) 다변량 mixed model
다중 반응변수에 대해, 랜덤효과들이 상관관계를 가지게 할 수 있다.
다음에서, ID1 는 다중 반응변수 y1 과 y2 에 있는 모델된 랜덤 효과를 연결/상관하기 위해 제공하는 랜덤한 라벨이다.
시간 indicator 변수에 대한 랜덤 기울기를 추가한다면 SEM 논문에서 이것은 병렬프로세스에 가까울 것이다.
bf(
y1 ~ x + z + (1 | ID1 |g),
y2 ~ x + z + (1 | ID1 |g)
)예를 들어, 이러한 접근법은 0-인플레이트된 모델에 대해 의미가 있을 수도 있다. 이는 같은 클러스터링이 count 모델과 0-인플레이티드 모델 모두에 대해 상관되기 위한 랜덤 효과를 원한다.
bf(y ~ x * z + (1 + x | ID1 | g),
zi ~ x + (1 | ID1 | g))Additive mixed model
mgcv 의 많은 기능들이 적용되고, 같은 문법으로 작동합니다.
brm(y ~ s(x) + z + (1 | g))비선형 mixed models
함수 형태가 nlme 로 알려진, 유사한 상황을 모델링할 수 있습니다. We can model similar situations where the functional form is known, as with nlme.
bf(
y ~ a1 - a2^x,
a1 ~ 1,
a2 ~ x + (x | g),
nl = TRUE
)Censored and truncated targets
censored 데이터에는, 생존/이벤트-히스토리 모델에서 하는 것 처럼 센서링 변수를 사용합니다.
bf(y | cens(censor_variable) ~ x + z + (1 | g), family = lognormal) # frailty
# see also stan_jm in the rstanarm package for joint modelstruncated 모델에 대해서는, lower, upper 바운드를 명시합니다.
brm(count | trunc(ub = 10) ~ x * z + (1 | g), family = poisson)측정오차
trial 들의 평균이나 다른 평균으로 측정된 잠재변수들과 같이, 하나의 변수가 오차와 함께 측정된 것으로 가정되는지를 알 수 있는 경우가 있습니다.
다음에서, sdx 는 x 의 알려진 표준편차인데, 상수이거나 관측값마다 변할 수 있습니다.
brm(y ~ me(x, sdx) + z + (1 | g))Mixture models
mixture 와 함께 다중 패밀리로 명시된 클러스터 두개.
따라서 이것이 기술적으로 mixture mixed model 인 것 같다.
brm(y ~ x + z + (1 | g), family = mixture(gaussian, gaussian))‘growth mixture model.’
brm(y ~ time + z + (1 + time | g), family = mixture(gaussian, gaussian))결측값
We can construct the model formula for missing values as follows, including using a mixed model as the imputation model (for x).
f =
bf(y ~ mi(x) + z + (1 | g)) +
bf(x | mi() ~ z + (1 | g)) +
set_rescor(FALSE)모델 외
Stan 과 rstanarm 과 brms 패키지와 같은 개발은 빠르고, 연관된 것들의 조합된 파워로 모델 결과를 탐색하는 도구들이 많이 있습니다. Even if one found a specialty package for a specific type of mixed model, it is doubtful you would have as many tools for model exploration such as posterior predictive checks, marginal effects, model comparison, basic model diagnostics and more. That said, the Stan ecosystem of R packages is notable at this point, and so use what works for your situation.