2 Variáveis Aleatórias Discretas

De modo mais formal, uma variável aleatória discreta $X$ é uma função definida num espaço amostral $\Omega$, assumindo valores em um conjunto enumerável dos números reais, como representado pela Figura 2.1.

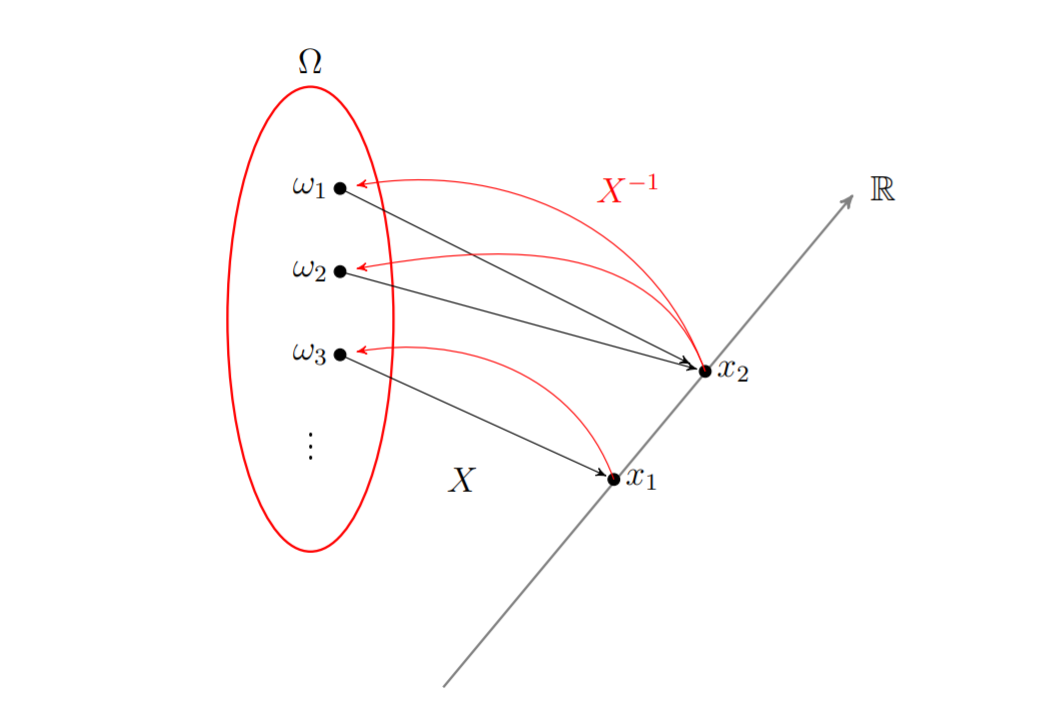
Figura 2.1: : Diagrama de Venn para os dados dos 209 estudantes que responderam ao questionário.

• Observe que:

$\Lambda=\left\lbrace x_1, x_2, \cdots \right\rbrace.$

• Pelo diagrama da Figura 2.1, vê-se:

$$\begin{equation} \begin{split} \left[ X=x_1\right]&=X^{-1}(x_1)=\lbrace \omega_3\rbrace,\\ \left[ X=x_2\right]&=X^{-1}(x_2)=\lbrace \omega_2, \omega_3\rbrace\\ \vdots & \\ \end{split} \tag{2.1} \end{equation}$$

• Como, $A=\left\lbrace \omega_1,\omega_2\right\rbrace=X^{-1}(x_2)=\left[X=x_2\right] \subset \Omega,$ então se $\omega_1$ ou $\omega_2$ ocorre, podemos pensar que $x_2$ ocorre;

• de um modo geral $\left[ X=x_i\right]$ representa a função inversa $X^{-1}$ no ponto $x_i$, sendo também um evento, ou seja

  $$\left[ X=x_i\right]=X^{-1}(x_i)=A \subset \Omega;$$

• como os eventos variam a cada realização do experimento, os valores numéricos que lhes são atribuídos também variarão,

• assim, faz sentido pensar em uma probabilidade associada ao valor numérico,

• a qual é induzida pelo evento ao qual este valor está associado.

• Portanto, tem-se:

  $$P\left(X=x_2\right)=P\left(X^{-1}(x_2)\right)=P\left(\lbrace \omega_2, \omega_3\rbrace\right).$$