2 Separatrizes e medidas de dispersão associadas
Nesta seção será discutido o cálculo e o uso da mediana como uma medida de tendência central, além de descrever como se dá a obtenção e interpretação de outras separatrizes. Também serão apresentadas medidas da dispersão em torno da mediana.
2.1 Mediana
A média, embora seja uma medida de tendência central muito utilizada, muitas vezes não descreve de maneira adequada um conjunto de dados, pois essa é uma medida que pode ser afetada por algumas características que os dados pode conter, como por exemplo a presença de assimetria acentuada na distribuição dos dados, ou presença de pontos que destoam dos demais, seja para cima ou para baixo. Nessas situações é importante que sejam obtidas outras medidas que não sejam afetadas por essas características. Uma medida que pode ser empregada nessas situações é a mediana, pois esta não é afetada por assimetria ou por pontos atípicos.
2.1.1 Mediana a partir de uma série de dados
A mediana de um conjunto de valores é o valor situado de tal forma no conjunto que o separa os dados ordenados (\(x_{(1)},x_{(2)},\cdots,x_{(n)}\)) em dois subconjuntos, de modo que 50% dos valores estão abaixo dele e os demais 50% estejam acima. Aqui, \(x_{(1)}\) denota o valor valor mínimo da série de dados e \(x_{(n)}\) corresponde ao valor máximo. Ou seja, têm-se:
\[x_{(1)} \leq x_{(2)} \leq \cdots \leq x_{(n)}.\]
A mediana é uma separatriz, pois esta divide o conjunto de dados ordenados em duas partes iguais.
A obtenção da mediana de uma série de dados \(\textbf{x}=(x_1,x_2, \cdots, x_n)\) pode ser feita da seguinte forma.
\[\begin{aligned} Med(\textbf{x}) &= \left\{ \begin{array}{ll} x_{(\frac{n+1}{2})}, &\ \text{se n é ímpar}; \\ \frac{x_{(\frac{n}{2})}+ x_{(\frac{n}{2}+1)}}{2}, &\ \text{se n par}. \end{array} \right.\\ \end{aligned}\]
- Para a série \(\textbf{x}=(5, 2, 6, 13, 9, 15, 10)\), a mediana pode ser obtida como segue:
\[\begin{aligned} (\underbrace{2, 5, 6,}_{3 \ elementos}\fbox{9,}\underbrace{10, 13, 15}_{3\ elementos}) \Rightarrow Med(\textbf{x})=9\\ \end{aligned}\]
- A série \(\textbf{y}=(1, 3, 0, 0, 2, 4, 1, 3, 5, 6)\) pode ser ordenada, e a mediana encontrada, da seguinte maneira:
\[\begin{aligned} (\underbrace {0,0,1,1,}_{4\ elementos}\fbox{2,3,}\underbrace{3,4,5,6}_{4\ elementos}) \Rightarrow Med(\textbf{y})=\frac{2+3}{2}= 2,5 \end{aligned}\]
2.1.2 Mediana a partir da tabela de frequência simples
Para obtenção da mediana a partir de uma tabela de frequência, considere a coluna das frequências relativas acumuladas. A frequência acumulada é útil devido a mediana ser um valor que acumula abaixo dele 50% dos dados ordenados, com isso pode-se encontrar facilmente a classe mediana olhando diretamente para a tabela. Para ilustrar a obtenção, considere o Exemplo 2.2.
Exemplo.2.2 Considere a Tabela 2.1, que mostra a distribuição de frequência das curvas da BR 116, compreendidas entre os quilômetros 52,90 e 113,20, dados vistos em Quaresma (2019). Considere o seguinte.
- População: todas as curvas existentes na BR 116 entre os quilômetros 52,90 e 113,20.
- Unidades amostrais ou indivíduos: as curvas investigadas.
- Variável: número de acidentes ocorridos entre 2014 e 2019 nessas curvas.
| Quant. Acidentes | \(Freq. Curvas\) | \(f_i\) | \(F_{ac}\) | \(X_i \times f_i\) |
|---|---|---|---|---|
| 0 | 13 | 0.34 | 0.34 | 0.00 |
| 1 | 5 | 0.13 | 0.47 | 0.13 |
| 2 | 5 | 0.13 | 0.61 | 0.26 |
| 3 | 3 | 0.08 | 0.68 | 0.24 |
| 4 | 3 | 0.08 | 0.76 | 0.32 |
| 5 | 2 | 0.05 | 0.82 | 0.26 |
| 6 | 3 | 0.08 | 0.89 | 0.47 |
| 7 | 1 | 0.03 | 0.92 | 0.18 |
| 12 | 1 | 0.03 | 0.95 | 0.32 |
| 17 | 1 | 0.03 | 0.97 | 0.45 |
| 48 | 1 | 0.03 | 1 | 1.26 |
| Total | 38 | 1.01 | - | 3.89 |
Para obter a mediana, observe que a até a terceira classe são acumulados mais de 50% dos dados (61%), sendo assim, esta é a classe que contém a mediana, deste modo não importa se o total de elementos na série é par ou ímpar, a mediana é o valor que está nessa classe, no caso, 2 acidentes, como mostra a linha a seguir, a qual foi destacada da Tabela 2.1. Ainda na tabela, pode ser visto que a média é \(\overline{x}=3,86\), a qual está a quase duas unidades distante da mediana, mostrando uma divergência dessas duas medidas de tendência central. Isso mostra que, neste caso, a média pode não ser uma boa medida de tendencial central.
| Mediana=2 | \(n_i\)=5 | \(f_i\)=0,13 | \(F_{ac}\)=0,61 |
|---|
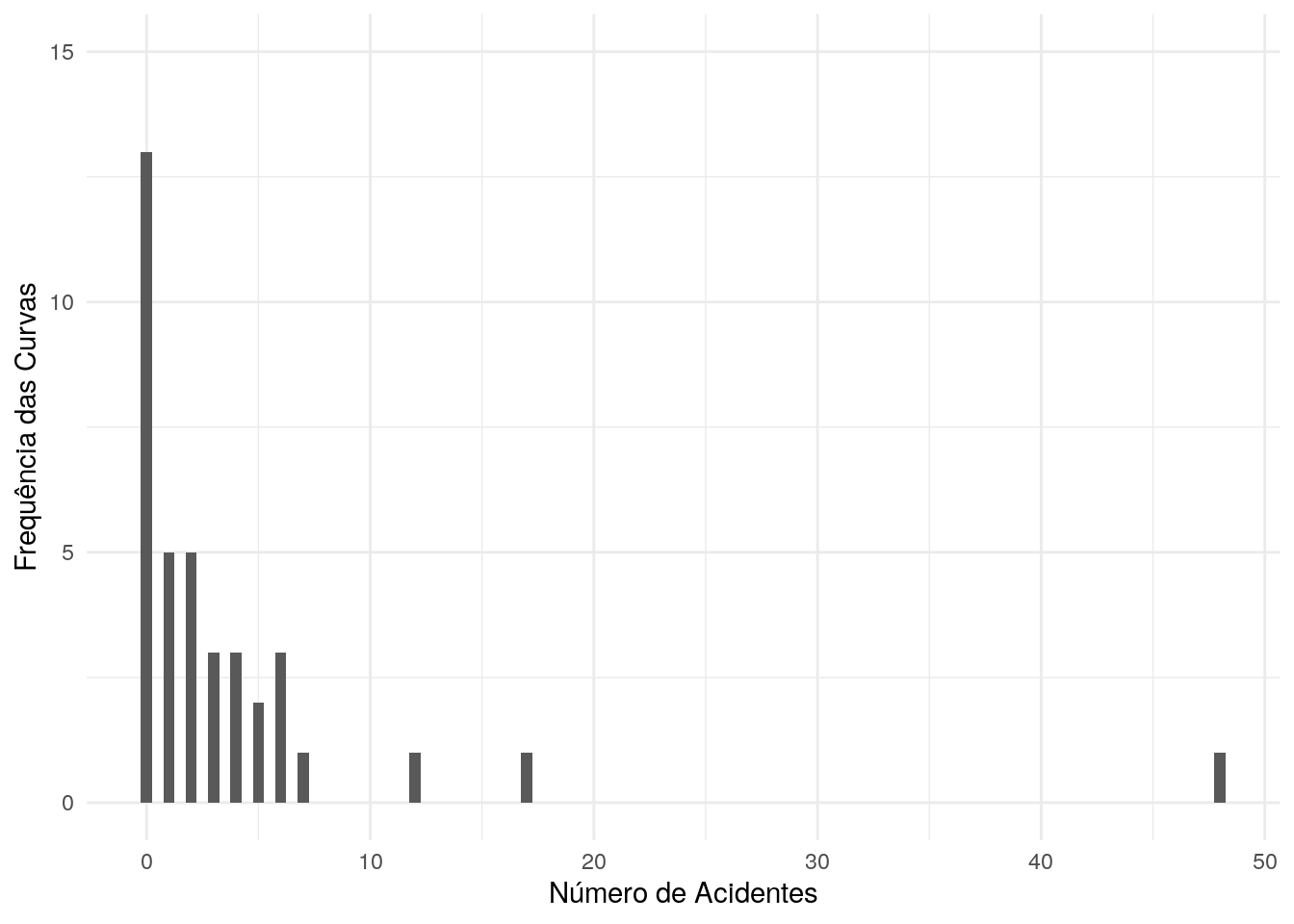
Figura 2.1: : Frequência das curvas por acidente.
2.1.3 Mediana a partir da tabela de frequência em intervalos de classe
A obtenção de uma aproximação da mediana a partir de dados agrupados em uma tabela de frequência em intervalos, assim como no caso de uma tabela de frequência simples, pode ser feita localizando a classe que contém a mediana. Neste caso, o valor da mediana não pode ser obtido de modo preciso, exigindo, pois é requerida uma aproximação dentro do intervalo que contém esse valor. Essa aproximação será feita aqui de modo a levar em consideração a distribuição de frequência por meio da relação: \[\begin{aligned} Med&=L_i+\left[\frac{\left( 0,5 - F_{ac(ant)}\right) }{f_i}\right] \times \delta \end{aligned}\] em que,
- \(L_i\): limite inferior da classe mediana,
- \(F_{ac(ant)}\): frequência relativa acumulada da classe anterior à classe mediana,
- \(\delta\): amplitude da classe
- e \(f_i\) é a frequência relativa da classe mediana.
O Exemplo 2.3 ilustra a obtenção dessa aproximação da mediana em tabela com intervalos.
| Km | \(Freq. Curvas\) | \(f_i\) | \(F_{ac}\) |
|---|---|---|---|
| (53.05,59.78] | 6 | 0.16 | 0.16 |
| (59.78,66.46] | 4 | 0.11 | 0.26 |
| (66.46,73.13] | 8 | 0.21 | 0.47 |
| (73.13,79.81] | 0 | 0.00 | 0.47 |
| (79.81,86.48] | 0 | 0.00 | 0.47 |
| (86.48,93.16] | 4 | 0.11 | 0.58 |
| (93.16,99.83] | 4 | 0.11 | 0.68 |
| (99.83,106.5] | 7 | 0.18 | 0.87 |
| (106.5,113.2] | 5 | 0.13 | 1 |
| Total | 38 | 1.00 | - |
Exemplo.2.3 A Tabela 2.1, mostra a distribuição de frequência das curvas da BR 116, compreendidas entre os quilômetros 52,90 e 113,20, segundo a quilometragem da via, dados vistos em Quaresma (2019). Neste caso, pode ser pensado as seguintes características para o estudo.
- População: todas as curvas existentes na BR 116 entre os quilômetros 52,90 e 113,20.
- Unidades amostrais ou indivíduos: as curvas investigadas.
- Variável: posição da curva na rodovia, medida pela quilometragem da via até a curva.
Note que a posição da curva é uma variável quantitativa contínua, sendo apropriado o uso de uma tabela de frequência com intervalos. Na sexta classe da tabela de frequência apresentada é localizada a mediana da quilometragem, ou seja, aquele valor para a variável local da curva que antes dele concentra 50\% dos locais das curvas para o trexo em questão. Essa classe é mostrada a seguir:
| Mediana \(\in\) (86,48;93,16] | \(n_6\)=4 | \(f_6\)=0,11 | \(F_{ac}\)=0,58 |
|---|
Uma vez que foi identificada a classe da mediana, basta aproximá-la dentro do intervalo, da seguinte forma:
\[\begin{aligned} Med&=L_6+\left[\frac{\left( 0,5 - F_{ac(5)}\right) }{f_6}\right] \times \delta \\ &=86,48+\frac{(0,5-0,47)}{0,11} \times (93.16-86,48)\\ &=86,48+\frac{0,03}{0,11} \times 6,68= 86,48 +2,73 \approx \textbf{88,3}. \end{aligned}\]
A Figura 2.2 mostra o histograma da frequência das curvas por quilometragem, onde pode ser visto o intervalo com maior frequência de curvas (65-70 km) e também o intervalo que contém a mediana (80-85 km).
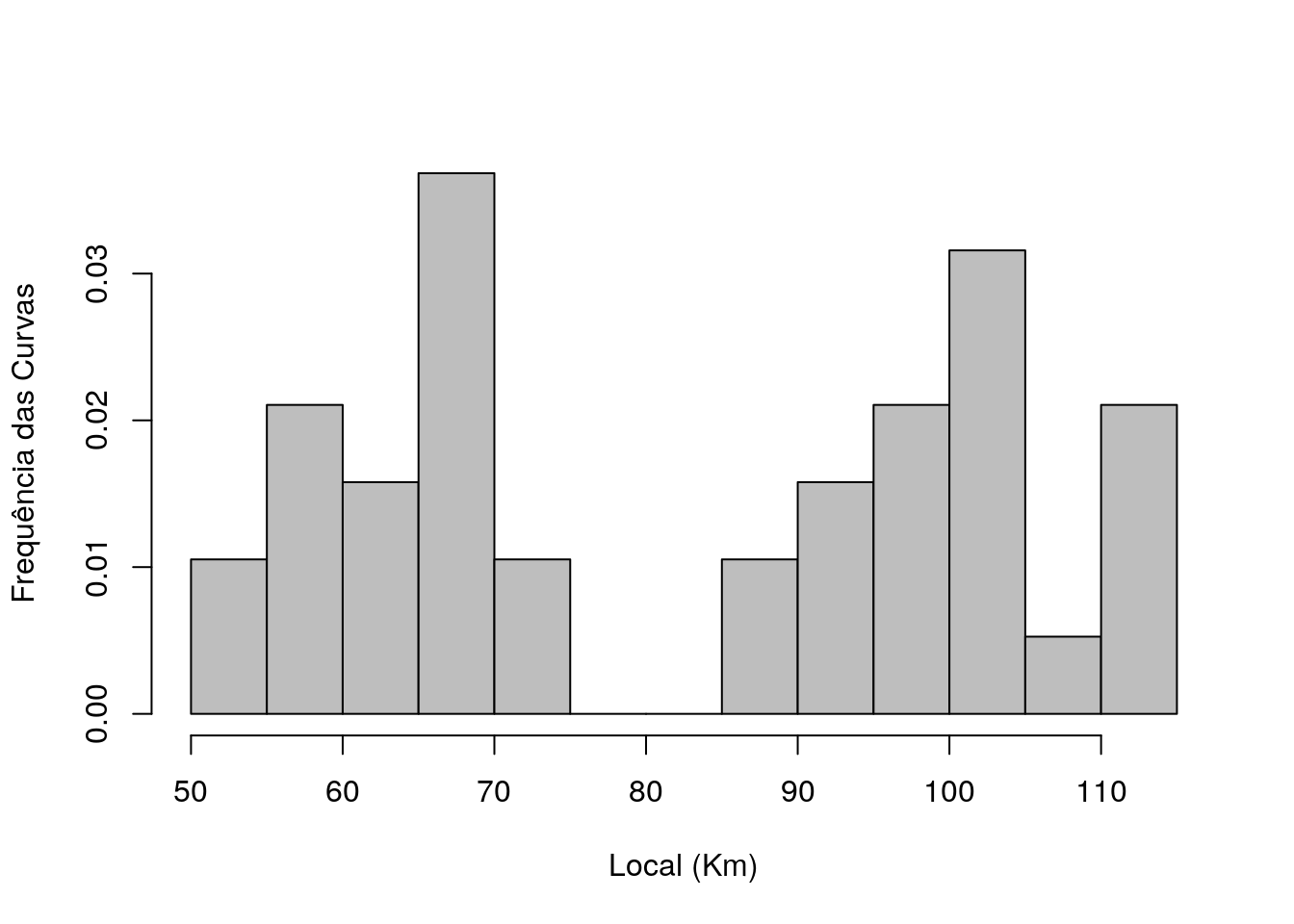
Figura 2.2: : Frequência das curvas.
2.2 Outras Separatrizes
Separatrizes (ou quantis) são valores que dividem uma série de dados ordenados (\(x_{(1)}, x_{(2)}, \cdots, x_{(n)}\)) em partes iguais. Assim como a mediana divide a série dados ordenados em duas partes iguais, podem ser obtidos valores que separam a série em mais parte iguais. As separatrizes mais importantes são:
- a mediana (uma medida que divide a série ordenada em duas partes iguais);
- os quartis (três medidas que dividem a série ordenada em quatro partes iguais);
- os decis (nove medidas que dividem a série ordenada em dez partes iguais)
- e os percentis (noventa e nove medidas que dividem a série ordenada em cem partes iguais).
A estratégia usada para a obtenção das demais separatrizes segue a mesma ideia aquela empregada para obter o valor da mediana. Então, para encontrar as medidas a partir de uma tabela de frequência, encontra-se a classe que contém a medida desejada observando as frequências relativas acumuladas. Se a tabela possuí intervalos, deve-se aproximar as medidas dentro de suas respectivas classes usando expressões que podem ser como segue.
- Para os quartis:
\[\begin{aligned} p_j&= \frac{ j}{4}, \mbox{ para } j = 1,2,3 \\ Q_j&=L_i+\left[\frac{\left( p_j- F_{ac(ant)}\right) }{f_i}\right] \times \delta \end{aligned}\] com:
- \(L_i\) é o limite inferior da classe definida por \(p_j\);
- \(F_{ac(ant)}\) é a frequência absoluta acumulada da classe anterior à que contém o \(j\)-ésimo quartil;
- \(\delta\) é a amplitude da classe e
- \(f_i\) é a frequência relativa da classe definida por \(p_j\).
- Para os decis:
\[\begin{aligned} p_j&= \frac{ j}{10}, \mbox{ para } j = 1,2,\cdots, 9\\ D_j&=L_i+\left[\frac{\left( p_j- F_{ac(ant)}\right) }{f_i}\right] \times \delta \end{aligned}\] com:
- \(L_i\) é o limite inferior da classe definida por \(p_j\);
- \(F_{ac(ant)}\) é a frequência absoluta acumulada da classe anterior à que contém o \(j\)-ésimo decil;
- \(\delta\) é a amplitude da classe e
- \(f_i\) é a frequência relativa da classe definida por \(p_j\).
- Para os percentis:
\[\begin{aligned} p_j&= \frac{ j}{100}, \mbox{ para } j = 1,2,\cdots, 99\\ P_j&=L_i+\left[\frac{\left( p_j- F_{ac(ant)}\right) }{f_i}\right] \times \delta \end{aligned}\] com:
- \(L_i\) é o limite inferior da classe definida por \(p_j\);
- \(F_{ac(ant)}\) é a frequência absoluta acumulada da classe anterior à que contém o \(j\)-ésimo percentil;
- \(\delta\) é a amplitude da classe e
- \(f_i\) é a frequência relativa da classe definida por \(p_j\).
2.2.1 Cálculo dos quartis
No Exemplo 2.3, os quartis podem ser obtidos da seguinte maneira:
2.2.1.1 Valor do primeiro quartil (\(Q_1\))
O valor \(Q_1\) está na segunda classe da tabela (tab:tabclass), pois essa acumula mais de 25\% dos dados, como pode ser visto na classe destacada a seguir.
| \(Q_1\) \(\in\) (59,78;66,46] | \(n_2\)=12 | \(f_2\)=0,32 | \(F_{ac}\)=0,26 |
|---|
Note que até essa classe concentra-se 26% dos dados, logo contém o \(Q_1\). Para aproximar essa medida dentro da classe encontrada, basta usar a relação:
\[\begin{aligned} p_1&= \frac{ 1}{4}=0,25\\ Q_1&=L_2+\left[\frac{\left( p_1- F_{ac(1)}\right) }{f_2}\right] \times \delta\\ Q_1&=59,78+\left[\frac{\left( 0,25- 0,16\right) }{0,32}\right] \times (66,46-59,78)\\ Q_1&=59,78+0,82 \times 6,68=59,78+5,47\approx 65,25 \end{aligned}\]
Então, \(Q_1\approx 65,25\)
2.2.1.2 Valor do segundo quartil (\(Q_2\))
O \(Q_2=Med=88,3\), ou seja esse valor é o valor da mediana e já foi calculado anteriormente.
2.2.1.3 Valor do terceiro quartil (\(Q_3\))
O valor \(Q_3\) está na quinta classe da tabela (tab:tabclass), pois essa acumula mais de 75% dos dados:
| \(Q_3\) \(\in\) (99,83;106,5] | \(n_8\)=7 | \(f_8\)=0,18 | \(F_{ac}\)=0,87 |
|---|
Note que até essa classe concentra-se 87% dos dados, logo contém o \(Q_3\). Assim:
\[\begin{aligned} p_3&= \frac{ 3}{4}=0,75\\ Q_3&=L_8+\left[\frac{\left( p_3- F_{ac(7)}\right) }{f_8}\right] \times \delta\\ Q_3&=99,83+\left[\frac{\left( 0,75- 0,68\right) }{0,18}\right] \times (106,5-99,83)\\ Q_3&=99,83+0,39\times 6,68=99,83+2,61\approx 102,45 \end{aligned}\]
Ou seja, \(Q_3\approx 102,45\)
2.3 Desenho Esquemático (Boxplot)
O desenho esquemático, também conhecido como Boxplot, é um gráfico bastante útil na análise do comportamento de uma variável a partir de um conjunto de valores observados. Dentre as vantagens do boxplot, podemos destacar:
- a detecção rápida de uma possível assimetria na distribuição de frequência dos dados;
- a capacidade de fornecer uma ideia sobre a existência de possíveis pontos atípicos (muito além ou muito aquém dos demais pontos);
- a exibição dos quartis.
2.3.1 Contrução do Boxplot
Para sua construção, é preciso obter mais duas medidas para decidir quais são os pontos atípicos da série de dados. Essas medidas serão chamadas aqui de limite superior (\(l_{sup}\)) e limite inferior (\(l_{inf}\)). Para obtê-los, fazemos:
\[\begin{aligned} l_{inf}&= Q_1-\frac{3}{2}(Q_3-Q_1) \mbox{ e }\\ l_{sup}&=Q_3+\frac{3}{2}(Q_3-Q_1).\\ \end{aligned}\]
Caso o valor mínimo no conjunto de dados seja maior que \(Q_1-\frac{3}{2}(Q_3-Q_1\), então: \(l_{sup}=min\).
Do mesmo modo, caso o valor máximo no conjunto de dados seja menor que \(Q_3+\frac{3}{2}(Q_3-Q_1)\), então: \(l_{inf}=min\)
Com essas medidas, podemos obter os valores que estão muito aquém de \(Q_1\) ou muito além de \(Q_3\). Tais pontos são chamados de pontos discrepantes (ou aberrantes, ou ainda outliers).
Após a obtenção dos limites (\(l_{inf}\) e \(l_{sup}\)), podemos construir o boxplot da seguindo os seguintes passos:
No eixo cartesiano, constrói-se um retângulo na vertical de modo que:
- A base no retângulo corresponda ao primeiro quartil (\(Q_1\))
- e o topo (lado superior) corresponda ao terceiro quartil (\(Q_3\));
- divide-se o retângulo em duas partes usando um segmento de reta orientado pela mediana;
- Acima do retângulo traça-se um segmento orientado por \(l_{sup}\);
- Abaixo do retângulo também é apresentado um traço orientado por \(l_{inf}\);
- acima de \(l_{sup}\) e abaixo de \(l_{inf}\), marcam-se os pontos discrepantes.
\[\begin{aligned} l_{inf}&= Q_1-\frac{3}{2}(Q_3-Q_1)= 65,25-\frac{3}{2}(102,45-65,25)=65,25-55,8=9,45 \\ l_{sup}&=Q_3+\frac{3}{2}(Q_3-Q_1)=102,45+\frac{3}{2}(102,45-65,25)=102,45+55,8=158,25.\\ \end{aligned}\]
Como, \(min=53,11\) e \(max=113,18\), então: \[\begin{aligned} l_{inf}&= 53,11 \\ l_{sup}&=113,18.\\ \end{aligned}\]
Usando esses limites e os quartis calculados anteriormente, pode-se costruir o gráfico apresentado na Figura @rer(fig:boxplotcurvas). Note que no intervalo delimitado pela caixa estão 50\% do total das curvas, e este intervalo vai dos quilometro \(Q_1=65,25\) até o quilometro \(Q_3=102,45\). Na caixa do gráfico pode ser notada uma assimetria, pois existem um lado, em relação a mediana, que é mais “largo” que o outro. Também pode ser notado que as curvas estão concentradas ao longo do trecho, ou seja, não existe uma isolada, pois não é observado pontos atípicos no conjunto de dados. Note, também, que a média e a mediana estão afastadas, indicando um deslocamento da média do centro da distribuição para a esquerda.
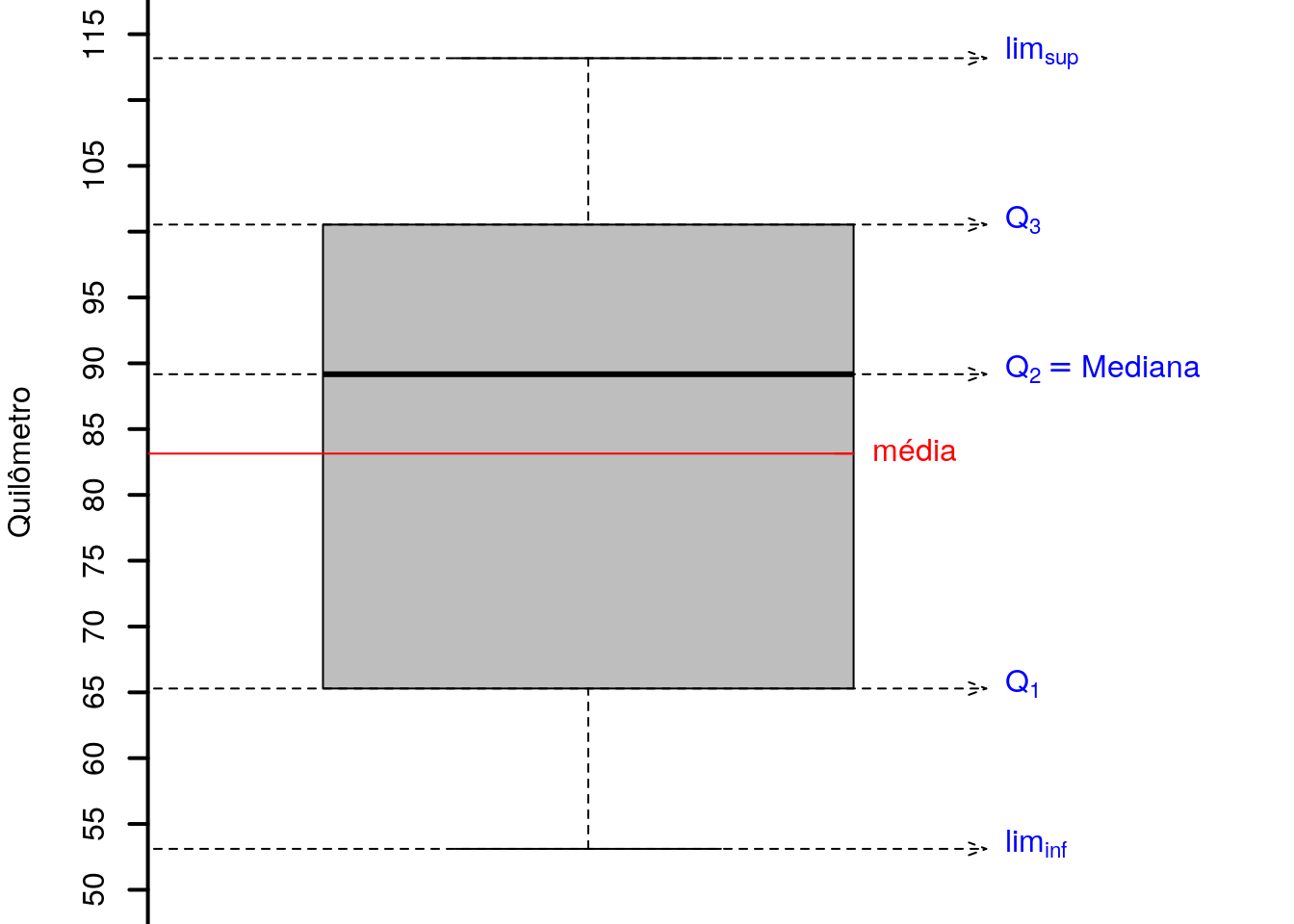
Figura 2.3: : Frequência das curvas pela sua localização na rodovia.
Exemplo.2.5 Considerando novamente a Tabela 2.1, que mostra a distribuição de frequência das curvas da BR 116, compreendidas entre os quilômetros 52,90 e 113,20, com as considerações seguintes.
- População: todas as curvas existentes na BR 116 entre os quilômetros 52,90 e 113,20.
- Unidades amostrais ou indivíduos: as curvas investigadas.
- Variável: número de acidentes ocorridos entre 2014 e 2019 nessas curvas.
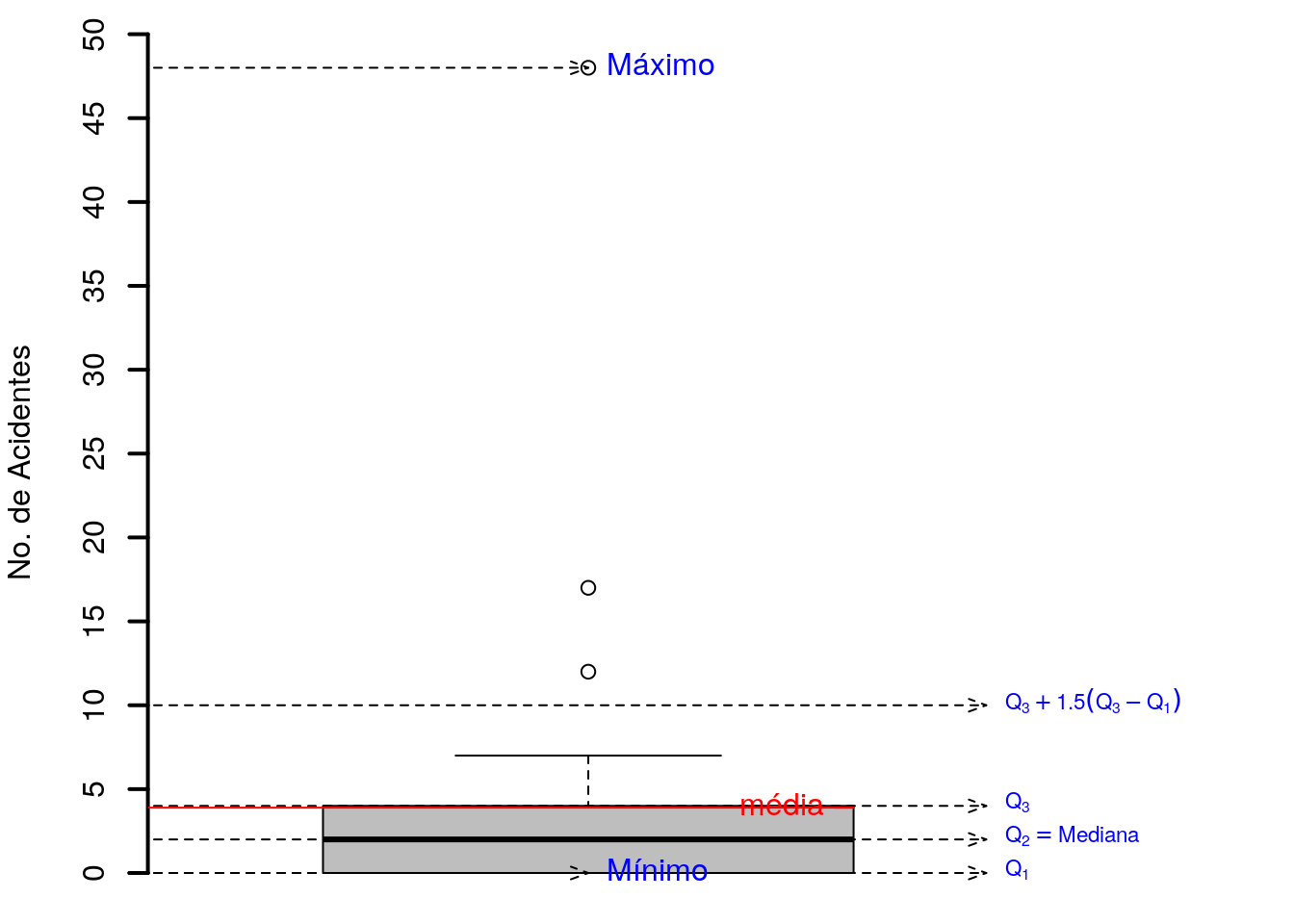
Figura 2.4: : Frequência das curvas pelo número de acidentes.
2.4 Medida da dispersão em torno da mediana
2.4.1 Distância interquartil
Se a mediana é usada como a medida de tendência central para um conjunto de dados, a distância entre o primeiro e o terceiro quartil pode ser usada como uma medida da variabilidade dos dados em torno da mediana. Essa medida é chamada de distância interquartil e é dada por:
\[D=Q_3-Q_1\]
Também é muito utilizado a "amplitude ou desvio semi-quartil’’, que seria o interquartil dividido por 2. Neste caso, essa é uma boa medida de dispersão, pois em um intervalo igual ao interquartil em torno da mediana estão 50% dos dados. Neste caso, o boxplot pode ser utilizado para visualizar o comportamento da variável que gerou os dos dados. Quanto maior for a distância entre os quartis \(Q_1\) e \(Q_2\), maior será a dispersão dos dados.
2.4.2 Amplitude Total
Também podem ser usadas outras medidas para se ter uma ideia da dispersão dos dados.
Um exemplo é a Amplitude Total (AT) que é a diferença entre o maior e o menor valor observado (valor máximo e valor mínimo).
\[AT = x_{\mbox{(max)}} - x_{\mbox{(min)}}\]
Observação: essa medida não é muito utilizada devido ser altamente afetada por pontos discrepantes, além de ser pouco informativa.
Referências
Quaresma, Renan Rocha. 2019. “Análise Da Influência de Parâmetros Geométricos de Rodovias Na Frequência E Severidade de Acidentes Rodoviários.” http://repositorio.ufc.br/bitstream/riufc/49429/1/2019_tcc_rrocha.pdf.