3 Gráficos para variáveis quantitativas
Um dos gráficos mais importantes para exibir distribuição de frequência de variáveis quantitativas é o histograma. Este gráfico pode ser pensado como uma representação gráfica da tabela de frequência com intervalos nas classes, em que as barras mostram o quão grande é a frequência nos intervalos. Assim, sua construção pode ser feita de forma similar ao procedimento empregado para construir a tabela de frequências com intervalos nas classes.
3.1 Histograma
O histograma é um gráfico de barras contíguas, e é apropriado para representar distribuições de frequências tando de variáveis quantitativas contínuas como discretas com muitos valores possíveis. Se a variável é quantitativa discreta, mas contém poucos valores possíveis, então os gráficos utilizados para apresentar a distribuição de frequência de variáveis qualitativas podem ser usados para representar sua frequência nos dados observados.
A construção do histograma será explicada aqui por meio de um exemplo, em que a variável “Nota do ENEM” do questionário aplicado aos estudantes das engenharias será utilizada para ilustrar essa construção. Dentre os entrevistados \(n=157\) declaram a sua nota do ENEM para ingressar no curso em se encontra. Os valores ordenados são apresentados a seguir.
## [1] 450,00 499,20 518,00 530,00 540,00 547,00 550,00 551,14 558,00 560,00
## [11] 561,30 570,00 570,00 570,00 575,00 578,00 578,00 588,00 588,00 589,00
## [21] 592,00 592,16 592,16 592,16 592,40 595,00 597,00 599,00 599,50 599,60
## [31] 600,00 602,00 602,00 604,05 604,50 604,50 605,00 609,00 614,00 614,66
## [41] 615,00 618,00 619,00 619,65 620,00 620,00 620,00 621,00 621,00 621,14
## [51] 622,00 622,20 622,30 624,00 624,00 624,00 624,80 624,80 627,80 627,80
## [61] 630,00 630,00 630,00 631,00 631,00 631,00 633,00 634,20 634,88 635,00
## [71] 636,10 636,10 639,50 640,00 640,00 640,00 640,75 642,00 643,20 643,60
## [81] 643,60 644,00 644,00 645,00 645,00 645,40 648,00 648,04 648,40 650,00
## [91] 650,00 650,00 650,00 650,00 651,00 651,00 651,00 651,30 651,50 652,00
## [101] 652,20 652,20 652,20 652,76 652,76 653,00 655,00 655,00 655,00 656,00
## [111] 657,00 657,56 660,00 660,00 661,00 661,48 663,00 664,62 664,94 664,94
## [121] 666,00 667,00 667,00 668,00 670,00 670,00 670,00 670,00 670,00 671,00
## [131] 671,90 671,90 676,14 676,50 680,00 680,00 680,00 680,00 683,00 684,50
## [141] 685,60 691,00 693,00 694,94 694,94 696,00 699,00 705,50 705,50 707,30
## [151] 709,00 720,12 720,30 728,00 750,00 750,00 765,28Para os dados da variável “Nota do ENEM”, vamos fixar \(L_{sup}=766\) e \(L_{inf}=450\) para determinar \[AT=L_{sup}-L_{inf}=766-450=316.\] Como \(n=157\), tem-se \(k\approx 1+log_{2}209\approx 8,29\approx 8\), assim \(k=8\) que fornece \(\delta=316/8 \approx 40\). Logo, tem-se:
\(450+40=490\) \(\Rightarrow\) \([450; 490)\)
\(490+40=530\) \(\Rightarrow\) \([490; 530)\)
\(530+40=570\) \(\Rightarrow\) \([530; 570)\)
\(570+40=610\) \(\Rightarrow\) \([570; 610)\)
\(610+40=650\) \(\Rightarrow\) \([610; 650)\)
\(650+40=690\) \(\Rightarrow\) \([650; 690)\)
\(690+40=730\) \(\Rightarrow\) \([690; 730)\)
\(730+40=770\) \(\Rightarrow\) \([730; 770)\)
Com isso, têm-se os intervalos que fornecerão as bases dos retângulos que utilizados para montar o gráfico de barras. No entanto, essas barras não serão construídas de qualquer modo, mas sim de modo que a área de cada barra seja igual à frequência relativa de ocorrência da variável no intervalo fornecido pela base dessa barra.
Para iniciar a construção do histograma, deve-se construir as escalas, usando os intervalos no eixo das abcissas, e para a ordenada, deve-se antes obter as alturas das barras, para finalmente construir a escala e desenhar as barras.
3.1.1 Altura da primeira barra do histograma
O primeiro intervalo construído, \([450; 490)\) , contém 20 valores de nota, assim sua frequêcia relativa é \(f_1=1/157\approx 0,006\), então a primeira barra deve ter área 0,006 Ou seja, a altura (\(h\)) da barra deve ser obtida como:
\[\delta \times h=0,006\]
em que \(\delta=490-450=40\) é a amplitude do intervalo em cada classe, então:
\[40\times h_1=0,006 \Rightarrow h_1=0,000159 \]
A Figura 3.1 mostra a primeira barra do histograma, cuja área é dada por: \[ h_1=0,000159 \Rightarrow \delta \times h_1 = f_1 \approx 0,006\]
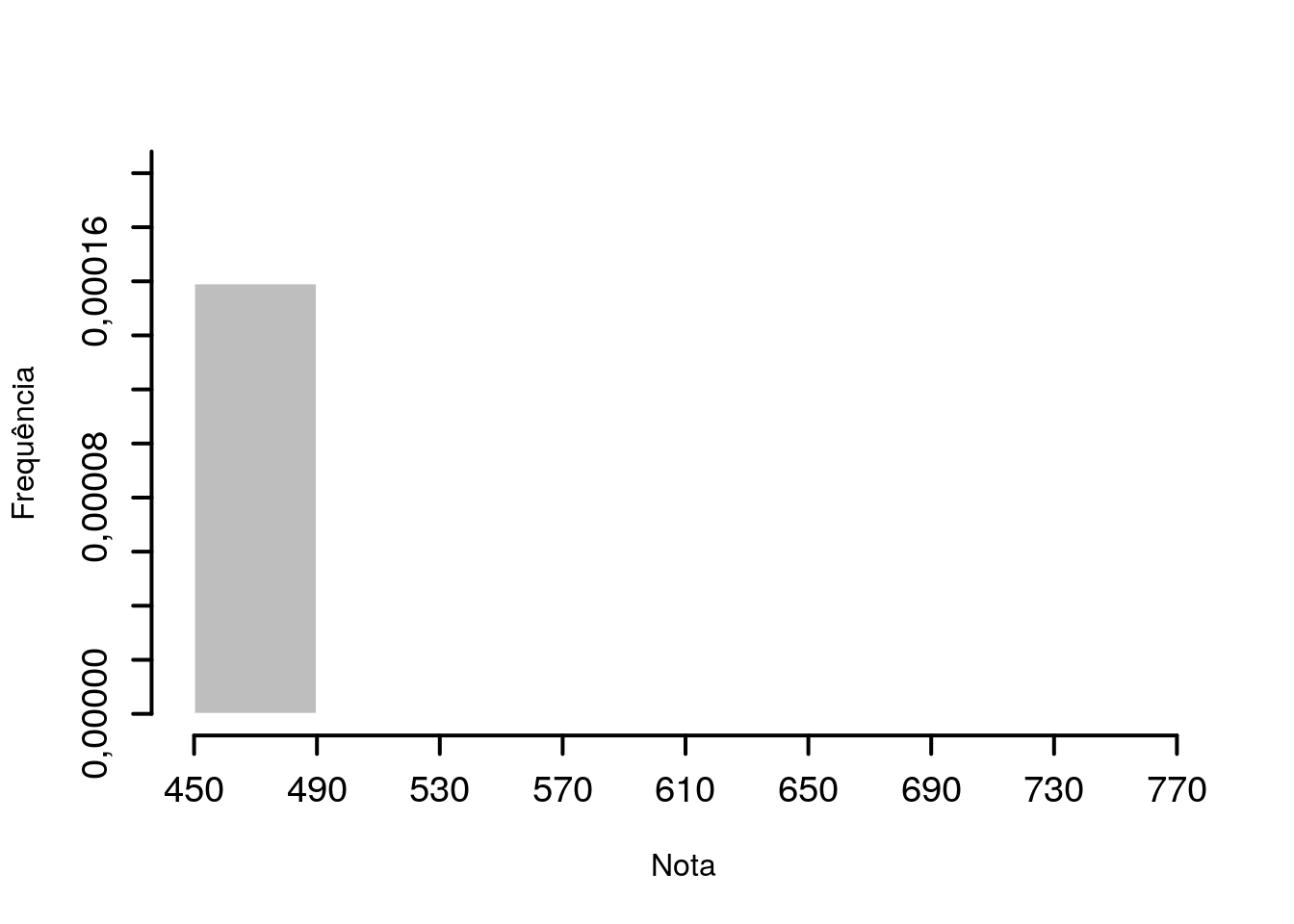
Figura 3.1: : Construção da primeira barra do histograma.
3.1.2 Altura da segunda barra do histograma
Para obter a segunda barra, basta usar o mesmo raciocínio, ou seja:
Obtém-se a segunda frequência relativa observando quantas observações contém o segundo intervalo \([490; 530)\), neste caso duas;
calcula-se a altura da barra dividindo essa frequência pela amplitudoe da classe:
\[f_2=2/157 = 0,01273885 \Rightarrow h_2=\frac{f_2}{40}=0,0003184713.\] Logo a altura da segunda barra é \(\approx 0.0003\), assim basta subir a barra até esse valor, como mostra a Figura 3.1.
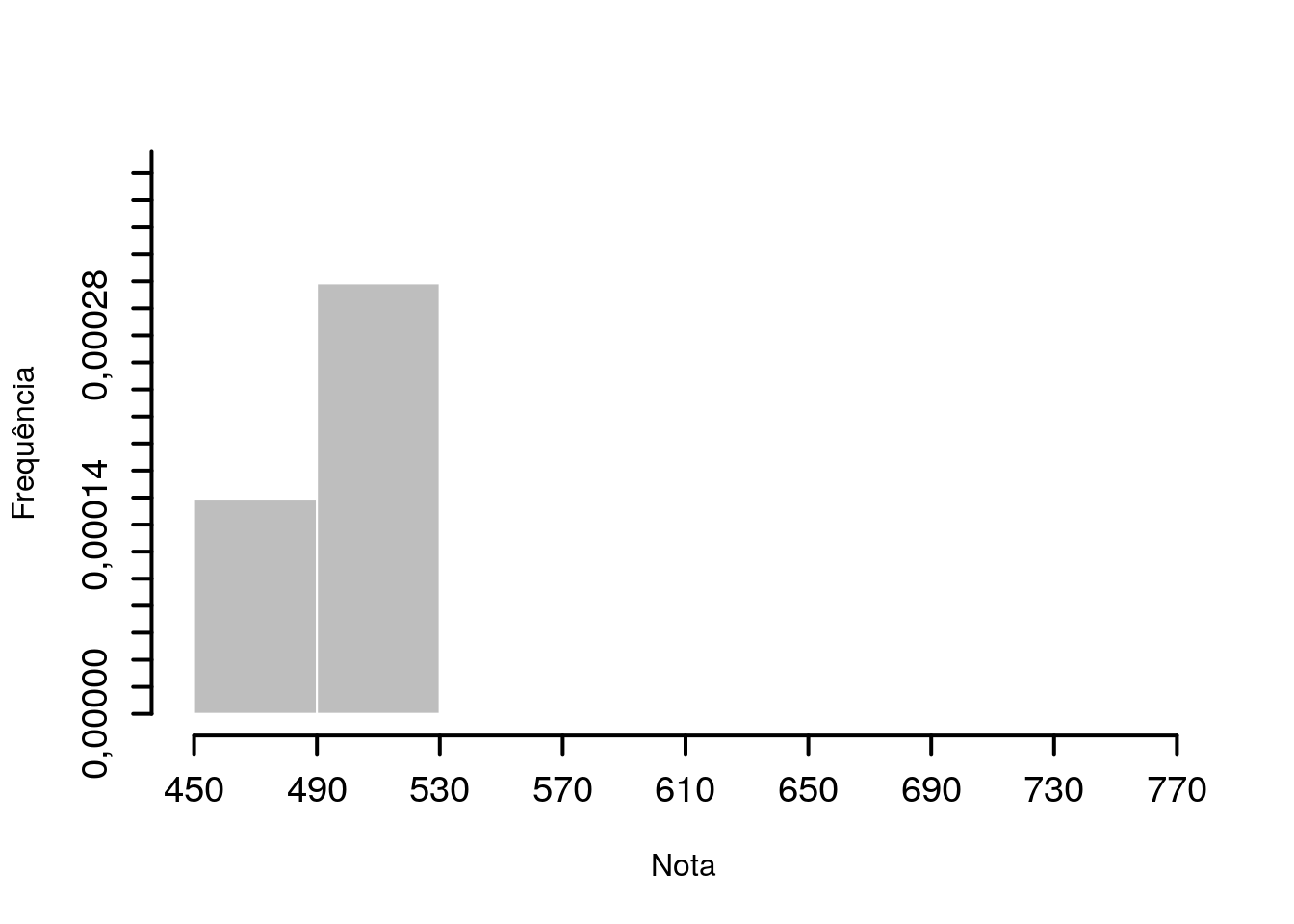
Figura 3.2: : Construção da segunda barra do histograma.
3.1.3 Alturas para as demais barras do histograma
o intervalo \([530; 570)\) contém 8 observações, então \[f_3=8/157 = 0,05095541 \Rightarrow h_3=\frac{f_3}{40}= 0,001273885.\]
O intervalo \([570; 610)\) contém 26 observações, então \[f_4=26/157 = 0,1656051 \Rightarrow h_4=\frac{f_4}{40}= 0,004140127.\]
- o intervalo \([610; 650)\) contém 49 observações, então:
\[f_5=49/157 = 0,3121019 \Rightarrow h_5=\frac{f_5}{40}= 0,007802548.\]
o intervalo \([650; 690)\) contém 55 observações, então: \[f_6=55/157 = 0,3503185 \Rightarrow h_6=\frac{f_6}{40}= 0,008757962.\]
o intervalo \([690; 730)\) contém 12 observações, então:
\[f_7=12/157 = 0,07643312 \Rightarrow h_7=\frac{f_7}{40}= 0,001910828.\]
- o intervalo \([730; 770)\) contém 4 observações, então:
\[f_8=4/157 = 0,1656051 \Rightarrow h_8=\frac{f_8}{40}= 0,004140127.\]
Deste modo, têm-se os seguinte valores de alturas para as barras:
- \(h_1= 0,0001592357 =1,592357\mbox{ e}^{-4}\)
- \(h_2= 0,0003184713 =3,184713 \mbox{ e}^{-4}\)
- \(h_3= 0,0012738854 =1,2738854\mbox{ e}^{-3}\)
- \(h_4= 0,0041401274 =4,1401274 \mbox{ e}^{-3}\)
- \(h_5= 0,0078025478 = 7,8025478 \mbox{ e}^{-3}\)
- \(h_6= 0,0087579618 = 8,7579618 \mbox{ e}^{-3}\)
- \(h_7= 0,0019108280 = 1,910828\mbox{ e}^{-3}\)
- \(h_8= 0,0006369427 = 6,369427 \mbox{ e}^{-4}\)
A escala no eixo das ordenadas deve ser construída observando o maior valor de altura, como mostra a Figura 3.3.
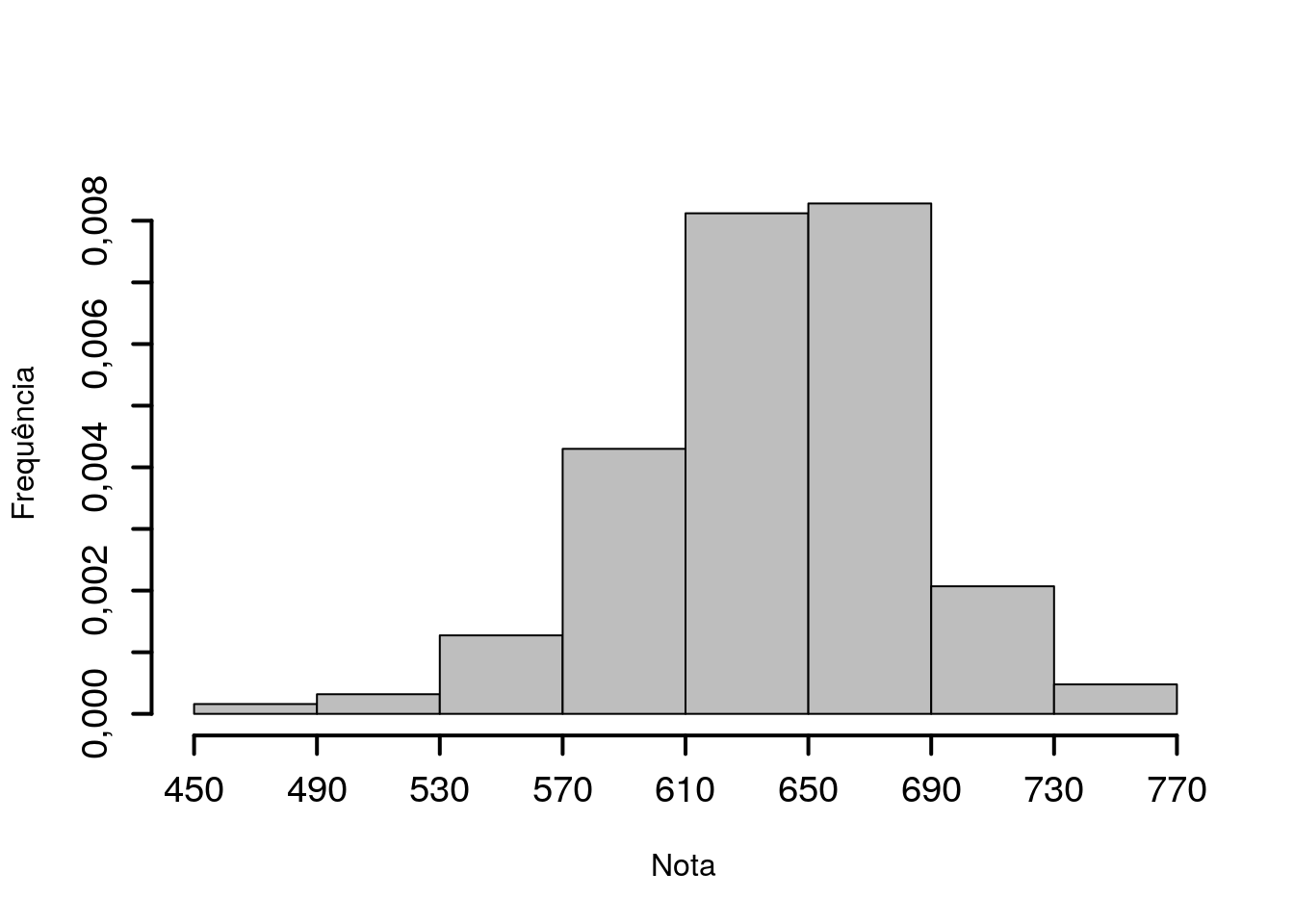
Figura 3.3: :Histograma para a variável Nota.
3.2 Polígono de frequência
Após a construção do histograma, é importante observar tendência de alturas das barras, para isso é interessante construir o polígono de frequência sobre as barras, que é um gráfico de linhas obtido ligando os pontos médios dos topos de cada barra, como mostra a Figura 3.4. Como pode ser visto nessa figura, usando o histograma é fácil observar para quais valores da variável tem-se a maior frequência. No caso da variável “Nota”, percebe-se que aproximadamente 66% dos entrevistados que declarou sua nota, obteve nota entre 610 e 690 pontos.
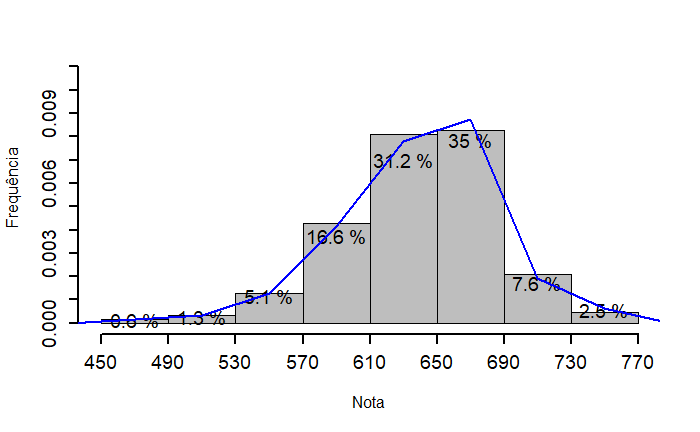
Figura 3.4: :Histograma e polígono de frequência para a variável Nota.
3.3 Exemplo de aplicação
3.4 Exemplos de aplicação
X=DadosEstudantes$Altura
hist(X,
breaks=9, # controla o número de classes
xlab="Nota", # rótulo do eixo das abcissas
ylab="Frequência", # rótulo do eixo das ordenadas
freq=FALSE, # se FALSE a soma da área das barras é 1
probability = TRUE, # se TRUE a soma da área das barras é 1
border="black", # cor para bordas
col="gray", # cor para as barras
main=" " )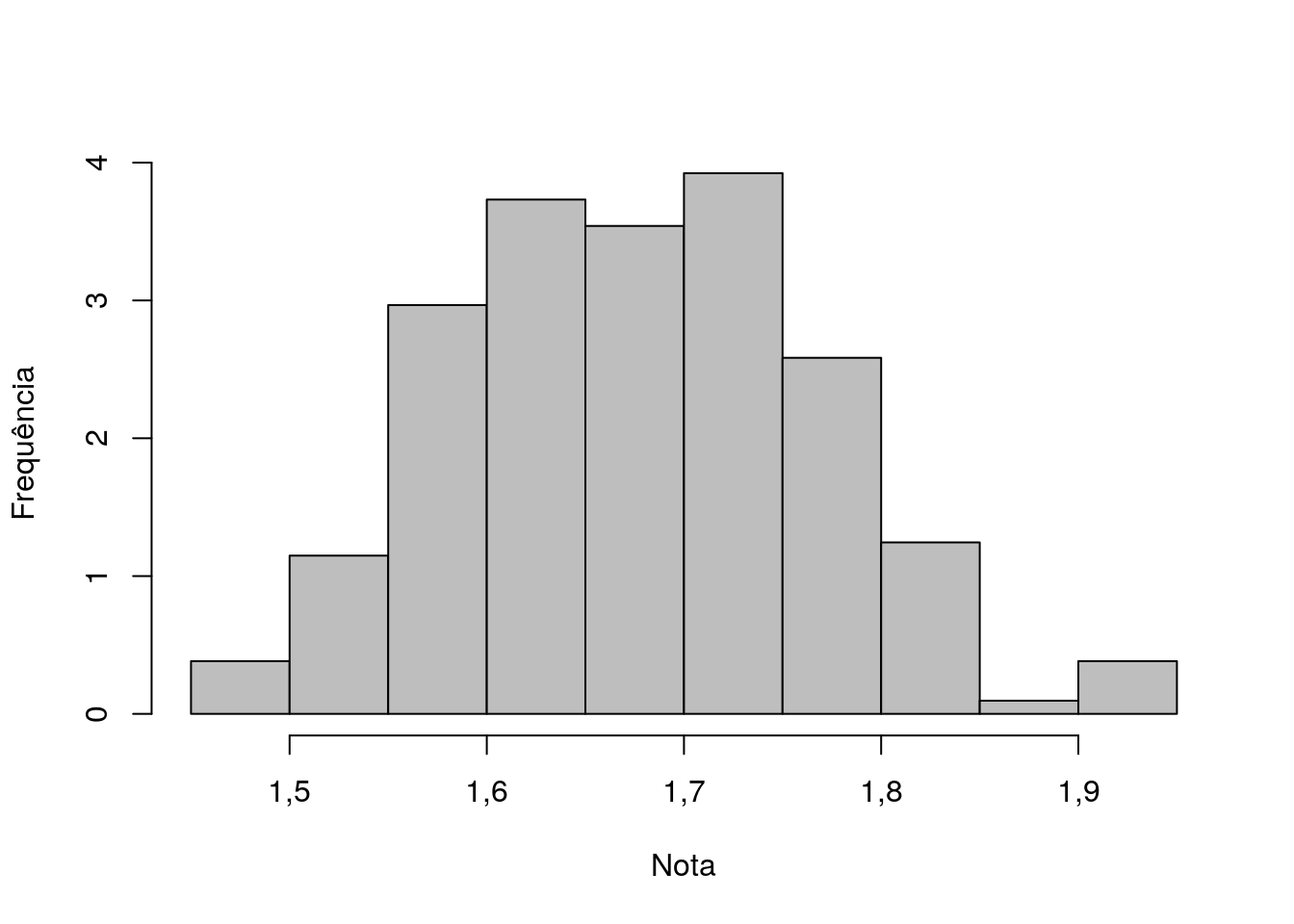
Figura 3.5: :Histograma para a variável Altura.
A Figura 3.5 mostra o histograma para a variável Altura dos estudantes, onde podemos ver que existe uma grande frequência de estudantes com altura entre 1,60 e 1,75 metro de altura (m), sendo a maior frequência entre 1,70 e 1,75 m.
X=DadosEstudantes$Idade
Y=DadosEstudantes$Idade.da.Escolha.do.Curso
## plot x
hist(X, breaks=15, xlab="Nota", ylab="Frequência", freq=FALSE, probability = TRUE, border="black", col="gray", main=" " )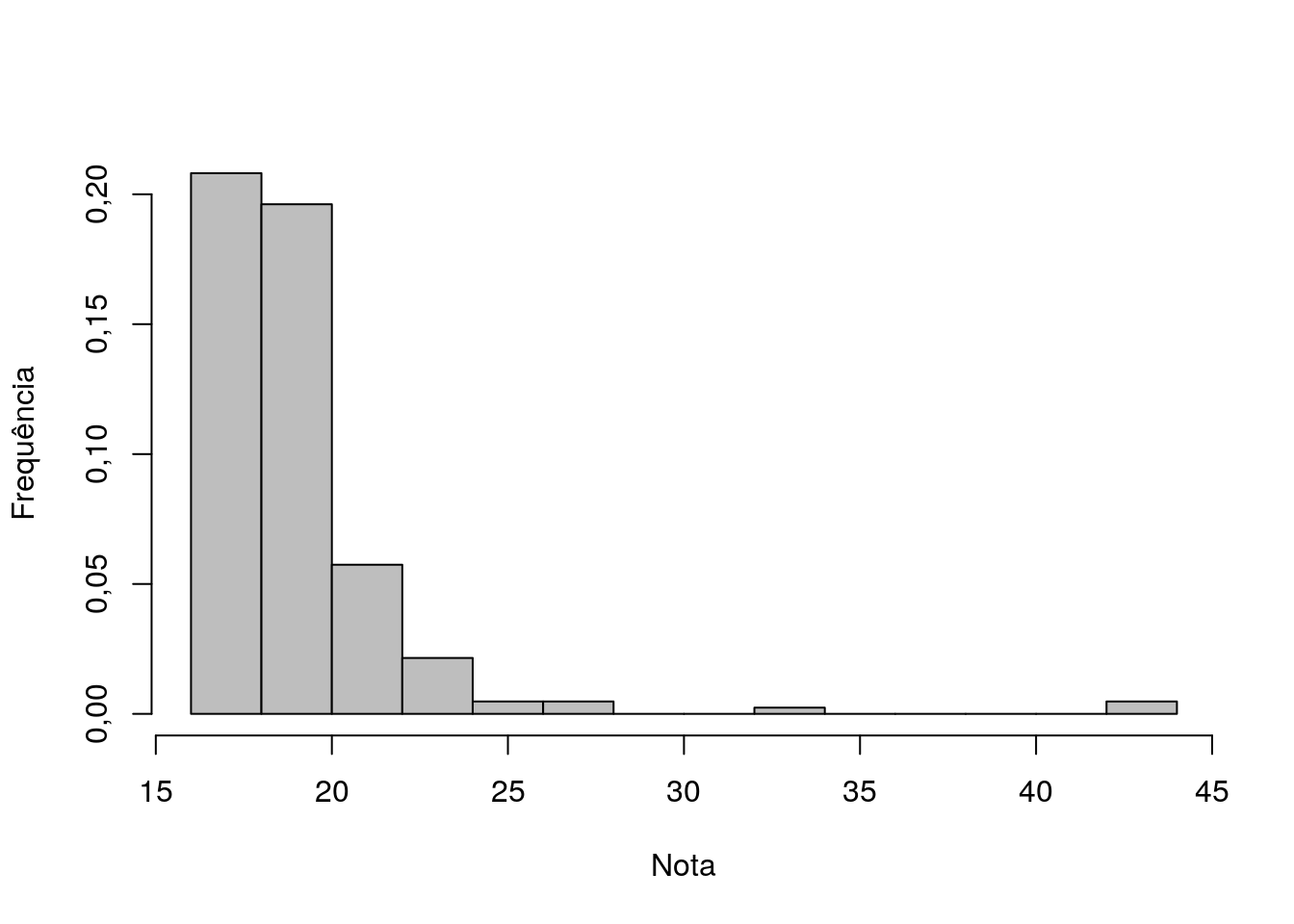
Figura 3.6: :Histograma para a variável Idade na epoca da entrevista
## plot y
hist(Y, breaks=15, xlab="Nota", ylab="Frequência", freq=FALSE, probability = TRUE, border="black", col="gray", main=" " )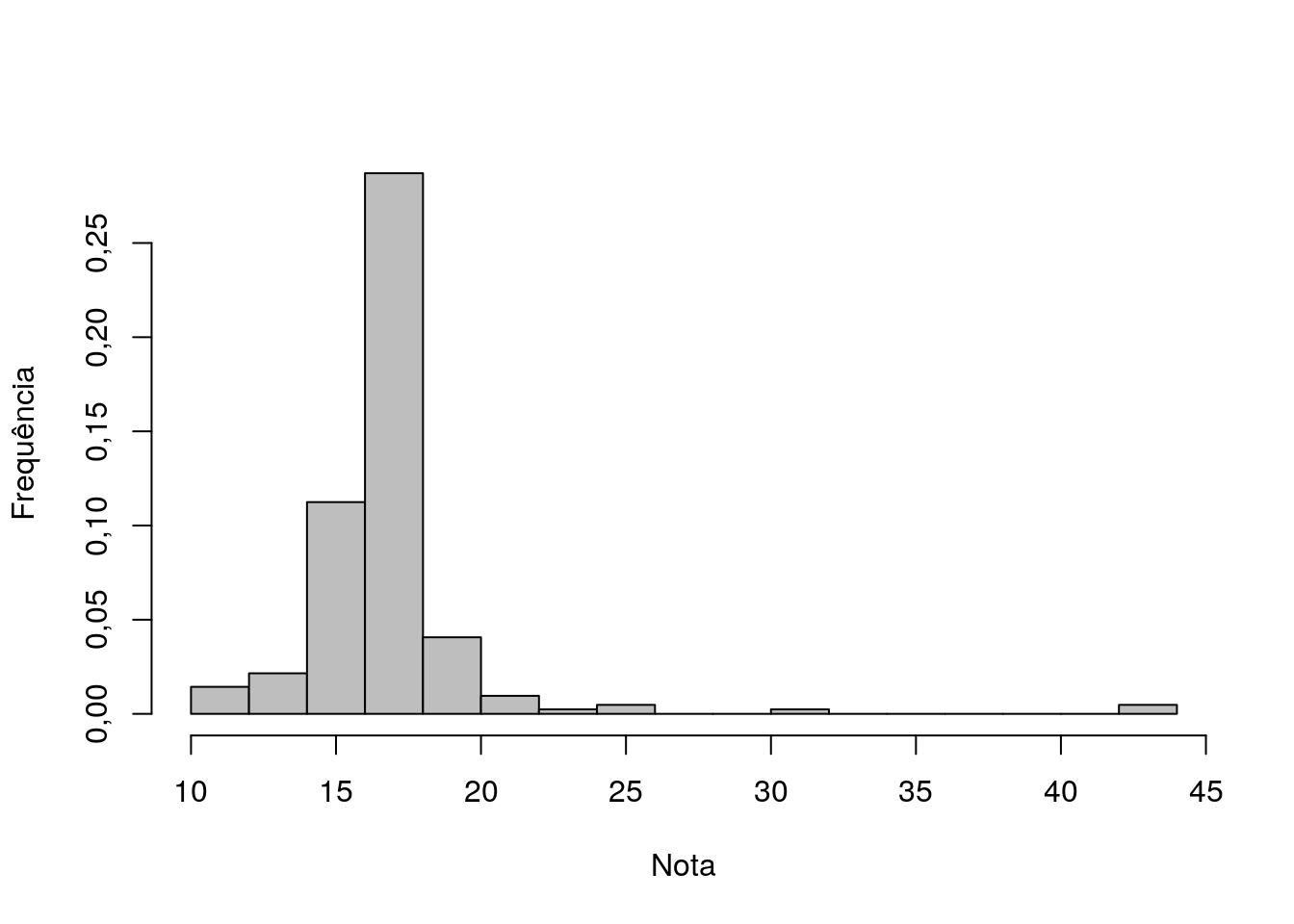
Figura 3.7: :Histograma para a variável Idade de escolha do curso.
As Figuras 3.6 e 3.7 mostram os histogramas das idades no ato da entrevista e as idades em que escolheram o curso em que estão matriculados. Observe que existe uma grande frequência de estudantes com idade em torno de 17 anos, enquanto as idades de escolha ficou em torno de 16, o que leva a conclusão de que existe uma alta frequência de estudantes que decidiram pelos seus cursos em época bem próxima a realização do exame para ingresso na universidade.