6 Marktprognose
Wir wollen den ambitionierten Versuch starten und Bewegungen des DAX vorhersagen. Hierzu verwenden wir das logistische Regressionsmodell und alle in der Vorlesung besprochenen Tools.
#notwendige Pakete
rm(list = ls())
library(tidyquant)
library(data.table)
library(plotly)
library(imputeTS)
library(caret)
library(glmnet)Wir beziehen zunächst die daten und interpolieren fehlende Werte linear.
#Wir beziehen manuell einen Datensatz mit den Daten der letzten 10 Jahre
our_data <- tq_get('^GDAXI'
, from = "1990-01-01", to = "2020-02-28")
#in data.table Format
dt <- data.table(our_data)
rm(our_data)
head(dt)## date open high low close volume adjusted
## 1: 1990-01-02 1788.89 1788.89 1788.89 1788.89 0 1788.89
## 2: 1990-01-03 1867.29 1867.29 1867.29 1867.29 0 1867.29
## 3: 1990-01-04 1830.92 1830.92 1830.92 1830.92 0 1830.92
## 4: 1990-01-05 1812.90 1812.90 1812.90 1812.90 0 1812.90
## 5: 1990-01-08 1841.47 1841.47 1841.47 1841.47 0 1841.47
## 6: 1990-01-09 1865.52 1865.52 1865.52 1865.52 0 1865.52#wir interpolieren fehlende Werte
cols <- names(dt)[-c(1)]
dt <- dt[ , (cols) := lapply(.SD, na_interpolation), .SDcols = cols]Im Anschluss erzeugen wir einige Features in Form technischer Indikatoren. Dies ist eine beliebige Auswahl und Sie können gerne mit anderen technischen Indikatoren herum experimentieren.
#nun bestimmen wir ein paar technische Indikatoren
#verschiedene Zeitfenster für die moving averages
n <- c(10, 20, 50)
#simple moving average
sma_list <- list()
for(i in 1:length(n)){
sma_list[[paste('sma_', n[i], sep = '')]] <- SMA(dt$close, n = n[i])
}
sma_dt <- as.data.table(sma_list)
#exponential moving average
ema_list <- list()
for(i in 1:length(n)){
ema_list[[paste('ema_', n[i], sep = '')]] <- EMA(dt$close, n = n[i])
}
ema_dt <- as.data.table(ema_list)
#Average True Range
atr <- ATR(dt[, .(high, low, close)], n = 14)[,2]
#Average Directional Index
adx <- ADX(dt[, .(high, low, close)], n = 14)[,4]
#Commodity Chanel Index
cci <- CCI(dt[, .(high, low, close)], n = 20, c = 0.015)
#Rate of Change
roc_01 <- ROC(dt$close, n = 1)
roc_05 <- ROC(dt$close, n = 5)
roc_14 <- ROC(dt$close, n = 14)
#Relative Strength Indey
rsi <- RSI(dt$close, n = 14)
#William's %R
will_r <- WPR(dt[, .(high, low, close)], n = 14)
#Stochastic %K
smi <- stoch(dt[, .(high, low, close)])[,1]Im Anschluss erzeugen wir einen Datensatz, der eine Variable “up_move” enthält, die den Wert 1 annimmt, wenn der heutige Schlusskurs über dem gestrigen Schlusskurs liegt. Zudem löschen wir alle Zeilen, in denen mindestens eine NA Beobachtung existiert. Wir teilen den Datensatz zunächst in zwei Perioden auf, die als Trainigs- und Testdaten dienen. Zudem bereiten wir die Daten noch weiter auf, indem wir alle metrischen Variablen auf den Wertebereich \(\left[0,1\right]\) normieren. Dies dient der Vergleichbarkeit der Fearures.
#stelle alle Variablen in einem Datensatz zusammen
pred_data_set <- data.table(dt, sma_dt, ema_dt, atr, adx, cci, roc_01, roc_05, roc_14, rsi, will_r, smi, to_predict = c(dt$close[-c(1)], NA))
#erzeuge Variable, die 1 ist, wenn der Kurs im Vergleich zum Vortag gestiegen ist
pred_data_set[, up_move := (pred_data_set$to_predict > pred_data_set$close) * 1 ]
#lösche die Zeilen mit mindestens einem NA
pred_data_set <- pred_data_set[!is.na(rowSums(pred_data_set[, -c(1)]))]
#Daten zum Schätzen
train_data <- pred_data_set[date < '2014-01-01', ]
#Daten um das Modell out-of-sample zu validieren
test_data <- pred_data_set[date >= '2014-01-01', ]
#Nun beginnen wir mit dem eigentlichen Modell
#um vergleichbare Einflüsse zu haben, standardisieren wir die Daten, auf Basis des
#empirischen Mittelwerts und der Standardabweichung der Trainingsdaten
pre_proc <- preProcess(train_data[, -c('date', 'up_move')], method = c('range'))
train_stand <- predict(pre_proc, train_data[, -c('date', 'up_move')])
train_stand[, date := train_data$date]
train_stand[, up_move := train_data$up_move]
test_stand <- predict(pre_proc, test_data[, -c('date', 'up_move')])
test_stand[, date := test_data$date]
test_stand[, up_move := test_data$up_move]Es erfolgt eine Schätzung des logistischen Regressionsmodells mittels der glm-Funktion.
#Wir schätzen ein logistische Regressionsmodell für die Trainingsdaten
glm_fit <- glm(up_move ~ sma_10 + sma_20 + sma_50 +
ema_10 + ema_20 + ema_50 +
atr + adx + cci + roc_01 + roc_05 + roc_14 + rsi + will_r + smi,
family = binomial(link = 'logit'),
data = train_stand)
#Zusammenfassung des Modells
summary(glm_fit)##
## Call:
## glm(formula = up_move ~ sma_10 + sma_20 + sma_50 + ema_10 + ema_20 +
## ema_50 + atr + adx + cci + roc_01 + roc_05 + roc_14 + rsi +
## will_r + smi, family = binomial(link = "logit"), data = train_stand)
##
## Deviance Residuals:
## Min 1Q Median 3Q Max
## -1.359 -1.237 1.079 1.115 1.399
##
## Coefficients: (1 not defined because of singularities)
## Estimate Std. Error z value Pr(>|z|)
## (Intercept) 0.48411 0.59666 0.811 0.417
## sma_10 2.82682 12.32002 0.229 0.819
## sma_20 8.89447 15.89927 0.559 0.576
## sma_50 6.98394 7.24162 0.964 0.335
## ema_10 0.75334 20.04211 0.038 0.970
## ema_20 -10.59700 37.72110 -0.281 0.779
## ema_50 -8.78678 5.85032 -1.502 0.133
## atr -0.15729 0.26160 -0.601 0.548
## adx 0.08017 0.16527 0.485 0.628
## cci 0.32110 0.65777 0.488 0.625
## roc_01 -0.05341 0.44841 -0.119 0.905
## roc_05 -1.06866 0.69879 -1.529 0.126
## roc_14 0.61948 0.73522 0.843 0.399
## rsi -0.35523 0.54979 -0.646 0.518
## will_r -0.14209 0.22458 -0.633 0.527
## smi NA NA NA NA
##
## (Dispersion parameter for binomial family taken to be 1)
##
## Null deviance: 8507.2 on 6156 degrees of freedom
## Residual deviance: 8495.5 on 6142 degrees of freedom
## AIC: 8525.5
##
## Number of Fisher Scoring iterations: 3Wir sehen, dass keines der Features einen statistisch signifikant von Null verschiedenen Einfluss hat. Dennoch erzeugen wir Prognosen für die Trainings- und Testdaten und betrachten die Accuracy.
#In sample Prognose
y_train_predict_glm <- (predict(glm_fit, train_stand, type = 'response') > 0.5) * 1## Warning in predict.lm(object, newdata, se.fit, scale = 1, type = if (type == :
## prediction from a rank-deficient fit may be misleading## [1] 0.5332142#Out of sample Prognose
y_test_predict_glm <- (predict(glm_fit, test_stand, type = 'response') > 0.5) * 1## Warning in predict.lm(object, newdata, se.fit, scale = 1, type = if (type == :
## prediction from a rank-deficient fit may be misleading## [1] 0.5259782Entsprechend schlecht ist die Prognose unseres Modells. Dies ist übrigens kein unerwartetes Ergebnis, da man bei effizienter Informationsverarbeitung des Marktes heutiger Kurse und daraus abgeleiteter Informationen keinerlei Informationsvorteil für zukünftige Entwicklungen besitzt. Nichts desto trotz kann man mit diesem Modell in ineffizienten Märkten sich zumindest temporär informativen Vorteil verschaffen und bessere Prognosen erzielen. In der Literatur werden hier bis zu 80% erreicht. Dennoch liefert das Ergebnis hier ein paar weitere Eigenheiten, die didaktisch sehr wertvoll sind. Zunächst gibt hier R eine Warnmeldung aus die auf einen nicht-vollen Rang der Matrix hinweist. Ohne darauf zu sehr im Detail einzugehen, kann dies ein Indiz für entweder zu viele Features oder für hohe Korrelationen zwischen den Features hindeuten. Da in unserem Fall das Verhältnis von Featureanzahl zu Datenpunkten relativ klein ist, liegt es näher, dass hohe Korrelation zwischen den Features besteht.
#potentiel kann es problematisch werden, wenn die Prediktoren zu stark korreliert sind
corr <- cor(train_stand[ , -c('open', 'high', 'low', 'close', 'volume', 'adjusted', 'to_predict', 'date', 'up_move')])
x <- names(train_stand[ , -c('open', 'high', 'low', 'close', 'volume', 'adjusted', 'to_predict', 'date', 'up_move')])
y <- x
plot_ly() %>%
add_trace(type = 'heatmap', x = x, y = y, z = corr) %>%
layout(title = 'Korrelationen der Features')Durch einen Blick auf die Heatmap bestätigt sich dieser Verdacht. Ein möglicher Umgang damit, ist es das Model mit einem Regularisierungsterm zu schätzen. Diese Möglichkeit ist durch die glmnet-Funktion im gleichnamigen Paket gegeben.
#hierfür benötigen wir die Prediktoren und die abhängige Variable in etwas anderem Format
X_train_stand <- as.matrix(train_stand[ , -c('open', 'high', 'low', 'close', 'volume', 'adjusted', 'to_predict', 'date', 'up_move')])
y_train_stand <- as.integer(train_stand$up_move)
X_test_stand <- as.matrix(test_stand[ , -c('open', 'high', 'low', 'close', 'volume', 'adjusted', 'to_predict', 'date', 'up_move')])
y_test_stand <- as.integer(test_stand$up_move)
#Schätzen mittels glm_net
glm_fit_reg <- glmnet(X_train_stand, y_train_stand, family = 'binomial')
#betrachte die geschätzten Koeffizienten mit steigender Regularisierung bzw. Erklärungsgüte
plot(glm_fit_reg, xvar = 'lambda', label = T)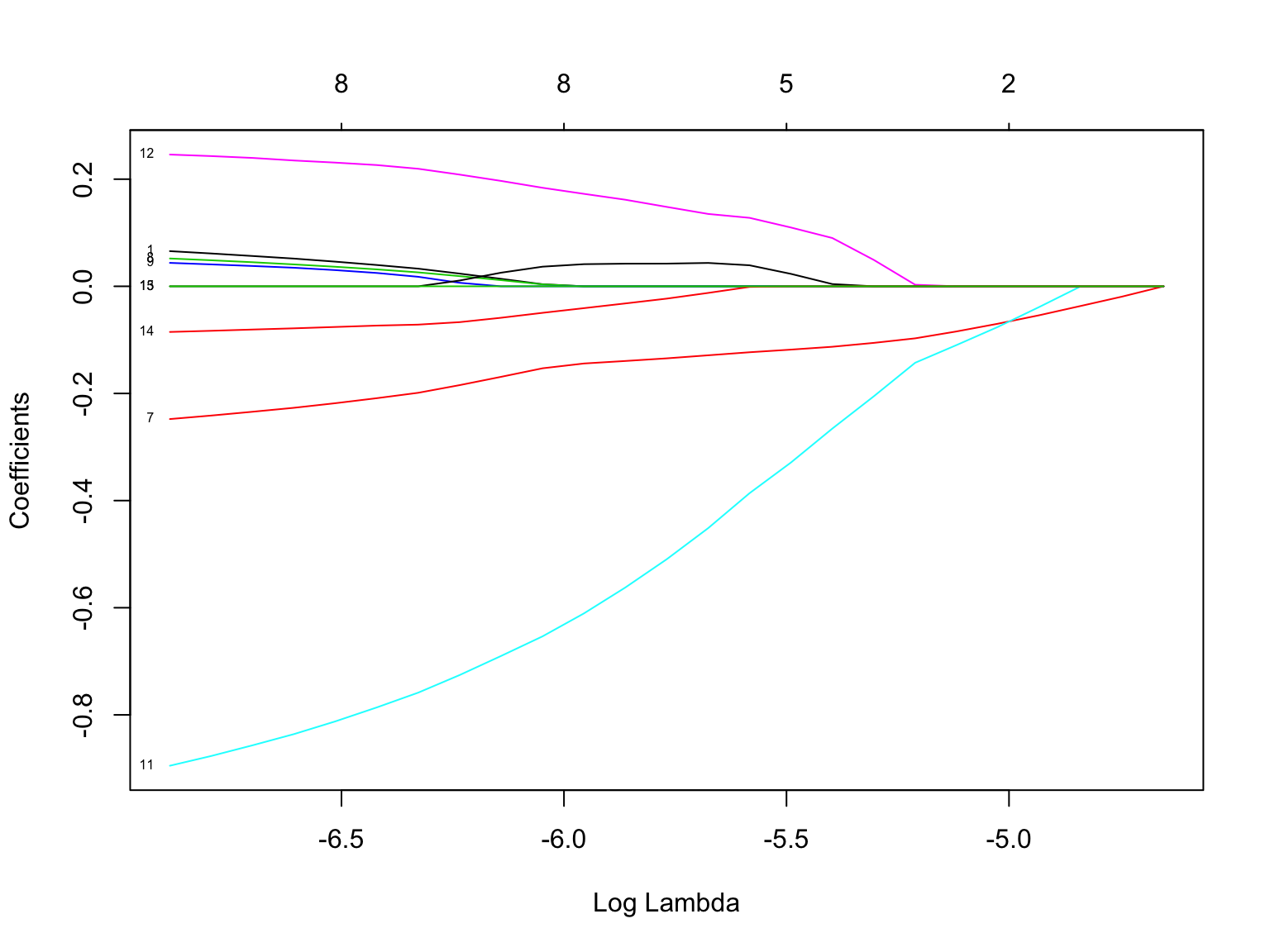
Diese Grafik zeigt auf einer Log-Skala, wie sich der Wert der Regressionskoeffizienten mit steigendem Gewicht der Regularisierung für alle Features verringert. Der \(\alpha\) Parameter der Regularisierung ist im Standard auf 1, womit wir es mit einer L1-Regularisierung zu tun haben. Diese ist dafür bekannt, dass sie die geschätzen Werte der Koeffizienten der nicht benötigten Features in Richtung 0 drückt. Bei einer L2-Regularisierung mit \(\alpha = 0\) ist es eher so, dass die geschätzten Werte korrelierter Features gleichermaßen kleiner werden.
Betrachten wir die Modellschätzung für verschiedene Werte von \(\lambda\):
##
## Call: glmnet(x = X_train_stand, y = y_train_stand, family = "binomial")
##
## Df %Dev Lambda
## 1 0 0.000e+00 0.009536
## 2 1 4.490e-05 0.008689
## 3 1 8.218e-05 0.007917
## 4 2 1.475e-04 0.007214
## 5 2 2.035e-04 0.006573
## 6 2 2.500e-04 0.005989
## 7 3 2.919e-04 0.005457
## 8 3 3.727e-04 0.004972
## 9 4 4.441e-04 0.004530
## 10 4 5.100e-04 0.004128
## 11 5 5.655e-04 0.003761
## 12 6 6.224e-04 0.003427
## 13 6 6.694e-04 0.003123
## 14 6 7.084e-04 0.002845
## 15 6 7.409e-04 0.002593
## 16 8 7.754e-04 0.002362
## 17 8 8.152e-04 0.002152
## 18 9 8.502e-04 0.001961
## 19 8 8.801e-04 0.001787
## 20 8 9.018e-04 0.001628
## 21 8 9.199e-04 0.001484
## 22 8 9.349e-04 0.001352
## 23 8 9.470e-04 0.001232
## 24 8 9.575e-04 0.001122
## 25 8 9.662e-04 0.001023Df steht hier für die Anzahl der (verlorenen) Freiheitsgrade und ist mit der Anzahl der Features im Modell gleichzusetzen deren geschätzter Koeffizient von null verschieden ist. %Dev ist eine Kennzahl der logistischen Regression, die man analog wie das \(R^2\) der linearen Regression interpretieren kann. Wir sehen das die Deviance (%Dev) mit sinkendem \(\lambda\) bzw. steigender Anzahl an null verschiedener Features zunimmt. Die Zunahme ab einem gewissen Wert sich nicht mehr stark verbessert. Insofern macht es ggf. Sinn nicht den kleinsten Wert für \(\lambda\) zu wählen, sondern einen Kompromiss aus Datenanpassung und Einbeziehung von null verschiedener Features einzugehen. Wir wählen für \(\lambda\) den Wert, den ersten, bei dem die Deviance Ratio mindesten bei 85% liegt und betrachten das hierzu geschätzte Regressionsmodell bzw. seine geschätzten Koeffizienten.
#verwenden wir zunächst aus den Lambdawerten den ersten, beim die Deviance Ratio 85% der maximal erreichbaren ist
lambda_dev <- glm_fit_reg$lambda[glm_fit_reg$dev.ratio - quantile(glm_fit_reg$dev.ratio, 0.8) > 0][1]
#man kann schön sehen, wie durch die Regularisierung Koeffzienten wegfallen, die untereinander stark korreliert sind
coef_shrink <- coef(glm_fit_reg, s = lambda_dev, exact = TRUE, x = as.matrix(X_train_stand), y = y_train_stand)
coef_shrink## 16 x 1 sparse Matrix of class "dgCMatrix"
## 1
## (Intercept) 5.179196e-01
## sma_10 4.600266e-02
## sma_20 .
## sma_50 .
## ema_10 .
## ema_20 .
## ema_50 .
## atr -2.181644e-01
## adx 3.645403e-02
## cci 3.020877e-02
## roc_01 .
## roc_05 -8.120283e-01
## roc_14 2.309009e-01
## rsi .
## will_r -7.589495e-02
## smi 1.631298e-15Man kann gut erkennen, dass gerade die Koeffizienten der Variablen bei null sind, deren Korrelation zu einer oder mehreren anderen Variablen sehr hoch ist. Genau dies soll die Regularisierung bewirken. Wie wir gleich sehen, verbessert dies leider nicht unsere Modellperformance was die Accuracy der Prognosen betrifft. Jedoch hat sich die Prognose der Testdaten zumindest ein wenig verbessert.
#Leider verbessert auch dies unsere Prognose nicht
acc_train_glm_shrink <- mean(y_train_stand == as.integer(predict(glm_fit_reg, newx = X_train_stand, type = 'class', s = lambda_dev)))
print(acc_train_glm_shrink)## [1] 0.5367874acc_test_glm_shrink <- mean(y_test_stand == as.integer(predict(glm_fit_reg, newx = X_test_stand, type = 'class', s =lambda_dev)))
print(acc_test_glm_shrink)## [1] 0.5355997Um den Wert für \(\lambda\) nicht willkürlich wählen zu müssen, führen wir eine Cross-Validation durch, bei der die Anzahl der Trainingsdaten über die Zeit sukzessive aufgefüllt werden. Wir verwenden dann den durchschnittlich Wert der \(\lambda\) Werten, die in den einzelnen Auswertungen, die beste Trainingsaccuracy erreichen.
test_size <- 1000
train_folds <- 5
window_length <- floor((dim(train_stand)[1] - test_size)/train_folds)
remaining <- (dim(train_stand)[1] - test_size) - window_length * train_folds
print(paste('The last ', remaining, ' observations are not used for pseudo-crossfold-validation'))## [1] "The last 2 observations are not used for pseudo-crossfold-validation"fold_results <- matrix(ncol = 2)
for(i in 1:train_folds){
train_fold <- train_stand[1:(window_length * i), ]
X_train_fold <- as.matrix(train_fold[ , -c('open', 'high', 'low', 'close', 'volume', 'adjusted', 'to_predict', 'date', 'up_move')])
y_train_fold <- as.integer(train_fold$up_move)
test_fold <- train_stand[((window_length * i) + 1):((window_length * i) + test_size), ]
X_test_fold <- as.matrix(test_fold[ , -c('open', 'high', 'low', 'close', 'volume', 'adjusted', 'to_predict', 'date', 'up_move')])
y_test_fold <- as.integer(test_fold$up_move)
glmnet_fold <- glmnet(X_train_fold, y_train_fold, family = 'binomial')
acc_fold <- c()
for(j in 1:length(glmnet_fold$lambda)){
acc_fold <- c(acc_fold, mean(y_test_fold == as.integer(predict(glmnet_fold,
newx = X_test_fold,
s = glmnet_fold$lambda[j],
type = 'class'))))
}
lambda_choose <- data.table(lambda = glmnet_fold$lambda, acc_fold = acc_fold)
fold_results <- rbind(fold_results, as.matrix(lambda_choose[acc_fold == max(acc_fold),][lambda == max(lambda), ]))
}
fold_results <- data.table(fold_results[-c(1), ])
acc_train_glm_cv_shrink <- mean(y_train_stand == as.integer(predict(glm_fit_reg, newx = X_train_stand, type = 'class', s = mean(fold_results$lambda))))
print(acc_train_glm_cv_shrink)## [1] 0.5338639acc_test_glm_cv_shrink <- mean(y_test_stand == as.integer(predict(glm_fit_reg, newx = X_test_stand, type = 'class', s = mean(fold_results$lambda))))
print(acc_test_glm_cv_shrink)## [1] 0.5381655Hier noch mal ein kleiner Überblick der drei Vorgehen:
results <- round(cbind(c(acc_train_glm, acc_train_glm_shrink, acc_train_glm_cv_shrink),
c(acc_test_glm, acc_test_glm_shrink, acc_test_glm_cv_shrink)), 4)
colnames(results) <- c('Training Acc', 'Test Acc')
rownames(results) <- c('GLM', 'GLM Shrinkage', 'GLM Crossfold Shrinkage')
library(knitr)
kable(results)| Training Acc | Test Acc | |
|---|---|---|
| GLM | 0.5332 | 0.5260 |
| GLM Shrinkage | 0.5368 | 0.5356 |
| GLM Crossfold Shrinkage | 0.5339 | 0.5382 |
Die hier durchgeführte Analyse kann an diversen Stellen anders durchgeführt werden. Zudem kann und sollte man verschiedene Märkte und Zeithorizonte ausprobieren. All dies steht Ihnen frei bzw. wird voraussichtlich Teil der Projektarbeit sein.