Chapter 4 Probability

4.1 Motivation

Perhaps the best formal definition of the field of Statistics is “the study of uncertainty.” No concept champions uncertainty better than Probability, the undisputed poster child of Statistics. Probability is to this day touted as one of the hardest concepts to master since it is often called the ‘least intuitive’ of academic subjects. Intuitive or not, it remains one of the most interesting fields in the empirical sciences with far reaching real world applications. By devoting time and effort to mastering the following concepts, you are establishing a valuable quantitative toolbox to help you succeed inside and outside of the classroom. Please refer to this book for a full treatise on Probability.

4.2 Basics of Probability

Naive Probability is likely what you have used up until this book when confronted with a probability problem. The method is simply the following: if you have some desired outcome (perhaps flipping tails on a coin) the way to find the probability of it occurring is $\frac{\# \; of \; desirable \; outcomes}{\# \; of \; total \; outcomes}$. So, since there are two outcomes to a fair coin flip (heads or tails) but only one desirable one (tails) we would just get $\frac{1}{2}$.

Probabilistic events or outcomes are events we are uncertain about; they have some probability, or chance, that they will occur. Flipping a fair coin and getting heads (certainly the most popular of probability examples) is a probabilistic event because there is a 50% chance (or .5 Probability) it occurs.

Random Experiments are functions with many possible probabilistic events/outcomes. For instance, rolling a fair, six sided die is a random experiment: in this case, there are six possible events/outcomes.

Random Experiments have Sample Spaces, which are collections of all possible outcomes of the event. In the die example, the sample space would be $\{1,2,3,4,5,6\}$. Sample spaces must be Exhaustive, meaning that we can list everything in the sample space, and Mutually Exclusive, meaning that no two outcomes can occur at the same time.

Can you think of sample spaces that would violate the two properties above? One example might be trying to make people’s weights a random experiment (where different outcomes have different probabilities). This violates both assumptions: it is not exhaustive because we can’t list every single weight (it’s continuous and there are infinite points) and it’s not mutually exclusive because two people can weigh the same amount.

A bit more quantitative are the widely feared Three Axioms (Rules) of Probability. They might seem basic, but a thorough understanding of them can make many problems much easier to solve. They are:

$P(A)$ is between 0 and 1 (inclusive of the endpoints). Basically, there can’t be less than a 0% chance of something happening, but there also can’t be over a 100% chance of it happening.

The sum of the associated probabilities for all of an experiment’s outcomes must add to 1. Again, best to think about this intuitively. If we are flipping a coin, there’s a 100% chance something will happen (heads or tails) so all of the different events must add up to 1.

$P(\bar{A}) = 1 - P(A)$. This is sort of an extension of Axiom 2 (the bar over the first $A$ means $A$ complement, or Event $A$ not occurring). If we isolate the outcome $A$, there are really only two possibilities: $A$ happening and $A$ not happening. Since the probabilities must add up to 1, we get the above equation.

Where $P(A)$ = Probability event $A$ occurs. If this confuses you, just remember that, when flipping a fair two-sided coin, $P(Heads) = .5$.

Finally, in this book, we will mostly deal with three types of probabilities: marginal, conditional and joint probabilities.

Marginal Probability is essentially basic probability: it is just the probability of a single event occurring (not worrying about anything else). So, the marginal probability of rolling a $2$ on a fair six sided dice is simply $\frac{1}{6}$.

Conditional Probability is a step beyond marginal. While it still gives the probability of a single event occurring, it now establishes some condition, or requirement that some other event occurs. An easy example to visualize is the question “Given that you roll above a $2$ on a fair, six sided die, what is the probability you roll a $5$?” Essentially, this parses the sample space down because it sets some outcome in addition to the event we are curious about (here, sample space goes from $\{1,2,3,4,5,6\}$ to $\{3,4,5,6\}$, because we are given that we rolled above $2$). So, you would be able to probably piece out (using naive probability) that the answer here is $\frac{1}{4}$ (we will formalize how to find this solution soon).

Joint Probability is a straightforward twist on marginal: it’s just the probability of multiple events occurring. So, while the probability of flipping heads on a coin and rolling a $3$ on a die are both marginal, the probability of both occurring is a joint probability. We will learn how to calculate these later (it largely depends on independence, which we will also discuss later).

Perhaps the most important problem solving skill of this section is being able to deal with probability tables. These appear with joint distributions, which we will discuss more later.

Consider the following table, which breaks down the probability that a randomly selected person attends Harvard or does not attend Harvard, and the probability that a randomly selected person’s favorite color is Crimson or some other color.

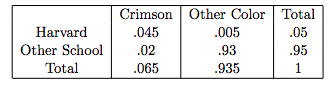
A quick comprehension key: according to this table, there is a $.045$ probability that someone goes to Harvard and has the favorite color Crimson.

Let’s learn how to read this table by using our three basic probabilities. First, we’ll start with a marginal probability: just the basic probability that a randomly selected person attends Harvard. In the table, we see two types of these people: Harvard students with the favorite color Crimson and (blasphemy) Harvard students with a different favorite color. What we are interested in for marginal probabilities is just the overall probability of attending Harvard, so here we want the total. This is clearly given by the column furthest, right: it is the sum of the two Harvard categories, $.05$. Therefore, overall, the marginal probability that someone attends Harvard is $.05$. We are lucky enough to have a convenient pneumonic here: the marginal probabilities are found in the margins.

So, extending this concept, we can find the rest of the marginals: $P(Other \; School) = .95$, $P(Crimson) = .065$, and $P(Other \; Color = .935)$.

We will next consider a conditional probability. Again, this is the probability of some event given some other event occurred. An example here would be the probability that someone’s favorite color is crimson given that they go to Harvard (remember, we are parsing the sample space down to students who attend Harvard!).

To find this in the table, we simply take the intersection of Harvard and Crimson ($.045$) and divide it by the marginal (total) probability that someone attends Harvard ($.05$).

If you aren’t clear on why we do this, don’t worry: we will formalize it with a definition and formula soon. However, it’s not too crazy to wrap your intuition around. We know that we are given that someone attends Harvard, so we’re already working within that $.05$ fraction of the sample space. Then, we just need to find the proportion of this parsed sample space that likes crimson. To do this, we just divide (for those following at home, the answer comes out to $.9$).

Finally, let’s do a joint probability. Again, this is the probability of two events occurring. One example would be the probability that someone goes to another school and the probability they like Crimson. This is just the intersection of the two: here, $.02$.

Don’t worry if you’re unsure how to actually calculate these probabilities; we haven’t learned that yet. This piece was just to establish how to read one of these tables, since it will often be your best weapon against these questions.

## Applications of Probability Axioms
Now that we have the qualitative based established, we will form some useful tools that arise from the concepts we’ve discussed. It’s going to get a little more ‘mathy,’ so roll up your sleeves.

First, a little notation. Two common expressions that you might see in Probability are $\cap$ and $\cup$. For example:

\[P(A\cap B), \; P(A \cup B)\]

The first one means, in english, probability of $A$ and $B$ occurring. This is commonly called the intersection of the two events $A$ and $B$. The second expression in english means the probability of $A$ or $B$ occurring}. This is often called the union of $A$ and $B$.

Familiarize yourself with these expressions since they will show up often!

Now for the application. We’ve discussed conditional probability but have yet to quantify the relationship of conditional events. Conditional events $A$ and $B$ are denoted with the notation $P(A|B)$, which means in english "the probability that event $A$ occurs given that event $B$ has occurred. The full equation is:

\[P(A|B) = \frac{P(A \cap B)}{P(B)}\]

Where, again, $P(A \cap B)$ = Probability $A$ and $B$ occur (the intersection). So, in english, the probability of event $A$ occurring given that event $B$ occurred equals the probability of both $A$ and $B$ occurring divided by the probability of $B$ occurring. This is an extremely common relationship that can help you find both conditional probabilities and intersections (probability of $A$ and $B$) depending on what a problem gives you (more on why this works later).

In fact, let’s return to the Harvard probability table. Remember when we calculated the conditional probability of liking crimson given someone goes to Harvard? This was the exact formula we used: dividing the intersection by the marginal (again, we’ll see soon just why this works if you are interested).

So, this formula will give us the tools to find conditional probabilities and intersections, but not union probabilities ($A$ or $B$ occurring). The formula needed for that is:

\[P(A \cup B) = P(A) + P(B) - P(A\cap B)\]

Again, we need the intersection.

The intuition behind this revolves around the fact that we do not want to overcount, so we have to subtract out the intersection of the two.

This is pretty difficult to think about, but pretty straightforward to visualize in a Venn Diagram.

Draw a two circle Venn Diagram with circles labeled $A$ and $B$. Let’s say $A$ is playing hockey, and $B$ is playing basketball. You took a survey of 50 people, and you fill in the Venn Diagram as follows: 15 play hockey only (in just the $A$ circle), 20 play basketball only (in just the $B$ circle), 3 play both (in the intersection of the circle) and 12 do not play either (outside the circle).

Say you want to find $P(A \cup B)$, the probability that someone plays hockey or they play basketball. You can easily find the probability they play hockey (just $\frac{18}{50} = .36$, or points in the $A$ circle divided by total points) and the probability they play basketball ($\frac{23}{50} = .46$). However, if you added these together, which is the intuitive thing to do, you would get a probability of $.82$. It’s clear that, since there are 12 people out of the 50 people sampled that play neither, the probability that someone plays a sport (hockey or basketball, or both: doesn’t matter, since all of those are playing a sport) is just $\frac{50 - 12}{50} = \frac{38}{50} = .76$.

Why did we get a different (larger) answer? The sharp eyed among you will notice that we added the intersection of 3 people that play both twice: once when we found each marginal probability of playing one of the sports. Therefore, we have to subtract it out once to make sure that we are only adding it in to the final equation one time. We wouldn’t want people that played both to be over-counted, since we are only looking for probability of playing a sport (don’t want to weight it if someone plays multiple sports).

So, given that we have all of the probabilities already, we do $\frac{18}{50} + \frac{23}{50} - \frac{3}{20} = .76$, which is the correct answer and thus the equation is validated.

Yes, you could have just added up the numbers inside the circle once (15 + 3 + 20) and then divided by the total number (50). Either way works, but the formula will likely be more handy in more complex applications.

Now we’ll discuss the concept of independence. We’ve mentioned it qualitatively but will now formally define it. This is one of the most important sections of probability and will also help to prove many other important results that we have already discussed.

First, the definition. Events $A$ and $B$ are independent if they are not related at all; that is, knowing the outcome of $A$ does not affect the probability of event $B$ occuring. We can write this statistical terms as:

\[P(A|B) = P(A)\]

Here, $A$ and $B$ are independent because the probability of $A$ given $B$ is the same as the probability of $A$ occurring (conditional equals the marginal). That means that even if $B$ occurs, the two events do not relate and therefore we have no information about $A$ and thus it’s probability doesn’t change. So, you can declare two events independent if:

\[P(A|B) = P(A) \; or \; P(B|A) = P(B)\]

We can apply this result to other important concepts. First, if we had to breakdown a joint probability ($P(A \cap B)$) in terms of marginals and conditionals, we would use the following formula:

\[P(A \cap B) = P(A|B)P(B)\]

For those interested, this is where we get the conditional formula we have already discussed: just divide $P(B)$ to both sides to get the exact same formula from earlier.

This is called the General Multiplication Rule. Why does it makes sense? Consider $P(A|B)P(B)$. If we know that both events $A$ and $B$ are going to occur, then we know we have some probability of event $B$ occurring (the $P(B)$ term) and then, since we know $B$ occurred, we need to multiply by the probability that $A$ occurs given that $B$ occurred (the conditional term $P(A|B))$. This gives the overall probability of both $A$ and $B$ occurring.

Consider an example to illustrate this principle. Say the probability that we use an umbrella is 10%, and the probability of rain on any given day is 20%. However, these are not independent. The probability that we use an umbrella depends on the weather: given that the day is raining, we have a higher probability of using an umbrella: 40%. Therefore, if we wanted to find the intersection probability of rainy day and wear umbrella, we would take the probability of a rainy day and, since it is now a given that it is a rainy day, multiply by the conditional probability that we wear an umbrella given that it is raining ($(.2)(.4) = .08$).

Anyways, you may have already seen where independence plays a role here. If events $A$ and $B$ are independent, then you know $P(A|B) = P(A)$, and you can substitute $P(A)$ into the above equation to get:

\[P(A \cap B) = P(A)P(B)\]

You can see, then, why it is very valuable to be able to prove independence: it allows us to easily find intersections by just multiplying marginal probabilities, instead of finding all of those tricky conditionals (as you can guess, not as easy to do). One example would be finding the probability of rolling a six on a fair die and flipping heads on a fair coin. Since the two are independent, you would just multiply: $(\frac{1}{6})(\frac{1}{2}) = \frac{1}{12}$.

Unfortunately, while independence is often a time-saver, a big pitfall of probability is assuming independence without actually checking it. Two events are only independent if the identity we discussed, $P(A|B) = P(A)$, holds.

One common probability problem will be testing the independence of jointly distributed variables. This is the first time we’ve seen this type of joint distribution in practice; it is a large part of probability and we will now discuss it.

4.2.1 Joint Distributions

We’re going to discuss distributions and random variables in much more depth later; for now, basically think of jointly distributed events as two variables $X$ and $Y$ with the probabilities broken down between them. It’s best illustrated via a table, and we’ve already seen one example in this text (the Harvard/Crimson example). Here is another joint distribution, illustrated in a table. This is from a sample of 100 Ivy League students, and measures the probability that they go to certain colleges and the probability that they are Rhodes Scholars.

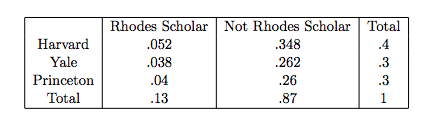
Remember that, since probability over all partitions must add up to one, the ‘Total’ row and column, as well as all the probabilities inside the table, should themselves all sum to one to be a valid table. A non-valid table would violate this summing to 1 property; it could also have a negative value, and we know that probabilities can’t be negative.

So, here are the two variables that are jointly distributed; ‘College’ and ‘Rhode Scholar status.’ While joint distributions are really pretty complex beasts, our work with them here is pretty cursory and usually just boils down to being able to read this table. We will thus illustrate the common concepts of a joint distribution through this table.

First (and we’ve already touched upon this) how do the marginal, conditional and joint probabilities show up here? We know that college is conditionally distributed on Rhodes Scholar status, but know little in terms of probabilities.

As we learned earlier, the marginal probabilities can be found in the margins. So, you would total all of the Harvard probabilities (Rhodes Scholar and Not Rhodes Scholar) to get the marginal $P(Harvard) = .4$. This makes sense, since we are looking for the overall probability of Harvard, which consists of it’s probability in both partitions of the conditional distribution (Rhodes Scholar and Not Rhodes Scholar).

Joint probabilities are relatively straightforward: they are just the actual numbers inside the table. For example, .04 gives the probability that someone attends Princeton and is a Rhodes Scholar. These may be written statistically as $P_{x,y}(x,y)$ or $P(X=x \cap Y=y)$.

Conditional probabilities, then, are easy, since they are just calculated using the joint and marginal (the joint divided by the marginal).

That is the method for reading these tables, and with this knowledge and the tools we’ve already discussed for probability, you should be comfortable with almost all of the table questions thrown at you. The most common example follows:

A very common question here would be “Is college independent of Rhodes Scholar?” (does the probability of being a Rhodes Scholar depend on being in a certain school, or vice versa).

To answer this, you would have to check the marginals versus the conditionals for each possible outcome. Here, we would start with if $P(Harvard) = P(Harvard | Rhodes \; Scholar)$. You should be comfortable calculating this from the table: $P(Harvard) = .4$, and $P(Harvard | Rhodes \; Scholar) = \frac{.052}{.13} = .4$, so the identity holds.

You might feel inclined to stop there and claim independence. However, you would have to check every single outcome to see if the same identity held. Here, $P(Yale) = .3$, which does not equal $P(Yale | Rhodes \; Scholar)$ (they are close, but they must be exactly the same to be independent) and thus we can say that the two variables are dependent.

Again, be careful: even if one cell seems to work, you must check all of them.

4.2.2 Return to the Probability Axioms

Finally, we have Bayes Rule. The formula is:

\[P(A|B) = \frac{P(B|A)P(A)}{P(B)}\]

This can prove extremely useful when switching between conditional probabilities: going from $P(A|B)$ to $P(B|A)$. We won’t delve into the intuition behind this since it’s not really a big factor in this book; just a useful little formula that might come in handy.

This has been a long section, so we will now summarize the most important applications that we’ve discussed:

\[P(A \cap B) = P(A|B)P(B) = P(B|A)P(A)\]

This is the General Multiplcation Rule, and can be rearranged to form the staple equation of conditional probability:

\[P(A|B) = \frac{P(A \cap B)}{P(B)}\]

When dealing with unions, remember the formula:

\[P(A \cup B) = P(A) + P(B) - P(A \cap B)\]

For two independent events $A$ and $B$:

\[P(A \cap B) = P(B)P(A)\]

And finally, Bayes Rule:

\[P(A|B) = \frac{P(B|A)P(A)}{P(B)}\]

One last bit about probability that hasn’t been covered: you may get asked on problem sets or exams to find the probability of ‘at least one event occurring.’ For example, if you flip a coin 5 times, what is the probability you get at least one heads?

This seems a little tricky to wrap your head around at first. You may find that find that the best way to approach it is to think that the only way to not get at least one heads is to get all tails. Therefore, the probability of getting at least one heads is the complement of getting all tails, or $\bar{P(All \; Tails)}$ (remember, the bar means complement!), or $1 - P(All \; Tails)$. In this case, the calculation would be $1 - .5^5 = .96875$. So, the probability of getting at least one heads is .96875.

## Random Variables

We’ve learned how probabilistic events are just events with some uncertainty. When you flip a coin, you aren’t sure of the outcome: there is some chance that it shows up tails, and some chance it shows up heads. We can apply this concept of uncertainty to creating Random Variables.

Perhaps the best way to think of a random variable is as a sort of machine that randomly spits out numbers in some fashion. Compare this to some function $f(x)$. Say you have a function $f(x) = 2x$. The behavior of the output of this function is very well defined and completely certain: whatever you plug in, you get twice back (plug in $5$, get $10$, etc.). Unlike a function, the output of a random variable has uncertainty; we’re never as sure as we are with the function (although the output follows some distribution, which we will get to later).

We generally denote random variables as having capital letters, and usually we use $X$. So, we know if you have some random variable $X$, it acts like a random function that spits out numbers (one example of such a ‘machine’ is flipping a coin 10 times; this certainly spits out random numbers and actually follows a distribution we will soon discuss).

1. Properties of Random Variables

This seems a little dicey (pun?) thus far, having some random ‘machine’ that spits out numbers willy-nilly. Thankfully, there are some properties of random variables that help us work out and nail down their nature.

First, random variables have distributions. This is essentially the name or type of the random variable. While there are many, many different types of random variables you could imagine, there are a few very common ones that we will be learning here: Binomial, Bernoulli, Poisson, Uniform and Normal distributions. So, a we call a random variable Binomial if it has a Binomial distribution. Each distribution has it’s own properties (expectation, variance, probability mass function, etc.), which will now be explained.

The simplest example of a property of a random variable is it’s expectation. A random variable’s expectation can be thought of as it’s average, and it is denoted as $E(X)$ (which means, in english, the expectation of random variable $X$). The expectation of the amount of heads in one coin flip (which is a random variable) is $.5$ (we will formalize why this is true later, but for now just use your intuition).

Next we have variance. As the name overtly suggests, this describes how much spread is inherent in a certain random variable, and is denoted as we have seen variance in the past: $Var(X)$ (variance of random variable $X$). We can’t calculate it just yet (we will learn) but it is reasonable to think about: you would expect higher variance from flipping a coin 10 times than just flipping it 5 times, for example.

Perhaps most importantly, random variables have probability mass functions (for discrete random variables) and probability density functions (for continuous random variables). The idea of these functions are the exact same (just called different things for discrete/continuous variables): they give the probability that the random variable takes on a certain value. Usually this is denoted $P(X=x)$, where $x$ represents the value that the random variable $X$ takes on. So, if we were flipping a coin 10 times, you could use the probability mass function to find $P(X=3)$. In this case, you would just plug $3$ into the function (we’ll learn more about the specific functions when we get into specific random variables: for now, just imagine plugging it into something like $3x + 4$).

A step further than the PMF (probability mass function) is the cumulative density function (which is the same for continuous and discrete variables; both have CDFs, there is no CMF). This gives the probability that a random variable takes on a certain value or smaller. We saw that if we plugged 3 into the PMF of a random variable, we would get the probability that the random variable takes on 3 (in the example of flipping a coin 10 times and measuring the number of heads, the probability that you flip exactly 3 heads). If you plug three into the cumulative distribution function, or CDF, then you get the probability that you flip three heads or less (so 0, 1, 2 or 3 heads). Perhaps not surprisingly, the CDF is the integral of the PMF (not something you have to know but a good way to remember them).

Don’t worry if the PMF or CDF concepts sound a ilttle confusing: the work with them here is relatively cursory. While you should understand the basics, you will usually only be tested on very simple mechanics that are totally doable without actually possessing a deep understanding of the machinery (PMF or CDF) behind the calculation. However, these are very helpful concepts in learning about random variables, so we are including them here.

One last thing: while we will usually be working with named variables that have well-defined means and variances, you will often have to work with a ‘rogue’ random variable (the best example is a simple gambling game). Here, you will have to use the general equations for expectation and variance, which are:

\[E(X) = \sum\limits_{all \; i} x_iP(X=x_i)\]

So, the expectation of random variable $X$ equals the sum of all it’s values $x_i$ times the probability that each value occurs. The best way to think of this is as a weighted average, where each value/outcome $x_i$ is weighted by the probability that it occurs.

\[Var(X) = \sum\limits_{all \; i} (x_i - \mu)^2P(X=x_i)\]

So, the variance is the sum of the distances from the mean squared of all the values weighted by the probability that each value/outcome occurs.

Let’s apply these concepts to a basic lottery game. Say that you are rolling a fair, six-sided die. You win $10 if the die roll is 5 or greater, $0 if the die roll is 2, 3 or 4, and lose $5 if the roll is 1.

It’s not immediately obvious if this is a good game to play. One way to find out is to calculate the expectation and variance of the game using the formulas above. There are three outcomes/values that your bet can take on: $10, $0 and -$5, all based on probabilities associated with the die: $\frac{2}{6}, \; \frac{3}{6}, \; \frac{1}{6}$, respectively. So:

\[E(X) = (10)(\frac{2}{6}) + (0)(\frac{3}{6}) - (5)(\frac{1}{6}) = 2.5\]

So the expectation of every game is $2.5. Since it’s a positive value, it seems like a pretty good bet to take, since on average you will win $2.5. Let’s find the variance, since we already found the expectation ($\mu$ is the average, or expected value):

\[Var(X) = (10 - 2.5)^2(\frac{2}{6}) + (0 - 2.5)^2(\frac{3}{6}) - (-5-2.5)^2(\frac{1}{6}) = 31.25\]

So the variance of every game is $31.25. It’s kind of hard to visualize what this means exactly (if it’s big or small); we can really only compare it to other variances (for some named variables, we will have a better gauge). For example, if there was another game with expectation $2.5 but variance of only $10, it would be a less risky game.

Speaking of risk, now is a good time to discuss risk aversion. You’ve probably learned in an economics or psychology class that humans are not totally rational; they don’t always act in ways that make sense. For example, consider two games $X$ and $Y$.

In game $X$, you win $5 with probability 1. In game $Y$, you win $0 with probability .5 and $10 with probability .5.

Which game would you prefer? Well, as a critically thinking statistician, you would be able to realize that the expected values of each game are exactly the same: $E(X) = (5)(1) = (10)(.5) + (0)(.5) = E(Y) = 5$. However, if is a fact of life that people prefer game $X$, the sure thing.

This is because people are risk averse for gains. Although the expectations are the same, the variances are certainly not: game $X$ clearly has a variance of $0$ while game $Y$ clearly has some positive variance. That means $Y$ is riskier than $X$, and when presented with a gain, people prefer to take the sure thing (the 100% chance you get 5 bucks) over this risk (the fifty-fifty chance you make a lot, 10, and make nothing). This doesn’t make that much sense mathematically because the risk is perfectly balanced: the upside risk equals the downside risk (.5 probability of winning $5 more than the sure thing and .5 probability of winning $5 less than the sure thing).

So, when presented with a gain, people tend to choose the more certain outcomes (they don’t like risk).

This is interestingly enough the exact opposite for losses: people are risk seeking when presented with losses. Consider the same games $X$ and $Y$ as before but with negative values (lose $5 in game $X$, and have a fifty-fifty chance of winning $0 and losing $10 in game $Y$).

Before, we saw that people usually prefer game $X$, the sure thing, despite the games having the same expectation. In this case, though, the result is the opposite: it’s clear that the two games have the same expectation, -$5, but now people prefer the risky game $Y$ because they are faced with a loss.

This isn’t a psychology book, so we won’t try to explain why this is the case. It may just be nice to think that, since people really don’t want to lose money, they are willing to take a chance to avoid it (even if it means giving them a chance to lose even more money) instead of suffering a sure loss.

4.3 Named Distributions

We’ve seen what random variables are and the properties that make each unique. Now, we will explore certain distributions that result in specific random variables. Here, we will discuss the Bernoulli, Binomial, Uniform, Poisson, and (the granddaddy of them all) the Normal distribution. Each one has their own expectation, variance, probability mass function, etc. This is not only one of the most interesting portions of the book but one of the most applicable to real life problems, and some of the best preparation for future Statistics study.

Hopefully this will clear things up a little bit; while we’ve discussed all of these properties, we haven’t yet seen them in action.

1. The Binomial Distribution

The Binomial Distribution is perhaps the best distribution to start with. It is a discrete distribution (meaning it takes on countable integer values - like ${1,2,3}$ - and not uncountably infinite values - like all the values between $1$ and $2$).

Each distribution has a story, which basically explains what the distribution is. The story of the Binomial is we perform $n$ trials, each with only two outcomes (usually success or failure) and with a probability of success $p$ that stays constant from trial to trial, where all trials are independent.

Sounds a little tricky, but consider flipping a fair coin $n$ times and hoping to get heads. This is the prototypical Binomial random variable. It meets all the requirements: there are a set of $n$ trials, each trial has only two outcomes (heads, which is success here, and tails, which is failure here), the probability of success/heads is .5 for every trial, and each flip of the coin is independent.

How about some more examples? Remember Charlie from Charlie and the Chocolate Factory? This is a perfect example of a Binomial. If chocolate bars are independent of each other, and Charlie buys $10$ bars, where each bar has a 1% chance of having a golden ticket, than the random variable $G$ that measures how many golden tickets Charlie wins has a Binomial distribution. What about a college student asking people out on dates? If prospective dates make their decisions independently, and the college student asks out 30 people where each has a probability .2 of saying yes, than the random variable $D$ that measures how many dates he gets is Binomial.

So, this is the general idea of what a Binomial represents. If indeed some random variable has a Binomial distribution, we use the following notation:

\[X \sim Bin(n,p)\]

Where $X$ is the random variable.

The ‘$\sim$’ means in English “approximately distributed by….” So here, the random variable $X$ is approximately distributed as a Binomial. The $n$ and $p$ are the parameters of the distribution. As you may have guessed, the $n$ represents the number of trials, while the $p$ represents the probability of success on each trial.

The parameters are very important, since they will soon fuel our calculations of expectation, variance and probability density. This is usually an exercise in recognizing that something has a Binomial distribution and then identifying the parameters. For example, if we were running an experiment for random variable $T$ that measures the number of tails and we flipped a fair coin 30 times, we could write:

\[T \sim Bin(30,.5)\]

Since (30 = $n$ = total number of trials) and (.5 = $p$ = probability of success on each trial).

Now that we’ve established the set-up for a Binomial, we can discuss the characteristics that make it unique: it’s expectation, variance, and probability density function. For a Binomial random variable $X$, we have:

\[E(X) = np, \; Var(X) = npq\] Where $q = 1 - p$. So, the expectation of successes in a Binomial random variable is the total number of trials times the probability of success on each trial (intuitive) and Variance is the number of trials times the probability of success times the complement of the probability of success (unfortunately not intuitive).

So, for our previous example $T \sim Bin(30,.5)$, where $T$ represents number of tails in 30 coin flips, we expect $(.5)(30) = 15$ tails on average, with the variance of these tails being $(30)(.5)(1-.5) = 7.5$ tails (remember, the standard deviation is the square root of the variance, so the standard deviation is $\sqrt{7.5}$).

We will not discuss the cumulative density function. Remember that it is the integral of the probability density function; however, we don’t work with it explicitly here so it won’t really be worth it to discuss it. This can be used to find, again, cumulative probabilities, like $P(X \leq 2)$.

Finally, then, we have the probability density function of a Binomial. Recall that a probability density function gives the probability that a random variable $X$ takes on any one value $x$: $P(X=x)$ for all $x$. For a Binomial, we have:

\[P(X=x) = {n \choose x}p^x q^{n - x}\]

We have not yet discussed what ${n \choose x}$ means; it is a concept central to counting/combinatorics. Since this is a concept immediately relevant to the Binomial random variable, we’ll run through that section now.

4.3.1 Counting

This sounds pretty trivial, but rest assured you that counting is one of the most difficult parts of Statistics. Thankfully, we will not delve very deep into the field here; just the basics for now.

First is the concept of the **factorial}. Represented in the field with a ‘!’ this basically means to multiply a number in descending integers until you get to 1. So, $3! = (3)(2)(1) = 6$. These get out of hand pretty fast, as $5! = 120$, $10! = 3,628,800$, and $70!$ factorial overflows my calculator. The factorial, then, is a very nice way to elegantly represent very large numbers.

What is it’s function in statistics? Say that we posed the question “how many ways can we order the letters A,B,C ?”

You could likely figure this out by just writing out the sample space: {ABC, ACB, BAC, BCA, CAB, CBA}, so there are six ways. However, you might not always be able to order these so conveniently. In that case, you could also use the strategy of the factorial. Since there are three distinct letters, the answer is 3! (which clearly comes out to $(3)(2)(1) = 6$).

Why does this work out so cleanly? Think about actually ordering the letters A,B,C. There are three ‘slots’ that the letters could take: they could either be the first letter in the sequence, the second letter or the third letter. How many different letters can we pick for the first ‘slot?’ Well, since no letters have been picked yet, there are 3 (we can pick A, B or C). How about the second slot? Since we know one letter has been picked (A, B or C, doesn’t matter) there are now 2 letters left that can go in the second slot. How about the last slot? We know two letters have been picked for the first two slots, so there is only 1 remaining letter.

Since we want the total number of combinations, we multiply each of the numbers, which is the same as taking the factorial of 3. So, if we asked the same question but this time wanted to know how many ways there are to order the entire alphabet, the answer would be $26!$ (of course, this is a disgustingly large number with around 30 digits, but our factorial gives us a clean way to represent it).

So, we now know that $x!$ gives the number of ways to order $x$ distinct objects. We can apply this concept to what we just talked about in the Binomial section: ${n \choose x}$, where the full formula is:

\[{n \choose x} = \frac{n!}{(n-x)! \; (x!)}\]

This is called the binomial coefficient, and in english it means “n choose x.” It gives the amount of ways that x objects can be chosen from a population of n objects. Perhaps the best way to visualize this is forming committees. Say you have a population of 300 parents at the local elementary school, and you want to choose 10 parents to be a part of the PTA (Parent Teacher Association). Since we have a population $n=300$ and we want to choose $x=10$ parents from the population, ${300 \choose 10}$ gives the number of ways that we can pick 10 parents from the pool of 300, or the number of combinations possible for the PTA committee. This is a very large number with 19 digits.

How on earth does the above formula give such a specific answer? Let’s break it down in a manageable example.

Say we have the 5 letters A,B,C,D,E, and we want to find out how many ways there are to select 3 letters from this set of 5 letters (like ABC, BCD, AEC, etc.).

We already know from out formulas that the answer is ${5 \choose 3}$, but it doesn’t make much intuitive sense. Let’s investigate using the binomial coefficient $\frac{n!}{(n-x)! \; (x!)}$, or in this case, plugging in for $n$ and $x$, $\frac{5!}{(5-3)! \; (3!)}$.

Let’s start from the top. The numerator $5!$ gives us the number of ways we can organize the letters A,B,C,D and E (turns out there are 120 ways). However, we aren’t asking for the number of ways that we can order the entire set, but the number of ways we can choose a certain amount of letters out of the entire set. Therefore, this $5!$ is giving us permutations like ACDBE and EDCBA, where we only want the permutations with 3 numbers, not all 5. You can look at this like it’s giving us a permutation of 3 letters followed by 2 letters, but we only want the permutation of 3 letters. So, we have to divide out the permutations that we don’t want.

So, if someone is putting together the 5 letters in a random order, we want to stop them at 3 letters. How can we do this? Well, once they have picked three letters to order out of the 5 (like BEC or DAB) they still have $2!$ combinations of letters in ways they can order the remaining letters. If they start with ABC, for example, there are 2!, or $(2)(1) = 2$, ways to order the remaining letters: DE and ED. The $5!$, then, is overcounting what we want by a factor of 2!, so we must divide the 5! by 2!, which is of course just $(n-x)!$ or $(5-3)!$.

Therefore, we are starting from the number of ways we can pick the 5 letters in a row, and then adjusting for the fact that we are picking the entire population of 5 instead of the 3 we asked for by dividing by (5-3)! or 2!, the letters we don’t care about. It’s sort of like dividing by the number of ways to not choose 3 letters.

That takes care of $n!$ in the numerator and $(n - x)!$ in the denominator. What about the ($x!$)? Well, where have we left off? After dividing, we’ve just found the number of ways to choose sets of 3 letters out of the 5 letters. However, we are still overcounting.

The key here is that order doesn’t matter. The division we just did, $\frac{5!}{(5-3)!}$, spits out the number of ways to choose 3 letters from A,B,C,D,E. This happens to come out to 60 (try it yourself to prove it). I’m going to start to write the sample space out to see if you notice any patterns:

\[ABC,ACB,BCA,BAC,CAB,CBA,ABD,ADB,BDA,BAD,DBA,DAB...\]

Did you catch it? Here I’ve written out 12 of the 60 permutations.

Consider the first six: ABC,ACB,BCA,BAC,CAB,CBA. They all have the same letters in them: A, B and C, the only factor that makes them unique is the order that they are presented in (ABC here is distinct from ACB). This is the same for the second six permutations that we wrote, but with the letters A, B and D.

Think back to one of the original examples of picking people for committees. Does it matter which order you pick the people for the committees in? No, it does not; as long as the same people are in a committee, it does not matter what order we picked them in.

Therefore, if A, B and C are people, than committees ABC and ACB are the exact same committee. Since we don’t really care which order they are selected in, this method again over-counts committees: the set of 6 permutations with the letters A, B and C should only count for 1 committee.

How do we fix this? Again, by dividing. Since there are 3! ways to order the people in the committee, but again, we don’t want to count these ways, we have to divide by 3!. You can see the intuition in this case: since $3! = 6$, and we just saw that 6 committees should have boiled down to 1. You can further convince yourself of this by the fact that there are 10 total permutations of these ‘false 6’ (two of which we wrote out) because there are 10 ways to group the letters ABCDE (ABC, ABD, ABE, ACD, ACE, ADE, BCD, BCE, BDE, CDE) and within each group $3! = 6$ ways to order the letters (which we don’t want).

So, we divide by the 3!, which completes the formula $\frac{5!}{(5-3)! \; (3!)}$. It comes out to 10 (in fact, we wrote out the complete answer at the end of the last paragraph) which means that there are 10 ways to select 3 letters from ABCDE. We learned that this formula adjusts for over-counting by $n!$ in selecting unnecessary orderings (dividing by $(5-3)!$ to get us down to just permutations of 3) and over-counting in giving extra ordering combinations (ABC and ACB are the same for our purposes).

As you probably now agree, counting can get very complicated very quickly. In this context, you really need to only understand the factorial and what ${n \choose x}$ means (number of ways to pick $x$ objects from a population of $n$ objects).

4.3.2 Return to Named Distributions

We left off discussing the probability density function of a Binomial. Now that we understand some basics of counting, let’s re-visit the function.

To jog your memory, the function that gave the probability that the random variable $X$ took on any value $x$ ($P(X=x)$) was:

\[P(X=x) = {n \choose x}p^x q^{n - x}\]

With our knowledge of counting, we can now break this formula down.

Let’s consider an easy example. Say $X$ is a random variable that represents the heads flipped from flipping a fair coin 5 times. We know this is Binomial (set number of trials, same probability across trials, only two outcomes on each trial, trials are independent), so we know $X \sim Bin(5,.5)$. Plugging in for $n$, $p$ and $q$ (remember, $q = 1 - p$):

\[P(X=x) = {5 \choose x}.5^x .5^{5 - x}\]

So, this becomes a function where we plug in $x$, the number of successes we are interested in seeing, to find the probability of $x$ amount of heads occurring.

A simple example would be finding the probability that exactly 3 heads occur in the 5 flips. Plugging in 3 for $x$ (since it is the number the random variable takes on), we would get:

\[P(X=x) = {5 \choose 3}.5^3 .5^{5 - 3}\]

Which comes out to .3125.

Why does this work? Let’s break down the components of the equation.

First, the probability portions, $.5^3$ and $.5^{5-3}$. Think about what these are saying. When you actually do get 3 heads out of 5 flips, what is the probability that it occurred? Remember, since each flip is independent, we can multiply the probabilities. Therefore, the probability of 3 heads is just $(.5)(.5)(.5)$, or just $.5^3$, and the probability of 2 tails (you must get 2 tails, since there are 5 total flips and exactly 3 are heads) is just (.5)(.5), or $.5^2$ (we have it written as $.5^{5-3}$, which is the same thing).

So, it turns out in this case that $.5^3 .5^2 = .5^5$ (again, we can multiply because flips are independent) gives the probability that any one permutation with three heads in five flips occurred. However, $.5^5 = .03125$, which is not the answer our probability density function gave us. Why is this?

What we just found is the probability of any one desirable permutation occurred. One example would be HHHTT. However, this is only one way of many that a desirable permutation (3 heads in 5 flips) can occur. Immediately, we can think of HHTTH and HHTHT as two more examples.

Of course, we know that the probability of each individual permutation is the exact same, since they all have 3 heads and 2 tails. Therefore, we merely have to multiply the probability of a desirable permutation, $.5^5$, by the number of desirable permutations that can occur. How many desirable permutations are there? Well, how many ways can you get 3 heads out of 5 flips? As we’ve just learned, this is exactly the concept captured by the binomial coefficient, ${n \choose x}$. In this case, ${5 \choose 3}$ gives the number of ways you can pick 3 heads out of 5 flips. In this case, it is 10.

So, we multiply the probability of each desirable permutation (3 heads in 5 flips) by the total number of desirable permutations to get the overall probability that we find a desirable permutation. Here, $(.03125)(10) = .3125$, so the formula checks out.

Remember, then, the $p^x q^{n - x}$ as the probability part of the desirable permutation, and the ${n \choose x}$ part as the number of desirable permutations.

Usually, though, you won’t have to use the probability density function, since we will often just ask for the endpoint probabilities of a random variable. These endpoint probabilities are exactly what they sound like: the probability extremes, or the probabilities of all failures or all successes. So, in the case we just discussed, the endpoints would be $P(5 \; Heads)$ and $P(0 \; Heads)$.

I say that you don’t need the function because you could just think about this using naive probability. Before, when we found the probability of a desired outcome, we needed to multiply it by the total possible permutations that had desired outcomes. Now, however, there’s only one way to list the endpoint probabilities. The extremes are HHHHH and TTTTT, which are totally unique in that you can’t rearrange them and make them different (whereas HHHTT and TTHHH were both desirable but definitely different). Mathematically, ${n \choose n} = {n \choose 0} = 1$.

So, the whole ${n \choose x}$ bit becomes 1, since there is only one way to choose the endpoints, and you just multiply by the probabilities. You know that since there is either all successes or all failures, you will be raising $p$ or $q$ to 0 and the other one to $n$. Think about getting all heads: $p^x$ becomes $.5^5$ and $q^{n-x}$ becomes $q^0 = 1$. Therefore, endpoint probabilities are given by $p^n$ and $q^n$.

That just about closes the Binomial distribution. Let’s do a quick example to make sure we are comfortable with all of the mechanics. Here is a sample question:

“Say that 200 students that took Statistics 101 are asked if they like the professor. The probability that each student likes the professor, independently of the rest, is .3 (the exams were especially hard this year). Let $P$ be the random variable that represents the amount of students that like the professor.”

What distribution does $P$ follow? Why? What is the expectation and variance of $P$? What are the endpoint probabilities? (Bonus: What is the probability that exactly half of the students like the professor?)

Right off the bat, we can identify this as a Binomial distribution. This is because there is a set number of trials (200 students), the probability of success (liking the professor) is a constant .3 across students, the trials have two outcomes (like or do not like) and students are independent from one another. So, for these reasons, $P \sim Bin(200, .3)$.

In terms of expectation and variance, we know that the expectation of a Binomial is $np$ and the variance is $npq$. Therefore, since we have already identified our parameters, we know $E(P) = (200)(.3) = 60$ and $Var(P) = (200)(.3)(.7) = 42$. So, we expect on average 60 students to like the professor with a variance of 42 students. The standard deviation would be the square root of the variance, or $\sqrt{42}$.

Finally, we are asked for the endpoint probabilities. We know that these are the probabilities of the extremes: all 200 students liking the professor or none of the students liking the professor. Using our knowledge of probability, we know the knowledge of all students liking him is $.3^{200}$or essentially 0 and the probability of exactly 0 students liking him is $.7^ {200} = 1.04*10^{-31}$, which is also essentially 0. It makes sense that these probabilities are very small, since there are a very large number of students and thus it is highly probable that somebody likes the Professor and somebody doesn’t like him.

For the bonus, we simply have to find $P(P=100)$, or the probability that $P$ takes on the value of 100, or half, the students. This is as simple as plugging into the probability density function, which becomes:

\[P(P=100) = {200 \choose 100}.3^{100} .7^{200 - 100}\]

Which is $1.509*10^{-9}$, or essentially 0. This makes sense because we expect 60 students to like the professor, and 100 is much higher than 60. It also makes sense that any one amount of students liking the professor is probabilistically unlikely, since there are such a large number of students sampled.

These are very similar to the types of questions you will deal with when encountering the Binomial in the wild. As a closing remark, remember that the main requirements of a Binomial distribution: set number of trials $n$, constant probability across trials $p$, two outcomes on each trial, independence across trials.

2. The Bernoulli Distribution

This is also discrete, and is in fact a much simpler distribution than the Binomial. In fact, the story of this distribution is that it is a special case of the Binomial: when there is only one trial, or $n=1$. So, whereas a Binomial might be 10 coin flips, the best way to visualize the Bernoulli distribution is that it is just one coin flip. In the professor example we just did, the Bernoulli version would be asking just one students. So, a Bernoulli distribution has one trial with some set probability that has exactly two outcomes. Since we know that there is only one trial, the only parameter needed is the probability $p$.

Since this is such a simple distribution, it’s expectation, variance and probability density function are pretty simple as well. If some random variable X is distributed Bernoulli with probability $p$ - that is, $X \sim Bern(p)$, then:

\[E(X) = p, \; Var(X) = pq , \; P(X=x) = p^x q^{1 - x}\]

Where, in the probability function, $x$ can be 1 or 0, since there can either be a success or failure on the one trial. It might be easier to write out the piecewise function:

\[P(X = 1) = p, \; P(X = 0) = q\]

So, if you flipped a biased coin once that had a probability of .3 of getting a heads, this would be a Bernoulli distribution (1 trial, constant probability, two outcomes on trial). The expected value would be .3, the variance would be $(.3)(.7) = .21$. The probability function makes sense, because the probability that $X=1$, or you get one heads, is .3 (which is $p$) and the probability $X=0$ is .7 (which is $q$).

4.3.3 Continuous Distributions

The random variables we have discussed thus far have been discrete; now, however, we will be working with continuous variables. We won’t get too deep into the mathematical definitions here; f our purposes, you can list out the whole sample space of a discrete distribution (like coin flips, which are just integers like 1,2,3,4,…$n$) where a continuous distribution has a sample space that is infinite and can’t be listed (like the space between 1 and 2, which has an infinite amount of numbers).

The biggest difference between discrete and continuous distributions in this book are the probability functions. A really interesting result is that, in Statistics, **the probability that a continuous random variable takes on any one value is $0$}. Mathematically, $P(X=x) = 0$ for all $x$. This is pretty crazy (the idea is to think of the continuous variable as a continuous integral. Remember how we construct integrals: by starting out with rectangles that then get smaller and smaller before approaching 0 width) and it means that we will be using the probability density function much less than we used the probability mass function for the discrete random variables.

Instead, we will be using cumulative distribution functions, which, as we mentioned before, give the cumulative probability between two points. In practice, the CDF looks like this: if we had weight as a random variable, we could use the CDF to find the probability that someone is in between two specific weights (represented as $P(a\leq X \leq b)$). Perhaps we would want to find the probability that our child is less than 80 pounds. Using the CDF of the weight distribution, we could just plug in 80 to get the probability that the child is 80 pounds or less).

So, remember this when we are finding probabilities for continuous distributions: the PDF doesn’t give us much, so we will use the CDF.

3. Uniform Distribution

This is perhaps the simplest of the continuous distributions. Imagine the shape of a uniform distribution as a rectangle with area 1 (since total probability must add up to 1). The simplest example is the standard uniform, which is a uniform distribution from 0 to 1. If $X$ is standard uniform, then $X \sim Unif(0,1)$.

So, the standard uniform looks like a square with height 1 from 0 to 1. The idea is that, since the distribution is uniform, the probabilities between intervals of the same length are the same all along the distribution. What we mean by that is, for the standard uniform, there is the same density between .1 and .2 as between .85 and .95, since the widths of the interval are both .1. In fact, the density of both of these intervals (and all intervals of length .1) is 10%, since the interval of .1 is one tenth of the entire, 1 unit long square. So, the probability that you are between .1 and .2 on the standard uniform distribution is just .1, since it is the probability density.

The key here is that this is really just geometry. Since the uniform distribution is a rectangle and the probability density is the same as the area in the rectangle (since, as we recall, the CDF is just an integral of the PDF, or area under a curve), density problems with the uniform are really just exercises in Geometry.

Anyways, for the general case of a random variable $X \sim Unif(a,b)$ (endpoints are $a$ and $b$), we use the following properties:

\[E(X) = \frac{a+b}{2}, Var(X) = \frac{(b-a)^2}{12}\]

The expected value makes sense, since it is just the average of the endpoints. The variance makes no intuitive sense, but that does not bother us because we are tough.

If we apply these formulas to the standard uniform, then, we an expected value of $\frac{0+1}{2} = \frac{1}{2}$ and a variance of $\frac{(1 - 0)^2}{12} = \frac{1}{12}$.

The CDF of a Uniform random variable is:

\[\frac{x-a}{b-a}\]

When $x$ is between $a$ and $b$. When $x \leq a$, it’s clear that the cumulative probability will be 0. Consider the standard uniform. If $x$ is 0 or negative, and we want to find the cumulative probability that the random variable takes on a value up to $x$, this must be 0 since we included none of the interval (if $x$ is -1, then none of the standard uniform ‘rectangle’ includes -1, so it has 0 density). In practice, the probability on the standard uniform that a value is less than -1 is 0. If $x\geq b$, that is, we are finding the cumulative probability of a value past the right bound, than we must get an answer of 1. That’s because, if $x$ was something like 2 on the standard uniform example, it would include the entire standard uniform rectangle, or 100% of the density. In practice, the probability on the standard uniform that a value is less than 2 is 1.

Anyways, the above relationship holds when $a \leq x \leq b$. Let’s try an example to see if this makes sense. We will use the standard uniform again because it is so simple; so $a$ and $b$ are 0 and 1, respectively. Let’s try and find the cumulative probability of .3. Intuitively, what should it be? What is the probability in the standard uniform that we take on a value up to .3? Well, we are essentially checking from 0 to .3, which is clearly 30% of the entire, 1 unit long square. Therefore, we should find a cumulative probability of 30%.

Plugging in, we get $\frac{.3-0}{1-0}= .3$. So, our intuition was confirmed.

Hopefully this example clears up any lingering confusion of the CDF; it’s simple after all, just plug and chug as always.

4. Normal Distribution

This is it: the big show. The Normal distribution is likely the most important concept you will learn here and one of the most central to all of Statistics (for reasons we will further explore in the second half of the book).

Imagine the Normal as the Bell Curve. Probability density, then, is most clustered around the middle, and decreases symmetrically as we move away from the middle/average.

To picture this, imagine a ‘Bell Curve’ result from scores on an academic test. Most students are clustered around the average score, while there are less and less students as we move away from the average (in either direction, as we have students that score above the average and below). Therefore, a random student has the highest probability of being somewhere around average, and that probability decreases as the score moves from the average.

Again, look for pictures if it helps you to learn it. Anyways, now that we have the shape, the Normal is just like any other continuous distribution. We have expectation, variance, and a cumulative distribution function.

So, if X is normally distributed, we say $X \sim N(\mu, \sigma^2)$. This means that $\mu$ is the mean and $\sigma^2$ is the variance. That’s right, we don’t have nice neat formulas to solve for them as we did before. We do, however, have certain properties that may help you identify them.

For instance, every Normal distribution is centered around the mean. Consider the standard Normal, which is distributed $N(0,1)$ (so a mean of 0 and variance of 1). The ‘bell’ here would be centered at 0. This can help you locate the mean of a Normal.

We can also recall the Empirical Rule that we learned in Chapter II. Here is a quote from Chapter II:

The concept (of the Empirical Rule) is that, for a mound shaped data set, about 68% of the data lies within $1$ standard deviation of the mean, about 95% of the data lies within $2$ standard deviations of the mean and about 99.7% of the data lies within $3$ standard deviations of the mean.

Aha! This will help us to contextualize the variance (which, remember, is the standard deviation squared). We know that a Normal distribution is certainly mound shaped (it’s a bell, for goodness sake), so the empirical rule certainly applies. So, let’s say that $D$ driving speed on a certain road is normally distributed such that $D \sim N(30,?)$ (mean driving speed of 30 mph, unknown variance). If the problem then told you that about 68% of drivers drive between 25 and 35 miles an hour, could you find the variance?

Well, you know by the empirical rule that about 68% of the data is between +/- 1 standard deviation of the mean. Since 25 and 35 are centered around the mean of 30 (off by 5 in either direction), and we are told that 68% of the data falls between them, we know that they are each 1 standard deviation from the mean. So, $\sigma = 5$ and thus variance is 25 ($\sigma$ represents standard deviation).

This is the type of problem solving required for understanding the mean and variance of a Normal. However, most important is the CDF of a Normal distribution.

This is a pretty interesting case because the CDF is so complicated that we don’t actually use it. Officially, the probability density function of a Normal is:

\[\frac{1}{\sigma \sqrt{2 \pi}} e^{\frac{-(x-\mu)^2}{2\sigma^2}}\]

Where $e$ is the mathematical constant such that $ln(e) = 1$.

So, the CDF is the integral with respect to $x$ of this very ugly thing. Luckily for you, you don’t have to deal with it unless you take more probability courses. We will mostly rely on the computer/given probability tables to calculate density in a Normal distribution.

However, while you won’t use this CDF directly, it’s important to understand how we get the output we do.

The key here is to go through the standard Normal - $N(0,1)$. That’s because its PDF is much simpler; since $\mu = 0$ and $\sigma^2 = 1$, the function becomes:

\[\frac{1}{\sqrt{2 \pi}} e^{\frac{-(x)^2}{2}}\]

Every computer and calculator has a program running this function. That is, computers are very good at giving us probability densities for the standard Normal distribution. It could very quickly tell you, for example, the cumulative density of -.5 on the standard Normal, or perhaps the density between -.2 and 1.5.

Standard Normals are also much easier to read for us humans. It basically creates a ‘standard’ for measuring things, where the units are always the same. We can apply the empirical rule with a quick glance, as you will soon see.

The point is, we would like to convert whatever Normal we get into a standard Normal. This is a process called standardization, and it allows us better understand and easily plug into the computer the results of our Normal random variable.

So, how do we get to a standard Normal from any other Normal? Recall transformations of a data set: when you multiply every value in a data set by a constant, the mean of the data set is multiplied by that constant and the variance is multiplied by the square of the constant, and when you add every value in a data set by a constant, the mean is increased by that constant and the variance is unchanged.

To formalize it, we’ll use the same sort of tools from the $a + bX$ rule, but this time applied to random variables and not data sets. The result, though, is really the exact same. If $X$ is a random variable with mean $\mu$ and variance $\sigma^2$:

\[E(a + bX) = a + bE(X)= a+b\mu\] \[Var(a + bX) = b^2Var(X) = b^2\sigma^2\]

Let’s apply this in going from a standard Normal to just a regular old Normal. Here, we will say that $Z$ is our standard normal, so $Z \sim N(0,1)$, and $N$ is the general normal, so $N \sim N(\mu, \sigma^2)$.

So, if we start from $Z$, how do we get to $N$? Well, we know that if we multiply $Z$ by some constant, then we will multiply the variance by the square of that constant. The variance of $Z$ is currently 1, and we want to go from this variance of 1 to the variance of the general Normal, $\sigma^2$. What do we multiply be 1 to get to $\sigma^2$? No tricks here, just $\sigma^2$. Remember, though, when we multiply by a constant the variance increases by the square of that constant, so we want to actually multiply $Z$ by $\sigma$, as this will multiply 1 by $\sigma^2$ to get to the variance of the general Normal, $\sigma^2$.

Thus far, then, we have $\sigma Z$. This creates a new random variable with the same variance as the Normal we are looking for ($Var(\sigma Z) = \sigma^2 Var(Z) = \sigma^2$). However, we still have to get the same mean. We know that multiplying by a constant multiplies the mean by the same constant; however, the mean of the standard normal is 0, so multiplying $Z$ by $\sigma$ does not affect the mean (part of why we use standardization is because of this convenience). So, we just have to add some constant to the mean of $Z$, which is 0, to get to the mean of the general Normal, $\mu$. What do you add to 0 to get $\mu$? Well, $\mu$ of course. Again, variance is not affected by adding constants, so we are still at the desired variance of $\sigma^2$.

Finally, then, we have:

\[\sigma Z + \mu = N\]

Solve for the variance and expectation of $\sigma Z + \mu$ to prove to yourself that it matches the variance and expectation of $N$.

If we solve for $Z$, we get:

\[Z = \frac{N - \mu}{\sigma}\]

Although perhaps not immediately obvious, this is the equation for the z-score, a concept most central to the field of statistics. You would use this to plug in a number from your general Normal distribution into $N$ and get some $z$ that is part of the standard Normal distribution.

Basically, what we have done is taken a general Normal random variable and converted it into a standard normal random variable, which is much easier to use with the tools of probability density. For example, say that the weights $W$ in a certain college are distributed normally with $W \sim N(120, 5^2)$. If you were asked “what is the probability of weighing less than 150 pounds,” how would you solve it?

This clearly requires the use of a CDF, since we have to find $P(W \leq 150)$. However, it’s not easy to apply the CDF to this Normal, since the CDF is so complicated. Instead, we can use the concept of a z-score to convert to a standardized normal, which is easier to work with.

Plugging in the mean, variance and value of 150 for $N$, we get $z = \frac{150 - 120}{5} = 6$. So, you have a z-score of 6. What does that mean? Well, since the standard deviation of the standard normal is 1 (a very nice property) the z-score essentially gives us how many standard deviations away from the mean we are in a standard normal. That is why it is so easy to read, since it immediately gives us a general clue of how extreme a point is. You couldn’t really wrap your head around how extreme 150 pounds was, but it’s much easier to think about being 6 standard deviations away from the mean.

That’s it - in terms of calculations at least. The computer/calculator can do the rest. All you have to do is plug the z-score into the correct program, and it will give you back the cumulative probability. All we’re doing is plugging in a value (the z-score) into the CDF of a standard normal. So, if you get a z-score of 2, what should happen when you plug it into the CDF? Well, harkening back to the Empirical rule, we know that $$2.5% of points are above 2 standard deviations above the mean (since the distribution is symmetric) so you should get about 97.5%.

The other common question involving z-scores is reverse lookup. This is essentially what it sounds like: doing the z-score process in reverse. Before, we got the z-score and used it to calculate the probability density. Now, we will be given probability density and asked to find the z-score (or the mean or the variance. However, once you find the z-score from the given probability density, you can solve for the mean or the variance, depending on what you’re given).

There are programs again on your calculator or computer that can do this. First, for the calculator. Again, hit ‘2nd’ then ‘Vars,’ but now scroll down to the third option that says “invNorm.” You should get a screen asking you for area, $\mu$ and $\sigma$. Again, the latter two should be already set as 0 and 1, respectively. All you have to do is enter the probability density (they call it area) and the calculator will spit out the z-score associated with that area. So, if you put in .5, or half the area, it will spit a z-score out of 0 (since the Normal distribution is symmetric).

In addition, that pretty much completes the first third of the material; everything before the first midterm. Congrats on making it to this milestone!