Chapter 2 Descriptive Statistics

2.1 Motivation

Whereas the last chapter provided a qualitative basis for statistics, this version will establish the most fundamental quantitative tools we will use for the remainder of the book Again, you have likely been exposed to learn much of this material in other quantitative-minded classes. However, it is nonetheless important to become extremely comfortable with these concepts, as they will likely appear in every chapter following.

2.2 Basic Descriptive Statistics

These are the core, most basic tools to describe any data set. They can be divided into two sections:

1. Measures of Center/Location

This includes the mean and median. As you likely know, the mean is the arithmetic average of a data set, and the median is the middle value. The official equation for the mean is:

\[\bar{X} = \frac{\sum\limits_{i=1}^n x_i}{n}\]

Where $\bar{X}$ denotes mean (a notation you must familiarize yourself with). In words, this equation says to add up all the values and divide by the number of values $n$.

The median, or middle of the data, is the middle number in a (sorted) data set with an odd amount of values and the average of the two middle numbers in a (sorted) data set with even values.

It’s most important to understand how these relate in an actual data set. Namely, the mean is much more affected by outliers (data points with extreme values that we will talk more about later). Consider if we were sampling bowling scores amongst a group of $10$ people and found the following sample:

\[S = \{96, 103, 121, 114, 98, 111, 107, 289, 115, 101\}\]

Where $S$ denotes the sample space, or all of the data points.

It’s clear that the outlier here is the point $289$ (we will formalize the definition of an outlier later, for now we will just assume this because it is so much larger than every other point). Let’s remove this outlier and generate a new sample space, $S_1$.

\[S_1 = \{96, 103, 121, 114, 98, 111, 107, 115, 101\}\]

Now let’s compare the mean and median of $S$ and $S_1$. The mean of $S_1$ is $107.\bar{3}$, while the mean of $S$ is a whopping $125.5$. However, the medians are much closer: $107$ and $109$ for $S_1$ and $S$, respectively (you can easily calculate these by hand, or with the mean and median functions in R).

It makes sense that the mean is more swayed than the median by the outlier $289$. That’s because, while this large number certainly brings up the average, it is only weighted into the median by it’s frequency count of $1$. In other words, for the median’s sake, it doesn’t matter how large the max number is, only that it is the max number. For the mean, since it is actually calculated from the data set, larger numbers will have larger results (changing numbers changes the mean every time, where it only changes the median if it changes the order of the numbers within the data set).

Therefore, it’s clear that while the mean is usually a good way to measure the center of a dataset, the median might be more well suited for diagnosing skewed data, since it is more robust against outliers.

2. Measures of Variation/Spread

This includes Range, IQR,Variance, Standard Deviation and MAD (the last of which will rarely be used).

Range is relatively simple. As you likely know, it is just the maximum value minus the minimum value. It measures the variation of a data set based on how wide the data set is. It’s clear that this can be pretty susceptible to outliers, since as the max or min of a data set move further from the center of the set, the range increases (you could make the argument that as long as an outlier is not the min or max point in the set, it does not affect the range at all. This would be correct, but in this book we will usually see outliers working as the min or max and thus affecting range; also, if an outlier is not the min or the max, that means we have another even larger - or smaller - outlier!).

The IQR (interquartile range) of a data set is simply the distance between the third quartile (or the 75th$\%$ of data points) and the first quartile (the 25th$\%$), commonly denoted as $Q3$ and $Q1$. So:

\[IQR = Q3 - Q1\]

If you’re having trouble grasping this concept, imagine the data set $1,2,3,....99,100$ (all of the integers going to $100$). We have that $Q3$, the 75th percentile, is here the point $75$, and $Q1$ is $25$. Therefore, $IQR = 75 - 25 = 50$.

It’s clear that the IQR is more robust to outliers than range, since usually outliers are extreme enough that they don’t fall within the 25th to 75th percentile of the data (they are usually above or below these cutoffs). Therefore, it would not affect the IQR directly.

MAD (Mean Absolute Deviation), which measures the spread of a data set, is a little more interesting. The equation is:

\[\frac{\sum\limits_{i=1}^n \mid x_i - \bar{x} \mid}{n}\]

In english, this means that to find the MAD you add up the distance from the mean for all points in a set and divide by the number of points (so the name makes sense: it is the average, or mean, of the distances, or absolute deviations). For example, if you were asked to find the MAD of a standard, fair dice roll, knowing that the mean is just $\frac{1+2+3+4+5+6}{6} = 3.5$, you would compute:

\[MAD = \frac{\mid 1- 3.5 \mid + \mid 2 - 3.5 \mid + \mid 3 - 3.5 \mid + \mid 4 - 3.5 \mid + \mid 5 - 3.5 \mid + \mid 6- 3.5 \mid}{6} = \frac{3}{2}\]

We need the absolute value signs because without it, based on symmetry and the fact that the mean is the arithmetic average, MAD would return $0$ for every data set (try it to prove it to yourself).

Variance, though, is the regularly preferred alternative method to measuring spread. It’s pretty similar to MAD:

\[Var(X) = \frac{\sum\limits_{i=1}^n (x_i - \bar{x})^2}{n}\]

And by extension, the standard deviation is:

\[ s_x = \sqrt{Var(X)} \] In fact, the standard deviation is always the square root of the variance.

Again, these are pretty similar (MAD and Variance), with the only discrepancy being that the differences between data points and mean ($x_i - \bar{x}$) are squared and not absolute valued.

In this book, we will be using variance and standard deviation almost every chapter (not MAD) so it is important to familiarize yourself with the concept and be able to calculate it for discrete distributions (like a roll of a fair, six-sided dice). Remember that variance is affected by outliers, since as $x_i$ increases, $(x_i - \bar{x})^2$ also increases (when $x_i>\bar{x}$, that is).

2.3 Applying Descriptive Statistics

This section will cover Linear Transformations of Data and Outliers.

1. Linear Transformations

As you have likely learned in an algebra class, a linear equation takes the form $Y = aX + b$, with $a$ being the slope and $b$ being the Y-intercept.

In statistics, linear transformations are usually applied to datasets when we need the output in terms of different units. For example, if we had a data set made up of measurements in inches and we needed to transform it to measurements in feet, we would use the transformation $Y_i = 12X_i$, where $X_i$ gives all the points in the old, inches data set and $Y_i$ gives all the points in the new foot data set.

This seems pretty rudimentary, but it will usually be applied to more monetary concepts. Take for example buying a car. Say that to buy a car, you have to pay $\$1000$ up front and then $\$50$ for each additional horsepower that the engine has. If you had data on the horsepower of each car but wanted to build a data set that includes the price of the car, you would use the transformation $P_i = (\$50)H_i+ \$1000$. Here, the intercept is the down payment of a thousand dollars, and then as horsepower $H$ increases by one unit, the price $P$ increases by fifty dollars.

The key with these transformations is how they affect the descriptive statistics we’ve already learned about. Most importantly is their relationship with the mean and variance:

\[E(a + bX) = a + bE(X)\] \[Var(a + bX) = b^2Var(X)\]

Note that E(X), or expected value of X, is the same as saying “the mean of X.”

This is the critically acclaimed “$a + bX$ rule,” and should be committed to memory (or at least understood thoroughly). It’s key to understand how this algebra works, since expectation and variance will show up in almost every unit in this book, and thus this rule will apply.

In english, this is describing what happens to the mean and variance when we transform a variable. The mean is straightforward: it is multiplied by the same multiplicative constant and increased by the same additive constant. In the car example we just did, the new mean could be found by multiplying by $50$ and then adding $1000$. So, the mean is affected by adding and/or multiplying constants (since the transformation affects every point individually, and the mean is calculated by adding up these points. Also, it is multiplied before it is added).

The variance is trickier, since it is clearly not affected by the additive constant (the “$a$” does not carry over to the right side of the equation). This makes intuitive sense, since if every value is increased by the same amount, then the spread between them doesn’t change (since $(x_i - \bar{x})^2$ does not change). However, multiplying should affect variance, since multiplying a small data point is much different than multiplying a large one. In fact, for reasons we won’t delve into here (they are more fit for a book on probability), we multiply by the constant squared. So, to find the new variance in our car example, we would just multiply the old variance by $50^2$ to get the new variance. So, variance is affected by multiplying constants but NOT by adding them (since variance measures the relationship between points, which is not affected by constant addition).

Less important are how other descriptive stats are affected by transformations, but we will include them anyways:

\[IQR_{new} = \mid b \mid (IQR_{old})\]

Or IQR is just multiplied by the absolute value of the multiplicative constant.

\[median_{new} = a + b(median_{old})\]

Or median is affected the same way the mean is by transformations.

Again, these are not really that important for our purposes and will probably not come up; even if they do, you will likely be able to derive the effects without remembering the formulas (trial and error, think about how data will be affected, etc.).

2. Outliers

These are decidedly inherently evil things with few redeeming qualities. We will see them in a more nuanced nature in later topics on regression and for now we will focus on detecting outliers.

As you can probably guess, an outlier is an extreme point that doesn’t really ‘lie’ with the rest of the data. Consider a sample I took of ten friends, testing how many cookies they could eat in an hour:

\[9, 37, 39, 39, 43, 44, 48, 48, 48, 89\]

It’s clear that there seem to be two outliers: the person who ate only $9$ cookies and the person who ate a whopping $89$ cookies. However, if someone asked you why these points are outliers, how would you respond? “Because they are really big or really small?” As in any field of analysis, it’s important to quantify exactly how we make these decisions. In this book, we will use two methods: the z-score and Box-Plot methods.

First is the z-score method. The idea of a z-score is arguably the most important concept you will learn in this book, and it’s introduction here does little justice to how central it is to the field of Statistics. Don’t worry though, you will soon enough be using the z-score for much more than just detecting outliers.

For now, we will calculate the z-score as:

\[z = \frac{x_i - \bar{x}}{s_x}\]

Or the data value minus the mean of the data set divided by the standard deviation of the data set. This result will be motivated and proved later, just trust it for now.

Although we don’t want to give too much away now, the z-score basically measures how significant a data point is relative to the mean (the larger the z-score, the farther away from the mean). It also standardizes these points, meaning that you can compare across units things totally unrelated (like SAT and ACT scores) by measuring performance based on the unitless z-score (it’s hard to compare a 1840 on the SATs versus a 27 on the ACTs; however, if you find the z-score, you can easily see which one is better).

Anyways, the z-score method for outlier is if a point has a z-score larger in magnitude than $+/- 2$, it is an outlier. This roughly means that the point is in either the top or bottom 2.5$\%$ of data, which we will further discuss later with the empirical rule.

With the cookie dataset, we see a mean of $44.4$ and standard deviation of $19.42$ (again, you can calculate this easily with the mean and sd functions in R). So, using the equation above, we get a z-score of $-1.82$ for the bottom point ($9$ cookies) and a z-score of $2.29$ for the top point ($89$ cookies). Therefore, using the $+/-2$ criteria, we would call the top point an outlier and remove it and fail to call the bottom point an outlier and would not remove it (although it certainly is unusual, it does not appear to be unusual enough). Of course, you would in theory have to check every point to see if it has a large enough z-score, but here it’s clear that no point other than $9$ or $89$ will have anywhere near a large enough z-score (nowhere near close to $+/-2$).

Next is the Box-Plot Method. Here, the criteria is if a point is lower than $1.5*IQR$ from $Q1$ or higher than $1.5*IQR$ from $Q3$, then it is an outlier.

We discussed these concepts in this chapter, but if you need a refresher, $Q1$ is just the 25th percentile of data, $Q3$ is the 75th percentile of data, and $IQR$ is the difference between the two ($Q3 - Q1$).

These points will usually show up as dots on a box plot, beyond (above or below) the box.

So, let’s use this method to test the cookie data. From the above cookie data, we find a $Q1$ value of $39$ and a $Q3$ value of $48$. So, $IQR = 48 - 39 = 9$, and $1.5*IQR = 1.5*9 = 13.5$.

Therefore, a point is an outlier if it is smaller than $Q1 - 1.5*IQR = 39 - 13.5 = 25.5$ or if it is larger than $Q3 + 1.5*IQR = 48 + 13.5 = 61.5$. The only point less than $25.5$ is $9$, and the only point greater than $61.5$ is $89$. So, the max and min are both outliers using this method!

Why did we get such a discrepancy between this and the z-score method? It is because, as we discussed earlier, mean and standard deviation (both used to find the z-score) are both heavily affected by extreme points, and thus might not tell the whole story in a skewed data set like this. The IQR is more robust to these extreme values, since it is not as directly affected by the, and thus perhaps gives a more accurate picture in this case.

However, you should be comfortable in using both methods and explaining their respective merits in varying situations.

2.4 Skewness

Ideally, we like to see well-behaved, mound shaped data that spreads out logically from the center. However, the (inconvenient?) truth is that real life data is usually skewed in some sense or another.

Visually, a skewed data set is not symmetric: the data spreads out farther in one direction (looks like a one-sided hill). We say a data set is right skewed if this “tail” points to the right, and left skewed if the tail points to the left. We like to remember these directions using what may be called the “sled-skew.” Imagine putting a little man on a sled on the highest bar of the data and think about which way he would want to sled down the slope (he likes long rides, so usually he will sled down the long way). The direction he sleds is the direction the data is skewed.

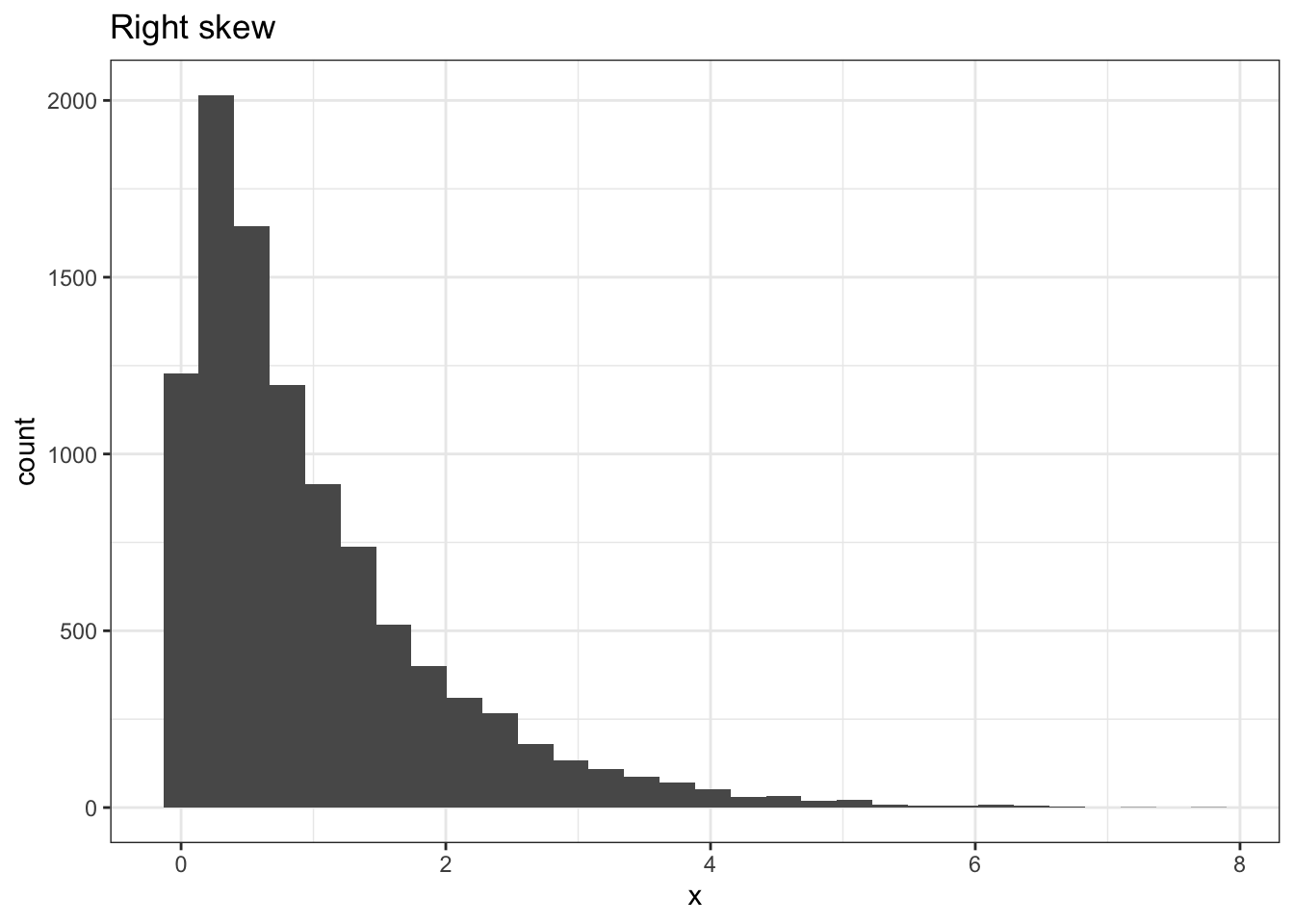
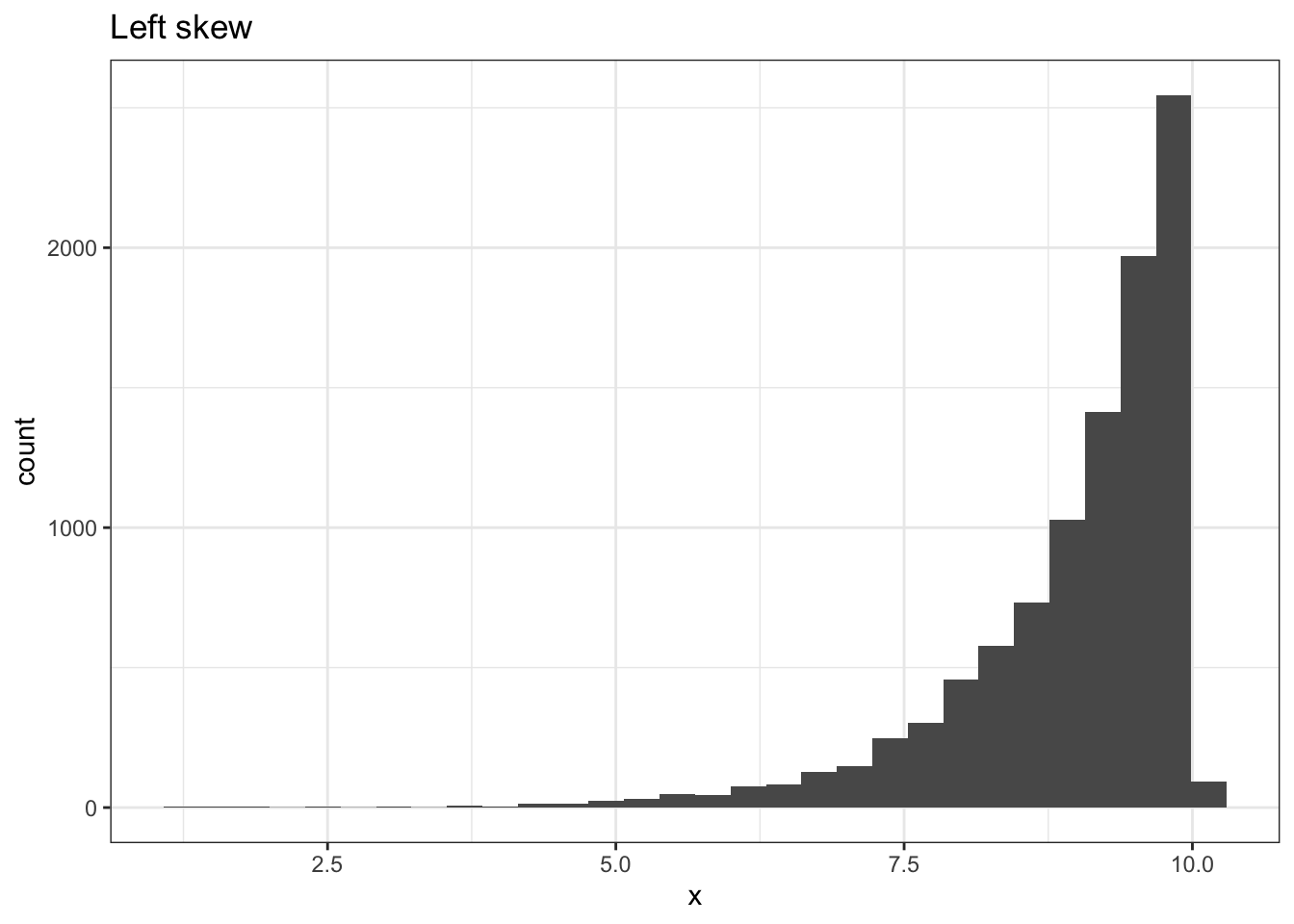
This is all fine and qualitative, but of course we need some way to quantify just what a skewed data set is instead of just looking at it subjectively. There is actually a numerical value that gives the skewness of a distribution, and it is the third standardized moment (3rd derivative) of the Moment Generating Function of a distribution. However, this is a probability concept that we won’t review in this book; instead, we run to R, or a similar tool, to find it for us. Usually, the rule of thumb is if the skew value is smaller in magnitude (absolute value) than .8, the data set is fine (not skewed). You can find the skewness value with the skewness function in the the e1071 package. This value will be positive for a right skew, negative for a left skew, and 0 (or close to it) for relatively no skew).

Of course, if we do encounter a skewed data set, we would like to (ideally) “un-skew” it: transform it until it is relatively normal looking (mound-shaped), since most of the tools we will earn in this book apply to mound-shaped data.

Usually, these transformations are a bit more involved than simple linear, $a + bX$ transformations. There is something called a ladder of powers, where the more skewed a data set is (the higher the skew value) the more powerful a transformation you need to correct it, and the higher you need to go on the ladder of powers.

In this book, our ladder will usually just consist of the square root transformation (take square root of every value), the log transformation (take log of every value) and the inverse transformation ($1$ divided by every value) where the first (square root) applies to the least-skewed sets (.8 to 1.5), log to slightly more skewed (1.5 to 3) and inverse to serious skews (over 3). In addition, a log transformation is usually applied to right-skewed distribution.

It sounds pretty dicey, but in this book we will just consider transforming a skewed data set and checking the new skewness statistic.

2.5 Chebyshev and the Empirical Rule

What sounds like an odd title for a children’s story is really a useful set of tools for describing data spread.

First, we’ll consider the Empirical Rule. This is a more specific and specialized rule, since it only applies to mound shaped data (we’ll see that Chebyshev’s rule applies to all data sets, regardless of shape).

You may have heard another name for the Empirical Rule: the “$68-95-99.7$ Rule.” The concept is that, for a mound shaped data set, about 68$\%$ of the data lies within $1$ standard deviation of the mean, about 95$\%$ of the data lies within $2$ standard deviations of the mean and about 99.7$\%$ of the data lies within $3$ standard deviations of the mean.

An important result of this rule is that, when we find the z-score of a data point, we are standardizing that point, or converting it to a random variable that has a standard deviation of 1. Therefore, the 68-95-99.7 rule is the same for z-scores: about 68$\%$ of data lies within +/- 1 z-score, etc. This does not have to make any sense now, as we will prove this in later sections. The important takeaway is that the same concept can be applied to z-scores}.

It’s also important to remember that the Empirical Rule gives the spread of data on both sides of the mean; that is, it’s not that 32$\%$ of data is more extreme than one standard deviation above the mean, but below as well. Since mound shaped data is symmetric, you can assume that the split is even, and that about 16$\%$ of the data is below the mean minus one standard deviation and about 16$\%$ is above the mean plus one standard deviation.

The Empirical rule, then, provides a quick and painless rough estimate of the relative position of a data point. It’s interesting to see how fast relative density accumulates: you only need to be $2$ standard deviations from the mean to be extraordinary (in the top 97.5th percentile).

While this proxy can only be used on mound shaped data, Chebyshev works on all data sets, regardless of shape.

It states that for any data set, the proportion of data within $k$ standard deviations of the mean is at least:

\[1 - \frac{1}{k^2}\]

Where $k>1$.

Let’s test this with $2$ standard deviations. If we plug in $2$ to the above equation, we get $1 - \frac{1}{2^2} = 1 - \frac{1}{4} = \frac{3}{4}$. Therefore, at least $75\%$ of the data is within $2$ standard deviations of the mean.

This value of $75\%$ is significantly smaller than the result from the Empirical Rule, which was $95\%$ for $+/- 2$ standard deviations. This makes sense, as the Empirical Rule requires more conditions to hold (mound shaped data) and thus should provide us with a better guess. We must also remember that Chebyshev gives us a strict lower bound (AT LEAST $75\%$), and thus may seem smaller by comparison.