Chapter 3 Greeks
As mentioned before, the price of an option can be modelled as a function of different parameters. The Greeks represent the sensitivities of the options with respect to this parameters, which translates by first (or even second) order derivatives.
3.1 Delta
The delta represents the sensitivity of the option with respect to the underlying \(S\).
For a call, we have \[ \boxed{\Delta_C= \frac{\partial C}{\partial S} = \mathcal{N}(d_1)} \] And for a put: \[ \boxed{\Delta_P= \frac{\partial P}{\partial S} = \mathcal{N}(d_1) -1} \]
- Since \(\mathcal{N}(.)\) is the repartition function of a gaussian, it lays between \(0\) and \(1\) for a call and \(-1\) and \(0\) for a put.
- If we are close to being ATM, \(\Delta \approx \mathcal{N}(d_2)= \mathbb{P}(ITM)\). Thus, \(\Delta\) is a good approximation of the probability of the ‘in-the-moneyness’ of the intrinsic value of the option.

Delta with respect to S
3.1.1 Delta evolution with T
- If we increase the maturity, \(\Delta\) flattens because the time value decreases.
- If we are deep OTM (on the left), we have more time to be ITM.
- If we are deep ITM (on the right), a higher maturity would give more time to fall OTM.

Delta with respect to Time
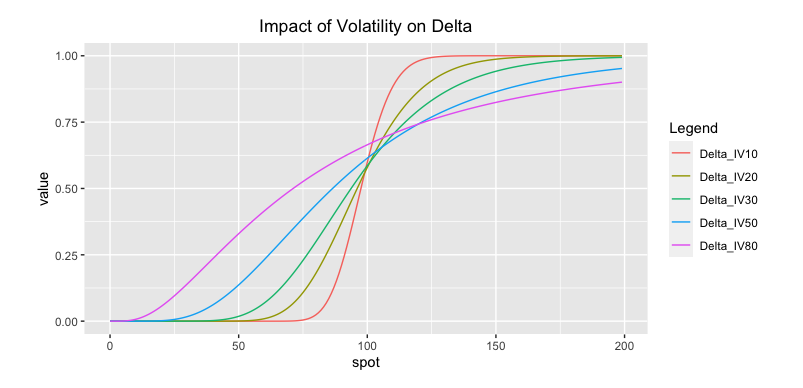
3.1.2 Delta evolution with volatility
- If we increase the volatility, \(\Delta\) flattens because small changes in the underlying will be less significant compared to low volatility environment : the volatility can compensate these changes.The delta therefore takes less extreme values, and flattens.
- If we are deep OTM (on the left), higher volatility implies more chance to finish ITM: The more OTM, the less chances we have to be “more OTM” compared to “more ITM”.
- If we are deep ITM (on the right), higher volatility implies more chance to finish OTM. The more ITM, the less chances we have to be “more ITM” compared to “more OTM”.
Delta with respect to Time
3.2 Gamma
The Gamma is the second order derivative of the option price with respect to the underlying price, or equivalently the first order derivative of the delta with respect to the underlying price. It measures the sensitivity of the delta with respect to underlying moves.
\[ \boxed{\Gamma=\frac{\partial^2 C}{\partial^2 S} = \frac{\partial \Delta}{\partial S} = \frac{\mathcal{N}'(d_1)e^{-qT}}{S\sigma \sqrt{T}}\geq 0} \]
First, we can notice that the gamma is the same for a long call and a long put and is positive. This is due to the fact that it is the derivative of the delta, so it models the slope of the curve. Thus, it has the shape of the density function of a Gaussian.
 ### Gamma vs Time to maturity
### Gamma vs Time to maturity
- The global shape of the gamma can be explained by time to maturity: shorter maturities have sharper and higher gamma because the delta has a sharper shape, so it is subject to bigger moves as we get closer to expiry. But looking more into detail with moneyness:
- For ‘deep’ OTM and ITM options, shorter maturities gamma is lower than higher maturities because there is less time for a change of moneyness, i.e. the time value of the option is lower.
- For ATM options, shorter maturities gamma is higher because there is a higher chance of a change of moneyness.
We can apply this notion of time value and obtain the same result with volatility.
3.2.1 Gamma vs Volatility
- When volatility decreases, the gamma globally increases, because as we saw, the shape of the delta is steeper.
But looking more into detail with moneyness:
- In the ATM region, lower volatility implies flatter delta, thus lower gamma.
- In ITM/OTM region, lower volatility implies steeper delta, thus higher gamma. Note: The time value is the difference between the option premium and its intrinsic value. For OTM options, since the intrinsic value is \(0\), the time value is just the option price.
3.3 Vega
Vega (\(\mathcal{V}\)) is the sensitivity of the option price with respect to a move of the volatility.
\[ \boxed{\mathcal{V}_C=\mathcal{V}_P = Se^{−qT}\mathcal{N}(d1)\sqrt{T}\geq 0} \]

Vega vs T and S
- \(\mathcal{V}\) is positive for calls and put: we want volatility because if underlying goes up (resp. down), the call (resp. put) is in the money, and otherwise, we don’t lose any money.
- On the opposite, the more ITM/OTM, the less impact will have volatility.
- vega is the highest at the strike because a small change in volatility can change the moneyness of the option.
- increased T increases vega: we have more time for volatility to affect the underlying and change moneyness.
- increased volatility increases the vega : the more volatility we have, the more sensible to it we are.
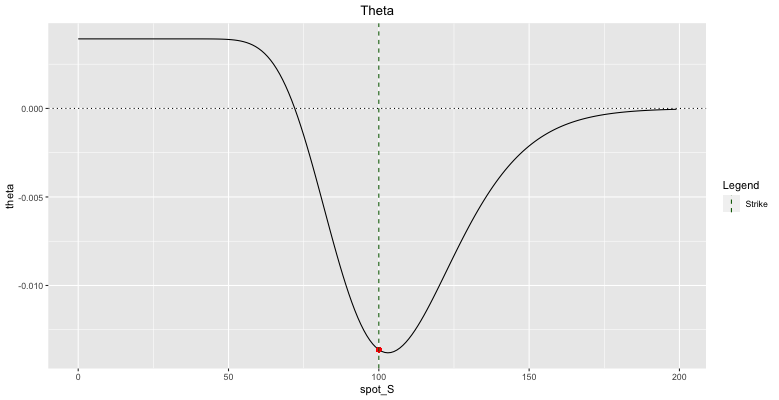
3.4 Theta
Theta represents the rate of change of an option’s price with respect to time. It measures the sensitivity of the option’s value to the passage of time, commonly referred to as time decay.
The theta is given by:
\[ \boxed{\Theta = \frac{\partial P}{\partial T}} \] The shape of Theta is as follows:

Theta vs S
It is to note that the theta of the call is always negative of null. We will see below cases where the theta of a put can be negative. Globally, Theta is negative, since the option loses time when times passes. However, we will see cases where theta can be positive.
3.4.3 Positive Theta
Consider a Deep ITM put option. We know the following relation:
\[ \boxed{P(t,T) =IV(t)+ + TV(t)} \]
Where \(TV\) is the time value of the option (hence, the opposite of the \(\Theta\)). As the value of the stock decreases to \(0\), the price naturally becomes \(e^{-r(T-t)}K\), and the payoff simplifies to \(K\).
\[
\boxed{e^{-r(T-t)}K=K+ TV(t)}
\]
Which simplifies to:
\[
\boxed{TV(t) = (e^{-r(T-t)}-1)K}
\]
We see that if:
* \(r>0\)
* \(S_t<<K\),
We can obtain a negative \(\Theta\)
3.5 Delta Bleed / Charm
It is the derivative of the delta with respect to the time, or also the derivative of the theta with respect to the underlying. \[ \boxed{\Delta_{charm}= -\frac{\partial \Delta}{\partial T} = \frac{\partial \Theta}{\partial S}} \] We put a minus sign because the above represents the variation of the delta when we increase the maturity instead of getting closer to expiry (so reducing the maturity).
- For ITM Calls (OTM Puts), the charm is positive: the \(\Delta\) increases as times passes, because it gives more time to finish OTM (ITM).
- For OTM Calls (ITM Puts), the charm is negative: the \(\Delta\) decreases as times passes, because it gives more time to finish ITM (OTM).
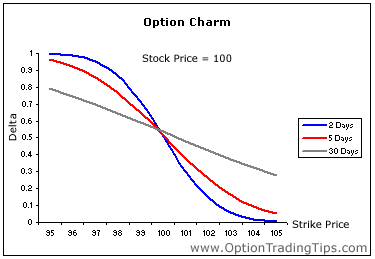
Delta Bleed of a Call option vs Time to maturity
To analyze the above curve, let us take a point in terms of moneyness (fix the strike): on the left, the longest to mature option (grey curve) has a lower delta than the two others, but we can see that as we get closer to maturity, the delta converges to one (hence the probability of finishing in the money).
The delta bleed is often used by traders to see how time will impact the delta, for instance before the week-end.