Chapter 4 Lab 2 - 14/10/2022

In questa lezione vedremo come importare dati disponibili in un file di tipo comma-separated (csv). Vedremo inoltre come analizzare i dati disponibili in un oggetto di tipo data frame. Il file Adjcloseprices.xlsx (o la sua versione equivalente Adjcloseprices.csv) contiene i prezzi giornalieri di alcuni titoli per una serie di date dal 2017 al 2021.

Si inizia però prima a vedere come fare a selezionare uno o più oggetti da un vettore.

4.1 Selezione di valori da un vettore

Si consideri il seguente vettore e si ricordi che il vettore è da considerarsi come un oggetto unidimensionale:

x = c(-44.5, 10.78, sqrt(77), log(3/5))

Per la selezione di elementi all’interno di un vettore si utilizzano le parentesi quadre. Ad esempio per selezionare il secondo elemento si usa il seguente codice (si noti che all’interno delle parentesi quadre si specifica la posizione del numero da selezionare).

x[2]

## [1] 10.78

Volendo selezionare più elemento si andrà a definire un vettore di posizioni tramite la funzione c:

x[c(2,4)] # 2 posizioni

## [1] 10.7800000 -0.5108256

Utilizzando gli operatori logici è possibile eseguire selezione di elementi e/o sostituzione per condizione. In questo caso non sarà necessario specificare le posizioni degli elementi da selezionare/sostitutire perchè R eseguirà la selezione/sostituzione solamente per quegli elementi che soddisfano la condizione (TRUE). Si selezionino ad esempio solo i valori negativi:

x < 0  #verifica condizione

## [1]  TRUE FALSE FALSE  TRUE

x[x < 0] #estratti gli elementi con TRUE

## [1] -44.5000000  -0.5108256

E’ possibile infine sostituire i numeri negativi con zero:

x[x < 0] = 0
x

## [1]  0.000000 10.780000  8.774964  0.000000

4.2 Import dei dati da file Excel

Un’anteprima dei dati contenuti nel file Excel Adjcloseprices.xlsx è rappresentata qui di seguito. Il file contiene un unico foglio di lavoro dove le righe si riferiscono alle osservazioni (date) e le colonne alle variabili misurate (prezzi per alcuni titoli).

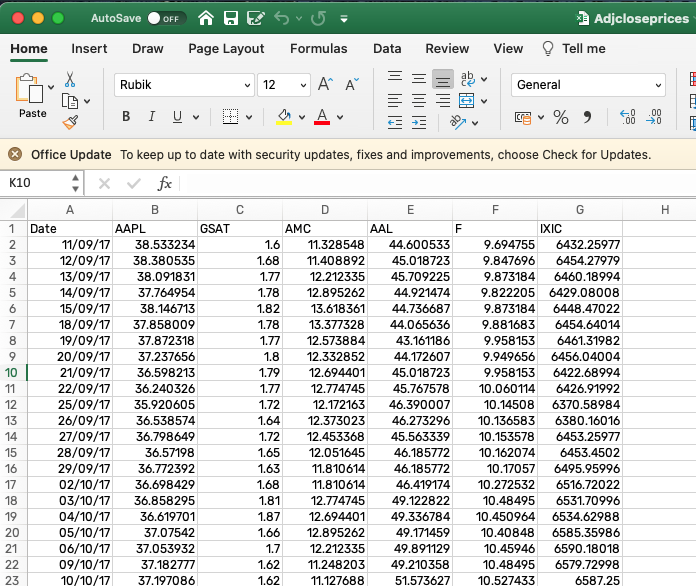
Figure 4.1: Anteprima di un file di esempio di tipo Excel contenente prezzi

E’ possibile utilizzare la funzionalità “Import Dataset” di RStudio per l’import di dati disponibili su file esterno: si veda qui per maggiori informazioni. La funzionalità “Import Dataset” è disponibile nel pannello in alto a destra (Environment) (si veda la Figura 4.2). Dopo aver scelto “From Excel” è possibile specificare alcuni settaggi del file nella finestra che compare (si veda un esempio simile in Figura 4.3. In particolare vanno definite tre cose:

il file che deve essere importato (utilizzare il testo Browse per identificarlo nel proprio computer)
nome dell’oggetto (Name) contenente i dati che verrà creato in RStudio
l’opzione “First row as Names” va selezionata in quanto significa che i nomi delle colonne sono incluse nella prima riga del file.

Figure 4.2: La funzione Import Dataset di RStudio

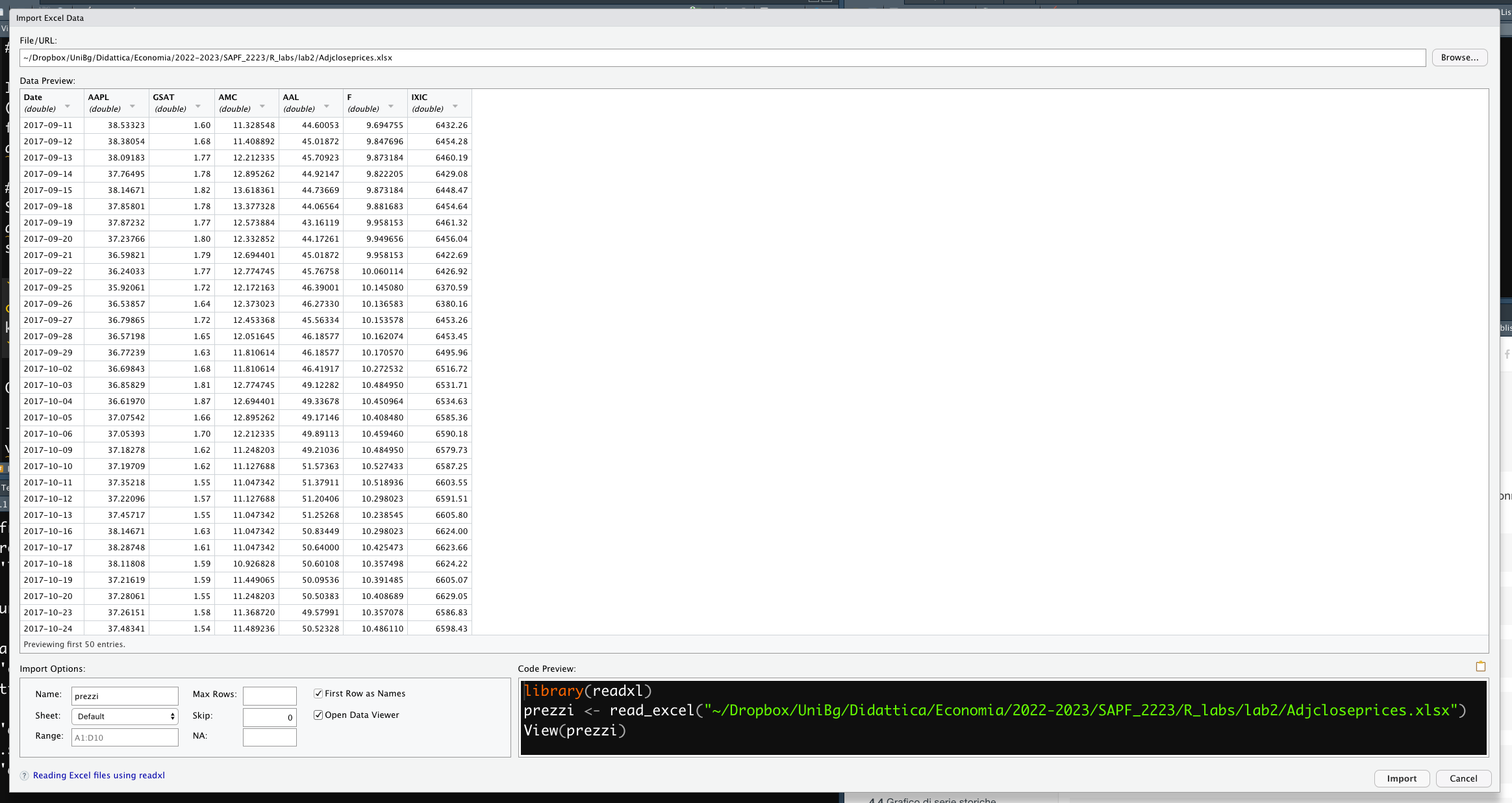
Figure 4.3: Finestra per la definizione delle caratteristiche del file Excel

Dopo aver cliccato su Import un oggetto di nome prezzi verrà creato.

Si noti che di fatto RStudio per l’import dei dati sta utilizzando la funzione read_excel contenuta nel pacchetto readxl (la cui installazione viene richiesta la prima volta che si tenta di usare questa opzione):

library(readxl)
prezzi = read_excel("./data/Adjcloseprices.xlsx")

A volte un file Excel può dare problemi in fase di import. In tal caso si suggerisce di salvare il foglio di lavoro come file di tipo csv (usando l’opzione File - Salva con Nome) e di procedere quindi come descritto nella Sezione 4.3.

4.3 Importazione dei dati da file csv

Si noti che il file di tipo .csv è di fatto un file di testo che può essere aperto con un editor di testo come TextNote, TextEdit o BloccoNote (si veda la Figura 4.4 per un esempio simile).

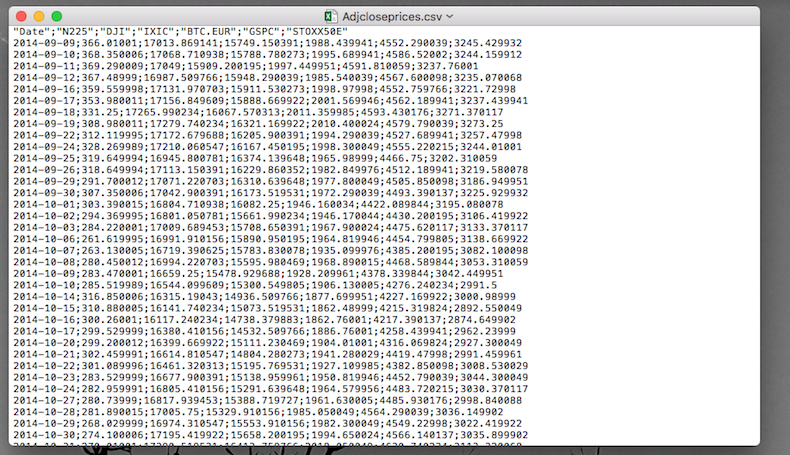
Figure 4.4: Anteprima di un file di esempio di tipo csv contenente prezzi

Ci sono 3 elementi che caratterizzano un file csv:

header (intestazione): la prima riga del file che contiene solitamente i nomi delle variabili;
il separatore di campo: il carattere utilizzato per separare le informazioni disponibili nel file (solitamente si utilizza il punto e virgola o la virgola);
il separatore decimale: il carattere utilizzato per i decimali (solitamente si usa la virgola o il punto).

Dall’anteprima del file riportata in Figura 4.4 si nota che:

le stringhe di testo riportate nella prima riga rappresentano i nomi delle variabili;
“;” è il separatore di campo;
“.” è il separatore decimale.

Queste informazioni devono necessariamente essere specificate in R quando si importano dei dati da un file csv. La funzione che si utilizza è read.csv i cui principali argomenti sono riportati di seguito (si veda anche ?read.csv):

file: il nome del file (specificato tra virgolette) da importare con eventualmente la specifica del percorso intero che porta alla cartella dove è contenuto il file;
header: valore logico (TRUE o FALSE) che indica se la prima riga del file contiene i nomi delle variabili;
sep: il carattere che rappresenta il separatore di campo (da specificare dentro le virgolette);
dec: il carattere che rappresenta il separatore decimale (da specificare dentro le virgolette).

Il seguente codice può quindi essere utilizzato per importare i dati disponibili in Adjcloseprices.csv (in particolare, il codice crea un oggetto di nome prezzi). La difficoltà consiste nello specificare il percorso del file per definirne la localizzazione nel proprio computer:

prezzi <- read.csv("./data/Adjcloseprices.csv", header=TRUE, sep=";")

In alternativa è possibile utilizzare la funzionalità “Import Dataset” disponibile nel pannello in alto a destra (Environment) (si veda la Figura 4.5). Dopo aver scelto “From text (base)” è possibile specificare tutti i settaggi del file csv nella finestra “Import Dataset” che segue (si veda un esempio simile in Figura 4.6.

Figure 4.5: La funzione Import Dataset di RStudio

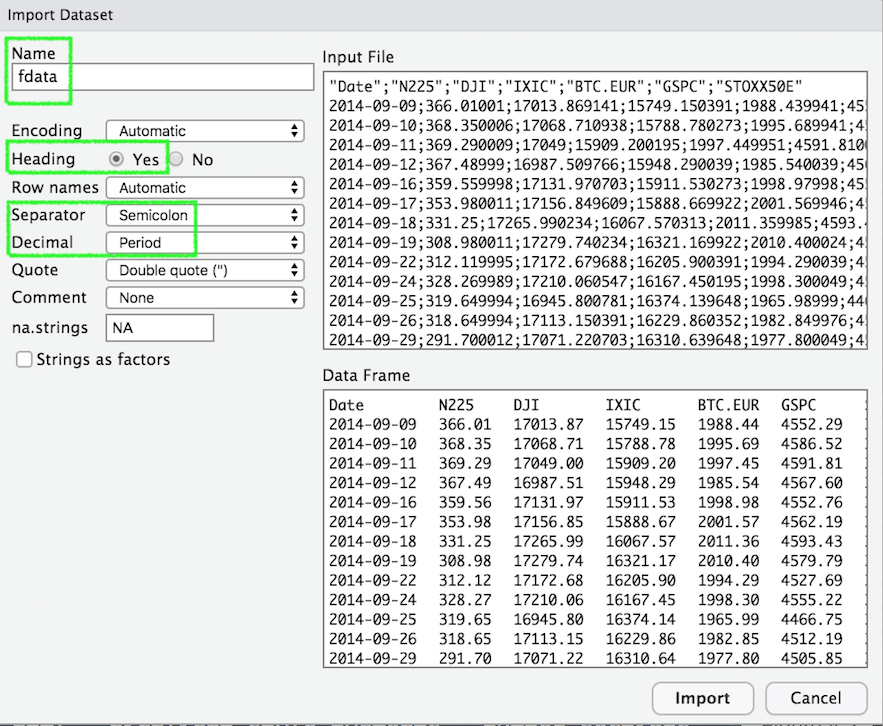
Figure 4.6: Finestra per la definizione delle caratteristiche del file csv

Dopo aver cliccato su Import un oggetto di nome prezzi verrà creato. Si noti che di fatto RStudio utilizza la funzione read.csv i cui argomenti vengono specificati tramite un’interfaccia user-friendly.

4.4 Data frame

L’oggetto prezzi è un oggetto di tipo data.frame:

class(prezzi)

## [1] "tbl_df"     "tbl"        "data.frame"

I data frame sono matrici di dati le cui righe si riferiscono ai soggetti (in questo caso ai diversi giorni finanziari) e le righe alle variabili (in questo caso le date e i prezzi dei titoli).

Utilizzando la funzione str si ottengono informazioni circa la tipologia delle variabili incluse nel data frame:

str(prezzi)

## tibble [1,008 × 7] (S3: tbl_df/tbl/data.frame)
##  $ Date: POSIXct[1:1008], format: "2017-09-11" "2017-09-12" ...
##  $ AAPL: num [1:1008] 38.5 38.4 38.1 37.8 38.1 ...
##  $ GSAT: num [1:1008] 1.6 1.68 1.77 1.78 1.82 1.78 1.77 1.8 1.79 1.77 ...
##  $ AMC : num [1:1008] 11.3 11.4 12.2 12.9 13.6 ...
##  $ AAL : num [1:1008] 44.6 45 45.7 44.9 44.7 ...
##  $ F   : num [1:1008] 9.69 9.85 9.87 9.82 9.87 ...
##  $ IXIC: num [1:1008] 6432 6454 6460 6429 6448 ...

Se il file importato è il file Excel la variabile Date è riconosciuta correttamente come tale (POSIXct è l’abbreviazione di calendar time, è quindi un vettore di date) mentre le altre variabili sono di tipo numerico (num). Se si lavora invece con il file csv qui sarebbe necessaria una trasformazione della colonna con le date.

Utilizzando le funzioni head e tail è possibile ottenere visualizzare la parte superiore e inferiore del data frame:

head(prezzi) #prime 6 righe in alto (date più remote)

## # A tibble: 6 × 7
##   Date                 AAPL  GSAT   AMC   AAL     F  IXIC
##   <dttm>              <dbl> <dbl> <dbl> <dbl> <dbl> <dbl>
## 1 2017-09-11 00:00:00  38.5  1.6   11.3  44.6  9.69 6432.
## 2 2017-09-12 00:00:00  38.4  1.68  11.4  45.0  9.85 6454.
## 3 2017-09-13 00:00:00  38.1  1.77  12.2  45.7  9.87 6460.
## 4 2017-09-14 00:00:00  37.8  1.78  12.9  44.9  9.82 6429.
## 5 2017-09-15 00:00:00  38.1  1.82  13.6  44.7  9.87 6448.
## 6 2017-09-18 00:00:00  37.9  1.78  13.4  44.1  9.88 6455.

tail(prezzi) #ultime 6 righe in basso (date più recenti)

## # A tibble: 6 × 7
##   Date                 AAPL  GSAT   AMC   AAL     F   IXIC
##   <dttm>              <dbl> <dbl> <dbl> <dbl> <dbl>  <dbl>
## 1 2021-09-02 00:00:00  154.  2.1   44.4  19.8  13.0 15331.
## 2 2021-09-03 00:00:00  154.  2.2   44.0  19.4  12.9 15364.
## 3 2021-09-07 00:00:00  157.  2.07  47.8  19.5  13.0 15374.
## 4 2021-09-08 00:00:00  155.  2.69  47.4  19.1  13.0 15287.
## 5 2021-09-09 00:00:00  154.  2.58  48.5  20.2  12.8 15248.
## 6 2021-09-10 00:00:00  149.  2.6   50.2  19.0  12.7 15115.

Per ottenere informazioni circa le dimensioni del data frame (numero di righe e colonne) si possono utilizzare le seguenti funzioni alternative:

nrow(prezzi) #n. di righe

## [1] 1008

ncol(prezzi) #n. di colonne

## [1] 7

dim(prezzi) #n. di righe e di colonne

## [1] 1008    7

Si fa notare che l’utilizzo della funzione length() non ha senso per un data frame essendo un oggetto di tipo bidimensionale (mentre length() si può utilizzare per oggetti monodimensionali come i vettori).

4.5 Selezione di dati da un data frame

La selezione di dati da un data frame si effettua utilizzando le parentesi quadre, in maniera simile a quanto visto durante il Lab 1 per i vettori. Nel caso di data frame però all’interno delle parentesi quadre dovranno essere specificati due indici, uno per le righe e uno per le colonne, separati da virgola. Per esempio il codice

prezzi[4,4]

## # A tibble: 1 × 1
##     AMC
##   <dbl>
## 1  12.9

seleziona l’elemento presente nella quarta riga e quarta colonna, corrispondente al prezzo del titolo AMC per il giorno 2017-09-14.

Per selezionare più elementi è possibile utilizzare un vettore di indici:

prezzi[ c(100,101,102) , 4] #righe 100, 101, 102, quarta colonna

## # A tibble: 3 × 1
##     AMC
##   <dbl>
## 1  11.0
## 2  11.4
## 3  10.9

Si noti che il vettore c(100,101,102) rappresenta una sequenza regolare di passo 1 da 100 a 102 il cui codice può essere semplificato con 100:102:

prezzi[ 100:102 , 4] #righe 100, 101, 102, quarta colonna

## # A tibble: 3 × 1
##     AMC
##   <dbl>
## 1  11.0
## 2  11.4
## 3  10.9

Per selezionare un’intera riga (contentente i prezzi di tutti i titoli per un particolare giorno) è necessario specificare solo l’indice di riga:

prezzi[4, ] #tutti i dati disponibili sulla quarta riga (quarto giorno)

## # A tibble: 1 × 7
##   Date                 AAPL  GSAT   AMC   AAL     F  IXIC
##   <dttm>              <dbl> <dbl> <dbl> <dbl> <dbl> <dbl>
## 1 2017-09-14 00:00:00  37.8  1.78  12.9  44.9  9.82 6429.

In maniera simile, per estrarre i dati di un’intera colonna (corrispondenti in questo caso all’intera serie storica di prezzi per il titolo selezionato), si specifica solamente l’indice di colonna:

prezzi[,4] #tutti i valori in quarta colonna

## # A tibble: 1,008 × 1
##      AMC
##    <dbl>
##  1  11.3
##  2  11.4
##  3  12.2
##  4  12.9
##  5  13.6
##  6  13.4
##  7  12.6
##  8  12.3
##  9  12.7
## 10  12.8
## # … with 998 more rows

Alternativamente è possibile selezionare una colonna utilizzando il nome di colonna preceduto dal simbolo di dollaro. Il seguente codice seleziona la colonna di nome AAPL e ne salva i valori in un nuovo oggetto (di tipo vettore) denominato x:

x = prezzi$AAPL #è un vettore
class(x)

## [1] "numeric"

length(x)

## [1] 1008

4.6 Analisi esplorativa su singole colonne

Dato un vettore di dati la funzione summary restituisce i valori dei principali indici statistici di posizione:

summary(prezzi$F)

##    Min. 1st Qu.  Median    Mean 3rd Qu.    Max. 
##   4.010   8.152   9.075   9.305  10.325  15.990

Per il calcolo della mediana si possono usare anche le seguenti funzioni (si ricordi che la mediana è il quantile di ordine 0.5):

median(prezzi$F)

## [1] 9.074938

quantile(prezzi$F, 0.5) #calcolo mediana

##      50% 
## 9.074938

Per calcolare misure di variabilità è possibile utilizzare la funzione var (varianza campionaria) sd (standard deviation, data dalla radice della varianza), o il coefficiente di variazione (indice relativo dato dal rapporto tra standard deviation e media):

var(prezzi$F)

## [1] 4.721864

sd(prezzi$F)

## [1] 2.172985

sd(prezzi$F) / mean(prezzi$F)

## [1] 0.2335304

4.7 Grafico di serie storiche

Si intende rappresentare graficamente le serie storiche dei prezzi per i titoli disponibili. Il grafico finale avrà le date sull’asse delle x e i prezzi sull’asse delle y. Iniziamo rappresentando la serie storica di F:

plot(prezzi$F)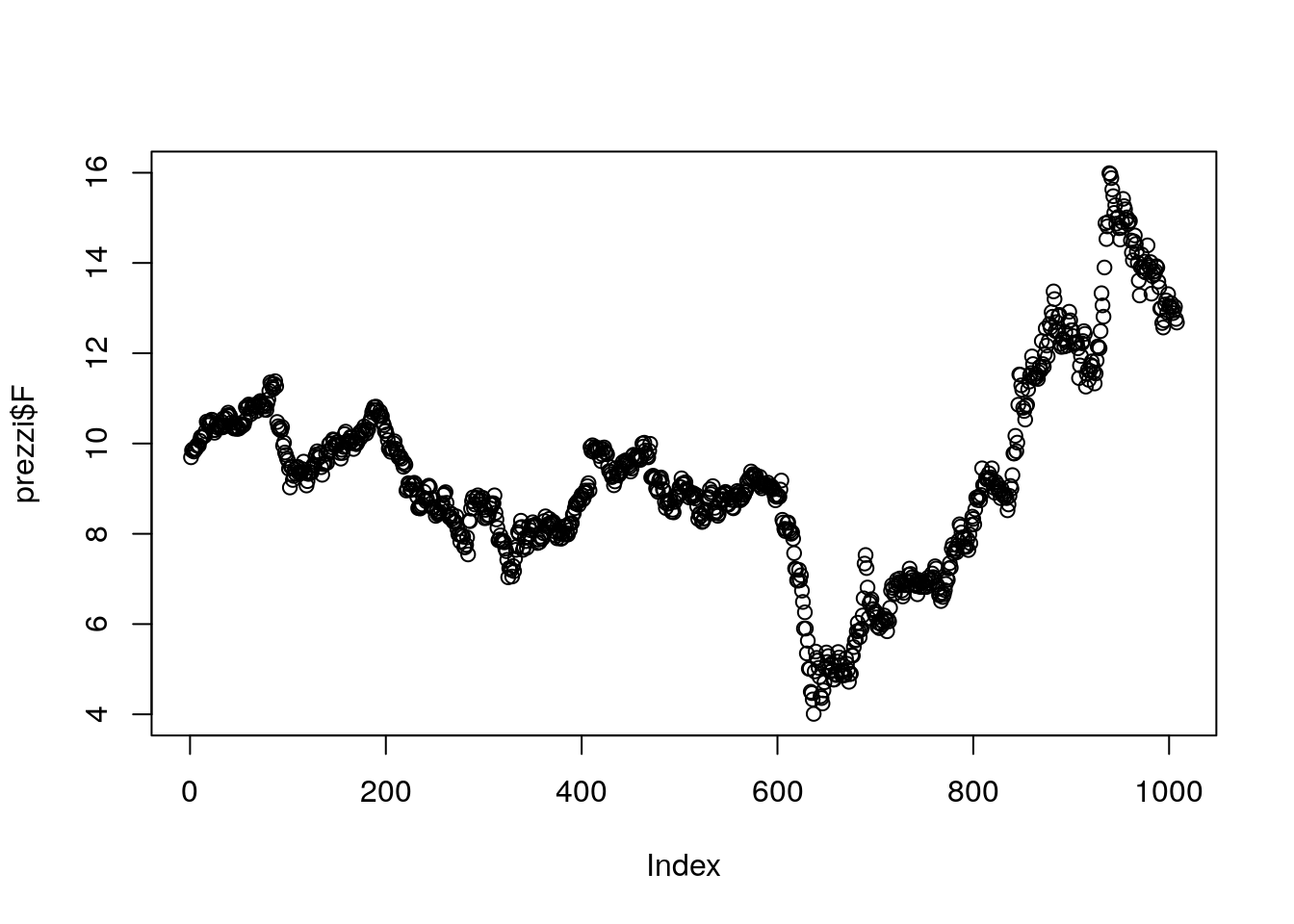

Ogni punto nel grafico rappresenta un giorno finanziario e la sua posizione nel grafico è data dal prezzo del titolo. Si noti che per il momento sull’asse delle x viene rappresentata, in maniera automatica, la variabile Index data da una sequenza regolare da 1 al numero totale di dati disponibili per la serie storica (in questo caso 1008). L’utilizzo dei punti non è la scelta migliore per rappresentare una serie storica perchè l’andamento temporale della serie non viene rappresentato chiaramente. Il codice che segue utilizza l’argomento type="l" (“l” sta per linea) al fine di avere una rappresentazione di tipo “linea” della serie storica:

plot(prezzi$F,type="l")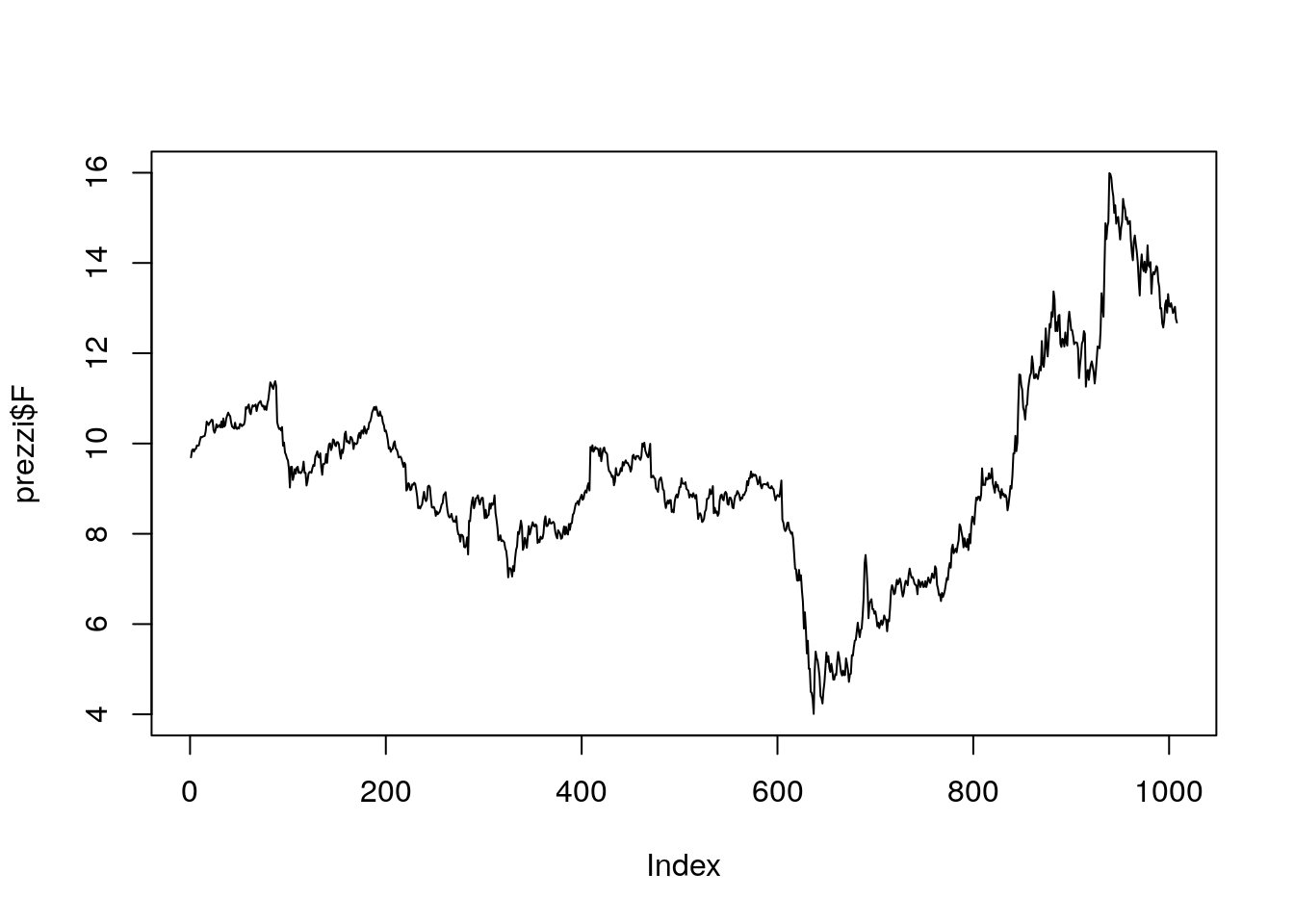

Per includere le date nell’asse delle x si va a specificare due vettori all’interno della funzione plot (il primo vettore verrà utilizzato per l’asse delle x, il secondo per l’asse delle y):

plot(prezzi$Date, prezzi$F,
     type="l")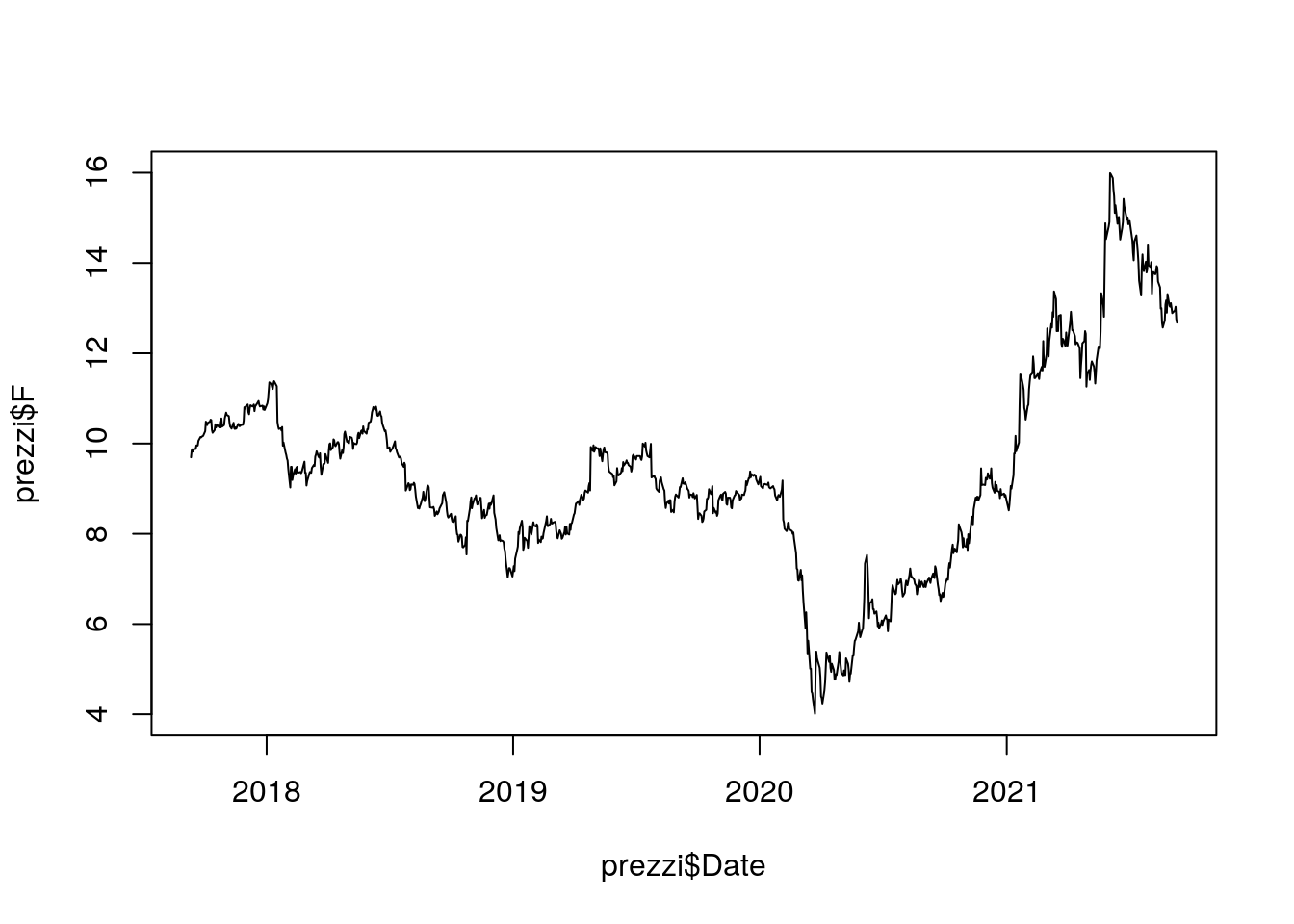

E’ possibile anche cambiare le etichette degli assi e definire un titolo per il grafico:

plot(as.Date(prezzi$Date), prezzi$F,
     type="l",
     xlab = "Date",
     main = "Serie storica del titolo FORD")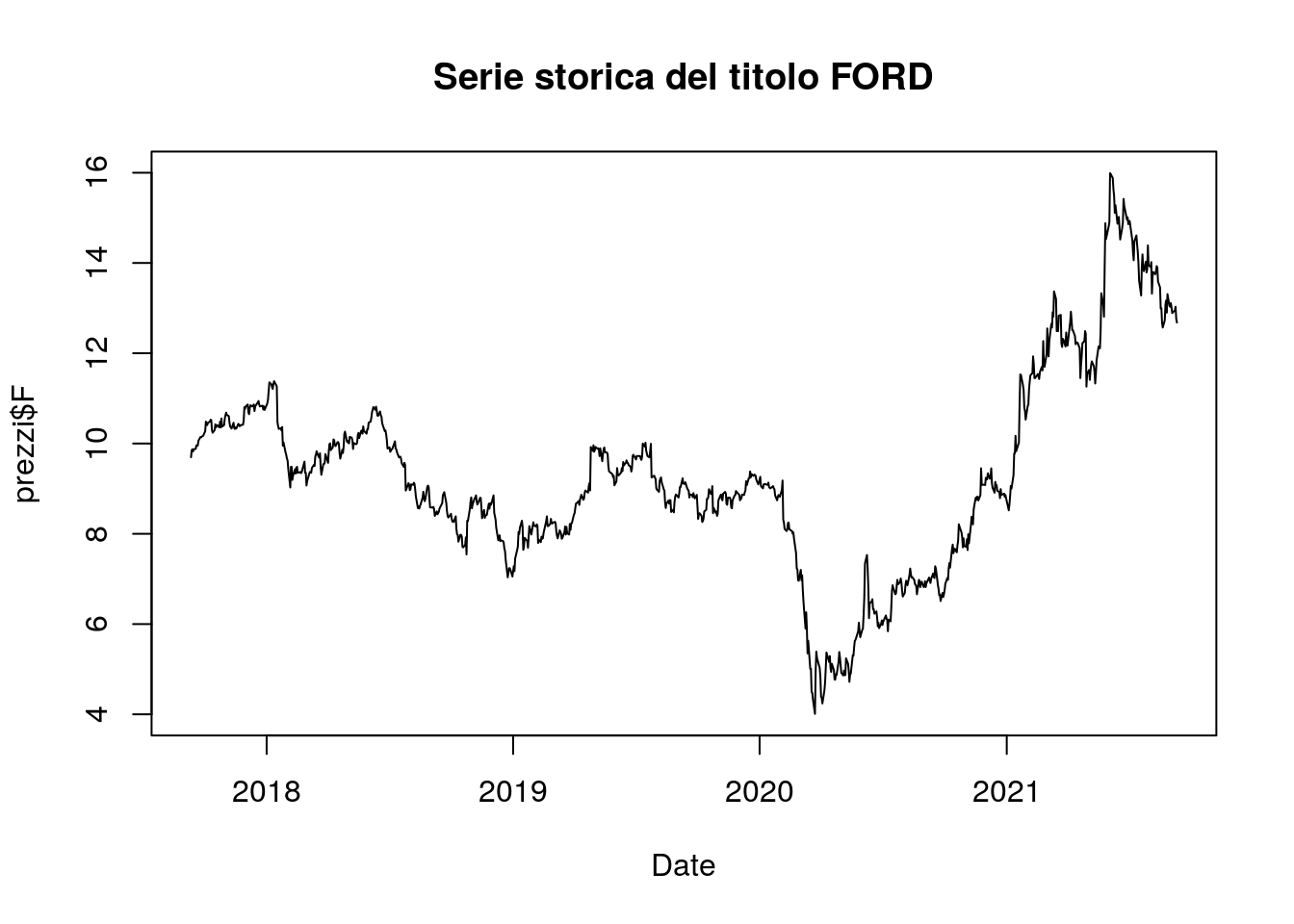

Il passo successivo consiste nel rappresentare più serie storiche nello stesso grafico (ad esempio F e AMC). La prima serie storica si rappresenta utilizzando la funzione plot mentre la seconda la funzione lines che va ad aggiungere una nuova linea ad un grafico esistente:

plot(prezzi$Date , prezzi$F,
     type="l")
#aggiungere una nuova serie storica
lines(prezzi$Date , prezzi$AMC,
      col = "red") #colore linea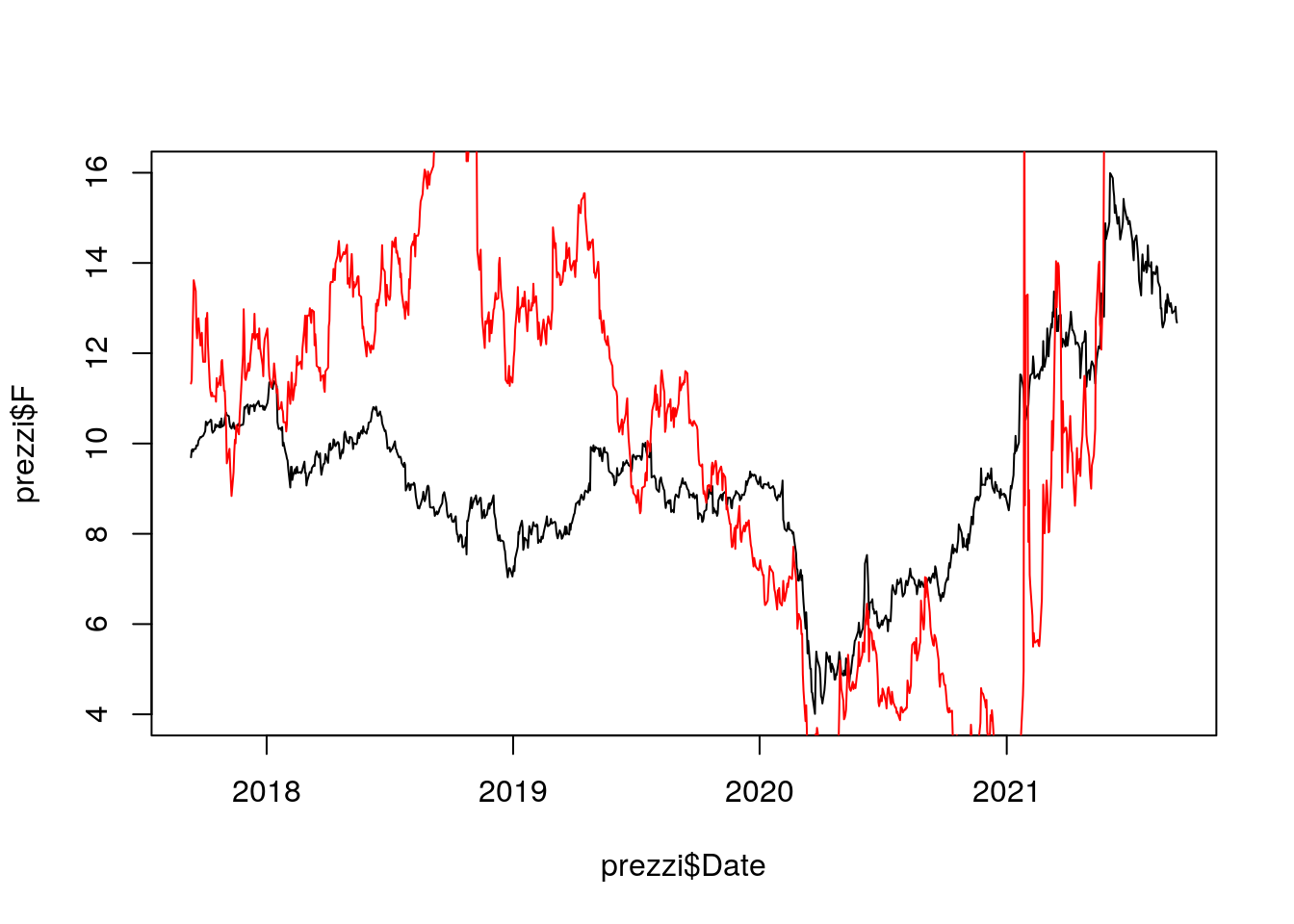

Si noti che la serie del titolo N225 non è visibile perchè ha un range di valori completamente diverso (controllare usando summary) e non incluso nell’intervallo di valori utilizzato per l’asse delle y e scelto in automatico da R. Per specificare in maniera diversa il range di valori dell’asse delle y si utilzza l’argomento ylim della funzione plot (andranno specificati il valore minimo e massimo per l’asse delle y):

plot(prezzi$Date,
      prezzi$F, 
      type = "l",#linea
      xlab = "Date",
      ylim = c(0,80)) 
lines(prezzi$Date,
      prezzi$AMC,
      col = "red")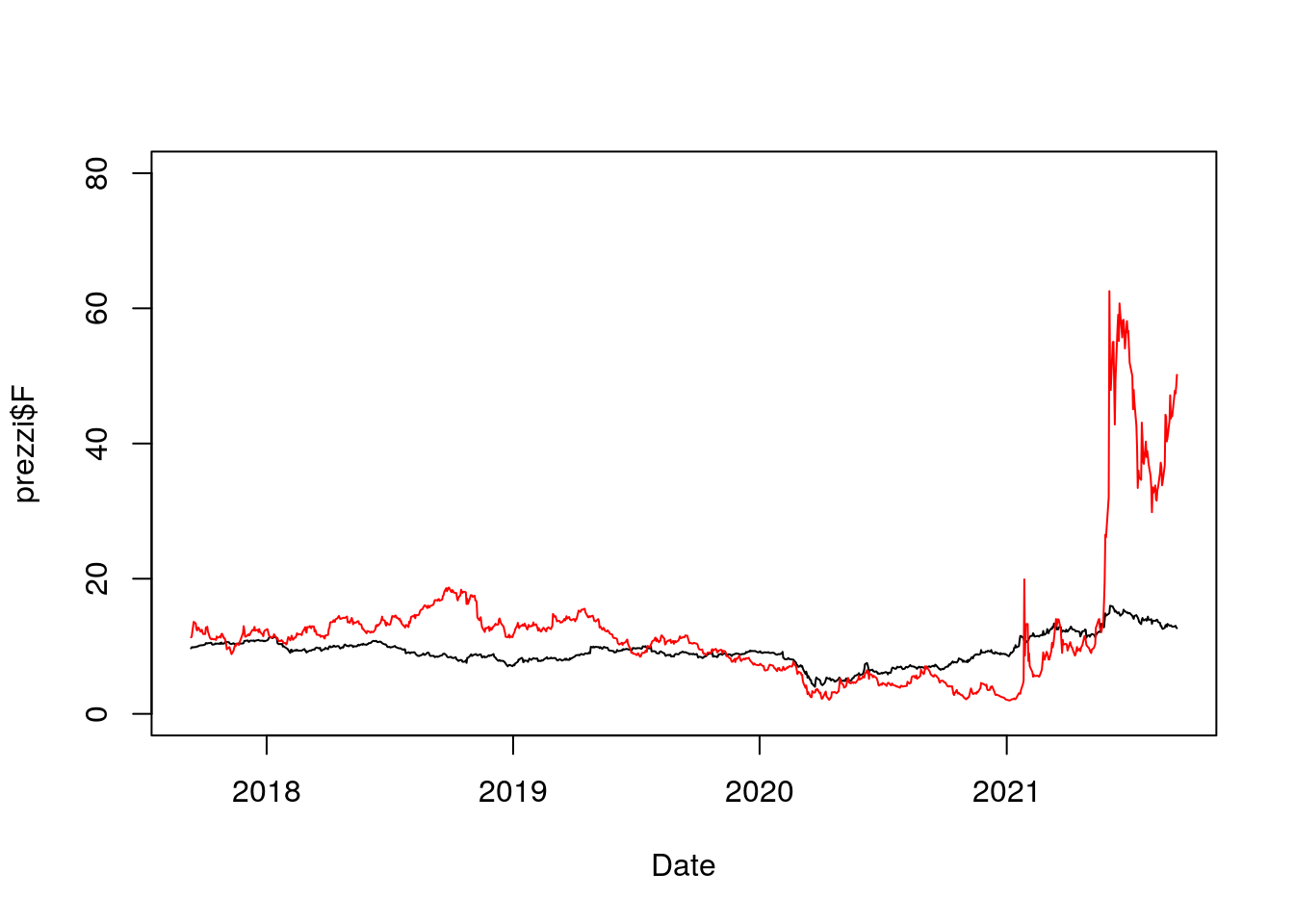

Utilizzando lo stesso approccio è quindi possibile rappresentare graficamente più serie storiche dei prezzi:

plot(prezzi$Date,
      prezzi$F, 
      type = "l",#linea
      xlab = "Date",
      main = "Serie storiche",
      ylim = c(0,200)) 
lines(prezzi$Date,
      prezzi$AMC,
      col = "red")
lines(prezzi$Date,
      prezzi$GSAT,
      col = "blue")
lines(prezzi$Date,
      prezzi$AAPL,
      col = "orange")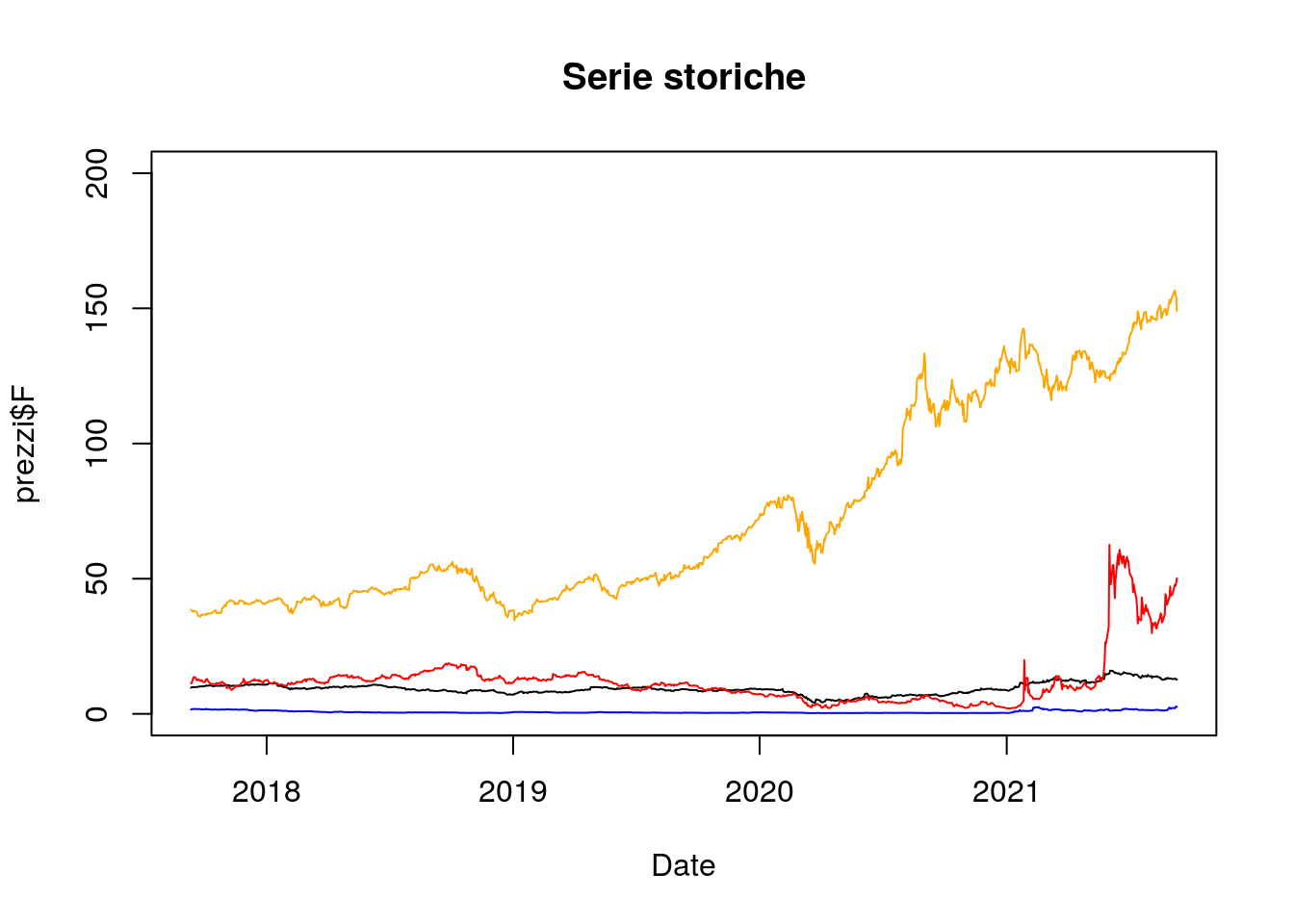

Si noti che gli argomenti xlab, ylab e main della funzione plot vengono utilizzati per specificare, rispettivamente, le etichette dell’asse delle x, dell’asse delle y e il titolo del grafico.

E’ anche possibile aggiungere una legenda al grafico utilizzando il seguente codice (non richiesto per l’esame!):

plot(prezzi$Date,
      prezzi$F, 
      type = "l",#linea
      xlab = "Date",
      main = "Serie storiche",
      ylim = c(0,200)) 
lines(prezzi$Date,
      prezzi$AMC,
      col = "red")
lines(prezzi$Date,
      prezzi$GSAT,
      col = "blue")
lines(prezzi$Date,
      prezzi$AAPL,
      col = "orange")
legend("topleft", 
       lty=c(1,1,1,1), #stile linea (1=linea continua)
       col=c("black","red","blue","orange"),
       legend = c("F","AMC","GSAT","AAPL")) #per ridurre il font size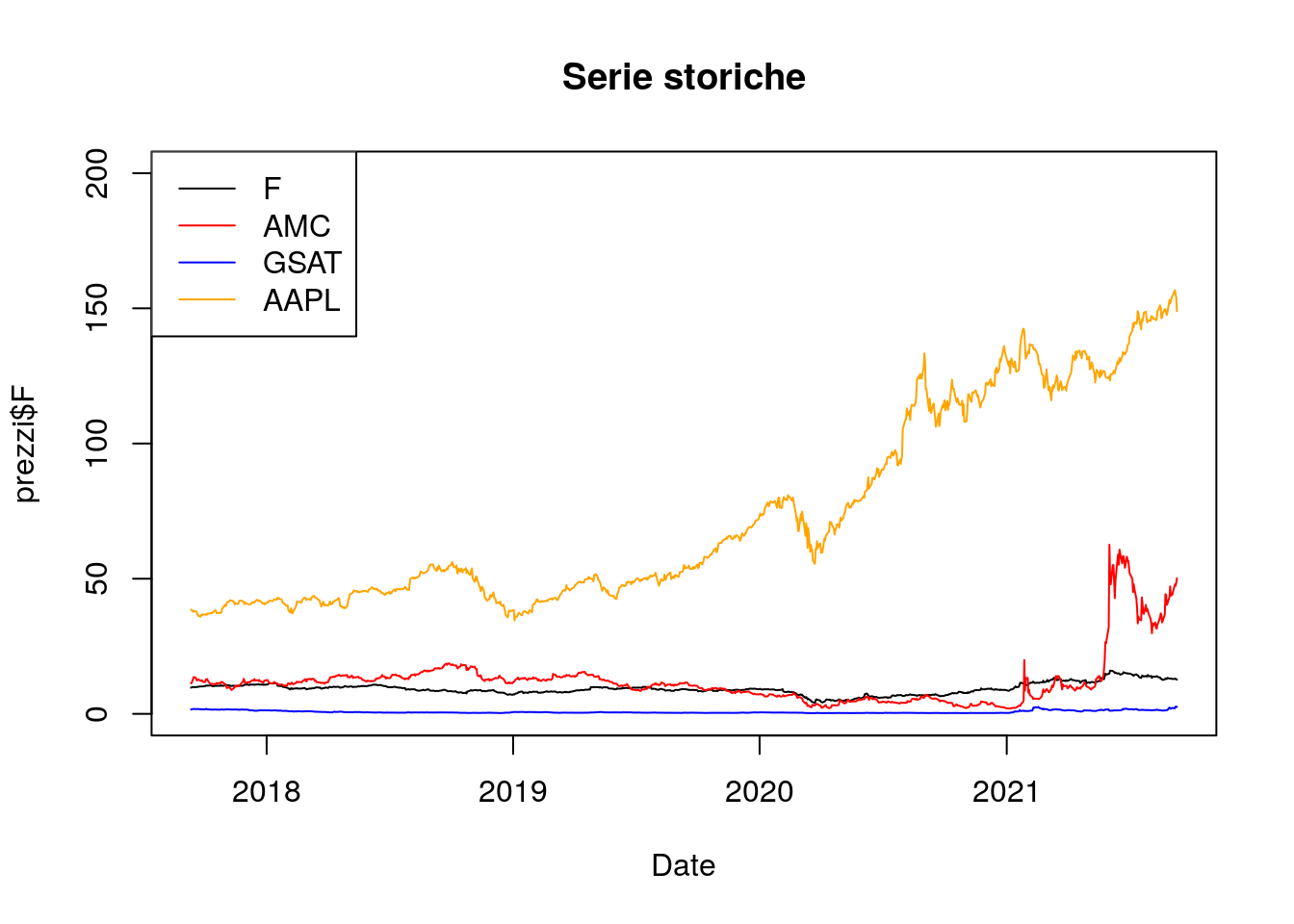

4.8 Approcciarsi al calcolo dei log-rendimenti

Per comodità si consiglia di iniziare a calcolare i log-rendimenti usando la seguente definizione: \[ r_t = \log\left(\frac{P_t}{P_{t-1}}\right) = \log (P_t) - \log (P_{t-1}) \] per \(t=2, \ldots, n\).

In particolare sfrutteremo il fatto che i dati in R sono ordinati dai più antichi (prime righe del data frame) ai più recenti (ultime righe del data frame) e che i rendimenti logaritmici sono dati da differenze consecutive dei prezzi logaritmici (\(log(P_t) - log(P_{t-1})\)). I prezzi logaritmici sono facilmente calcolabili utilizzando la funzione log. Le differenze consecutive (per un vettore di prezzi) while differences posso essere ottenute utilizzando la funzione diff. Al fine di apprendere il funzionamento della funzione diff si consideri un piccolo vettore contenente i primi 5 prezzi di F:

mini = prezzi$F[1:5]
mini

## [1] 9.694755 9.847696 9.873184 9.822205 9.873184

Applicando la funzione log all’oggetto (vettore) mini si ottiene il seguente vettore di prezzi logaritmici:

log(mini)

## [1] 2.271585 2.287238 2.289822 2.284646 2.289822

Successivamente si applica la funzione diff per calcolare le differenze tra log-prezzi:

diff(log(mini))

## [1]  0.015652502  0.002584876 -0.005176756  0.005176756

il cui primo elemento è dato dalla differenza tra il secondo log-prezzo (2.2872375) e il primo (2.271585). Analogamente la seconda differenza è data dalla differenza tra il terzo log-prezzo (2.2898224) e il secondo (2.271585). Ripetendo la procedura per ogni giorno si otterrà un vettore di log-rendimenti la cui lunghezza è \(n-1\).

A titolo di controllo si può calcolare “manualmente” il primo log-rendimento:

log(mini[2]/mini[1])

## [1] 0.0156525

log(mini[2])-log(mini[1])

## [1] 0.0156525

E’ assolutamente importante ricordare che l’ordine delle due funzioni è importante: con diff(log(mini)) calcoliamo prima i log-prezzi e poi le loro differenze. E’ assolutamente sbagliato utilizzare il codice log(diff(mini)).

4.9 Esercizi Lab 2

4.9.1 Esercizio 1

Scaricare dall’e-learning i tre file CSV JNJ.xlsx, PFE.xlsx e NVS.xlsx (fonte dei dati: https://finance.yahoo.com/). Essi si riferiscono alle serie storiche dei prezzi dei seguenti titoli per il periodo 3/10/2013 - 3/10/2018: Johnson & Johnson (JNJ), Pfizer Inc. (PFE) e Novartis AG (NVS). Ogni file contiene le seguenti variabili:

Date: data
Open: prezzo di apertura
High: prezzo massimo registrato dal titolo nella giornata di negoziazione
Low: prezzo minimo registrato dal titolo nella giornata di negoziazione
Close: prezzo di chiusura
Adj.Close: prezzo di chiusura aggiustato per dividendi e frazionamenti
Volume: quantita’ complessiva di titoli scambiati nella giornata

Importare i 3 file in R creando 3 oggetti diversi con nomi JNJ, PFE e NVS.

Visualizzare le prime righe dei 3 dataframe. Verificare inoltre la dimensione dei 3 dataframe e la loro struttura. Si riferiscono i dati alle stesse date?
Considerare solamente per i 3 dataframe la variabile Adj.Close. Calcolare per i tre titoli delle statistiche descrittive. Quale titolo presenta maggiore variabilità?
Utilizzando la funzione quantile (vedere ?quantile) calcolare il quantile di ordine 0.99 per i prezzi Adj.Close di JNJ. Commentare il valore.
Per i prezzi Adj.Close di JNJ si considerano estremi i valori inferiori al quantile di ordine 0.1 o superiori al quantile di ordine 0.99.

Calcolare quanti sono in valore assoluto i valori estremi. Suggerimento: in questo caso la condizione e’ doppia e di tipo OR che in R si traduce con l’operatore |.
Quanto vale la media dei prezzi estremi?
In quali date si verificano i valori estremi?

Rappresentare sullo stesso grafico le tre serie storiche dei prezzi Adj.Close
Per ogni titolo calcolare la percentuale di prezzi superiori alla media. Per quale titolo si osserva una percentuale maggiore di prezzi maggiori della media?
Si considerino i più recenti 5 prezzi per Pfizer Inc. (PFE). Calcolare i log-rendimenti usando le funzioni log e diff e verificare poi manualmente la correttezza del calcolo.

4.9.2 Esercizio 2

Importare i dati del file worldbankdata.xlsx che contiene per 25 paesi europei i dati relativi alle seguenti variabili: Population density (people per sq. km of land area) 2016, Electric power consumption (kWh per capita) 2014, Proportion of seats held by women in national parliaments (%) 2016, Mobile cellular subscriptions 2016, Rail lines (total route-km) 2014

Estrarre tutti i valori disponibili per la variabile pop_density.
Calcolare la mediana e la media per tutte le variabili quantitative. Verificare per quali variabili la media è maggiore della mediana.
Selezionare tutti i dati disponibili per il paese in 3a riga.
Selezionare tutti i dati disponibili per il paese il cui nome Country e’ Croatia (in questo caso sarà necessario vedere quale nome di paese è esattamente uguale (==) a "Croatia").
Trovare il paese con la maggiore densità di popolazione utilizzando all’interno del proprio codice la funzione max. Sostituire poi il valore con la densità media.