Chapter 4 기타 분포

4.1 시작하면서

이번 단원에서는 정규분포 말고 다른 분포들에 대해 알아보겠다. 그렇다고 모든 분포를 다 다루지는 않고 실제 통계분석에서 주로 활용되는 분포인 카이제곱, \(t\), \(F\)의 3가지 분포만 살펴보겠다. 각 분포의 유래와 기본적인 성질을 알고 실제 통계분석에서 어떻게 활용되는지 미리 대략적인 감을 잡는 정도가 목표이니, 편안한 마음으로 한번 훑어보면서 자유도의 개념 정도만 챙기고 넘어가도록 하자.

4.2 카이제곱분포(Chi-square distribution)

앞단원에서도 잠깐 언급한 카이제곱분포에서 카이(\(\chi\))는 \(X\)의 그리스 알파벳 버전으로 평균 0, 분산 1인 표준정규분포를 의미한다. 따라서 카이제곱이라는 이름에는 표준정규분포를 제곱한다는 의미가 내포되어 있고, 실제로 자유도 \(v\)인 카이제곱분포를 \(X^2\)을 \(v\)개 합한 것의 분포로 정의한다. 더 정확히 말하자면 \(X_1, X_2,\cdots, X_v\)가 표준정규분포를 따를 때

\[Q = X_1^2+X_2^2+\cdots+X_v^2\] 의 분포는 자유도가 \(v\)인 카이제곱 분포를 따른다고 정의하고 \(Q\sim\chi^2(v)\)로 표현한다. 아래 그림를 통해 대략적인 모양을 확인해 보자.

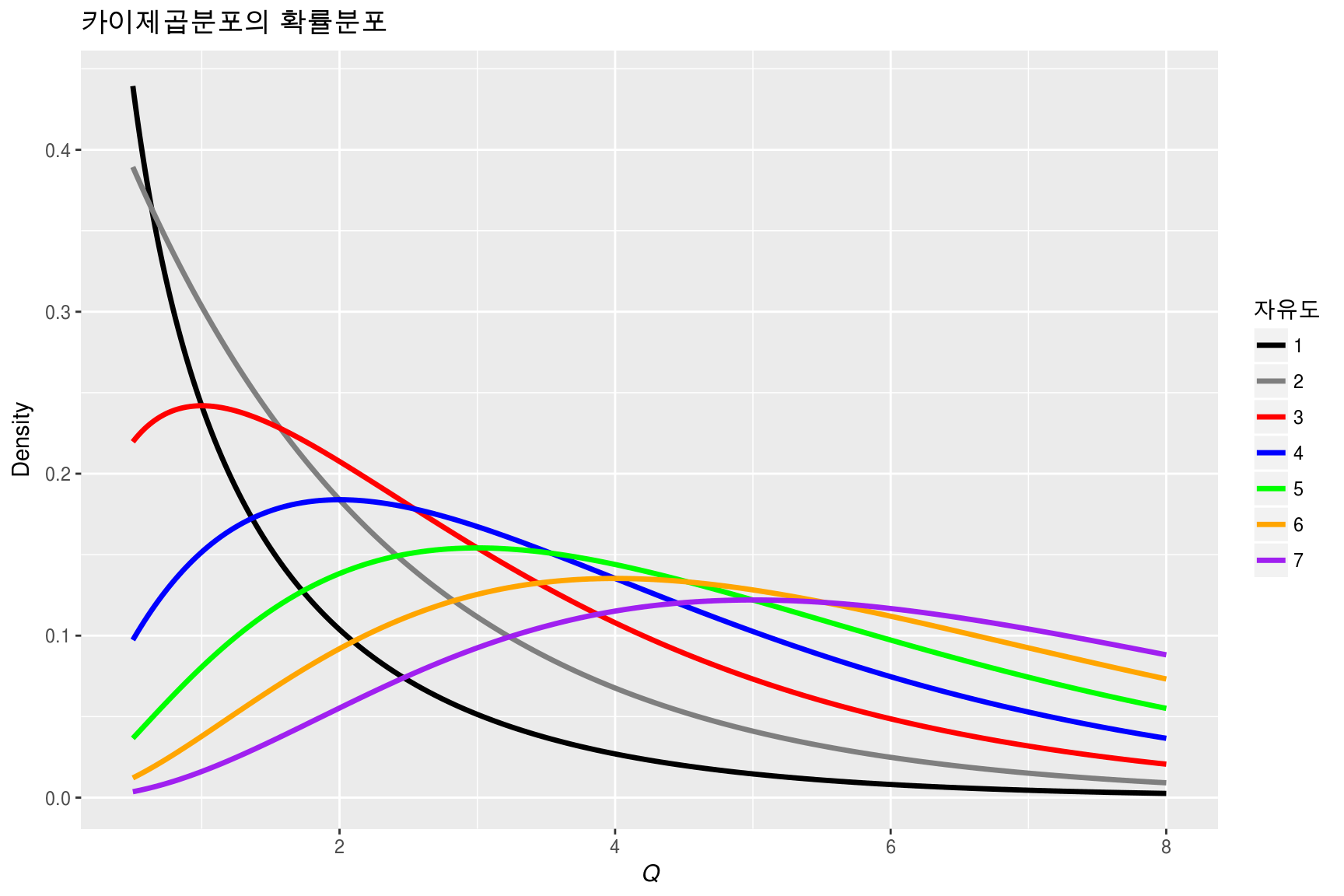
Figure 4.1: 카이제곱분포

우선 Q값은 제곱들의 합이므로 0 이상만 가질 수 있다는 것을 알 수 있으며 \(\chi^2(v)\)의 평균은 \(v\), 분산은 \(2v\)임이 알려져 있다.

4.2.1 자유도(Degree of Freedom)란?

미지수의 갯수

4.2.2 카이제곱 분포의 활용: \(2\times2\) 테이블.

4.3 \(t\)-분포

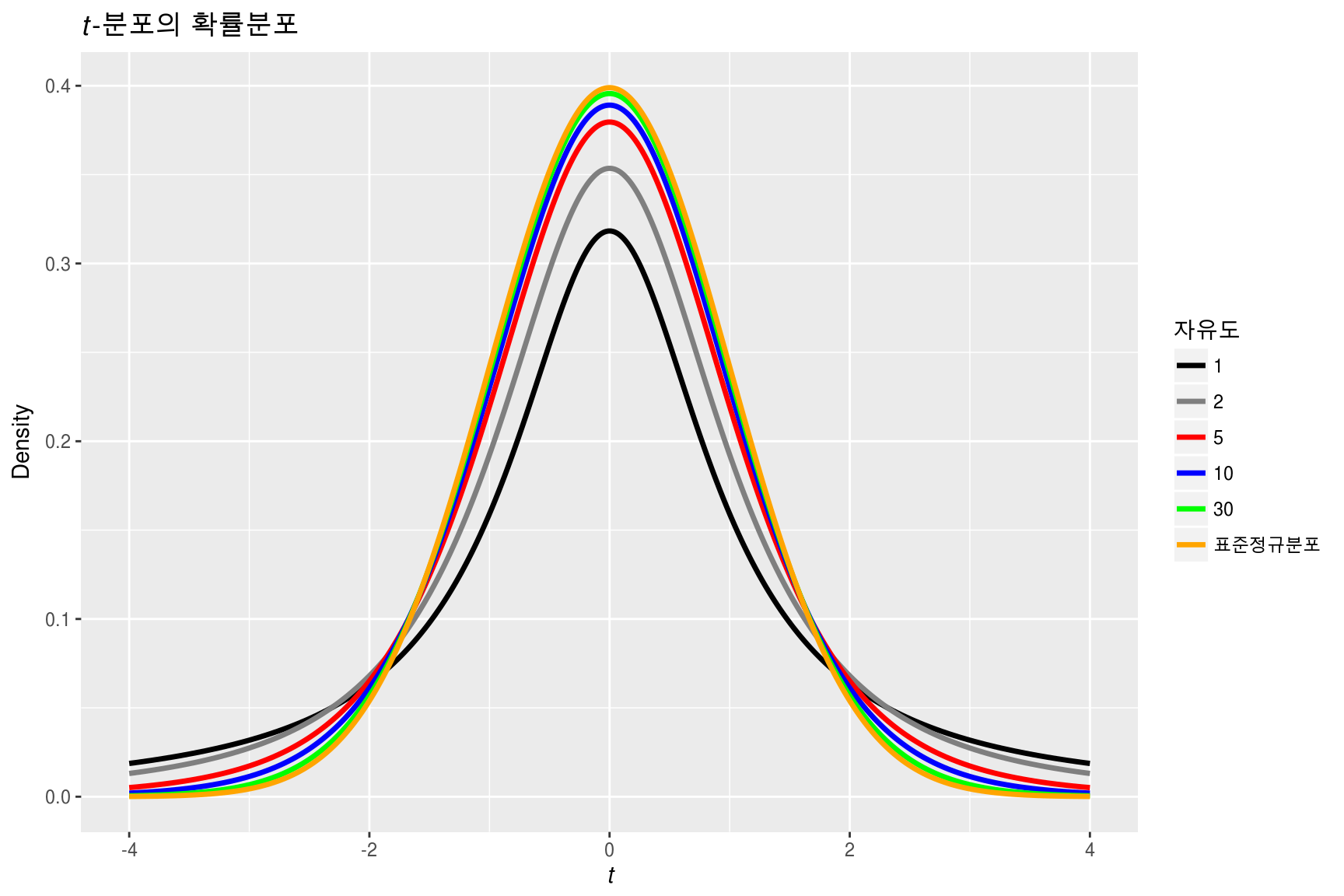
Figure 4.2: \(t\)-분포

4.4 \(F\)-분포

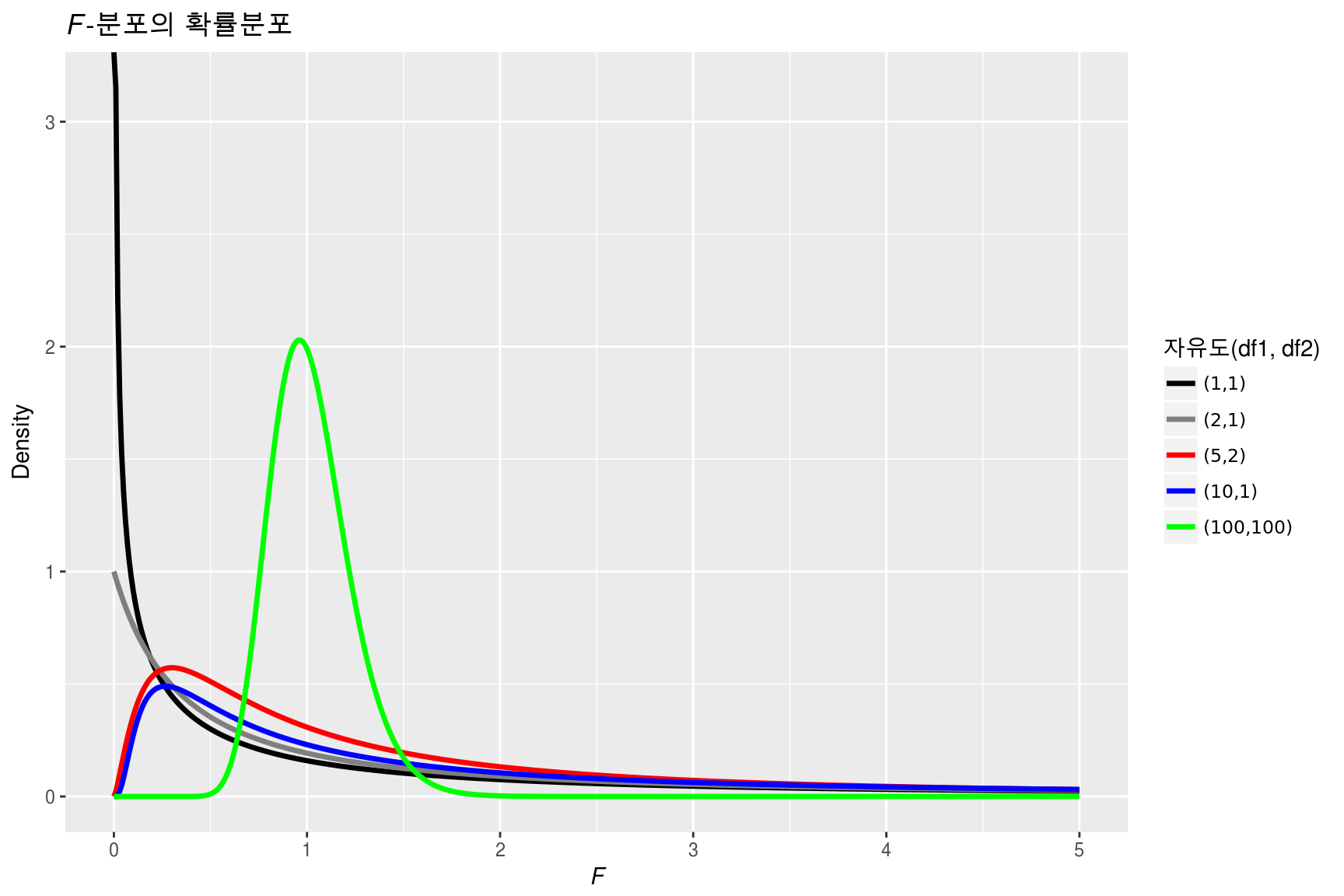
Figure 4.3: \(F\)-분포

4.5 마치며

이번 단원에서는 정규분포의 당위성을 뒷받침하는 3가지의 근거를 다양한 예시와 실험을 통해 알아보았으며, 그 중 중심극한정리에 대해서는 따로 그 의미를 되새겨보았다. 다음 단원에서는 정규분포 외에 알아야 하는 확률분포를 딱 3개만 더 알아보도록 하겠으며, 그 후에는 본격적으로 통계분석의 세계로 들어가 보도록 하겠다.