8 Collecting and Merging Data
8.1 Collecting Data
For the final project in this class you are to find your own data and to generate a short presentation and blog post. The first step in this process is going to be looking for your own data.
This is going to be an iterative process. That is: you aren’t likely to just go out and grab the right data on the first pass. You are going to have to think about your area of inquiry, then look for data, refine your area of inquiry based on the data thats available, think about adding data based on this new question etc.
For this process keep in mind that we are here to help! We really want you to come to office hours to talk to us about what you are looking for and what problems you are facing. We’ve been doing this for awhile and can help you think through things if you hit dead ends, or to suggest extra data to supplement what it is that you are finding. Please come talk to us!
The remainder of this section will go over some guidelines for looking for data and some places to go and find it. The second section of this chapter deals with the critical step of merging two datasets together: the functions we use to combine two datasets that have common units of analysis.
8.1.1 What to look for?
To start off with: I would not encourage your first step to be to look for a dataset.
The first thing you should be doing is thinking about a realtionship in terms of concepts and not measures. What do I mean by this?
Let’s take a look at this graph I generated from American National Election Study looking at the relationship between the self-reported 7-point ideology measure and family income.
anes <- rio::import("https://github.com/marctrussler/IIS-Data/raw/main/ANES2020Clean.csv")
boxplot(anes$income ~ anes$ideology7, xlab="Ideology",
ylab="Reported Family Income (Thousands)", outline=F, axes=F)
axis(side=2)
axis(side=1, at=1:7,
labels=c("Very Liberal","2","3","4","5","6","Very Conservative"), cex.axis=0.8)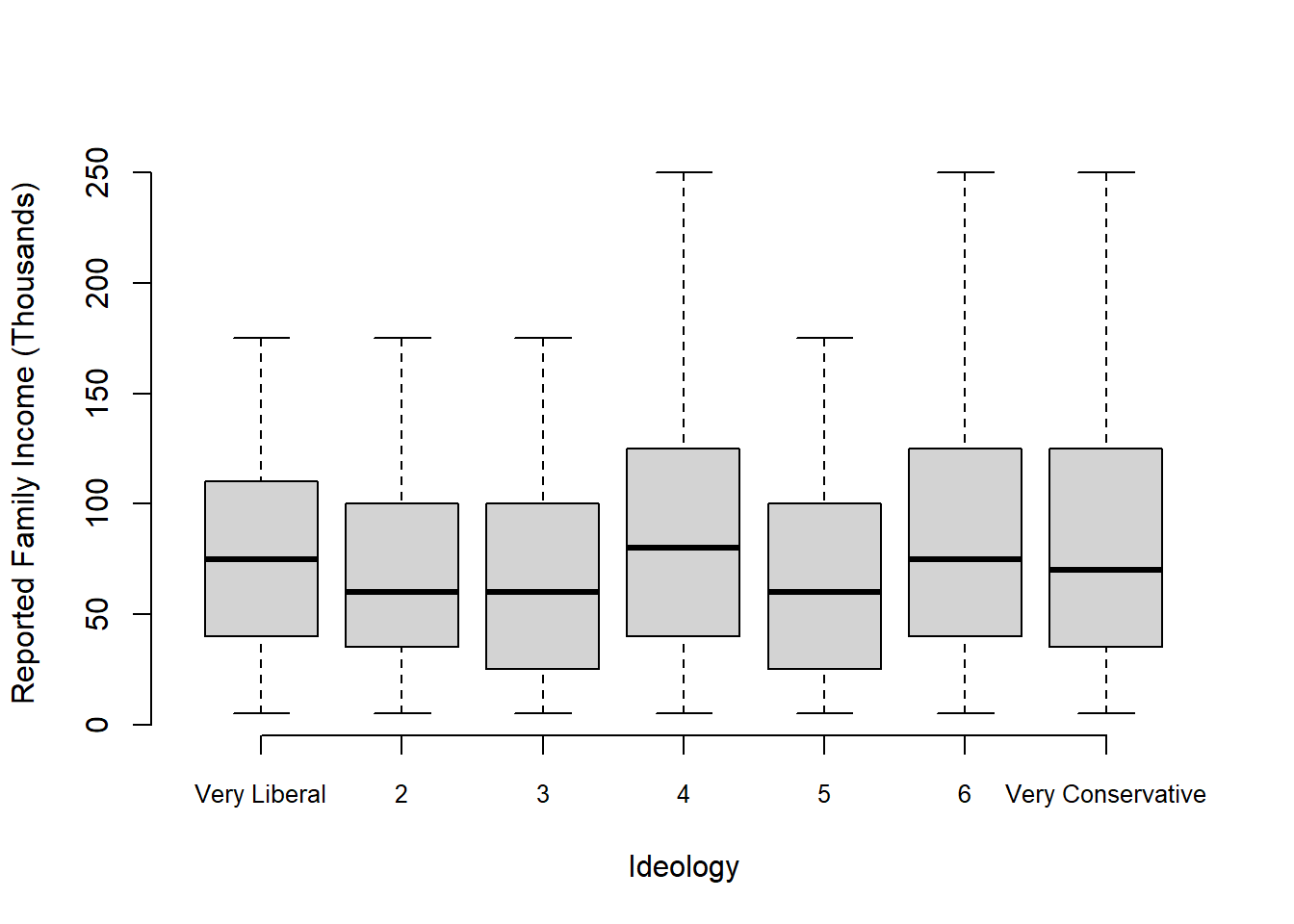
How should we describe the question this graph is answering?
We could say: What is the relationship between self reported 7-point ideology measures and reported family income?
But that’s pretty unsatisfying! We don’t really want to answer questions about questions in the ANES, we are interested in the broader concepts that these things represent. The question we actually want to answer is:
What is the relationship between ideology and wealth?
Asking the question this way makes us (1) think about what we really care about; and (2) forces us to grapple with the question: how well do these things measure the concepts we care about?
“Ideology” is a concept about how people think politics and society should be organized. The labels “liberal” and “conservative” are an interpretation of these fundamental positions, and the facto of putting it on a 7 point scale is a further abstraction that assumes a single dimensional scale. This may, or may not, do a good job of capturing the concept (lots of evidence suggests it does not), but at the very least, explicitly defining this as a measure makes us think about and defend this choice.
Indeed, even something basic like “family income” may or may not capture the concept of “wealth” correctly. This doesn’t take into account assets, investments, or generational wealth in a way that may matter for fully capturing this concept.
So: the first step in thinking about what sort of data you want to get is to think about the concepts you want to explore, and what sort of measures may do a good job in representing these concepts.
As I said before, this is going to be an iterative process. It’s nice to start with an ideal world: these are the measures that would perfectly represent my concept. But this will also happen backwards: redefining the concepts you are interested in based on the real world measures that are available.
Once you have your concepts you wish to measure the next step is to think through which unit of analysis you expect these things to be measured on.
To take our above example of “What is the relationship between ideology and wealth?” For this question we pretty much have to use individual data. We can measure wealth, at say, the county level, but it’s hard to measure ideology at that level. What is the collective ideology of Philadelphia? (Such measures actually exist, but the point remains that ideology is really thought of as an individual concept.)
But if our question was: “How did COVID-19 affect voter turnout?” this might be a question that is answered with aggregate data. We can measure COVID-19 exposure by the number of cases at the county level, and also measure voter turnout using election results at the county level. That being said, this relationship could also be answered at the individual level: measuring COVID exposure through self-reports of infection and voter turnout through self-reported turnout.
So sometimes the question you are answering forces you into a particular unit of analysis, and sometimes it allows you to make a choice. How should you think about those choices?
Individual data is often great when you can find it, and gives us the opportunity to look at more specific attitudes and behaviors that can only really be captured at the individual level. However, individual survey data is expensive! The National Exit Poll, which we help to administer at NBC, costs several million dollars. So with individual data you are limited to what other people have collected and made available. Further, most survey data is meant to be representative at the national or state level. It’s hard to get enough people in different counties to be representative. So if your question is about specific small geographies (like Philadelphia) it would be hard to do that with survey data.
Aggregated data will have less detail about individual behaviors and attitudes, but it is much more prevalent. A lot of aggregated data (at, say, the county, state, or national level) is produced by administrative bodies more or less automatically. Further, this data is often produced regularly which allows us to look at the same units over time.
Another benefit of aggregate data is that it is very easy to add extra contextual information for cases. For example if we look at election results at the county level, we can add any other information that has been collected at the county level to these cases and build a very rich dataset. With individual level data that information we have for individuals is all the information that we are going to get.
Some more fundamental things to look for:
- Your data should have, at minimum, 100 observations. Anything less than that becomes very hard to work with.
- Try to look for data where you get extra contextual information about cases. For individuals you want survey data that has things like demographics and geographic location. For aggregate data you can often add contextual information gathered elsewhere.
- Data with repeated observations over time – what we call “panel” data – is extremely powerful and always a good fine.
8.1.2 Beware Ecological Inference
The above sells aggregated data pretty hard, but there is one particular concern when using aggregate data that you should be aware of, which is the “ecological inference fallacy.”
In short, the risk here is when you conclude that a relationship that is happening at the aggregate level is also happening at the individual level.
Here are three aggregate relationships:
In the 19th Century, areas with higher numbers of protestants had more suicides.
Areas with fattier diets have higher incidence of breast cancer.
States with higher median incomes are more likely to vote democratic.
All of these relationships are true at the aggregate level. Critically, none of these relationships are true at the individual level. Protestants were not more likely to commit suicide in the 19th C; having a fattier diet does not lead to breast cancer; having a higher income does not make you more likely to vote Democratic.
There are, of course, cases where the aggregate and individual cases line up: states with a higher percentage of voters with a college degree are more likely to vote Democratic; individuals with a college degree are more likely to vote Democratic. But we cannot automatically assume the second thing from the first thing.
You don’t have the budgets or bandwidth to look into these things, but this is something that should be thought about and avoided when you are making conclusions based on aggregate data.
8.1.3 Where to get data?
Really? Anywhere. We live in an amazing time of data availability.
Here are some options, with notes below.
– Data on election outcomes at all levels. Particularly interesting are Presidential election results by county.
– Access to Census Data. (Log in through library)
American National Election Study
– Individual level data about politics. Gold standard “academic” source.
– More individual level data about politics. VOTER Survey is a panel study.
– Data for all of 538’s articles
– Data for academic articles. Can be a bit of a hassle.
– Geographic Covid data.
– Amazing resource for city data. Great when paired with Census data.
– Public opinion data. (Log in through library and create an account.)
8.1.4 What Census data should I use?
When you go to Social Explorer and look for Census data you will see two options: the Decennial Census and the American Community Survey (ACS). The latter further has availability across different time periods.
How can you sort these things out?
The decennial Census is exactly what you think it is. As mandated by the constitution the government counts the whole population of the United States every 10 years. In addition to simply asking “Do you exist?” the Census additionally asks Sex, Age, Race, and Hispanic Origin. Because the census literally counts everyone, it is extremely helpful if you want to know information about these particular variables at extremely specific geographies. Right down to the block level you can determine what the population looks like. (Sort of. Out of privacy concerns the Census has started to add some random noise at very low levels of geography, which is a controversial practice).
That’s great if you want to know about those variables and aren’t specific about time. But what if you want to know things like income and education, and want to know about years other than 2000,2010, or 2020? That is where the American Community Survey (ACS) comes in. The ACS is a traditional survey completed by the Census Bureau that is constantly ongoing. They ask a wide range of questions and are doing so constantly. This allows us to get good information on a wide range of variables in-between census years.
But why are there 5-year, 3-year, and 1-year ACS versions? For a given geographic area the Census has to collect a certain amount of people before they feel that what they have is representative of that area. For a state the ACS can collect that information within a calendar year, so they can produce an estimate of (for example) the percent of people with a college degree in Pennsylvania for the year 2022. But for a very small geographic unit – like a census tract, which is a subset of a county – there is not way they can collect enough people in just a year to form a representative estimate. Therefore, they pool together answers over a 5 year span to get an estimate.
In short: the 5-year ACS will have information on smaller geographic units, with the trade-off being that you can’t be as specific about time. The 1-year ACS allows you to be very specific about time but you don’t get very specific geographies included (not even all counties are included in 1-year estimates).
8.1.5 What filetypes to look for?
R can, helpfully, open almost anything. We have seen that The “rio” package is built to handle most any sort of data, so that should be your default for loading in information. But, it is important to always do a spot check. When you open data use the View() command to have a look. Does the data look correct?
If given options, .csv filetypes are usually the most straightforward to work with and are pretty foolproof. rio has no problem opening excel files (xls or xlsx) but if that is the source of your data be aware if the file has multiple “sheets” of data. rio actually has an option to select which sheet you want to read in.
Sometimes you will be looking for data and it will be in tabular format but hosted in a pdf. (Secretaries of State posting election results are terrible for this.) There are ways to read these files but it is beyond the scope of this class to cover. I would encourage you to look elsewhere in these situations. Do make a mental note that: anyone who publishes data in a pdf is purposefully doing it to prevent people from using it.
8.1.6 Remember: Everyting in R!
For your final project you will hand in a Rmarkdown that will take us from the raw data downloaded from the internet (you will include links so that we know you are using the raw data) to your final tables and graphs. Every step along the way needs to be documented. This means that you are prohibited from doing any pre-processing in Excel. Even if you must delete rows of description or something like that, you cannot quickly open it in excel and then re-save as a new file. I know this is persnickety, but we’re are trying to being transparent, replicable, and avoid catastrophic and irreversible errors.
8.2 Merging Data
We’ve learned a lot about cleaning individual datasets, but what about working with multiple datasets from different sources that have the same identifiers in each? If we have one dataset that has counties, and another dataset that has counties, we should be able to combine those two things. Well, we can! The way we do so is through “merging” data.
Let’s say that we want to know the % of voting age population that turned out to vote in each county in 2016.
The first thing we are going to need is data on election results. Let’s load in data from MIT Elections on the presidential election results in each county from 2000-2016:
x <- rio::import("https://github.com/marctrussler/IDS-Data/raw/main/MITElectionDataPres0016.Rds")What does this data look like?
head(x)
#> year state state_po county FIPS office
#> 1 2000 Alabama AL Autauga 1001 President
#> 2 2000 Alabama AL Autauga 1001 President
#> 3 2000 Alabama AL Autauga 1001 President
#> 4 2000 Alabama AL Autauga 1001 President
#> 5 2000 Alabama AL Baldwin 1003 President
#> 6 2000 Alabama AL Baldwin 1003 President
#> candidate party candidatevotes totalvotes
#> 1 Al Gore democrat 4942 17208
#> 2 George W. Bush republican 11993 17208
#> 3 Ralph Nader green 160 17208
#> 4 Other NA 113 17208
#> 5 Al Gore democrat 13997 56480
#> 6 George W. Bush republican 40872 56480
#> version
#> 1 20191203
#> 2 20191203
#> 3 20191203
#> 4 20191203
#> 5 20191203
#> 6 20191203The data is in long format (county-candidate units of observation), and we have no variable here for the voting age population in each county!
Let’s do some basic cleaning. I want it so that we have one row per county, and I just want data from 2016. I’m also going to only keep the variables that I need.
x$candidate <- NULL
elect <- spread(x,
key=party,
value=candidatevotes)
keep <- c("year","state","county","FIPS","totalvotes")
elect <- elect[keep]
elect.all <- elect
elect <- elect[elect$year==2016,]
elect <- elect[!is.na(elect$FIPS),]
#Removing this dataset x, only because it makes things confusing below, usually
#i'd keep it in the environment.
rm(x)This leaves us with:
head(elect)
#> year state county FIPS totalvotes
#> 12468 2016 Alabama Autauga 1001 24973
#> 12469 2016 Alabama Baldwin 1003 95215
#> 12470 2016 Alabama Barbour 1005 10469
#> 12471 2016 Alabama Bibb 1007 8819
#> 12472 2016 Alabama Blount 1009 25588
#> 12473 2016 Alabama Bullock 1011 4710To this we need to add the voting age population in each of these counties. This is something we can get from Social Explorer. So i’m going to go to the website and show you where to get that.
In the real world I would download this to my computer and put in the file-path to reach that file. For the sake of brevity in this class we are going to load the data from github.
acs <- rio::import("https://github.com/marctrussler/IDS-Data/raw/main/R12662248_SL051.csv")Let’s see what these data look like:
head(acs)
#> Geo_FIPS Geo_GEOID Geo_NAME
#> 1 1001 05000US01001 Autauga County
#> 2 1003 05000US01003 Baldwin County
#> 3 1005 05000US01005 Barbour County
#> 4 1007 05000US01007 Bibb County
#> 5 1009 05000US01009 Blount County
#> 6 1011 05000US01011 Bullock County
#> Geo_QName Geo_STUSAB Geo_SUMLEV Geo_GEOCOMP
#> 1 Autauga County, Alabama al 50 0
#> 2 Baldwin County, Alabama al 50 0
#> 3 Barbour County, Alabama al 50 0
#> 4 Bibb County, Alabama al 50 0
#> 5 Blount County, Alabama al 50 0
#> 6 Bullock County, Alabama al 50 0
#> Geo_FILEID Geo_LOGRECNO Geo_US Geo_REGION Geo_DIVISION
#> 1 ACSSF 13 NA NA NA
#> 2 ACSSF 14 NA NA NA
#> 3 ACSSF 15 NA NA NA
#> 4 ACSSF 16 NA NA NA
#> 5 ACSSF 17 NA NA NA
#> 6 ACSSF 18 NA NA NA
#> Geo_STATECE Geo_STATE Geo_COUNTY Geo_COUSUB Geo_PLACE
#> 1 NA 1 1 NA NA
#> 2 NA 1 3 NA NA
#> 3 NA 1 5 NA NA
#> 4 NA 1 7 NA NA
#> 5 NA 1 9 NA NA
#> 6 NA 1 11 NA NA
#> Geo_PLACESE Geo_TRACT Geo_BLKGRP Geo_CONCIT Geo_AIANHH
#> 1 NA NA NA NA NA
#> 2 NA NA NA NA NA
#> 3 NA NA NA NA NA
#> 4 NA NA NA NA NA
#> 5 NA NA NA NA NA
#> 6 NA NA NA NA NA
#> Geo_AIANHHFP Geo_AIHHTLI Geo_AITSCE Geo_AITS Geo_ANRC
#> 1 NA NA NA NA NA
#> 2 NA NA NA NA NA
#> 3 NA NA NA NA NA
#> 4 NA NA NA NA NA
#> 5 NA NA NA NA NA
#> 6 NA NA NA NA NA
#> Geo_CBSA Geo_CSA Geo_METDIV Geo_MACC Geo_MEMI Geo_NECTA
#> 1 NA NA NA NA NA NA
#> 2 NA NA NA NA NA NA
#> 3 NA NA NA NA NA NA
#> 4 NA NA NA NA NA NA
#> 5 NA NA NA NA NA NA
#> 6 NA NA NA NA NA NA
#> Geo_CNECTA Geo_NECTADIV Geo_UA Geo_UACP Geo_CDCURR
#> 1 NA NA NA NA NA
#> 2 NA NA NA NA NA
#> 3 NA NA NA NA NA
#> 4 NA NA NA NA NA
#> 5 NA NA NA NA NA
#> 6 NA NA NA NA NA
#> Geo_SLDU Geo_SLDL Geo_VTD Geo_ZCTA3 Geo_ZCTA5 Geo_SUBMCD
#> 1 NA NA NA NA NA NA
#> 2 NA NA NA NA NA NA
#> 3 NA NA NA NA NA NA
#> 4 NA NA NA NA NA NA
#> 5 NA NA NA NA NA NA
#> 6 NA NA NA NA NA NA
#> Geo_SDELM Geo_SDSEC Geo_SDUNI Geo_UR Geo_PCI Geo_TAZ
#> 1 NA NA NA NA NA NA
#> 2 NA NA NA NA NA NA
#> 3 NA NA NA NA NA NA
#> 4 NA NA NA NA NA NA
#> 5 NA NA NA NA NA NA
#> 6 NA NA NA NA NA NA
#> Geo_UGA Geo_BTTR Geo_BTBG Geo_PUMA5 Geo_PUMA1
#> 1 NA NA NA NA NA
#> 2 NA NA NA NA NA
#> 3 NA NA NA NA NA
#> 4 NA NA NA NA NA
#> 5 NA NA NA NA NA
#> 6 NA NA NA NA NA
#> SE_A01001B_001 SE_A01001B_002 SE_A01001B_003
#> 1 55200 51937 47928
#> 2 208107 196498 184809
#> 3 25782 24392 22942
#> 4 22527 21252 20074
#> 5 57645 54160 50528
#> 6 10352 9756 9122
#> SE_A01001B_004 SE_A01001B_005 SE_A01001B_006
#> 1 44358 41831 37166
#> 2 170486 162430 146989
#> 3 21265 20346 18173
#> 4 18785 17868 15780
#> 5 46533 44177 39627
#> 6 8582 8202 7104
#> SE_A01001B_007 SE_A01001B_008 SE_A01001B_009
#> 1 30102 22728 14875
#> 2 123663 98286 69956
#> 3 14498 11394 7942
#> 4 12705 9810 6371
#> 5 32841 25688 17741
#> 6 5984 4385 3063
#> SE_A01001B_010 SE_A01001B_011 SE_A01001B_012
#> 1 8050 3339 815
#> 2 40665 16114 3949
#> 3 4634 1814 422
#> 4 3661 1539 427
#> 5 10233 4101 866
#> 6 1616 605 175That looks terrible!
One of the first things we see, however, is that these data also have FIPS codes, which is great news!
To figure out which data I want I can use the data dictionary that Social Explorer provided to figure out which column has the data we need in it.With that we learned that”A01001_005” has the county population that is greater than 18.
I’m going to create a new variable that is just a copy of that variable, and call it vap for voting-age-population.
acs$vap <- acs$SE_A01001B_005What we want to do here is to use the fact that both variables have fips codes to combine these two datasets. We want to be able to match up the row for FIPS code 1001 in the elect dataset to the 1001 row in the acs dataset.
Why didn’t we do this with the county names? We have already seen the problem that there are lots of “Jefferson Counties”, but potentially we could create a variable that is something “KY-Jefferson” to get around that. But even if we did that we would potentially get into trouble.
Look at this:
acs$Geo_NAME[acs$Geo_FIPS==27137]
#> [1] "St. Louis County"
elect$county[elect$FIPS==27137]
#> [1] "Saint Louis"Same county spelled two different ways! No reason to deal with that if you don’t have to. Having FIPS codes as unique identifiers fixes this problem.
(There have been lots of times in my life where I have had to merge based on county and precinct names! Nothing to do there but hard work to make them match.)
OK Let’s reduce the dataset down:
keep <- c("Geo_FIPS","vap")
acs <- acs[keep]Alright, now we have a dataset of election results by county, and a dataset of voting age population, by county. Now we need to stick them together.
head(acs)
#> Geo_FIPS vap
#> 1 1001 41831
#> 2 1003 162430
#> 3 1005 20346
#> 4 1007 17868
#> 5 1009 44177
#> 6 1011 8202
head(elect)
#> year state county FIPS totalvotes
#> 12468 2016 Alabama Autauga 1001 24973
#> 12469 2016 Alabama Baldwin 1003 95215
#> 12470 2016 Alabama Barbour 1005 10469
#> 12471 2016 Alabama Bibb 1007 8819
#> 12472 2016 Alabama Blount 1009 25588
#> 12473 2016 Alabama Bullock 1011 4710Now the merge is going to work based off of exact matches. It’s a good idea, then, to make sure that the fips codes are formatted in the same way.
First, are these both of the same class?
A FIPS code is a two digit state code and a three digit county code. Autgua county Alabama is “01001” because Alabama is the first state and Autgua is the first county in that state. Philadelphia is “42101” because PAs state code is 42. Now sometimes the leading 0 will get dropped for a state like Alabama because the FIPS code is being treated as numeric. So Autgua will be “1001”. You don’t want a situation where all of the counties in the first 9 states don’t merge because one datset has the leading 0 and the other doesn’t. (This is also a potential problem with Zip codes).
We can check that the two are formatted similarly with nchar()
Not exact matches but pretty close!
If we wanted to change this to have leading 0s we could write code like this:
acs2 <- acs
#Use the paste command to add leading 0 to those fips codes with
#only 4 characters
acs2$Geo_FIPS[nchar(acs2$Geo_FIPS)==4] <- paste("0",acs2$Geo_FIPS[nchar(acs2$Geo_FIPS)==4], sep="")
table(nchar(acs2$Geo_FIPS))
#>
#> 5
#> 3220
head(acs2$Geo_FIPS)
#> [1] "01001" "01003" "01005" "01007" "01009" "01011"Back to merging, we can determine the degree to which we are going to have overlap using the %in% command. How many of our elect counties are matched in the acs data?
So for 41 electoral counties we don’t have a matching FIPS code. What are those?
unmatched <- elect[!(elect$FIPS %in% acs$Geo_FIPS),]
head(unmatched,41)
#> year state county FIPS totalvotes
#> 14266 2016 Missouri Kansas City 36000 128601
#> 14856 2016 South Dakota Oglala Lakota 46113 2905
#> 15355 2016 Virginia Bedford 51515 0
#> 15749 2016 Alaska District 1 2001 6638
#> 15750 2016 Alaska District 2 2002 5492
#> 15751 2016 Alaska District 3 2003 7613
#> 15752 2016 Alaska District 4 2004 9521
#> 15753 2016 Alaska District 5 2005 7906
#> 15754 2016 Alaska District 6 2006 8460
#> 15755 2016 Alaska District 7 2007 8294
#> 15756 2016 Alaska District 8 2008 8073
#> 15757 2016 Alaska District 9 2009 8954
#> 15758 2016 Alaska District 10 2010 9040
#> 15759 2016 Alaska District 11 2011 9689
#> 15760 2016 Alaska District 12 2012 9543
#> 15762 2016 Alaska District 14 2014 10420
#> 15763 2016 Alaska District 15 2015 4982
#> 15765 2016 Alaska District 17 2017 6788
#> 15766 2016 Alaska District 18 2018 7402
#> 15767 2016 Alaska District 19 2019 4792
#> 15769 2016 Alaska District 21 2021 8647
#> 15770 2016 Alaska District 22 2022 8372
#> 15771 2016 Alaska District 23 2023 6924
#> 15772 2016 Alaska District 24 2024 9080
#> 15773 2016 Alaska District 25 2025 8127
#> 15774 2016 Alaska District 26 2026 8905
#> 15775 2016 Alaska District 27 2027 8783
#> 15776 2016 Alaska District 28 2028 11427
#> 15777 2016 Alaska District 29 2029 9394
#> 15778 2016 Alaska District 30 2030 8950
#> 15779 2016 Alaska District 31 2031 10182
#> 15780 2016 Alaska District 32 2032 7472
#> 15781 2016 Alaska District 33 2033 9934
#> 15782 2016 Alaska District 34 2034 9431
#> 15783 2016 Alaska District 35 2035 9042
#> 15784 2016 Alaska District 36 2036 8264
#> 15785 2016 Alaska District 37 2037 5062
#> 15786 2016 Alaska District 38 2038 5095
#> 15787 2016 Alaska District 39 2039 5639
#> 15788 2016 Alaska District 40 2040 4610
#> 15789 2016 Alaska District 99 2099 5056In two cases we have counties that no longer exist for the Census (Bedford and Oglala Lakota) but MIT still uses for vote reporting. Kansas City reports its votes seprately from Jackson county. Alaska doesn’t actually have counties and instead reports votes in election districts. For class I’m not going to fix this stuff, but if this was “real” work I would find ways around each of these discrepancies, otherwise I would be lying if I said my analysis was true of the whole country.
But for the vast majority of cases we have a good match.
After all this, the merge function is very straightforward:
merged.data <- merge(elect, acs, by.x="FIPS", by.y="Geo_FIPS")
head(merged.data)
#> FIPS year state county totalvotes vap
#> 1 1001 2016 Alabama Autauga 24973 41831
#> 2 1003 2016 Alabama Baldwin 95215 162430
#> 3 1005 2016 Alabama Barbour 10469 20346
#> 4 1007 2016 Alabama Bibb 8819 17868
#> 5 1009 2016 Alabama Blount 25588 44177
#> 6 1011 2016 Alabama Bullock 4710 8202That’s just what we wanted! Alright!
Now by default R deleted the rows where we didn’t have a match. We can see this by:
If we want to preserve those rows (which is probably a good idea) we can do:
merged.data <- merge(elect, acs, by.x="FIPS", by.y="Geo_FIPS", all.x=T)
sum(is.na(merged.data$vap))
#> [1] 41To continue with our analysis, let’s calculate the percent of voting age peoplt that turned out to vote in each county:
merged.data$perc.turnout <- (merged.data$totalvotes/merged.data$vap)*100I know that Alaska is going to mess things up here, so i’m going to set the turnout to missing for Alaska
merged.data$perc.turnout[merged.data$state=="Alaska"] <- NAOverall the average county turnout is:
mean(merged.data$perc.turnout,na.rm=T)
#> [1] 57.2615approximately 57% of the voting age population.
Question: is that the nationwide turnout rate?
No! That is the average of the county rates, but counties are all different sizes. We can get the nationwide turnout rate by adding up all of the votes and dividing by all of the people over 18:
Slightly lower.
We can look at how this turnout varies by state using a boxplot:
boxplot(merged.data$perc.turnout ~ merged.data$state)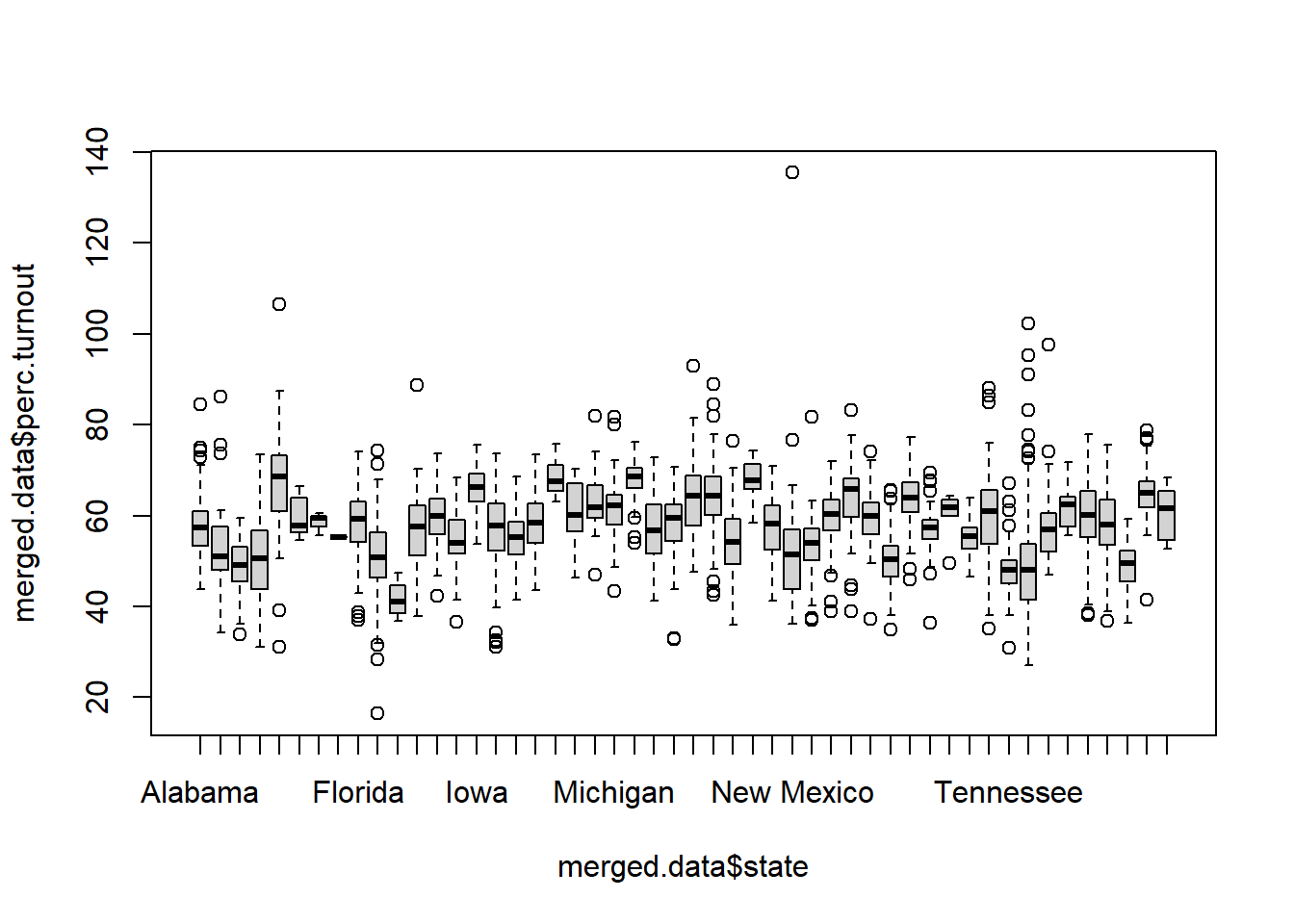
Hm, we’re still getting some points above 100, why is that??
ACS numbers are estimates! Things can get weird for very small counties where it may look like more than 100% of people are voting.
Let’s recode all values above 100 to 100/l
merged.data$perc.turnout[merged.data$perc.turnout>100] <- 100
boxplot(merged.data$perc.turnout ~ merged.data$state, outline=F)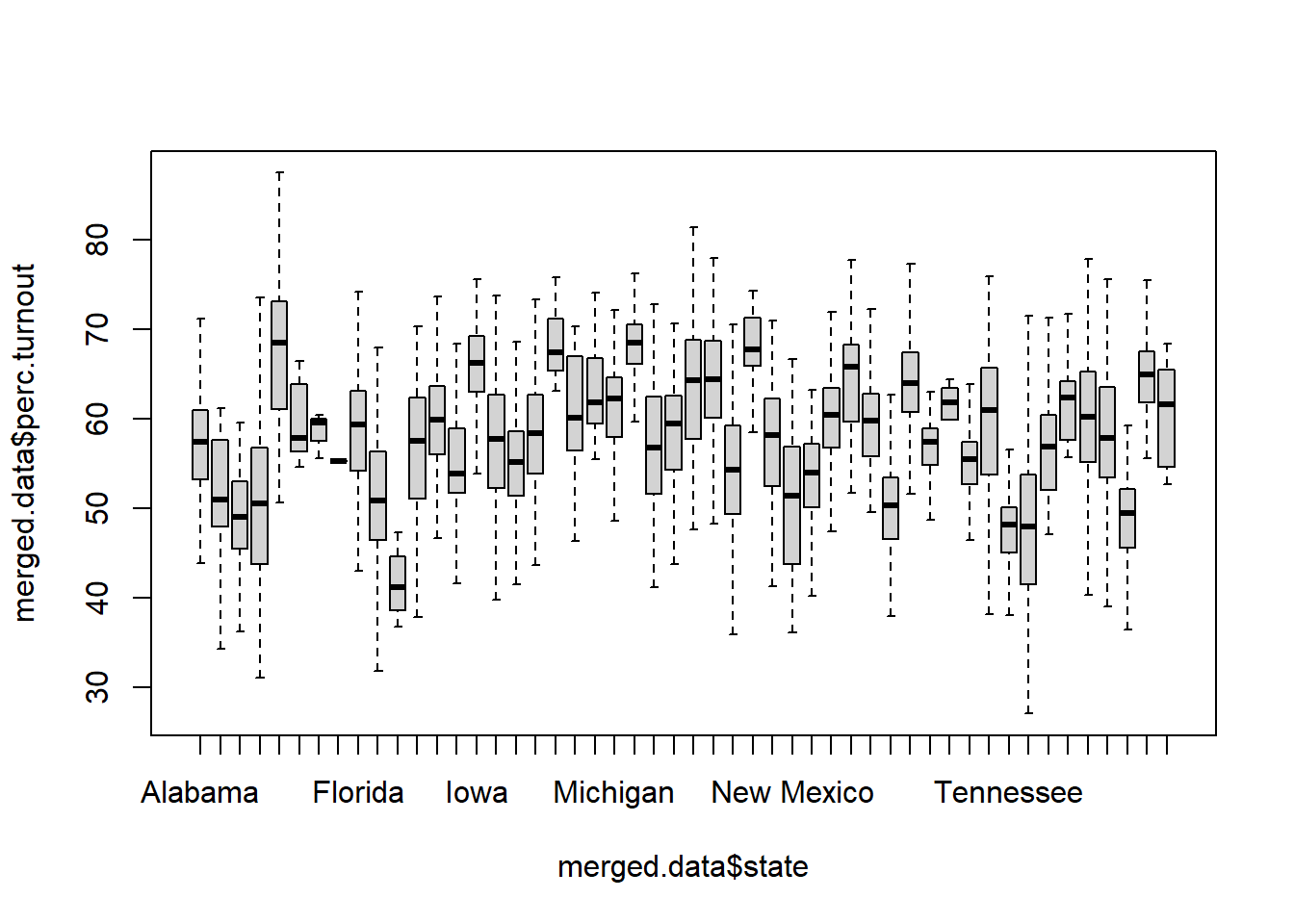
Is this a good or correct decision? To recode places about to 100 to 100? I think it’s a good one, but the rule is less “always do it this way” and more “be transparent”. This is a decision I would note in my script, and one that I would note in any report I was writing on this.
What if we wanted to do this for every year in the original elect dataset? That is, what if we wanted to merge in the county population figures for every observation in elect.all which is for all elections from 2000-2016.
Now there are 5 different Autagua Alabamas in the dataset. For each of these rows we want to merge in the vap number from our acs file. (Let’s ignore that this vap number would be changing over time for right now).
head(elect.all[order(elect.all$FIPS),])
#> year state county FIPS totalvotes
#> 1 2000 Alabama Autauga 1001 17208
#> 3117 2004 Alabama Autauga 1001 20081
#> 6234 2008 Alabama Autauga 1001 23641
#> 9351 2012 Alabama Autauga 1001 23932
#> 12468 2016 Alabama Autauga 1001 24973
#> 2 2000 Alabama Baldwin 1003 56480This is actually really easy, because R will do all of the work for us with the same command. It will know that every time there is FIPS 1001 in the elect dataset it should put in the appropriate number from the acs dataset.
full.merge <- merge(elect.all, acs, by.x="FIPS",by.y="Geo_FIPS",all.x=T)
head(full.merge[order(full.merge$FIPS),])
#> FIPS year state county totalvotes vap
#> 1 1001 2000 Alabama Autauga 17208 41831
#> 2 1001 2012 Alabama Autauga 23932 41831
#> 3 1001 2016 Alabama Autauga 24973 41831
#> 4 1001 2004 Alabama Autauga 20081 41831
#> 5 1001 2008 Alabama Autauga 23641 41831
#> 6 1003 2008 Alabama Baldwin 81413 162430That looks right!
We can think about the limits to this process though: we can have one dataset that has multiple rows for a merging variable, but the other dataset must have one and only one row for the merging variable. So here, the elect data has many rows for each FIPS code and the acs data has one row for each FIPS code. We couldn’t complete this merge if the acs data had multiple rows for each FIPS code.
What if we had ACS Data like this, where we have a new vap number for each election year:
acs.series <- rio::import("https://github.com/marctrussler/IDS-Data/raw/main/ACSSeries.Rds")
head(acs.series)
#> Geo_FIPS vap year
#> 1 1001 39249 2000
#> 2 1003 162016 2000
#> 3 1005 18659 2000
#> 4 1007 21349 2000
#> 5 1009 43670 2000
#> 6 1011 6169 2000How can we perform this merge? Now we have multiple FIPS codes for each year….
Thinking back to units of analysis, we are interested in what variable (or sets of variables) uniquely identifies rows. In both cases now the combination of FIPS and year uniquely identifies cases. So now we want to merge on both variables: matching FIPS 1001 in year 2000 to FIPS 1001 in year 2000 etc.
There are two ways to do this.
First we can create a new variable that simple combines these two variables into a new variable:
acs.series$county.year <- paste(acs.series$Geo_FIPS,acs.series$year,sep="")
head(acs.series)
#> Geo_FIPS vap year county.year
#> 1 1001 39249 2000 10012000
#> 2 1003 162016 2000 10032000
#> 3 1005 18659 2000 10052000
#> 4 1007 21349 2000 10072000
#> 5 1009 43670 2000 10092000
#> 6 1011 6169 2000 10112000
elect.all$county.year <- paste(elect.all$FIPS,elect.all$year,sep="")
head(elect.all)
#> year state county FIPS totalvotes county.year
#> 1 2000 Alabama Autauga 1001 17208 10012000
#> 2 2000 Alabama Baldwin 1003 56480 10032000
#> 3 2000 Alabama Barbour 1005 10395 10052000
#> 4 2000 Alabama Bibb 1007 7101 10072000
#> 5 2000 Alabama Blount 1009 17973 10092000
#> 6 2000 Alabama Bullock 1011 4904 10112000
#If the variable is called the same thing in both datasets you don't have to do by.x and by.y:
merge.series <- merge(elect.all,acs.series, by="county.year", all.x=T)
head(merge.series)
#> county.year year.x state county FIPS totalvotes
#> 1 100012000 2000 Delaware Kent 10001 48247
#> 2 100012004 2004 Delaware Kent 10001 55977
#> 3 100012008 2008 Delaware Kent 10001 66925
#> 4 100012012 2012 Delaware Kent 10001 68696
#> 5 100012016 2016 Delaware Kent 10001 74598
#> 6 100032000 2000 Delaware New Castle 10003 212995
#> Geo_FIPS vap year.y
#> 1 10001 133347 2000
#> 2 10001 134028 2004
#> 3 10001 134468 2008
#> 4 10001 134360 2012
#> 5 10001 134211 2016
#> 6 10003 435787 2000This works ok, but note that we now have copies of FIPS and year now. Indeed, because there was the variable year in both datasets R has changed the names to year.x and year.y. Now we could fix this with some cleanup (or deleting out the FIPS and year variables from one of the datasets before merging).
The other way of doing this is to simply explicitly merge on both variables:
#Going to delete the merging variable we made first:
elect.all$county.year <- NULL
acs.series$county.year <- NULL
merge.series2 <- merge(elect.all, acs.series, by.x=c("FIPS","year"), by.y=c("Geo_FIPS","year"))
head(merge.series2)
#> FIPS year state county totalvotes vap
#> 1 10001 2000 Delaware Kent 48247 133347
#> 2 10001 2004 Delaware Kent 55977 134028
#> 3 10001 2008 Delaware Kent 66925 134468
#> 4 10001 2012 Delaware Kent 68696 134360
#> 5 10001 2016 Delaware Kent 74598 134211
#> 6 10003 2000 Delaware New Castle 212995 435787