1 Introduction
1.1 Historical Introduction
1.1.1 Exercises I 1.4
1.a Modify the region in Figure I.3 by assuming that the ordinate at each \(x\) is \(2x^2\) instead of \(x^2\). Draw the new figure. Check through the principal steps in the foregoing section and find what effect this has on the calculation of the area.
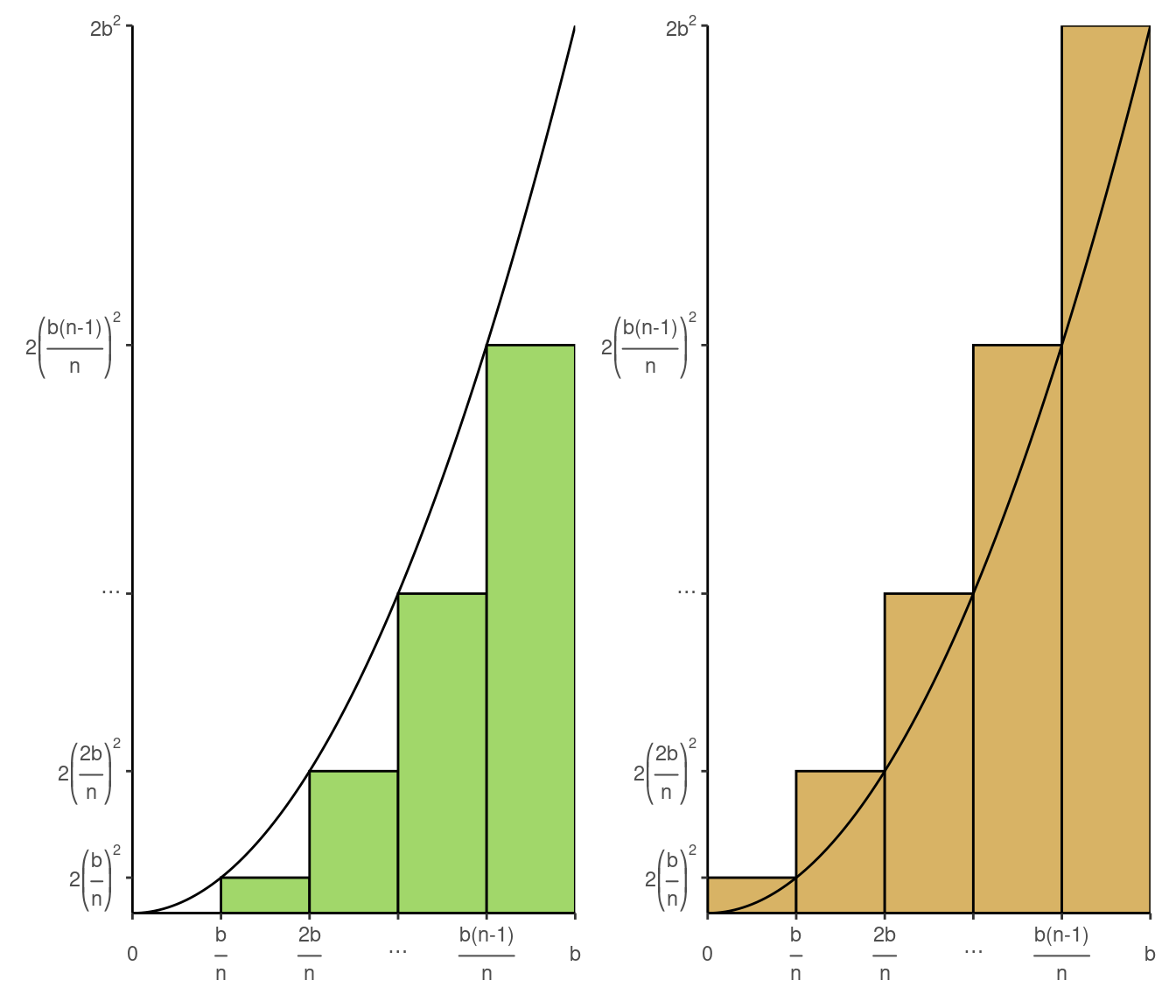
First we need to calculate the area of each rectangle:
\[\frac{b}{n} \mathbf{2}\left[\frac{kb}{n}\right]^2 = \mathbf{2}\frac{k^2b^3}{n^3}\]
Second we need to calculate \(s_n\)
\[\begin{split} s_n & = \sum_{k=1}^{n-1} \mathbf{2}\frac{k^2b^3}{n^3} \\ & = \mathbf{2}\frac{b^3}{n^3} \sum_{k=1}^{n-1} k^2 \\ & = \mathbf{2}\frac{b^3}{n^3} \left[\frac{n^3}{3} - \frac{n^2}{2} + \frac{n}{6} \right] \end{split}\]
Third we need to calculate \(S_n\)
\[\begin{split} S_n & = \sum_{k=1}^{n} \mathbf{2}\frac{k^2b^3}{n^3} \\ & = \mathbf{2}\frac{b^3}{n^3} \sum_{k=1}^{n} k^2 \\ & = \mathbf{2}\frac{b^3}{n^3} \left[\frac{n^3}{3} + \frac{n^2}{2} + \frac{n}{6} \right] \end{split}\]
Fourth we use the following inequalities where \(n \geq 1\)
\[\begin{split} \frac{n^3}{3} - \frac{n^2}{2} + \frac{n}{6} & < \frac{n^3}{3} & < \frac{n^3}{3} + \frac{n^2}{2} + \frac{n}{6} \\ \mathbf{2}\frac{b^3}{n^3} \left[\frac{n^3}{3} - \frac{n^2}{2} + \frac{n}{6}\right] & < \mathbf{2}\frac{b^3}{3} & < \mathbf{2}\frac{b^3}{n^3} \left[\frac{n^3}{3} + \frac{n^2}{2} + \frac{n}{6}\right] \\ s_n & < \mathbf{2}\frac{b^3}{3} & < S_n \end{split}\]
Fifth we assume that there is some \(A\) such that \(s_n < A < S_n\) and prove that \(A = \mathbf{2}\frac{b^3}{3}\) using the following inequalities: \(\frac{n^3}{3} - \frac{n^2}{2} + \frac{n}{6} < \frac{n^3}{3}\) and \(\frac{n^3}{3} < \frac{n^3}{3} + \frac{n^2}{2} + \frac{n}{6}\)
\[\begin{split} \frac{n^3}{3} - \frac{n^2}{2} + \frac{n}{6} < \frac{n^3}{3} & \iff \frac{n^3}{3} + \frac{n^2}{2} + \frac{n}{6} < \frac{n^3}{3} + n^2 \\ & \iff \mathbf{2}\frac{b^3}{n^3}\left[\frac{n^3}{3} + \frac{n^2}{2} + \frac{n}{6}\right] < \mathbf{2}\frac{b^3}{n^3}\left[\frac{n^3}{3} + n^2\right] \\ & \iff S_n < \mathbf{2}\left[\frac{b^3}{3} + \frac{b^3}{n}\right] \end{split}\]
\[\begin{split} \frac{n^3}{3} < \frac{n^3}{3} + \frac{n^2}{2} + \frac{n}{6} & \iff \frac{n^3}{3} - n^2 < \frac{n^3}{3} - \frac{n^2}{2} + \frac{n}{6} \\ & \iff \mathbf{2}\frac{b^3}{n^3}\left[\frac{n^3}{3} - n^2\right] < \mathbf{2}\frac{b^3}{n^3}\left[\frac{n^3}{3} - \frac{n^2}{2} + \frac{n}{6}\right] \\ & \iff \mathbf{2}\left[\frac{b^3}{3} - \frac{b^3}{n}\right] < s_n \\ \end{split}\]
Therefore we have also that \(\mathbf{2}\left[\frac{b^3}{3} - \frac{b^3}{n}\right] < A < \mathbf{2}\left[\frac{b^3}{3} + \frac{b^3}{n}\right]\). If \(A > \mathbf{2}\frac{b^3}{3}\) then \(A - \mathbf{2}\frac{b^3}{3} > 0\) so using \(A < \mathbf{2}\left[\frac{b^3}{3} + \frac{b^3}{n}\right]\) we can conclude that \(n < \frac{\mathbf{2}b^3}{A - \mathbf{2}\frac{b^3}{3}}\) but \(n \geq 1\) so there are some values of \(n\) where \(n < \frac{\mathbf{2}b^3}{A - \mathbf{2}\frac{b^3}{3}}\) is false. If \(A < \mathbf{2}\frac{b^3}{3}\) then \(0 < \mathbf{2}\frac{b^3}{3} - A\) so using \(\mathbf{2}\left[\frac{b^3}{3} - \frac{b^3}{n}\right] < A\) we can also conclude that \(n < \frac{\mathbf{2}b^3}{\mathbf{2}\frac{b^3}{3} - A}\) and again this is false. The only possibility is that \(A = \mathbf{2}\frac{b^3}{3}\) so there is a unique value \(A\) such that \(s_n < A < S_n\).
1.b Do the same if the ordinate at each \(x\) is \(3x^2\)
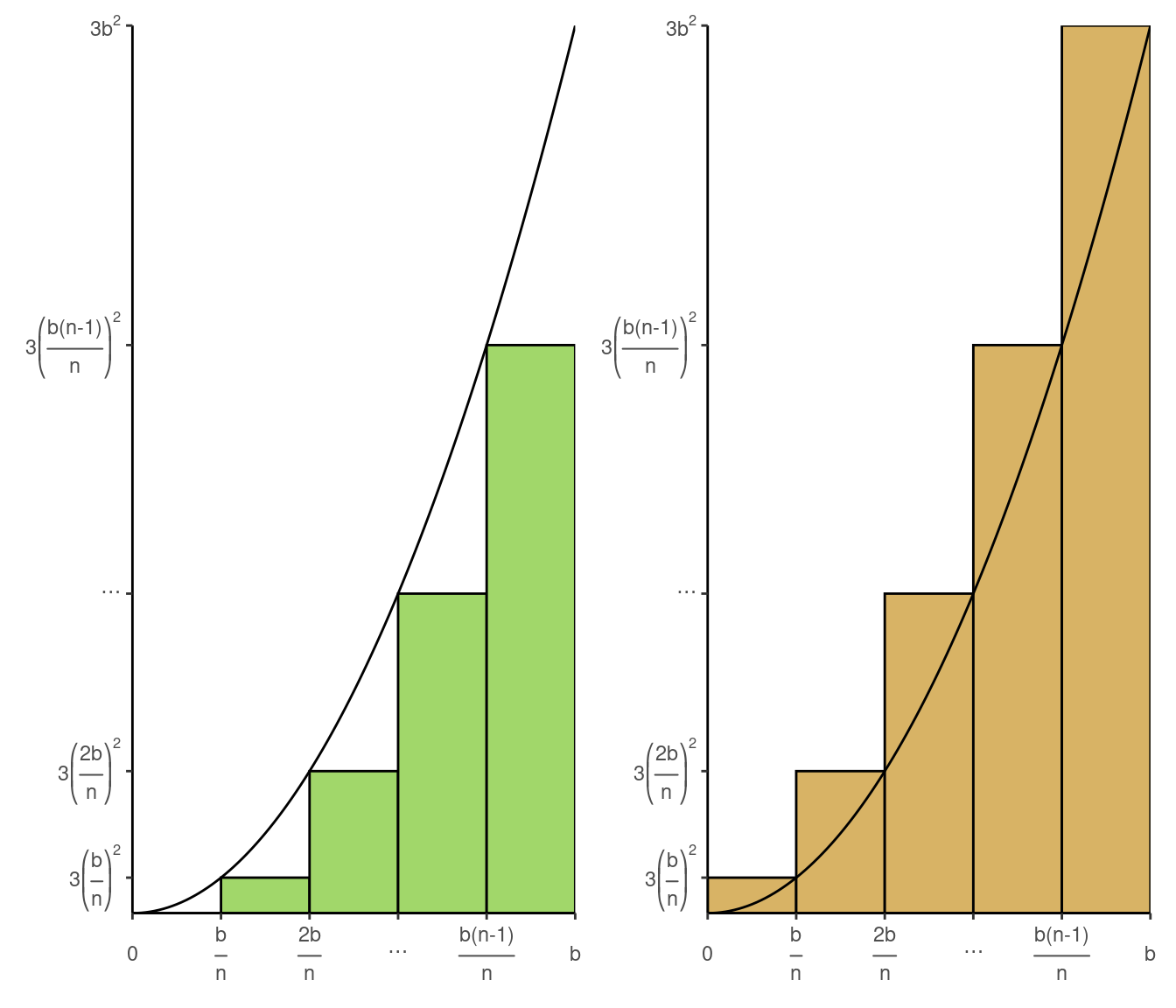
The process is similar as in 1.a where we only need to change \(\mathbf{2}\) with \(\mathbf{3}\).
1.c Do the same if the ordinate at each \(x\) is \(\frac{1}{4}x^2\)
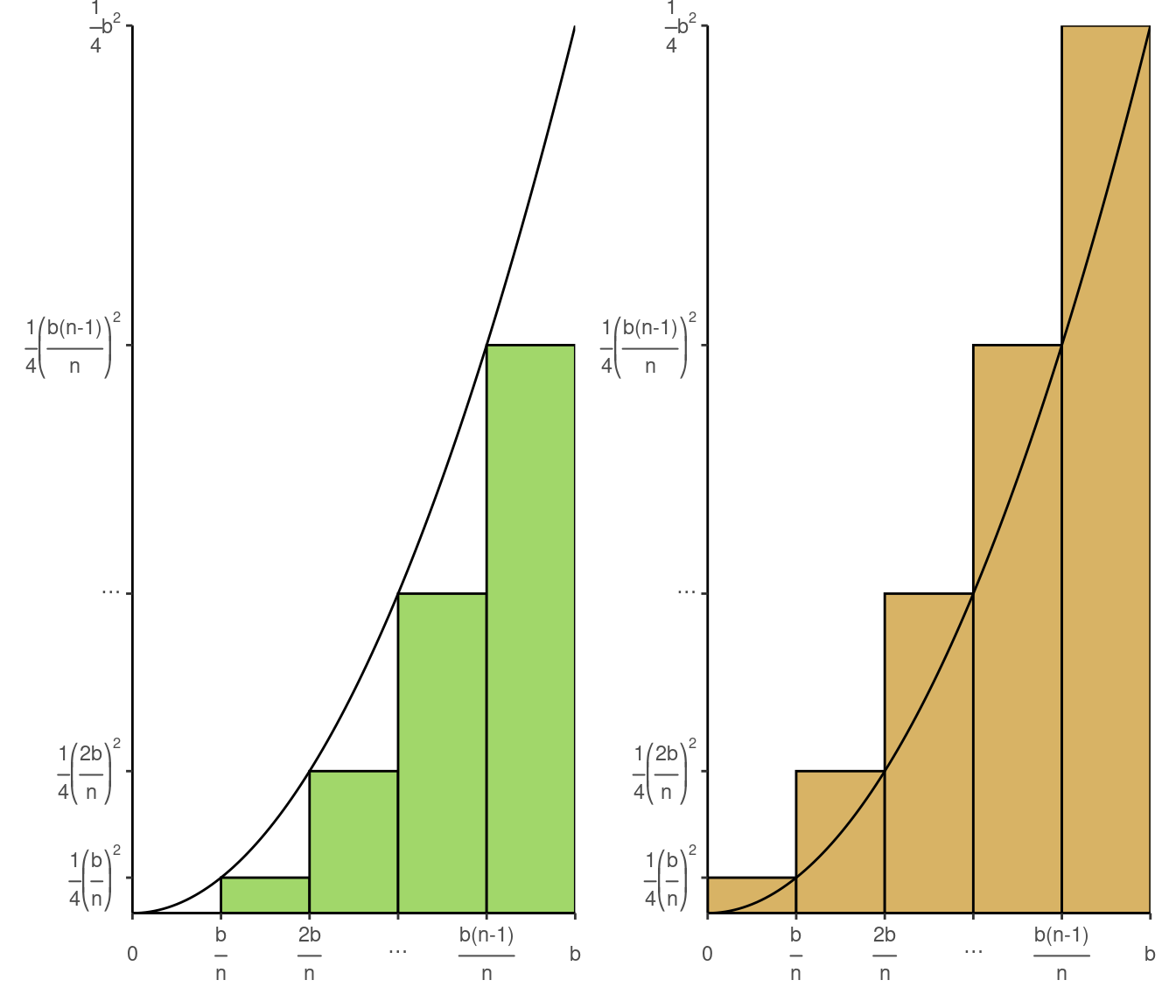
The process is similar as in 1.a where you only need to change \(\mathbf{2}\) with \(\mathbf{\frac{1}{4}}\).
1.d Do the same if the ordinate at each \(x\) is \(2x^2 + 1\)
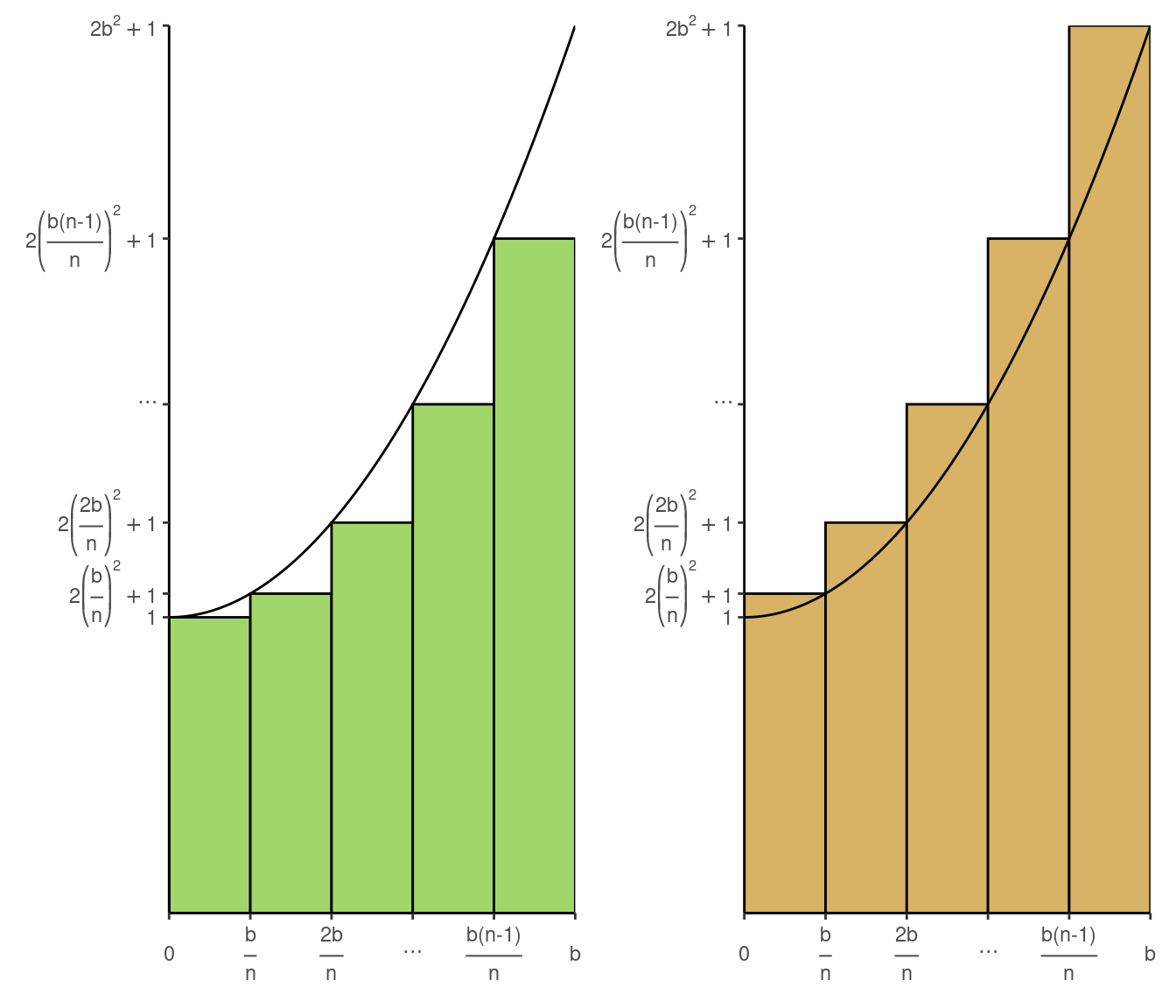
First we need to calculate the area of each rectangle:
\[\frac{b}{n} \left[\mathbf{2}\left[\frac{kb}{n}\right]^2 + \mathbf{1}\right] = \mathbf{2}\frac{k^2b^3}{n^3} + \mathbf{1}\frac{b}{n}\]
Second we need to calculate \(s_n\)
\[\begin{split} s_n & = \sum_{k=1}^{n-1} \left[\mathbf{2}\frac{k^2b^3}{n^3} + \mathbf{1}\frac{b}{n}\right] \\ & = \mathbf{2}\frac{b^3}{n^3} \sum_{k=1}^{n-1} k^2 + \mathbf{1}\frac{b(n-1)}{n} \\ & = \mathbf{2}\frac{b^3}{n^3} \left[\frac{n^3}{3} - \frac{n^2}{2} + \frac{n}{6} \right] + \mathbf{1}\frac{b(n-1)}{n} \end{split}\]
Third we need to calculate \(S_n\)
\[\begin{split} S_n & = \sum_{k=1}^{n} \left[\mathbf{2}\frac{k^2b^3}{n^3} + \mathbf{1}\frac{b}{n}\right] \\ & = \mathbf{2}\frac{b^3}{n^3} \sum_{k=1}^{n} k^2 + \mathbf{1}b \\ & = \mathbf{2}\frac{b^3}{n^3} \left[\frac{n^3}{3} + \frac{n^2}{2} + \frac{n}{6} \right] + \mathbf{1}b \end{split}\]
Fourth we use the following inequalities where \(n \geq 1\)
\[\begin{split} \frac{n^3}{3} - \frac{n^2}{2} + \frac{n}{6} & < \frac{n^3}{3} < \frac{n^3}{3} + \frac{n^2}{2} + \frac{n}{6} \\ \mathbf{2}\frac{b^3}{n^3} \left[\frac{n^3}{3} - \frac{n^2}{2} + \frac{n}{6}\right] + \mathbf{1}b & < \mathbf{2}\frac{b^3}{3} + \mathbf{1}b < \mathbf{2}\frac{b^3}{n^3} \left[\frac{n^3}{3} + \frac{n^2}{2} + \frac{n}{6}\right] + \mathbf{1}b \\ \mathbf{2}\frac{b^3}{n^3} \left[\frac{n^3}{3} - \frac{n^2}{2} + \frac{n}{6}\right] + \mathbf{1}\frac{b(n-1)}{n} & < \mathbf{2}\frac{b^3}{3} + \mathbf{1}b < \mathbf{2}\frac{b^3}{n^3} \left[\frac{n^3}{3} + \frac{n^2}{2} + \frac{n}{6}\right] + \mathbf{1}b s_n & < \mathbf{2}\frac{b^3}{3} + \mathbf{1}b < S_n \end{split}\]
Fifth we assume that there is some \(A\) such that \(s_n < A < S_n\) and prove that \(A = \mathbf{2}\frac{b^3}{3} + \mathbf{1}b\) using the following inequalities: \(\frac{n^3}{3} - \frac{n^2}{2} + \frac{n}{6} < \frac{n^3}{3}\) and \(\frac{n^3}{3} < \frac{n^3}{3} + \frac{n^2}{2} + \frac{n}{6}\)
\[\begin{split} \frac{n^3}{3} - \frac{n^2}{2} + \frac{n}{6} < \frac{n^3}{3} & \iff \frac{n^3}{3} + \frac{n^2}{2} + \frac{n}{6} < \frac{n^3}{3} + n^2 \\ & \iff \mathbf{2}\frac{b^3}{n^3}\left[\frac{n^3}{3} + \frac{n^2}{2} + \frac{n}{6}\right] + \mathbf{1}b < \mathbf{2}\frac{b^3}{n^3}\left[\frac{n^3}{3} + n^2\right] + \mathbf{1}b \\ & \iff S_n < \mathbf{2}\left[\frac{b^3}{3} + \frac{b^3}{n}\right] + \mathbf{1}b \end{split}\]
\[\begin{split} \frac{n^3}{3} < \frac{n^3}{3} + \frac{n^2}{2} + \frac{n}{6} & \iff \frac{n^3}{3} - n^2 < \frac{n^3}{3} - \frac{n^2}{2} + \frac{n}{6} \\ & \iff \mathbf{2}\frac{b^3}{n^3}\left[\frac{n^3}{3} - n^2\right] + \mathbf{1}b < \mathbf{2}\frac{b^3}{n^3}\left[\frac{n^3}{3} - \frac{n^2}{2} + \frac{n}{6}\right] + \mathbf{1}b \\ & \iff \mathbf{2}\left[\frac{b^3}{3} - \frac{b^3}{n}\right] + \mathbf{1}b < s_n \\ \end{split}\]
Therefore we have also that \(\mathbf{2}\left[\frac{b^3}{3} - \frac{b^3}{n}\right] + \mathbf{1}b < A < \mathbf{2}\left[\frac{b^3}{3} + \frac{b^3}{n}\right] + \mathbf{1}b\). If \(A > \mathbf{2}\frac{b^3}{3} + \mathbf{1}b\) then \(A - \mathbf{2}\frac{b^3}{3} - \mathbf{1}b > 0\) so using \(A < \mathbf{2}\left[\frac{b^3}{3} + \frac{b^3}{n}\right] + \mathbf{1}b\) we can conclude that \(n < \frac{\mathbf{2}b^3}{A - \mathbf{2}\frac{b^3}{3} - \mathbf{1}b}\) but \(n \geq 1\) so there are some values of \(n\) where \(n < \frac{\mathbf{2}b^3}{A - \mathbf{2}\frac{b^3}{3} - \mathbf{1}b}\) is false. If \(A < \mathbf{2}\frac{b^3}{3} + \mathbf{1}b\) then \(0 < \mathbf{2}\frac{b^3}{3} + \mathbf{1}b - A\) so using \(\mathbf{2}\left[\frac{b^3}{3} - \frac{b^3}{n}\right] + \mathbf{1}b < A\) we can also conclude that \(n < \frac{\mathbf{2}b^3}{\mathbf{2}\frac{b^3}{3} + \mathbf{1}b - A}\) and again this is false. The only possibility is that \(A = \mathbf{2}\frac{b^3}{3} + \mathbf{1}b\) so there is a unique value \(A\) such that \(s_n < A < S_n\).
1.e Do the same if the ordinate at each \(x\) is \(ax^2 + c\)
In this part we are going to assume that \(a > 0\) and \(c > 0\). If \(a = 0\) then it is not possible to calculate the area of the rectangles and if \(a < 0\) we would need to define the concept of a negative area. Also if \(c = 0\) it is a case we already cover and if \(c < 0\) we would need again to define the concept of a negative area.
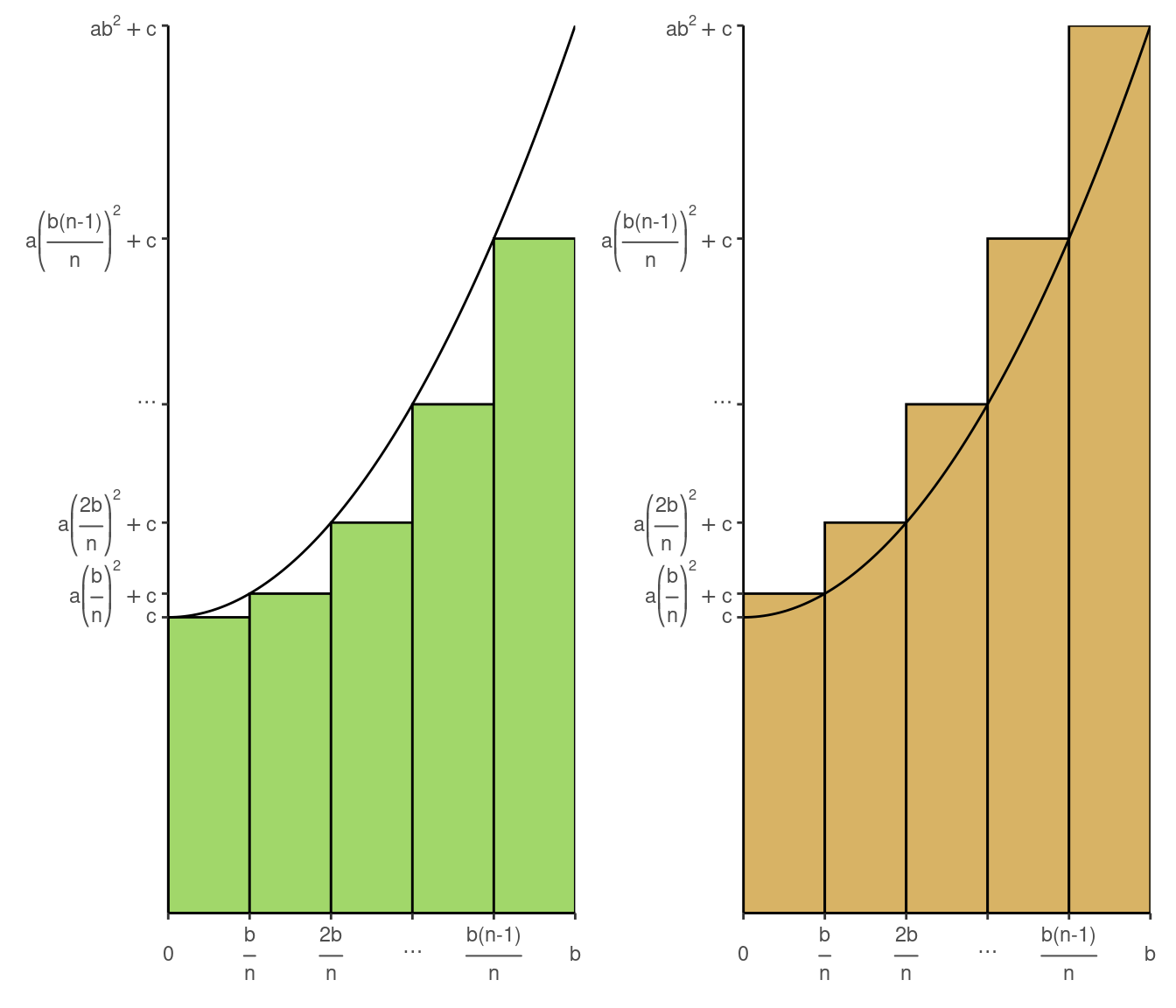
The process is similar as in 1.d where we only need to change \(\mathbf{2}\) with \(\mathbf{a}\) and \(\mathbf{1}\) with \(\mathbf{c}\).
2 Modify the region in Figure I.3 by assuming that the ordinate at each \(x\) is \(x^3\) instead of \(x^2\). Draw a new figure.
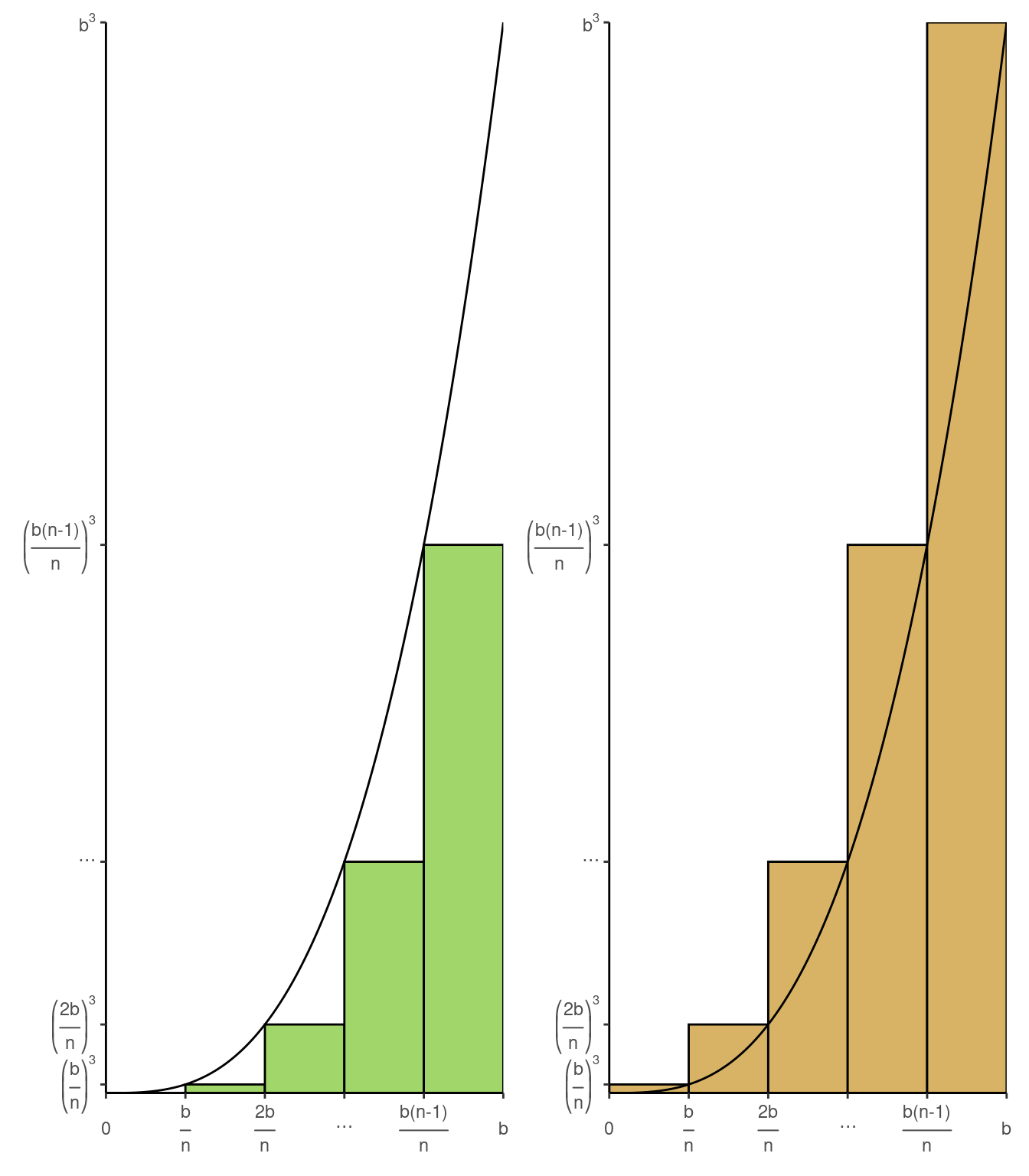
2a Use a construction similar to that illustrated in Figure I.3 and show that the outer and inner sums \(S_n\) and \(s_n\) are given by
\[S_n = \frac{b^4}{n^4}\left[1^3 + 2^3 + \cdots + n^3\right] \; , \; s_n = \frac{b^4}{n^4}\left[1^3 + 2^3 + \cdots + (n-1)^3\right]\]
First we need to calculate the area of each rectangle:
\[\frac{b}{n} \left[\frac{kb}{n}\right]^3 = \frac{k^3b^4}{n^4}\]
Second we need to calculate \(s_n\)
\[\begin{split} s_n & = \sum_{k=1}^{n-1} \frac{k^3b^4}{n^4} \\ & = \frac{b^4}{n^4} \sum_{k=1}^{n-1} k^3 \end{split}\]
Third we need to calculate \(S_n\)
\[\begin{split} S_n & = \sum_{k=1}^{n} \frac{k^3b^4}{n^4} \\ & = \frac{b^4}{n^4} \sum_{k=1}^{n} k^3 \end{split}\]
2b Use the inequalities (which can be proved by mathematical induction; see Section I4.2)
\[1^3 + 2^3 + \cdots + (n-1)^3 < \frac{n^4}{4} < 1^3 + 2^3 + \cdots + n^3\]
to show that \(s_n < \frac{b^4}{4} < S_n\) for every \(n\), and prove that \(\frac{b^4}{4}\) is the only number which lies between \(s_n\) and \(S_n\) for every \(n\)
First we use the following inequality where \(n \geq 1\)
\[\begin{split} 1^3 + 2^3 + \cdots + (n-1)^3 & < \frac{n^4}{4} & < 1^3 + 2^3 + \cdots + n^3 \\ \frac{b^4}{n^4} \sum_{k=1}^{n-1} k^3 & < \frac{b^4}{4} & < \frac{b^4}{n^4} \sum_{k=1}^{n} k^3 \\ s_n & < \frac{b^4}{4} & < S_n \end{split}\]
Second we assume that there is some \(A\) such that \(s_n < A < S_n\) and prove that \(A = \frac{b^4}{4}\) using the following inequalities: \(s_n < \frac{b^4}{4}\) and \(\frac{b^4}{4} < S_n\)
If \(A > \frac{b^4}{4}\) and \(s_n < \frac{b^4}{4}\) then \(S_n > \frac{b^4}{4}\) and \(0 < \frac{b^4}{4} - s_n\). Therefore because \(S_n - s_n > \frac{b^4}{4} - s_n\) this implies that \(\frac{b^4}{\frac{b^4}{4} - s_n} > n\) but \(n \geq 1\) so there are some values of \(n\) where \(\frac{b^4}{\frac{b^4}{4} - s_n} > n\) is false.
If \(A < \frac{b^4}{4}\) and \(\frac{b^4}{4} < S_n\) then \(\frac{b^4}{4} > s_n\) and \(0 < S_n - \frac{b^4}{4}\). Therefore because \(S_n - \frac{b^4}{4} < S_n - s_n\) this implies that \(n < \frac{b^4}{S_n - \frac{b^4}{4}}\) but \(n \geq 1\) so there are some values of \(n\) where \(n < \frac{b^4}{S_n - \frac{b^4}{4}}\) is false.
2c What numbers takes the place of \(\frac{b^4}{4}\) if the ordinate at each \(x\) is \(ax^3 + c\)?
The process to answer this question is similar to the answer in 2b and 2a
First we need to calculate the area of each rectangle:
\[\frac{b}{n} \left[ a\left[\frac{kb}{n}\right]^{\mathbf{3}} + c\right] = a\frac{k^{\mathbf{3}}b^{\mathbf{4}}}{n^{\mathbf{4}}} + c \frac{b}{n}\]
Second we need to calculate \(s_n\)
\[\begin{split} s_n & = \sum_{k=1}^{n-1} \left[a\frac{k^{\mathbf{3}}b^{\mathbf{4}}}{n^{\mathbf{4}}} + c \frac{b}{n}\right] \\ & = a\frac{b^{\mathbf{4}}}{n^{\mathbf{4}}} \sum_{k=1}^{n-1} k^{\mathbf{3}} + c\frac{b(n-1)}{n} \end{split}\]
Third we need to calculate \(S_n\)
\[\begin{split} S_n & = \sum_{k=1}^{n} \left[a\frac{k^{\mathbf{3}}b^{\mathbf{4}}}{n^{\mathbf{4}}} + c \frac{b}{n}\right] \\ & = a\frac{b^{\mathbf{4}}}{n^{\mathbf{4}}} \sum_{k=1}^{n} k^{\mathbf{3}} + cb \end{split}\]
Fourth we use the following inequality where \(n \geq 1\)
\[\begin{split} 1^{\mathbf{3}} + 2^{\mathbf{3}} + \cdots + (n-1)^{\mathbf{3}} & < \frac{n^{\mathbf{4}}}{{\mathbf{4}}} < 1^{\mathbf{3}} + 2^{\mathbf{3}} + \cdots + n^{\mathbf{3}} \\ a\frac{b^{\mathbf{4}}}{n^{\mathbf{4}}} \sum_{k=1}^{n-1} k^{\mathbf{3}} + cb & < a\frac{b^{\mathbf{4}}}{{\mathbf{4}}} + cb < a\frac{b^{\mathbf{4}}}{n^{\mathbf{4}}} \sum_{k=1}^{n} k^{\mathbf{3}} + cb \\ a\frac{b^{\mathbf{4}}}{n^{\mathbf{4}}} \sum_{k=1}^{n-1} k^{\mathbf{3}} + c\frac{b(n-1)}{n} & < a\frac{b^{\mathbf{4}}}{{\mathbf{4}}} + cb < a\frac{b^{\mathbf{4}}}{n^{\mathbf{4}}} \sum_{k=1}^{n} k^{\mathbf{3}} + cb \\ s_n & < a\frac{b^{\mathbf{4}}}{{\mathbf{4}}} + cb < S_n \end{split}\]
Sixth we assume that there is some \(A\) such that \(s_n < A < S_n\) and prove that \(A = a\frac{b^{\mathbf{4}}}{{\mathbf{4}}} + cb\) using the following inequalities: \(s_n < a\frac{b^{\mathbf{4}}}{{\mathbf{4}}} + cb\) and \(a\frac{b^{\mathbf{4}}}{{\mathbf{4}}} + cb < S_n\)
If \(A > a\frac{b^{\mathbf{4}}}{{\mathbf{4}}} + cb\) and \(s_n < a\frac{b^{\mathbf{4}}}{{\mathbf{4}}} + cb\) then \(S_n > a\frac{b^{\mathbf{4}}}{{\mathbf{4}}} + cb\) and \(0 < a\frac{b^{\mathbf{4}}}{{\mathbf{4}}} + cb - s_n\). Therefore because \(S_n - s_n > a\frac{b^{\mathbf{4}}}{{\mathbf{4}}} + cb - s_n\) this implies that \(\frac{ab^{\mathbf{4}} + cb}{a\frac{b^{\mathbf{4}}}{{\mathbf{4}}} + cb - s_n} > n\) but \(n \geq 1\) so there are some values of \(n\) where \(\frac{ab^{\mathbf{4}} + cb}{a\frac{b^{\mathbf{4}}}{{\mathbf{4}}} + cb - s_n} > n\) is false.
If \(A < a\frac{b^{\mathbf{4}}}{{\mathbf{4}}} + cb\) and \(a\frac{b^{\mathbf{4}}}{{\mathbf{4}}} + cb < S_n\) then \(a\frac{b^{\mathbf{4}}}{{\mathbf{4}}} + cb > s_n\) and \(0 < S_n - a\frac{b^{\mathbf{4}}}{{\mathbf{4}}} - cb\). Therefore because \(S_n - a\frac{b^{\mathbf{4}}}{{\mathbf{4}}} - cb < S_n - s_n\) this implies that \(n < \frac{ab^4 + cb}{S_n - a\frac{b^{\mathbf{4}}}{{\mathbf{4}}} - cb}\) but \(n \geq 1\) so there are some values of \(n\) where \(n < \frac{ab^{\mathbf{4}} + cb}{S_n - a\frac{b^{\mathbf{4}}}{{\mathbf{4}}} - cb}\) is false.
3 The inequalities (I.5) and (I.12) are special cases of the more general inequalities
\[1^{\mathbf{m}} + 2^{\mathbf{m}} + \cdots + (n-1)^{\mathbf{m}} < \frac{n^{\mathbf{m + 1}}}{\mathbf{m + 1}} < 1^{\mathbf{m}} + 2^{\mathbf{m}} + \cdots + n^{\mathbf{m}}\]
that are valid for every integer \(n \geq 1\) and every integer \({\mathbf{m}} \geq 1\). Asumme the validity of (I.13) and generalize the results of Exercise 2.
We can generalize this result to \(ax^{\mathbf{m}} + c\) where the process is similar as in 2.c. We only need to change \(\mathbf{3}\) with \(\mathbf{m}\) and \(\mathbf{4}\) with \(\mathbf{m + 1}\).
1.2 Some Basic Concepts of the Theory of Sets
1.2.1 Exercises I 2.5
1 Use the roster notation to designate the following sets of real numbers.
\[A = \{x | x^2 - 1 = 0 \} = \{ -1, 1 \}\]
\[B = \{x | (x - 1)^2 = 0 \} = \{ 1 \}\]
\[C = \{x | x + 8 = 9 \} = \{ 1 \}\]
In this part \(x^3 - 2x^2 + x = 2 \Longleftrightarrow (x^2 + 1)(x - 2) = 0\). In that sense there are also 2 complex roots \(x = -i\) and \(x = i\) but they are not real numbers (Remember that \(S = \mathbb{R}\))
\[D = \{x | x^3 - 2x^2 + x = 2 \} = \{ 2 \}\]
\[E = \{x | (x + 8)^2 = 9^2 \} = \{ -17, 1 \}\]
\[F = \{x | (x^2 + 16x)^2 = 17^2 \} = \{ -17, -8 - \sqrt{47}, 1, \sqrt{47} - 8 \}\]
2 For the sets in Exercise 1, note that \(B \subseteq A\). List all the inclusion relations \(\subseteq\) that hold among the sets \(A\), \(B\), \(C\), \(D\), \(E\), \(F\).
\(B \subseteq A\), \(C \subseteq A\), \(C \subseteq B\), \(B \subseteq C\), \(E \subseteq B\), \(E \subseteq C\), \(E \subseteq F\)
3 Let \(A = \{ 1 \}\), \(B = \{ 1, 2 \}\). Discuss the validity of the following statements (prove the ones that are true and explain why the others are not true).
3a \(A \subset B\)
It is true because \(1 \in A\) and \(1 \in B\) but \(2 \notin A\) and \(2 \in B\) so \(A \subseteq B\) and \(A \neq B\)
3b \(A \subseteq B\)
It is true because \(1 \in A\) and \(1 \in B\) but \(2 \notin A\) and \(2 \in B\) so \(A \subset B\) or \(A = B\) is true
3c \(A \in B\)
It is false because \({1}\) is not an element of \(B\). Remember that \(1\) is not the same as \(\{ 1 \}\)
3d \(1 \in A\)
It is true because \(1\) is an element of \(A\).
3e \(1 \subseteq A\)
It is false because the subsets of \(A\) are \(\emptyset\) and \(\{ 1 \}\)
3f \(1 \subset B\)
It is false because the proper subsets of \(B\) are \(\emptyset\), \(\{ 1 \}\) and \(\{ 2 \}\)
4 Solve Exercise 3 if \(A = \{ 1 \}\) and \(B = \{ \{ 1 \}, 1 \}\).
4a \(A \subset B\)
It is true because \(1 \in A\) and \(1 \in B\) but \(\{ 1 \} \notin A\) and \(\{ 1 \} \in B\) so \(A \subseteq B\) and \(A \neq B\)
4b \(A \subseteq B\)
It is true because \(1 \in A\) and \(1 \in B\) but \(\{ 1 \} \notin A\) and \(\{ 1 \} \in B\) so \(A \subset B\) or \(A = B\) is true
4c \(A \in B\)
It is true because \(\{ 1 \} \in B\) and \(A = \{ 1 \}\) so \(A \in B\)
4d \(1 \in A\)
It is true because \(1\) is an element of \(A\).
4e \(1 \subseteq A\)
It is false because the subsets of \(A\) are \(\emptyset\) and \(\{ 1 \}\)
4f \(1 \subset B\)
It is false because the proper subsets of \(B\) are \(\emptyset\), \(\{ \{1 \} \}\) and \(\{ 1 \}\)
5 Given the set \(S = \{ 1, 2, 3, 4 \}\). Display all subsets of \(S\). There are 16 altogether, counting \(\emptyset\) and \(S\).
\(\emptyset\), \(\{ 1 \}\), \(\{ 2 \}\), \(\{ 3 \}\), \(\{ 4 \}\), \(\{ 1, 2 \}\), \(\{ 1, 3 \}\), \(\{ 1, 4 \}\), \(\{ 2, 3 \}\), \(\{ 2, 4 \}\), \(\{ 3, 4 \}\), \(\{ 1, 2, 3 \}\), \(\{ 1, 2, 4 \}\), \(\{ 1, 3, 4 \}\), \(\{ 2, 3, 4 \}\), \(\{ 1, 2, 3, 4 \}\)
6 Given the following four sets
\[A = \{ 1, 2 \}, \;\; B = \{ \{ 1 \}, \{ 2 \} \}, \;\; C = \{ \{ 1 \}, \{ 1, 2 \} \}, \;\; D = \{ \{ 1 \}, \{ 2 \}, \{ 1, 2 \} \}\]
discuss the validity of the following statements (prove the ones that are true and explain why the others are not true).
6a \(A = B\)
It is false because \(1 \in A\) and \(1 \notin B\)
6b \(A \subseteq B\)
It is false because \(1 \in A\) and \(1 \notin B\)
6c \(A \subset C\)
It is false because \(1 \in A\) and \(1 \notin C\)
6d \(A \in C\)
It is true because \(\{ 1, 2 \} \in C\) and \(A = \{ 1, 2 \}\) so \(A \in C\)
6e \(A \subset D\)
It is false because \(1 \in A\) and \(1 \notin D\)
6f \(B \subset C\)
It is false because \(\{ 2 \} \in B\) and \(\{ 2 \} \notin C\)
6g \(B \subset D\)
It is true because \(\{ 1 \} \in B\), \(\{ 2 \} \in B\) and \(\{ 1 \} \in D\), \(\{ 2 \} \in D\) but \(\{ 1, 2 \} \notin B\) and \(\{ 1, 2 \} \in D\)
6h \(B \in D\)
It is not true because the elements of \(D\) are \(\{ 1 \}\), \(\{ 2 \}\) and \(\{ 1, 2 \}\) so \(\{ \{ 1 \}, \{ 2 \} \}\) is not an element of \(D\)
6i \(A \in D\)
It is true because \(\{ 1, 2 \} \in D\) and \(A = \{ 1, 2 \}\) so \(A \in D\)
7 Prove the following properties of set equality.
7a \(\{ a, a \} = \{ a \}\)
\[\begin{split} a \in \{ a, a \} & \Longleftrightarrow a \in \{ a \} \end{split}\]
7b \(\{ a, b \} = \{ b, a \}\)
\[\begin{split} a \in \{ a, b \} \land b \in \{ a, b \} & \Longleftrightarrow b \in \{ a, b \} \land a \in \{ a, b \} \\ & \Longleftrightarrow b \in \{ b, a \} \land a \in \{ b, a \} \end{split}\]
7c \(\{ a \} = \{ b, c \}\) if and only if \(a = b = c\)
\[\begin{split} \{ a \} = \{ b, c \} & \Longleftrightarrow a \in \{ b, c \} \land (b \in \{ a \} \land c \in \{ a \}) \\ & \Longleftrightarrow (a = b \lor a = c) \land (b = a \land c = a) \\ & \Longleftrightarrow (a = b \lor a = c) \land (a = b = c) \\ & \Longleftrightarrow a = b = c \end{split}\]
Prove the set relations in Exercises 8 through 19. (Sample proofs are given at the end of this section)
8 Commutative laws: \(A \cup B = B \cup A\), \(A \cap B = B \cap A\)
\[\begin{split} x \in A \cup B & \Longleftrightarrow x \in A \lor x \in B \\ & \Longleftrightarrow x \in B \lor x \in A \\ & \Longleftrightarrow \in B \cup A \end{split}\]
\[\begin{split} x \in A \cap B & \Longleftrightarrow x \in A \land x \in B \\ & \Longleftrightarrow x \in B \land x \in A \\ & \Longleftrightarrow \in B \cap A \end{split}\]
9 Associative laws: \(A \cup (B \cup C) = (A \cup B) \cup C\), \(A \cap (B \cap C) = (A \cap B) \cap C\)
\[\begin{split} x \in A \cup (B \cup C) & \Longleftrightarrow x \in A \lor x \in (B \cup C) \\ & \Longleftrightarrow x \in A \lor (x \in B \lor x \in C) \\ & \Longleftrightarrow (x \in A \lor x \in B) \lor x \in C \\ & \Longleftrightarrow x \in A \cup B \lor x \in C \\ & \Longleftrightarrow x \in (A \cup B) \cup C \\ \end{split}\]
\[\begin{split} x \in A \cap (B \cap C) & \Longleftrightarrow x \in A \land x \in (B \cap C) \\ & \Longleftrightarrow x \in A \land (x \in B \land x \in C) \\ & \Longleftrightarrow (x \in A \land x \in B) \land x \in C \\ & \Longleftrightarrow x \in A \cap B \land x \in C \\ & \Longleftrightarrow x \in (A \cap B) \cap C \\ \end{split}\]
10 Distributive laws: \(A \cap (B \cup C) = (A \cap B) \cup (A \cap C)\), \(A \cup (B \cap C) = (A \cup B) \cap (A \cup C)\)
\[\begin{split} x \in A \cap (B \cup C) & \Longleftrightarrow x \in A \land x \in (B \cup C) \\ & \Longleftrightarrow x \in A \land (x \in B \lor x \in C) \\ & \Longleftrightarrow (x \in A \land x \in B) \lor (x \in A \land x \in C) \\ & \Longleftrightarrow x \in A \cap B \lor x \in A \cap C \\ & \Longleftrightarrow x \in (A \cap B) \cup (A \cap C) \\ \end{split}\]
\[\begin{split} x \in A \cup (B \cap C) & \Longleftrightarrow x \in A \lor x \in (B \cap C) \\ & \Longleftrightarrow x \in A \lor (x \in B \land x \in C) \\ & \Longleftrightarrow (x \in A \lor x \in B) \land (x \in A \lor x \in C) \\ & \Longleftrightarrow x \in A \cup B \land x \in A \cup C \\ & \Longleftrightarrow x \in (A \cup B) \cap (A \cup C) \\ \end{split}\]
11 \(A \cup A = A\), \(A \cap A = A\)
\[\begin{split} x \in A \cup A & \Longleftrightarrow x \in A \lor x \in A \\ & \Longleftrightarrow x \in A \end{split}\]
\[\begin{split} x \in A \cap A & \Longleftrightarrow x \in A \land x \in A \\ & \Longleftrightarrow x \in A \end{split}\]
12 \(A \subseteq A \cup B\), \(A \cap B \subseteq A\)
\[\begin{split} x \in A & \Longrightarrow x \in A \lor x \in B \\ & \Longrightarrow x \in A \cup B \end{split}\]
In this part we also have \(A \cap B \subseteq B\) but because \(A\) and \(B\) are arbitrary sets the proof related to \(A \cap B \subseteq A\) include this case.
\[\begin{split} x \in A \cap B & \Longrightarrow x \in A \land x \in B \\ & \Longrightarrow x \in A \end{split}\]
13 \(A \cup \emptyset = A\), \(A \cap \emptyset = \emptyset\)
In this part remember that \(x \in \emptyset\) is false but \(x \in A \lor x \in \emptyset\) is true if and only if \(x \in A\)
\[\begin{split} x \in A \cup \emptyset & \Longleftrightarrow x \in A \lor x \in \emptyset \\ & \Longleftrightarrow x \in A \end{split}\]
In this part remember that \(\emptyset\) is always a subset of every set and that \(\emptyset\) is a set containing no elements whatsoever. Taking into account these true statements we can prove that \(A \cap \emptyset = \emptyset\).
First, \(A \cap \emptyset \supseteq \emptyset\) is true because \(\emptyset\) is always a subset of every set.
Second, if \(x \in A \cap \emptyset\) then \(x \in A \land x \in \emptyset\) but \(x \notin \emptyset\) so \(x \in A \cap \emptyset\) is false. Therefore for any \(x\) we have that \(x \notin A \cap \emptyset\) must be true. Also let’s assume that \(A \cap \emptyset \nsubseteq \emptyset\) where this would mean that there is some \(y\) such that \(y \in A \cap \emptyset \land y \notin \emptyset\) but this is false because \(A \cap \emptyset\) is a set containing no elements whatsoever. Therefore \(A \cap \emptyset \nsubseteq \emptyset\) is false and \(A \cap \emptyset \subseteq \emptyset\) must be true.
Third, because \(A \cap \emptyset \supseteq \emptyset\) and \(A \cap \emptyset \subseteq \emptyset\) are true we have that \(A \cap \emptyset = \emptyset\).
14 \(A \cup (A \cap B) = A\), \(A \cap (A \cup B) = A\)
First we prove \(A \cup (A \cap B) = A\) in 2 parts:
\[\begin{split} x \in A \cup (A \cap B) & \Longleftrightarrow x \in A \lor x \in A \cap B \\ & \Longleftrightarrow x \in A \lor (x \in A \land x \in B) \\ & \Longleftrightarrow (x \in A \lor x \in A) \land (x \in A \lor x \in B) \\ & \Longleftrightarrow x \in A \land x \in (A \cup B) \\ & \Longrightarrow x \in A \\ x \in A & \Longrightarrow x \in A \lor x \in A \cap B \\ & \Longleftrightarrow x \in A \cup (A \cap B) \end{split}\]
\[\begin{split} x \in A & \Longrightarrow x \in A \lor x \in A \cap B \\ & \Longleftrightarrow x \in A \cup (A \cap B) \end{split}\]
Second we prove \(A \cap (A \cup B) = A\) using \(A \cup (A \cap B) = A\):
\[\begin{split} A \cap (A \cup B) & = (A \cap A) \cup (A \cap B) \\ & = A \cup (A \cap B) \\ & = A \end{split}\]
15 If \(A \subseteq C\) and \(B \subseteq C\), then \(A \cup B \subseteq C\)
\[\begin{split} (A \subseteq C \land B \subseteq C) \land x \in A \cup B & \Longleftrightarrow (A \subseteq C \land B \subseteq C) \land (x \in A \lor x \in B) \\ & \Longrightarrow (A \subseteq C \land x \in A) \lor (B \subseteq C \land x \in B) \\ & \Longrightarrow x \in C \end{split}\]
16 If \(C \subseteq A\) and \(C \subseteq B\), then \(C \subseteq A \cap B\)
\[\begin{split} (C \subseteq A \land C \subseteq B) \land x \in C & \Longrightarrow (C \subseteq A \land x \in C) \land (C \subseteq B \land x \in C) \\ & \Longrightarrow x \in A \land x \in B \\ & \Longrightarrow x \in A \cap B \end{split}\]
17a If \(A \subset B\) and \(B \subset C\), prove that \(A \subset C\)
\[\begin{split} (A \subset B \land B \subset C) \land x \in A & \Longrightarrow (x \in B \land B \subset C) \land \exists y: y \notin A \land y \in B \\ & \Longrightarrow x \in C \land \exists y: y \notin A \land y \in C \end{split}\]
17b If \(A \subseteq B\) and \(B \subseteq C\), prove that \(A \subseteq C\)
\[\begin{split} (A \subseteq B \land B \subseteq C) \land x \in A & \Longrightarrow x \in B \land B \subseteq C \\ & \Longrightarrow x \in C \end{split}\]
17c What can you conclude if \(A \subset B\) and \(B \subseteq C\)?
First, if \(B = C\) we can conclude that \(A \subset C\).
Second, if \(B \subset C\) using the proof in 17a we can conclude again that \(A \subset C\).
17d If \(x \in A\) and \(A \subseteq B\), is it necessarily true that \(x \in B\)?
Yes, because \(A \subseteq B\) means that \(\forall y: y \in A \Longrightarrow y \in B\) and if \(x \in A\) is true also \(x \in B\) must be true.
17e If \(x \in A\) and \(A \in B\) is it necessarily true that \(x \in B\)?
No, for example in 6 a counterexample was presented where \(A = \{ 1, 2 \}\) and \(C = \{ \{ 1\}, \{ 1, 2 \} \}\). In this case we have that \(1 \in A\), \(A \in C\) and \(1 \notin C\).
18 \(A - (B \cap C) = (A - B) \cup (A - C)\)
\[\begin{split} x \in A - (B \cap C) & \Longleftrightarrow x \in A \land x \notin B \cap C \\ & \Longleftrightarrow x \in A \land (x \notin B \lor x \notin C) \\ & \Longleftrightarrow (x \in A \land x \notin B) \lor (x \in A \land x \notin C) \\ & \Longleftrightarrow x \in A - B \lor x \in A - C \\ & \Longleftrightarrow x \in A - B \cup A - C \end{split}\]
19 Let \(\mathscr{F}\) be a class of sets. Then
\[B - \bigcup_{A \in \mathscr{F}} A = \bigcap_{A \in \mathscr{F}} (B - A) \text{ and } B - \bigcap_{A \in \mathscr{F}} A = \bigcup_{A \in \mathscr{F}} (B - A)\]
\[\begin{split} x \in B - \bigcup_{A \in \mathscr{F}} A & \Longleftrightarrow x \in B \land x \notin \bigcup_{A \in \mathscr{F}} A \\ & \Longleftrightarrow x \in B \land \forall A: A \in \mathscr{F} \land x \notin A \\ & \Longleftrightarrow (\forall A: A \in \mathscr{F} \land x \in B) \land (\forall A: A \in \mathscr{F} \land x \notin A) \\ & \Longleftrightarrow \forall A: A \in \mathscr{F} \land (x \in B \land x \notin A) \\ & \Longleftrightarrow \forall A: A \in \mathscr{F} \land x \in B - A \\ & \Longleftrightarrow x \in \bigcap_{A \in \mathscr{F}} B - A \end{split}\]
\[\begin{split} x \in B - \bigcap_{A \in \mathscr{F}} A & \Longleftrightarrow x \in B \land x \notin \bigcap_{A \in \mathscr{F}} A \\ & \Longleftrightarrow x \in B \land \exists A: A \in \mathscr{F} \land x \notin A \\ & \Longleftrightarrow (\exists A: A \in \mathscr{F} \land x \in B) \land (\exists A: A \in \mathscr{F} \land x \notin A) \\ & \Longleftrightarrow \exists A: A \in \mathscr{F} \land (x \in B \land x \notin A) \\ & \Longleftrightarrow \exists A: A \in \mathscr{F} \land x \in B - A \\ & \Longleftrightarrow x \in \bigcup_{A \in \mathscr{F}} B - A \end{split}\]
20a Prove that one of the following two formulas is always right and the other one is sometimes wrong:
\[\text{(i) } A - (B - C) = (A - B) \cup C\]
\(\text{(i)}\) is false because \(A \cap C = C\) is not always true:
\[\begin{split} x \in A - (B - C) & \Longleftrightarrow x \in A \land x \notin B - C \\ & \Longleftrightarrow x \in A \land (x \notin B \lor x \in C) \\ & \Longleftrightarrow (x \in A \land x \notin B) \lor (x \in A \land x \in C) \\ & \Longleftrightarrow x \in A - B \lor x \in A \cap C \\ & \Longleftrightarrow x \in (A - B) \cup (A \cap C) \end{split}\]
\[\text{(ii) } A - (B \cup C) = (A - B) - C\]
\(\text{(ii) }\) is true because:
\[\begin{split} x \in A - (B \cup C) & \Longleftrightarrow x \in A \land x \notin B \cup C \\ & \Longleftrightarrow x \in A \land (x \notin B \land x \notin C) \\ & \Longleftrightarrow (x \in A \land x \notin B) \land x \notin C \\ & \Longleftrightarrow x \in A - B \land x \notin C \\ & \Longleftrightarrow x \in (A - B) - C \end{split}\]
20b State an additional necessary and sufficient condition for the formula which is sometimes incorrect to be always right.
For \(\text{(i)}\) to be true we need that \(A \cap C = C\). Also because \(A \cap C = C \Longleftrightarrow C \subseteq A\) another alternative is to point out that \(C \subseteq A\) is a necessary and sufficient condition for \(\text{(i)}\) to be true.
1.3 A Set of Axioms for the Real-Number System
1.3.1 Exercises I 3.3
1 Prove Theorems I.5 through I.15, using Axioms 1 through 6 and Theorems I.1 through I.4.
Theorem I.5 \(a(b - c) = ab - ac\)
\[\begin{split} a(b - c) & = a(b + (-c)) & \text{ Theorem I.3} \\ & = ab + a(-c) & \text{ Axiom 3} \\ & = (ab + a(-c)) + 0 & \text{ Axiom 4} \\ & = (ab + a(-c)) + (ac + (-ac)) & \text{ Theorem I.2} \\ & = ab + (a(-c) + (ac + (-ac))) & \text{ Axiom 2} \\ & = ab + ((a(-c) + ac) + (-ac)) & \text{ Axiom 2} \\ & = ab + (a((-c) + c) + (-ac)) & \text{ Axiom 3} \\ & = ab + (a( c + (-c)) + (-ac)) & \text{ Axiom 1} \\ & = ab + (a0 + (-ac)) & \text{ Theorem I.2} \\ & = (ab + a0) + (-ac) & \text{ Axiom 2} \\ & = a(b + 0) + (-ac) & \text{ Axiom 3} \\ & = ab + (-ac) & \text{ Axiom 4} \\ & = ab -ac & \text{ Theorem I.3} \end{split}\]
Theorem I.6 \(0a = a0 = 0\)
First
\[0a = a0 \text{ Axiom 1}\]
Second
\[\begin{split} a0 & = a(0 + 0) & \text{ Axiom 4} \\ & = a0 + a0 & \text{ Axiom 3} \end{split}\]
Third
\[\begin{split} a0 & = a0 + 0 \text{ Axiom 4} \end{split}\]
Fourth
\[\begin{split} a0 + a0 & = a0 + 0 \Longrightarrow a0 = 0 \text{ Theorem I.1} \end{split}\]
Therefore \(0a = a0 = 0\)
Theorem I.7 CANCELLATION LAW OF MULTIPLICATION. If \(ab = ac\) and \(a \neq 0\), then \(b = c\). (In particular, this shows that the number \(1\) of Axiom 4 is unique)
First
\[\begin{split} a \neq 0 \Longrightarrow \exists y: y \in \mathbb{R} \land ay = 1 \text{ Axiom 6} \end{split}\]
Second
\[\begin{split} b & = 1b & \text{ Axiom 4} \\ & = (ay)b \\ & = (ya)b & \text{ Axiom 1} \\ & = y(ab) & \text{ Axiom 2} \\ & = y(ac) \\ & = c & \text{ Axioms 2, 1, 4} \\ \end{split}\]
Theorem I.8 POSSIBILITY OF DIVISION. Given \(a\) and \(b\) with \(a \neq 0\), there is exactly one \(x\) such that \(ax = b\). This \(x\) is denoted by \(b/a\) or \(\frac{a}{b}\) and is called the quotient of \(b\) and \(a\). In particular, \(1/a\) is also written \(a^{-1}\) and is called the reciprocal of a.
First
\[\begin{split} a \neq 0 \Longrightarrow \exists y: y \in \mathbb{R} \land ay = 1 \text{ Theorem I.3} \end{split}\]
Second
\[\begin{split} b & = 1b & \text{ Axiom 4} \\ & = (ay)b \\ & = a(yb) & \text{ Axiom 2} \\ & = ax & \text{ where } x = yb \end{split}\]
Third, if \(ax = b\) and \(az = b\) then by Theorem I.7 \(x = z\) so \(x\) is unique.
Theorem I.9 If \(a \neq 0\), then \(b/a = ba^{-1}\)
First
\[\begin{split} a \neq 0 \land 1 \in \mathbb{R} \Longrightarrow \exists! a^{-1}: a^{-1} \in \mathbb{R} \land aa^{-1} = 1 \text{ Theorem I.8} \end{split}\]
Second
\[\begin{split} a \neq 0 \land b \in \mathbb{R} \Longrightarrow \exists! b/a: b/a \in \mathbb{R} \land ab/a = b \text{ Theorem I.8} \end{split}\]
Third
\[\begin{split} b & = 1b & \text{ Axiom 4} \\ & = (aa^{-1})b \\ & = a(a^{-1}b) & \text{ Axiom 2} \\ & = a(ba^{-1}) & \text{ Axiom 1} \\ \end{split}\]
Fourth
\[\begin{split} ab/a = b \land b = a(ba^{-1}) \Longrightarrow b/a = ba^{-1} \text{ Theorem I.7} \end{split}\]
Theorem I.10 If \(a \neq 0\), then \((a^{-1})^{{-1}} = a\)
First, if \(a \neq 0\) we can use Theorem I.8
Second
\[\begin{split} 1 & = a^{-1}(a^{-1})^{{-1}} \text{ Theorem I.8} \\ \end{split}\]
Third
\[\begin{split} 1 & = aa^{-1} & \text{ Theorem I.8} \\ & = a^{-1}a & \text{ Axiom 1} \end{split}\]
Fourth
\[\begin{split} 1 = a^{-1}(a^{-1})^{{-1}} \land 1 = a^{-1}a \Longrightarrow (a^{-1})^{{-1}} = a \text{ Theorem I.7} \end{split}\]
Theorem I.11 If \(ab = 0\), then \(a = 0\) or \(b = 0\)
To prove this statement we are going to use the method of reductio ad absurdum and the equivalence between the statements \(A \Longrightarrow B\) and \(\neg(A \land (\neg B))\). Please check out (Mendelson 2008, Chapter 1, p 7, Exercises 2 and 5)
First
\[\begin{split} (ab = 0 \Longrightarrow (a = 0 \lor b = 0)) & \Longleftrightarrow \neg(ab = 0 \land \neg(a = 0 \lor b = 0)) \\ & \Longleftrightarrow \neg(ab = 0 \land (a \neq 0 \land b \neq 0)) \end{split}\]
Second, we are going to assume \((ab = 0 \land (a \neq 0 \land b \neq 0)\), find a contradiction and conclude that \(\neg(ab = 0 \land (a \neq 0 \land b \neq 0)\) is true where this means that the original statement is true: \(ab = 0 \Longrightarrow (a = 0 \lor b = 0)\)
Third
\[\begin{split} a0 = 0 \text{ Theorem I.6} \end{split}\]
Fourth
\[\begin{split} a0 = 0 \land ab = 0 \Longrightarrow b = 0 \text{ Theorem I.7} \end{split}\]
Fifth, there is a contradiction because we assume initially that \(b \neq 0\) so \(\neg(ab = 0 \land (a \neq 0 \land b \neq 0)\) is true by the method of reductio ad absurdum. Therefore the original statement is true: \(ab = 0 \Longrightarrow (a = 0 \lor b = 0)\)
Theorem I.12 \((-a)b = -(ab)\) and \((-a)(-b) = ab\)
In the case of \((-a)b = -(ab)\):
First
\[\begin{split} 0 & = (-a)b + (-(-a)b) & \text{ Theorem I.8} \\ & = (-a)b + (ab) & \text{ Theorem I.4} \\ & = (ab) + (-a)b & \text{ Axiom 1} \end{split}\]
Second
\[\begin{split} 0 & = (ab) + (-(ab)) \text{ Theorem I.8} \end{split}\]
Third
\[\begin{split} 0 = (ab) + (-a)b \land 0 = (ab) + (-(ab)) \Longrightarrow (-a)b = (-(ab)) \text{ Theorem I.1} \end{split}\]
Fourth
\[\begin{split} -(ab) & = 0 - (ab) & \text{ Theorem I.2} \\ & = 0 + (-(ab)) & \text{ Theorem I.3} \\ & = (-(ab)) + 0 & \text{ Axiom 1} \\ & = (-(ab)) & \text{ Axiom 4} \end{split}\]
Fifth
\[\begin{split} (-a)b & = (-(ab)) \\ & = -(ab) \end{split}\]
In the case of \((-a)(-b) = ab\) we use the first part in Theorem I.12:
\[\begin{split} (-a)(-b) & = -(a(-b)) \\ & = -((-b)a) & \text{ Axiom 1} \\ & = (-(-b))a \\ & = -(-b)a & \text{ Theorem I.2, Theorem I.3, Axiom 4} \\ & = ba & \text{ Theorem I.4} \\ & = ab & \text{ Axiom 1} \end{split}\]
Theorem I.13 \((a / b) + (c / d) = (ad + bc) / (bd)\) if \(b \neq 0\) and \(d \neq 0\)
First we prove that \(bd(b^{-1}d^{-1}) = 1\)
\[\begin{split} bd(b^{-1}d^{-1}) & = bb^{-1}(dd^{-1}) \text{ Axiom 2, Axiom 1} \\ & = 1\cdot1 \text{ Theorem I.8} \\ & = 1 \text{ Axiom 4} \end{split}\]
Second we prove that \((b^{-1}d^{-1}) = (bd)^{-1}\) taking into account that \(bd(bd)^{-1} = 1\) by Theorem I.8
\[\begin{split} bd(b^{-1}d^{-1}) = 1 \land bd(bd)^{-1} = 1 \Longrightarrow (b^{-1}d^{-1}) = (bd)^{-1} \text{ Theorem I.11, Theorem I.7} \end{split}\]
Third
\[\begin{split} (a / b) + (c / d) & = (ab^{-1}) + (cd^{-1}) & \text{ Theorem I.9} \\ & = 1(ab^{-1}) + 1(cd^{-1}) & \text{ Axiom 4} \\ & = dd^{-1}(ab^{-1}) + bb^{-1}(cd^{-1}) & \text{ Theorem I.8, Theorem I.9} \\ & = (b^{-1}d^{-1})ad + (b^{-1}d^{-1})bc & \text{ Axiom 2, Axiom 1} \\ & = (ad + bc)(b^{-1}d^{-1}) & \text{ Axiom 3, Axiom 1} \\ & = (ad + bc)(bd)^{-1} \\ & = (ad + bc) / (bd) & \text{ Theorem I.9} \end{split}\]
Theorem I.14 \((a / b)(c / d) = (ac) / (bd)\) if \(b \neq 0\) and \(d \neq 0\)
First, check out the proof of Theorem I.13 where we prove that \((b^{-1}d^{-1}) = (bd)^{-1}\)
Second
\[\begin{split} (a / b)(c / d) & = (ab^{-1})(cd^{-1}) & \text{ Theorem I.9} \\ & = (ac)(b^{-1}d^{-1}) & \text{ Axiom 2, Axiom 1} \\ & = (ac)(bd)^{-1} & \text{ Axiom 2, Axiom 1} \\ & = (ac) / (bd) & \text{ Theorem I.9} \end{split}\]
Theorem I.15 \((a / b) / (c / d) = (ad) / (bc)\) if \(b \neq 0\), \(c \neq 0\) and \(d \neq 0\)
First, check out the proof of Theorem I.13 where we prove that \((b^{-1}d^{-1}) = (bd)^{-1}\). Using this result we can also prove that \((b^{-1}(d^{-1})^{-1}) = (bd^{-1})^{-1}\) where \(b\) and \(d\) are any real numbers different from \(0\)
Second
\[\begin{split} (a / b) / (c / d) = (ad) / (bc) & = (ab^{-1}) / (cd^{-1}) & \text{ Theorem I.9} \\ & = (ab^{-1})(cd^{-1})^{-1} & \text{ Theorem I.9} \\ & = (ab^{-1})(c^{-1}(d^{-1})^{-1}) \\ & = (ab^{-1})(c^{-1}d) & \text{ Theorem I.10} \\ & = (ad)(b^{-1}c^{-1}) & \text{ Axiom 2, Axiom 1} \\ & = (ad)(bc)^{-1} \\ & = (ad) / (bc) & \text{ Theorem I.9} \end{split}\]
In Exercises 2 through 10, prove the given statements or establish the given questions. You may use Axioms 1 through 6 and Theorems I.1 through I.15.
2 \(-0 = 0\)
\[\begin{split} -0 \land 0 & \Longleftrightarrow 0 + (-0) = 0 \land 0 + 0 = 0 & \text{ Axiom 4, Theorem I.2} \\ & \Longleftrightarrow (-0) = 0 & \text{ Theorem I.1} \\ & \Longleftrightarrow -0 = 0 & \text{ Theorem I.3, Theorem I.2, Axiom 4} \end{split}\]
3 \(1^{-1} = 1\)
\[\begin{split} 1^{-1} \land 1 & \Longleftrightarrow 1\cdot 1^{-1} = 1 \land 1 \cdot 1 = 1 & \text{ Axiom 4, Axiom 6, Theorem I.8} \\ & \Longleftrightarrow 1^{-1} = 1 & \text{ Theorem I.7} \end{split}\]
4 Zero has no reciprocal
To prove this statement we are going to use the method of reductio ad absurdum. Please check out (Mendelson 2008, Chapter 1, p 7, Exercises 2 and 5)
First, let’s assume that \(x\) is the reciprocal of \(0\). Then by Theorem 1.8 \(0 \cdot x = 1\).
Second by Theorem 1.6 \(0 \cdot x = 0\) but we are assuming that \(0 \cdot x = 1\) so \(0 = 1\).
Third, there is a contradiction because by Axiom 4 \(0\) and \(1\) are distinct.
Fourth \(0 \cdot x = 1\) is false and \(0 \cdot x \neq 1\) is true so zero has no reciprocal.
5 \(-(a + b) = -a - b\)
\[\begin{split} -(a + b) & = -1(a + b) & \text{ Axiom 4} \\ & = -1a + (-1b) & \text{ Axiom 3} \\ & = -a + (-b) & \text{ Axiom 4} \\ & = -a - b & \text{ Theorem I.3} \\ \end{split}\]
6 \(-(a - b) = -a + b\)
\[\begin{split} -(a - b) & = -1(a - b) & \text{ Axiom 4} \\ & = -1a + (-1)(-b) & \text{ Axiom 3} \\ & = -1a + 1b & \text{ Theorem I.12} \\ & = -a + b & \text{ Axiom 4} \end{split}\]
7 \((a - b) + (b - c) = a + c\)
\[\begin{split} (a - b) + (b - c) & = (a + (-b)) + (b + (-c)) & \text{ Theorem I.3} \\ & = (a + ((-b) + b)) + (-c) & \text{ Axiom 2} \\ & = (a + 0) + (-c) & \text{ Axiom 1, Axiom 4} \\ & = a - c & \text{ Axiom 4, Theorem I.3} \\ \end{split}\]
8 If \(a \neq 0\) and \(b \neq 0\), then \((ab)^{-1} = (a^{-1}b^{-1})\)
Check out the proof of Theorem I.13 where we prove that \((b^{-1}d^{-1}) = (bd)^{-1}\)
9 \(-(a / b) = (-a / b) = a / (-b)\) if \(b \neq 0\)
First we prove that \(-1 \neq 0\). If \(-1 = 0\) then \(1 + (-1) = 0\) and \(0 + 0 = 0\) will imply that \(1 = 0\) which is not true by Axiom 4. Therefore by reductio ad absurdum (please check out (Mendelson 2008, Chapter 1, p 7, Exercises 2 and 5)) \(-1 \neq 0\) must be true.
Second we prove that \(-b^{-1} = (-b)^{-1}\). Because \((-b)(-b)^1 = 1\) by Theorem I.8, \((-b)(-b^{-1}) = bb^{-1} = 1\) by Theorem I.12, Theorem I.8 and \(-b = -1b \neq 0\) by Theorem I.11 we can conclude that \(-b^{-1} = (-b)^{-1}\) using Theorem I.7.
\[\begin{split} -(a / b) & = -(ab^{-1}) & \text{ Theorem I.9} \\ & = (-ab^{-1}) & \text{ Theorem I.3, Axiom 4} \\ & = (-a / b) & \text{ Theorem I.9} \\ & = (-ab^{-1}) & \text{ Theorem I.9} \\ & = (-b^{-1}a) & \text{ Axiom 1} \\ & = -(b^{-1}a) & \text{ Theorem I.3, Axiom 4} \\ & = (-b^{-1})a & \text{ Theorem I.12} \\ & = (-b)^{-1}a \\ & = a(-b)^{-1} & \text{ Axiom 1} \\ & = a / (-b) & \text{ Theorem I.9} \end{split}\]
10 \((a / b) - (c / d) = (ad - bc) / (bd)\) if \(b \neq 0\) and \(d \neq 0\)
In this part remember exercise 8
\[\begin{split} (a / b) - (c / d) & = (ab^{-1}) - (cd^{-1}) & \text{ Theorem I.9} \\ & = 1(ab^{-1}) - 1(cd^{-1}) & \text{ Axiom 4} \\ & = dd^{-1}(ab^{-1}) - bb^{-1}(cd^{-1}) & \text{ Theorem I.8, Theorem I.9} \\ & = (b^{-1}d^{-1})ad - (b^{-1}d^{-1})bc & \text{ Axiom 2, Axiom 1} \\ & = (ad - bc)(b^{-1}d^{-1}) & \text{ Axiom 3, Theorem I.5, Axiom 1} \\ & = (ad - bc)(bd)^{-1} \\ & = (ad - bc) / (bd) & \text{ Theorem I.9} \end{split}\]
1.3.2 Exercises I 3.5
1 Prove Theorems I.22 through I.25, using the earlier theorems and Axioms 1 through 9
Theorem I.22 If \(a < b\) and \(c < 0\), then \(ac > bc\)
\[\begin{split} 0 > c \land b > a & \Longrightarrow 0 - c \in \mathbb{R}^+ \land b - a \in \mathbb{R}^+ & \text{ By definition} \\ & \Longrightarrow -c \in \mathbb{R}^+ \land b - a \in \mathbb{R}^+ & \text{ Theorem I.2} \\ & \Longrightarrow -c(b - a) \in \mathbb{R}^+ & \text{ Axiom 7} \\ & \Longrightarrow -c(b + (-a)) \in \mathbb{R}^+ & \text{ Theorem I.3} \\ & \Longrightarrow -cb + -c(-a) \in \mathbb{R}^+ & \text{ Axiom 3} \\ & \Longrightarrow -cb + ca \in \mathbb{R}^+ & \text{ Theorem I.5} \\ & \Longrightarrow ca + (-cb) \in \mathbb{R}^+ & \text{ Axiom 1} \\ & \Longrightarrow ca - cb \in \mathbb{R}^+ & \text{ Theorem I.3} \\ & \Longrightarrow ca > cb & \text{ By definition} \end{split}\]
Theorem I.23 If \(a < b\), then \(-a > -b\). In particular, if \(a < 0\), then \(-a > 0\).
\[\begin{split} b > a & \Longrightarrow & b - a \in \mathbb{R}^+ & \text{ By definition} \\ & \Longrightarrow & b + (- a) \in \mathbb{R}^+ & \text{ Theorem I.3} \\ & \Longrightarrow & (- a) + -(-b) \in \mathbb{R}^+ & \text{ Axiom 1, Theorem I.4} \\ & \Longrightarrow & (- a) + (-(-b)) \in \mathbb{R}^+ & \text{ Theorem I.3, Theorem I.2, Axiom 4} \\ & \Longrightarrow & (- a) - (-b) \in \mathbb{R}^+ & \text{ Theorem I.3} \\ & \Longrightarrow & (- a) > (-b) & \text{ By definition} \\ & \Longrightarrow & -a > -b & \text{ Theorem I.3, Theorem I.2, Axiom 4} \end{split}\]
\[\begin{split} a < 0 & \Longrightarrow -a > -0 & \text{ Theorem I.23} \\ & \Longrightarrow -a > 0 & \text{ Exercises I 3.3 2} \end{split}\]
Theorem I.24 If \(ab > 0\), then both \(a\) and \(b\) are positive or both are negative
To prove this statement we are going to use the method of reductio ad absurdum. Please check out (Mendelson 2008, Chapter 1, p 7, Exercises 2 and 5)
First, we assume that \(\neg((a > 0 \land b > 0) \lor (a < 0 \land b < 0))\) is true and find a contradiction by inspecting each case.
Second, if \(a = 0\) or \(b = 0\) then \(ab = 0\) by Theorem I.6. But we would have that \(ab > 0\) and \(ab = 0\) which is a contradiction by Theorem I.16
Third, if \(a < 0\) and \(b > 0\) then \(ab < a0 = 0\) by Theorem I.19 and Theorem I.6. But we would have that \(ab < 0\) and \(ab = 0\) which is a contradiction by Theorem I.16
Fourth, if \(b < 0\) and \(a > 0\) then \(ab = ba < b0 = 0\) by Theorem I.19, Theorem I.6 and Axiom 1. But we would have that \(ab < 0\) and \(ab = 0\) which is a contradiction by Theorem I.16
Fifth, we conclude that the original statement is true: \((a > 0 \land b > 0) \lor (a < 0 \land b < 0)\).
Theorem I.25 If \(a < c\) and \(b < d\) then \(a + b < c + d\)
\[\begin{split} c > a \land d > b & \Longrightarrow c - a \in \mathbb{R}^+ \land d - b \in \mathbb{R}^+ & \text{ By definition} \\ & \Longrightarrow (c - a) + (d - b) \in \mathbb{R}^+ & \text{ Axiom 7} \\ & \Longrightarrow (c + (-a)) + (d + (-b)) \in \mathbb{R}^+ & \text{ Theorem I.3} \\ & \Longrightarrow (c + ((-a) + d)) + (-b) \in \mathbb{R}^+ & \text{ Axiom 2} \\ & \Longrightarrow (c + (d + (-a))) + (-b) \in \mathbb{R}^+ & \text{ Axiom 1} \\ & \Longrightarrow (c + d) + ((-a) + (-b)) \in \mathbb{R}^+ & \text{ Axiom 2} \\ & \Longrightarrow (c + d) + (-a + (-b)) \in \mathbb{R}^+ & \text{ Theorem I.3, Theorem I.2, Axiom 4} \\ & \Longrightarrow (c + d) + (-a - b) \in \mathbb{R}^+ & \text{ Theorem I.3} \\ & \Longrightarrow (c + d) + (-(a + b)) \in \mathbb{R}^+ & \text{ Exercises I 3.3 5} \\ & \Longrightarrow (c + d) - (a + b) \in \mathbb{R}^+ & \text{ Theorem I.3} \\ & \Longrightarrow c + d > a + b & \text{ By definition} \end{split}\]
2 There is no real number \(x\) such that \(x^2 + 1 = 0\)
To prove this statement we are going to use the method of reductio ad absurdum. Please check out (Mendelson 2008, Chapter 1, p 7, Exercises 2 and 5)
First, we assume that \(x^2 + 1 = 0\) is true and find a contradiction
Second, if \(x = 0\) then \(x^2 = 0\) by Theorem I.6. But we would have that \(0 + 1 = 1 = 0\) by Axiom 4 and Axiom 1. But \(1 > 0\) by Theorem I.21 where this is a contradiction by Theorem I.16
Third, if \(x \neq 0\) then \(x^2 + 1 = 1 + x^2 = 0\) and therefore \(x^2 = -1\) by Axiom 1 and Theorem I.2
Fourth, \(-1 < 0\) by Theorem I.21, Theorem I.23 and Exercises I 3.3 2 so \(-1 = x^2 < 0\). But \(x^2 > 0\) by Theorem I.20 where this is a contradiction by Theorem I.16
Fifth, we conclude that \(x^2 + 1 = 0\) is false so \(x^2 + 1 \neq 0\) must be true.
3 The sum of two negative numbers is negative
\[\begin{split} a < 0 \land b < 0 & \Longrightarrow -a > 0 \land -b > 0 & \text{ Theorem I.23} \\ & \Longrightarrow -a \in \mathbb{R} \land -b \in \mathbb{R} & \text{ By definition} \\ & \Longrightarrow -a + (-b) \in \mathbb{R} & \text{ Axiom 7} \\ & \Longrightarrow -a - b \in \mathbb{R} & \text{ Theorem I.3} \\ & \Longrightarrow -(a + b) \in \mathbb{R} & \text{ Exercises I 3.3 5} \\ & \Longrightarrow -(a + b) > 0 & \text{ By definition} \\ & \Longrightarrow -(-(a + b)) < 0 & \text{ Theorem I.23, Exercises I 3.3 2} \\ & \Longrightarrow a + b < 0 & \text{ Theorem I.4} \\ \end{split}\]
4 If \(a > 0\), then \(1/a > 0\); if \(a < 0\), then \(1/a < 0\)
\[\begin{split} a > 0 & \Longrightarrow a > 0 \land aa^{-1} = 1 \land 1 > 0 & \text{ Theorem I.8, Theorem I.21} \\ & \Longrightarrow a^{-1} > 0 & \text{ Theorem I.24} \\ & \Longrightarrow 1/a > 0 & \text{ By definition} \end{split}\]
\[\begin{split} a < 0 & \Longrightarrow a < 0 \land aa^{-1} = 1 \land 1 > 0 & \text{ Theorem I.8, Theorem I.21} \\ & \Longrightarrow a^{-1} < 0 & \text{ Theorem I.24} \\ & \Longrightarrow 1/a < 0 & \text{ By definition} \end{split}\]
5 If \(0 < a < b\), then \(0 < b^{-1} < a^{-1}\)
\[\begin{split} 0 < a < b & \Longrightarrow 0 < b \land aa^{-1} < ba^{-1} & \text{ Theorem I.17, Theorem I.19} \\ & \Longrightarrow 0 < b \land 1 < a^{-1}b & \text{ Theorem I.8, Axiom 1} \\ & \Longrightarrow 0 < b \land 1b^{-1} < (a^{-1}b)b^{-1} & \text{ Theorem I.19} \\ & \Longrightarrow 0 < b \land b^{-1} < a^{-1}1 & \text{ Axiom 2, Theorem I.8} \\ & \Longrightarrow 0 < b \land b^{-1} < a^{-1} & \text{ Axiom 2, Axiom 4} \\ & \Longrightarrow 0 < b^{-1} < a^{-1} & \text{ Exercises I 3.5 4} \\ \end{split}\]
6 If \(a \leq b\) and \(b \leq c\), then \(a \leq c\)
\[\begin{split} a \leq b \land b \leq c & \Longrightarrow (a < b \lor a = b) \land (b < c \lor b = c) & \text{ By definition} \\ & \Longrightarrow (a < b \land b < c) \lor (a < c) \lor (a = c) \\ & \Longrightarrow (a < c) \lor (a = c) & \text{ Theorem I.17} \\ & \Longrightarrow a \leq c & \text{ By definition} \\ \end{split}\]
7 If \(a \leq b\) and \(b \leq c\), and \(a = c\), then \(b = c\)
\[\begin{split} a \leq b \land b \leq c \land a = c & \Longrightarrow c \leq b \land b \leq c \\ & \Longrightarrow (c < b \land b < c) \lor (b < b) \lor (c = b) \\ & \Longrightarrow c = b & \text{ Theorem I.16} \end{split}\]
8 For all real \(a\) and \(b\) we have \(a^2 + b^2 \geq 0\). If \(a\) and \(b\) not both \(0\), then \(a^2 + b^2 > 0\)
\[\begin{split} a \in \mathbb{R} \land b \in \mathbb{R} & \Longrightarrow a^2 \geq 0 \land b^2 \geq 0 & \text{ Theorem I.20, Theorem I.6} \\ & \Longrightarrow \left[ \begin{split} (a^2 > 0 \land b^2 > 0) & \lor \\ (a^2 = 0 \land b^2 > 0) & \lor \\ (a^2 > 0 \land b^2 = 0) & \lor \\ (a^2 = 0 \land b^2 = 0) \end{split} \right] \\ & \Longrightarrow \left[ \begin{split} (a^2 + b^2 > 0 + 0) & \lor \\ (0 + b^2 > 0 + 0) & \lor \\ (a^2 + 0 > 0 + 0) & \lor \\ (a^2 + b^2 = 0 + 0) \end{split} \right] & \text{ Theorem I.25, Theorem I.18} \\ & \Longrightarrow \left[ \begin{split} (a^2 + b^2 > 0) & \lor \\ (0 + b^2 > 0) & \lor \\ (a^2 + 0 > 0) & \lor \\ (a^2 + b^2 = 0) \end{split} \right] & \text{ Axiom 4, Theorem I.18} \\ & \Longrightarrow \left[ \begin{split} (a^2 + b^2 > 0) & \lor \\ (a^2 + b^2 = 0) \end{split} \right] \\ & \Longrightarrow a^2 + b^2 \geq 0 & \text{ By definition} \end{split}\]
9 There is no real number \(a\) such that \(x \leq a\) for all real \(x\)
To prove this statement we are going to use the method of reductio ad absurdum. Please check out (Mendelson 2008, Chapter 1, p 7, Exercises 2 and 5)
First, let’s assume that there is a real number \(a\) such that \(x \leq a\) for all real \(x\) and find a contradiction.
Second, \(1 > 0\) by Theorem 1.21 therefore:
\[\begin{split} 1 > 0 & \Longrightarrow & 1 + 0 > 0 & \text{ Theorem I.4} \\ & \Longrightarrow & 1 + (a + (-a)) > 0 & \text{ Theorem I.2} \\ & \Longrightarrow & (1 + a) + (-a) > 0 & \text{ Axiom 2} \\ & \Longrightarrow & (1 + a) - a > 0 & \text{ Theorem I.2} \\ & \Longrightarrow & (1 + a) - a \in \mathbb{R}^+ & \text{ By definition} \\ & \Longrightarrow & 1 + a > a & \text{ By definition} \\ \end{split}\]
Third, there is a contradiction because it exists a real number \(1 + a\) such that \(1 + a > a\). Therefore the original statement is true: \(\neg (\exists a: a \in \mathbb{R} \land (\forall x:x \in \mathbb{R} \Longrightarrow x \leq a))\)
10 If \(x\) has the property that \(0 \leq x < h\) for every positive real number \(h\), then \(x = 0\)
To prove this statement we are going to use the method of reductio ad absurdum. Please check out (Mendelson 2008, Chapter 1, p 7, Exercises 2 and 5)
First, let’s assume that \(x > 0\) then \(x \in \mathbb{R}^+\). Therefore it must be the case that \(0 \leq x < x\) because \(x\) is a positive number. But \(x = x\) so there is a contradiction by Theorem I.16. We can conclude that \(x > 0\) is false and \(x \leq 0\) must be true.
Second, apart from \(x \leq 0\) we also have that \(x \geq 0\). Therefore because \((x < 0 \lor x = 0) \land (x > 0 \lor x = 0)\) by Theorem I.16 it must be the case that \(x = 0\).
1.3.3 Exercises I 3.12
1 If \(x\) and \(y\) are arbitrary real numbers with \(x < y\), prove that there is at least one real \(z\) satisfying \(x < z < y\)
Let choose an arbitary \(w \in \mathbb{R}^+\) and use \(\mathbb{Z}^+\) to denote the set of positive integers:
\[\begin{split} w \in \mathbb{R}^+ \land y - x \in \mathbb{R}^+ & \Longrightarrow n(y - x) > w \land n \in \mathbb{Z}^+ \text{ Theorem I.30} \\ & \Longrightarrow n(y - x) > w \land n^{-1} \in \mathbb{R}^+ \text{ Exercises I 3.5 4, Theorem I.8} \\ & \Longrightarrow 1(y - x) > wn^{-1} \text{ Theorem I.19, Axiom 1, Theorem I.18} \\ & \Longrightarrow y - x > w/n \text{ Axiom 4, Theorem I.9} \\ & \Longrightarrow y > w/n + x \text{ Theorem I.18, Axiom 4, Axiom 5} \\ & \Longrightarrow y > w/n + x \land wn^{-1} \in \mathbb{R}^+ \text{ Axiom 7} \\ & \Longrightarrow y > w/n + x > x \text{ Theorem 1.18, Axiom 4, Theorem 1.9} \\ & \Longrightarrow z = w/n + x \end{split}\]
Some examples of \(z\) are \(|y - x| / n + x\) for \(n = 2, 3, \ldots\) where \(|y - x|\) is the absolute value of \(y - x\)
2 If \(x\) is an arbitrary real number, prove that there are integers \(m\) and \(n\) such that \(m < x < n\)
First, by Theorem I.29 \(n > x\) were \(n\) is a positive integer and therefore an integer.
Second, let’s use \(\mathbb{Z}^-\) to denote the set of negative integers, and prove analogous results similar to Theorem I.28 and Theorem I.29 for \(\mathbb{Z}^-\).
Third, we prove the set \(\mathbb{Z}^-\) of negative integers \(-1, -2, -3, \ldots\) is unbounded below using the method of reductio ad absurdum. Please check out (Mendelson 2008, Chapter 1, p 7, Exercises 2 and 5). Assume to the contrary that \(\mathbb{Z}^-\) is bounded below so by Theorem I.27 \(\mathbb{Z}^-\) has a greatest lower bound. Therefore exists \(c \in \mathbb{R}\) such that \(c \leq x\) for all \(x \in \mathbb{Z}^-\). Then \(c + 1\) can not be a lower bound for \(\mathbb{Z}^-\) because \(c < c + 1\) so there is some \(m \in \mathbb{Z}^-\) such that \(m < c + 1\). So it must be the case that \(-(-m + 1) < c\) where \(-(-m + 1) \in \mathbb{Z}^-\) but this is a contradiction because \(c\) is the greatest lower bound of \(\mathbb{Z}^-\). Therefore we must conclude that \(\mathbb{Z}^-\) is unbounded below.
Fourth, we prove that for every real \(x\) there exists a negative integer \(m\) such that \(x > m\). We prove this statement using the method of reductio ad absurdum. Please check out (Mendelson 2008, Chapter 1, p 7, Exercises 2 and 5). If this is not the case \(x\) would be a lower bound for \(\mathbb{Z}^-\) but this is not true. So we must conclude that for every real \(x\) there exists a negative integer \(m\) such that \(x > m\).
Fifth, we have that if \(x\) is an arbitrary real number there are integers \(m\) and \(n\) such that \(n > x > m\) where in this case \(n\) is a positive integer and \(m\) is a negative integer.
3 If \(x > 0\), prove that there is a positive integer \(n\) such that \(1 / n < x\)
\[\begin{split} x > 0 & \Longrightarrow nx > 1 & \text{ Theorem I.30} \\ & \Longrightarrow x > n^{-1}1 & \text{ Theorem I.19, Axiom 1, Theorem I.8, Axiom 4} \\ & \Longrightarrow x > 1 / n & \text{ Axiom 1, Theorem I.9} \end{split}\]
4 If \(x\) is an arbitrary real number, prove that there is exactly one integer \(n\) which satisfies the inequalities \(n \leq x < n + 1\). This \(n\) is called the greatest integer in \(x\) and is denoted by \([x]\). For example \([5] = 5\), \(\left[ \frac{5}{2} \right] = 2\), \(\left[ -\frac{8}{3} \right] = -3\)
First, we prove that if \(S \subseteq \mathbb{Z}\), \(S \neq \emptyset\) and \(S\) is bounded above then \(sup \; S\) exists and \(sup \; S = max \; S\). We have that \(sup \; S\) exists by Axiom 10. Now, we prove that \(sup \; S = max \; S\) using the method of reductio ad absurdum. Please check out (Mendelson 2008, Chapter 1, p 7, Exercises 2 and 5). Let’s assume that \(sup \; S \notin S\) then for all \(s \in S\) we have that \(sup \; S > s\). Because \(sup \; S > Sup \; S - 1\) then \(sup \; S - 1\) is not an upper bound so there exists some \(s^* \in S\) such that \(s^* > sup \; S - 1\). Also because \(s^*\) is not an upper bound there exists some \(s^{**} \in S\) such that \(s^{**} > s^*\). Therefore we have that \(sup \; S > s^{**} > s^* > sup \; S - 1\) so we have that \(1 = sup \; S - (sup \; S - 1) > s^{**} - (sup \; S - 1) > s^{**} - s^*\) where this means that \(1 > s^{**} - s^* > 0\). But this is a contradiction because if \(s^{**} \in S\) and \(s^* \in S\) then \(s^{**} \in \mathbb{Z}\) and \(s^* \in \mathbb{Z}\) so if \(s^{**} > s^*\) it must be that \(s^{**} - s^* \geq 1\). In that case \(sup \; S \in S\) so \(sup \; S = max \; S\).
Second, let \(S = \{y: y \leq x \land y \in \mathbb{Z} \text{ where } x \in \mathbb{R} \}\). We have that \(S \subseteq \mathbb{Z}\), \(S\) is bounded above by \(x\) and also by Exercises I 3.12 2 \(S \neq \emptyset\). Therefore by the first part \(sup \; S\) exists and \(sup \; S = max \; S\). Because \(sup \; S \in S\) then \(sup \; S \leq x\) and \(sup \; S \in \mathbb{Z}\). Also \(sup \; S = max \; S\), \(sup \; S < sup \; S + 1\) and \(sup \; S + 1 \in \mathbb{Z}\) then \(sup \; S + 1 \notin S\) so \(x < sup \; S + 1\). Finally, we have that \(sup \; S < x < sup \; S + 1\), \(sup \; S \in \mathbb{Z}\) and \(sup \; S\) is unique by Theorem I.26.
Observation 1: Also we have that:
\[\begin{split} n \leq x < n + 1 & \Longrightarrow \left[ x \right] \leq x \land x < \left[ x \right] + 1 & \text{ By definition} \\ & \Longrightarrow \left[ x \right] + 1 \leq x + 1 \land x < \left[ x \right] + 1 & \text{ Theorem I.18} \\ & \Longrightarrow x < \left[ x \right] + 1 \leq x + 1 & \text{ Theorem I.17} \\ \end{split}\]
Observation 2: A better notation would be \(n = \lfloor x \rfloor\) for \(n \leq x < n + 1\) to differentiate it from \(m = \lceil x \rceil\) for \(m - 1 < x \leq m\). For example \(\lfloor 2.5 \rfloor = 2\), \(\lceil 2.5 \rceil = 3\) and \(\lfloor 2 \rfloor = 2 = \lceil 2 \rceil\)
5 If \(x\) is an arbitrary real number, prove that there is exactly one integer \(n\) which satisfies \(x \leq n < x + 1\).
First, we prove that if \(S \subseteq \mathbb{Z}\), \(S \neq \emptyset\) and \(S\) is bounded below then \(inf \; S\) exists and \(inf \; S = min \; S\). We have that \(inf \; S\) exists by Theorem I.27. Now let \(-S = \{-y: y \in S \}\) then \(-S \subseteq \mathbb{Z}\), \(-S \neq \emptyset\) and \(-S\) is bounded above. By the first part in the proof of Exercises I 3.12 4 \(-S\) we have that \(sup -S = max -S\) so \(-(-sup -S) = -(-max -S)\) by Theorem I.4. Because \(-(-sup -S) \in -S\) then \(-sup -S \in S\) and also we have that \(-sup -S = inf \; S\). Therefore \(inf \; S = min \; S\).
Second, let \(S = \{y: x \leq y \land y \in \mathbb{Z} \text{ where } x \in \mathbb{R} \}\). We have that \(S \subseteq \mathbb{Z}\), \(S\) is bounded below by \(x\) and also by Exercises I 3.12 2 \(S \neq \emptyset\). Therefore by the first part \(inf \; S\) exists and \(inf \; S = min \; S\). Because \(inf \; S \in S\) then \(x \leq inf \; S\) and \(inf \; S \in \mathbb{Z}\).
Third, if \(inf^* \; S\) is another greater lower bound then \(inf \; S \geq inf^* \; S\). But \(inf \; S\) is also a greater bound so \(inf^* \; S \geq inf \; S\). Therefore \(inf \; S = inf^* \; S\) where this means that \(inf \; S\) is unique.
Fourth, if \(inf \; S = x\) then by Exercises I 3.12 4 \(inf \; S = x < inf \; S + 1 = x + 1\). Also if \(x < inf \; S = (inf \; S - 1) + 1\) by Exercises I 3.12 4 \(inf \; S - 1 < x\) so \(inf \; S < x + 1\).
Fifth, we have that \(x \leq inf \; S < x + 1\), \(inf \; S \in \mathbb{Z}\) and \(sup \; S\) is unique.
Observation: We can denote this \(inf \; S = n\) as \(n = \lceil x \rceil\) for \(x \leq \lceil x \rceil < x + 1\). For example \(\lceil 2.5 \rceil = 3\) and \(\lceil 2 \rceil = 2\)
6 If \(x\) and \(y\) are arbitrary real numbers, \(x < y\), prove that there exists at least one rational number \(r\) satisfying \(x < r < y\), and hence infinitely many. This property is often described by saying that the rational numbers are dense in the real-number system.
First, we have that:
\[\begin{split} y > x & \Longrightarrow y - x > 0 \text{ By definition} \\ & \Longrightarrow (y - x)^{-1} \text{ Theorem I.8} \\ & \Longrightarrow (y - x)^{-1} + 1 \geq \left[ (y - x)^{-1} \right] + 1 > (y - x)^{-1} \text{ Exercises I 3.12 4 Observation 1} \\ & \Longrightarrow (y - x)(\left[ (y - x)^{-1} \right] + 1) > 1 \text{ Theorem I.19, Theorem I.8} \\ & \Longrightarrow (y - x)n > 1 \text{ where } n = \left[ (y - x)^{-1} \right] + 1 \land n \in \mathbb{Z}^+ \\ \end{split}\]
Second, we have that:
\[\begin{split} y > x & \Longrightarrow y - x > 0 & \text{ By definition} \\ & \Longrightarrow n(y - x) > 1 \text{ where } n \geq \left[ (y - x)^{-1} \right] + 1 & \text{ Theorem I.30} \\ & \Longrightarrow ny > 1 + nx \\ & \Longrightarrow ny > 1 + nx \geq 1 + \left[ nx \right] > nx & \text{ Exercises I 3.12 4 Observation 1} \\ & \Longrightarrow ny > 1 + \left[ nx \right] > nx \\ & \Longrightarrow y > \frac{1 + \left[ nx \right]}{n} > x \\ & \Longrightarrow y > r > x \end{split}\]
Observation 1: For example, \(2\pi > \pi\) and \(2\pi - \pi > 1 > 0\). Therefore we can fix \(n = \left[ \pi^{-1} \right] + 1 = 1\) where \(1*(2\pi - \pi) > 1\) and \(r = \frac{1 + [1\pi]}{1} = \frac{1 + 3}{1} = \frac{4}{1}\).
Observation 2: For example, \(\pi > e\) and \(1 \geq \pi - e > 0\). Therefore we can fix \(n = \left[ (\pi - e)^{-1} \right] + 1 = 2 + 1 = 3\) where \(3*(\pi - e) > 1\) and \(r = \frac{1 + [3e]}{3} = \frac{1 + 8}{3} = \frac{3}{1}\).
Third, we have that \(y > r > x\) so we can choose \(n = \left[ (y - x)^{-1} \right] + 1, \left[ (y - x)^{-1} \right] + 2, \ldots\) to fix \(r\). Therefore there are countable infinite \(r\)’s between \(y\) and \(x\) that we can build in this way.
7 If \(x\) is rational, \(x \neq 0\) and \(y\) irrational, prove that \(x + y\), \(x - y\), \(xy\), \(x/y\) and \(y/x\) are all irrational.
To prove these statements we are going to use the method of reductio ad absurdum. Please check out (Mendelson 2008, Chapter 1, p 7, Exercises 2 and 5)
First, assume that \(x + y\) is rational:
\[\begin{split} x + y = \frac{a}{b} & \Longrightarrow \frac{c}{d} + y = \frac{a}{b} & \text{ By definition} \\ & \Longrightarrow y = \frac{a}{b} - \frac{c}{d} \\ & \Longrightarrow y = \frac{ad - bc}{bd} & \text{ Exercises I 3.3 10} \\ & \Longrightarrow y \in \mathbb{Q} & \text{ This is a contradiction} \end{split}\]
Therefore \(x + y \notin \mathbb{Q}\) but \(x + y \notin \mathbb{R}\) so \(x + y\) is irrational.
Second, for \(x - y\) we prove that if \(y\) is irrational then \(-y\) is irrational. Assume that \(y\) is irrational and \(-y\) rational so \(- y = \frac{a}{b}\) for \(a \in \mathbb{Z}\), \(b \in \mathbb{Z}\) and \(b \neq 0\) but \(y = -\frac{a}{b}\) would be rational where this is a contradiction. Therefore if \(y\) is irrational then \(-y\) is irrational is a true statement. Now we can apply the first part to \(x + (-y)\) and we have that \(x + (-y)\) is irrational.
Third, assume that \(xy\) is rational:
\[\begin{split} xy = \frac{a}{b} & \Longrightarrow \frac{c}{d}y = \frac{a}{b} & \text{ By definition} \\ & \Longrightarrow y = \frac{d}{c}\frac{a}{b} & \text{ Theorem I.9, Axiom 2, Theorem 1.8, Axiom 4} \\ & \Longrightarrow y = \frac{da}{cb} & \text{ Theorem I.14} \\ & \Longrightarrow y \in \mathbb{Q} & \text{ This is a contradiction} \end{split}\]
Therefore \(xy \notin \mathbb{Q}\) but \(xy \notin \mathbb{R}\) so \(xy\) is irrational.
Fourth, for \(x / y = xy^{-1}\) we prove that if \(y\) is irrational then \(y^{-1}\) is irrational. Assume that \(y\) is irrational and \(y^{-1}\) rational so \(y^{-1} = \frac{a}{b}\) for \(a \in \mathbb{Z}\), \(b \in \mathbb{Z}\) and \(b \neq 0\) but \(y = (y^{-1})^{-1} = (a / b)^{-1} = \frac{1}{a / b} = \frac{1 \cdot 1^{-1}}{a / b} = \frac{1 / 1}{a / b} = \frac{b}{a}\) would be rational where this is a contradiction. Therefore if \(y\) is irrational then \(y^{-1}\) is irrational is a true statement. Now we can apply the first part to \(x / y = xy^{-1}\) and we have that \(x / y\) is irrational.
Fifth, for \(y / x = yx^{-1} = x^{-1}y\) we prove that if \(x\) is rational then \(x^{-1}\) is rational. If \(x\) is rational then \(x^{-1} = \left( \frac{a}{b} \right)^{-1} = \frac{1}{a / b} = \frac{1 \cdot 1^{-1}}{a / b} = \frac{1 / 1}{a / b} = \frac{b}{a}\) so \(x^{-1}\) is rational. Now we can apply the third part to \(y / x = yx^{-1} = x^{-1}y\) and we have that \(y / x\) is irrational.
8 Is the sum or product of two irrational numbers always irrational?
The answer is no. If \(x\) is rational, \(x \neq 0\) and \(y\) is irrational then \(x + y\), \(-y\) and \(y^{-1}\) are irrationals by Exercises I 3.12 7. However \((x + y) + (-y) = x\) and \((xy)y^{-1} = x\) are rationals.
9 If \(x\) and \(y\) are arbitrary real numbers, \(x < y\), prove that there exists at least one irrational number \(z\) satisfying \(x < z < y\), and hence infinitely many.
First, let \(w > 0\) and \(w \in \mathbb{R} - \mathbb{Q}\). The condition \(w > 0\) is not restrictive because if \(w < 0\) and \(w \in \mathbb{R} - \mathbb{Q}\) then \(-w > 0\) and \(-w \in \mathbb{R} - \mathbb{Q}\). What we need is at least one \(w \in \mathbb{R} - \mathbb{Q}\).
Second, if \(y > x\), \(w > 0\) and \(w \in \mathbb{R} - \mathbb{Q}\)
\[\begin{split} y > x & \Longrightarrow y > r_1 > x \text{ where } r_1 \in \mathbb{Q} & \text{ Exercises I 3.12 6} \\ & \Longrightarrow y > r_1 > r_2 > x & \text{ Exercises I 3.12 6} \\ & \Longrightarrow n(r_1 - r_2) > w & \text{ Theorem I.30} \\ & \Longrightarrow r_1 - r_2 > \frac{w}{n} \text{ where } \frac{w}{n} \in \mathbb{R} - \mathbb{Q} & \text{ Exercises I 3.12 7} \\ & \Longrightarrow r_1 > \frac{w}{n} + r_2 \text{ where } \frac{w}{n} + r_2 \in \mathbb{R} - \mathbb{Q} & \text{ Exercises I 3.12 7} \\ & \Longrightarrow r_1 > \frac{w}{n} + r_2 > r_2 \\ & \Longrightarrow y > r_1 > \frac{w}{n} + r_2 > r_2 > x \\ & \Longrightarrow y > \frac{w}{n} + r_2 > x \end{split}\]
Third, we have that \(w(r_1 - r_2)^{-1} + 1 \geq \left[ w(r_1 - r_2)^{-1} \right] + 1 > w(r_1 - r_2)^{-1}\) by Exercises I 3.12 4 Observation 1. Therefore \((\left[ w(r_1 - r_2)^{-1} \right] + 1)(r_1 - r_2) > w\) by Theorem I.19, Exercises I 3.5 4 Observation 1, Theorem I.8 and Axiom 4. Also by Exercises I 3.5 4 and because \(\left[ w(r_1 - r_2)^{-1} \right] \geq 0 \land 1 > 0\) we have that \(\left[ w(r_1 - r_2)^{-1} \right] + 1) \in \mathbb{Z^+}\). In that sense we can fix \(n = \left[ w(r_1 - r_2)^{-1} \right] + 1), \left[ w(r_1 - r_2)^{-1} \right] + 2), \ldots\)
Fourth, we have that \(y > \frac{w}{n} + r_2 > x\) where \(n \geq \left[ w(r_1 - r_2)^{-1} \right] + 1\), \(n \in \mathbb{Z}^+\), \(y > r_1 > r_2 > x\), \(r_1 \in \mathbb{Q}\), \(r_2 \in \mathbb{Q}\), \(w \in \mathbb{R} - \mathbb{Q}\) and \(\frac{w}{n} + r_2 \in \mathbb{R} - \mathbb{Q}\)
Observation 1: In Exercises I 3.12 11 we are going to prove that \(\sqrt{2} \in \mathbb{R} - \mathbb{Q}\) and also we have that \(\sqrt{2} > 0\) because \(\sqrt{2}\) is the positive root of \(2\). Therefore we can fix \(w = \sqrt{2}\)
Observation 2: For example, \(\pi > e\) and \(1 \geq \pi - e > 0\). Therefore we can fix \(r_2 = \frac{1 + [(\left[ (\pi - e)^{-1} \right] + 1)e]}{\left[ (\pi - e)^{-1} \right] + 1} = \frac{1 + [3e]}{3} = \frac{1 + 8}{3} = 3\) and \(r_2 = \frac{1 + [(\left[ (\pi - e)^{-1} \right] + 2)e]}{\left[ (\pi - e)^{-1} \right] + 2} = \frac{1 + [4e]}{4} = \frac{1 + 10}{4} = \frac{11}{4}\). Furthermore we can fix \(\frac{w}{n} + r_2 = \frac{w}{\left[ w(r_1 - r_2)^{-1} \right] + 1} + r_2 = \frac{\sqrt{2}}{\left[ \sqrt{2}(3 - \frac{11}{4})^{-1} \right] + 1} + \frac{11}{4} = \frac{\sqrt{2}}{5 + 1} + \frac{11}{4} = \frac{2\sqrt{2} + 33}{12}\). So \(\pi > \frac{2\sqrt{2} + 33}{12} > e\) where \(\frac{2\sqrt{2} + 33}{12} \in \mathbb{R} - \mathbb{Q}\)
10 An integer \(n\) is called even if \(n = 2m\) for some integer \(m\), and odd if \(n + 1\) is even. Proof the following statements.
10a An integer cannot be both even and odd
To prove this statement we are going to use the method of reductio ad absurdum. Please check out (Mendelson 2008, Chapter 1, p 7, Exercises 2 and 5)
First, if \(m \in \mathbb{Z}\) and \(s \in \mathbb{Z}\) then \(m - s \in \mathbb{Z}\)
Second, assume that for some \(n \in \mathbb{Z}\) we have that \(n\) is even and odd:
\[\begin{split} n = 2m \land n + 1 = 2s & \Longrightarrow n = 2m \land n = 2s - 1 \\ & \Longrightarrow 2m = 2s - 1 \\ & \Longrightarrow 2(m - s) = - 1 \\ & \Longrightarrow m - s = -\frac{1}{2} \\ & \Longrightarrow m - s \notin \mathbb{Z} & \text{ This is a contradiction} \end{split}\]
Therefore, there is a contradiction so \(n\) can not be even and odd at the same time.
10b Every integer is either even or odd
First, we prove that if \(n \in \mathbb{Z}\) and if \(s < s + 2\) then there is a unique \(t \in \mathbb{Z}\) and is \(t = s + 1\).
\[\begin{split} s < s + 2 & \Longrightarrow s = s < s + 1 \land s + 1 = s + 1 < s + 2 & \text{ where } s \text{ is unique } \text{ Exercises I 3.12 5} \\ & \Longrightarrow s < s + 1 < s + 2 \end{split}\]
Second
\[\begin{split} n \in \mathbb{Z} & \Longrightarrow \frac{n}{2} \in \mathbb{Q} \subset \mathbb{R} \\ & \Longrightarrow m \leq \frac{n}{2} < m + 1 & \text{ Exercises I 3.12 5} \\ & \Longrightarrow 2m \leq n < 2(m + 1) \\ & \Longrightarrow 2m + 1 \leq n + 1 < 2m + 3 \\ \end{split}\]
Third, if \(2m = n\) then \(n\) is even. But if \(2m < n\) then \(2m + 1 < n + 1\) so \(2m + 1 < n + 1 < 2m + 3\). Because \(2m + 1 < 2m + 2 < 2m + 3\) by the first part \(n + 1 = 2m + 2 = 2(m + 1)\) so \(n + 1\) is even and \(n\) is odd. Therefore \(n\) is even or odd but no both because of Exercises I 3.12 10a
10c The sum or product of two even integers is even. What can you say about the sum or product of two odd integers?
First, the sum of two even integers
\[\begin{split} 2m = n \in \mathbb{Z} \land 2s = p \in \mathbb{Z} & \Longrightarrow n + p = 2m + 2s \\ & \Longrightarrow n + p = 2(m + s) \text{ where } m + s \in \mathbb{Z} \\ & \Longrightarrow n + p \text{ is even} \end{split}\]
Second, the product of two even integers
\[\begin{split} 2m = n \in \mathbb{Z} \land 2s = p \in \mathbb{Z} & \Longrightarrow np = (2m)(2s) \\ & \Longrightarrow np = 2(m(2s)) \text{ where } m(2s) \in \mathbb{Z} \\ & \Longrightarrow np \text{ is even} \end{split}\]
Third, the sum of two odd integers
\[\begin{split} n \text{ and } p \text{ are odd} & \Longrightarrow n + 1 = 2m \land p + 1 = 2s \\ & \Longrightarrow (n + 1) + (p + 1) = 2m + 2s \\ & \Longrightarrow (n + p) + 2 = 2(m + s) \\ & \Longrightarrow n + p = 2(m + s) - 2 \\ & \Longrightarrow n + p = 2((m + s) - 1) \text{ where } 2((m + s) - 1) \in \mathbb{Z} \\ & \Longrightarrow n + p \text{ is even} \\ \end{split}\]
Fourth, the product of two odd integers
\[\begin{split} n \text{ and } p \text{ are odd} & \Longrightarrow n + 1 = 2m \land p + 1 = 2s \\ & \Longrightarrow (n + 1)(p + 1) = 2m(2s) \\ & \Longrightarrow (np + 1) + (n + p) = 2m(2s) \\ & \Longrightarrow np + 1 = 2m(2s) - (n + p) \\ & \Longrightarrow np + 1 = 2m(2s) - 2t \text{ where } t \in \mathbb{Z} & \text{ By the third part} \\ & \Longrightarrow np + 1 = 2(m(2s) - t) \text{ where } 2(m(2s) - t) \in \mathbb{Z} \\ & \Longrightarrow np + 1 \text{ is even} \\ & \Longrightarrow np \text{ is odd} \end{split}\]
10d If \(n^2\) is even, so is \(n\). If \(a^2 = 2b^2\), where \(a\) and \(b\) are integers, then both \(a\) and \(b\) are even.
First, assume \(n^2\) is even. Also by Exercises I 3.12 10a and 10b \(n\) is even or odd but not both. If \(n\) is odd by Exercises I 3.12 10c third part \(n^2\) would be odd so \(n\) must be even.
Second, because \(a^2 = 2b^2\) then \(a^2\) is even. By the first part \(a\) is even. Therefore \(a^2 = (2t)^2\) where \(t \in \mathbb{Z}\) so:
\[\begin{split} a^2 = (2t)^2 \land a^2 = 2b^2 & \Longrightarrow (2t)^2 = 2b^2 \\ & \Longrightarrow 4t^2 = 2b^2 \\ & \Longrightarrow 2t^2 = b^2 \text{ where } t^2 \in \mathbb{Z} \\ & \Longrightarrow b^2 \text{ is even} \\ & \Longrightarrow b \text{ is even } & \text{ By the first part} \end{split}\]
Third, \(a\) and \(b\) are even.
10e Every rational number can be expressed in the form \(a / b\), where \(a\) and \(b\) are integers, at least one of which is odd.
First, we assume that every rational number, \(c \in \mathbb{Q}\), has a unique representation as an irreducible fraction1, \(c = \frac{a}{b}\), where \(a \in \mathbb{Z}\), \(b \in \mathbb{Z}\), \(b > 0\) and \(a, b\) have no common divisors except \(1\). For example, \(\frac{3}{12}\) or \(\frac{-3}{-12}\), \(\frac{-2}{10}\) or \(\frac{2}{-10}\) and \(\frac{0}{-1}\) or \(\frac{0}{2}\) can be represented as \(\frac{1}{4}\), \(\frac{-1}{5}\) and \(\frac{0}{1}\) in its reduced form.
Second, assume \(a \text{ is even } \land b \text{ is even }\) and \(c = \frac{a}{b} \in \mathbb{Q}\) where \(\frac{a}{b}\) is the unique representation as an irreducible fraction of \(c\). Then \(a = 2s\) and \(b = 2t\) so \(c = \frac{a}{b} = \frac{2s}{2t} = \frac{s}{t}\). But this contradicts that \(\frac{a}{b}\) is the unique representation as an irreducible fraction of \(c\). Therefore \(a \text{ is even } \land b \text{ is even }\) is false so \(a \text{ is odd } \lor b \text{ is odd }\) must be true.
11 Prove that there is no rational number whose square is \(2\). \([\)Hint: Argue by contradiction. Assume \((a/b)^2 = 2\), where \(a\) and \(b\) are integers, at least one of which is odd. Use parts of Exercise 10 to deduce a contradiction.\(]\)
To prove this statement we are going to use the method of reductio ad absurdum. Please check out (Mendelson 2008, Chapter 1, p 7, Exercises 2 and 5)
First, assume \(\left( \frac{a}{b} \right)^2 = 2\) where \(\frac{a}{b}\) is the unique representation as an irreducible fraction of a rational number.
Second, using the results of Exercises I 3.12 10 we have that \(a \text{ is even } \land b \text{ is even }\) but this is a contradiction because \(\frac{a}{b}\) is the unique representation as an irreducible fraction of a rational number. Therefore \(\frac{a}{b} \notin \mathbb{Q}\) so it must be the case that \(a/b = ab^{-1} \in \mathbb{R} - \mathbb{Q}\) because \(a \in \mathbb{Z} \subset \mathbb{R} \land b \in \mathbb{Z}^+ \subset \mathbb{R}\)
12 The Archimedean property of the real-number system was deduced as a consequence of the least-upper-bound axiom. Prove that the set of rational numbers satisfies the Archimedean property but not the least-upper-bound property. This shows that the Archimedean property does not imply the least-upper-bound axiom.
First, the archimedean property was deduced by proving that \(\mathbb{Z}^+\) was unbounded above. Also because \(\mathbb{Q} \subset \mathbb{R}\) if \(c \in \mathbb{Q}\) then we can apply Theorem I.29 and Theorem I.30 to \(c\). Therefore any \(c \in \mathbb{Q}\) satisfies the archimedean property.
Second, if we apply the least-upper-bound axiom to \(\mathbb{Q}\) we would have that every \(S \subseteq \mathbb{Q} \land S \neq \emptyset\) which is bounded above has a supremum; that is, there is a rational number \(B\) such that \(B = \text{sup } S\).
Third, let \(S = \{s: s \in \mathbb{Q} \land s^2 < 2 \}\). We have that \(S \subset \mathbb{Q}\) and \(S \neq \emptyset\) because \(0 \in \mathbb{Q}\) and \(0^2 = 0 < 2\) so \(0 \in S\).
Fourth, by Theorem 1.16 if \(s \in S \subset \mathbb{Q} \subset \mathbb{R}\) we must have that \(s = 0\), \(s < 0\) or \(s > 0\). If \(s = 0\) or \(s < 0\) then \(s \leq 0 < 2\). If \(s > 0\) then \(s \geq 1\) or \(1 > s > 0\). In the case of \(s \geq 1\) we have that \(s^2 \geq s\) by Theorem 1.16 so \(2 > s^2 \geq s\) and in the case of \(1 > s > 0\) we have that \(2 > 1 > s > 0\). Therefore in any case if \(s \in S\) we have that \(2 > s\) so \(2\) is an upper bound of \(S\).
Fifth, now we assume that there is some \(B \in \mathbb{Q}\) such that for all \(s \in S\) we have that \(s \leq B\). However by Exercises I 3.12 6 there is some \(r \in \mathbb{Q}\) such that \(B < r < 2\) so \(B\) is not a least upper bound of \(S\). Therefore not every \(S \subseteq \mathbb{Q} \land S \neq \emptyset\) which is bounded above has a supremum \(B\) where \(B \in \mathbb{Q}\).
References
The complete proof can be found in Existence of Canonical Form of Rational Number and Canonical Form of Rational Number is Unique↩︎