Chapter 4 Statistical Programming

Since we are now able to extract and aggregate data, we can start working on a first small project. When deploying a new data science project the following steps should be taken into consideration.

Data Exploration

Data Processing

Model Development

Model Evaluation

Model Deployment

We will look into the different steps during this section of the course. Some general concepts this section elaborates on are summarized within

Python for Probability, Statistics and Machine Learning - Unpingco (2014)

4.1 Data Exploration

Data exploration is the process of analyzing and understanding a dataset to gain insights and knowledge about it. It is an important first step in the data analysis process and involves a wide range of techniques and tools to discover patterns, trends, relationships, and anomalies. During the data exploration process, you may perform tasks such as visualizing the data, summarizing its key statistics, identifying missing values and outliers, and assessing the quality and validity of the data.

4.2 Visualization

Data visualization is the process of representing data in graphical or pictorial way to reduce the degree of abstraction. This can be especially useful when dealing with large amounts of data. It is a powerful tool for exploring and communicating complex data in a clear and concise way. By using visual elements like charts, graphs, maps, and infographics, data visualization can make patterns, trends, seasonalities, anomalies and correlations within the data more easily recognizable.

There are several packages to visualize data, such as matplotlib, plotly or ggplot. This course uses Plotnine for visualization but you are free to chose your preferred tool of visualization. We are also using numpy to handle mathematic calculations.

# Import modules
from plotnine import *
import numpy as np

In order to allow proper visualization of the data it is necessary to identify relevant metrics that require plotting plus a selection of the appropriate visual. We start by plotting trade price and volume throughout the day discretized on a 1-minute time interval for AAPL on the 2022-02-01.

# Plot average trading price throughout day
ggplot() + \
  geom_line(data = trades_lowfreq, 
            mapping = aes(x="parttime_trade", y="price")) + \
  xlab("Time") + \
  scale_x_datetime(date_labels = "%H:%M") + \
  ylab(f"Price") + \
  theme_custom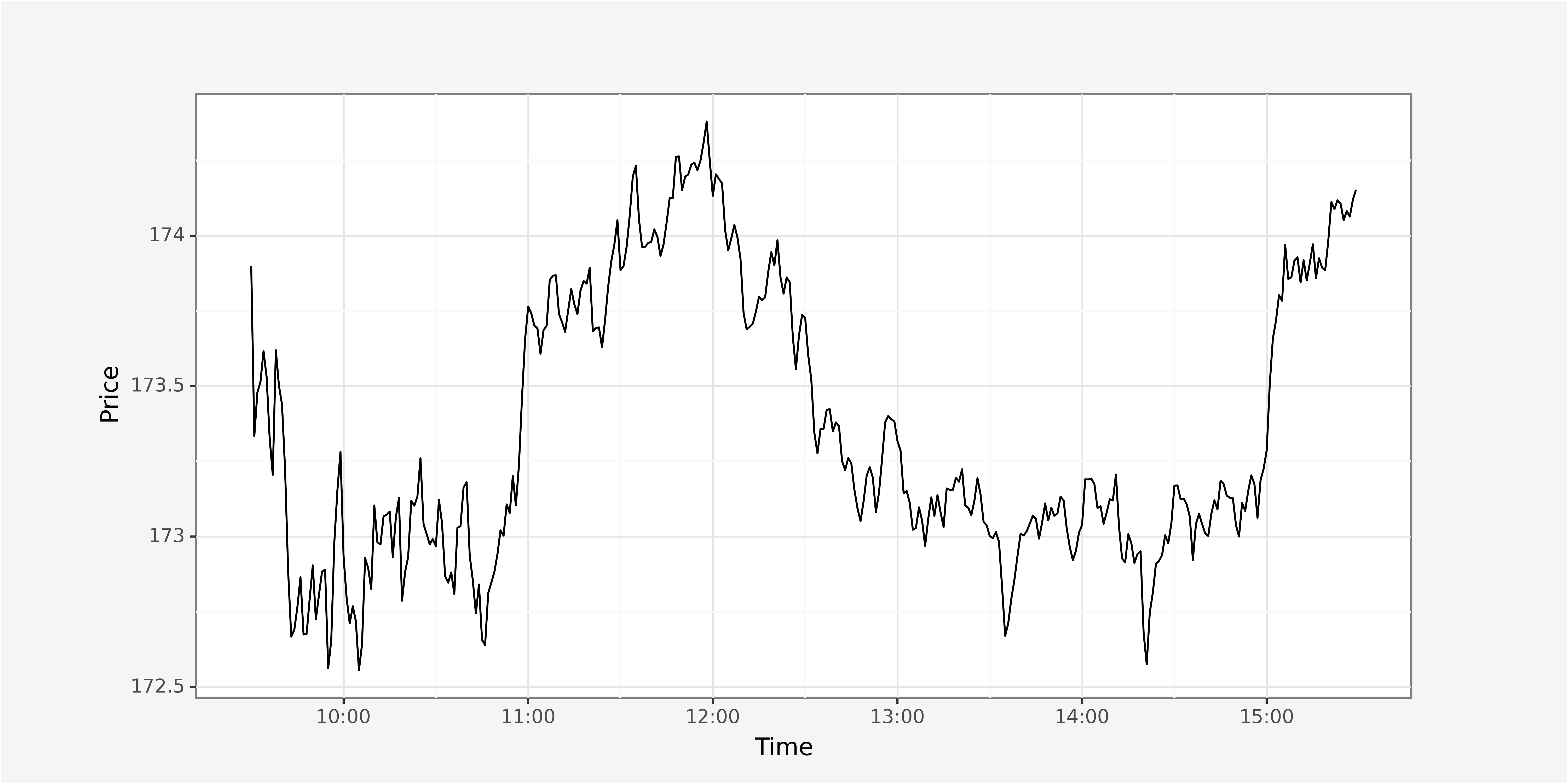

Additionally, we want to compute some initial measures of distribution for the aggregated trades.

# Compute standard deviation of trading quantity
std_quantity = np.std(trades_lowfreq.quantity).round(4)
mean_quantity = np.mean(trades_lowfreq.quantity).round(4)
median_quantity = np.median(trades_lowfreq.quantity).round(4)

Plotting the volume throughout the trading day yields the following graphic.

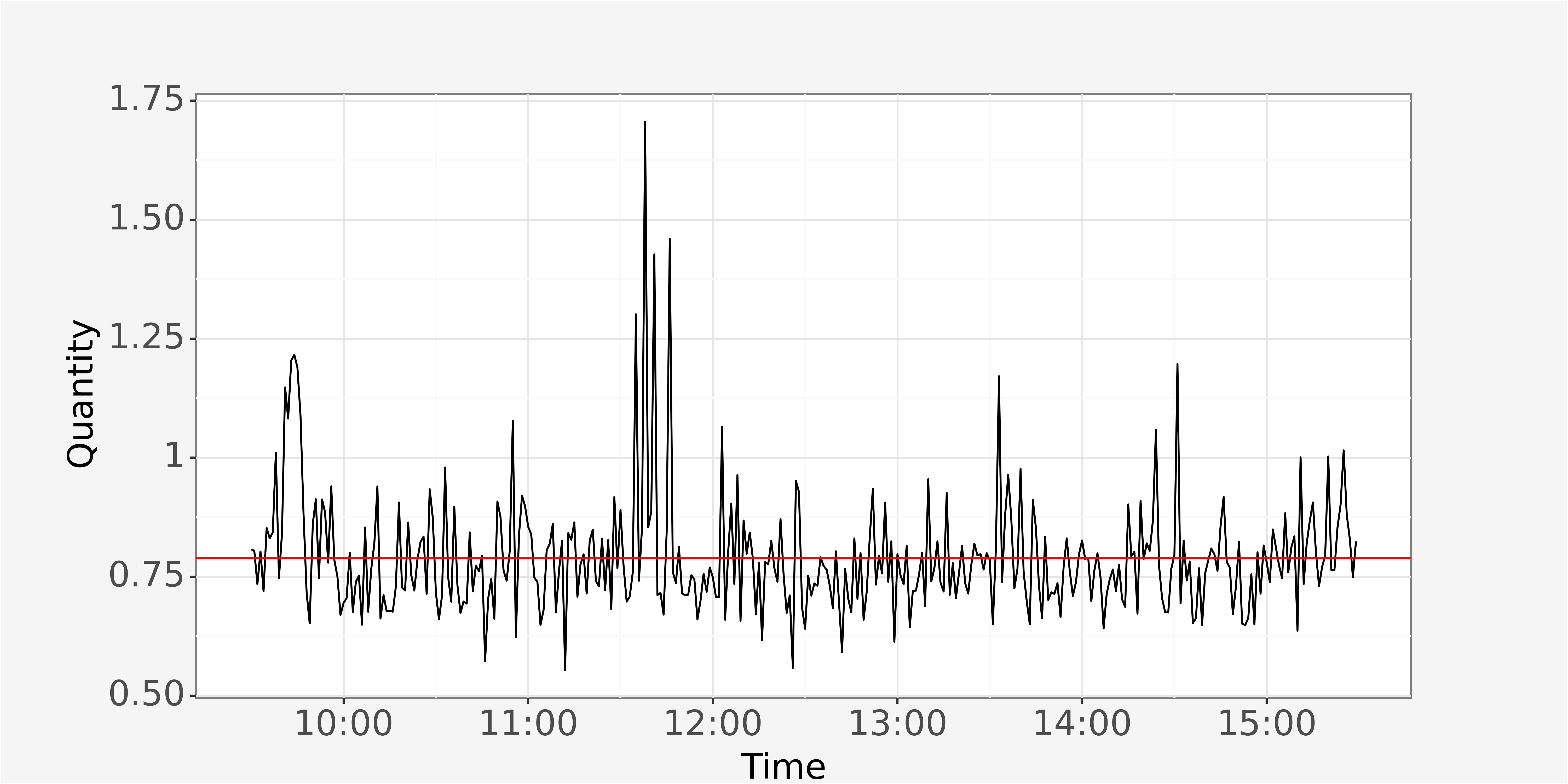
The red line indicates the mean traded quantity per day.

4.3 Preprocessing

Data preprocessing is the process of transforming raw data into a form suitable for analysis and model development. It is an essential step in data analysis because real-world data is often incomplete, inconsistent, or contains errors, which can lead to inaccurate or biased results if not handled properly. Dependent on how reliable your datasource is, you might want (or need) to run the following checks of data quality, to ensure you are working with proper data for your analysis.

Notice, that the relevant preprocessing steps are highly dependent on the underlying dataset.

Data Cleaning
Data cleaning is the process of identifying and correcting or removing errors, inconsistencies, and inaccuracies in a dataset. It might be necessary to run statistical tests on the data to identify outliers which look like they have been generated by a different data generating process. Additionally, domain knowledge can help to identify obvious erroneous data within the dataset. When investigating quote data, e.g., a negative bid-ask spread would be considered erroneous or a date which lies in the future.

Data Transformation
Data transformation refers to the process of converting data from one format, structure, or representation to another. It involves manipulating and changing data in order to make it more suitable for a particular purpose.

Feature Engineering	Creating new features or variables from existing data, such as calculating ratios, differences, or percentages between different variables.
Encoding	Converting categorical data into numerical values, such as assigning numeric codes to represent different categories
Aggregation	Combining multiple data points or records into a single value, such as computing the average, sum, ratio of a set of values

Handling Missing Data
Handling missing data requires a a-priori definition of what missing data is. An entire row can be defined as being subject to missing data if only a single attribute is missing (however, this should not happen and would be evidence for a bad database setup with a lack of constraints). This row might entirely be excluded from the analysis, or could still be used if it contains all relevant variables. Dealing with missing data heavily depends on the context of the data (time series, cross-sectional…) and should be decided after computing the fraction of missing values within the dataset. Missing values can be interpolated, set to equal zero or discarded entirely.

In our time series data, we could consider missing values as timestamps which do not have any trading data available. This can only be done after discretization of data and is not suitable for data in a continous setting.

If we are looking at values on a discrete timegrid of a single minute, the data looks complete.

# Number of minutes throughout the trading day
trading_minutes = (15.5 - 9.5) * 60
print(f"Number of trading minutes: {trading_minutes}")

# Length of trade dataframe aggregated on minute basis
print(f"Number of trades aggregated to low frequency: {len(trades_lowfreq)}")

However we can see, that the data is not evenly spaced if we look at it on a microsecond level. When dealing with unevenly spaced data in continuous time, detecting missing values is not feasible unless the data is aggregated to a higher level.

Summing the resulting boolean values using the function function isna() we are able to identify the number of missing values per row.

trades_lowfreq.isna().sum()

The dataset can therefore be considered complete with regard to the variables we are currently investigating.

Duplicates
Identification of duplicate values is also highly dependent on the dataset and requires identification of a primary key which distinguishes between the different row entries. Since our data has been aggregated as a time series on a one-minute basis, we determine the timestamp as a unique identifier for all rows.

Do we take the average (in case of two different values for a single observation). Another interesting question would be to identify the origin of those outliers.

# Checking for duplicate values of the non-aggregated dataset
trades_filtered.reset_index(drop=True).groupby(["parttime_trade", "part_time_nano"])["quantity"].count().head(10)

On the nanosecond level we can see that we have a certain amount of duplicate values, which originate from the occurence of metaorders.

The data aggregated on a one minute level does not show duplicate values after its aggregation.

# Checking for duplicate values of the non-aggregated dataset
trades_lowfreq.reset_index(drop=True).groupby(["parttime_trade", "part_time_nano"])["quantity"].count().head(10)

Attribute Transformation
Attribute transformation might also contain the scaling of data which we will look at at a later point of our project. The concept of feature engineering allows to modify variables in a way they remain highly significant for our model development. This might include computation of lagged values, first differences, computation of ratios etc. Transforming categorical or literal variables into numerical variables (or vice versa).

Data Reduction
Oftentimes, the relevant dataset contains a variety of variables which will not be necessary for the entire analysis. To allow for smooth computation times, especially within the exploratory part of your analysis, you might want to subset your dataset horizontally or vertically. Furthermore, different techniques of variable reduction exist to aggregate information within the data.

4.3.1 Outliers

An outlier is an individual point of data that is distant from other points in the dataset. It is an anomaly in the dataset that may be caused by a range of errors in capturing, processing or manipulating data. The outlier is not necessarily due to erroneous measurements, but might be classified as contextual outlier which does not seem to have been produced by the underlying data generating process. Outliers can easily skew the data and cause bias in the development of the model.

Point Outlier	In data analysis, a point outlier is an observation or data point that significantly differs from other observations in a dataset. Point outliers can occur due to measurement errors, data entry mistakes, or genuine deviations in the data.
Contextual Outlier	A contextual outlier is also known as conditional outlier and refers to an observation or data point that is unusual within a specific context of observation. This means that it is unusual within a certain (sub)sample of the dataset but may not be considered an outlier when looking at the entire dataset.
Collective Outlier	A collective outlier, also known as a group outlier or a contextual collective outlier, is a pattern or group of observations in a dataset that is significantly different from the rest of the data.

Detecting contextual and collective outliers often involves using advanced statistical techniques, such as cluster analysis or principal component analysis.

4.3.2 Sampling strategies

When working with especially big datasets while encountering restrictions of technical infrastructure it might make sense to reduce the entire data sample to a smaller sample to allow feasible handling of data. Therefore, we might want to reduce our sample size using one of the following sampling strategies.

Random Sampling	In simple random sampling, the researcher selects the relevant datapoints randomly. There are a number of data analytics tools like random number generators and random number tables used that are based entirely on chance.
Systematic Sampling	In systematic sampling, every population is given a number as well like in simple random sampling. However, instead of randomly generating numbers, the samples are chosen at regular intervals.
Stratified Sampling	In stratified sampling, the population is clustered into subgroups, called strata, based on a predefined set of characteristics. After identifying the subgroups, random or systematic sampling can be employed to select a sample for each subgroup. This method allows you to draw more precise conclusions because it ensures that every subgroup is properly represented.
Cluster Sampling	In cluster sampling, the population is divided into subgroups, but each subgroup has similar characteristics to the whole sample. Instead of selecting a sample from each subgroup, you randomly select an entire subgroup. This method is helpful when dealing with large and diverse populations.

4.3.3 Normalization and Scaling

When dealing with scaling features we differentiate between scaling a feature within a single homogenous dataset, or scaling a single feature within a heterogenous dataset with multiple categorical subgroups. Normalization and scaling are especially relevant if we are looking at a heterogenous dataset.

Most scaling techniques incorporate (a) centering data horizontally and (b) scaling data vertically to make the data more or less dense. While the horizontal centering allows for a comparison of the datavalues regarding the centering factor, the vertical scaling adjusts and equalizes the variances across a set of different features of the dataset. The scaling can either be done on all features, given our dataset is mostly homogenous, or on different subgroups of the data, if we deal with a heterogenous dataset.

Standard Scaler
The standard scaler implements a Z-score standardization

\(x_z = \frac{x - \overline{x}}{\sigma_x}\)

with the translational term being the attributes’ mean \(\overline{x}\) and the scaling factor as standard deviation \(\sigma_x\). Since the scaling factor of standard deviation is sensitive to outliers, it might make the scaled distribution relatively narrow. To alleviate this problem, the scaling factor might be altered to \(\sqrt{\sigma_x}\) to reduce the influence of outliers. Such a scaling is called Pareto scaling.

Min-Max Scaler
The Min-Max Scaler alters an attribute’s scale and shifts its values horizontally, causing the transformed attributes to range within \([0,1]\).

\(x_{mm} = \frac{x - min(x)}{max(x) - min(x)}\)

The scaling factor consists of the range of the attribute \(max(x) - min(x)\) while the translational term is its minimum value \(min(x)\). This approach is especially sensitive to outliers due to scaling with extreme values of the observed realizations. Therefore, it fails to equalize means and variances of distributions. It can therefore be considered rather unsuitable for machine learning problems.

Robust Scaler
The robust scaler allows a more robust scaling approach due to is horizontal transformation with the data’s mean (second quantile \(Q_{2}(x)\)) and scaling with an interquantile range \(Q_{3}(x) - Q_{1}(x)\).

\(x_r = \frac{x - Q_{2}(x)}{Q_{3}(x) - Q_{1}(x)}\)

This scaler therefore seems to allow for equalization of both, mean and variance even in the presence of outliers.

Scaling Factors
When dealing with heterogenous datasets with a multitude of categorical subgroups, the underlying realization of the response variable might differ in magnitude for the single groups. We then usually encounter scaling factors. It indicates, e.g., that a higher capitalized stock will have a lower price impact, while a lower capitalized stock has a higher price impact with the stock’s capitalization indicating the scaling factor. We assume the scaling factor to be (highly) correlated to our response variable.

\(x_{sf} = x \times scale\_factor\).

Identifying the scaling factor can allow for another procedure of normalization to generate a more homogenous dataset.

Normalizing Qualitative Values
The normalization procedures defined above can be applied to numerical values. Qualitative data can be subject to normalization procedures as well, however different techniques apply which will not be discusses within the scope of this course.

4.4 Exercise

Extract the trading data for the stocks AAPL and AMZN on the 2022-02-01 to work on the following tasks.

Discretization

(1)	Discretize the data from microseconds (\(10^{-6}\)) to miliseconds (\(10^{-3}\))
(2)	Discretize the data from microseconds (\(10^{-6}\)) to seconds (\(10^{0}\))

Visualization
Due to performance reasons, perform the following analysis on the data based on one-minute aggregates.

(3)	Plot the price series throughout the trading day for both stocks
(4)	Plot the return series throughout the trading day for both stocks
(5)	Plot the correlation of the returns throughout the trading day using a rolling window of 100 observations on (i) microsecond and (ii) second aggregated data. How do the correlation values compare?
(6)	Plot the autocorrelation function of the returns for both of the stocks separately
(6)	Plot the intraday volatility as \(\sigma_{r,t} = \sqrt{\sum_{i=1}^{n}r_i^2}\) for both of the stocks separately with different parameter values for \(n=10\) and \(t in [1,390]\).
(6)	Plot the intraday orderbook imbalance as \(imb_t = \frac{V_{bid,t} - V_{ask,t}}{V_{bid,t} + V_{ask,t}}\) with \(imb_t \in (-1,1)\) following Cartea et al. (2015) and \(V_{bid,t}, V_{ask,t}\) indicating the bid and ask volumes respectively. Can you plot an histogram of the order imbalance realizations per stock?

Descriptive Analysis
Now, go back to the aggregated data on microsecond level.

(7)	Investigate the data for potential anomalies. Can you think about suitable measures to identify statistical outliers in this dataset?
(8)	Compute the average traded quantity, price and volatility for each of the two stocks
(9)	Create a new variable within the dataframe that scales the quantity for each trade with the mean quantity traded per day for each stock
(10)	Create a new variable that indicates the direction of a trade. Assign the values of \(1\) for a buy and \(-1\) for a sell. According to Lee and Ready (1991), a trade is classified as buy if \(P_{trade,t} < P_{mid,t-1}\). Analogously, a trade is classified as sell if \(P_{trade,t} > P_{mid,t-1}\). Can you plot the autocorrelation function of the trade direction based on the unaggregated data?
(11)	Compute a few descriptive statistics of your choice based on the trading direction. What is the overall quantity bought and sold for each of the stocks per day? What is the average price of buy and sell trades?

Python 3.11.1 (C:/Program Files/python.exe)
Reticulate 1.26 REPL -- A Python interpreter in R.
Enter 'exit' or 'quit' to exit the REPL and return to R.