Componente G - ENEL
2022-08-16
Capítulo 1 Entregable 1. Análisis estadístico de comportamiento de variables de precios y cantidades y su efecto sobre la recuperación de costos (Análisis transversal - Análisis de regresión (Multivariada y logística)
1.1 Ideas por trabajar y Marco Conceptual
- Caracterización de cambios en variables para determinar rangos y probabilidades por escenarios en distintos experimentos en el modelo matemático. Podría utilizarse la volatilidad (implícita o esperada para medir valores futuros (bajo ciertos escenarios futuros, ya que la volatiliad implicita produce una estimación de la volatilidad dependiendo de varios factores regresores) o histórica para medir los cambios vistos)
- Indagación de cambios de comportamiento de estas variables en escenarios de penetración de renovables para evaluar su efecto en las propuestas o experimentos sobre el calculo de G.
- Evaluación del efecto de IPP mediante comparación de resultados considerando IPP o no. Es decir, deflactando y sin deflactar. De esta manera se puede determinar ele efecto del IPP sobre las estimaciones.
De acuerdo a la regulación vigente, la componente G está determinada por:
\[\begin{equation} \label{G} \begin{split} G_{m,i,j} & = Qc_{m-1}*[P_{{Contratos}_{m-1}}]+(1-Qc_{m-1})*P_{{bolsa}_{m-1}} + AJ_{m} \\ G_{m,i,j} & = Qc_{m-1}*[\alpha*Pc_{m-1} + (1-\alpha)*Mc_{m-1}]+(1-Qc_{m-1})*Pb_{m-1} + AJ_{m} \end{split} \end{equation}\]
donde:
\(Qc_{m-1}\) : Porción de la demanda de mercado regulado del comercializador que es atendida mediantes compras en contratos bilaterales en el mes \(m-1\). \ \(Pc_{m-1}\) : Costo promedio ponderado de compras por el comericializador \(i\) para el mercado regulado mediante contratos bilaterales, liquidados en el mes \(m-1\).\ \(Mc_{m-1}\) : Costo promedio ponderado de compras de TODOS los contratos bilaterales para atender mercado regulado del país, liquidados en el mes \(m-1\).\ \(Pb_{m-1}\) : Precio de la energía comprada en Bolsa por el comercializador para atender el mercado regulado en el mes \(m-1\) definida en la ecuación
\[\begin{equation} \label{Pb} Pb_{m-1} = \frac{\sum_{k=1}^{n}P_{h,m-1}*D_{h,m-1}}{\sum_{k=1}^{n} D_{h,m-1}} \end{equation}\]
donde \(P_{h,m-1}\) y \(D_{h,m-1}\) corresponden al precio de bolsa y demanda comprada para el mercado regulado a la hora \(h\) del mes \(m-1\) por el comercializador.
\(\alpha\) : corresponde a un factor de ponderación del precio de contratos para Enero de 2007, calculado de acuerdo al procedimiento mostrado en según la ecuación :
\[\begin{equation} \label{alfa} \alpha = 1- \left[\frac{C_{m,t}*(1-P)}{C_{t-1}*\frac{IPP_{m-1}}{IPP_{junio,t-1}}}\right] \end{equation}\]
En términos generales, el Costo medio unitario de compra (\(\overline{Cu_{c}}\)) corresponde al costo incurrido por el comercializador en sus compras de energía en Contratos bilaterales y Bolsa para suplir la Demanda comercial descontando las pérdidas, tal como se muestra en la ecuación .
\[\begin{equation} \label{Cucompra} \begin{split} \overline{Cu_{c}}=\frac{Q_{c}*P_{c}+Q_{b}*P_{b}}{Q_{c}+Q_{b}} \\ \overline{P_{c}}=\frac{Compras_{Contratos}}{Q_{c}} \\ \overline{P_{b}}=\frac{Compras_{Bolsa}}{Q_{b}} \\ \end{split} \end{equation}\]
Por su parte, el Costo medio unitario recuperable (\(\overline{Cu_{r}}\)) corresponde al costo recaudado a través de la componente \(G\) de la tarifa y está definido según la ecuación .
\[\begin{equation} \label{Curecuperable} \begin{split} \overline{Cu_{r}}=\frac{\alpha*Q_{c}*P_{c}+(1-\alpha)*Q_{c}*M_{c}+Q_{b}*P_{b}}{Q_{c}+Q_{b}} \end{split} \end{equation}\]
Consecuentemente, se puede calcular la desviación entre ambos costos como una prima (\(Prima_{costos}\)) como la diferencia entre ambos tipos de costo, tal como se muestra en la ecuación .
Dado que,
\[\begin{equation} \label{Prima} \begin{split} Prima_{costos}=Costo_{mes}-Costo_{recuperable}\\ Prima_{costos}=Q_{c}\overline{P_{c}}+Q_{b}\overline{P_{b}}-[\alpha*Q_{c}*P_{c}+(1-\alpha)*Q_{c}*M_{c}]-Q_{b}*P_{b} \\ Si P_{c}=\overline{P_{c}} y P_{b}=\overline{P_{b}}\\ Prima_{costos}=(P_{c}-M_{c})(1-\alpha)Qc \\ Prima_{costos}=f(P_{c},M_{c},Q_{ç},\alpha) \end{split} \end{equation}\]
El análisis estadístico comprenderá los siguientes ítems:
Estadística descriptiva de variables \(Pc\), \(Qc\),\(Mc\), \(Pb\), \(Pb_{pais}\), \(\alpha_{real}\)
Distribuciones estadísticas y posibles ajustes paramétricos ( . Posible uso en VaR Paramétrico o No paramétrico).
Análisis de regresión transversal multivariada para explicar la variabilidad de la prima de costos en términos de las variables regresoras de precios y cantidades. : El aporte consiste en averiguar las variables que impacten más sensiblemente a esta desviación.
\[\begin{equation} Prima_{costos} = \beta_{1}Qc + \beta_{2}Pc + \beta_{3}Mc + \beta_{4}Pb + \beta_{5}Pb_{pais} \end{equation}\]
Análisis de Regresión Logística. Basado en la distribución estadística de la prima de costos y sus regresoras, se ensayará otro modelo de regresión cuyo resultado no intente explicar la variabilidad () sino establecer probabilidades (Odds ratio) de que las primas de costos sean (Altas o Bajas/ Positivas o negativas) cuando las regresoras sean Altas o Bajas. Por ejemplo, resultados del tipo: “Si el precio de contratos es alto, la probabilidad de que la prima de costos sea alta es de X a 1 con respecto al escenario en que el precio de contratos sea bajo.” Si X>1, los precios de contrato altos serán más determinates que los precios de contrato bajos.
\[\begin{equation} \label{logisticas} \small log\frac{p}{1-p}=\kappa + \alpha_{W}Pc_{Altos} \end{equation}\]
Esta misma formulación se puede hacer contra Qc o Mc.
1.2 Estadística descriptiva de variables \(Pc\), \(Qc\),\(Mc\), \(Pb\), \(Pb_{pais}\), \(\alpha_{real}\)
1.2.1 Deflactación
Para la deflactación se trabajara con la serie de IPP del DANE disponible en : \url(https://www.dane.gov.co/index.php/estadisticas-por-tema/precios-y-costos/indice-de-precios-del-productor-ipp). Esta serie trabaja con los precios base de Diciembre de 2014 y se trabaja con las series de IPP del producto Nacional y del IPP Minero.
Figure 1.1: Comportamiento de variable IPP (Base Diciembre 2014)
A continuación se presentan los valores estadísticos de las variables de análisis.
| Demanda | Qc | Pcontratos | PcontratosdefNal | Qb | Pbolsa | PbolsadefNal | Mc | McdefNal | Rc | RcdefNal | |
|---|---|---|---|---|---|---|---|---|---|---|---|
| X | Min. :774522052 | Min. :525339468 | Min. :168.2 | Min. :144.8 | Min. : 11559043 | Min. : 63.01 | Min. : 52.81 | Min. :172.9 | Min. :158.0 | Min. :-1.943e+09 | Min. :-1.742e+09 |
| X.1 | 1st Qu.:852566101 | 1st Qu.:656046934 | 1st Qu.:199.5 | 1st Qu.:160.7 | 1st Qu.: 74797607 | 1st Qu.:105.57 | 1st Qu.: 83.53 | 1st Qu.:188.8 | 1st Qu.:162.8 | 1st Qu.:-7.047e+08 | 1st Qu.:-5.036e+08 |
| X.2 | Median :871630445 | Median :742904312 | Median :206.7 | Median :174.3 | Median :125275571 | Median :147.47 | Median :127.53 | Median :208.8 | Median :171.9 | Median : 2.255e+08 | Median : 2.111e+08 |
| X.3 | Mean :866650478 | Mean :727661020 | Mean :213.4 | Mean :172.7 | Mean :142066171 | Mean :180.82 | Mean :147.51 | Mean :213.5 | Mean :172.4 | Mean : 1.240e+08 | Mean : 8.105e+07 |
| X.4 | 3rd Qu.:886036514 | 3rd Qu.:798713827 | 3rd Qu.:237.2 | 3rd Qu.:181.4 | 3rd Qu.:201706087 | 3rd Qu.:258.99 | 3rd Qu.:194.94 | 3rd Qu.:232.1 | 3rd Qu.:181.9 | 3rd Qu.: 8.471e+08 | 3rd Qu.: 6.751e+08 |
| X.5 | Max. :915197739 | Max. :868416423 | Max. :273.2 | Max. :190.0 | Max. :348640751 | Max. :437.01 | Max. :368.20 | Max. :288.3 | Max. :194.7 | Max. : 2.237e+09 | Max. : 1.360e+09 |
1.2.2 Variables de Precio
A continuación se muestran gráficamente los comportamientos de los estadísticos descriptivos de los precios.
1.2.2.1 Precios reales y deflactados
1.2.2.1.1 Precios reales
Figure 1.2: Comportamiento de variables de precios y cantidades sin deflactar
1.2.2.1.2 Precios deflactados
(#fig:DescEstadistica1_def)Comportamiento de variables de precios constantes Diciembre 2014
1.2.2.2 Variaciones de precios
1.2.2.2.1 Cambios en precios reales (\(P_{t}- P_{t-1}\))
Figure 1.3: Comportamiento de variables de cambios de precios y cantidades sin deflactar
1.2.2.2.2 Cambios de precios deflactados (\(P_{t}- P_{t-1}\))
(#fig:DescEstadistica1_defDiff)Comportamiento de cambios de precios constantes Diciembre 2014
1.2.3 Variables de Cantidades
1.2.3.1 Cantidades
A continuación se muestran gráficamente los comportamientos de los estadísticos descriptivos de las cantidades
(#fig:DescEstadistica1_Q)Comportamiento de variables de precios y cantidades sin deflactar
1.2.3.2 Variaciones de Cantidades
(#fig:DescEstadistica1Diff_Q)Comportamiento de cambios de cantidades sin deflactar
1.2.4 Variables de primas
1.2.4.1 Primas Rc y U
Figure 1.4: Comportamiento de variables de montos Rc y U (millones de pesos)
1.2.4.2 Variaciones de Primas
Figure 1.5: Comportamiento de cambios de primas Rc y U sin deflactar
1.2.5 Segmentación en escenarios de Prima de costos positiva o negativa
Se puede segmentar los datos cuando la prima de costos es Alta o Baja (RcNivel) y ver el comportamiento de las variables y sus estadísticos.
1.2.5.1 Variables de Precios
1.2.5.1.1 Precios reales y deflactados vs. Prima de Costo
Figure 1.6: Comportamiento de los precios por Prima de costos sin deflactar
Figure 1.7: Comportamiento de los precios por Prima de costos deflactada a precios constantes Diciembre 2014
1.2.5.1.2 Cambios de Precios reales y deflactados vs. Prima de costo
Figure 1.8: Comportamiento de los cambios de precios por Prima de costos sin deflactar
Figure 1.9: Comportamiento de los cambios de precios por Prima de costos deflactada a precios constantes Diciembre 2014
1.2.5.2 Variables de Cantidades
1.2.5.2.1 Cantidades vs. Prima de costo deflactada y sin deflactar
(#fig:DescEstadistica_Qdiff)Comportamiento de las Cantidades por Prima de costos
(#fig:DescEstadisticadef_Qdiffdef)Comportamiento de las Cantidades por Prima de costos deflactada
1.2.5.2.2 Variación de cantidades vs Prima de costo deflactada y sin deflactar
(#fig:DescEstadistica_Qdiff2)Comportamiento de las variaciones de cantidades por Prima de costos
(#fig:DescEstadisticadef_Qdiffdef2)Comportamiento de las Cantidades por Prima de costos deflactada
1.2.6 Correlogramas
1.2.6.1 Diagrama de correlaciones sin deflactar
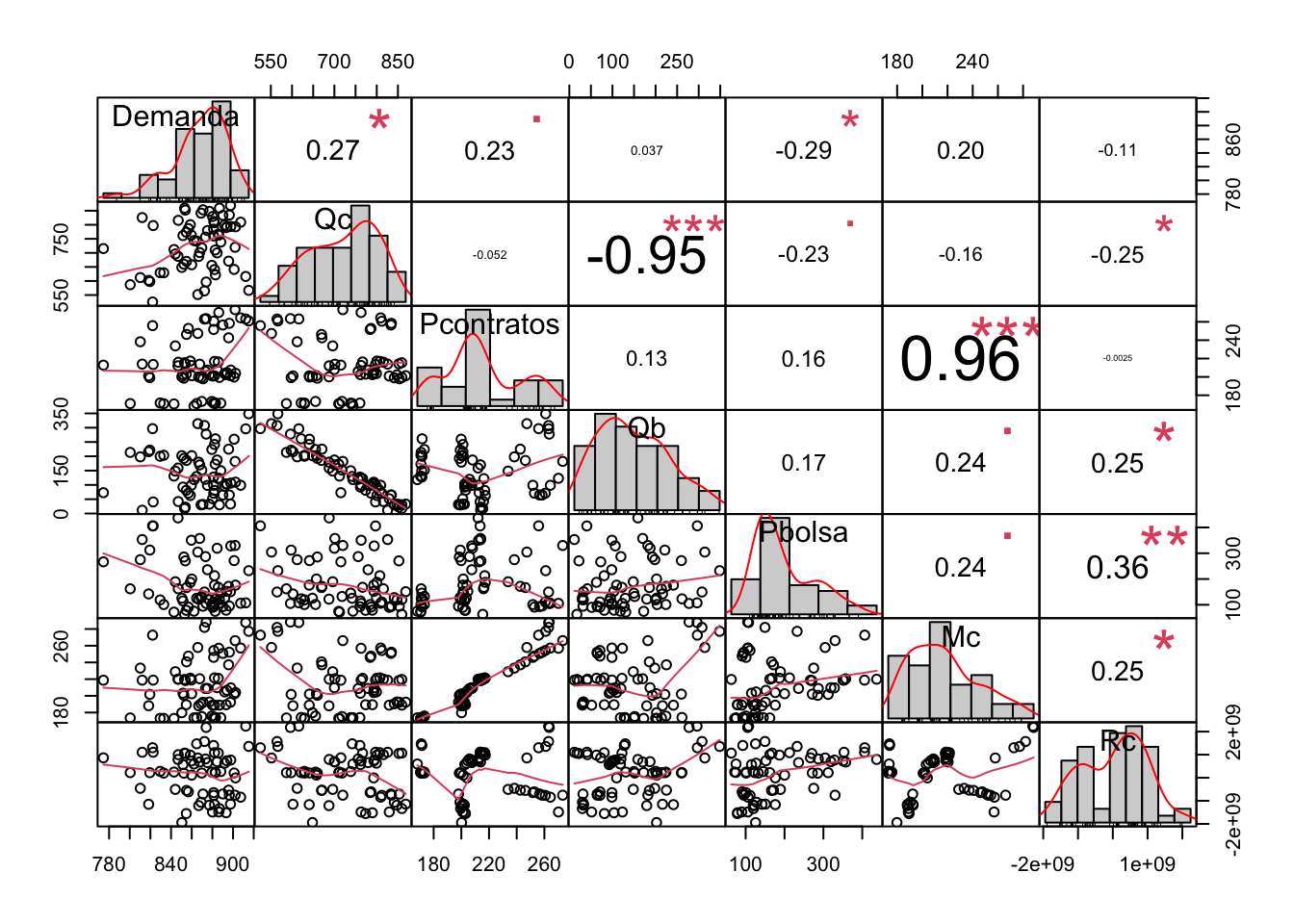
Figure 1.10: Comportamiento de las Cantidades por Prima de costos deflactada
1.2.6.2 Diagrama de correlaciones luego de deflactar
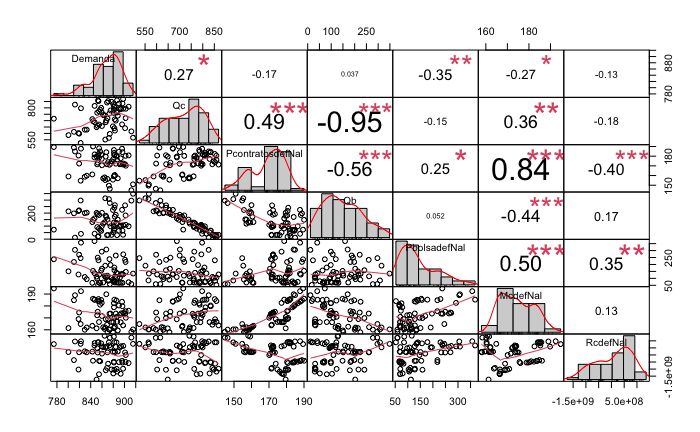
Figure 1.11: Comportamiento de las Cantidades por Prima de costos deflactada
1.2.7 Conclusiones - Ideas principales.
Existe un comportamiento creciente, acentuado y diferenciado para el IPP Minero a partir de la pandemia del COVID-19.
Sobre los precios,
- Pc y Mc son superiores a los precios de Bolsa!!! Con una prima de riesgo de casi 20%, (17-18%)
- Pc y Mc son casi idénticos. incluso existe una tendencia donde los precios de contrato deflactados de ENEL son más altos que el mercado (Mc). - Escaso margen de competitividad?
- Sobre los precios, estos exhiben distribuciones asimétricas donde la media supera a la mediana.
Sobre las cantidades,
Existe una relación casi de 5 a 1 entre lo que se compromete en contratos vs. lo que se exponen en bolsa. () Exposición a bolsa del 20%
Sobre las cantidades, estos exhiben distribuciones asimétricas donde la mediana supera a la media.
Sobre las variaciones de los precios,
- Comportamientos crecientes, donde el mayor crecimiento lo tiene Mc (1.8) mientras que Pc crece un poco menos (1.4), mientras que el precio de bolsa prácticamente no ha crecido.
- Si estos mismos valores se miran con precios constantes, tanto Pc como Mc no han disminuido, lo cual es esperable en un mercado de contratos, es decir, el hecho de colocar un alfa constante ha hecho que no hayan incentivos para bajar los precios de los contratos. Por su parte, el precio de bolsa si ha experimentado una disminución, es decir, el precio indicativo del mercado baja pero el precio de contratación se mantiene constante. Esto es contraintuitivo pues se espera que el precio de bolsa sea una señal de precio que viene bajando pero los contratos no lo hacen respectivamente. Es como si existiera una ineficiencia creciente.
Sobre las variaciones de demanda,
- Es esperable un creciemiento de la demanda de ENEL, la cual se encuentra alrededor de 0.7 GWh/mes. Lo interesante es que el cubrimiento en contratos Qc viene disminuyendo mes a mes (- 0.5 GWh/mes) mientras que la exposición a bolsa viene creciendo (1.2 GWh/mes). En otras palabras hay una creciente exposición a bolsa.
Sobre el comportamiento de la prima de costo,
- Las primas de costo tienen media y mediana positiva, siendo una distribución asimétrica hacia los valores positivos, lo que implica que esta prima de costos es la mayor parte del tiempo favorable o positiva.
- Por su parte, la desviación operativa U, tiene media negativa, lo que implica que por motivos operativos, esta prima de gestión de compras pasa de un valor positivo a un valor negativo cuando se incluye la operación en la facturación y sus calendarios o ciclos.
- Los cambios o variaciones mes a mes en la prima de costo son positivas tanto en media como en mediana, mientras que los cambios en la prima operativa son negativos, de hecho, la mitad del tiempo (mediana) han estado con valores de -1490 millones de pesos. Cabe resaltar que estos valores no son sostenidos, sino más bien, un valor de los cambios sin contar el punto inicial.
Primas de costo vs. Precios y Cantidades
- Las primas de costo tienden a ser negativas, es decir, el costo mes es menor que el costo recuperable, lo cual es algo indeseable cuando:
- Los precios de bolsa son más bajos
- Los precios de contratos son más altos
- Las cantidades contratadas son más altas (Menor exposición a bolsa)
- Las cantidades de bolsa son más bajas (Menor exposición a bolsa)
- Las primas de costo tienden a ser negativas, es decir, el costo mes es menor que el costo recuperable, lo cual es algo indeseable cuando:
Primas de costo vs. Variaciones de precios y cantidades. Aún más, las primas de costo tienden a ser más discriminadas por los cambios en las variables de precio y cantidad.
- Las primas de costo tienden a ser negativas, es decir, el costo mes es menor que el costo recuperable, lo cual es algo indeseable cuando:
- Los precios de bolsa son crecientes respecto a t-1. Cunado los precios de bolsa son decrecientes, las primas son positivas.
- Los precios de contratos son crecientes respecto a t-1. Cuando los precios de contrato son constantes, la prima es positiva.
- Las cantidades contratadas son crecientes respecto a t-1, (Exposición a bolsa decreciente).
- Las cantidades de bolsa son decrecientes respecto a t-1 (Exposición a bolsa decreciente)
- Las primas de costo tienden a ser negativas, es decir, el costo mes es menor que el costo recuperable, lo cual es algo indeseable cuando:
Sobre las correlaciones,
- Las correlaciones entre las variables son más altas para precios deflactados.
- Hay una correlación negativa y casi perfecta entre Qb y Qc, lo cual es esperable y lógica.
- Hay una correlación positiva muy alta (0.84) entre Pc y Mc, como si ENEL estuviera fijando el precio Mc.
- Aunque no es muy fuerte (0.5), hay una correlación positiva entre los precios Pc y las cantidades Qc, como si el precio de contrato subiera cuando el margen de contratación aumentara.
- Algo opuesto ocurre con los Precios de contratos y las cantidades compradas en bolsa. Cuando suben los precios de contratos, disminuyen las cantidades compradas en bolsa, esto puede ser consecuencia de la anterior correlación donde suben las cantidades contratadas. Esto no parece tan justo, ya que los precios de contrato son mayores a los de bolsa. En otras palabras, se compra más y más caro.
Sobre los rangos,
- No se exhiben demasiados outliers en las distribuciones de precios y cantidades (en GWh/mes). Este fenómeno es importante para la normalización.
- Tanto primas Rc (Millones de pesos), Qc (GWh/mes), Qb (GWh/mes), Pc (\(/Kwh) y Pb (\)/KWh) se encuentran en los mismos rangos.
1.3 Ajuste a distribuciones paramétricas o no paramétricas de variables de precio y cantidades
Se utilizará el siguiente procedimiento para cada una de las variables a analizar :
- Ajuste a distribuciones paramétricas y elección de mejores ajustes usando criterio AIC y BIC (paquete univariateML).
- Estimación de parámetros de los mejores modelos por Máxima verosimilitud (paquete UnivariateML).
- Estimación de incertidumbre e intervalos de confianza de los parámetros obtenidos mediante bootstrap.
- Presentación de curvas QQ, PP y curvas de densidad para diagnóstico (paquete fitdistrplus).
- Estimación de funciones para nuevos valores a simular en el caso de los Valores a Riesgo paramétricos y no paramétricos (paquete UnivariateML).
- Estimación de bondad de ajuste de las funciones de densidad utilizando la distancia de Kolmogorov-Smirnov (Máxima distancia entre densidad acumulada teórica aproximada vs. densidad empírica) Con esta prueba o test se determina si se puede trabajar con modelos paramétricos o no paramétricos.
1.3.1 Análisis de Precios de Contratos
1.3.1.1 Precios sin deflactar
El primer paso consiste en descubrir la distribución que mejor ajusta siguiendo el criterio de AIC.
| distribucion | df | AIC |
|---|---|---|
| mlinvgamma(DatosObjetivo) | 2 | 636.6676 |
| mlbetapr(DatosObjetivo) | 2 | 636.6701 |
| mlinvgauss(DatosObjetivo) | 2 | 636.8849 |
| mllnorm(DatosObjetivo) | 2 | 636.9724 |
| mlgumbel(DatosObjetivo) | 2 | 637.3198 |
| mlgamma(DatosObjetivo) | 2 | 637.5261 |
| mlnorm(DatosObjetivo) | 2 | 639.5414 |
| mlinvweibull(DatosObjetivo) | 2 | 640.3303 |
| mllaplace(DatosObjetivo) | 2 | 641.2499 |
| mllogis(DatosObjetivo) | 2 | 642.7499 |
| mlweibull(DatosObjetivo) | 2 | 645.6588 |
| mlcauchy(DatosObjetivo) | 2 | 656.1154 |
| mlrayleigh(DatosObjetivo) | 1 | 754.2683 |
| mlexp(DatosObjetivo) | 1 | 841.9362 |
| mllgamma(DatosObjetivo) | 2 | Inf |
El paso siguiente consiste en la estimación de parámetros por Maxima verosimilitud y sus correspondientes intervalos de confianza utilizando el método de bootstrap.
##
## Maximum likelihood for the Lognormal model
##
## Call: mllnorm(x = DatosObjetivo)
##
## Estimates:
## meanlog sdlog
## 5.3535182 0.1384548
##
## Data: DatosObjetivo (66 obs.)
## Support: (0, Inf)
## Density: stats::dlnorm
## Log-likelihood: -316.4862## 5% 95%
## meanlog 5.3267932 5.3808009
## sdlog 0.1168725 0.1577421El siguiente paso es la representación gráfica del ajuste seleccionado.
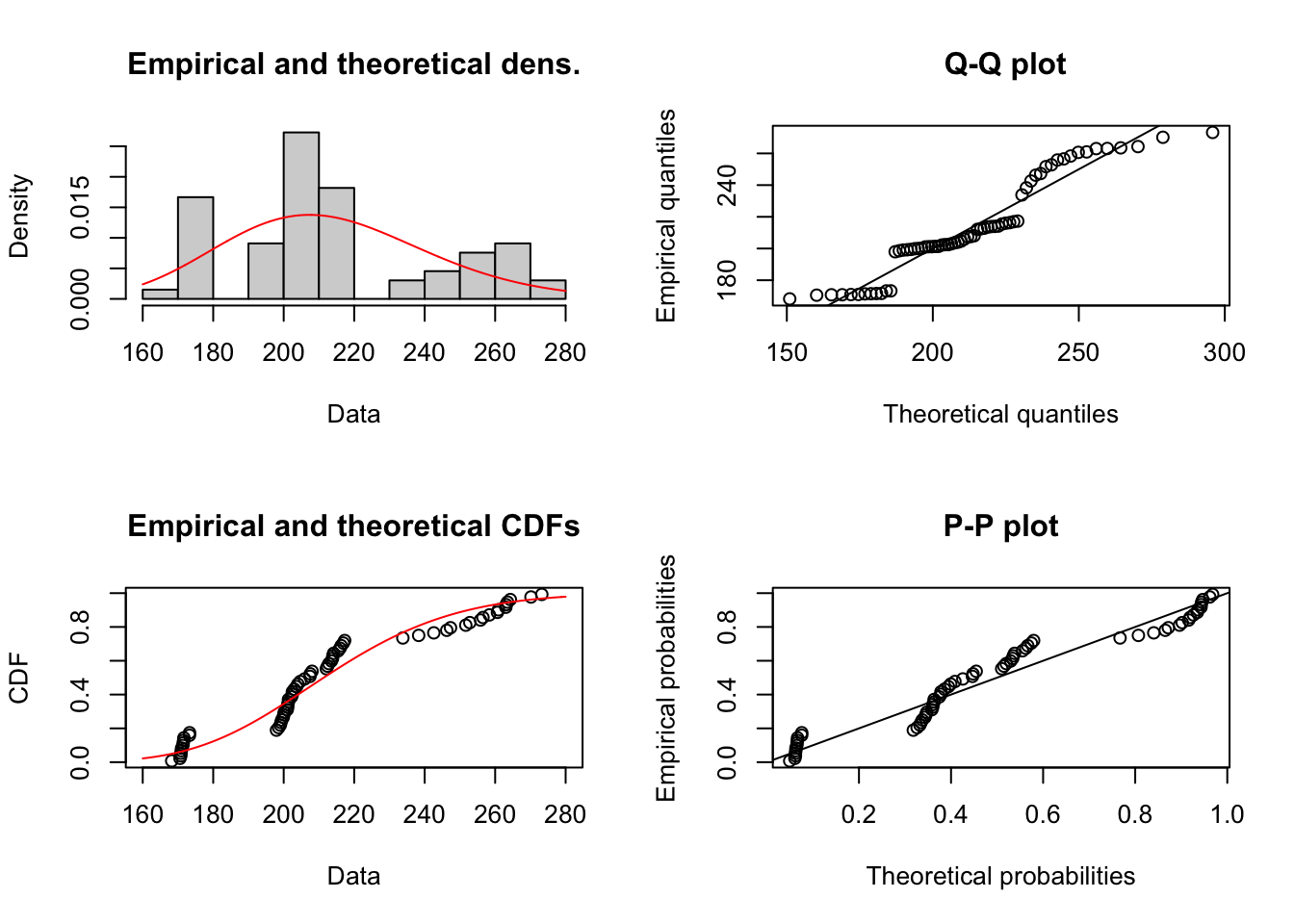
Figure 1.12: Comportamiento de las Cantidades por Prima de costos deflactada
Se dejan las funciones listas para generar los datos de acuerdo a la distribución seleccionada. (Con las funciones dml(), pml(), qml() y rml() se puede calcular la densidad, probabilidad de acumulada, cuantiles, y muestreo de nuevos valores de cualquiera de las distribuciones disponibles en el paquete. Por ejemplo, se pueden simular 5 nuevos valores de diamantes acorde a la distribución ajustada.)
## [1] 195.5698 204.7212 262.2580 213.4239 215.1679 267.9974 225.2778 177.3924
## [9] 192.1776 198.7036Se realiza un Test de Kolmogorov-Smirnov. Una vez calculada la distancia de Kolmogorov–Smirnov, hay que determinar si el valor de esta distancia es suficientemente grande, teniendo en cuenta las muestras disponibles, como para considerar que las dos distribuciones son distintas (p-value). Esto puede conseguirse calculando la probabilidad de observar distancias iguales o mayores si ambas muestras procediesen de la misma distribución, es decir, que las dos distribuciones son la misma.
Para el estadístico de Kolmogorov–Smirnov existen dos tipos de solución:
Solución analítica (exacta): si se cumple que las muestras son grandes y que no hay ligaduras, esta solución es mucho más rápida y genera p-values exactos. Esta solución está implementada en la función ks.test() del paquete stats.
Mediante un test de resampling: consiste en simular, mediante permutaciones o bootstrapping, las distancias de Kolmogorov–Smirnov que se obtendrían si ambas muestras procediesen de la misma distribución. Una vez obtenidas las simulaciones, se calcula el porcentaje de distancias iguales o mayores a la observada.
##
## Two-sample Kolmogorov-Smirnov test
##
## data: DatosGenerados and DatosObjetivo
## D = 0.18182, p-value = 0.2264
## alternative hypothesis: two-sidedEl p-value es demasiado alto, debiera ser menor a 0.05 de forma tal que la probabilidad de encontrar una distancia de Kolmogorov mayor a 0.1363 sea muy baja. Sin embargo, la probabilidad es alta (0.22). Se debe modelar no paramétricamente.
1.3.1.2 Precios deflactados
El primer paso consiste en descubrir la distribución que mejor ajusta siguiendo el criterio de AIC.
| distribucion | df | AIC |
|---|---|---|
| mlweibull(DatosObjetivo) | 2 | 508.1084 |
| mlnorm(DatosObjetivo) | 2 | 516.3770 |
| mlinvgauss(DatosObjetivo) | 2 | 519.2987 |
| mllnorm(DatosObjetivo) | 2 | 519.3099 |
| mllogis(DatosObjetivo) | 2 | 519.7255 |
| mlbetapr(DatosObjetivo) | 2 | 520.4057 |
| mllaplace(DatosObjetivo) | 2 | 525.5567 |
| mlgumbel(DatosObjetivo) | 2 | 533.6291 |
| mlinvweibull(DatosObjetivo) | 2 | 538.6509 |
| mlcauchy(DatosObjetivo) | 2 | 541.0667 |
| mlrayleigh(DatosObjetivo) | 1 | 723.4300 |
| mlexp(DatosObjetivo) | 1 | 814.0022 |
| mlinvgamma(DatosObjetivo) | 2 | Inf |
| mlgamma(DatosObjetivo) | 2 | Inf |
| mllgamma(DatosObjetivo) | 2 | Inf |
El paso siguiente consiste en la estimación de parámetros por Maxima verosimilitud y sus correspondientes intervalos de confianza utilizando el método de bootstrap.
##
## Maximum likelihood for the Weibull model
##
## Call: mlweibull(x = DatosObjetivo)
##
## Estimates:
## shape scale
## 18.77511 177.90166
##
## Data: DatosObjetivo (66 obs.)
## Support: (0, Inf)
## Density: stats::dweibull
## Log-likelihood: -252.0542## 5% 95%
## shape 16.49473 22.71341
## scale 175.79271 179.82700El siguiente paso es la representación gráfica del ajuste seleccionado.
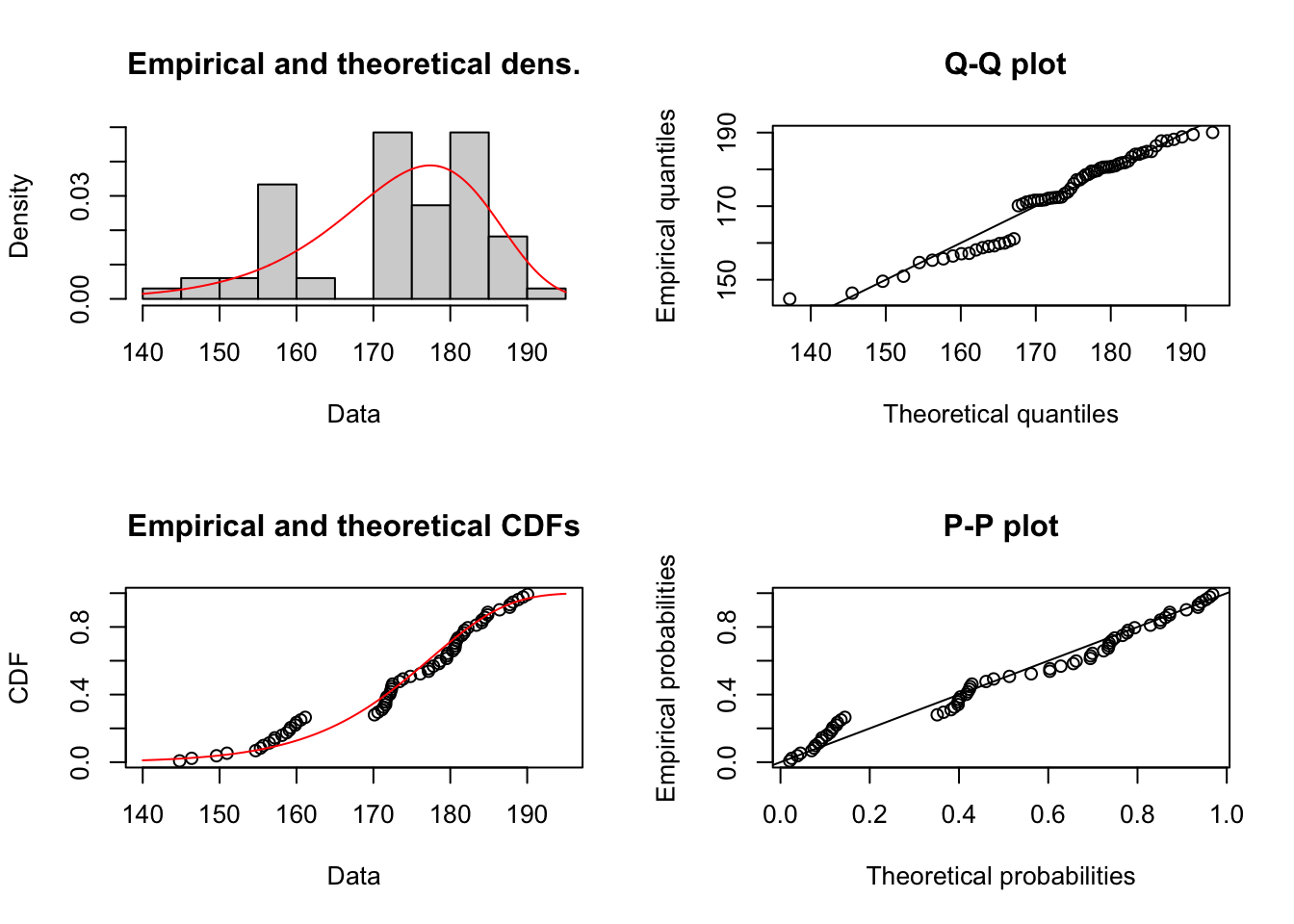
Figure 1.13: Comportamiento de las Cantidades por Prima de costos deflactada
Se dejan las funciones listas para generar los datos de acuerdo a la distribución seleccionada. (Con las funciones dml(), pml(), qml() y rml() se puede calcular la densidad, probabilidad de acumulada, cuantiles, y muestreo de nuevos valores de cualquiera de las distribuciones disponibles en el paquete. Por ejemplo, se pueden simular 5 nuevos valores de diamantes acorde a la distribución ajustada.)
## [1] 179.9999 164.8020 176.8441 159.2100 153.3301 188.9153 173.7005 158.4573
## [9] 173.0531 175.6097Se realiza un Test de Kolmogorov-Smirnov. Una vez calculada la distancia de Kolmogorov–Smirnov, hay que determinar si el valor de esta distancia es suficientemente grande, teniendo en cuenta las muestras disponibles, como para considerar que las dos distribuciones son distintas (p-value). Esto puede conseguirse calculando la probabilidad de observar distancias iguales o mayores si ambas muestras procediesen de la misma distribución, es decir, que las dos distribuciones son la misma.
Para el estadístico de Kolmogorov–Smirnov existen dos tipos de solución:
Solución analítica (exacta): si se cumple que las muestras son grandes y que no hay ligaduras, esta solución es mucho más rápida y genera p-values exactos. Esta solución está implementada en la función ks.test() del paquete stats.
Mediante un test de resampling: consiste en simular, mediante permutaciones o bootstrapping, las distancias de Kolmogorov–Smirnov que se obtendrían si ambas muestras procediesen de la misma distribución. Una vez obtenidas las simulaciones, se calcula el porcentaje de distancias iguales o mayores a la observada.
##
## Two-sample Kolmogorov-Smirnov test
##
## data: DatosGenerados and DatosObjetivo
## D = 0.090909, p-value = 0.9505
## alternative hypothesis: two-sidedEl p-value es demasiado alto, debiera ser menor a 0.05 de forma tal que la probabilidad de encontrar una distancia de Kolmogorov mayor a 0.09 sea muy baja. Sin embargo, la probabilidad es alta (0.95). Se debe modelar no paramétricamente.
1.3.2 Análisis de Precios de Bolsa
1.3.2.1 Precios sin deflactar
El primer paso consiste en descubrir la distribución que mejor ajusta siguiendo el criterio de AIC.
| distribucion | df | AIC |
|---|---|---|
| mlinvgamma(DatosObjetivo) | 2 | 768.1587 |
| mlbetapr(DatosObjetivo) | 2 | 768.1881 |
| mlinvweibull(DatosObjetivo) | 2 | 768.3657 |
| mlinvgauss(DatosObjetivo) | 2 | 768.7240 |
| mllgamma(DatosObjetivo) | 2 | 769.0624 |
| mllnorm(DatosObjetivo) | 2 | 770.3519 |
| mlgamma(DatosObjetivo) | 2 | 775.0331 |
| mlgumbel(DatosObjetivo) | 2 | 776.4875 |
| mlrayleigh(DatosObjetivo) | 1 | 779.3744 |
| mlweibull(DatosObjetivo) | 2 | 781.3680 |
| mlnorm(DatosObjetivo) | 2 | 795.0280 |
| mllogis(DatosObjetivo) | 2 | 796.2847 |
| mllaplace(DatosObjetivo) | 2 | 798.0207 |
| mlcauchy(DatosObjetivo) | 2 | 806.6529 |
| mlexp(DatosObjetivo) | 1 | 820.0707 |
El paso siguiente consiste en la estimación de parámetros por Maxima verosimilitud y sus correspondientes intervalos de confianza utilizando el método de bootstrap.
##
## Maximum likelihood for the InvGamma model
##
## Call: mlinvgamma(x = DatosObjetivo)
##
## Estimates:
## alpha beta
## 4.334467 609.083866
##
## Data: DatosObjetivo (66 obs.)
## Support: (0, Inf)
## Density: extraDistr::dinvgamma
## Log-likelihood: -382.0794## 5% 95%
## alpha 3.367789 5.931205
## beta 466.841362 848.380865El siguiente paso es la representación gráfica del ajuste seleccionado.
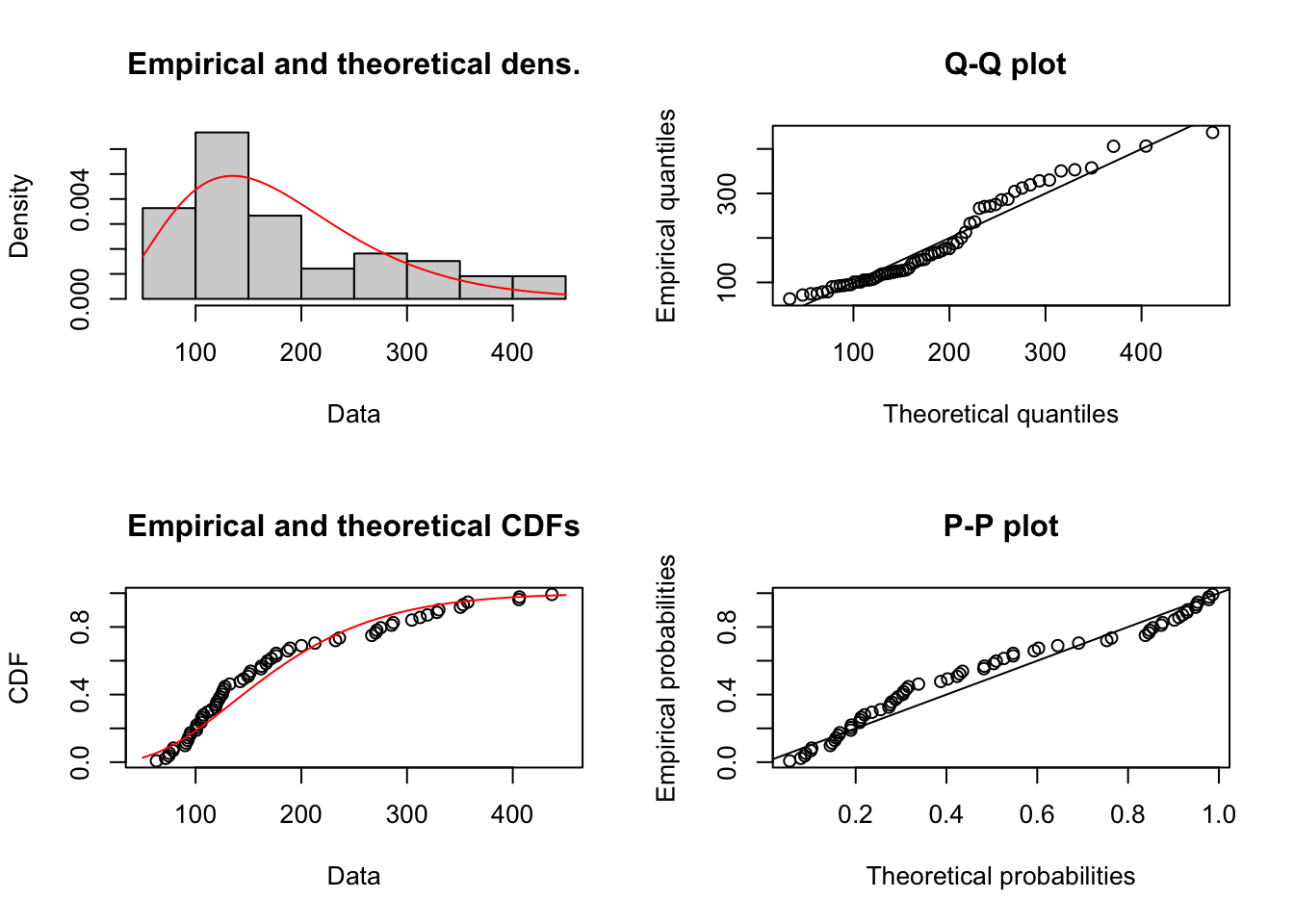
Figure 1.14: Comportamiento de las Cantidades por Prima de costos deflactada
Se dejan las funciones listas para generar los datos de acuerdo a la distribución seleccionada. (Con las funciones dml(), pml(), qml() y rml() se puede calcular la densidad, probabilidad de acumulada, cuantiles, y muestreo de nuevos valores de cualquiera de las distribuciones disponibles en el paquete. Por ejemplo, se pueden simular 5 nuevos valores de diamantes acorde a la distribución ajustada.)
## [1] 216.33329 93.42847 491.33004 148.85422 76.82465 127.15381 346.59320
## [8] 508.40575 92.20115 133.23753Test de Kolmogorov
##
## Two-sample Kolmogorov-Smirnov test
##
## data: DatosGenerados and DatosObjetivo
## D = 0.24242, p-value = 0.04099
## alternative hypothesis: two-sidedEl p-value es demasiado alto, debiera ser menor a 0.05 de forma tal que la probabilidad de encontrar una distancia de Kolmogorov mayor a 0.1363 sea muy baja. En este caso, la probabilidad es baja (0.04). Se debe modelar paramétricamente con una función inversa de gamma.
1.3.2.2 Precios deflactados
El primer paso consiste en descubrir la distribución que mejor ajusta siguiendo el criterio de AIC.
| distribucion | df | AIC |
|---|---|---|
| mlinvgauss(DatosObjetivo) | 2 | 742.8038 |
| mlinvgamma(DatosObjetivo) | 2 | 742.8669 |
| mlbetapr(DatosObjetivo) | 2 | 742.8927 |
| mllgamma(DatosObjetivo) | 2 | 743.2881 |
| mlinvweibull(DatosObjetivo) | 2 | 743.7603 |
| mllnorm(DatosObjetivo) | 2 | 744.3384 |
| mlgamma(DatosObjetivo) | 2 | 748.4645 |
| mlgumbel(DatosObjetivo) | 2 | 750.0135 |
| mlrayleigh(DatosObjetivo) | 1 | 752.5828 |
| mlweibull(DatosObjetivo) | 2 | 754.5785 |
| mlnorm(DatosObjetivo) | 2 | 768.1041 |
| mllogis(DatosObjetivo) | 2 | 768.4197 |
| mllaplace(DatosObjetivo) | 2 | 769.4201 |
| mlcauchy(DatosObjetivo) | 2 | 781.1126 |
| mlexp(DatosObjetivo) | 1 | 793.1977 |
El paso siguiente consiste en la estimación de parámetros por Maxima verosimilitud y sus correspondientes intervalos de confianza utilizando el método de bootstrap.
##
## Maximum likelihood for the InvGamma model
##
## Call: mlinvgamma(x = DatosObjetivo)
##
## Estimates:
## alpha beta
## 4.232914 483.424691
##
## Data: DatosObjetivo (66 obs.)
## Support: (0, Inf)
## Density: extraDistr::dinvgamma
## Log-likelihood: -369.4335## 5% 95%
## alpha 3.284454 5.848535
## beta 372.487871 667.391989El siguiente paso es la representación gráfica del ajuste seleccionado.
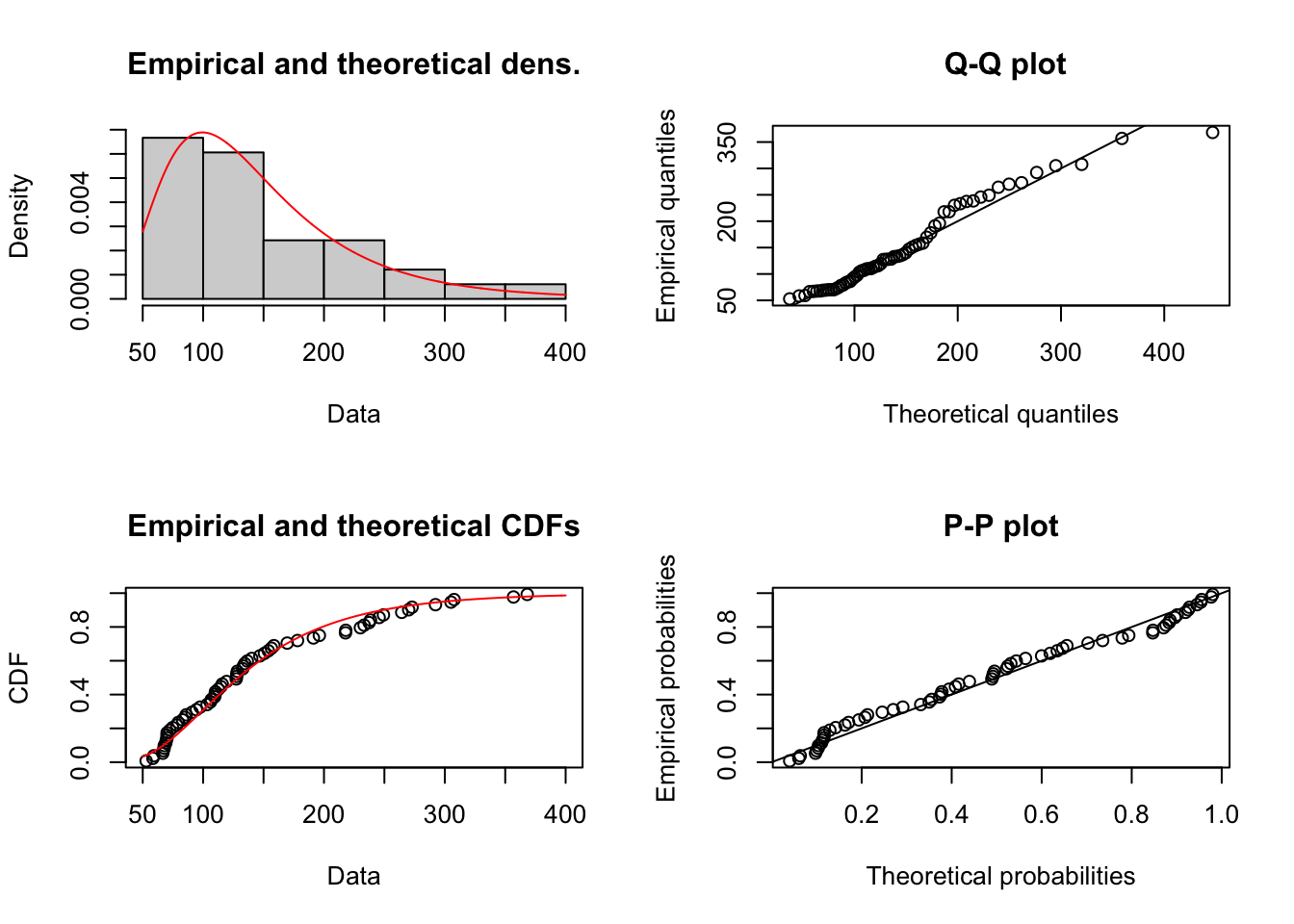
Figure 1.15: Comportamiento de las Cantidades por Prima de costos deflactada
Se dejan las funciones listas para generar los datos de acuerdo a la distribución seleccionada. (Con las funciones dml(), pml(), qml() y rml() se puede calcular la densidad, probabilidad de acumulada, cuantiles, y muestreo de nuevos valores de cualquiera de las distribuciones disponibles en el paquete. Por ejemplo, se pueden simular 5 nuevos valores de diamantes acorde a la distribución ajustada.)
## [1] 96.95608 114.78885 286.43354 133.85991 137.94288 310.26609 163.42527
## [8] 67.63327 90.89080 102.81658Se realiza un Test de Kolmogorov-Smirnov. Una vez calculada la distancia de Kolmogorov–Smirnov, hay que determinar si el valor de esta distancia es suficientemente grande, teniendo en cuenta las muestras disponibles, como para considerar que las dos distribuciones son distintas (p-value). Esto puede conseguirse calculando la probabilidad de observar distancias iguales o mayores si ambas muestras procediesen de la misma distribución, es decir, que las dos distribuciones son la misma.
Para el estadístico de Kolmogorov–Smirnov existen dos tipos de solución:
Solución analítica (exacta): si se cumple que las muestras son grandes y que no hay ligaduras, esta solución es mucho más rápida y genera p-values exactos. Esta solución está implementada en la función ks.test() del paquete stats.
Mediante un test de resampling: consiste en simular, mediante permutaciones o bootstrapping, las distancias de Kolmogorov–Smirnov que se obtendrían si ambas muestras procediesen de la misma distribución. Una vez obtenidas las simulaciones, se calcula el porcentaje de distancias iguales o mayores a la observada.
##
## Two-sample Kolmogorov-Smirnov test
##
## data: DatosGenerados and DatosObjetivo
## D = 0.12121, p-value = 0.7215
## alternative hypothesis: two-sidedEl p-value es demasiado alto, debiera ser menor a 0.05 de forma tal que la probabilidad de encontrar una distancia de Kolmogorov mayor a 0.12 sea muy baja. Sin embargo, la probabilidad es alta (0.72). Sin embargo, elcomportamiento a lo largo de la distribucion acumulada es muy buena. Se podría trabajar paramétricabemente como una log normal.
1.3.3 Análisis de Precios Mc
1.3.3.1 Precios sin deflactar
El primer paso consiste en descubrir la distribución que mejor ajusta siguiendo el criterio de AIC.
| distribucion | df | AIC |
|---|---|---|
| mlgumbel(DatosObjetivo) | 2 | 640.8032 |
| mlinvweibull(DatosObjetivo) | 2 | 640.9515 |
| mlinvgamma(DatosObjetivo) | 2 | 643.1323 |
| mlbetapr(DatosObjetivo) | 2 | 643.1426 |
| mlinvgauss(DatosObjetivo) | 2 | 644.1442 |
| mllnorm(DatosObjetivo) | 2 | 644.2492 |
| mlgamma(DatosObjetivo) | 2 | 645.6268 |
| mlnorm(DatosObjetivo) | 2 | 649.3652 |
| mllogis(DatosObjetivo) | 2 | 651.9493 |
| mllaplace(DatosObjetivo) | 2 | 657.3226 |
| mlweibull(DatosObjetivo) | 2 | 657.8210 |
| mlcauchy(DatosObjetivo) | 2 | 674.7770 |
| mlrayleigh(DatosObjetivo) | 1 | 754.9082 |
| mlexp(DatosObjetivo) | 1 | 842.0060 |
| mllgamma(DatosObjetivo) | 2 | Inf |
El paso siguiente consiste en la estimación de parámetros por Maxima verosimilitud y sus correspondientes intervalos de confianza utilizando el método de bootstrap.
##
## Maximum likelihood for the Gumbel model
##
## Call: mlgumbel(x = DatosObjetivo)
##
## Estimates:
## mu sigma
## 198.5177 25.3556
##
## Data: DatosObjetivo (66 obs.)
## Support: (-Inf, Inf)
## Density: extraDistr::dgumbel
## Log-likelihood: -318.4016## 5% 95%
## mu 193.40261 204.09729
## sigma 21.06161 28.91131El siguiente paso es la representación gráfica del ajuste seleccionado.
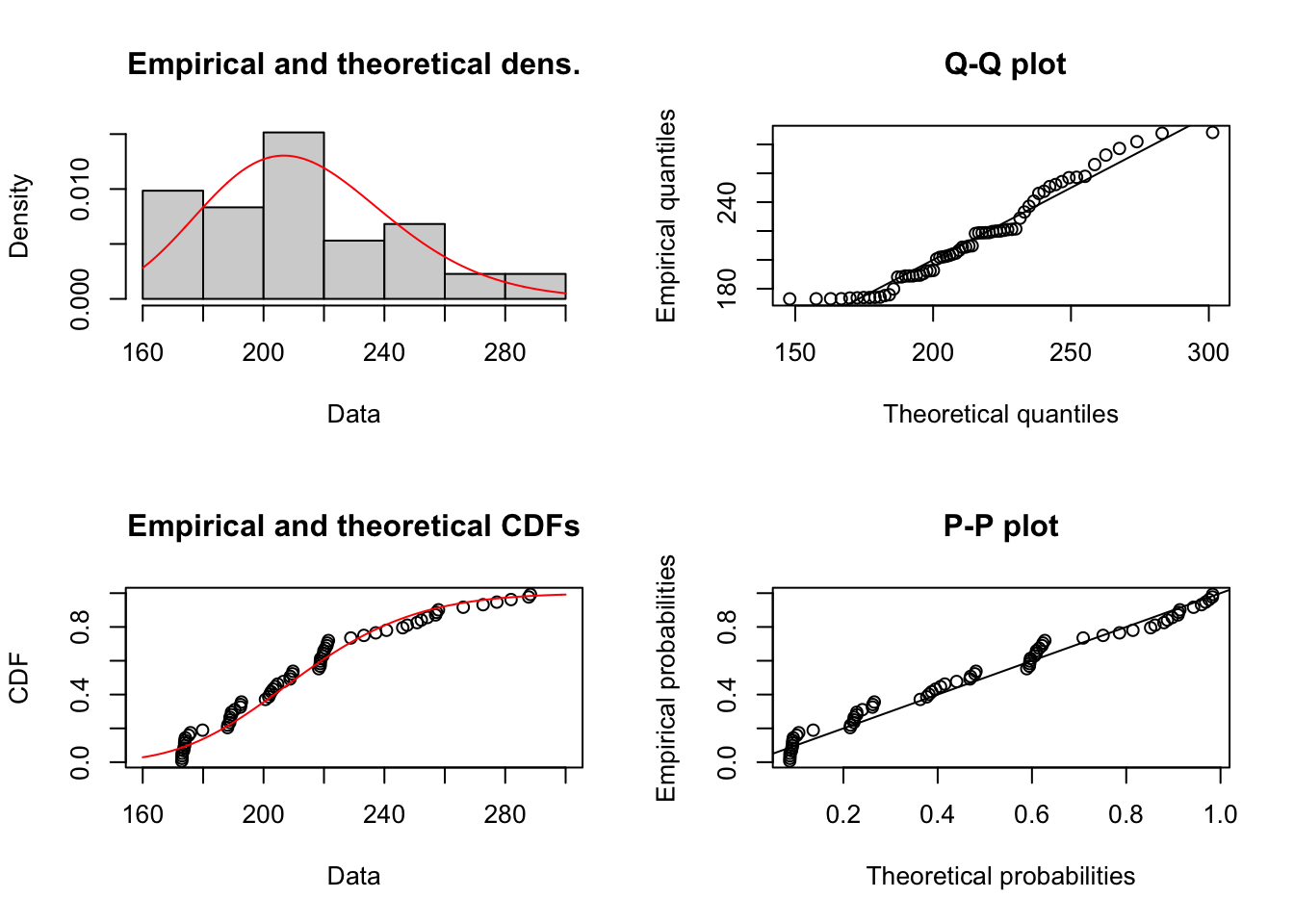
Figure 1.16: Comportamiento de las Cantidades por Prima de costos deflactada
Se dejan las funciones listas para generar los datos de acuerdo a la distribución seleccionada. (Con las funciones dml(), pml(), qml() y rml() se puede calcular la densidad, probabilidad de acumulada, cuantiles, y muestreo de nuevos valores de cualquiera de las distribuciones disponibles en el paquete. Por ejemplo, se pueden simular 5 nuevos valores de diamantes acorde a la distribución ajustada.)
## [1] 195.4943 206.1110 263.6110 215.7760 217.6653 268.6368 228.3248 172.8469
## [9] 191.4322 199.1847Test de Kolmogorov
##
## Two-sample Kolmogorov-Smirnov test
##
## data: DatosGenerados and DatosObjetivo
## D = 0.15152, p-value = 0.4376
## alternative hypothesis: two-sidedEl p-value es demasiado alto, debiera ser menor a 0.05 de forma tal que la probabilidad de encontrar una distancia de Kolmogorov mayor a 0.15152 sea muy baja. En este caso, la probabilidad es alta (0.43). No se puede modelar paramétricamente.
1.3.3.2 Precios deflactados
El primer paso consiste en descubrir la distribución que mejor ajusta siguiendo el criterio de AIC.
| distribucion | df | AIC |
|---|---|---|
| mlgumbel(DatosObjetivo) | 2 | 491.5170 |
| mlinvweibull(DatosObjetivo) | 2 | 491.9053 |
| mlbetapr(DatosObjetivo) | 2 | 493.4328 |
| mlinvgauss(DatosObjetivo) | 2 | 493.7130 |
| mllnorm(DatosObjetivo) | 2 | 493.7341 |
| mlnorm(DatosObjetivo) | 2 | 494.8694 |
| mllogis(DatosObjetivo) | 2 | 500.3632 |
| mlweibull(DatosObjetivo) | 2 | 503.4347 |
| mllaplace(DatosObjetivo) | 2 | 510.5954 |
| mlcauchy(DatosObjetivo) | 2 | 531.1531 |
| mlrayleigh(DatosObjetivo) | 1 | 722.9721 |
| mlexp(DatosObjetivo) | 1 | 813.8082 |
| mlinvgamma(DatosObjetivo) | 2 | Inf |
| mlgamma(DatosObjetivo) | 2 | Inf |
| mllgamma(DatosObjetivo) | 2 | Inf |
El paso siguiente consiste en la estimación de parámetros por Maxima verosimilitud y sus correspondientes intervalos de confianza utilizando el método de bootstrap.
##
## Maximum likelihood for the Lognormal model
##
## Call: mllnorm(x = DatosObjetivo)
##
## Estimates:
## meanlog sdlog
## 5.14840580 0.05742717
##
## Data: DatosObjetivo (66 obs.)
## Support: (0, Inf)
## Density: stats::dlnorm
## Log-likelihood: -244.867## 5% 95%
## meanlog 5.13673426 5.15964542
## sdlog 0.04876042 0.06485509El siguiente paso es la representación gráfica del ajuste seleccionado.
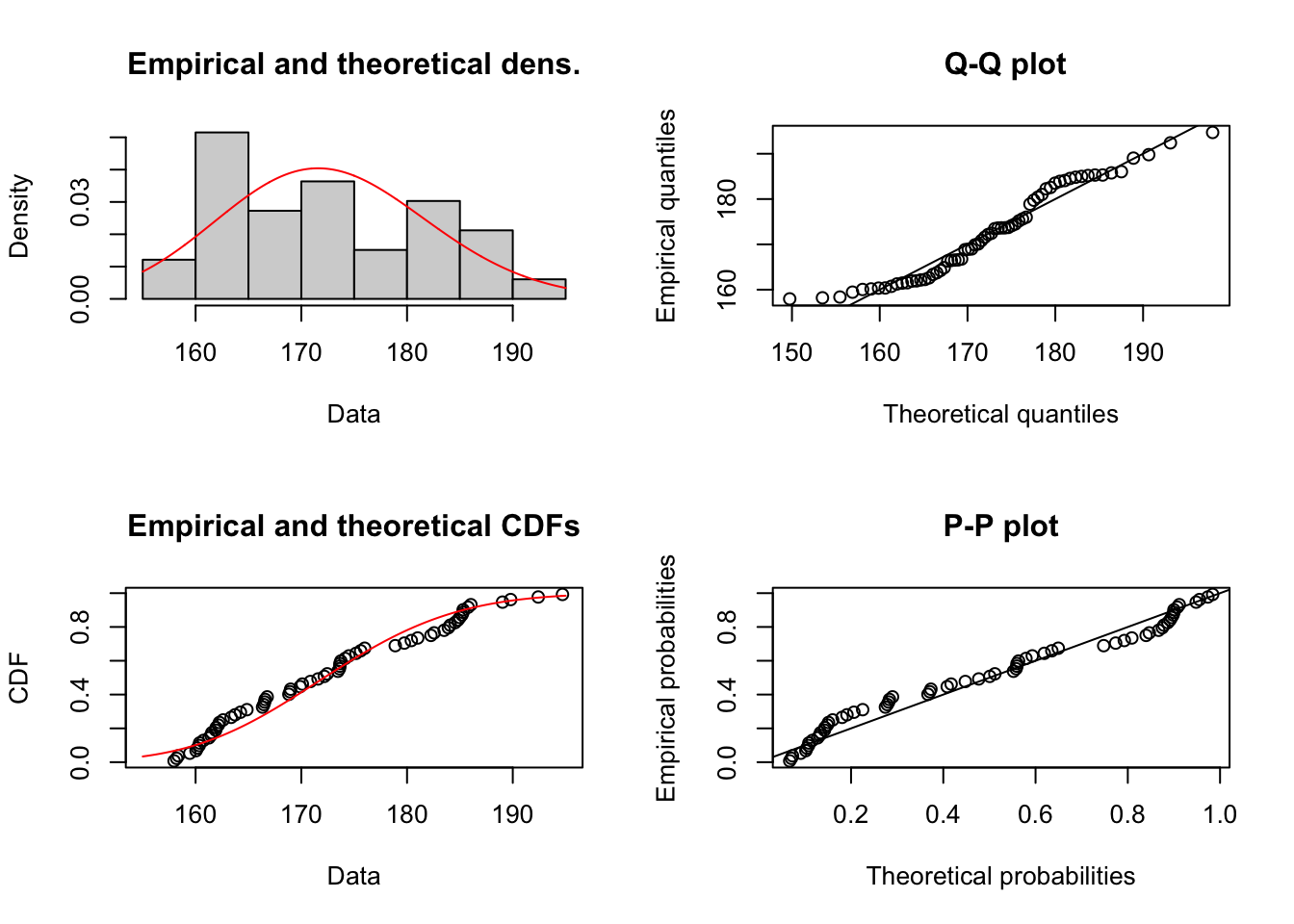
Figure 1.17: Comportamiento de las Cantidades por Prima de costos deflactada
Se dejan las funciones listas para generar los datos de acuerdo a la distribución seleccionada. (Con las funciones dml(), pml(), qml() y rml() se puede calcular la densidad, probabilidad de acumulada, cuantiles, y muestreo de nuevos valores de cualquiera de las distribuciones disponibles en el paquete. Por ejemplo, se pueden simular 5 nuevos valores de diamantes acorde a la distribución ajustada.)
## [1] 166.7039 169.8961 188.2777 172.8553 173.4398 189.9759 176.7745 160.0933
## [9] 165.4984 167.8067Se realiza un Test de Kolmogorov-Smirnov. Una vez calculada la distancia de Kolmogorov–Smirnov, hay que determinar si el valor de esta distancia es suficientemente grande, teniendo en cuenta las muestras disponibles, como para considerar que las dos distribuciones son distintas (p-value). Esto puede conseguirse calculando la probabilidad de observar distancias iguales o mayores si ambas muestras procediesen de la misma distribución, es decir, que las dos distribuciones son la misma.
Para el estadístico de Kolmogorov–Smirnov existen dos tipos de solución:
Solución analítica (exacta): si se cumple que las muestras son grandes y que no hay ligaduras, esta solución es mucho más rápida y genera p-values exactos. Esta solución está implementada en la función ks.test() del paquete stats.
Mediante un test de resampling: consiste en simular, mediante permutaciones o bootstrapping, las distancias de Kolmogorov–Smirnov que se obtendrían si ambas muestras procediesen de la misma distribución. Una vez obtenidas las simulaciones, se calcula el porcentaje de distancias iguales o mayores a la observada.
##
## Two-sample Kolmogorov-Smirnov test
##
## data: DatosGenerados and DatosObjetivo
## D = 0.15152, p-value = 0.4376
## alternative hypothesis: two-sidedEl p-value es demasiado alto, debiera ser menor a 0.05 de forma tal que la probabilidad de encontrar una distancia de Kolmogorov mayor a 0.15 sea muy baja. Sin embargo, la probabilidad es alta (0.43). Se debe modelar no paramétricamente.
1.3.4 Análisis de cantidades compradas en Contrato (Qc)
El primer paso consiste en descubrir la distribución que mejor ajusta siguiendo el criterio de AIC.
| distribucion | df | AIC |
|---|---|---|
| mlweibull(DatosObjetivo) | 2 | 781.5049 |
| mlnorm(DatosObjetivo) | 2 | 785.2429 |
| mlgamma(DatosObjetivo) | 2 | 787.3335 |
| mlinvgauss(DatosObjetivo) | 2 | 788.6791 |
| mllnorm(DatosObjetivo) | 2 | 788.7312 |
| mllogis(DatosObjetivo) | 2 | 790.1910 |
| mlbetapr(DatosObjetivo) | 2 | 790.3202 |
| mlinvgamma(DatosObjetivo) | 2 | 790.3247 |
| mllaplace(DatosObjetivo) | 2 | 800.8843 |
| mlinvweibull(DatosObjetivo) | 2 | 805.0141 |
| mlcauchy(DatosObjetivo) | 2 | 819.9270 |
| mlrayleigh(DatosObjetivo) | 1 | 915.4215 |
| mlexp(DatosObjetivo) | 1 | 1003.8583 |
| mllgamma(DatosObjetivo) | 2 | Inf |
El paso siguiente consiste en la estimación de parámetros por Maxima verosimilitud y sus correspondientes intervalos de confianza utilizando el método de bootstrap.
##
## Maximum likelihood for the Weibull model
##
## Call: mlweibull(x = DatosObjetivo)
##
## Estimates:
## shape scale
## 9.791492 766.688593
##
## Data: DatosObjetivo (66 obs.)
## Support: (0, Inf)
## Density: stats::dweibull
## Log-likelihood: -388.7524## 5% 95%
## shape 8.541512 11.8957
## scale 750.348558 781.9120El siguiente paso es la representación gráfica del ajuste seleccionado.
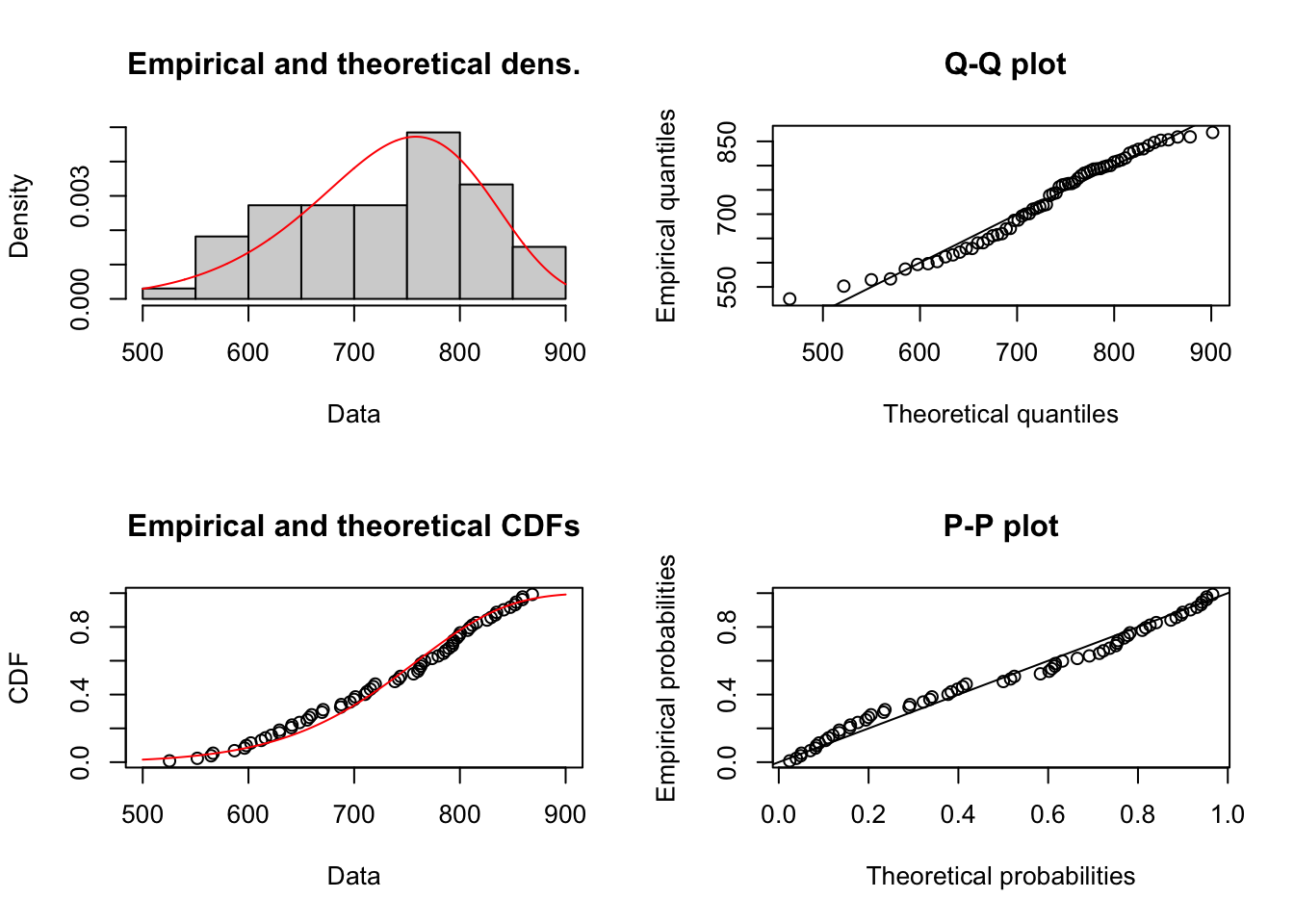
Figure 1.18: Comportamiento de las Cantidades por Prima de costos deflactada
Se dejan las funciones listas para generar los datos de acuerdo a la distribución seleccionada. (Con las funciones dml(), pml(), qml() y rml() se puede calcular la densidad, probabilidad de acumulada, cuantiles, y muestreo de nuevos valores de cualquiera de las distribuciones disponibles en el paquete. Por ejemplo, se pueden simular 5 nuevos valores de diamantes acorde a la distribución ajustada.)
## [1] 784121865 662102007 757973318 619693836 576553583 860282336 732347754
## [8] 614088400 727122820 747860788Test de Kolmogorov
##
## Two-sample Kolmogorov-Smirnov test
##
## data: DatosGenerados and DatosObjetivo
## D = 0.075758, p-value = 0.9923
## alternative hypothesis: two-sidedEl p-value es demasiado alto, debiera ser menor a 0.05 de forma tal que la probabilidad de encontrar una distancia de Kolmogorov mayor a 0.07 sea muy baja. En este caso, la probabilidad es alta (0.99). Sin embargo, la distancia entre las cdfs es la más baja de todas. Se puede considerar modelable con un modelo weibull ya que las diferencias en las cdfs son muy bajas y no sinteresa el tema de las colsas de la distribución para el cálculo del VaR.
1.3.5 Análisis de cantidades compradas en bolsa (Qb)
El primer paso consiste en descubrir la distribución que mejor ajusta siguiendo el criterio de AIC.
| distribucion | df | AIC |
|---|---|---|
| mlweibull(DatosObjetivo) | 2 | 766.0764 |
| mlrayleigh(DatosObjetivo) | 1 | 766.3077 |
| mlgamma(DatosObjetivo) | 2 | 768.8097 |
| mlnorm(DatosObjetivo) | 2 | 775.4146 |
| mllnorm(DatosObjetivo) | 2 | 778.6151 |
| mllogis(DatosObjetivo) | 2 | 778.8292 |
| mlinvgauss(DatosObjetivo) | 2 | 783.8729 |
| mllgamma(DatosObjetivo) | 2 | 786.4256 |
| mllaplace(DatosObjetivo) | 2 | 787.0305 |
| mlexp(DatosObjetivo) | 1 | 788.2307 |
| mlbetapr(DatosObjetivo) | 2 | 797.7771 |
| mlinvgamma(DatosObjetivo) | 2 | 798.5241 |
| mlinvweibull(DatosObjetivo) | 2 | 803.4579 |
| mlcauchy(DatosObjetivo) | 2 | 805.7396 |
El paso siguiente consiste en la estimación de parámetros por Maxima verosimilitud y sus correspondientes intervalos de confianza utilizando el método de bootstrap.
##
## Maximum likelihood for the Weibull model
##
## Call: mlweibull(x = DatosObjetivo)
##
## Estimates:
## shape scale
## 1.732965 159.272717
##
## Data: DatosObjetivo (66 obs.)
## Support: (0, Inf)
## Density: stats::dweibull
## Log-likelihood: -381.0382## 5% 95%
## shape 1.511735 2.105382
## scale 141.060714 177.986569El siguiente paso es la representación gráfica del ajuste seleccionado.
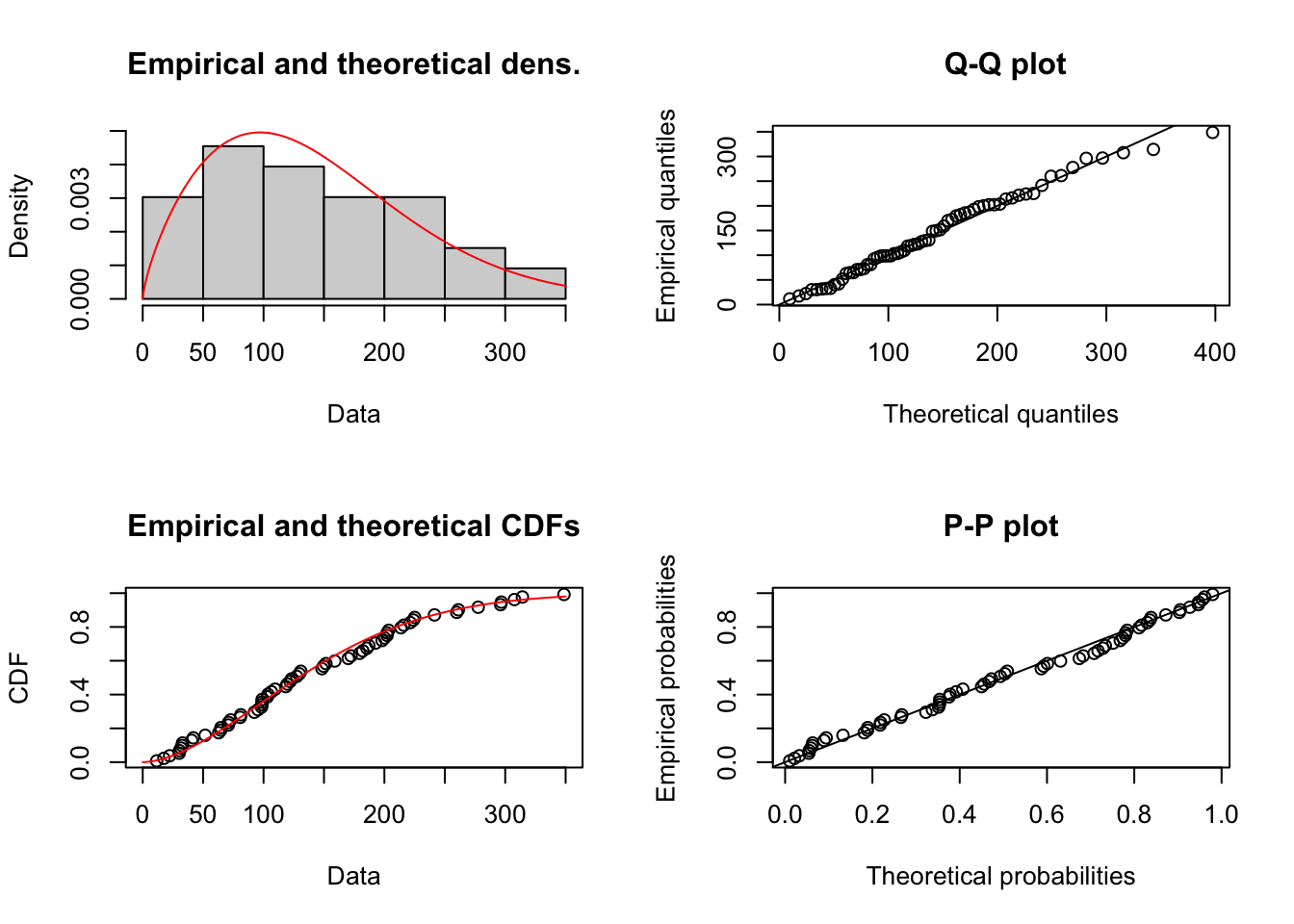
Figure 1.19: Comportamiento de las Cantidades por Prima de costos deflactada
Se dejan las funciones listas para generar los datos de acuerdo a la distribución seleccionada. (Con las funciones dml(), pml(), qml() y rml() se puede calcular la densidad, probabilidad de acumulada, cuantiles, y muestreo de nuevos valores de cualquiera de las distribuciones disponibles en el paquete. Por ejemplo, se pueden simular 5 nuevos valores de diamantes acorde a la distribución ajustada.)
## [1] 180.84750 69.54420 149.30968 47.84453 31.82519 305.33222 122.94031
## [8] 45.45014 118.06598 138.39801Test de Kolmogorov
##
## Two-sample Kolmogorov-Smirnov test
##
## data: DatosGenerados and DatosObjetivo
## D = 0.075758, p-value = 0.9923
## alternative hypothesis: two-sidedEl p-value es demasiado alto, debiera ser menor a 0.05 de forma tal que la probabilidad de encontrar una distancia de Kolmogorov mayor a 0.07 sea muy baja. En este caso, la probabilidad es alta (0.99). Sin embargo, la distancia entre las cdfs es la más baja de todas. Se puede considerar modelable con un modelo weibull ya que las diferencias en las cdfs son muy bajas y no sinteresa el tema de las colsas de la distribución para el cálculo del VaR.
1.4 Análisis de regresión (Análisis Transversal)
1.4.1 Regresión multivariada
Análisis de regresión transversal multivariada para explicar la variabilidad de la prima de costos en términos de las variables regresoras de precios y cantidades. : El aporte consiste en averiguar las variables que impacten más sensiblemente a esta desviación.
\[\begin{equation} Prima_{costos} = \beta_{1}Qc + \beta_{2}Pc + \beta_{3}Mc + \beta_{4}Pb + \beta_{5}Pb_{pais} \end{equation}\]
Se irá variando el modelo añadiendo o eliminando variables con el fin de encontrar el mejor modelo utilizando algunas métricas estadisticas (AIC). Si se trabaja el Rc en millones de pesos, y las cantidades en GWh/mes, las escalas son similares.
1.4.1.1 Con valores sin deflactar
## Start: AIC=758.94
## Rc ~ Qc + Pcontratos + Qb + Pbolsa + Mc
##
## Df Sum of Sq RSS AIC
## - Qb 1 27846 5454661 757.27
## - Qc 1 38718 5465533 757.40
## <none> 5426815 758.94
## - Pbolsa 1 289858 5716673 760.37
## - Pcontratos 1 46322459 51749274 905.77
## - Mc 1 46648404 52075219 906.18
##
## Step: AIC=757.27
## Rc ~ Qc + Pcontratos + Pbolsa + Mc
##
## Df Sum of Sq RSS AIC
## <none> 5454661 757.27
## + Qb 1 27846 5426815 758.94
## - Pbolsa 1 375283 5829944 759.66
## - Qc 1 1327233 6781895 769.65
## - Pcontratos 1 46488886 51943547 904.02
## - Mc 1 47718706 53173367 905.56##
## Call:
## lm(formula = Rc ~ Qc + Pcontratos + Pbolsa + Mc, data = datosregresion)
##
## Residuals:
## Min 1Q Median 3Q Max
## -535.12 -193.05 -60.24 210.15 880.42
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) -363.6133 428.7618 -0.848 0.399723
## Qc 1.7340 0.4501 3.853 0.000283 ***
## Pcontratos -115.2470 5.0545 -22.801 < 2e-16 ***
## Pbolsa 0.8385 0.4093 2.049 0.044809 *
## Mc 110.8501 4.7986 23.101 < 2e-16 ***
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 299 on 61 degrees of freedom
## Multiple R-squared: 0.9139, Adjusted R-squared: 0.9082
## F-statistic: 161.8 on 4 and 61 DF, p-value: < 2.2e-16\[\begin{equation} Prima_{costos} = -363.61 + 1.734*Qc -115.24*Pcontratos +0.83*Pbolsa + 110.85*Mc \end{equation}\]
Los precios de contratos Pc y Mc son los que más explican la variabilidad de la prima de costos, pero de manera distinta:
- Cuando Mc sube, la prima sube.
- Cuando Pc sube, la prima baja.
Validación regresión lineal
Validación regresión lineal
1.4.1.1.1 Residuos aleatoriamente distribuidos
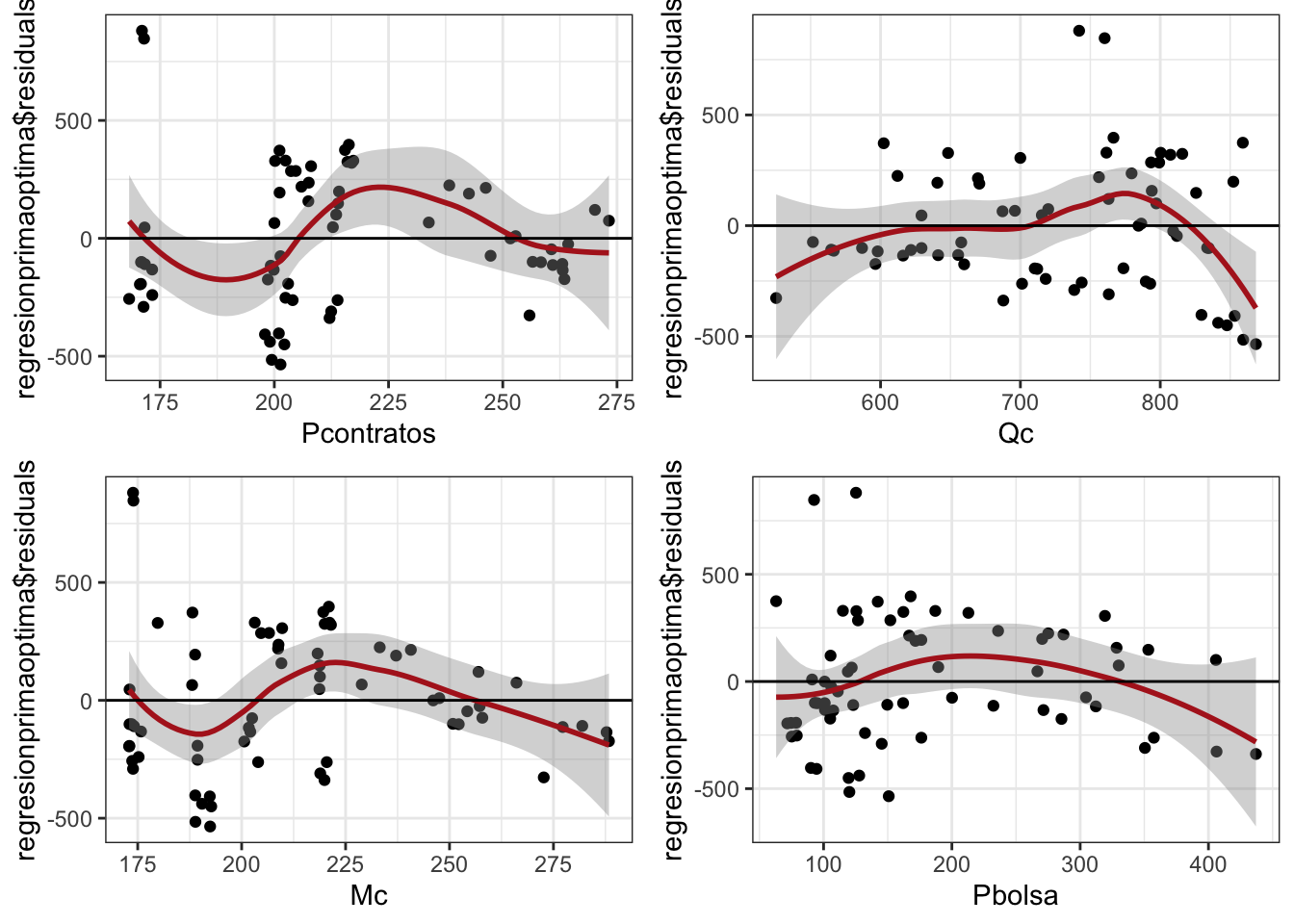
Figure 1.20: Comportamiento de las Cantidades por Prima de costos deflactada
Si la relación es lineal, los residuos deben de distribuirse aleatoriamente en torno a 0 con una variabilidad constante a lo largo del eje X.
1.4.1.1.2 Normalidad de residuos
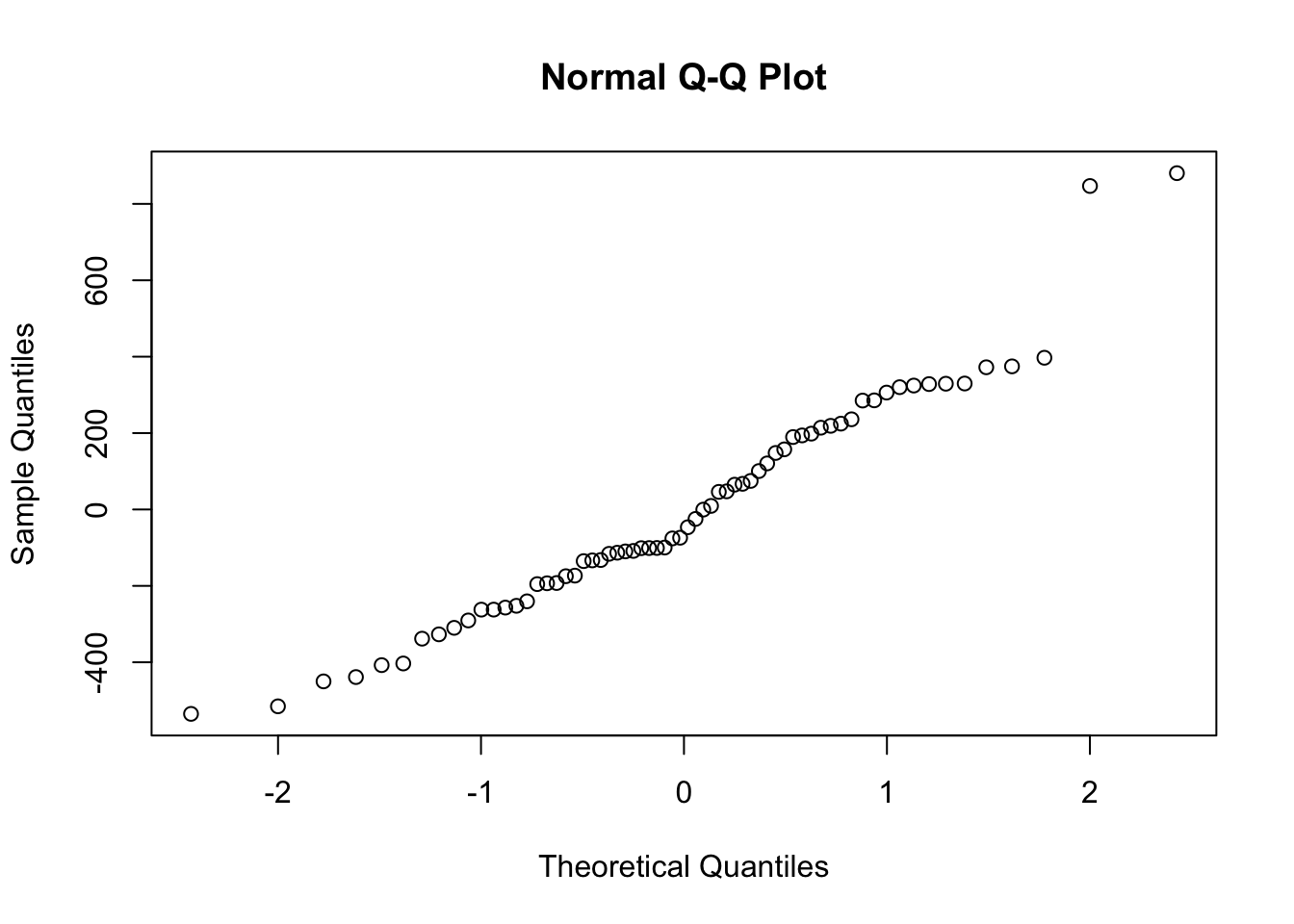
Figure 1.21: Comportamiento de las Cantidades por Prima de costos deflactada
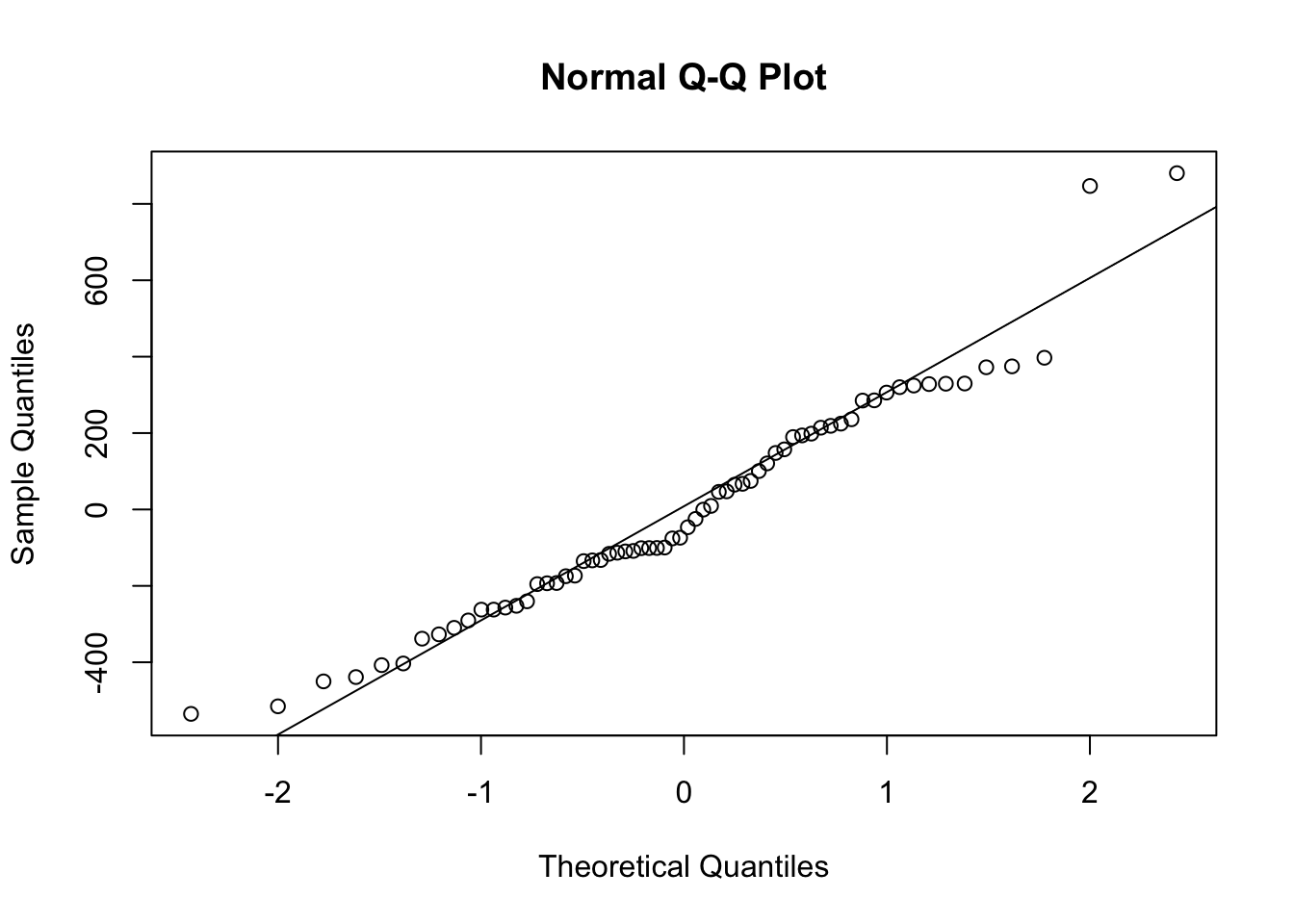
Figure 1.22: Comportamiento de las Cantidades por Prima de costos deflactada
##
## Shapiro-Wilk normality test
##
## data: regresionprimaoptima$residuals[1:66]
## W = 0.96142, p-value = 0.03825Los residuos superan la prueba de normalidad dado que los puntos de la muestra y los teóricos de una distribución normal coinciden a lo largo de la linea. Shapiro puede fallar en grandes muestras.
1.4.1.1.3 Homocedasticidad de residuos.
Test Beach-Pagan que asume hipótesis nula=homocedasticidad. Si el p-value<0.05, se rechaza la hipótesis nula, osea se rechaza homocedasticidad.
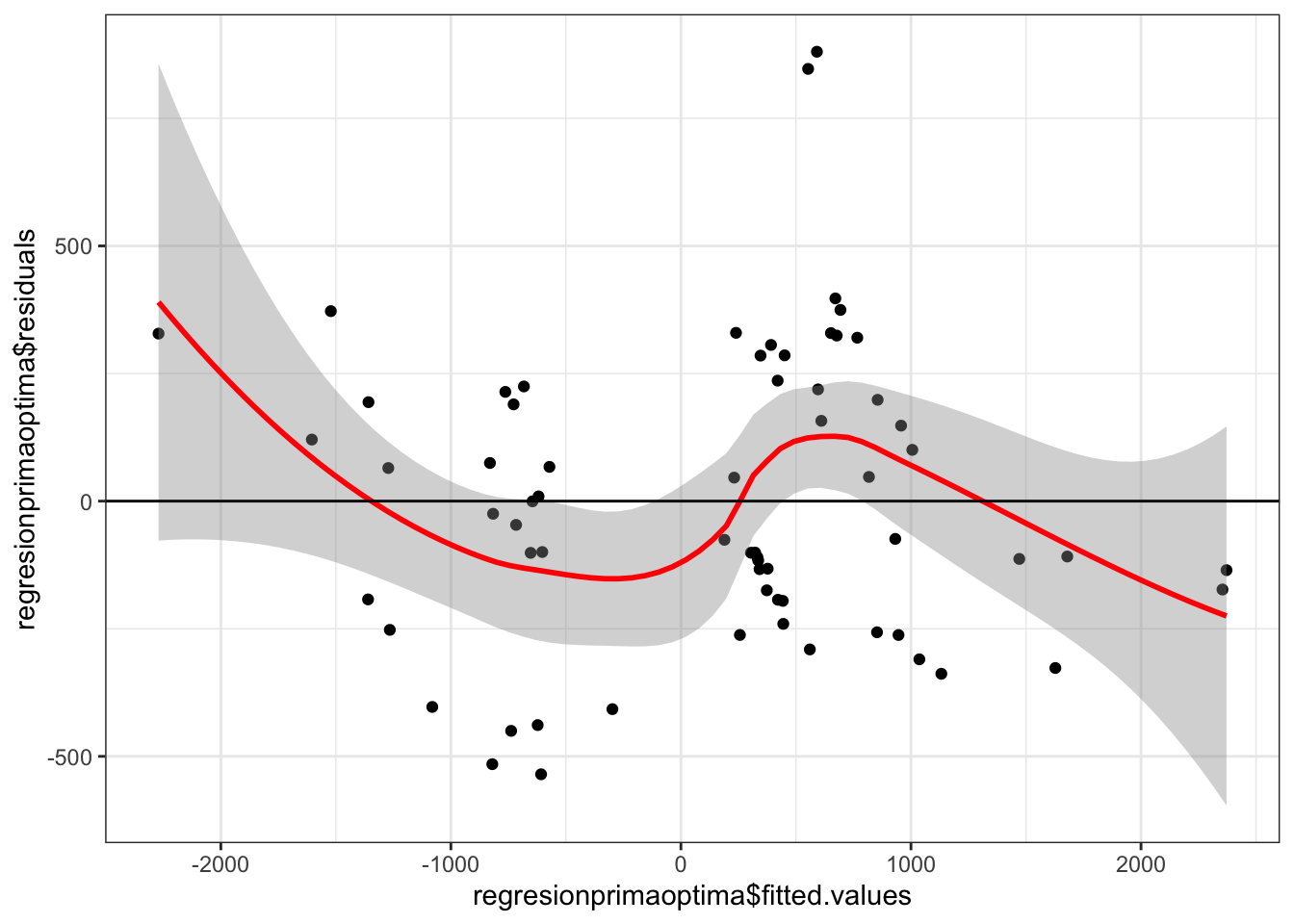
Figure 1.23: Comportamiento de las Cantidades por Prima de costos deflactada
##
## studentized Breusch-Pagan test
##
## data: regresionprimaoptima
## BP = 11.662, df = 4, p-value = 0.02005No se cumple la condición de homocedasticidad, dado que no pasa el test, por lo tanto se trabaja con mínimos cuadrados ponderados (WLS).
1.4.1.1.4 Correlación entre predictores
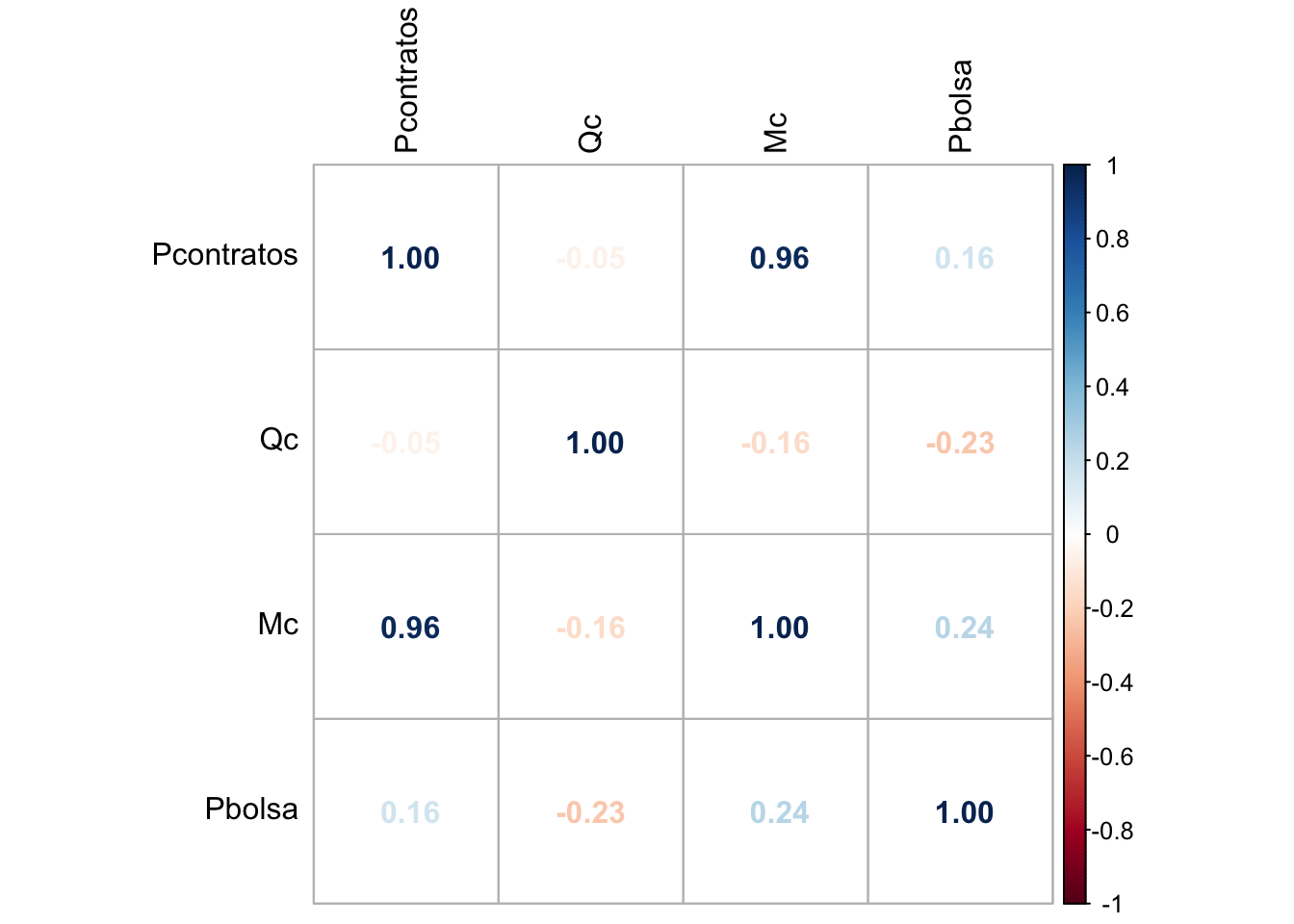
Figure 1.24: Comportamiento de las Cantidades por Prima de costos deflactada
## Qc Pcontratos Pbolsa Mc
## 1.210507 16.787349 1.161146 17.558897OJO!!!Hay predictores que muestran una correlación lineal muy alta Pc y Mc. Análisis de Inflación de Varianza (VIF): VIF = 1: Ausencia total de colinealidad 1 < VIF < 5: La regresión puede verse afectada por cierta colinealidad, como es este caso para Pc y Mc.
1.4.1.1.5 Autocorrelación.
Evalúa si los errores o residuos adyacentes o consecutivos están correlacionados. Ho: No existe correlación. Si p<0.05 se puede rechazar la hipótesis nula.
## lag Autocorrelation D-W Statistic p-value
## 1 0.5904285 0.8132553 0
## Alternative hypothesis: rho != 0OJO!!Como p=0, se rechaza la hipótesis Ho de que no existe correlación. No Pasa la prueba de Durbin & Watson de autocorrelación y por lo tanto, hay autocorrelación de orden 1 entre los errores. El estadistico deDurbin-watson da 0.81, lo que indica Esto quiere decir que hay que incluir rezagos en las variables regresoras.
1.4.1.1.6 Valores atípicos
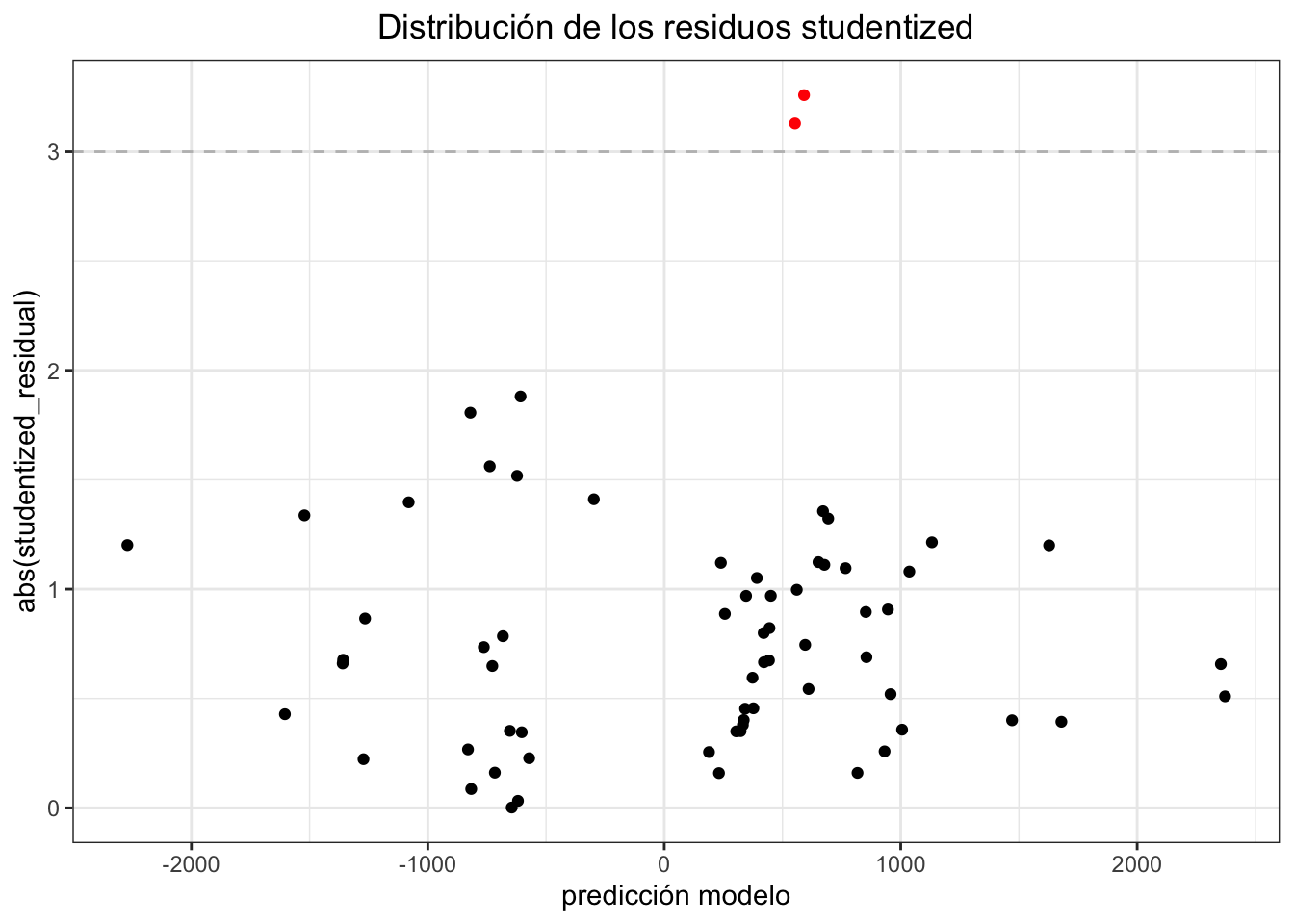
Figure 1.25: Comportamiento de las Cantidades por Prima de costos deflactada
Existen algunas pocas observaciones atípicas 2 de 66. Son pocos y por lo tanto no afectan la capacidad predictiva del modelo pero pueden ser interesantes.
1.4.1.1.7 Regresión WLS – Corrección de Heterocedasticidad.
Criterio para los pesos: defining the weights in such a way that the observations with lower variance are given more weight
##
## Call:
## lm(formula = Rc ~ Qc + Pcontratos + Mc, data = datosregresion,
## weights = wt)
##
## Weighted Residuals:
## Min 1Q Median 3Q Max
## -350.32 -179.16 -69.75 208.82 508.80
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) -191.8872 488.3875 -0.393 0.6958
## Qc 1.1733 0.4541 2.584 0.0122 *
## Pcontratos -128.2685 5.3696 -23.888 <2e-16 ***
## Mc 125.9661 5.2021 24.214 <2e-16 ***
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 228.4 on 61 degrees of freedom
## Multiple R-squared: 0.907, Adjusted R-squared: 0.9024
## F-statistic: 198.3 on 3 and 61 DF, p-value: < 2.2e-16La regresión lineal multivariada resultante es la siguiente:
\[\begin{equation} Prima_{costos} = -191.8 + 1.17*Qc -128.26*Pcontratos + 125.996*Mc \end{equation}\]
Rechequeo de heterocedasticidad.
Test Beach-Pagan que asume hipótesis nula=homocedasticidad. Si el p-value<0.05, se rechaza la hipótesis nula, osea se rechaza homocedasticidad.
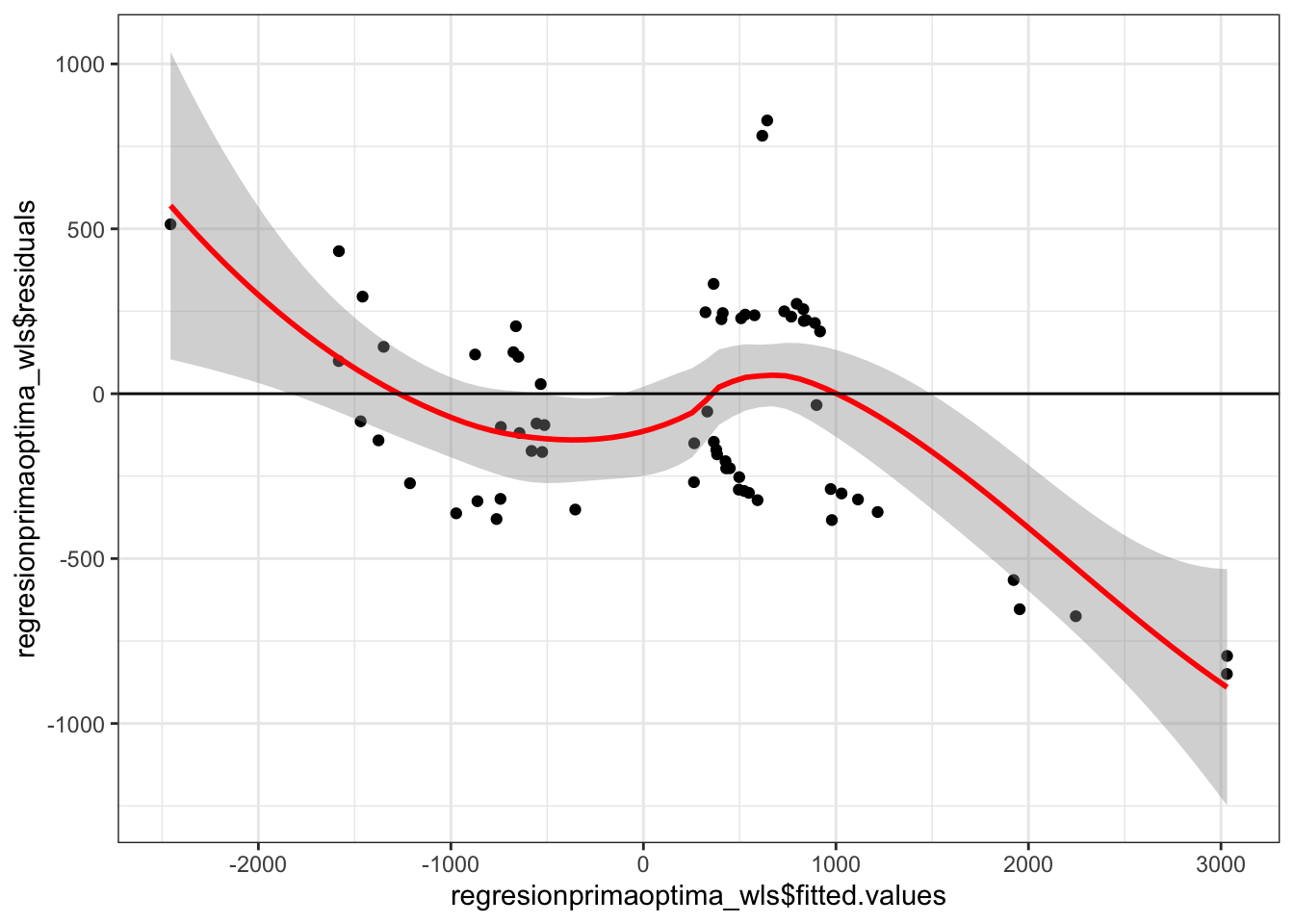
(#fig:homocedasticidadresiduos_wls)Comportamiento de las Cantidades por Prima de costos deflactada
##
## studentized Breusch-Pagan test
##
## data: regresionprimaoptima_wls
## BP = 12.844, df = 3, p-value = 0.0049871.4.1.2 Conclusiones de las regresiones multivariadas.
- Hay colinealidad entre Mc y Pc como regresoras, por lo tanto, se debe evitar su uso simultáneo.
- Hay autocorrelación positiva de orden 1, por lo tanto, los errores o residuos se pueden estar subestimando, ya que los errores en t, son explicados o estan correlacionados con t-1. Es decir, existe un efecto memoria en las series de Prima de costo y sus regresores y por ello, un análisis transversal puede tener problemas de estimación.
- Se tiene varianza variable, es decir, heterocedasticidad entre los valores ajustados y los errores. Este comportamiento podría determinar modelos en series de tiempo que aborden esa heterocedasticidad.
- No hay valores de outliers suficientes que alteren la estimación de la prima de costos.
1.4.1.3 Regresiones incluyendo rezagos
## Start: AIC=749.9
## Rc ~ Qc + Pcontratos + lag(Pcontratos) + Qb + Pbolsa + lag(Pbolsa) +
## Mc + lag(Mc)
##
## Df Sum of Sq RSS AIC
## - Qb 1 17168 5064624 748.12
## - Qc 1 41822 5089278 748.44
## - lag(Pbolsa) 1 44854 5092310 748.48
## <none> 5047456 749.90
## - lag(Mc) 1 269412 5316868 751.28
## - lag(Pcontratos) 1 339630 5387086 752.13
## - Pbolsa 1 339693 5387149 752.13
## - Mc 1 2095729 7143185 770.47
## - Pcontratos 1 10140239 15187695 819.50
##
## Step: AIC=748.12
## Rc ~ Qc + Pcontratos + lag(Pcontratos) + Pbolsa + lag(Pbolsa) +
## Mc + lag(Mc)
##
## Df Sum of Sq RSS AIC
## - lag(Pbolsa) 1 47005 5111629 746.72
## <none> 5064624 748.12
## - lag(Mc) 1 274006 5338630 749.55
## + Qb 1 17168 5047456 749.90
## - lag(Pcontratos) 1 348477 5413102 750.45
## - Pbolsa 1 398413 5463037 751.04
## - Qc 1 1078613 6143237 758.67
## - Mc 1 2079135 7143760 768.48
## - Pcontratos 1 10147576 15212200 817.61
##
## Step: AIC=746.72
## Rc ~ Qc + Pcontratos + lag(Pcontratos) + Pbolsa + Mc + lag(Mc)
##
## Df Sum of Sq RSS AIC
## <none> 5111629 746.72
## - lag(Mc) 1 227606 5339235 747.55
## + lag(Pbolsa) 1 47005 5064624 748.12
## + Qb 1 19319 5092310 748.48
## - lag(Pcontratos) 1 311111 5422740 748.56
## - Pbolsa 1 475544 5587173 750.50
## - Qc 1 1107762 6219391 757.47
## - Mc 1 2457379 7569008 770.24
## - Pcontratos 1 10285731 15397360 816.40##
## Call:
## lm(formula = Rc ~ Qc + Pcontratos + lag(Pcontratos) + Pbolsa +
## Mc + lag(Mc), data = datosregresion)
##
## Residuals:
## Min 1Q Median 3Q Max
## -503.07 -186.76 -45.48 206.82 887.16
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) -409.9972 439.0063 -0.934 0.354217
## Qc 1.6533 0.4663 3.545 0.000783 ***
## Pcontratos -100.0750 9.2635 -10.803 1.64e-15 ***
## lag(Pcontratos) -17.0134 9.0552 -1.879 0.065293 .
## Pbolsa 0.9647 0.4153 2.323 0.023714 *
## Mc 87.3081 16.5342 5.280 2.02e-06 ***
## lag(Mc) 25.8655 16.0951 1.607 0.113477
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 296.9 on 58 degrees of freedom
## (1 observation deleted due to missingness)
## Multiple R-squared: 0.9192, Adjusted R-squared: 0.9109
## F-statistic: 110 on 6 and 58 DF, p-value: < 2.2e-16## lag Autocorrelation D-W Statistic p-value
## 1 0.5424666 0.8992941 0
## Alternative hypothesis: rho != 01.4.2 Regresión logística
- Análisis de Regresión Logística. Basado en la distribución estadística de la prima de costos y sus regresoras, se ensayará otro modelo de regresión cuyo resultado no intente explicar la variabilidad () sino establecer probabilidades (Odds ratio) de que las primas de costos sean (Positivas o negativas) cuando las regresoras sean Altas o Bajas. Por ejemplo, resultados del tipo: “Si el precio de contratos es alto, la probabilidad de que la prima de costos sea alta es de X a 1 con respecto al escenario en que el precio de contratos sea bajo.” Si X>1, los precios de contrato altos serán más determinates que los precios de contrato bajos.
\[\begin{equation} log\frac{p}{1-p}=\kappa + \alpha_{W}Pc_{Altos} \end{equation}\]
donde,
- p: probabilidad de que la prima de costos sea Positiva.
- \(\kappa\): Intersecto
- \(\alpha_{W}\): \(log(OddsRatio)\) siendo el precio de contratos Bajo. En otras palabras, la razón entre las chances (odds ratio) de obtener una prima de costos positiva a negativa, cuando los precios de contratos son bajos.
Esta misma formulación se puede hacer contra Qc o Mc.
1.4.2.1 Precios como variables regresoras
## PcontratosNivel
## RcNivel Alto Bajo
## Negativo 12 13
## Positivo 15 261.4.2.1.1 Precios de Contratos vs. Prima de Costo
##
## Call:
## glm(formula = RcNivel ~ PcontratosNivel, family = "binomial",
## data = datos)
##
## Deviance Residuals:
## Min 1Q Median 3Q Max
## -1.4823 -1.2735 0.9005 0.9005 1.0842
##
## Coefficients:
## Estimate Std. Error z value Pr(>|z|)
## (Intercept) 0.2231 0.3873 0.576 0.565
## PcontratosNivelBajo 0.4700 0.5152 0.912 0.362
##
## (Dispersion parameter for binomial family taken to be 1)
##
## Null deviance: 87.578 on 65 degrees of freedom
## Residual deviance: 86.744 on 64 degrees of freedom
## AIC: 90.744
##
## Number of Fisher Scoring iterations: 4La regresión logística resultante es la siguiente:
\(PrimaCostosPositiva = 0.2231 + 0.47*PcontratoBajo\)
Esto quiere decir que \(Ln(Odds)\) de tener una prima de costos positiva en el mercado con precios de contrato Altos corresponde a 0.2231, lo que significa 1.2625 (exp(0.2231)) a 1 de tener una prima de costos positiva a una prima negativa cuando hay precios de contrato alto. Ahora bien, si los precios de contrato son bajos, el \(ln(Odds)\) aumenta debido al signo positivo del coeficiente que acompaña a PcontratoBajo (pasa a 0.6931 (0.2231+0.47)), lo que hace que pase de 1.2625 (exp(0.2231)) a 1 a unos chances de a 2 (exp(0.6931)) a 1 de tener una prima de costos positiva a una negativa cuando se tienen precios de contrato bajos. Este incremento es evidenciada dado que el \(Ln(OddsRatio)\) es +0.47, lo que significa que el \(OddsRatio\) es 1.56 (exp(0.47)). Esto quiere decir, que los precios de contrato bajos tienen un 156% de probabilidades respecto a los precios de contrato altos de causar una prima de costos positiva en el mercado.
Es decir,
- Con precios de contrato altos (por encima de la media), ya hay mayores chances de tener primas positivas respecto a obtener primas negativas. (1.26 a 1)
- Si los precios de contratos son bajos (por debajo de la media), las chances ahora son de 2 a 1 de obtener una prima de costos positiva.