2.3 Research and experimentation | 研究和实验

Eager execution provides an imperative, define-by-run interface for advanced operations. Write custom layers, forward passes, and training loops with auto differentiation. Start with these notebooks, then read the eager execution guide.

2.3.1 Eager execution | Eager Execution 模式

View source on GitHub | Run in Google Colab

本节将介绍如何在 Tensorflow 中使用 Eager execution，包括：

• 载入需要的包
• 构建和使用张量
• 使用 GPU 加速
• 数据集

2.3.1.1 Import Tesorflow | 载入 Tensorflow

最开始，让我们首先载入 Tensorflow 并开启 Eager Execution 选项。Eager execution 提供了一个 Tensorflow 的可交互天端，具体详细的内容我们在之后再介绍。

import tensorflow as tf

tf.enable_eager_execution()

2.3.1.2 Tensors | 张量

一个张量 (Tensor) 是一个多维的数组。类似于 NumPy 中的 ndarray 对象，张量对象也包含数据类型 (datatype) 和形状 (shape) 属性。此外，张量也可以驻留在加速器 (例如 GPU) 的内存中。Tensorflow 提供了丰富的算子 (例如：tf.add，tf.matmul，tf.linalg.inv 等) 来操作张量。这些操作可以自动的将原生的 Python 类型进行转换，例如：

print(tf.add(1, 2))
print(tf.add([1, 2], [3, 4]))
print(tf.square(5))
print(tf.reduce_sum([1, 2, 3]))
print(tf.encode_base64("hello world"))

# Operator overloading is also supported
print(tf.square(2) + tf.square(3))

tf.Tensor(3, shape=(), dtype=int32)
tf.Tensor([4 6], shape=(2,), dtype=int32)
tf.Tensor(25, shape=(), dtype=int32)
tf.Tensor(6, shape=(), dtype=int32)
tf.Tensor(b'aGVsbG8gd29ybGQ', shape=(), dtype=string)
tf.Tensor(13, shape=(), dtype=int32)

每个张量包含一个形状和数据类型属性

x = tf.matmul([[1]], [[2, 3]])
print(x.shape)
print(x.dtype)

(1, 2)
<dtype: 'int32'>

NumPy 中的数组和 Tensorflow 中的张量最主要的区别在于：

• 张量可以贮存在加速器内存中 (例如：GPU，TPU)
• 张量是不可变的

2.3.1.2.1 NumPy Compatibility | NumPy 兼容性

Tensorflow 的张量和 NumPy 的 ndarrays 之间的转换十分容易：

• Tensorflow 算子可以自动的将 NumPy 的 ndarrays 转换为张量。
• NumPy 算子可以自动的将张量转换为 NumPy 的 ndarrays。

张量可以通过调用 .numpy() 方法显式的转换为 NumPy ndarrays。如果两者底层共用相同的内存，则这种转换通常是高效的。但是，并不是所有的情况下都会共享相同的内存，例如：张量肯能寄存在 GPU 的内存中，而 NumPy 数组则存储在主机的内存中，因此这种转换将会包含一个从 GPU 内存到主机内存的拷贝过程。

import numpy as np

ndarray = np.ones([3, 3])

print("TensorFlow operations convert numpy arrays to Tensors automatically")
tensor = tf.multiply(ndarray, 42)
print(tensor)

print("And NumPy operations convert Tensors to numpy arrays automatically")
print(np.add(tensor, 1))

print("The .numpy() method explicitly converts a Tensor to a numpy array")
print(tensor.numpy())

TensorFlow operations convert numpy arrays to Tensors automatically
tf.Tensor(
[[42. 42. 42.]
 [42. 42. 42.]
 [42. 42. 42.]], shape=(3, 3), dtype=float64)
And NumPy operations convert Tensors to numpy arrays automatically
[[43. 43. 43.]
 [43. 43. 43.]
 [43. 43. 43.]]
The .numpy() method explicitly converts a Tensor to a numpy array
[[42. 42. 42.]
 [42. 42. 42.]
 [42. 42. 42.]]

2.3.1.3 GPU acceleration | GPU 加速

大多数的 Tensorflow 运算都能够通过 GPU 来加速。无需任何说明，Tensorflow 会自动的选择使用 GPU 还是 CPU 来进行运算 (如果必要还包括 CPU 和 GPU 内存之间的拷贝)。通常张量将和产生该张量的运算存储在相同的内存中，例如：

x = tf.random_uniform([3, 3])

print("Is there a GPU available: "),
print(tf.test.is_gpu_available())

print("Is the Tensor on GPU #0:  "),
print(x.device.endswith('GPU:0'))

Is there a GPU available: 
True
Is the Tensor on GPU #0:  
True

2.3.1.3.1 Device Names | 设备名称

张量的 .device 属性提供了承载其值的设备的名称字符串。这个名称是由很多信息编码而成，例如程序所执行的主机的网络标识和运行所在的设备。在分布式的 Tensorflow 程序中才会是这样，不过我们现在先暂时跳过这些。现在，这个字符串应该是以 GPU:<N> 的样式结尾，这表明该张量在第 <N> 个 GPU 类型的设备上。

2.3.1.3.2 Explicit Device Placement | 指定设备

在 Tensorflow 中 placement 一词指的是一个运算是如何被指定给一个设备去执行的。如上文中提及的，当没有明确的指明的时候，Tensorflow 将会自动的为一个运算分配设备，如需要也会在设备间进行数据的拷贝。同时，我们也可以通过 tf.device 上下文管理器显式的指定需要放置张量的设备。

def time_matmul(x):
  %timeit tf.matmul(x, x)

# Force execution on CPU
print("On CPU:")
with tf.device("CPU:0"):
  x = tf.random_uniform([1000, 1000])
  assert x.device.endswith("CPU:0")
  time_matmul(x)

# Force execution on GPU #0 if available
if tf.test.is_gpu_available():
  with tf.device("GPU:0"): # Or GPU:1 for the 2nd GPU, GPU:2 for the 3rd etc.
    x = tf.random_uniform([1000, 1000])
    assert x.device.endswith("GPU:0")
    time_matmul(x)

On CPU:
10 loops, best of 3: 29.1 ms per loop
The slowest run took 161.37 times longer than the fastest. This could mean that an intermediate result is being cached.
1000 loops, best of 3: 1.04 ms per loop

2.3.1.4 Datasets | 数据集

本小节我们将使用 tf.data.Dataset API 构建一个数据管道将数据喂给你的模型，包括：

• 构建一个数据集。
• 在 Eager Execution 开启时在一个数据集上不断迭代。

我们建议使用 Dataset API 对简单和可复用的数据来构建高性能，复杂的数据管道，并未模型的训练和评估提供支持。

如果你对 Tensorflow 计算图并不熟悉，用于构建数据对象的 API 在 Eager Execution 开启后也是完全相同的，仅是数据集上元素的迭代略有不同。你可以直接在 tf.data.Dataset 对象上应用 Python 迭代器，而无需显式的创建一个 tf.data.Interator 对象。总结一下，在 Tensorflow Guide 中有关迭代器的讨论与 Eager Execution 模式是否开启无关。

2.3.1.4.1 Create a source Dataset | 构建一个原始数据集

一个原始 (source) 数据集可以用如下函数构建：Dataset.from_tensors，Dataset.from_tensor_slices，或是可以从文件读取信息的函数 TextLineDataset 和 TFRecordDataset。更多的信息请参考 Tensorflow Guide。

ds_tensors = tf.data.Dataset.from_tensor_slices([1, 2, 3, 4, 5, 6])

# Create a CSV file
import tempfile
_, filename = tempfile.mkstemp()

with open(filename, 'w') as f:
  f.write("""Line 1
Line 2
Line 3
  """)

ds_file = tf.data.TextLineDataset(filename)

2.3.1.4.2 Apply transformations | 数据变换

我们可以利用如下函数对数据级中的记录进行变换，例如：map，batch，shuffle 等。更多详细信息请参见 tf.data.Dataset API 文档。

ds_tensors = ds_tensors.map(tf.square).shuffle(2).batch(2)

ds_file = ds_file.batch(2)

2.3.1.4.3 Iterate | 迭代

当 Eager Execuation 模式开始后，Dataset 对象就支持迭代了。如果你熟悉 Tensorflow 计算图中的 Dataset，即可对其进行迭代使用了，需要注意的是此模式下无需调用 Dataset.make_one_shot_iterator() 或 get_next() 函数。

print('Elements of ds_tensors:')
for x in ds_tensors:
  print(x)

print('\nElements in ds_file:')
for x in ds_file:
  print(x)

Elements of ds_tensors:
tf.Tensor([1 9], shape=(2,), dtype=int32)
tf.Tensor([16  4], shape=(2,), dtype=int32)
tf.Tensor([36 25], shape=(2,), dtype=int32)

Elements in ds_file:
tf.Tensor([b'Line 1' b'Line 2'], shape=(2,), dtype=string)
tf.Tensor([b'Line 3' b'  '], shape=(2,), dtype=string)

2.3.2 Automatic differentiation and gradient tape | 自动微分和梯度带

View source on GitHub | Run in Google Colab

上节中，我们介绍了张量和及其相关的操作，本节我们将介绍自动微分 (Automatic Defferentiation)，一种在机器学习中关键的优化技术。

2.3.2.1 Setup | 设置

import tensorflow as tf
tf.enable_eager_execution()

tfe = tf.contrib.eager # Shorthand for some symbols

2.3.2.2 Derivatives of a function | 函数的导数

Tensorflow 提供一套 API 用于自动微分，即计算一个函数的导数。和数学表示最接近的一种方式就是将整个计算过程包装成一个 Python 函数，例如 f，我们可以使用 tfe.gradients_function 来构建其导数，并根据传入的参数计算其导数值。如果你对 NumPy 中的微分函数 autogard 熟悉的话，这里的情况类似，例如：

from math import pi

def f(x):
  return tf.square(tf.sin(x))

assert f(pi/2).numpy() == 1.0


# grad_f will return a list of derivatives of f
# with respect to its arguments. Since f() has a single argument,
# grad_f will return a list with a single element.
grad_f = tfe.gradients_function(f)
assert tf.abs(grad_f(pi/2)[0]).numpy() < 1e-7

2.3.2.2.1 Higher-order gradients | 高阶导数

通过执行相同的 API 多次我们可得到高阶导数：

def f(x):
  return tf.square(tf.sin(x))

def grad(f):
  return lambda x: tfe.gradients_function(f)(x)[0]

x = tf.lin_space(-2*pi, 2*pi, 100)  # 100 points between -2π and +2π

import matplotlib.pyplot as plt

plt.plot(x, f(x), label="f")
plt.plot(x, grad(f)(x), label="first derivative")
plt.plot(x, grad(grad(f))(x), label="second derivative")
plt.plot(x, grad(grad(grad(f)))(x), label="third derivative")
plt.legend()
plt.show()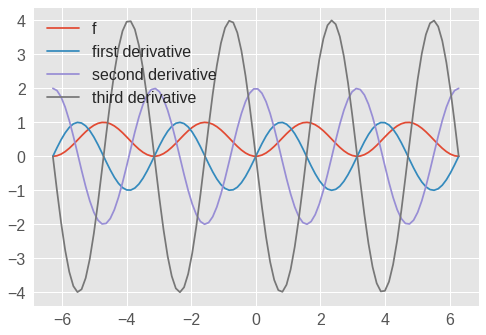

图 1.13: 高阶导数

2.3.2.3 Gradient taps | 梯度带

每一个可微的 Tensorflow 操作都有一个相关的梯度函数，例如：tf.square(x) 的梯度函数为 2.0 * x。为了计算一个用户自定义函数 (如上文中的 f(x)) 的梯度，Tensorflow 会首先记录所有用于计算最终输出的运算，我们称这个记录为一个带子 (tape)。接下来，将使用这个记录带和每个原始操作对应的梯度函数通过反向微分模式 (reverse mode differentiation) 计算用户自定义函数的梯度。

因为运算在被执行后才被记录，所以 Python 的控制流 (例如：ifs 和 whiles) 也能够很好的被处理：

def f(x, y):
  output = 1
  # Must use range(int(y)) instead of range(y) in Python 3 when
  # using TensorFlow 1.10 and earlier. Can use range(y) in 1.11+
  for i in range(int(y)):
    output = tf.multiply(output, x)
  return output

def g(x, y):
  # Return the gradient of `f` with respect to it's first parameter
  return tfe.gradients_function(f)(x, y)[0]

assert f(3.0, 2).numpy() == 9.0   # f(x, 2) is essentially x * x
assert g(3.0, 2).numpy() == 6.0   # And its gradient will be 2 * x
assert f(4.0, 3).numpy() == 64.0  # f(x, 3) is essentially x * x * x
assert g(4.0, 3).numpy() == 48.0  # And its gradient will be 3 * x * x

有时候，可能并不是很方便将计算封装在一个函数中，例如：输出的梯度和函数中的一些中间计算值有关。在这种情况下，显式的使用 tf.GradientTape 上下文将会很有用，尽管这样会显得比较啰嗦。所有在 tf.GradientTape 上下文中的计算都将会被记录。

x = tf.ones((2, 2))
  
# TODO(b/78880779): Remove the 'persistent=True' argument and use
# a single t.gradient() call when the bug is resolved.
with tf.GradientTape(persistent=True) as t:
  # TODO(ashankar): Explain with "watch" argument better?
  t.watch(x)
  y = tf.reduce_sum(x)
  z = tf.multiply(y, y)

# Use the same tape to compute the derivative of z with respect to the
# intermediate value y.
dz_dy = t.gradient(z, y)
assert dz_dy.numpy() == 8.0

# Derivative of z with respect to the original input tensor x
dz_dx = t.gradient(z, x)
for i in [0, 1]:
  for j in [0, 1]:
    assert dz_dx[i][j].numpy() == 8.0

2.3.2.3.1 Higher-order gradients | 高阶导数

在 GradientTape 上下文管理器中所有的运算都会被记录用于自动微分。如果梯度是在上下文中计算的，那么这个梯度的计算过程也会被记录。所以，相同的 API 对高阶梯度也同样适用，例如：

# TODO(ashankar): Should we use the persistent tape here instead? Follow up on Tom and Alex's discussion

x = tf.constant(1.0)  # Convert the Python 1.0 to a Tensor object

with tf.GradientTape() as t:
  with tf.GradientTape() as t2:
    t2.watch(x)
    y = x * x * x
  # Compute the gradient inside the 't' context manager
  # which means the gradient computation is differentiable as well.
  dy_dx = t2.gradient(y, x)
d2y_dx2 = t.gradient(dy_dx, x)

assert dy_dx.numpy() == 3.0
assert d2y_dx2.numpy() == 6.0

2.3.2.4 Next Steps | 接下来

在本节中，我们介绍了 Tensorflow 中的梯度计算。有了这些，我们就有足够多的知识去构建和训练一个神经网络，我们将在下面的教程中对其进行介绍。

2.3.3 Custom training: basics | 自定义训练：基础

View source on GitHub | Run in Google Colab

在上一节中，我们介绍了如何利用 Tensorflow API 进行自动微分，一个机器学习基础的一块内容。在本节，我们将利用上节中的内容来进行一些简单的机器学习实践。

Tensorflow 同样包含了神经网络的高阶 API (tf.keras)，它提供了大量实用抽象来简化我们的代码。我们强烈建议使用这些高级 API 来构建神经网络模型。但是在本节中，我们将介绍神经网络模型训练的一些基础内容。

2.3.3.1 Setup | 设置

import tensorflow as tf

tf.enable_eager_execution()
tfe = tf.contrib.eager # ADD BY LEO

2.3.3.2 Variables | 变量

在 Tensorflow 中张量是一个不可变状态的对象。但在机器学习模型训练的过程中，有些是需要改变的，例如用相同代码在不同时间点上进行预测的损失，当然我们是希望这个损失越来越小。为了表示这种随着计算而发生改变的状态，你可以选择依赖 Python 这种有状态的编程语言 (stateful programming language) 特性。

# Using python state
x = tf.zeros([10, 10])
x += 2  # This is equivalent to x = x + 2, which does not mutate the original
        # value of x
print(x)

tf.Tensor(
[[2. 2. 2. 2. 2. 2. 2. 2. 2. 2.]
 [2. 2. 2. 2. 2. 2. 2. 2. 2. 2.]
 [2. 2. 2. 2. 2. 2. 2. 2. 2. 2.]
 [2. 2. 2. 2. 2. 2. 2. 2. 2. 2.]
 [2. 2. 2. 2. 2. 2. 2. 2. 2. 2.]
 [2. 2. 2. 2. 2. 2. 2. 2. 2. 2.]
 [2. 2. 2. 2. 2. 2. 2. 2. 2. 2.]
 [2. 2. 2. 2. 2. 2. 2. 2. 2. 2.]
 [2. 2. 2. 2. 2. 2. 2. 2. 2. 2.]
 [2. 2. 2. 2. 2. 2. 2. 2. 2. 2.]], shape=(10, 10), dtype=float32)

当然，Tensorflow 也有内置的有状态的运算，这些运算通常要比低级的 Python 表示方法更容易使用。例如，在表示模型的权重的时候，使用 Tensorflow 中的变量会更加方便和有效。

一个变量是一个存储了数值的对象，在 Tensorflow 计算过程中，其会隐式的读取这个值。有很多运算 (例如：tf.assign_sub，tf.scatter_update 等) 可以改变 Tensorflow 变量中的值。

# MODIFIED BY LEO
# v = tf.Variable(1.0)
v = tfe.Variable(1.0)
assert v.numpy() == 1.0

# Re-assign the value
v.assign(3.0)
assert v.numpy() == 3.0

# Use `v` in a TensorFlow operation like tf.square() and reassign
v.assign(tf.square(v))
assert v.numpy() == 9.0

在计算梯度的时候，使用变量进行计算可以自动被追踪。对于表示 Embeddings 的变量，Tensorflow 将会进行稀疏更新，这样会更加高效和节省内存。

2.3.3.3 Example: Fitting a linear model | 示例：构建一个线性模型

让我们用到目前位置引入的概念 (包括：Tensor，GradientTape，Variable) 来构建和训练一个简单的模型。这个过程主要包括：

1. 定义模型。
2. 定义损失韩式。
3. 获取训练数据。
4. 利用训练数据和一个“优化器”来调整变量拟合数据。

在本节中，我们将以一个简单的线性模型为示例：\(f\left(x\right) = Wx + b\)，它仅包含两个变量 \(W\) 和 \(b\)。此外，我们利用现有数据，对模型进行充分训练，理想的有 \(W = 3.0\) 和 \(b = 2.0\)。

2.3.3.3.1 Define the model | 定义模型

让我们定义一个包含变量和运算的简单类：

class Model(object):
  def __init__(self):
    # Initialize variable to (5.0, 0.0)
    # In practice, these should be initialized to random values.
    self.W = tfe.Variable(5.0) # MODIFIED BY LEO
    self.b = tfe.Variable(0.0) # MODIFIED BY LEO
    
  def __call__(self, x):
    return self.W * x + self.b
  
model = Model()

assert model(3.0).numpy() == 15.0

2.3.3.3.2 Define a loss function | 定义损失函数

损失函数度量了给定的输入和模型的输出之间的匹配程度，在这里我们使用标准的 L2 损失。

def loss(predicted_y, desired_y):
  return tf.reduce_mean(tf.square(predicted_y - desired_y))

2.3.3.3.3 Obtain training data | 获取训练数据

让我们利用一些噪音合成训练数据。

TRUE_W = 3.0
TRUE_b = 2.0
NUM_EXAMPLES = 1000

inputs  = tf.random_normal(shape=[NUM_EXAMPLES])
noise   = tf.random_normal(shape=[NUM_EXAMPLES])
outputs = inputs * TRUE_W + TRUE_b + noise

在我们训练模型之前，让我们可视化一下模型当前的状态，图中模型的预测值为红色，训练数据为蓝色。

import matplotlib.pyplot as plt

plt.scatter(inputs, outputs, c='b')
plt.scatter(inputs, model(inputs), c='r')
plt.show()

print('Current loss: '),
print(loss(model(inputs), outputs).numpy())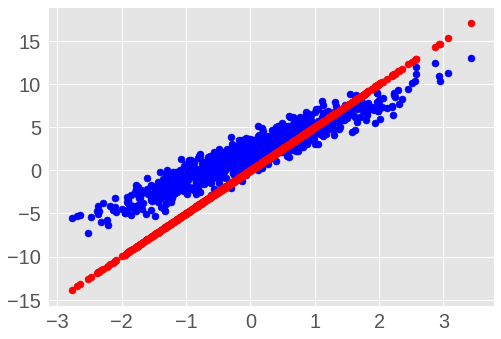

图 1.14: 简单的线性模型的初始状态

Current loss: 
8.717568

2.3.3.3.4 Define a training loop | 定义一个循环训练

我们已经准备好了网络和训练数据，接下来让我们开始训练这个模型。使用训练数据对模型中的变量 (\(W\) 和 \(b\)) 通过梯度下降进行更新。tf.train.Optimizer 中包含了大量的梯度下降方案，我们强烈建议使用这些优化器。但是本着构建我们第一个示例模型的原则，我们将利用基本的数学知识手动实现这个过程。

def train(model, inputs, outputs, learning_rate):
  with tf.GradientTape() as t:
    current_loss = loss(model(inputs), outputs)
  dW, db = t.gradient(current_loss, [model.W, model.b])
  model.W.assign_sub(learning_rate * dW)
  model.b.assign_sub(learning_rate * db)

最后，利用训练数据进行迭代训练，并观察 \(W\) 和 \(b\) 如何变化。

model = Model()

# Collect the history of W-values and b-values to plot later
Ws, bs = [], []
epochs = range(10)
for epoch in epochs:
  Ws.append(model.W.numpy())
  bs.append(model.b.numpy())
  current_loss = loss(model(inputs), outputs)

  train(model, inputs, outputs, learning_rate=0.1)
  print('Epoch %2d: W=%1.2f b=%1.2f, loss=%2.5f' %
        (epoch, Ws[-1], bs[-1], current_loss))

# Let's plot it all
plt.plot(epochs, Ws, 'r',
         epochs, bs, 'b')
plt.plot([TRUE_W] * len(epochs), 'r--',
         [TRUE_b] * len(epochs), 'b--')
plt.legend(['W', 'b', 'true W', 'true_b'])
plt.show()

Epoch  0: W=5.00 b=0.00, loss=8.71757
Epoch  1: W=4.61 b=0.39, loss=5.95636
Epoch  2: W=4.29 b=0.70, loss=4.18297
Epoch  3: W=4.04 b=0.95, loss=3.04401
Epoch  4: W=3.84 b=1.15, loss=2.31250
Epoch  5: W=3.67 b=1.31, loss=1.84267
Epoch  6: W=3.54 b=1.44, loss=1.54092
Epoch  7: W=3.44 b=1.55, loss=1.34711
Epoch  8: W=3.36 b=1.63, loss=1.22263
Epoch  9: W=3.29 b=1.70, loss=1.14268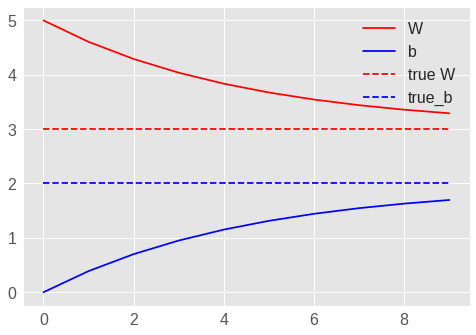

图 1.15: 简单的线性模型的 W 和 b 变化

2.3.3.4 Next Steps | 接下来

在本接种，我们介绍了变量 (Variables)，并利用但目前位置介绍的 Tensorflow 中的原始操作来构建和训练一个简单的线性模型。

理论上，这差不多已经够你在机器学习研究中所需的 Tensorflow 相关内容了。在实践中，特别是对于神经网络而言，高级的 API 例如 tf.kears 使用起来更为便捷。因为它提供了更高阶的模块 (叫做 “layers”)，用于存储和恢复信息的工具，一系列的损失函数，一系列的优化器等等。

接下来的教程中将逐步介绍这些高级 API。

2.3.4 Custom layers | 自定义层

View source on GitHub | Run in Google Colab

我们强烈建议使用 tf.keras 中的高级 API 构建神经网络，也就是说大多数的 Tensorflow API 对于 Eager Execuation 模式都是可用的。

import tensorflow as tf
tfe = tf.contrib.eager

tf.enable_eager_execution()

2.3.4.1 Layers: common sets of useful operations | 层：常用运算的一般设置

在我们编写机器学习模型代码时，我们期望能够在更高的抽象层级上操作，而不是进行更加底层的操作，甚至操作单个变量。

大多数机器学习模型可以表示成一些简单的层的组合和堆叠。Tensorflow 提供了一组常用的网络层，同时也提供了便捷的完全从同或依据现有网络层来构建用户自定义网络层的方法。

Tensorflow 的 tf.keras 包中包含了 Keras 的全部 API，Keras 中的层在我们构建自己的模型时十分有用。

# In the tf.keras.layers package, layers are objects. To construct a layer,
# simply construct the object. Most layers take as a first argument the number
# of output dimensions / channels.
layer = tf.keras.layers.Dense(100)
# The number of input dimensions is often unnecessary, as it can be inferred
# the first time the layer is used, but it can be provided if you want to 
# specify it manually, which is useful in some complex models.
layer = tf.keras.layers.Dense(10, input_shape=(None, 5))

内置的网络层的列表可以 API 文档 中获取，主要包含：Dense (全链接层)，Conv2D (二维卷积层)，LSTM (长短时记忆)，BatchNormalization (批标准化)，Dropout 等等。

# To use a layer, simply call it.
layer(tf.zeros([10, 5]))

<tf.Tensor: id=30, shape=(10, 10), dtype=float32, numpy=
array([[0., 0., 0., 0., 0., 0., 0., 0., 0., 0.],
       [0., 0., 0., 0., 0., 0., 0., 0., 0., 0.],
       [0., 0., 0., 0., 0., 0., 0., 0., 0., 0.],
       [0., 0., 0., 0., 0., 0., 0., 0., 0., 0.],
       [0., 0., 0., 0., 0., 0., 0., 0., 0., 0.],
       [0., 0., 0., 0., 0., 0., 0., 0., 0., 0.],
       [0., 0., 0., 0., 0., 0., 0., 0., 0., 0.],
       [0., 0., 0., 0., 0., 0., 0., 0., 0., 0.],
       [0., 0., 0., 0., 0., 0., 0., 0., 0., 0.],
       [0., 0., 0., 0., 0., 0., 0., 0., 0., 0.]], dtype=float32)>

# Layers have many useful methods. For example, you can inspect all variables
# in a layer by calling layer.variables. In this case a fully-connected layer
# will have variables for weights and biases.
layer.variables

[<tf.Variable 'dense_1/kernel:0' shape=(5, 10) dtype=float32, numpy=
 array([[-0.38186976, -0.57403755, -0.28538084, -0.29921725,  0.6323789 ,
         -0.22408262, -0.558205  ,  0.20939457, -0.13509727, -0.4790057 ],
        [-0.02313542, -0.43945417,  0.01707488,  0.4670754 , -0.58452326,
         -0.62444955,  0.33546197,  0.45212358, -0.20420289, -0.14902249],
        [-0.56579435,  0.16514385, -0.24310723, -0.18096009,  0.6025618 ,
          0.4940943 ,  0.2489987 , -0.31508538,  0.198874  ,  0.5320404 ],
        [ 0.3744052 , -0.01636934,  0.15089905,  0.2619381 ,  0.45835572,
         -0.18408775,  0.22304171, -0.6093193 ,  0.5606211 ,  0.1611399 ],
        [-0.0149563 , -0.24973878,  0.5764479 ,  0.02765155, -0.50330853,
         -0.40767083,  0.17201573, -0.08274871, -0.27955824, -0.07600993]],
       dtype=float32)>,
 <tf.Variable 'dense_1/bias:0' shape=(10,) dtype=float32, numpy=array([0., 0., 0., 0., 0., 0., 0., 0., 0., 0.], dtype=float32)>]

# The variables are also accessible through nice accessors
layer.kernel, layer.bias

(<tf.Variable 'dense_1/kernel:0' shape=(5, 10) dtype=float32, numpy=
 array([[-0.38186976, -0.57403755, -0.28538084, -0.29921725,  0.6323789 ,
         -0.22408262, -0.558205  ,  0.20939457, -0.13509727, -0.4790057 ],
        [-0.02313542, -0.43945417,  0.01707488,  0.4670754 , -0.58452326,
         -0.62444955,  0.33546197,  0.45212358, -0.20420289, -0.14902249],
        [-0.56579435,  0.16514385, -0.24310723, -0.18096009,  0.6025618 ,
          0.4940943 ,  0.2489987 , -0.31508538,  0.198874  ,  0.5320404 ],
        [ 0.3744052 , -0.01636934,  0.15089905,  0.2619381 ,  0.45835572,
         -0.18408775,  0.22304171, -0.6093193 ,  0.5606211 ,  0.1611399 ],
        [-0.0149563 , -0.24973878,  0.5764479 ,  0.02765155, -0.50330853,
         -0.40767083,  0.17201573, -0.08274871, -0.27955824, -0.07600993]],
       dtype=float32)>,
 <tf.Variable 'dense_1/bias:0' shape=(10,) dtype=float32, numpy=array([0., 0., 0., 0., 0., 0., 0., 0., 0., 0.], dtype=float32)>)

2.3.4.2 Implementing custom layers | 构建自定义的网络层

构建自定义的网络层的最好实践是继承 tf.keras.Layer 类并实现：

• __init__，在此进行与输入无关的初始化
• build，在此可以得知输入张量的形状，并进行后续的初始化
• call，在此进行前向的计算

需要注意的是，我们无需在调用 build 时再创建变量，你也可以在 __init__ 中创建他们。但是，在 build 中创建他们的好处是可以根据输入张量的形状在创建后续变量，也就是说，在 __init__ 中创建变量需要显式的指定所需的一些形状参数。

class MyDenseLayer(tf.keras.layers.Layer):
  def __init__(self, num_outputs):
    super(MyDenseLayer, self).__init__()
    self.num_outputs = num_outputs
    
  def build(self, input_shape):
    self.kernel = self.add_variable("kernel", 
                                    shape=[input_shape[-1].value, 
                                           self.num_outputs])
    
  def call(self, input):
    return tf.matmul(input, self.kernel)
  
layer = MyDenseLayer(10)
print(layer(tf.zeros([10, 5])))
print(layer.variables)

tf.Tensor(
[[0. 0. 0. 0. 0. 0. 0. 0. 0. 0.]
 [0. 0. 0. 0. 0. 0. 0. 0. 0. 0.]
 [0. 0. 0. 0. 0. 0. 0. 0. 0. 0.]
 [0. 0. 0. 0. 0. 0. 0. 0. 0. 0.]
 [0. 0. 0. 0. 0. 0. 0. 0. 0. 0.]
 [0. 0. 0. 0. 0. 0. 0. 0. 0. 0.]
 [0. 0. 0. 0. 0. 0. 0. 0. 0. 0.]
 [0. 0. 0. 0. 0. 0. 0. 0. 0. 0.]
 [0. 0. 0. 0. 0. 0. 0. 0. 0. 0.]
 [0. 0. 0. 0. 0. 0. 0. 0. 0. 0.]], shape=(10, 10), dtype=float32)
[<tf.Variable 'my_dense_layer/kernel:0' shape=(5, 10) dtype=float32, numpy=
array([[ 0.10101604, -0.3224442 ,  0.01233709,  0.511952  , -0.37625661,
         0.17313367, -0.3861404 , -0.49091217, -0.5357712 , -0.48490155],
       [-0.32566747,  0.35822678, -0.45985532, -0.1619854 ,  0.42522162,
         0.60397416, -0.5726387 , -0.13526723, -0.02939123,  0.17975879],
       [ 0.57780296, -0.04614013,  0.27127117,  0.5906159 ,  0.44118112,
        -0.49981686,  0.25520337,  0.4067822 ,  0.1510328 , -0.02576578],
       [ 0.4620852 ,  0.1791476 , -0.55509675, -0.25070927, -0.38807744,
        -0.00608116,  0.4826128 , -0.31024626, -0.30914158,  0.57044727],
       [-0.5274048 , -0.55100423, -0.53232807, -0.37151748,  0.13543159,
        -0.02298492,  0.08317608,  0.15291196,  0.50038236, -0.07125527]],
      dtype=float32)>]

注意，当不需要在 build 中创建你的变量的时候，你可以在 __init__ 中创建他们。

由于代码阅读者会更加熟悉标准的网络层的使用方式，因此当你的代码中更多的使用标准网络层会更加友好。如果你想使用一个在 tf.kears.layers 和 tf.contrib.layers 中并不包含的层的时，可以考虑提一个 Github Issue，或者自己实现一个并提交一个 Pull Request 贡献你的代码。

2.3.4.3 Models: composing layers | 模型：组合网络层

在机器学习模型中很多有趣的网络层往往是由一些简单的网络层组合而成。例如，ResNet 中的残差模块就是由卷积，批标准化和 ShortCut 支路构成。

当构建一个包含其他网络层的自定义网络层时，主要会用到 tf.keras.Model 这个类，通常通过继承 tf.keras.Model 这个类实现。

class ResnetIdentityBlock(tf.keras.Model):
  def __init__(self, kernel_size, filters):
    super(ResnetIdentityBlock, self).__init__(name='')
    filters1, filters2, filters3 = filters

    self.conv2a = tf.keras.layers.Conv2D(filters1, (1, 1))
    self.bn2a = tf.keras.layers.BatchNormalization()

    self.conv2b = tf.keras.layers.Conv2D(filters2, kernel_size, padding='same')
    self.bn2b = tf.keras.layers.BatchNormalization()

    self.conv2c = tf.keras.layers.Conv2D(filters3, (1, 1))
    self.bn2c = tf.keras.layers.BatchNormalization()

  def call(self, input_tensor, training=False):
    x = self.conv2a(input_tensor)
    x = self.bn2a(x, training=training)
    x = tf.nn.relu(x)

    x = self.conv2b(x)
    x = self.bn2b(x, training=training)
    x = tf.nn.relu(x)

    x = self.conv2c(x)
    x = self.bn2c(x, training=training)

    x += input_tensor
    return tf.nn.relu(x)

    
block = ResnetIdentityBlock(1, [1, 2, 3])
print(block(tf.zeros([1, 2, 3, 3])))
print([x.name for x in block.variables])

tf.Tensor(
[[[[0. 0. 0.]
   [0. 0. 0.]
   [0. 0. 0.]]

  [[0. 0. 0.]
   [0. 0. 0.]
   [0. 0. 0.]]]], shape=(1, 2, 3, 3), dtype=float32)
['resnet_identity_block/conv2d/kernel:0', 'resnet_identity_block/conv2d/bias:0',
 'resnet_identity_block/batch_normalization/gamma:0',
 'resnet_identity_block/batch_normalization/beta:0',
 'resnet_identity_block/conv2d_1/kernel:0',
 'resnet_identity_block/conv2d_1/bias:0',
 'resnet_identity_block/batch_normalization_1/gamma:0',
 'resnet_identity_block/batch_normalization_1/beta:0',
 'resnet_identity_block/conv2d_2/kernel:0',
 'resnet_identity_block/conv2d_2/bias:0',
 'resnet_identity_block/batch_normalization_2/gamma:0',
 'resnet_identity_block/batch_normalization_2/beta:0',
 'resnet_identity_block/batch_normalization/moving_mean:0',
 'resnet_identity_block/batch_normalization/moving_variance:0',
 'resnet_identity_block/batch_normalization_1/moving_mean:0',
 'resnet_identity_block/batch_normalization_1/moving_variance:0',
 'resnet_identity_block/batch_normalization_2/moving_mean:0',
 'resnet_identity_block/batch_normalization_2/moving_variance:0']

大多数情况下，模型是有多个网络层构成的，并一个接一个的被调用，这种情况可以通过 tf.keras.Sequential 来组合网络层实现。

my_seq = tf.keras.Sequential([tf.keras.layers.Conv2D(1, (1, 1)),
                              tf.keras.layers.BatchNormalization(),
                              tf.keras.layers.Conv2D(2, 1, 
                                                     padding='same'),
                              tf.keras.layers.BatchNormalization(),
                              tf.keras.layers.Conv2D(3, (1, 1)),
                              tf.keras.layers.BatchNormalization()])
my_seq(tf.zeros([1, 2, 3, 3]))

<tf.Tensor: id=508, shape=(1, 2, 3, 3), dtype=float32, numpy=
array([[[[0., 0., 0.],
         [0., 0., 0.],
         [0., 0., 0.]],

        [[0., 0., 0.],
         [0., 0., 0.],
         [0., 0., 0.]]]], dtype=float32)>

2.3.4.4 Next steps | 接下来

现在你可以回到上一节中，利用本节中网络层和模型的概念对之前的线性回归模型的例子进行更好的重构。

2.3.5 Custom training: walkthrough | 自定义训练：完整流程

View source on GitHub | Run in Google Colab

本节我们将通过机器学习模型对鸢尾花 (iris flowers) 进行种类划分。我们将利用 TensorFlow 的 Eager Execuation 模式：

1. 构建模型
2. 在样本数据上训练模型
3. 利用模型在未知数据上进行预测

2.3.5.1 TensorFlow programming | TensorFlow 编程

本节将使用如下 TensorFlow 的高阶概念：

• 开启 Eager Execuation 开发模式。
• 利用 Datasets API 导入数据。
• 利用 TensorFlow Kears API 都建模型和网络层。

本教程同其他 TensorFlow 代码结构类似：

1. 导入数据集
2. 选择模型
3. 训练模型
4. 评估模型性能
5. 利用训练好的模型进行预测

2.3.5.2 Setup program | 设置

2.3.5.2.1 Configure imports and eager execution | 设置导入和 Eager Execution 模式

导入相关的 Python 模块，包括 TensorFlow，同时开启 Eager Execution 模式。Eager Execution 模式可以使 TensorFlow 的每一个操作立即被执行并返回具体的值，而不是建立一个 计算图 稍后再执行。如果你使用过交互式解析器 (REPL) 或 Python 的交互式控制台，该模式与其类似。Eager Execution 模式要求 Tensorflow 的版本大于等于 1.8。

一旦 Eager Execution 模式开启后，在这个程序中则无法再将其关闭，更过细节，请参见 eager executuion guide。

from __future__ import absolute_import, division, print_function

import os
import matplotlib.pyplot as plt

import tensorflow as tf
import tensorflow.contrib.eager as tfe

tf.enable_eager_execution()

print("TensorFlow version: {}".format(tf.VERSION))
print("Eager execution: {}".format(tf.executing_eagerly()))

TensorFlow version: 1.10.0
Eager execution: True

2.3.5.3 The Iris classification problem | 鸢尾花分类问题

假设你是一名植物学家，你正在寻找一种自动化的方法对你发现的鸢尾花进行分类。机器学习提供了大量的算法用于对花朵进行分类，例如一个复杂的机器学习程序可以根据鸢尾花的图片对其进行分类。我们的方案更加简单些，我们将利用鸢尾花的萼片 (sepals) 和花瓣 (petals) 的长度和宽度进行分类。

整个鸢尾花大约包含 300 个种类，本节我们仅对如下 3 种进行分类：

• Iris setosa
• Iris virginica
• Iris versicolor

图 1.16: Iris setosa (by Radomil, CC BY-SA 3.0), Iris versicolor, (by Dlanglois, CC BY-SA 3.0), 和 Iris virginica (by Frank Mayfield, CC BY-SA 2.0)

幸运的是已经有人构建了一个包含 120 个样本及其萼片和花瓣长宽信息的 鸢尾花数据集，这是在机器学习分类问题中初学者常用的一个经典数据集。

2.3.5.4 Import and parse the training dataset | 导入训练数据

下载数据集文件，并将其转换为 Python 可以使用的数据结构。

2.3.5.4.1 Download the dataset | 下载数据集

利用 tf.keras.utils.get_file 工具函数下载训练数据集，该函数将返回已下载的文件的路径。

train_dataset_url = "http://download.tensorflow.org/data/iris_training.csv"

train_dataset_fp = tf.keras.utils.get_file(fname=os.path.basename(train_dataset_url),
                                           origin=train_dataset_url)

print("Local copy of the dataset file: {}".format(train_dataset_fp))

Downloading data from http://download.tensorflow.org/data/iris_training.csv
8192/2194 [=========================================================] - 0s 0us/step
Local copy of the dataset file: /root/.keras/datasets/iris_training.csv

2.3.5.4.2 Inspect the data | 探索数据

数据文件 (iris_training_csv) 是一个逗号分隔符文件 (CSV)，使用 head -n5 命令插线前 4 条数据：

!head -n5 {train_dataset_fp}

120,4,setosa,versicolor,virginica
6.4,2.8,5.6,2.2,2
5.0,2.3,3.3,1.0,1
4.9,2.5,4.5,1.7,2
4.9,3.1,1.5,0.1,0

从中我们可以得知：

1. 第一行包含了数据集的一些相关信息
   • 数据集共包含 120 个样本，每个样本包含 4 个特征和 1 个分类标签名。
2. 其他行为数据记录，每行一个 样本
   • 前 4 列为 特征：即为样本的一些特征属性。本数据集中为花朵的一些衡量指标。
   • 最后一列为 标签：也就是我们想预测的值。本数据集中为 0，1 或 2 分别对应不同的种类。

让我们写一些代码：

# column order in CSV file
column_names = ['sepal_length', 'sepal_width', 'petal_length', 'petal_width', 'species']

feature_names = column_names[:-1]
label_name = column_names[-1]

print("Features: {}".format(feature_names))
print("Label: {}".format(label_name))

Features: ['sepal_length', 'sepal_width', 'petal_length', 'petal_width']
Label: species

每个标签对应一个类型的名称 (例如：setosa)，但机器学习通常会采用数值性进行处理。不同的类型数字会对应到不同的名称上，例如：

• 0：Iris setosa
• 1：Iris versicolor
• 2：Iris virginica

更多有关特征和标签的内容，请参见 ML Terminology section of the Machine Learning Crash Course。

class_names = ['Iris setosa', 'Iris versicolor', 'Iris virginica']

2.3.5.4.3 Create a tf.data.Dataset | 构建一个 tf.data.Dataset

TensorFlow 的 Dataset API 能够处理许多将数据加载到模型中的常见情况。这是一套用于读取和转换数据的高阶 API，更多信息请参见 Datasets Quick Start guide。

因为数据集为逗号分隔符文件，因此我们使用 make_csv_dataset 函数进行解析。这个函数适用于为模型的训练提供数据，默认情况下会对数据进行混洗 (shuffle=True, shffle_buffer_size=10000) 并且一直重复数据 (num_epochs=None)。我们还可以设置批大小 (batch_size)：

batch_size = 32

train_dataset = tf.contrib.data.make_csv_dataset(
    train_dataset_fp,
    batch_size, 
    column_names=column_names,
    label_name=label_name,
    num_epochs=1)

make_csv_dataset 函数返回一个值为 (features, label) 对的 tf.data.Dataset 对象，其中 features 是一个词典：{'feature_name': value}。

当 Eager Execution 模式开启时，这些 Dataset 对象是可以递归的，让我们来看一下一批特征：

features, labels = next(iter(train_dataset))

features

OrderedDict([('sepal_length',
              <tf.Tensor: id=115377, shape=(32,), dtype=float32, numpy=
              array([6.4, 5.1, 6.5, 5.1, 4.4, 6.5, 6.8, 5.3, 6.4, 6.3, 5.5, 6. , 7.9,
                     7.2, 4.7, 6.4, 4.8, 5.8, 7.7, 6.5, 5. , 7.7, 6.4, 4.9, 5. , 5. ,
                     7.6, 5.5, 5.8, 6.1, 5. , 6.1], dtype=float32)>),
             ('sepal_width',
              <tf.Tensor: id=115378, shape=(32,), dtype=float32, numpy=
              array([2.8, 3.7, 2.8, 3.8, 3.2, 3. , 3.2, 3.7, 3.2, 3.3, 2.4, 3. , 3.8,
                     3.6, 3.2, 2.7, 3.1, 2.7, 2.8, 3. , 3.5, 2.6, 2.8, 3.1, 3.6, 3.4,
                     3. , 2.4, 2.7, 2.6, 2.3, 2.8], dtype=float32)>),
             ('petal_length',
              <tf.Tensor: id=115375, shape=(32,), dtype=float32, numpy=
              array([5.6, 1.5, 4.6, 1.5, 1.3, 5.5, 5.9, 1.5, 4.5, 6. , 3.8, 4.8, 6.4,
                     6.1, 1.6, 5.3, 1.6, 4.1, 6.7, 5.8, 1.3, 6.9, 5.6, 1.5, 1.4, 1.6,
                     6.6, 3.7, 5.1, 5.6, 3.3, 4. ], dtype=float32)>),
             ('petal_width',
              <tf.Tensor: id=115376, shape=(32,), dtype=float32, numpy=
              array([2.1, 0.4, 1.5, 0.3, 0.2, 1.8, 2.3, 0.2, 1.5, 2.5, 1.1, 1.8, 2. ,
                     2.5, 0.2, 1.9, 0.2, 1. , 2. , 2.2, 0.3, 2.3, 2.2, 0.1, 0.2, 0.4,
                     2.1, 1. , 1.9, 1.4, 1. , 1.3], dtype=float32)>)])

需要注意的是这些特征是以一组或一批的形式存在的，每个样本的每列的值都被添加到对应的特征数组中。通过改变 batch_size 可以设置这些特征数组中存储的样本个数。

你可以将一批数据中一些特征做图来观察一些分群现象：

plt.scatter(features['petal_length'],
            features['sepal_length'],
            c=labels,
            cmap='viridis')

plt.xlabel("Petal length")
plt.ylabel("Sepal length")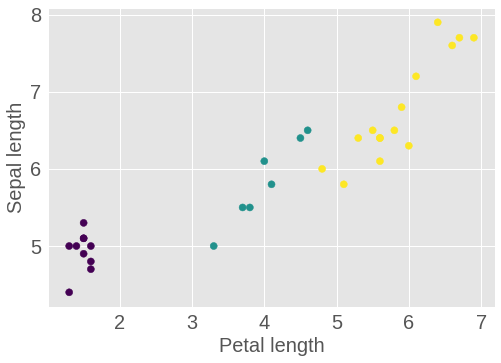

图 1.17: 一批 Iris 数据的 Petal 长度和 Sepal 长度

为了简化模型的构建步骤，我们创建一个函数将特征词典重新封装成为一个形状为 (batch_size, num_features) 的数组。

这个函数使用 tf.stack 方法，这个方法可以将一个张量的列表按照指定的维度合并成一个张量。

def pack_features_vector(features, labels):
  """Pack the features into a single array."""
  features = tf.stack(list(features.values()), axis=1)
  return features, labels

接下来我们使用 tf.data.Dataset.map 将每一个 (features, label) 对打包成 features 并放入训练数据集中：

train_dataset = train_dataset.map(pack_features_vector)

现在 Dataset 的特征元素变成了形状为 (batch_size, num_features) 的数组，让我们来看一写样本：

features, labels = next(iter(train_dataset))

print(features[:5])

tf.Tensor(
[[5.8 2.6 4.  1.2]
 [5.6 2.9 3.6 1.3]
 [4.6 3.6 1.  0.2]
 [6.4 2.8 5.6 2.1]
 [5.6 2.7 4.2 1.3]], shape=(5, 4), dtype=float32)

2.3.5.5 Select the type of model | 选择一个模型

2.3.5.5.1 Why model? | 为什么需要模型？

模型 是特征和标签之间的一个桥梁。对于 Iris 分类问题，模型定义了萼片和花瓣的一些度量与 Iris 种类之间的关系。一些简单的模型可以用几行简单的数学公式描述，但复杂的机器学习模型包含很多难以概括的参数。

你能否在不使用机器学习的情况下确定 Iris 种类和这四个特征之间的关系呢？也就是说，你是否可以利用传统的编程技术 (例如很多的条件语句) 来构建模型呢？如果你对数据集进行了足够长时间的分析，也许你可以得出一个特定的种类与花瓣和萼片的度量之间的关系，但是对于更复杂的数据集，这将变得很困难，甚至不可能。一个好的机器学习方法可以帮助你确定一个合适的模型，如果你选取了一个适合的机器学习模型，并提供了足够多的有代表性的样本，那么程序将能够为你找出其中的关系。

2.3.5.5.2 Select the model | 选择模型

我们需要选取一种模型用于训练，模型多种多样，选择一个合适的模型需要丰富的经验。本节将使用一个神经网络模型解决 Iris 分类问题。神经网络模型 能够识别特征和标签之间复杂的关系。其是一个高度结构化的图，包含一个或多个 隐含层，没一层包含一个或多个 神经元。神经网络也包含很多种不同的类型，本例中我们将使用一个稠密或叫做 全链接的神经网络，即一个层中的一个神经元接收上一层中所有神经元的输出为输入。例如：下图展示了一个包含一个输入层，两个隐含层和一个输出层的神经网络。

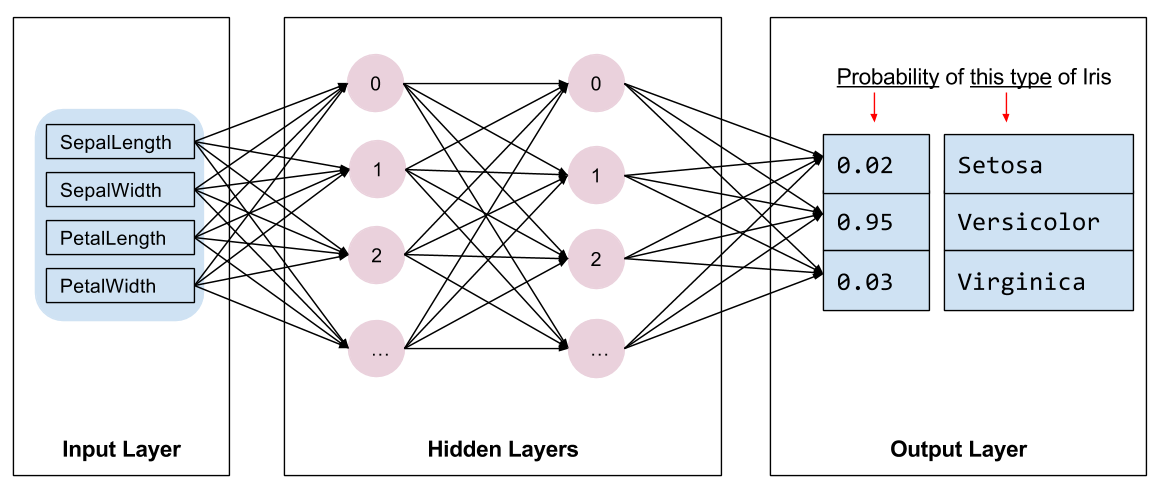
图 1.18: 全链接神经网络

当上图中的模型训练好并喂给一个未打标的样本时，起降产生三个预测值，每个值即为属于这个分类的可能性，这个预测的流程我们称之为 推理 (inference)。在本例中，输出的预测值之和为 1.0，图中预测值分别为：Iris setosa 为 0.02，Iris versicolor 为 0.95，Iris virginica 为 0.03。也就是说模型对这个未标注的数据预测，其有 95% 的可能性属于 Iris versicolor 分类。

2.3.5.5.3 Create a model using Keras | 利用 Keras 构建一个模型

我们强烈建议使用 TensorFlow 中的 tf.keras API 构建模型和网络层。Keras 能够处理复杂的网络层的连接，这使得我们更加容易的构建模型和进行实验。

tf.keras.Sequential 是一系列网络层的线性堆叠。其构造器接受一个层实例的列表，本例中，共有两个 全链接层，每层 10 个节点，输出层包含 3 个节点分别表示不同的类型的预测值。第一层中的 input_shape 参数表示数据集中特征的个数，是必需的。

model = tf.keras.Sequential([
  tf.keras.layers.Dense(10, activation=tf.nn.relu, input_shape=(4,)),  # input shape required
  tf.keras.layers.Dense(10, activation=tf.nn.relu),
  tf.keras.layers.Dense(3)
])

激活函数 决定了每一层每一个节点输出的形状。在这里非线性 (non-linearities) 至关重要，缺少了它模型将等同于一个单层的网络。激活函数有 很多种，其中 ReLU 是一种常用于隐含层的激活函数。

理想的网络层数和神经元数量取决于问题和数据集。想机器学习的许多方面一样，选择一个合适的网络结构需要大量的知识和实验。一般来说，增加隐含层和神经元的数量通常会构建一个更强大的模型，同时也需要更多的数据来进行有效的训练。

2.3.5.5.4 Using the model | 使用模型

让我们快速的看一下模型对一批特征数据的处理结果：

predictions = model(features)
predictions[:5]

<tf.Tensor: id=115517, shape=(5, 3), dtype=float32, numpy=
array([[-0.25014448,  0.4518844 , -0.19731727],
       [-0.24891749,  0.45386022, -0.2008579 ],
       [-0.5100661 ,  0.8423368 , -0.16162065],
       [-0.00567953,  0.02502966, -0.02036327],
       [-0.16325398,  0.30432606, -0.1388951 ]], dtype=float32)>

这里，每个样本都返回了每个类对应的 Logit 值。

使用 softmax 函数可以将这些 logits 转换为每个类所对应的概率值。

tf.nn.softmax(predictions[:5])

<tf.Tensor: id=115523, shape=(5, 3), dtype=float32, numpy=
array([[0.24557413, 0.49552992, 0.2588959 ],
       [0.24578558, 0.49632812, 0.2578864 ],
       [0.15914522, 0.6153677 , 0.22548702],
       [0.33149803, 0.34183598, 0.32666594],
       [0.27618322, 0.44082347, 0.28299332]], dtype=float32)>

利用 tf.argmax 函数获取预测的类型。由于我们的模型并没有进行训练，因此预测效果比较糟糕。

print("Prediction: {}".format(tf.argmax(predictions, axis=1)))
print("    Labels: {}".format(labels))

Prediction: [1 1 1 1 1 1 1 1 1 0 1 1 1 1 0 1 0 1 1 1 0 1 1 1 1 1 1 1 1 1 1 1]
    Labels: [1 1 0 2 1 0 1 2 1 2 1 0 2 1 2 0 2 2 0 1 2 0 0 1 0 0 1 0 2 0 1 0]

2.3.5.6 Train the model | 训练模型

训练 是指机器学习中模型不断优化，也就是不断利用数据集进行学习的过程。目标就是从训练数据中学习到足够的信息从而可以对未知数据进行预测。但如果从训练数据中学习了过多的信息，模型则会仅对已知的数据有较高的预测效果，但缺乏泛化能力。这个问题我们称之为 过拟合 (overfitting)，就像我们仅记住了已知问题的答案，而并没有真正去理解如何解决这个问题。

Iris 分类问题是一个 有监督学习 (supervised machine learning) 的示例，模型需要从带有标签的样本中进行学习。在 无监督学习 (unsupervised machine learning)，样本数据没有标签，模型仅是在特征中寻找不同的模式。

2.3.5.6.1 Define the loss and gradient function | 定义损失和梯度函数

在训练和评估阶段，我们都需要计算模型的 损失 (loss)。其用于衡量模型的预测与真实标签之间的差异程度，也就是模型的表现，我们期望优化，也就是最小化这个值。

我们利用 tf.losses.sparse_softmax_cross_entropy 函数计算模型的损失，其将模型的 logits 值和真实便签作为参数，返回在样本上的平均损失。

def loss(model, x, y):
  y_ = model(x)
  return tf.losses.sparse_softmax_cross_entropy(labels=y, logits=y_)


l = loss(model, features, labels)
print("Loss test: {}".format(l))

Loss test: 1.2565419673919678

利用 tf.GradientTape 可以计算用于优化模型的 梯度 (gradients)。更多内容和示例，请参见 Eager Execution Guide。

def grad(model, inputs, targets):
  with tf.GradientTape() as tape:
    loss_value = loss(model, inputs, targets)
  return loss_value, tape.gradient(loss_value, model.trainable_variables)

2.3.5.6.2 Create an optimizer | 构建一个优化器

一个 优化器 (optimizer) 将计算得到的梯度应用在模型的参数上，从而最小化损失函数。你可以将损失函数想想成为一个曲面 (见图 1.19)，我们需要的是找到其最低点。梯度即为曲面上最陡的上升的方向，因此我们将以梯度的反方向进行移动。通过迭代计算在每一批次数据上的损失和梯度，在训练过程中对模型不断调整，逐渐地，模型将找到最合适的权重和偏置以实现最小化损失。对于模型而言，其损失越小，模型的预测效果越好。

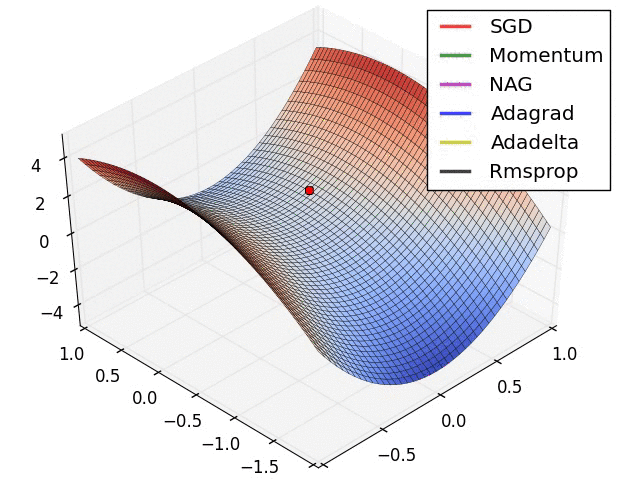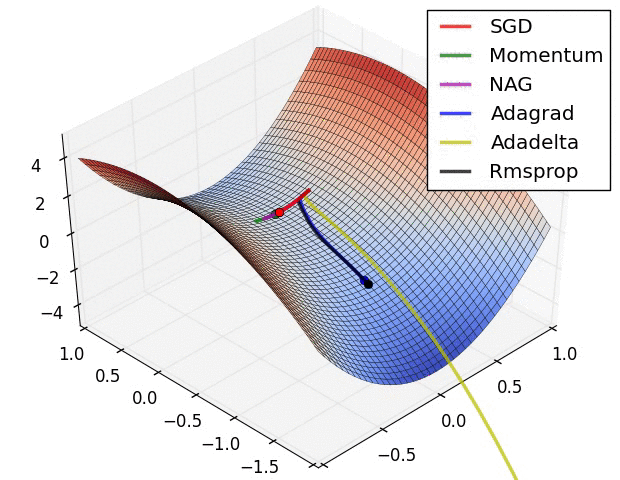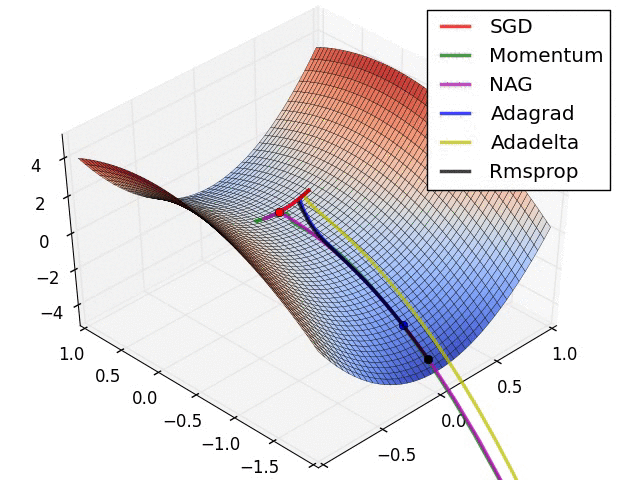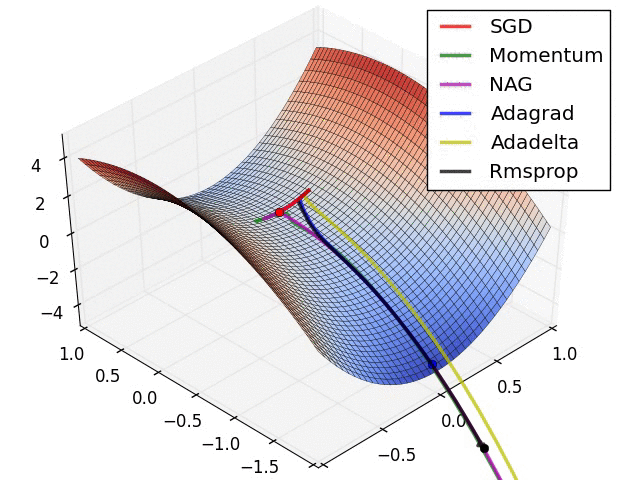
图 1.19: 3 维空间优化算法可视化 (Source: Stanford class CS231n, MIT License)

TensorFlow 有很多用于训练的 优化算法。本例我们使用 tf.train.GradientDescentOptimizer 优化器，其实现了 随机梯度下降 (stochastic gradient descent, SGD) 算法。参数 learning_rate 表示每一次步长，这是一个超参数 (hyperparameter)，通常情况下你需要不断调整才能取得一个不错的结果。

让我们来设置优化器和 global_step 计数器。

optimizer = tf.train.GradientDescentOptimizer(learning_rate=0.01)

global_step = tf.train.get_or_create_global_step()

我们使用它来计算一个单步的优化：

loss_value, grads = grad(model, features, labels)

print("Step: {}, Initial Loss: {}".format(global_step.numpy(),
                                          loss_value.numpy()))

optimizer.apply_gradients(zip(grads, model.variables), global_step)

print("Step: {},         Loss: {}".format(global_step.numpy(),
                                          loss(model, features, labels).numpy()))

Step: 0, Initial Loss: 1.2565419673919678
Step: 1,         Loss: 1.2273242473602295

2.3.5.6.3 Training loop | 循环训练

准备工作已经完毕，至此我们可以开始进行模型训练了。一个循环训练是将数据集中的样本不断的喂给模型帮助其能够更好的进行预测。如下为训练中的相关步骤：

1. 遍历每一轮 (epoch)，一轮是指将整个数据集使用一遍。
2. 在每一轮中，遍历训练数据集 (Dataset) 中每个样本，获取其特征 (x) 和标签 (y)。
3. 利用样本的特征进行预测，与其标签进行对比。度量预测的精准度并计算模型的损失和梯度。
4. 利用一个优化器 (optimizer) 更新模型的参数。
5. 跟踪整个过程的一些统计信息。
6. 在下一轮中重复该过程。

num_epochs 是重复整个数据集的次数。可能与我们的直觉相反，对模型训练更长的时间并不能够保证其效果会越来越好。num_epochs 是一个需要你调整的 超参数 (hyperparameter)，选择合适的轮数往往需要丰富的经验和大量的实验。

## Note: Rerunning this cell uses the same model variables

# keep results for plotting
train_loss_results = []
train_accuracy_results = []

num_epochs = 201

for epoch in range(num_epochs):
  epoch_loss_avg = tfe.metrics.Mean()
  epoch_accuracy = tfe.metrics.Accuracy()

  # Training loop - using batches of 32
  for x, y in train_dataset:
    # Optimize the model
    loss_value, grads = grad(model, x, y)
    optimizer.apply_gradients(zip(grads, model.variables),
                              global_step)

    # Track progress
    epoch_loss_avg(loss_value)  # add current batch loss
    # compare predicted label to actual label
    epoch_accuracy(tf.argmax(model(x), axis=1, output_type=tf.int32), y)

  # end epoch
  train_loss_results.append(epoch_loss_avg.result())
  train_accuracy_results.append(epoch_accuracy.result())
  
  if epoch % 50 == 0:
    print("Epoch {:03d}: Loss: {:.3f}, Accuracy: {:.3%}".format(epoch,
                                                                epoch_loss_avg.result(),
                                                                epoch_accuracy.result()))

Epoch 000: Loss: 1.205, Accuracy: 29.167%
Epoch 050: Loss: 0.616, Accuracy: 77.500%
Epoch 100: Loss: 0.331, Accuracy: 96.667%
Epoch 150: Loss: 0.214, Accuracy: 97.500%
Epoch 200: Loss: 0.160, Accuracy: 97.500%

2.3.5.6.4 Visualize the loss function over time | 可视化损失函数变化

打印出模型训练的过程会对我们很有帮助，当然可视化这个过程将会更好。TensorBoard 是一个很好的用于 TensorFlow 的可视化工具，同时我们可以利用 matplotlib 包绘制简单的图形。

对这些图进行解释会需要一定的经验，简单一点我们希望看到的是损失的下降和准确率的上升。

fig, axes = plt.subplots(2, sharex=True, figsize=(12, 8))
fig.suptitle('Training Metrics')

axes[0].set_ylabel("Loss", fontsize=14)
axes[0].plot(train_loss_results)

axes[1].set_ylabel("Accuracy", fontsize=14)
axes[1].set_xlabel("Epoch", fontsize=14)
axes[1].plot(train_accuracy_results)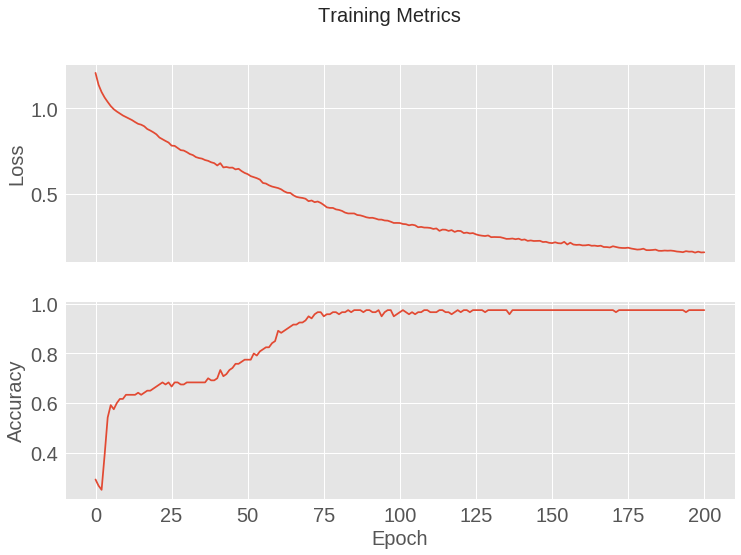

图 1.20: 模型损失和准确率变化曲线

2.3.5.7 Evaluate the model’s effectiveness | 评估模型的性能

模型已经训练完毕，现在我们可以对其性能进行一些统计。

评估 (Evaluating) 意味着要判断模型的预测效果如何。为了确定模型在 Iris 分类问题上的效果，我们可以将萼片和花瓣的一些度量值喂给模型，让其预测 Iris 的种类，然后将预测值同真实的标签进行比对。例如：如果一个模型能够将输入样本冲的一半预测正确，其准确率则为 0.5。表 1.3 展示了一个效果更好的模型，其将 5 个预测对了 4 个，准确率为 80%。

表 1.3: 一个准确率为 0.8 的 Iris 分类器

Sepal length	Sepal width	Petal length	Petal width	Label	Model prediction
5.9	3.0	4.3	1.5	1	1
6.9	3.1	5.4	2.1	2	2
5.1	3.3	1.7	0.5	0	0
6.0	3.4	4.5	1.6	1	2
5.5	2.5	4.0	1.3	1	1

2.3.5.7.1 Setup the test dataset | 准备测试集

评估模型和训练模型类似，最大的区别就是数据来自于一个单独的 测试集 而不是训练集。为了公平的评估模型的效果，用于评估的数据必须与训练模型时所用的数据不同。

准备测试数据集同训练集类似，下载对应的 CSV 文件并读取其中的数据：

test_url = "http://download.tensorflow.org/data/iris_test.csv"

test_fp = tf.keras.utils.get_file(fname=os.path.basename(test_url),
                                  origin=test_url)

Downloading data from http://download.tensorflow.org/data/iris_test.csv
8192/573 [============================================================] - 0s 0us/step

test_dataset = tf.contrib.data.make_csv_dataset(
    train_dataset_fp,
    batch_size, 
    column_names=column_names,
    label_name='species',
    num_epochs=1,
    shuffle=False)

test_dataset = test_dataset.map(pack_features_vector)

2.3.5.7.2 Evaluate the model on the test dataset | 在测试集上评估模型

不同于训练阶段，模型仅需在测试数据集上执行一 轮 即可。在下面的代码块中，我们遍历测试集的所有样本，并比较其真实的标签和模型的预测值，用于衡量模型在整个测试集上的准确率。

test_accuracy = tfe.metrics.Accuracy()

for (x, y) in test_dataset:
  logits = model(x)
  prediction = tf.argmax(logits, axis=1, output_type=tf.int32)
  test_accuracy(prediction, y)

print("Test set accuracy: {:.3%}".format(test_accuracy.result()))

Test set accuracy: 96.667%

我们可以看一下测试集最后一批数据的预测结果，大部分都是正确的：

tf.stack([y,prediction], axis=1)

<tf.Tensor: id=230521, shape=(24, 2), dtype=int32, numpy=
array([[0, 0],
       [2, 2],
       [1, 2],
       [0, 0],
       [0, 0],
       [1, 1],
       [0, 0],
       [1, 1],
       [0, 0],
       [0, 0],
       [0, 0],
       [0, 0],
       [1, 1],
       [0, 0],
       [2, 2],
       [1, 1],
       [0, 0],
       [2, 2],
       [0, 0],
       [1, 1],
       [1, 1],
       [0, 0],
       [0, 0],
       [1, 1]], dtype=int32)>

2.3.5.8 Use the trained model to make prediction | 利用训练好的模型进行预测

我们已经训练好一个模型，并且“证明”了其在 Iris 分类问题上的效果还不错 (并不是很完美)。接下来，我们可以利用训练好的模型对一些 未标注的数据 进行预测，也就是仅包含特征而不包含标签的数据。

在现实生活中，未标注的数据可能来自于不同的渠道，例如：APP，CSV 文件，数据流等等。现在，我们手动构造一些为标注的数据并对其进行预测。标签的数值及其对应的种类如下：

• 0: Iris setosa
• 1: Iris versicolor
• 2: Iris virginica

predict_dataset = tf.convert_to_tensor([
    [5.1, 3.3, 1.7, 0.5,],
    [5.9, 3.0, 4.2, 1.5,],
    [6.9, 3.1, 5.4, 2.1]
])

predictions = model(predict_dataset)

for i, logits in enumerate(predictions):
  class_idx = tf.argmax(logits).numpy()
  p = tf.nn.softmax(logits)[class_idx]
  name = class_names[class_idx]
  print("Example {} prediction: {} ({:4.1f}%)".format(i, name, 100*p))

Example 0 prediction: Iris setosa (96.4%)
Example 1 prediction: Iris versicolor (84.3%)
Example 2 prediction: Iris virginica (67.9%)