Capítulo 4 Teste de hipóteses

4.1 Distribuição normal

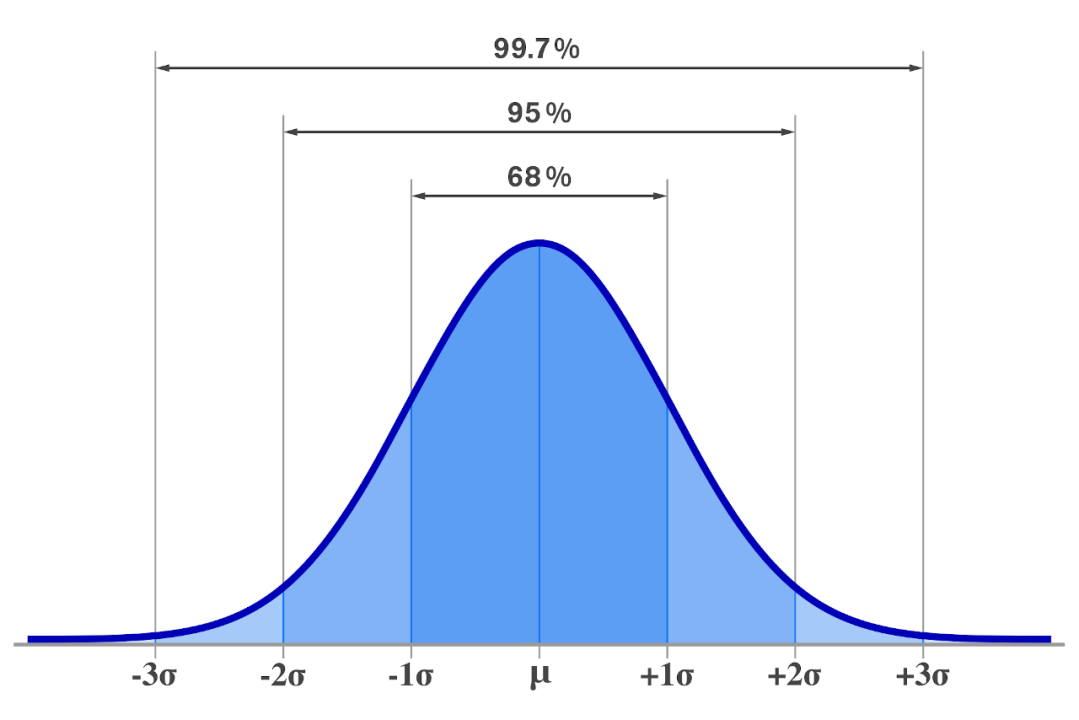
Figura 1.1: Função densidade de probabilidade da distribuição gaussiana (distribuição normal): $X \sim N(\mu,\sigma^2)$.

Figura 2.1: Várias funções densidade de probabilidade da distribuição distribuição normal: Em $\mu=0$ e $\sigma^2=1$ (curva vermelha) temos a distribuição normal padrão $X \sim N(0,1)$

$$f(x) = \frac{1}{\sigma \sqrt{2\pi} } e^{-\frac{1}{2}\left(\frac{x-\mu}{\sigma}\right)^2}$$

Onde: $\mu$ = média, $\sigma$ = desvio padrão.

Exemplos:

1. Curva normal [https://www.geogebra.org/m/muusbweq].
2. Curva normal 2 [https://www.geogebra.org/m/whcwmx4w].

Propriedades:

1. O ponto máximo de $f(x)$ está em $\mu$.
2. Os pontos de inflexão da função são: $X = \mu + \sigma$ e $X = \mu - \sigma$ (desvio-padrão).
3. A curva é simétrica em relação a $\mu$.
4. $E(X) = \mu$ e $Var(X) = \sigma^2$.
5. A área compreendida pela curva nesse intervalo é exatamente igual a 1, valor que, em estatística, corresponde a 100% de probabilidade.

4.2 Teorema do limite central

• Materiais de apoio (clique para acessar):
  • Rice Virtual Lab in Statistics: Sampling Distributions (em inglês).
  • Applet Central (em inglês).
  • Distribuição normal (em inglês).
  • Calculadora da distribuição normal.
  • Geogebra:
    • Central Limit Theorem (reproduced from Adam Knowles).
    • Distribuição Normal(0,1).

Quando o tamanho n da amostra aumenta, a distribuição amostral da sua média aproxima-se cada vez mais de uma distribuição normal.

Figura 1.2: Comparação das funções densidade de probabilidade, $p(k)$, para a soma de $n$ pares de dados de seis faces mostrando a convergência para uma distribuição normal quando se aumenta $n$ em acordo com o teorema do limite central. No gráfico abaixo a direita os perfis suaves estão reescalados e superpostos e comparados a uma distribuição normal (curva preta). Fonte: https://en.wikipedia.org/wiki/Normal_distribution

Teorema do limite central:

Se $\bar{x}$ é a média de uma amostra aleatória de tamanho $n$ de uma população infinita com a média $\mu$ e desvio-padrão $\sigma$ e se $n$ é grande, então $z$ é uma nova variável aleatória dada por

$$z=\frac{\bar{x} - \mu}{\sigma/\sqrt{n}} = \frac{\bar{x} - \mu}{\sigma_{\bar{x}}} \tag{4.1}$$

que tem uma nova distribuição normal padrão dada por $Z \sim N(\mu=0,\sigma^2 = 1)$, isto é, $Z \sim N(0,1)$.

Onde: $\sigma_{\bar{x}}=\sigma/\sqrt{n}$ na igualdade (4.1).

Em particular é importante lembrar que:

• Para população infinita: $\sigma_\bar{x} = \frac{\sigma_{pop}}{\sqrt{n}}$

• Para população finita: $\sigma_\bar{x} = \frac{\sigma_{pop}}{\sqrt{n}} \times \sqrt{\frac{N-n}{n-1}}$, onde $N$ é o tamanho da população.

4.3 Teste de hipóteses

Uma hipótese estatística é uma afirmação ou conjectura sobre um parâmetro, ou parâmetros, de uma população (ou populações). Pode também se referir ao tipo, ou natureza, da população (ou populações).

• Procedimentos gerais para um teste de hipótese:
  1. Definir a hipótese nula ($H_0$) e a alternativa ($H_A$).
  2. Definir um nível de significância $\alpha$, que irá determinar o nível de confiança $100 \times (1−\alpha)%$ do teste.
  3. Definir o tipo de teste, com base na hipótese alternativa.
  4. Calcular a estatística de teste, com base na distribuição amostral do estimador do parâmetro sob teste → valor calculado.
  5. Determinar a região crítica (região de rejeição), com base no nível de significância $\alpha$ → valor crítico.
  6. Concluir o teste.

4.3.1 Hipótese nula ($H_0$) × hipótese alternativa ($H_A$)

• A hipótese nula ($H_0$) é a alegação inicial assumida como verdadeira. A hipótese alternativa representado por $H_A$ é a afirmação contraditória.
• A hipótese nula será rejeitada em favor da hipótese alternativa somente se a evidência da amostra sugerir que $H_0$ seja falsa.
• Se a amostra não contradizer fortemente $H_0$, continuaremos a acreditar na verdade da hipótese nula.
• As duas conclusões possíveis de uma análise do teste de hipóteses são rejeitar $H_0$ ou não rejeitar $H_0$.

---

• Exemplo: Em um estudo sobre a proporção de homens e mulheres de uma mesma população, deseja-se testar a hipótese de que a proporção de mulheres é maior do que a proporção de homens. Clique aqui para baixar o arquivo (nesse arquivo vamos considerar $1$ como mulher, mas depende de como o dado foi coletado pelo pesquisador).

1. Definir a hipótese nula ($H_0$) e a alternativa ($H_A$).

Resolução: Supõe-se inicialmente que a população de mulheres é de 50 %, ou seja, $H_0$ é tal que a proporção $p_M = 0,5$. Então as hipóteses são:

$H_0: p_M = 0,5$ × $H_A: p_M > 0,5$

Com isso, deseja-se que a hipótese nula $p_M = 0,5$ seja rejeitada, de modo que a hipótese alternativa $p_M > 0,5$ seja apoiada.

Apoiar a hipótese alternativa de que $p_M > 0,5$ é o mesmo que apoiar a afirmativa de que a proporção de mulheres na população é maior do que a de homens.

2. Nível de significância: erros de decisão.

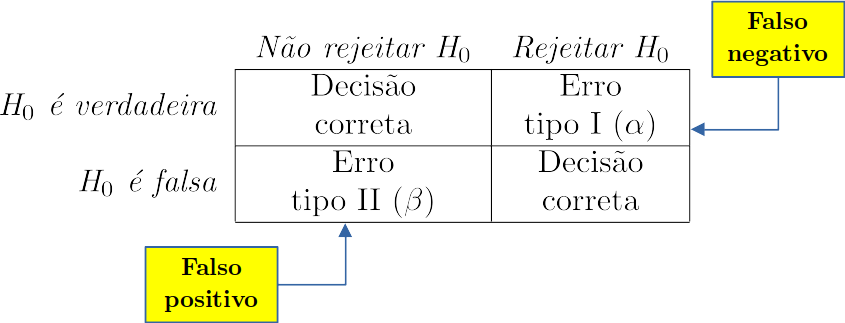
Figura 1.3: Erros de decisão no teste de hipóteses.

• $\alpha$ = Pr(erro tipo I) = Pr(rejeitar $H_0$ | $H_0$ verdadeira) (leia-se: probabilidade de rejeitar $H_0$, sendo $H_0$ verdadeira).
• $\beta$ = Pr(erro tipo II) = Pr(não rejeitar $H_0$ | $H_0$ falsa).
• $\alpha$ é o nível de significância do teste.
• $1-\alpha$ é o nível de confiança do teste.

No exemplo anterior, se $H_0$: $p_M$ = 0,5 e $H_A$: $p_M$ > 0,5, então:

• $\alpha$ = Pr(concluir que a proporção de mulheres é maior quando na verdade não é).
• $\beta$ = Pr(concluir que a proporção é igual quando na verdade não é).

3. Definir o tipo de teste, com base na hipótese alternativa:

A hipótese alternativa determinará o sentido do teste de hipótese, que pode ser:

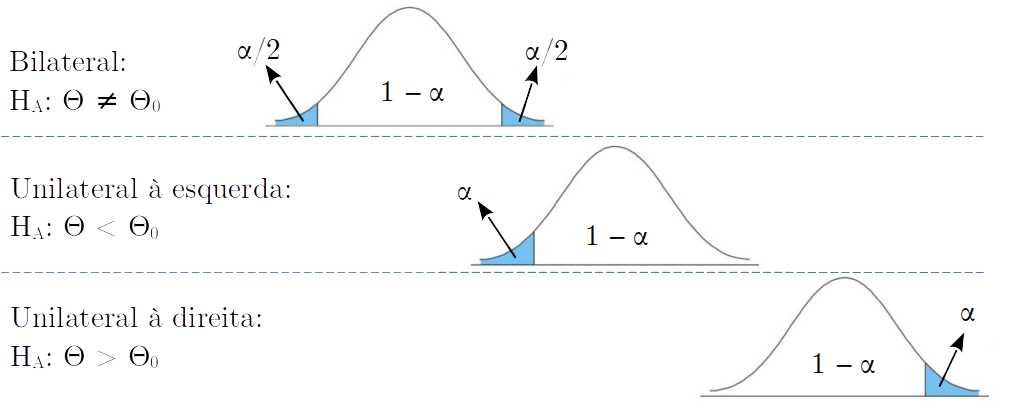
Figura 1.4: Diferentes testes para a hipótese alternativa.

3.1 Teste bilateral:

Uma hipótese do tipo:

$H_0: \Theta = \Theta_0$

$H_A: \Theta \ne \Theta_0$

É bilateral.

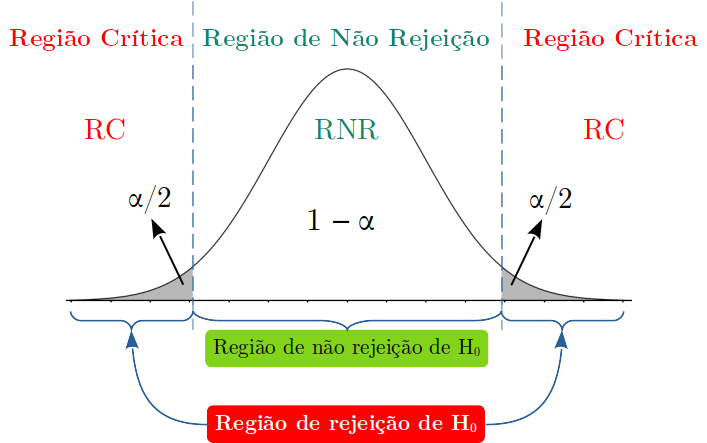
Figura 2.2: Teste bilateral com as regiões de rejeição e de não rejeição da $H_0$.

3.2 Teste unilaterais:

Uma hipótese do tipo:

$H_0: \Theta = \Theta_0$

$H_0: \Theta < \Theta_0$

É unilateral à esquerda.

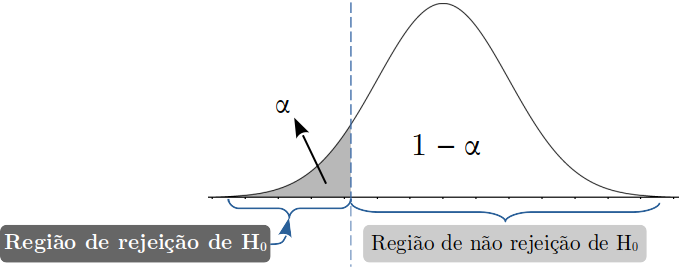
Figura 1.5: Teste unilateral a esquerda com as regiões de rejeição e de não rejeição da $H_0$.

Uma hipótese do tipo:

$H_0: \Theta = \Theta_0$

$H_0: \Theta > \Theta_0$

É unilateral à direita.

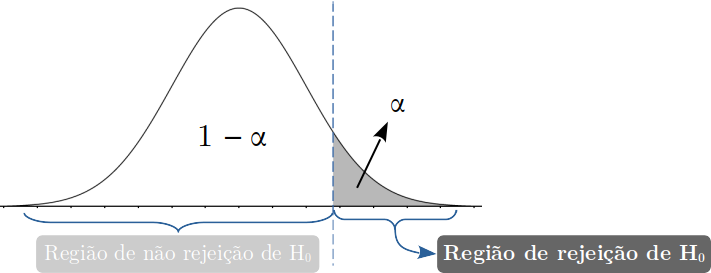
Figura 1.6: Teste unilateral a direita com as regiões de rejeição e de não rejeição da $H_0$.

4. Calcular a estatística de teste para a proporção:

Pode se demonstrar (Morettin, 2010¹) que a distribuição para proporções de $p$ sucessos pode ser defininida como uma variável aleatória da seguinte forma:

Seja $p$ conhecida A população pode ser definida como uma variável $X$ tal que:

$$X= \begin{cases} 1 & \text{se o elemento da população tem a característica}\\ 0 & \text{se o ele1nento da população não tem a característica} \end{cases}$$

e $Pr(X=1)=p$, $P(X=0)=1-p$.

Foi demonstrado² que: $\mu=E(X)=p$ e $\sigma^2=Var(X)=p(1-p)$.

Retira-se uma grande amostra³ ($n \rightarrow \infty$) $x_1$, $x_2$, $...$, dessa população, com reposição e define-se $x$ como o número de sucessos na amostra, isto é, o número de elementos da amostra com a característica que se quer estudar.

O estimador de $p$ é definido por $\hat{p}=\frac{x}{n}$: proporção de sucessos na amostra.

$X: B(n,p)$, $E(X) = np$ e $Var(X) = np(1-p)$.

Calculando esperança e variância de $p$:

$E(\hat{p})=E(\frac{x}{n})=\frac{1}{n}E(x)=\frac{1}{n} np = p$ $\therefore \mu_p = E(\hat{p})=p$.

$Var(\hat{p})=Var(\frac{x}{n})=\frac{1}{n^2}Var(x)=\frac{1}{n^2}np(1-p)=\frac{p(1-p)}{n}$ $\therefore \sigma_p=\sqrt{\frac{p(1-p)}{n}}$

Portanto a variável normalizada $z$ para proporção será:

$$z=\frac{\bar{x} - \mu}{\sigma} = \frac{E(x) - \mu}{\sigma_p} = \frac{p-p_0}{\sqrt{\frac{p_0(1-p_0)}{n}}}$$

5. Determinar a região crítica (região de rejeição), com base no nível de significância $\alpha$ → valor crítico

• Estabelecer um valor crítico que divide a região de rejeição da região de não rejeição da hipótese nula.
• A região crítica de um teste de hipótese é a região de rejeição da hipótese nula.

6. Concluir o teste. Com base na estatística do teste e do valor crítico:

• Se a estatística estiver dentro da região crítica rejeita-se $H_0$.
• Se a estatística estiver fora da região crítica não se rejeita $H_0$.

No R:

Temos duas funções que podem executar o teste de hipóteses: prop.test() (que usa a distribuição normal para o cálculo da probabilidade e que faz uso da correção de continuidade de Yates) e binom.test() (que é o teste exato para uma distribuição binomial).

O uso da distribuição Normal (distribuição contínua) em vez da distribuição Binomial (distribuição discreta) usa a correção de continuidade que tem por objetivo tornar as probabilidades calculadas pelo modelo Normal mais próximas daquelas obtidas usando o modelo Binomial⁴.

mulheres_homens=read.csv("mulheres-homens.csv")
table(mulheres_homens$resposta) # proporção de 1's e 0's.
#> 
#>  0  1 
#> 38 62
prop.test(x=62,n=100,alternative = "greater",correct = T)
#> 
#>  1-sample proportions test with continuity correction
#> 
#> data:  62 out of 100, null probability 0.5
#> X-squared = 5.29, df = 1, p-value = 0.01072
#> alternative hypothesis: true p is greater than 0.5
#> 95 percent confidence interval:
#>  0.5329359 1.0000000
#> sample estimates:
#>    p 
#> 0.62
binom.test(x=62,n=100,p=0.5,alternative = "greater")
#> 
#>  Exact binomial test
#> 
#> data:  62 and 100
#> number of successes = 62, number of trials = 100,
#> p-value = 0.01049
#> alternative hypothesis: true probability of success is greater than 0.5
#> 95 percent confidence interval:
#>  0.5332465 1.0000000
#> sample estimates:
#> probability of success 
#>                   0.62