Capítulo 3 Estatísticas descritivas

3.1 Escalas de medida

• O resultado de uma medição é chamada de variável.
• Nem todas as variáveis são do mesmo tipo.

Escala nominal ou categórica: não há relação entre as variáveis usadas, isto é, não há relação entre elas como “maior” ou “melhor”. Exemplos: cor do olho, gênero. Não faz sentido falar em “média do olho” ou “média do gênero”. Nesta escala somente podemos afirmar que uma medida é diferente ou não de outra, e ela é usada para categorizar indivíduos de uma população.

Operações aritméticas não são permitidas e uma medida de posição apropriada é a moda.

Escala ordinal: Uma medida é diferente e maior do que outra. As categorias são ordenadas, e a ordem dos numerais associados ordena as categorias. Por exemplo, a classe socioeconômica de um indivíduo pode ser baixa (1 ou X), média (2 ou Y) e alta (3 ou Z). Transformações que preservam a ordem não alteram a estrutura de uma escala ordinal.

Medidas de posição apropriadas são a mediana e a moda.

Escala intervalar: Uma medida é igual ou diferente, maior e quanto maior do que outra. Pode-se quantificar a diferença entre as categorias da escala ordinal. Necessita-se de uma origem arbitrária e de uma unidade de medida. Por exemplo, considere a temperatura de um indivíduo, na escala Fahrenheit. A origem é 0º F e a unidade é 1º F. Transformações que preservam a estrutura dessa escala são do tipo \(y = ax + b\), \(a > 0\). Por exemplo, a transformação \(y = 5/9 (x – 32)\) transforma graus Fahrenheit em graus Celsius.

Operações aritméticas, e média, mediana e moda são medidas de posição apropriadas.

Escala razão: Dadas duas medidas nessa escala, podemos dizer se são iguais, ou se uma é diferente, maior, quanto maior e quantas vezes a outra. A diferença com a escala intervalar é que agora existe um zero absoluto. A altura de um indivíduo é um exemplo de medida nessa escala. Se ela for medida em centímetros (cm), 0 cm é a origem e 1 cm é a unidade de medida. Um indivíduo com 190 cm é duas vezes mais alto do que um indivíduo com 95 cm, e esta relação continua a valer se usarmos 1 m como unidade. Ou seja, a estrutura da escala razão não é alterada por transformações da forma \(y = cx\), \(c > 0\). Por exemplo, \(y = x/100\) transforma cm em m.

As estatísticas apropriadas para a escala intervalar são também apropriadas para a escala razão.

• Tente você indicar quais são as escolas usadas:

1. Salários dos empregados de uma indústria.
2. Opinião de consumidores sobre determinado produto.
3. Número de respostas certas de alunos num teste com dez itens.
4. Temperatura diária da cidade de Manaus.
5. Porcentagem da receita de municípios aplicada em educação.
6. Opinião dos empregados da Companhia MB sobre a realização ou não de cursos obrigatórios de treinamento.
7. QI de um indivíduo.

3.1.1 Variáveis contínuas × discretas

• Uma variável contínua pode assumir quaisquer valores. Entre dois valores podem existir outros valores.
• Uma variável discreta não é continua e não há valores possíveis entre dois valores.

Tipos de escala e tipos de variáveis.

	contínua	discreta
nominal	-	Sim
ordinal	-	Sim
intervalar	Sim	Sim
razão	Sim	Sim

3.2 Preditores × resultados

• Usa-se a notação matemática de que \(Y\) é uma variável que se deseja que seja explicada pelas variáveis \(X_1\), \(X_2\), \(...\) .

• Os nomes clássicos para essas variáveis são:

  • Variáveis independentes (VI): as variáveis \(X\)’s (preditoras) são usadas para explicar a variável dependente.
  • Variáveis dependentes (VD): a variável \(Y\) (resultado) é explicada pelas variáveis \(X\)’s (independentes).

Variáveis e seus nomes clássicos e modernos.

Variável	Nome clássico	Nome moderno
a ser explicada	variável dependente (VD)	resultado
explicativa	variável independente (VI)	preditor

3.3 Medidas de tendência central:

Média: soma de \(N\) números dividida por \(N\).

\[ \overline{x} = \frac{x_1+x_2+x_3+\dots+ x_{N-1} +x_N }{N} = \frac{1}{N} \sum_{i=1}^{N} x_i \]

• O Símbolo \(\sum_{}^{}\) (sigma, letra S maiúscula grega) é usado para indicar o somatório . A soma é realizada sobre o índice \(i\). Nesse caso de \(1\) até \(N\).

Mediana: divide os valores ao meio. É o valor do \(\frac{N+1}{2}\)-ésimo item.

Exemplo: sejam os valores 30, 10, 15, 40, 35 e 20, logo N = 6. Sua mediana é o (6+1)/2 = 3,5, ou seja, o valor entre o 3º e 4º elemento. Valores ordenados: 10, 15, 20, 30, 35, 40. \(\therefore \textrm{Mediana}= \frac{20+30}{2} = 25\).

Moda: valor que mais aparece.

No R os respectivos comandos são: mean(), median(), para moda há um truque.

Exemplos:

• Usando o data frame dados:

library(readr)
dados <- read_csv("Dados_EB.csv", locale = locale(decimal_mark = ",", grouping_mark = "."))
# média
mean(dados$`Idade Anos`)
#> [1] 34.58333
mean(dados$`N de Filhos`,na.rm = T)
#> [1] 1.65
#
# mediana
median(dados$`Salario (x Sal Min)`)
#> [1] 10.165
#
# moda
sort(table(dados$`Região de Procedência`))
#> 
#>  capital interior    outra 
#>       11       12       13

Exemplo usando um applet do Geogebra: https://www.geogebra.org/classroom/zvktmetd/results/q7dzawwkpb

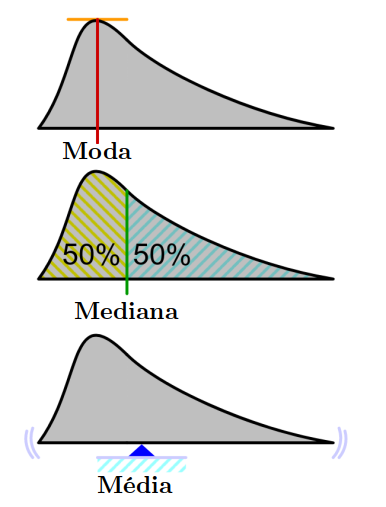
Figura 1.1: Medidas de tendência central. Fonte: https://commons.wikimedia.org/wiki/File:Visualisation_mode_median_mean.svg

Quantis: dividem os dados em duas ou mais partes aproximadamente tão iguais quanto possível. Há quartis, decis e percentis que dividem em 4, 10 e 100 partes os dados.

Quartis:

\[\begin{array}{l} Q_1 = \textrm{posição } x_{(\frac{N}{4})} \\ Q_2 = \textrm{posição da } \textrm{mediana} \\ Q_3 = \textrm{posição } x_{(\frac{3N}{4})} \\ \textrm{limite inferior} = Q_1 - 1,5(Q_3 - Q_1) \\ \textrm{limite superior} = Q_3 + 1,5(Q_3 - Q_1) \\ \textrm{IQR} = Q_3 - Q_1 \end{array}\]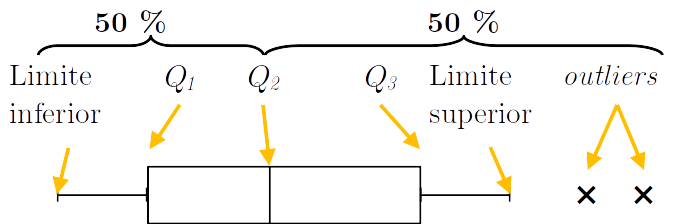

Figura 2.1: Box-plot.

No R, com os pacotes básicos, usam-se as funções boxplot.stats() e boxplot() (ver respectivos help para uso e resultados):

boxplot.stats(dados$`Idade Anos`)
#> $stats
#> [1] 20.0 30.0 34.5 40.0 48.0
#> 
#> $n
#> [1] 36
#> 
#> $conf
#> [1] 31.86667 37.13333
#> 
#> $out
#> numeric(0)
boxplot(dados$`Idade Anos`~dados$`Grau de Instrução`,xlab="Idade (anos)",ylab="Grau de instrução",width=c(.5,3,6),names=c("EF","EM","SU"),horizontal = T)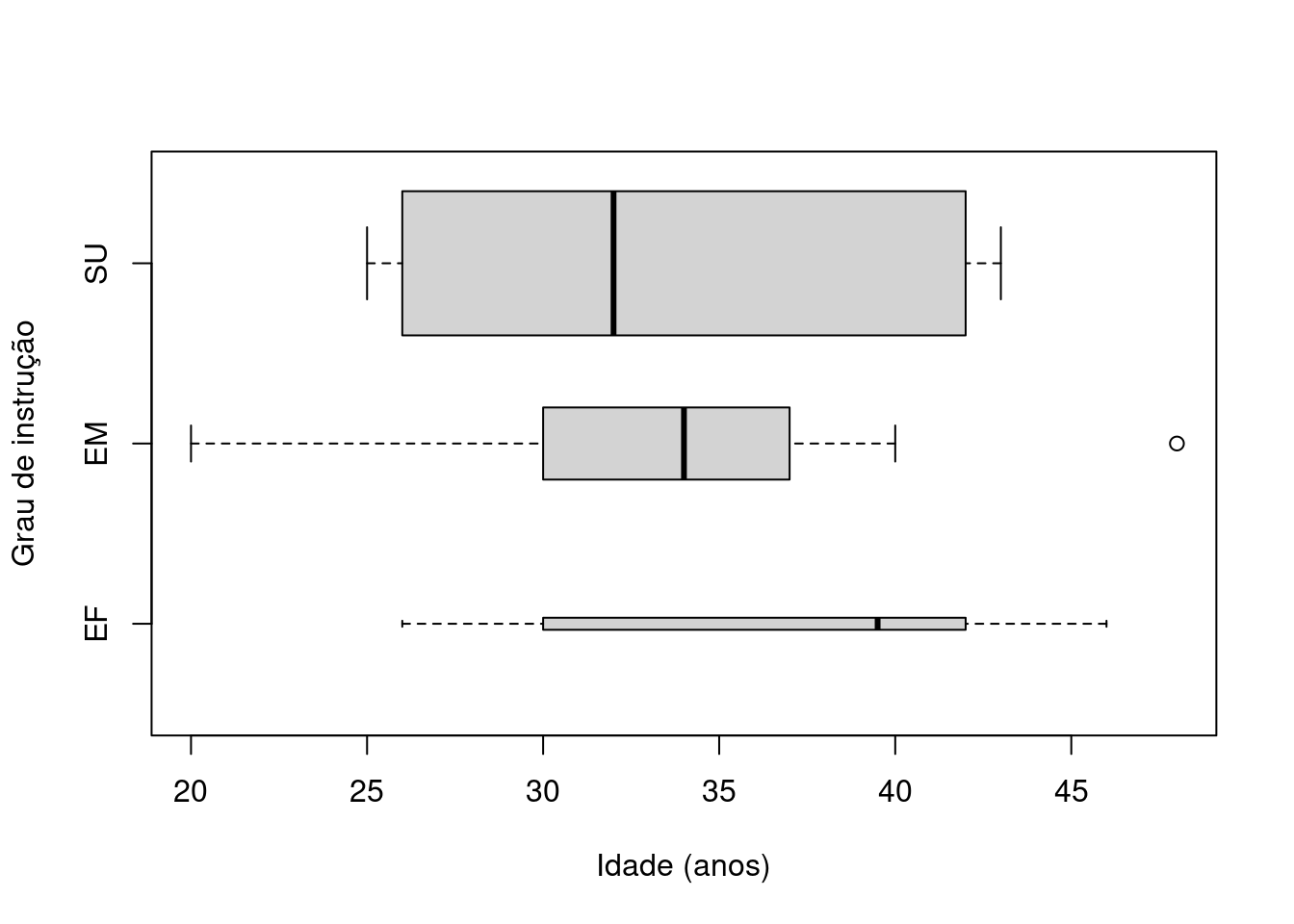

3.4 Histograma

Exemplo usando um applet do Geogebra: https://www.geogebra.org/classroom/ncetwurd

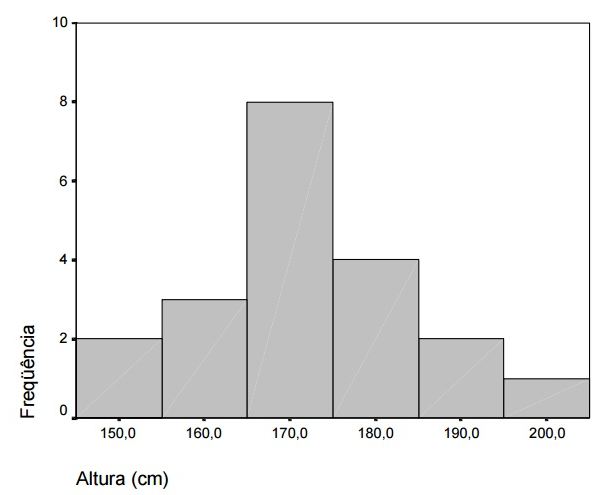
Figura 1.3: Histograma da altura.

• Quantos tem altura até 170 cm?

• Qual é a média da altura?

No R usa-se hist():

table(dados$`N de Filhos`)
#> 
#> 0 1 2 3 5 
#> 4 5 7 3 1
# para right = F as classes têm invervalo [a,b)
hist(dados$`N de Filhos`,freq = T,ylim = c(0,8),right = F,main = "Histograma de nº de filhos",xlab="Classes [a,b)",ylab="Frequência")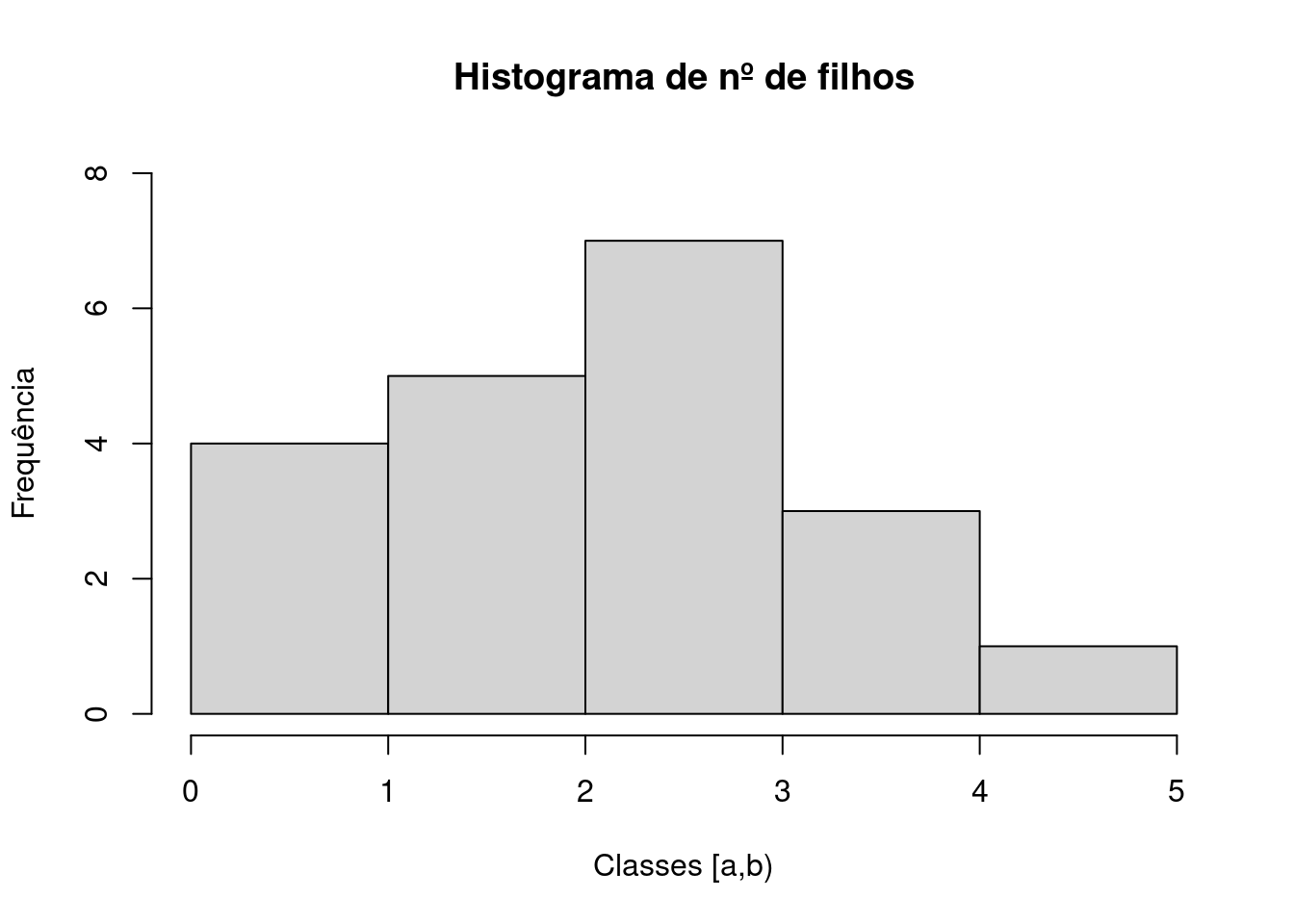

3.5 Medidas de dispersão:

Amplitude: diferença entre o maior e o menor valor.

Desvio padrão amostral: média do quanto em média os dados (da amostra) se desviam da média.

\[ s=\sqrt{\frac{\displaystyle\sum\limits_{i=1}^N ( x_i-\bar{x} )^2 }{N-1}} \]

O valor \(s^2\) é a variância.

3.5.1 Esperança matemática e Variância

Em estatística a média é também conhecida com esperança matemática (média artimética ponderada ou valor esperado). A esperança matemática de uma variável aleatória \(X\) é dada por \[E(X)=\sum_{ i=1 }^{ n } X_i \times p(X_i)\] Notações usuais: \(E(X)\), \(\mu(X)\), \(\mu_X\), \(\mu\).

O desvio padrão ao quadrado é também conhecido com variância (grau de dispersão em torno da média): \[Var(X)=E{[X-E(X)]^2} = E[X-\mu(X)]^2 = E[X^2]-E[X]^2\] No caso discreto, seja \(X\): \(x_1\), \(x_2\), \(...\), \(x_n\) e \(P(X=x_i) = p(x_i)\), \(i=1,2,...,n\): \[Var(X)=\sum_{i=1}^{n}(x_i-\mu_x)^2 \times p(x_i)\]

O desvio padrão é a raiz quadrada da variância de \(X\): \(\sigma_X = \sqrt{Var(X)}\)

Quanto menor a variância, menor o grau de dispersão de probabilidades em torno da média e vice-versa; quanto maior a variância, maior o grau de dispersão da probabilidade em torno da média.

Usando, como exemplo, uma função de distribuição normal (Fig. 3.1) (o que é uma “função de distribuição” será visto adiante) temos que no intervalo \((\sigma - \mu)\) a \((\sigma + \mu)\) o grau de concentração de probabilidades em torno da média é 68,2% (=34,1%\(\times 2\)), entre \((\sigma - 2 \mu)\) a \((\sigma + 2 \mu)\) (=(34,1% + 13,6%)\(\times 2\)) o grau de concentração de probabilidades em torno da média é de 95,2% e entre \((\sigma - 3 \mu)\) a \((\sigma + 3 \mu)\) o grau de concentração de probabilidades em torno da média é de 99,6%.

Figura 3.1: Função de distribuição normal e medidas de probabilidades entre os intervalos de um, dois e três desvio-padrão. Fonte: https://en.wikipedia.org/wiki/Normal_distribution

3.6 Variáveis aleatórias

Quando se realiza um experimento (uma coleta de dados) há interesse principalmente em alguma função do resultado e não do resultado em si.

Exemplos:

• Jogando dois dados estamos interessados na soma deles e não os valores individuais. Se quisermos saber quando a soma será 7 podemos ter os seguintes resultados (1, 6), (2, 5), (3, 4), (4, 3), (5, 2) ou (6, 1).

• Ao se jogar uma moeda pode se estar interessado no número de caras que aparecerá, mas não na sequência de caras ou coroas que teremos como resultados.

Essas grandezas de interesse são conhecidas como variáveis aleatórias.

Variável aleatória discreta: quando a variável aleatória assume no máximo um número contável de valores possíveis. A soma das probabilidades associado a contagem dos valores deve ser 1 (100 %).

Define-se para uma variável aleatória discreta a função discreta de probabilidade (ou função densidade de probabilidade) \(p(a)\) de \(X\) como:

\[ p(a)=P(X=a) \] A função \(p(a)\) é positiva para no máximo um número contável de valores de \(a\).

Isto é, se \(X\) deve assumir um dos valores \(x_1\), \(x_2\), \(...\), então os seguintes axiomas são válidos:

\[ \begin{align*} \begin{array}{l} p(x_i) \ge 0 \quad \textrm{ para } i = 1, 2, \dots \\ p(x) = 0 \quad \textrm{ para todos os demais valores de } x \\ \textrm{e} \\ \sum_{ i=1 }^{ \infty } p(x_i) = 1 \tag{3.1} \end{array} \end{align*} \]

Exemplo 1: Verique que a função densidade de probabilidade do fenômeno com variáveis aleatórias \(p(0)=\frac{1}{4}\), \(p(1) = \frac{1}{2}\) e \(p(2)=\frac{1}{4}\) valida os axiomas de (3.1).

variavel_aleatoria=data.frame(p=c(1/4,1/2,1/4))
barplot(variavel_aleatoria$p,xlab = c("x"),ylab = c("p(x)"),names.arg = c("p(0)","p(1)","p(2)"))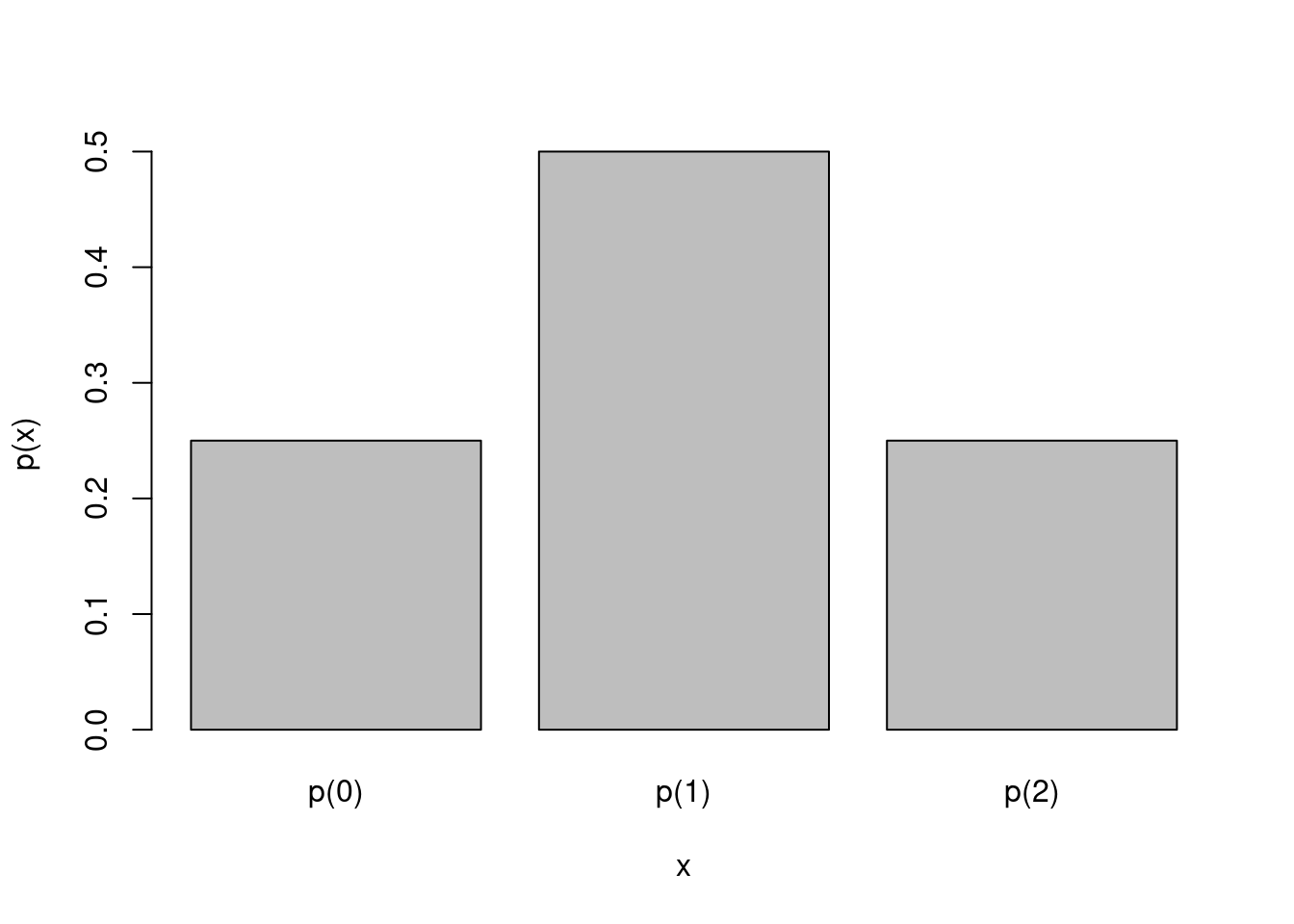

Exemplo 2: Suponha-se o lançamento de um par de dados honestos e que \(x\) indique a soma dos pontos obtidos. Qual é a distribuição de probabilidade desta soma?

Figura 1.5: Espaço amostral (6x6) do lançamento de um par de dados honestos.

Há 36 pontos ao todo e, a cada ponto, atribui-se uma probabilidade de \(1/36\). A soma de todas as probabilidades de todos os pontos do espaço é \(1\).

Soma das probabilidades do lançamento de um par de dados honestos.

\(x\)	\(2\)	\(3\)	\(4\)	\(5\)	\(6\)	\(7\)	\(8\)	\(9\)	\(10\)	\(11\)	\(12\)
\(p(x)\)	\(\frac{1}{36}\)	\(\frac{2}{36}\)	\(\frac{3}{36}\)	\(\frac{4}{36}\)	\(\frac{5}{36}\)	\(\frac{6}{36}\)	\(\frac{5}{36}\)	\(\frac{4}{36}\)	\(\frac{3}{36}\)	\(\frac{2}{36}\)	\(\frac{1}{36}\)

prob_df=data.frame(x=2:12, y=c(seq(1,6)/36,seq(5,1)/36))
barplot(prob_df$y,xlab = "x",ylab = c("p(x)"),names.arg = c(2:12),ylim = c(0,.2),axis.lty = 1)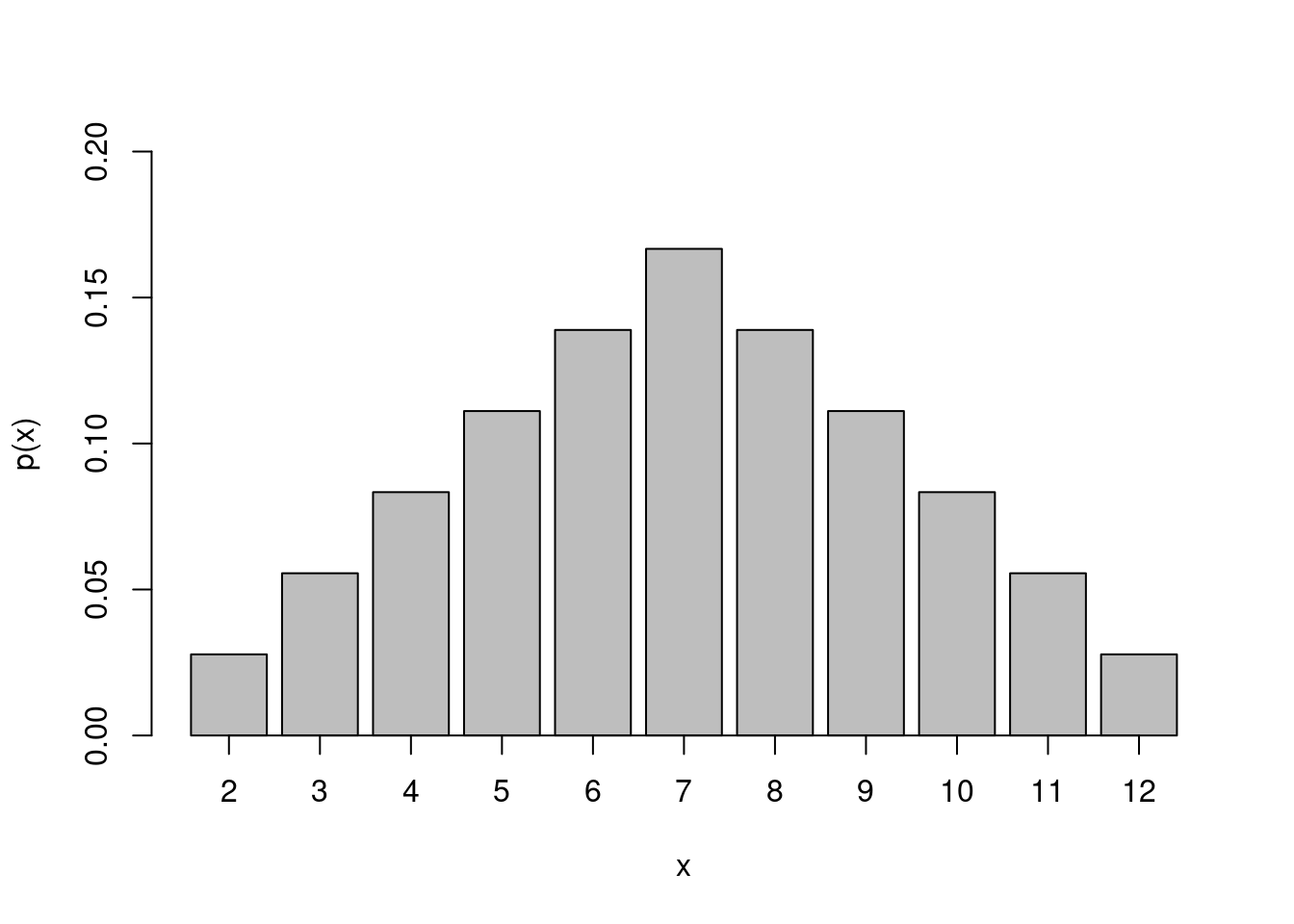

Figura 1.6: Distribuição de probabilidade do espaço amostral (6x6) do lançamento de um par de dados honestos.

Onde \(\bar{x}=7\) (média) e \(s = 2,42\) (desvio padrão) (ver seção Esperança matemática e Variância).

Variável aleatória contínua: quando a variável aleatória assume um número incontável de valores possíveis.

Define-se para uma variável aleatória contínua a função densidade de probabilidade (ou função de probabilidade) \(f(x)\) de \(X\) como:

\[ Pr(X\in (a,b)) = \int_a^b f(x)dx \]

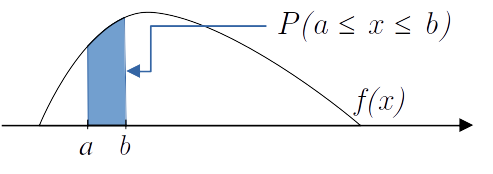
Figura 3.2: Probabilidade no intervalo \(Pr(a ≤ x ≤ b)\)

\(P(a ≤ x ≤ b)\) representa a área sob a curva da função densidade de probabilidade \(f(x)\).

A área sob a curva é igual a \(1\):

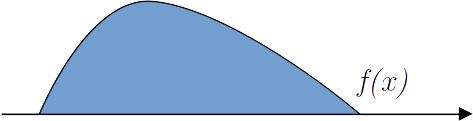
Figura 3.3: Probabilidade no intervalo -∞ a +∞.

\[ Pr(X\in ({-\infty},{\infty})) = \int_{-\infty}^{\infty} f(x)dx = 1. \]

• Esperança: pode ser entendida como um “centro de distribuição de probabilidades”. \[ E(X)=\int_{-\infty}^{\infty} x \times f(x)dx.\]
• Variância: \[ Var(X)=\int_{-\infty}^{\infty} [x - E(X)]^2 \times f(x) dx.\]

3.7 Distribuições teóricas de probabilidades de variáveis aleatórias discretas

Alguns modelos matemáticos probabilísticos que representam os fenômenos.

3.7.1 Distribuição de Bernoulli

Distribuição discreta de espaço amostral {0, 1}, que tem valor 1 com a probabilidade de sucesso \(p\) e valor 0 com a probabilidade de falha \(q = 1 − p\).

Pode ser pensar num modelo com vários resultados de um tipo de experimento com respostas do tipo sim/não, verdadeiro/falso, 1/0, etc. (respostas dicotômicas). Cada resultado assume apenas um possível valor lógico: o resultado verdadeiro, 1 ou sim (acerto) têm uma probabilidade \(p\), a não ocorrência desses resultados (falha) tem uma probabilidade \(q\) (\(=1-p\)). No caso de uma moeda com resultados Cara e Coroa a probabilidade de ocorrência de uma Cara (ou Coroa) é \(p=1/2\) (50%) (se a moeda for enviesada pode se ter \(p \ne 1/2\)).

• Média: \(E[x]=p\).

Pois sendo \(Pr(X=1)=p\) e \(Pr(X=0)=q\):

\(E[x]=Pr(X=1) \times 1 + Pr(X=0) \times 0 = p \times 1+q \times 0 = p\).

• Variância: \(Var[X]= pq\).

Pois sendo:

\(E[X^2]=Pr(X=1) \times 1^2 + Pr(X=0) \times 0^2\)

\(E[X^2]= p \times 1+q \times 0 = p = E[X]\), segue:

\(Var[X]=E[X^2]-E[X]^2=E[X]-E[X]^2=p-p^2=p(1-p)=pq\).

Obs.: uma séria de experimentos de Bernoulli gera uma distribuição binomial (ver Distribuição binomial a seguir).

3.7.2 Distribuição Hipergeométrica

Considerando uma população com \(N\) elementos, dos quais \(r\) têm uma determinada característica (a retirada de um desses elementos corresponde ao sucesso). Retira-se dessa população, sem reposição, uma amostra de tamanho \(n\). Seja \(X\): número de sucessos na amostra. Qual é a \(P(X=k)\)?, onde \(k\) é um número.

\[Pr(X=k)=\frac{\binom{r}{k} \binom{N-r}{n-k} }{\binom{N}{n} }\] onde: \(\binom{r}{k} = \frac{r!}{(r-k)!k!}\).

3.7.3 Distribuição binomial

Distribuição de probabilidade discreta, com parâmetros \(n\) e \(p\), do número de sucessos em uma sequência de \(n\) experimentos independentes, cada um sendo o resultado de uma variável dicotômica (sucesso com probabilidade \(p\) e falha com probabilidade \(q=1-p\)).

Um único sucesso/falha no experimento é chamada de experimento de Bernoulli e sua sequência de resultados é chamado de processo de Bernoulli. Para uma única tentativa (\(n=1\)) a distribuição binomial é uma distribuição de Bernoulli.

• As variáveis (ou dados) são coletadas sob condições idênticas.
• Cada variável comporta apenas dois resultados possíveis (verdadeiro ou falso, 0 ou 1 etc.).
• A probabilidade de sucesso (ou de falha) \(p\) é a mesma para cada variável.
• As variáveis são independentes uma das outras.
• Notação: \(X\) tem distribuição binomial com parâmetros \(n\) e \(p\): \(X \sim B(n,p)\).

\[Pr(X=k)= \binom{n}{k} p^{k} q^{n-k}\] onde: \(\binom{n}{k} = \frac{n!}{(n-k)!k!}\).

• Exemplo: Uma moeda é lançada 20 vezes. Qual a probabilidade de saírem 8 Caras?

Resolução: \(X\): número de sucessos (Cara). \(X = 0, 1, 2, ..., 20 \implies p(\text{Caras})=\frac{1}{2} \implies X \sim B(20, \frac{1}{2})\). \(P(X=8)=\binom{20}{8} \left( \frac{1}{2} \right)^8 \left( \frac{1}{2} \right)^{12}=0,120134\).

dbinom(8,20,1/2)
#> [1] 0.1201344

3.7.4 Distribuição Poisson

Distribuição discreta de probabilidade que expressa a probabilidade de um dado número de eventos ocorrer num intervalo de tempo fixo se esses eventos ocorrerem a uma taxa média constante e independente do tempo do último evento.

A probabilidade de \(k\) sucessos de \(\lambda\) eventos (em média) num intervalo (de tempo) é dada por: \[Pr(X=k)=\frac{e^{-\lambda} \times \lambda^k}{k!}\] Obs.: \(\lambda = E[X]= Var[X]\).

Pode também ser usada para número de eventos em outros tipos de intervalo como tempo e outras dimensões maiores que um (ex.: nº eventos em uma dada área ou volume). Assim, as variáveis são o resultado de contagem de eventos discretos em meios contínuos (tempo, volume etc.).

• Exemplo: Numa central telefônica chegam 300 telefonemas por hora. Qual a probabilidade de que: a) num minuto não haja nenhum chamado? b) em 3 minutos haja 2 chamados?

Resolução: Seja \(X\): nº de chamadas por minuto.

\(\lambda_1=\frac{300}{1\text{h}}=\frac{300}{60\text{min}}=5\text{ chamadas/min}\).

a) \(Pr(X=0)=\frac{e^{-5} \times 5^0}{0!}=0,0067379\).

dpois(0,5)
#> [1] 0.006737947

b) Como agora temos 3 min., \(\lambda=15\) (\(=3 \times \lambda_1\)): \(Pr(X=2)=\frac{e^{-15} \times 15^2}{2!}=0.0001721\).

dpois(3,15)
#> [1] 0.0001720701