Capítulo 9 Regresión logística
9.1 Resumen
En este instructivo, estimamos e interpretamos modelos de regresión logística para variables dependientes categóricas.
Vamos a utilizar las siguientes librerías:
library(tidyverse)## Warning: package 'tidyverse' was built under R version 4.0.3## -- Attaching packages --------------------------------------- tidyverse 1.3.0 --## v ggplot2 3.3.2 v purrr 0.3.4
## v tibble 3.0.6 v dplyr 1.0.4
## v tidyr 1.1.2 v stringr 1.4.0
## v readr 1.3.1 v forcats 0.5.0## Warning: package 'tibble' was built under R version 4.0.3## Warning: package 'dplyr' was built under R version 4.0.3## -- Conflicts ------------------------------------------ tidyverse_conflicts() --
## x dplyr::filter() masks stats::filter()
## x dplyr::lag() masks stats::lag()library(ggeffects) # efectos en modelos de regresion
library(sjPlot) # tablas de regresion
library(haven) # datos en formato .dta9.2 Repaso
Estimar modelos de regresión lineal:
- Operacionalización de modelos teóricos para evaluar hipótesis sobre relaciones entre variables.
- Interpretar coeficientes: dirección, magnitud, significancia.
- Regresión múltiple para controlar por otros factores.
9.3 Variables dependientes categóricas
No todos los fenómenos que estudiamos se pueden expresar como variables numéricas, ordenadas de menor a mayor y en las que cada intervalo (cada aumento de una unidad) es constante. En ocasiones, nos interesa estudiar cualidades o categorías, como el tipo de régimen, la adopción de una política pública o la presencia de guerra civil en un país.
El modelo de regresión lineal por mínimos cuadrados ordinarios (OLS) no es ideal para modelar variables dependientes categóricas. Sin embargo, sí lo podemos utilizar, una aplicación que llamamos el modelo de probabilidad lineal (MPL). Una mejor opción es utilizar la regresión logística o logit. En este instructivo, veremos cómo podemos usar ambos.
9.4 Datos
Pero primero, necesitamos datos. Carguemos unos datos directamente de la web. Se trata de información sobre la admisión a programas de posgrado universitario en una univerdiad de Estados Unidos:
dat <- read_csv("https://stats.idre.ucla.edu/stat/data/binary.csv")## Parsed with column specification:
## cols(
## admit = col_double(),
## gre = col_double(),
## gpa = col_double(),
## rank = col_double()
## )dat## # A tibble: 400 x 4
## admit gre gpa rank
## <dbl> <dbl> <dbl> <dbl>
## 1 0 380 3.61 3
## 2 1 660 3.67 3
## 3 1 800 4 1
## 4 1 640 3.19 4
## 5 0 520 2.93 4
## 6 1 760 3 2
## 7 1 560 2.98 1
## 8 0 400 3.08 2
## 9 1 540 3.39 3
## 10 0 700 3.92 2
## # ... with 390 more rowsTenemos cuatro variables:
admit: dummy de admisión (0=no admitio; 1=admitido).gre: nota en el examen GRE. Puede tomar valores de 200 a 800.gpa: promedio crédito acumulado de pregrado. Puede tomar valores de 0 a 4.rank: ránquin de la universidad de pregrado. Hay 4 categorías, de mayor (1) a menor (4) calidad.
Estamos interesados en la probabilidad de que un individuo sea admitido a la universidad (admit = 1). Convertimos dos variables categóricas -amit y rank- a tipo factor, porque pese a que conceptualmente son categóricas, están codificadas como numéricas en R. Hacemos esto con la funciones case_when() (para recodificar números como categorías) y as.factor() (un cambio de clase simple):
dat <- dat %>%
mutate(
admit_fct = case_when(
admit == 0 ~ "No", # usar los valores de la variable admit
admit == 1 ~ "Sí"
),
admit_fct = as.factor(admit_fct),
rank_fct = as.factor(rank)
)Ya que recodificamos y limpiamos un poco los datos, veamos la distribución de la variable dependiente con una gráfica de frecuencias:
dat %>%
ggplot(aes(x = admit_fct)) +
geom_bar() +
labs(x = "Admitido",
y = "Número de observaciones")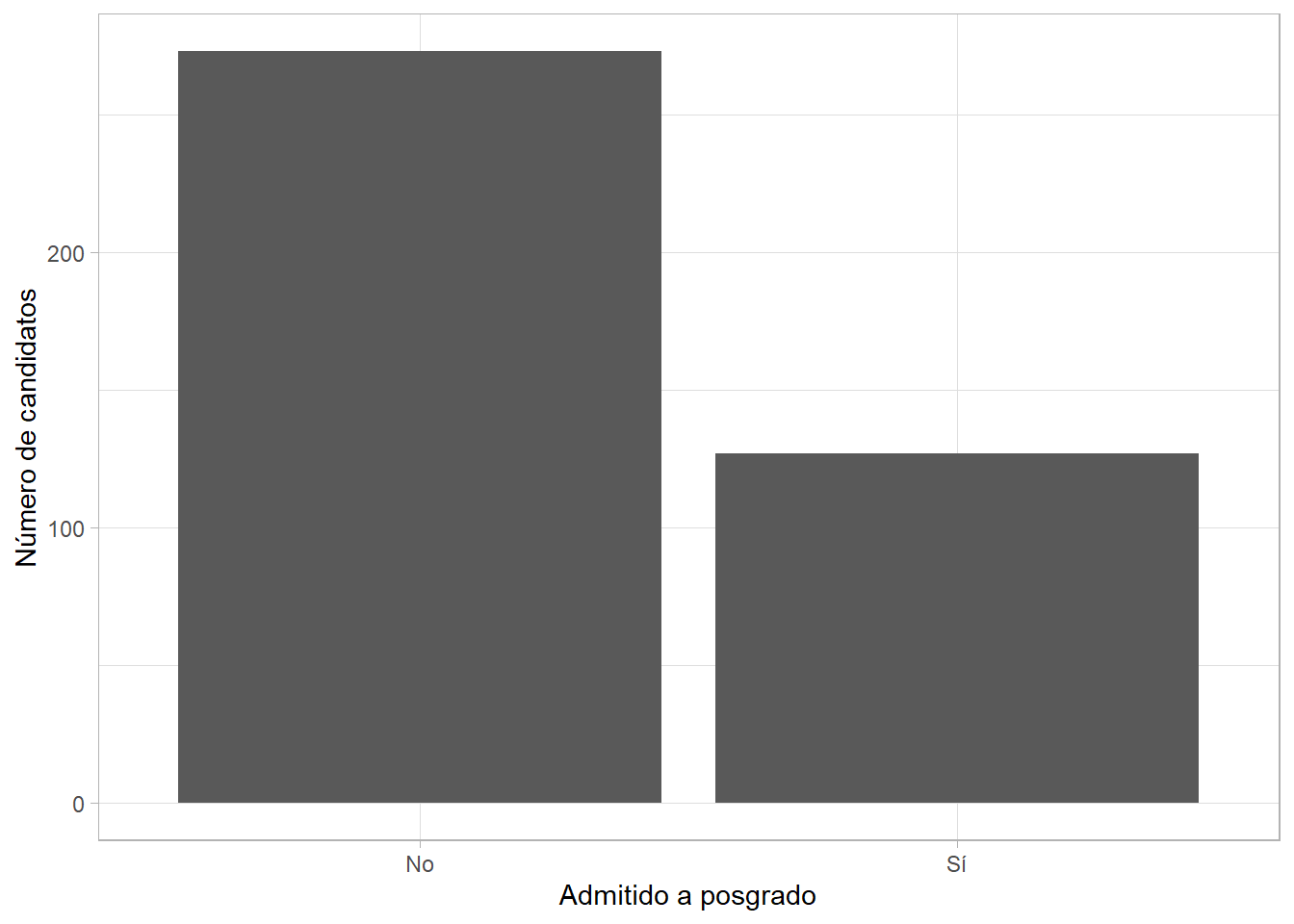
Y veamos la relaciones entre esta variable y las dos variables numéricas en la base de datos:
dat %>%
group_by(admit_fct) %>%
summarize(
obs = n(),
media_gre = mean(gre),
media_gpa = mean(gpa)
)## # A tibble: 2 x 4
## admit_fct obs media_gre media_gpa
## * <fct> <int> <dbl> <dbl>
## 1 No 273 573. 3.34
## 2 Sí 127 619. 3.49Veamos una de estas relaciones como una gráfica de dispersión con una línea de tendencia (¡estimada por ggplot2 con OLS!):
dat %>%
ggplot(aes(x = gre, y = admit)) +
geom_point(alpha = 0.25, size = 2) +
geom_smooth(method = "lm", se = FALSE, color = "red") +
scale_y_continuous(breaks = c(0, 1), labels = c("No", "Sí")) +
labs(x = "Puntaje GRE", y = "Admisión")## `geom_smooth()` using formula 'y ~ x'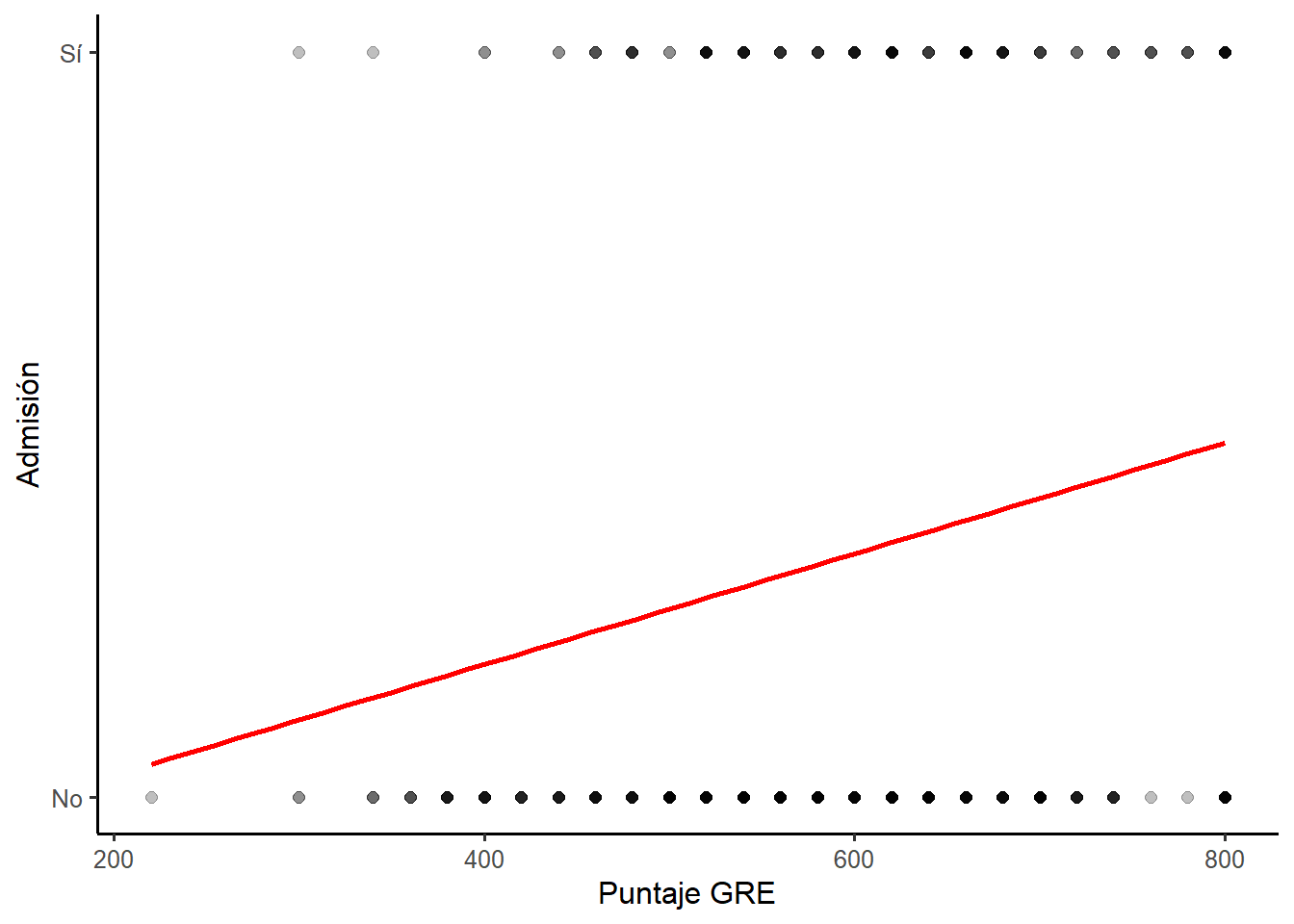
Algo no está bien… La línea de tendencia de geom_smooth() es estimada usando OLS - el modelo hace lo posible por ajustarse a los datos, pero tratar de conectar las observaciones no admitidas y sus puntajes con las de estudiantes admitidos es difícil. Busquemos una alternativa.
9.5 El model de probabilidad lineal (MPL)
Recordemos: nos interesa ver la probabilidad de que un estudiante sea admitido, dadas sus notas en el examen GRE, su promedio crédito acumulado (GPA) y el ránquin de su universidad de pregrado (1-4).
Podemos hacer una primera aproximación estimando un modelo de probabilidad lineal (MPL). Usamos lm() como si estuviéramos estimando cualquier otro modelo de regresión lineal - ¡porque eso es lo que estamos haciendo! Noten que la variable dependiente en la fórmula es la versión numérica de la misma (admit) y no el factor que creamos arriba (admit_fct):
mpl <- lm(
admit ~ gre + gpa + rank_fct,
data = dat
)Usemos summary() para ver un resumen de los resultados del modelo:
summary(mpl)##
## Call:
## lm(formula = admit ~ gre + gpa + rank_fct, data = dat)
##
## Residuals:
## Min 1Q Median 3Q Max
## -0.7022 -0.3288 -0.1922 0.4952 0.9093
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) -0.2589102 0.2159904 -1.199 0.2314
## gre 0.0004296 0.0002107 2.038 0.0422 *
## gpa 0.1555350 0.0639618 2.432 0.0155 *
## rank_fct2 -0.1623653 0.0677145 -2.398 0.0170 *
## rank_fct3 -0.2905705 0.0702453 -4.137 4.31e-05 ***
## rank_fct4 -0.3230264 0.0793164 -4.073 5.62e-05 ***
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 0.4449 on 394 degrees of freedom
## Multiple R-squared: 0.1004, Adjusted R-squared: 0.08898
## F-statistic: 8.795 on 5 and 394 DF, p-value: 6.333e-08La interpretación es similar a OLS, excepto que conceptualizamos los coeficientes como cambios en la probabilidad de que la variable dependiente sea igual a 1 (\(Pr(Y|X) = 1\)) asociados a cambios en las variables independientes. En este caso, se trata de la probabilidad de que admit sea igual 1, o sea, de ser admitido a la universidad. Así, los resultados indican que:
- Un incremento de 1 unidad en la nota del examen GRE, se asocia con un incremento de 0.04% en la probabilidad de ser amitido.
- Un incremento de 1 unidad en el promedio crédito acumulado, se asocia con un incremento de 16% en la probabilidad de ser amitido.
- Comparado con estudiantes de universidades en la categoría 1 del ránquin, estudiantes de la categoría 2 tienen 16% menos probabilidad de ser admitidos.
- Comparado con estudiantes de universidades en la categoría 1 del ránquin, estudiantes de la categoría 3 tienen 29% menos probabilidad de ser admitidos.
- Comparado con estudiantes de universidades en la categoría 1 del ránquin, estudiantes de la categoría 4 (la más baja) tienen 32% menos probabilidad de ser admitidos.
- Finalmente, el intercepto nos dice que la probabilidad de ser admitido para un estudiante de una universidad en la categoría 1 del ránquin, con notas de 0 en el GRE y promedio crédito acumulado (GPA) de 0 es de -25%. ¿¡Cómo!?
La interpretación del intercepto apunta a uno de los problemas principales del MPL: el modelo puede arrojar “probabilidades” por debajo de 0. Veamos otros ejemplo. Calculemos el valor esperado de \(Y\) (la probabilidad esperada de ser admitido) para un estudiante de una universidad en la categoría 4 y los valores más bajos de GRE y GPA observados en los datos. Reemplazamos en la ecuación del modelo y extraemos los coeficientes usando la función coef():
coef(mpl)[[1]] +
coef(mpl)[[2]]*min(dat$gre) +
coef(mpl)[[3]]*min(dat$gpa) +
coef(mpl)[[4]]*0 +
coef(mpl)[[5]]*0 +
coef(mpl)[[6]]*1## [1] -0.1359216¡Este pobre estudiante tiene una probabilidad de -13% de ser admitido! Y esto no es un caso aislado, sino que pasa frecuentemente con el MPL. Para ver qué tan frecuentemente ocurre con nuestro modelo, miremos la distribución de las predicciones que estima. Para varias observaciones, el modelo predice probabilidades negativas (por debajo de 0):
mpl %>%
predict() %>% # extrae las predicciones o "fitted values" del modelo
as_tibble() %>%
ggplot(aes(x = value)) +
geom_histogram(binwidth = 0.01) +
geom_vline(xintercept = 0, linetype = "dashed", color = "red") +
scale_x_continuous(labels = scales::percent) +
labs(x = expression(hat(Y)), y = "Número de observaciones")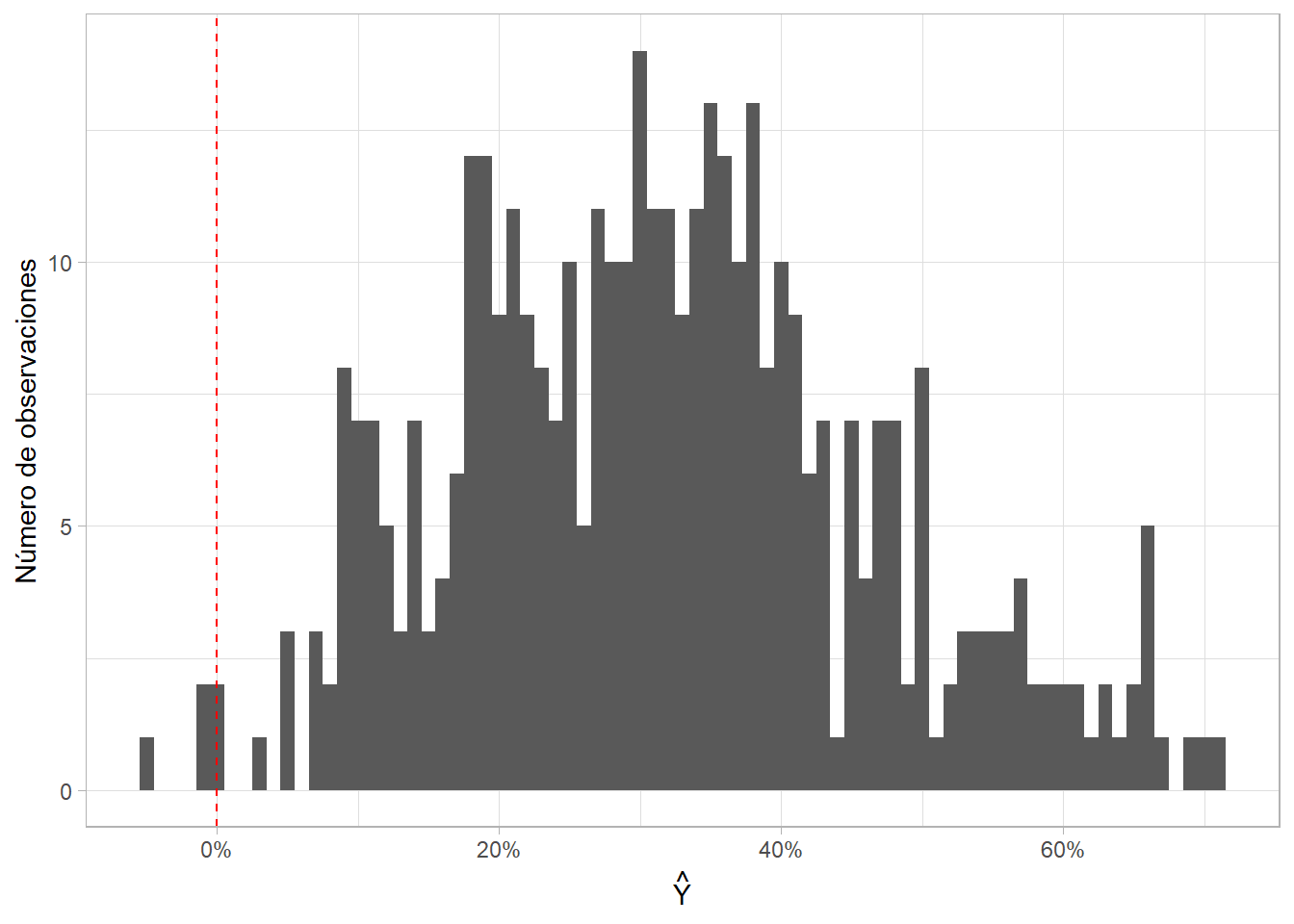
Esto no significa que el MPL sea inútil. Estas probabilidades negativas (y en otras ocasiones, por encima de 1.0 o 100%) solo suceden para valores extremos de las variables independientes. Además, las podemos interpretar como que la probabilidad de que el evento ocurra es extremadamente baja o extremadamente alta. Finalmente, el MPL es utilizado frecuentemente en la literatura académica de experimentos o evaluación técnica de políticas públicas con experimentos.
Pese a sus limitaciones, las predicciones de un modelo como este tienen valor. Veamos los efectos de las distintas variables independientes usando ggpredict() de ggeffects:
mpl %>%
ggpredict()## $gre
##
## # Predicted values of admit
## # x = gre
##
## x | Predicted | SE | 95% CI
## -------------------------------------
## 220 | 0.36 | 0.10 | [0.17, 0.56]
## 295 | 0.40 | 0.09 | [0.23, 0.56]
## 365 | 0.43 | 0.08 | [0.28, 0.57]
## 435 | 0.46 | 0.07 | [0.32, 0.59]
## 510 | 0.49 | 0.06 | [0.37, 0.61]
## 585 | 0.52 | 0.06 | [0.41, 0.63]
## 655 | 0.55 | 0.06 | [0.44, 0.66]
## 800 | 0.61 | 0.07 | [0.47, 0.75]
##
## Adjusted for:
## * gpa = 3.39
## * rank_fct = 1
##
##
## $gpa
##
## # Predicted values of admit
## # x = gpa
##
## x | Predicted | SE | 95% CI
## --------------------------------------
## 2.00 | 0.30 | 0.11 | [0.09, 0.52]
## 2.50 | 0.38 | 0.08 | [0.22, 0.54]
## 3.00 | 0.46 | 0.06 | [0.34, 0.58]
## 3.50 | 0.54 | 0.06 | [0.43, 0.65]
## 4.00 | 0.62 | 0.07 | [0.48, 0.75]
##
## Adjusted for:
## * gre = 587.70
## * rank_fct = 1
##
##
## $rank_fct
##
## # Predicted values of admit
## # x = rank_fct
##
## x | Predicted | SE | 95% CI
## -----------------------------------
## 1 | 0.52 | 0.06 | [0.41, 0.63]
## 2 | 0.36 | 0.04 | [0.29, 0.43]
## 3 | 0.23 | 0.04 | [0.15, 0.31]
## 4 | 0.20 | 0.05 | [0.09, 0.30]
##
## Adjusted for:
## * gre = 587.70
## * gpa = 3.39
##
##
## attr(,"class")
## [1] "ggalleffects" "list"
## attr(,"model.name")
## [1] "."O para un “perfil” específico:
mpl %>%
ggpredict(
terms = c("gpa", "rank_fct[1, 4]"), # mantiene gre constante en la media
) %>%
plot() +
scale_y_continuous(labels = scales::percent) +
labs(title = "Valores esperados: probabilidad de ser admitido",
x = "GPA", y = "Pr(Y=1)", color = "Rank pregrado")## Scale for 'y' is already present. Adding another scale for 'y', which will
## replace the existing scale.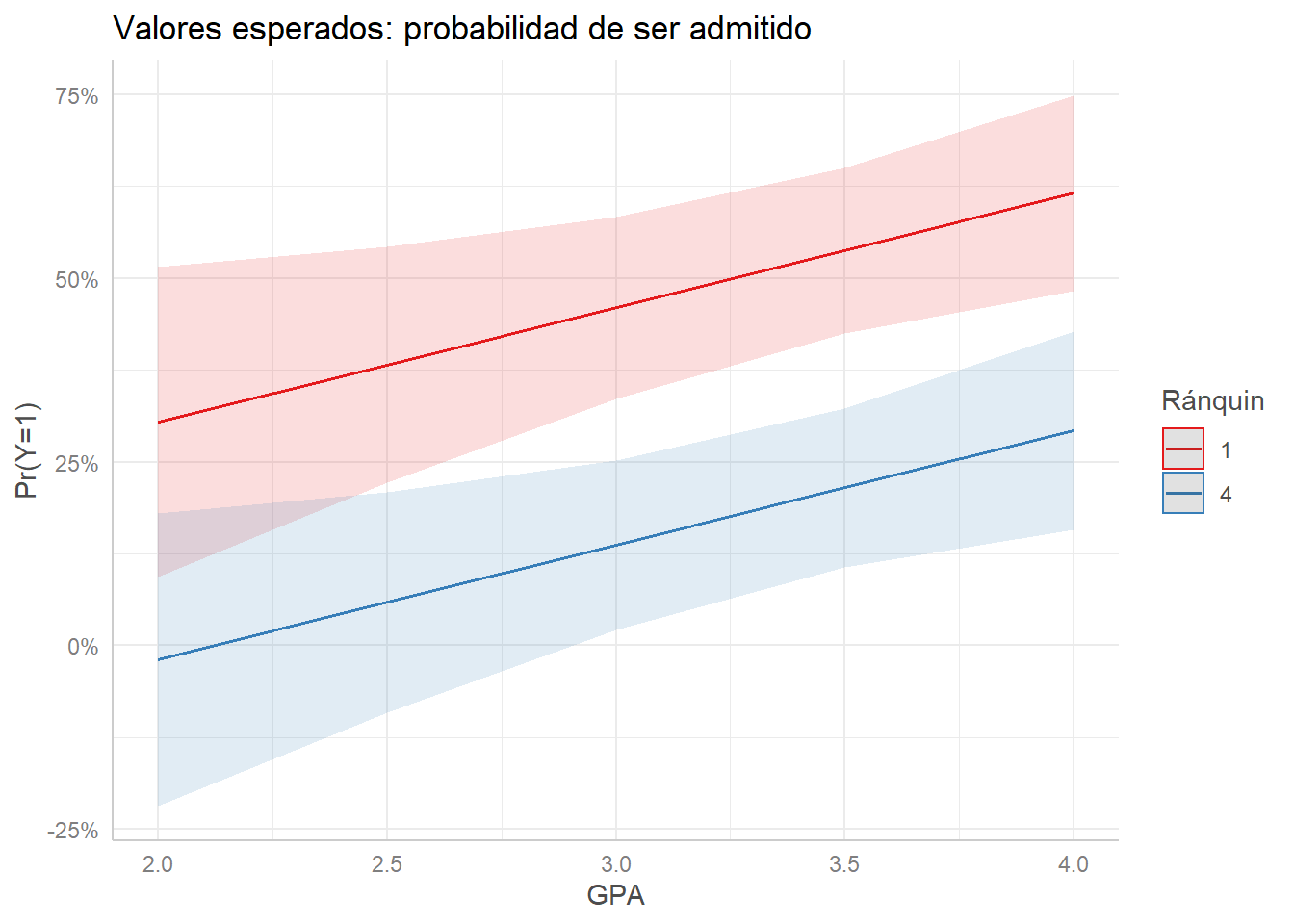
Vemos que la probabilidad de ser admitido aumenta a medida que sube el promedio crédito acumulado o GPA, pero que los estudiantes que provenienen de universidades con un mejor ránquin tienen una ventaja comparados con los de universidades menos prestigiosas.
9.6 Regresión logística
La alternativa al MPL es la regresión logística o el modelo logit.12. A diferencia de OLS, la regresión logística, está diseñada explícitamente para modelar variables dependientes categóricas (específicamente binarias) y se estima via máxima verosimilitud (o maximum likelihood estimation, MLE), no mínimos cuadrados ordinarios.13 El logit está diseñadao para ver la asociación entre una serie de variables independientes y la probabilidad de que \(Y = 1\) dado \(X\) (\(Pr(Y|X) = 1\)).
Estimemos el mismo modelo que trabajamos arriba, pero esta vez usando regresión logística. En R, usamos la funciónm glm() y especificamos que el modelo usa una distribución binomial, lo cual le indica a R que es una regresión logística:
logit <- glm( # modelos lineales generalizados estimados por MLE
admit_fct ~ gre + gpa + rank_fct, # formula
data = dat, # datos
family = binomial() # tipo de modelo/distribucion
)Aparte: podemos estimar un modelo de regresión lineal con glm() y obtener los mismos resultados que con lm() - comparen con los resultados del MPL:
glm( # modelos lineales generalizados estimados por MLE
admit ~ gre + gpa + rank, # formula
data = dat, # datos
family = "gaussian" # tipo de modelo/distribucion
) %>%
summary() # ver coeficientes##
## Call:
## glm(formula = admit ~ gre + gpa + rank, family = "gaussian",
## data = dat)
##
## Deviance Residuals:
## Min 1Q Median 3Q Max
## -0.6617 -0.3417 -0.1947 0.5061 0.9556
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) -0.1824127 0.2169695 -0.841 0.4010
## gre 0.0004424 0.0002101 2.106 0.0358 *
## gpa 0.1510402 0.0633854 2.383 0.0176 *
## rank -0.1095019 0.0237617 -4.608 5.48e-06 ***
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## (Dispersion parameter for gaussian family taken to be 0.1978669)
##
## Null deviance: 86.677 on 399 degrees of freedom
## Residual deviance: 78.355 on 396 degrees of freedom
## AIC: 493.07
##
## Number of Fisher Scoring iterations: 2Volviendo al modelo logit, coeficientes que vemos en los resultados del modelo son “log-odds” y, por el momento, solo interpretamos la dirección de la relación (el signo del coeficiente, positivo o negativo) y la significancia estadística de los mismos. Los log-odds son el logaritmo de los odds:14 la tasa o razón entre el número veces que algo sucede y el número de veces que no sucede. Mientras, probabilidad es la tasa de casos positivos a casos posibles. Si yo llego tarde a clase 1 de cada 5 veces, los odds de yo llegar tarde son \(\frac{1}{4} = 0.25\) (y los log-odds son \(\log(0.25) = -1.39\)), pero la probabilidad de que llegue tarde es \(\frac{1}{5} = 0.20\). Son formas distintas de expresar ideas muy similares.
En ese orden de ideas, los resultados del modelo logístico que estimamos corroboran lo encontrado con el MPL - aumentos en el GRE y GPA se asocian con aumentos la probabilidad de admisión, mientras que los estudiantes de universidades de universidades mejor ranqueadas tienen una mayor probabilidad de admisión que los demás:
summary(logit)##
## Call:
## glm(formula = admit_fct ~ gre + gpa + rank_fct, family = binomial(),
## data = dat)
##
## Deviance Residuals:
## Min 1Q Median 3Q Max
## -1.6268 -0.8662 -0.6388 1.1490 2.0790
##
## Coefficients:
## Estimate Std. Error z value Pr(>|z|)
## (Intercept) -3.989979 1.139951 -3.500 0.000465 ***
## gre 0.002264 0.001094 2.070 0.038465 *
## gpa 0.804038 0.331819 2.423 0.015388 *
## rank_fct2 -0.675443 0.316490 -2.134 0.032829 *
## rank_fct3 -1.340204 0.345306 -3.881 0.000104 ***
## rank_fct4 -1.551464 0.417832 -3.713 0.000205 ***
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## (Dispersion parameter for binomial family taken to be 1)
##
## Null deviance: 499.98 on 399 degrees of freedom
## Residual deviance: 458.52 on 394 degrees of freedom
## AIC: 470.52
##
## Number of Fisher Scoring iterations: 4Podemos convertir los log-odds a odds usando la función exponencial exp(). En este caso, valores por encima de 1 indican que hay una asociación positiva (aumentos en la variable independiente se asocian con aumentos en \(Pr(Y) = 1\)) y valores por debajo de 1 indican una asociación negativa (reducciones en \(Pr(Y) = 1\)):
coef(logit) %>%
as_tibble() %>%
mutate(odds = exp(value))## # A tibble: 6 x 2
## value odds
## <dbl> <dbl>
## 1 -3.99 0.0185
## 2 0.00226 1.00
## 3 0.804 2.23
## 4 -0.675 0.509
## 5 -1.34 0.262
## 6 -1.55 0.212Veamos una tabla resumen comparando ambos modelos -el MPL y el logit. Por defecto, tab_model() nos muestra odds en los coeficientes:
tab_model(
mpl, logit,
dv.labels = c("MPL", "Logit")
)| MPL | Logit | |||||
|---|---|---|---|---|---|---|
| Predictors | Estimates | CI | p | Odds Ratios | CI | p |
| (Intercept) | -0.26 | -0.68 – 0.17 | 0.231 | 0.02 | 0.00 – 0.17 | <0.001 |
| gre | 0.00 | 0.00 – 0.00 | 0.042 | 1.00 | 1.00 – 1.00 | 0.038 |
| gpa | 0.16 | 0.03 – 0.28 | 0.015 | 2.23 | 1.17 – 4.32 | 0.015 |
| rank_fct [2] | -0.16 | -0.30 – -0.03 | 0.017 | 0.51 | 0.27 – 0.94 | 0.033 |
| rank_fct [3] | -0.29 | -0.43 – -0.15 | <0.001 | 0.26 | 0.13 – 0.51 | <0.001 |
| rank_fct [4] | -0.32 | -0.48 – -0.17 | <0.001 | 0.21 | 0.09 – 0.47 | <0.001 |
| Observations | 400 | 400 | ||||
| R2 / R2 adjusted | 0.100 / 0.089 | 0.102 | ||||
Los resultados son prácticamente idénticos… ¿por qué hacer una regresión logística, entonces? Porque el logit nos permite pasar entre log-odds, odds y probabilidades de forma tal que podemos hacer mejores predicciones.
9.6.1 Coeficientes como probabilidades
La mejor forma de interpretar los resultados de un modelo de regresión logística (más fácil y más informativa) pasa por convertir los log-odds a probabilidades. Esto lo hacemos pasando los log-odds por la función logística:
\[ \text{logistic}(\alpha) = \frac{\exp(\alpha)}{1 + \exp(\alpha)} \]
En R, podríamos calcular probabilidades usando la función logística así:
exp(coeficiente) / (1 + exp(coeficiente))Sin embargo, ya existe la función plogis, que es el “link” o vínculo entre probabilidades y log-odds. Gráficamente, la función logística se ve así (y describe mejor la relación entre una variable numérica y una categórica que el OLS que hicimos arriba):
tibble(x = -15:15, y = plogis(x)) %>%
ggplot(aes(x, y)) +
geom_line(size = 1, color = "red")
Volviendo a nuestro modelo de regresión, la probabilidad que resulta de pasar el coeficiente (en log-odds) por la función logística es \(Pr(Y) = 1\) en la mitad de la curva de la función logística:
coef(logit) %>%
as_tibble() %>%
mutate(
odds = exp(value),
prob = plogis(value)
)## # A tibble: 6 x 3
## value odds prob
## <dbl> <dbl> <dbl>
## 1 -3.99 0.0185 0.0182
## 2 0.00226 1.00 0.501
## 3 0.804 2.23 0.691
## 4 -0.675 0.509 0.337
## 5 -1.34 0.262 0.207
## 6 -1.55 0.212 0.1759.6.1.1 Visualizar probabilidades
Estos resultados son más interpretables de forma gráfica. Podemos usar ggpredict() nuevamente, especificando las variables independientes cuyos efectos queremos ver usando terms =:
logit %>%
ggpredict(terms = c("gpa", "rank_fct")) %>%
plot() +
labs(title = "Valores esperados: probabilidad de ser admitido",
color = "Rank", x = "GPA", y = "Pr(Y=1)")## Data were 'prettified'. Consider using `terms="gpa [all]"` to get smooth plots.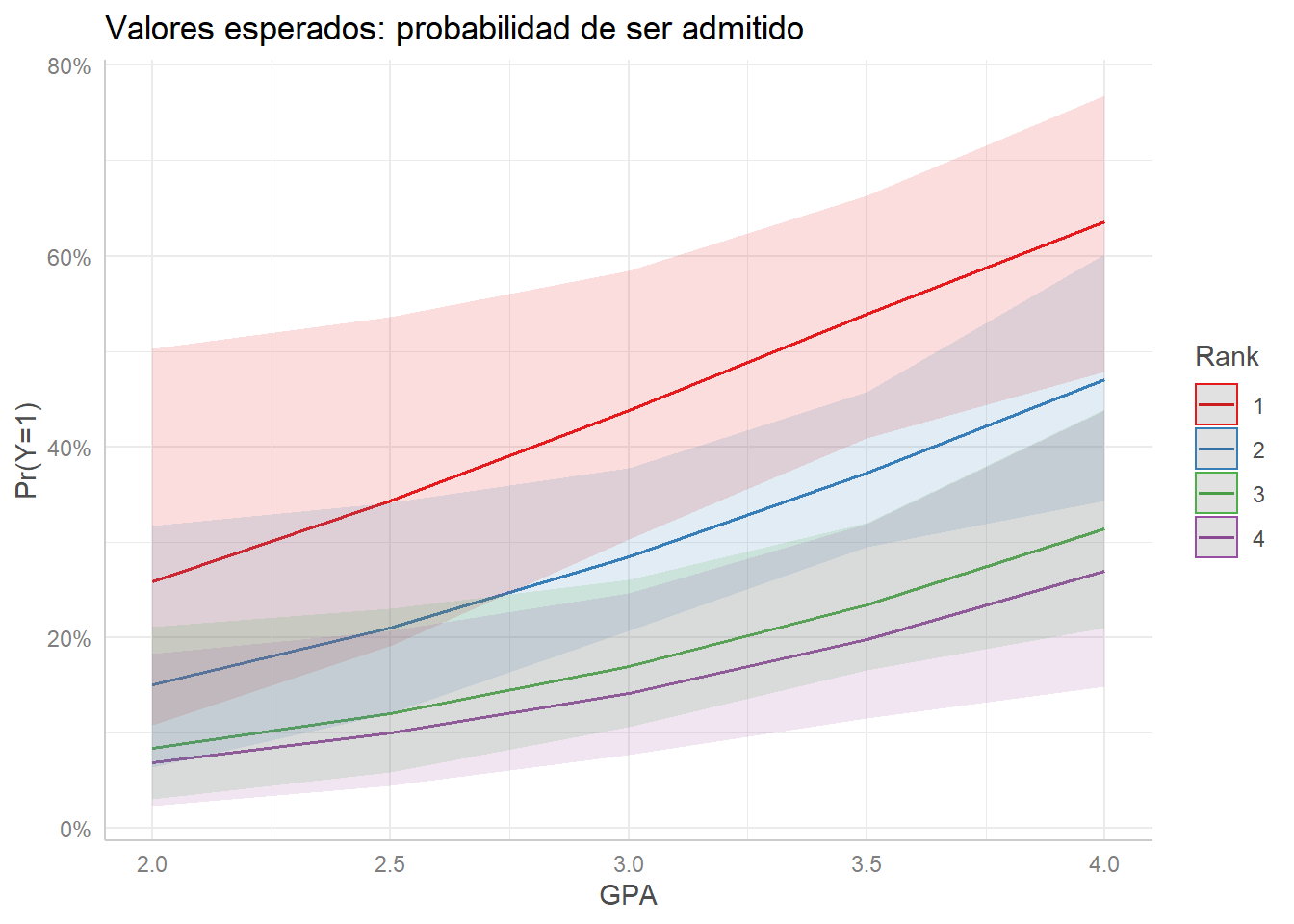
Una representación gráfica del modelo de regresión logística nos permite evidenciar dos elementos muy importantes en su interpretación:
- La pendiente de la línea cambia levemente a lo largo de su trayecto, indicando que se trata de una curva y que la asociación entre \(X\) (GPA) y \(Y\) (probabilidad de ser admitido) no es constante, sino que depende del valor de \(X\).
- La pendiente de la curva para cada grupo definido por la variable categórica \(Z\) (ránquin) también es distinta, lo cual indica que la asociación entre \(X\) y \(Y\) depende de las demás variables incluidas en el modelo. En otras palabras, ¡hay una interacción inherente!
9.6.2 Evaluar el modelo
¿Cómo evaluar un modelo de regresión logística? Miremos dos opciones.
9.6.2.1 Variables omitidas
Esta es una evaluación tanto teórica, como metodológica. Al igual que en la regresión lineal por OLS, para que uno modelo de regresión logística tenga coeficientes insesgados, es necesario que hayamos incluido todas las variables relevantes (causales). Así mismo, es importante que no hayamos incluido otras variables irrelevantes.
9.6.2.2 Predicciones y falsos positivos
Otra forma común de evaluar un modelo de regresión logística es comparando las predicciones del modelo con los valores reales. Recordemos que para cada observación en nuestros datos, sabemos si fue admitido o no. Además, podemos calcular la probabilidad de ser admitido a partir de los resultados del modelo.
Para facilitar la comparación entre probabilidades (probabilidad de ser admitido o no) y valores de 0 o 1 (admitido o no), asumimos que si el modelo estimó una probabilidad de admisión por encima del 50% (0.5) para una observación, la predicción del modelo es que ese individuo será “admitido”:
modelo_aug <- as_tibble(logit$model)
modelo_aug <- modelo_aug %>%
mutate(fitted = logit$fitted.values,
residuals = logit$residuals,
std_residuals = rstandard(logit),
cooks_d = cooks.distance(logit))
preds <- modelo_aug %>%
mutate(
model_prob = plogis(fitted), # probabilidad de ser admitido
model_pred = if_else(
model_prob > 0.5, "Sí", "No" # convertir a binario (clasificar)
)
)
preds## # A tibble: 400 x 10
## admit_fct gre gpa rank_fct fitted residuals std_residuals cooks_d
## <fct> <dbl> <dbl> <fct> <dbl> <dbl> <dbl> <dbl>
## 1 No 380 3.61 3 0.173 -1.21 -0.621 0.000579
## 2 Sí 660 3.67 3 0.292 3.42 1.58 0.00450
## 3 Sí 800 4 1 0.738 1.35 0.788 0.00145
## 4 Sí 640 3.19 4 0.178 5.61 1.87 0.0132
## 5 No 520 2.93 4 0.118 -1.13 -0.505 0.000302
## 6 Sí 760 3 2 0.370 2.70 1.43 0.00631
## 7 Sí 560 2.98 1 0.419 2.39 1.33 0.00535
## 8 No 400 3.08 2 0.217 -1.28 -0.704 0.000610
## 9 Sí 540 3.39 3 0.201 4.98 1.80 0.00573
## 10 No 700 3.92 2 0.518 -2.07 -1.22 0.00268
## # ... with 390 more rows, and 2 more variables: model_prob <dbl>,
## # model_pred <chr>Para ver el desempeño del modelo, podemos ver:
- Positivos verdaderos: datos dicen sí, modelo predice sí.
- Falsos positivos: datos dicen no, modelo predice sí.
- Negativos verdaderos: datos dicen no, modelo predice no.
- Falsos negativos: datos dicen sí, modelo predice no.
Organicemos una tabla cruzada con esa información (una matriz de confusión):
preds %>%
group_by(admit_fct, model_pred) %>% # agrupar
summarize(casos = n()) %>%
ungroup() %>%
mutate(prop = casos/sum(casos)) %>%
pivot_wider(admit_fct, names_from = model_pred, values_from = prop) # organizar## `summarise()` has grouped output by 'admit_fct'. You can override using the `.groups` argument.## # A tibble: 2 x 2
## admit_fct Sí
## <fct> <dbl>
## 1 No 0.682
## 2 Sí 0.318El modelo predice correctamente (No-No y Sí-Sí) el 71% de las observaciones. Sin embargo, tenmos aproximadamente un 24% de falsos negativos. Si nuestra pretensión es construir un modelo que identifique correctamente los admitidos, claramente podríamos mejorar. Esto lo haríamos a) agregando variables, b) transformando las existentes de forma tal que haya una relación más clara con la variable dependiente o c) cambiando el modelo.
9.7 Conclusión
Con frecuencia queremos explicar, entender, describir o predecir variable dependientes categóricas binarias. Para esto, podemos estimar un modelo de probabilidad lineal, pero es mejor utilizar una regresión logística. Un modelo de regresión logística nos permite estimar la probabilidad de que un evento ocurra dadas unas variables independientes. Así mismo, nos permite cómo cambios en las variables independientes se asocian con cambios en la probabilidad de que ocurra un evento. Finalmente, podemos evaluar estos modelos según su capacidad de predecir correctamente.
9.8 Ejercicios
9.8.1 Explicando el voto nominal
¿Por qué algunos legisladores votan a favor de un proyecto de ley? ¿Cómo se relaciona la identificación partidista con la probabilidad de que un legislador vote “sí”? Utilicemos datos (el archivo nafta.dta disponibles en https://github.com/josefortou/lab-book/tree/master/data) para intentar responder estas preguntas.
9.8.1.1 Los datos
Miremos cómo votaron los representates a la cámara de Estados Unidos frente al Tratado de Libre Comercio de América del Norte (TLCAN o NAFTA):
nafta <- read_dta("data/nafta.dta") %>%
zap_label()
nafta## # A tibble: 434 x 4
## vote democrat pcthispc cope93
## <dbl> <dbl> <dbl> <dbl>
## 1 0 1 8 92
## 2 0 1 1 92
## 3 0 1 40 100
## 4 1 0 0 42
## 5 0 0 22 8
## 6 1 0 5 0
## 7 1 1 66 83
## 8 1 1 14 83
## 9 0 1 0 100
## 10 0 1 3 92
## # ... with 424 more rowsAdemás de la variable de voto a favor/en contra (vote que toma los valores “Yes” y “No”), tenemos tres variables más:
democrat: dummy de membrecía partidista (Republicano o Demócrata).pcthispc: porcentaje de la población que es de origen latino en el distrito de donde viene el representante.cope93: indicador COPE de posiciones pro-sindicato de cada legislador (0=anti-sindicatos, 100=pro-sindicatos).
Recodifiquemos las variables categóricas:
nafta <- nafta %>%
mutate(
vote = factor(vote, levels = c(0, 1),
labels = c("No", "Yes")),
democrat = factor(democrat, levels = c(0, 1),
labels = c("Rep./other", "Dem."))
)Ahora, veamos cuántos representantes votaron a favor o en contra en cada partido:
nafta %>%
count(vote, democrat)## # A tibble: 4 x 3
## vote democrat n
## <fct> <fct> <int>
## 1 No Rep./other 47
## 2 No Dem. 153
## 3 Yes Rep./other 133
## 4 Yes Dem. 1019.8.1.2 Hipótesis
Tenemos las siguientes hipótesis:
- Mayores valores COPE (más pro-sindicalismo) se asocian con una menor probabilidad de votar por NAFTA.
- El efecto de COPE sobre la probabilidad de votar por NAFTA depende de la afiliación partidista: el efecto será mayor para Demócratas que para Republicanos.
Además, controlamos por una explicación alternativa: es posible que una mayor población latina en el distrito de origen se asocie con una mayor probabilidad de votar por NAFTA por razones de lobby, presión política y deseos de reelección.
Así que estimamos el siguiente modelo:
\[ Pr(Y = 1|X) = \lambda(\beta_0 + \beta_1\text{Dem.} + \beta_2\text{COPE} + \beta_3\text{Dem.}\times\text{COPE} + \beta_4\text{Porc. latino}) \]
Donde \(\lambda\) es la función de distribución acumulada (CDF) logística.
9.8.1.3 Estimación
Estime el modelo usando la función glm().
9.8.1.4 Resultados
Presente los resultados en una tabla de regresión:
Presente los resultados utilizando gráficas:
Otros modelos como el probit son similares, pero menos populares y con frecuencia equivalentes en su interpretación o resultados.↩︎
Mientras que OLS busca los parámetros que minimizan una distancia -los cuadrados de los residuos-, MLE busca los parámetros que maximizan la probabilidad o likelihood de observar los datos que tenemos.↩︎
En español, a veces se usan los términos “oportunidades”, “probabilidades” o “momios”. Porque no hay una terminología equivalente en español, usamos odds.↩︎