Capítulo 4 Elementos básicos
4.1 Resumen
En este capítulo:
- Seguimos profundizando nuestro conocimiento sobre las bases del lenguaje de programación estadística R usando RStudio.
- Introducimos una característica central de este lenguaje: los objetos.
- Mostramos cómo cargar bases de datos, cómo guardar objetos de R y cómo hacer algunas operaciones básicas con datos.
Principales conceptos: objeto; bases de datos; importar, cargar y guardar datos.
Funciones clave: c(); read_csv(); read_excel(); write_csv(); head(); tibble(); plot(); ggplot().
4.1.1 Librerías
Vamos a utilizar las siguientes librerías:
library(tidyverse)Recordemos que para poder cargar una librería, primero debe estar instalada. Podemos revisar si una librería está instalada de esta manera:
"tidyverse" %in% rownames(installed.packages())4.1.2 Datos
Debemos descargar los siguientes archivos de datos y guardarlos en la carpeta /data de nuestro proyecto:
- Ingreso de empleados de un hospital en Riverside, California: link. Para descargar, hacer click derecho, “Guardar como…”.
4.2 Objetos, vectores y nombres
En R, todo es (potencialmente) un objeto y a los objetos les asignamos un nombre. Podemos crear objetos sencillos, como un vector de números. La función c() pega o combina valores, los cuales separamos por comas. El siguiente bloque de código imprime el objeto (en este caso, un vector) a la consola:
c(1, 1, 2, 3, 5, 8, 13, 21)## [1] 1 1 2 3 5 8 13 21Sin embargo, el objeto no queda guardado en el Environment de R (el listado de objetos disponibles en la sesión) y entonces no podemos usarlo más adelante. Podemos asignarle un nombre a este vector, usando el operador de asignación <- y así, guardarlo como un objeto de R. Podemos darle cualquier nombre, pero es aconsejable usar un estándar (camelCase o snake_case, por ejemplo) y ser consistente. No es recomendable usar espacios ni acentos en los nombres de objetos.
Una vez le asignamos nombre, este vector queda guardado en el Environment global ![]() de la sesión y estará ahí hasta que lo borremos manualmente (con la función
de la sesión y estará ahí hasta que lo borremos manualmente (con la función rm()) o cerremos la sesión de R. El listado de todos los objetos cargados en la sesión de R, incluyendo los que vienen de librerías cargadas ![]() , aparece en la pestaña
, aparece en la pestaña Environment.
Aquí, entonces, la asignamos un nombre a nuestro vector de números:
misNumeros <- c(1, 1, 2, 3, 5, 8, 13, 21)Ejecutar en la consola el nombre de un objeto creado imprime su contenido a la misma consola:
misNumeros## [1] 1 1 2 3 5 8 13 21Un vector puede ser un objeto simple, pero su composición puede ser algo más compleja. Puede tener caracteres o texto y mezclar distintos tipos de información. A continuación, creamos un vector que combina números, texto (usamos comillas para indicarle a R que interprete "rojo" como texto) y condiciones lógicas (TRUE):
vector_mixto <- c(10, "rojo", TRUE, log(10)) # los valores que son caracteres van entre comillas
vector_mixto## [1] "10" "rojo" "TRUE" "2.30258509299405"Podemos crear otro objeto, con otro nombre, pero el mismo contenido. Esto es equivalente a un flujo al que estamos acostumbrados cuando movemos archivos en un computador o en la nube: Copiar-Pegar-Cambiar nombre.
mis_numeros <- misNumeros
mis_numeros## [1] 1 1 2 3 5 8 13 21La función rm() sirve para remover o eliminar cualquier objeto existente en la sesión de R:
rm(misNumeros)Pero, la copia que hicimos bajo otro nombre todavía existe:
mis_numeros## [1] 1 1 2 3 5 8 13 21Si queremos borrar todos los objetos cargados en la sesión de R actual, podemos usar la función ls(), que nos da un listado de los objetos disponibles, en conjunción con rm():
rm(list = ls())4.2.1 Clases de objetos
Todo objeto en R tiene una clase, esto es, hay distintos tipos de objetos: vector numéricos, lógicos o de texto, matrices, bases de datos, modelos estadísticos, tablas, gráficas, etc. Podemos consultar la clase de un objeto con la función class():
class(mis_numeros)## [1] "numeric"Es importante tener en cuenta la clase de un objeto, porque algunas operaciones solo funcionan en objetos de cierto tipo. Por ejemplo, mean() solo funciona si la aplicamos a un objeto numérico; de lo contrario, arroja un error:
mean("1") # por que nos arroja error?## Warning in mean.default("1"): argument is not numeric or logical: returning NA## [1] NAPor defecto, un vector con números, caracteres y otros tipos de información (o sea, mixto), es clasificado como de tipo caracter:
class(vector_mixto)## [1] "character"Alternativamente, podemos evaluar lógicamente qué clase de objeto tenemos usando la familia de funciones is.*():
is.numeric(mis_numeros)## [1] TRUEis.integer(vector_mixto)## [1] FALSELos objetos también tiene una estructura (qué contiene el objeto) que podemos ver con la función str(). En este caso, vemos que mis_numeros es un objeto numérico, con 8 elementos (los números 1, 1, 2, 3, 5, 8, 13 y 21):
str(mis_numeros)## num [1:8] 1 1 2 3 5 8 13 214.3 Bases de datos en R
Los vectores como los que hemos visto hasta ahora son relativamente simples: tienen una sola dimensión. Pero este no es la realidad de la mayoría de los datos que nos encontramos en el mundo real: frecuentemente, trabajos con bases de datos que tienen filas y columnas (o sea, dos dimensiones). A este tipo de bases de datos las llamamos “rectangulares”.
Podemos crear objetos más complejos en R, como un data.frame, un tipo de base de datos rectangular. Un data.frame es el objeto base para trabajar con datos en R. Posteriormente, veremos cómo el tibble, un objeto similar, ofrece algunas mejorías y facilidades para el análisis de datos. Los objetos de tipo matrix son más simples: matrices sin nombres de filas o columnas. Todos estos objetos son “rectangulares” en el sentido de que tienen dos dimensiones: filas y columnas.
Idealmente, en una base de datos rectangular las filas deben corresponder a observaciones o casos y las columnas deben corresponder a variables o características de los casos. Una base de datos con estas características es “ordenada” (o tidy). Para entender mejor este concepto, comparemos dos formas de ver los mismos datos: la población de una muestra de 5 países latinoamericanos, por año, de 2015 a 2017. Estos datos ya vienen incluidos en la librería ggplot2, la cual viene con tidyverse. Aquí están los datos en un formato “ancho”:
Y ahora, en un formato más “largo”, que se ajusta a los principios de los datos ordenados o “tidy”:
4.4 Bases de datos incluidas en R
Como vemos, R tiene una serie de bases de datos que sirven como ejemplos para practicar. Carguemos una base de datos sobre automóviles (información sobre su peso, eficiencia, número de cilindros, etc.) ya incluida en R usando la función data().
data(mtcars)¿Qué clase de objeto es mtcars? Es un data.frame:
class(mtcars)## [1] "data.frame"Utilizando la función dim() vemos además que mtcars tiene 32 filas y 11 columnas:
dim(mtcars)## [1] 32 11Podemos combinar estos dos pasos. Indaguemos por la estructura del objeto mtcars (que ya debe aparecer en nuestro ambiente de trabajo) con str(). Como vemos, es un objeto tipo data.frame con 32 observaciones y 11 variables. Además, vemos los valores de las primeras filas de cada columna:
str(mtcars)## 'data.frame': 32 obs. of 11 variables:
## $ mpg : num 21 21 22.8 21.4 18.7 18.1 14.3 24.4 22.8 19.2 ...
## $ cyl : num 6 6 4 6 8 6 8 4 4 6 ...
## $ disp: num 160 160 108 258 360 ...
## $ hp : num 110 110 93 110 175 105 245 62 95 123 ...
## $ drat: num 3.9 3.9 3.85 3.08 3.15 2.76 3.21 3.69 3.92 3.92 ...
## $ wt : num 2.62 2.88 2.32 3.21 3.44 ...
## $ qsec: num 16.5 17 18.6 19.4 17 ...
## $ vs : num 0 0 1 1 0 1 0 1 1 1 ...
## $ am : num 1 1 1 0 0 0 0 0 0 0 ...
## $ gear: num 4 4 4 3 3 3 3 4 4 4 ...
## $ carb: num 4 4 1 1 2 1 4 2 2 4 ...Ahora, miremos las primeras 5 observaciones de esta base de datos usando la función head():
head(mtcars, n = 5) ## mpg cyl disp hp drat wt qsec vs am gear carb
## Mazda RX4 21.0 6 160 110 3.90 2.620 16.46 0 1 4 4
## Mazda RX4 Wag 21.0 6 160 110 3.90 2.875 17.02 0 1 4 4
## Datsun 710 22.8 4 108 93 3.85 2.320 18.61 1 1 4 1
## Hornet 4 Drive 21.4 6 258 110 3.08 3.215 19.44 1 0 3 1
## Hornet Sportabout 18.7 8 360 175 3.15 3.440 17.02 0 0 3 2Si queremos abrir la base de datos en una pestaña aparte, utilizamos la función View(). Ojo, aunque no es recomendable incluir esta función en documentos tipo RMarkdown, pues impide que compilen:
View(mtcars)En esta base de datos, cada fila es un modelo de carro distinto y cada columna es una característica variable. Cada fila (cada carro) puede tener distintos valores en cada variable (distinto peso, puede ser automático o manual, etc.). En ese sentido, la base de datos está “ordenada” (es tidy).
Podemos mirar elementos individuales (o “atómicos”) de objetos usando el operador $. En el caso de bases de datos, estos elementos individuales son las columnas que guardan la información de variables. La variable mpg indica las millas por galón de cada carro en la base de datos. A continuación, vemos el contenido de esta variable:
mtcars$mpg## [1] 21.0 21.0 22.8 21.4 18.7 18.1 14.3 24.4 22.8 19.2 17.8 16.4 17.3 15.2 10.4
## [16] 10.4 14.7 32.4 30.4 33.9 21.5 15.5 15.2 13.3 19.2 27.3 26.0 30.4 15.8 19.7
## [31] 15.0 21.4Si estamos interesados en conocer el promedio de la eficiencia de los carros en la base de datos:
mean(mtcars$mpg)## [1] 20.09062Usar las bases de datos incluidas en “base R” es una manera fácil de cargar datos a R, pero no es la más útil, pues la mayoría de las bases de datos incluidas por defecto son para practicar y no para realizar análisis novedosos3.
4.5 Crear una base de datos
Una segunda opción para traer bases de datos a R es crear un data.frame o similar manualmente, como si estuviéramos llenando una hoja de cálculo. Por ejemplo, creemos unos datos simulados. Son dos columnas (las variables x y y) con 10000 filas que siguen una distribución normal, usando la función rnorm(). La variable z en cambio, está distribuida binomial, pues la creamos usando rbinom(). En ambos casos, argumentos opcionales nos permite definir características de estas distribuciones. Como rnorm() y rbinom() toman muestras de distribuiones de variables aleatorias, incluimos un llamado a la función set.seed() para asegurarnos que el resultado de la simulación pueda ser reproducido en otros equipos y sesiones de R:
set.seed(8675309) # puede ser cualquier número
dat <- data.frame(
x = rnorm(10000, mean = 0, sd = 1),
y = rnorm(10000, mean = 3, sd = 2),
z = rbinom(10000, size = 1, prob = 0.2)
)Como estos datos no caben en la consola, podemos ver las primeras 10 observaciones con head() (noten que especificamos el argumento n = 10):
head(dat, n = 10) ## x y z
## 1 -0.99658235 4.3779393 0
## 2 0.72182415 5.1581324 0
## 3 -0.61720882 2.5572035 0
## 4 2.02939157 3.9708548 0
## 5 1.06541605 3.3928724 0
## 6 0.98721974 3.5707338 0
## 7 0.02745393 1.1724984 0
## 8 0.67287232 0.8631819 0
## 9 0.57206650 2.2093646 0
## 10 0.90367770 -0.7277716 0Miremos cuántas observaciones tienen un valor de x que excede la media de la muestra (0 por definición, como lo establecimos en el bloque de código anterior). Para esto, usamos if_else(), una función que evalúa si un objeto cumple con ciertas condiciones; en este caso, si una observación tiene un valor x por encima de la media de x (“if”), lo marcamos como "por encima", de lo contrario (“else”) lo marcamos como "por debajo". Tabulamos los resultados de esta evaluación anidando if_else() en la función table():
table(if_else(dat$x > mean(dat$x), "por encima", "por debajo"))##
## por debajo por encima
## 5033 4967Este resultado tiene sentido, porque sabemos que x sigue una distribución normal y en estas distribuciones aproximadamente el 50% de las observaciones se encuentra por encima de la media. Mientras, ¿cuántas observaciones fueron clasificadas como 1 en la variable z? ¿Y por qué?
table(dat$z)##
## 0 1
## 7982 20184.5.1 Crear “tibbles”
Por supuesto, los datos en R no tienen que ser totalmente abstractos y simulados. Al fin y al cabo, nuestro objetivo es tener las herramientas para hacer análisis de datos políticos con más contenido sustantivo.
A continuación, creamos una pequeña base de datos con 7 observaciones (filas) y 4 variables (columnas), con información sobre la edad, ingreso y ciudad de vivienda de siete personas. Se trata de una base de datos rectangular en formato tidy, con una fila para cada observación (persona) y una columna para cada variable (características de las personas).
Esta vez, en vez de usar data.frame(), usamos tibble(). Los “tibbles” son versiones mejoradas de un data.frame. Para poder usar la función tibble(), debemos cargar la librería tibble. Esta viene incluida en tidyverse. Recuerden que ya cargamos esta librería al principio de este capítulo, por lo que podemos usar la función.
El uso de tibble() es sencillo e intuitivo si estamos creando una base de datos pequeña. Le damos nombre a las columnas e insertamos su contenido -los datos- fila a fila. Cuando se trata de texto, lo incluimos entre comillas ("):
datos_ingreso <- tibble(
"nombre" = c("José", "Antonio", "María", "Inés", "Pablo", "Catalina", "Cristóbal"),
"edad" = c(28, 25, 32, 30, 35, 33, 42),
"ciudad" = c("Barranquilla", "Medellín", "Medellín", "Medellín", "Barranquilla", "Bogotá", "Bogotá"),
"ingreso" = c(8000000, 4000000, 9500000, 7300000, 6500000, 6000000, 9000000)
)Veamos nuestra pequeña base de datos:
datos_ingreso## # A tibble: 7 x 4
## nombre edad ciudad ingreso
## <chr> <dbl> <chr> <dbl>
## 1 José 28 Barranquilla 8000000
## 2 Antonio 25 Medellín 4000000
## 3 María 32 Medellín 9500000
## 4 Inés 30 Medellín 7300000
## 5 Pablo 35 Barranquilla 6500000
## 6 Catalina 33 Bogotá 6000000
## 7 Cristóbal 42 Bogotá 9000000Si tibble() no les parece muy intuitivo, tenemos la opción de usar tribble() (una “tibble() transpuesta”):
datos_ingreso <- tribble(
~nombre, ~edad, ~ciudad, ~ingreso,
"José", 28, "Barranquilla", 8000000,
"Antonio", 25, "Medellín", 4000000,
"María", 32, "Medellín", 9500000,
"Inés", 30, "Medellín", 7300000,
"Pablo", 35, "Barranquilla", 6500000,
"Catalina", 33, "Bogotá", 6000000,
"Cristóbal", 42, "Bogotá", 9000000,
)Corroboremos que el resultado es el mismo:
datos_ingreso## # A tibble: 7 x 4
## nombre edad ciudad ingreso
## <chr> <dbl> <chr> <dbl>
## 1 José 28 Barranquilla 8000000
## 2 Antonio 25 Medellín 4000000
## 3 María 32 Medellín 9500000
## 4 Inés 30 Medellín 7300000
## 5 Pablo 35 Barranquilla 6500000
## 6 Catalina 33 Bogotá 6000000
## 7 Cristóbal 42 Bogotá 9000000Podemos conocer las propiedades (clase y estructura) de este objeto que creamos, así como las propiedades de algunos de sus componentes:
str(datos_ingreso)## tibble [7 x 4] (S3: tbl_df/tbl/data.frame)
## $ nombre : chr [1:7] "José" "Antonio" "María" "Inés" ...
## $ edad : num [1:7] 28 25 32 30 35 33 42
## $ ciudad : chr [1:7] "Barranquilla" "Medellín" "Medellín" "Medellín" ...
## $ ingreso: num [1:7] 8000000 4000000 9500000 7300000 6500000 6000000 9000000Si ya tenemos un data.frame, lo podemos convertir a tibble con la función as_tibble():
as_tibble(mtcars)## # A tibble: 32 x 11
## mpg cyl disp hp drat wt qsec vs am gear carb
## <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl>
## 1 21 6 160 110 3.9 2.62 16.5 0 1 4 4
## 2 21 6 160 110 3.9 2.88 17.0 0 1 4 4
## 3 22.8 4 108 93 3.85 2.32 18.6 1 1 4 1
## 4 21.4 6 258 110 3.08 3.22 19.4 1 0 3 1
## 5 18.7 8 360 175 3.15 3.44 17.0 0 0 3 2
## 6 18.1 6 225 105 2.76 3.46 20.2 1 0 3 1
## 7 14.3 8 360 245 3.21 3.57 15.8 0 0 3 4
## 8 24.4 4 147. 62 3.69 3.19 20 1 0 4 2
## 9 22.8 4 141. 95 3.92 3.15 22.9 1 0 4 2
## 10 19.2 6 168. 123 3.92 3.44 18.3 1 0 4 4
## # ... with 22 more rowsSi queremos que permanentemente sea un tibble(), debemos asignar la operación:
mtcars <- as_tibble(mtcars)4.6 Guardar datos
Si queremos usar este objeto (y otros) después, por ejemplo en otra sesión, en otro computador o compartirlo con un colega, tenemos dos opciones. Primero, podemos repetir el código que produjo el objeto. Segundo, podemos guardar este objeto como un archivo. A continuación, guardamos estos datos como un archivo de valores separados por comas con extensión .csv. Estos archivos pueden abrirse en Excel y Google Spreadsheets y ahorran espacio, así que son una excelente opción.
A continuación, grabamos la base de datos como un archivo .csv en la carpeta data/ de nuestro proyecto. La función write_csv() viene de la librería readr, también incluida en tidyverse y toma un objeto de R y lo guarda como un archivo en una ubicación especificada en el argumento path =:
write_csv(datos_ingreso, path = "data/datos_ingreso.csv")El archivo ahora está guardado y podemos utilizarlo en el futuro. Podemos ver la lista de archivos en la carpeta data/ con la función list.files():
list.files("data/")## [1] "camara2018.csv" "cede-agro.csv"
## [3] "cede-conf.csv" "cede-edu.csv"
## [5] "cede-gen.csv" "cede-gob.csv"
## [7] "cede-salud.csv" "codebooks"
## [9] "DahlDims.sav" "data.zip"
## [11] "datos_ingreso.csv" "datos_polity_dpi.csv"
## [13] "datos_taller1.csv" "DPI2017.dta"
## [15] "gapminder_america.xlsx" "gp0070_cronograma_20211.xlsx"
## [17] "gp0070_cronograma_20212.xlsx" "mde_df.csv"
## [19] "mde_homicidio.csv" "nafta.dta"
## [21] "nes_2004_data.csv" "OECD_country_data.csv"
## [23] "OECD_country_data.xls" "p4v2017.xls"
## [25] "p5v2018.xls" "riverside_final.csv"
## [27] "wb_tidy.csv"4.7 Gráficas simples
Al final, podemos visualizar la información de una base de datos usando unas funciones muy simples. Veremos mejores formas de visualizar datos usando la librería ggplot2 (otro miembro del tidyverse… son como los Avengers), pero inicialmente trabajemos con funciones básicas de R (base).
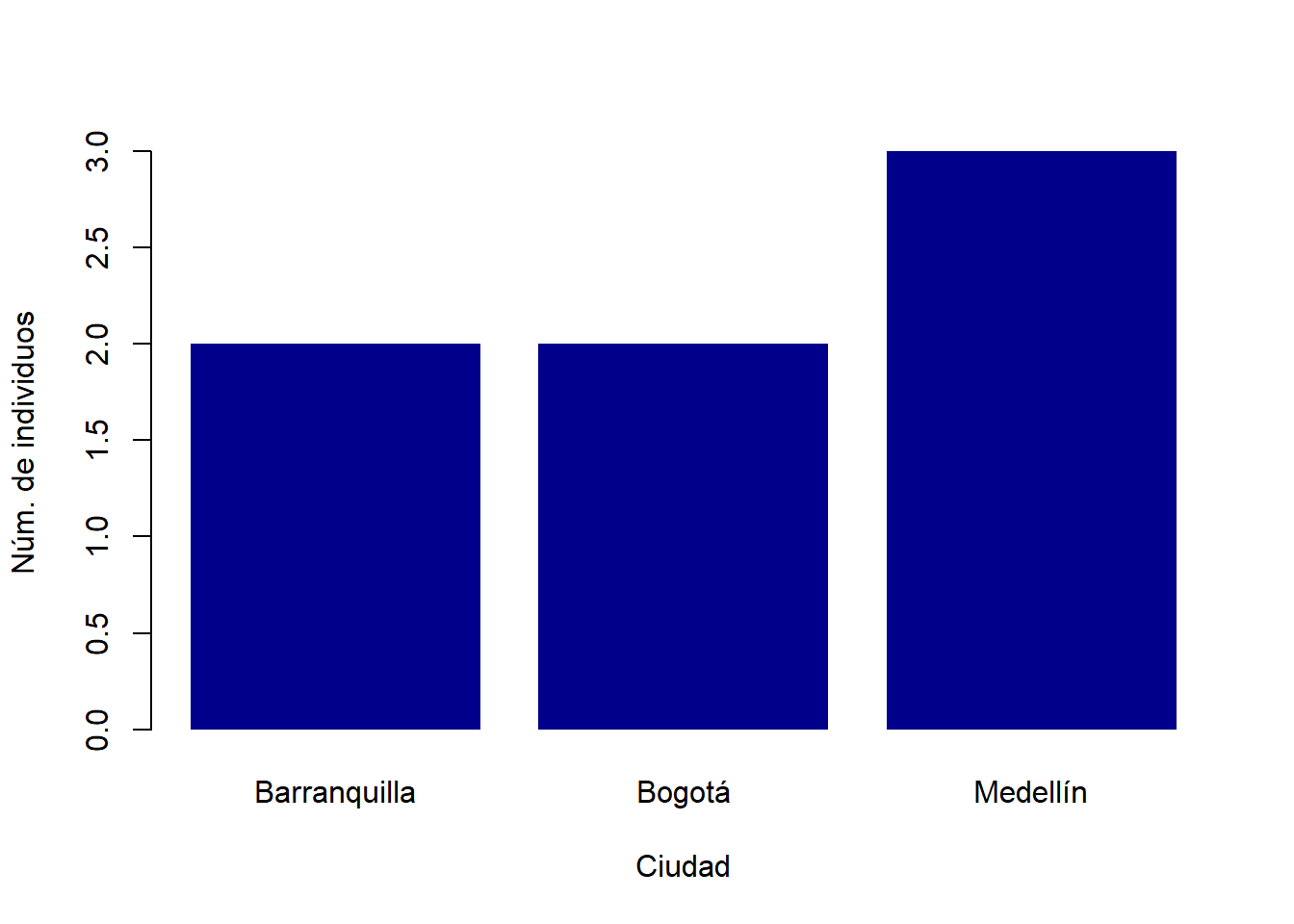
Si nos preguntamos “¿cuántos individuos hay en cada ciudad?” estamos indagando por la distribución de la variable ciudad. En otras palabras, queremos una gráfica de barras que “cuente” el número de observaciones (individuos en este caso) por cada valor de una variable. Lo podemos hacer con la función barplot(). Esta función toma una tabla de frecuencias y construye una gráfica de barras. Entonces, primero construimos una tabla de frecuencias de la variable ciudad (noten el uso del operador $) utilizando la función table():
tabla_ciudades <- table(datos_ingreso$ciudad)
tabla_ciudades##
## Barranquilla Bogotá Medellín
## 2 2 3Ahora, le pasamos esa tabla a la función barplot(), especificando las etiquetas de los ejes (xlab = y ylab =), el relleno de las barras (col =) y eliminamos el borde de las mismas (border =):
barplot(
tabla_ciudades,
xlab = "Ciudad", ylab = "Núm. de individuos",
border = NA, col = "darkblue"
)
¿Hay una relación entre la edad de las personas y el ingreso de cada una? Son pocos datos, pero podemos intentar explora esta pregunta. Para graficar la relación entre dos variables numéricas, creamos una gráfica de dispersión con plot(). Además, especificamos la forma de los puntos (pch =) y su color y el relleno (col = y bg =). Finalmente, agregamos una línea de tendencia roja con la función abline()4:
plot(
datos_ingreso$edad, datos_ingreso$ingreso,
pch = 21, col = "darkblue", bg = "darkblue",
xlab = "Edad en años", ylab = "Ingreso en COP"
)
abline(
lm(datos_ingreso$ingreso ~ datos_ingreso$edad), # regresion lineal simple
col = "darkred"
)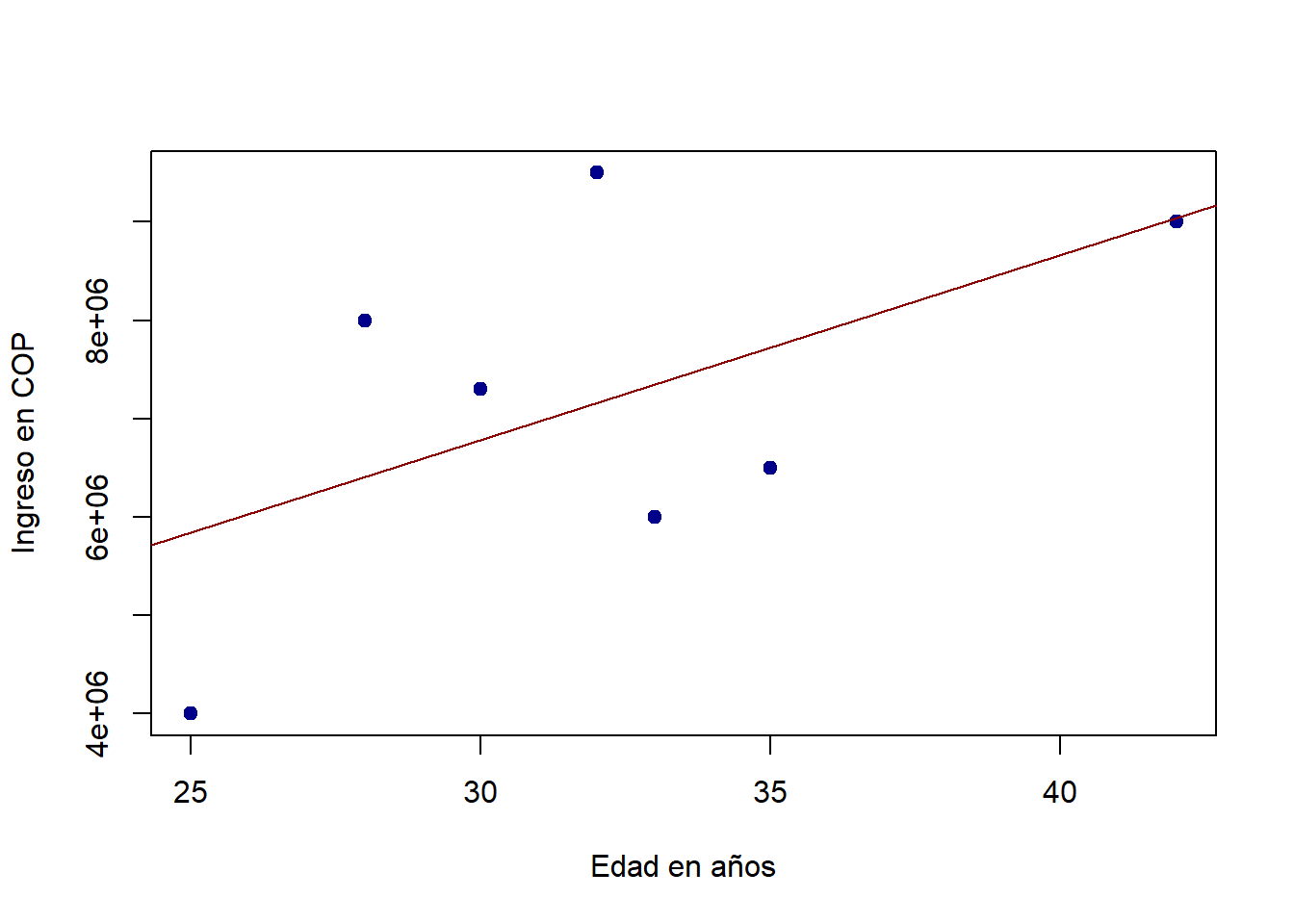
Efectivamente, en esta muestra, la edad se relaciona de forma positiva con el ingreso, pero no deberíamos tener mucha confianza en este resultado con tan pocas observaciones.
4.8 Importar datos
Ya vimos cómo crear una base de datos a mano y cómo hacer uso de datos ya incluídos en R. Sin embargo, es más común (y más fácil) hacer una base de datos en otro programa e importarla a R o utilizar una base de datos ya existente (LAPOP, V-Dem, Banco Mundial…) e importarla. R tiene funciones para importar datos de todo tipo, dependiendo del tipo de archivo, utilizando distintas librerías y funciones:
| Archivo o programa | Extensión | Función en R | Librería |
|---|---|---|---|
| R | .rds |
read_rds() |
readr |
| Valores separados por comas | .csv |
read_csv() o read_tab() |
readr |
| Excel | .xlsx o .xls |
read_excel |
readxl |
| Stata | .dta |
read_dta() |
haven |
| SPSS | .sav |
read_sav |
haven |
Ya mencionamos que un formato popular para archivos de datos es el .csv, porque es portable entre sistemas y programas y, además, ocupa poco espacio. CSV significa comma separated values o archivo de valores separados por comas. Estos archivos se leen con read_csv(). A continuación, cargamos un CSV que se encuentra en la carpeta /data:
datos_lewisbeck <- read_csv("data/riverside_final.csv")##
## -- Column specification --------------------------------------------------------
## cols(
## edu = col_double(),
## income = col_double(),
## senior = col_double(),
## gender = col_double(),
## party = col_double()
## )Esta es una base de datos con información sobre empleados de un hospital en la ciudad de Riverside, California.5 Confirmemos que cargamos bien el archivo mirando las primeras 10 filas:
head(datos_lewisbeck, 10)## # A tibble: 10 x 5
## edu income senior gender party
## <dbl> <dbl> <dbl> <dbl> <dbl>
## 1 8 26430 9 0 1
## 2 8 37449 7 1 0
## 3 10 34182 16 0 1
## 4 10 25479 1 0 2
## 5 10 47034 14 1 0
## 6 12 37656 14 1 0
## 7 12 50265 24 1 0
## 8 12 46488 11 0 0
## 9 12 52480 16 0 1
## 10 14 32631 5 0 1Para cada empleado (cada fila), hay información sobre su nivel educativo, ingreso, experiencia laboral, género (0 = “mujer”) y hasta su filiación partidista.
Rápidamente, visualicemos la relación entre los años de experiencia laboral de cada empleado y su ingreso (en USD), incorporando también información sobre el género de cada uno. En esta ocasión, en vez de usar las funciones de base, usemos funciones de la librería ggplot2 (todo hay que decirlo, esta también está incluida en tidyverse). A partir de ahora, utilizaremos ggplot2 para todas nuestras gráficas.
La función básica es ggplot(), en donde especificamos los datos utilizados, y a partir de ella construimos la gráfica capa a capa con más funciones, separadas por el operador +:
ggplot(data = datos_lewisbeck, aes(x = senior, y = income, color = factor(gender))) +
geom_point() +
labs(x = "Experiencia (en años)", y = "Ingreso (en USD)", color = "Género")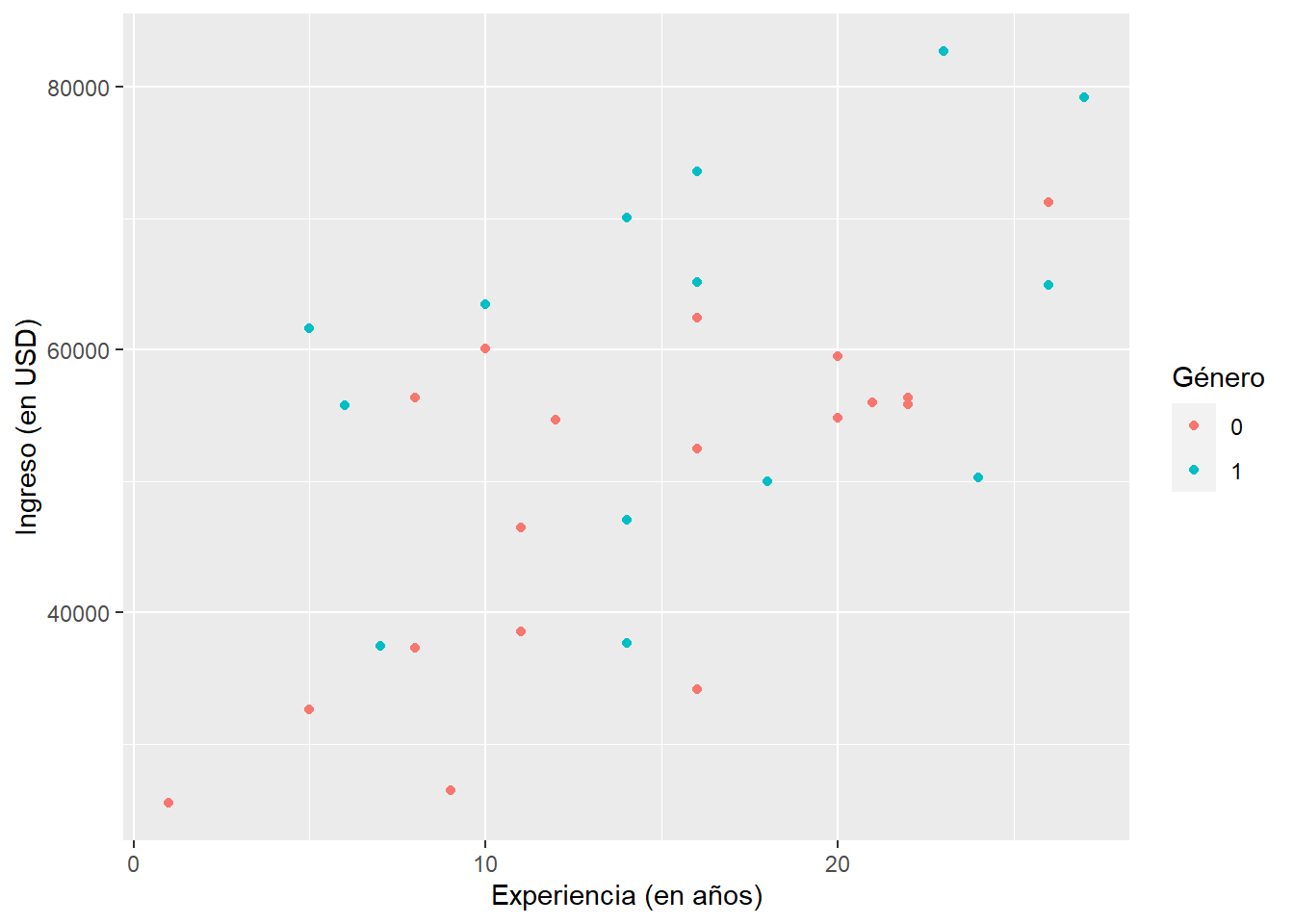
En el Capítulo “Visualización con datos” profundizamos en el uso efectivo de ggplot2 para transmitir información estadística. Parece que hay una relación positiva entre experiencia e ingreso (mayor experiencia se asocia con mayor ingreso). Aunque no es sustancialmente diferente para hombres y mujeres, sí notamos que las mujeres perciben un ingreso un poco menor que los hombres.
4.9 Ejercicios
- Utilizando la función
tibble(), crear una base de datos sencilla que consigne la siguiente información en filas y columnas:
- La ciudad de Medellín, Antioquia, tiene 16 comunas.
- Cali está dividida en 22 comunas. La ciudad está ubicada en el departamento de Valle del Cauca.
- La capital Bogotá, Distrito Capital, está dividida en 20 localidades.
- La ciudad de Barranquilla, Atlántico, tiene 5 localidades.
- Hay 3 localidades en Cartagena, capital de Bolívar.
Utilizando
ggplot()ygeom_col()y los datos del punto anterior, construir una gráfica de barras que compare el número de divisiones administrativas entre los distintos municipios. Pueden encontrar toda la información sobre la libreríaggplot2en este sitio web. Alternativamente, pueden usarbarplot(). Pista: la información necesaria ya está en la base de datos que crearon, así que no hace falta calcularla usandotable().Calcular el promedio del número de divisiones administrativas de las cinco ciudades principales del país.
Si estamos en RStudio Cloud, debemos empezar por subirlos y ubicarlos en una carpeta dentro del proyecto. Vamos al panel inferior derecho, pestaña
Files, click enUploady seguimos las indicaciones.↩︎Aquí,
abline()estima una regresión lineal simple deingresosobreedady grafica la línea \(\text{ingreso} = b \times \text{edad} + a\).↩︎Estos datos vienen de: Lewis-Beck, Colin y Michael Lewis-Beck. Applied regression: An introduction. Thousand Oaks, Sage Publications, 2015.↩︎