TEMA 2: Aproximaciones Lineales y Cuadráticas
Clase 1: Ampliación de la idea y necesidad de la aproximación de funciones
En el capítulo anterior ya introdujimos una de las aplicaciones más famosas de la derivada en funciones de una variable: la aproximación de imágenes de funciones en entornos de puntos donde existe la derivada (y, por lo tanto, se puede trazar una recta tangente a la función en dicho punto). Recuerda que, entonces, usamos la recta tangente como la función más sencilla que me permite aproximar una función complicada (recuerda que, por ejemplo, vimos que si quiero obtener el valor para \(x=0.1\) de \(f(x)=e^{x}\) cerca de \(x=0,\) usamos aproximadamente \(f(x)\simeq1+x,\) es decir, \(e^{0.1}\simeq1.1).\) Recuerda, por tanto, que:
Diferenciabilidad de una función en una variable: \(f\) es una función diferenciable en el entorno de \(x_{0}\) si el error de aproximación se hace lo más pequeño posible cuando \(\triangle x\rightarrow0\).
En funciones de una variable, si existe la derivada en un punto (es decir, la función es derivable en dicho punto), podemos aproximarla en el entorno de dicho punto y, por tanto, automáticamente diremos que es diferenciable (y, por tanto, continua y sin picos). En el caso de las funciones de \(n\) variables, esto no es automático.
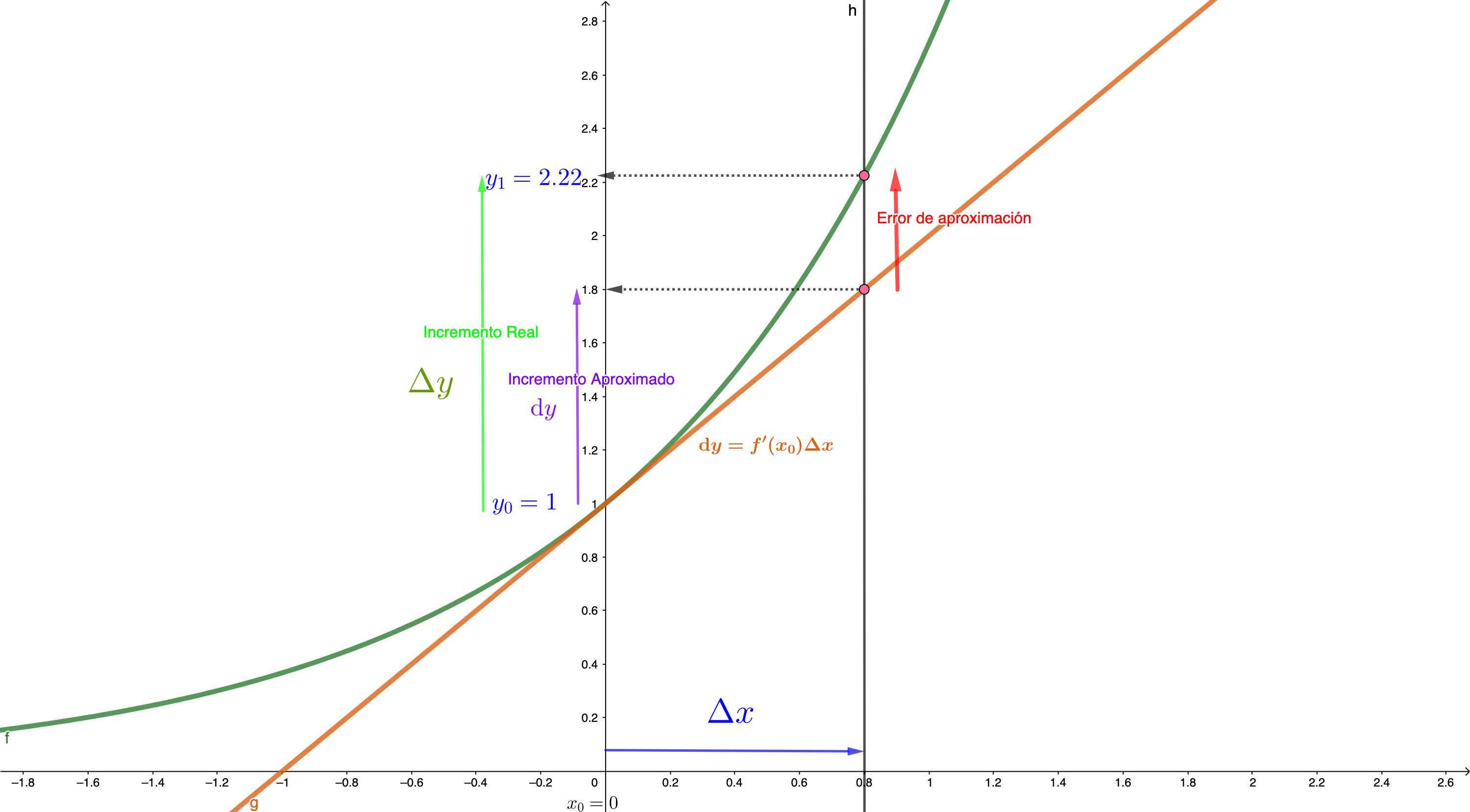
FIG1A. Volvemos a la idea de aproximar una función mediante una recta.
Donde nos damos cuenta de que \(\mathrm{d}y\) es el valor aproximado de cambio de la variable \(y\), si incrementamos la \(x\) en la cantidad \(\triangle x\). Ese incremento se calcula como \(\mathrm{d}y=f'(x_0)\triangle x\) y se llama “la diferencial de \(y\).” Es muy común encontrarse la diferencial como \(\mathrm{d}y=f'(x_0)\mathrm{d}x\), donde \(\mathrm{d}x=\triangle x\). En nuestra notación, generalmente, preferiremos la primera y diremos, además, que el error de aproximación que cometemos será menor cuanto “más pequeño” sea \(\triangle x\).
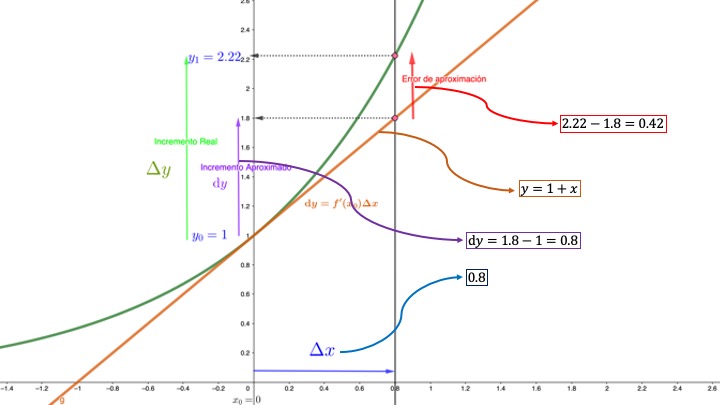
FIG1B. En números.
¿Qué significa error de aproximación ? Necesitamos:
- Darnos cuenta de que \(\frac{\triangle y}{\triangle x}=f'(x)+error\) (es decir, que este cociente-que es la tasa de variación media- es igual a la tasa de variación instantánea más un error arbitrario). Es lo mismo que decir que \(\frac{\triangle y}{\triangle x}\simeq f'(x)\). Cambiamos el aproximadamente igual por el igual al añadir el término de error en la ecuación.
- \(\triangle y=f'(x)\triangle x+error(\triangle x)\triangle x\), si \(\triangle x\rightarrow0\), el error tenderá a decrecer (más rápido, puesto que depende a su vez de \(\triangle x,\) como ves en el dibujo).
- Llamaremos a \(f'(x)\triangle x\) la diferencial \(\rightarrow\mathrm{d}f(x)\). Es decir: \(\triangle y\approx\mathrm{d}f(x)\) (o lo que es lo mismo, aproximamos el incremento de la variable \(y\) mediante la diferencial).
- La función en el punto la escribimos como \(y_{0}=f(x_{0})\)
- La función en el punto en el que se quiere aproximar \(y=f(x)\)
- Entonces, \(\underset{\triangle y}{\underbrace{f(x)-f(x_{0})}}\approx\mathrm{d}f(x)\) si \(\triangle x\rightarrow0\)
Una función será diferenciable (que, en nuestro caso, lo traduciremos como aproximable) si, en esta ecuación,
\[ f(x)-f(x_{0})=\mathrm{d}f(x)+error(\triangle x)\triangle x \]
el error tiende a cero segun \(\triangle x\rightarrow0\). Claro, de la expresión \[ f(x)-f(x_{0})=f'(x_0)\Delta x+error(\triangle x)\triangle x \]
Dividiendo por \(\Delta x\) en ambos lados
\[ \frac{f(x)-f(x_{0})}{\Delta x}=f'(x_0)+error(\triangle x) \]
si hacemos que \(\Delta x\rightarrow0\), entonces tendremos la definición de derivada y el error se irá disipando. Para ello, en el caso de una sola variable, esto es equivalente a pedir que la función sea derivable en el punto (o lo que es lo mismo, que exista su derivada en dicho punto). Entonces, es automáticamente diferenciable.
¿De qué dependerá el error de aproximación? Piensa que, por un lado, dependerá del punto en el que aproximes la función y del valor que elijas para \(\Delta x\).Pero también dependerá de la propia curvatura de la función (cuanto más curva, peor será la aproximación). En realidad, podemos intuir, entonces, que el error de aproximación, del que no vamos a dar una expresión analítica, dependerá de la derivada segunda de la función. Luego, cuando veamos expresiones cuadráticas, desarrollaremos algo más esta idea.
Piensa ¿Tiene sentido tratar de aproximar la función \(f(x)=2x+3\)?
La aproximación de funciones \(\mathbb{R}^{2}\rightarrow\mathbb{R}\)
Para poder llevar este concepto a funciones de dos variables deberemos, primero, repasar la ecuación del plano en \(\mathbb{R}^{3}\).
¿Sabrías cuál es la ecuación de un plano en 3D que pase por los puntos \((0,0,0)\)?
\[ ax+by+cz=0 \]
Es normal escribirlo como una función de dos variables:
\[ z=f(x,y)=-\frac{a}{c}x-\frac{b}{c}y \]
si vamos a google y tecleamos “z=3x-2y,” entonces obtenemos:
FIG2. La ecuación del plano que nos da Google.
De hecho, en general, un plano que pase por un punto arbitrario en \(\mathbb{R}^{3}\) : \(\left(x_{0},y_{0},z_{0}\right)\) se escribe como:
\[\begin{equation} 0=a\left(x-x_{0}\right)+b\left(y-y_{0}\right)+c(z-z_{0}) \tag{1.4} \end{equation}\]
y, de nuevo, puedes dejar la \(z\) en la parte izquierda de la ecuación y obtendrás
\[ z-z_{0}=-\frac{a}{c}(x-x_{0})-\frac{b}{c}(y-y_{0}) \]
y que, para simplificar, llamaremos \(A=-a/c\), \(B=-b/c\). Es decir, finalmente, tendremos que
\[ z-z_{0}=A(x-x_{0})+B(y-y_{0}) \]
Pensemos ahora:
¿Qué son \(A,B?\)?
son pendientes del plano: Entonces, como queremos aproximar la función \(f(x,y),\) de manera similar a como hacíamos en funciones de una variable, ahora utilizaremos-en vez de una recta- un plano para hacer dicha aprocimación. ¿Cómo buscamos \(A,B\)?
Vamos a pensar con lo que ya sabemos de derivadas y derivadas parciales:
Si congelo el eje \(y\), entonces, me muevo en torno al eje de las \(x\).}
\[ z-z_{0}=A(x-x_{0}) \]
si te fijas, tengo una recta \(z=z_{0}+A(x-x_{0}).\) Esta recta buscaremos que sea tangente a la función en el punto \(x_{0}.\) Entonces, \(A=\frac{\partial f}{\partial x}(x_{0},y_{0})\) Claro, \(A\) es la pendiente de la recta que da lugar al plano en el eje \(x\) y que es tangente a la función en el punto \(x_{0},y_{0}\).
Si congelo el eje \(x\), es decir, me quedo con que \(x=x_{0}\). Entonces, me muevo en torno al eje de las \(y\).}
\[ z-z_{0}=B(y_{0}-y_{0}) \]
Si te fijas,de manera análoga, tengo una recta \(z=z_{0}+B(y-y_{0}).\) Esta recta será tangente a la función en el punto \(y_{0}.\) Entonces, \(B=\frac{\partial f}{\partial y}(x_{0},y_{0})\). De nuevo, \(B\) es la pendiente de la recta que da lugar al plano en el eje \(y\) y que es tangente a la función en el punto \(x_{0},y_{0}\).
Bueno, pues teniendo la función \(z=f(x,y),\) y conociendo su valor en el punto \((x_{0},y_{0},z_{0})\) definimos la ecuación del plano tangente a dicha función \(f:\mathbb{R}^{2}\rightarrow\mathbb{R}\)
\[ z-z_{0}=\frac{\partial f}{\partial x}(x_{0},y_{0})(x-x_{0})+\frac{\partial f}{\partial y}(x_{0},y_{0})(y-y_{0}) \]
De la misma forma, si quisiéramos conocer la aproximación de la función en unos puntos arbitrarios \(x,y\), en el entorno de los puntos \((x_{0},y_{0})\) podríamos usar ese plano y los razonammientos anteriores
\[ f(x,y)-f(x_{0},y_{0})=\frac{\partial}{\partial x}f(x_{0},y_{0})(x-x_{0})+\frac{\partial f}{\partial y}(x_{0},y_{0})(y-y_{0})+e_{1}\triangle x+e_{2}\triangle y \]
donde \(e_{1}\) y \(e_{2}\) son términos de error que dependen, como pasaba en el caso de funciones en una variable, de la distancia a \(x_{0},y_{0}\) con la que pretendamos aproximar la función. Ya sabes que también se puede escribir como:
\[\begin{equation} \triangle f=\frac{\partial f}{\partial x}(x_{0},y_{0})\triangle x+\frac{\partial f}{\partial y}(x_{0},y_{0})\triangle y+e_{1}(\triangle x,\triangle y)\triangle x+e_{2}(\triangle x,\triangle y)\triangle y \tag{1.5} \end{equation}\]
Haciendo \(\left(\triangle x,\triangle y\right)\rightarrow(0.0)\) en la ecuación (1.5) entonces, las cantidades que miden los errores \((e_{1}(\triangle x,\triangle y),e_{2}(\triangle x,\triangle y))\) que dependen de \(\Delta x,\Delta y\) y de los valores \(x_{0},y_{0}\) se irán antes que nada a cero y tendremos la aproximación:
\[ f(x,y)-f(x_{0},y_{0})\approx\frac{\partial f}{\partial x}(x_{0},y_{0})(x-x_{0})+\frac{\partial f}{\partial y}(x_{0},y_{0})(y-y_{0}) \]
o también:
\[ \triangle f\approx\frac{\partial f}{\partial x}(x_{0},y_{0})\Delta x+\frac{\partial f}{\partial y}(x_{0},y_{0})\triangle y \]
es decir, podemos usar la diferencial de la misma forma que antes:
\[ \mathrm{d}f(x,y)=\frac{\partial f}{\partial x}(x_{0},y_{0})\Delta x+\frac{\partial f}{\partial y}(x_{0},y_{0})\Delta y \]
Y, además, podemos aproximar el valor de la función modificando a la vez tanto la \(x\) como la \(y\)
\[ f(x,y)\approx f(x_{0},y_{0})+\underset{\mathrm{d}f(x,y)}{\underbrace{\frac{\partial f}{\partial x}(x_{0},y_{0})\triangle x+\frac{\partial f}{\partial y}(x_{0},y_{0})\triangle y}} \]
De igual manera, es común encontrarse \(\mathrm{d}f(x,y)=\frac{\partial f}{\partial x}(x_{0},y_{0}) \mathrm{d}x+\frac{\partial f}{\partial y}(x_{0},y_{0}) \mathrm{d}y\), usando \(\mathrm{d}x,\mathrm{d}y\).
En realidad, de manera análoga a como planteamos en funciones de una variable, buscamos ser capaces de aproximar cualquier función en 2 variables (que tenga buenas propiedades) utilizando un plano. Esto lo puedes ver en este vídeo de Maths & GO
Clase 2: ¿Qué funciones se pueden aproximar?
Diremos que una función podrá ser aproximable (diferenciable) si el error de aproximación de la ecuación (1.5) en ambas variables tiende a cero cuando nos acercamos al punto en el que el plano es tangente a la función.
En este curso, y de manera general, utilizaremos la condición suficiente de diferenciabilidad
Una función es diferenciable si sus derivadas parciales primeras existen y son continuas en su dominio
OJO!
Es importante darse cuenta de que es una condición suficiente:
Si no se cumple, no quiere decir que la función no sea diferenciable, sino que deberás analizar con mayor detalle este aspecto. Lo que escapa de los objetivos de este curso.
Si se cumple, ya te garantizas que la función es diferenciable
Aunque quizás te sorprenda que no valga con que la derivada parcial exista, sino que se exige algo más que cuando teníamos una variable. Esto ocurre porque una función de dos o más variables puede tener derivadas parciales (existen), pero la función no ser continua.
Ejemplo
Fíjate en esta función: \(f(x,y)=x^{3}+8xy-y^{2}\). Sus derivadas parciales \(f'_{x}=3x^{2}+8y\) y \(f_{y}'=8x-2y\) como ves, existen (son polinomios), y son continuas para todos los valores de \(x,y\).
Esto implica que la función es diferenciable en dicho punto. Como ves, en la FIG3, al trazar un plano tangente por un punto cualquiera de estas funciones suaves, en un entorno (delimitado por la bola roja), la aproximación usando un plano es lo suficientemente buena.
Sin embargo, y de manera análoga a lo que ya vimos en una dimensión,
hay funciones con picos cuyas derivadas parciales existen
pero que no satisfacen la condición suficiente de diferenciabilidad.
Si las dibujas, puedes ver enseguida que hay puntos donde la función
no podría aproximarse mediante planos puesto que estos no serían únicos.
FIG4. Típica función que parece un papel arrugado. No diferenciable en varios puntos, aunque sea continua.
En este curso generalmente trabajaremos con funciones diferenciables (puedes ir al oráculo de Matemáticas I para profundizar más en esto, si te interesa). Si son diferenciables, decimos que \(f\in C^{1}\left[(x_{0},y_{0})\right]\) es decir, que \(f\) es una función de clase 1 en el entorno del punto \(x_{0},y_{0}.\) Ser una función de clase 1 implica que sus derivadas parciales primeras existen y son continuas en el entorno de dicho punto, esto es, cumple la condición suficiente de diferenciabilidad.
Aproximaciones cuadráticas
De la misma manera que hemos aproximado funciones utilizando la recta y el plano, ahora vamos a ver cómo mejorar la calidad de la aproximación. ¿Qué función conocida podemos tratar de incorporar para minimizar el error de aproximación cuando nos alejamos del punto \(x_{0}\) en el dibujo de la FIG 5?
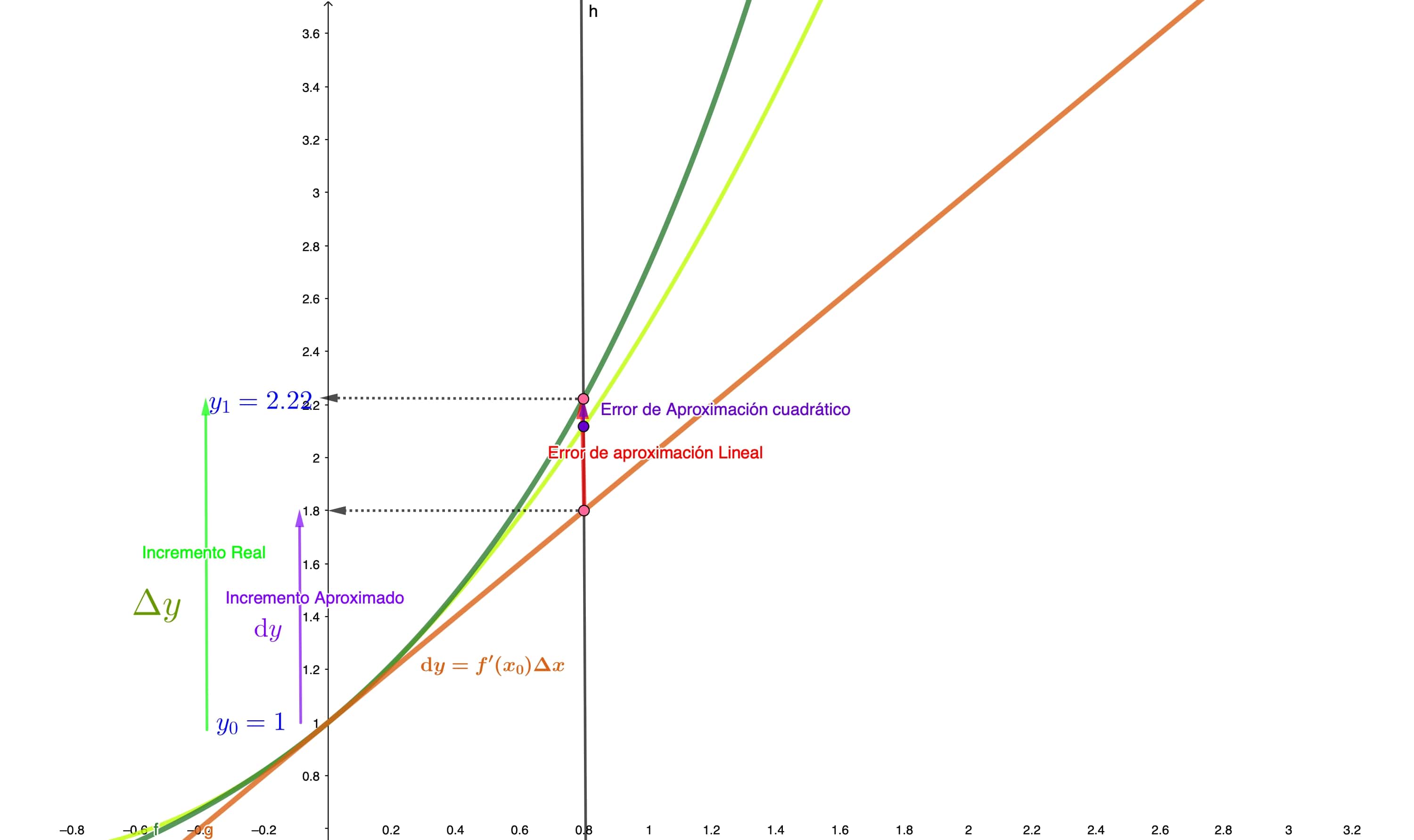
FIG5.¡¡ Usando una parábola!!.
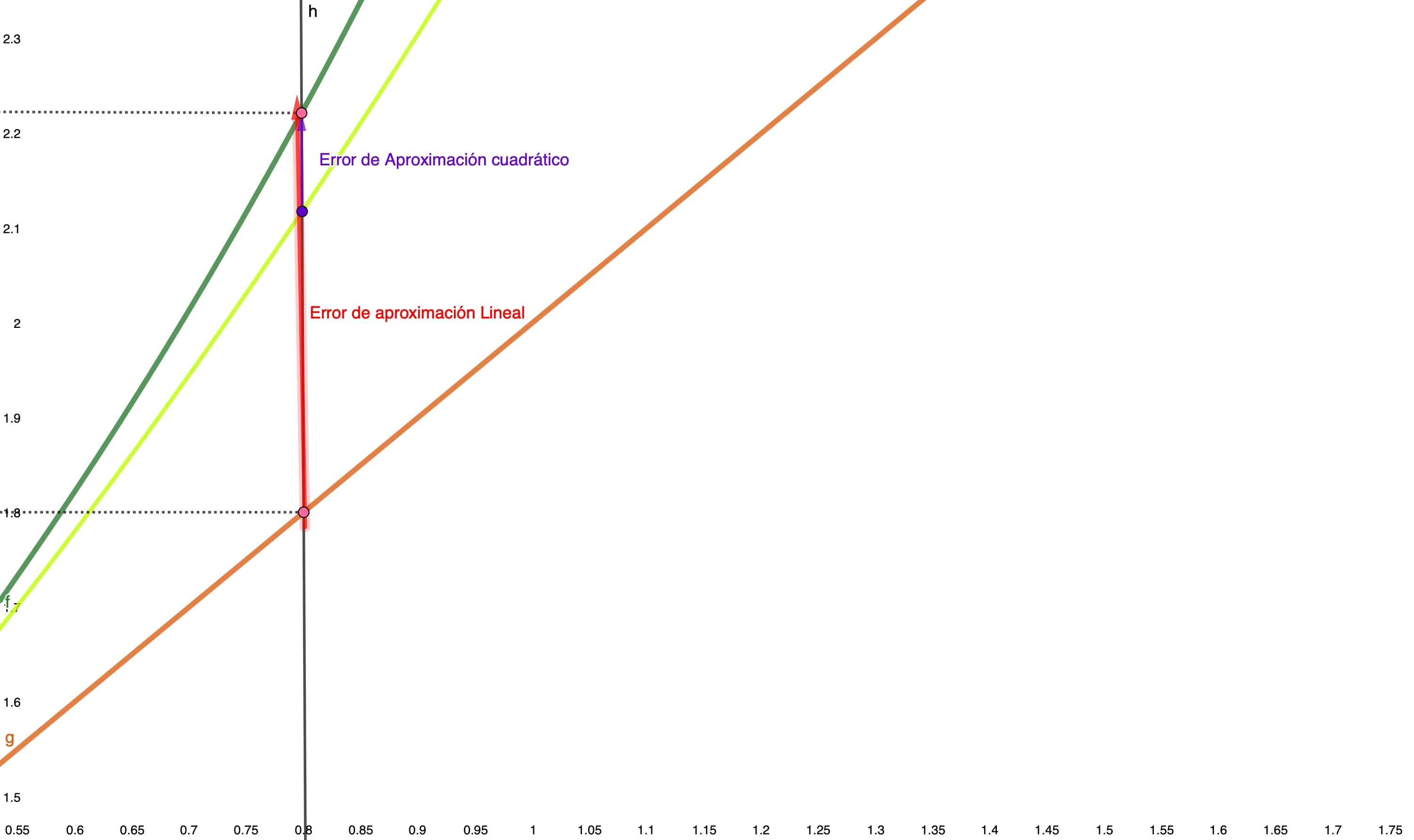
FIG5B.¡¡ Usando una parábola!!.
En el siguiente vídeo, te explicamos de dónde sale la expresión
\[ f(x)\simeq f(x_{0})+f'(x_{0})(x-x_{0})+\frac{f''(x_{0})}{2}(x-x_{0})^{2}, \]
que nos permite aproximar una función utilizando un polinomio de segundo grado:
Es importante que notes que en el punto \(x_0\) la función y las derivadas primeras y segundas valen lo mismo.
Como ves, nos permitirá aproximar el valor de una función \(f(x)\) en el entorno de un punto \(x_{0}\), con mayor precisión. Diremos que es una aproximación de orden 2, o cuadrática y, si te fijas, incorpora a la aproximación lineal (o de orden 1), marcado en negrita
\[ f(x)\simeq \textbf{{f(x_{0})+f'(x_{0})(x-x_{0})}}+ \frac{f''(x_{0})}{2}(x-x_{0})^{2}, \]
El uso de estas aproximaciones polinómicas se conoce como los polinomios de Taylor de orden \(n\)
Ahora, decimos que trabajamos con un polinomio de Taylor de orden 2.
OJO!
El polinomio de Taylor de orden \(n\) lo usamos para aproximar una función que sea, al menos, \(n+1\) diferenciable. Además, decimos que el error de aproximación dependerá de la derivada \(n+1\). Por ejemplo, en el caso del polinomio de orden 1, para aproximar una curva tenemos que \[ f(x)={f(x_{0})+f'(x_{0})(x-x_{0})}+R, \]
donde \(R\) se denomina “resto.” Se puede probar que este resto dependerá de la segunda derivada de la función (aunque no se puede precisar en qué valor está evaluada). La idea la puedes ver en la FIG 5
En el caso de Taylor de orden 2
\[ f(x)={f(x_{0})+f'(x_{0})(x-x_{0})}+\frac{f''(x_{0})}{2}(x-x_{0})^{2}+R, \]
de nuevo, el error de aproximación dependerá, en este caso, de la tercera derivada de la función.
Piensa ¿Tiene entonces sentido aproximar utilizando Taylor de orden 2 la función \(f(x)=x^2\)?
¿Cómo lo generalizamos a una función en dos dimensiones? Hay una forma larga y otra más breve o compacta. Empezamos con la compacta. Para ello, te pedimos que recuerdes del bachillerato la notación vectorial. Vamos a definir \(\overrightarrow{x}_{0}=\left(x_{1}^{0},x_{2}^{0}\right)\), como un vector en \(\mathbb{R}^{2}\) con los valores iniciales de \(x_{1}\)y \(x_{2}\). Diremos que la aproximación para una función \(f(\overrightarrow{x})\) en un entorno del punto \(f(\overrightarrow{x}_{0}):\)
\[ f(\overrightarrow{x})\simeq f(\overrightarrow{x}_{0})+\nabla f(\overrightarrow{x}_{0})\left(\overrightarrow{x}-\overrightarrow{x}_{0}\right)^{t}+\frac{1}{2}\left(\overrightarrow{x}-\overrightarrow{x}_{0}\right)Hf(\overrightarrow{x}_{0})\left(\overrightarrow{x}-\overrightarrow{x}_{0}\right)^{t} \]
Fíjate que usamos la traspuesta: si
\(\left(\overrightarrow{x}-\overrightarrow{x}_{0}\right)=\left(x_{1}-x_{1}^{0},x_{2}-x_{2}^{0}\right)\) su traspuesta \(\left(\overrightarrow{x}-\overrightarrow{x}_{0}\right)^{t}=\left(\begin{array}{c} x_{1}-x_{1}^{0}\\ x_{2}-x_{2}^{0} \end{array}\right)\).
Es decir, vamos a ir deshaciendo estas operaciones para obtener la forma larga del polinomio:
\[ \small f(\overrightarrow{x})\simeq f(\overrightarrow{x}_{0})+\left(\frac{\partial f}{\partial x_{1}},\frac{\partial f}{\partial x_{2}}\right)_{\overrightarrow{x}_{0}}\left(\begin{array}{c} x_{1}-x_{1}^{0}\\ x_{2}-x_{2}^{0} \end{array}\right)+\frac{1}{2}\left(\left(x_{1}-x_{1}^{0},x_{2}-x_{2}^{0}\right)\left[\begin{array}{cc} \frac{\partial^{2}f}{\partial x_{1}^{2}} & \frac{\partial^{2}f}{\partial x_{1}\partial x_{2}}\\ \frac{\partial^{2}f}{\partial x_{2}\partial x_{1}} & \frac{\partial^{2}f}{\partial x_{2}^{2}} \end{array}\right]_{\overrightarrow{x_{0}}}\left(\begin{array}{c} x_{1}-x_{1}^{0}\\ x_{2}-x_{2}^{0} \end{array}\right)\right) \]
Lo cual nos deja esta expresión:
\[ \small f(\overrightarrow{x})\simeq f(\overrightarrow{x_{0}})+f_{x_{1}}^{'}(\overrightarrow{x_{0}})\left(x_{1}-x_{1}^{0}\right)+f_{x_{2}}^{'}(\overrightarrow{x_{0}})\left(x_{2}-x_{2}^{0}\right)+\frac{1}{2}f''_{x_{1}}(\overrightarrow{x_{0}})\left(x_{1}-x_{1}^{0}\right)^{2}+\frac{1}{2}f''_{x_{2}}(\overrightarrow{x_{0}})\left(x_{2}-x_{2}^{0}\right)^{2}+f_{x_{1},x_{2}}^{''}(\overrightarrow{x_{0}})\left(x_{1}-x_{1}^{0}\right)\left(x_{2}-x_{2}^{0}\right) \]
Fíjate cómo en el último término, hemos usado el teorema de Schwartz (es decir, las derivadas segundas cruzadas son iguales).
Ejercicios resueltos para practicar Ejercicio resuelto 1 Sea \(g(x,y)=2xy^{\frac{1}{2}}+x\). Diga si son ciertas o falsas las siguientes afirmaciones:
La función \(g(x,y)\) es diferenciable en el punto \((2,4)\)
Para puntos \((x,y)\) próximos al punto \((2,4)\) se cumple \(g(x,y)\approx5x+y-4\)
soluciones
- Comprobamos si se cumple la condición suficiente de diferenciabilidad
\(g_{x}^{\prime }=2y^{1/2}+1\); \(g_{y}^{\prime }=xy^{-1/2}\)
Puesto que ambas parciales existen y son continuas “en el entorno” del punto \((2,4)\) la función es diferenciable en ese punto, y la afirmación es cierta.
- Puesto que es diferenciable podemos aproximarla por la función lineal cuya gráfica es el plano tangente a la gráfica en ese punto. Necesitamos hallar el gradiente de la función en el punto, y el valor de la función en el punto para hallar esta función lineal:%
\(\nabla g(2,4)=(5,1)\); \(g(2,4)=10\)
luego para puntos \((x,y)\) próximos a \((2,4)\) se cumple
\(g(x,y)\approx g(2,4)+g_{x}^{\prime }(2,4)(x-2)+g_{y}^{\prime}(2,4)(y-4)=10+5(x-2)+(y-4)=5x+y-4\)
y, por tanto, la afirmación es cierta.
Ejercicio resuelto 2
Sea \(\Pi(r,w)=100\frac{r+w}{rw}\) la función de beneficios de una empresa donde \(r\) es el precio del capital y \(w\) es el precio del trabajo. Se pide: a) Calcule el vector gradiente del la función de beneficios en el punto \((r_{0},w_{0})=(2,1)\) e interprete económicamente el signo de cada una de las derivadas parciales. b) Calcule la matriz Hessiana de la función dada en el punto \((r_{0},w_{0})=(2,1).\) c) Utilizando la diferencial, calcule el valor aproximado de \(\Pi(1.99,1.01).\)
Solución a)
\(\nabla \Pi (r,w)=(-\frac{100}{r^{2}},-\frac{100}{w^{2}})\Rightarrow \nabla\Pi (2,1)=(-25,-100)\)
\[ H\Pi(r,w)=\left(\begin{array}{cc} 200/r^3 & 0\\ 0 & 200/w^3 \end{array}\right) \] de donde \[ H\Pi(2,1)=\left(\begin{array}{cc} 25 & 0\\ 0 & 200 \end{array}\right) \] c) \(\Pi(2,1)=150\Rightarrow \Pi(1.99,2.01)\simeq \Pi (2,1)-25\cdot(-0.01)-100(0.01)=150+0.25-1=149.25\)
Clase 3: Las propiedades del gradiente
Vamos a tratar de entender las propiedades interesantes del gradiente, y muy útiles en optimización, con un ejemplo. Analicemos una función sencilla:
\[ f(x,y)=ln(4x-y) \]
Supongamos que estamos en el punto inicial \(x_{0},y_{0}=(1,3)\). Vamos a calcular el vector gradiente de la función:
\[ \nabla f(x,y)=\left[\frac{4}{4x-y},\frac{-1}{4x-y}\right] \]
que, evaluado en el punto \((1,3)\),
\[ \nabla f(x_{0},y_{0})=\left[4,-1\right] \]
¿Recuerdas qué información nos daba un vector? En este caso, al tener dos coordenadas, nos está marcando en qué dirección nos movemos. Por ejemplo, el vector (4,-1) nos dice que andemos siempre 4 pasos en dirección eje \(x\) (es decir, a la derecha) y menos 1 pasos (es decir, hacia abao) en dirección eje \(y\). Si lo dibujamos, estamos recorriendo esta dirección:
FIG6. El mismo vector en \(\mathbb{R}^{2}\).
Nota que los vectores marcan la misma dirección, da igual que empecemos del (0,0). Es decir, donde empieces da igual, que es lo mismo que decir que el punto de aplicación del vector no es importante. Todos esos vectores son, en definitiva, el (4,-1).
Bueno, ya tenemos pillada la idea de para qué nos sirve un vector (por lo menos, para nosotros). Ahora vamos a por el siguiente argumento. Pinta las curvas de nivel de la función del ejemplo. Para ello:
\[ C=ln(4x-y)\Rightarrow e^{C}=4x-y \]
FIG7. las curvas de nivel para diferentes valores de c.
Como ves en la FIG 7, la función crece según nos vamos en sentido sureste. ¿Se puede mejorar esta descripción?. Ahora nos preguntamos ¿cuál de estas flechas (sí, sí, vectores) es la que permite avanzar hacia el siguiente valor mayor de la función de forma más rápida? Mira estos candidatos. ¿Qué flecha (vector) te parece el mejor?
FIG8. ¡La verde!
estarás de acuerdo conmigo que el mejor candidato es el verde. Esa es la forma más rápida que encontramos para avanzar al siguiente punto de la función. Pues fíjate, ese vector es proporcional a otro que ya hemos dibujado antes:
FIG8. ¿De qué vector es proporcional?
¡Del gradiente! En efecto. De hecho, ahora vamos a mostrar lo siguiente:
El gradiente marca la dirección de máximo crecimiento/decrecimiento de la función
¿En qué consiste buscar la dirección de máximo crecimiento/decrecimiento de la función?
Necesitamos,en este caso, encontrar el vector de desplazamientos \((\Delta x,\Delta y)\). Que me permita crecer/decrecer lo más rápido a partir de un punto dado \(x_0,y_0\). Un momento, si tienes dudas sobre vectores lo mejor es que antes veas este vídeo
Para probar esto de una forma más precisa (no sólo con un dibujo), vamos a necesitar algunos argumentos que están fuera de los objetivos de esta asignatura, pero que debemos contar (basados en el vídeo que acabas de ver). La idea es la siguiente:
Ya sabemos que el cambio en la función se puede escribir, de forma aproximada como:
\[ \triangle f\approx\frac{\partial f(x_{0},y_{0})}{\partial x}\triangle x+\frac{\partial f(x_{0},y_{0})}{\partial y}\triangle y \]
Esto se puede escribir como: \[ \triangle f\approx\left[\frac{\partial f(x_{0},y_{0})}{\partial x},\frac{\partial f(x_{0},y_{0})}{\partial y}\right]\left[\begin{array}{c} \triangle x\\ \triangle y \end{array}\right]=\nabla f(x_{0},y_{0})\left[\begin{array}{c} \triangle x\\ \triangle y \end{array}\right] \]
usando el producto escalar de vectores. Aunque, también se puede escribir de esta otra forma:
\[ \triangle f\approx\left\Vert \nabla f(x_{0},y_{0})\right\Vert \left\Vert \left[\triangle x,\triangle y\right]\right\Vert cos\left(\nabla f(x_{0},y_{0}),\left[\triangle x,\triangle y\right]\right) \]
¡No dramas! esta última manera es cómo se escribe el producto escalar de dos vectores usando la regla del coseno. En el vídeo se dedica algo de detalle a ello. Ahora, aquí me importa que te lo creas. Y que recuerdes que el coseno de 90º y 270º es 0 y que el coseno de 0º es 1 y el coseno de 180º es -1. Recuerda que la función coseno tiene su rango (o imagen) entre el -1 y el 1. Entonces,
buscamos un vector de desplazamientos (\(\Delta x \Delta y\)) que me permita llegar lo antes posible al siguiente valor de la función, es decir, que se incremente lo más rápido posible.
Eso implicará que querremos que esta magnitud
\[ \nabla f(x_{0},y_{0})\left[\begin{array}{c} \triangle x\\ \triangle y \end{array}\right] \]
sea lo mayor posible. Dado que
\[ \nabla f(x_{0},y_{0})\left[\begin{array}{c} \triangle x\\ \triangle y \end{array}\right]=\vert\vert \nabla f(x_{0},y_{0})\vert\vert \vert\vert (\Delta x,\Delta y)\vert\vert cos(\nabla f(x_{0},y_{0}),(\Delta x,\Delta y)) \]
en este caso, dado que el gradiente es un vector dado, y el vector de desplazamientos es lo que estamos buscando, sólo podemos controlar qué ángulo han de tener el gradiente y el vector de desplazamientos para que este desplazamiento sea el más rápido. Muy sencillo:
| Grados entre el gradiente y la curva de nivel | coseno | producto escalar | dirección | |
|---|---|---|---|---|
| 0 | \(cos(0)=1\) | \(\left\Vert \nabla f(x_{0},y_{0})\right\Vert \left\Vert \left[\triangle x,\triangle y\right]\right\Vert \times 1\) | crecimiento más rápido | |
| 90 | \(cos(90)=0\) | \(\left\Vert \nabla f(x_{0},y_{0})\right\Vert \left\Vert \left[\triangle x,\triangle y\right]\right\Vert \times 0\) | no varía | |
| 180 | \(cos(180)=-1\) | \(\left\Vert \nabla f(x_{0},y_{0})\right\Vert \left\Vert \left[\triangle x,\triangle y\right]\right\Vert \times (-1)\) | decrecimiento más rápido | |
| 270 | \(cos(270)=0\) | \(\left\Vert \nabla f(x_{0},y_{0})\right\Vert \left\Vert \left[\triangle x,\triangle y\right]\right\Vert \times 0\) | no varía |
Entonces, vemos que:
La dirección de máximo crecimiento es aquella en la que el ángulo entre el gradiente y el vector de incrementos es nulo (es decir, son el mismo vector). Esto quiere decir que \(\triangle x,\triangle y\) se han de mover proporcionales al vector gradiente.
La dirección de mayor decrecimiento es la contaria (es decir, formando 180 grados respecto a la curva de nivel)
Hay direcciones en las que no varía: si el vector de incrementos es perpendicular al vector gradiente.
Recta tangente a una curva de nivel o derivada de la función implícita
Siguiendo el hilo, podríamos preguntarnos ¿cuál es la ecuación de la recta tangente a la curva de nivel en un punto? Para ello, debemos pensar que, gráficamente, consiste en algo del estilo de lo que tenemos en la FIG9, imaginando que son las curvas de nivel de una función \(f(x,y)\) en dos variables.
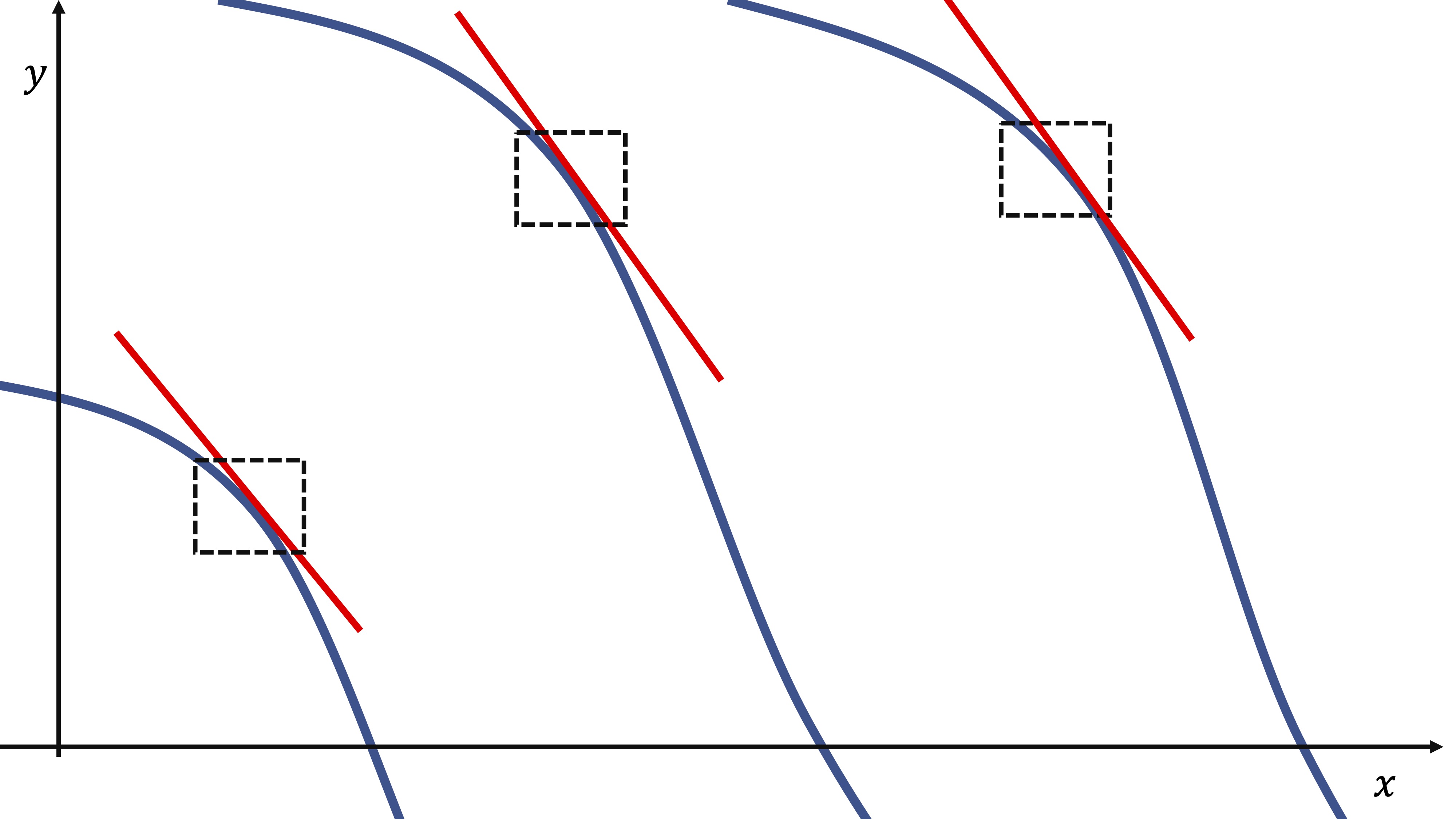
FIG9. ¿De qué vector es proporcional?
Debemos pensar, por tanto, que al buscar la pendiente de la curva de nivel de la función en un punto \((x^*,y^*)\), podemos confundir- en un entorno del punto-la curva de nivel con la recta tangente. Eso quiere decir que, en ese entorno, la función no varía, aproximadamente, es decir, de la aproximación utilizando la diferencial de la función, \[ \triangle f\approx\frac{\partial f(x_{0},y_{0})}{\partial x}(x-x_{0})+\frac{\partial f(x_{0},y_{0})}{\partial y}(y-y_{0}) \]
como queremos buscar la ecuación de la recta que hace que la función no varíe, pues necesitamos que \(\triangle f=0\), por lo que:
\[ 0\approx\frac{\partial f(x_{0},y_{0})}{\partial x}(x-x_{0})+\frac{\partial f(x_{0},y_{0})}{\partial y}(y-y_{0}) \]
De tal forma que la ecuación será:
\[ y-y_{0}=-\frac{\frac{\partial f(x_{0},y_{0})}{\partial x}}{\frac{\partial f(x_{0},y_{0})}{\partial y}}(x-x_{0}) \]
Como ves, es condición necesaria para obtener dicha ecuación que \(\frac{\partial f(x_{0},y_{0})}{\partial y}\) sea distinta de cero. Si no es así, entonces, no seremos capaces de encontrar dicha ecuación.
FIG9. ¿De qué vector es proporcional?
Como ves en la FIG9, en realidad, para poder buscar la tangente a la curva de nivel en un punto, en dicho entorno-sea como sea la curva- deberá poder identificarse una función del tipo \(y=f(x)\). Si eso ocurre, entonces, \(\frac{\partial f(x_{0},y_{0})}{\partial y}\neq 0\). En el punto en el que esto no ocurra, será imposible definir dicha función y-por tanto- encontrar la pendiente a la recta tangente.
Ejercicio Busca la ecuación de la recta tangente a la función \(f(x,y)=2x^2+3y^2\) en el punto \((1,1)\) y en el punto \((0,0)\).
Como resumen de lo aprendido:
FIG10. Un buen resumen
La ventaja de esta aproximación es que, sin conocer la curva de nivel (sólo conociendo el gradiente y el valor de la función en el punto) podemos aproximar la relación entre la \(x\) y la \(y\) que permite:
- Ir en la dirección de máximo cambio
- Ir en la dirección de mínimo cambio
- Ir en la dirección de cambio nulo.
Chuleta-resumen aproximación por la diferencial
Tengo la función: \[ z=f(x,y) \]
tenemos la función \(z=f(x,y)\): y me preguntan ¿cuánto se incrementa \(z\) si aumento la \(x\) y la \(y\) en una unidad?
Me preguntan \(\triangle z=(z-z_{0})\) y me dan \(\triangle x=\triangle y=1\). Entonces, \[ \triangle z\simeq\frac{\partial f}{\partial x}(x_{0},y_{0})\triangle x+\frac{\partial f}{\partial y}(x_{0},y_{0})\triangle y \]
Si me dicen, por ejemplo : que SÓLO \(\triangle x=1\), entendemos que \(\triangle y=0\), entonces
\[ \triangle z\simeq\frac{\partial f}{\partial x}(x_{0},y_{0})\triangle x \]
Cuánto se incrementa \(z\) si : aumento la \(x\) y la \(y\) en un tanto por ciento (por ejemplo, \(a\%\) para la \(x\) y \(b\%\) para la \(y\)?
En este caso, te siguen preguntando \(\triangle z=(z-z_{0})\) y me dan \(\triangle\%x=a,\triangle\%y=b\). Pero es mejor que uses esta expresión: \[ \triangle z\simeq\frac{\partial f}{\partial x}(x_{0},y_{0})\triangle x+\frac{\partial f}{\partial y}(x_{0},y_{0})\triangle y \]
Para ello, convierte los porcentajes en incrementos de \(x\) y de \(y\), \(\triangle x=\frac{ax_{0}}{100}\)\(\triangle y=\frac{by_{0}}{100}\) y aplica la fórmula
Cuánto se incrementa en tanto por ciento \(z\) si : aumento la \(x\) y la \(y\) en un tanto por ciento (por ejemplo, \(a\%\) para la \(x\) y \(b\%\) para la \(y\)?
Usa en este caso, esta expresión, que involucra a las elasticidades parciales \[ \triangle\%z\simeq\varepsilon_{x}\triangle\%x+\varepsilon_{y}\triangle\%y \]
Ahora \(\triangle\%x=a\), \(\triangle\%y=b\): son directamente los porcentajes
Cuánto vale \(z\) si : aumento la \(x\) y la \(y\) en una unidad?
Ahora, deshaces el incremento: \[ z\simeq z_{0}+\frac{\partial f}{\partial x}(x_{0},y_{0})\triangle x+\frac{\partial f}{\partial y}(x_{0},y_{0})\triangle y \]
Lo demás sigue igual (y es análogo para el resto de casos: elasticidades, etc…).
Ejercicio resuelto 3
Sea \(t_{2}(x,y)=1+x-2y+\frac{1}{2}x^{2}+3y^{2}-2xy\) el polinomio de Taylor de segundo orden de una función \(f(x,y)\) en el punto \((x,y)=(0,1)\) a) Di, justificando tu respuesta, si es cierta la siguiente afirmación: "si aumentamos \(y\) ligeramente el valor de \(f\) aumenta, y ese aumento es mayor cuanto mayor es \(y\)
- Diga qué relación deben satisfacer las variaciones \((\Delta x,\Delta y)\) de las variables para que partiendo del punto \((0,1)\) se aumente la función \(f\) lo más rápidamente posible.
Solución
- El polinomio de Taylor de segundo orden coincide en el punto con la función , y tiene el mismo gradiente y hessiana que la función en el punto. Por tanto
\(f(0,1)=t_{2}(0,1)=1-2+3=2\), \(\nabla t_{2}(x,y)=(1+x-2y,-2+6y-2x)\Longrightarrow \nabla f(0,1)=\nabla t_{2}(0,1)=(-1,4)\) \
\[ Hf(0,1)=Ht_{2}(0,1)=\left(\begin{array}{cc} 1 & -2\\ -2 & 6 \end{array}\right) \]
Puesto que \(f_{y}^{\prime }(0,1)=(t_{2})_{y}^{\prime }(0,1)=4\) es cierto que si aumentamos ligeramente \(y\) dejando \(x\) fija, partiendo del punto \((0,1)\) entonces el valor de la función aumenta. Puesto que \(f_{yy}^{\prime \prime}(0,1)=(t_{2})_{yy}^{\prime }(0,1)=6>0\) es cierto que ese aumento es mayor cuanto mayor es \(y\).
- La relación debe ser tal que \((\Delta x,\Delta y)\) tenga la dirección y sentido del vector gradiente,
\(\frac{\Delta x}{\Delta y}=\frac{-1}{4},\text{ }\Delta y>0\)


