TEMA 1: Introducción al cálculo en 2 variables

Clase 1: conceptos básicos

Recordemos, primeramente, ciertos aspectos del cálculo en 1 variable. Recuerda que puedes asistir al grupo 0- si te has matriculado- aunque aquí se dejarán links a algunos de los vídeos de dicho curso que te pueden ayudar a refrescar esa información.

Función de una variable: Decimos que \(f\) es una función de \(x\), y lo escribimos así: \[ y=f(x) \] si a cada valor de \(x\) la regla o función \(f\) asigna un único valor a \(y\). ¿Dónde buscamos los valores de \(x\)? Decimos que en "el dominio’’ de las \(x\). El dominio no es más que un subconjunto de los números reales (¿recuerdas cuáles son los números reales?, ¿Los reconoces todos?} donde la función tiene sentido matemático. Entonces, diremos que \(f\,:\,D\subset\mathbb{R}\rightarrow\mathbb{R}\) si la regla o función \(f\) asigna a cada valor del dominio \(D\) (que, recuerda, es un subconjunto de los números reales) un valor real. Todos los posibles valores \(f(x)\) se denominan el recorrido (o rango, o imagen) de la función. Por ejemplo, \[ f(x)=\frac{1}{x-1} \] Implica que el dominio son todos los valores reales salvo el 1, puesto que la función no está definida , y lo escribimos así \[ D=\left\{ x\in\mathbb{R}|x\neq1\right\} \] El recorrido (o rango, o imagen) son los posibles valores que puede tomar la \(y.\) En este caso, será todo \(\mathbb{R}\) salvo el valor 0.

Puedes usar Geogebra para hacer los gráficos de muchas de las funciones que se presentarán en este curso. Por ejemplo, aquí representamos la función anterior:

Si tenemos \(n\) variables, que es lo nuevo de este curso,la idea será similar: necesitamos una regla que le asigne un único output a un conjunto de \(n\) variables input.

Functión de n variables: Una función de variables se define como \[ y=f(x_{1},x_{2},...,x_{n}) \]

\(y\)	\(x_{1},...,x_{n}\)
endógena	exógenas
explicada	explicativas
dependiente	independientes

Y necesitamos \(n\) variables porque los modelos que estudiará en Ciencias Sociales suelen basarse en un conjunto amplio de factores que explican un hecho. Piensa que, en general, nosotros vamos a pasar de trabajar en \(\mathbb{R}\) a trabajar en \(\mathbb{R}^n\)

[]

Ejercicio 1

¿Cómo se dibujarán los conjuntos (o espacios) : > - \(\mathbb{R}\) > - \(\mathbb{R^2}\) > - \(\mathbb{R^3}\) sabrías dibujar algún otro?

Entonces:

Decimos que \(f\,:\,D\subset\mathbb{R}^{n}\rightarrow\mathbb{R}\) si la regla o función \(f\) asigna a cada valor del dominio \(D\) (que es un subconjunto de los numeros reales \(n\) dimensionales) un valor real. En este texto usaremos, generalmente, funciones de dos variables, es decir:

\[ y=f\left(x_{1},x_{2}\right), \]

donde \(f\,:\,D\subset\mathbb{R}^{2}\rightarrow\mathbb{R}\).

Pero, por supuesto, podríamos tener una función de \(n\) variables

\[ y=f\left(x_{1},x_{2},...,x_{n}\right), \]

donde \(f\,:\,D\subset\mathbb{R}^{n}\rightarrow\mathbb{R}\).

En el siguiente vídeo puedes hacerte con una idea de la relación entre las funciones de una variable y las de varias variables. Además, al final aparece una función de 4 variables que nos encontramos, nada más y nada menos, que en Ponferrada (León)

• ¿Cómo se escribirá un dominio de una función de \(n\) variables?

[]

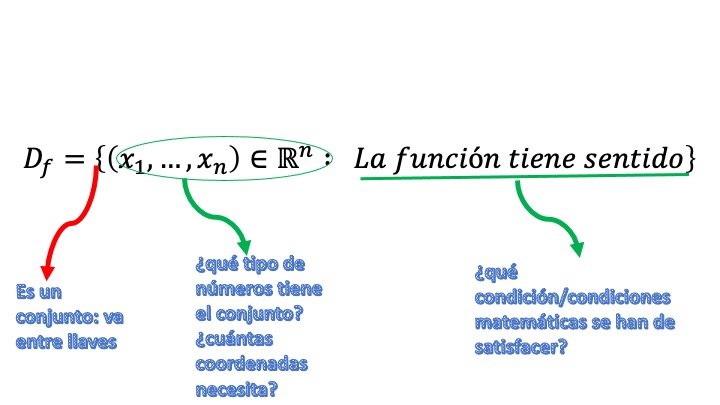Funciones de 2 (y más) variables

En el vídeo anterior aparece una función de dos variables muy famosa, que conoces, y que -a lo mejor- no te habías parado a pensar en que lo era: el índice de masa corporal.

FIG 2. Este es el IMC que te encuentras en la farmacia. En los ejercicios trabajaremos sobre él.

El índice de masa corporal (IMC) es una función que tiene su dominio en dos dimensiones (el par \((p,a)\)) y cuya imagen es un un valor (el valor del índice para cada individuo). Es decir, \(f\::D\subset\mathbb{R}^{2}\rightarrow\mathbb{R}\):

\[\begin{equation} IMC=\frac{p}{a^{2}} \tag{1.1} \end{equation}\]

En este caso, la función se puede escribir de esta forma:

\[ IMC=f(p,a) \]

Si te das cuenta, la variable output o endógena es el IMC, mientras que \(p,a\) son los inputs o exógenas de la función. Pertenecen a valores en \(\mathbb{R}^{2}\). ¿Pero cualquier para en \(\mathbb{R}^{2}\) será válido? Por ejemplo, valdrá decir que el peso de un individuo es -15 kg y su altura -1,75 metros?

¿Cuál será el dominio? En principio, si analizamos la función de una manera "fría’’ sin saber qué es \(p\) ni \(a\), tenemos que pensar qué valores de la función harían que no esté correctamente definida. En este caso, si \(a=0\), el IMC no estará definido, puesto que no podemos dividir por cero. Por lo que el dominio de la función será:

\[ D=\left\{ \left(p,a\right)\in\mathbb{R}^{2}|a\neq0\right\} \]

(que se lee: el dominio de la función es el conjunto de todos los valores reales en dos dimensiones de \(p\) y \(a\) tales que \(a\neq0\))

Sin embargo, este dominio parece no tener sentido. ¿Puede ser el peso de un individuo -8 kilogramos en el planeta Tierra tal y como están las cosas? ¡NO! Por ello, definimos el dominio natural de una función que será aquel que tenga sentido económico, de una manera amplia (por económico también entendemos social, psicológico, biológico, etc…). En nuestro caso, dado que el peso y la altura son siempre valores positivos, el domino natural:

\[ D_{N}=\left\{ \left(p,a\right)\in\mathbb{R}^{2}|p>0,a>0\right\} \]

Por tanto, el dominio, al final, es el subconjunto de los números reales \(n\)-dimensionales (en este caso, \(n\)=2) para los cuales la función tiene sentido. El rango (recorrido o imagen) lo buscaremos en el conjunto: \(\mathbb{R}\)). La imagen es el resultado de aplicarle la expresión de la función al conjunto de \(n\) valores cualesquiera que pertenezcan al dominio.

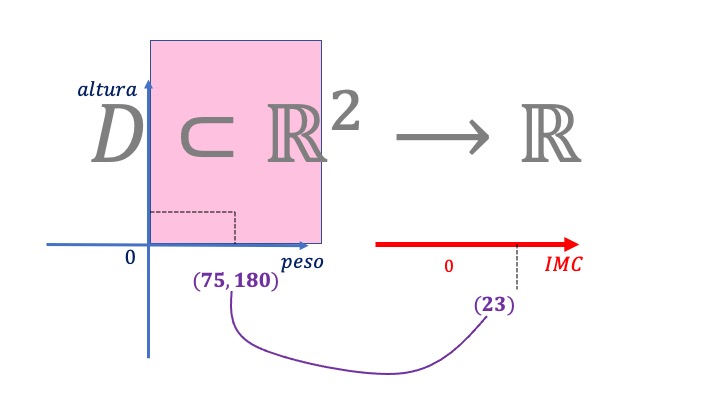
FIG3 Esta es la idea esquemática del IMC. El dominio está en dos dimensiones, mientras que la imagen en una dimensión.

Ejercicio 2

Ahora es el momento de estudiar el dominio de diferentes funciones. Discute y representa su dominio.

• \(f(x,y)=x^{2}+(y-1)^{2}\)
• \(g(x,y)=9x^{2}+(y-1)^{2}\)
• \(h(x,y)=2x^{2}+y\)
• \(j(x,y)=2+y-\sqrt{x}\)
• \(l(x,y)=y+\ln(x+1)\)
• \(m(x,y)=(x-2)y\)
• \(n(x,y)=(x+1)^{2}+y^{2}\)
• \(p(x,y,z)=\sqrt{2x+y-z}\)

Ejercicio del vídeo 1

Escribe el dominio de la función que nos encontramos en el banco de Ponferrada. Para ello, piensa bien las variables explicativas en qué conjunto de números están definidas (naturales, enteros, reales, etc…) y sus valores sensatos. \[ M=C_{0}\frac{\left(1+\frac{i}{m}\right)^{n\times m}\left(\frac{i}{m}\right)}{\left(1+\frac{i}{m}\right)^{n\times m}-1} \]

Ahora, volvamos a la FIG 3. Como ves, cada intersección de un valor del peso y de la altura (lo que se llama par ordenado) proporciona un IMC (usando la fórmula que te damos en la ecuación (1.1). Sin embargo, siempre es útil tener una impresión visual de las funciones con las que trabajamos (lo llevas haciendo en todos tus cursos previos de matemáticas en funciones de una variable). Pensemos sobre esta función cuyo dominio tiene dos variables y su imagen tiene una

• El gráfico ahora tiene tres ejes (de forma general \(x_{1},x_{2},y\)) con el objetivo de pintar la función \(y=f(x_{1},x_{2}).\) Es decir, el gráfico de una función \(\mathbb{R}^{2}\rightarrow\mathbb{R}\) está definido en tres dimensiones: una para cada variable
• El gráfico de la función son los puntos \((x_{1},x_{2},y=f(x_{1},x_{2})\) tales que \(\left(x_{1},x_{2}\right)\) pertencen al dominio \(D\). Esto lo escribimos así: \(G(f)=\left\{ x_{1},x_{2},f(x_{1},x_{2})|\left(x_{1},x_{2}\right)\in D\right\}\)
• Imagina que la función que tenemos es \(f(x_1,x_2)=x_1+x_2-0.2\). Entonces, un punto de la función será \(x_{1}=0.6,x_{2}=0.4\) con \(f(x_{1},x_{2})=0.8.\). En la FIG4 dibujamos ese punto (de los infinitos que dan lugar a la función)
• En la FIG 5, hacemos lo mismo pero ahora yo con la función para calcular el IMC \(Graf(f)=\left\{ p,a,f(p,a)|\left(p,a\right)\in D\right\}\)

FIG4 Así se representa un punto en 3 dimensiones.

FIG5 Así se representa la función IMC.

Sin embargo, dibujar funciones en 3D está muchas veces fuera de nuestro alcance, a no ser que tengamos a mano un ordenador (O Google: si pones en el buscador una función, automáticamente te saca el gráfico. Prueba, por ejemplo, en escribir z=x/y^2 y dar a buscar ¿qué sale? ) Sin embargo, a veces podremos esbozar la pinta del gráfico. Para ello, podemos aprovechar que conocemos la pinta que tienen las funciones elementales y ver que esta función es una ``mezcla’’ de dos fuciones famosas:

\[ f(p,a)=\frac{p}{a^{2}} \]

Para ello, primeramente nos olvidamos de que existe la variable \(a\). ¡Que deje de ser una variable y que sea una constante!. Por ejemplo, digamos que \(C=\frac{1}{a^{2}}.\) Al hacer eso, nos estamos olvidando del eje asociado a la variable altura y estamos representando esta función:

\[ f(p)=Cp \]

Que, como ves, es una ecuación lineal con pendiente \(C\). Por eso las líneas amarillas de la FIG 6 son rectas. Esas rectas quieren decir que ``si nos olvidamos de la variable altura, la función tiene pinta de recta con respecto a la variable peso’’.

FIG6 Si miramos la gráfica del IMC olvidándonos primero la altura y luego el peso.

Por otro lado, si nos olvidamos de la variable \(p\), y decimos que sea una constante, tendremos esta función con respecto a \(a\):

\[ f(a)=\frac{C}{a^{2}} \]

En este caso, tú, que eres un gran conocedor de las funciones elementales, habrás detectado que es una de tipo potencial (y con una relación inversa con el IMC). De ahí, las líneas marcadas en rosa. Y así quedaría esbozada la función.

Ejercicio 3

Dibuja en Geogebra las funciones del Ejercicio 1. Usa Geogebra para imaginarte la forma que tienen si “bloqueas” mentalmente cada uno de los ejes alternativamente

Ejercicio 4

Mira este ejercicio de examen ¿sabrías hacerlo? Mira bien los valores de los ejes y recuerda la ecuación de una recta y de una parábola :)

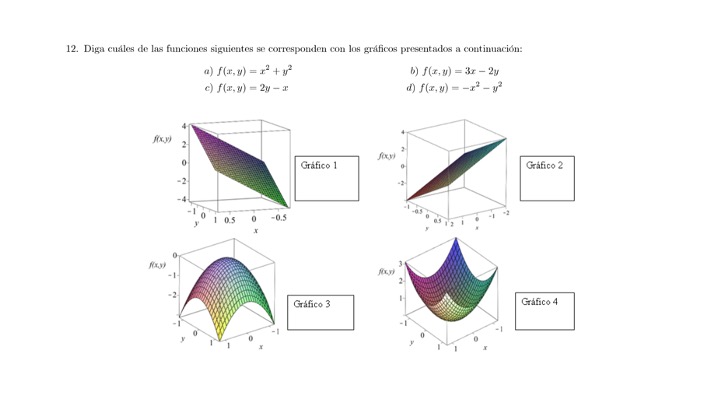
Ejercicio de Examen.

solución Las funciones \(b)\) y \(c)\) son lineales, luego sus gráficas son planos. Las funciones \(a)\) y \(d)\) son cuadráticas y sus gráficas son paraboloides . Puesto que la función en \(a)\) toma siempres valores mayores o iguales que cero, y la de d) valores menores o iguales que cero, se tiene que el gráfico 3 es el \(d)\) y el 4 es el \(a)\). Es inmediato ver que el gráfico 1 es el \(b),\) y el gráfico 2 es el \(c)\). Podemos verlo, por ejemplo, de la siguiente manera: en b) podemos ver que si x aumenta el valor de la función aumenta: esto sucede en el gráfico 1 y no en el 2. Por descarte, entonces, el gráfico 2 corresponde a \(c)\).

Clase 2: Las curvas de nivel

Las curvas de nivel son una nueva herramienta de análisis visual que, aunque no lo creas, llevas mucho tiempo viéndolas hasta por la televisión. Mira el siguiente vídeo para familiarizarte con las curvas de nivel

Como ya vimos, es complicado tratar de dibujar funciones en 3D. Pero tiene que haber alguna manera de que entendamos los aspectos más importantes de una función sin que nos cueste mucho esfuero. ¡La hay! Es una técnica de representación que se utiliza en muchos contextos. Las curvas de nivel. ¿Recuerdas haberlas visto?

FIG1 Todas las noches en tu TV.

Efectivamente, en "El Tiempo’’ siempre las ponen. Esas curvas unen coordenadas del planeta Tierra que tienen la misma presión atmosférica. ¡Espera un momento! vamos a volver a los datos del IMC. Si te fijas, pesar 75 kilos y medir 1.75 te da el mismo IMC que si pesas 80 kilos y mides 1.80, es decir, un IMC de 25. Por lo tanto, podemos buscar esos valores de peso y altura que te dan el mismo IMC

FIG2 Curvas de nivel de la función IMC generadas por ordenador: en el vídeo te explicamos de dónde vienen.

Fíjate que en las curvas de nivel de la FIG2 hemos restringido el dominio a una altura y pesos sensatos. Si ampliáramos la figura, se vería la parábola. Por otro lado, tú puedes decidir qué quieres que sea la ordenada o la abscisa (peso/altura o altura/peso)

Pues ya podemos definir una curva de nivel. Consiste en los puntos del dominio que nos proporcionan un valor, \(C\in\ Im(f)\) (es decir, constante y que pertenezca a la imagen de la función) o lo que es lo mismo

\[ Nivel=\left\{ \left(x_{1},x_{2}\right)\in D\::\:f(x_{1},x_{2})=C\right\} \]

De esta forma, dando diferentes valores a \(C\) podemos esbozar el comportamiento de nuestra función. Por ejemplo, si damos valor \(C=20\), en el ejemplo del IMC, tendremos que

\[ 20=\frac{p}{a^{2}}\Rightarrow p=20a^{2} \]

si te fijas, \(p=20a^{2}\) es una parábola (es como si tuvieras \(y=20x^{2}\)) por eso, las curvas de nivel de la FIG 3 tienen esa pinta de curva (aunque mostramos sólo una parte).

FIG3 Curvas de nivel de la función IMC, remarcando la de nivel 20 y el sentido de crecimiento de la función.

Una vez dibujas la curva de nivel 20, puedes darte cuenta enseguida de que si aumentas el valor de \(C\), en este caso la parábola se irá haciendo cada vez más estrecha (claro, \(p=25a^{2}\) te devuelve un valor mayor para \(p\) por cada \(a\), comparada con \(p=20a^{2})\). De esta forma, ya puedes dibujar unas flechas que indiquen hacia dónde crece la función (es decir, hacia dónde tiene mayor nivel).

Mira, ahora, estas funciones, que están dibujadas en FIG4 y FIG5:
\[ f_{1}\left(x_{1},x_{2}\right)=x_{1}^{2}+x_{2}^{2} \] \[ f_{2}\left(x_{1},x_{2}\right)=Ln\left(x_{1}^{2}+x_{2}^{2}\right) \] Puedes pintarlas primero usando google. Con poner en el buscador z=x^2 + y^2 y z=ln(x^2 + y^2) puedes ver qué pinta tienen. Si mueves el cursor, podrás obtener la visión de la función ``desde arriba’’. Esa vista cenital te permite ver la proyección de la función en 3D sobre el plano. Y, por tanto, puedes deducir la pinta que tendrán las curvas de nivel.

FIG4 Curvas de nivel de la función \(z=x^2+y^2\), obtenids de Google

FIG5 Curvas de nivel de la función \(z=ln(x^2+y^2)\), obtenidqs de Google.

Analíticamente, nota que la imagen de \(f_{1}\) siempre es \(Im(f_{1})\geq0\) ( ya que la función sólo puede tomar valores iguales o mayores que cero), por lo que las curvas de nivel \[ Nivel_{1}=\left\{ \left(x_{1},x_{2}\right)\in D\::\:x_{1}^{2}+x_{2}^{2}=C,C\geq0\right\} \] tendremos, entonces, circunferencias concéntricas de radio \(\sqrt{C}.\) Por otro lado, para las curvas de \(f_{2}\) , la imagen será \(Im(f_{2})=\mathbb{R}\) aunque en el dominio, \(x_{1}^{2}+x_{2}^{2}>0\). Esto hace que \[ Nivel_{2}=\left\{ \left(x_{1},x_{2}\right)\in D\::\:x_{1}^{2}+x_{2}^{2}=e^{C},C\in\mathbb{R}\right\} \] y serán circunferencias concéntricas de radio \(\sqrt{e^{C}}\)

¿Por qué tienen la misma pinta las curvas de nivel? Pues porque \(f_{2}\) es una transformación monótona de \(f_{1}\). Eso implica que el logaritmo neperiano respeta el orden dado (esto es, si \(f_{1}(x_{1},x_{2})>f_{1}(y_{1},y_{2})\), entonces,\(f_{2}(x_{1},x_{2})>f_{2}(y_{1},y_{2})\)).

Ejercicio 1

Dibuja 3 curvas de nivel de cada función e indica con una flecha el sentido hacia el que crece.

• \(f(x,y)=x^{2}+(y-1)^{2}\)
• \(g(x,y)=\frac{1}{9}x^{2}+(y-1)^{2}\)
• \(h(x,y)=2x^{2}+y\)
• \(j(x,y)=2+y-\sqrt{x}\)
• \(l(x,y)=y-\ln(x)\)
• \(l(x,y)=y+\ln(x+1)\)
• \(m(x,y)=(x-2)y\)
• \(n(x,y)=(x+1)^{2}+(y-3)^{2}\)
• \(p(x,y,)=\sqrt{2x+y}\)

Ejercicio 2

Mira este ejercicio de examen ¿sabrías hacerlo? En este caso debes saber perfectamente dibujar rectas, parábolas, e hipérbolas

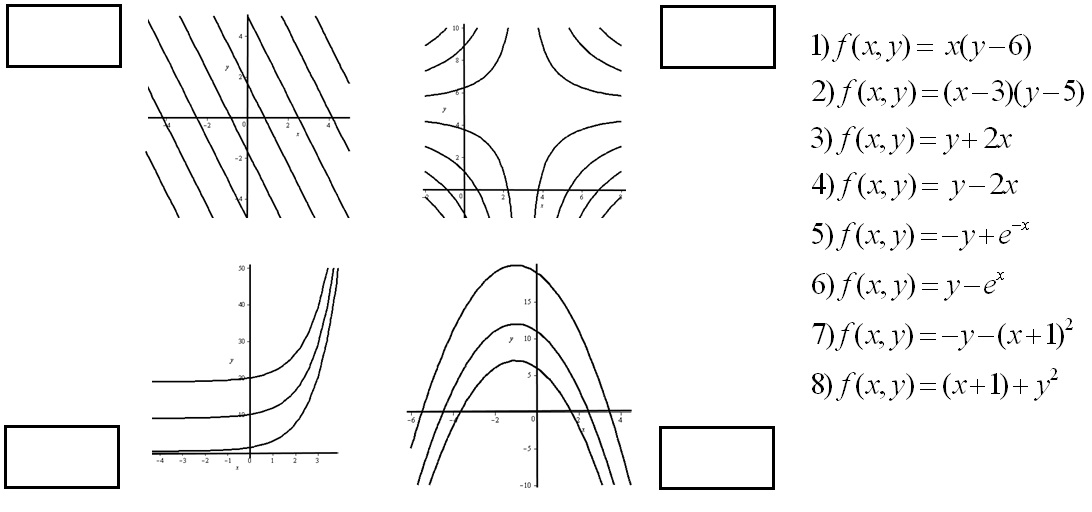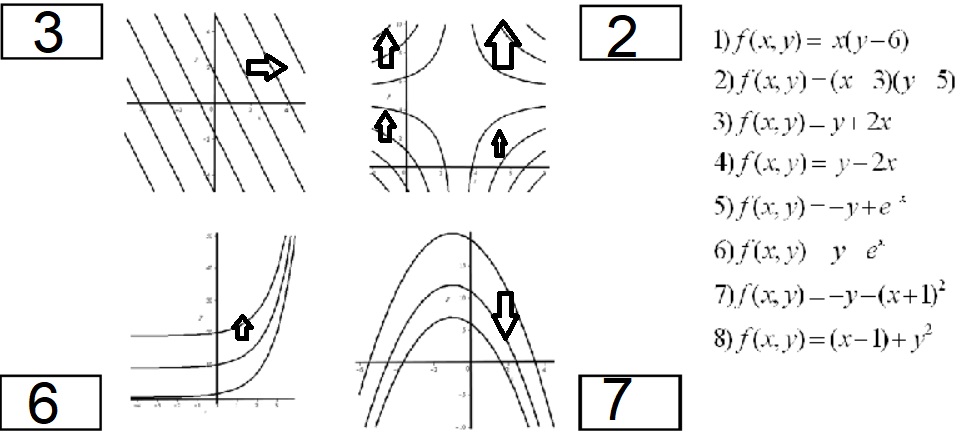
solución Es inmediato ver que 1 y 2 son hipérbolas. Como la que tiene el centro en el (3,5) es la 2, esta corresponde al gráfico de la esquina superior derecha. Las funciones 3 y 4 son lineales, luego sus curvas de nivel son rectas. Como la que tiene pendiente negativa es la 3, esta es la que tiene por curvas de nivel las de la esquina superior izquierda. Las funciones 5 y 6 son exponenciales. La que tiene curvas de nivel crecientes es la 6, que corresponde entonces con las de la parte inferior izquierda. Las funciones 7 y 8 son cuadráticas. Sus curvas de nivel son parábolas. Las que tienen el vértice en puntos con coordenada \(x=-1,\) orientadas en el eje vertical y que miran hacia abajo corresponden a la función 7. En la siguiente figura, ponemos las flechas que indican hacia dónde crece la función

Ejercicio 3

Este ejercicio no es necesario que lo sepas hacer. Sin embargo, si lo consigues, habrás aprendido mucho. Entre otras, cosas: EXCEL. Ánimo, recuerda que para eso estamos los profesores: para que nos pregunten :)

Volvamos a la función del Banco de Ponferrada (vídeo 1): \[ M=C_{0}\frac{\left(1+\frac{i}{m}\right)^{n\times m}\left(\frac{i}{m}\right)}{\left(1+\frac{i}{m}\right)^{n\times m}-1}, \]

como seguro que ya has entendido, de esta función (que a valores del número de años, meses, tipo de interés y capital inicial te dice cuánto tienes que pagar al mes del préstamo) no podemos obtener una gráfica en 3D (puesto que estaría en 5D), ni un conjunto de curvas de nivel (que estarían en 4D). Vamos a suponer que fijamos ciertos valores: \(n=1\), \(m=12\), de tal forma que la función se reescribe así

\[ M=C_{0}\frac{\left(1+\frac{i}{12}\right)^{12}\left(\frac{i}{12}\right)}{\left(1+\frac{i}{12}\right)^{12}-1}, \]

Si sólo podemos pagar una mensualidad de \(M=100\) euros, obtén el conjunto de los tipos de interés y capitales iniciales que nos podemos permitir (inténtalo primero a mano, haz unas cuentas y acude a Excel, que te vendrá como agua de mayo).

Recuerda que los tipos de interés están en tanto por uno (es decir, \(i\in(0,1)\)).

Las curvas de nivel van a ser una herramienta que estaremos utilizando constantemente. Deberías practicar mucho con ellas y entender perfectamente las claves de estas. Los profesores de Matemáticas III te lo agradecerán ;)

Más información Aquí te incluyo tres vídeos que te servirán para repasar gráficas de funciones en una variable

Repaso de la recta y la parábola

Repaso de la exponencial y la logarítmica

Repaso de cónicas

Clase 3: Las derivadas parciales

En esta clase vamos a utilizar una herramienta de cálculo que es básica: la derivada. En la Universidad es muy importante que entiendas el concepto. De hecho, vas a aprender una nueva derivada la derivada parcial que no es compleja de calcular (si sabes derivar funciones de una variable), pero que deberás entender para aplicarla en muchos contextos.

Para que puedas entender el concepto de derivada parcial, primero tendrás que recuperar la idea de derivada de una función. Para recordar la idea de derivada de una función, vamos a definir algunos conceptos que necesitas tener claros. Antes, puedes ver este vídeo que, seguramente, te ayude a recordar algunas ideas.

También puedes acudir al Grupo 0, donde se trabajará con esta idea más a fondo

La ecuación de una recta: es \[ y=ax+b \] donde \(b\) es el valor que toma la \(y\) cuando \(x=0\) (por eso se le llama la ordenada en el origen y \(a\) es la pendiente (que indica cuánto crece la \(y\) cuando la \(x\) aumenta una unidad). Para poder definir la ecuación de una recta, necesitamos dos puntos de esta. Por ejemplo, los puntos \((x_{0},y_{0})=(1,3)\), \((x_{1},y_{1})=(3,7)\) definen una recta (que puedes dibujar inmediatamente). Para calcular \(a\), lo que hacemos es: \(a=\frac{y_{1}-y_{0}}{x_{1}-x_{0}}=\frac{7-3}{3-1}=2\). Otra forma de escribir esto que, en este curso será muy habitual, \(\triangle x=x_{1}-x_{0}=3-1=2\), \(\triangle y=y_{1}-y_{0}=7-3=4.\) Recuerda que \(\triangle\) significa incremento. Por tanto, \[ a=\frac{\triangle y}{\triangle x} \]

La recta, además, puedes escribirla de manera que en su expresión aparezca uno de los puntos (por ejemplo: (\(x_{0},y_{0}\))) de esta forma:

\[ y=y_{0}+a(x-x_{0}) \]

donde, en este caso, \(b=y_{0}-ax_{0}\). Trabajaremos habitualmente con esta expresión (y enseguida verás por qué). En el caso que nos ocupa, \(y=3+2(x-1).\)

La tasa de variación media: Ahora imaginemos que un virus provoca una cantidad de contagios (en miles) que viene dada por la siguiente función \[ y=x^{2} \] donde \(x\) es el tiempo medido en meses. Su gráfica (FIG 1) será la siguiente:

FIG1 Gráfica con una supuesta evolución del virus.

De tal forma que, si estamos en el mes 1, hay mil contagiados y si estamos en el mes 4 hay 16 mil contagiados (como se puede ver en la FIG1). Ahora bien, si queremos resumir la información, podemos hacer lo siguiente: cogemos los dos puntos que conocemos \((x_{0},y_{0})=(1,1)\), \((x_{1},y_{1})=(4,16)\) y podemos hacer la cuenta de cuántos contagiados promedio hay por mes: lo que llamaremos la tasa de variación media: \[ TVM=\frac{16-1}{4-1}=5 \] podemos, entonces, decir que se han contagiado, en promedio 5000 individuos cada mes. Si te das cuenta, esa tasa de variación media se calcula igual que ¡la pendiente de una recta! En realidad, estamos calculando la pendiente de una recta secante a la curva anterior (es decir, \(y=1+5(x-1)\Rightarrow y=-4+5x\)

FIG2 Esta es justo la secante: prueba a hacerlo tú en Geogebra.

Comprueba, ahora, que puedes hacer muchas más secantes. ¡Todas las que quieras!

FIG3 Más secantes a la curva \(y=x^2\).

la particularidad de estas secantes es que vamos cogiendo, cada vez, puntos más cercanos al \((x_{0},y_{0})=(1,1)\). Según nos acercamos a ese punto (que lo hemos elegido como referencia, de la misma manera que podríamos haber elegido otro cualquiera) ¿qué pinta tiene la secante?

La tasa de variación instantánea: Pues lo has averiguado. La secante se acaba convirtiendo en una tangente. De hecho, la pendiente de la tangente podemos encontrarla. Como ves, en la FIG3, para definir la tangente tenemos que acercarnos todo lo posible al punto \((x_{0},y_{0}).\) La forma que tenemos, en Matemáticas, de escribir eso es con un límite. Diremos que la pendiente de la recta tangente a la función en el punto \((x_{0},y_{0})\) es \[ \lim_{\triangle x\rightarrow0}\frac{\triangle y}{\triangle x} \]

El concepto de “instantánea” está heredado de la época de Newton, donde estaban preocupados modelando problemas físicos. Puedes pensar en un coche que está circulando por una carretera. Si se apunta a cada instante la velocidad que lleva, la tasa de variación instantánea consistiría en analizar el cambio en la velocidad en cada momento del tiempo. En Economía es preferible asociar el concepto de derivada a “cambio marginal,” esto es, cómo cambia una función (producción, costes, etc…) ante cambios pequeños en el input (trabajadores, productos, etc…)

Fíjate: usamos el límite para decir que nos movemos muy poquito (un pelín, ligeramente, etc…) de \(x_{0}\). Para no llamar a esto la pendiente de la recta tangente a la función en el punto \((x_{0},y_{0})\), que es muy largo, lo llamamos DERIVADA y lo escribimos como \(y',f',\frac{\mathrm{d}y}{\mathrm{d}x}\) entre otras notaciones, de tal forma que:

\[ f'(x_{0})=\lim_{\triangle x\rightarrow0}\frac{\triangle y}{\triangle x}=\lim_{\triangle x\rightarrow0}\frac{f(x_{0}+\triangle x)-f(x_{0})}{\triangle x} \]

Si te cuesta entender este lenguaje:

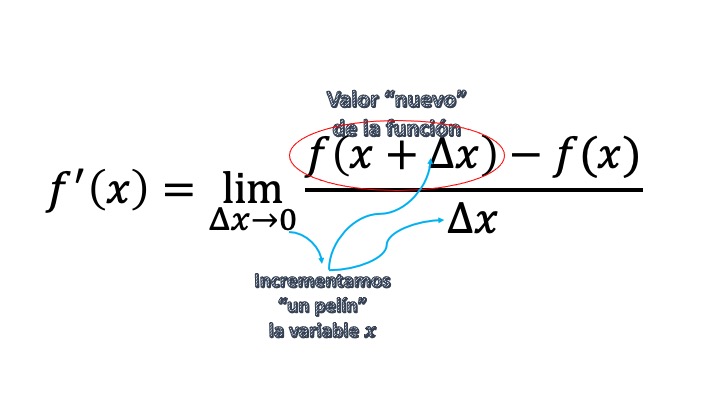
La derivada, algo garabateada

Entonces, vamos a pensar:

Si estoy en el punto (1,1) y la derivada de la función es \(f'(x)=2x\), entonces, la ecuación de la recta tangente a ese punto será:

\[ y=y_{0}+f'(x_{0})(x-x_{0}) \]

En este caso, \(f'(1)=2,\) por lo que \[ y=1+2(x-1)\Rightarrow y=-1+2x \]

Puedes ver en la FIG4 que, efectivamente, es la recta tangente al punto (1,1)

FIG4 Aquí se ve claramente, usando GEOGEBRA que esa recta es la tangente a la curva en el punto deseado.

Si te das cuenta, en el entorno del punto (1,1) la curva y la recta se parecen mucho. No ocurría así con las otras secantes trazadas, ¿verdad?. Vamos a aprovechar que en el entorno del punto (1,1) la recta tangente se “parece” a la función y diremos que será una aproximación de la curva en el entorno de ese punto. Es decir:

\[ \left.f(x)\right|_{x_{0}}\simeq y_{0}+f'(x_{0})(x-x_{0}) \]

y leemos como que la función en el entorno del punto \(x_{0}\) (así es cómo se interpreta \(\left.f(x)\right|_{x_{0}})\) es aproximadamente igual a la recta tangente. Ahora bien, como \(y=f(x),\) podemos reescribir la ecuación anterior como \[ y\simeq y_{0}+f'(x_{0})(x-x_{0}) \] y, si pasamos restando \(y_{0},\) entonces

\[ y-y_{0}\simeq f'(x_{0})(x-x_{0}) \]

Como ya has visto, podemos escribir \(\triangle y=(y-y_{0})\), \(\triangle x=(x-x_{0})\) y, por tanto, tendremos que \[ \triangle y\simeq f'(x_{0})\triangle x \] de tal forma que podemos decir que, si \(\triangle x=1,\) entonces

\[ \triangle y\simeq f'(x_{0}) \]

es decir:

la derivada es el incremento aproximado de la \(y\) si aumentamos \(x\) en una unidad.

Nota, por favor, que se introduce claramente el adjetivo aproximado. A esto, además, se lo conoce como la tasa de variación instantánea para diferenciarla de la anterior, que llamábamos tasa de variación media. El adjetivo instantánea aquí implica incrementar “muy poquito” la \(x\).

Siempre que queramos analizar cómo cambia una variable cuando modificamos otra , el cálculo diferencial es imprescindible. En Economía es estándar añadir el adjetivo “marginal” a la interpretación de una derivada (como ya habrás visto en Teoría Económica). Si \(f(x)\) denota la producción de un bien, su derivada \(f'(x)\)- que representa el incremento de la producción ante un incremento pequeño (marginal) del input- se interpreta directamente como la productividad marginal. Otra de las expresiones que se utiliza para la derivada es el concepto de ritmo de variación puesto que nos permite analizar si el cambio que se produce en \(f(x)\) es o no grande al aumentar \(x\).

Recuerda que has de conocer las derivadas de las funciones elementales.

Entonces, ¿para qué usaremos este resultado? ¿Te has preguntado alguna vez cómo hace el ordenador este cálculo? \[ e^{0.1} \]

quizás creas que el ordenador sabe hacerlo de alguna manera extrañaa que tú no sepas. Pero no: el ordenador aproxima el resultado usando la idea anterior. Como hemos visto, si calculamos la recta tangente a una curva, podemos obtener una ecuación más sencilla que nos permitirá aproximar el valor de una función en el entorno de un punto. Si, en este caso, tomamos que \(f(x)=e^{x}\) y que, ya que \(x=0.1\) está cerquita de \(x=0\), tomaremos que \(x_{0}=0.\) Entonces, como ya sabemos, \(f'(x)=e^{x}\) y, por tanto, \(f(0)=1,f'(0)=1,\) por lo que \[ \left.f(x)\right|_{x_{0}=0}\simeq1+1(x-0), \]

es decir, la función que que nos permite aproximar \(e^{0.1}\) es

\[ \left.f(x)\right|_{x_{0}=0}\simeq1+x, \]

en valores cercanos a cero (como ya sabes). Por lo que \[ e^{x}\simeq1+x \]

entonces, \(e^{0.1}\simeq1+0.1=1.1\) (como podrás comprobar con la calculadora, que hace una aproximación mejor, no está nada mal y ha sido sencillo). Eso sí, sólo si lo usamos en el entorno de \(x=0.\) Más adelante, veremos cómo mejorar la aproximación. Míralo en la FIG5

Puedes revisar esta idea en el siguiente vídeo de Maths & GO

FIG5 La idea de la aproximación lienal para la función exponencial hecho en Geogebra.

Con todas estas ideas, repasadas de las Matemáticas de otros años, es el momento de introducir la derivada parcial. Lo positivo de todo esto es que, si controlas bien lo anterior, no te va a costar nada entender la idea de derivada parcial.

1.3.1 La derivada parcial

Es el momento de hablar de cómo aplicamos esta idea en funciones de dos (o más variables). Introducimos la derivada parcial, que es otro contenido nuevo en este curso. Para entender la idea de la derivada parcial, vamos a empezar a trabjar de manera intuitiva con la función, ya famosa, “paraboloide de revolución” (mira el vídeo 2, si no la recuerdas)

\[ y=x_{1}^{2}+x_{2}^{2} \]

que ya dibujamos en 3D e hicimos sus curvas de nivel en las clases previas. En el gráfico siguiente, la FIG 6, ponemos la función y algunas curvas de nivel

FIG6 Curvas de nivel de la función \(y=x_1^2+x_2^2\)

Como puedes ver, sobre las curvas de nivel hemos puesto una flecha (un vector) que indica que nos movemos una unidad en el eje de las abscisas y 0 unidades en las ordenadas. Es decir, incrementamos la variable \(x_{1}\) en una unidad y no tocamos la variable \(x_{2}.\) De hecho, tenemos que \(f(0,0)=0,\)y \(f(1,0)=1.\) Podemos decir, por ejemplo, que el incremento \(\triangle f=f(1,0)-f(0,0)=1.\) Escrito de otra forma ese incremento: \(f(x_{1}^{0}+\triangle x_{1},x_{2}^{0})-f(x_{1}^{0},x_{2}^{0})\). Fíjate que podríamos hacer cálculos similares a los que hicimos con una sola variable. Podríamos, por tanto, calcular la tasa de variación media de la función, ante el cambio que ha sufrido \(x_{1}.\) De esta forma:

\[ TVM_{x_{1}}=\frac{f(x_{1}^{0}+\triangle x_{1},x_{2}^{0})-f(x_{1}^{0},x_{2}^{0})}{\triangle x_{1}} \]

FIG7 tratamos de analizar qué pasará en la función si incrementamos \(x_1\) “una migaja.”

la cual nos dice el cambio promedio de la función al incrementar \(x_{1}\) y dejando \(x_{2}\) constante (lo que se conoce como ceteris paribus ). Ahora bien, ¿qué pasaría si, de nuevo, hacemos \(x_{1}\) tan pequeño como queramos dejando \(x_{2}\) quieto?

FIG8 tratamos de analizar qué pasará en la función si incrementamos \(x_1\) “una migaja.”

Como vemos, nos encontraremos en una curva de nivel, marcada en azul en la FIG7, que tiene un valor de la función mucho más pequeño que el de antes. De esta manera, podemos calcular, al igual que con una sola variable, la tasa de variación instantánea:

\[ TV{\color{red}I}_{x_{1}}=\lim_{\triangle x_{1}\rightarrow0}\frac{f(x_{1}^{0}+\triangle x_{1},x_{2}^{0})-f(x_{1}^{0},x_{2}^{0})}{\triangle x_{1}} \]

que se va a llamar derivada parcial . Como ves, nos permitirá analizar el impacto que tiene un incremento pequeño de \(x_{1}\), haciendo que \(x_{2}\) no varíe. La derivada parcial tiene su propia notación:

Sea la función \(f\left(x_{1},x_{2},...,x_{n}\right)\), la derivada parcial de la función con respecto a \(x_{i}\) (donde \(i\) es cualqueira de los posibles inputs): \[ \frac{\partial f}{\partial x_{i}} \] o, también, \[ f_{x_{i}}' \]

En el caso de una función con dos inputs, se concreta en

\[ \frac{\partial f}{\partial x_{1}}=\underset{\triangle x_{1}\rightarrow0}{\lim}\frac{f(x_{1}+\triangle x_{1},x_{2})-f(x_{1},x_{2})}{\triangle x_1} \]

\[ \frac{\partial f}{\partial x_{2}}=\underset{\triangle x_{2}\rightarrow0}{\lim}\frac{f(x_{1},x_{2}+\triangle x_{2})-f(x_{1},x_{2})}{\triangle x_2} \]

De ahí que, efectivamente, derivar de manera parcial consista en dejar constantes todas las variables con respecto a la que no se derive y utilizar las reglas de derivación habituales con la variable \(i\)-ésima. Destripamos, un momento, la fórmula de la derivada parcial

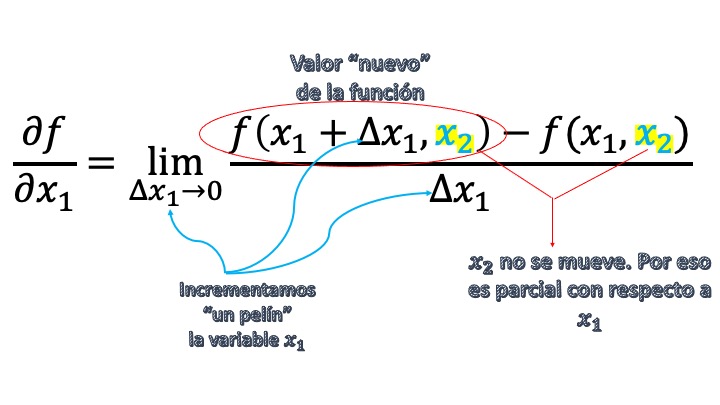
…por si se entiende mejor.

Seguro que entiendes que, en el caso de \(x_{2}\) podríamos realizar el mismo análisis visual pero, en este caso, cambiando la orientación del vector \(\overrightarrow{v}.\)

FIG9 Lo mismo, pero en la dirección del otro eje coordenado.

Las derivadas parciales en la práctica

Para hacer una derivada parcial con respecto a la variable \(i\)-ésima, deberás imaginar que el resto de variables son constantes (números) y usar las normas de derivación habituales. Por ejemplo, si queremos hacer la derivada parcial de la función \(f(x_{1},x_{2})=x_{1}^2+x_{2}^2\) con respecto a \(x_{1}\), entonces

\[ f(x_{1},x_{2})=x_{1}^{2}+{\color{red}x_{\color{red}2}^{2}} \]

deberemos imaginar que \(x_{2}\) es un escalar. Si es así, como la derivada de un escalar es 0, entonces:

\[ \frac{\partial f}{\partial x_{1}}=2x_{1} \]

De la misma manera, si queremos derivar con respecto a \(x_{2}\), la función ahora podemos verla así: \(f(x_{1},x_{2})=\color{red}x_{\color{red}1}^{2}+{x_{2}^{2}}\) y, de nuevo,

\[ \frac{\partial f}{\partial x_{2}}=2x_{2} \]

Ejercicios resueltos:

haz las siguientes derivadas parciales

• \(f(x_{1},x_{2})=x_{1}+6x_{2}^{2}\)

  • \(\frac{\partial f}{\partial x_{1}}=1\)
  • \(\frac{\partial f}{\partial x_{2}}=12x_{2}\)

• \(g(x_{1},x_{2})=\left(x_{1}+6x_{2}^{2}\right)^{2}\) (ten en cuenta la aplicación de la regla de la cadena)

  • \(\frac{\partial g}{\partial x_{1}}=2\left(x_{1}+6x_{2}^{2}\right)\)
  • \(\frac{\partial g}{\partial x_{2}}=24x_{2}\left(x_{1}+6x_{2}^{2}\right)\)

• \(h(x_{1},x_{2})=Ax_{1}^{1/3}x_{2}^{2}\)

  • \(\frac{\partial h}{\partial x_{1}}=\frac{A}{3}x_{1}^{-2/3}x_{2}^{2}\)
  • \(\frac{\partial h}{\partial x_{2}}=2Ax_{1}^{1/3}x_{2}\)

Ejercicio de examen

Aquí tienes un ejercicio de examen que te ayudará a utilizar todos los conceptos que ya sabes

Ejercicio de Examen.

Clase 4: Las derivadas parciales (II)

El objetivo, ahora, es entender la interpretación de una derivada parcial. Para ello, volveremos- de nuevo- a hablar de la relación entre la tasa de variación media y la(s) derivada(s) parciales de una función. Hasta ahora, lo que hemos hecho es aprender las técnicas para obtener derivadas parciales de funciones que son, a su vez, funciones (salvo que derivemos una función lineal). Ahora vamos a ver cómo, evaluándolas en un punto, obtenemos un significado con interpretación económica.

Para seguir entendiendo la idea, veamos el caso del índice de masa corporal, recordemos \(IMC=\frac{p}{a^{2}}\), de tal forma que \(p\) es el peso en kilogramos y \(a\) es la altura en metros del individuo. Ahora vamos a imaginarnos a un individuo que mide 1.65 metros y pesa 70 kilos (por lo que su IMC es 25.71). En el diagrama de las figuras 17 y 18 podemos ver que han redondeado el IMC y que pone 26. La idea de la derivada parcial es la siguiente (FIG10)

• Si no variamos la altura (es decir, nos quedamos en \(a=1.65\)) podemos analizar cómo se modifica el IMC al ir variando el peso. Por ejemplo ¿y si pasamos de pesar 65 kilos a 70?

Vamos a calcular, primeramente, la varaición del IMC, es decir \(\Delta IMC\), para ello:

\[ \Delta IMC=IMC(70,1.65)-IMC(65,1.65)=25.71-23.87=1.84, \]

es decir, un individuo que pasa de \((65,1.65)\) a \((70,1.65)\), incrementa su IMC en 1.84 puntos. Ahora vamos a analizar la variación promedio, es decir, por cada kilo que aumenta, cuánto aumenta su IMC:

\[ \frac{\Delta IMC}{\Delta p}=\frac{IMC(p+\triangle p, a)-IMC(p,a)}{\triangle p}=\frac{1.84}{5}=0.37 \]

es decir, en promedio, por cada kilo que engorda nuestro individuo, su IMC sube 0.37 unidades.

Por otro lado, como vimos, la derivada consiste en calcular la tasa anterior cuando \(\Delta p\rightarrow 0\). Esto, en realidad, es difícil de interpretar. Nuestra imaginación no entiende muy bien qué quiere decir que el incremento del peso se acerque todo lo que queramos a cero, pero que nunca sea cero. Sin embargo, lo traduciremos como “cuánto cambia el IMC si incrementamos ligeramente el peso.”

la derivada parcial será \[ \frac{\partial IMC}{\partial p}=\frac{1}{a^{2}} \] que, evaluada en el punto en el que está el individuo

\[ \frac{\partial IMC}{\partial p}(65,1.65)=\frac{1}{1.65^{2}}=0.36 \]

En este caso, como ves, la derivada parcial se parece bastante a la tasa de variación media. Esto ocurre porque el cambio que ha sufrido la función (en este caso, aumentar 5 kilos) no parece ser muy grande. Esto nos lleva a decir que, si \(\Delta p\) es lo suficientemente pequeño, entonces:

\[ \frac{\Delta IMC}{\Delta p}\approx \frac{\partial IMC}{\partial p}(65,1.65) \]

De esta forma, podemos también decir que

\[ \Delta IMC\approx \frac{\partial IMC}{\partial p}(65,1.65)\Delta p \]

y, por ejemplo, es normal en economía atribuir como “pequeño” un incremento unitario en la variable independiente (trabajadores, precios, capital, etc…). En este caso, parece sensato, y entonces,haciendo \(\Delta p=1\)

\[ \Delta IMC\approx \frac{\partial IMC}{\partial p}(65,1.65)=0.36 \] y, por tanto, diremos que el incremento aproximado del IMC, ante cambios en una unidad del peso,manteniendo la altura constante, cuando el individuo está en el punto \((65,1.65)\) es de 0.36 unidades.

Sin embargo, no siempre es cierto que un incremento unitario en la variable independiente nos asegure que es “pequeño” y que, por tanto, podemos interpretar así la derivada

FIG11 Ahora, la idea de la derivada parcial del IMC con respecto a la estatura, dejando fijo el peso en un valor arbitrario.

Imaginemos un individuo que pesa \(70\) kilos y mide \(1.65\). Su IMC ya sabemos que es \(25.71\). Si fuera capaz de crecer un metro, mediría \(2.65\) y, manteniendo el peso constante, su IMC sería \(9.96\), por lo que

\[ \Delta IMC=IMC(70,2.65)-IMC(70,1.65)=9.96-25.71=-15,75, \]

es decir, el IMC se reduce en 15.75 unidades. Si calculamos la tasa de variación media \[ \frac{\Delta IMC}{\Delta a}=\frac{IMC(p, a+\triangle a)-IMC(p,a)}{\triangle a}=\frac{-15.75}{1}=-15.75, \] como es obvio, por cada metro que crece, el IMC cae -en este caso- 15.75 unidades. Si hacemos la derivada parcial y la evaluamos en el punto

\[ \frac{\partial IMC}{\partial a}=\frac{-2p}{a^{3}}, \] es decir

\[ \frac{\partial IMC}{\partial a}(70,1.65)=-31.16, \]

como ves, la derivada parcial y la tasa de variación media ya no se parecen. La derivada parcial está sobreestimando la verdadera variación. En este caso, si quisiéramos usar la derivada parcial, volveríamos a este resultado:

\[ \Delta IMC\approx \frac{\partial IMC}{\partial a}(70,1.65)\Delta a \]

donde \(\Delta a\) deberá ser mucho más pequeño que la unidad. Por ejemplo, si el individuo creciera cinco centímetros, tendríamos que

\[ \Delta IMC\approx \frac{\partial IMC}{\partial a}(70,1.65)\times 0.05=-31.16\times 0.05=-1.55 \]

es decir, el IMC se reduciría-aproximadamente-en 1.55 unidades si manteniendo el peso constante, el individuo pasa de 1.65 a 1.70. Utilizando la variación real obtendríamos:

\[ \Delta IMC=IMC(70,1.70)-IMC(70,1.65)=24.22-25.71=-1.49 \] que, como ves, ahora sí que se parece a la derivada.

Entonces:

• El incremento de la función (\(\Delta IMC\), en este caso) nos da la variación exacta de la función ante cambios en una de sus variables independientes
• La derivada parcial nos da la variación aproximada de la función, ante cambios “pequeños” en un input dejando el resto constantes.
• En Economía, muchas veces, un cambio pequeño suele ser una unidad, pero no siempre.
• Las derivadas parciales se utilizan, por ejemplo, para analizar cambios marginales en funciones (productividad marginal de los factores, coste marginal, etc…)

Puedes ver este vídeo de Maths & GO que te explica, con ayuda del inefable Homer Simpson, la idea de derivada parcial.

Ejercicio 1

Calcula las derivadas parciales de las siguientes funciones

1: \(f(a,b)=\frac{ae^{2b+1}}{1+3a}+(b+3)\sqrt{a^{2}+\ln b}\)

2: \(f(m,n)=me^{2m-n}\)

3: \(f(p,q)=\ln\left(\frac{p^{2}}{p+q}\right)\)

4: \(f(x,y,z)=xe^{z}\left(\frac{y+x}{z^{2}+1}\right)\)

5: \(f(a,b)=\frac{a}{a+b}+\sin(2a)\)

La elasticidad y las elasiticidades parciales

El concepto de la elasticidad va a ser de los más manejados a lo largo del grado. En muchas disciplinas recurrirán a él (marketing, macroeconomía, microeconomía)….y es el concepto sobre el que más dudáis.

Quizás, este vídeo te ayude a entender mejor la idea: haz click en la imagen

Por tanto, la elasticidad nos ayuda a entender “cambios” (sí, otra vez la idea del principio: cambios, cambios, cambios) porcentuales de la función cuando la variable input también cambia un un tanto por ciento. Por ejemplo, en la función

\[\begin{equation} y=f(x),\tag{1.2} \end{equation}\]

nos interesa analizar el cambio porcentual de la variable \(y\) ante un incremento porcentual de la variable \(x\) y escribamos la aproximación lineal de (1.2)

\[ \triangle y\simeq f'(x)\triangle x \]

vamos ahora a jugar un poco. Haremos cambios en la ecuación, pero para llegar a otra expresión en tantos por ciento para ambas variables. Para ello, dividamos en ambos lados por \(y\)

\[ \frac{\triangle y}{y}\simeq f'(x)\frac{1}{y}\triangle x, \]

ahora dividamos en ambos lados por \(x\)

\[\begin{equation} \frac{\triangle y}{y}\frac{1}{x}\simeq f'(x)\frac{1}{y}\frac{\triangle x}{x},\tag{1.3} \end{equation}\]

como quiero que me quede en la izquierda de la ecuación (1.3) el cambio porcentual en la \(y\), paso la \(x\) a la derecha:

\[ \frac{\triangle y}{y}\simeq f'(x)\frac{x}{y}\frac{\triangle x}{x}, \]

multiplico por 100 en ambos lados

\[ \left(\frac{\triangle y}{y}\right)\times100\simeq f'(x)\frac{x}{y}\left(\frac{\triangle x}{x}\right)\times100, \]

y obtengo

\[\begin{equation} \Delta\%y\simeq{f'(x)\frac{x}{y}}\Delta\%x, \end{equation}\]

donde \(\Delta\%y\) y \(\Delta\%x\) se leen como cambio porcentual de la y y cambio porcentual de la x . Por otro lado, \({f'(x)\frac{x}{y}}\) es la elasticidad. La interpretación, por lo tanto, es clara:

OJO, la elasticidad!

si hacemos que \(\Delta\%x=1\), estamos incrementando la variable \(x\) en un 1%. Entonces, si llamamos \(\epsilon_{y,x}\) a la elasticidad de la variable \(y\) con respecto a la \(x\)

Entonces, \(\epsilon_{y,x}=f'(x)\frac{x}{y}\)

este valor indica el incremento porcentual aproximado de la \(y\) ante cambios en un 1% de la variable \(x\).

Ejemplo

Si la demanda de un bien sigue la función \(y(p)=\frac{2}{p^{2}}\), la elasticidad-precio (\(\epsilon_{y,p}\)) será:

\[ \epsilon_{y,p}=\frac{-4}{p^{3}}\frac{p}{y(p)} \]

Como ves, este resultado es una función. Dependerá del valor del precio actual. De tal forma que si, por ejemplo, en estos momentos, el precio es \(p=1\),la elasticidad será

\[ \epsilon_{y,p}=\frac{-4}{1}\frac{1}{2}=-2 \]

OJO, interpretamos una elasticidad!

si incremento el precio en un 1%, la demanda caerá -aproximadamente- en un 2%. ¡No olvides que la elasticidad es un concepto porcentual! ¡Por favor!

En el caso de que tengamos una función de más de una variable, todo se mantiende muy similar. En este caso, la función sera:

\[ y=f(x_{1},x_{2},...,x_{n}) \]

de tal forma que si quieres analizar el cambio marginal en tantos por ciento de la \(y\) ante cambios en tantos por ciento de cualquiera de las variables \(x_1,...x_n\), manteniendo el resto constante, deberás hacer lo siguiente:

\[ \triangle\%y\simeq\underset{\varepsilon_{y,x_{i}}}{\underbrace{\frac{\partial f}{\partial x_{i}}(x_{1},...,x_{n})\frac{x_{i}}{f(x_{1},...,x_{n})}}}\triangle\%x_{i} \]

donde \(i=1,..,n\). Es decir, como ves, sólo hay que cambiar la derivada por la derivada parcial de cualquiera de las posibles \(x_i\) que componen la función y usar la misma fórmula. Tendremos, entonces, la elasticidad parcial puesto que no hay que olvidarse de que el resto de inputs de la función no los hemos modificado. Por ejemplo, en la función:

\[ y=3x_{1}^{2/3}x_{2}^{-1/2} \]

si queremos obtener la elasticidad parcial de la primera variable cuando \(x_{1}=8\) y \(x_{2}=1,\) haremos lo siguiente

\[ \varepsilon_{y,x_{1}}=\frac{\partial f}{\partial x_{1}}(x_{1},x_{2})\frac{x_{1}}{f(x_{1},x_{2})}=\frac{2}{3}3x_{1}^{-1/3}x_{2}^{-1/2}\frac{x_{1}}{3x_{1}^{2/3}x_{2}^{-1/2}}=2/3 \]

Esto implica que, si incrementamos \(x_{1}\) un 1%, la \(y\) incrementará, aproximadamente, un 0.66%, es decir:

\[ \triangle\%y\simeq2/3. \]

Pregunta

Busca la función Cobb-Douglas, muy famosa en Economía, y analiza la particularidad de sus elasticidades. Descubrirás por qué esta función tiene un “sobrenombre” asociado a sus elasticidades ¿cuál es?

Clase 5: Derivadas parciales segundas, gradiente y Hessiano

De la misma manera que ocurre con las funciones de una variable, las funciones de \(n\) variables también tienen derivadas segundas, terceras, etc… siempre que sea posible seguir derivando.

OJO, interpretamos las derivadas parciales primeras, de manera geométrica, de una función \(f(x,y)\)

Como en el caso de una variable, las derivadas parciales primeras de una función, nos informan sobre si la función es creciente o decreciente respecto a la variable con la que derivamos, manteniendo la(s) otra(s) constante(s).

Ejemplo Sea la función \(f(x,y)=e^{-x}/y^2\) ¿Es la función decreciente con respecto a \(x\) e \(y\) para cualquier \((x,y)\)? En la FIG1, puedes observar la función en el gráfico en 3D (sí, para entender este concepto te vamos a pedir que mires gráficos en 3D)

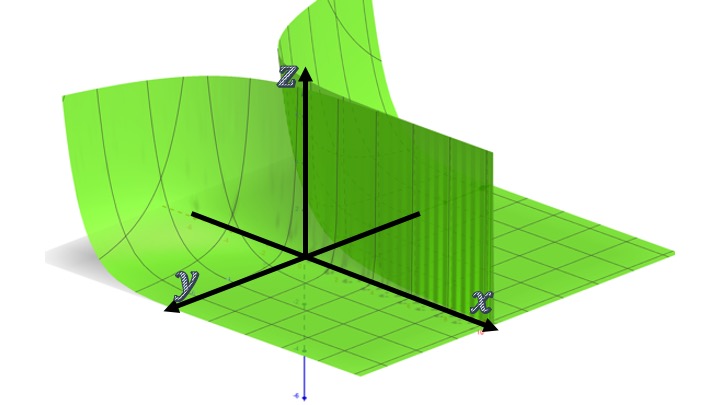
FIG1 La función \(f(x,y)=e^{-x}/y^2\).

Para ello, obtenemos la derivada parcial primera con respecto a \(x\) y a \(y\)

\[ f'_{x}=\frac{-e^{-x}}{y^2}. \] en este caso, para cualquier valor de \((x,y)\) la derivada parcial con respecto a \(x\) es negativa. Eso quiere decir que, si miramos la función, obviando el eje de las \(y\), el perfil de esta será el de una función decreciente. Lo puedes ver en la FIG2, según la \(x\) crece, la \(z\) va disminuyendo.

FIG2 Giramos la función \(f(x,y)=e^{-x}/y^2\) para ver la idea de la derivada parcial con respecto a \(x\).

Por otro lado,

\[ f'_{y}=\frac{-2e^{-x}}{y^3}. \] Como vemos, el numerador es siempre negativo para cualquier \(x\). El denominador es negativo para \(y<0\) y positivo para \(y>0\). Por lo tanto, para cualquier valor de \(x\), la relación entre \(z\) e \(y\) será creciente si \(y<0\) y decreciente si \(y>0\). Puedes ver en la FIG3 cómo, efectivamente, al “olvidarnos” del eje de las “x” y analizar la relación entre \(z\) e \(y\), vemos la función creciente y decreciente.

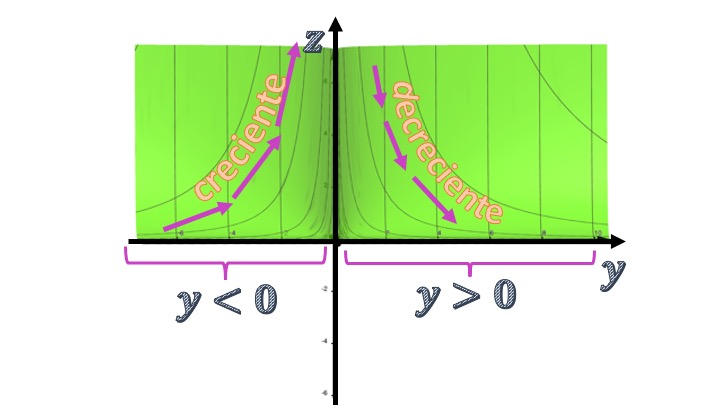
Recuerda que en la función de una variable \(y=f(x)\), podemos definir, en el entorno de un punto \(x_{0}\) los siguientes conceptos:

FIG4 Clasificación de funciones de una variable respecto a su convexidad/concavidad.

Una función convexa se caracteriza por que desde su punto mínimo (es decir, con \(f'(x)=0\)) las pendientes de las rectas tangentes tanto a la derecha como a la izquierda son crecientes. Como las pendientes (es decir, las primeras derivadas \(f'(x)\)) crecen, es lo mismo que decir que las segundas derivadas (que representan el cambio de la pendiente en cada punto) serán mayores que cero (\(f''(x)>0\)). En el caso de las funciones cóncavas ocurrirá lo contrario. Las pendientes (primeras derivadas) de las rectas tangentes que parten tanto a derecha como a izquierda del máximo (derivada nula) serán decrecientes. De nuevo, la derivada segunda es la encargada de modelar el cambio de las pendientes y, por tanto, \(f''(x)>0\).

OJO, las derivadas segundas

Una derivada mide siempre el cambio de una función cuando incrementamos un input. La derivada segunda es la derivada de una derivada. Por lo tanto, la derivada segunda mide el cambio de la derivada al incrementar el input.

De tal manera que, mirando de esta otra forma la FIG4, podemos analizar dos formas de crecer y de decrecer

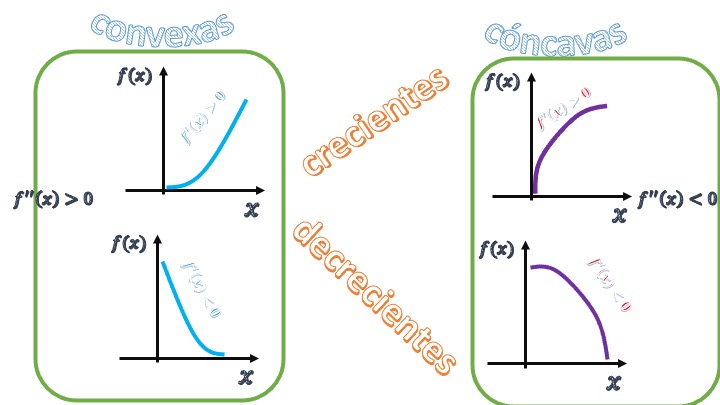
FIG5 Reinterpretamos el crecimiento/decrecimiento.

• Función creciente y convexa: \(f'(x)>0\), \(f''(x)>0\) presenta un crecimiento acelerado. Cuanto mayor es \(x\), mayor es la pendiente de la función. Es equivalente a decir que la función sufre una aceleración (o crecimiento acelerado) según avanza la \(x\).
• Función creciente y cóncava: \(f'(x)>0\) y \(f''(x)<0\) presenta un crecimiento amortiguado. Cuanto mayor es \(x\), menor es la pendiente de la función. Es equivalente a decir que sufre una desaceleración (o crecimiento frenado) según avanza la \(x\)
• Función decreciente y convexa \(f'(x)<0\), \(f''(x)>0\) presenta un decrecimiento desacelerado: cuanto mayor es \(x\) menor es la caída de la pendiente de la función.
• Función decreciente y cóncava \(f'(x)<0\), \(f''(x)<0\) presenta un decrecimiento acelerado: cuanto mayor es \(x\) mayor es la caída de la pendiente de la función.

Por cierto, este análisis se ha hecho con funciones que se comportan muy bien. Con funciones algo más complicadas puede replicarse la idea pensando en que los comportamientos cóncavos y convexos pueden darse en entornos de puntos concretos de la función.

Ahora,aplicando esto en en una función con n variables, tendremos dos tipos de derivadas segundas parciales. Asumamos una función \(z=f(x,y)\)

La derivada segunda con respecto a la misma variable

\[ \frac{\partial^{2}f}{\partial x^{2}}\left(x_{0},y_{0}\right) \]

que representa el cambio de la pendiente de la función con respecto al eje de las \(x\), estando en el punto \((x_{0},y_{0}).\) y dejando fija la variable \(y\). Nos permite analizar la concavidad, convexidad de la función en la dirección de \(x\) (es decir, dejando fijo \(y=y_0\). También se escribe \(f''_{xx}(x_{0},y_{0}).\)

En el ejemplo con el que estamos trabajando, tendremos que

\[ f''_{xx}=\frac{e^{-x}}{y^2}. \]

que será siempre positiva. Esto quiere decir que las pendientes de la función respecto al eje \(x\) serán crecientes y que, por tanto, dejando fijo el eje \(y\), el perfil de la función será convexo:

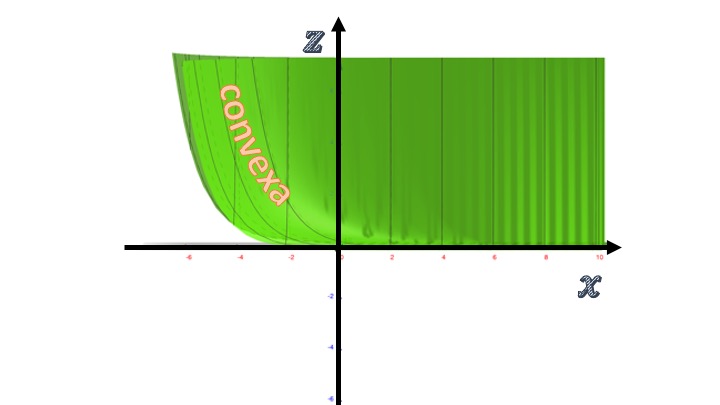
FIG6 Analizamos ahora la convexidad/concavidad de la función respecto al eje de las \(x\).

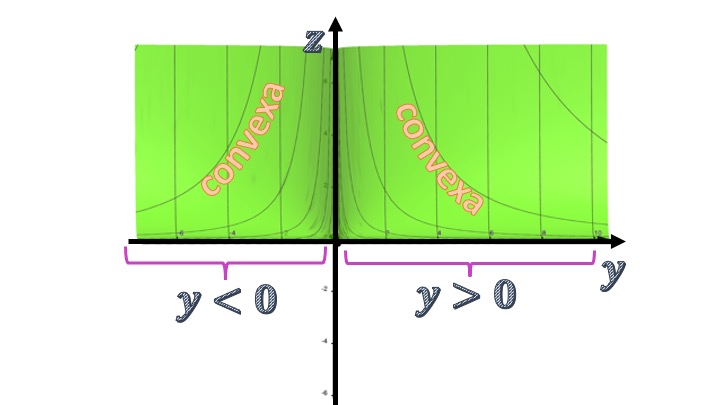
FIG7 Analizamos ahora la convexidad/concavidad de la función respecto al eje de las \(y\).

Por otro lado,

\[ f''_{yy}=\frac{6e^{-x}}{y^4}. \]

de tal forma que, para cualquier valor de \(y\) la segunda derivada es positiva y, por tanto, la función, si nos olvidamos del eje de las \(x\), tendrá un perfil de función convexa al relacionar el eje de las \(y\) con el de \(z\).

Ojo, la función se ha elegido para que sea fácil “olvidar” el eje de las \(x\) y el de las \(y\). En funciones más complicadas no es tan fácil de ver gráficamente, ya que la concavidad /convexidad puede depender del valor de la otra variable

Ojo(2): si te cuesta verlo en el gráfico te recomiendo que trates de hacerte el dibujo en Geogebra y navegar por la función tratando de ver con calma todos los detalles. Si, aún así, no te es posible: RELAX!, los argumentos geométricos sólo intentan ayudar mediante la ilustración de conceptos: pero no es la única manera de aprender

La derivada segunda con respecto a otra variable (derivada segunda cruzada)

\[ \frac{\partial^{2}f}{\partial x\partial y}\left(x_{0},y_{0}\right) \]

, que representa el cambio de la derivada parcial con respecto a la \(x\) , es decir, \(\frac{\partial f}{\partial x}\) al incrementar la variable \(y\), estando en el punto \((x_{0},y_{0}).\) Es una forma de analizar efectos cruzados de una variable sobre los cambios en la función proporcionados por la otra variable. También se escribe como \(f_{xy}(x_{0},y_{0}).\)

Es decir, debemos coger la derivada parcial con respecto a \(x\) y, ahora, derivarla con respecto a \(y\):

\[ f''_{xy}=\frac{2e^{-x}}{y^3}. \]

que nos dice:

• si \(y<0\), la pendiente \(f'_x\) decrecerá con la \(y\) (como se puede ver en el dibujo: diferentes perfiles de pendientes en un punto de \(x\) para distintos valores de \(y\))
• Si \(y>0\), la pendiente \(f'_x\) crecerá con la \(y\) (eso no se aprecia mucho en el gráfico).

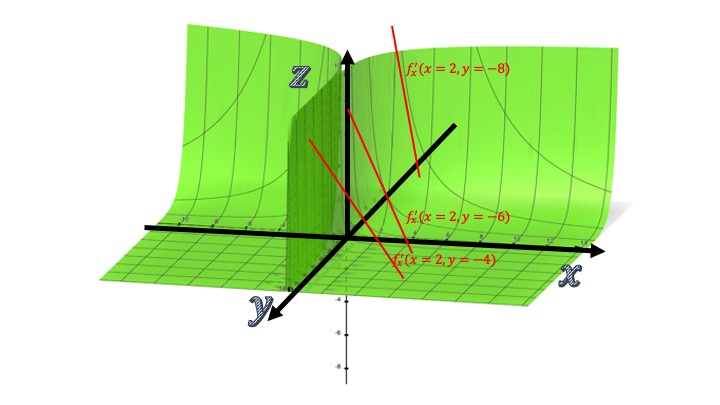
FIG8 Analizamos ahora cómo evoluciona \(f'_x\) para distintos valores de la \(y\)

Por otro lado, tenemos que si derivamos con respecto a \(x\) la derivada que ya teníamos con respecto a \(y\):

\[ f''_{yx}=\frac{2e^{-x}}{y^3}. \]

• si \(y<0\), la pendiente \(f'_y\) decrecerá con la \(x\)
• Si \(y>0\), la pendiente \(f'_y\) crecerá con la \(x\)

Nota importante: ¡ Las derivadas parciales cruzadas son iguales! ¿Esto será siempre así? Enseguida lo vemos.

Ejercicio de Examen

Mira este ejercicio de examen. Se sabe que es falsa ¿por qué?.

La respuesta La primera derivada parcial que nos dan implica que a mayor \(y\), menor \(h\) (manteniendo la \(x\) constante), es decir, \(h_y<0\) implica que \(h\) es decreciente dejando \(x\) constante. Por otro lado, ese decrecimiento es “más negativo” cuanto mayor sea \(x\), debido a que \(h_{yx}<0\). No confundir que algo se haga “más negativo” con “menor.”

El gradiente y la Hessiana

Por otra parte, vamos a necesitar dos instrumentos para almacenar la información que estamos capturando de las funciones. Definiremos el vector gradiente de la función \(f(x_{1},...,x_{n})\) a un vector en \(\mathbb{R}^{n}\) tal que

\[ \nabla f(x_{1},...,x_{n})=\left[\frac{\partial f}{\partial x_{1}},...,\frac{\partial f}{\partial x_{n}}\right] \]

Es decir, se denota \(\nabla\) (no confundir con el signo de incremento). Como ves, por ahora, lo único que necesitamos saber del gradiente es que es un vector… Sí, la palabra temida. VECTOR! Piérdele el miedo. En este vector, introducimos de forma ordenada las derivadas parciales. Por ejemplo, de la función \(f(x,y,z)=x^{2}y+z\), este es el vector gradiente:

\[ \nabla f(x,y,z)=\left[2xy,x^{2},1\right]. \]

Por otro lado, las derivadas parciales segundas, las introduciremos en…una MATRIZ! Sí, recuerda que, por ahora, una matriz es la forma más elegante que conocemos para almacenar la información. Pues bien, definiremos la matrix Hessiana de la funci?n \(f(x_{1},...,x_{n})\) a una matrix de números reales de dimensión \(n\times n\) tal que

\(Hf(x_{1},...,x_{n})=\left[\begin{array}{cccc} \frac{\partial^{2}f}{\partial x_{1}^{2}} & {\frac{\partial^{2}f}{\partial x_{1}\partial x_{2}}} & ... & \frac{\partial^{2}f}{\partial x_{1}\partial x_{n}}\\ \frac{\partial^{2}f}{\partial x_{2}\partial x_{1}} & \frac{\partial^{2}f}{\partial x_{2}^{2}} &...&...\\ ...&...&...&...\\ \frac{\partial^{2}f}{\partial x_{n}\partial x_{1}} &... &... & \frac{\partial^{2}f}{\partial x_{n}^{2}} \end{array}\right]\).

De hecho, gracias al Teorema de Schwartz, , es decir:

El teorema de Schwartz

en funciones con derivadas cruzadas segundas continuas definidas en su dominio de \(\mathbb{R}^{n}\), las segundas derivadas cruzadas serán simétricas:

\[ \frac{\partial^{2}f}{\partial x_{i}\partial x_{j}}=\frac{\partial^{2}f}{\partial x_{j}\partial x_{i}} \] \(i \neq j\)

En este curso utilizaremos funciones que siempre satisfacerán el teorema de Schwartz.

Un punto muy importante es la interpretación económica de las derivadas anteriores Ya sabemos que una derivada parcial indica el cambio marginal aproximado de una función ante cambios unitarios en un input dejando el resto constante. Por ejemplo, si \(z=f(K,L)\) es una función de producción, \(f'_K\) es la productividad marginal del capital (dejando los trabajadores constantes). De esta forma, \(f''_KK\) indicará la variación de la productividad marginal del capital (es decir, como es una derivada segunda, indica cómo varía la derivada primera), mientras que \(f''_K,L\) indica cómo varía la productividad marginal del capital ante cambios en la otra variable (\(L\)).

Ejercicio resuelto 1

Los beneficios de una empresa dependen del precio por unidad de capital \(r\) y del precio por unidad de trabajo \(w\) según una función \(\varPi(r,w)\) de la que sabemos su gradiente \(\nabla\varPi(r,w)=(\frac{-100}{r^{2}},\frac{-100}{w^{2}})\) y su Hessiana \(H\varPi=\left[\begin{array}{cc} \frac{200}{r^{2}} & 0\\ 0 & \frac{200}{w^{2}} \end{array}\right]\).

Razone si es cierto que la variación en el beneficio, al incrementarse r, es en valor absoluto, mayor cuanto mayor es \(r\).

Como vemos, la variación en el beneficio, al aumentar \(r\) será negativa. Es decir, a mayor \(r\), menor beneficio. Esto sería, entonces, lo mismo a analizar la velocidad en el cambio del beneicio. Ahora veamos su aceleración . Si te fijas, al tener derivada primera negativa, estamos en los casos inferiores de la FIG 21. Como, en nuestro caso, la derivada segunda es positiva, estamos en el primero de ellos. Si te das cuenta, la variación en el beneficio, según aumenta \(r\) es cada vez menor. Por lo tanto, es falsa la afirmación.

Ejercicio resuelto 2

Calcule el gradiente de la función \(f(a,b)=\frac{3a+2b^{2}}{\sqrt{2a+1}}\) en el punto \((a_{0},b_{0})=(0,4)\) e interprete el signo de sus componentes.

solución \(f_{a}^{'}(a,b)=\frac{3\sqrt{2a+1}-\frac{2(3a+2b^{2})}{2\sqrt{2a+1}}}{2a+1}\Longrightarrow f_{a}^{'}(0,4)=3-32=-29\)

\(f_{b}^{'}(a,b)=\frac{4b}{\sqrt{2a+1}}\Longrightarrow f_{b}^{'}(0,4)=16\)

El gradiente es el vector \((-29,16).\) Que \(f_{a}^{\prime }(0,4)<0\) quiere decir que si partiendo de \((0,4)\) la variable \(a\) aumenta ligeramente y la variable b permanece fija entonces el valor de la funci?n disminuye. Que \(f_{b}^{\prime }(0,4)>0\) quiere decir que si \(b\) aumenta ligeramente dejando \(% a\) fijo entonces el valor de la función aumenta.

Ejercicio resuelto 3

Sea \(f(x,y)\) una función cuyo gradiente es

\(\nabla f(x,y)=\left( \frac{1+y^{2}}{(x+1)^{2}},\frac{-2y}{x+1}\right)\)

Actualmente, los valores de las variables son \((x_{0},y_{0})\). Se sabe que si se incrementa la variable \(y\) en una unidad, dejando la \(x\) constante, entonces la función \(f\) disminuye aproximadamente en una unidad. Dibuje todos los puntos \((x_{0},y_{0})\) que tienen esa propiedad.

solución Los puntos \((x_{0},y_{0})\) con esa propiedad son aquellos cuya derivada parcial respecto de \(y\) es igual a \(-1,\)

\(\frac{-2y}{x+1}=-1\Longleftrightarrow y=\frac{1}{2}x+\frac{1}{2}\)

que son los puntos de una recta.

Ejercicio resuelto 4

Cuando se producen \(x\) unidades del bien X e \(y\) unidades del bien Y se incurre en unos costes dados por la función

\(C(x,y)=8\sqrt{x^{2}+3y}\).

Actualmente \(x_{0}=2\) e \(y_{0}=4.\)

1. Calcule los costes marginales (derivadas parciales) en cualquier punto y en el punto \((x_{0},y_{0})\) e interpreta su signo.

2. ¿Cuál es aproximadamente la variación en el coste si \(x\) se incrementa en una décima?

3. ¿Cuál es aproximadamente la variación en el coste si \(y\) se incrementa un \(10\%?\)

4. ¿Cuál es aproximadamente la variación porcentual en el coste si \(y\) se incrementa un \(8\%?\)

Soluciones a)

\(C_{x}^{'}(x,y)=\frac{8x}{\sqrt{x^{2}+3y}}\) \(C_{y}^{'}(x,y)=\frac{12}{\sqrt{x^{2}+3y}}\)

Ambas son positivas en cualquier punto, luego si se incrementa la cantidad producida de cualquiera de los dos bienes el coste aumenta.

\(\Delta C\simeq C_{x}^{\prime }(2,4)\Delta x=4\Delta x=0.4\)

\(\Delta C\simeq C_{y}^{\prime }(2,4)\Delta y=3\Delta y=3\frac{10}{100}4=1.2\)

\(\Delta C\simeq C_{y}^{\prime }(2,4)\Delta y=3\frac{8}{100}4\Longrightarrow\) \(\Delta C\%=\frac{\Delta C}{C(2,4)}100\simeq \frac{3\frac{8}{100}4}{32}100=3\)

También podía haberse hecho con la elasticidad de \(C\) respecto de \(y\). Prueba que te sale lo mismo.

Ejercicio resuelto 5

Sea \(f(L,K)\) la cantidad de producto que se obtiene empleando \(L\) unidades de trabajo y \(K\) unidades de capital. Actualmente \(f(120,20)=240\) y \(\nabla f(120,20)=(3,2).\) Diga, justificando tu respuesta, si son ciertas o falsas las siguientes afirmaciones: a) Si se despide a un \(4\%\) de los trabajadores la cantidad de producto se reduce un \(6\%.\) b) Si \(K\) se incrementa un \(2\%\) la cantidad producida es aproximadamente 240.04 unidades.

soluciones

1. La elasticidad respecto de \(L\) viene dada por

\(\varepsilon_{L}(120,20)=\frac{f_{L}^{\prime }(120,20)}{f(120,20)}\cdot 120=\frac{3\cdot 120}{240}=\frac{3}{2}\)

\(\Delta f\% \simeq \varepsilon_{L}(120,20)\cdot\Delta L\%=\frac{3}{2}\cdot(-4)=-6\)

luego la afirmación es cierta.

2. \(\Delta f\simeq f_{K}^{\prime }(120,20)\Delta K=2\frac{2}{100}\cdot 20=\frac{80\%}{100}=0.8\)

y, por tanto, la cantidad producida será aproximadamente \(240.8.\) La afirmación es falsa.

Ejercicio resuelto 6

La demanda \(x\) de mantequilla (en toneladas) es función del precio \(p\) del kilo de mantequilla y del precio \(q\) del kilo de margarina (ambos precios vienen dados en euros). Actualmente, los precios son \(p_{0}\) y \(q_{0}\) y la demanda es \(x_{0}.\) Exprese, utilizando derivadas parciales primeras y/o segundas o elasticidades los siguiente hechos:

1. La demanda de mantequilla aumenta al aumentar el precio de la margarina y este aumento es mayor cuanto menor es el precio de la mantequilla.

2. Si el precio de la mantequilla aumenta un \(2\%\) la demanda de mantequilla disminuye aproximadamente en un \(4\%.\)

3. Si el precio de la mantequilla aumenta en 20 céntimos de euro el kilo, entonces la demanda de mantequilla disminuye aproximadamente en 100 kilogramos.

solución

1. La demanda de mantequilla aumenta al aumentar el precio de la margarina: \(\frac{\partial x}{\partial q}(p_{0},q_{0})>0\) y al decir que ese aumento es mayor cuanto menor es el precio de la mantequilla nos están diciendo que esta parcial es decreciente en \(p,\) es decir, \(x_{qp}^{\prime \prime }(p_{0},q_{0})<0\)

2. Nos está diciendo que la elasticidad parcial de la demanda respecto de la mantequilla es \(-2.\)

3. Hay que tener en cuenta que el precio se mide en euros, no en céntimos de euro. Y que la demanda se mide en toneladas, no en kilos. Un aumento de \(20\) céntimos de euro es un aumento de \(\frac{20}{100}=0.2\). Y \(100\) kilogramos son \(\frac{100}{1000}=0.1\) toneladas. Entonces \(\Delta p=0.2\) y \(\Delta x=-0.1\) luego

\(-0.1=\Delta x\simeq x_{p}^{\prime }(p_{0},q_{0})\Delta p=0.2x_{p}^{\prime}(p_{0},q_{0})\Longrightarrow x_{p}^{\prime }(p_{0},q_{0})=-\frac{1}{2}\)

La cantidad producida de cierto bien viene dada por la función \(y=f(L,K)=4L^{1/2}K^{\beta },\) \(\beta >0.\) Halle, si fuese posible, todos los valores del parámetro $$ de manera que: a) La función \(\partial f/\partial K\) sea decreciente en \(K.\) b) La función \(\partial f/\partial L\) sea creciente en \(K\) y decreciente en \(L.\) c) La función \(\partial f/\partial K\) sea decreciente en \(L\) y la función \(\partial f/\partial L\) sea creciente en \(K.\)

solución

La parcial respecto de \(K\) es \(f_{K}^{\prime }=4\beta L^{1/2}K^{\beta -1}\)

1. Esta parcial es decreciente en \(K\) si al derivarla respecto de \(K\) la derivada es negativa

\(f_{KK}^{\prime \prime }=4\beta (\beta -1)L^{1/2}K^{\beta -2}\) que es negativa si \(0<\beta <1.\)

2. Para que \(\partial f/\partial L\) sea creciente en \(K\) debe cumplirse \(f_{LK}^{\prime \prime }>0\) y para que sea decreciente en \(L\) debe cumplirse \(f_{LL}^{\prime \prime }<0\) . Puesto que \(f_{L}^{\prime }=2L^{-1/2}K^{\beta }\) se tiene

\(f_{LK}^{\prime \prime }=2\beta L^{-1/2}K^{\beta -1}\) \(f_{LL}^{\prime \prime }=-L^{-3/2}K^{\beta }<0\)

luego \(\beta >0.\)

3. Debería cumplirse \(f_{KL}^{\prime \prime }<0\) y \(f_{LK}^{\prime\prime}>0\) lo que es imposible pues al ser la función \(C^{2}\) el teorema de Schwarz asegura que las derivadas parciales cruzadas deben ser iguales.