TEMA 6: Cálculo Matricial
Clase 1: Introducción a las matrices
Las matrices conforman uno de los instrumentos más inteligentes creados por los humanos para guardar información. Una matriz, por ejemplo, es la base de datos de Amazon. Amazon, para poder predecir qué producto ofrecerte, estudia y maneja esas matrices con métodos que involucrarán álegbra matricial, que es lo que veremos aquí.
FIG1. Una base de datos es una matriz
En definitiva, si ya sabías del bachillerato que una matriz es una tabla de valores ordenadas por filas y columnas, este curso tienes que ser consciente de que casi cualquier dato sobre nosotros se alamacena en una matriz que, a su vez, da lugar a una base de datos y que, con métodos estadísticos basados en el cálculo matricial, se obtienen patrones, aprendizajes y predicciones sobre estos. ¡Con el cálculo matricial se puede dominar el mundo!
FIG2. Espero que hayas visto Matrix, un clásico
Una matriz real está formada por números reales en \(m\) filas y en \(n\) columnas. Forman el conjunto \(\mathcal{M_{\mathit{m\times n}}}\) (es decir, el conjunto de las matrices de dimensión \(m\)-filas, \(n\)-columnas rellena con números reales). Una matriz de 4 filas y 3 columnas pertenece al conjunto \(\mathcal{M_{\mathit{4\times3}}}\). Los elementos de la matriz se suelen notar con \(a_{ij}\) donde \(i=1,...,m\) \(j=1,...,n.\) También podrás encontrarlo como \(\left[\mathbf{A}\right]_{ij}=a_{ij}\). Las matrices se suelen notar con letras mayúsculas en negrita. Por ejemplo, la matriz \(\mathbf{A}\in M_{\mathit{m\times n}}\) se escribe
\[ \mathbf{A=\left(\mathit{\begin{array}{cccc} a_{11} & a_{12} & { ...} & a_{1n}\\ a_{21} & a_{22} & { {...}} & a_{2n}\\ { ...} & { ...} & { \ddots} & { ...}\\ a_{m1} & a_{m2} & { ...} & { a_{mn}} \end{array}}\right)} \]
donde, además, si es cuadrada el número de filas será igual al número de columnas (es decir, \(m=n)\), y la matriz contará con un conjunto de elementos (los \(a_{ii}\), por ejemplo, \((a_{11},a_{22},...)\) que conforman la diagonal principal.
\[ \mathbf{A=\left(\mathit{\begin{array}{cccc} {\mathit{a_{11}}} & a_{12} & ... & a_{1n}\\ a_{21} & {a_{22}} & {...} & a_{2n}\\ ... & ... & \ddots & ...\\ a_{n1} & a_{n2} & ... & {a_{nn}} \end{array}}\right)} \]
A menudo, aparecerá también la matriz traspuesta: consiste en cambiar las filas por las columnas (es decir, el elemento \(a_{ij}\) pasa a convertirse en el elemento \(a_{ji}\)) y se denota como
\[ \mathbf{A^{\mathit{t}}}, \]
de tal forma que \(\mathbf{A}^{t}\in M_{\mathit{n\times m}}\) y, por tanto \[ \mathbf{A^{\mathit{t}}}=\left(\begin{array}{cccc} a_{11} & a_{21} & ... & a_{m1}\\ a_{12} & a_{22} & ... & a_{m2}\\ ... & ... & \ddots & ...\\ a_{1n} & a_{2n} & ... & a_{mn} \end{array}\right). \]
Ejemplo
Si \(\mathbf{A}=\left(\begin{array}{ccc} 2 & 3 & 4\\ 1 & 5 & 1 \end{array}\right)\), entonces, \[ \mathbf{A^{\mathit{t}}}=\left(\begin{array}{cc} 2 & 1\\ 3 & 5\\ 4 & 1 \end{array}\right) \]
Es importante remarcar que es fácil ver que podemos pensar que las matrices, en realidad, están compuestas por vectores fila o vectores columna. Nosotros, como hicimos en el tema anterior, usaremos la convención de que los vectores son columnas, de tal forma que un vector \(\overrightarrow{a}\in\mathcal{M}_{m\times1}\), quiere decir que
\[ \overrightarrow{a}=\left[\begin{array}{c} a_{1}\\ a_{2}\\ ...\\ a_{m} \end{array}\right] \]
por otro lado, el vector \(\overrightarrow{a}^{t}\in\mathcal{M}_{1\times m}\) será el anterior vector pero como una fila, es decir \[ \overrightarrow{a}^{t}=\left[\begin{array}{cccc} a_{1} & a_{2} & ... & a_{m}\end{array}\right] \]
Presta atención
De esta forma, para querer decir que nos centramos en una columna de una matriz, ponemos \(\overrightarrow{a}_{\bullet j}\), es decir, \(\overrightarrow{a}_{\bullet1}\) querrá decir: trabajamos con el vector que da lugar a la primera columna de la matriz \(\mathbf{A}\). De otro modo, si queremos verlo por filas, podemos escribir el vector \(\overrightarrow{a}_{i\bullet}\) , donde, escribiendo \(\overrightarrow{a}_{1\bullet}\) nos estaríamos refiriendo al vector que da lugar la fila primera de la matriz \(\mathbf{A}\).
Por lo tanto, si una matriz \(\mathbf{A}\) de dimensión \(m\times n\) la queremos ver como si estuviera compuesta de vectores columna, tendríamos;
\[ \mathbf{A}=\left[\begin{array}{cccc} col_{1} & col_{2} & ... & col_{n}\end{array}\right]=\left[\begin{array}{cccc} \overrightarrow{a}_{\bullet1} & \overrightarrow{a}_{\bullet2} & ... & \overrightarrow{a}_{\bullet n}\end{array}\right] \]
mientras que la misma matriz podríamos verla escrita por vectores filas como
\[ \mathbf{A}=\left[\begin{array}{c} fil_{1}\\ fil_{2}\\ ...\\ fil_{m} \end{array}\right]=\left[\begin{array}{c} \overrightarrow{a}_{1\bullet}\\ \overrightarrow{a}_{2\bullet}\\ ...\\ \overrightarrow{a}_{m\bullet} \end{array}\right] \]
Ejemplo
Si \(\mathbf{A}=\left(\begin{array}{ccc} 2 & 3 & 4\\ 1 & 5 & 1 \end{array}\right)\),
\[ \mathbf{A}=\left(\left[\begin{array}{c} 2\\ 1 \end{array}\right]\left[\begin{array}{c} 3\\ 5 \end{array}\right]\left[\begin{array}{c} 4\\ 1 \end{array}\right]\right), \]
Entonces, \(\overrightarrow{a}_{\bullet1}=\left[\begin{array}{c} 2\\ 1 \end{array}\right]\), o, \(\overrightarrow{a}_{\bullet3}=\left[\begin{array}{c} 4\\ 1 \end{array}\right]\).
Del mismo modo,
\[ \mathbf{A}=\left(\begin{array}{c} \left[\begin{array}{ccc} 2 & 3 & 4\end{array}\right]\\ \left[\begin{array}{ccc} 1 & 5 & 1\end{array}\right] \end{array}\right) \]
\(\overrightarrow{a}_{1\bullet}=\left[\begin{array}{ccc} 2 & 3 & 4\end{array}\right]\)
Hay diferentes tipos de matrices de interés.
- Matriz cuadrada: si \(m=n\)
por ejemplo: \(\left[\begin{array}{ccc} 1 & 2 & 3\\ 2 & 4 & 6\\ 2 & -8 & 7 \end{array}\right]\)
- matriz diagonal: matriz cuadrada donde todos los elementos son cero salvo los de la diagonal principal
por ejemplo \(\left[\begin{array}{ccc} 1 & 0 & 0\\ 0 & 4 & 0\\ 0 & 0 & 7 \end{array}\right]\);
Ojo si estos elementos son la unidad, esta matriz diagonal se conoce como la matriz identidad (generalmente se nota como \(\mathbf{I}_{m}\):
\(\left[\begin{array}{ccc} 1 & 0 & 0\\ 0 & 1 & 0\\ 0 & 0 & 1 \end{array}\right]\).
- Matriz triangular (superiores e inferiores)
\(\left[\begin{array}{ccc} 1 & 3 & 2\\ 0 & 4 & 1\\ 0 & 0 & 7 \end{array}\right]\),\(\left[\begin{array}{ccc} 1 & 0 & 0\\ 3 & 4 & 0\\ 2 & 1 & 7 \end{array}\right]\)
Respecto a las operaciones con matrices, al igual que en las operaciones que definen un espacio vectorial, tenemos
- Suma de matrices
Para que se puedan sumar matrices tienen que tener la misma dimensión. Definimos la suma como:
\[ \mathbf{A}+\mathbf{B}=\mathbf{C} \]
donde \(\left[\mathbf{C}\right]_{ij}=\left[a_{ij}+b_{ij}\right]\):
para ello, ambas matrices tienen que tener la misma dimensión. Si no, la suma no está correctamente definida. Entonces, no es difícil probar que las operaciones de adición tienen las mismas propiedades que en los números reales
\(\mathbf{A}+\mathbf{B}=\mathbf{B+A}\)
\(\mathbf{A}+\left(\mathbf{B}+\mathbf{D}\right)=\mathbf{\left(\mathbf{A}+\mathbf{B}\right)+\mathbf{D}}\)
\(\mathbf{A}+\mathbf{0}=\mathbf{A}\)
\(\mathbf{A}+(-\mathbf{A})=\mathbf{\mathbf{0}}\)
- producto por un escalar \(\lambda\)
Respecto al producto por escalares, el cual se define como:
\[ \mathbf{\lambda A}=\lambda\left[\mathbf{A}\right]_{ij} \]
tenemos como propiedades
\(\left(\lambda+\mu\right)\mathbf{A}=\lambda\mathbf{A}+\mu\mathbf{A}\)
\(\lambda\left(\mathbf{B}+\mathbf{D}\right)=\lambda\boldsymbol{\mathbf{B}}+\lambda\mathbf{D}\)
\(\left(\lambda\mu\right)\mathbf{A=\lambda\left(\mu A\right)}\)
El conjunto de matrices \(\mathcal{M_{\mathit{m\times n}}}\) tiene estructura de espacio vectorial, puesto que satisface las propiedades requeridas
- Producto de matrices
Podemos entender el producto de matrices como un conjunto ordenado de productos escalares de vectores. Para que el producto que vamos a exponer de matrices tenga sentido, debe ocurrir que:
- El número de columnas de la primera matriz coincida con el número de filas de la segunda
- La dimensión final será número de filas de la primera \(\times\) número de columnas de la segunda
Es decir, tenemos que
\[ \underset{\color{green}m\times{\color{red}n}}{\mathbf{A}}\mathbf{\underset{\mathit{{\color{red}n}\times \color{blue}r}}{B}=\underset{\mathit{{ \color{green}m}\times \color{blue}r}}{C}} \]
y, entonces, debemos realizar los productos escalares “fila por columna”
\[ \left({\color{blue}{ { \mathit{\begin{array}{cccc} a_{11} & a_{12} & ... & a_{1n}\\ {\color{red}a_{21}} & {\color{red}a_{22}} & {\color{red}{\color{magenta}...}} & {\color{red}a_{2n}}\\ ... & ... & \ddots & ...\\ a_{m1} & a_{m2} & ... & a_{mn} \end{array}}}}}\right)\left(\begin{array}{ccc} {\color{red}b_{11}} & ... & b_{1r}\\ {\color{red}b_{21}} & ... & b_{2r}\\ {\color{red}...} & \ddots & ...\\ {\color{red}b_{n1}} & ... & b_{nr} \end{array}\right) \]
Por ejemplo, en el caso que marcamos en rojo, el elemento
\[ c_{21}=\left[a_{21},a_{22},...a_{2n}\right]\left[\begin{array}{c} b_{11}\\ b_{21}\\ ...\\ b_{n1} \end{array}\right]=\overrightarrow{a}_{2\bullet}\cdot\overrightarrow{b}_{\bullet1} \]
Importante
Veamos cómo funciona el producto de matrices como combinaciones lineales de las filas y columnas. Sea \(\mathrm{A}\in\mathcal{M}_{3\times3}\)y \(\mathrm{B}\in\mathcal{M}_{3\times2}\), su producto se puede escribir como
\[ \left[\begin{array}{ccc} a_{11} & a_{12} & a_{13}\\ a_{21} & a_{22} & a_{23}\\ a_{31} & a_{32} & a_{33} \end{array}\right]\left[\begin{array}{cc} b_{11} & b_{12}\\ b_{21} & b_{22}\\ b_{31} & b_{32} \end{array}\right]= \] \[ \left[\begin{array}{cc} a_{11}b_{11}+a_{12}b_{21}+a_{13}b_{31} & a_{11}b_{12}+a_{12}b_{22}+a_{13}b_{32}\\ a_{21}b_{11}+a_{22}b_{21}+a_{23}b_{31} & a_{21}b_{12}+a_{22}b_{22}+a_{23}b_{32}\\ a_{31}b_{11}+a_{32}b_{21}+a_{33}b_{31} & a_{31}b_{32}+a_{12}b_{22}+a_{33}b_{32} \end{array}\right]=\left[\begin{array}{cc} \overrightarrow{a}_{1\bullet}\cdot\overrightarrow{b}_{\bullet1} & \overrightarrow{a}_{1\bullet}\cdot\overrightarrow{b}_{\bullet2}\\ \overrightarrow{a}_{2\bullet}\cdot\overrightarrow{b}_{\bullet1} & \overrightarrow{a}_{2\bullet}\cdot\overrightarrow{b}_{\bullet2}\\ \overrightarrow{a}_{3\bullet}\cdot\overrightarrow{b}_{\bullet1} & \overrightarrow{a}_{3\bullet}\cdot\overrightarrow{b}_{\bullet2} \end{array}\right] \]
Entonces,
¿Cómo son las filas del resultado de \(AB?\)? ¿Cómo son las columnas? responde respecto a combinaciones lineales de filas/columnas de las matrices \(A,B\):
- Las columnas de \(AB\) son una combinación lineal de las columnas de \(A\). Veamos, la primera columna de \(AB\):
\(\left[\begin{array}{ccc} a_{11} & a_{12} & a_{13}\\ a_{21} & a_{22} & a_{23}\\ a_{31} & a_{32} & a_{33} \end{array}\right]\left[\begin{array}{c} b_{11}\\ b_{21}\\ b_{31} \end{array}\right]=\left[\begin{array}{c} a_{11}b_{11}+a_{12}b_{21}+a_{13}b_{31}\\ a_{21}b_{11}+a_{22}b_{21}+a_{23}b_{31}\\ a_{31}b_{11}+a_{32}b_{21}+a_{33}b_{31} \end{array}\right]=b_{11}\left[\begin{array}{c} a_{11}\\ a_{21}\\ a_{31} \end{array}\right]+b_{21}\left[\begin{array}{c} a_{12}\\ a_{22}\\ a_{32} \end{array}\right]+b_{31}\left[\begin{array}{c} a_{13}\\ a_{23}\\ a_{33} \end{array}\right]\)
como ves, es una combinación de las columnas de la matriz \(A\) con los “pesos” \(b_{11},b_{21},b_{31}\).
Por otro lado, \(\left[\begin{array}{ccc} a_{11} & a_{12} & a_{13}\\ a_{21} & a_{22} & a_{23}\\ a_{31} & a_{32} & a_{33} \end{array}\right]\left[\begin{array}{c} b_{12}\\ b_{22}\\ b_{32} \end{array}\right]=\left[\begin{array}{c} a_{11}b_{12}+a_{12}b_{22}+a_{13}b_{32}\\ a_{21}b_{12}+a_{22}b_{22}+a_{23}b_{32}\\ a_{31}b_{32}+a_{12}b_{22}+a_{33}b_{32} \end{array}\right]=b_{12}\left[\begin{array}{c} a_{11}\\ a_{21}\\ a_{31} \end{array}\right]+b_{22}\left[\begin{array}{c} a_{12}\\ a_{22}\\ a_{32} \end{array}\right]+b_{32}\left[\begin{array}{c} a_{13}\\ a_{23}\\ a_{33} \end{array}\right]\)
es decir
\[ \left[\begin{array}{ccc} a_{11} & a_{12} & a_{13}\\ a_{21} & a_{22} & a_{23}\\ a_{31} & a_{32} & a_{33} \end{array}\right]\left[\begin{array}{cc} b_{11} & b_{12}\\ b_{21} & b_{22}\\ b_{31} & b_{32} \end{array}\right]=\] \[\left[{b_{11}\left[\begin{array}{c} a_{11}\\ a_{21}\\ a_{31} \end{array}\right]+b_{21}\left[\begin{array}{c} a_{12}\\ a_{22}\\ a_{32} \end{array}\right]+b_{31}\left[\begin{array}{c} a_{13}\\ a_{23}\\ a_{33} \end{array}\right]},{\color{blue}{\color{blue}{b_{12}\left[\begin{array}{c} a_{11}\\ a_{21}\\ a_{31} \end{array}\right]+b_{22}\left[\begin{array}{c} a_{12}\\ a_{22}\\ a_{32} \end{array}\right]+b_{32}\left[\begin{array}{c} a_{13}\\ a_{23}\\ a_{33} \end{array}\right]}}}\right] \]
- Las filas de \(AB\) son una combinación lineal de las filas de \(B\):
\[\left[\begin{array}{ccc} a_{11} & a_{12} & a_{13}\\ \\ \\ \end{array}\right]\left[\begin{array}{cc} b_{11} & b_{12}\\ b_{21} & b_{22}\\ b_{31} & b_{32} \end{array}\right]=\] \[\left[\begin{array}{cc} {\color{red}a_{11}b_{11}+a_{12}b_{21}+a_{13}b_{31}} & {\color{blue}a_{11}b_{12}+a_{12}b_{22}+a_{13}b_{32}}\\ \\ \\ \end{array}\right]=\] \[\left[\begin{array}{c} a_{11}\left[\begin{array}{cc} b_{11} & b_{12}\end{array}\right]+a_{12}\left[\begin{array}{cc} b_{21} & b_{22}\end{array}\right]+a_{13}\left[\begin{array}{cc} b_{31} & b_{32}\end{array}\right]\\ \\ \\ \end{array}\right]\]
Mostremos estas conclusiones con un ejemplo sencillo
\(A=\left[\begin{array}{cc} 2 & 1\\ 3 & 0 \end{array}\right],B=\left[\begin{array}{cc} 1 & 0\\ 2 & 1 \end{array}\right]\)
- las columnas de \(AB\) son combinación lineal de las columnas de \(A\)
\[ AB=\left[{1}{\left[\begin{array}{c} 2\\ 3 \end{array}\right]}+{2}{\left[\begin{array}{c} 1\\ 0 \end{array}\right]},{0}{\left[\begin{array}{c} 2\\ 3 \end{array}\right]}+{1}{\left[\begin{array}{c} 1\\ 0 \end{array}\right]}\right]=\left[\begin{array}{cc} 4 & 1\\ 3 & 0 \end{array}\right] \]
- las filas de \(AB\) son combinación lineal de las filas de \(B\)
\[ AB=\left[\begin{array}{c} {2}{\left[\begin{array}{cc} 1 & 0\end{array}\right]}+{1}{\left[\begin{array}{cc} 2 & 1\end{array}\right]}\\ {3}{\left[\begin{array}{cc} 1 & 0\end{array}\right]}+{0}{\left[\begin{array}{cc} 2 & 1\end{array}\right]} \end{array}\right]=\left[\begin{array}{cc} 4 & 1\\ 3 & 0 \end{array}\right] \]
Ojo, esto es complicado. ¡ Hay que dedicarle un tiempo hasta entenderlo y manejarlo!
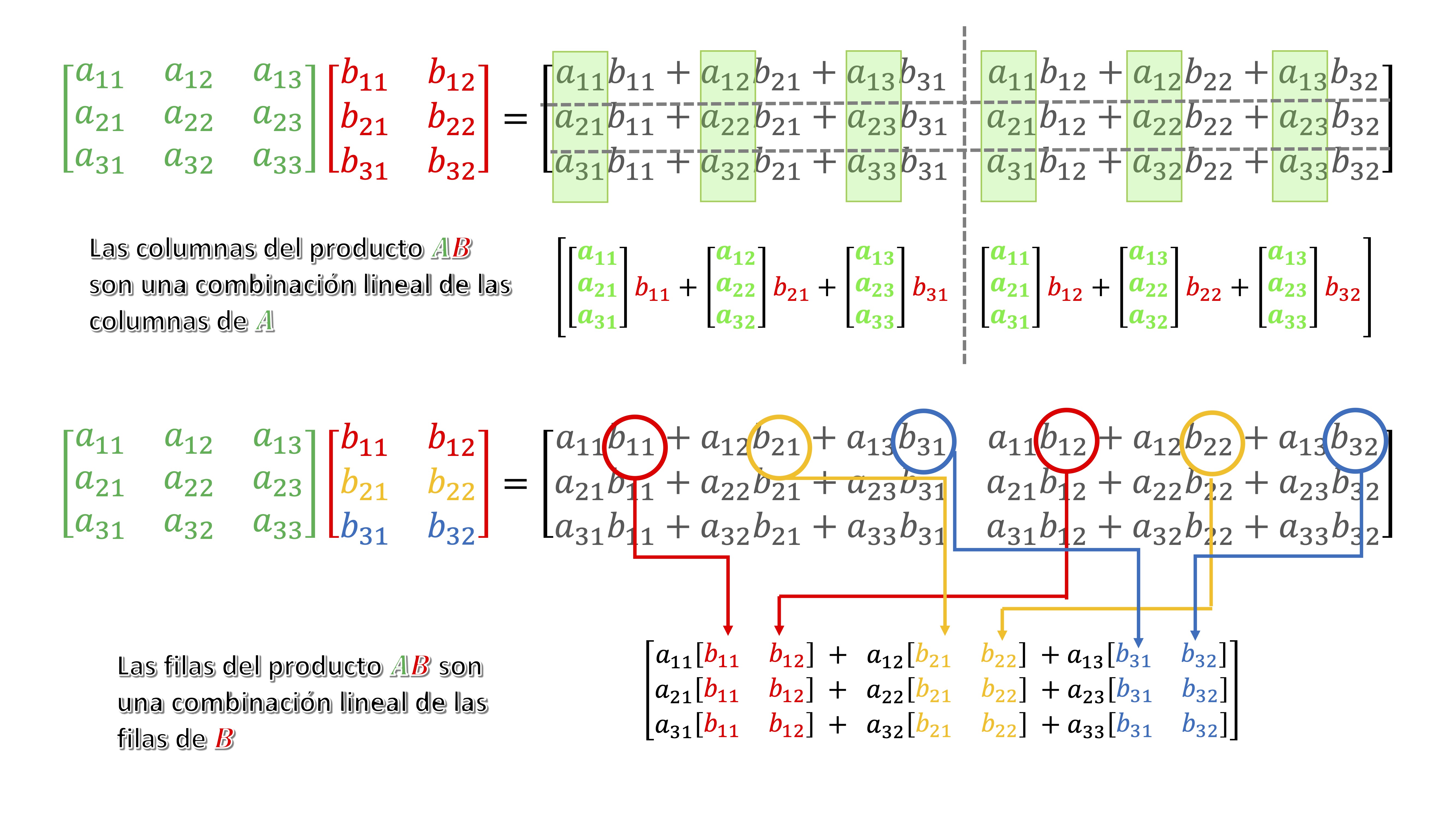
FIG1. Lo puedes ver aquí esquematizado.
El producto de matrices tiene diferentes propiedades (siempre que tengan las dimensiones adecuadas para poder realizar las operaciones)
\(\mathbf{A}\mathbf{B}\neq\mathbf{BA}\) (no se cumple la conmutatividad del producto)
\(\mathbf{A}\left(\mathbf{B}\mathbf{C}\right)=\mathbf{\left(\mathbf{A}\mathbf{B}\right)\mathbf{C}}\) (asociativa)
\(\mathbf{A}\left(\mathbf{B}+\mathbf{C}\right)=\mathbf{A}\mathbf{B+\mathbf{A}\mathbf{C}}\) (distributiva)
\(\left(\mathbf{A}+\mathbf{B}\right)\mathbf{C}=\mathbf{A}\mathbf{C+\mathbf{B}\mathbf{C}}\) (distributiva)
\(\mathbf{I_{\mathit{m}}A=A=AI_{\mathit{n}}}\) para \(\mathbf{A\mathcal{\in M_{\mathit{m\times n}}}}\)
Importante
¿Por qué funciona que \(\mathbf{A}\left(\mathbf{B}+\mathbf{C}\right)=\mathbf{A}\mathbf{B+\mathbf{A}\mathbf{C}}\) ? donde asumimos que \(\mathbf{A}\in\mathcal{M}_{m\times n},\mathbf{B,C}\in\mathcal{M}_{n\times r}\)}
Si las matrices tienen las dimensiones adecuadas para que se pueda realizar este cálculo, entonces
- \(\left[\begin{array}{ccc} a_{11} & ... & a_{1n}\\ ... & & ...\\ a_{m1} & ... & a_{mn} \end{array}\right]\left[\begin{array}{ccc} b_{11}+c_{11} & ... & b_{1r}+c_{1r}\\ ... & & ...\\ b_{n1}+c_{n1} & & b_{nr}+c_{nr} \end{array}\right]\)
- estos productos, pueden ponerse como el producto escalar de cada vector fila de la matriz \(\mathbf{A}\) por las columnas de la suma de \(\mathbf{\mathbf{\mathrm{B+C}}}\) \[ \left(\begin{array}{ccc} \overrightarrow{a}_{1\bullet}\cdot\left(\overrightarrow{b}_{\bullet1}+\overrightarrow{c}_{\bullet1}\right) & ... & \overrightarrow{a}_{1\bullet}\cdot\left(\overrightarrow{b}_{\bullet r}+\overrightarrow{c}_{\bullet r}\right)\\ ... & ... & ...\\ \overrightarrow{a}_{m\bullet}\cdot\left(\overrightarrow{b}_{\bullet n}+\overrightarrow{c}_{\bullet n}\right) & ... & \overrightarrow{a}_{m\bullet}\cdot\left(\overrightarrow{b}_{\bullet r}+\overrightarrow{c}_{\bullet r}\right) \end{array}\right) \]
- Por las propiedades del cálculo vectorial, podemos reescribir como \[ \left(\begin{array}{ccc} \overrightarrow{a}_{1\bullet}\cdot\overrightarrow{b}_{\bullet1}+\overrightarrow{a}_{1\bullet}\cdot\overrightarrow{c}_{\bullet1} & ... & \overrightarrow{a}_{1\bullet}\cdot\overrightarrow{b}_{\bullet r}+\overrightarrow{a}_{1\bullet}\cdot\overrightarrow{c}_{\bullet r}\\ ... & ... & ...\\ \overrightarrow{a}_{m\bullet}\cdot\overrightarrow{b}_{\bullet1}+\overrightarrow{a}_{m\bullet}\cdot\overrightarrow{c}_{\bullet1} & ... & \overrightarrow{a}_{m\bullet}\cdot\overrightarrow{b}_{\bullet r}+\overrightarrow{a}_{m\bullet}\cdot\overrightarrow{c}_{\bullet r} \end{array}\right) \]
- lo cual, dado que sabemos las propiedades del producto de matrices, es lo mismo que poner \(\mathbf{A}\mathbf{B+\mathbf{A}\mathbf{C}}\)
Pregunta
Si \(\mathbf{A}\) y \(\mathbf{B}\) son matrices cuadradas del mismo tamaño…¿se cumplirá: }\(\left(\mathbf{A}+\mathbf{B}\right)^{2}=\mathbf{A}^{2}+2\mathbf{A}\mathbf{B}+\mathbf{B}^{2}\)?
veamos que eso no es así:
\[ \left(\mathbf{A}+\mathbf{B}\right)^{2}=\left(\mathbf{A}+\mathbf{B}\right)\left(\mathbf{A}+\mathbf{B}\right)=\mathbf{A}^{2}+\mathbf{{\color{red}B\mathbf{\color{red}A}+\mathbf{A}\mathbf{B}}+\mathbf{B}^{2}} \]
Y, como hemos visto, en general, \(\mathbf{A}\mathbf{B}\neq\mathbf{BA}\).
Más operaciones con matrices
Vamos a presentar matrices que usaremos muy a menudo ya que aparecen en distintos cálculos matriciales
- La matriz traspuesta: ya se vio anteriormente. Ahora, presentamos sus propiedades más relevantes
- \(\left(\mathbf{A}+\mathbf{B}\right)^{t}=\mathbf{A}^{t}+\mathbf{B}^{t}\) (fácil de verificar)
- \(\left(\mathbf{A}\mathbf{B}\right)^{t}=\mathbf{B}^{t}\mathbf{A}^{t}\). Veamos por qué. Para ello, hagamos el producto de dos matrices
\(\mathbf{A}\mathbf{B}\): \[ \left(\begin{array}{ccc} a_{11} & ... & a_{1n}\\ {\color{red}a_{21}} & {\color{red}{\color{magenta}{...}}} & {\color{red}a_{2n}}\\ ... & \ddots & ...\\ a_{m1} & ... & a_{mn} \end{array}\right)\left(\begin{array}{ccc} {\color{red}b_{11}} & ... & b_{1r}\\ {\color{red}b_{21}} & ... & b_{2r}\\ {\color{purple}{\color{purple}{\color{purple}...}}} & \ddots & ...\\ {\color{red}b_{n1}} & ... & b_{nr} \end{array}\right), \] donde hemos marcado, por ejemplo, el elemento 2.1 de la matriz producto resultante que resultaría ser: \[ \left[\begin{array}{cccc} a_{21} & a_{22} & ... & a_{2n}\end{array}\right]\left[\begin{array}{c} b_{11}\\ b_{21}\\ ...\\ b_{n1} \end{array}\right]=c_{21} \] nota que, si traspones ambos vectores, \(\left[\begin{array}{c} a_{21}\\ a_{22}\\ ...\\ a_{2n} \end{array}\right]\) \(\left[\begin{array}{cccc} b_{11} & b_{21} & ... & b_{n1}\end{array}\right]\)
este resultado no coincide con un escalar (sería una matriz \(nxn\)) su traspuesta, por tanto, sería, para que salga lo mismo:
\[ \left[\begin{array}{cccc} b_{11} & b_{21} & ... & b_{n1}\end{array}\right]\left[\begin{array}{c} a_{21}\\ a_{22}\\ ...\\ a_{2n} \end{array}\right] \]
Lo que implica el resultado anterior.
- \(\left(\mathbf{\lambda A}\right)^{t}=\lambda\mathbf{A}^{t}\)
- \(\left(\mathbf{A}^{t}\right)^{t}=\mathbf{A}\)
Clase 2: el método de Gauss-Jordan de inversión de matrices
Primeramente, hagamos algunos ejercicios
Ejercicio resuelto 1
Producto escalar utilizando la traspuesta. Escribe el producto escalar entre dos vectores utilizando la traspuesta y asumiendo, como desde el principio del curso, que un vector lo veremos como una columna de una matriz.
Por ejemplo, sean los vectores \[ \overrightarrow{x}=\left[\begin{array}{c} 1\\ 2\\ 3\\ 1 \end{array}\right],\overrightarrow{y}=\left[\begin{array}{c} -1\\ -2\\ 3\\ 1 \end{array}\right] \]
el producto escalar se escribirá, pensando ahora los vectores como matrices columna, como:
\[ \overrightarrow{x}^{t}\overrightarrow{y}, \] es decir
\(\left[\begin{array}{cccc} 1 & 2 & 3 & 1\end{array}\right]\left[\begin{array}{c} -1\\ -2\\ 3\\ 1 \end{array}\right]=-1-4+9+1=5\).
Nota que es equivalente a esta otra escritura
\[ \overrightarrow{x}\cdot\overrightarrow{y}=\left[\begin{array}{c} 1\\ 2\\ 3\\ 1 \end{array}\right]\cdot\left[\begin{array}{c} -1\\ -2\\ 3\\ 1 \end{array}\right]=5 \]
y que, dependiendo del contexto, usarás una u otra notación.
Nota, por favor, que de ninguna manera ponemos \(\mathbf{{\color{red}xy}}\). Ese producto no tendría sentido porque las dimensiones no permiten hacer ningún producto. Por otro lado, otro producto que podemos definir es
\[ \overrightarrow{x}\overrightarrow{y}^{t} \]
de tal forma que tenemos
\[ \left[\begin{array}{c} 1\\ 2\\ 3\\ 1 \end{array}\right]\left[\begin{array}{cccc} -1 & -2 & 3 & 1\end{array}\right] \]
como ves, es un producto generado por una matriz \(4\times1\) y otra \(1\times4\). Cumple con la norma del producto y el resultado que debemos esperar es una matriz \(4\times4\). De hecho:
\[ \left[\begin{array}{c} 1\\ 2\\ 3\\ 1 \end{array}\right]\left[\begin{array}{cccc} -1 & -2 & 3 & 1\end{array}\right]=\left[\begin{array}{cccc} -1 & -2 & 3 & 1\\ -2 & -4 & 6 & 2\\ -3 & -6 & 9 & 3\\ -1 & -2 & 3 & 1 \end{array}\right] \]
Ejercicio resuelto 2
- escribe la norma de un vector en \(\mathbb{R}^{n}\) utilizando la traspuesta
Sabemos que \(\left\Vert \overrightarrow{x}\right\Vert =\sqrt{x_{1}^{2}+x_{2}^{2}+...+x_{n}^{2}}=\sqrt{\left[\begin{array}{c} x_1\\ x_2\\ ...\\ x_n\end{array}\right]\cdot\left[\begin{array}{c} x_1\\ x_2\\ ...\\ x_n\end{array}\right]}\) entonces, es igual a \(\sqrt{\left(x_{1},x_{2},...,x_{n}\right)\left(\begin{array}{c} x_{1}\\ x_{2}\\ ...\\ x_{n} \end{array}\right)}\), es decir, \(\sqrt{\overrightarrow{x}^{t}\overrightarrow{x}}\)
Ejercicio sobre propiedades producto matricial
Camino a la inversión de una matriz: las matrices elementales
Las matrices elementales (que denotaremos como \(\mathbf{E}\) ) nos permitirán, mediante el producto de matrices, realizar operaciones por filas aprovechando las propiedades vistas en la clase anterior. Date cuenta de que si queremos operar por filas en la matriz \(\mathbf{A}\)
\[ \mathbf{E}\mathbf{A} \]
Deberemos elegir convenientemente la matriz \(\mathbf{E}\) para que el resultado sea una nueva matriz construida a partir de combinaciones lineales de las filas de \(\mathbf{A}\)
Las matrices elementales son matrices cuadradas y sucedáneas de la matriz identidad. Cuando premultiplicamos a una matriz \(\mathbf{A}\) por una matriz elemental, procedemos a hacer modificaciones por filas a las matrices \(m\times n\) que queramos transformar. Por ejemplo:
- Multiplica una fila (\(i\)) por una constante \(\lambda\): \(\mathbf{E}_{i}(\lambda)\). Esto significa que la matriz identidad cambia el 1 de la fila \(i\) por \(\lambda\).
Imagina una matriz \(3\times3\), tendremos \(\mathbf{E}_{2}(\lambda)=\left[\begin{array}{ccc} 1 & 0 & 0\\ 0 & \lambda & 0\\ 0 & 0 & 1 \end{array}\right]\)
- Suma a la fila \(i\) la fila \(j\) multiplicado por \(\lambda\): \(\mathbf{E}_{ij}(\lambda)\) cambia el elemento \(ij\) de la matriz por el escalar.
En la matriz anterior, tendríamos, \(\mathbf{E}_{32}(\lambda)=\left[\begin{array}{ccc} 1 & 0 & 0\\ 0 & 1 & 0\\ 0 & \lambda & 1 \end{array}\right]\)
- Permuta la fila \(i\) por la fila \(j\) \(\mathbf{P}_{ij}\).
En el caso de la matriz anterior \(\mathbf{P}_{23}=\left[\begin{array}{ccc} 1 & 0 & 0\\ 0 & 0 & 1\\ 0 & 1 & 0 \end{array}\right]\)
- ¿Y si lo quiero hacer por columnas? Pues tendrás que postmultiplicar la matriz que quieres cambiar.
Ejemplos
Las matrices elementales hacen cambios por filas siempre premultiplicando. Sea \(\mathbf{A}=\left[\begin{array}{cccc} 1 & 3 & 5 & 7\\ 2 & 4 & 6 & 8 \end{array}\right]\), los cambios que provocan las matrices elementales son, por ejemplo,
- multiplica la segunda fila por -2 \(\Rightarrow\overset{\mathbf{E}_{2}(-2)}{\left[\begin{array}{cc} 1 & 0\\ 0 & {\color{red}-2} \end{array}\right]}\left[\begin{array}{cccc} 1 & 3 & 5 & 7\\ 2 & 4 & 6 & 8 \end{array}\right]=\left[\begin{array}{cccc} 1 & 3 & 5 & 7\\ -4 & -8 & -12 & -16 \end{array}\right]\)
- súmale a la primera fila la segunda fila multiplicada por -1 \(\Rightarrow\overset{\mathbf{E}_{12}(-1)}{\left[\begin{array}{cc} 1 & {\color{red}-1}\\ 0 & 1 \end{array}\right]}\left[\begin{array}{cccc} 1 & 3 & 5 & 7\\ 2 & 4 & 6 & 8 \end{array}\right]=\left[\begin{array}{cccc} -1 & -1 & -1 & -1\\ 2 & 4 & 6 & 8 \end{array}\right]\)
La matriz inversa
Matriz Inversa. La matriz inversa es análoga (aunque con “peros”) a la división en escalares. Recuerda que, en escalares:
\[ a^{-1}=\frac{1}{a}\Rightarrow a^{-1}a=1 \]
¿Cómo calcular, entonces, la inversa de \(\mathbf{A=\left(\mathit{\mathrm{\begin{array}{cc} 1 & 1\\ 0 & 1 \end{array}}}\right)}\)?
Necesitamos encontrar una matriz cuadrada \(\mathbf{B}\) tal que \(\mathbf{BA=I}\). Te avisamos ya que esto no siempre será posible (es decir, no todas las matrices serán invertibles).
Intentemos hacerlo usando las ideas aprendidas manejando sistemas de ecuaciones sencillos. Sea \(\mathbf{B}=\left(\begin{array}{cc} a & b\\ c & d \end{array}\right)\) tal que
\[ \left(\begin{array}{cc} a & b\\ c & d \end{array}\right)\left(\mathit{\mathrm{\begin{array}{cc} 1 & 1\\ 0 & 1 \end{array}}}\right)=\left(\mathit{\mathrm{\begin{array}{cc} 1 & 0\\ 0 & 1 \end{array}}}\right) \]
Obtenemos que \(a=1,a+b=0,c=0,c+d=1\), esto es
\[ \mathbf{B=A^{-1}=\left(\mathit{\mathrm{\begin{array}{cc} 1 & -1\\ 0 & 1 \end{array}}}\right)} \]
Nota, como hemos visto que si una matriz \(\mathbf{A}\) tiene inversa:
\[ \mathbf{A}^{-1}\mathbf{A}=\mathbf{I}=\mathbf{A\mathbf{A}^{-1}} \]
Veamos ahora el algoritmo para invertir matrices: Gauss-Jordan
Así funciona
Lo primero que tienes que hacer es ampliar la matriz \(\mathbf{A}\) de tal forma que anexes la identidad, es decir, tendrás una nueva matriz \(\mathbf{A}^{*}\)
\[ A^{*}=\left[\left.\mathbf{A}\right|\mathbf{I}\right] \]
El objetivo será conseguir, mediante transformaciones elementales por filas, que la matriz de la izquierda se convierta en \(\mathbf{I}\) de tal forma que la matriz de la derecha se convertirá en \(\mathbf{A}^{-1}\). Para conseguir este objetivo:
- El elemento \(a_{11}\) ha de convertirse en un 1. Para ello, si es 0, deberás permutar las filas de \(\mathbf{A}^{*}\). Si no, deberás hacer la operación elemental correspondiente.
- Los elementos por debajo del \(a_{11}\) deberán ser 0 mediante operaciones elementales.
- Sucesivamente, irás convirtiendo en 1 los elementos \(a_{ii}\) de la matriz. Si en alguno de ellos lo encuentras imposible, entonces la matriz no tiene inversa. Posteriormente deberás hacer ceros los elementos inferiores a cada \(a_{ii}\) para, después, convertir en ceros los elementos que están por encima.
Ejemplo Resuelto
Vamos a aplicarlo con la siguiente matriz
\[ \mathbf{A}=\left[\begin{array}{ccc} 2 & 0 & 1\\ -1 & 1 & -1\\ 0 & 2 & 1 \end{array}\right] \]
Sigamos los pasos:
- \(\left(\left.\begin{array}{ccc} 2 & 0 & 1\\ -1 & 1 & -1\\ 0 & 2 & 1 \end{array}\right|\begin{array}{ccc} 1 & 0 & 0\\ 0 & 1 & 0\\ 0 & 0 & 1 \end{array}\right)\underrightarrow{\mathbf{E}_{1}(1/2)}\) (multiplicamos la primera fila por \(\frac{1}{2}\) para tener un 1 en el primer elemento)
- \(\left(\left.\begin{array}{ccc} 1 & 0 & 1/2\\ -1 & 1 & -1\\ 0 & 2 & 1 \end{array}\right|\begin{array}{ccc} 1/2 & 0 & 0\\ 0 & 1 & 0\\ 0 & 0 & 1 \end{array}\right)\underrightarrow{\mathbf{E}_{21}(1)}\) A la fila 2, le sumamos la fila 1 ( y así nos hacemos con un cero en el elemento 2,1)
- \(\left(\left.\begin{array}{ccc} 1 & 0 & 1/2\\ 0 & 1 & -1/2\\ 0 & 2 & 1 \end{array}\right|\begin{array}{ccc} 1/2 & 0 & 0\\ 1/2 & 1 & 0\\ 0 & 0 & 1 \end{array}\right)\underrightarrow{\mathbf{E}_{32}(-2)}\) Ahora a la fila 3, le sumamos la fila 2 multiplicada por -2
- \(\left(\left.\begin{array}{ccc} 1 & 0 & 1/2\\ 0 & 1 & -1/2\\ 0 & 0 & 2 \end{array}\right|\begin{array}{ccc} 1/2 & 0 & 0\\ 1/2 & 1 & 0\\ -1 & -2 & 1 \end{array}\right)\underrightarrow{\mathbf{E}_{3}(1/2)}\) A la fila 3 la multiplicamos por \(1/2\), para así tener un 1
- \(\left(\left.\begin{array}{ccc} 1 & 0 & 1/2\\ 0 & 1 & -1/2\\ 0 & 0 & 1 \end{array}\right|\begin{array}{ccc} 1/2 & 0 & 0\\ 1/2 & 1 & 0\\ -1/2 & -1 & 1/2 \end{array}\right)\underrightarrow{\mathbf{E}_{23}(1/2)}\) Ahora a la fila 2, le sumamos la fila 3 multiplicada por \(1/2\)
- \(\left(\left.\begin{array}{ccc} 1 & 0 & 1/2\\ 0 & 1 & 0\\ 0 & 0 & 1 \end{array}\right|\begin{array}{ccc} 1/2 & 0 & 0\\ 1/4 & 1/2 & 1/4\\ -1/2 & -1 & 1/2 \end{array}\right)\underrightarrow{\mathbf{E}_{13}(-1/2)}\) finalmente, a la fila 1 le sumamos la fila 3 multiplicada por \(-1/2\)
- \(\left(\left.\begin{array}{ccc} 1 & 0 & 0\\ 0 & 1 & 0\\ 0 & 0 & 1 \end{array}\right|\begin{array}{ccc} 3/4 & 1/2 & -1/4\\ 1/4 & 1/2 & 1/4\\ -1/2 & -1 & 1/2 \end{array}\right)\)
Fíjate que, en este ejemplo, hemos hecho todos estos cambios, que se traducen en un conjunto de multiplicaciones de matrices elementales:
\[ \left[\begin{array}{ccc} 1 & 0 & -1/2\\ 0 & 1 & 0\\ 0 & 0 & 1 \end{array}\right]\left[\begin{array}{ccc} 1 & 0 & 0\\ 0 & 1 & 0\\ 0 & 0 & 1/2 \end{array}\right]\left[\begin{array}{ccc} 1 & 0 & 0\\ 0 & 1 & 0\\ 0 & -2 & 1 \end{array}\right]\left[\begin{array}{ccc} 1 & 0 & 0\\ 1 & 1 & 0\\ 0 & 0 & 1 \end{array}\right] \] \[ \left[\begin{array}{ccc} 1/2 & 0 & 0\\ 0 & 1 & 0\\ 0 & 0 & 1 \end{array}\right]\mathbf{\left[\begin{array}{ccc} 2 & 0 & 1\\ -1 & 1 & -1\\ 0 & 2 & 1 \end{array}\right]=\left[\begin{array}{ccc} 3/4 & 1/2 & -1/4\\ 1/4 & 1/2 & 1/4\\ -1/2 & -1 & 1/2 \end{array}\right]} \]
Pero… ¿Por qué funciona este algoritmo? Es sencillo: nota que partimos de una expresión así:
\[ \left(\mathbf{A}|\mathbf{I}\right) \]
A la cual le aplicamos operaciones elementales \(\mathbf{E}\), las que correspondan, en ambos lados
\[ \left(\mathbf{EA}|\mathbf{E}\mathbf{I}\right) \]
Al final, esas operaciones están diseñadas para que obtengamos que
\(\mathbf{EA}=\mathbf{I}\), por lo que no queda otra que \(\mathbf{E}=\mathbf{A^{-1}}\).
Las siguientes propiedades se corresponden con las de la matriz inversa
- Si una matriz tiene inversa, esta es única. Para demostrarlo, supongamos que \(\mathbf{B}\) y \(\mathbf{C}\) son ambas inversas de \(\mathbf{A}\). Se cumple, entonces, que \(\mathbf{AB}=\mathbf{I}\). Si multiplico por \(\mathbf{C},\) tenemos que \(\mathbf{CA}\mathbf{B}=\mathbf{CI}\), usando la definición de inversa, \(\mathbf{\underset{CA}{I}B=CI}\), (como \(\mathbf{C}\) es la inversa de \(\mathbf{A})\), entonces \(\mathbf{IB=CI}\Rightarrow\mathbf{B=C}\).
- \(\mathbf{(A}^{-1})^{-1}=\mathbf{A}\)
- \(\mathbf{(A}^{t})^{-1}=\mathbf{\left(A^{-1}\right)^{\mathit{t}}}\). Esto nos dice que la inversa de una matriz traspuesta equivale a la traspuesta de su inversa. Necesitamos mostrar que \(\mathbf{\left(A^{-1}\right)^{t}}\) es la inversa de \(\mathbf{A}^{t}\). Entonces, \(\left(\mathbf{A}^{t}\right)\left(\mathbf{A}^{-1}\right)^{t}=\)\(\left(\mathbf{A}^{\text{-1}}\mathbf{A}\right)^{t}=\mathbf{I}\), lo cual es cierto
- \(\mathbf{(AB})^{-1}=\mathbf{B^{-1}A^{-1}}\). Para ver cuál es la inversa de \(\mathbf{AB}\), necesitamos buscar una \(\mathbf{X}\) tal que \(\mathbf{(AB)X=I}\) esto es, si hacemos que \(\mathbf{X=B^{-1}A^{-1}}\) \(\mathbf{A\underset{{\color{purple}BB^{-1}}}{I}A^{-1}}=\mathbf{I}\), es decir \(\mathbf{B^{-1}A^{-1}}\) es la inversa de\(\mathbf{AB}\) (es la propiedad más usada e importante)
- \(\left(\mathbf{A}^{k}\right)^{-1}=\left(\mathbf{A}^{-1}\right)^{k}\) Podemos empezar pensando en qué hacer si \(k=2\Rightarrow(AA)^{-1}=A^{-1}A^{-1}=(A^{-1})^{2}\) dada la propiedad anterior. Podemos generalizarlo en una prueba \(\left(\mathbf{A}^{k}\right)^{-1}=\left(\mathbf{A}^{k-1}\mathbf{A}\right)^{-1}=\mathbf{A}^{-1}\mathbf{A}^{-k+1}=\left(\mathbf{A}^{-1}\right)^{k}\)
Ejemplo Resuelto
-Simplifica
\[ \mathbf{\left(AB\right)^{-1}\left(AC^{-1}\right)\left(D^{-1}C^{-1}\right)^{-1}D^{-1}} \] utilizaremos que \[ \mathbf{\left(AB\right)^{-1}=B^{-1}A^{-1}} \] entonces, tenemos que
\[ \mathbf{\left(AB\right)^{-1}\left(AC^{-1}\right)\left(D^{-1}C^{-1}\right)D^{-1}=B^{-1}A^{-1}AC^{-1}CDD^{-1}=B^{-1}} \]
-Despeja \(D\) en la expresión
\[ \mathbf{C^{t}B^{-1}A^{2}BAC^{-1}DA^{-2}B^{t}C^{-2}=C^{t}} \] necesitamos invertir \(\mathbf{\left(C^{t}B^{-1}A^{2}BAC^{-1}\right)^{-1}=CA^{-1}B^{-1}A^{-2}B\left(C^{-1}\right)^{t}}\) entonces, premultiplicando en ambos lados
\[ \mathbf{CA^{-1}B^{-1}A^{-2}B\left(C^{-1}\right)^{t}C^{t}B^{-1}A^{2}BAC^{-1}DA^{-2}B^{t}C^{-2}=CA^{-1}B^{-1}A^{-2}B\left(C^{-1}\right)^{t}C^{t}} \]
\[ \mathbf{DA^{-2}B^{t}C^{-2}=CA^{-1}B^{-1}A^{-2}B} \]
Ahora necesitamos invertir \(\mathbf{\left(A^{-2}B^{t}C^{-2}\right)^{-1}=C^{2}\left(B^{t}\right)^{-1}A^{2}}\) y postmultiplicando:
\[ \mathbf{DA^{-2}B^{t}C^{-2}C^{2}\left(B^{t}\right)^{-1}A^{2}=CA^{-1}B^{-1}A^{-2}BC^{2}\left(B^{t}\right)^{-1}A^{2}} \]
\[ \mathbf{D=CA^{-1}B^{-1}A^{-2}BC^{2}\left(B^{t}\right)^{-1}A^{2}} \]
Clase 3: El determinante y sus propiedades
En este curso, vamos a entender el determinante como una función que te proporciona, para cada matriz cuadrada en el espacio vectorial \(\mathcal{M}_{n\times n}\) un número real (es decir, \(\left|\right|\::\mathcal{M}_{n\times n}\rightarrow\mathbb{R}\)). El determinante es un gran “misterio.” Tiene aplicaciones sorprendentes pero no es eficiente su cálculo (ni a mano ni a ordenador), por lo que no siempre será aconsejado su uso a la hora de obtener resultados.
Cálculo del determinante
En matrices \(2\times2\) es sencillo: \(\left|\mathbf{A}\right|=\left|\begin{array}{cc} a_{11} & a_{12}\\ a_{21} & a_{22} \end{array}\right|=a_{11}a_{22}-a_{21}a_{12}\)
En matrices \(3\times3\) es algo menos sencillo: \[ \left|\mathbf{A}\right|=\begin{cases} \left(\begin{array}{ccc} {\color{red}a_{11}} & {\color{green}a_{12}} & {\color{purple}a_{13}}\\ {\color{purple}a_{21}} & {\color{red}a_{22}} & {\color{green}a}_{{\color{green}23}}\\ {\color{green}a_{31}} & {\color{purple}a_{32}} & {\color{red}a_{33}} \end{array}\right) & signo+\\ \left(\begin{array}{ccc} {\color{purple}a_{11}} & {\color{green}a_{12}} & {\color{red}a_{13}}\\ {\color{green}a_{21}} & {\color{red}a_{22}} & {\color{purple}a_{23}}\\ {\color{green}{\color{red}a_{31}}} & {\color{purple}a_{32}} & {\color{green}{\color{green}{\color{green}a_{33}}}} \end{array}\right) & signo- \end{cases} \]
\[ \underset{signo+}{\underbrace{{\color{red}a}_{11}{\color{red}a_{22}\color{red}{a}_{33}}+{\color{green}a_{12}\color{green}a_{23}\color{green}a_{31}}+{\color{purple}a_{13}\color{purple}a_{21}\color{purple}a_{32}}}}-\underset{signo-}{\underbrace{{\color{red}a_{31}\color{red}a_{22}\color{red}a_{13}}-{\color{green}a_{21}\color{green}a_{12}\color{green}a_{33}}-\color{purple}a_{11}\color{purple}a_{23}\color{purple}a_{32}}} \]
Sacando factor común a la expresión anterior,
\(\left|\mathbf{A}\right|=a_{11}\left[a_{22}a_{33}-a_{32}a_{23}\right]+{a_{12}\left[a_{23}a_{31}-a_{21}a_{33}\right]}+a_{13}\left[a_{21}a_{32}-a_{31}a_{22}\right]\)
Nota cómo en esta factorización tienes que “reordenarlo” para que te quede como sigue, en forma de producto de elementos de una fila por un conjnto de determinantes:
\(\left|\mathbf{A}\right|=a_{11}\left|\begin{array}{cc} a_{22} & a_{23}\\ a_{32} & a_{33} \end{array}\right|-a_{12}\left|\begin{array}{cc} a_{21} & a_{23}\\ a_{31} & a_{33} \end{array}\right|+a_{13}\left|\begin{array}{cc} a_{21} & a_{22}\\ a_{31} & a_{32} \end{array}\right|\)
Esta última expresión se obtiene hallando los “menores” y sus “cofactores” asociados.
Los menores, \(M_{ij}\) consisten en el determinante de la submatriz que se forma al tapar la fila \(i\) y la columna \(j\) de la matriz.
Por ejemplo, de la matriz
\[ \mathbf{A}=\left(\begin{array}{ccc} a_{11} & a_{12} & a_{13}\\ a_{21} & a_{22} & a_{23}\\ a_{31} & a_{32} & a_{33} \end{array}\right) \]
Su menor \(M_{11}\) consiste en deshacerse de la fila 1 y la columna 1 y obtener el determinante
\[ \left(\begin{array}{ccc} {\color{gray}{\color{gray}a_{11}}} & {\color{gray}{a_{12}}} & {\color{gray}{a_{13}}}\\ {\color{gray}{a_{21}}} & a_{22} & a_{23}\\ {\color{gray}{a_{31}}} & a_{32} & a_{33} \end{array}\right) \]
y el menor, por tanto, será:
\[ M_{11}= \left|\begin{array}{cc} a_{22} & a_{23}\\ a_{32} & a_{33} \end{array}\right| \]
Finalmente, definimos el cofactor \(C_{ij}\), consiste en utilizar esta “regla de signos”:
\[ C_{ij}=(-1)^{i+j}M_{ij} \]
El determinante, por tanto, de una matriz \(n\times n\), lo podemos escribir como:
\[ \left|\mathbf{A}\right|=a_{i1}C_{i1}+a_{i2}C_{i2}+...+a_{in}C_{in} \]
o
\[ \left|\mathbf{A}\right|=a_{1j}C_{1j}+a_{2j}C_{2j}+...+a_{nj}C_{nj} \]
Es decir, elegimos una fila (o columna) y lo desarrollamos de esta forma. Como da lo mismo la fila (o columna) que se elija, será sensato obtener el determinante usando la fila (o columna) con más ceros, si eres afortunado y tu matriz tiene alguno.
De hecho, hay dos determinantes muy sencillos:
- El de una matriz triangular (el producto de los elementos de la diagonal principal)
- El de una matriz diagonal (el producto de los elementos de la diagonal principal, nuevamente).
Ahora, anotemos las propiedades principales del determinante:
- P1. Una sencillita \(\left|\mathbf{I}\right|=1\)
- P2. Si mutltiplicas una fila (columna) de una matriz por un escalar, \(\lambda\) , el determinante queda multiplicado por el escalar: Efectivamente, \[ \left|\begin{array}{cc} \lambda a_{11} & \lambda a_{12}\\ a_{21} & a_{22} \end{array}\right|=\lambda\left|\begin{array}{cc} a_{11} & a_{12}\\ a_{21} & a_{22} \end{array}\right|. \] \(\lambda a_{11}a_{22}-\lambda a_{21}a_{12}=\lambda(a_{11}a_{12}-a_{21}a_{12}).\)
- P3. Si multiplicas toda la matriz (\(n\times n)\) por un escalar, \(\lambda,\) el determinante queda multiplicado por el escalar elevado a \(n\).
- Respecto a las filas (columnas) de la matriz, el determinante actúa como una función lineal: \[ \left|\begin{array}{cc} a_{11}+\lambda & a_{12}+\mu\\ a_{21} & a_{22} \end{array}\right|=\left|\begin{array}{cc} a_{11} & a_{12}\\ a_{21} & a_{22} \end{array}\right|+\left|\begin{array}{cc} \lambda & \mu\\ a_{21} & a_{22} \end{array}\right| \]
- P4. Si dos filas (columnas) de una matriz son iguales, su determinante es cero
- P5. Las operaciones elementales no afectan al determinante \[ \left|\begin{array}{cc} a_{11} & a_{12}\\ a_{21}+\lambda a_{11} & a_{22}+\lambda a_{12} \end{array}\right|=\underset{propiedad\:4}{\left|\begin{array}{cc} a_{11} & a_{12}\\ a_{21} & a_{22} \end{array}\right|+\left|\begin{array}{cc} a_{11} & a_{12}\\ \lambda a_{11} & \lambda a_{12} \end{array}\right|}=\] \[ \underset{propiedad\:5}{\left|\begin{array}{cc} a_{11} & a_{12}\\ a_{21} & a_{22} \end{array}\right|+\lambda\left|\begin{array}{cc} a_{11} & a_{12}\\ a_{11} & a_{12} \end{array}\right|=\left|\begin{array}{cc} a_{11} & a_{12}\\ a_{21} & a_{22} \end{array}\right|} \]
- P6. Si la matriz tiene una fila de ceros, (es decir, en 2, \(\lambda=0)\) el determinante será 0
- P7. \(\left|\mathbf{AB}\right|=\left|\mathbf{A}\right|\left|\mathbf{B}\right|\) (no así en la suma) Para probar esto, se puede particionar la matriz de tal forma que \(C=\left(\begin{array}{cc} \mathbf{A} & \mathbf{0}\\ \mathbf{-I} & \mathbf{B} \end{array}\right)\) Ahora bien, si se multiplican las \(n\) últimas filas de la matriz C por \(\mathbf{A}\) y se le suman a las \(n\) primeras filas, tendremos \(C*=\left(\begin{array}{cc} \mathbf{0} & \mathbf{AB}\\ \mathbf{-I} & \mathbf{B} \end{array}\right)\). Entonces, sabemos por las propiedades anteriores que \(\left|\mathbf{C}\right|=\left|\mathbf{C}*\right|\). Por las reglas del determinante \(\left|C\right|=\left|A\right|\left|B\right|\) mientras que \(\left|C*\right|=\left|AB\right|\)
- P8. \(\left|\mathbf{A^{T}}\right|=\left|\mathbf{A}\right|\)
- P9. Si cambias el orden de una fila, el determinante es el mismo pero con signo opuesto.
- P10. Si \(\mathbf{A}\) es invertible, \(\left|\mathbf{A^{-1}}\right|=\frac{1}{\left|\mathbf{A}\right|}\). Esta prueba es sencillita, puesto que \(\mathbf{A^{-1}}\mathbf{A}=\mathbf{I}\), calculando determinantes\(\left|\mathbf{A^{-1}}\mathbf{A}\right|=\left|\mathbf{I}\right|\), de las propiedades \(\left|\mathbf{A^{-1}}\right|=\frac{1}{\left|\mathbf{A}\right|}\)
Clase 4: Usos del determinante para el cálculo de inversas
Ejercicio resuelto
Usa las propiedades del determinante para calcular el de esta matriz
\[ A=\left(\begin{array}{cccccc} 2 & -3 & 0 & 0 & -2 & 6\\ 0 & 7 & 1 & 1 & 0 & 0\\ 0 & 5 & 1 & -1 & 1 & 2\\ 0 & 1 & 0 & -2 & 1 & 3\\ -1 & 2 & 0 & 0 & 1 & -3\\ 0 & 1 & 2 & 0 & 0 & 3 \end{array}\right) \]
- Lo primero que podemos notar es que la fila 1 es casi el doble que la 5 (multiplicada por menos 1). Si hacemos una operaci?n elemental, entonces, podremos conseguir la primera fila toda de ceros menos un número. Recuerda que las operaciones elementales no alteran el determinante (propiedad #6) \[ E_{14}(2)A=\left(\begin{array}{cccccc} {\color{red}0} & {\color{red}1} & {\color{red}0} & {\color{red}0} & {\color{red}0} & {\color{red}0}\\ 0 & 7 & 1 & 1 & 0 & 0\\ 0 & 5 & 1 & -1 & 1 & 2\\ 0 & 1 & 0 & -2 & 1 & 3\\ -1 & 2 & 0 & 0 & 1 & -3\\ 0 & 1 & 2 & 0 & 0 & 3 \end{array}\right) \]
- Ahora podemos usar que el determinante será: \[ \left|A\right|=1(-1)^{1+2}\left|\begin{array}{ccccc} {\color{red}0} & 1 & 1 & 0 & 0\\ {\color{red}0} & 1 & -1 & 1 & 2\\ {\color{red}0} & 0 & -2 & 1 & 3\\ {\color{red}-1} & 0 & 0 & 1 & -3\\ {\color{red}0} & 2 & 0 & 0 & 3 \end{array}\right| \]
- Y, de nuevo, tenemos \(\left|A\right|=-(-1)^{4+1}\left|\begin{array}{cccc} 1 & 1 & 0 & 0\\ 1 & -1 & 1 & 2\\ 0 & -2 & 1 & 3\\ 2 & 0 & 0 & 3 \end{array}\right|=\left|\begin{array}{cccc} {\color{red}1} & {\color{red}1} & {\color{red}0} & {\color{red}0}\\ 1 & -1 & 1 & 2\\ 0 & -2 & 1 & 3\\ 2 & 0 & 0 & 3 \end{array}\right|\) \(\left|A\right|=1(-1)^{1+1}\left|\begin{array}{ccc} -1 & 1 & 2\\ -2 & 1 & 3\\ 0 & 0 & 3 \end{array}\right|+1(-1)^{1+2}\left|\begin{array}{ccc} 1 & 1 & 2\\ 0 & 1 & 3\\ 2 & 0 & 3 \end{array}\right|=\left|\begin{array}{ccc} -1 & 1 & 2\\ -2 & 1 & 3\\ {\color{red}0} & {\color{red}0} & {\color{red}3} \end{array}\right|-\left|\begin{array}{ccc} 1 & 1 & 2\\ 0 & 1 & 3\\ 2 & 0 & 3 \end{array}\right|\) Finalmente \(\left|A\right|=3(-1)^{3+3}\left|\begin{array}{cc} -1 & 1\\ -2 & 1 \end{array}\right|-\left|\begin{array}{ccc} 1 & 1 & 2\\ 0 & 1 & 3\\ 2 & 0 & 3 \end{array}\right|=3\times1-(3+6+0-4-0-0)=-2\)
El uso del determinante para el cálculo de una inversa
Ahora, resolvamos una inversa \(2\times2\) tal que \(A=\left[\begin{array}{cc} a & b\\ c & d \end{array}\right]\)
usando el algoritmo de Gauss Jordan
\[ \left[\left.\begin{array}{cc} a & b\\ c & d \end{array}\right|\begin{array}{cc} 1 & 0\\ 0 & 1 \end{array}\right]\underrightarrow{E_{1}\left(\frac{1}{a}\right)}\left[\left.\begin{array}{cc} 1 & b/a\\ c & d \end{array}\right|\begin{array}{cc} 1/a & 0\\ 0 & 1 \end{array}\right]\underrightarrow{E_{21}\left(-c\right)} \] \[ \left[\left.\begin{array}{cc} 1 & b/a\\ 0 & d-\frac{cb}{a} \end{array}\right|\begin{array}{cc} 1/a & 0\\ -c/a & 1 \end{array}\right]=\left[\left.\begin{array}{cc} 1 & b/a\\ 0 & \left|A\right|/a \end{array}\right|\begin{array}{cc} 1/a & 0\\ -c/a & 1 \end{array}\right]\underrightarrow{E_{2}\left(a/\left|A\right|\right)} \] \[ \left[\left.\begin{array}{cc} 1 & b/a\\ 0 & 1 \end{array}\right|\begin{array}{cc} 1/a & 0\\ -c/\left|A\right| & a/\left|A\right| \end{array}\right]\underrightarrow{E_{12}\left(-b/a\right)}\left[\left.\begin{array}{cc} 1 & 0\\ 0 & 1 \end{array}\right|\begin{array}{cc} \frac{1}{a}\left(1+\frac{bc}{\left|A\right|}\right) & -b/\left|A\right|\\ -c/\left|A\right| & a/\left|A\right| \end{array}\right]= \]
\[ \left[\left.\begin{array}{cc} 1 & 0\\ 0 & 1 \end{array}\right|\begin{array}{cc} d/\left|A\right| & -b/\left|A\right|\\ -c/\left|A\right| & a/\left|A\right| \end{array}\right] \]
De este resultado podemos obtener que:
- Si el determinante de una matriz (por ahora \(2\times2\)) es cero, NO TIENE INVERSA
- La inversa de una matriz \(2\times2\) es \(\frac{1}{\left|A\right|}\left[\begin{array}{cc} {\color{red}d} & -b\\ -c & {\color{red}a} \end{array}\right]\)
Enseguida vemos que \(\left[\begin{array}{cc} {\color{red}d} & -b\\ -c & {\color{red}a} \end{array}\right]\) se conoce como la “traspuesta de la adjunta.” Primero, veamos qué es la matriz adjunta.
- Otra forma de escribir lo anterior es como, respecto a los “menores,” nota , por ejemplo, que \(M_{11}=\left(\begin{array}{cc} {\color{gray}{\color{gray}a}} & {\color{gray}b}\\ {\color{gray}c} & d \end{array}\right)\)
\[ \left[\begin{array}{cc} {\color{red}d} & -b\\ -c & {\color{red}a} \end{array}\right]=\left[\begin{array}{cc} M_{11} & -M_{21}\\ -M_{12} & {\color{red}{\color{blue}M_{22}}} \end{array}\right] \]
- Pero, a su vez, podemos ver que estamos usando los cofactores:
\[ \left[\begin{array}{cc} {\color{red}d} & -b\\ -c & {\color{red}a} \end{array}\right]=\left[\begin{array}{cc} C_{11} & C_{21}\\ C_{12} & {{C_{22}}} \end{array}\right] \]
La adjunta de una matriz
Llamaremos “matriz adjunta” a aquella que se forma con los cofactores de una matriz como la adjunta de la matriz. Por ejemplo, si \(\mathbf{A}\in M_{2\times2}\)
\[ adj\left(\mathbf{A}\right)=\left[\begin{array}{cc} C_{11} & C_{12}\\ C_{21} & C_{22} \end{array}\right] \]
De esta forma, diremos que, hemos descubierto que en la matriz \(2\times2\), la inversa será:
\[ \mathbf{A}^{-1}=\frac{1}{|\mathbf{A}|}adj\left(\mathbf{A}\right)^t \]
Demostremos ahora, entonces, que se puede utilizar este resultado para calcular cualquier inversa:
Sea \(\mathbf{A}\in\mathcal{M}_{n\times n}\), la inversa existe si y solo si \(\left|\mathbf{A}\right|\neq0\), entonces
\[ \mathbf{A}^{-1}=\frac{1}{\left|\mathbf{A}\right|}adj(\mathbf{A})^t \]
Desarrollando por el cofactor, por filas, tendremos, que para cada posible fila de la matriz, el determinante es siempre el mismo:
\[ \left|\mathbf{A}\right|=a_{11}C_{11}+a_{12}C_{12}+...+a_{1n}C_{1n} \]
\[ \left|\mathbf{A}\right|=a_{21}C_{21}+a_{22}C_{22}+...+a_{2n}C_{1n} \]
\[ .... \]
\[ \left|\mathbf{A}\right|=a_{n1}C_{n1}+a_{n2}C_{n2}+...+a_{nn}C_{nn} \]
Esto, sistemáticamente es
\[ \left[\begin{array}{cccc} a_{11} & ... & ... & a_{1n}\\ a_{21} & ... & ... & a_{2n}\\ ... & ... & ... & ...\\ a_{n1} & ... & ... & a_{nn} \end{array}\right]\left[\begin{array}{cccc} {C_{11}} & ... & ... & C_{n1}\\ {C_{12}} & ... & ... & C_{n2}\\ {...} & ... & ... & ...\\ {C_{1n}} & ... & ... & C_{nn} \end{array}\right]=\left[\begin{array}{cccc} \left|\mathbf{A}\right| & 0 & ... & 0\\ ... & \left|\mathbf{A}\right| & ... & 0\\ {0} & ... & ... & ...\\ 0 & ... & ... & \left|\mathbf{A}\right| \end{array}\right]\] \[ \Longrightarrow\frac{1}{\left|\mathbf{A}\right|}\left[\begin{array}{cccc} a_{11} & ... & ... & a_{1n}\\ a_{21} & ... & ... & a_{2n}\\ ... & ... & ... & ...\\ a_{n1} & ... & ... & a_{nn} \end{array}\right]\left[\begin{array}{cccc} {C_{11}} & ... & ... & C_{1n}\\ {C_{12}} & ... & ... & C_{2_{n}}\\ {...} & ... & ... & ...\\ {C_{1n}} & ... & ... & C_{nn} \end{array}\right]=\mathbf{I}\]
Entonces,
\[ \mathbf{A}\frac{1}{\left|\mathbf{A}\right|}adj(\mathbf{A})^t=\mathbf{I} \]
si premultiplico por la inversa
\[ \frac{1}{\left|\mathbf{A}\right|}adj(\mathbf{A})^t=\mathbf{A}^{-1} \]
Algunas matrices cuadradas relevantes
A continuación, mostramos algunas matrices con propiedades especiales e interesantes, con las que trabajaremos en el seminario
- Matriz ortogonal: es aquella cuya traspuesta es igual a su inversa. \(\mathbf{A}\) es ortogonal si \(\mathbf{A}^{t}=\mathbf{A}^{-1},\)por lo que \(\mathbf{A}\mathbf{A}^{t}=\mathbf{I}\)
Prueba que si \(\mathbf{A}\) es ortogonal, entonces su determinante es o 1 o -1.
\(\mathbf{A}^{t}\mathbf{A}=\mathbf{I}\) por definición de ortogonal \(\left|\mathbf{A}^{t}\right|\left|\mathbf{A}\right|=1\) propiedades 8 y 1 del determinante \(\left|\mathbf{A}\right|\left|\mathbf{A}\right|=1\) propiedad 9 del determinante \(\left|\mathbf{A}\right|^{2}=1\)
\(\left|\mathbf{A}\right|=1\\ \left|\mathbf{A}\right|=-1\)
- Matriz idempotente: es aquella que, al multiplicarla por ella misma, te devuelve ella misma (idem=idéntica, potente=potencia) \(\mathbf{A}\mathbf{A}=\mathbf{A}\)
Sea \(\mathbf{A}\) una matriz idempotente. Determina para qué valores del escalar \(k\), la expresión \(\mathbf{I}-k\mathbf{A}\) es idempotente
Necesitamos que \(\left(\mathbf{I}-k\mathbf{A}\right)\left(\mathbf{I}-k\mathbf{A}\right)=\left(\mathbf{I}-k\mathbf{A}\right)\), entonces, vamos primero a operar:
\[ \left(\mathbf{I}-k\mathbf{A}\right)\left(\mathbf{I}-k\mathbf{A}\right)=\mathbf{I}\mathbf{I}-k\mathbf{A}\mathbf{I}-k\mathbf{A}\mathbf{I}-k^{2}\mathbf{A}\mathbf{A} \]
con lo que sabemos
\[ \left(\mathbf{I}-k\mathbf{A}\right)\left(\mathbf{I}-k\mathbf{A}\right)=\mathbf{I}-2k\mathbf{A}-k^{2}\mathbf{A} \]
ahora, pretendemos que \[ \mathbf{I}-2k\mathbf{A}-k^{2}\mathbf{A}=\mathbf{I}-k\mathbf{A}\Rightarrow-k\mathbf{A}-k^{2}\mathbf{A}=\mathbf{0}\Rightarrow-(k+k^{2})\mathbf{A}=\mathbf{0}\Rightarrow\begin{cases} k=0\\ k=-1 \end{cases} \]
- Matriz Nilpotente: es aquella matriz \(\mathbf{A}\) que, multiplicada por ella misma, te devuelve la matriz de ceros
\[\mathbf{A}\mathbf{A}=\mathbf{0} \]
por ejemplo,
\[\mathbf{A}=\left[\begin{array}{cc} 2 & -4 \\ 1 & -2 \end{array}\right]\]
Prueba que el producto te devuelve la matriz de ceros (\(\mathbf{0}\)) ¿No te parece curioso? Una matriz (distinta de cero) que se multiplica por ella misma y te devuelve ceros. ¡¡¡Eso no ocurre con los números reales!!! Haz algunos ejercicios para reforzar estas ideas
Ejercicios resueltos
Sean \[ A=\left[\begin{array}{cccc} 0 & 0 & 0 & 1\\ b & 0 & 0 & 0\\ 0 & -1 & 0 & 0\\ 0 & 0 & 1 & a \end{array}\right],B=\left[\begin{array}{cccc} 1 & 0 & 0 & 2\\ 0 & 2 & 0 & 1\\ 1 & 0 & 1 & 1\\ 0 & 0 & 1 & 2 \end{array}\right], \] obtén los valores de \(a,b\) para que \(A\) sea ortogonal.
- Necesitamos que \(A^{t}A=I,\)entonces \(\left(\begin{array}{cccc} 0 & b & 0 & 0\\ 0 & 0 & -1 & 0\\ 0 & 0 & 0 & 1\\ 1 & 0 & 0 & a \end{array}\right)\left(\begin{array}{cccc} 0 & 0 & 0 & 1\\ b & 0 & 0 & 0\\ 0 & -1 & 0 & 0\\ 0 & 0 & 1 & a \end{array}\right)=\left(\begin{array}{cccc} 1 & 0 & 0 & 0\\ 0 & 1 & 0 & 0\\ 0 & 0 & 1 & 0\\ 0 & 0 & 0 & 1 \end{array}\right)\Rightarrow\left(\begin{array}{cccc} b^{2} & 0 & 0 & 1\\ 0 & 1 & 0 & 0\\ 0 & 0 & 1 & 1\\ 0 & 0 & a & 1+a^{2} \end{array}\right)=\left(\begin{array}{cccc} 1 & 0 & 0 & 0\\ 0 & 1 & 0 & 0\\ 0 & 0 & 1 & 0\\ 0 & 0 & 0 & 1 \end{array}\right)\) de donde sacamos que \(a=0,b=\pm1\)
- ¿Es \(B\) invertible? Para que sea invertible, \(\left|B\right|\neq0.\) Usando la expresi?n del determinante por cofactores, nos fijamos en la segunda columna: \[ \left|B\right|=b_{12}C_{12}+b_{22}C_{22}+b_{32}C_{32}+b_{42}C_{42}\Rightarrow\left|B\right|=2(-1)^{2+2}M_{22}=2\left|\begin{array}{ccc} 1 & 0 & 2\\ 1 & 1 & 1\\ 0 & 1 & 2 \end{array}\right|=6 \] al ser distinto de cero, es invertible.
- Sea \(C\) una matriz tal que \(CB=A\). Muestre que \(C\) es invertible y calcule \(C^{-1}\)sin necesidad de usar ningún método de inversión.
- Para que \(C\) sea invertible, necesitamos calcular su determinante y asegurarnos que es distinto de cero. Usando las propiedades del determinante \[ \left|CB\right|=\left|A\right|\Rightarrow\left|C\right|\left|B\right|=\left|A\right|\Rightarrow\left|C\right|=\frac{\left|A\right|}{\left|B\right|} \] como sabemos que\(\left|A\right|\neq0\) por ser ortogonal y hemos obtenido que \(\left|B\right|\neq0,\)entonces \(\left|C\right|\) es invertible.
- Para obtener la inversa, podemos aprovechar la ortogonalidad de \(A\), de tal forma que \(AA^{t}=I\), entonces \[ CB{\color{red}A^{t}}=A{\color{red}A^{t}}\Rightarrow CBA^{t}=I \] ahora, introducimos la inversa de \(C,\)para despejar \[ {\color{red}C^{-1}}CBA^{t}={\color{red}C^{-1}}\Rightarrow BA^{t}=C^{-1} \] es decir, haciendo el producto de \(BA^{t},\)obtenemos la inversa de \(C.\)
Clase 5: La matriz escalonada y el rango de una matriz
Matriz escalonada
Definamos, visualmente, una matriz escalonada
\[ \left[\begin{array}{cccccc} * & \blacktriangleright & \blacktriangleright & \blacktriangleright & \blacktriangleright & \blacktriangleright\\ {\color{red}0} & {\color{red}0} & * & \blacktriangleright & \blacktriangleright & \blacktriangleright\\ {\color{red}0} & {\color{red}0} & {\color{red}0} & * & \blacktriangleright & \blacktriangleright\\ {\color{red}0} & {\color{red}0} & {\color{red}0} & {\color{red}0} & {\color{red}0} & {\color{red}0} \end{array}\right] \]
Donde;
- El elemento \(*\) Se llama pivote
- \(\blacktriangleright\) es un escalar cualquiera (incluso cero)
- El primer pivote tiene todo ceros debajo de él (primera columna)
- El resto de pivotes tienen todo ceros debajo de ellos en su columna y todo ceros a su izquierda.
- No puede haber un pivote encima de otro.
- Las últimas filas pueden ser todo de ceros.
Veamos diferentes matrices escalonadas:
\[ \left[\begin{array}{ccc} 2 & 4 & 1\\ {\color{red}0} & -1 & 2\\ {\color{red}0} & {\color{red}0} & {\color{red}0} \end{array}\right],\left[\begin{array}{ccc} 1 & 0 & 1\\ {\color{red}0} & 1 & 5\\ {\color{red}0} & {\color{red}0} & 4 \end{array}\right],\left[\begin{array}{cccc} 1 & 2 & 2 & 1\\ {\color{red}0} & {\color{red}0} & 2 & 3\\ {\color{red}0} & {\color{red}0} & {\color{red}0} & {\color{red}0} \end{array}\right] \]
Cualquier matriz puede escalonarse. Para ello, deberás trabajar con matrices elementales (es decir, realizar combinaciones lineales por filas) para obtener el resultado deseado
Rango de una matriz
El rango de una matriz es el número de filas/columnas linealmente independientes. Piensa por ejemplo en esta matriz:
\[ \left[\begin{array}{cc} 1 & 3\\ 2 & 6 \end{array}\right] \]
Recuerda que la idea de independencia lineal de los vectores (elijamos, por ejemplo, las columnas de la matriz) requiere que la solución a este sistema:
\[ \alpha_{1}\left[\begin{array}{c} 1\\ 2 \end{array}\right]+\alpha_{2}\left[\begin{array}{c} 3\\ 6 \end{array}\right]=\left[\begin{array}{c} 0\\ 0 \end{array}\right] \]
sea exactamente \(\alpha_{1}=\alpha_{2}=0\). ¿Qué quiere decir eso? Pues que conociendo uno de los dos vectores no puedo decir nada del otro. Por ejemplo, en este caso, es fácil ver que una posible solución al sistema es \(\alpha_{1}=3,\alpha_{2}=-1\), entonces
\[ 3\left[\begin{array}{c} 1\\ 2 \end{array}\right]-1\left[\begin{array}{c} 3\\ 6 \end{array}\right]=\left[\begin{array}{c} 0\\ 0 \end{array}\right] \]
En este caso, no son linealmente independientes. Si lo haces por filas, entonces
\[ \alpha_{1}\left[\begin{array}{c} 1\\ 3 \end{array}\right]+\alpha_{2}\left[\begin{array}{c} 2\\ 6 \end{array}\right]=\left[\begin{array}{c} 0\\ 0 \end{array}\right] \]
donde, enseguida, puedes ver que \(\alpha_{1}=1,\alpha_{2}=-1/2.\) Diremos, por lo tanto, que el rango de esta matriz es 1, puesto que hay un único vector “independiente” (cualquiera de los dos).
Una manera de obtener el rango de una matriz es mediante el cálculo de los determinantes de las submatrices cuadradas más grandes que pueden formarse. Recuerda que el determinante de una matriz será cero si una fila/columna es combinación lineal de otra(s). El rango será igual a la dimensión de la submatriz mayor con determinante distinto de cero. Por ejemplo:
\[ \left[\begin{array}{cccc} 1 & 0 & 2 & 1\\ 0 & 2 & 4 & 2\\ 0 & 2 & 2 & 3 \end{array}\right] \]
De los que tenemos:
Cuatro submatrices de orden 3 \(\left|\begin{array}{ccc} 1 & 0 & 2\\ 0 & 2 & 4\\ 0 & 2 & 3 \end{array}\right|,\left|\begin{array}{ccc} 1 & 0 & 1\\ 0 & 2 & 2\\ 0 & 2 & 3 \end{array}\right|,\left|\begin{array}{ccc} 0 & 2 & 1\\ 2 & 4 & 2\\ 2 & 2 & 3 \end{array}\right|,\left|\begin{array}{ccc} 1 & 2 & 1\\ 0 & 4 & 2\\ 0 & 2 & 3 \end{array}\right|\) como sus determinantes son distintos de cero, el rango de esta matriz es 3
Por ejemplo,
\[ \left[\begin{array}{cccc} 1 & 0 & 1 & 1\\ 1 & 2 & 3 & 3\\ 1 & 1 & 2 & 3 \end{array}\right] \]
si te das cuenta, la tercera columna la he generado sumando las dos primeras columnas (es decir, la tercera columna “depende” de las dos primeras). Tenemos cuatro submatrices de orden 3, empezamos
\(\left|\begin{array}{ccc} 1 & 0 & 1\\ 1 & 2 & 3\\ 1 & 1 & 2 \end{array}\right|=0\),
donde hemos encontrado ya un primer determinante igual a 0. Ya no puede tener rango 3. Veamos ahora con las submatrices de orden 2. Ojo, aquí tendremos ¡18! submatices. Fíjate que no vas a encontrar ninguna con determinante cero: \(\left|\begin{array}{cc} 1 & 0\\ 1 & 2 \end{array}\right|,\left|\begin{array}{cc} 0 & 1\\ 2 & 3 \end{array}\right|,...\)
Por lo que el rango de esta matriz es 2.
Sin embargo, esta manera de obtener el rango no es operativa. Podemos aprovechar el hecho de que el rango de una matriz no se va a ver afectado por sus operaciones elementales. Por ello, tratemos de escalonarla. Entonces, el rango será:
El rango de una matriz escalonada consiste en el número de filas de esta DISTINTAS de CERO. Y el rango de cualquier matriz coincide con el de su matriz escalonada.
Por ejemplo, calculemos el rango de la siguiente matriz (donde la segunda columna es dos veces la primera)
\[ \left[\begin{array}{cccc} 1 & 2 & 1 & 0\\ 2 & 4 & 1 & 1\\ 1 & 2 & -1 & 0\\ 0 & 0 & 1 & 1 \end{array}\right] \]
La escalonamos:
\[ \left[\begin{array}{cccc} 1 & 2 & 1 & 0\\ 2 & 4 & 1 & 1\\ 1 & 2 & -1 & 0\\ 0 & 0 & 1 & 1 \end{array}\right]\underrightarrow{E_{21}(-2)}\left[\begin{array}{cccc} 1 & 2 & 1 & 0\\ 0 & 0 & -1 & 1\\ 1 & 2 & -1 & 0\\ 0 & 0 & 1 & 1 \end{array}\right]\underrightarrow{E_{31}(-1)}\left[\begin{array}{cccc} 1 & 2 & 1 & 0\\ 0 & 0 & -1 & 1\\ 0 & 0 & -2 & 0\\ 0 & 0 & 1 & 1 \end{array}\right]\underrightarrow{E_{32}(-2)}\left[\begin{array}{cccc} 1 & 2 & 1 & 0\\ 0 & 0 & -1 & 1\\ 0 & 0 & 0 & -2\\ 0 & 0 & 1 & 1 \end{array}\right] \]
\[ \underrightarrow{E_{42}(1)}\left[\begin{array}{cccc} 1 & 2 & 1 & 0\\ 0 & 0 & -1 & 1\\ 0 & 0 & 0 & -2\\ 0 & 0 & 0 & 2 \end{array}\right]\underrightarrow{E_{43}(1)}\left[\begin{array}{cccc} {\color{red}1} & 2 & 1 & 0\\ 0 & 0 & {\color{red}{-1}} & 1\\ 0 & 0 & 0 & {\color{red}{-2}}\\ 0 & 0 & 0 & 0 \end{array}\right] \]
Como ya sabemos, tiene rango 3.
El rango de la matriz \(\mathbf{A\in\mathcal{M}_{\mathit{m\times n}}}\) ,escrito como \(rg(\mathbf{A})\) es el máximo número de vectores fila/columna linealmente independientes en la matriz \(\mathbf{A}\). Esto es, el rango de una matriz es igual al rango de su traspuesta :
\[ rg(\mathbf{A})=rg(\mathbf{A}^{t}). \]
Propiedades del rango:
FALTAAAAA
Ejercicio resuelto calcula el rango de la matriz \(\mathbf{A}\) en función del parámetro \(a\)
\[ \mathbf{A}=\left[\begin{array}{cccc} 2 & 4 & 0 & 2\\ 1 & 0 & 3 & -1\\ 3 & 4a & 3 & a \end{array}\right] \]
solución Escalonamos la matriz,
\(\left[\begin{array}{cccc} 2 & 4 & 0 & 2\\ 1 & 0 & 3 & -1\\ 3 & 4a & 3 & a \end{array}\right]\rightarrow E_{21}(-\frac{1}{2})\left[\begin{array}{cccc} 2 & 4 & 0 & 2\\ 0 & -2 & 3 & -2\\ 3 & 4a & 3 & a \end{array}\right]\rightarrow E_{31}(-\frac{3}{2})\left[\begin{array}{cccc} 2 & 4 & 0 & 2\\ 0 & -2 & 3 & -2\\ 0 & -6+4a & 3 & -3+a \end{array}\right]E_{32}(-3+2a)\left[\begin{array}{cccc} 2 & 4 & 0 & 2\\ 0 & -2 & 3 & -2\\ 0 & 0 & -6+6a & 3-3a \end{array}\right]\)
Como vemos, si \(a=1\), entonces, la matriz escalonada que obtenemos es\(\left[\begin{array}{cccc} {\color{red}2} & 4 & 0 & 2\\ 0 & {\color{red}-2} & 3 & -2\\ 0 & 0 & 0 & 0 \end{array}\right]\) cuyo rango es 2. En caso de que \(a\neq1\), el rango de la matriz es 3.
Clase 6: Subespacios fila y columna de una matriz: dimensión y base de un subespacio
Atención
Antes de empezar esta sesión, es bueno que recuerdes esto que ya sabías
Subespacios de En \(\mathbb{R}^{2}\):
- El punto \((0,0)\)
- Cualquier recta que pase por el origen (un vector director, una ecuación cartesiana)
- Todo \(\mathbb{R}^{2}\)
Subespacios de En \(\mathbb{R}^{3}\):
- El punto \((0,0,0)\)
- Cualquier recta que pase por el origen (un vector director/dos ecuaciones cartesianas)
- Cualquier plano que pase por el origen (dos vectores directores/una ecuación cartesiana)
- Todo \(\mathbb{R}^{3}\)
Volvemos a recuperar una idea con la que ya trabajamos en el primer tema: el conjunto generador. Sea un conjunto de vectores \(\overrightarrow{v}_{1},...,\overrightarrow{v}_{k}\in\mathbb{R}^{n}\) (recuerda, también, que esto quiere decir que los \(k\) vectores están definidos en un espacio vectorial de dimensión \(n\)) definimos generador (o sistema generador)
\[ Gen\left\{ \overrightarrow{v}_{1},\overrightarrow{v}_{2},...,\overrightarrow{v}_{k}\right\} =\alpha_{1}\overrightarrow{v}_{1}+\alpha_{2}\overrightarrow{v}_{2}+...+\alpha_{k}\overrightarrow{v}_{k}, \]
como ves, son las posibles combinaciones lineales que pueden “generarse” con los vectores del conjunto
Ejercicio resuelto
Indica qué figura geométrica en el plano/espacio representan los siguientes conjuntos generadores
- Caso 1 \[ Gen\left\{ \left[\begin{array}{c} 1\\ 0\\ 1 \end{array}\right],\left[\begin{array}{c} -1\\ 1\\ 0 \end{array}\right]\right\} \]
solución
como ves, representa
\[ Gen\left\{ \left[\begin{array}{c} 1\\ 0\\ 1 \end{array}\right],\left[\begin{array}{c} -1\\ 1\\ 0 \end{array}\right]\right\} =\alpha_{1}\left[\begin{array}{c} 1\\ 0\\ 1 \end{array}\right]+\alpha_{2}\left[\begin{array}{c} -1\\ 1\\ 0 \end{array}\right] \]
un plano en \(\mathbb{R}^{3}\) que pasa por el origen.
- Caso 2
\[ Gen\left\{ \left[\begin{array}{c} 1\\ 0\\ 1 \end{array}\right],\left[\begin{array}{c} -1\\ 1\\ 0 \end{array}\right],\left[\begin{array}{c} 0\\ 1\\ 1 \end{array}\right]\right\} \]
si te fijas,
\[ Gen\left\{\left[\begin{array}{c} 1\\ 0\\ 1 \end{array}\right],\left[\begin{array}{c} -1\\ 1\\ 0 \end{array}\right],\left[\begin{array}{c} 0\\ 1\\ 1 \end{array}\right]\right\}=\alpha_{1}\left[\begin{array}{c} 1\\ 0\\ 1 \end{array}\right]+\alpha_{2}\left[\begin{array}{c} -1\\ 1\\ 0 \end{array}\right]+\alpha_{3}\left[\begin{array}{c} 0\\ 1\\ 1 \end{array}\right] \]
el tercer vector es la suma de los otros dos. Es decir, el tercer vector no es linealmente independiente de los otros dos (analiza el rango de la matriz \(A=\left[\begin{array}{ccc} 1 & -1 & 0\\ 0 & 1 & 1\\ 1 & 0 & 1 \end{array}\right])\). Entonces, en realidad aunque haya tres vectores en el conjunto, estamos representando el mismo plano. Puedes verlo con Geogebra.
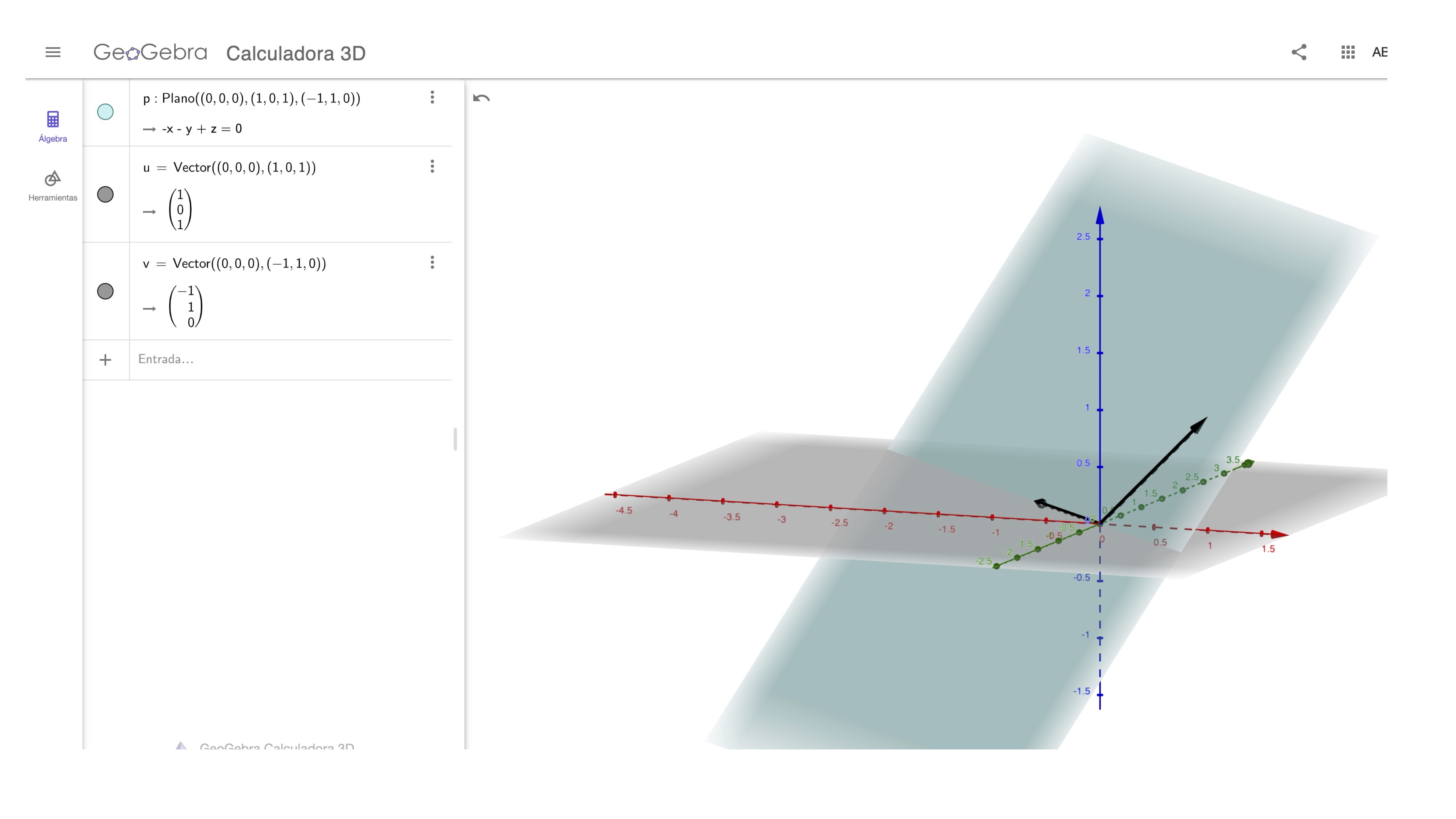
FIG1: el plano, definido con los dos vectores directores
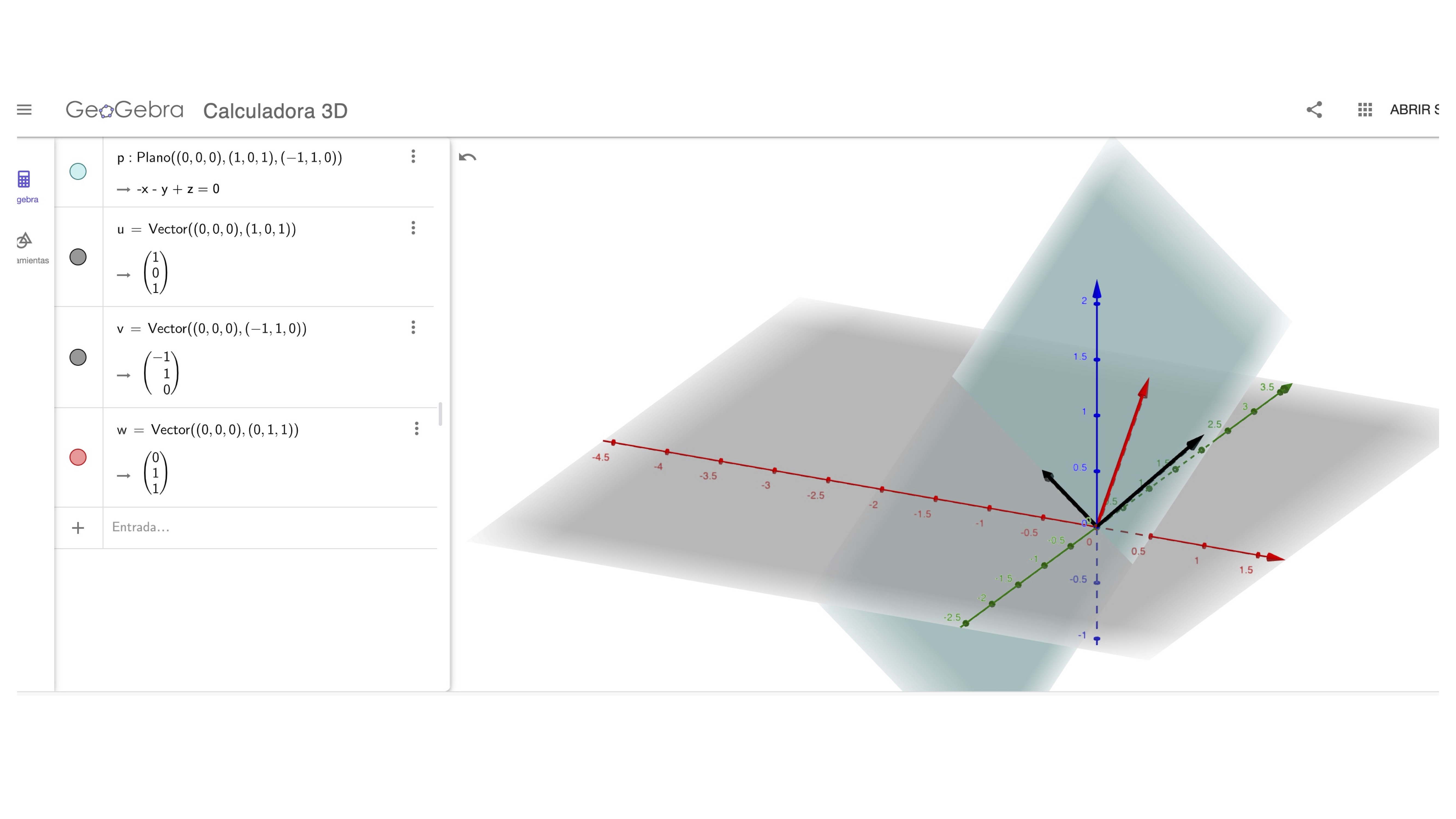
FIG2: el plano, definido con un vector que no aporta nada nuevo
En realidad, aquí ocurre que
\[ Gen\left\{ \left[\begin{array}{c} 1\\ 0\\ 1 \end{array}\right],\left[\begin{array}{c} -1\\ 1\\ 0 \end{array}\right]\right\} =Gen\left\{ \left[\begin{array}{c} 1\\ 0\\ 1 \end{array}\right],\left[\begin{array}{c} -1\\ 1\\ 0 \end{array}\right],\left[\begin{array}{c} 0\\ 1\\ 1 \end{array}\right]\right\} \]
ya que ambos representan lo mismo. Nota que estamos representando las ecuaciones paramétricas de un plano en tres dimensiones que pasa por el origen. Recuerda que es un subespacio. Sin embargo, diremos que el primer conjunto es “más eficiente” que el segundo. El primer conjunto contiene el mínimo número de vectores que necesitamos para representar el subespacio. El segundo, contiene uno que-en realidad- sobra. Para diferenciar el primer tipo del segundo, llamaremos base al sistema generador donde los vectores son linealmente independientes y sistema generador a cualquier conjunto de vectores que no es linealmente independiente y que generan un (sub)espacio.
Entonces…
Estamos interesados en caracterizar los subespacios que conocemos mediante conjuntos generadores
Definición de base
Sea \(H\subseteq\mathbb{R}^{n}\), un (sub)espacio vectorial. Diremos que \(B\left\{ \overrightarrow{v}_{1},\overrightarrow{v}_{2},...,\overrightarrow{v}_{k}\right\}\) es una base del subespacio si los vectores son sistema generador (es decir, \(H=Gen\left\{ \overrightarrow{v}_{1},\overrightarrow{v}_{2},...,\overrightarrow{v}_{k}\right\}\)) y son linealmente independientes (es decir, no sobra ningún vector).
cuando te damos los vectores directores de una recta o un plano que pasan por el origen, te estamos dando, en realidad, una base de estos subespacios.
Fijémonos en \(\mathbb{R}^{3}\). Un plano que pasa por el origen puede tener, como ecuaciones paramétricas
\[\begin{equation} \left(\begin{array}{c} x\\ y\\ z \end{array}\right)=\alpha_{1}\left(\begin{array}{c} 1\\ 0\\ 1 \end{array}\right)+\alpha_{2}\left(\begin{array}{c} -1\\ 1\\ o \end{array}\right) \end{equation}\]
Entonces, diremos que: Una base para el plano con el que estamos trabajando será
\[ B_{plano}=\left\{ \left(\begin{array}{c} 1\\ 0\\ 1 \end{array}\right),\left(\begin{array}{c} -1\\ 1\\ 0 \end{array}\right)\right\} \]
La idea intuitiva de base de un subespacio es un “esqueleto” sobre el que asentaremos la figura.
1.4 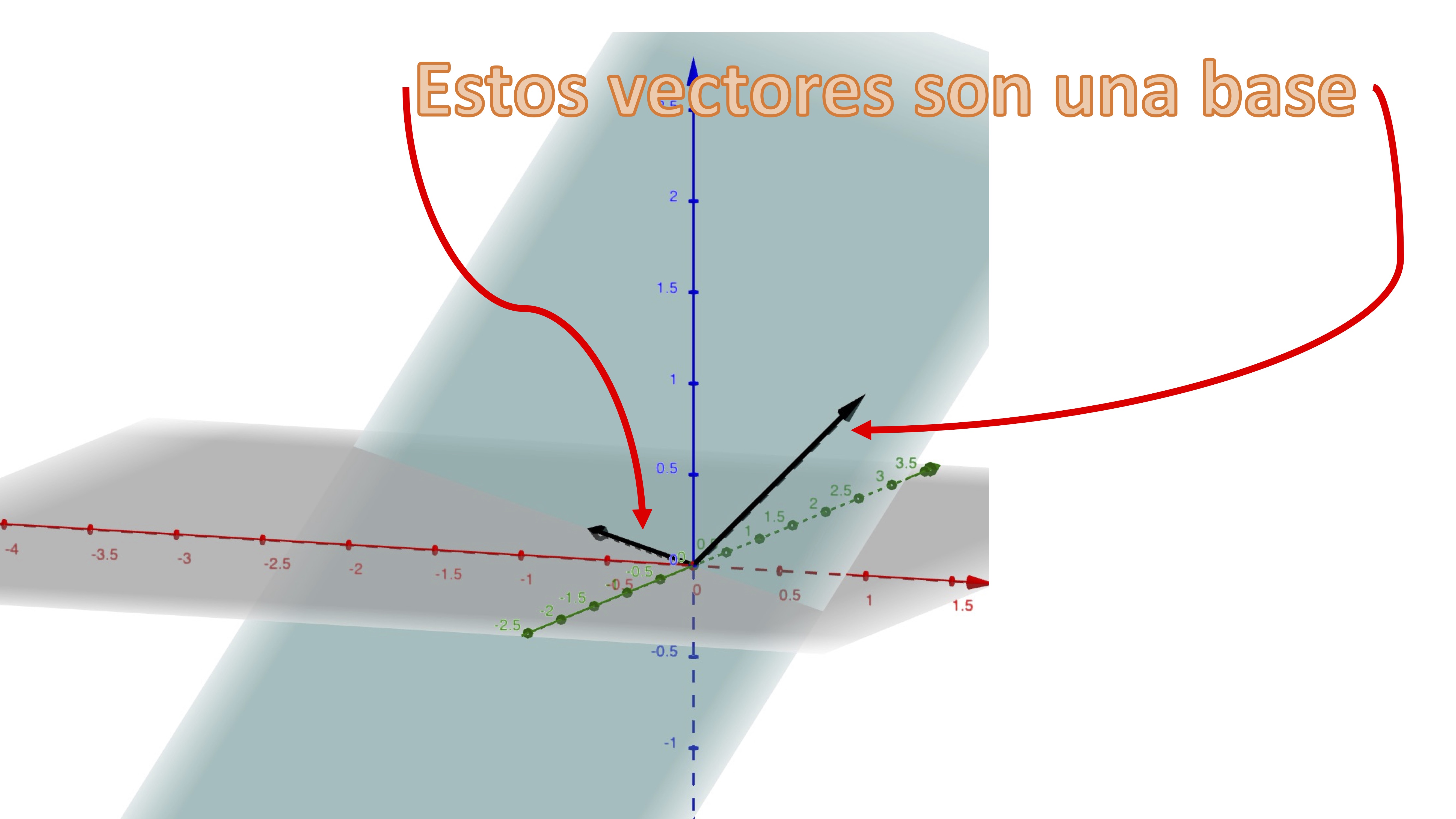
Ejercicio resuelto
¿Es el conjunto siguiente generador de un plano en \(\mathbb{R}^{3}\)?
\[ Gen\left\{ \left(\begin{array}{c} 1\\ 0\\ 5 \end{array}\right),\left(\begin{array}{c} 2\\ 0\\ 10 \end{array}\right)\right\} \]
Si nos damos cuenta, el segundo vector es el doble del primero. No son linelamente independientes, por lo que no puede generar un plano. Este conjunto genera una recta que pasa por el origen en \(\mathbb{R}^{3}\):
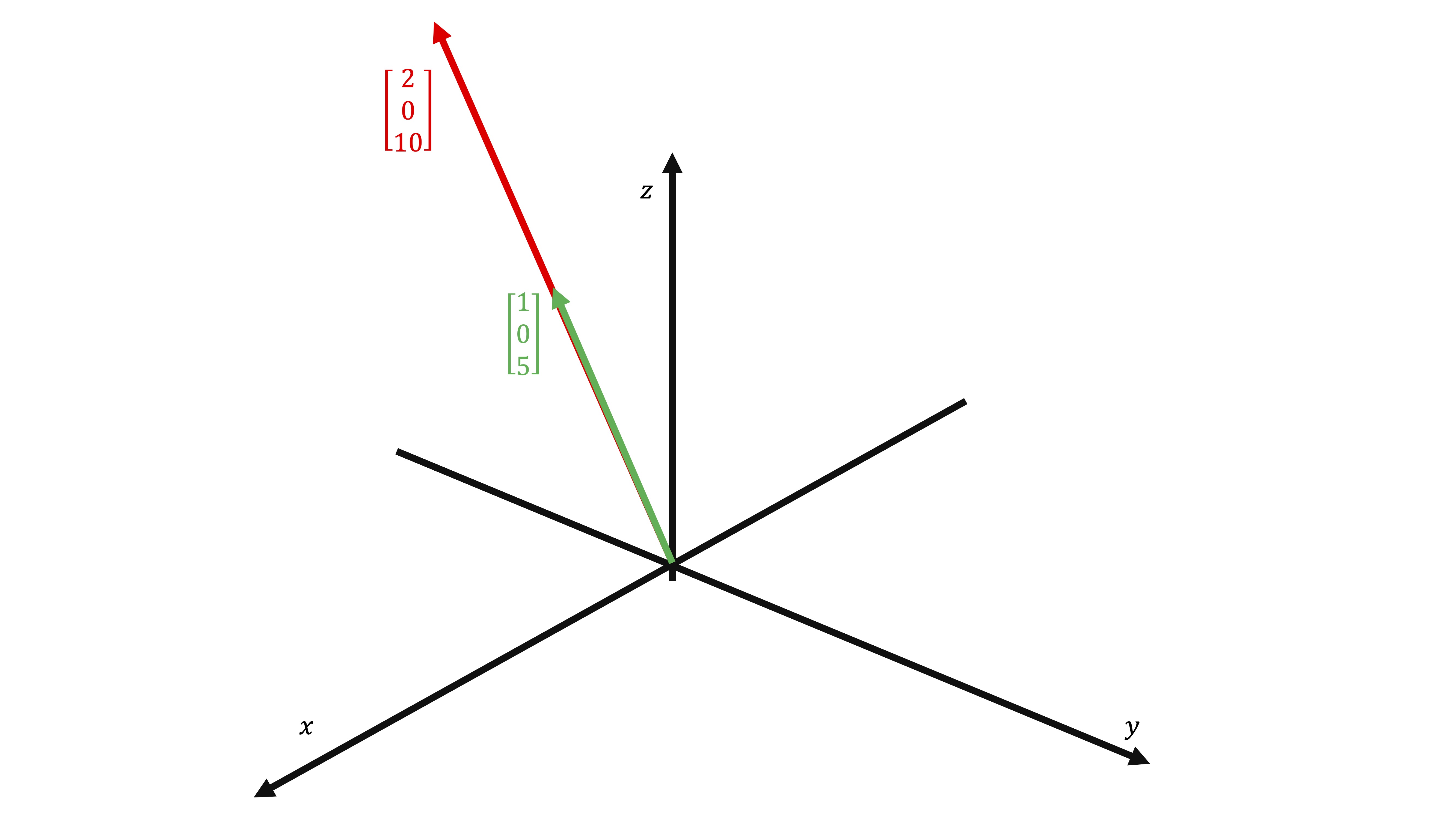
FIG4: ¡Esto es una base!
De hecho, una base posible de este subespacio será \[ B_{recta}=\left\{ \left(\begin{array}{c} 1\\ 0\\ 5 \end{array}\right)\right\} \]
otra, podría ser
\[ B_{recta}=\left\{ \left(\begin{array}{c} 2\\ 0\\ 10 \end{array}\right)\right\} \]
etc…
Dimensión de un subespacio
La dimensión de \(H\subseteq\mathbb{R}^{n}\), un (sub)espacio vectorial, es el número de elementos que tiene la base. Aunque te parezca muy abstracto, en el caso de la recta y el plano, enseguida lo vas a entender.
Podemos pensar en un plano como en una tabla de una mesa. Cuando la vas a comprar, necesitas saber las dimensiones. La mesa Lagkapten, por ejemplo, tiene un largo de 120 centímetros y un ancho de 60
FIG4: La mesa Lagkapten
es decir, necesitamos dos dimensiones. Una recta es, por ejemplo, un lápiz que, como sabes, tiene una dimensión (el largo). ¡Esto ya lo has visto en el primer tema!.
¿Qué pasa en \(\mathbb{R}^{4}?\)
- Una recta tendrá un vector director y, por tanto, dimensión 1
- Un plano tendrá dos vectores directores y, por tanto, dimensión 2
¿Qué pasa en \(\mathbb{R}^{n}?\)
- Una recta tendrá un vector director y, por tanto, dimensión 1
- Un plano tendrá dos vectores directores y, por tanto, dimensión 2
Vamos a profundizar más en estas ideas, dándonos cuenta de que en una matriz podemos obtener un conjunto de vectores fila y columna, como ya sabemos. Lo veremos con un ejemplo de una matriz sencilla
Definamos una matriz \(\mathbf{A\in\mathcal{M}}_{2\times3}\)
\[ \mathbf{A}=\left[\begin{array}{ccc} 1 & 0 & 1\\ 1 & 1 & 2 \end{array}\right] \]
que tendrça dos conjuntos de vectores. Por filas:
\[ F(A)=\left\{ \left[\begin{array}{c} 1\\ 0\\ 1 \end{array}\right],\left[\begin{array}{c} 1\\ 1\\ 2 \end{array}\right]\right\} \] como ves, las filas de la matriz pertenecen al espacio vectorial \(\mathbb{R}^{3}\), mientras que las columnas
\[ C(A)=\left\{ \left[\begin{array}{c} 1\\ 1 \end{array}\right],\left[\begin{array}{c} 0\\ 1 \end{array}\right],\left[\begin{array}{c} 1\\ 2 \end{array}\right]\right\} \]
pertenecen a \(\mathbb{R}^{2}.\) Es decir, una matriz \(\mathbf{A\in\mathcal{M}}_{m\times n}\) nos proporciona un conjunto de \(m\) vectores fila \(F(A)\in\mathbb{R}^{n}\) y un conjunto de \(n\) vectores columna \(C(A)\in\mathbb{R}^{m}\). Ahora veremos que este conjunto de vectores conforman subespacios de distintos espacios vectoriales
(Sub)espacio fila F(A)
Tenemos \(m\) filas en \(\mathbb{R}^{n}.\) El (sub)espacio lo podemos crear realizando una combinación lineal de las filas de la matriz, expresadas como vectores columna:
\[ F(\mathbf{A})=Gen\left\{ \left[\begin{array}{c} \\ fila\\ \\ \end{array}1\right]\left[\begin{array}{c} \\ fila\\ \\ \end{array}2\right],...,\left[\begin{array}{c} \\ fila\\ \\ \end{array}m\right]\right\} \]
El (sub)espacio fila de la matriz \(\mathbf{A}\) , \(F(\mathbf{A})\subseteq\) \(\mathbb{R}^{n}\) . El subespacio serán todos los vectores \(\left[\begin{array}{c} x_{1}\\ ...\\ x_{n} \end{array}\right]\) que podemos obtener como combinación lineal de las filas. Por supuesto, una base para este subespacio será el conjunto de vectores linealmente independientes.
Ejemplo: calcula Una base para el el subespacio de las filas de la Matriz \[ \mathbf{A}=\left[\begin{array}{ccc} 1 & 0 & 1\\ 1 & 1 & 2 \end{array}\right] \]
Tenemos, por un lado, que \[ F(\mathbf{A})=Gen\left\{ \left[\begin{array}{c} 1\\ 0\\ 1 \end{array}\right],\left[\begin{array}{c} 1\\ 1\\ 2 \end{array}\right]\right\} \] que es fácil de ver que son linelamente independientes, por lo que la base
\[ B_{F(\mathbf{A})}=\left\{ \left[\begin{array}{c} 1\\ 0\\ 1 \end{array}\right],\left[\begin{array}{c} 1\\ 1\\ 2 \end{array}\right]\right\} \]
y, la dimensión
\[ dim\left(B_{F(A)}\right)=2 \]
es decir, tenemos un plano en \(\mathbb{R}^{3}\) que pasa por el origen de coordenadas.
(sub)espacio columna C(A)
El (sub)espacio columna es aquel que podemos construir mediante una combinación lineal con las columnas de la matriz.
\[ C(\mathbf{A})=Gen\left\{ \left[\begin{array}{c} \\ col\\ \\ \end{array}1\right]\left[\begin{array}{c} \\ col\\ \\ \end{array}2\right],...,\left[\begin{array}{c} \\ col\\ \\ \end{array}n\right]\right\} \]
El (sub)espacio columna de la matriz \(\mathbf{A}\) , \(C(\mathbf{A})\subseteq\) \(\mathbb{R}^{m}\) . El subespacio serán todos los vectores \(\left[\begin{array}{c} x_{1}\\ ...\\ x_{m} \end{array}\right]\) que podemos obtener como combinación lineal de las columas. Por supuesto, una base para este subespacio será el conjunto de vectores linealmente independientes.
Ejemplo: Una base para el el subespacio de las columnas de la Matriz \[ \mathbf{A}=\left[\begin{array}{ccc} 1 & 0 & 1\\ 1 & 1 & 2 \end{array}\right] \]
Tenemos, por un lado, que \[ C(\mathbf{A})=Gen\left\{ \left[\begin{array}{c} 1\\ 1 \end{array}\right],\left[\begin{array}{c} 0\\ 1 \end{array}\right],\left[\begin{array}{c} 1\\ 2 \end{array}\right]\right\} \] Si escalonamos la matriz para analizar su rango \[ \mathbf{A}=\left[\begin{array}{ccc} 1 & 0 & 1\\ 1 & 1 & 2 \end{array}\right]\rightarrow E_{21}(-1)\left[\begin{array}{ccc} {\color{red}1} & 0 & 1\\ 0 & {\color{red}1} & 1 \end{array}\right] \]
como vemos, tenemos dos pivotes, por lo que el rango de \(\mathbf{A}\)(ya lo sab?amos) es 2. Dos vectores linealmente independientes son los de la matriz \(\mathbf{A}\) que se corresponden con los pivotes de la matriz escalonada
\[ B_{C(\mathbf{A})}=\left\{ \left[\begin{array}{c} 1\\ 1 \end{array}\right],\left[\begin{array}{c} 0\\ 1 \end{array}\right]\right\} \]
y, la dimensión \[ dim\left(B_{C(A)}\right)=2 \]
es decir, estamos generando todo \(\mathbb{R}^{2}\)%
Es fácil deducir:
La dimensión del (sub)espacio fila y columna de la matriz \(\mathbf{A}\) es la misma:
\[ dim(R(\mathbf{A}))=dim(C(\mathbf{A}))=rango(\mathbf{A}) \]
Y, con esto, se termina el capítulo. Recuerda que has aprendido muchas, muchas cosas. Es el momento de ordenarlas en tu cabeza.

FIG. y yo, que creía que ya sabía mucho de matrices