Tema 3: Sistemas de Ecuaciones

Clase 1: Introducción a los sistemas de ecuaciones

Un sistema de ecuaciones es una aplicación práctica de todo lo que hemos visto anteriormente. Por ejemplo, el sistema:

\[ \begin{cases} a_{11}x+a_{12}y=b_{1}\\ a_{21}x+a_{22}y=b_{2} \end{cases} \]

se puede escribir, mediante notación matricial, como:

\[ \left[\begin{array}{cc} a_{11} & a_{12}\\ a_{21} & a_{22} \end{array}\right]\left[\begin{array}{c} x_{1}\\ x_{2} \end{array}\right]=\left[\begin{array}{c} b_{1}\\ b_{2} \end{array}\right] \]

Donde tenemos:

Una matriz (que llamaremos matriz de coeficientes)

\[ \mathbf{A}=\left[\begin{array}{cc} a_{11} & a_{12}\\ a_{21} & a_{22} \end{array}\right] \]

Un vector de variables /incógnitas

\[ \overrightarrow{x}=\left[\begin{array}{c} x_{1}\\ x_{2} \end{array}\right] \]

Un vector de términos independientes

\[ \overrightarrow{b}=\left[\begin{array}{c} b_{1}\\ b_{2} \end{array}\right] \]

El uso del producto matricial, pudiendo escribir- de manera compacta- el sistema como

\[ \mathbf{A}\overrightarrow{x}=\overrightarrow{b} \]

Ejericio resuelto

Escribe el sistema anterior de tal forma que lo pongas como una combinación lineal de las columnas de la matriz $\mathbf{A}$? ¿Cómo será el vector $\overrightarrow{b}$ con respecto al espacio $Col(\mathbf{A})$?

solución: El sistema podemos escribirlo como

\[ \left[\begin{array}{c} a_{11}\\ a_{21} \end{array}\right]x_{1}+\left[\begin{array}{c} a_{12}\\ a_{22} \end{array}\right]x_{2}=\left[\begin{array}{c} b_{1}\\ b_{2} \end{array}\right] \]

Si el sistema tiene solución, entonces, somos capaces de encontrar valores para $x_{1},x_{2}$ de tal forma que $\overrightarrow{b}$ está contenido en el espacio columna de $\mathbf{A}.$ Es decir, si un sistema es resoluble, entonces $\overrightarrow{b}{\subseteq Col(A)}$

Por ejemplo, planteamos el siguiente sistema

\[ \left[\begin{array}{cc} -1 & 1\\ 2 & -1 \end{array}\right]\left[\begin{array}{c} x_{1}\\ x_{2} \end{array}\right]=\left[\begin{array}{c} -0.5\\ 1.5 \end{array}\right] \]

Pero también lo puedes ver como una combinación lineal de las columnas de la matriz de coeficientes $\mathbf{A}$

\[ x_{1}\left[\begin{array}{c} -1\\ 2 \end{array}\right]+x_{2}\left[\begin{array}{c} 1\\ -1 \end{array}\right]=\left[\begin{array}{c} -0.5\\ 1.5 \end{array}\right], \]

entonces, diremos que el sistema tiene solución si somos capaces de encontrar los valores de $x_{1}$y $x_{2}$ que permiten que el vector $\left[\begin{array}{c} -0.5\\ 1.5 \end{array}\right]$

esté generado por la combinación lineal propuesta. Veámoslo gráficamente

$FIG1:Dibujamos las dos rectas en \mathbb{R}^{2} que dan lugar al sistema representado abajo$

FIG1:Dibujamos las dos rectas en $\mathbb{R}^{2}$ que dan lugar al sistema representado abajo

\[ \begin{cases} x_{2}=x_{1}-0.5\\ x_{1}=\frac{1}{2}x_{2}+0.75 \end{cases}\]

En este caso, la solución es un punto, es decir,

\[ \overrightarrow{x}=\left[\begin{array}{c} 1\\ 0.5 \end{array}\right], \]

que, sustituyendo en el sistema

\[ \left[\begin{array}{c} -1\\ 2 \end{array}\right]\times 1+\left[\begin{array}{c} 1\\ -1 \end{array}\right]\times 0.5=\left[\begin{array}{c} -0.5\\ 1.5 \end{array}\right] \]

Es decir, la única forma que tenemos de que el vector $\left[\begin{array}{c} -0.5\\ 1.5 \end{array}\right]$ pertenezca al espacio de las columnas de la matriz de coeficientes $\mathbf{A}$ es asignando $x_{1}=1,x_{2}=0.5.$ Decimos que, cuando la solución es un punto el sistema es COMPATIBLE DETERMINADO (compatible es que tiene solución y determinado que esta es única). Si tuviéramos infinitas soluciones, lo llamaríamos compatible indeterminado (es decir, tiene solución, pero son infinitas) y si no tiene solución: incompatible. Geométricamente, representan:

FIG2: Distintos tipos de soluciones

Ejercicio resuelto

Escribe dos sistemas: uno que sea compatible indeterminado y, a partir de este, modifícalo para que sea incompatible. Explica cómo lo has hecho.

Es muy fácil construir un sistema que cumpla con ciertas características. Por ejemplo, partimos de la ecuación \[ 2x+3y=4 \]

si queremos que sea compatible indeterminado, deberemos hacer que esta recta sea proporcional . Por ejemplo, la podemos multiplicar por 3: \[ \begin{cases} 2x+3y=4\\ 6x+9y=12 \end{cases} \]

En realidad, ambas ecuaciones están dando la misma información.

Si queremos que sea incompatible, entonces partiremos de caulquiera de las dos ecuaciones anteriores y diremos algo que sea imposible. Por ejemplo, \[ \begin{cases} 2x+3y=4\\ 6x+9y=11 \end{cases} \]

No puede ocurrir que, si una ecuación es el triple que la otra, la suma no dé el triple. Esto es imposible y, por lo tanto, se dice que es incompatible.

Ahora, una pregunta

¿Cómo escribimos cualquier sistema, general, en forma matricial? ¿cuáles han de ser sus dimensiones?

\[ \underset{\left[\begin{array}{cccc} a_{11} & a_{12} & ... & a_{1n}\\ a_{21} & a_{22} & ... & a_{2n}\\ ... & ... & ... & ...\\ a_{m1} & a_{m2} & ... & a_{mn} \end{array}\right]}{\mathbf{A}}\underset{\left[\begin{array}{c} x_{1}\\ x_{2}\\ ...\\ x_{n} \end{array}\right]}{\overrightarrow{x}}=\underset{\left[\begin{array}{c} b_{1}\\ b_{2}\\ ...\\ b_{m} \end{array}\right]}{\overrightarrow{b}} \]

Donde definimos:

$\mathbf{A}$ matriz de coeficientes $\mathbf{A}\in\mathcal{M}_{m\times n}$

$\overrightarrow{x}$ vector de incógnitas $\overrightarrow{x}\in\mathcal{M}_{n\times1}$

$\overrightarrow{b}$ vector de término independiente $\overrightarrow{b}\in\mathcal{M}_{m\times1}$

Importante: si $\overrightarrow{b}=\left[\begin{array}{c} 0\\ 0\\ ...\\ 0 \end{array}\right]$, decimos que el sistema es ``homogéneo’’.

Otro ejemplo que puede visualizarse es un sistema de tres ecuaciones con tres incógnitas. Nota que, en realidad, tienes tres ecuaciones cartesianas de tres planos en $\mathbb{R}^{3}$

\[ \left[\begin{array}{ccc} a_{11} & a_{12} & a_{13}\\ a_{21} & a_{22} & a_{23}\\ a_{31} & a_{32} & a_{33} \end{array}\right]\left[\begin{array}{c} x_{1}\\ x_{2}\\ x_{3} \end{array}\right]=\left[\begin{array}{c} b_{1}\\ b_{2}\\ b_{3} \end{array}\right] \]

Nada nos asegura que el sistema tenga solución, incluso que sea única. De hecho, se pueden presentar diferentes casos, como puedes ver en la siguiente figura.

FIG3: El sistema tiene una única solución

Por ejemplo:

\[ \left[\begin{array}{ccc} 1 & -2 & 1\\ 0 & 2 & -1\\ 1 & -1 & 2 \end{array}\right]\left[\begin{array}{c} x_{1}\\ x_{2}\\ x_{3} \end{array}\right]=\left[\begin{array}{c} 1\\ 1\\ 3 \end{array}\right] \]

Como ves, la solución viene dada por un punto en $\mathbb{R}^3$. Diremos, entonces, que el conjunto solución es:

\[ Sol=\left\{ \left(2,1,1\right)\right\} , \]

FIG4: El sistema tiene infinitas soluciones

Por ejemplo,

\[ \left[\begin{array}{ccc} 1 & -2 & 1\\ {\color{red}{0.5}} & {\color{red}{-1}} & {\color{red}{0.5}}\\ 1 & -1 & 2 \end{array}\right]\left[\begin{array}{c} x_{1}\\ x_{2}\\ x_{3} \end{array}\right]=\left[\begin{array}{c} 1\\ {\color{red}{0.5}}\\ 3 \end{array}\right] \]

fíjate, para conseguir un sistema compatible indeterminado, hemos hecho que la segunda ecuación se construya con la primera dividida por 2: esto es, una de las dos ecuaciones “sobra” puesto que no aporta información.

En este caso, la solución es un conjunto de puntos que da lugar a una recta. Ya sabes, del primer capítulo, que una recta en $\mathbb{R}^3$ se construye con dos ecuaciones cartesianas

\[ \begin{cases} x_{1}-2x_{2}+x_{3}=1\\ x_{1}-x_{2}+2x_{3}=3 \end{cases} \]

podemos tener, enseguida, la solución como ya sabes del primer capítulo:

Obtengo la recta que representan estas ecuaciones cartesianas del plano

Hago $x_{3}={{\lambda}}$, entonces, si restas las ecuaciones, obtienes $x_{2}=2-\lambda$ y, si sustituyes, obtienes $x_{1}=5-3\lambda$. Entonces, la solución de este sistema resulta ser \[ \left[\begin{array}{c} x_{1}\\ x_{2}\\ x_{3} \end{array}\right]=\left[\begin{array}{c} 5\\ 2\\ 0 \end{array}\right]+\lambda\left[\begin{array}{c} -3\\ -1\\ 1 \end{array}\right] \]

que es una recta en $\mathbb{R}^{3}$. El conjunto solución se dice que es: \[ Sol=\left\{ \overrightarrow{x}\in\mathbb{R}^{3}\::\:\left[\begin{array}{c} x_{1}\\ x_{2}\\ x_{3} \end{array}\right]=\left[\begin{array}{c} 5\\ 2\\ 0 \end{array}\right]+\lambda\left[\begin{array}{c} -3\\ -1\\ 1 \end{array}\right]\right\} \]

Si miras con más atención el dibujo, donde incluimos la recta que representa el conjunto solución:

FIG5: La recta que conforma la solución al sistema

Y, finalmente, cuando el sistema no tiene solución:

FIG6: La recta que conforma la solución al sistema

\[ \left[\begin{array}{ccc} {\color{lime}1} & {\color{lime}{-2}} & {\color{lime}1}\\ {\color{red}1} & {\color{red}{-2}} & {\color{red}1}\\ {\color{blue}1} & {\color{blue}{-2}} & {\color{blue}1} \end{array}\right]\left[\begin{array}{c} x_{1}\\ x_{2}\\ x_{3} \end{array}\right]=\left[\begin{array}{c} {\color{lime}1}\\ {\color{red}{-1}}\\ {\color{blue}3} \end{array}\right] \]

como ves, escribimos en la parte izquierda los mismos coeficientes para las ecuaciones cartesianas de los planos pero, en la parte izquierda, ponemos diferentes valores para el término independiente. Esto da lugar a la FIG 6, donde los planos son paralelos: no hay intersección posible.

Método de resolución de sistemas (1): Cramer

Si la matriz $\mathbf{A}$ que define el sistema es cuadrada $(n\times n)$, tenemos que:

\[ \mathbf{A}\overrightarrow{x}=\overrightarrow{b} \]

Imaginemos que es un sistema $3\times3$, y entonces:

\[ a_{11}x_{1}+a_{12}x_{2}+a_{13}x_{3}=b_{1} \]

\[ a_{21}x_{1}+a_{22}x_{2}+a_{23}x_{3}=b_{2} \]

\[ a_{31}x_{1}+a_{32}x_{2}+a_{33}x_{3}=b_{3} \]

es decir, \[ x_{1}\left[\begin{array}{c} a_{11}\\ a_{21}\\ a_{31} \end{array}\right]+x_{2}\left[\begin{array}{c} a_{12}\\ a_{22}\\ a_{32} \end{array}\right]+x_{3}\left[\begin{array}{c} a_{13}\\ a_{23}\\ a_{33} \end{array}\right]=\left[\begin{array}{c} b_{1}\\ b_{2}\\ b_{3} \end{array}\right] \]

o también, si escribimos las columnas de la matriz $\mathbf{A}$ como vectores, $\mathbf{A}=\left[\overrightarrow{a}_{\bullet1},\overrightarrow{a}_{\bullet2},\overrightarrow{a}_{\bullet3}\right]$, (no olvides, por ejemplo $\overrightarrow{a}_{\bullet1}=\left[\begin{array}{c} a_{11}\\ a_{21}\\ a_{31} \end{array}\right])$ el sistema se puede escribir de forma compacta como

\[ x_{1}\overrightarrow{a}_{\bullet1}+x_{2}\overrightarrow{a}_{\bullet2}+x_{3}\overrightarrow{a}_{\bullet3}=\overrightarrow{b} \]

Recuerda que, por el método de Cramer, este sistema tiene solución mediante el siguiente cálculo (algo tedioso) \[ \begin{cases} \frac{\left|\begin{array}{ccc} {\overrightarrow{b}} & \overrightarrow{a}_{\bullet2} & \overrightarrow{a}_{\bullet3}\end{array}\right|}{\left|A\right|}=x_{1}\\ \frac{\left|\begin{array}{ccc} \overrightarrow{a}_{\bullet1} & {\overrightarrow{b}} & \overrightarrow{a}_{\bullet3}\end{array}\right|}{\left|A\right|}=x_{2}\\ \frac{\left|\begin{array}{ccc} \overrightarrow{a}_{\bullet1} & \overrightarrow{a}_{\bullet2} & {\overrightarrow{b}}\end{array}\right|}{\left|A\right|}=x_{3} \end{cases} \]

Este método no es conveniente aplicarlo a sistemas de mayor dimensión

También puede aplicarse a sistemas compatibles indeterminados.

Para entender de dónde viene el método de Cramer, basta con mirar con detenimiento este determinante. Es el determinante de la matriz de coeficientes donde, en la primera columna, hemos puesto el vector $\overrightarrow{b}$ de términinos independientes

\[ \left|\begin{array}{ccc} \overrightarrow{b} & \overrightarrow{a}_{\bullet2} & \overrightarrow{a}_{\bullet3}\end{array}\right| \]

Nótese que el sistema podemos escribirlo como $x_{1}\overrightarrow{a}_{\bullet1}+x_{2}\overrightarrow{a}_{\bullet2}+x_{3}\overrightarrow{a}_{\bullet3}=\overrightarrow{b}$,

de tal forma que

\[ \left|\begin{array}{ccc} \overrightarrow{b} & \overrightarrow{a}_{\bullet2} & \overrightarrow{a}_{\bullet3}\end{array}\right|=\left|\begin{array}{ccc} {\color{blue}x_{1}\overrightarrow{a}_{\bullet1}+x_{2}\overrightarrow{a}_{\bullet2}+x_{3}\overrightarrow{a}_{\bullet3}} & \overrightarrow{a}_{\bullet2} & \overrightarrow{a}_{\bullet3}\end{array}\right| \]

Usando las propiedades del determinante, tenemos que

\[ \left|\begin{array}{ccc} x_{1}\overrightarrow{a}_{\bullet1}+{x_{2}\overrightarrow{a}_{\bullet2}+x_{3}\overrightarrow{a}_{\bullet3}} & \overrightarrow{a}_{\bullet2} & \overrightarrow{a}_{\bullet3}\end{array}\right|=\left|\begin{array}{ccc} x_{1}\overrightarrow{a}_{\bullet1} & \overrightarrow{a}_{\bullet2} & \overrightarrow{a}_{\bullet3}\end{array}\right|+\left|\begin{array}{ccc} {x_{2}\overrightarrow{a}_{\bullet2}+x_{3}\overrightarrow{a}_{\bullet3}} & \overrightarrow{a}_{\bullet2} & \overrightarrow{a}_{\bullet3}\end{array}\right|. \]

Entonces, recuerda que

Si multiplicamos una columna (o fila) por un valor, este multiplica al determinante de la matriz $\left|\begin{array}{ccc} x_{1}\overrightarrow{a}_{\bullet1} & \overrightarrow{a}_{\bullet2} & \overrightarrow{a}_{\bullet3}\end{array}\right|=x_{1}\left|\begin{array}{ccc} \overrightarrow{a}_{\bullet1} & \overrightarrow{a}_{\bullet2} & \overrightarrow{a}_{\bullet3}\end{array}\right|=x_{1}\left|A\right|$

por otro lado, $\left|\begin{array}{ccc} x_{2}\overrightarrow{a}_{\bullet2}+x_{3}\overrightarrow{a}_{\bullet3} & \overrightarrow{a}_{\bullet2} & \overrightarrow{a}_{\bullet3}\end{array}\right|=\left|\begin{array}{ccc} x_{2}\overrightarrow{a}_{\bullet2} & \overrightarrow{a}_{\bullet2} & \overrightarrow{a}_{\bullet3}\end{array}\right|+\left|\begin{array}{ccc} x_{3}\overrightarrow{a}_{\bullet3} & \overrightarrow{a}_{\bullet2} & \overrightarrow{a}_{\bullet3}\end{array}\right|=0$

Entonces, tenemos que \[ \frac{\left|\begin{array}{ccc} \overrightarrow{b} & \overrightarrow{a}_{\bullet2} & \overrightarrow{a}_{\bullet3}\end{array}\right|}{\left|A\right|}=x_{1} \]

De tal forma que, para cualquier $x_{i}$, tenemos que sustituir en la columna correspondiente $i$ del determinante por el vector $\overrightarrow{b}.$ De esta forma,

\[ x_{i}=\frac{1}{\left|\mathbf{A}\right|}\left|\begin{array}{cccccc} a_{11} & ... & a_{1i-1} & b_{1}&a_{1i+1} & ... & a_{1n}\\ a_{21} & ... & a_{2i-1} & b_{2}&a_{2i+1} & ... & a_{2n}\\ ... & ... & ... & ... & ... & ...\\ a_{n1} & ... & a_{ni-1} & b_{n}&a_{ni+1} & ... & a_{nn} \end{array}\right| \]

Ejercicio resuelto

Resuelve por Cramer el siguiente sistema \[ \left[\begin{array}{cc} -1 & 1\\ 2 & -1 \end{array}\right]\left[\begin{array}{c} x_{1}\\ x_{2} \end{array}\right]=\left[\begin{array}{c} -0.5\\ 1.5 \end{array}\right] \]

donde \[ x_{1}=\frac{\left|\begin{array}{cc} -0.5 & 1\\ 1.5 & -1 \end{array}\right|}{\left|\begin{array}{cc} -1 & 1\\ 2 & -1 \end{array}\right|}=1, \] \[ x_{1}=\frac{\left|\begin{array}{cc} -1 & -0.5\\ 2 & 1.5 \end{array}\right|}{\left|\begin{array}{cc} -1 & 1\\ 2 & -1 \end{array}\right|}=0.5 \]

Clase 2: métodos de resolución de sistemas de ecuaciones

Fíjate en este sistema de ecuaciones:

\[ \underset{\left[\begin{array}{ccccc} 2 & 0 & 1 & 1 \\ 0 & 3 & 0 & 1 \\ 0 & 0 & 1 & 2 \\ 0 & 0 & 0 & 4 \end{array}\right]}{\mathbf{A}}\underset{\left[\begin{array}{c} x_{1}\\ x_{2}\\ x_{3}\\ x_{4} \end{array}\right]}{\overrightarrow{x}}=\underset{\left[\begin{array}{c} 2\\ -1\\ 0\\ 4 \end{array}\right]}{\overrightarrow{b}} \]

Este sistema es muy sencillo de resolver, dada la disposición de la matriz de coeficientes $\mathbf{A}$. Si empezamos en la última fila, tenemos que

\[ 4x_{4}=4\implies x_4=1 \]

ya tenemos la cuarta incógnita, si vamos ahora a la tercera fila, donde tenemos

\[ x_{3}+2x_{4}=0 \] y sabiendo ya que $x_{4}=1$, entonces

\[ x_{3}=-2 \]

Es fácil, por tanto, de la misma manera obtener $x_2=-\frac{2}{3}$ y, finalmente,$x_1=\frac{3}{2}$. Diremos que la solución de este sistema (recuerda que la solución es el valor-o conjunto de valores- que pueden tomar las incógnitas) es

\[ sol=\{\vec{x}\in \mathbb{R}^4: x_1=\frac{3}{2},x_2=-\frac{2}{3},x_{3}=-2, x_4=1\} \]

que, como ves, es un punto en un espacio vectorial de 4 dimensiones.

La solución de este sistema es inmediata debido a la estructura triangular de la matriz de coeficientes. Parece sensato que debamos aspirar a algo similar. Nuestro objetivo, por tanto, a la hora de resolver sistemas de ecuaciones será escalonar la matriz de coeficientes. Otro ejemplo sería este sistema \[ \left[\begin{array}{ccccc} a_{11} & a_{12} & a_{13} & a_{14} & a_{15}\\ {\color{blue}{\color{blue}0}} & {\color{blue}{\color{blue}0}} & a_{23} & a_{24} & a_{25}\\ {\color{blue}0} & {\color{blue}0} & {\color{blue}0} & a_{34} & a_{35} \end{array}\right]\left[\begin{array}{c} x_{1}\\ x_{2}\\ x_{3}\\ x_{4}\\ x_{5} \end{array}\right]=\left[\begin{array}{c} b_{1}\\ b_{2}\\ b_{3}\\ b_{4}\\ b_{5} \end{array}\right] \] sin embargo, este no es triangular. Veremos que para resolverlo, tendremos que distinguir entre variables endógenas y exógenas.

El método de Gauss por filas

Nuestro objetivo es, como ya has averiguado, resolver sistemas de la forma

\[ \mathbf{A}\overrightarrow{x}=\overrightarrow{b}, \]

donde $\mathbf{A}\in M_{(m\times n)}.$

De la misma forma que ya hicimos con el método de Gauss para invertir matrices, vamos a utililizarlo para resolver de una manera cómoda sistemas de ecuaciones con matrices (en plarticular, grandes). Para ello, deberemos escribir la matriz ampliada del sistema $A^{*}$, que consiste en aquella matriz de coeficientes a la que se le anexiona el vector de términos independientes:

\[ A^{*}=\left(\mathbf{A}|\overrightarrow{b}\right) \]

Antes de resolver el sistema, nos interesará saber si este tiene solución:

Teorema de Existencia de Solución

Teorema de Rocher-Frobenius.

Del sistema de ecuaciones $\mathbf{A}\overrightarrow{x}=\overrightarrow{b}$ donde $\mathbf{A}\in\mathcal{M}_{m\times n}$ sea $\mathbf{A}^{*}$ la matriz ampliada (es decir $\left[\mathbf{A}\mathrm{\mathit{\overrightarrow{b}}}\right]$), entonces:

Si $rg(\mathbf{A})<rg(\mathbf{A^{*})}$ entonces el sistema es incompatible

Si $rg(\mathbf{A})=rg(\mathbf{A^{*})}$ entonces el sistema es compatible determinado

Si $rg(\mathbf{A})=rg(\mathbf{A^{*})}<n$ entonces el sistema es compatible indeterminado

Para ello, deberemos escalonar la matriz ampliada. Veámoslo con un ejemplo. Sea el sistema

\[ \begin{array}{ccccccc} 2x & +y & & -w & & = & 4\\ & y & & +w & +u & = & 4\\ x & & -z & +2w & & = & 0 \end{array} \]

(por cierto, no importa el orden en el que coloques las variables del sistema, pues se satisface la propiedad conmutativa!) Podemos escribir la matriz ampliada $\left(\mathbf{A}|\overrightarrow{b}\right)$ del sistema como:

\[ \left(\left.\begin{array}{ccccc} 2 & 1 & 0 & -1 & 0\\ 0 & 1 & 0 & 1 & 1\\ 1 & 0 & -1 & 2 & 0 \end{array}\right|\begin{array}{c} 4\\ 4\\ 0 \end{array}\right) \]

Buscamos la forma escalonada del sistema. Para ello, utilizamos operaciones elementales

\[ \left(\left.\begin{array}{ccccc} 2 & 1 & 0 & -1 & 0\\ 0 & 1 & 0 & 1 & 1\\ 1 & 0 & -1 & 2 & 0 \end{array}\right|\begin{array}{c} 4\\ 4\\ 0 \end{array}\right)\underrightarrow{E_{31}(-1/2)}\left(\left.\begin{array}{ccccc} 2 & 1 & 0 & -1 & 0\\ 0 & 1 & 0 & 1 & 1\\ 0 & -1/2 & -1 & 5/2 & 0 \end{array}\right|\begin{array}{c} 4\\ 4\\ -2 \end{array}\right) \]

\[ \underrightarrow{E_{32}(1/2)}\left(\left.\begin{array}{ccccc} {\color{blue}2} & 1 & 0 & -1 & 0\\ {\color{red}0} & {\color{blue}1} & 0 & 1 & 1\\ {\color{red}0} & {\color{red}0} & {\color{blue}{-1}} & 3 & 1/2 \end{array}\right|\begin{array}{c} 4\\ 4\\ 0 \end{array}\right) \]

Ya tenemos la forma escalonada.

Tanto la matriz de coeficientes como la ampliada tienen rango 3 (igual, pero menor al número de variables). El sistema es compatible indeterminado.

Fíjate que podemos reescribirlo como

\[ \left[\begin{array}{ccccc} {\color{blue}2} & 1 & 0 & -1 & 0\\ {\color{red}0} & {\color{blue}1} & 0 & 1 & 1\\ {\color{red}0} & {\color{red}0} & {\color{blue}{-1}} & 3 & 1/2 \end{array}\right]\left[\begin{array}{c} {\color{brown}x}\\ {\color{brown}y}\\ {\color{brown}z}\\ w\\ u \end{array}\right]=\left[\begin{array}{c} 4\\ 4\\ 0 \end{array}\right] \]

Los pivotes, en este caso están asociados con las variables $(x,y,z)$ que serán, entonces, denominadas variables endógenas. Mientras que las variables libres (o exógenas) son $u,w$.El resultado del sistema será (poniendo las endógenas en función de las exógenas):

\[ -z+3w+\frac{1}{2}u=0\implies z=3w+\frac{1}{2}u \]

\[ y+w+u=4\implies y=4-w-u \]

\[ 2x+y-w=4\implies x=w+\frac{1}{2}u \]

¿Cómo escribir el resultado con la notación aprendida en el curso? Como ves, tienes un conjunto de variables $(x,y,z)$ que dependen de parámetros $(u,w)$. Además, el espacio de soluciones se encuentra en $\mathbb{R}^{5}$ (es decir, la solución de este sistema ha ser este vector con cinco componentes reales$\left[\begin{array}{c} x\\ y\\ z\\ w\\ u \end{array}\right].$ Entonces, escribiendo la solución en forma de paramétricas, tendremos

\[ \left[\begin{array}{c} x\\ y\\ z\\ w\\ u \end{array}\right]=\underbrace{\underbrace{\left[\begin{array}{c} 0\\ 4\\ 0\\ 0\\ 0 \end{array}\right]}_{PARTICULAR}+\underbrace{w\left[\begin{array}{c} 1\\ -1\\ 3\\ 1\\ 0 \end{array}\right]+u\left[\begin{array}{c} 1/2\\ -1\\ 1/2\\ 0\\ 1 \end{array}\right]}_{NO-RESTRINGIDA}} \]

En este caso, parece sencillo ver que se divide en dos partes. La primera, una solución “concreta” que es el vector $\left(0,4,0,0,0\right)$ que consiste en hacer $w=0,u=0$. Esta solución se corresponde con uno de los vectores posibles que resuelven el sistema anterior. Podríamos dar valores $w\neq0,u\neq0$ y obtendríamos un conjunto infinito de vectores que son solución del sistema.

Nota importante. En una matriz escalonada como esta, por ejemplo,

\[ \left[\begin{array}{cccc} 1 & 2 & 2 & |1\\ {\color{red}0} & {\color{red}0} & 2 & |3\\ {\color{red}0} & {\color{red}0} & {\color{red}0} & {\color{red}{|0}} \end{array}\right] \]

{cuya solución está formada por vectores en $\mathbb{R}^{4}$, es decir, $\left[\begin{array}{cccc} x_{1} & x_{2} & x_{3} & x_{4}\end{array}\right]$ está claro que una de las variables exógenas será la variable $x_{4}$. Sin embargo, puedes decidir, alternativamente, que $x_{1}$ o $x_{2}$ sean exógenas. Pero no ambas a la vez. Por lo tanto, tienes dos alternativas:

alternativa 1:$x_{1},x_{3}$ endógenas y $x_{2},x_{4}$ exógenas

alternativa 2: $x_{2},x_{3}$ endógenas y $x_{1},x_{4}$ exógenas.

Clase 3: Los sistemas homogéneos y los subespacios asociados a la solución

Diremos que un sistema lineal de ecuaciones es homogéneo si se presenta de esta manera:

\[ \mathbf{A}\overrightarrow{x}={\overrightarrow{0}} \]

De nuestro sistema anterior, siempre podemos proponer la forma homogénea, que consiste en cambiar el vector de términos independientes por ceros

\[ \begin{array}{ccccccc} 2x & +y & & -w & & = & 0\\ & y & & +w & +u & = & 0\\ x & & -z & +2w & & = & 0 \end{array} \]

Estos sistemas tienen siempre una posible solución: la trivial que implica que todas las incógnitas serán cero (piensa que eso siempre satisface el sistema). En este caso, será $(x,y,z,w,u)=(0,0,0,0,0)$. Sin embargo, obtendremos una solución “no trivial” si el rango de la matriz ampliada es menor que el número de filas. Busquemos, por tanto, el rango y veamos que es 3.

\[ \left(\left.\begin{array}{ccccc} 2 & 1 & 0 & -1 & 0\\ 0 & 1 & 0 & 1 & 1\\ 1 & 0 & -1 & 2 & 0 \end{array}\right|\begin{array}{c} 0\\ 0\\ 0 \end{array}\right)\underrightarrow{E_{31}(-1/2)}\left(\left.\begin{array}{ccccc} 2 & 1 & 0 & -1 & 0\\ 0 & 1 & 0 & 1 & 1\\ 0 & -1/2 & -1 & 5/2 & 0 \end{array}\right|\begin{array}{c} 0\\ 0\\ 0 \end{array}\right) \]

Entonces, la solución de este sistema, llamado “homogéneo” implica que :

\[ -z+3w+\frac{1}{2}u=0\implies z=3w+\frac{1}{2}u \]

\[ y+w+u=0\implies y=-w-u \]

\[ 2x+y-w=0\implies x=-w+\frac{1}{2}u \]

Es decir, es compatible indeterminado.

\[ \left[\begin{array}{c} x\\ y\\ z\\ w\\ u \end{array}\right]=w\left[\begin{array}{c} -1\\ -1\\ 3\\ 1\\ 0 \end{array}\right]+u\left[\begin{array}{c} 1/2\\ -1\\ 1/2\\ 0\\ 1 \end{array}\right] \]

Presta atención: del sistema de la clase anterior, teníamos que la solución era \[ \left[\begin{array}{c} x\\ y\\ z\\ w\\ u \end{array}\right]=\underbrace{\underbrace{\left[\begin{array}{c} 0\\ 4\\ 0\\ 0\\ 0 \end{array}\right]}_{PARTICULAR}+\underbrace{{w\left[\begin{array}{c} 1\\ -1\\ 3\\ 1\\ 0 \end{array}\right]+u\left[\begin{array}{c} 1/2\\ -1\\ 1/2\\ 0\\ 1 \end{array}\right]}}_{{\color{red}{HOMOGÉNEO}}}} \]

y del homogéneo, como ves:

\[ \left[\begin{array}{c} x\\ y\\ z\\ w\\ u \end{array}\right]=w\left[\begin{array}{c} -1\\ -1\\ 3\\ 1\\ 0 \end{array}\right]+u\left[\begin{array}{c} 1/2\\ -1\\ 1/2\\ 0\\ 1 \end{array}\right] \]

No es casualidad: veremos que un sistema \[ \mathbf{A}\overrightarrow{x}=\overrightarrow{b} \]

presentará siempre, en sus soluciones la suma de una particular (un punto) más la del homogéneo (que se corresponderá con los vectores directores de esta).

La prueba de ello es la siguiente. Llamamos $\overrightarrow{x_{h}}$ la solución de un sistema homogéneo

\[ \mathbf{A}\overrightarrow{x_{h}}=\overrightarrow{0} \]

Llamamos $\overrightarrow{x_{p}}$ una solución particular de un sistema no homogéneo

\[ \mathbf{A}\overrightarrow{x_{p}}=\overrightarrow{b} \]

Vamos a demostrar que la solución del sistema

\[ \mathbf{A}\overrightarrow{x}=\overrightarrow{b} \]

la podemos poner como la suma de la particular más la homogénea, es decir:

\[ \overrightarrow{x}=\overrightarrow{x_{p}}+\overrightarrow{x_{h}} \]

Para ello, partimos de \[ \mathbf{A}\overrightarrow{x_{p}}=\overrightarrow{b} \]

si sumamos el vector de ceros, nada cambia

\[ \mathbf{A}\overrightarrow{x_{p}}+\overrightarrow{0}=\overrightarrow{b} \]

pero nos permite introducir el sistema homogéneo, ya que $\mathbf{A}\overrightarrow{x_{h}}=\overrightarrow{0}$, entonces

\[ \mathbf{A}\overrightarrow{x_{p}}+\mathbf{A}\overrightarrow{x_{h}}=\overrightarrow{b} \] sacando factor común \[ \mathbf{A}(\overrightarrow{x_{p}}+\overrightarrow{x_{h}})=\overrightarrow{b} \]

Esto implica que resolviendo un sistema de ecuaciones cualquiera, puedes obtener también la solución del homogéneo. Por ejemplo, de este sistema:

\[ \begin{cases} x+2y-3z=1\\ y-z=-1\\ \end{cases} \]

obtenemos la matriz ampliada:

\[ \left(\begin{array}{cccc} 1 & 2 & -3 &|1\\ 0 & 1 & -1 &|-1 \end{array}\right) \]

De donde obtenemos que \[ y=-1+z \]

\[ x=3+z \]

por lo que este sistema, escrito en paramétricas:

\[ \left[\begin{array}{c} x\\ y\\ z \end{array}\right]=\left[\begin{array}{c} 3\\ -1\\ 0 \end{array}\right]+z\left[\begin{array}{c} 1\\ 1\\ 1 \end{array}\right] \]

La solución particular es $\left[\begin{array}{c} 3\\ -1\\ 0 \end{array}\right]$

mientras que la solución al homogéneo es $\left[\begin{array}{c} x\\ y\\ z \end{array}\right]=z\left[\begin{array}{c} 1\\ 1\\ 1 \end{array}\right]$.

Para que te des cuenta, si este es el homogéneo asociado \[ \begin{cases} x+2y-3z=0\\ y-z=0\\ \end{cases} \]

la solución es $\left[\begin{array}{c} x\\ y\\ z \end{array}\right]=z\left[\begin{array}{c} 1\\ 1\\ 1 \end{array}\right]$

puedes sustituir en $x,y,z$ y verás que satisface el sistema.

La solución del sistema homogéneo es un subespacio vectorial

Nuevo ejemplo de subespacio vectorial que debes conocer

Ejercicio resuelto

Muestra que la solución de un sistema homogéneo es un subespacio vectorial, mientras que la solución de un sistema no homogéneo no lo es.

Sea el sistema homogéneo \[ \mathbf{A}\overrightarrow{x}=\overrightarrow{0} \]

será subespacio si:

Como condición necesaria, el cero es un elemento del conjunto, como es el caso

\[ \mathbf{A}\overrightarrow{0}=\overrightarrow{0} \]

Una vez cumpliendo esta condición,dos soluciones del sistema (por ejemplo $\overrightarrow{w},\overrightarrow{z})$ sumadas, también son solución del sistema:

\[ \begin{cases} \mathbf{A}\overrightarrow{w}=\overrightarrow{0}\\ \mathbf{A}\overrightarrow{z}=\overrightarrow{0}\\ \mathbf{A}\left(\overrightarrow{w}+\overrightarrow{z}\right)=\overrightarrow{0} \end{cases} \]

Un vector proporcional a uno que sea solución, también lo es. Por ejemplo, sea $\overrightarrow{x}$ solución del sistema, y sea $\lambda\overrightarrow{x}$, entonces \[ \begin{cases} \mathbf{A}\overrightarrow{x}=\overrightarrow{0}\\ \mathbf{A}\lambda\overrightarrow{x}=\lambda\overrightarrow{0}=\overrightarrow{0} \end{cases} \]

Veamos cómo esto no pasa con un sistema no homogéneo. Por ejemplo,

\[ \mathbf{A}\overrightarrow{x}=\overrightarrow{b} \]

Como condición necesaria, el cero es un elemento del conjunto, pero…¿es esto cierto? \[ \mathbf{A}\overrightarrow{0}=\overrightarrow{b} \] ,en general, NO, a no ser que $\overrightarrow{b}=\overrightarrow{0}$ y, entonces, estamos ante un sistema homogéneo.

Aunque ya sepamos que un sistema no homogéneo no es un subespacio, sigamos viendo si cumpliría las otras condiciones. ¿Es la suma de soluciones solución del sistema? (por ejemplo $\overrightarrow{w},\overrightarrow{z})$ sumadas, también son solución del sistema: \[ \begin{cases} \mathbf{A}\overrightarrow{w}=\overrightarrow{b}\\ \mathbf{A}\overrightarrow{z}=\overrightarrow{b}\\ \mathbf{A}\left(\overrightarrow{w}+\overrightarrow{z}\right)=2\overrightarrow{b} \end{cases} \] No! obtenemos $2\overrightarrow{b}$ en vez de $\overrightarrow{b}$. Puedes comprobar que tampoco se cumple cuando utilizamos un múltiplo de un vector solución.

Ya hemos visto que la solución a un sistema homogéneo es un subespacio. De hecho, se le suele llamar el espacio nulo o núcleo de la matriz $\mathbf{A}$.

Sea $\mathbf{A}\in\mathcal{M}_{m\times n}$. El conjunto $N$ de soluciones al sistema

\[ \mathbf{A}\overrightarrow{x}=\overrightarrow{0} \]

Es decir: $N(\mathbf{A})\in\left\{\overrightarrow{x}\in\mathbb{R}^{n}\::\:\mathbf{A}\overrightarrow{x}=\overrightarrow{0}\right\}$

es un subespacio de $\mathbb{R}^{n}$ (el número de columnas de la matriz, que se corresponde con el número de variables). Este subespacio se conoce también como el $Nulo(\mathbf{A})$ o el núcleo $Ker(A)$

De hecho, la dimensión del subespacio solución será igual al número de variables exógenas que tenga el sistema, ya que esas variables serán los parámetros de las ecuaciones paramétricas de la solución y, por tanto, con los vectores directores podremos formar una base del subespacio

La dimensión del subespacio nulo matriz $\mathbf{A}$ es

\[ dim(N(\mathbf{A}))=n-rango(\mathbf{A}) \]

Además, este subespacio tiene una propiedad muy importante:

De un sistema como este $\mathbf{A}\overrightarrow{x}=\overrightarrow{0}$, con $\mathbf{A}\in\mathcal{M}_{m\times n}$ las $m$ filas de la matriz son perpendiculares a la solución del sistema $\overrightarrow{x}$ . \[ \left[\begin{array}{cccc} \color{red}{a_{11}} & \color{red}{a_{12}} & ... & \color{red}{a_{1n}}\\ a_{21} & & & a_{2n}\\ ... & & & ....\\ a_{m1} & ... & ... & a_{mn} \end{array}\right]\left[\begin{array}{c} \color{red}{x_{1}}\\ \color{red}{x_{2}}\\ ...\\ \color{red}{x_{n}} \end{array}\right]=\overrightarrow{0} \]

¿Por qué sucede esto? Fíjate que el producto de matrices implica que cada fila es ortogonal a la solución del sistema. Es decir, las filas de la matriz $\mathbf{A}$ siempre serán ortogonales a la solución del homogéneo. De aquí podemos concluir que el espacio fila de una matriz $\mathbf{A}$ es perpendicular al $N(A):$

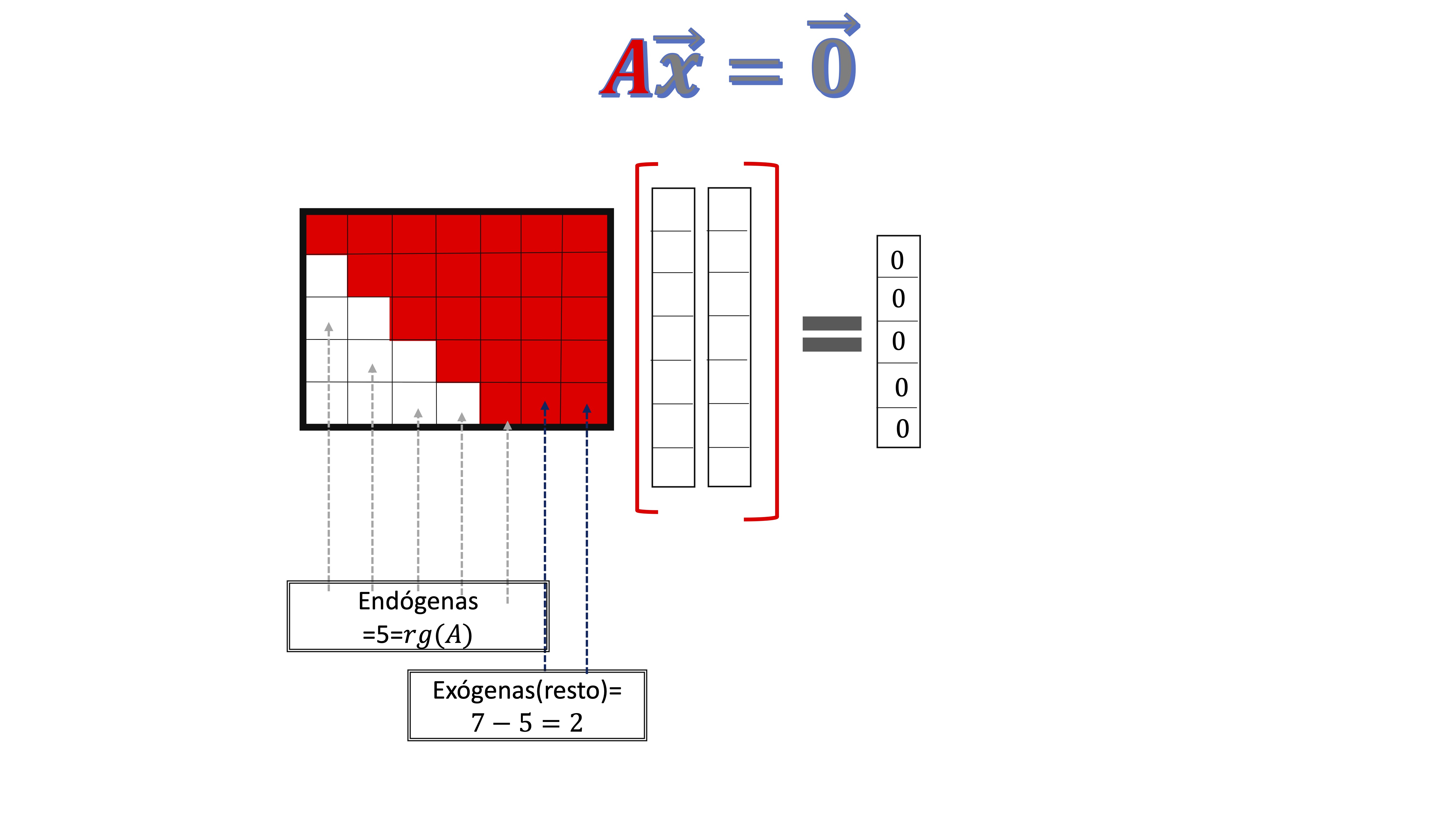FIG1: Un dibujo de la idea Como ves, la solución del sistema (que son los dos vectores que están en el corchete rojo) es ortogonal a las filas de la matriz $\mathbf{A}$.

Ejemplo

Queremos resolver \[ \left[\begin{array}{ccc} 2 & 0 & 4\\ 1 & 1 & 3 \end{array}\right]\left[\begin{array}{c} x_{1}\\ x_{2}\\ x_{3} \end{array}\right]=\left[\begin{array}{c} 0\\ 0 \end{array}\right] \]

la forma escalonada es $\left[\begin{array}{ccc} 1 & 0 & 1\\ 0 & 1 & 1 \end{array}\right]\left[\begin{array}{c} x_{1}\\ x_{2}\\ x_{3} \end{array}\right]=\left[\begin{array}{c} 0\\ 0 \end{array}\right]$

la solución de este sistema es una recta en $\mathbb{R}^{3}$ \[ \left[\begin{array}{c} x_{1}\\ x_{2}\\ x_{3} \end{array}\right]=x_{3}\left[\begin{array}{c} -2\\ -1\\ 1 \end{array}\right] \]

El subespacio nulo de la matriz $\mathbf{A}=\left[\begin{array}{ccc} 2 & 0 & 4\\ 1 & 1 & 3 \end{array}\right]$, es decir $N(A)$ tiene dimensión 1 y una base es $B_{N(A)}=\left\{ \left[\begin{array}{c} -2\\ -1\\ 1 \end{array}\right]\right\}$

Al tener dimensión 1 es una recta (en 3 dimensiones)

Por otro lado, sabemos que los vectores del espacio fila $\left(\begin{array}{c} 2\\ 0\\ 4 \end{array}\right),\left(\begin{array}{c} 1\\ 1\\ 3 \end{array}\right)$ son los vectores ortogonales a la solución (es decir, el subespacio fila es ortogonal al espacio nulo). Por la propia definci?n de sistema homogéneo:

\[ \left[\begin{array}{ccc} 2 & 0 & 4\\ 1 & 1 & 3 \end{array}\right]\left[\begin{array}{c} x_{1}\\ x_{2}\\ x_{3} \end{array}\right]=\left[\begin{array}{c} 0\\ 0 \end{array}\right] \]

si sutituímos por la solución:

\[ \left[\begin{array}{ccc} 2 & 0 & 4\\ 1 & 1 & 3 \end{array}\right]\left[\begin{array}{c} -2\\ -1\\ 1 \end{array}\right]=\left[\begin{array}{c} 0\\ 0 \end{array}\right] \]

los dos productos escalares: $\left(2,0,4\right)\cdot(-2,-1,1)$ y $\left(1,1,3\right)\cdot(-2,-1,1)$ son ambos nulos.

Clase 4: El (sub)espacio nulo traspuesto $N(A^{t})$

Veamos un ejercicio: sea el sistema

$\mathbf{A}\overrightarrow{x}=\overrightarrow{0}$ tal que

\[ \left[\begin{array}{cccc} {\color{orange}1} & 1 & 0 & 2\\ 0 & {\color{orange}1} & 0 & 1\\ 0 & 0 & {\color{orange}2} & 1 \end{array}\right]\left[\begin{array}{c} x_{1}\\ x_{2}\\ x_{3}\\ x_{4} \end{array}\right]=\left[\begin{array}{c} 0\\ 0\\ 0 \end{array}\right] \]

Obtén una base para el subespacio nulo de $\mathbf{A}$, es decir, $N(\mathbf{A})$.

Obtén una base para el subespacio de vectores perpendiculares al espacio nulo de $\mathbf{A}$

Como ves, la matriz asociada al sistema de ecuaciones ya está escalonada. Tenemos tres variables endógenas ($x_{1},x_{2},x_{3})$ y una exógena. Si lo resolvemos, tenemos \[ \begin{cases} 2x_{3}+x_{4}=0 & x_{3}=-\frac{1}{2}x_{4}\\ x_{2}+x_{4}=0 & x_{2}=-x_{4}\\ x_{1}+x_{2}+2x_{4}=0 & x_{1}=-x_{4} \end{cases} \]

de tal forma que la solución del sistema, en ecuaciones paramétricas será:

\[ N(\mathbf{A})=\left\{ \left[\begin{array}{c} x_{1}\\ x_{2}\\ x_{3}\\ x_{4} \end{array}\right]=x_{4}\left[\begin{array}{c} -1\\ -1\\ -1/2\\ -1 \end{array}\right]\right\} \]

que representa una recta en $\mathbb{R}^{4}$. Una base para el subespacio será:

\[ B_{N(A)}=\left\{ \left[\begin{array}{c} -1\\ -1\\ -1/2\\ -1 \end{array}\right]\right\} \]

Por otro lado, debemos encontrar una base del subespacio de vectores perpendiculares a $N(\mathbf{A})$. Si nos fijamos, el sistema se puede escribir, resuelto como

\[ \left[\begin{array}{cccc} {\color{orange}1} & 1 & 0 & 2\\ 0 & {\color{orange}1} & 0 & 1\\ 0 & 0 & {\color{orange}2} & 1 \end{array}\right]\lambda\left[\begin{array}{c} -1\\ -1\\ -1/2\\ -1 \end{array}\right]=\left[\begin{array}{c} 0\\ 0\\ 0 \end{array}\right] \]

indicando que cualquier vector de la forma $\lambda\left[\begin{array}{c} -1\\ -1\\ -1/2\\ -1 \end{array}\right]$

es solución. Además, sabemos que los vectores filas, multiplicados por este vector son perpendiculares en el sistema homogéneo (compruébalo).

Por lo que una base de vectores que son perpendiculares al subespacio nulo es la base del subespacio fila de la matriz, es decir

\[ B_{F(A)}=\left\{ \left[\begin{array}{c} 1\\ 1\\ 0\\ 2 \end{array}\right],\left[\begin{array}{c} 0\\ 1\\ 0\\ 1 \end{array}\right],\left[\begin{array}{c} 0\\ 0\\ 2\\ 1 \end{array}\right]\right\} \]

Ahora, el ejercicio propone lo siguiente:

Sea el sistema $\mathbf{A}^{t}\overrightarrow{y}=\overrightarrow{0}$,

busca una base para el subespacio nulo de la matriz $\mathbf{A}^{t}$, es decir, $N(\mathbf{A}^{t})$

\[ \left[\begin{array}{ccc} 1 & 0 & 0\\ 1 & 1 & 0\\ 0 & 0 & 2\\ 2 & 1 & 1 \end{array}\right]\left[\begin{array}{c} y_{1}\\ y_{2}\\ y_{3} \end{array}\right]=\left[\begin{array}{c} 0\\ 0\\ 0\\ 0 \end{array}\right] \]

Fijémenos ahora que la solución estará en otro espacio: $\mathbb{R}^{3}$, puesto que ahora tenemos tres variables. Debemos escalonar la matriz

\[ \left[\begin{array}{ccc} 1 & 0 & 0\\ 1 & 1 & 0\\ 0 & 0 & 2\\ 2 & 1 & 1 \end{array}\right]\underrightarrow{E_{21}(-1)}\left[\begin{array}{ccc} 1 & 0 & 0\\ 0 & 1 & 0\\ 0 & 0 & 2\\ 2 & 1 & 1 \end{array}\right]\underrightarrow{E_{41}(-2)}\left[\begin{array}{ccc} 1 & 0 & 0\\ 0 & 1 & 0\\ 0 & 0 & 2\\ 0 & 1 & 1 \end{array}\right]\underrightarrow{E_{42}(-1)}\left[\begin{array}{ccc} 1 & 0 & 0\\ 0 & 1 & 0\\ 0 & 0 & 2\\ 0 & 0 & 1 \end{array}\right]\underrightarrow{E_{43}(-1/2)}\left[\begin{array}{ccc} 1 & 0 & 0\\ 0 & 1 & 0\\ 0 & 0 & 2\\ 0 & 0 & 0 \end{array}\right] \]

por lo que la resolución del sistema, nos lleva a

\[ \left[\begin{array}{ccc} 1 & 0 & 0\\ 0 & 1 & 0\\ 0 & 0 & 2\\ 0 & 0 & 0 \end{array}\right]\left[\begin{array}{c} y_{1}\\ y_{2}\\ y_{3} \end{array}\right]=\left[\begin{array}{c} 0\\ 0\\ 0\\ 0 \end{array}\right] \]

es decir, \[ y_{3}=0,y_{2}=0,y_{1}=0 \]

que es la solución trivial, esto es, el sistema es compatible determinado y sólo tiene esa solución:

\[ N(\mathbf{A}^{t})=\left\{ \left[\begin{array}{c} x_{1}\\ x_{2}\\ x_{3} \end{array}\right]=\left[\begin{array}{c} 0\\ 0\\ 0 \end{array}\right]\right\} \]

que es un punto (dimensión 0).

Ejercicio propuesto ¿Cuál será la base de vectores perpendiculares a $N(\mathbf{A}^{t})$ ?

Respuesta:

\[ B_{C(A)}=\left\{ \left[\begin{array}{c} 1\\ 0\\ 0 \end{array}\right],\left[\begin{array}{c} 1\\ 1\\ 0 \end{array}\right],\left[\begin{array}{c} 0\\ 0\\ 2 \end{array}\right]\right\} \]

¿Por qué es el espacio columna de la matriz $\mathbf{A}$?

De la misma forma que analizamos antes el sistema que se conforma con la matriz $\mathbf{A}$, vamos a pensar el sistema que da lugar la matriz de coeficientes $\mathbf{A}^t$:

Sea $\mathbf{A}\in\mathcal{M}_{m\times n}$. El conjunto $N$ de soluciones al sistema

\[ \mathbf{A}^{t}\overrightarrow{y}=\overrightarrow{0} \]

Es decir: $N(\mathbf{A}^{t})\in\left\{ \overrightarrow{y}\in\mathbb{R}^{m}\::\:\mathbf{A}^{t}\overrightarrow{y}=\overrightarrow{0}\right\}$

es un subespacio de $\mathbb{R}^{m}$. Este subespacio se conoce como el $Nulo(\mathbf{A}^{t})$ o el núcleo $Ker(\mathbf{A}^{t})$

De hecho, la dimensión del subespacio será el número de variables exógenas que tenga el sistema, ya que esas variables nos permitirán generar una base del subespacio:

La dimensión del subespacio nulo matriz $\mathbf{A}$ es \[ dim(N(\mathbf{A}))=n-rango(\mathbf{A}) \]

La dimensión del (sub)espacio nulo matriz $\mathbf{A}^{t}$ es

\[ dim(N(\mathbf{A}^{t}))=m-rango(\mathbf{A}) \]

Sin embargo, este subespacio tiene una propiedad muy importante:

De un sistema como este $\mathbf{A}^{t}\overrightarrow{y}=\overrightarrow{0}$, con $\mathbf{A}^{t}\in\mathcal{M}_{{\color{red}n\times m}}$ las $n$ filas de la matriz $\mathbf{A}^{t}$ (que coinciden con las $n$ columnas de la matriz $\mathbf{A})$ son perpendiculares a la solución del sistema $\overrightarrow{y}$, como puedes comprobar en el ejemplo anterior

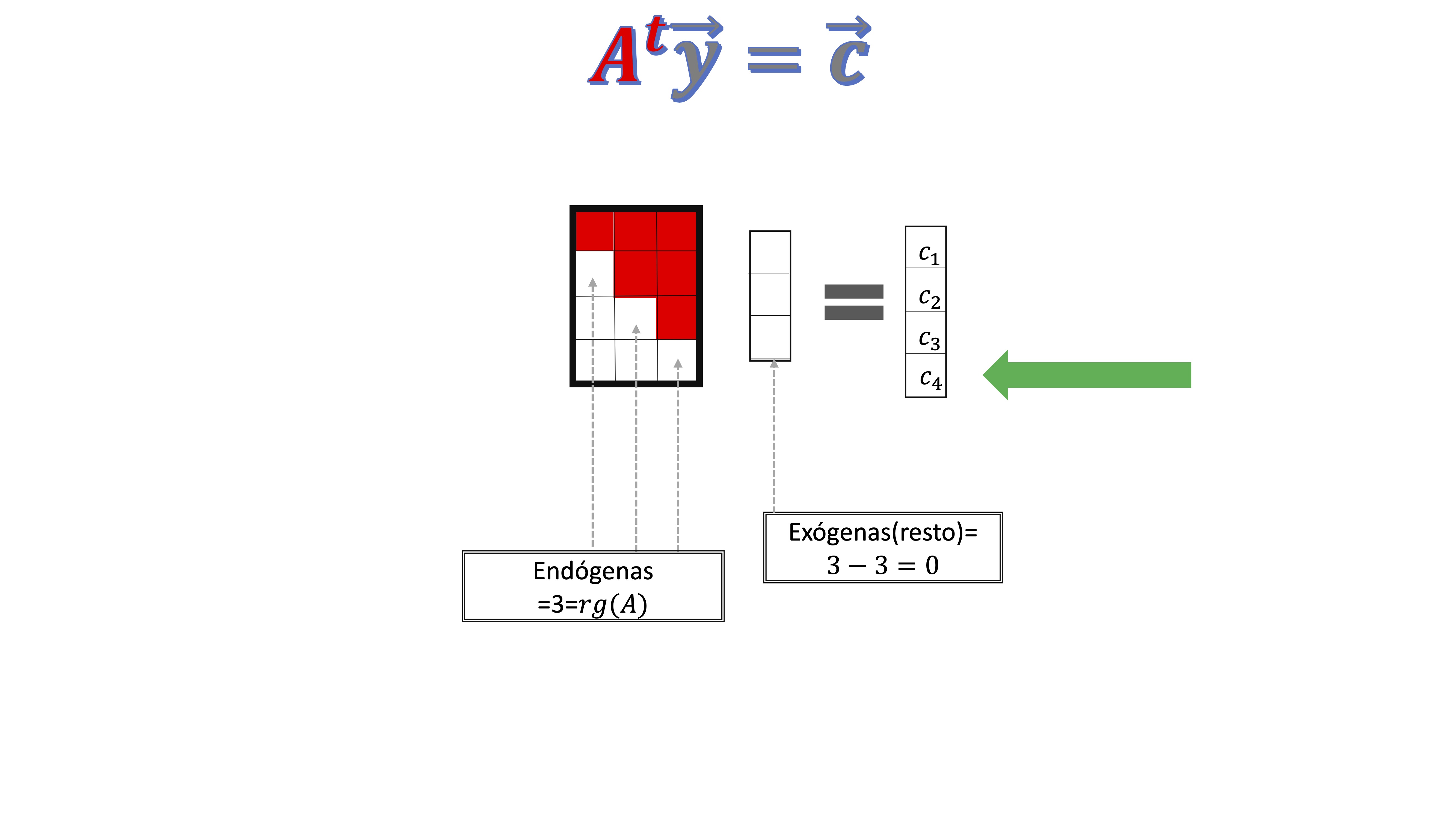FIG1: Esa idea la puedes ver aquí Las filas de la matriz traspuesta (que son las columnas de la matriz original) son, de nuevo, perpendiculares a la solución del sistema homogéneo (subespacio nulo de $\mathbf{A}^t$)

Aplicaciones importantes

Veamos un resumen de ideas importantes:

$dim(C(\mathbf{A}))=dim(F(\mathbf{A}))=rg(\mathbf{A})$

la dimensión de los (sub)espacios fila y columna de una matriz es la misma, no así los espacios en los que están (el espacio fila está en $\mathbb{R}^n$) y el espacio columna en $\mathbb{R}^m$.

$dim(N(\mathbf{A}))=n-rg(\mathbf{A})$

es decir, la dimensión del subespacio nulo de la matriz $\mathbf{A}$ es igual al número de variables exógenas que tiene el sistema (piensa en cuando lo resuelves)

$n=$#paramétricas$+$#cartesianas

Es decir, el espacio en el que están las soluciones de un sistema $n$ es igual al número de vectores que tienen las paramétricas (es decir, número de exógenas) y número de ecuaciones cartesianas. Piensa en un plano o una recta en $\mathbb{R}^3$.

Llamamos coordenadas del vector $\overrightarrow{b}$ en una base $B$ a la solución de un sistema de ecuaciones donde la base son las columnas de la matriz $\mathbf{A}$, el término independiente es el vector $\overrightarrow{b}$ y las coordenadas son las soluciones del sistema.

Por ejemplo, sea la base \[ B_{F(A)}=\left\{ \left[\begin{array}{c} 1\\ 1\\ 0\\ 2 \end{array}\right],\left[\begin{array}{c} 0\\ 1\\ 0\\ 1 \end{array}\right],\left[\begin{array}{c} 0\\ 0\\ 2\\ 1 \end{array}\right]\right\} \]

¿Cuáles son las coordenadas del vector

\[ \left[\begin{array}{c} 1\\ 2\\ 2\\ 4 \end{array}\right] \]

en dicha base? comprueba que son $x_1=1,x_2=1,x_3=1,x_4=1$.

Nota Estas mismas propiedades puedes adaptarlas de manera muy sencilla para $\mathbf{A}^t$

Un esquema sobre los subespacios de una matriz

Entre el tema anterior y este hemos definido lo que se conoce como los “cuatro subespacios” de una matriz $A$. Una idea clave en álgebra lineal.

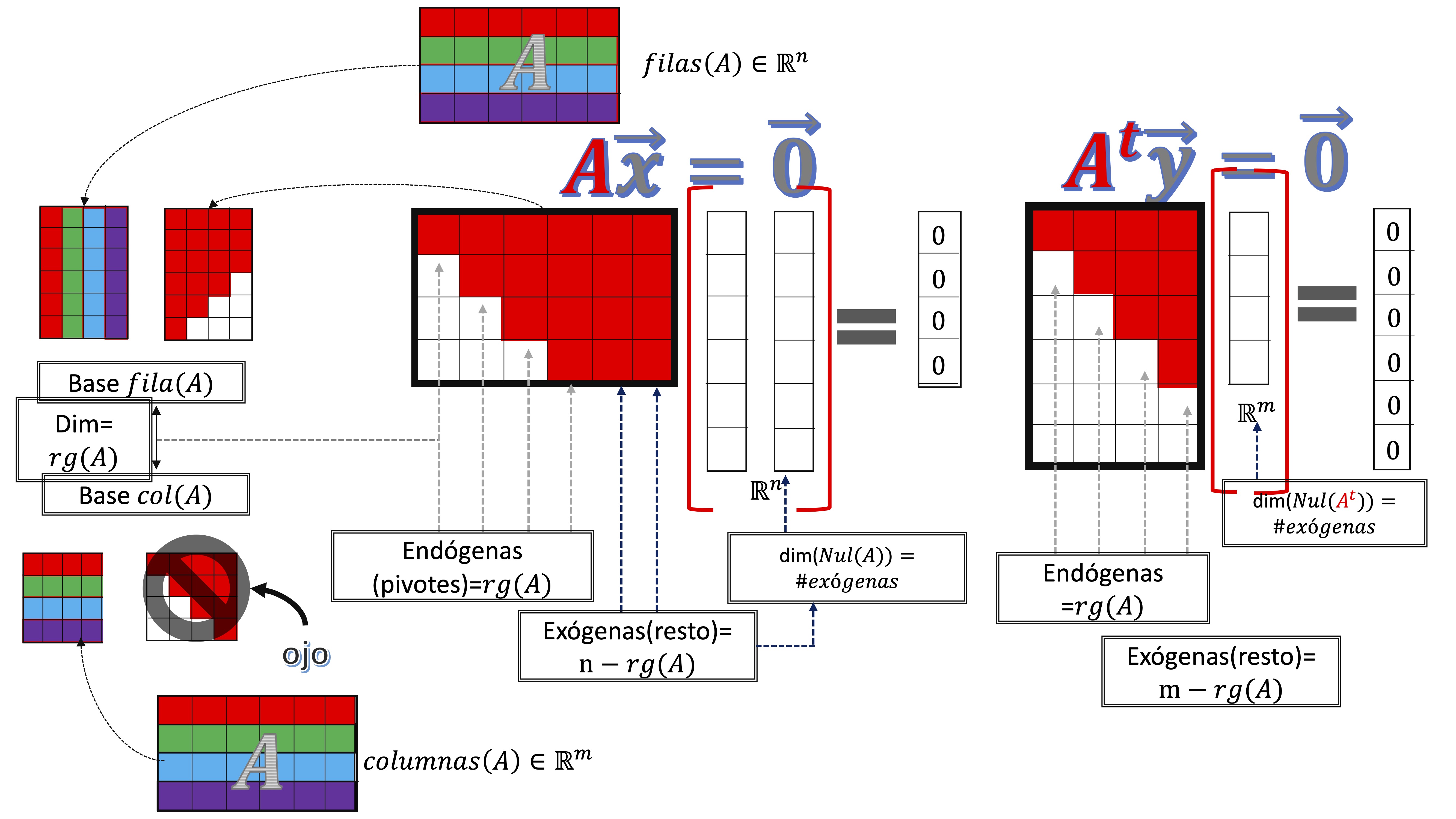
FIG1: Los cuatro subespacios de una matriz

La idea de este esquema es que, con tiempo, te ayude a tener claro, en la mente, la idea de lo que representan. Básicamente:

La matriz $\mathbf{A}$ (de $m$ filas y $n$ columnas) tendrá como rango un valor menor o igual al menor valor entre $m,n$

Ese rango $rg(\mathbf{A})$ es la dimensión del espacio fila $dim(fila(\mathbf{A}))=rg(\mathbf{A})$ y la del espacio columna $dim(col(\mathbf{A}))=rg(\mathbf{A})$.

Al escalonar la matriz por filas, una base del espacio fila son aquellas filas que son pivote en la matriz escalonada o aquellas de la matriz original, que se corresponden con pivotes (piensa que al escalonar por fila haces combinaciones lineales de las filas originales)

Al escalonar la matriz por filas, una base del espacio columna son aquellas columnas de la matriz original que se corresponden con los pivotes de la matriz escalonada Nunca directamente las columnas de la matriz escalonada.

La solución del sistema homogéneo asociado, es un subespacio cuya base vendrá dada por los vectores directores de la solución. Es decir, dependerá del número de exógenas (que serán $n-pivotes(\mathbf{A})=n-rg(\mathbf{A})).$ De hecho, la dimensión del subespacio nulo será, exactamente, el número de exógenas del sistema.

Es fácil de ver cómo se aplica, de manera análoga, al sistema con la matriz de coeficientes traspuesta

Ejercicio (de examen) para practicar con el esquema

Considere un sistema de ecuaciones lineales $A\overrightarrow{x}=\overrightarrow{b}$, donde la matriz $\mathbf{A}$ tiene tres filas y cuatro columnas.

Un sistema como este ¿tiene siempre solución? Si no es así, escriba un ejemplo de sistema que no tenga solución.

respuesta: para entender que no siempre tiene solución, pensemos en los dos casos que se muestran a continuación:

FIG2:

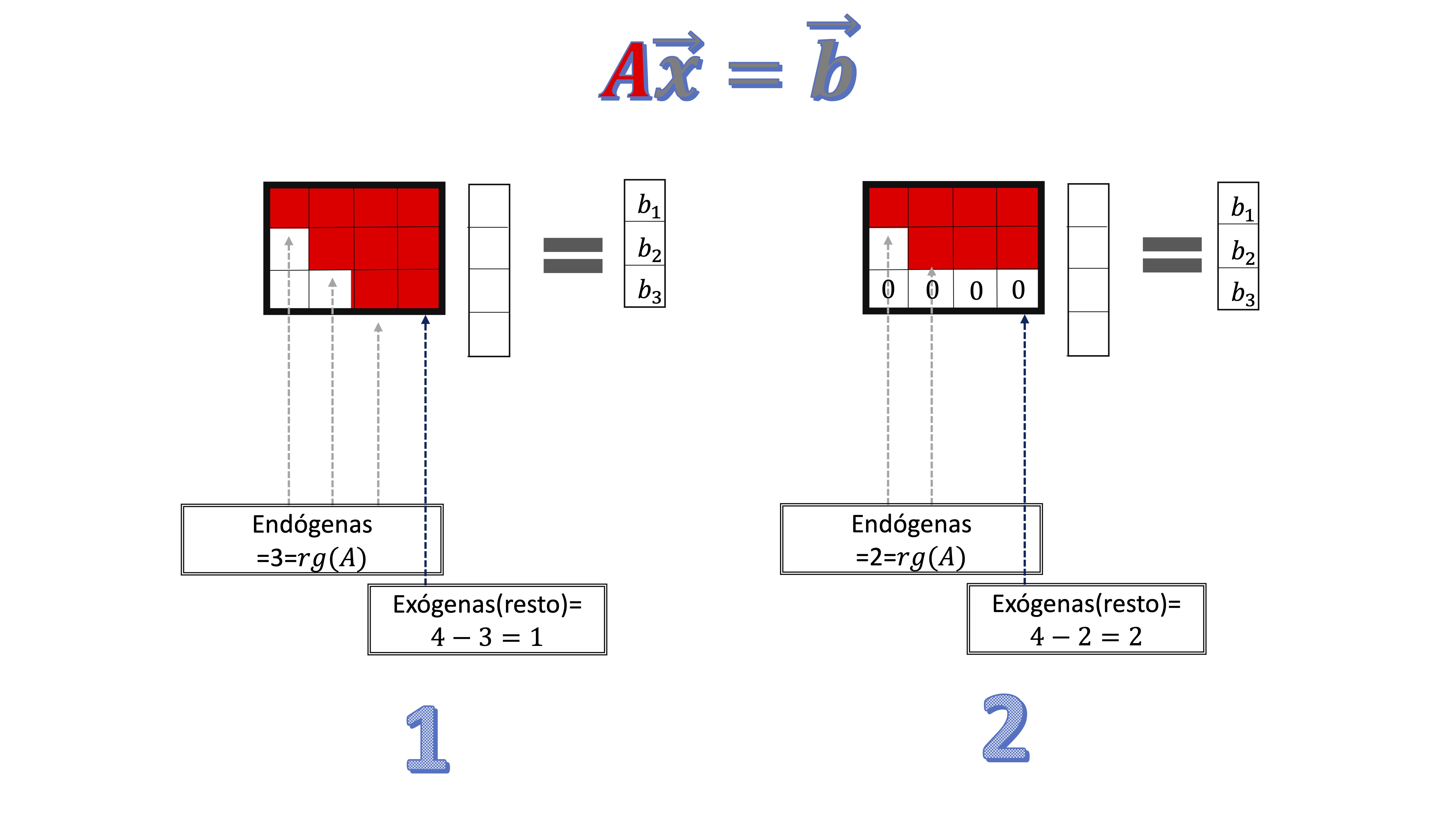
En el caso 1, el rango de la matriz de coeficientes es 3 (que es el máximo rango que puede tener, dada la información que tenemos). Entonces, el rango será igual al de la ampliada (podremos poner cualquier valor para $b_{1},b_{2},b_{3}$ ) y el sistema tiene solución. Sin embargo, en el segundo caso, donde el rango de la matriz de coeficientes es 2 (tiene dos pivotes) la última fila es toda de ceros. Al anexionar el vector $\overrightarrow{b}$, si su última componente no tiene un cero, entonces el rango de la ampliada será mayor que el de la de coeficientes y el sistema NO TENDRÁ SOLUCIÓN.

¿Es posible que el sistema tenga una única solución? Si es así, proporcione un ejemplo

Para que eso fuera así, el rango de la matriz de coeficientes debería ser 4 y eso es imposible en este contexto.

Formule, si es posible, una condición necesaria y suficiente sobre $\mathbf{A}$ y $\overrightarrow{b}$ que garantice que el sistema tiene, al menos, una solución:

Como condición suficiente, sabemos que si el rango de la matriz de coeficientes es igual al de la matriz amplida, el sistema tiene, al menos una solución. ¿Es esa condición necesaria? También. Es imposible encontrar un ejemplo que no satisfaga esta condición y tenga, al menos, una solución.

Formule, si es posible, una condición sólo para $\mathbf{A}$ que garantice que el sistema tiene, al menos, una solución

Como vemos, para que el sistema tenga solución, $\overrightarrow{b}\in Col(\mathbf{A})$, es decir, el vector de términos independientes debe pertenecer al espacio columna de la matriz de coeficientes. Como $\overrightarrow{b}\in\mathbb{R}^{3}$, entonces, necesitamos que el espacio columna de $A$ sea todo $\mathbb{R}^{3}$. Eso lo coseguimos pidiendo a $A$ que su rango sea 3.

Considere ahora el sistema $A^{t}\overrightarrow{y}=\overrightarrow{c}$ . ¿Es posible que el sistema tenga infinitas soluciones?

Para ello, mira esta imagen

FIG3:

De nuevo, el rango de la matriz de coeficientes deberá ser igual al de la matriz ampliada. Hay que tener en cuenta que si $c_{4}\neq0$, entonces el rango de la ampliada será mayor que el de la matriz de coeficientes y, por tanto, el sistema será incompatible. Pero siempre que $c_{4}=0$, el sistema será compatible indeterminado y tendrá, por tanto, infinitas soluciones.

Otro problema de examen para practicar

Suponga que $\mathbf{A}$ es una matriz de orden $5\times7$ y que $\mathbf{A}\overrightarrow{x}=\overrightarrow{b}$ tiene solución para todo $\overrightarrow{b}$. Entonces.

¿Cómo es el espacio generado por las columnas de $\mathbf{A}$?

Fíjate en la figura: como el sistema tiene siempre que tener solución, el rango de la matriz de coeficientes ha de ser 5, esto es, hay cinco columnas linealmente independientes. Sin embargo, FIG4:

la matriz $\mathbf{A}$ tiene siete columnas. Entonces, las columnas serán: \[ Gen\left\{ \overrightarrow{a}_{\bullet1},\overrightarrow{a}_{\bullet2},\overrightarrow{a}_{\bullet3},\overrightarrow{a}_{\bullet4},\overrightarrow{a}_{\bullet5},\overrightarrow{a}_{\bullet6},\overrightarrow{a}_{\bullet7}\right\} \] pero, como sabemos, sólo cinco de ellas son linealmente independientes. Entonces, lo que tenemos es un “generador” de las columnas de $\mathbf{A}$

¿Cómo es el espacio generado por el conjunto de soluciones de $\mathbf{A}\overrightarrow{x}=\overrightarrow{0}?$ Puedes verlo en la figura

FIG4:

De nuevo, al tener dos exógenas, sabemos que la dimensión del espacio nulo (es decir, las soluciones al sistema homogéneo) es dos. Por lo que tenemos un plano en $\mathbb{R}^{7}$.

¿Cómo es el espacio generado por el conjunto de soluciones a $A^{t}\overrightarrow{y}=\overrightarrow{0}?$

De nuevo, en la figura

FIG5:

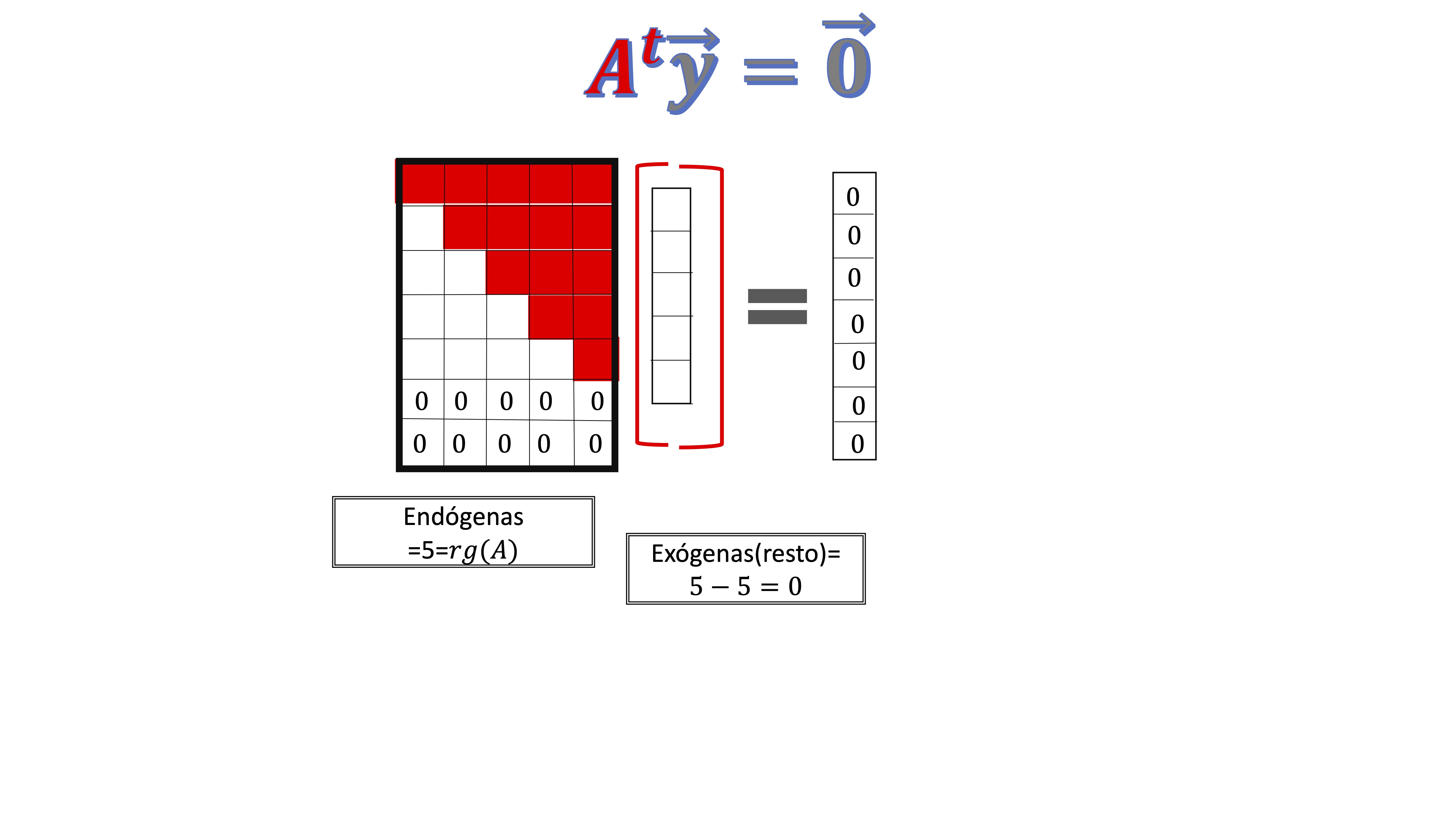
como ves, el rango (que sigue siendo indefectiblemente 5) implica que, ahora, hay 5 endógenas. Como la solución está en $\mathbb{R}^{5}$ y el rango de la ampliada coincide con el de la matriz de coeficientes y es 5, el sistema es compatible determinado y, por tanto, la única solución que admite es el vector de ceros (por eso, la dimensión del espacio solución es cero: es un punto).

FIG6: oh my god!

Ejercicio resuelto

Sea el sistema de ecuaciones $\mathbf{A}\overrightarrow{x}=\left(\begin{array}{c} 2\\ 4\\ 2 \end{array}\right)$, cuya solución completa es

\[ \overrightarrow{x}=\left(\begin{array}{c} 2\\ 0\\ 0 \end{array}\right)+c\left(\begin{array}{c} 1\\ 1\\ 0 \end{array}\right)+d\left(\begin{array}{c} 0\\ 0\\ 1 \end{array}\right) \]

¿Cuál es la dimensión del espacio vectorial generado por las filas de $\mathbf{A}$?

El espacio de soluciones se puede dividir entre la solución completa más la solución del sistema homogéneo (clase 3), es decir:

\[ \overrightarrow{x}=\underbrace{\underbrace{\left[\begin{array}{c} 2\\ 0\\ 0 \end{array}\right]}_{PARTICULAR}+\underbrace{{\color{red}c\left[\begin{array}{c} 1\\ 1\\ 0 \end{array}\right]+d\left[\begin{array}{c} 0\\ 0\\ 1 \end{array}\right]}}_{{\color{red}HOMOG\acute{E}NEO}}} \]

Esto implica que la solución del homogéneo tiene dos vectores directores, por lo que es un plano en $\mathbb{R}^{3}$, o lo que es lo mismo, un subespacio de dimensión 2. Esto implica que el sistema tiene dos exógenas y una endógena. Para ello, el rango de la matriz $A$ será 1. Entonces, esto quiere decir que la matriz $A$, que será de orden $3\times3$, tiene una sola fila linealmente independiente y su dimensión será 1.

¿Quién es $A$?

Apliquemos la solución del sistema que conocemos. Es decir,

$A\overrightarrow{x}=\left(\begin{array}{c} 2\\ 4\\ 2 \end{array}\right)$, entonces, sabemos que $\left(\begin{array}{c} 2\\ 0\\ 0 \end{array}\right)$ es una solución particular. Eso quiere decir que

\[ A\left(\begin{array}{c} 2\\ 0\\ 0 \end{array}\right)=\left(\begin{array}{c} 2\\ 4\\ 2 \end{array}\right) \]

y ya podemos conocer ¡La primera columna de la matriz $\mathbf{A}$! Esto ya lo sabes del capítulo anterior: el producto de una matriz $A$ por otra, resulta de la combinación lineal de las columnas de la matriz $\mathbf{A}$. Entonces, si \[ A=\left[\begin{array}{ccc} 1 & * & *\\ 2 & * & *\\ 1 & * & * \end{array}\right], \] ya tenemos la pimera columna. Sigamos. Ahora, sabemos que $\overrightarrow{x}=\underbrace{{\color{red}c\left[\begin{array}{c} 1\\ 1\\ 0 \end{array}\right]+d\left[\begin{array}{c} 0\\ 0\\ 1 \end{array}\right]}}$

es solución al homogéneo. Es decir:

\[ A\left[c\left(\begin{array}{c} 1\\ 1\\ 0 \end{array}\right)+d\left(\begin{array}{c} 0\\ 0\\ 1 \end{array}\right)\right]=\left(\begin{array}{c} 0\\ 0\\ 0 \end{array}\right) \]

para cualquier $c,d\neq0.$ Si los hacemos valer 1 (lo más sencillo), entonces

\[ \left[A\left(\begin{array}{c} 1\\ 1\\ 0 \end{array}\right)+A\left(\begin{array}{c} 0\\ 0\\ 1 \end{array}\right)\right]=\left(\begin{array}{c} 0\\ 0\\ 0 \end{array}\right)\Rightarrow A\left(\begin{array}{c} 1\\ 1\\ 1 \end{array}\right)=\left(\begin{array}{c} 0\\ 0\\ 0 \end{array}\right) \]

de donde sabemos que la matriz $\mathbf{A}$ \[ \left[\begin{array}{ccc} 1 & * & *\\ 2 & * & *\\ 1 & * & * \end{array}\right]\left(\begin{array}{c} 1\\ 1\\ 1 \end{array}\right)=\left(\begin{array}{c} 0\\ 0\\ 0 \end{array}\right). \]

Debemos buscar valores que, al multiplicar por el vector de unos nos devuelvan el vector de ceros. Es fácil, y hay muchas opciones. Una de ellas:

\[ \left[\begin{array}{ccc} 1 & -1 & 0\\ 2 & -2 & 0\\ 1 & -1 & 0 \end{array}\right]\left(\begin{array}{c} 1\\ 1\\ 1 \end{array}\right)=\left(\begin{array}{c} 0\\ 0\\ 0 \end{array}\right). \]

¡Ya tenemos la matriz $\mathbf{A}$! Puedes asegurarte, resolviendo el sistema, que obtienes la solución del enunciado.

Ejercicio resuelto^ {Sea $\mathbf{A}\in\mathcal{M}_{m\times n}$ una matriz de rango completo por filas, tal que el conjunto de soluciones del sistema homogéneo $\mathbf{A}\overrightarrow{x}=\overrightarrow{0}$ es \[ \left\{ \overrightarrow{x}\in\mathbb{R}^{4}:\overrightarrow{x}=a\left[\begin{array}{c} -1\\ 2\\ -3\\ 1 \end{array}\right],a\in\mathbb{R}\right\} \] }

Indique (explicando su respuesta, el número de filas y columnas de la matriz $\mathbf{A})$

Aquí piensa que la idea de rango completo por filas es que el rango de la matriz $\mathbf{A}$ es $m$. Es decir, tiene $m$ filas (y columnas) linealmente independientes. Ahora bien, la solución presenta una variable exógena (tiene un vector director), por lo que el sistema es compatible indeterminado. Esto quiere decir que, según el teorema de Rocher, el rango de la matriz $A$ al ser compatible indeterminado, tiene que ser menor que el número de columnas (variables) $n$. Como tiene 4 columnas y una variable exógena, $m=3$.

Otra manera de verlo es pensar que, al ser $n=4$ y la solución tener una exógena, la matriz, escalonada por filas, va a tener $3$ pivotes. Y el rango es justo el número de pivotes que tiene la matriz escalonada.

Encuentre un ejemplo de una matriz como $\mathbf{A}$

Aquí tienes que encontrar una matriz que satisfaga $\mathbf{A}\overrightarrow{x}=\overrightarrow{0}$ cuando sabes que $\overrightarrow{x}=a\left[\begin{array}{c} -1\\ 2\\ -3\\ 1 \end{array}\right]$ , esto es,$\mathbf{A}a\left[\begin{array}{c} -1\\ 2\\ -3\\ 1 \end{array}\right]=\overrightarrow{0}$. Un ejemplo de esa matriz $\mathbf{A}$ implica que puedes dar a $a$ cualquier valor (por ejemplo $a=1)$ así que, tienes que buscar \[ \mathbf{A}\left[\begin{array}{c} -1\\ 2\\ -3\\ 1 \end{array}\right]=\left[\begin{array}{c} 0\\ 0\\ 0 \end{array}\right] \]

Es decir, tienes que buscar una matriz $\mathbf{A}$ formada por 3 vectores fila de $4$ coordenadas que sean perpendiculares a $\left[\begin{array}{c} -1\\ 2\\ -3\\ 1 \end{array}\right]$.

Entonces, una matriz $A$, será, por ejemplo

\[ \left[\begin{array}{cccc} 2 & 1 & 0 & 0\\ -3 & 0 & 1 & 0\\ 1 & 0 & 0 & 1 \end{array}\right] \]

como ves, tienes muchas más candidatas a matriz $A$.

Existen vectores $\overrightarrow{b}$ para los cuales el sistema $\mathbf{A}\overrightarrow{x}=\overrightarrow{b}$ no tiene solución? Especifique cuáles%

La dimensión de $\overrightarrow{b}$ es $3\times1$ y el rango de $\mathbf{A}$es 3, por lo que es comaptible indeterminado y siempre tiene una solución (infinitas, de hecho)

Las filas de $\mathbf{A}$ pertenecen a $\mathbb{R}^{n}.$? Podemos hallar vectores en$\mathbb{R}^{n}$ que no sean combinación lineal de las filas de $\mathbf{A}?$ En caso afirmativo, dé un ejemplo.

Tomemos como ejemplo la matriz que dimos en la parte 2.

\[ \left[\begin{array}{cccc} 2 & 1 & 0 & 0\\ -3 & 0 & 1 & 0\\ 1 & 0 & 0 & 1 \end{array}\right] \]

Una cominación lineal es

\[ a_{1}\left[\begin{array}{c} 2\\ 1\\ 0\\ 0 \end{array}\right]+a_{2}\left[\begin{array}{c} -3\\ 0\\ 1\\ 0 \end{array}\right]+a_{3}\left[\begin{array}{c} 1\\ 0\\ 0\\ 1 \end{array}\right]=\left[\begin{array}{c} x_{1}\\ x_{2}\\ x_{3}\\ x_{4} \end{array}\right] \]

Si damos valores a $a_{1},a_{2},a_{3}$ obtendremos el vector$\left[\begin{array}{c} x_{1}\\ x_{2}\\ x_{3}\\ x_{4} \end{array}\right]$ que será combinaci?n lineal de las filas de $\mathbf{A}$. Ahora bien, hay un vector que sabemos que no es combinación lineal de estos tres: el perpendicular. Con decir que al ser $\left[\begin{array}{c} -1\\ 2\\ -3\\ 1 \end{array}\right]$ un vector perpendicular a las filas de la matriz, no habrá manera de encontrar una combinación lineal que te dé ese vector.

Si no, prueba a resolver este sistema. Será incompatible.

CURIOSIDAD: ¿Por qué el rango de una matriz es el número de filas no nulas al hacer la forma escalonada?

Para darte cuenta, lo que vamos a hacer, primero, es ver un ejemplo para entender la relación de la prueba de este teorema con los sistemas homog?neos. Mira esta matriz, donde la columna 2 es el doble de la columna 1 (por lo que esperamos que el rango sea 3):

\[ \left[\begin{array}{cccc} 1 & 2 & 1 & 0\\ 2 & 4 & 1 & 1\\ 1 & 2 & -1 & 0\\ 0 & 0 & 1 & 1 \end{array}\right] \]

La escalonamos y llegamos a \[ \left[\begin{array}{cccc} 1 & 2 & 1 & 0\\ 0 & 0 & -1 & 1\\ 0 & 0 & 0 & 2\\ 0 & 0 & 0 & 0 \end{array}\right] \]

Como sabemos, el rango es el número de filas/columnas linealmente independientes. En este caso, vamos a ver por qué las filas de esta matriz escalonada, son LI:

\[ \left[\begin{array}{c} 1\\ 2\\ 1\\ 0 \end{array}\right]\alpha_{1}+\left[\begin{array}{c} 0\\ 0\\ -1\\ 1 \end{array}\right]\alpha_{2}+\left[\begin{array}{c} 0\\ 0\\ 0\\ 2 \end{array}\right]\alpha_{3}=\left[\begin{array}{c} 0\\ 0\\ 0\\ 0 \end{array}\right] \]

la única solución posible a este sistema es que $(\alpha_{1}=\alpha_{2}=\alpha_{3}=0):$ \[ \alpha_{1}1=0 \]

\[ \alpha_{2}(-1)=0 \]

\[ \alpha_{3}2=0 \]

Es decir, tenemos tres vectores linealmente independientes.

En general, una matriz escalonada tiene esta forma:

\[ \left[\begin{array}{ccccc} * & \# & \# & ... & \#\\ 0 & 0 & * & ... & \#\\ ... & ... & ... & ... & ...\\ 0 & 0 & 0 & ... & *\\ 0 & 0 & 0 & ... & 0 \end{array}\right] \]

Y ocurrirá que si analizamos la dependencia, independencia lineal de los $p$ vectores fila distintos de cero:

\[ \left[\begin{array}{c} *\\ \#\\ \#\\ ...\\ \# \end{array}\right]\alpha_{1}+\left[\begin{array}{c} 0\\ 0\\* \\ ...\\ \# \end{array}\right]\alpha_{2}+...+\left[\begin{array}{c} 0\\ 0\\ 0\\ ...\\* \end{array}\right]\alpha_{p}=\left[\begin{array}{c} 0\\ 0\\ 0\\ ...\\ 0 \end{array}\right] \]

si te fijas, la idea de la forma escalonada obliga a que hasta la coordenada $j-$ ésima del vector, son todo ceros. Por lo tanto, la solución del sistema obligará a: \[ pivote_{j}\alpha_{j}=0 \]

por lo que no queda otra que $\alpha_{j}=0.$

Notas para Matemáticas II, UCM Somosaguas

Tema 3: Sistemas de Ecuaciones

Clase 1: Introducción a los sistemas de ecuaciones

Método de resolución de sistemas (1): Cramer

Clase 2: métodos de resolución de sistemas de ecuaciones

El método de Gauss por filas

Clase 3: Los sistemas homogéneos y los subespacios asociados a la solución

Clase 4: El (sub)espacio nulo traspuesto \(N(A^{t})\)

Aplicaciones importantes

Un esquema sobre los subespacios de una matriz

CURIOSIDAD: ¿Por qué el rango de una matriz es el número de filas no nulas al hacer la forma escalonada?