TEMA 1: Geometría del Plano y del Espacio: el espacio vectorial

Clase 1: ¿Para qué @#¢∞ necesitamos un espacio vectorial?

Ya has trabajado con ellos

De forma intuitiva, ya has trabajado durante la ESO y el bachillerato con los espacios vectoriales. Por ejemplo, para resolver este problema:

---

Problema 1

Busca \(x_1\),\(x_2\),\(x_3\) \(\in \mathbb{R}\) que resuelvan el sistema siguiente:

\[ 3x_1+2x_2=8\\ x_1+x_3=2\\ 2x_1+3x_2+8x_3=7 \]

Antes de nada, puedes escribirlo de dos formas distintas

1. Con una matriz (de coeficientes)

\[ \left[\begin{array}{ccc} 3 & 2 & 0\\ 1 & 0 & 1\\ 2 & 3 & 8 \end{array}\right]\left[\begin{array}{c} x_{1}\\ x_{2}\\ x_{3} \end{array}\right]=\left[\begin{array}{c} 8\\ 2\\ 7 \end{array}\right] \]

2. Con vectores (de coeficientes)

\[ \left[\begin{array}{c} 2\\ 1\\ 2 \end{array}\right]x_{1}+\left[\begin{array}{c} 2\\ 0\\ 3 \end{array}\right]x_{2}+\left[\begin{array}{c} 0\\ 1\\ 8 \end{array}\right]x_{3}=\left[\begin{array}{c} 8\\ 2\\ 7 \end{array}\right] \]

donde \(x_1,x_2,x_3\) -nuestras incógnitas- decimos que son escalares, esto es, números reales.

---

Como ves, tienes tanto matrices: \(\left[\begin{array}{ccc} 3 & 2 & 0\\ 1 & 0 & 1\\ 2 & 3 & 8 \end{array}\right]\), como escalares (\(x_1,x_2,x_3\)) y como vectores (por ejemplo, \(\left[\begin{array}{c} 2\\ 1\\ 2\end{array}\right]\)) en las distintas formulaciones del mismo problema. Cuando tenemos elementos matemáticos que puedo sumar entre ellos (por ejemplo cualquiera de los vectores de antes que forman el sistema) o multiplicar por un escalar (por ejemplo \(x_{3}\left[\begin{array}{c} 8\\ 2\\ 7 \end{array}\right]\)), y siguen siendo el mismo elemento (es decir, la suma de vectores te devuelve un vector, el producto de un escalar por un vector te devuelve-de nuevo- un vector), diremos que estamos trabajando con un espacio vectorial.

La necesidad fundamental de definir un espacio vectorial es tratar de ver cómo trasladar las operaciones básicas con números reales a los vectores definidos en el conjunto de los números reales.

---

Recuerda

con los números reales (\(1,6.25,\pi,e,-532,...\)) tenías aseguradas diversas propiedades. Sean \(a,b,c\in\mathbb{R}\), entonces,

1.- Conmutativa de la suma \(a+b=b+c\)

2.- Asociativa de la suma \((a+b)+c=a+(b+c)\)

3.- Elemento neutro \(a+0=a\)

4.- Elemento simétrico \(a+(-a)=0\)

Mientras que, con el producto, tendremos

5.- propiedad conmutativa \(a\times b=b \times a\)

6.- Propiedad asociativa \(a\times (b\times c)=(a\times b)\times c\)

7.- propiedad distributiva (respecto de la suma) \(a\times (b+c)=a\times b+ a\times c\)

8.- elemento neutro \(a\times 1=a\)

9.- elemento absorbente \(a\times 0=0\)

Como ves, todas estas operaciones se realizan con números reales y su resultado son números reales. ¿Podremos emular algo parecido con vectores y matrices? La respuesta está en el sistema de ecuaciones del principio en cualquiera de sus tres maneras de verlo.

---

Un espacio vectorial puede verse como un lugar en el que las operaciones de suma (y resta) de vectores/matrices… y producto de un vector/matriz por un escalar (número real) tienen sentido: esto es, te devuelven un vector/matriz de las dimensiones “adecuadas” y satisfacen ciertas propiedades parecidas a las que hemos visto antes para \(\mathbb{R}\) Por ejemplo, un ejemplo de espacio vectorial es \(\mathbb{R}^{2}\), que es el que contiene a infinitos pares de números reales ordenados \((x,y)\), o el espacio \(\mathbb{R}^{3}\), que contiene las infinitas ternas ordenadas de valores reales \((x,y,z)\). En estos espacios, hay operaciones con vectores que vamos a ver tienen sentido: ¿qué significa que tengan sentido? Pues que, al realizarlas, te devuelven otro vector/matriz que permanecen en el espacio inicial.

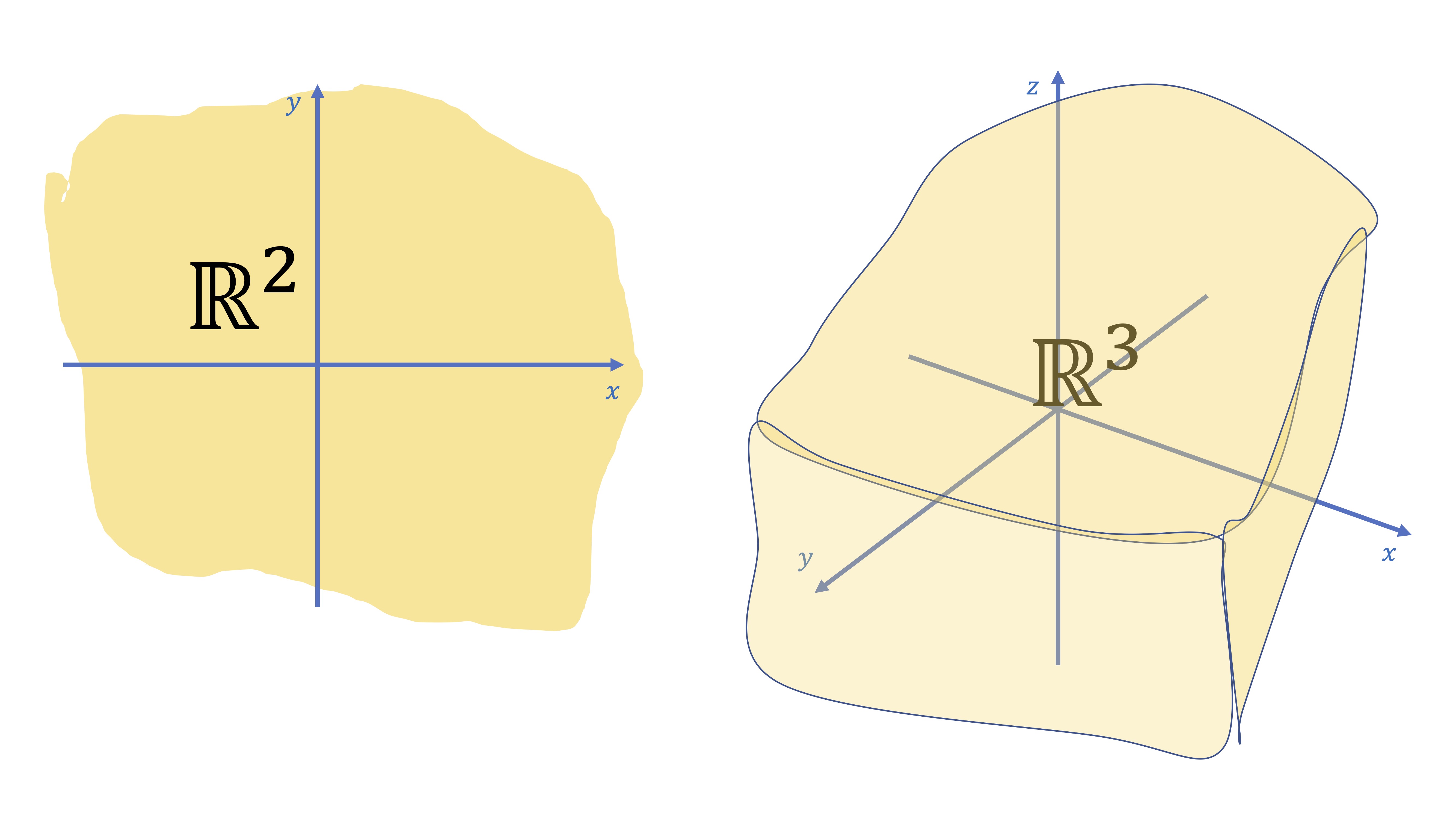Las operaciones de las que hablamos son las siguientes:

• Suma de vectores (siempre de igual dimensión) \(\overrightarrow{x}+\overrightarrow{y}=\left[\begin{array}{c} x_{1}\\ ...\\ x_{n} \end{array}\right]+\left[\begin{array}{c} y_{1}\\ ...\\ y_{n} \end{array}\right]=\left[\begin{array}{c} x_{1}+y_{1}\\ ...\\ x_{n}+y_{n} \end{array}\right]\)

• Propiedad asociativa de la suma de vectores \(\overrightarrow{x}+\left(\overrightarrow{y}+\overrightarrow{z}\right)=\left(\overrightarrow{x}+\overrightarrow{y}\right)+\overrightarrow{z}=\left[\begin{array}{c} x_{1}\\ ...\\ x_{n} \end{array}\right]+\left(\left[\begin{array}{c} y_{1}\\ ...\\ y_{n} \end{array}\right]+\left[\begin{array}{c} z_{1}\\ ...\\ z_{n} \end{array}\right]\right)=\left(\left[\begin{array}{c} x_{1}\\ ...\\ x_{n} \end{array}\right]+\left[\begin{array}{c} y_{1}\\ ...\\ y_{n} \end{array}\right]\right)+\left[\begin{array}{c} z_{1}\\ ...\\ z_{n} \end{array}\right]\)

• Elemento neutro de la suma de vectores \(\overrightarrow{x}+\overrightarrow{0}=\overrightarrow{x}\) es decir, \(\overrightarrow{0}=\left[\begin{array}{c} 0\\ ...\\ 0 \end{array}\right]\)

• Elemento opuesto \(\overrightarrow{x}-\overrightarrow{x}=\overrightarrow{0}\)

• Producto de un escalar \(\lambda\) por un vector \(\overrightarrow{x}\): \(\lambda\overrightarrow{x}=\left[\begin{array}{c} \lambda x_{1}\\ ...\\ \lambda x_{n} \end{array}\right]\)

• Propiedad distributiva con respecto a la suma de escalares \(\left(\alpha+\beta\right)\overrightarrow{x}=\alpha\overrightarrow{x}+\beta\overrightarrow{x}=\alpha\left[\begin{array}{c} x_{1}\\ ...\\ x_{n} \end{array}\right]+\beta\left[\begin{array}{c} x_{1}\\ ...\\ x_{n} \end{array}\right]\)

• propiedad distributiva con respecto a la suma de vectores \(\alpha\overrightarrow{x}+\alpha\overrightarrow{y}=\alpha(\overrightarrow{x}+\overrightarrow{y})=\alpha\left(\left[\begin{array}{c} x_{1}\\ ...\\ x_{n} \end{array}\right]+\left[\begin{array}{c} y_{1}\\ ...\\ y_{n} \end{array}\right]\right)\)

• propiedad asociativa (escalares y vector) \(\left(\alpha\beta\right)\overrightarrow{x}=\alpha\left(\beta\overrightarrow{x}\right)=\alpha\beta\left[\begin{array}{c} x_{1}\\ ...\\ x_{n} \end{array}\right]\)

• Elemento neutro del producto \(1\overrightarrow{x}=\overrightarrow{x}\)

• Elemento absorbente del producto \(0\overrightarrow{x}=\overrightarrow{0}\) mira qué es escalar y qué vector: \(0,\overrightarrow{0}).\)

Como ves, la operación “vector por vector” no está definida en el listado (piensa en qué sale de ahí), ni la de “matriz por matriz”. Claro, no satisfacen estas propiedades (ya lo sabes de Bachillerato). Entonces, el espacio vectorial se define de tal forma que haya dos operaciones (suma y producto) que funcionen adecuadamente

Formalizamos,ahora, la idea de espacio vectorial real

Un espacio vectorial real consiste en un conjunto no vacío \(E\), de objetos que llamaremos vectores, con dos operaciones \(+\) y \(\cdot\), de tal forma que el conjunto \(E\) está “cerrado” por ambas operaciones.

veamos qué significa “estar cerrado por las operaciones”

Definimos los vectores \(\overrightarrow{u},\overrightarrow{v},\overrightarrow{w}\in E\) y los escalares \(\lambda,\mu\in\mathbb{R}\). Entonces:

El conjunto \(E\) está “cerrado” por la operación suma.

Eso quiere decir que la suma de dos vectores cualesquiera que pertenezcan a \(E\) tiene que pertenecer también a \(E\), es decir, \(\overrightarrow{u}+\overrightarrow{v}\in E\). Entonces:

• Hay un vector \(\overrightarrow{0}\in E\) tal que ejerce de elemento neutro de la suma (es decir, \(\overrightarrow{u}+\overrightarrow{0}=\overrightarrow{u}\))

• Cada vector \(\overrightarrow{v}\) tiene un inverso aditivo, tal que \(\overrightarrow{w}+\overrightarrow{v}=\overrightarrow{0}\) (entonces, \(\overrightarrow{v}=-\overrightarrow{w})\)

• Y se cumplen las propiedades conmutativa y asociativa de la suma.

El conjunto \(E\) está “cerrado” por el producto de un vector por un escalar.

Esto quiere decir que \(\lambda\overrightarrow{v}\in E\)

• Entonces, tenemos propiedad distributiva en los escalares y el producto \((\lambda+\mu)\overrightarrow{v}=\lambda\overrightarrow{v}+\mu\overrightarrow{v}\)

• Así como en la suma de vectores \(\lambda\left(\overrightarrow{v}+\overrightarrow{w}\right)=\lambda\overrightarrow{v}+\lambda\overrightarrow{w}\)

• Debe existir el elemento neutro del producto escalar \(1\cdot\overrightarrow{v}=\overrightarrow{v}\) así como el absorbente \(0\cdot\overrightarrow{v}=\overrightarrow{0}\)

En esta asignatura, los espacios vectoriales con los que trabajaremos, en general, serán \(\mathbb{R}^{2},\mathbb{R}^{3},...,\mathbb{R}^{n}\) ya que es obvio ver que satisfacen estas propiedades (debido a que las heredan de las propiedades de los números reales con las que has trabajado desde siempre y con las propiedades de las operaciones con vectores ya explicados.

Piensa ¿Son los polinomios de grado 2 espacios vectoriales?

Claro. Por ejemplo, el polinomio \(P(x)=2x^2+3x+1\). Si le sumas otro polinomio de grado 2, \(Q(x)=x^2+1\), obtienes….¡un polinomio de grado 2! (\(P(x)+Q(x)=3x^2+3x+2\)). Si lo multiplicas por un escalar (por ejemplo, 3), obtienes un ¡polinomio de grado 2! (\(3P(x)=6x^2+9x+3\)). Sin embargo, ¿¿si multiplicas ambos polinomios?? Pues obtendrás un polinomio de grado 4. En este caso, la operación producto entre polinomios tiene sentido matemático, pero no conforma un espacio vectorial. Por lo tanto, para que los polinomios sean objetos de un espacio vectorial, se debe usar sólo la operación producto por un escalar.

---

Clase 2: El concepto de vector

Uno de los elementos más representativos de un espacio vectorial es un vector. En general, dar una definición de vector es sencillo (nos debería bastar con la típica de segmento de recta, contado a partir de un punto del espacio, cuya longitud representa a escala una magnitud, en una dirección determinada y en uno de sus sentidos) pero no suele entenderse, ya que está especialmente diseñada para la física. Piensa que, para nosotros, un vector es un instrumento algebráico que nos permite almacenar información de una manera ordenada, sencilla y clara. Vamos a entenderlo de forma intuitiva. Para ello, imaginemos primeramente que visualizamos la información del precio de una acción en bolsa:

FIG1. La trayectoria de una acción en la bolsa.

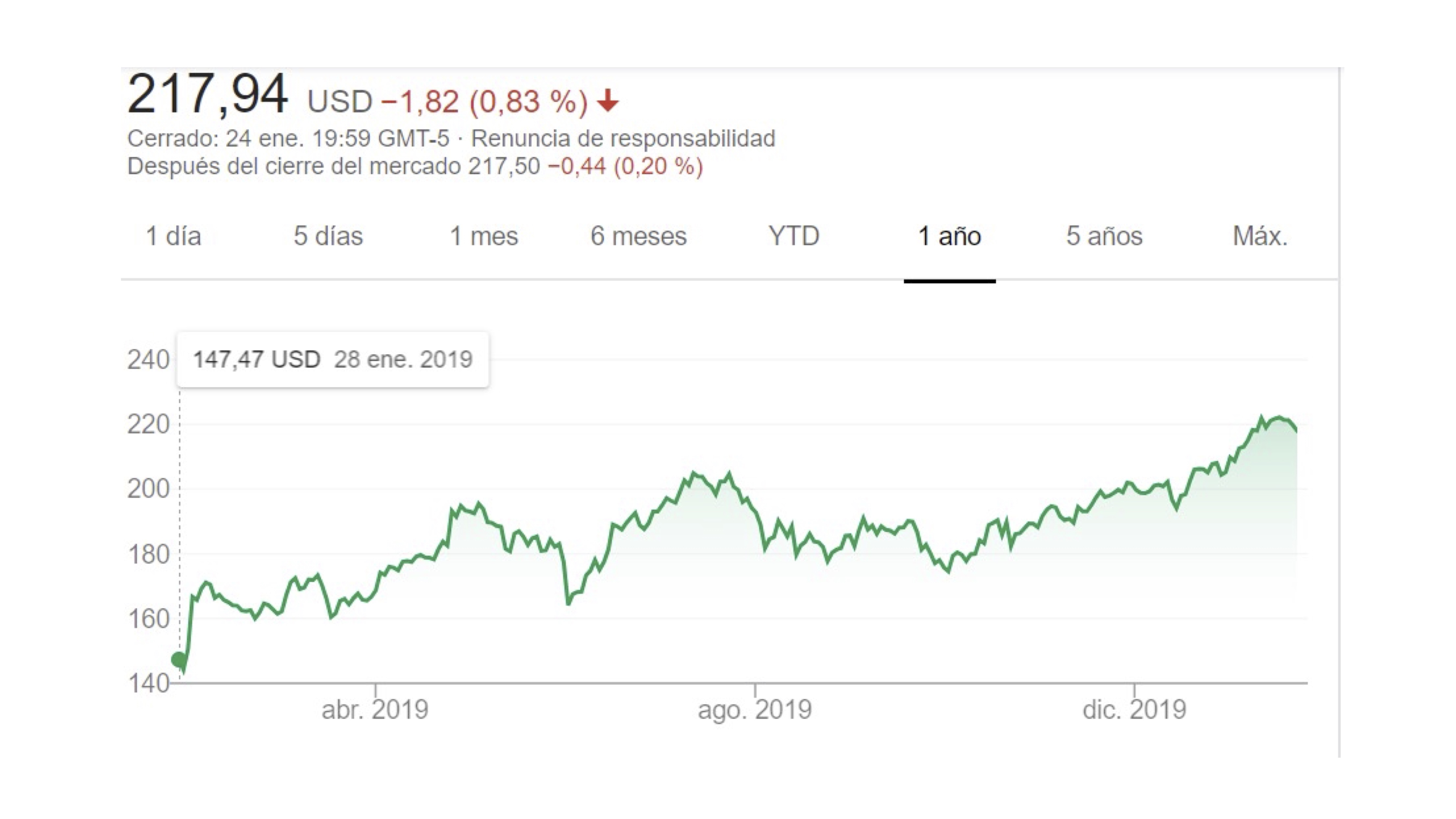
Los homo sapiens sapiens intentamos entender rápidamente los movimientos más sobresalientes. De esta forma, no prestamos atención a los pequeños cambios con forma de diente de sierra. Como el ojo humano tiende a abstraer y quedarse con un “esquema” del movimiento, en realidad vemos algo así:

FIG2. Una abstracción de dicho movimiento con vectores.

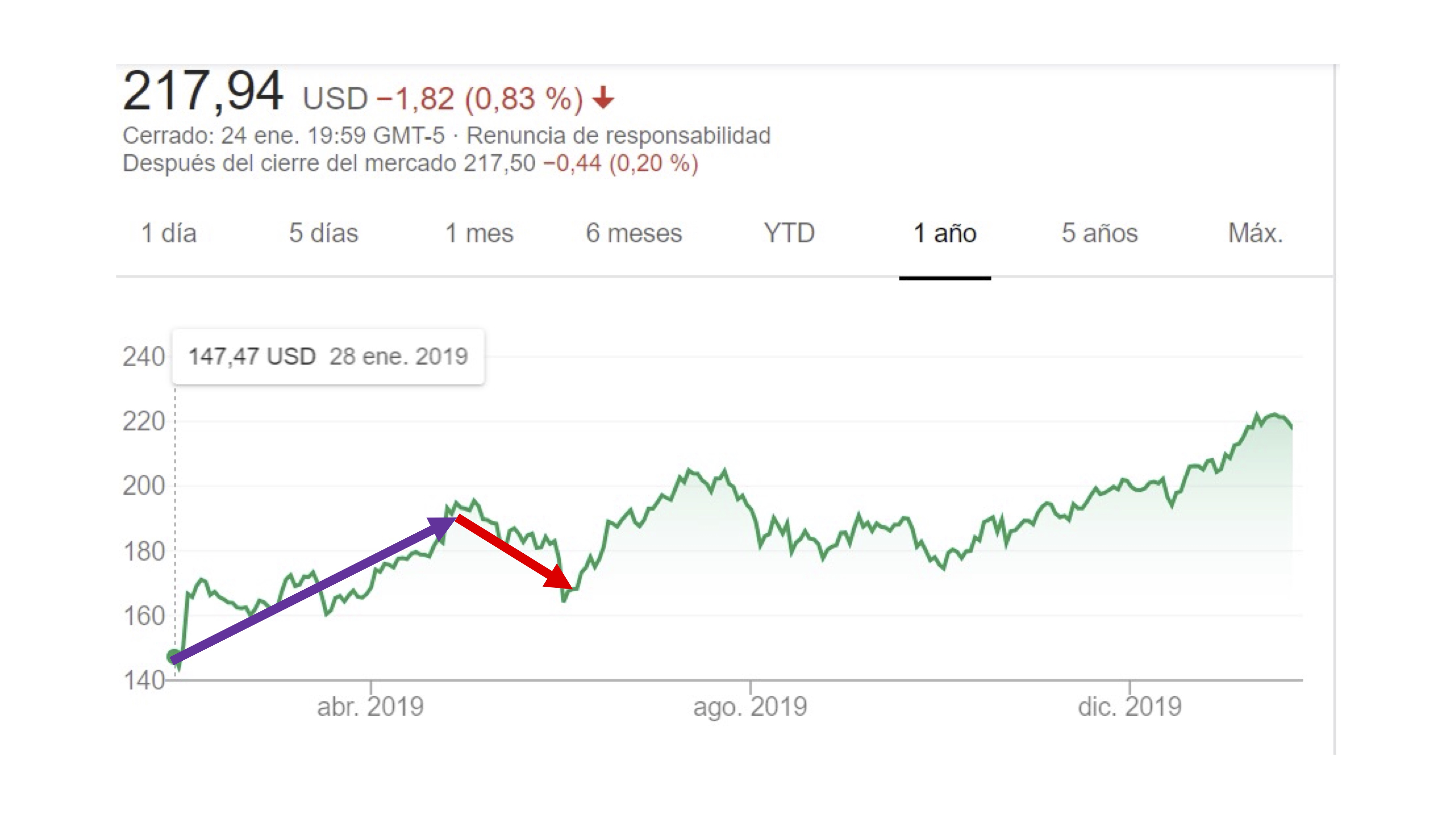
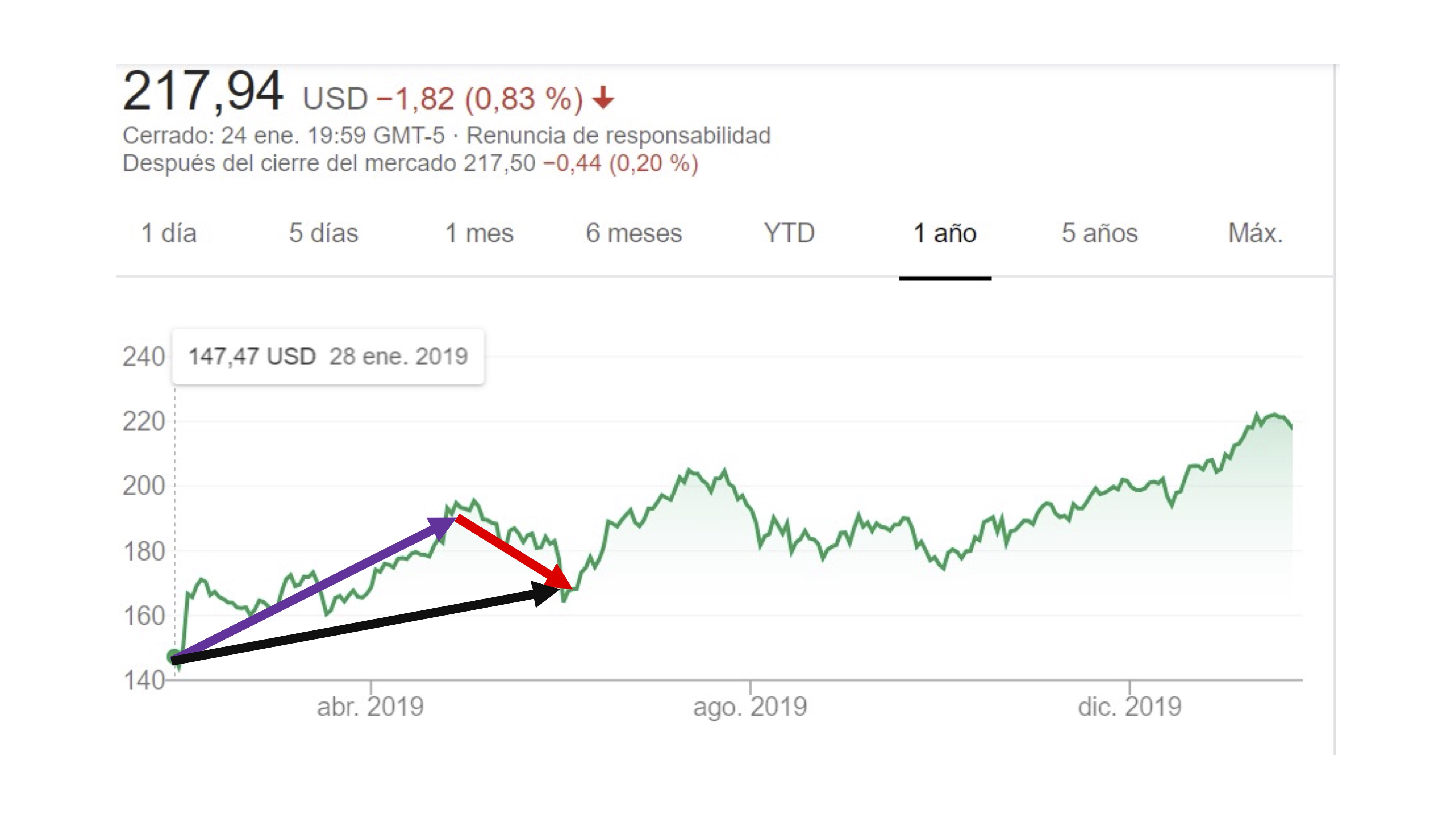
Las flechas representan la idea de vector. La primera flecha, la morada, nos está indicando un “crecimiento” sostenido en el tiempo, mientras que la roja, un “decrecimiento” algo menos prolongado en el tiempo.

Estos vectores tienen sentido porque están contextualizados. Ese contexto viene dado por los ejes de coordenadas. En el eje de las \(x\), representamos el tiempo y en el eje de las \(y\) el incremento en el valor.

De hecho, las operaciones básicas, como la suma y la resta, tienen pleno sentido. La suma de los dos vectores está representada aquí por el negro. Si te das cuenta, indica de dónde partes y a dónde llegas. Es el resultado de subir con cierto ritmo (vector morado) pero luego bajar (vector rojo). Es una manera de tener un buen resumen del efecto de ambas fuerzas.

FIG3. La idea de la suma como el efecto de dos fuerzas.

Puedes ver un pequeño vídeo donde hablamos más de la idea de vector

Sin embargo, verás que un vector puede tener muchos significados. En esta asignatura, para nosotros, simplemente será un “contenedor” de información numérica que, en el caso de 2 y 3 dimensiones, podremos representarlo pero que, en general, será un objeto abstracto. Veremos, además, que nos permitirá definir rectas en el plano y en el espacio y planos en el espacio. Esto es, efectivamente, una aplicación geométrica que nos será de utilidad para poder entender más ideas abstractas.

Los vectores, en este curso, los escribiremos-casi siempre- en columnas. Es decir, sea \(\overrightarrow{x}\in\mathbb{R}^{2},\overrightarrow{y}\in\mathbb{R}^{3},\overrightarrow{w}\in\mathbb{R}^{n}\) \[ \overrightarrow{x}=\left[\begin{array}{c} 2\\ -1 \end{array}\right],\overrightarrow{y}=\left[\begin{array}{c} 3\\ -1\\ 2 \end{array}\right],\overrightarrow{w}=\left[\begin{array}{c} w_{1}\\ w_{2}\\ w_{3}\\ ...\\ w_{n} \end{array}\right], \]

con letras minúsculas y, además, con una flecha por encima. Trabajaremos sólo con números reales, de tal forma que seguiremos esta notación:

FIG4. Con esta notación nos referiremos al espacio en el que convivirán los vectores.

Idea final: un vector puede ser “muchas cosas”. No tengas miedo a abstraer la idea y aprender a manipular los objetos (lo cual, en esencia, es empezar a jugar con elementos que uno no puede visualizar pero que, sin embargo, satisfacen propiedades muy estimulantes)

Suma y diferencia de vectores

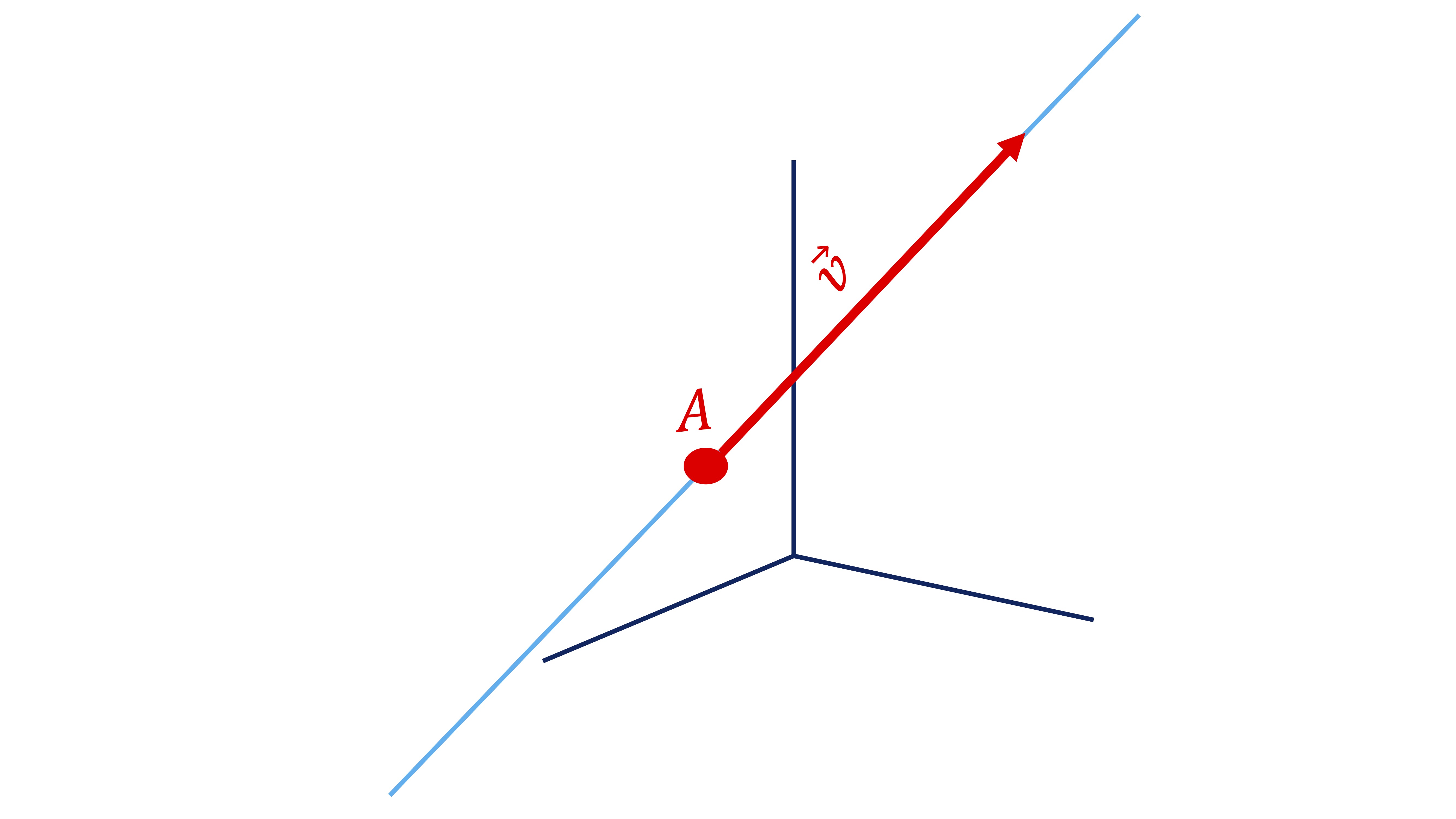
Es interesante remarcar, primeramente, la diferencia entre un punto y un vector (tal y como va a usarse en esta asignatura): la diferencia fundamental es que el punto \(A(1,3)\) tiene un único lugar en los ejes coordenados, mientras que el vector \(\overrightarrow{u}=(1,3)\) lo podemos situar donde queramos siempre y cuando respetemos su dirección y sentido.

FIG5. Un punto y un vector.

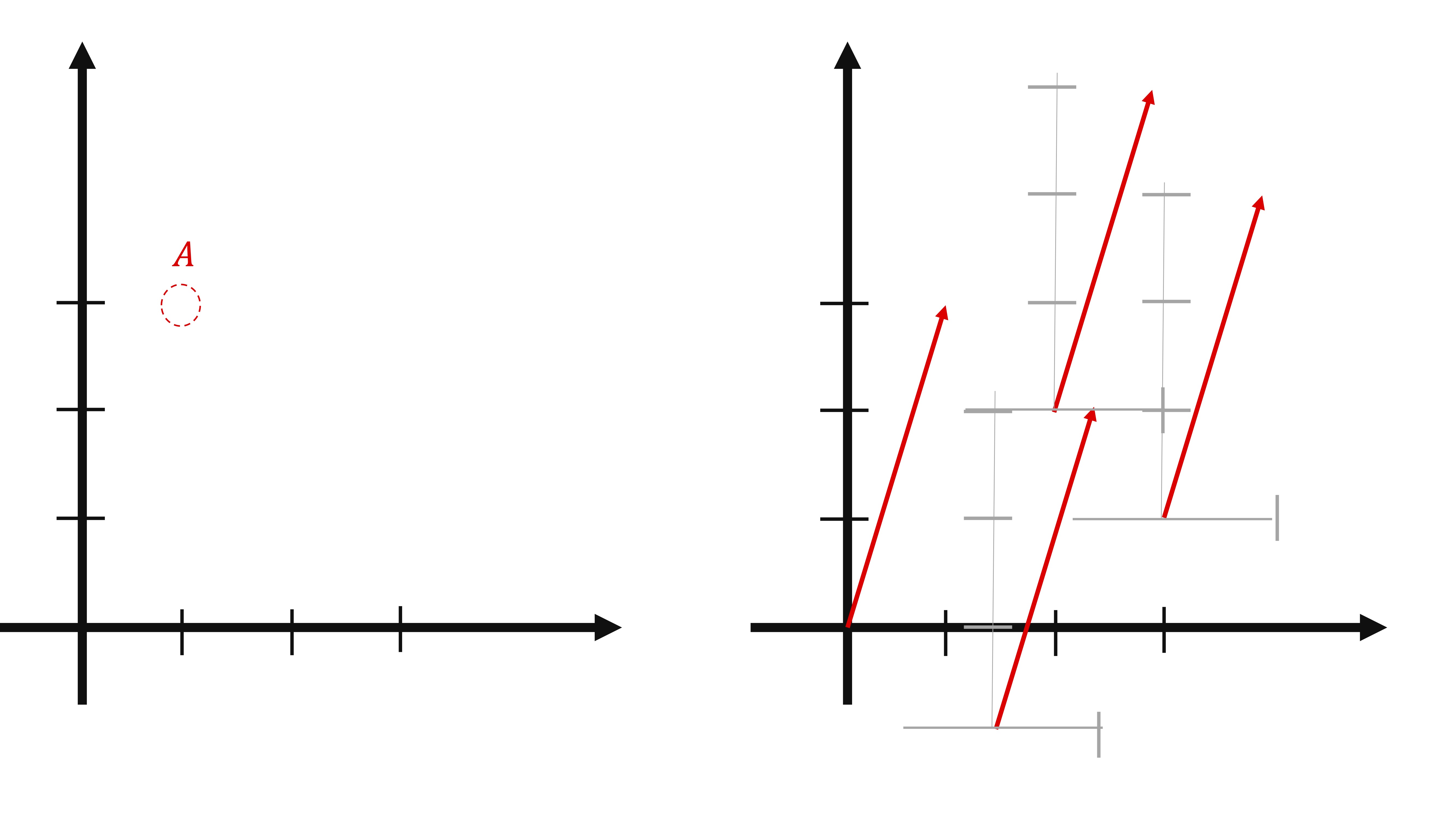
En la FIG 5 representamos el punto \(A=(1,3)\) y el vector \(\overrightarrow{u}=(1,3).\) Como ves, el vector lo podemos situar donde queramos. Simplemente, en el inicio (punto de aplicación) nos imaginamos unos ejes coordenados para poder trazar la flecha que une cualquier punto que represente el origen de coordenadas con el punto que indica la dirección y sentido correspondientes.

Por otro lado, si multiplicamos un vector por un escalar positivo, obtendremos vectores proporcionales a este en la misma dirección y sentido. Si lo multiplicamos por un escalar negativo, obtendremos un vector en la misma dirección pero sentido opuesto

Por ejemplo, en la FIG 6 representamos el vector \(\overrightarrow{x}\) y algunos vectores proporcionales a este (es decir, \(\lambda\overrightarrow{x}\))

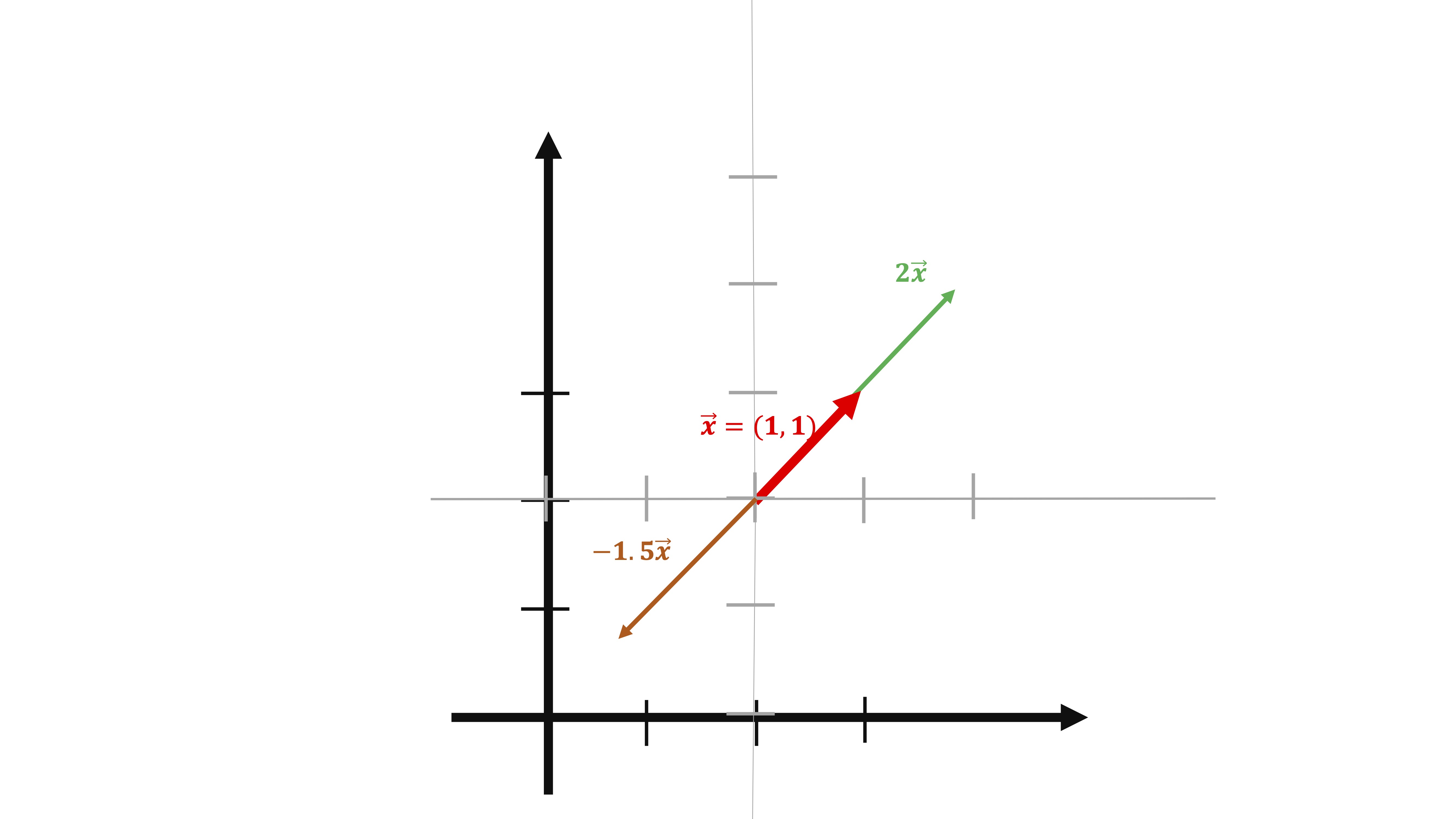Como ves, el signo y la magnitud de \(\lambda\) indica si el nuevo vector va en el mismo sentido (\(\lambda\) positivo), si va en sentido contrario (\(\lambda\) negativo) o si tiene mayor longitud (valor absoluto de \(\lambda\) mayor que 1) o si tiene menor longitud (valor absoluto de \(\lambda\) menor que 1)

Finalmente, sean dos vectores \(\overrightarrow{u}=\left(1,3\right)\) y \(\overrightarrow{v}=\left(2,1\right)\), la suma y la diferencia se realizarán componente a componente. Es decir:

\[ \overrightarrow{u}+\overrightarrow{v}=\left[\begin{array}{c} 3\\ 4 \end{array}\right] \]

\[ \overrightarrow{u}-\overrightarrow{v}=\left[\begin{array}{c} -1\\ 2 \end{array}\right] \]

Gráficamente, en el caso de la suma podemos ilustrarla mediante la “regla del paralelogramo”, mientras que, en el caso de la diferencia, lo que tenemos es el vector que se genera uniendo las puntas de flecha de estos.

FIG7. La suma y diferencia de vectore.

Podemos dibujar, asimismo, un vector en tres dimensiones. Por ejemplo,

\[ \overrightarrow{w}=\left[\begin{array}{c} 1\\ -1\\ 3 \end{array}\right], \]

para ello, define los tres ejes de coordenadas correspondientes. Primero busca el punto donde se cruzan las dos primeras componentes (asociadas, en nuestro ejemplo, al eje \(x\) y al eje \(y\)). Después, traza un eje paralelo al \(z\) y avanza tres unidades tomando la intersección del punto \(x=1,y=-1\) como origen de coordenadas. Y ya tienes el vector que querías representar.

---

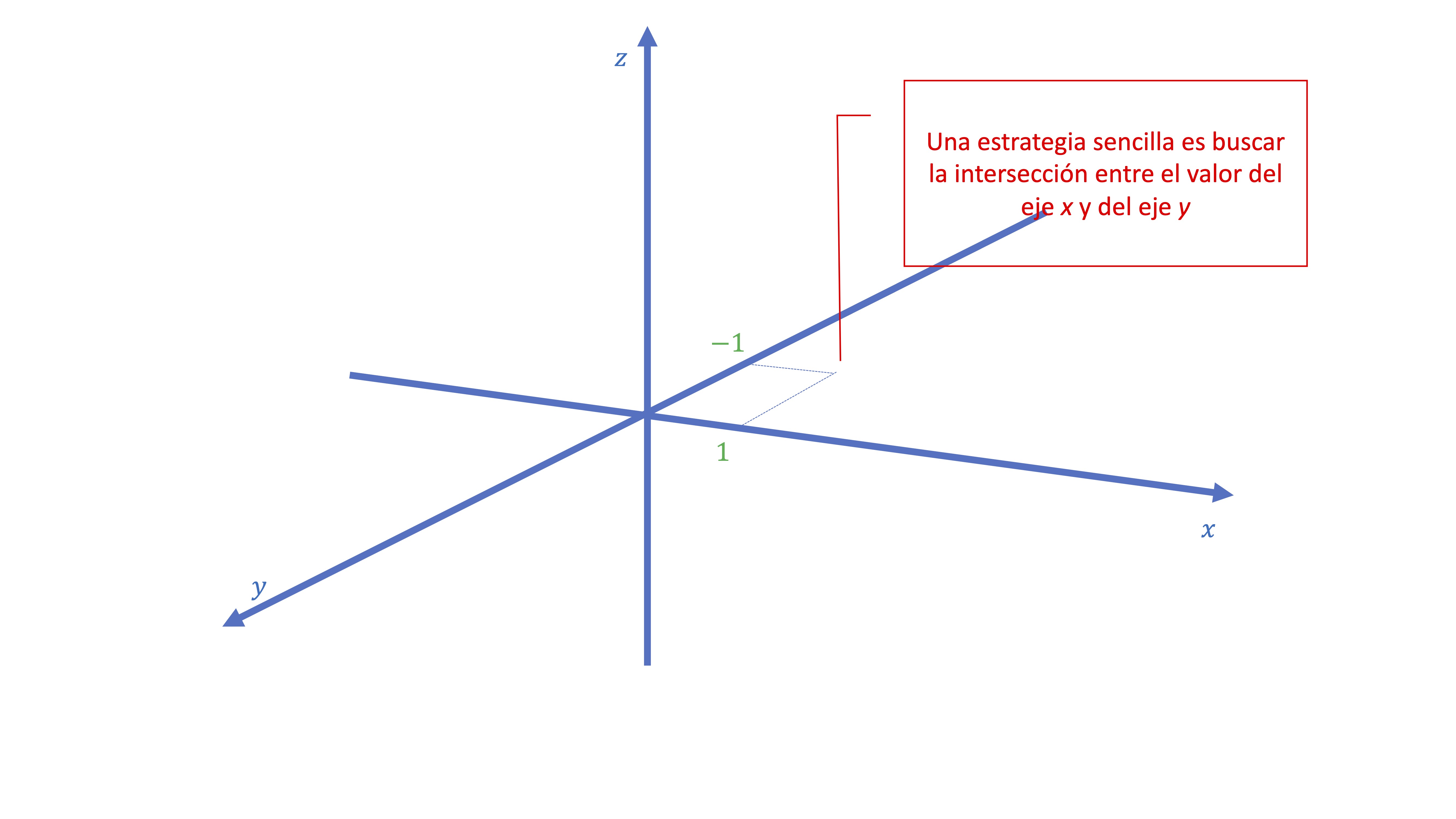
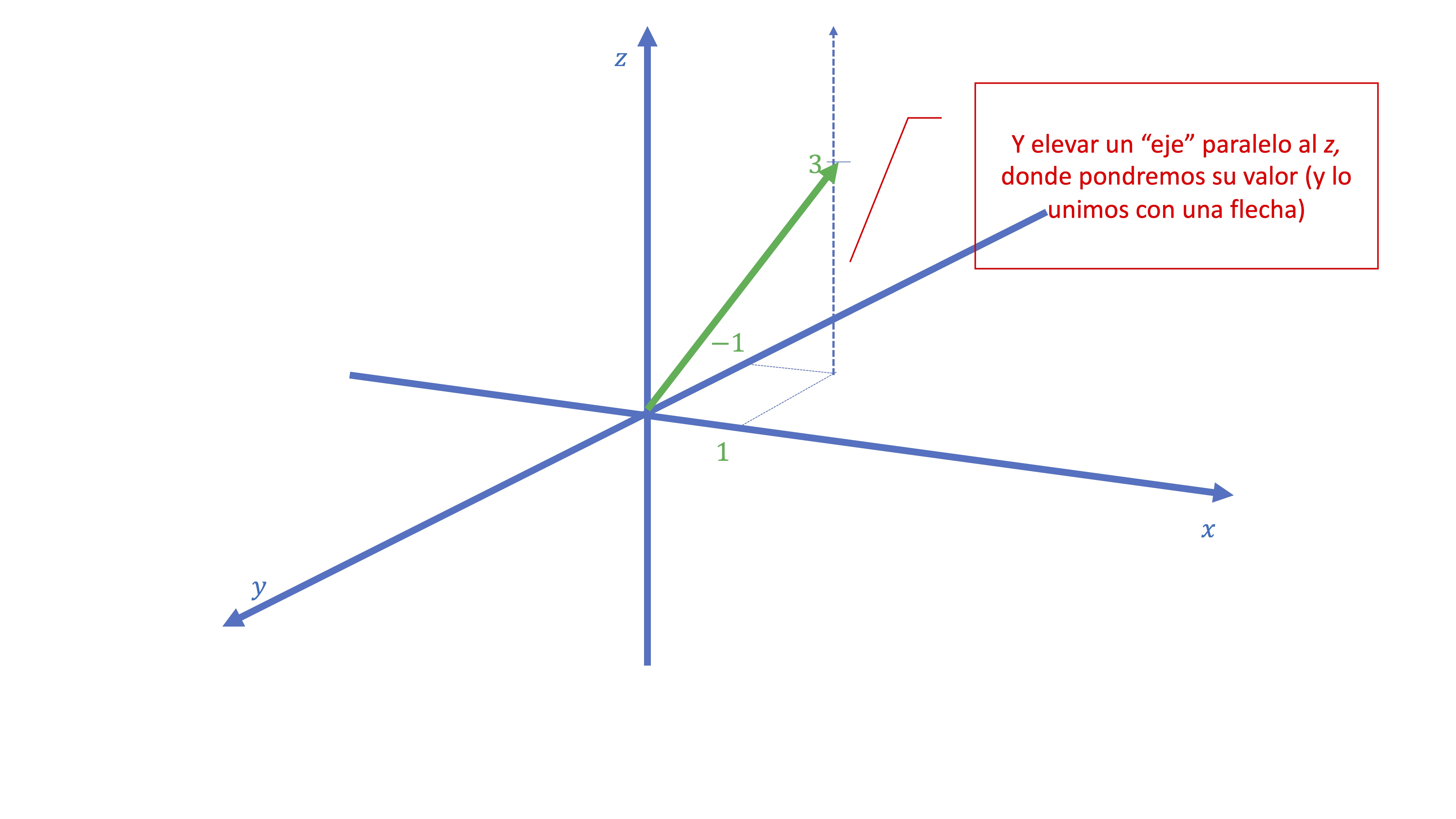
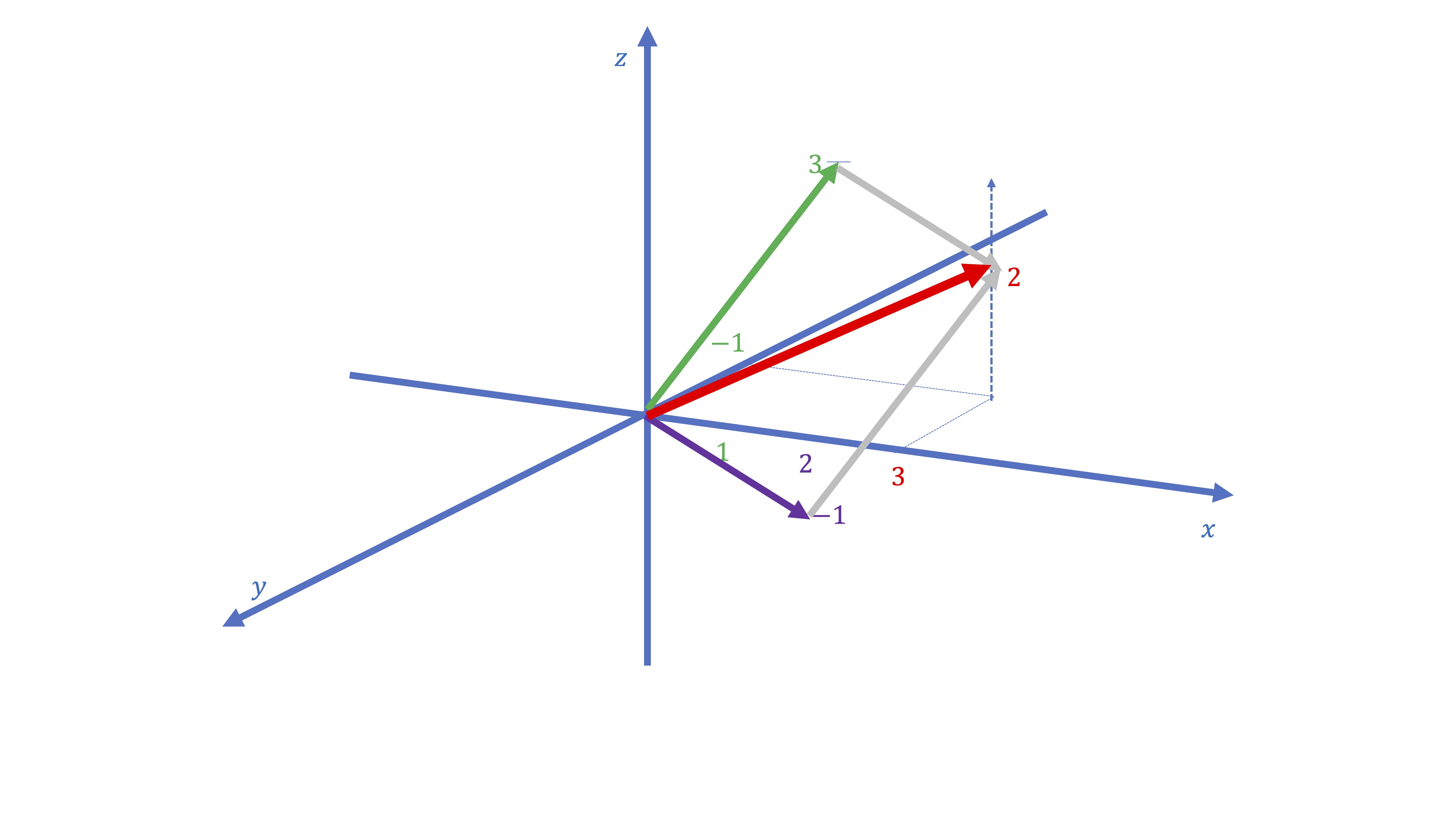
*Ejemplo resuelto*
Dibuja los siguientes vectores y su suma, mediante la regla del paralelogramo: 

\(\overrightarrow{x}=\left[\begin{array}{c} 1\\ -1\\ 3 \end{array}\right],\overrightarrow{y}=\left[\begin{array}{c} 2\\ 0\\ -1 \end{array}\right]\)

FIG9. La regla del paralelogramo en 3 dimensiones.

---

Clase 3: Operaciones en el espacio vectorial

la combinación lineal

Vuelve a ver el sistema enunciado en el Problema 1, de la clase 1. Si te fijas, una de las maneras de escribir este sistema fue

\[ \left[\begin{array}{c} 2\\ 1\\ 2 \end{array}\right]x_{1}+\left[\begin{array}{c} 2\\ 0\\ 3 \end{array}\right]x_{2}+\left[\begin{array}{c} 0\\ 1\\ 8 \end{array}\right]x_{3}=\left[\begin{array}{c} 8\\ 2\\ 7 \end{array}\right] \]

Si te das cuenta, estamos sumando vectores (multiplicados por un escalar) con el objetivo de que esa suma nos proporcione otro vector. De hecho, si hacemos \(x_1=\frac{7}{3}\),\(x_2=\frac{5}{3}\),\(x_3=-\frac{1}{3}\)

puedes comprobar que la suma proporciona el vector a la derecha del igual:

\[ \frac{7}{3}\left[\begin{array}{c} 2\\ 1\\ 2 \end{array}\right]+\frac{5}{3}\left[\begin{array}{c} 2\\ 0\\ 3 \end{array}\right]-\frac{1}{3}\left[\begin{array}{c} 0\\ 1\\ 8 \end{array}\right]=\left[\begin{array}{c} 8\\ 2\\ 7 \end{array}\right] \]

Podemos decir que el vector \(\left[\begin{array}{c} 8\\ 2\\ 7 \end{array}\right]\) “depende” de los vectores \(\left[\begin{array}{c} 2\\ 1\\ 2 \end{array}\right],\left[\begin{array}{c} 2\\ 0\\ 3 \end{array}\right],\left[\begin{array}{c} 0\\ 1\\ 8 \end{array}\right]\) ya que, al multiplicar convenientemente esos vectores por escalares y sumarlos, obtenemos el vector \(\left[\begin{array}{c} 8\\ 2\\ 7 \end{array}\right]\). Entonces, decimos que \(\left[\begin{array}{c} 8\\ 2\\ 7 \end{array}\right]\) es un vector linealmente dependiente de \(\left[\begin{array}{c} 2\\ 1\\ 2 \end{array}\right],\left[\begin{array}{c} 2\\ 0\\ 3 \end{array}\right],\left[\begin{array}{c} 0\\ 1\\ 8 \end{array}\right]\) y también decimos que esta operación:

\[ \frac{7}{3}\left[\begin{array}{c} 2\\ 1\\ 2 \end{array}\right]+\frac{5}{3}\left[\begin{array}{c} 2\\ 0\\ 3 \end{array}\right]-\frac{1}{3}\left[\begin{array}{c} 0\\ 1\\ 8 \end{array}\right]\]

es una *combinación lineal”. Piensa, entonces, que un sistema de ecuaciones compatible permite poner el término independiente como una combinación lineal de los vectores (columna) que forman la matriz de coeficientes.

De manera más formal

Sea \[ \overrightarrow{y}\in\mathbb{R}^{n} \]

se dice que es combinación lineal de \(k\) vectores \(\overrightarrow{x}_{1},...,\overrightarrow{x}_{k}\in\mathbb{R}^{n}\) si existen números reales \(\lambda_{1},...,\lambda_{k}\) tales que

\[ \overrightarrow{y}=\alpha_{1}\overrightarrow{x}_{1}+...+\alpha_{k}\overrightarrow{x}_{k} \]

Nota que, en este caso, \(k\) es el número de vectores que intervienen en la suma y que \(n\) es la dimensión del espacio vectorial en el que se buscan los vectores.

Al conjunto de todas las combinaciones lineales \(\overrightarrow{x}_{1},...,\overrightarrow{x}_{k}\in\mathbb{R}^{n}\) que se pueden obtener dando valores a \(\alpha_{1},\alpha_{2},...\alpha_{k}\in\mathbb{R}\) se le denota

sistema generador \[ Gen\left\{ \overrightarrow{x}_{1},...,\overrightarrow{x}_{k}\right\} , \]

de tal forma que \[ Gen\left\{ \overrightarrow{x}_{1},...,\overrightarrow{x}_{k}\right\} =\alpha_{1}\overrightarrow{x}_{1}+...+\alpha_{k}\overrightarrow{x}_{k} \]

Diremos que un conjunto de vectores, por ejemplo, \(\overrightarrow{x}_{1},...,\overrightarrow{x}_{k}\) son linealmente dependientes si alguno de ellos es combinación lineal de los restantes. Podría ocurrir que haya un subconjunto de vectores que sean linealmente independientes y otros que sean linealmente dependientes. Al mayor número de vectores linealmente independientes se llamará rango de ese conjunto de vectores. Definimos, ahora, una manera operativa para trabajar con la dependencia lineal de vectores

Diremos que los vectores \(\overrightarrow{x}_{1},...,\overrightarrow{x}_{k}\in\mathbb{R}^{n}\) son lineamente dependientes si existen números (reales) \(\alpha_{1},...,\alpha_{k}\) no todos nulos tales que \[ \alpha_{1}\overrightarrow{x}_{1}+...+\alpha_{k}\overrightarrow{x}_{k}=\overrightarrow{0} \]

Por otro lado, un conjunto de vectores es linealmente independiente si para obtener \[ \alpha_{1}\overrightarrow{x}_{1}+...+\alpha_{k}\overrightarrow{x}_{k}=\overrightarrow{0} \]

obligatoriamente todos los \(\alpha_{i}=0\), para \(i=1,....,k.\)

---

*Ejercicio resuelto*

Entonces, para saber si un conjunto de vectores es linealmente independiente,
habrá que resolver el sistema de ecuaciones asociado

\[ \alpha_{1}\overrightarrow{x}_{1}+...+\alpha_{k}\overrightarrow{x}_{k}=\overrightarrow{0} \]

 y, si la única solución posible es
 

\[ \alpha_{1},..,\alpha_{k}=(0,...,0). \]

entonces, son linealmente independientes.

• Nos preguntamos si el conjunto de vectores \(V=\left\{ \left[\begin{array}{c} 2\\ 4\\ 2 \end{array}\right],\left[\begin{array}{c} 1\\ 1\\ 1 \end{array}\right],\left[\begin{array}{c} 0\\ 2\\ 0 \end{array}\right]\right\}\) es linealmente dependiente.

Entonces,

\[ \lambda_{1}\left[\begin{array}{c} 2\\ 4\\ 2 \end{array}\right]+\lambda_{2}\left[\begin{array}{c} 0\\ 2\\ 0 \end{array}\right]+\lambda_{3}\left[\begin{array}{c} 1\\ 1\\ 1 \end{array}\right]=\left[\begin{array}{c} 0\\ 0\\ 0 \end{array}\right] \]

Fíjate que esto da lugar a un sistema de ecuaciones

\[ \begin{cases} 2\lambda_{1}+\lambda_{3}=0\\ 4\lambda_{1}+2\lambda_{2}+\lambda_{3}=0\\ 2\lambda_{1}+\lambda_{3}=0 \end{cases} \]

cuya solución es, \(\lambda_{3}=-2\lambda_{1},\lambda_{2}=-\lambda_{1}\), por lo que, para cualquier valor de \(\lambda_{1}\neq0\), podemos tener un valor de \(\lambda_{2}\)y de \(\lambda_{3}\). Por lo que el conjunto de vectores es linealmente dependiente.

• Nos preguntamos si el conjunto de vectores \(W=\left\{ \left[\begin{array}{c} 1\\ 1\\ 1 \end{array}\right],\left[\begin{array}{c} 1\\ 1\\ -1 \end{array}\right],\left[\begin{array}{c} -1\\ 1\\ 1 \end{array}\right]\right\}\) es linealmente dependiente.

Entonces, planteamos

\[ \lambda_{1}\left[\begin{array}{c} 1\\ 1\\ 1 \end{array}\right]+\lambda_{2}\left[\begin{array}{c} 1\\ 1\\ -1 \end{array}\right]+\lambda_{3}\left[\begin{array}{c} -1\\ 1\\ 1 \end{array}\right]=\left[\begin{array}{c} 0\\ 0\\ 0 \end{array}\right] \]

Fíjate que esto da lugar a un sistema de ecuaciones:

\[ \begin{cases} \lambda_{1}+\lambda_{2}-\lambda_{3}=0\\ \lambda_{1}+\lambda_{2}+\lambda_{3}=0\\ \lambda_{1}-\lambda_{2}+\lambda_{3}=0 \end{cases} \]

la única solución posible es

\[ {\color{red}0}\left[\begin{array}{c} 1\\ 1\\ 1 \end{array}\right]+{\color{red}0}\left[\begin{array}{c} 1\\ 1\\ -1 \end{array}\right]+{\color{red}0}\left[\begin{array}{c} -1\\ 1\\ 1 \end{array}\right]=\left[\begin{array}{c} 0\\ 0\\ 0 \end{array}\right] \]

es que todos los parámetros sean cero.

El producto escalar

Es una operación entre vectores que genera un número real (escalar). Los ingleses lo llaman “dot product” y, es cierto, usamos el punto (o este símbolo \(\left\langle \cdot\right\rangle )\) para indicar la siguiente operación de dos vectores \(\overrightarrow{x},\overrightarrow{y}\in\mathbb{R}^{n}\) tal que \[ \overrightarrow{x}=\left[\begin{array}{c} x_{1}\\ x_{2}\\ ...\\ x_{n} \end{array}\right],\overrightarrow{y}=\left[\begin{array}{c} y_{1}\\ y_{2}\\ ...\\ y_{n} \end{array}\right], \]

entonces, el producto escalar se define como

\[ \overrightarrow{x}\cdot\overrightarrow{y}=\left\langle \overrightarrow{x},\overrightarrow{y}\right\rangle =\left(x_{1}y_{1}+...+x_{n}y_{n}\right) \]

Por ejemplo, si

\[ \overrightarrow{x}=\left[\begin{array}{c} 1\\ -1\\ 0\\ 2 \end{array}\right],\overrightarrow{y}=\left[\begin{array}{c} 0\\ 1\\ -1\\ 3 \end{array}\right], \]

calculamos el producto escalar de ambos vectores como

\[ \overrightarrow{x}\cdot\overrightarrow{y}=\left[\begin{array}{c} 1\\ -1\\ 0\\ 2 \end{array}\right]\cdot\left[\begin{array}{c} 0\\ 1\\ -1\\ 3 \end{array}\right]=1\times 0 +(-1)\times 1 + 0\times(-1)+2\times3=5 \]

¿qué quiere decir este valor? está relacionado con el ángulo que abarca ambos vectores. Para probarlo, necesitaríamos invocar al teorema del coseno pero no vamos a hacerlo. Lo único importante en este caso es saber que si el producto escalar es 0, eso implica que ambos vectores comprenden un ángulo recto y decimos que son perpendiculares u ortogonales.

El producto escalar tiene las siguientes propiedades:

• \(\overrightarrow{x}\cdot\overrightarrow{y}=\overrightarrow{y}\cdot\overrightarrow{x}\) (conmutativa)

• \(\overrightarrow{x}\cdot\left(\overrightarrow{y}+\overrightarrow{z}\right)=\overrightarrow{x}\cdot\overrightarrow{y}+\overrightarrow{x}\cdot\overrightarrow{z}\) (distributiva)

• \(\alpha\left(\overrightarrow{x}\cdot\overrightarrow{y}\right)=\left(\alpha\overrightarrow{x}\right)\cdot\overrightarrow{y}=\overrightarrow{x}\cdot\left(\alpha\overrightarrow{y}\right)\)
• \(\overrightarrow{x}\cdot\overrightarrow{x}>0\) si \(\overrightarrow{x}\neq0\)

Veamos algunas ideas que necesitaremos en este curso y que están relacionadas con el producto escalar.

---

Clase 4: Operaciones en el espacio vectorial(II)

• ¿Cuánto mide un vector? Calcularemos su longitud

FIG 1. La longitud de un vector en ^2 usando el teorema de Pitágoras

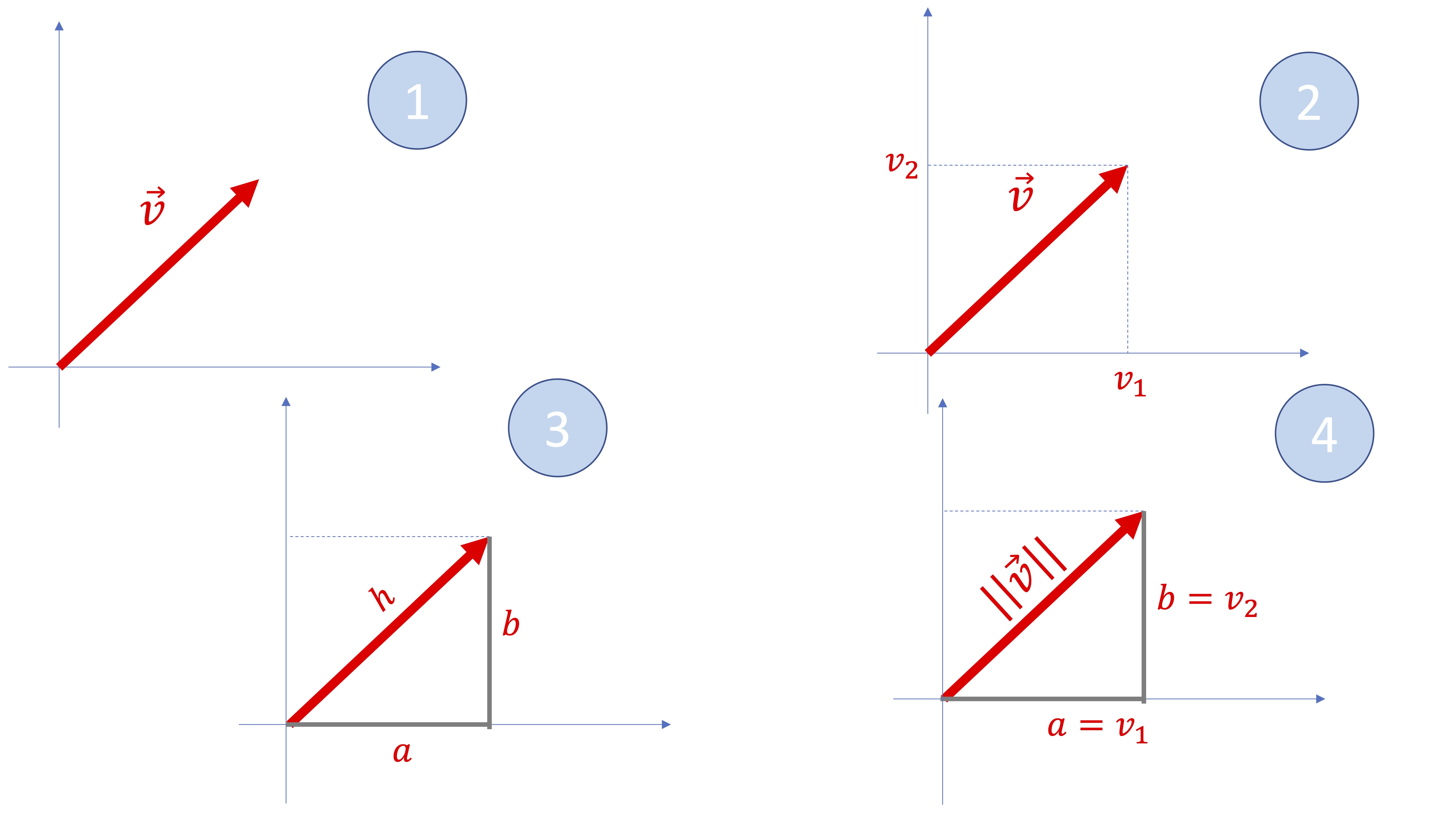
La longitud, que es la medida del vector, se puede analizar tomando como referencia el Teorema de Pitágoras (como en FIG 1):

1. representamos un vector cualquiera: el vector \(\overrightarrow{v}=\left[\begin{array}{c} v_{1}\\ v_{2} \end{array}\right]\)

2. marcamos claramente sus componentes en el plano \(xy\)

3. Notamos que tenemos un triángulo rectángulo. Por lo tanto, la hipotenusa \(h\) es la longitud que estamos buscando. Y sabemos que cumple \(h^{2}=a^{2}+b^{2}\Rightarrow h=\sqrt{a^{2}+b^{2}}\)

4. Lo adaptamos a nuestro contexto. En general, a la longitud la vamos a bautizar como “norma” de un vector. La norma del vector \(\overrightarrow{v}\) se denotará como \(\left\Vert \overrightarrow{v}\right\Vert\) y, viendo lo que hemos obtenido anteriormente, resulta ser \(\left\Vert \overrightarrow{v}\right\Vert =\sqrt{v_{1}^{2}+v_{2}^{2}}\)

---

Importante Reescribiendo la norma utilizando el producto escalar, resulta inmediato comprobar que \(\left\Vert \overrightarrow{v}\right\Vert =\sqrt{v_{1}^{2}+v_{2}^{2}}=\sqrt{\left(v_{1}v_{1}+v_{2}v_{2}\right)}=\sqrt{\overrightarrow{v}\cdot\overrightarrow{v}}\)

En general, para un vector \(\overrightarrow{v}\in\mathbb{R}^{n},\)

\[ \left\Vert \overrightarrow{v}\right\Vert =\sqrt{\overrightarrow{v}\cdot\overrightarrow{v}}=\sqrt{v_{1}^{2}+...+v_{n}^{2}} \]

---

• Calcular la distancia entre dos vectores (es la longitud del vector diferencia)

FIG 2. La distancia de dos vectores en ^2 usando el teorema de Pitágoras

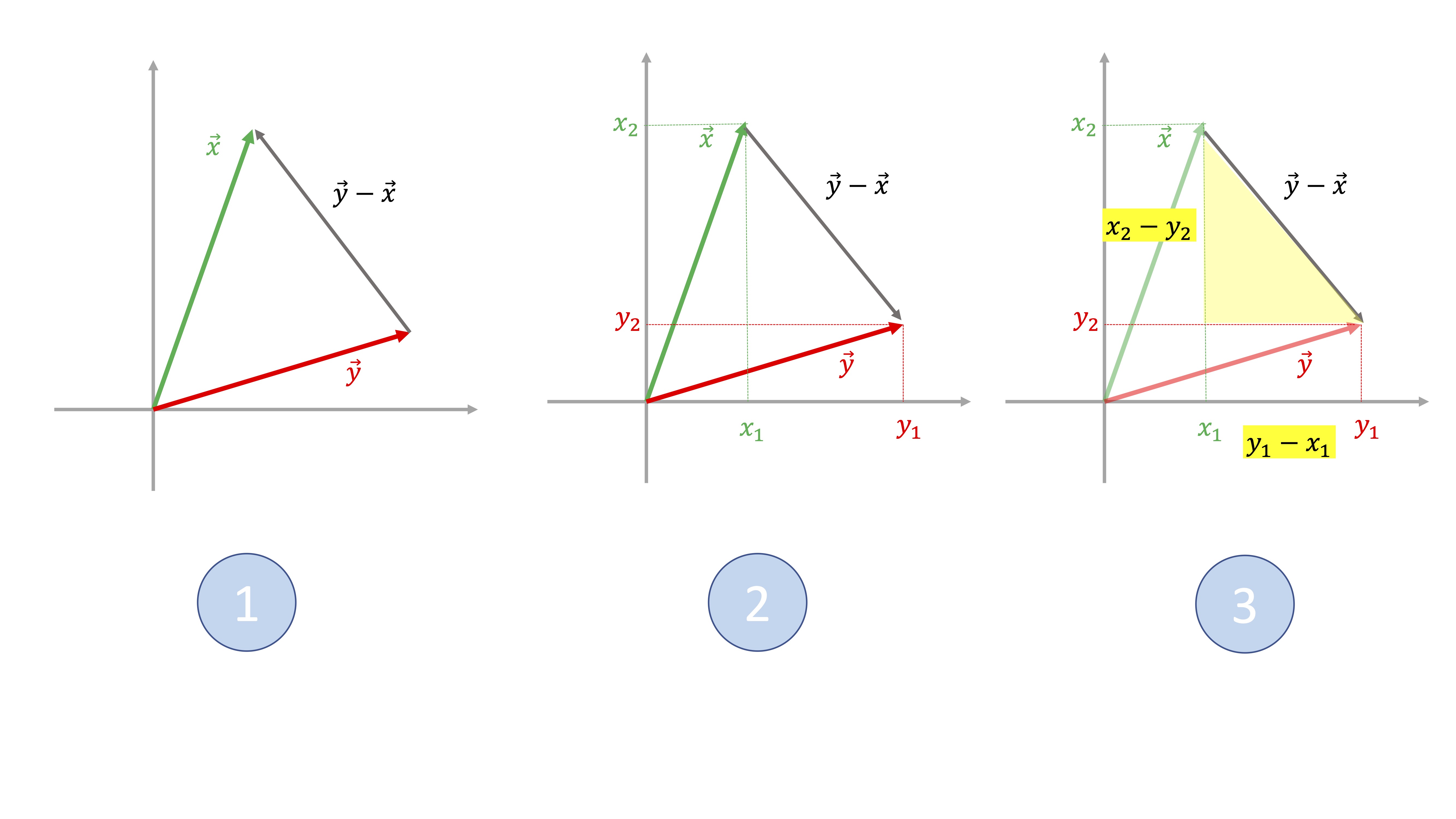
1. representamos dos vectores cualesquiera: \(\overrightarrow{x}=\left[\begin{array}{c} x_{1}\\ x_{2} \end{array}\right],\overrightarrow{y}=\left[\begin{array}{c} y_{1}\\ y_{2} \end{array}\right]\) así como su diferencia, \(\overrightarrow{y}-\overrightarrow{x}=\left[\begin{array}{c} y_{1}-x_{1}\\ y_{2}-x_{2} \end{array}\right]\)

2. marcamos claramente sus componentes en el plano \(xy\), y encontramos un triángulo rectángulo. Vamos a utilizarlo.

3. En este caso, la hipotenusa es la longitud de la diferencia de vectores ($-$) y los catetos son \((x_{2}-y_{2}),(y_{1}-x_{1}).\) Por lo que \[ \left\Vert \overrightarrow{y}-\overrightarrow{x}\right\Vert =\sqrt{(y_{1}-x_{1})^{2}+(x_{2}-y_{2})^{2}} \]

date cuenta de que, al estar al cuadrado, puedes reescribirlo “más bonito” como

\[ \left\Vert \overrightarrow{y}-\overrightarrow{x}\right\Vert =\sqrt{(y_{1}-x_{1})^{2}+(y_{2}-x_{2})^{2}} \]

---

lo que nos lleva a que para dos vectores, en general, \(\overrightarrow{x},\overrightarrow{y}\in\mathbb{R}^{n}\), su distancia se calculará como:

\[ d\left(\overrightarrow{x},\overrightarrow{y}\right)=\left\Vert \overrightarrow{y}-\overrightarrow{x}\right\Vert =\sqrt{\left(y_{1}-x_{1}\right)^{2}+....+\left(y_{n}-x_{n}\right)^{2}} \]

---

• Calcular un vector perpendicular a otro.

Ahora, claramente en la FIG 3, el vector \(\overrightarrow{x}\) y el \(\overrightarrow{y}\) son perpendiculares, ya que los hemos dibujado en los ejes de coordenadas cartesianos. La longitud de la hipotenusa es \(\left\Vert \overrightarrow{x}-\overrightarrow{y}\right\Vert\), la longitud de los catetos es \(\left\Vert \overrightarrow{x}\right\Vert ,\left\Vert \overrightarrow{y}\right\Vert\) por lo que, según el Teorema de Pitágoras \(\left\Vert \overrightarrow{x}-\overrightarrow{y}\right\Vert ^{2}=\left\Vert \overrightarrow{x}\right\Vert ^{2}+\left\Vert \overrightarrow{y}\right\Vert^{2}\)

FIG 3. Dos vectores perpendiculares en ^2

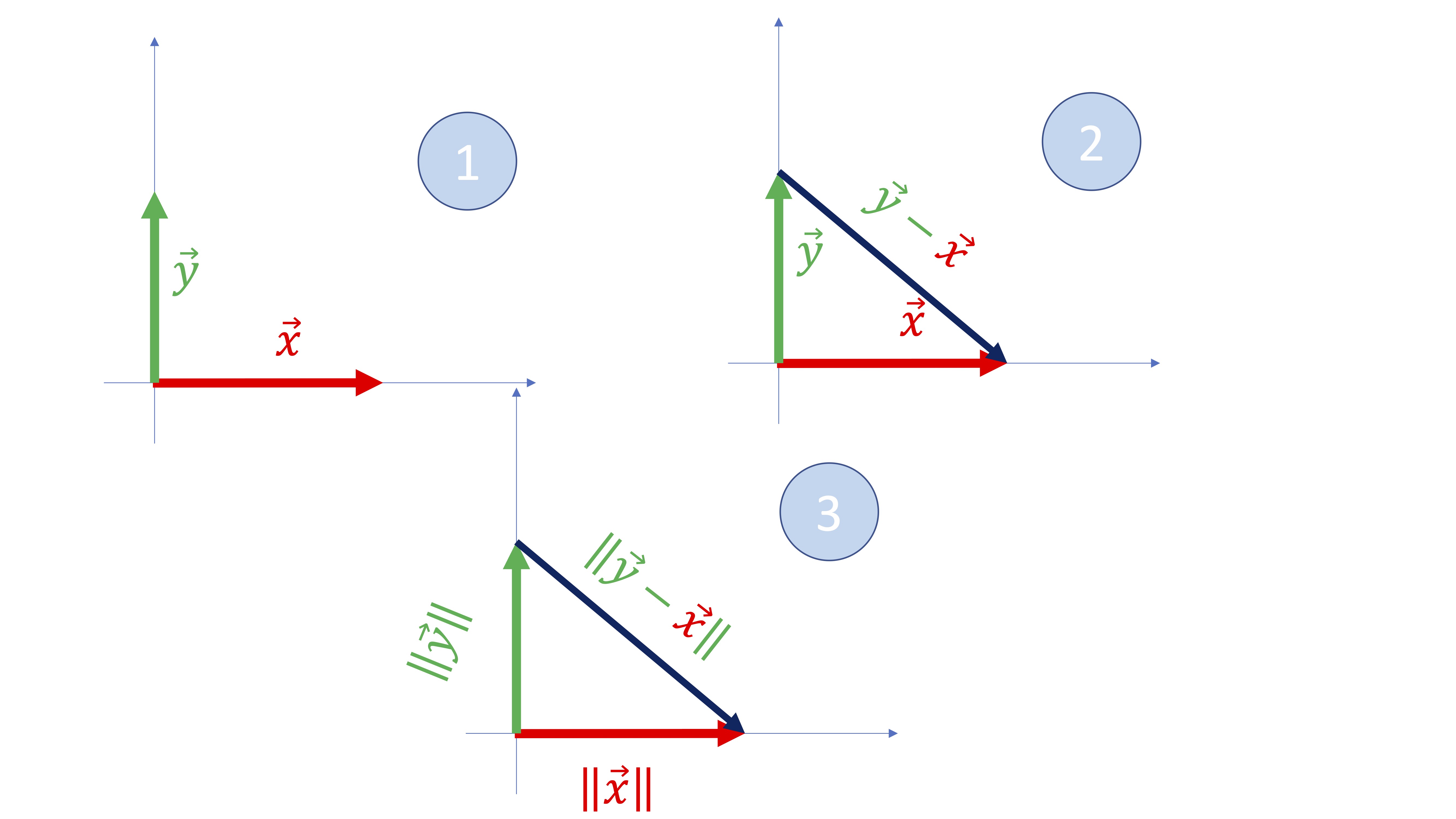
Por otro lado, tenemos que, según la definición de producto escalar

\[ \left\Vert \overrightarrow{x}-\overrightarrow{y}\right\Vert ^{2}=\left(\overrightarrow{x}-\overrightarrow{y}\right)\cdot\left(\overrightarrow{x}-\overrightarrow{y}\right)=\overrightarrow{x}\cdot\overrightarrow{x}-\overrightarrow{x}\cdot\overrightarrow{y}-\overrightarrow{y}\cdot\overrightarrow{x}+\overrightarrow{y}\cdot\overrightarrow{y}=\left\Vert \overrightarrow{x}\right\Vert ^{2}+\left\Vert \overrightarrow{y}\right\Vert ^{2}-2\overrightarrow{x}\cdot\overrightarrow{y} \]

(este desarrollo consiste en ver, usando propiedades del producto escalar, cuánto vale \(\left\Vert \overrightarrow{x}-\overrightarrow{y}\right\Vert ^{2}\). Míralo con calma, porque utiliza todo lo aprendido en esta clase). Entonces,

\[ \begin{cases} \left\Vert \overrightarrow{x}-\overrightarrow{y}\right\Vert ^{2}=\left\Vert \overrightarrow{x}\right\Vert ^{2}+\left\Vert \overrightarrow{y}\right\Vert ^{2} & (1)\\ \left\Vert \overrightarrow{x}-\overrightarrow{y}\right\Vert ^{2}=\left\Vert \overrightarrow{x}\right\Vert ^{2}+\left\Vert \overrightarrow{y}\right\Vert ^{2}-2\overrightarrow{x}\cdot\overrightarrow{y} & (2) \end{cases} \]

Para que se igualen ambas expresiones (1) y (2) , resulta que tiene que ocurrir que \(\overrightarrow{x}\cdot\overrightarrow{y}=0\) y esta es, por tanto, la condición necesaria (y suficiente) para que dos vectores sean perpendiculares.

---

Dos vectores son perpendiculares/ortogonales si su producto escalar es cero

---

*Ejemplo resuelto*
Busca todos los vectores que sean ortogonales a los siguientes:

\[ \overrightarrow{v}=\left[\begin{array}{c} 1\\ 0\\ -2 \end{array}\right],\overrightarrow{w}=\left[\begin{array}{c} -1\\ -1\\ 2 \end{array}\right] \]

Encuentra, asimismo, aquellos vectores ortogonales que tengan norma:

\(\sqrt{5}.\)

solución

Buscamos un vector \(\overrightarrow{x}\) tal que satisfaga el siguiente sistema:

\[ \begin{cases} \overrightarrow{x}\cdot\overrightarrow{v}=0\\ \overrightarrow{x}\cdot\overrightarrow{w}=0 \end{cases}, \]

que, en este caso, será:

\[ \begin{cases} x_{1}-2x_{3}=0 & (1)\\ -x_{1}-x_{2}+2x_{3}=0 & (2) \end{cases}. \]

Si resolvemos:

\(\Rightarrow\) de (1) tenemos \(x_{1}=2x_{3}\)

\(\Rightarrow\) sustituímos en (2), donde tendremos \(-2x_{3}-x_{2}+2x_{3}=0\Rightarrow x_{2}=0\).

Ya lo tenemos: el conjunto de vectores que son ortogonales a \(\overrightarrow{v},\overrightarrow{w}\) son los que tienen por componentes

\[ \overrightarrow{x}=\left[\begin{array}{c} 2x_{3}\\ 0\\ x_{3} \end{array}\right] \]

Como ves (en esto os soléis equivocar mucho) el vector dependerá de \(x_{3}\). Hay, por tanto, infinitos vectores ortogonales a

\(\overrightarrow{v},\overrightarrow{w}:\left[\begin{array}{c} 2\\ 0\\ 1 \end{array}\right],\left[\begin{array}{c} -2\\ 0\\ -1 \end{array}\right],\left[\begin{array}{c} 1\\ 0\\ 1/2 \end{array}\right],...\)

Ahora debemos buscar aquellos que tengan norma \(\sqrt{5}\), es decir,

\[ \left\Vert \overrightarrow{x}\right\Vert =\sqrt{5}. \]

En ese caso,

\[ \left\Vert \overrightarrow{x}\right\Vert =\sqrt{4x_{3}^{2}+x_{3}^{2}}=\sqrt{5x_{3}^{2}} \]

Es fácil ver que, como queremos que la norma sea \(\sqrt{5}\), entonces,

\[ x_{3}=\pm1 \]

es decir:

\[ \overrightarrow{x}_{1}=\left[\begin{array}{c} 2\\ 0\\ 1 \end{array}\right],\overrightarrow{x}_{2}=\left[\begin{array}{c} -2\\ 0\\ -1 \end{array}\right] \]

---

Clase 5: geometría del plano y del espacio (I)

Rectas en \(\mathbb{R}^{2}\)

Recordemos, de cursos anteriores, la ecuación lineal

\[ y-y_{0}=m(x-x_{0}), \]

que, geométricamente, es la ecuación de una recta que pasa por el punto \((x_{0},y_{0})\) y tiene pendiente \(m\). Por ejemplo, \(y-2=-1(x-3)\), la recta pasa por el punto (3,2) y tiene pendiente \(-1\). Esta ecuación la llamaremos cartesiana y, diremos, representa una recta en \(\mathbb{R}^{2}\).

Hoy vamos a ver otra manera de escribir la ecuación de una recta en \(\mathbb{R}^{2}:\) las ecuaciones paramétricas. Pensemos en una recta cualquiera en un espacio de dos dimensiones, como por ejemplo la recta verde de la FIG 1:

FIG 1. Una recta en \(\mathbb{R}^{2}\)

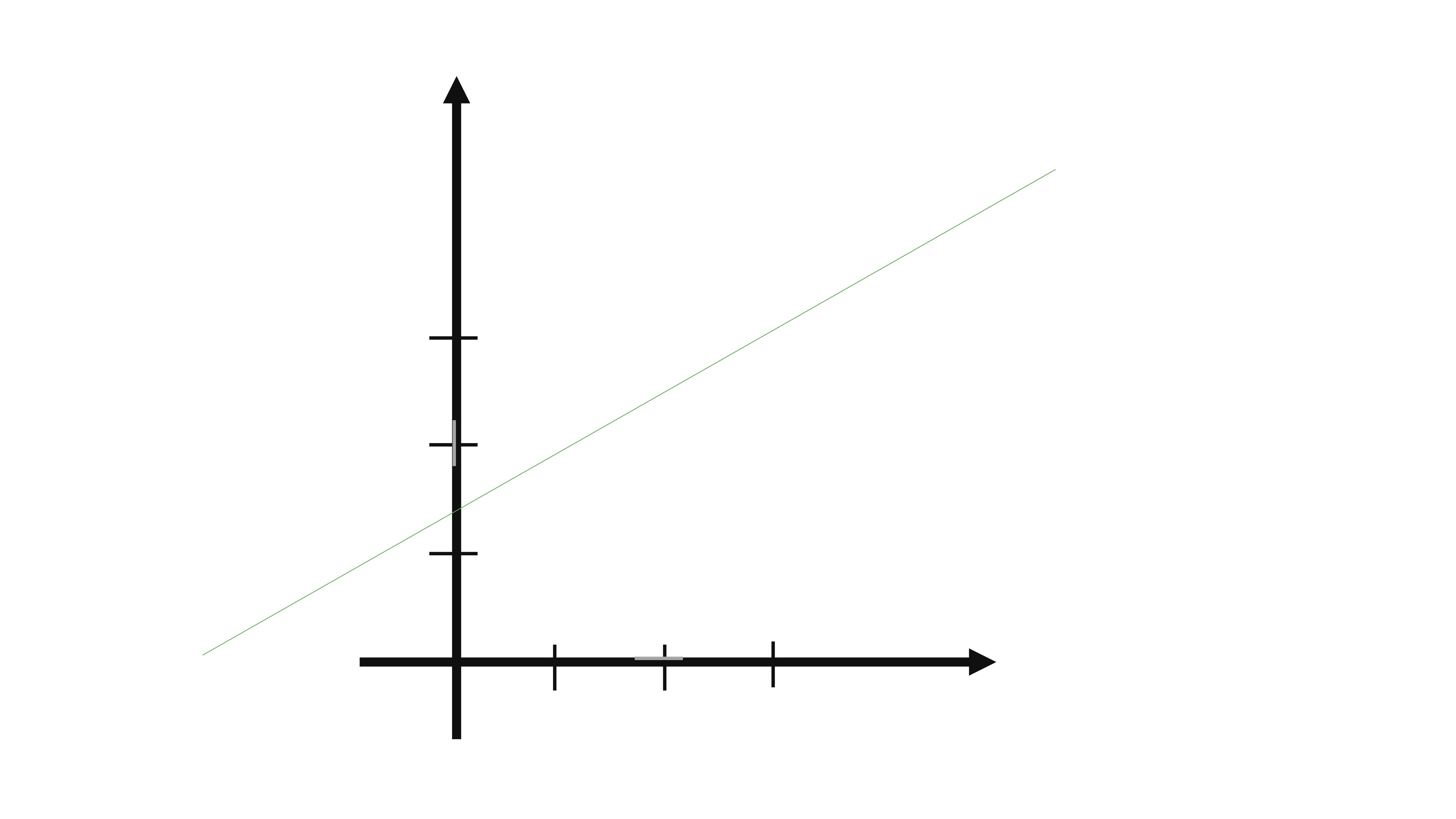
Podemos intuir que en esta recta la dirección está maracada por un vector, llamémosle \(\overrightarrow{v}\). Sin embargo, nota que un vector tiene un punto de aplicación (clase 1) y que el vector \(\overrightarrow{v}\)-por sí solo- puedes ponerlo donde quieras en el plano (FIG5)

FIG 2. El mismo vector en \(\mathbb{R}^{2}\)

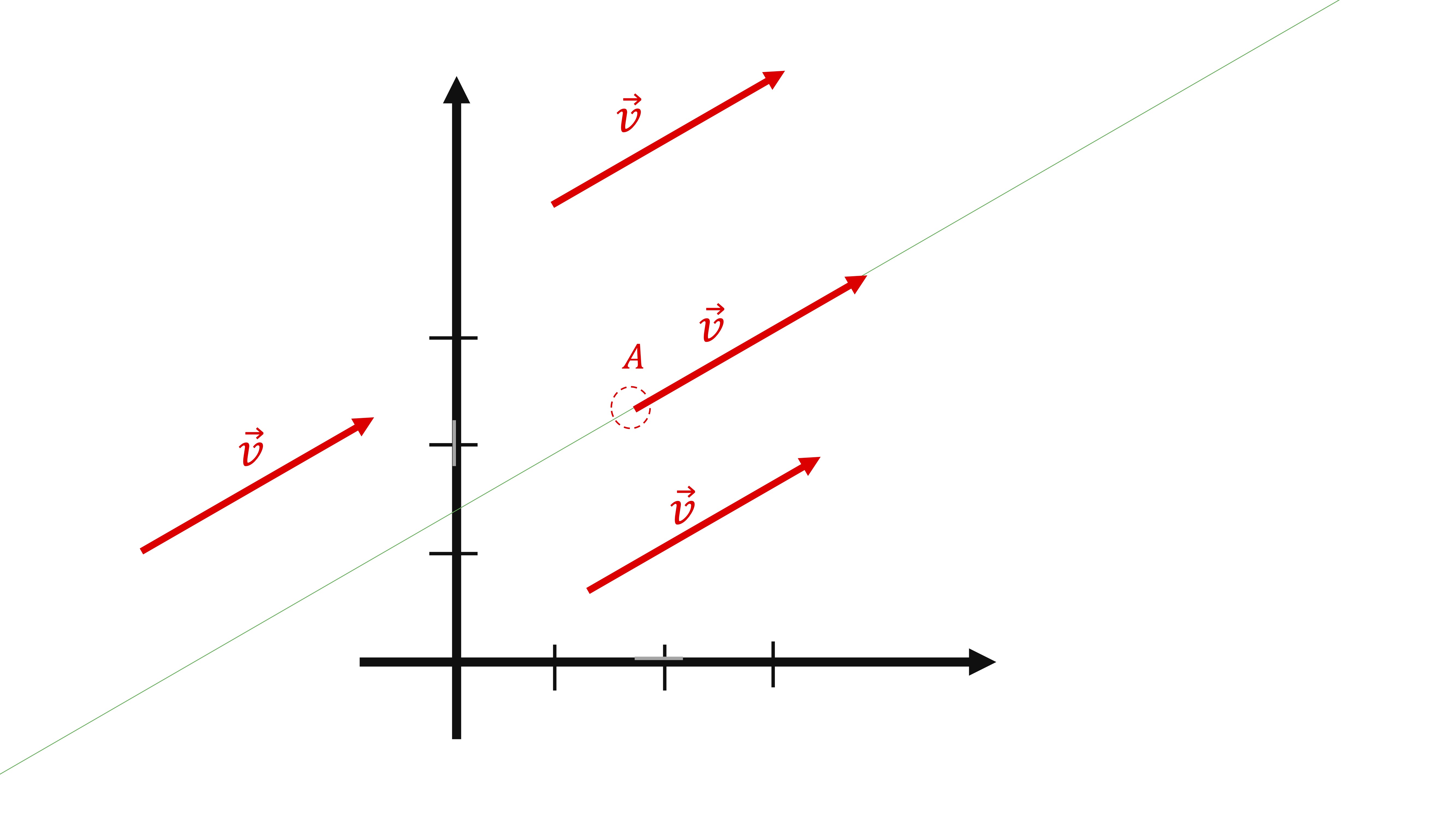
Es por ello que, para definir la recta, necesitaremos un punto que pertenezca a esta (punto de aplicación), que lo llamaremos \(A\). Por lo tanto:

La ecuación paramétrica de una recta en \(\mathbb{R}^{2}\) viene determinada por un punto \(A\in\mathbb{R}^{2}\) y un vector \(\overrightarrow{v}\in\mathbb{R}^{2}\) y tiene la forma

\[ recta\equiv\left(\begin{array}{c} x\\ y \end{array}\right)=A+\lambda\overrightarrow{v} \]

donde \(\lambda\) es un parámetro en \(\mathbb{R}\) y a \(\overrightarrow{v}\) lo llamamos vector director.

Como se hace tradicionalmente (aunque no es obligatorio), las coorednadas de la recta se definirán usando \(x,y\). Esta ecuación, por tanto, nos servirá para obtener puntos \((x,y)\) que pertenecen a la recta. La idea de esta expresión es que \(A\) marca un punto contenido en la recta y \(\lambda\) permite calcular un vector proporcional al vector director \(\overrightarrow{v}\), el cual marca la dirección de la recta. Por ejemplo, si \(A(A_{1},A_{2})\) y \(\overrightarrow{v}=\left[\begin{array}{c} v_{1}\\ v_{2} \end{array}\right]\), entonces la ecuación paramétrica será:

\[ \begin{cases} x=A_{1}+\lambda v_{1}\\ y=A_{2}+\lambda v_{2} \end{cases} \]

también puedes escribirlo como

\[ \left[\begin{array}{c} x\\ y \end{array}\right]=\left[\begin{array}{c} A_{1}\\ A_{2} \end{array}\right]+\lambda\left[\begin{array}{c} v_{1}\\ v_{2} \end{array}\right] \]

como ves, esta ecuación nos permite obtener puntos \((x,y)\) que pertenecen a la recta en cuestión (tan sólo hay que dar valores a \(\lambda\)).

¿Qué necesitaremos, entonces, para poder definir una recta ?

1) Un punto y un vector director

Por un lado, ya tenemos el caso de que conocemos un punto y el vector director. Por ejemplo, si queremos definir unas ecuaciones paramétricas de una recta que pasa por el punto \(A(5,3)\) y con vector director \(\overrightarrow{v}=\left[\begin{array}{c} 1\\ -1 \end{array}\right]\), deberemos escribir

\[ \left[\begin{array}{c} x\\ y \end{array}\right]=\left[\begin{array}{c} 5\\ 3 \end{array}\right]+\lambda\left[\begin{array}{c} 1\\ -1 \end{array}\right] \]

y esta es la ecuación paramétrica. ¿Para qué sirve? Puedes verla como una máquina que proporciona puntos que pertenecen a la recta (para ello, dale valores reales a \(\lambda\)). Si quieres obtener la ecuación cartesiana, es muy fácil: deberás eliminar el parámetro \(\lambda\). Para ello, despéjalo en ambas ecuaciones

\[ x=5+\lambda\Rightarrow x-5=\lambda \]

\[ y=3-\lambda\Rightarrow3-y=\lambda \]

Si igualas, tendrás que \(x-5=3-y\), que puedes reescribir como

\[ y=2-x \]

que es, como sabes, una ecuación cartesiana.

2) Dos puntos

Supongamos que \(A(1,2),B(3,1)\) son dos puntos contenidos en una recta desconocida (FIG 3):

FIG 3. Dos puntos en \(\mathbb{R}^{2}\)

Si te das cuenta, en la figura nos están dando el punto \(A\) y el punto \(B\). Construímos el vector director como la diferencia entre los vectores que se generan del origen de coordenadas a cada punto (nota que puedes tener, alternativamente, dos vectores directores que son, en realidad, el mismo pero con sentidos distintos):

\[ \overrightarrow{v}=\overrightarrow{OA}-\overrightarrow{OB} \]

\[ \overrightarrow{w}=\overrightarrow{OB}-\overrightarrow{OA} \]

Entonces, tomando cualesquiera de los puntos como origen, y de los vectores directores, podemos escribir cualquiera de estas ecuaciones paramétricas:

\[ recta\equiv A+\lambda\overrightarrow{v} \]

\[ recta\equiv A+\lambda\overrightarrow{w} \]

\[ recta\equiv B+\lambda\overrightarrow{v} \]

\[ recta\equiv B+\lambda\overrightarrow{w} \]

Cualquiera de estas ecuaciones paramétricas es válida: es decir, hay múltiples ecuaciones paramétricas que deberán proporcionarte la misma ecuación cartesiana (si no, algo va mal).

---

Mira este ejemplo

Halla la ecuación paramétrica de la recta que pasa por los puntos \(A=(1,2)\) y \(B(3,-1)\)

Para obtener el vector director, usamos la expresión: \[ \overrightarrow{v}=\overrightarrow{OA}-\overrightarrow{OB}=\left[\begin{array}{c} 1\\ 2 \end{array}\right]-\left[\begin{array}{c} 3\\ -1 \end{array}\right]=\left[\begin{array}{c} -2\\ 3 \end{array}\right] \]

Entonces unas- de las posibles- ecuaciones paramétricas serán

\[ \left[\begin{array}{c} x\\ y \end{array}\right]=\left[\begin{array}{c} 1\\ 2 \end{array}\right]+\lambda\left[\begin{array}{c} -2\\ 3 \end{array}\right] \]

¡Genera puntos que están en la recta dando valores a \(\lambda\)!

Por otro lado, si quieres obtener la ecuación cartesiana asociada a la recta anterior, lo que tienes que hacer es eliminar el parámetro. Para ello, puedes resolver el sistema de ecuaciones:

\[ \begin{cases} x=1-2\lambda\\ y=2+3\lambda \end{cases} \]

de donde obtenemos

\[ y+\frac{3}{2}x=\frac{7}{2} \]

Es decir, la ecuación cartesiana será

\[ y=\frac{7}{2}-\frac{3}{2}x \]

Para asegurarte de que cualquiera de las ecuaciones paramétricas que hayas tomado están bien, debes obtener la misma ecuación cartesiana. Es decir: hay infinitas ecuaciones paramétricas pero sólo unas ecuaciones cartesianas.

---

3) Un punto y un vector perpendicular a
la recta

Si tenemos un punto \(A\in\mathbb{R}^{2}\) y un vector perpendicular a la recta, podemos calcular el vector director con la famosa regla del producto escalar.

FIG 7. Un punto y un vector director en \(\mathbb{R}^{2}\) que definen la recta verde

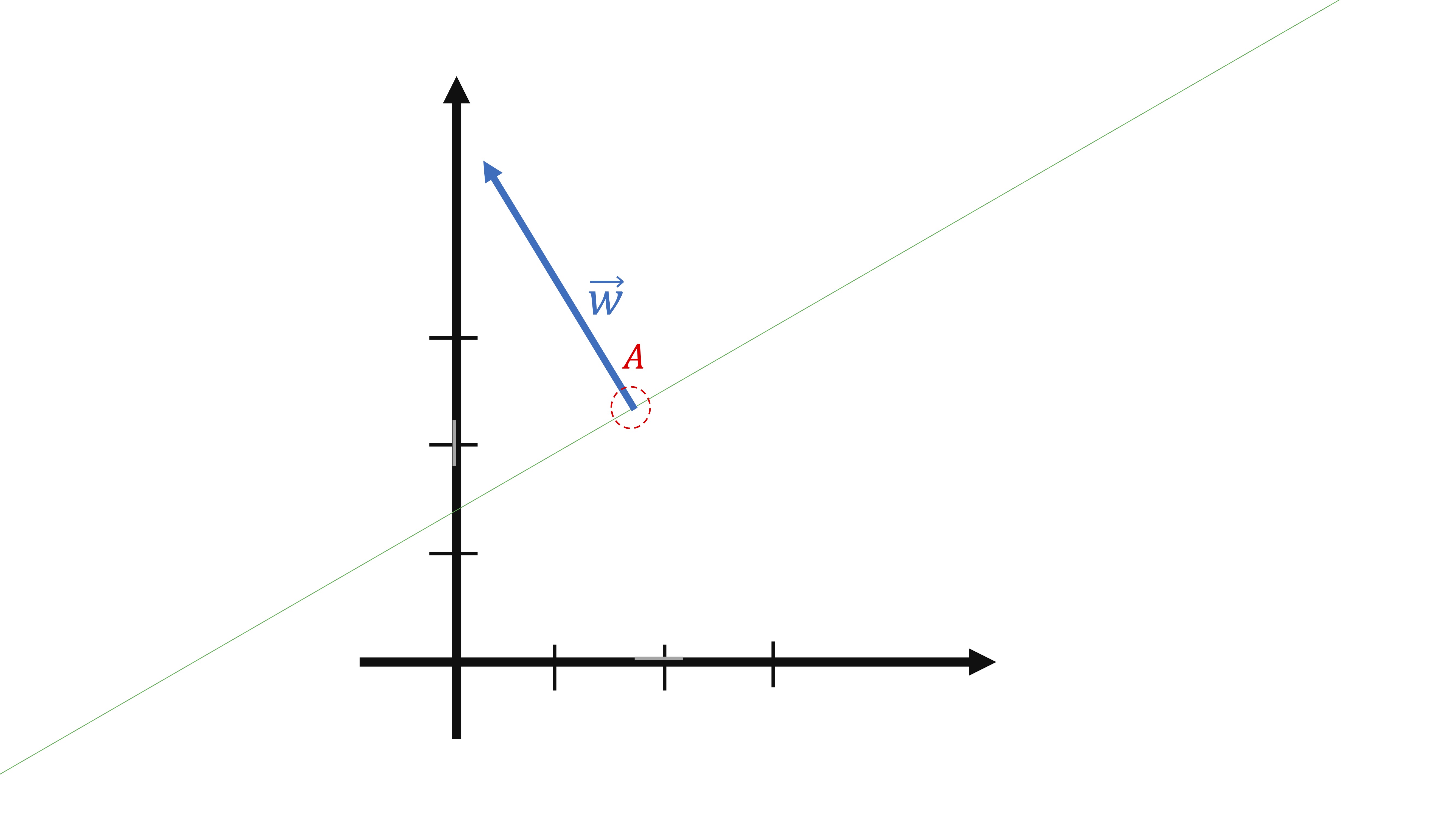
Por ejemplo, supón que quieres hallar la ecuación paramétrica de la recta que pasa por el punto \(A(1,2)\) y es perpendicular a \(\overrightarrow{w}=\left[\begin{array}{c} 3\\ 2 \end{array}\right]\) El vector director será perpendicular a \(\overrightarrow{w}\), para ello, ha de cumplirse que

\[ \overrightarrow{w}\cdot\overrightarrow{v}=0 \]

Entonces,

\[ 3v_{1}+2v_{2}=0 \]

es decir, \[ v_{1}=\frac{-2v_{2}}{3} \]

Esto nos muestra que los vectores de esta familia:

\[ \overrightarrow{v}=\left[\begin{array}{c} -\frac{2}{3}v_{2}\\ v_{2} \end{array}\right] \]

nos proporcionan vectores perpendiculares a \(\overrightarrow{w}\). Por ejemplo, si \(v_{2}=3\), un vector director de la recta será

\[ \overrightarrow{v}=\left[\begin{array}{c} -2\\ 3 \end{array}\right] \]

y unas ecuaciones paramétricas serán

\[ \left[\begin{array}{c} x\\ y \end{array}\right]=\left[\begin{array}{c} 1\\ 2 \end{array}\right]+\lambda\left[\begin{array}{c} -2\\ 3 \end{array}\right] \]

---

Clase 6: el plano y las rectas en el espacio

Hoy empezamos con una ecuación que, seguramente, has visto en años anteriores:

\[\begin{equation} a(x-x_{0})+b(y-y_{0})+c(z-z_{0})=0 \tag{1} \end{equation}\]

Es la ecuación cartesiana de un plano que pasa por el punto \(\left(x_{0},y_{0},z_{0}\right)\), donde \((a,b,c)\) son los coeficientes asociados a \((x,y,z)\). De hecho, fijémonos en otra manera de escribir la ecuación

\[ \left[\begin{array}{c} a\\ b\\ c \end{array}\right]\cdot\left[\begin{array}{c} x-x_{0}\\ y-y_{0}\\ z-z_{0} \end{array}\right]=0\]

donde \(\left[\begin{array}{c} a\\ b\\ c\end{array}\right]\) es el vector de las “pendientes” que se corresponden, respectivamente, con las variables \(x,y,z\) del plano y \(\left[\begin{array}{c} x-x_{0}\\ y-y_{0}\\ z-z_{0}\end{array}\right]\)

es el vector que representa todos los puntos que pertenecen al plano.

---

Mira estos ejemplos

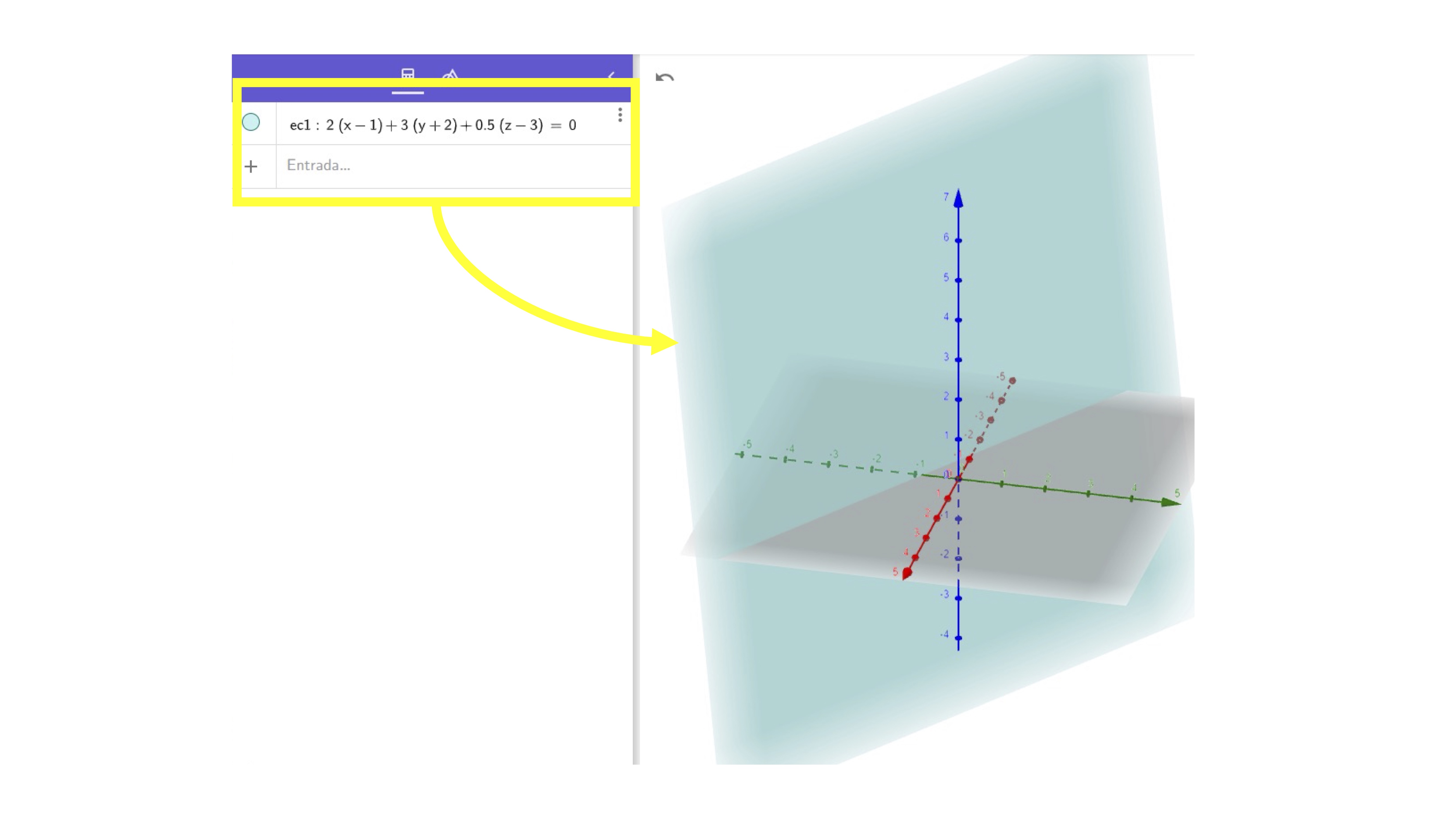
Si estamos en \(\mathbb{R}^{3}\) la que sigue, es la ecuación de un plano que pasa por el punto \(A(1,-2,3)\) y que tiene por pendientes \(2,3,0.5\) para las variables \(x,y,z\)

\[ 2(x-1)+3(y+2)+0.5(z-3)=0 \]

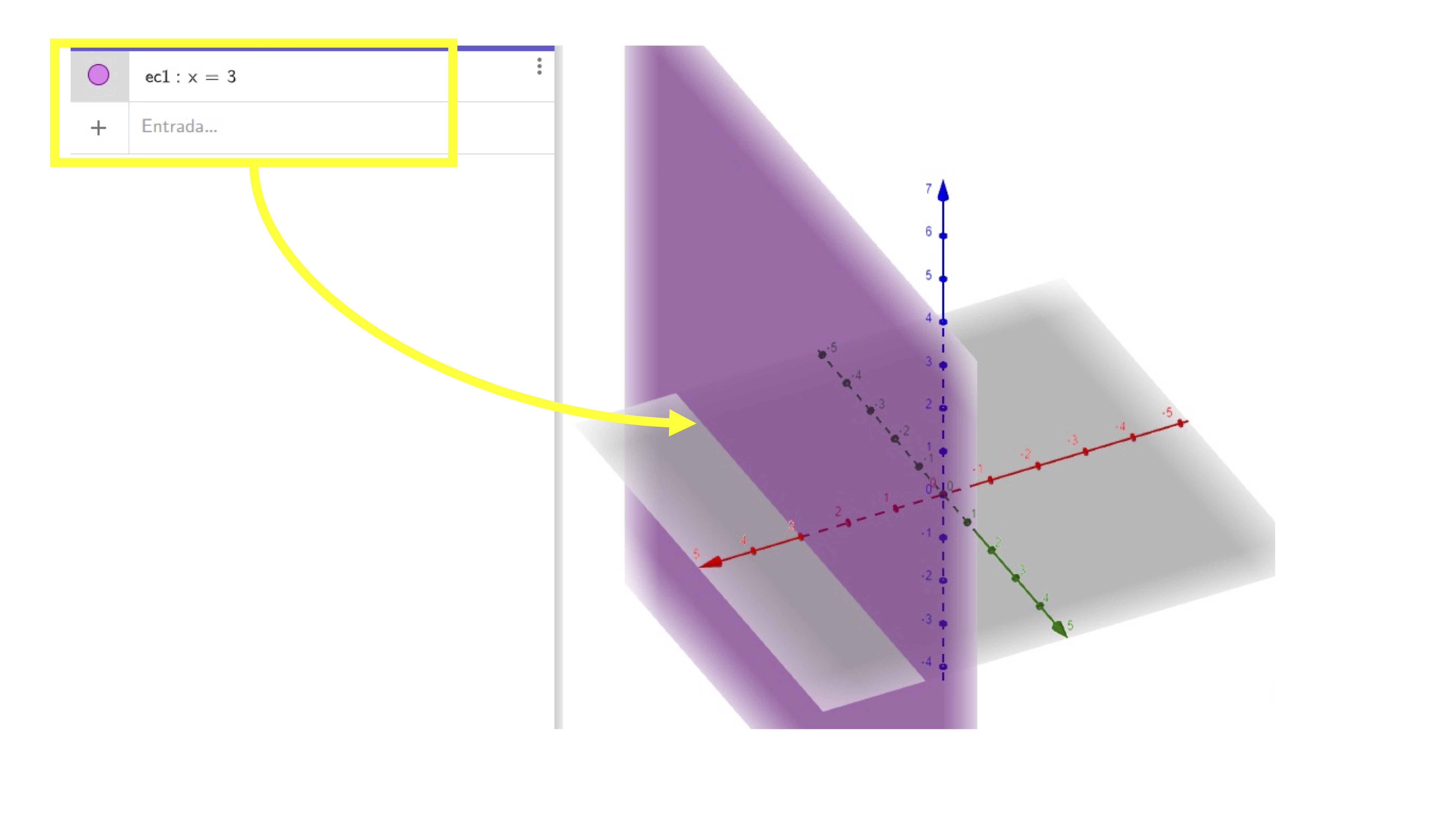
Para verlo, no hace falta más que escribirlo en Geogebra:

FIG 1. Un plano en \(\mathbb{R}^{3}\) a través de sus ecuaciones paramétricas

OJO, error muy común!

Pero, atención, si estás en \(\mathbb{R}^{3}\), esta ecuación:

\[ x=3 \]

representa un plano (para el que las variables \(y,z\) son “libres”, esto es, toman todos los valores reales). Es decir, es un plano en el que la coordenada \(x\) toma siempre valor 3.

Un error muy común es decir que en el plano \(x=3\) las variables \(y,z\) son cero. Eso no es verdad. Lo que sí ocurre es que \(b=c=0\) en la ecuación del plano (1). Es decir, la ecuación de este plano, será:

\[ 1(x-3)+0(y-0)+0(z-0)=0 \]

\(y,z\) son, en general, distintos de cero. Míralo en Geogebra:

FIG 2. El plano \(x=3\)

---

Vamos ahora, como ya hicimos con la recta en \(\mathbb{R}^{2}\) , a ver cómo podemos definir un plano en \(\mathbb{R}^{3}\) utilizando vectores directores. Necesitaremos dos vectores directores y un punto de aplicación. Pero, además, los vectores deben ser linealmente independientes (mira la FIG 3) :

FIG 3. Un plano en \(\mathbb{R}^{3}\) a través de sus dos vectores directores (en la izquierda: OK, en la derecha: KO)

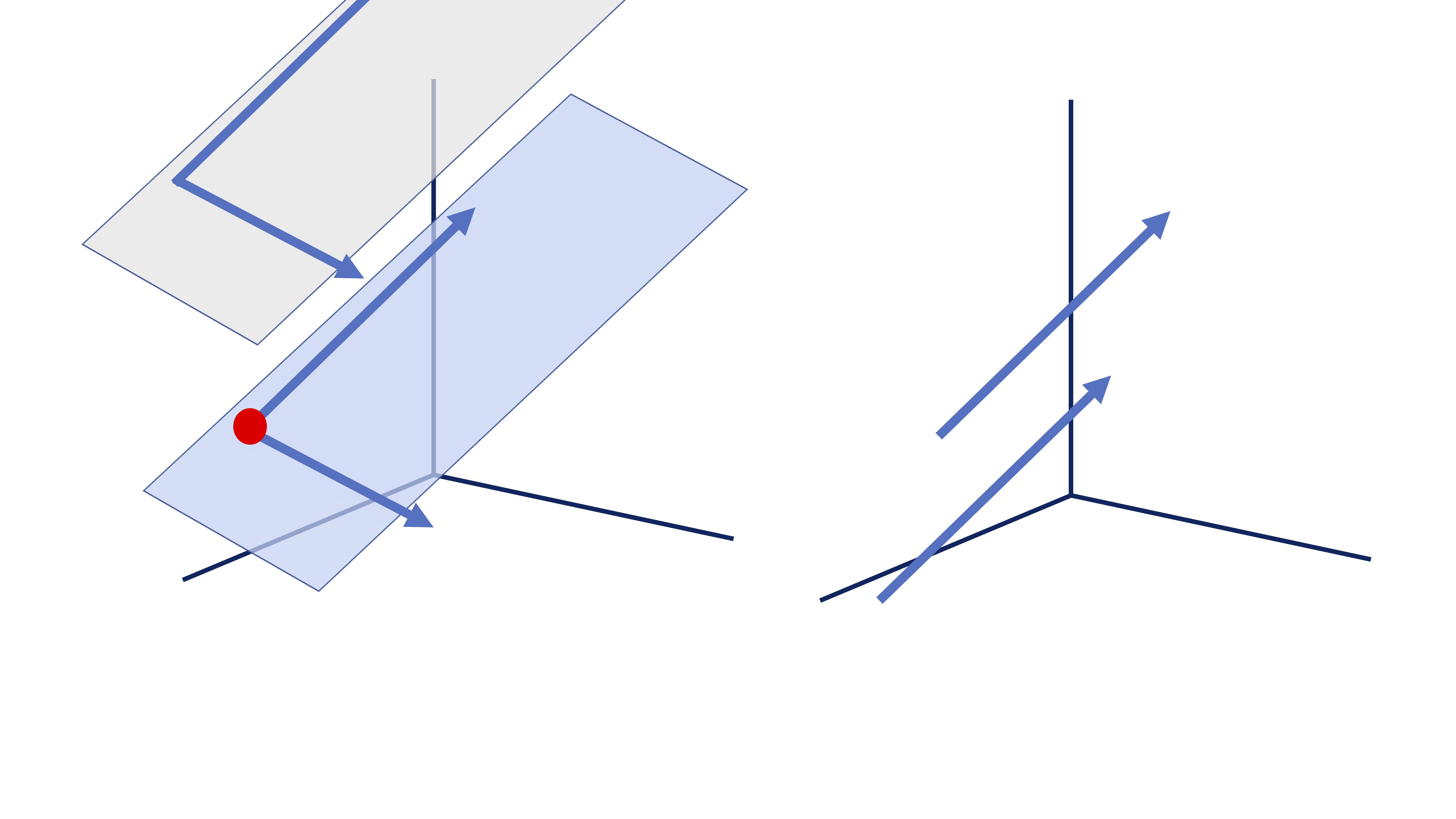
• En el primero de ellos, tenemos dos vectores linealmente independientes (tienen dirección distinta), entonces, queda perfectamente definido el plano. \(\left\{ \left(\begin{array}{c} 1\\ 2\\ 3 \end{array}\right),\left(\begin{array}{c} 1\\ 0\\ 1 \end{array}\right)\right\}\)

• En el segundo, los dos vectores tienen misma dirección (sólo que punto de aplicación distinto). Entonces, no definen un plano, sino dos rectas.\(\left\{ \left(\begin{array}{c} 1\\ 2\\ 3 \end{array}\right),\left(\begin{array}{c} 2\\ 4\\ 6 \end{array}\right)\right\}\)

Mira, además, en la FIG3, necesitamos el punto de aplicación para definir completamente dónde se encuentra el plano en el espacio. Si no, podríamos ponerlo en infinitos lugares siguiendo a los vectores directores.

Las ecuaciones paramétricas del plano en \(\mathbb{R}^{3}\) se determinan con dos vectores L.I en \(\mathbb{R}^{3}\) y un punto en \(\mathbb{R}^{3}\).

\[ plano\equiv\Pi=A+\lambda_{1}\overrightarrow{v}+\lambda_{2}\overrightarrow{w} \] Donde \(\Pi=(x,y,z).\) Es decir:

\[ \begin{cases} x=A_{1}+\lambda_{1}v_{1}+\lambda_{2}w_{1}\\ y=A_{2}+\lambda_{1}v_{2}+\lambda_{2}w_{2}\\ z=A_{3}+\lambda_{1}v_{3}+\lambda_{2}w_{3} \end{cases} \]

OJO, como ya hemos dicho, los vectores directores no tienen que ser proporcionales (o no tendremos un plano). Por ejemplo, si \(\overrightarrow{v}\left[\begin{array}{c} 1\\ -1\\ 1\end{array}\right]\) y \(\overrightarrow{w}\left[\begin{array}{c} -1\\ 1\\ -1\end{array}\right]\)
en realidad \(\overrightarrow{v}=-\overrightarrow{w}\), esto quiere decir que no estamos acotando un plano (dibújalo) sino describiendo una recta (con información redundante, puesto que el vector director es el mismo).

Veamos diferentes formas de definir un plano

---

1) Un punto y dos vectores directores

Por ejemplo, sea el punto \(A(6,0,1)\) y los vectores directores \(\overrightarrow{v}\left[\begin{array}{c} 3\\ 0\\ -1\end{array}\right]\) y \(\overrightarrow{v}\left[\begin{array}{c} 0\\ 3\\ -1\end{array}\right]\)

Nos proporcionan las siguientes ecuaciones paramétricas

\[ \begin{cases} x=6+3\lambda_{1} & (1)\\ y=3\lambda_{2} & (2)\\ z=1-\lambda_{1}-\lambda_{2} & (3) \end{cases} \]

o, de igual modo

\[ \left[\begin{array}{c} x\\ y\\ z \end{array}\right]=\left[\begin{array}{c} 6\\ 0\\ 1 \end{array}\right]+\lambda_{1}\left[\begin{array}{c} 0\\ 0\\ -1 \end{array}\right]+\lambda_{2}\left[\begin{array}{c} -3\\ 3\\ -1 \end{array}\right] \]

---

Como siempre, puedes buscar la ecuación cartesiana del plano. Para ello, puedes resolver el sistema. si despejas \(\lambda_{1}\) en la ecuación (1)

\(\Rightarrow\lambda_{1}=\frac{x-6}{3}\)

De la ecuación (2)

\(\Rightarrow\lambda_{2}=\frac{y}{3}\)

y, finalmente, en la ecuación (3)

\(\Rightarrow z=1-\left(\frac{x-6}{3}\right)-\frac{y}{3}\Rightarrow z=3-\frac{x}{3}-\frac{y}{3}.\)

---

2) Tres puntos del plano cualesquiera (no alineados)

Supongamos que tenemos los puntos \(A=(6,0,1)\) \(B=(3,3,0)\) y \(C=(9,0,1)\).

¿Cómo construimos los vectores directores? Asgurándonos, primero, que los puntos no están alineados (proporcionales). Entonces, tomamos como referencia uno de ellos (A, por ejemplo) y:

\[ \overrightarrow{BA}=\overrightarrow{v}=\left[\begin{array}{c} 3\\ 3\\ 0\end{array}\right]-\left[\begin{array}{c} 6\\ 0\\ 1\end{array}\right]=\left[\begin{array}{c} -3\\ 3\\ 1\end{array}\right] \]

y,

\[ \overrightarrow{CA}=\overrightarrow{w}=\left[\begin{array}{c} 9\\ 0\\ 1\end{array}\right]-\left[\begin{array}{c} 6\\ 0\\ 1\end{array}\right]=\left[\begin{array}{c} 3\\ 0\\ -1\end{array}\right] \]

El plano, por tanto, pasa por el punto \(A\):

\[ \left[\begin{array}{c} x\\ y\\ z \end{array}\right]=\underset{A}{\left[\begin{array}{c} 6\\ 0\\ 1 \end{array}\right]}+\lambda_{1}\underset{\overrightarrow{BA}}{\left[\begin{array}{c} -3\\ 3\\ -1 \end{array}\right]}+\lambda_{2}\underset{\overrightarrow{CA}}{\left[\begin{array}{c} 3\\ 0\\ 0 \end{array}\right]} \]

por lo que, finalmente, \[ \begin{cases} x=6+3\lambda_{1}-3\lambda_{2} & (1)\\ y=3\lambda_{1} & (2)\\ z=1-\lambda_{1} & (3) \end{cases} \]

---

¿Cómo se halla la ecuación cartesiana? Tendremos que ir sustituyendo, de nuevo:

Empezamos en la ecuación (2)

\(\Rightarrow\lambda_{1}=\frac{y}{3}\).

De la ecuación (3)

\(\Rightarrow\lambda_{1}=1-z\)

Igualando ambas ecuaciones:

\[ y=3-3z \]

y ¡esta es la ecuación cartesiana!. Como ves, la \(x\) es “libre”, es decir, en este plano \(x\) toma todos los valores reales.

Ejercicio resuelto

Obtén las ecuaciones paramétricas del plano anterior eligiendo otro punto de aplicación y muestra que tienes distintas ecuaciones paramétricas pero que llegas a la misma ecuación cartesiana:

Tomamos como referencia el punto B

\[ \overrightarrow{BA}=\overrightarrow{v}=\left[\begin{array}{c} 3\\ 3\\ 0\end{array}\right]-\left[\begin{array}{c} 6\\ 0\\ 1\end{array}\right]=\left[\begin{array}{c} -3\\ 3\\ -1\end{array}\right] \]

\[ \overrightarrow{CB}=\overrightarrow{w}=\left[\begin{array}{c} 9\\ 0\\ 1\end{array}\right]-\left[\begin{array}{c} 3\\ 3\\ 0\end{array}\right]=\left[\begin{array}{c} 6\\ -3\\ 1\end{array}\right] \]

El plano, por tanto, pasa por el punto \(A\):

\[ \left[\begin{array}{c} x\\ y\\ z \end{array}\right]=\underset{B}{\left[\begin{array}{c} 3\\ 3\\ 0 \end{array}\right]}+\lambda_{1}\underset{\overrightarrow{BA}}{\left[\begin{array}{c} -3\\ 3\\ -1 \end{array}\right]}+\lambda_{2}\underset{\overrightarrow{CB}}{\left[\begin{array}{c} 6\\ -3\\ 1 \end{array}\right]} \]

\[ \begin{cases} x=3-3\lambda_{1}+6\lambda_{2} & (1)\\ y=3+3\lambda_{1}-3\lambda_{2} & (2)\\ z=0-\lambda_{1}+\lambda_{2} & (3) \end{cases} \]

¿Cómo se halla la ecuación cartesiana? Tendremos que ir sustituyendo:

Si sumamos las ecuaciones (2) y la (3) multiplicada por 3

\(\Rightarrow y+3z=3\)

Despejando \[ y=3-3z. \]

---

3) Un punto y un vector perpendicular al plano

La intuición de esto está al principio de la clase

FIG 4. Un plano en \(\mathbb{R}^{3}\) a través de un punto y un vector normal ( o perpendicular)

Tenemos el punto \(A(6,0,1)\) y un vector que sabemos que es perpendicular al plano, por ejemplo, \(\overrightarrow{n}=\left[\begin{array}{c} 1\\ 2\\ 3 \end{array}\right]\) . A este vector se le suele llamar vector normal. En este caso, no resulta inmediato obtener las ecuaciones paramétricas (¿cómo obtenemos dos vectores directores?). Sin embargo, se pueden obtener, de manera muy sencilla, las ecuaciones cartesianas. Si te fijas en la figura, tenemos un vector perpendicular al plano en un punto con coordenadas \(x,y,z\), mientras que conocemos el punto \(A\) del plano, un punto arbitrario \(A(A_{1},A_{2},A_{3})\) y perpendicular a un vector \(\overrightarrow{n}\), entonces, las ecuaciones cartesianas tienen que cumplir que el vector \(\overrightarrow{n}\) sea perpendicular al vector generado por la diferencia \(\overrightarrow{d}=(x,y,z)-(A_{1},A_{2},A_{3})\), esto es \[ \overrightarrow{n}\cdot\overrightarrow{d}=0\Rightarrow\overrightarrow{n}\cdot\left[\begin{array}{c} x-A_1\\ y-A_2\\ z-A_3\end{array}\right]=0 \]

En este caso, \[ \left[\begin{array}{c} 1\\ 2\\ 3\end{array}\right]\cdot\left[\begin{array}{c} x-6\\ y-0\\ z-1\end{array}\right]=0 \]

y, por lo tanto: \[ x+2y+3z=9 \]

---

Podemos obtener, además, las ecuaciones paramétricas. Para ello, despejamos una coordenada en función del resto:

\[ x=-2y-3z+9 \]

y a las otras dos coordenadas les asignamos un parámetro (recordamos que un plano necesita dos vectores directores)

\[ y=\lambda_{1},z=\lambda_{2} \]

Tenemos, entonces

\[ \begin{cases} x=9-2\lambda_{1}-3\lambda_{2}\\ y=\lambda_{1}\\ z=\lambda_{2} \end{cases} \]

que dan lugar a las ecuaciones paramétricas

\[ \left[\begin{array}{c} x\\ y\\ z \end{array}\right]=\left[\begin{array}{c} 9\\ 0\\ 0 \end{array}\right]+\lambda_{1}\left[\begin{array}{c} -2\\ 1\\ 0 \end{array}\right]+\lambda_{2}\left[\begin{array}{c} -3\\ 0\\ 1 \end{array}\right] \]

Ejercicio resuelto

Del plano \(\Pi=\left\{ (x,y,z)\in\mathbb{R}^{3}\::\:2x+3y+4z=3\right\}\) calcula dos vectores directores de este que sean perpendiculares entre sí. Como nosotros sabemos calcular vectores directores, podemos empezar obteniéndolos. Como es un plano, necesitamos definir dos parámetros. Entonces:

\[ y=\lambda_{1},z=\lambda_{2} \]

Sustituyendo en la ecuación de nuestro plano,

\[ 2x+3\lambda_{1}+4\lambda_{2}=3, \] por lo que \[ x=\frac{3}{2}-\frac{3}{2}\lambda_{1}-2\lambda_{2}. \]

Entonces, nota que podemos reescribirlo como:

\[ \left[\begin{array}{c} x\\ y\\ z \end{array}\right]=\left[\begin{array}{c} 3/2\\ 0\\ 0 \end{array}\right]+\lambda_{1}\left[\begin{array}{c} -3/2\\ 1\\ 0 \end{array}\right]+\lambda_{2}\left[\begin{array}{c} -2\\ 0\\ 1 \end{array}\right] \]

Ahora bien, los vectores directores que hemos obtenido (ya sería demasiada suerte) no son ortogonales. ¿Cómo buscamos un par de vectores directores que sean ortogonales? Una manera rápida (y que ya conocemos) es darnos cuenta de que necesitamos buscar un vector \(\overrightarrow{v}\) que, a su vez, sea perpendicular al vector normal del plano (el que viene proporcionado por los coeficientes \((2,3,4)\)) y que sea perpendicular a cualquiera de los dos vectores directores que ya conocemos (en este caso, podríamos quedarnos con \((-2,0,1)\). Da lo mismo cuál elijas, pero nos proporcionará cuentas más sencillas). Entonces, de acuerdo con lo que se nos pide, debemos resolver:

\[ \begin{cases} \left[\begin{array}{c} -2\\ 0\\ 1\end{array}\right]\cdot\left[\begin{array}{c} v_1\\ v_2\\ v_3\end{array}\right]=0\\ \left[\begin{array}{c} 2\\ 3\\ 4\end{array}\right]\cdot\left[\begin{array}{c} v_1\\ v_2\\ v_3\end{array}\right]=0 \end{cases} \]

De aquí, sacamos que:

\[ \begin{cases} v_{3}=2v_{1}\\ 3v_{2}=-2v_{1}-4v_{3} \end{cases} \]

donde \(3v_{2}=-2v_{1}-8v_{1}\Rightarrow v_{2}=\frac{-10}{3}v_{1}\).

Es decir, el vector que cumple con las dos condiciones (es un vector director y es perpendicular al otro) consiste en:

\[ \overrightarrow{v}=\left[\begin{array}{c} v_1\\ \frac{-10}{3}v_{1}\\ 2v_{1}\end{array}\right] \]

Por ejemplo, si hacemos \(v_{1}=3\), el vector será:

\[ \overrightarrow{v}=\left[\begin{array}{c} 3\\ -10\\ 6\end{array}\right] \]

Ahora que lo tenemos, podríamos tratar de ver que, efectivamente, dadas las paramétricas- con estos dos vectores- obtenemos la misma cartesiana. Veamos:

\[ \left[\begin{array}{c} x\\ y\\ z \end{array}\right]=\left[\begin{array}{c} 3/2\\ 0\\ 0 \end{array}\right]+{\lambda_{1}\left[\begin{array}{c} 3\\ -10\\ 6 \end{array}\right]}+\lambda_{2}\left[\begin{array}{c} -2\\ 0\\ 1 \end{array}\right] \]

Donde \[ \begin{cases} x=3/2+3\lambda_{1}-2\lambda_{2} & (1)\\ y=-10\lambda_{1} & (2)\\ z=6\lambda_{1}+\lambda_{2} & (3) \end{cases} \]

De la ecución (2), tenemos que \(\lambda_{1}=-\frac{y}{10}\). Por otro lado, de la ecuación (3) \(z=-\frac{3}{5}y+\lambda_{2}\Rightarrow\lambda_{2}=z+\frac{3}{5}y.\) Si sustituímos en la ecuación (1),

\[ x=\frac{3}{2}-\frac{3y}{10}-2z-\frac{6}{5}y\Rightarrow x=\frac{3}{2}-\frac{(3+12)}{10}y-2z \]

es decir, \(x=\frac{3}{2}-\frac{3}{2}y-2z\Rightarrow x+\frac{3}{2}y+2z=\frac{3}{2}\).

Si la multiplico por 2, obtengo:

\[ 2x+3y+4z=3. \]

Rectas en el espacio

En el espacio 3D también se pueden visualizar rectas (imagínate un bolígrafo flotando). Ahora bien, vamos a ver cómo las modelizamos utilizando álgebra.

Una recta en el espacio 3D queda definida por un vector director y un punto. Por ejemplo la recta que pasa por el punto \(A(3,0,1)\) y es paralela al vector \(\overrightarrow{v}=\left[\begin{array}{c} 1\\ -1\\ 0 \end{array}\right]\)

esquemáticamente, lo que tenemos es la FIG 1:

Echemos las cuentas:

-Las ecuaciones paramétricas serán: \[\left[\begin{array}{c} x\\ y\\ z \end{array}\right]=\left[\begin{array}{c} A_{1}\\ A_{2}\\ A_{3} \end{array}\right]+\lambda\left[\begin{array}{c} v_{1}\\ v_{2}\\ v_{3} \end{array}\right], \] con \(\lambda\in\mathbb{R}\).

• En nuestro ejemplo, \[\left[\begin{array}{c} x\\ y\\ z \end{array}\right]=\left[\begin{array}{c} 3\\ 0\\ 1 \end{array}\right]+\lambda\left[\begin{array}{c} 1\\ -1\\ 0 \end{array}\right]\],

• Por otro lado, ¿qué sabemos de las ecuaciones cartesianas? Recuerda que lo que hay que hacer es eliminar el parámetro \(\lambda\). Entonces:

\[ \begin{cases} x=3+\lambda & (1)\\ y=-\lambda & (2)\\ z=1 & (3) \end{cases} \]

Es fácil ver que de la ecuación (2) podemos introducir su resultado en la ecuación (1), es decir

\[ \begin{cases} x=3-y\\ z=1 \end{cases} \]

OJO, error muy común!

La primera forma os cuesta mucho verla y es la más inmediata. Una recta en 3D queda determinada por dos planos que se intersecan. Un momento ¡¡Dos ecuaciones cartesianas!! ¿Es eso posible? Acudamos un momento a Geogebra:

FIG 1. Como puedes ver, definimos una recta introduciendo dos ecuaciones cartesianas de planos

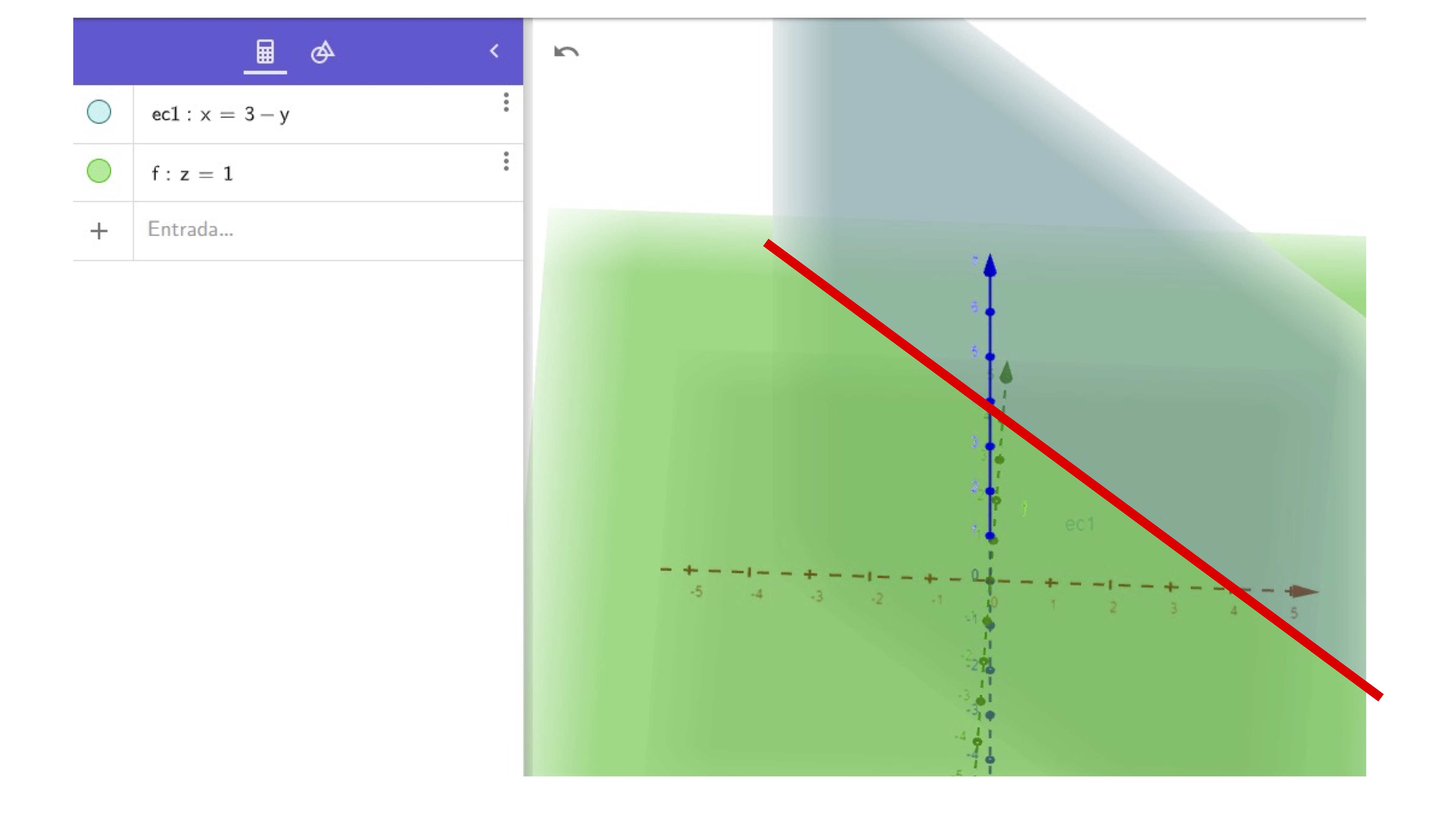
Por lo que, una recta en 3D, queda definida como

---

1) Dos planos que se cortan

Efectivamente, eso os cuesta en general bastante: dos planos que se intersecan forman una recta en \(\mathbb{R}^{3}:\)

FIG 2. No lo olvides!!!

Por lo tanto, como sabemos que un plano está determinado por UNA ecuación cartesiana: en el caso de la recta, necesitaremos dos ecuaciones cartesianas que formen un sistema compatible indeterminado (infinitas soluciones). Si es incompatible, entonces los planos no se cortarán. Al ser sólo dos ecuaciones, entonces el sistema nunca podrá ser compatible determinado.

---

Ejercicio resuelto

Halla unas ecuaciones paramétricas para la recta con estas ecuaciones cartesianas

\[ \begin{cases} x+y-z=1\\ x+2y-2z=2 \end{cases}. \]

Para resolverlo, podemos hacer que \(z=\lambda\), entonces \(\begin{cases} x+y=1+\lambda\\ x+2y=2+2\lambda \end{cases}\).

Resolviendo el sistema, tenemos que \(y=1+\lambda\), \(x=0\).

La ecuación paramétrica que obtenemos es \(\left(\begin{array}{c} x\\ y\\ z \end{array}\right)=\left(\begin{array}{c} 0\\ 1\\ 0 \end{array}\right)+\lambda\left(\begin{array}{c} 0\\ 1\\ 1 \end{array}\right)\).

---

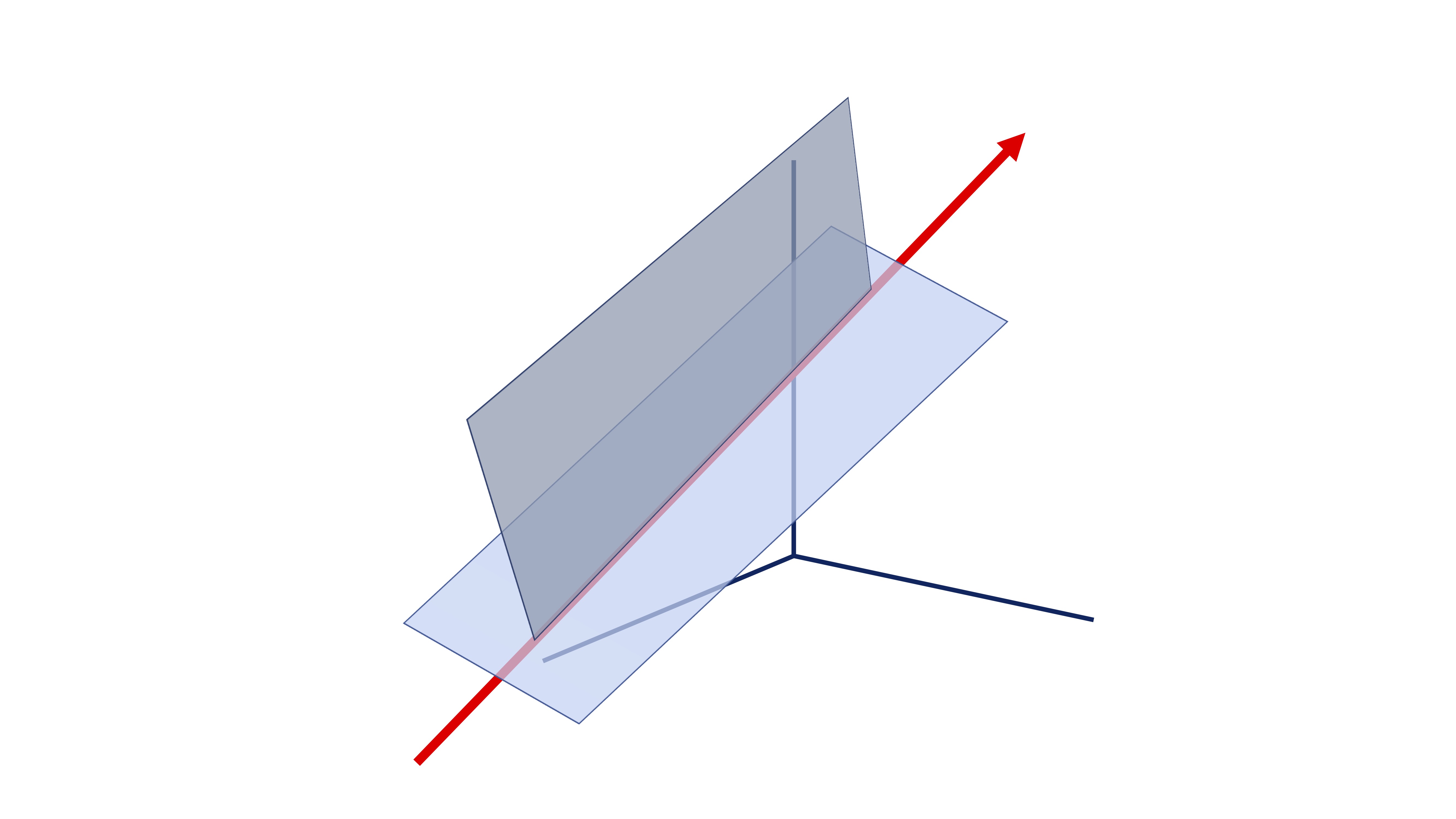
2) Dos vectores perpendiculares a la recta y un punto

Otra opción es que nos den dos vectores perpendiculares a la recta (necesitamos que nos den dos para que quede perfectamente determinada dicha recta). Además, lógicamente, de un punto de la recta:

FIG 3. Definimos una recta en 3D

---

Ejercicios resueltos

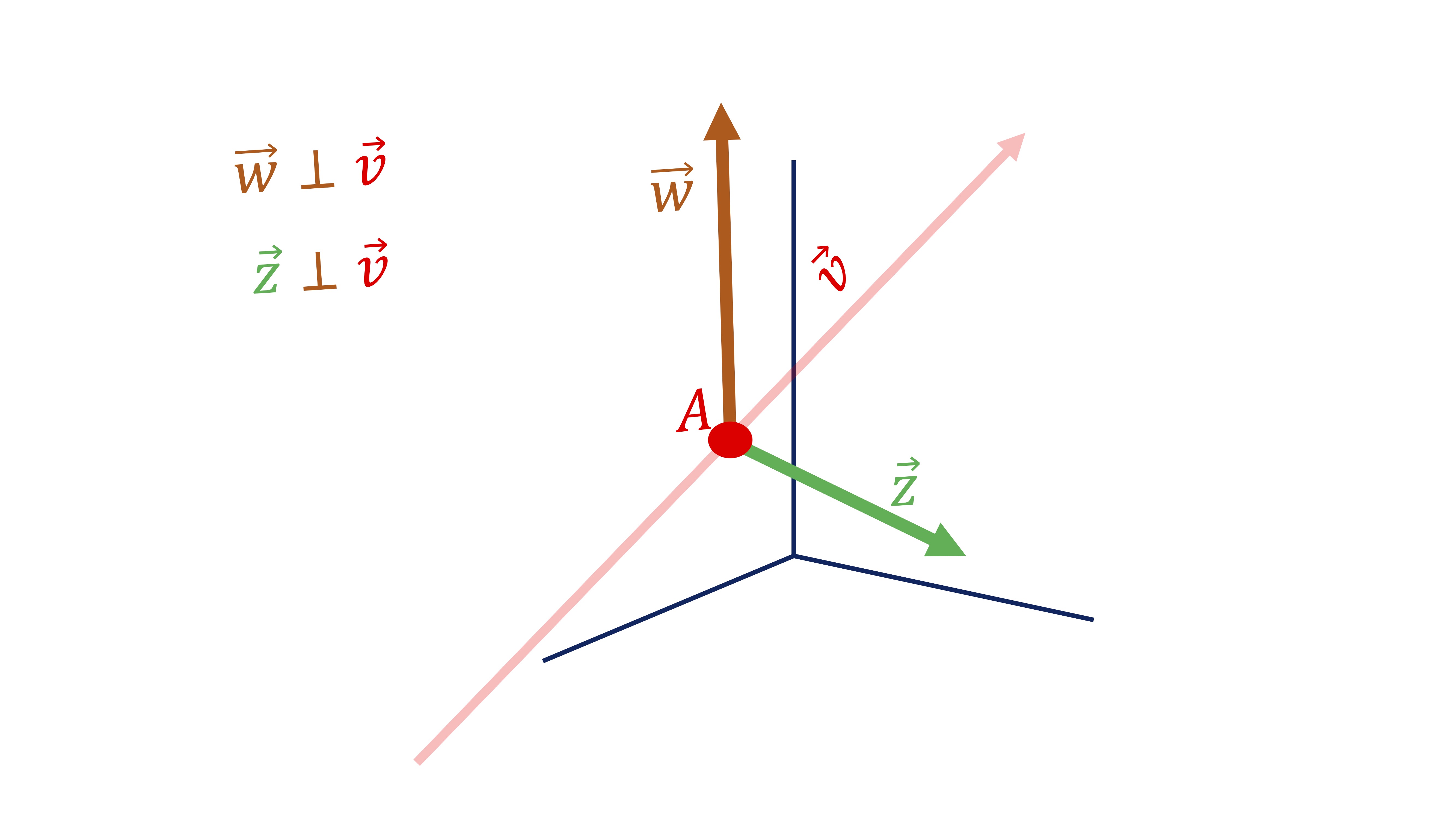
• De estas ecuaciones cartesianas, \[ \begin{cases} x+y-z=1\\ x+2y-2z=2 \end{cases}. \] obtén el vector director a travás de los vectores perpendiculares a esta.

solución Los vectores perpendiculares podemos sacarlos de las ecuaciones cartesianas. De la primera, tenemos que el vector

\(\overrightarrow{w}=\left[\begin{array}{c} 1\\ 1\\ -1 \end{array}\right]\) es perpendicular al plano \(x+y-z=1\). De la segunda, obtenemos que \(\overrightarrow{z}=\left[\begin{array}{c} 1\\ 2\\ -2 \end{array}\right]\)

es perpendicular al plano \(x+2y-2z=2\). Entonces, debemos buscar un vector que sea perpendicular a ambos a la vez, y este será el vector director \(\overrightarrow{v}\)

\[ \begin{cases} \overrightarrow{v}\cdot\overrightarrow{w}=0\\ \overrightarrow{v}\cdot\overrightarrow{z}=0 \end{cases} \]

de lo que tenemos

\[ \begin{cases} v_{1}+v_{2}-v_{3}=0 & (1)\\ v_{1}+2v_{2}-2v_{3}=0 & (2) \end{cases} \]

si trabajamos en este sistema:

Ecuación (1) - Ecuación (2) nos da \(-v_{2}+v_{3}=0\Rightarrow v_{3}=v_{2}\)

si sistuímos en cualquiera de las dos ecuaciones, obtenemos que \(v_{1}=0\)

Tenemos, entonces, el siguiente vector (no pierdas detalle):

\[ \overrightarrow{v}=\left[\begin{array}{c} 0\\ v_{2}\\ v_{2} \end{array}\right] \] por ejemplo \[ \overrightarrow{v}=\left[\begin{array}{c} 0\\ 1\\ 1 \end{array}\right] \]

• Sea el plano \(\Pi=\left\{ (x,y,z)\in\mathbb{R}^{3}\::\:2x+3y+4z=3\right\}\). Di si la recta \(r=\left\{ (x,y,z)\in\mathbb{R}^{3}\::\:(x,y,z)=(0,1,0)+\lambda(2,4,-4),\lambda\in\mathbb{R}\right\}\) está contenida en el plano.

solución Este es muy sencillo. Puedes buscar dos puntos de la recta y luego verificar si esos dos puntos pertenecen al plano (si \(\lambda=0,\lambda=1)\), tenemos esos dos puntos \((0,1,0),(2,5,-4)\) y es fácil verificar que están en el plano con la ecuación cartesiana, ¿no?

Clase 7: Subconjuntos de Espacios vectoriales: subespacios

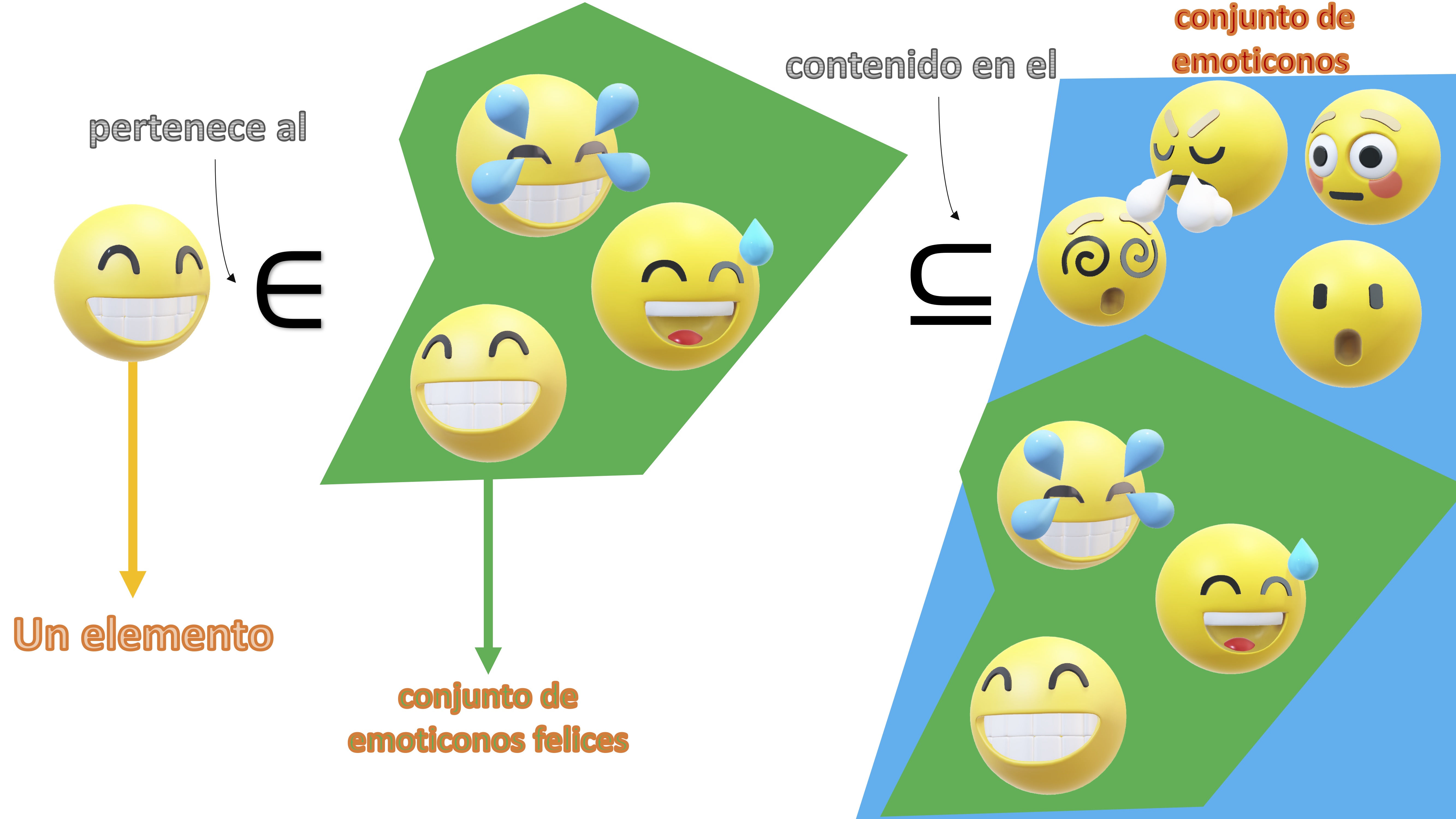
Primera idea importante para la clase de hoy: un subconjunto

FIG 1. \(W\) es un subconjunto de \(E\)

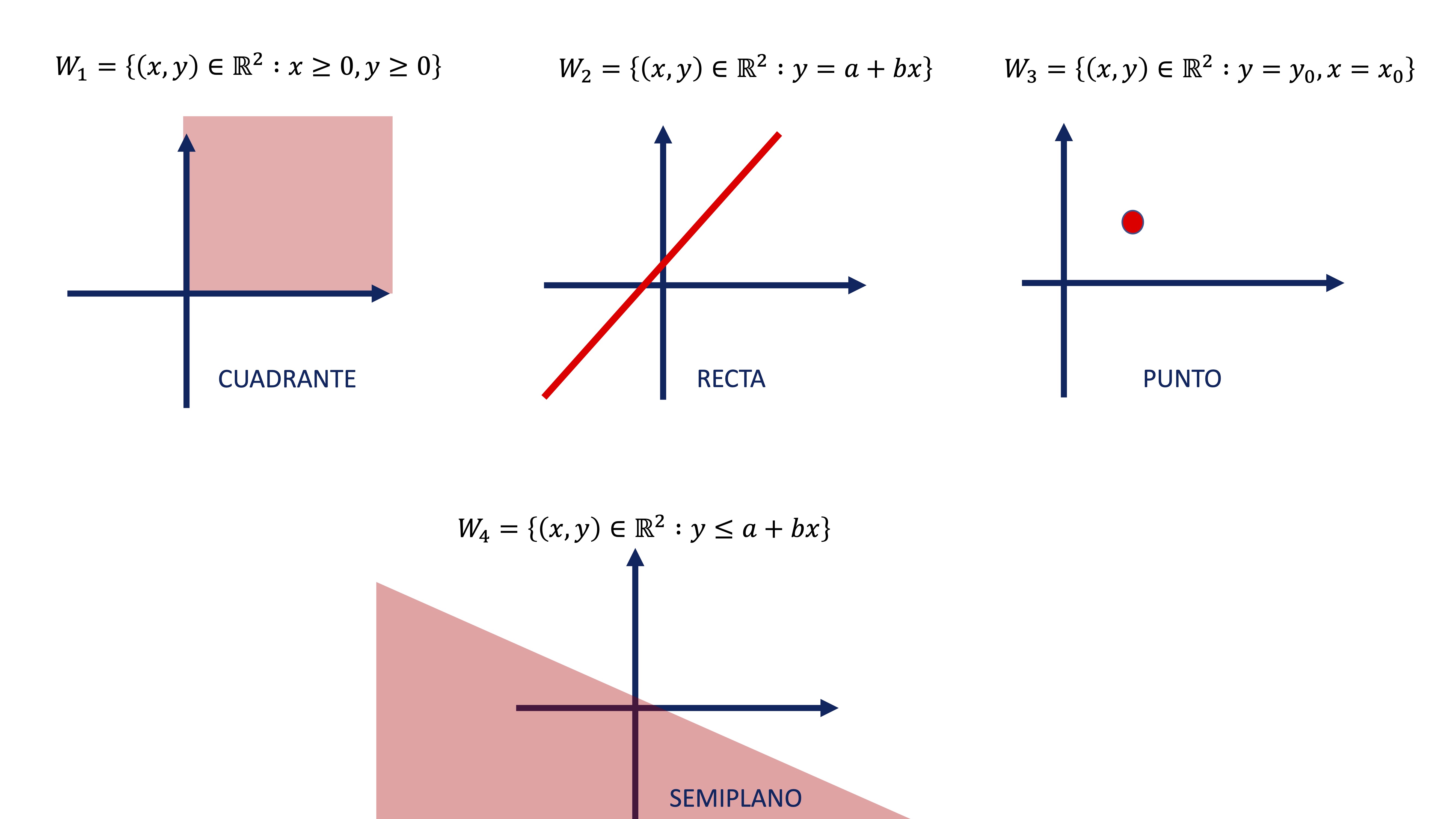
Un conjunto \(W\) es subconjunto de un conjunto \(E\) si \(W\) está contenido en \(E\) y lo escribimos como \[ W\subseteq E \]

Recuerda cosas básicas de la notación de conjuntos: cuándo se usa “pertenece” y cuándo “contenido en”

FIG 2.

Podemos pensar en un conjunto, por ejemplo, \(\mathbb{R}^{2}\), que en este tema ya hemos visto que tiene un nombre: “espacio vectorial”. ¿Qué objetos serán subconjuntos de \(\mathbb{R}^{2}?\)? Por ejemplo, aquí mostramos algunos

FIG 2. Subconjuntos de \(\mathbb{R}^{2}?\)

Ejercicio resuelto

• ¿Es \(\mathbb{R}^{2}\) un subconjunto de \(\mathbb{R}^{2}?\) ¿Es \(\mathbb{R}^{2}\) un subconjunto de \(\mathbb{R}^{3}\)?

solución

\(\mathbb{R}^{2}\) es el conjunto de todos los vectores con dos componentes reales que pueden representarse en el plano. Entonces, \(\mathbb{R}^{2}\) es un subconjunto de sí mismo (ya que está contenido en sí mismo). Sin embargo, \(\mathbb{R}^{2}\) NO es un subconjutno de \(\mathbb{R}^{3}\), ya que no cumple con las normas de \(\mathbb{R}^{3}\): estas son vectores de números reales con tres componentes.

Por lo tanto, veamos subconjuntos de \(\mathbb{R}^{3}\)

Un punto: \[ (1,2,5) \]

Una recta:

\[ \left[\begin{array}{c} x\\ y\\ z \end{array}\right]=\left[\begin{array}{c} 1\\ 2\\ 3 \end{array}\right]+\lambda\left[\begin{array}{c} 0\\ -\text{1}\\ 1 \end{array}\right] \]

Un plano

\[ \left[\begin{array}{c} x\\ y\\ z \end{array}\right]=\left[\begin{array}{c} 1\\ 2\\ 3 \end{array}\right]+\lambda_{1}\left[\begin{array}{c} 0\\ -\text{1}\\ 1 \end{array}\right]+\lambda_{2}\left[\begin{array}{c} 1\\ 2\\ 1 \end{array}\right] \]

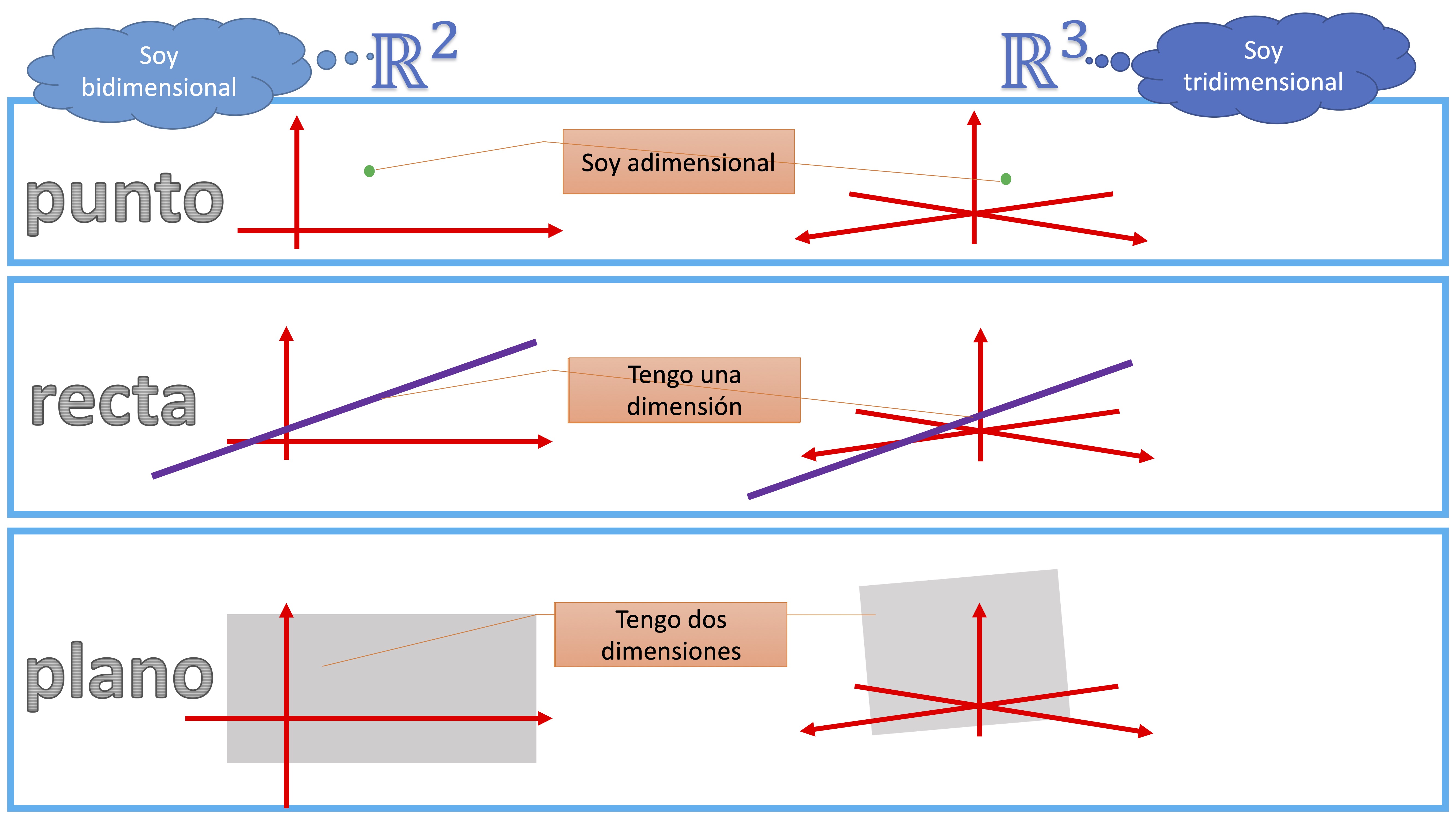
y el propio \(\mathbb{R}^{3}.\) Como sabes, el punto tiene dimensión 0, pero está en \(\mathbb{R}^{3}\) (Es decir, es un objeto sin dimensión que necesita tres valores para ser definido en el conjunto). La recta tiene una dimensión (un vector director), pero sigue necesitando definirse en \(\mathbb{R}^{3}\), por lo que el vector y el punto por el que pasa necesitan de 3 valores. Mientras que el plano es un objeto bidimensional, de nuevo definido en\(\mathbb{R}^{3}\). No tenemos que confundir la dimensión del objeto geométrico con la dimensión del espacio donde se define

---

Importante

\(\mathbb{R}^{2}\) es un espacio vectorial BIDIMENSIONAL. Es decir, para describir cualquier objeto que esté en él , necesitaremos dar dos coordenadas. Por otro lado, \(\mathbb{R}^{3}\) es un espacio vectorial TRIDIMENSIONAL. Para describir cualquier objeto que esté en él, necesitaremos dar tres coordenadas. Por otro lado, un punto es siempre un objeto adimensional (no tiene ni ancho, ni largo ni nada). Lo que ocurre es que un punto en \(\mathbb{R}^{2}\) se describe con dos coordenadas y en \(\mathbb{R}^{3}\) con tres. Una recta es un objeto unidimensional (piensa en el metro de medir). Para definir una recta en \(\mathbb{R}^{2}\) necesitarás un vector director en \(\mathbb{R}^{2}\) y para definir una recta en \(\mathbb{R}^{3}\), necesitarás un vector director en \(\mathbb{R}^{3}\). Finalmente, un plano es un objeto bidimensional (piensa en un folio), lo que ocurre es que para definirlo en \(\mathbb{R}^{2}\), necesitas dos vectores directores de \(\mathbb{R}^{2}\) y para definirlo en \(\mathbb{R}^{3}\), dos vectores directores de \(\mathbb{R}^{3}\) ( que sean linealmente independientes).

FIG 3. Una cosa es la dimensión del espacio y otra cosa la dimensión del objeto

---

Nuestro objetivo de hoy es definir un subconjunto concreto de un espacio vectorial que se denomina: subespacio vectorial

Para ello, tenemos que ver que hay dos tipos de subconjuntos. Unos que pasan por el origen de coordenadas (es decir, que contienen a \(\overrightarrow{0}\)), mientras que hay otros que no. Pensemos, por ejemplo, en un plano en \(\mathbb{R}^{3}\). Vamos a elegir \[ 2x-3y+z=5 \]

como ejemplo de un plano que no pasa por el \(\overrightarrow{0}\) (\(2\times0-3\times0+0\neq5)\) y una versión que sí pasa por el origen: \[ 2x-3y+z=0 \]

Ahora, elegimos un par de puntos que pertenecen a ese plano:

Puntos	\(2x-3y+z=5\)	\(2x-3y+z=0\)
\(A\)	\((1,0,2)\)	\((1,1,1)\)
\(B\)	\((0,-2,-1)\)	\((0,1,3)\)
\(A+B\)	\((1,-2,1)\)	\((1,2,4)\)

Si te fijas, en el plano que no pasa por el origen, la suma de ambos puntos nos proporciona un punto que no está en el plano original (\(2\times1-3\times0+2\neq5)\) mientras que en la versión del plano que sí que pasa por el origen, la suma de ambos puntos pertenece al plano (\(2\times1-3\times2+4=0)\).

Nota, además, que si multiplicamos cualquiera de los puntos por una constante, en el caso del plano que no pasa por el \((0,0,0)\) el nuevo punto (por ejemplo, \(2A\)) no está en el plano (no satisface la ecuación \(2x-3y+z=5\)) mientras que en el plano definido por \(2x-3y+z=0\), el nuevo punto pertenece también al plano

Puntos	\(2x-3y+z=5\)	\(2x-3y+z=0\)
\(A\)	\((1,0,2)\)	\((1,1,1)\)
\(2A\)	\((2,0,4)\)	\((2,2,2)\)

A los subconjuntos de un espacio vectorial que preservan estas propiedades (la suma de dos vectores pertence al subconjunto y el producto de un vector por un escalar pertenece también a este) los llamaremos SUBESPACIOS VECTORIALES

Un subespacio, por ejemplo \(W\), de un espacio vectorial \(E\) es un conjunto tal que \(W\subseteq E\). \(W\), entonces, deberá estar cerrado bajo la suma de vectores y el producto escalar, o lo que es lo mismo, debe heredar las propiedades del espacio vectorial.

---

Test para detectar subespacios vectoriales

Para ver que estamos ante un subespacio vectorial, debemos comprobar que el subconjunto \(W\) cumple:

• Debemos asegurarnos que, si \(\overrightarrow{u},\overrightarrow{v}\in W\), entonces \(\overrightarrow{u}+\overrightarrow{v}\in W\),

• y que \(\lambda\overrightarrow{u}\in W\).

Esto tiene una consecuencia clara, como \(\lambda\) puede ser cualquier número real, si \(\lambda=0\), necesitamos que \(\overrightarrow{0}\subseteq W\), esto implica que un subespacio es un subconjunto de un espacio vectorial que necesita pasar por el punto \(\overrightarrow{0}\).

Ejercicio

Definimos dos subconjuntos de \(\mathbb{R}^{2}:\)

\[ S_{1}=\left\{ \overrightarrow{x}\in\mathbb{R}^{2}:y=3x+2\right\} \]

\[ S_{2}=\left\{ \overrightarrow{x}\in\mathbb{R}^{2}:y=3x\right\} \]

Nota que, en este caso, \(\overrightarrow{x}=\left[\begin{array}{c} x\\ y \end{array}\right]\). Vamos a ver si los dos subconjuntos satisfacen la condición de subespacio.

• ¿Es \(S_{1}\) un subespacio?

Para verlo, usamos dos vectores en \(\mathbb{R}^{2}\) que sigan las normas del subconjunto, ya sabes, \(\overrightarrow{u}=\left[\begin{array}{c} 1\\ 5 \end{array}\right]\)\(\in S_{1}\) y \(\overrightarrow{v}=\left[\begin{array}{c} 2\\ 8 \end{array}\right]\)\(\in S_{1}\)

• ¿Está cerrado bajo la suma? \(\overrightarrow{u}+\overrightarrow{v}\Rightarrow\left[\begin{array}{c} 3\\ 13 \end{array}\right]\notin S_{1}\), pues no está cerrado bajo la suma puesto que si \(x=3\), entonces \(y\) debería ser \(11\).

• ¿Está cerrado bajo el producto escalar? \(\lambda\left(\overrightarrow{u}\right)\Rightarrow\left[\begin{array}{c} \lambda1\\ \lambda5 \end{array}\right]\notin S_{1}\). Coge un valor \(\lambda\neq1\), el vector que obtienes no cumple con la “regla” que impone \(S_{1}\)

• Pero… ¿Pertenece el \(\overrightarrow{0}\)? Si te das cuenta, si \(x=0\),entonces \(y=2\) por lo que el origen no es un vector del subconjunto. Entonces:

ESTE SUBCONJUNTO NO ES UN SUBESPACIO

• ¿Es \(S_{2}\) un subespacio ?

Para verlo, usamos dos vectores en \(\mathbb{R}^{2}\) que sigan las normas del subconjunto, ya sabes, \(\overrightarrow{u}=\left[\begin{array}{c} 1\\ 3 \end{array}\right]\)\(\in S_{2}\) y \(\overrightarrow{v}=\left[\begin{array}{c} 2\\ 6 \end{array}\right]\)\(\in S_{2}\)

• ¿Está cerrado bajo la suma? \(\overrightarrow{u}+\overrightarrow{v}\Rightarrow\left[\begin{array}{c} 3\\ 9 \end{array}\right]\in S_{2}\), Sí, lo está, puestoque si \(x=3\), entonces \(y=9\)

• ¿Está definido bajo el producto escalar? \(\lambda\left(\overrightarrow{u}\right)\Rightarrow\left[\begin{array}{c} \lambda3\\ \lambda9 \end{array}\right]\in S_{2}\). Coge un valor \(\lambda\neq1\), el vector que obtienes sí cumple con la “regla” que impone \(S_{2}\)

• ¿Pertenece el \(\overrightarrow{0}\)? Si te das cuenta, si \(x=0\), entonces \(y=0\) por lo que el origen es un vector del subconjunto. Entonces:

ESTE SUBCONJUNTO ES UN SUBESPACIO

Ejercicio propuesto

Define todos los subespacios que podemos encontrarnos en \(\mathbb{R}^{2}\) y en \(\mathbb{R}^{3}.\)

Ampliación

La proyección ortogonal de un vector sobre otro

La idea de proyectar un vector sobre otro consiste en buscar la sombra de un vector sobre otro. En nuestro caso, en la imgagen (1) pretendemos buscar la sombra del vector \(\overrightarrow{w}\) sobre el vector \(\overrightarrow{v}\).

De forma más precisa, querremos buscar un vector proporcional a \(\overrightarrow{v}\), es decir, un nuevo vector \(\lambda\overrightarrow{v}\) tal que esté lo más cerca posible del vector \(\overrightarrow{w}.\)

FIG 1. La proyección ortogonal

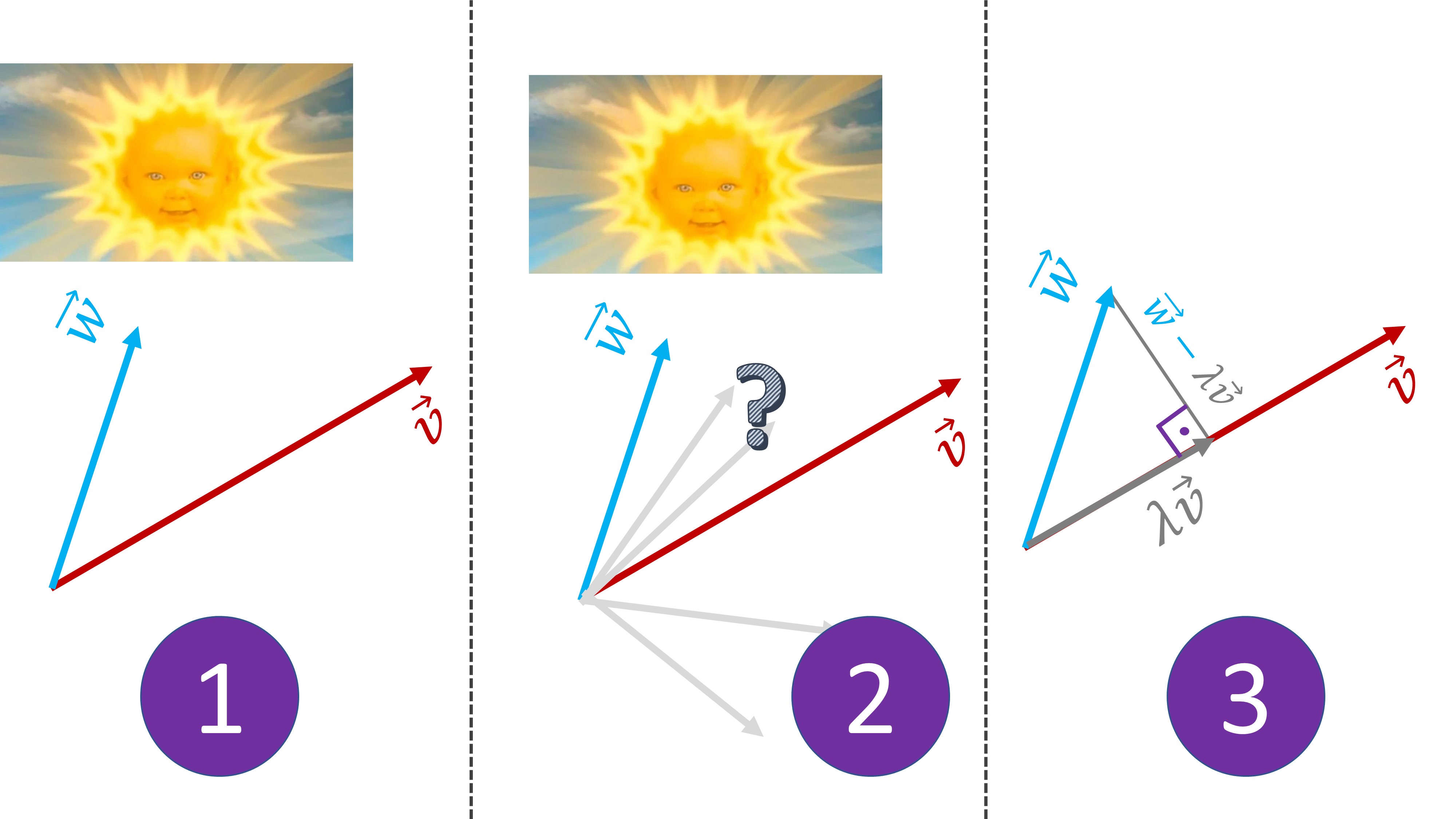
Como vemos en (2), la única posibilidad de encontrar un vector proporcional a \(\overrightarrow{v}\), que esté lo más cerca posible de \(\overrightarrow{w}\), es un vector que tenga distancia (Ver (3)) \(\overrightarrow{w}-\lambda\overrightarrow{v}\) y que esa distancia sea perpendicular al vector \(\overrightarrow{v}\). Entonces, impondremos:

\[ \overrightarrow{v}\cdot\left(\overrightarrow{w}-\lambda\overrightarrow{v}\right)=0 \]

Es decir, queremos ambos vectores sean perpendiculares: su producto escalar ha de ser cero. Entonces, operando:

\[ \overrightarrow{v}\cdot\overrightarrow{w}-\lambda\overrightarrow{v}\cdot\overrightarrow{v}=0 \]

despejamos \(\lambda\), que es nuestra incógnita:

\[ \lambda=\frac{\overrightarrow{v}\cdot\overrightarrow{w}}{\overrightarrow{v}\cdot\overrightarrow{v}} \]

Ojo: este resultado es un escalar porque, tanto \(\overrightarrow{v}\cdot\overrightarrow{w}\) como \(\overrightarrow{v}\cdot\overrightarrow{v}\) son ambos escalares y, por eso, podemos dividir ambos valores. Sin embargo, ojo, date cuenta de que no puedes “simplificar” las \(\overrightarrow{v}\), puesto que, para que tenga sentido, debes hacer el producto escalar antes.

---

Ejemplo:

Obtén la proyección ortogonal del vector \(\overrightarrow{w}=\left[\begin{array}{c} 1\\ 1 \end{array}\right]\) sobre el vector \(\overrightarrow{v}=\left[\begin{array}{c} 5\\ 3 \end{array}\right]\). Para ello, debemos obtener, primero, el valor de \(\lambda\), es decir:

\[ \lambda=\frac{\left[\begin{array}{c} 5\\ 3 \end{array}\right]\cdot\left[\begin{array}{c} 1\\ 1 \end{array}\right]}{\left[\begin{array}{c} 5\\ 3 \end{array}\right]\cdot\left[\begin{array}{c} 5\\ 3 \end{array}\right]}=\frac{5\times1+3\times1}{5\times5+3\times3}=\frac{8}{34}=\frac{4}{17} \]

Entonces, el vector proporcional a \(\overrightarrow{v}\), que es la proyección ortogonal del vector \(\overrightarrow{w}\) sobre \(\overrightarrow{v}\), es

\[ \frac{4}{17}\left[\begin{array}{c} 5\\ 3 \end{array}\right]=\left[\begin{array}{c} 20/17\\ 12/17 \end{array}\right] \]

---