TEMA 4: Cálculo Integral

• Las integrales están presentes en todas las ciencias, puesto que-como seguro ya sabes- las necesitamos para calcular, entre otras cosas, áreas. En economía también es necesario calcular áreas, pero en este caso, no de terrenos ni de cuestiones físicas, sino de “conceptos” que, de forma abstracta, representan también un área. Un área podrá ser un beneficio acumulado, un excedente de un consumidor, incluso una probabilidad. Por eso, es importante que manejemos bien este instrumento. Para ello, necesitarás:

1. Derivar bien en una variable
2. Entender el concepto de área
3. Tener nociones del concepto de límite
4. Conocer cómo dibujar una recta, una parábola y regiones más generales en el plano

Clase 1: la función primitiva

Vamos a empezar definiendo una función clave para el cálculo integral: la primitiva de una función \(f(x)\).

Una primitiva (o antiderivada) de una función \(f(x)\) es otra función, \(F(x)\), tal que si derivamos \(F(x)\) obtenemos \(f(x).\) Es decir:

\[ F'(x)=f(x). \]

Como puedes apreciar, estamos estableciendo una operación “inversa” a derivar: buscamos una función \(F(x)\) cuya derivada sea la función original \(f(x)\). Por eso, también, llamamos a esta operación “antiderivar”. Por ejemplo, si mi función es \(f(x)=3\), ¿Cuál será la primitiva o antiderivada? Pues tenemos que buscar una función \(F(x)\) que, al derivarla, nos dé 3. Seguro que has adivinado que

\[ F(x)=3x \]

Sin embargo, hay un detalle que quizás no hayas observado: no es la única posible función que, al derivarse, nos da \(3\). Hay más: de hecho, hay infinitas:

\[ F(x)=3x+C \]

donde \(C\) es una constante. Como sabemos, la derivada de una constante es \(0\). De esta forma,

\[ (F(x)+C)'=3. \]

Por lo tanto, si una función tiene primitiva, en realidad, tiene ¡infinitas primitivas (mira la FIG 1)!

FIG1. Te dibujamos unas cuantas de esas primitivas

Ahora bien, para referirnos a esta operación sin la necesidad de tener que escribir la palabra “primitiva” o “antiderivada”, vamos a usar un símbolo:

\[ F(x)=\int f(x) \]

donde \(\int\) es el “símbolo” de la integral y \(f(x)\) es el integrando (o la función a la que queremos calcularle la primitiva). Es habitual, sin embargo, añadir con respecto a qué variable integramos mediante el símbolo “diferencial” \(\mathrm{"d}x"\)

\[ F(x)=\int f(x)\mathrm{d}x \]

Nuestros objetivos serán: Construir una tabla de antiderivadas (con el objeto de aprenderla de memoria y simplificar nuestro trabajo), estudiar la tabla y practicar con ellas!

Por ejemplo, calcula la antiderivada de \(f(x)=3x\)

Ahora me están pidiendo que calcule esto:

\[ F(x)=\int3x\mathrm{d}x \]

Entonces, tengo que pensar una función que, al derivarla, me dé \(3x\). Mira esta candidata:

\[ F(x)=\frac{3}{2}x^{2}+C \]

¿Es la antiderivada? Para saberlo, tenemos que derivarla y ver que se cumple lo que buscamos:

\[ F'(x)=\frac{3}{2}{\color{red}2x} \]

simplificando, obtenemos que:

\[ F'(x)=3x=f(x) \]

¡vaya, este método parece imbatible!.

Si te das cuenta, podemos pensar alguna estrategia para obtener las primitivas más famosas. Estas se suelen llamar primitivas inmediatas. Para ello, hay que pensar en cómo se deriva esa función y hacer lo contrario.

Algunas Integrales Inmediatas Comunes

1. \(\int x^{n}\mathrm{d}x=\frac{x^{n+1}}{n+1}+C\) cuidado, si \(n\neq-1\)

2. \(\int x^{-1}\mathrm{d}x=\int\frac{1}{x}\mathrm{d}x=\ln\left|x\right|+C\) (Es el caso anterior con \(n=-1)\)

3. \(\int e^{x}\mathrm{d}x=e^{x}+C\)

4. \(\int a^{x}\mathrm{d}x=\frac{a^{x}}{ln(a)}+C\)

5. \(\int\sin x\mathrm{d}x=-\cos(x)+C\)

6. \(\int\cos x\mathrm{d}x=\sin(x)+C\)

Además, hay dos propiedades de la obtención de primitivas que son particularmente muy interesantes:

propiedad 1 \[ \int kf(x)\mathrm{d}x=k\int f(x)\mathrm{d}x \]

(es decir, la integral de una constante por una función es igual a la constante multiplicada por la función). Así que, en nuestro ejemplo anterior, podríamos haber hecho perfectamente \[ F(x)=\int3x\mathrm{d}x=3\int x\mathrm{d}x \]

y, usando la regla 1 de la tabla:

\[ F(x)=3\frac{x^{1+1}}{1+1}+C=3\frac{x^{2}}{2}+C \]

La otra propiedad, dice que

propiedad 2

\[ \int\left[f(x)+g(x)\right]\mathrm{d}x=\int f(x)\mathrm{d}x+\int g(x)\mathrm{d}x \]

(Es decir, que la integral de una suma de funciones es igual a la suma de la integral de cada función).

Ejemplo 1 ¿cuál es la integral de \(\int\left(x^{2}+\frac{1}{x^{2}}+\sqrt{x}\right)\mathrm{d}x\)

• Primero, escríbelo todo de una forma más clara \(\int\left(x^{2}+\frac{1}{x^{2}}+\sqrt{x}\right)\mathrm{d}x=\int\left(x^{2}+x^{-2}+x^{1/2}\right)\mathrm{d}x\)
• Haciendo caso a dicha propiedad \(\intop x^{2}\mathrm{d}x+\int x^{-2}\mathrm{d}x+\int x^{1/2}\mathrm{d}x=\frac{x^{3}}{3}+\frac{x^{-1}}{-1}+\frac{x^{1/2+1}}{1/2+1}=\frac{x^{3}}{3}-\frac{1}{x}+\frac{2x\sqrt{x}}{3}+C\)

Estas integrales las llamamos integrales indefinidas (porque se hacen para cualquier valor de \(x\) para el que estas funciones tengan sentido) e inmediatas (porque podemos utilizar la tabla de integrales que has hecho antes). Con el paso de las clases, veremos que no siempre será posible tener integrales inmediatas.

Ahora, por ejemplo, ¿qué ocurrirá si, en vez de tener \(\int x^{2}dx\) , pasamos a tener una función de \(x\)? ¿Cómo integraríaamos \(\int(2x+3)^{2}dx\)? Si te das cuenta, no puedes seguir las reglas anteriores al pie de la letra. Si hicieras esto NO te saldría la primitiva. Mira algo que es incorrecto:

\[ \int(2x+3)^{2}dx=\frac{(2x+3)^{3}}{3}+C \]

ESTO NO es la primitiva. ¿Por qué? Vamos a derivarla:

\[ \frac{d\frac{(2x+3)^{3}}{3}}{dx}=\frac{3(2x+3)^{2}}{3}2={\color{red}2\left(2x+3\right)^{2}} \]

¡no es la función original! Si te das cuenta, ese “2”, en rojo, es la derivada de \(f(x)=2x+3\), que es la función “interna”. Para que esta integral se pueda hacer de una forma similar a la de las inmediatas, deberíamos conseguir ese “2”. Como sabemos que si multiplicamos y dividimos por el mismo número nada cambia, podemos hacer esto:

\[ \frac{\color{red}1}{\color{red}2}\int\color{red}2(2x+3)^{2}dx=\frac{\color{red}1}{\color{red}2}\frac{(2x+3)^{3}}{3}+C \]

porque, ahora, si la derivamos, ¡tachán! \[ \frac{d(\frac{1}{2}\frac{(2x+3)^{3}}{3}+C)}{dx}={\left(2x+3\right)^{2}} \]

Ahora sí que, si derivas la primitiva, obtienes la función \(f(x)\) original. Como ves, hemos manipulado en ambos lados para conseguir que aparezca la derivada de la función (estamos aplicando la regla de la cadena). Ojo, estas manipulaciones sólo puedes hacerlas con números, nunca multiplicando y dividiendo por la variable \(x\) (propiedad 1).

Ahora, reformulemos la tabla de integrales inmediatas para tener funciones compuestas:

Algunas Integrales Inmediatas Compuestas

1. \(\int f'(x)f(x)^{n}\mathrm{d}x=\frac{f(x)^{n+1}}{n+1}+C\) cuidado, si \(n\neq-1\)

2. \(\int f'(x)f(x)^{-1}\mathrm{d}x=\int\frac{f'(x)}{f(x)}\mathrm{d}x=\ln\left|f(x)\right|+C\) (Es el caso anterior con \(n=-1)\)

3. \(\int f'(x)e^{f(x)}\mathrm{d}x=e^{f(x)}+C\)

4. \(\int f'(x)a^{f(x)}\mathrm{d}x=\frac{a^{f(x)}}{ln{a}}+C\)

5. \(\int f'(x)\sin f(x)\mathrm{d}x=-\cos(f(x))+C\)

6. \(\int f'(x)\cos f(x)\mathrm{d}x=\sin(f(x))+C\)

Esto es importante: Muchas veces tendrás que decidir si una integral es como la primera de la lista o la segunda. Por ejemplo:

• 1. \(\int\left(\frac{x+2}{\sqrt{x^{2}+4x+10}}\right)\mathrm{d}x\)

• 2. \(\int\left(\frac{x-8}{x^{2}-16}\right)\mathrm{d}x\label{eq:INT2}\)

En el caso 1, tenemos en el numerador algo parecido a la derivada de la función que está dentro de la raíz cuadrada. Entonces, no tenemos la derivada del denominador, sino de la función que interviene en la composición. Y, además, una raíz cuadrada es una potencia, por lo que tenemos, en realidad:

\[ \int\left(x+2\right)\left(x^{2}+4x+10\right)^{-1/2}\mathrm{d}x \]

por lo que es una integral de la forma (1) del listado. Para resolverla, tendrás que multiplicar y dividir por 2,

\[ \frac{\color{red}1}{\color{red}2}\int\color{red}2\left(x+2\right)\left(x^{2}+4x+10\right)^{-1/2}\mathrm{d}x \]

y resolverla como una del tipo (1) (hazlo tú y asegúrate de que está bien integrada derivando lo que obtienes).

En el caso de la integral dada por (2), en el numerador tenemos “casi” la derivada del denominador. Por lo que será del tipo logarítmico. De nuevo, tendrás que multiplicar por 2.

\[ \frac{\color{red}1}{\color{red}2}\int\color{red}2\left(\frac{x-8}{x^{2}-16}\right)\mathrm{d}x \]

y ver que, el resultado, es tipo logarítmico. Asegúrate de que está bien derivándola de nuevo.

Clase 2: Integración por partes

Este método resulta adecuado cuando tenemos un producto de funciones.

\[ \int f(x)g(x)\mathbf{d}x \]

Estas integrales, obviamente, no son inmediatas. Por ejemplo, \(\int xsen(x)\mathrm{d}x\), donde \(f(x)=x\), \(g(x)=sen(x)\). Vamos a ver un método que, basado en las propiedades de la derivada de un producto, nos va a permitir obtener la primitiva correspondiente.

Ahora, para seguir trabajando, vamos a simplificar la notación, teniendo

\[ u=f(x) \] \[ v=g(x) \]

Asimismo, sabemos que \(\frac{\mathrm{d}u}{\mathrm{d}x}=f'(x)\Rightarrow \mathrm{d}u=f'(x)\mathrm{d}x\) y que \(\frac{\mathrm{d}v}{\mathrm{d}x}=g'(x)\Rightarrow \mathrm{d}v=g'(x)\mathrm{d}x\). De esta manera,

\[ \int f(x)g'(x)\mathrm{d}x=f(x)g(x)-\int g(x)f'(x)\mathrm{d}x \]

puede reescribirse como:

\[ \int u\mathrm{d}v=uv-\int v\mathrm{d}u \]

Esto nos permite, además, acordarnos de la expresión:

\[ \int u\mathrm{d}v={\color{red}u}\mathrm{\mathrm{n\,d\acute{\imath}a\,vi\,una}}\,{\color{red}v}\mathrm{aca}-\int{\color{red}v}\mathrm{estida\:{\color{red}d}e}{\color{red}u}\mathrm{niforme} \]

Y ahora nos queda ponerla en práctica. Lo aconsejable es seguir el procedimiento siguiente (que aplicaremos para la integral \(\int x\ln x\))

Ejemplo del procedimiento: Elijamos la función \(u\), y el resto será \(\mathrm{d}v\). Lo normal es que elijamos para \(u\) una función que no tenga integral inmediata. Por ejemplo, en nuestro caso, \(u=\ln x\). Sin embargo, podemos usar como criterio una regla nemotécnica que establece un orden de prioridades para elegir \(u\): ALPES, por

• A: funciones arco (arcoseno, arcotangente, etc….)
• L: funci?n logaritmo
• P: potencias y polinomios
• E: exponenciales
• S: senos y cosenos.

FIG1. Un día vi una vaca vestida de uniforme en los ALPES

• Una vez tenemos \(u=\ln x\), el resto es \(\mathrm{d}v\). En nuestro caso, \(\mathrm{d}v=x\mathrm{d}x\).
• Obtenemos \(du=f'(x)dx\). En nuestro caso, \(du=\frac{1}{x}dx\)
• Obtenemos \(v=\int dv\). En nuestro caso \(v=\int xdx\Rightarrow v=\frac{x^{2}}{2}\)
• Aplicamos la expresión

\[ \int x\ln x=\ln x\left(\frac{x^{2}}{2}\right)-\int\frac{x^{2}}{2}\frac{1}{x}dx=\ln x\left(\frac{x^{2}}{2}\right)-\frac{x^{2}}{4}+C \]

Es importante notar que la regla ALPES es una regla nemotécnica (no científica). Por lo tanto, ayuda a tomar decisiones. Si, siguiendo la regla, la integral que queda en \(\int{\color{red}v}\mathrm{estida\:{\color{red}d}e}{\color{red}u}\mathrm{niforme}\) no es inmediata pueden pasar dos cosas:

• O que hayas elegido mal las funciones y debas deshacer lo andado
• Que tengas que volver a integrar por partes

Estas cosas se aprenden con la práctica :)

Ejemplo

-\(\int t\sin t\mathrm{d}t\)

Operando,

• \(u=t\Rightarrow\mathrm{d}u=\mathrm{d}t\)
• \(\mathrm{d}v=\sin t\mathrm{d}t\Rightarrow v=\int\sin t\mathrm{d}t\Rightarrow v=-\cos t\)
• \(\int t\sin t\mathrm{d}t=t(-\cos t)-\int-\cos t\mathrm{d}t=-t(\cos t)+\sin t+C\)

¿De dónde sale la expresión de la integral por partes?

Empecemos con la derivada de un producto:

\[ \left(f(x)g(x)\right)'=f'(x)g(x)+f(x)g'(x) \]

Como queremos ver cómo integrar estas funciones, apliquemos integración en ambos lados:

\[ \int\left(f(x)g(x)\right)'\mathrm{d}x=\int f'(x)g(x)\mathrm{d}x+\int f(x)g'(x)\mathrm{d}x \]

Fíjate que, aprovechando que integral y derivada son funciones inversas:

\[ f(x)g(x)=\int f'(x)g(x)\mathrm{d}x+\int f(x)g'(x)\mathrm{d}x \]

Ahora, para seguir trabajando vamos a llamar a dos variables que serán el resultado de las funciones anteriores:

\[ u=f(x) \] \[ v=g(x) \]

Asimismo, sabemos que \(\mathrm{d}u=f'(x)\mathrm{d}x\) y que \(\mathrm{d}v=g'(x)\mathrm{d}x\). De esta manera: \[ uv=\int v\mathrm{d}u+\int u\mathrm{d}v \]

es decir:

\[ uv-\int v\mathrm{d}u=\int u\mathrm{d}v \]

Clase 3: El Teorema Fundamental del Cálculo

En realidad, históricamente, la primera integral en introducirse fue la integral definida, puesto que está íntimamente relacionada con el cálculo de áreas. En el apéndice podrás ver, con más detalle, cómo se llegó al Teorema Fundamental del Cálculo. En este vídeo también se explica, de manera visual, la idea del teorema.

Dado que la idea, detrás del teorema, es poder utilizar la integral para calcular áreas de figuras representadas por funciones acotadas inferiormente por el eje \(x\),

Funciones integrables Diremos que una función \(f(x)\) es integrable en un intervalo \(x\in(a,b)\) si presenta alguna de estas características:

1. Funciones continuas y acotadas superiormente: como ves, puedes “ver” el área comprendida entre la función y el eje de las \(x\)

FIG1. Función continua y acotada superiormente

2.- Funciones continuas, acotadas, a trozos (con discontinuidad evitable): de nuevo, puedes visualizar el área comprendida entre la función y el eje \(x\).

¿Por qué? Como ves, se puede rellenar perfectamente con el “rectangulito”

FIG3. Función continua a trozos acotada

El Teorema Fundamental del cálculo dice:

OJO!

Sea \(f\) una función integrable en el interalo \((a,b)\), sea \(F(x)\) una función definida en dicho intervalo, tal que \[ F(x)=\int_a^xf \] Si \(f\) es continua en cualquier punto \(c\in(a,b)\), entonces

\[ F'(c)=f(c). \]

Este resultado es muy potente, pues le da un significado a la operación que hemos definido anteriormente como “la operación inversa a derivar”.

OJO!

Cuando en la función integral tengas que poner en el límite superior el valor \(x\), entonces, deberás cambiar la letra de la función (queda muy raro, matemáticamente, que un mismo símbolo haga de número y de variable). Entonces, el Teorema Fundamental del cálculo, también dice:

\[ \frac{\mathrm{d}}{\mathrm{d}x}\int_{a}^{x}f(t)dt=f(x) \]

• La función integral \(F(x)\) puede interpretarse como el área de la entre el punto \(a\) y el punto \(x\in(a,b)\) siempre que \(f(x)\geq0\) para esos valores de \(x\).

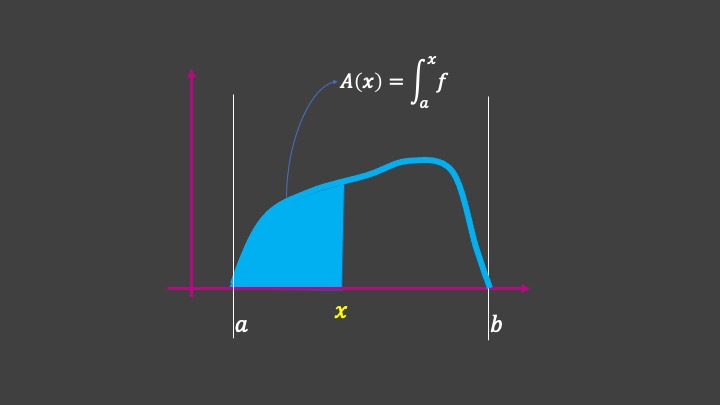
FIG4. Así obtenemos el área de una función continua \(F(x)=\int_{a}^{x}f\)

• Si la función \(f(x)\) cambia de signo, entonces, la interpretación de \(F(x)\) es la diferencia entre áreas.

La idea de la función integral es clave en esta parte, por lo que vamos a entenderla con un ejemplo

Piensa, ahora, sobre la siguiente función, \(f(x)\), definida a trozos:

\[ f(x)=\begin{cases} x & 0\leq x\leq2\\ 3 & 2<x\leq3\\ 5-x & 3<x\leq6 \end{cases} \]

¿Es \(f(x)\) derivable?

Si te fijas, esta función presenta la siguiente derivada: \[ f'(x)=\begin{cases} 1 & 0\leq x\leq2\\ 0 & 2<x\leq3\\ -1 & 3<x\leq6 \end{cases} \]

en los puntos \(x=2,x=3\) las derivadas no son iguales por la derecha y por la izquierda, por lo que no lo es en dichos puntos.

¿Es \(f(x)\) integrable?

Sí, porque es una función continua a trozos (cada trozo está formado por funciones continuas).%

Si ves el siguiente gráfico, FIG5, esta idea te quedará más clara:

FIG5. La función \(f\) no es derivable, pero cumple con las hipótesis de integrabilidad de Riemann

En la FIG 5, vemos cómo podemos obtener el área debajo de la función \(f(x)\). Son figuras sencillitas y, por tanto, resulta inmediato.

Recuerda que en la clase hemos definido la función integral \(F(x)\) como aquella función que te devuelve el área debajo de la curva \(f(x)\) para cada valor de \(x\). En este caso, es fácil de construir cada uno de los trozos:

**OJO: aviso de notación* Si ponemos una \(x\) en el límite superior de la integral, debemos cambiar la variable que define la función. Por ejemplo: no se pone \({\color{red}\int_{\color{red}0}^\color{red}{x}\color{red}f(\color{red}x)\mathrm{d}x}\), sino \({\color{green}\int_{\color{green}0}^\color{green}{x}\color{green}f(\color{green}t)\mathrm{d}t}\). Es una cuestión de significado: la \(x\) no puede ser a la vez un límite de integración (un número) y una variable.

Construimos, a continuación, la función integral como \(\int_{0}^{x}f(t)\mathrm{d}t\):

• Primer trozo (primer triángulo para \(x\in[0,2]\)) \[ F(x)=\int_{0}^{x}t\mathrm{d}t=\left[\frac{t^{2}}{2}\right]_{0}^{x}=\frac{x^{2}}{2},\:x\in[0,2] \]

Fíjate que coincide con el área del triángulo.

• Segundo trozo (la suma del primer trozo y el rectángulo) \[ F(x)=F(2)+\int_{2}^{x}3\mathrm{d}t=F(2)+\left[3t\right]_{2}^{x}=2+3(x-2)\:\:x\in(2,3] \]

**OJO: error muy común* Como ves, tenemos que sumarle el valor del área en el tramo anterior, es decir, \(F(2)\). Si no, no tendríamos la función integral (porque recuerda que esta función te dice el área acumulada para cada valor de \(x\)). Fíjate, \(F(3)=2+3=5\), que es la suma de las áreas del triángulo gris y el rectángulo amarillo.

Finalmente, dibujamos el tercer trozo:

• Tercer trozo \[ F(x)=F(3)+\int_{3}^{x}(5-t)\mathrm{d}t=F(3)+\left[5t-\frac{t^{2}}{2}\right]_{3}^{x}=5+\left[5x-\frac{x^{2}}{2}-\frac{19}{2}\right]=-\frac{11}{2}+5x-\frac{x^{2}}{2}\:\:x\in(3,6] \]

De nuevo, \(F(6)=6.5\), como esperaríamos (al tener un último trozo con resultado negativo).

Es decir, obtenemos:

\[ F(x)=\begin{cases} \frac{x^{2}}{2} & 0\leq x\leq2\\ 3x-4 & 2<x\leq3\\ -\frac{x^{2}}{2}+5x-\frac{11}{2} & 3<x\leq6 \end{cases} \]

que, además, podemos mostrar gráficamente en la FIG 6

FIG6. La función integral \(F(x)\) correspondiente a \(f(x)\)

Dediquemos ahora unos minutos a observar las dos funciones de la FIG 6: \(f(x)\) es discontinua y no diferenciable en \(x=2\) ni en \(x=3\). \(F(x)\), la función integral de \(f(x)\) es continua. Es decir, al integrar una función, su función integral siempre será continua \(F(x)\) (parece lógico, ¿no? lo que hace es ir acumulando el área). Sin embargo, en los puntos en los que la función \(f(x)\) es discontinua, la función \(F(x)\) será no derivable (de nuevo es lógico, porque resulta que \(f(x)\) es la derivada de \(F(x)\). Recuerda que el TFC nos dice que \(F'(x)=f(x)\)).

Entonces….

• \(f(x)\) es integrable\(\Rightarrow\)\(F(x)\) será continua [piensa en el trozo \(x\in[0,3]\): \(f(x)\) es integrable pero no continua.]
• \(f(x)\) es continua\(\Rightarrow F(x)\) es derivable [piensa en cualquier integral inmediata que has visto de una función continua]
• \(f(x)\) es derivable \(p\) veces\(\Rightarrow F(x)\) es derivable \(p+1\) veces [piensa en el tramo \(x\in(3,6):\) es una recta y la integral se convierte en una parábola].

Aplicaciones al cálculo de áreas

Podemos definir el segundo teorema fundamental del cálculo como:

OJO!

Sea \(f\) una función integrable en el intervalo \((a,b)\), la integral definida

\[ \int_a^bf(x)\mathrm{d}x=F(b)-F(a). \]

Este teorema, conocido como la regla de Barrow, tiene muchas aplicaciones en el cálculo de áreas.

Veamos cómo usarlo en la práctica:

• Trata de dibujar las funciones involucradas (es bueno saber cómo están orientadas y esbozar el punto de corte)

• Analiza si hay alguna simetría que simplifique los cálculos

• Obtén el punto de corte con el eje de las “x”.

Veamos un ejemplo: calcula el area de la región acotada por las funciones \(y=x+2\) y \(y=x^{2}\). Mira la FIG 12

FIG12. Dos opciones para ver la integral

Si eliges (1) como el camino:

• Los puntos de corte los hallas como \((x+1)=x^{2}\). La ecuación de segundo grado que tienes, proporciona como soluciones \(x=-1,x=2\)

• La integral que tenemos que resolver será: \(\int_{-1}^{2}\left[(x+2)-x^{2}\right]\mathrm{d}x\)

• El resultado, vía la regla de Barrow: \(\int_{-1}^{2}\left[(x+2)-x^{2}\right]\mathrm{d}x\)=\(\left[\frac{x^{2}}{2}+2x-\frac{x^{3}}{3}\right]_{-1}^{2}=\frac{9}{2}\)

Si, en cambio, eliges (2) como el camino, ahora las funciones son \(x=y-2\), \(x=\pm\sqrt{y}\) (piensa que ahora es como si hubieras rotado los ejes). Por lo tanto

• Los puntos de corte se obtienen igualando \(y-2=\pm\sqrt{y}\) implica que \(y=4,y=1.\)

• Nótese que hay que añadir otro punto: \(y=0\). Por eso es bueno dibujar las funciones implicadas con precisión.

• Entre los valores de \(0<y<1\), el área viene dada por \(\sqrt{y}\),\(-\sqrt{y}\), es decir, \(\int_{0}^{1}\left[\sqrt{y}-(-\sqrt{y})\right]\mathrm{d}y\)

• Entre los valores \(1<y<4\), el área viene dada por \(\int_{1}^{4}\left[\sqrt{y}-(y-2)\right]\mathrm{d}y\)

Es decir:\(\int_{0}^{1}\left[\sqrt{y}-(-\sqrt{y})\right]\mathrm{d}y+\int_{1}^{4}\left[\sqrt{y}-(y-2)\right]\mathrm{d}y\)

La práctica (y la habilidad dibujando) te permitirá analizar qué estrategia es más sencilla. De todas formas, de cara a las integrales dobles, te interesa saber, cuanto antes, moverte en ambos ejes.

Por otro lado, debes tener en cuenta qué ocurre si tienes que calcular un área de una función con respecto al eje de las \(x\). Si la función cambia de signo, la integral, tal cual, no podría interpretarse como un área. Mira este ejemplo en la FIG 13: la integral es 0

Lo que tienes que hacer, en ese caso, es partir la integral y , en la parte negativa, quedarte con su valor absoluto (mira la FIG 14)

FIG13. Una área que da cero (II)

Por otro lado, cuando tienes que calcular el área entre dos funciones, lo que tienes que hacer es dibujarlas para ver cuál está por encima de cuál. En función de esto, te interesará, como en la figura, obtener \(\int_{a}^{b}\left[f(x)-g(x)\right]\mathrm{d}x\) o, al revés

FIG14. ¿Por qué se restan la función que está por encima de la que está por debajo?

En realidad, da igual en dónde se sitúen en los ejes coordenados. Siempre podrás calcular el área como diferencia de la función que está por encima menos la que está por debajo. Si piensas en términos de “rellenar” la función con rectángulos, la altura de cada rectángulo será, en este caso, el valor de la función de arriba menos el de la función de abajo:

Ejercicios resueltos de cálculo de áreas

Clase 3: la función integral y el TFC

Ejemplos de aplicación del TFC

• Derivar una función integral

Dada la función \[ F(x)=\int_{2x}^{x^{2}}\ln\left(t^{2}+1\right)\mathrm{d}t \]

se pide obtener la derivada primera \(F'(x)\).

Del TFC, sabemos que \[ F'(x)=\frac{\mathrm{d}}{\mathrm{d}x}\int\ln\left(t^{2}+1\right)\mathrm{d}x=\ln\left(x^{2}+1\right) \]

Del lema de Barrow, sabemos que \[ \int_{2x}^{x^{2}}\ln\left(t^{2}+1\right)\mathrm{d}x=F(x^{2})-F(2x) \]

Por lo que, por la regla de la cadena, la derivada será:

\[ F'(x^{2})2x-F'(2x)2 \]

Evaluando, tendremos que la derivada pedida es

\[ F'(x)=\ln\left(x^{2}+1\right)2x-2\ln\left(2x+1\right) \]

También lo podemos hacer para una función en dos variables:

\[ F(x,y)=\frac{3x}{e^{y}}+\int_{2-x}^{2y+1}\sqrt{s^{2}+3}\mathrm{d}s \]

Nnos piden las derivadas parciales de la función \(F\) en el punto \((x,y)=(1,0)\). Usando el TFC, es muy sencillo operar \[ \frac{\partial F}{\partial x}(x,y)=\frac{3}{e^{y}}+\underset{BARROW}{\underbrace{\left[\left(\sqrt{\left(2y+1\right)^{2}+3}\right)\frac{\partial}{\partial x}(2y+1)\right]-\left[\left(\sqrt{(2-x)^{2}+3}\right)\frac{\partial}{\partial x}(2-x)\right]}} \]

es decir, \[ \frac{\partial F}{\partial x}(x,y)=\frac{3}{e^{y}}+\left[\left(\sqrt{\left(2y+1\right)^{2}+3}\right)0\right]-\left[\left(\sqrt{(2-x)^{2}+3}\right)\frac{\partial}{\partial x}(2-x)\right] \]

y, por tanto,

\[ \frac{\partial F}{\partial x}(x,y)=\frac{3}{e^{y}}+\left(\sqrt{(2-x)^{2}+3}\right) \]

Por otro lado, podemos llegar a que \(\frac{\partial F}{\partial y}=\frac{-3x}{e^{y}}+2\sqrt{(2y+1)^{2}+3}\).

Otro uso del TFC: recuperar una función “total” sabiendo su “marginal”

Sean \(C(q)\) los costes de una empresa. Por lo tanto, \(C'(q)\) son los costes marginales. Por el TFC:

\[ C(q)-C(q_{0})=\int_{q_{0}}^{q}{\color{magenta}C'(t)}\mathrm{d}t, \]

es decir, si \(q_{0}=0\), entonces

\[ C(q)=C(0)+\int_{0}^{q}C'(t)\mathrm{d}t. \]

Esto tiene una lectura claramente económica:

• \(C(0)\) son los costes fijos (los que incurre en ellos aunque no fabrique nada)

• \(\int_{0}^{q}C'(t)\mathrm{d}t\) son los costes variables (que, obviamente, dependen de las \(q\) unidades que fabriquen)

Esto nos sirve, entonces, para todas las variables stock y flujo que conoces. Las derivadas (variables marginales) son flujos, mientras que la función integral es la variable stock (es decir, la acumulación del flujo). En general, recuerda que:

\[ F(x)-F(0)=\int_{0}^{x}f(t)\mathrm{d}t \]

donde \(F(x)-F(0)\) es la variación de la función integral. Por lo tanto,

\[ F(x)=F(0)+\int_{0}^{x}f(t)\mathrm{d}t \]

Ejemplo resuelto

El ritmo de variación de la prima de riesgo de España en los últimos 30 días ha sido \[ r(t)=\begin{cases} 1-\frac{16}{(t+1)^{2}} & 0\leq t\leq15\\ 2 & 15\leq t\leq30 \end{cases} \]

la prima de riesgo en \(t=0\) fue de \(345\) puntos.

• Explicación 1: Como ves, se trata de una función continua a trozos, la variación de la prima de riesgo es la derivada con respecto al tiempo (la variable flujo) y la prima de riesgo es la función integral (la variable stock).

1. Sea \(R(t)\) el valor de la prima de riesgo el día \(t\) ¿Es continua? ¿Es derivable?

solución: \(R(t)\) es la función integral. Sabemos que siempre es continua (ya que \(r(t)\) está bien definida: es continua a trozos y está acotada en el dominio), por lo que acabamos de ver. Para que sea derivable, \(r(t)\) deberá ser continua. Veamos si lo es \(\lim_{r(t)\rightarrow15^{-}}=1-\frac{1}{16},\) \(\lim_{r(t)\rightarrow15^{+}}=2,\) por lo que-al no ser \(r(t)\) continua en todo su dominio-no será derivable en \(R(15)\).

2. ¿Cuál ha sido la variación en la prima de riesgo en los 15 primeros días?

_solución: \(R(t)\) es la prima de riesgo. Nos piden \(R(15)-R(0)\). Usaremos la siguiente expresión:

\[ R(15)-R(0)=\int_{0}^{15}1-\frac{16}{(t+1)^{2}}\mathrm{d}t \]

Esta integral se resuelve así

\[ \int_{0}^{15}1-\frac{16}{(t+1)^{2}}\mathrm{d}t=\left[t+\frac{16}{t+1}\right]_{0}^{15}=0, \] por lo que no ha variado en los primeros 15 días.

3. Obtén la función \(R(t)\) que da el valor de la prima de riesgo el día \(t\in[0,30]\)

Solución: La función \(R(t)\) debemos obtenerla a partir de la ecuación inicial, teniendo en cuenta que está compuesta por dos trozos y que \(R(0)=345\) \[ R(t)=\begin{cases} 345+\int_{0}^{t}\left(1-\frac{16}{(x+1)^{2}}\right)\mathrm{d}x & 0\leq t\leq15\\ R(15)+\int_{15}^{t}2\mathrm{d}x & 15\leq t\leq30 \end{cases} \]

entonces,

\[ R(t)=\begin{cases} 345+\left[t+\frac{16}{t+1}\right]_{0}^{t}=329+t+\frac{16}{t+1} & 0\leq t\leq15\\ R(15)+\int_{15}^{t}2\mathrm{d}x=315+2t & 15\leq t\leq30 \end{cases} \]

Como ves, nos proporciona una función \(R(t)\) que nos da el valor de la prima de riesgo (variable stock) para cada momento \(t\).

Clase 5: el concepto de integral doble como volumen

La integral doble aparece con la necesidad de calcular volúmenes de figuras no obvias (con una amplia utilidad en cálculo de probabilidades en funciones de densidad bivariantes). Por un lado, conocemos el volumen de un prisma rectangular,

\[ Areabase\times altura \] por ejemplo, este:

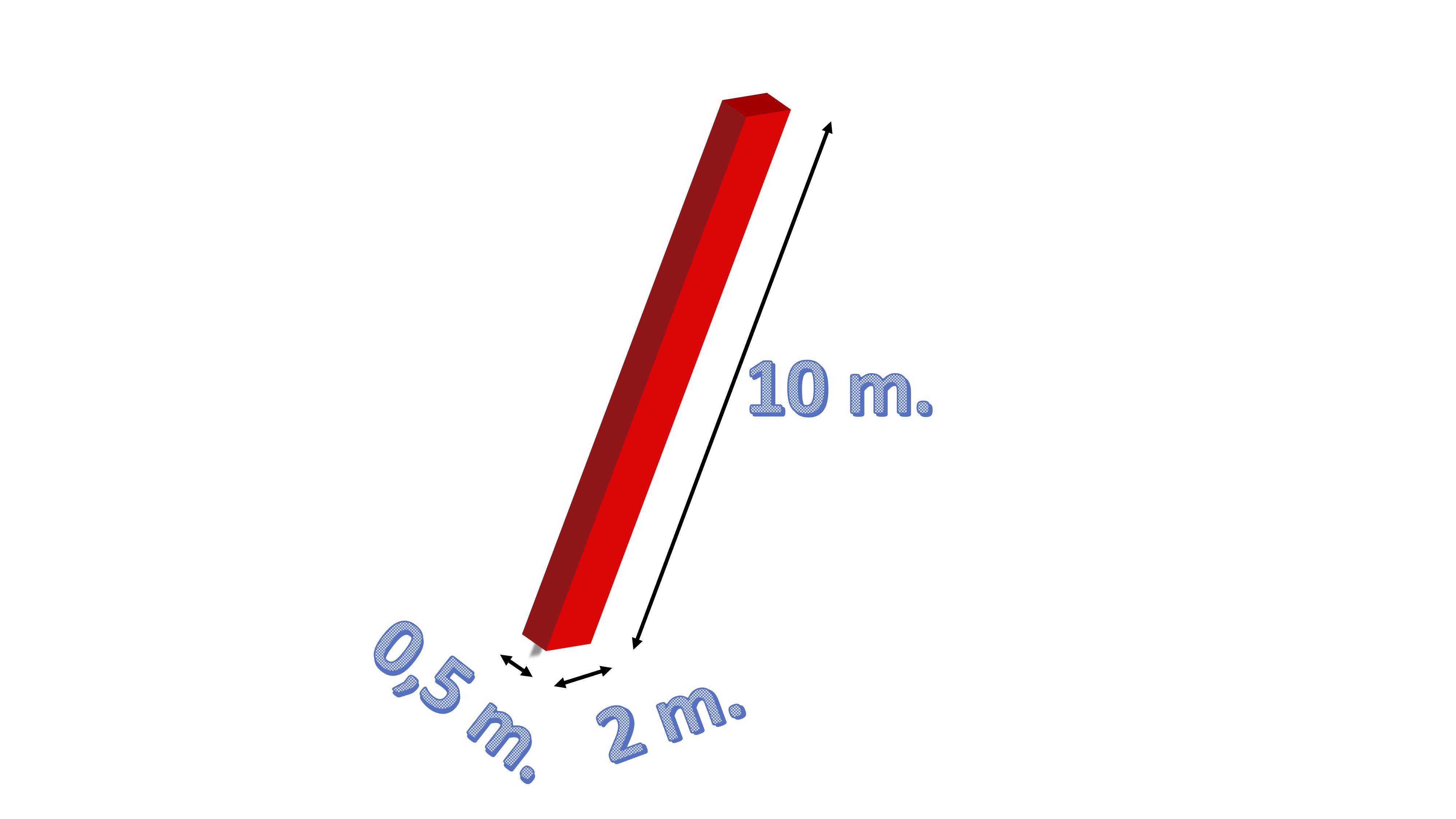
FIG1. Un prisma rectangular

\[ Volumen=2\times0.5\times10=10m^{3} \]

Ahora bien, si queremos calcular el volumen de un sólido que está comprendido en el recinto \(R\)

\[ R=\left\{ \left(x,y\right)\in\mathbb{R}^{2}:0\leq x\leq a,0\leq y\leq b\right\} \]

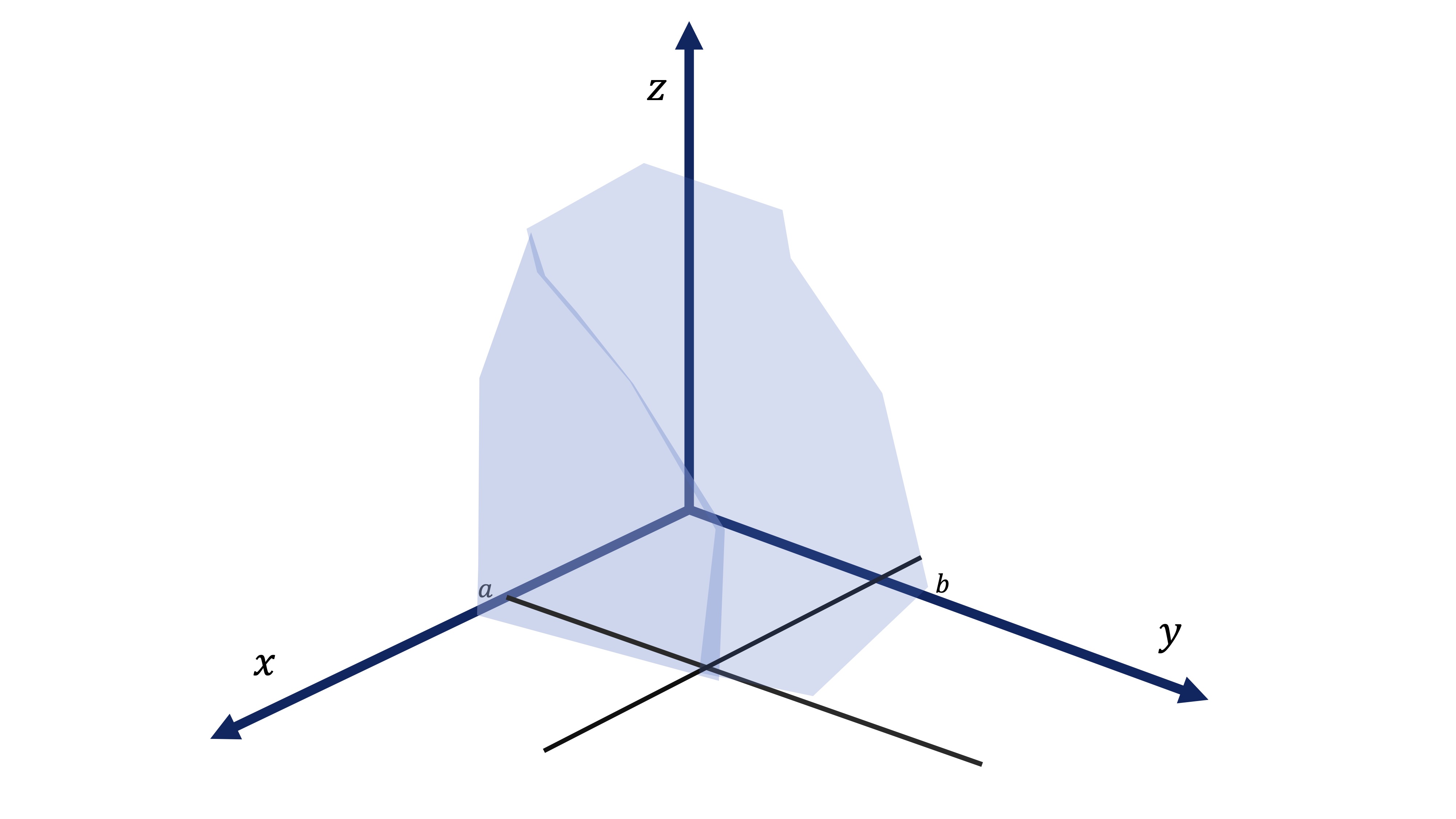
FIG2. sólido al que calcularle el volumen

y cuya altura viene definida por la función \(z=f(x,y)\):

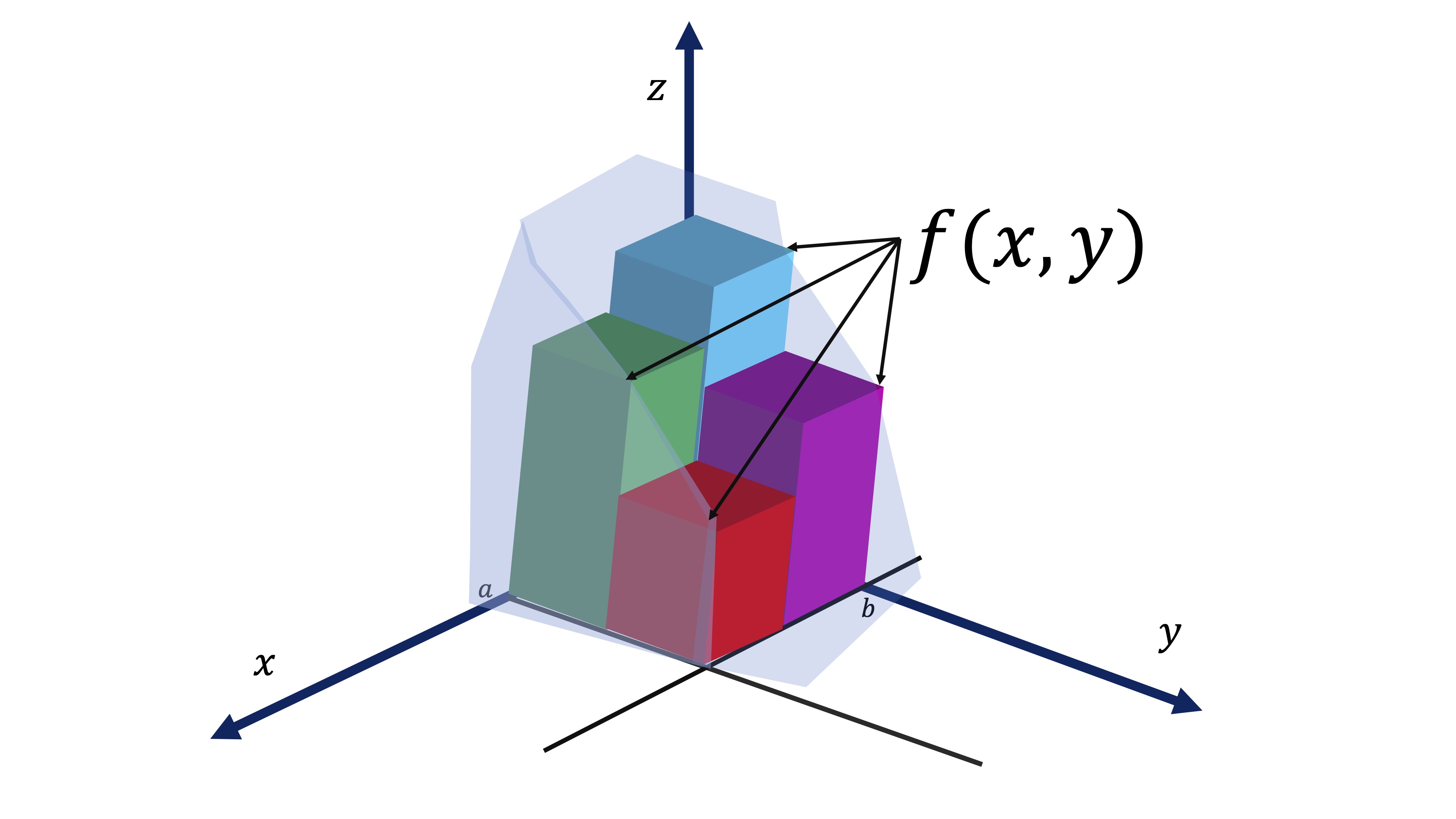
FIG3. Que puede aproximarse “rellenándolo con prismas”

• Podemos empezar aproximándola mediante un número pequeño de prismas (por ejemplo, cuatro).
• El volumen será el área de cada cuadrado (la base del prisma) por la altura (medida por el valor que tome \(z=f(x,y)\).

De hecho, tendremos que elegir cuatro puntos que se correspondan con valores de \(x\) e \(y\) y que están en cada cuadrado. Es decir:

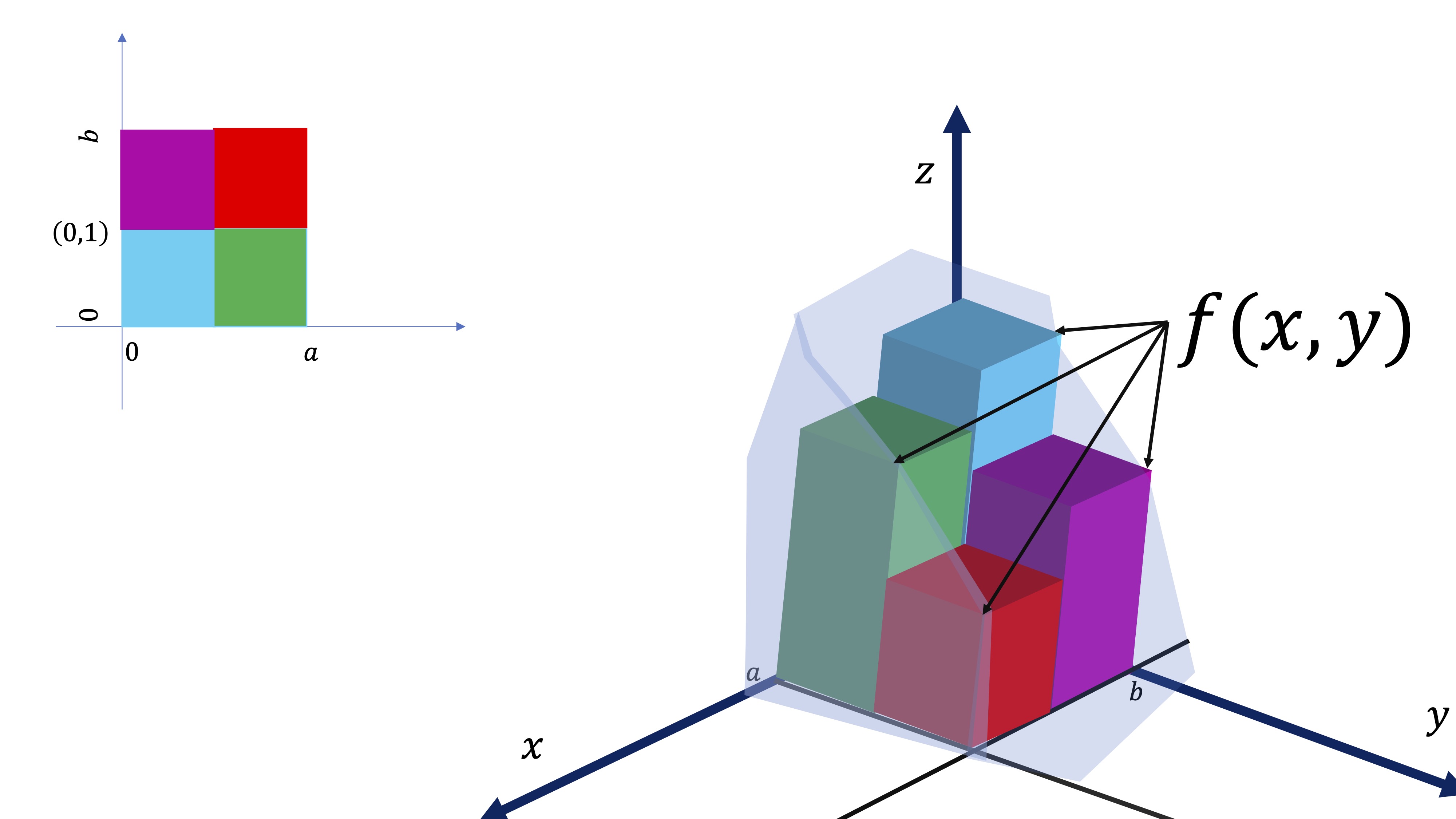
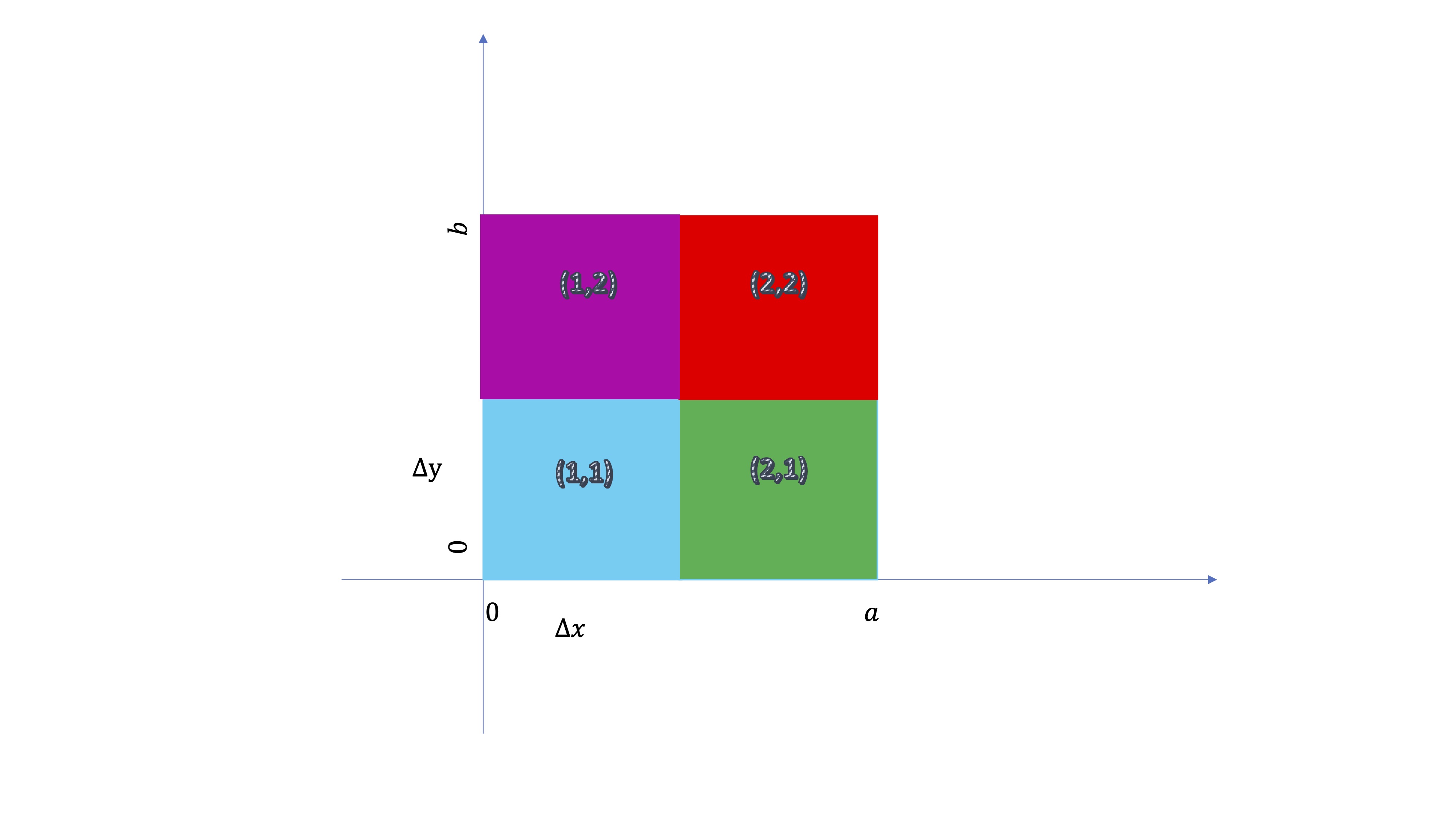
Ahora tendremos que definir los valores de \((x,y)\) que pertenezcan a cada uno de los cuadrados posibles:

\(i\)	\(j\)	\((x,y)\)
\(1\)	\(1\)	\(x_1,y_1\)
\(1\)	\(2\)	\(x_1,y_2\)
\(2\)	\(1\)	\(x_2,y_1\)
\(2\)	\(2\)	\(x_2,y_2\)

Finalmente, el volumen lo calcularemos mediante esta expresión:

\[ V\simeq\sum_{i=1}^{2}\sum_{j=1}^{2}f(x_{i},y_{j})\times Area\:cuadrado \]

Por ejemplo, supongamos que \(a=1,b=2\). Entonces, el recinto será:

\[ 0\leq x\leq1,0\leq y\leq2 \]

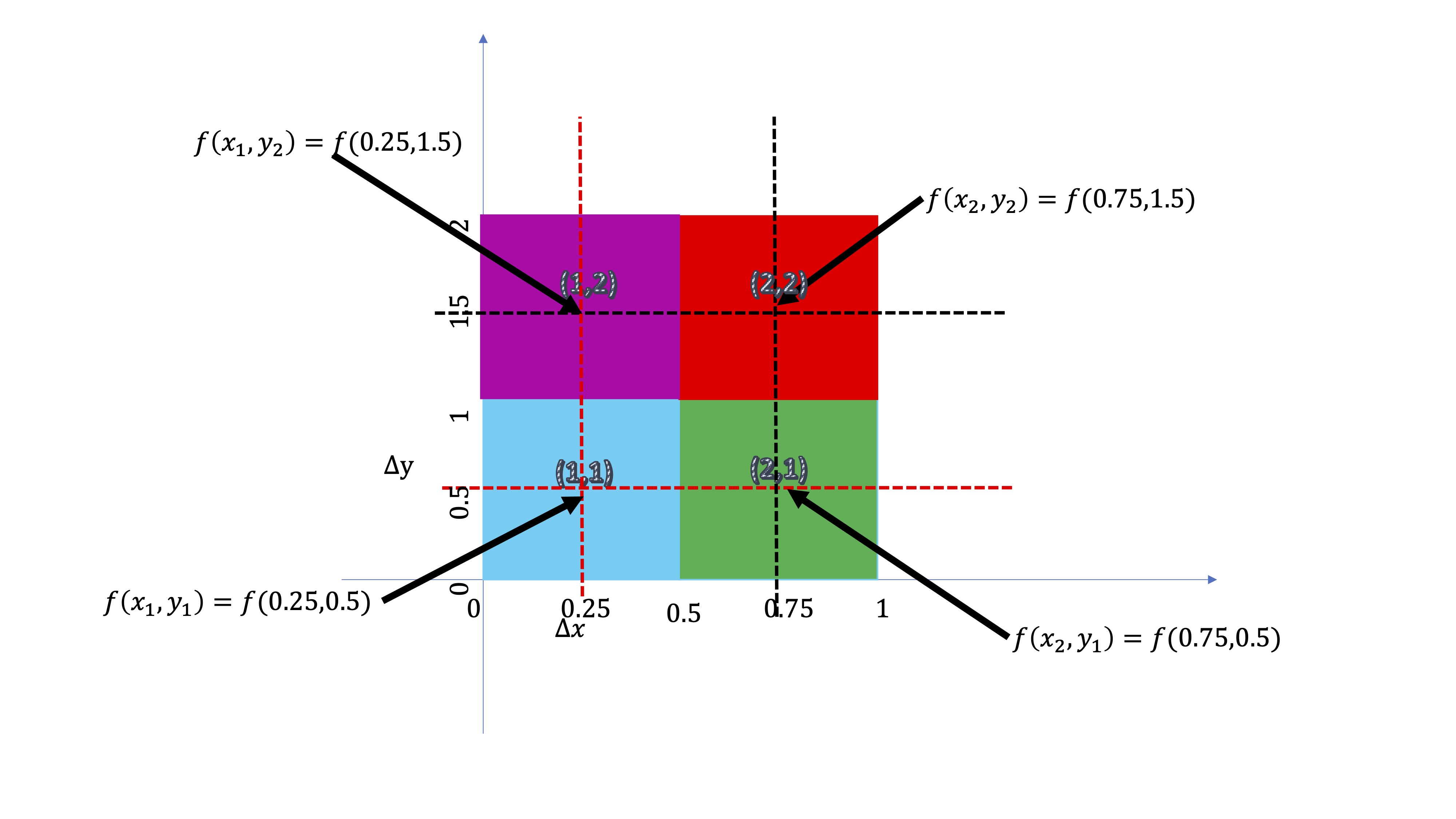
FIG6. Recinto en el que trabajaremos

y supongamos (ver FIG6) también que la altura del sólido viene definida por la función \(f(x,y)=8-x^{2}-y^{2}.\) Vamos a aproximar el volumen haciendo las cuentas anteriores. Para empezar, el área de cada cuadrado será

\[ \mathrm{\Delta}x\mathrm{\Delta}y \] que, en este caso, es

\[ \Delta x\Delta y=0.5\times1=0.5 \]

Eligiendo, de manera arbitraria, un valor para cada par \(x,y\)

\(i\)	\(j\)	\((x,y)\)	\(f(x,y)\)
\(1\)	\(1\)	\(x_1=0.25,y_1=0.5\)	\(7.6875\)
\(1\)	\(2\)	\(x_1=0.25,y_2=1.5\)	\(5.6875\)
\(2\)	\(1\)	\(x_2=0.75,y_1=0.5\)	\(7.1875\)
\(2\)	\(2\)	\(x_2=0.75,y_2=1.5\)	\(5.1875\)

Entonces, el volumen aproximado, será:

\[ V\simeq\left(f(x_{1}y_{1})+f(x_{1},y_{2})+f(x_{2},y_{1})+f(x_{2},y_{2})\right)\Delta x\Delta y \]

Es decir,

\[ V\simeq\left(7.6875+5.6875+7.1875+5.1875)\right)0.5=12.875m^{3} \]

Fíjate que estas cuentas que acabamos de echar pueden escribirse de forma más compacta como: \[ V\simeq\sum_{i=1}^{2}\sum_{j=1}^{2}f(x_{i},y_{j})\times\Delta x\Delta y \]

Ahora pensemos: podemos hacer, como en la integral definida en funciones de una variable, que \(\Delta x\rightarrow0,\Delta y\rightarrow0\). Esto implicaría hacer que la base de los prismas sea “infinítamente” pequeña. Todo lo pequeña que queramos sin ser cero. Esto, a su vez, hará que el número de prismas sea infinítamente grande (\(n\rightarrow\infty).\) Es decir, el volumen exacto consistirá en

\[ V=\lim_{n\rightarrow\infty}\sum_{i=1}^{n}\sum_{j=1}^{n}f(x_{i},y_{j})\times\Delta x\Delta y \]

Y a esta operación, siguiendo la lógica aplicada a las sumas de Riemmann, la denominaremos “integral doble sobre el recinto \(R\)”

\[ \int\int_{R}f(x,y)\mathrm{d}x\mathrm{d}y \]

que, en este caso, será

\[ \int_{0}^{2}\int_{0}^{1}\left(8-x^{2}-y^{2}\right)\mathrm{d}x\mathrm{d}y \]

Ahora veremos las propiedades más destacables y cómo operar con ellas. Para, finalmente, calcular el volumen exacto de este problema.

La integral doble iterada en recinto rectangular

Vamos a practicar la mecánica de integrar respecto a una variable en una función de dos variables \(f(x,y).\) Por ejemplo: \[ \int_{1}^{y}\left(2x^{2}y\right)\mathrm{d}x \]

En esta integral, estamos considerando \(y\) como un número (constante), e integramos con respecto a \(x\). Entonces, tendremos que:

\[ \int_{1}^{{\color{red}y}}\left(2x^{2}{\color{red}y}\right)\mathrm{d}x=\left[\frac{2{\color{red}y}x^{3}}{3}\right]_{1}^{y}=\frac{2{\color{red}y}^{4}}{3}-\frac{2{\color{red}y}}{3} \]

Como ves, al integrar, tenemos que dejar la \(y\) constante y, por supuesto, al aplicar “Barrow”, el resultado quedará en función de \(y\). Podemos, de nuevo, hacerlo con respecto a \(y\) y dejando, por tanto, la \(x\) constante

\[ \int_{1}^{{\color{green}x}}\left(2{\color{green}x}^{2}y\right)\mathrm{d}y=\left[{\color{green}x}^{2}y^{2}\right]_{1}^{x}={\color{green}x}^{4}-{\color{green}x}^{2} \]

Fíjate cómo nos tiene que quedar dependiendo de \(x\), que es ahora la constante.

Esta idea de integración parcial puede utilizarse para integrar, convenientemente, una función de dos variables. Supongamos que \(1<x<2\) y \(0<y<3\) de la función \(f(x,y)=2x^{2}y.\) Es muy importante el orden en que se escriben los términos. Si empezamos por la \(x\), debemos escribir así:

\[ \int_{1}^{2}2x^{2}y\mathrm{d}x=2y\int_{1}^{2}x^{2}\mathrm{d}x=2y\left[\frac{x^{3}}{3}\right]_{1}^{2}=2y\left(\frac{8}{3}-\frac{1}{3}\right)=\frac{14}{3}y \]

Ahora, lo que hemos obtenido, lo integramos respecto de \(y\):

\[ \int_{0}^{3}\frac{14}{3}y\mathrm{d}y=\frac{14}{3}\left[\frac{y^{2}}{2}\right]_{0}^{3}=\frac{14}{3}\frac{9}{2}=21u^{3} \]

En realidad, esto es lo mismo que escribirla así:

\[ \int_{0}^{3}\int_{1}^{2}2x^{2}y\mathrm{d}x\mathrm{d}y \]

como ves, el orden de los límites de integración de cada signo integral está en consonancia con las diferenciales: \(\mathrm{d}x,\mathrm{d}y\). De esta forma, si quieres hacer la integral doble, puedes trabajar de esta forma:

\[ \int_{0}^{3}\int_{1}^{2}2x^{2}y\mathrm{d}x\mathrm{d}y=\int_{0}^{3}\underset{\mathrm{integro\:respecto\:a}\:x}{2y\left[\frac{x^{3}}{3}\right]_{1}^{2}}\mathrm{d}y=\int_{0}^{3}2y\left(\frac{8}{3}-\frac{1}{3}\right)\mathrm{d}y=\int_{0}^{3}\left(\frac{14}{3}y\right)\mathrm{d}y=\frac{14}{3}\left[\frac{y^{2}}{2}\right]_{0}^{3}=21u^{3} \]

Ahora bien, el orden no debería afectar al resultado, ¿no? Si la rehacemos cambiando el orden

\[ \int_{1}^{2}\int_{0}^{3}2x^{2}y\mathrm{d}ydx \]

como ves, modificamos tanto los límites de integración como las diferenciales:

\(\mathrm{d}x,\mathrm{d}y\). De esta forma, operando \[ \int_{1}^{2}2x^{2}\left[\frac{y^{2}}{2}\right]_{0}^{3}dx=\int_{1}^{2}9x^{2}dx=9\left[\frac{x^{3}}{3}\right]_{1}^{2}=9\left(\frac{8}{3}-\frac{1}{3}\right)=21u^{3} \]

Esto se conoce como el teorema de Fubini para integrales dobles en regiones rectangulares:

\[ \int_{c}^{d}\int_{a}^{b}f\left(x,y\right)\mathrm{d}x\mathrm{d}y=\int_{a}^{b}\int_{c}^{d}f\left(x,y\right)\mathrm{d}y\mathrm{d}x \]

Ejemplo: Seguimos con el cálculo del volumen anterior (que sólo habíamos aproximado) \[ \int_{0}^{2}\int_{0}^{1}\left(8-x^{2}-y^{2}\right)\mathrm{d}x\mathrm{d}y \]

Lo primero, e interesante, es que podemos descomponer los sumandos de la integral:

\[ \int_{0}^{2}\int_{0}^{1}\left(8-x^{2}-y^{2}\right)\mathrm{d}x\mathrm{d}y=\int_{0}^{2}\int_{0}^{1}8\mathrm{d}x\mathrm{d}y-\int_{0}^{2}\int_{0}^{1}x^{2}\mathrm{d}x\mathrm{d}y-\int_{0}^{2}\int_{0}^{1}y^{2}\mathrm{d}x\mathrm{d}y= \]

\[ \int_{0}^{2}8\left[x\right]_{0}^{1}\mathrm{d}y-\int_{0}^{2}\left[\frac{x^{3}}{3}\right]_{0}^{1}\mathrm{d}y-\int_{0}^{2}y^{2}\left[x\right]_{0}^{1}\mathrm{d}y=\int_{0}^{2}8\mathrm{d}y-\frac{1}{3}\int_{0}^{2}\mathrm{d}y-\int_{0}^{2}y^{2}\mathrm{d}y= \]

\[ 8\left[y\right]_{0}^{2}-\frac{1}{3}\left[y\right]_{0}^{2}-\left[\frac{y^{3}}{3}\right]_{0}^{2}=16-\frac{2}{3}-\frac{8}{3}=\frac{48-10}{3}=\frac{38}{3}=12.66u^{3} \]

(por cierto, no está nada mal la aproximación que hicimos con los cuatro prismas, ¿no?).

Ejercicio Haz la misma integral, pero cambiando los órdenes de integración. Deberías obtener lo mismo.

La integral doble cuando el recinto no es rectangular

Vamos a ampliar algo más el concepto. Supongamos, por ejemplo, que queremos buscar el volumen de una figura cuyo recinto no es rectangular, sino que tiene alguno de estos dos “perfiles” \[ a\leq x\leq b,g_{1}(x)\leq y\leq g_{2}(x) \]

\[ h_{1}(y)\leq x\leq h_{2}(y),c\leq y\leq d \]

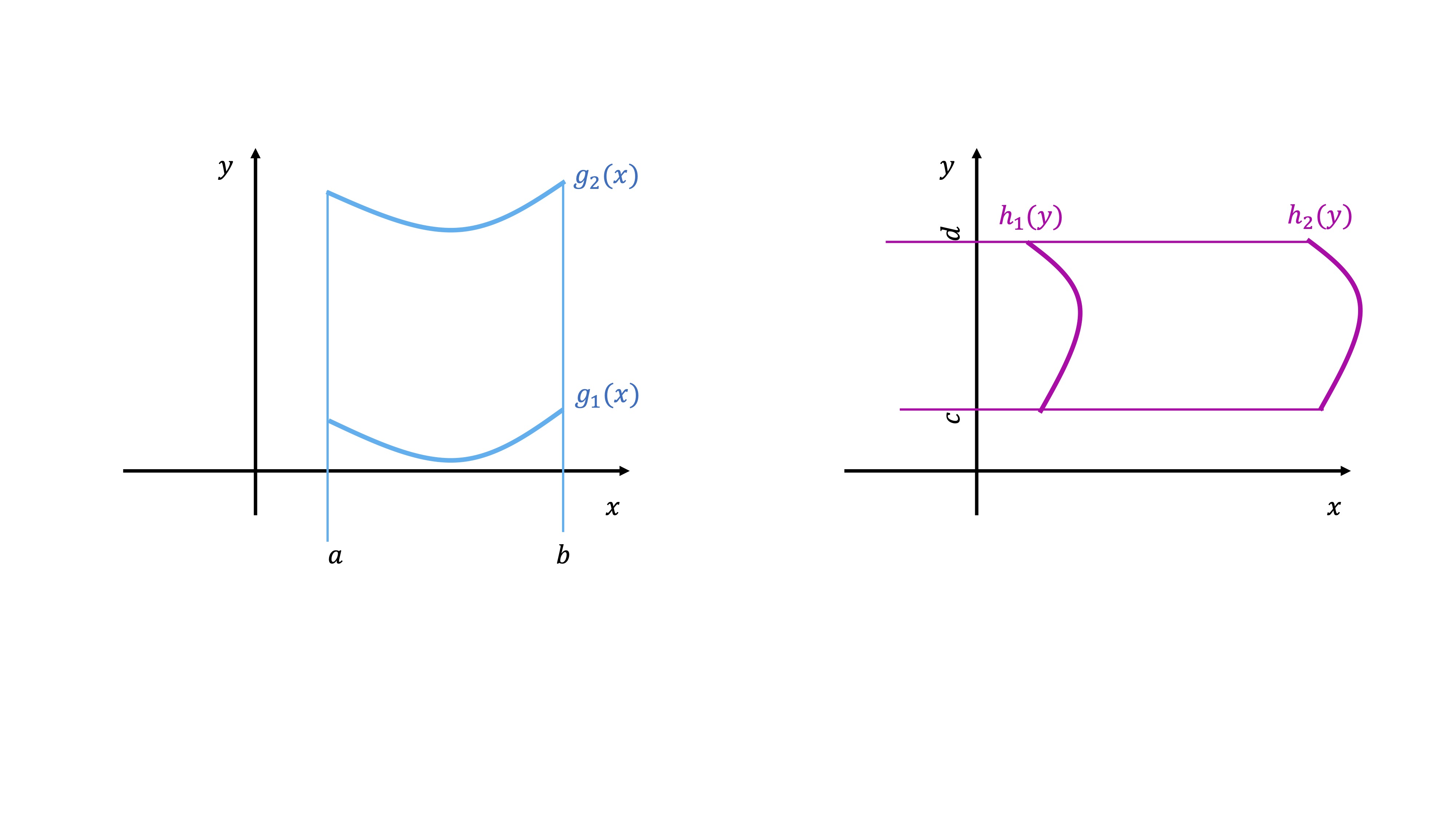
FIG7. posibles recintos de integración

Es decir, que uno de los ejes del recinto sea “función” del otro eje. Esto ocurre cuando el recinto de integraciómn no es rectangular. Veamos, cómo plantear la integral doble de la funci?n \(f(x,y)\)

**IDEA BÁSICA* Al plantear la integral doble, primero debes integrar con respecto a la variable cuyos límites de integración son funciones y, posteriormente, respecto a la variable cuyos límites de integración son números: si no , no te saldrá un volumen.

CASO 1 \(a\leq x\leq b,g_{1}(x)\leq y\leq g_{2}(x)\)

Debes formular la integral de tal forma que primero integres con respecto a la \(y\) (que es la que sus límites son función de \(x\)) y, después, integral con respecto a la \(x\), cuyos límites de integración son ya constantes. Es decir:

\[ \int_{a}^{b}\int_{g_{1}(x)}^{g_{2}(x)}f(x,y)\mathrm{d}y\mathrm{d}x \]

y ojo, aquí no se cumple el Teorema de Fubini de la manera inmediata que pensarás. Es decir, esto NO SE PUEDE HACER

\[ \int_{g_{1}(x)}^{g_{2}(x)}\int_{a}^{b}f(x,y)\mathrm{d}x\mathrm{d}y \]

ya que, al operar aquí el resultado te quedará como función de \(x.\) Después, veremos cómo se cambia el orden de integración en estos casos.

CASO 2 \(c\leq y\leq d,h_{1}(y)\leq x\leq h_{2}(y)\)

Debes formular la integral de tal forma que primero integres con respecto a la \(x\) (que es la que sus límites son función de \(y\)) y, después, integral con respecto a la \(y\), cuyos límites de integración son ya constantes. Es decir:

\[ \int_{c}^{d}\int_{h_{1}(x)}^{h_{2}(x)}f(x,y)\mathrm{d}x\mathrm{d}y \]

De la misma manera que en el caso 1, no se pueden cambiar los límites de integración de manera directa.

Ejemplo: obtén la integral doble de la funcion \(f(x,y)=x^{2}y\) sobre la región \[ R=\left\{ \left(x,y\right)\in\mathbb{R}^{2}:0\leq x\leq2,0\leq y\leq\frac{x}{2}\right\} \]

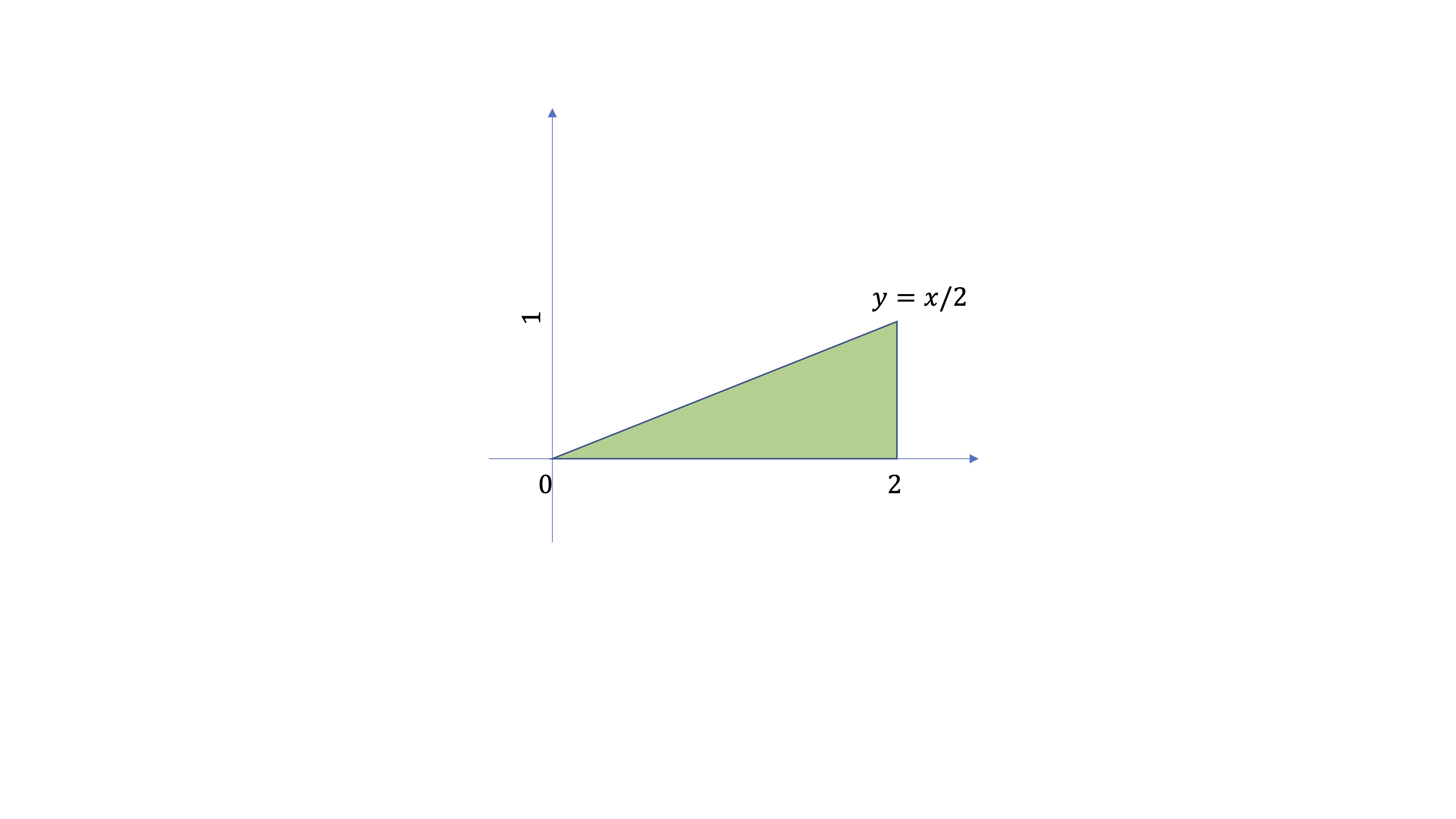
FIG8. El recinto de integración

Como puedes ver, en este caso, tal y como lo enuncian, la \(x\) “se mueve” entre dos valores, por lo que será la integral “exterior” (la última) es la \(y\) la que es función de \(x\). Entonces \[ \int_{0}^{2}\int_{0}^{x/2}x^{2}y\mathrm{d}y\mathrm{d}x \]

la cual, de nuevo, puede obtenerse como \[ \int_{0}^{2}x^{2}\left[\frac{y^{2}}{2}\right]_{0}^{x/2}\mathrm{d}x=\int_{0}^{2}x^{2}\frac{x^{2}}{8}\mathrm{d}x=\left[\frac{x^{5}}{40}\right]_{0}^{2}=\frac{32}{40}=\frac{2}{5} \]

En el gráfico de abajo puedes ver cómo, efectivamente, esos son los límites de integración.

• Usamos el esquema para ver cómo, si fijamos una variable, la otra toma valores que dependen de este
• En este caso, fijamos \(x\). La \(y\) vale 0 en el extremo inferior y en el superior, al estar en la frontera del recinto, vale \(x/2\), que viene dado por la fórmula del recinto.

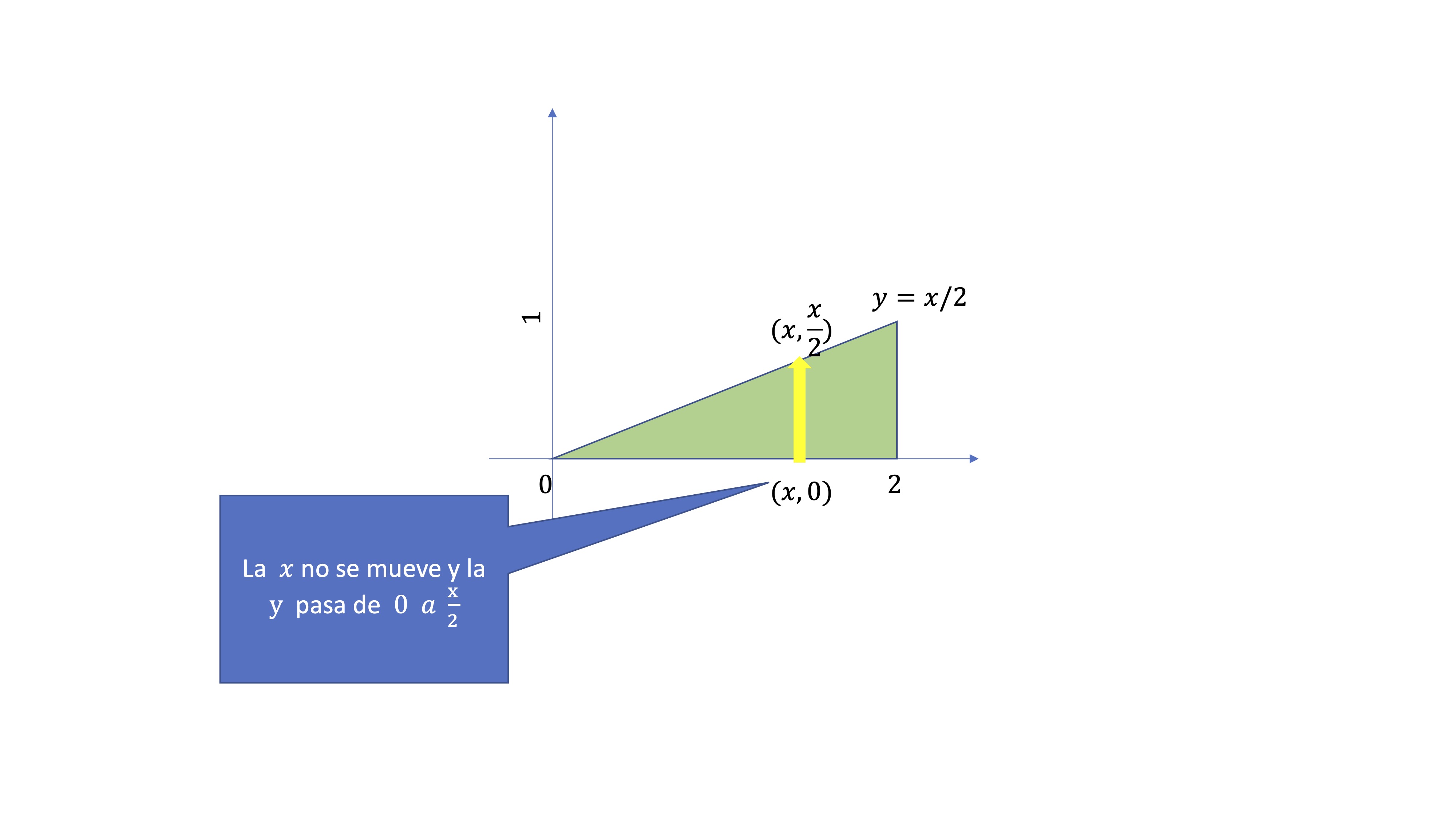
FIG9. Si dejamos la \(x\) constante

Ahora, lo que vamos a hacer es integrar primero con respecto a la \(y\) y después con respecto a la \(x\). Recuerda que no es tan fácil como cambiar los órdenes de integración. Ahora, necesitaremos tener \[ \int_{c}^{d}\int_{g_{1}(y)}^{g_{2}(y)}x^{2}y\mathrm{d}x\mathrm{d}y \]

Necesitamos, entonces, conocer \(g_{1}(y),g_{2}(y),c,d.\) Vemos, primeramente, que \(c=0,d=1\), en la FIG 8. Ya tenemos los valores entre los que fluctúa la \(y\). Deberemos, entonces, obtener

\[ \int_{0}^{1}\int_{g_{1}(y)}^{g_{2}(y)}x^{2}y\mathrm{d}x\mathrm{d}y \]

¿Quiénes son \(g_{1}(y),g_{2}(y)?\)

Piensa sobre este esquema:

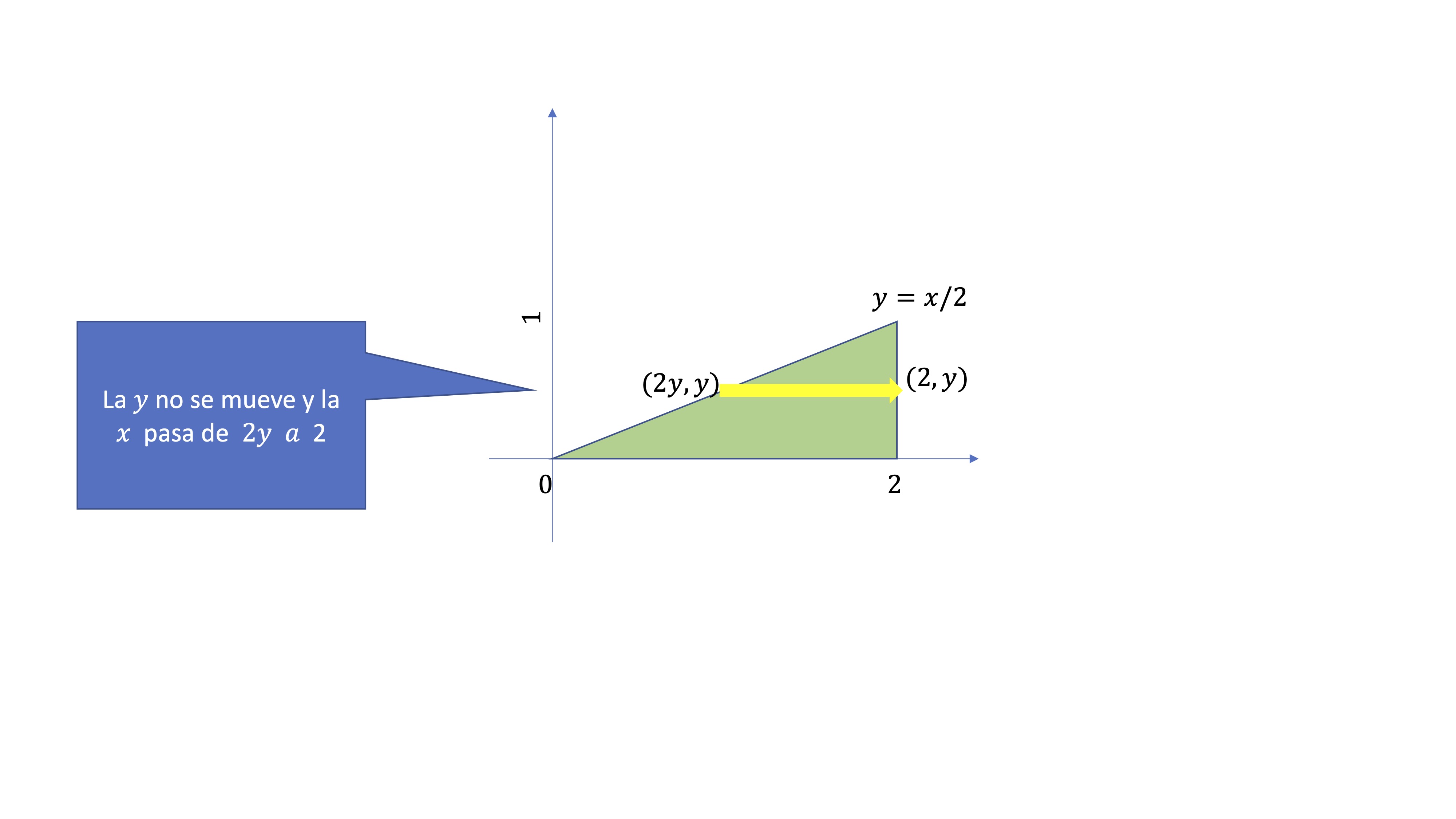Dejas fija la \(y\), porque ahora quieres ver cómo para cualquier \(y\), la \(x\) toma valores. Entonces, fíjate que en el extremo inferior, para un valor \(y\) dado, la \(x\), al ser \(y=x/2\), la \(x=2y\). Y en el extremo superior, la \(x\) siempre vale \(2\). Entonces, la integral doble será:

\[ \int_{0}^{1}\int_{2y}^{2}x^{2}y\mathrm{d}x\mathrm{d}y \]

Ejercicio: opera en esta integral para comprobar que obtienes el mismo volumen.

APÉNDICE: CÓMO SE LLEGÓ AL TFC

A continuación vamos a desgranar uno de los mayores éxitos del cálculo hace un par de siglos. La historia empieza suave pero, presta atención, acaba con una pelea.

Los Griegos

Uno de los problemas que más interesó en la antigüedad fue el cálculo de áreas (imagina que, en aquellos tiempos, eran muy importantes los terrenos, n o c o m o a h o r a). Una manera de poder calcular áreas de ciertas figuras no obvias (como podría ser un rectángulo, un cuadrado o un triángulo) era siendo exhaustivos. Es decir, rellenando la figura en cuestión con otras figuras cuya área es conocida y más fácil de obtener (rectángulos, ¿no?). De hecho, el método de la exhaución, consiste en inscribir y circunscribir rectangulitos en la figura de esta forma:

FIG1. La idea del método de Exhaución con un área que conocemos de sobra (en este caso será \(1/2\))

De tal forma que sabemos que el área que estamos buscando se encontrará entre la figura de la izquierda (con rectángulos inscritos) y la de la derecha (con rectángulos circunscritos). Claro, los inscritos aproximan el área por “defecto” y los circunscritos, por “exceso”. Por ejemplo, en este caso, vamos a poner algunos números. Nota que esta figura, que es un triángulo rectángulo, podemos verla como una función \(f(x)=x,\:x\in[0,1]\), es decir, la bisectriz del primer cuadrante acotada en el eje de las \(x\) por el intervalo \([0,1]\). Entonces, como hemos inscrito y circunscrito cuatro rectángulos, se nos presenta lo siguiente (FIG 2)

FIG2. Presta atención a los valores numéricos

Tendremos dos “sumas” que darán lugar a la aproximación del área que buscamos. La suma inferior, \(s\), que consiste en \(\frac{1}{4}\left(\frac{1}{4}+\frac{1}{2}+\frac{3}{4}\right)=0.375\), es decir, la base de cada rectángulo es \(\frac{1}{4}\) y los valores entre paréntesis son las diferentes alturas. Por otro lado, la suma superior, denotada con una ese mayúscula, \(S=\frac{1}{4}\left(\frac{1}{4}+\frac{1}{2}+\frac{3}{4}+1\right)=0.625\). Tenemos, por tanto, una primera aproximación al área del triángulo (que ya sabemos que es 0.5). La intuición nos dice, entonces, que será razonable rellenar con muchos más rectangulitos: todos los que podamos. Vamos a pensar ahora de manera algo más abstracta: Empecemos inscribiendo y circunscribiendo \(n\) rectángulos. Entonces, la base de cada rectángulo será \(\frac{1}{n}\).

FIG3. Partición para “\(n\)” rectángulos

Podemos, también, deducir las sumas inferiores y superiores: si nos damos cuenta, la altura de la suma inferior llegará hasta la altura del rectángulo \(n-1\)-ésimo y será \(\frac{h-1}{n}\). Entonces, la suma inferior consistirá en

\[ s=\frac{\text{1}}{n}\left(\frac{1}{n}+\frac{2}{n}+...+\frac{n-1}{n}\right) \]

mientras que la superior llegará al rectángulo \(n-\)ésimo y, por tanto, su suma será:

\[ S=\frac{1}{n}\left(\frac{1}{n}+\frac{2}{n}+...+\frac{n}{n}\right) \]

Donde hemos puesto \(\frac{n}{n}\) para remarcar la idea. Si te das cuenta, podemos reescribir las sumas como

\[ \begin{cases} s=\frac{1}{n^{2}}\left(1+2+...+n-1\right)\\ S=\frac{1}{n^{2}}\left(1+2+....+n\right) \end{cases} \]

y ahí un resultado muy famoso que nos permite escribir la suma de los \(N\) primeros números naturales (por ejemplo, \(1+2+3+...+N=\frac{N(N+1)}{2}).\) Esto nos lleva a que:

\[ \begin{cases} s=\frac{1}{n^{2}}\left(\frac{\left[n-1\right]n}{2}\right)=\frac{n-1}{2n}\\ S=\frac{1}{n^{2}}\left(\frac{n\left[n+1\right]}{2}\right)=\frac{n+1}{2n} \end{cases} \]

Por lo que, elige cuántos rectángulos quieres y tendrás una aproximación del área por exceso y por defecto. En la siguiente tabla, lo hacmos para distintas particiones (valor de \(n\))

\(n\)	\(s\)	\(S\)
4	\(0.375\)	\(0.625\)
10	\(0.45\)	\(0.55\)
100	\(0.495\)	\(0.505\)
1000	\(0.4995\)	\(0.5005\)

FIG4. Partición para “\(n\)” rectángulos

como ves, según se hace \(n\) todo lo grande que desees, ambas sumas se parecen cada vez más. Tanto que no es difícil calcular:

\[ s_{n\rightarrow\infty}=S_{n\rightarrow\infty}=\frac{1}{2}, \]

que es el área que buscábamos. ¡Bien!

Riemman: hace un siglo

Este matemático alemán se dedicó a darle forma al método de la exhaución y estudiar sus propiedades. Comprobó que a una función continua (o continua a trozos) acotada, se le puede calcular el área usando el método de la exhaución. Lo que hizo fue estudiar las propiedades de las funciones a las que se les podía calcular el área con este método:

• Funciones acotadas, en un intervalo,superiormente: es decir, debemos ser capaces de rellenar con rectangulitos y para ello, necesitamos un “tope”. Las funciones continuas en un intervalo son un caso particular de funciones acotadas que nos interesan en este curso

>- También se pueden integrar (en el sentido de Riemann) las funciones continuas a trozos, acotadas

¿Por qué? Como ves, se puede rellenar perfectamente con el “rectangulito”

Ojo, porque si no está acotada:

es decir, esta función:

\[ \begin{cases} f(x)=\frac{1}{x}\; \; si\;\; 0<x<5\\ f(x)=0 \; \; si \;\; x=0 \end{cases} \]

cuando nos acerquemos a cero \((x\rightarrow0)\) no vamos a poder meter el rectangulito, por lo que esta función no es integrable según Riemann.

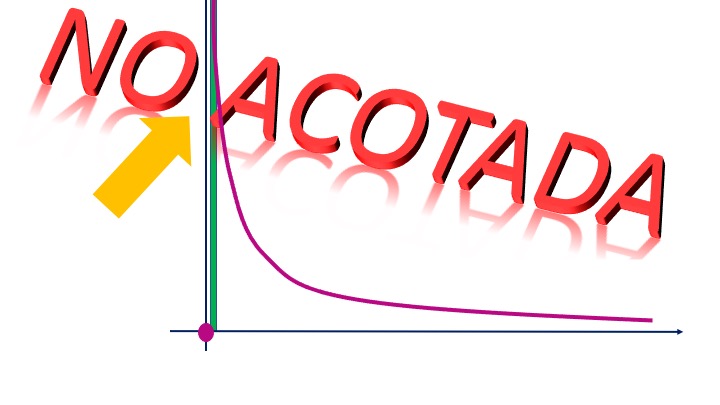
FIG9. (algo así)

Por cierto, la función, sin embargo, sería integrable en cualquier intervalo que no contenga al cero. Por ejemplo, \(f(x)=\frac{1}{x}\; si \; x\in(1,5)\).

Riemman, en definitiva, probó que se podía calcular el área comprendida entre las funciones anteriores continuas (o continuas a trozos) y acotadas y el eje \(x\) mediante las sumas de rectángulos (o trapecios) inscritos o circunscritos en la figura que forma la función. A esto se le llamó integral definida de Riemann. Básicamente dice que una función \(f(x)\) es Riemann integrable en un intervalo \((a,b)\) si las sumas inferiores y las superiores convergen en un único número cuando \(n\rightarrow\infty\) en la expresión:

\[ \sum_{n=0}^{\infty}\triangle x_{n}f(x_{n})\;x\in[a,b] \]

y, para abreviar, y no escribir tanto, se decidió denotar así al área \[ \sum_{n=0}^{\infty}\triangle x_{n}f(x_{n})\;,x\in[a,b]=\int_{a}^{b}f(x)\mathrm{d}x \]

Ahora bien ¿quién se atreve a calcular áreas usando sumas de Riemann?

Siglo XVII: La gran pelea del cálculo y el gran teorema

Por otro lado, y un siglo antes del trabajo de Riemann, Newton (UK) y Leibniz (Alemania) estaban trabajando en las grandes ideas de cálculo que ya has estudiado (generalmente la derivada aplicada a problemas físicos). El caso es que -según cuenta la historia- ambos llegaron al mismo resultado. Se dieron cuenta de que el cálculo de la integral como un área era una tarea trivial. Vamos a ver cómo:

Lo primero es definir la “función integral”. Si tenemos una función \(f\:[a,b]\rightarrow\mathbb{R}\), continua, definimos la función integral \(A(x)=\int_{a}^{x}f\) como aquella que te proporciona el área comprendida por la función y el eje de abscisas entre el punto \(a\) y un punto cualquiera \(x\in[a,b].\) Es decir, algo así, concretamente, \(A(x)\):

FIG10. Así obtenemos el área de una función continua \(A(x)=\int_{a}^{x}f\)

Avancemos un poco en el eje de las \(x\) y calculemos otra área, por ejemplo, \(A(x+\Delta x)\).

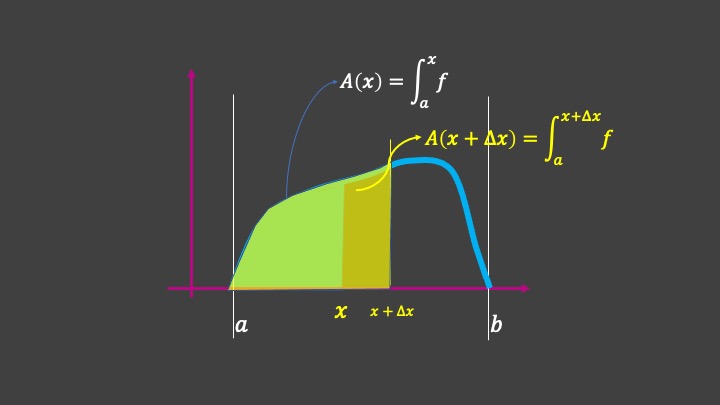
FIG10. \(A(x+\Delta x)=\int_{a}^{x+\Delta x}f\)

Ahora, fíjate bien en la FIG11, que vamos a analizar las diferencias entre ambas

FIG11. \(A(x+\Delta x)=\int_{a}^{x+\Delta x}f\)

La diferencia \(A(x+\Delta x)-A(x)\) es el trocito amarillo que, como ves, podemos aproximar por un rectángulo (como ya sabemos). De hecho, podemos tener un rectángulo inscrito y otro circunscrito \[ \Delta xf(x)\leq A(x+\Delta x)-A(x)\leq\Delta xf(x+\Delta x) \]

Ahora bien, si pasamos dividiendo \(\Delta x\), tendremos que

\[ f(x)\leq\frac{A(x+\Delta x)-A(x)}{\Delta x}\leq f(x+\Delta x) \]

Ahora, como sabemos, debemos hacer \(\Delta x\rightarrow0\) lo que nos lleva a

\[ f(x)\leq\lim_{\Delta x\rightarrow0}\frac{A(x+\Delta x)-A(x)}{\Delta x}\leq f(x) \]

y, como ya sabes, el límite \(\lim_{\Delta x\rightarrow0}\frac{A(x+\Delta x)-A(x)}{\Delta x}\) define una derivada : la de la función \(A\) en el punto \(x\). Es decir: resultado importante:

\[ A'(x)=f(x). \]

O, lo que es lo mismo,

Si \(f\) es continua en \([a,b]\), entonces, \[ A(x)=\int_{a}^{x}f \]

es derivable en cualquier punto \(x\in[a,b]\) y, además, \[ A'(x)=f(x), \]

para todo \(x\in[a,b]\)

Como verás, hemos omitido por comodidad en la integral \(\int_{a}^{x}f\) el término \(f{(x)\mathrm{d}x}\). En realidad, no es común omitirlo (salvo que no haya duda con respecto a qué variable estamos integrando). Eso sí, tenemos que llamar la atención en una cuestión de notación

OJO!

Cuando en la función integral tengas que poner en el límite superior el valor \(x\), entonces, deberás cambiar la letra de la función (queda muy raro, matemáticamente, que un mismo símbolo haga de número y de variable). Entonces, el Teorema Fundamental del cálculo, también dice:

\[ \frac{\mathrm{d}}{\mathrm{d}x}\int_{a}^{x}f(t)dt=f(x) \]

Este resultado muestra, por tanto, por qué decimos que calcular una integral consiste en buscar una primitiva. Algo que ya has hecho antes de manera mecánica. Es el vínculo entre los griegos y las matemáticas del siglo XIX. Nos queda un último paso. Como ya sabemos, una primitiva \(F(x)\) cumple que:

\[ F(x)=\int_{a}^{x}f(t)\mathrm{d}t+C \]

para \(x\in[a,b].\) De hecho, fíjate que \[ F(a)={\color{red}\int_{\color{red}a}^{\color{red}a}f(t)\mathrm{d}t}+C\equiv{\color{red}0}+C \]

puesto que en un punto no tenemos área. Esto nos dice que \(F(a)=C\), por lo que

\[ F(x)=\int_{a}^{x}f(t)\mathrm{d}t+C\Rightarrow F(x)=\int_{a}^{x}f(t)\mathrm{d}t+F(a) \]

de tal forma que, ¡sorpresa!

\[ F(x)-F(a)=\int_{a}^{x}f(t)\mathrm{d}t \]

y, particularizando en un intervalo concreto \(x\in[a,b]\)

\[ F(b)-F(a)=\int_{a}^{b}f(t)\mathrm{d}t, \]

A esta técnica se la conoce como “regla de Barrow” y nos dice que resolver una integral definida es facilísimo: sólo hay que buscar la primitiva y evaluarla en los extremos de los límites de integración y, finalmente, restarlos.

Llegar a este resultado no fue fácil y estuvo rodeado de polémica. Tanto Newton como Leibniz consiguieron llegar a conclusiones parecidas en fechas parecidas. Bueno, parece ser que Newton llegó antes, pero sin haberlo publicado. Leibniz, sin embargo, lo “descubrió” algo más tarde pero lo publicó con éxito. Estuvieron muy peleados (algo que afectó, de hecho, a las relaciones entre los científicos de Reino Unido y del continente europeo) y, a día de hoy, hay pruebas a favor de que ambos llegaron- cada uno por su lado- al mismo resultado. Newton está enterrado en la abadía de Westmister, con todos los honores. Sin embargo, Leibniz murió abandonado. Aunque hoy en día se usa su notación, ya que supo dotar al lenguaje del cálculo elegancia y concisión. Eso sí, a Newton se le otorgó el nombramiento de Sir.