Chapter 3 Simple Linear Regression
In this chapter, we’ll introduce the basic simple linear regression framework. You’ve probably seen this in your Business Statistics class, but we’ll begin with the basics. We continue to work with the CPS data from chapter 2, and we continue to explore this relationship between average wages (represented by \(Y\)) and years of schooling (represented by \(X\)).
3.1 The Simple Linear Regression Model
We begin with the conditional expectation function. Recall the definition from 2.3.1:
\[\begin{gather} E\left[Y|X=x\right] = \sum_{j=1}^m y_j \times Pr(Y = y_j | X = x) \tag{3.1} \end{gather}\]Now, we propose a linear parameterization for this function:
\[\begin{gather} E\left[Y|X=x\right] = \alpha_0 + \alpha_1 x, \end{gather}\]which we often abbreviate to
\[\begin{gather} E\left[Y|X\right] = \alpha_0 + \alpha_1 X. \tag{3.2} \end{gather}\]There are two ways to think about this. First, we are assuming that the sum in @ref(eq.CE) simplifies to a linear function of \(X\). This is usually an aggressive assumption, but there are some important benefits. Chief among these benefits is its simplicity, as we will soon see. Nonetheless, because we are assuming things, we call (3.2) a model. More specifically, it is called a population model, and it covers our population of interest. In this applicaton, our population is American workers in 1994.
The second way to think about our linear model is that we are specifying a linear approximation to the actual conditional expectation function in (3.1). In this view, the simple linear model seems less like an aggressive assumption and more like a modest approximation.
Any particular observation of \(Y\) equals the conditional average plus an error term:
\[\begin{gather} Y_i = \alpha_0 + \alpha_1 X_i + e_i. \tag{3.3} \end{gather}\]There are two mathematical facts about the error term, \(e\).
- \(E[e|X] = 0\).
- \(E[e] = 0\).
The first of these results is a direct implication of our modelling assumption in (3.2). To see this, we can take the conditional expectation of both sides of (3.3). To follow these steps, you need to know a few things.
- The expectation (or average) of a sum of two random variables equals the sum of their expectation: \(E[X + Y] = E[X] + E[Y]\), for example.
- Second, only \(Y\), \(X\), and \(e\) are random varialbes in (3.3), and \(\alpha_0\) and \(\alpha_1\) are parameters. Parameters are not random variables and they have no probability distribution. Parameters equal some number with probability 100%; we just don’t know wha that number is. Therefore, the expected value of a parameter is simply the parameter itself; \(E[\alpha_0] = \alpha_0\), for example.
- Third, when we condition the expectation on some random variable, that random variable is no longer uncertain. This means that \(E[X|X] = X\), for example.
With these ideas in mind, we can derive the implication that \(E[e|X]\) = 0:
\[\begin{align} E[Y|X] &= E[\alpha_0 + \alpha_1 X + e | X] \\ &= E[\alpha_0|X] + E[\alpha_1 X | X] + E[e|X] \\ &= \alpha_0 + \alpha_1 X + E[e|X] \end{align}\]And from (3.2), we can infer that \(E[e|X]\) must equal zero.
Furthermore, we can apply the law of iterated expectations and prove that \(E[e] = 0\):
\[\begin{align} E[e] &= E[E[e|X]] \\ &= E[0] \\ &= 0. \end{align}\]3.1.1 Quick Questions
- What is the Law of Iterated Expectations (LIE)? Can you come up with an example, or find one on the internets (😂), that help you understand LIE better?
- What is the difference between \(E[e]\) and \(E[e|X]\)? Does \(E[e] = 0\) imply that \(E[e|X] = 0\)?
3.2 Intepreting the Model
Before we get on to estimation, let’s explore an important feature of our linear regression model in (3.2):
A one unit increase in X is associated with an \(\alpha_1\) unit increase in the average value of Y.
Or, we could say:
A one unit increase in X is associated with an \(\alpha_1\) unit increase in Y, on average.
Thus, we call \(\alpha_1\) the marginal effect of X on Y. We can arrive at this observation in two ways. First, we could simply take an algebraic difference of the average value of \(Y\) whenever \(X\) equals \(x+1\) and \(x\):
\[\begin{align} E[Y|X = x+1] - E[Y|X = x] &= \alpha_0 + \alpha_1(x+1) - \left(\alpha_0 - \alpha_1(x)\right) \\ &= \alpha_1 \end{align}\]Alternatively, we could take the derivative of the conditional expectation with respect to \(X\):
\[\begin{gather} \frac{d E[Y|X]}{d X} = \alpha_1 \end{gather}\]When taking the derivative with respect to \(X\), everything that is not \(X\) is treated as a constant. In this introductory econometrics class, the only derivative formula you will need is the power rule.
Remember that the derivative provides the slope of the conditional expectation function at various possible values of \(X\). Since our conditional expectation function is a straight line, the slope is constant and does not vary (or depend on) the value of \(X\). Generally, however, the derivative might vary with \(X\), and in that case it is an approximation to the discrete marginal effect of \(X\) on \(Y\). We’ll come back to this when we consider regression models that are nonlinear.
3.2.1 Quick Questions
- We often shorten the marginal effect statement to “a one unit increase in \(X\) is associated with an \(\alpha_1\) unit increase in Y.” Why would it be wrong to take this–the omission of “average”–literally?
- What is the power rule from Calculus?
3.3 Estimating the Regression Model
Now, we take up the issue of estimating (3.3). Estimation involves using a sample of data from the population to obtain estimates of the parameters, \(\alpha_0\) and \(\alpha_1\). One method of estimation involves choosing these two parameters so that the sample analogues of the two mathematical facts about \(e\) above are satisfied as closely as possible. This is called the method of moments estimator.
However, the more common approach, and the one we take here, is called ordinary least squares (OLS). We begin by labeling our estimates with “hats”: \(\hat{\alpha}_0\) and \(\hat{\alpha}_1\) represents our estimates of \(\alpha_0\) and \(\alpha_1\), respectively. Then, we define predicted \(Y\) and the residual:
\[ \hat{Y}_i = \hat{\alpha}_0 + \hat{\alpha}_1 X_i \\ \hat{u}_i = Y_i - \hat{Y}_i \]
Residuals are also known as predicted errors. The OLS strategy involves picking \(\hat{\alpha}_0\) and \(\hat{\alpha}_1\) so that the residuals are as small in size as possible. More specifically, we choose our estimates to solve the following minimization problem:
\[\begin{gather} \min_{\hat{\alpha}_0, \hat{\alpha}_1} \sum_{i=1}^n \hat{u}_i^2 \tag{3.4} \end{gather}\]
While we won’t derive the solution to this minimization problem here, I’ll not that we can use standard multivariable Calculus methods to do so: Take the derivatives with respect to each parameter, set those derivates equal to zero, and solve. The parameters that minimize the sum of squared residuals (SSR) are,
\[\begin{equation} \begin{gathered} \hat{\alpha_1} = \frac{\sum_{i=1}^n \left(X_i - \bar{X}\right)\left(Y_i - \bar{Y}\right)}{\sum_{i=1}^n \left(X_i - \bar{X}\right)^2} \\ \hat{\alpha}_0 = \bar{Y} - \hat{\alpha}_1 \bar{X} \end{gathered} \tag{3.5} \end{equation}\]
3.3.1 Questions
- Here are the first six rows of the data. Using just these six observations, use the formulas in equations (3.5) to estimate the following regression model:
\[ AHE = \alpha_0 + \alpha_1 YRSEDUC + e \tag{3.6} \]
head(ch8_cps)## # A tibble: 6 × 8
## ahe yrseduc female age northeast midwest south west
## <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl>
## 1 12.5 14 0 40 1 0 0 0
## 2 19.2 12 0 30 1 0 0 0
## 3 17.5 12 0 29 1 0 0 0
## 4 13.9 12 0 40 1 0 0 0
## 5 7.21 14 1 40 1 0 0 0
## 6 7.60 12 1 35 1 0 0 0What is the estimated effect of one year of schooling on average hourly earnings?
Make a scatterplot with AHE on the vertical axis and YRSEDUC on the horiztonal axis. Add the fitted regression line to the plot.
Using your estimates, compute the standard error of the regression (SER):
\[ SER = \sqrt{\frac{1}{n-2} \sum_{i=1}^n \hat{u}_i^2}. \]
- In a sentence, what interpretation or meaning does the SER have?
3.4 Example: Regressing Wages on Schooling
Hopefully, you’ve successfully used (3.5) to compute ols estimates of (3.6) above. Whether you did this by hand, with Excel, or with R, you probably observed that this could be tedious with a larger sample of data. However, we can write computer programs to perform these steps. In R, we have the lm() function that estimates regression models. I use it now to estimate the following model with all 59485 observations from our dataset. This time, I am going to replace variable names in (3.6) with names that are more recognizable and easier to read aloud.
\[ Wage = \alpha_0 + \alpha_1 Schooling + e \tag{3.7} \]
est1 <- lm(ahe ~ yrseduc, data = ch8_cps)
summary(est1)##
## Call:
## lm(formula = ahe ~ yrseduc, data = ch8_cps)
##
## Residuals:
## Min 1Q Median 3Q Max
## -36.23 -8.92 -2.75 5.86 360.56
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) -14.77458 0.32319 -45.71 <2e-16 ***
## yrseduc 2.74270 0.02256 121.59 <2e-16 ***
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 14.12 on 59483 degrees of freedom
## Multiple R-squared: 0.1991, Adjusted R-squared: 0.199
## F-statistic: 1.478e+04 on 1 and 59483 DF, p-value: < 2.2e-16We can write out our estimated result in the following way,
\[ \widehat{Wage} = -14.77 + 2.74 Schooling \tag{3.8} \]
Here are a few immediate observations:
- We estimate that a one year increase in schooling is associated with a $2.74 increase in wages.
- The standard error of the regression is 14.12.
- The R-squared value is 0.2.
3.4.1 Quick Questions
- What is the predicted wage for someone with 13 years of schooling?
- What is the predicted wage for someone with 0 years of schooling? How do you make sense of a negative predicted wage?
- Read about the R-squared value in Stock and Watson (2019). What does it represent?
3.5 Visualizing the Estimated Model
A picture may help solidify our understanding about OLS estimation. Let’s create a scatterplot and add the fitted regression line in (3.8).
ggplot(ch8_cps, aes(x = yrseduc, y = ahe)) +
geom_point() +
geom_abline(intercept = alphas[[1]], slope = alphas[[2]] ) +
labs(x = "Years of Schooling",
y = "Average Hourly Earnings")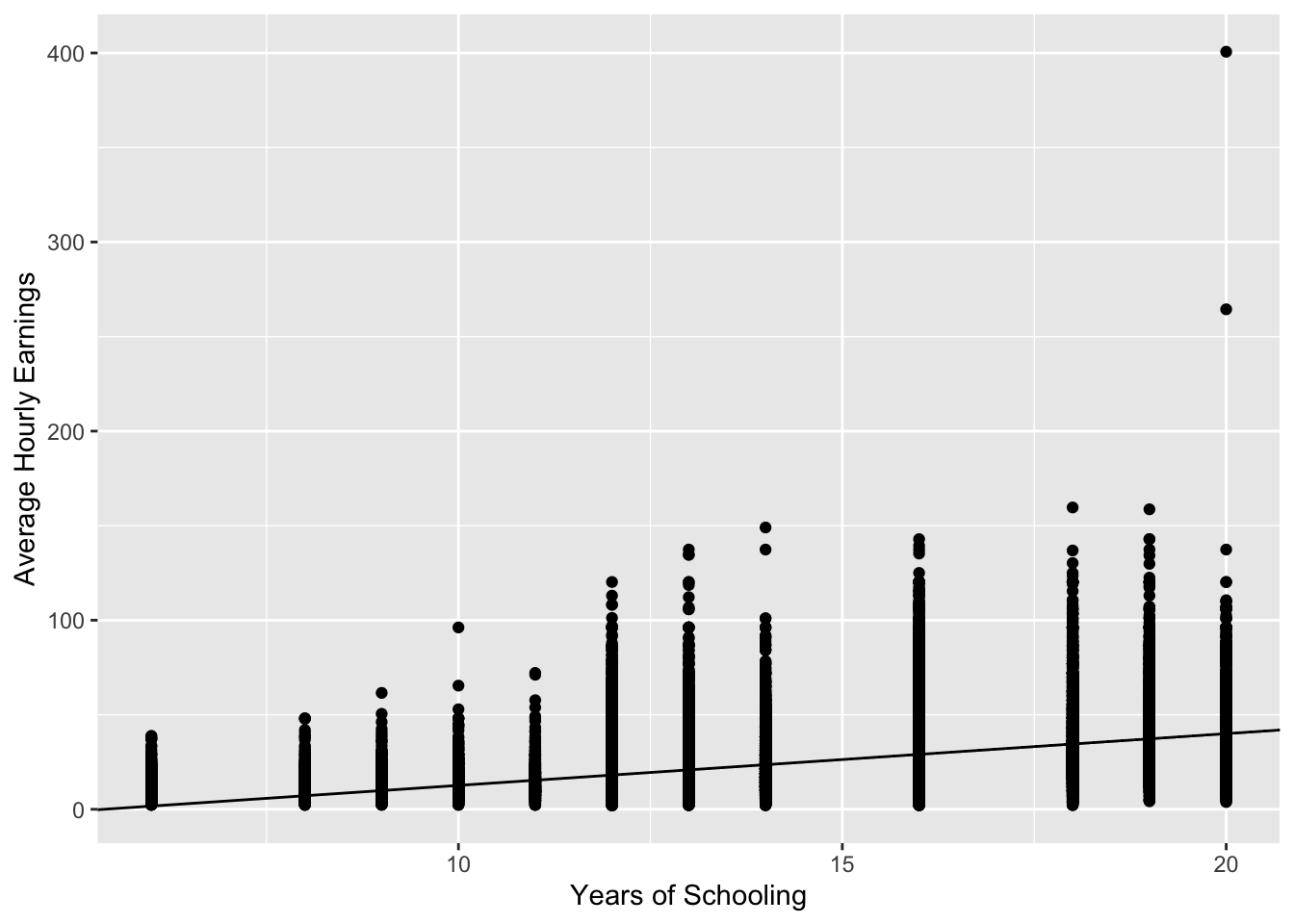
So far, this doesn’t appear to be a line that fits the data very well. However, that’s because there are so many observations, and years of schooling only takes on discrete values between 6 and 20. Therefore, the dots in the scatter plot overlap and it’s hard to tell how many are at (15 years, $20). We can remedy this a bit by slightly and somwhat randomly moving each dot just a bit so that they are not overlaying each other as much. We can do this with the geom_jitter() function. I also adjust the opaqueness by setting alpha equal to 0.1. In this image, it looks more plausibly that our regression line is the line of best fit. (Here, I also switch to the geom_smooth geometry, since it saves us from needing to input the intercept and slope.)
ggplot(ch8_cps, aes(x = yrseduc, y = ahe)) +
geom_jitter(alpha = .1) +
geom_smooth(method = "lm") +
labs(x = "Years of Schooling",
y = "Average Hourly Earnings") +
theme_bw()## `geom_smooth()` using formula 'y ~ x'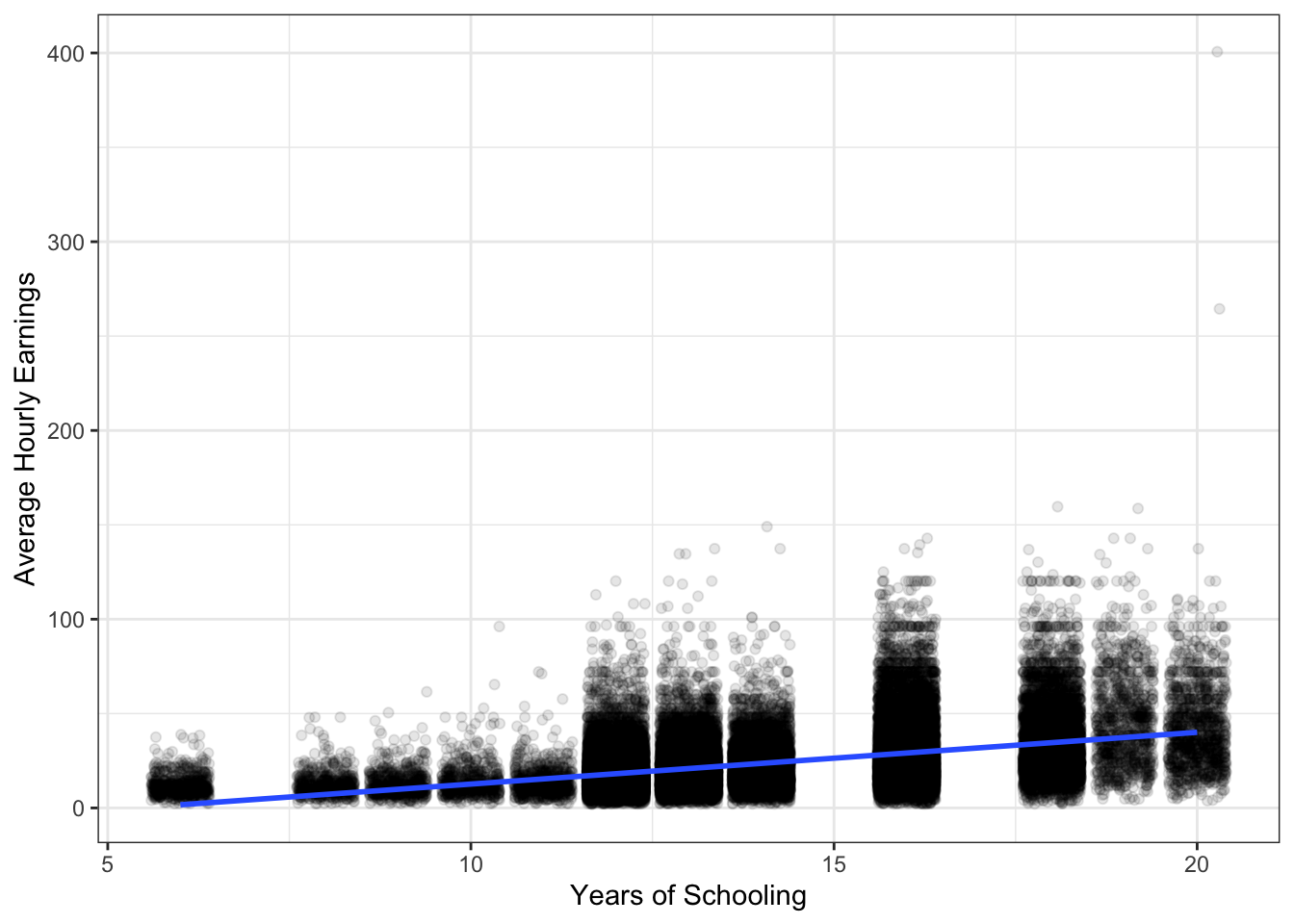
Figure 3.1: Earnings and Schooling
3.6 A Few Statistics
There are few terms and statistics that emerge from OLS. I’ll list them here,
\[\begin{gather} TSS = \sum_{i=1}^n (Y_i - \bar{Y})^2 \\ ESS = \sum_{i=1}^n (\hat{Y}_i - \bar{Y})^2 \\ SSR = \sum_{i=1}^n (Y_i - \hat{Y}_i)^2 \\ R^2 = 1 - \frac{SSR}{TSS} = \frac{ESS}{TSS} \end{gather}\]
TSS, or total sum of squares, measures the amount of total variation in the dpendent variable. (If we devided TSS by \(n-1\) and took the square root, then we’d have the sample standard deviation of \(Y\).)
ESS, or explained sum of squares, measures the amount of variation in the predicted dependent variable.
SSR, or sum of squared residuals, measures the amount of variation in the residuals. It is this oject that OLS makes as small as possible by choosing the right estimates, \(\hat{\beta}_0\) and \(\hat{\beta}_1\).
\(R^2\), or R-squared, is the fraction of total variation in the dependent variable that is explained by our model.
3.6.1 Quick Questions
Using the range, can you illustrate an analogous measure to \(R^2\)? In other words, try to show in Figure 3.1 the “explained range” and the “total range,” and then compare the two visually. Remember that range is simply the maximum observed value less the minimum observed value.
In a regression model, can we have a categorical variable as a regressor? Examples of categorical variables might be sex (male or female) or region-of-residence (perhaps northeast, southeast, midwest, or west).
3.7 Causality
So far, we’ve described \(\alpha_1\) as the associated effect of schooling on wages. That is because we want to avoid taking a causal interpretation until we have some confidence that we’ve identified the causal relationship between schooling and wages, which we’ll take up in the next chapter. For now, it will be helpful to think about the following questions.
3.7.1 Questions
- We’ve observed a positive relationship between schooling and wages in our sample of data. How might schooling cause wages to be higher?
- Suppose that schooling did not have any causal effect on wages. What else might explain this observed positive relationship?