Capítulo 4 Modelos con respuesta normal

En este capítulo se describirán los métodos y modelos estadísticos para analizar medidas respetidas cuando la variable respuesta sigue una distribución normal o gaussiana.

4.1 Respuesta Multivariante

4.1.1 Ecuación

$$\vec{y}_i = \vec{\mu} + \sum_{k=1}^K \beta_k x_{ki} + \vec{e}_i$$

Donde

• $\vec{y_i}=(y_{i1},\ldots,y_{iT})$ es el vector de medidas para el individuo $i$.

• $\vec{\mu}=(\mu_1,\ldots,\mu_T)$ es el vector con las medias de cada momento.

• $\vec{e_i} \sim N(\vec{0},\Sigma)$, donde $\Sigma$ es la matrix de covarianzas de los errores y tiene que ser la misma para todos los individuos. Su estructura, pero, puede ser cualquiera.

• $x_{ki}$ valor de la variable independiente $k$ del individuo $i$.

Observaciones

• Para ajustar este modelo los datos se disponen de forma horizontal.

• En este modelo los tiempos en que se toman las $T$ medidas tienen que ser los mismos para todos los individuos.

• Para estudiar la evolución en el tiempo se puede realizar un contraste polinómico en el vector de medias $\vec{\mu}$.

• Para comparar grupos de medidas, por ejemplo si se tienen cinco medidas, las dos primeras corresponden al tratamiento A y las otras tres al tratamiento B, se puede realizar un contraste lineal para comparar los dos tratamientos.

• Cuando hay un valor faltante en alguna medida, toda la fila del individuo se tiene que eliminar.

• Cada variable independiente, $x_{ki}$ es un único valor por individuo. O sea, que este modelo no contempla que las variables independientes sean de medidas repetidas. Si tuviéramos una variable que cambiara en el tiempo, se tienen que poner como variables diferentes (una para cada momento).

• Los factores contribuyen con tantas dummy variables como categorías menos uno en los términos $x_{ik}$.

• Los términos $x_{ik}$ pueden ser también interacciones entre variables, como el producto de sus términos.

Datos				Matriz de diseño ~ fumador + edad + sexo + edad:fumador
indiv	edad	fumador	sexo	fumadorEx	fumadorNunca	edad	sexomujer	fumadorEx:edad	fumadorNunca:edad
1	50	Ex	mujer	1	0	50	1	50	0
2	55	Actual	mujer	0	0	55	1	0	0
3	60	Actual	hombre	0	0	60	0	0	0
4	65	Nunca	mujer	0	1	65	1	0	65
5	62	Ex	hombre	1	0	62	0	62	0

4.2 Modelos Lineales Mixtos (LMM)

4.2.1 Ecuación

$$y_{ij} = \beta_{0i} + \sum_{k=1}^K \beta_{ki} x_{ijk} + e_{ij}$$

Donde $i$ representa al individuo, $j$ representa el momento (de uno hasta hasta el número de observaciones del individuo $i$),

• $\beta_{0i} \sim N\left(\beta_0, \sigma_{\beta_0}^2\right)$ es la constante del modelo aunque en general se supone aleatoria, o sea que tiene cierta varianza entre individuos y está centrada en la contaste $\mu$.

• $\beta_{ki} \sim N\left(\beta_k, \sigma_{\beta_k}^2\right)$: pendientes o coeficientes de las variables del modelo. Pueden ser aleatorias, o sea, variar entre individuos. Se denominan efectos aleatorios.

• $x_{ijk}$ valor de la $k$-ésima variable independiente del individuo $i$ en el momento $j$.

En general puede haber correlación entre la contante $\beta_{0i}$ y las pendientes $\beta_{ki}$. Y entre los efectos aleatorios entre ellos.

Por lo tanto, el vector formado por la constante y por los coeficientes (efectos aleatorios) se supone que sigue una distribución normal:

$$\vec{\beta}_i = (\beta_{0i},\beta_{1i},\ldots,\beta_{Ki})^t \sim N\left(\vec{\beta}, \Omega) \right)$$

• El vector formado por los errores de un individuo $\vec{e_i} \sim N(\vec{0},\Sigma_i)$, sigue una distribuión normal multivariante con una cierta matriz de covarianzas $\Sigma_i$ que no tiene porqué ser la misma ni del mismo tamaño para todos los individuos ya que no todos los individuos tendrán el mismo número de observaciones. Los errores son independientes de la constante aleatoria y de los coeficientes aleatorios.

Observaciones

• Para ajustar este modelo los datos se disponen de forma vertical.

• El modelo LMM es muy flexible y potente. Permite especificar efectos aleatorios con lo que evaluar la variabilidad de ciertos efectos o variables entre individuos sinó también permite especificar la correlación residual entre las distintas medidas repetidas en un mismo individuo.

• Cuando hay missings en una observación no hace falta eliminar las otras del mismo individuo, ya que cada fila aquí es una observación y no un individuo.

• La esperanza de la constante y coeficientes aleatorios $\vec{\beta}_i$ es la misma para todos los individuos, $\vec{\beta}$, y la matriz de covarianzas, $\Omega$, también.

• Si un coeficiente no es aleatorio, se puede notar como $\beta_{ki'} = \beta_{k'}$ en lugar de suponer que sigue una distribución normal. También se podría pensar que sigue una distribución “normal” con varianza cero.

• Los efectos fijos son la esperanza de los efectos aleatorios ($\beta_0, \beta_1, \ldots, \ldots, \beta_k$). Además, cuando un coeficiente no es aleatorio (tiene varianza cero) se denomina fijo directamente. Un coeficiente que multiplique a un término que no sea tiempo dependiente (p.e. la edad o el sexo), o a una interacción que incluya a un término constante en el tiempo (p.e. la interacción entre el sexo y el tiempo), tiene que ser fijo. Veremos un ejemplo más adelante.

• La presencia de efectos aleatorios inducen correlación entre medidas de un mismo individuo. Sin embargo, según que estructura de correlación sólo se puede conseguir definiendo también una estructura de correlación entre residuos no nula (no diagonal).

4.2.2 Casos particulares

4.2.2.1 Modelo con constante aleatoria

$$y_{ij} = \beta_{0i} + \beta_{1} t_{ij} + e_{ij}$$

Donde $\beta_{0i} \sim N(0, \sigma_{\beta_0})$, y $\beta_1$ es la constante del tiempo. En este caso se supone que el tiempo tiene un efecto lineal. Podríamos añadir un término cuadrático, cúbico, etc. si el efecto no fuera lineal.

$$y_{ij} = \beta_{0i} + \beta_{1} t_{ij} + \beta_{2} t_{ij}^2 + e_{ij}$$

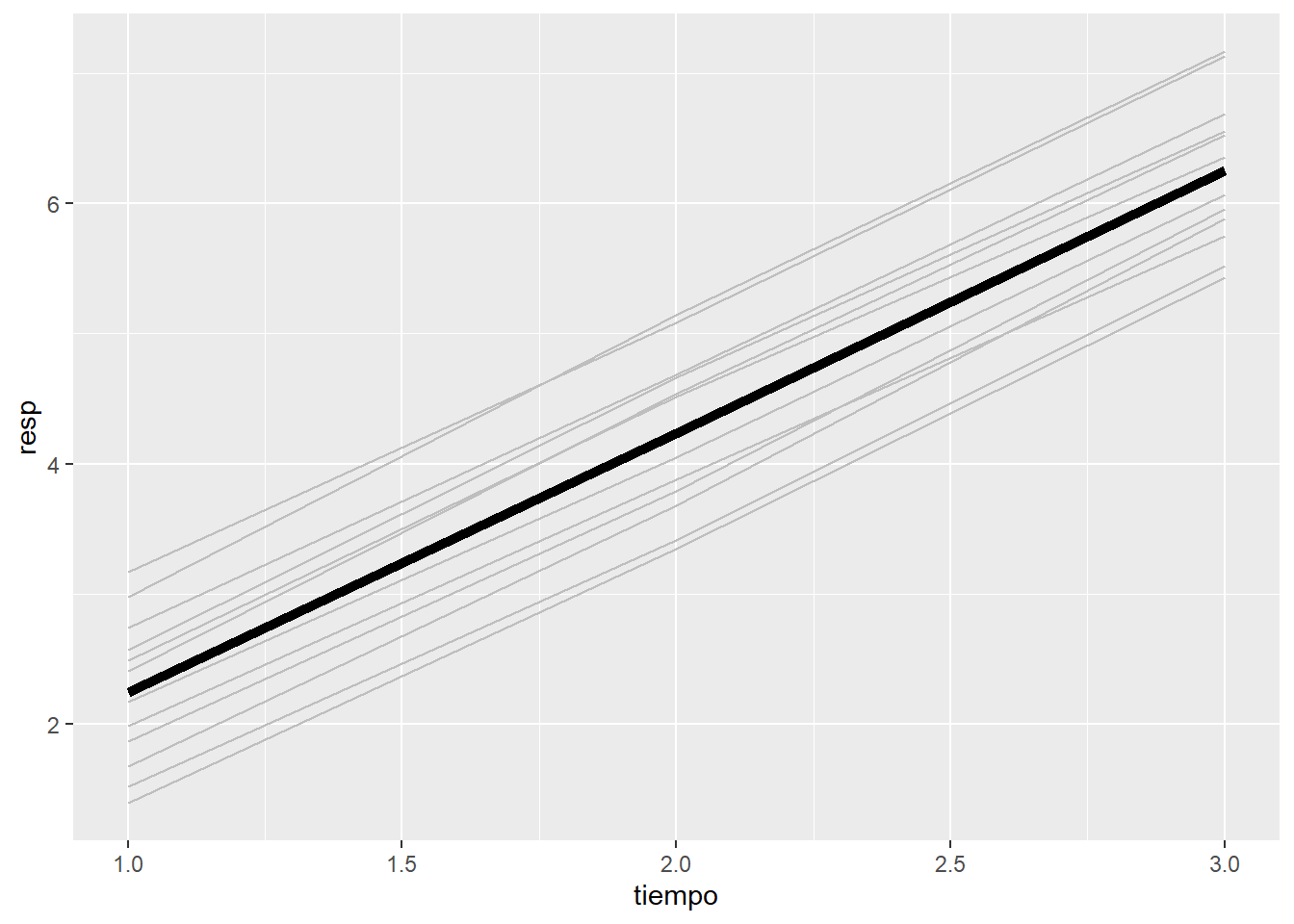
4.2.2.2 Modelo con pendiente y constante aleatoria

$$y_{ij} = \beta_{0i} + \beta_{1i} t_{ij} + e_{ij}$$

$\vec{\beta} = (\beta_{0i}, \beta_{1i})^t \sim N\left(\vec{0}, \Omega\right)$, donde

$$\Omega= \begin{pmatrix} \sigma_{\beta_0}^2 & \sigma_{\beta_0,\beta_1} \\ \sigma_{\beta_0,\beta_1} & \sigma_{\beta_1}^2 \end{pmatrix}$$

El término $\sigma_{\beta_0,\beta_1}$ es la covarianza entre la constante y la pendiente. Ésta en general puede no ser cero.

En este gráfico se observa primero que las pendientes son diferentes entre los individuos. Y además, que los individuos que empiezan de más arriba bajan más rápido y viceversa. Así pues, la correlación entre la constante y la pendiente es negativa.

4.2.3 Simplificación del modelo

Empezaremos con el modelo más general, o sea, sin asumir independencia de los residuos, con efectos aleatorios (todos los que se admitan) correlacionados.

En cuanto a los efectos fijos, se incluyrán también los máximos que se puedan, interacciones si es pertinente.

A partir de aquí se simplificará el modelo en el siguiente orden:

1. Estructura de correlación de los errores

Mediante el test de razón de verosimilitudes (LRT), se comparan las verosimilitudes de dos modelos.

Hay que ajustar el modelo mediante el criterio de máxima verosimilutud.

Los modelos tienen que estar anidados: la matriz de covarianzas de los errores de un modelo se pueda expresar como un caso particular de la del otro modelo. Por ejemplo, la matriz sin estructura sería la más general de todas, y la matriz de simetría compuesta sería un caso particular en que todas las correlación son iguales. No están anidadas las matrices con estructura MA(1) y una AR(1).

La simetría compuesta es un caso particular de matriz sin estructura.

$$\begin{pmatrix} 1 & \rho_{12} & \rho_{13} \\ \rho_{12} & 1 & \rho_{23} \\ \rho_{13} & \rho_{23} & 1 \\ \end{pmatrix} \Rightarrow \color{blue}{(\rho_{12}=\rho_{13}=\rho_{23} =\rho)} \Rightarrow \begin{pmatrix} 1 & \rho & \rho \\ \rho & 1 & \rho \\ \rho & \rho & 1 \\ \end{pmatrix}$$

La matriz que supone independencia entre los residuos es un caso particular de matriz de simetría compuesta.

$$\begin{pmatrix} 1 & \rho & \rho \\ \rho & 1 & \rho \\ \rho & \rho & 1 \\ \end{pmatrix} \Rightarrow \color{blue}{(\rho=0)} \Rightarrow \begin{pmatrix} 1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \\ \end{pmatrix}$$

Pero no se puede pasar de una AR(1) a una MA(1) ni viceversa

$$\begin{pmatrix} 1 & \rho & \rho^2 \\ \rho & 1 & \rho \\ \rho^2 & \rho & 1 \\ \end{pmatrix} \Rightarrow \color{blue}{(????)} \Rightarrow \begin{pmatrix} 1 & \frac{\theta}{1+\theta^2} & 0 \\ \frac{\theta}{1+\theta^2} & 1 & \frac{\theta}{1+\theta^2} \\ 0 & \frac{\theta}{1+\theta^2} & 1 \\ \end{pmatrix}$$

Heterocedesticidad:

La heterocedesticidad se produce cuando los parámetros de la matriz de covarianzas $\Sigma$ dependen de variables. Por ejemplo, del sexo o de la edad, etc, o de una combinación lineal de las variables (valor esperado).

Por ejemplo, que la varianza sea distinta según el sexo, mientras que la correlación sea la misma:

para hombres

$$\Sigma_{\text{H}} = \sigma_{\text{H}}^2 \begin{pmatrix} 1 & \rho & \rho^2 \\ \rho & 1 & \rho \\ \rho^2 & \rho & 1 \\ \end{pmatrix}$$ ,

y para las mujeres

$$\Sigma_{\text{M}} = \sigma_{\text{M}}^2 \begin{pmatrix} 1 & \rho & \rho^2 \\ \rho & 1 & \rho \\ \rho^2 & \rho & 1 \\ \end{pmatrix}$$

También podríamos definir las varianzas (diagonal de $\Sigma$), en función del tiempo.

Veremos como es posible modelizar diferentes varianzas distintas entre grupos de individuos con la función lme de R que se describirá en esta sección.

2. Elección matriz covarianzas de los efectos aleatorios

Se puede simplificar el modelo considerando que la correlación entre los efectos aleatorios es cero. Es decir, H$_0$ postula que la matriz $\Omega$ es diagonal, mientras que la H$_1$ se asume que las correlaciones pueden ser no nulas.

Como la matriz diagonal es un caso particular de la matriz general, en que las correlaciones son cero se puede aplicar el test de razón de verosimilitudes.

3. Varianzas de los efectos aleatorios

La hipótesis nula para contrastar los factores de efectos aleatorios es que su varianza es igual a cero. Por ejemplo para la constante aleatoria:

$$\begin{array}{l} H_0: \sigma_{\beta_0}^2 = 0 \\ H_1: \sigma_{\beta_0}^2 > 0 \end{array}$$

Hay diferentes técnicas estadísticas para contrastar estos tests, pero no son estándard. El problema es que la varianza de una distribución normal no puede ser cero, por lo tanto la hipótesis nula está fuera del espacio parametrico (“beyond boundary”). Existen, pero, algunas herramientas en R que lo realizan mediante técnicas de remuestreo (“bootstrap”). Éstas son complejas desde el punto de visto teórico y no se explicarán en este curso..¹ Otra alternativa es usar índices como el AIC o BIC (cuanto más bajo mejor), que proporciona la función anova en la comparación de dos modelos: uno considerando el coeficiente como aleatorio ($\beta_{ik}$) el otro considerando el coeficiente como fijo ($\beta_{k}$).

4. Efectos fijos

Una vez escogida la estructura de covarianzas de los efectos aleatorios, de los errores, y qué efectos son aleatorios (contraste sobre sus varianzas), vamos a contrastar la significación de los efectos fijos:

Para ello, se puede usar el test de Wald para testar un único parámetro:

$$\begin{array}{l} \text{H}_0: \beta_1 = 0\\ \text{H}_1: \beta_1 \neq 0 \end{array}$$

o LRT para testar más de un parámetro a la vez, por ejemplo las dummies de un factor de más de dos categorías:

$$\begin{array}{l} \text{H}_0: \beta_1 = \beta_2 = 0\\ \text{H}_1: \text{alguno diferente de 0} \end{array}$$

4.2.4 Validación del modelo

Una vez simplificado y seleccionado el modelo, hay que validarlo.

De todas las premisas a comprobar en este curso nos limitaremos a las asumciones sobre los residuos. Para ellos se realizarán dos gráficos:

• Residuos estandarizados vs valores predichos: en este gráficos debería aparecer una nube de puntos uniformemente distribuida sin ninguna tendencia. Ésto nos indicaría que no nos hemos dejado ninguna variable, o ningún término cuadrático o cúbico del tiempo.

• QQ-norm: éste gráfico está pensado para comprobar la normalidad. Si los puntos se encuentran alrededor de la diagonal sin seguir ningún patrón, dará evidencia de que los residuos siguen una distribución normal

Hay otras premisas que se deberían comprobar, como por ejemplo la normalidad de los efectos aleatorios. Pero, por su complejidad, no se verá en este curso.

4.2.5 Función lme

Para ajustar los modelos lineales mixtos usaremos la función lme del paquete nlme. Esta función permite incorporar efectos aleatorios, así como especificar la estructura de la matriz de correlaciones de los residuos.

Para usar esta función, los datos deben estar en formato horizontal. No hace falta que haya el mismo número de medidas para cada individuo.

La variable respuesta debe seguir una distribución normal.

library(nlme)

?lme

Los argumentos más importantes de la función lme

• fixed:

Fórmula de la forma

respuesta ~ var1 + var2 + var3

La constante se presupone que está y no hace falta escribir 1+. La sintaxis es la misma que para el “formula environment” de otras funciones estándard como lm para regresión lineal ordinaria (los términos van separados con +, las interacciones se especifican con :, etc.). A la izquierda de ~ se especifica la variable respuesta.

• random:

 ~ var1 + var2 + ... + varK | indiv

sin ninguna variable a la izquierda de ~, donde indiv es la variable sujeto y var1, var2, … varK son las variables con coeficiente aleatorio. Por defecto se supone que la constante está incluida.

Si se desea que la constante no sea aleatoria ~ var1 + var2 + ... + varK - 1 | indiv.

Si sólo la constante es aleatoria, ~ 1 | indiv

Para especificar que la matriz $\Omega$ es diagonal se usa la función pdDiag

list(indiv = pdDiag( ~ var1 + var2 + ... + varK))

Si los individuos estuvieran anidados en clusters aleatorios: ~ var1+..| clusters / indiv

• correlation

Para especificar la forma de la matriz de covarianzas de los residuos $\Sigma_i$.

Estructura	Valor
Residuos independientes (valor por defecto)	NULL
Simetría compuesta	corCompSymm()
AR(1)	corAR1()
ARMA(p,q)	corARMA(p,q)
ARMA(p,q)	corARMA(p,q)
Sin estructura	corSymm()

Para más estructuras: ?corClasses

• weights

Este argumento modeliza la varianza, $\sigma^2$ según variables

Por defecto, NULL que supone que la matriz de covarianzas es la misma para todos los individuos.

Expresión	Función
varPower()	$\sigma^2(x) = |x|^{2*\theta}$
varFixed()	$\sigma^2(x) = |x|$
varConstPower()	$\sigma^2(x) = (\theta_1 + |x|^{\theta_2})^2$

En lugar de una variable, puede ser el valor predicho:

varFixed(fitted(.))

Para ver más ?varClasses

• method

Método usado para estimar los parámetros

• REML (“REstricted Maximum Likelihood”): método por defecto y que proporciona estimaciones no sesgadas de los parámetros.

  • ML (“Maximum Likelihood”): proporciona estimaciones de los parámetros sesgados.

Para usar el LRT, o calcular los índices AIC o BIC se usa el método ML. La función anova que compara dos modelos por AIC, reajusta los modelos automàticamente bajo el método ML si han sido estimados con REML.

4.3 Técnica de la suma de cuadrados

Ésta técnica sólo permite analizar cierto tipo limitado de diseños: balanceados, sin variables independientes cuantitativas (covariables), sólo cualitativas o factores y con un número limitado de factores que tienen que estar cruzados (no anidados).

4.3.1 Diseño 1W+1S

Cuando el diseño es balanceado (mismo número de individuos por grupo), las medidas son las mismas y para todos los individuos, y no hay covariables, se puede usar la técnica de suma de cuadrados o tabla ANOVA.

En el contexto de los modelos lineales para ANOVA, para este diseño la ecuación del modelo sería

$$y_{ijk} = \mu + \alpha_i + \beta_j + \alpha\beta_{ij} + \pi_{k(i)} + e_{ijk}$$

Donde

• $\mu$ es la constante del modelo,
• $\alpha_i$, son los efectos del grupo o tratamiento
• $\beta_j$, son los efectos del tiempo
• $\alpha\beta_{ij}$ es la interacción del tiempo con el grupo
• $\pi_{k(i)}$ es el efecto aleatorio del individuo que está anidado al grupo
• $e_{ijk}$ son los errores

$\sum_{i=1}^a \alpha_i=0$, $\sum_{j=1}^b \beta_j=0$, $\sum_{i=1}^a \alpha\beta_{ij}=0, \forall j$, $\sum_{j=1}^b \alpha\beta_{ij}=0, \forall i$,

$\pi_{k(i)} \sim N(0, \sigma_{ind})$ $e_{ijk} \sim N(0, \sigma)$ indep

En este contexto se dice que el tiempo y la interacción tratamiento:tiempo son términos o componentes “intra sujeto” (within subject). Mientras que el grupo es un componente “entre sujeto” (between subject). Por lo tanto, se trata de un diseño 1W+1B.

Las técnicas clásicas de la tabla ANOVA y su inferencia són válidas siempre y cuando se cumpla la condició de esfericidad: simetría computuesta o también que la variancia de la diferencia entre dos medidas es constante. Para comprobar la condición de esfericidad se puede aplicar el test de Mauchly.

Si no se cumplela condición de esfericidad, hay que corregir los grados de libertad de los términos “intra sujetos” de la tabla ANOVA y se recalculan sus p-valores. Hay dos métodos para corregir los grados de libertad: método “Huynh and Feldt” (H-F) y el método “Greenhouse-Geisser” (G-G) .

4.3.2 Diseño 1W

Si en el diseño no hay grupos, luego el modelo se simplifica a un diseño de un factor “intra sujeto” (1W)

$$y_{ij} = \mu + \beta_i + \pi_{j(i)} + e_{ij}$$

En ambos casos, tanto en el diseño en que tenemos grupos como en el que no, no nos interesa evaluar el efecto del individuo; ya sabemos que hay variabilidad entre ellos. Veremos en un ejemplo como el paquete ez que se usará para esta técnica de suma de cuadrados omite los resultados sobre el factor aleatorio individuo.

4.3.3 Función ezANOVA

Para ajustar los modelos de medidas repetidas balanceados mediante la técnica de suma de cuadrados existe la función ezANOVA del paquete ez

library(ez)

?ezANOVA

Tanto la corrección por H-F o G-G, como el test de esfericidad de Mauchly estan implementados en el package ez de R, y se printan por pantalla en los resultados.

Para visualizar los resultados, se usará la función ezPlot. Más adelante en esta sección se verá en un ejemplo.

Los datos deben estar en formato vertical. Es obligatorio que las variables estén en una base de datos (“data.frame”).

• data: base de datos donde se encuentran las variables ANT[ANT$error==0,]

• dv: variable respuesta o variable dependiente

• wid: variable individuo

• within: factor o factores “intra sujeto”. Típicamente en este argumento se espedificará el tiempo. Si se especifica más de un factor, éstos deben estar cruzados y se escribirá .(var1,var2).

• between: factor o factores “entre sujetos”. Si no hay ningún factor “intra-sujeto” se deja a NULL. Como en el argumento within, si hay más de un factor “entre sujetos”, éstos deben estar cruzados y se escribirá .(var1,var2).

Observaciones:

• La variable respuesta y los factores deben escribirse sin comillas.
• Los factores “intra”, “entre” y el sujeto deben estar en format factor.
• El factor individuo debe tener tantos niveles como individuos.
• Aunque es en teoría la función permite covariables (variables independientes contínuas), la implementación está en versión “beta”.
• Los factores deben ser todos de efectos fijos, a excepción del individuo.

4.4 Ejemplos

Vamos a ver algunos ejemplos que se analizarán mediante las técnicas que se acaban de describir.

4.4.1 Ejemplo 1

En la base de datos “Ejemplo_1W.csv” se tienen los datos de un diseño con 12 individuos en los que se toman los niveles en sangre de un cierto parámetro lipídico. Para cada invidivuo se miden los niveles a 1, 2 y 3 horas.

datos <- read.csv2("./datos/Ejemplo_1W.csv")
datos

   indiv tiempo medida
1      1      1   39.4
2      2      1   33.5
3      3      1   27.1
4      4      1   30.9
5      5      1   32.2
6      6      1   26.6
7      7      1   28.5
8      8      1   37.7
9      9      1   35.7
10    10      1   30.6
11    11      1   24.4
12    12      1   38.8
13     1      2   65.3
14     2      2   53.2
15     3      2   42.3
16     4      2   52.3
17     5      2   57.4
18     6      2   42.5
19     7      2   37.5
20     8      2   56.0
21     9      2   50.3
22    10      2   43.2
23    11      2   39.9
24    12      2   56.1
25     1      3   68.6
26     2      3   54.3
27     3      3   41.3
28     4      3   45.7
29     5      3   53.5
30     6      3   36.7
31     7      3   36.4
32     8      3   55.3
33     9      3   46.4
34    10      3   38.3
35    11      3   37.3
36    12      3   52.6

4.4.1.1 Exploración de los datos

library(ggplot2)
p <- ggplot(data = datos, aes(x = tiempo, y = medida, group = indiv))
p + geom_line(col="grey") + stat_summary(aes(group = 1),
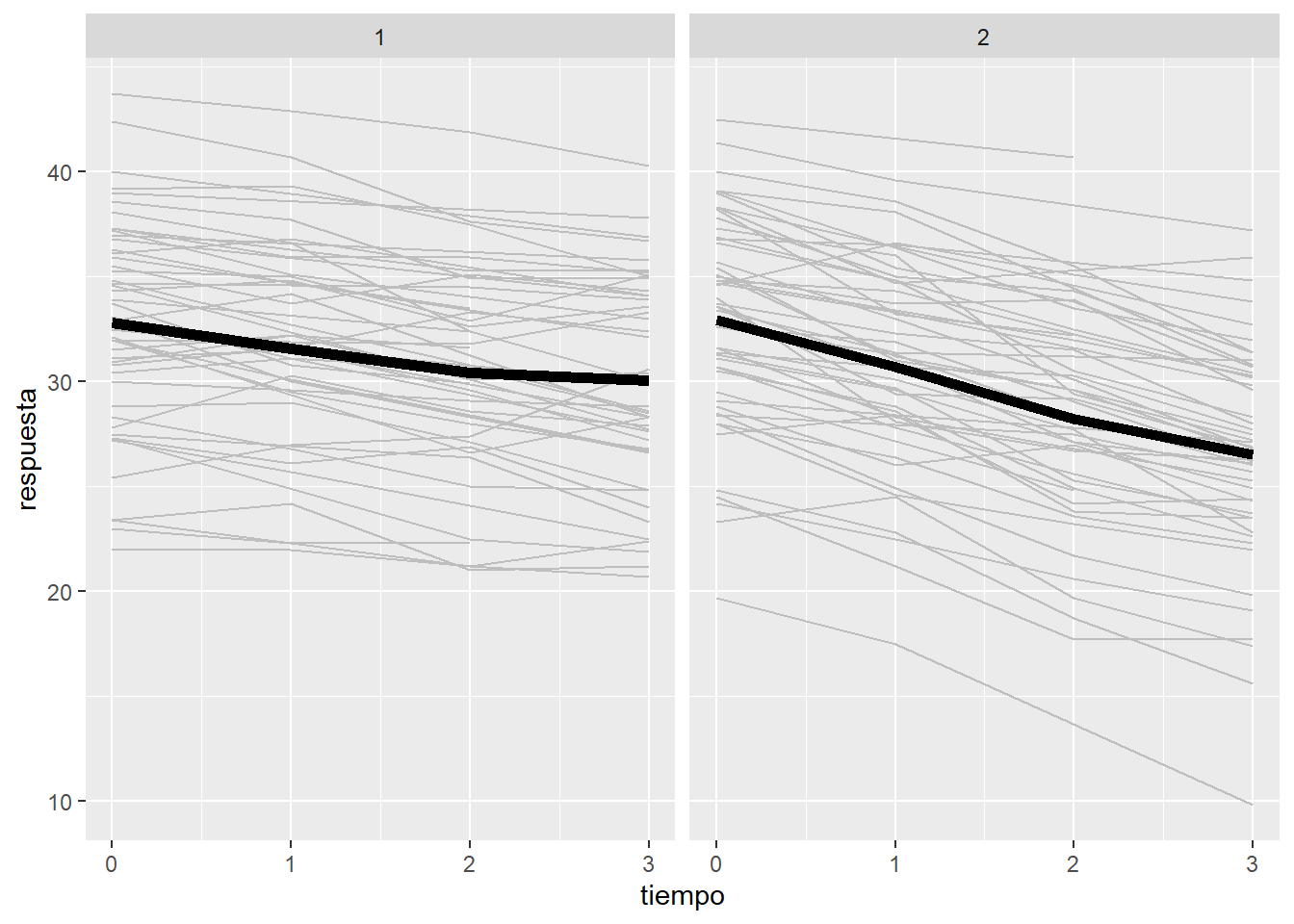
    geom = "line", fun = mean, size=2)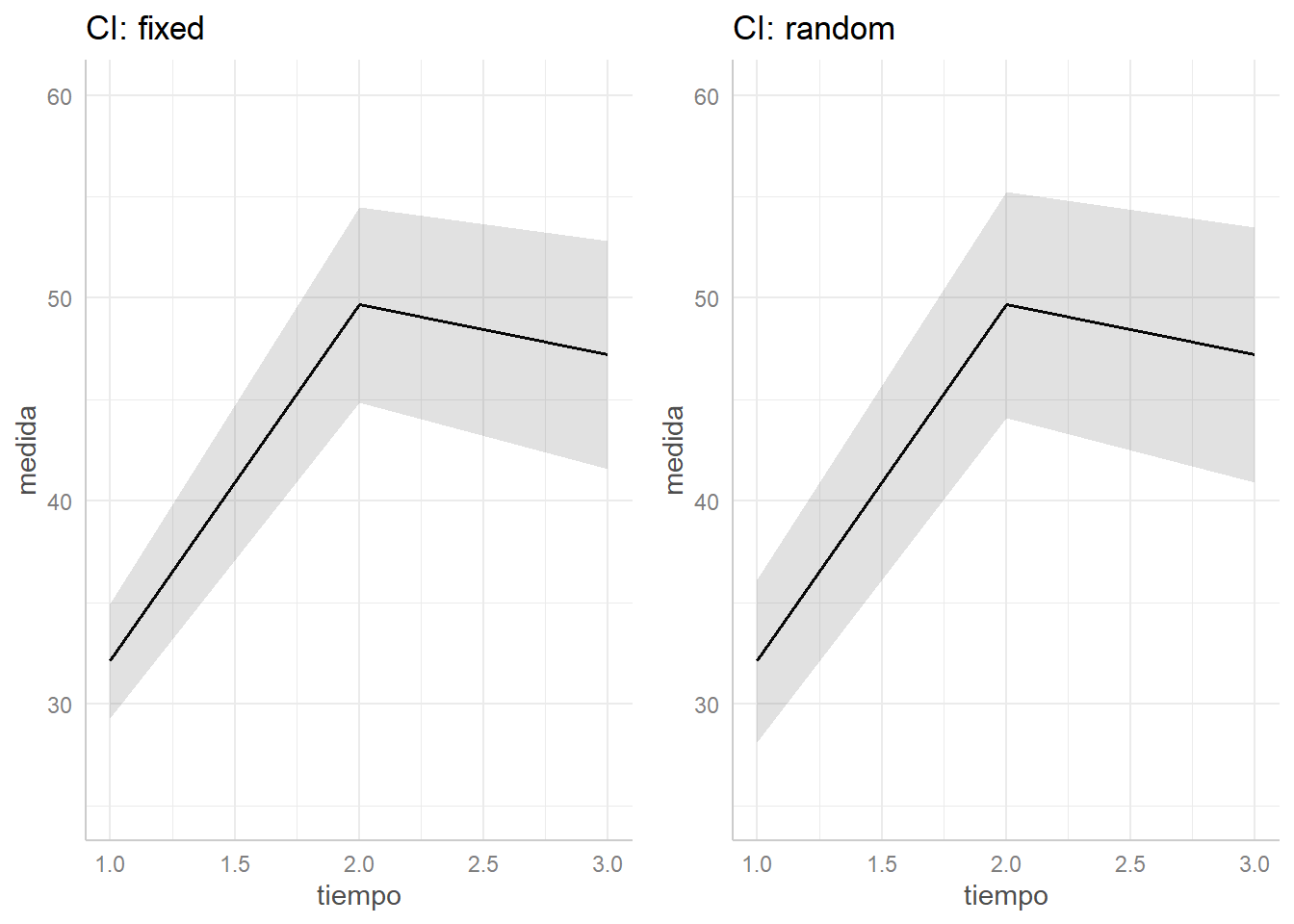

Cada línea representa a un individuo, mientras que la línea más gruesa es el promedio de los 12 individuos.

Vemos como el efecto del tiempo no es del todo lineal. Además las líneas están bastante separadas indicando variabilidad entre los individuos.

4.4.1.2 Modelo de respuesta multivariante

Para analizar los datos mediante el modelo de respuesta multivariante hay que disponer los datos de forma horizontal.

datosh <- reshape(data=datos, 
              direction="wide", 
              v.names=c("medida"), 
              times=1:3, 
              timevar="tiempo", 
              idvar="indiv")
datosh

   indiv medida.1 medida.2 medida.3
1      1     39.4     65.3     68.6
2      2     33.5     53.2     54.3
3      3     27.1     42.3     41.3
4      4     30.9     52.3     45.7
5      5     32.2     57.4     53.5
6      6     26.6     42.5     36.7
7      7     28.5     37.5     36.4
8      8     37.7     56.0     55.3
9      9     35.7     50.3     46.4
10    10     30.6     43.2     38.3
11    11     24.4     39.9     37.3
12    12     38.8     56.1     52.6

Para ajustar un modelo de regresión lineal con respuesta multivariante se puede usar la función lm. Y hay que poner la variable respuesta a la izquierda de ~ como una matriz de las tres variables (medida.1, medida.2 y medida.3):

respuesta <- as.matrix(datosh[,c("medida.1","medida.2","medida.3")])
modelo <- lm(respuesta ~ 1, data=datosh)
modelo

Call:
lm(formula = respuesta ~ 1, data = datosh)

Coefficients:
             medida.1  medida.2  medida.3
(Intercept)  32.12     49.67     47.20   

vcov(modelo)

                     medida.1:(Intercept) medida.2:(Intercept)
medida.1:(Intercept)             2.088308             3.049141
medida.2:(Intercept)             3.049141             6.033232
medida.3:(Intercept)             3.507273             6.775000
                     medida.3:(Intercept)
medida.1:(Intercept)             3.507273
medida.2:(Intercept)             6.775000
medida.3:(Intercept)             8.216970

summary(modelo)

Response medida.1 :

Call:
lm(formula = medida.1 ~ 1, data = datosh)

Residuals:
    Min      1Q  Median      3Q     Max 
-7.7167 -3.9667 -0.5667  4.0833  7.2833 

Coefficients:
            Estimate Std. Error t value Pr(>|t|)    
(Intercept)   32.117      1.445   22.23 1.72e-10 ***
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Residual standard error: 5.006 on 11 degrees of freedom


Response medida.2 :

Call:
lm(formula = medida.2 ~ 1, data = datosh)

Residuals:
    Min      1Q  Median      3Q     Max 
-12.167  -7.217   1.633   6.358  15.633 

Coefficients:
            Estimate Std. Error t value Pr(>|t|)    
(Intercept)   49.667      2.456   20.22 4.75e-10 ***
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Residual standard error: 8.509 on 11 degrees of freedom


Response medida.3 :

Call:
lm(formula = medida.3 ~ 1, data = datosh)

Residuals:
   Min     1Q Median     3Q    Max 
-10.80  -9.15  -1.15   6.50  21.40 

Coefficients:
            Estimate Std. Error t value Pr(>|t|)    
(Intercept)   47.200      2.867   16.47 4.25e-09 ***
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Residual standard error: 9.93 on 11 degrees of freedom

anova(modelo)

Analysis of Variance Table

            Df  Pillai approx F num Df den Df    Pr(>F)    
(Intercept)  1 0.98347   178.54      3      9 2.463e-08 ***
Residuals   11                                             
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Con el summary se contrasta si la media de cada momento por separado es igual a cero.

Con el print simplemente se reporta la media estimada para cada momento.

El estadístico de la tabla ANOVA “Pillai” tiene un rango de 0 a 1. Cuando el valor es próximo a uno hay más evidencia que el efecto es significativo. Es útil cuando las suposiciones del modelo no se cumplen.

El p-valor de (Intercept) de la tabla ANOVA contrasta la siguiente hipótesis

$$\begin{array}{l} H_0: \mu_1 = \mu_2 = \mu_3 = 0 \\ H_1: \text{alguna media es diferente de cero} \end{array}$$

que no es en realidad la hipótesis que nos interesaria contrastar que sería $H_0: \mu_1 = \mu_2 = \mu_3$

4.4.1.3 Suma de cuadrados

Para ajustar este modelo hay que usar los datos en disposición vertical. Además hay que convertir las variables tiempo e indiv a factor.

library(ez)
datos.ez <- datos
datos.ez$tiempo <- factor(datos.ez$tiempo)
datos.ez$indiv <- factor(datos.ez$indiv)

ezANOVA(data=datos.ez, dv=medida, wid=indiv, within=tiempo, detailed = TRUE)

$ANOVA
       Effect DFn DFd       SSn       SSd         F            p p<.05
1 (Intercept)   1  11 66546.801 1892.0589 386.88796 6.390053e-10     *
2      tiempo   2  22  2166.376  264.6244  90.05264 2.542699e-11     *
        ges
1 0.9686088
2 0.5011210

$`Mauchly's Test for Sphericity`
  Effect         W          p p<.05
2 tiempo 0.4433135 0.01712201     *

$`Sphericity Corrections`
  Effect       GGe        p[GG] p[GG]<.05       HFe        p[HF] p[HF]<.05
2 tiempo 0.6423901 5.662497e-08         * 0.6905331 1.998401e-08         *

La condición de esfericidad no se cumple dado que el test de Mauchly es significativo. Por lo tanto, hay que corregir los grados de libertad y en consecuencia el p-valor del factor tiempo. Después de la corrección, éste sigue siendo significativo.

Nota: Es posible tener más de un factor “entre sujetos”. Para incorporar dos factores hay que especificar el argumento within=.(var1,var2). Ambos factores tienen que estar cruzados.

4.4.1.4 Modelo lineal mixto

Primero, ajustamos el modelo más complejo con constante y pendiente aleatoria, y añadimos el tiempo al cuadrado ya que vemos por el gráfico que la tendencia no es lineal.

modelo <- lme(fixed = medida ~ poly(tiempo, 2), 
              data=datos,
              random = ~ poly(tiempo, 2) | indiv,
              # correlation = corSymm()
              correlation = corAR1()
              )
summary(modelo)

Linear mixed-effects model fit by REML
 Data: datos 
       AIC      BIC    logLik
  208.6888 225.1504 -93.34439

Random effects:
 Formula: ~poly(tiempo, 2) | indiv
 Structure: General positive-definite, Log-Cholesky parametrization
                 StdDev    Corr         
(Intercept)       7.526056 (Intr) p(,2)1
poly(tiempo, 2)1 14.559990  0.881       
poly(tiempo, 2)2  5.178443 -0.663 -0.729
Residual          1.441564              

Correlation Structure: AR(1)
 Formula: ~1 | indiv 
 Parameter estimate(s):
         Phi 
0.0001428372 
Fixed effects: medida ~ poly(tiempo, 2) 
                     Value Std.Error DF    t-value p-value
(Intercept)       42.99444  2.185832 22  19.669598       0
poly(tiempo, 2)1  36.94647  4.443447 22   8.314823       0
poly(tiempo, 2)2 -28.30784  2.076632 22 -13.631610       0
 Correlation: 
                 (Intr) p(,2)1
poly(tiempo, 2)1  0.828       
poly(tiempo, 2)2 -0.475 -0.497

Standardized Within-Group Residuals:
       Min         Q1        Med         Q3        Max 
-1.0450552 -0.4346930 -0.1931843  0.5001057  1.1924184 

Number of Observations: 36
Number of Groups: 12 

• Valor esperado de la constante y coeficientes, $\beta_0, \ldots, \beta_K$. También se conoce como los coeficientes fijos. Para obtener la tabla de sus estimaciones y los p-valores:

coef(summary(modelo))

                     Value Std.Error DF    t-value      p-value
(Intercept)       42.99444  2.185832 22  19.669598 1.886788e-15
poly(tiempo, 2)1  36.94647  4.443447 22   8.314823 3.092000e-08
poly(tiempo, 2)2 -28.30784  2.076632 22 -13.631610 3.311649e-12

• Estimación de los efectos aleatorios, $\color{green}{(\beta_{0i}^{*},\beta_{1i}^{*},\beta_{2i}^{*})}$

ranef(modelo)

    (Intercept) poly(tiempo, 2)1 poly(tiempo, 2)2
1  14.730441065       30.8722315       -6.5833764
2   4.054046210       11.0739532       -1.2028619
3  -5.907126225       -5.2717958        2.8619041
4   0.001779692        0.6665792       -3.8718583
5   4.796479128       13.7400443       -6.6013406
6  -7.601895827      -11.9016785        1.3545235
7  -8.829202865      -17.6630563        7.7680601
8   6.499328908        7.4984525       -0.9466624
9   0.924045128       -6.5624802        1.6842059
10 -5.693831230      -15.1669218        3.7578624
11 -8.860625561       -8.7246544        2.6200805
12  5.886561577        1.4393264       -0.8405368

• Matriz de covarianzas de la constante y coeficientes aleatorios, $\Omega$:

getVarCov(modelo)

Random effects variance covariance matrix
                 (Intercept) poly(tiempo, 2)1 poly(tiempo, 2)2
(Intercept)           56.642           96.553          -25.856
poly(tiempo, 2)1      96.553          211.990          -54.998
poly(tiempo, 2)2     -25.856          -54.998           26.816
  Standard Deviations: 7.5261 14.56 5.1784 

• Matriz de correlaciones de los residuos, $\Sigma_i$

modelo$modelStruct$corStruct

Correlation structure of class corAR1 representing
         Phi 
0.0001428372 

Podemos especificar que la correlación entre efectos aleatorios sea cero con la función pdDiag en el argumento random:

modelo2 <- lme(fixed = medida ~ poly(tiempo, 2), 
              data=datos,
              random = list(indiv=pdDiag(~ poly(tiempo, 2))),
              correlation = corAR1()
              )
summary(modelo2)

Linear mixed-effects model fit by REML
 Data: datos 
       AIC      BIC    logLik
  217.8098 229.7819 -100.9049

Random effects:
 Formula: ~poly(tiempo, 2) | indiv
 Structure: Diagonal
        (Intercept) poly(tiempo, 2)1 poly(tiempo, 2)2 Residual
StdDev:  0.00304907         9.921619     6.785107e-05 7.683502

Correlation Structure: AR(1)
 Formula: ~1 | indiv 
 Parameter estimate(s):
     Phi 
0.896943 
Fixed effects: medida ~ poly(tiempo, 2) 
                     Value Std.Error DF    t-value p-value
(Intercept)       42.99444  2.116748 22  20.311555       0
poly(tiempo, 2)1  36.94647  4.443466 22   8.314786       0
poly(tiempo, 2)2 -28.30784  2.065204 22 -13.707045       0
 Correlation: 
                 (Intr) p(,2)1
poly(tiempo, 2)1  0.000       
poly(tiempo, 2)2 -0.098  0.000

Standardized Within-Group Residuals:
        Min          Q1         Med          Q3         Max 
-1.58347912 -0.87272384  0.04840927  0.77580090  2.40352231 

Number of Observations: 36
Number of Groups: 12 

getVarCov(modelo2)

Random effects variance covariance matrix
                 (Intercept) poly(tiempo, 2)1 poly(tiempo, 2)2
(Intercept)       9.2968e-06            0.000       0.0000e+00
poly(tiempo, 2)1  0.0000e+00           98.439       0.0000e+00
poly(tiempo, 2)2  0.0000e+00            0.000       4.6038e-09
  Standard Deviations: 0.0030491 9.9216 6.7851e-05 

Y para contrastar esta asunción

anova(modelo, modelo2)

        Model df      AIC      BIC     logLik   Test  L.Ratio p-value
modelo      1 11 208.6888 225.1504  -93.34439                        
modelo2     2  8 217.8098 229.7819 -100.90491 1 vs 2 15.12105  0.0017

El modelo mejor es el modelo más complejo con correlación no nula entre los efectos aleatorios.

Simplificación del modelo

Primero miramos si podemos simplificar la matriz de correlación de los residuos.

Comparamos mediante el LRT el modelo ajustado con uno que suponga independencia de los residuos:

anova(modelo, update(modelo, correlation=NULL))

                                   Model df      AIC      BIC    logLik   Test
modelo                                 1 11 208.6888 225.1504 -93.34439       
update(modelo, correlation = NULL)     2 10 206.6888 221.6539 -93.34439 1 vs 2
                                        L.Ratio p-value
modelo                                                 
update(modelo, correlation = NULL) 3.668106e-10       1

Como el p-valor > 0.05, elegimos el modelo más simple (el de independencia de los residuos). Además, según el criteria AIC, o BIC (cuánto más bajo mejor), también nos decantamos por el modelo de independencia de los residuos.

modelo <- update(modelo, correlation=NULL)

Posteriormente constrastamos si los coeficientes del tiempo pueden ser constantes (su varianza es cero):

anova(modelo, update(modelo, random = ~ 1 | indiv))

                                    Model df      AIC      BIC     logLik
modelo                                  1 10 206.6888 221.6539  -93.34439
update(modelo, random = ~1 | indiv)     2  5 218.5762 226.0587 -104.28808
                                      Test  L.Ratio p-value
modelo                                                     
update(modelo, random = ~1 | indiv) 1 vs 2 21.88739   6e-04

Con la función anova se comparan los dos modelos mediante el LRT, uno con los coeficientes aleatorios y el otro sólo con la constante aleatoria. En este caso, y como se ha dicho, el LRT para constrastar si las varianzas son cero no es del todo adecuado. Existen otros tests basados en remuestreo, pero hasta la fecha no funcionan con lme y no se explicarán en este curso.

Basándonos en el LRT, y también el criterio AIC o BIC, se tiene que el modelo más complejo (el que supone que los coeficientes son aleatorios) es el que se eligirá.

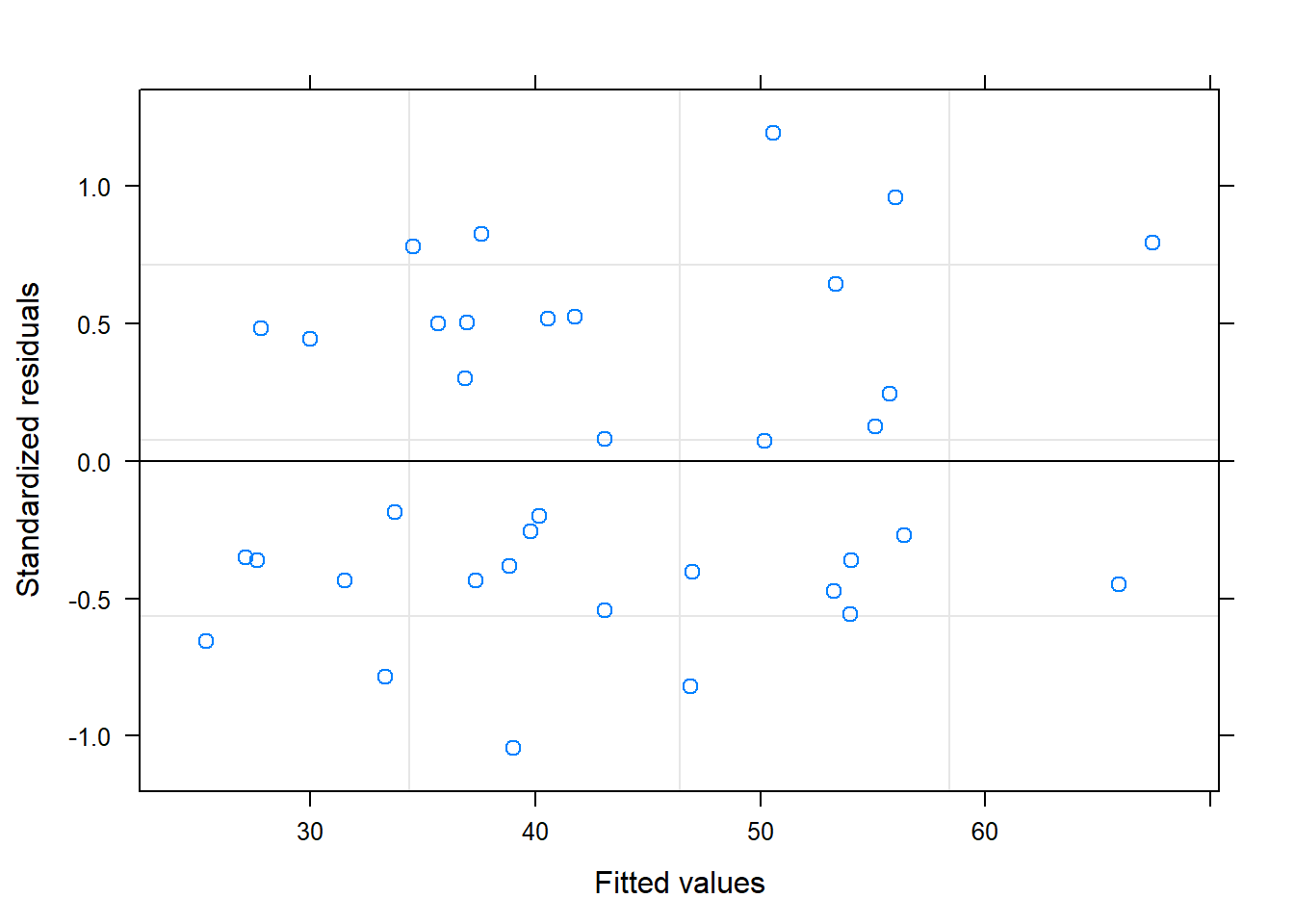
Finalmente, validamos el modelo:

par(mfrow=c(1,2))
plot(modelo)

qqnorm(modelo)

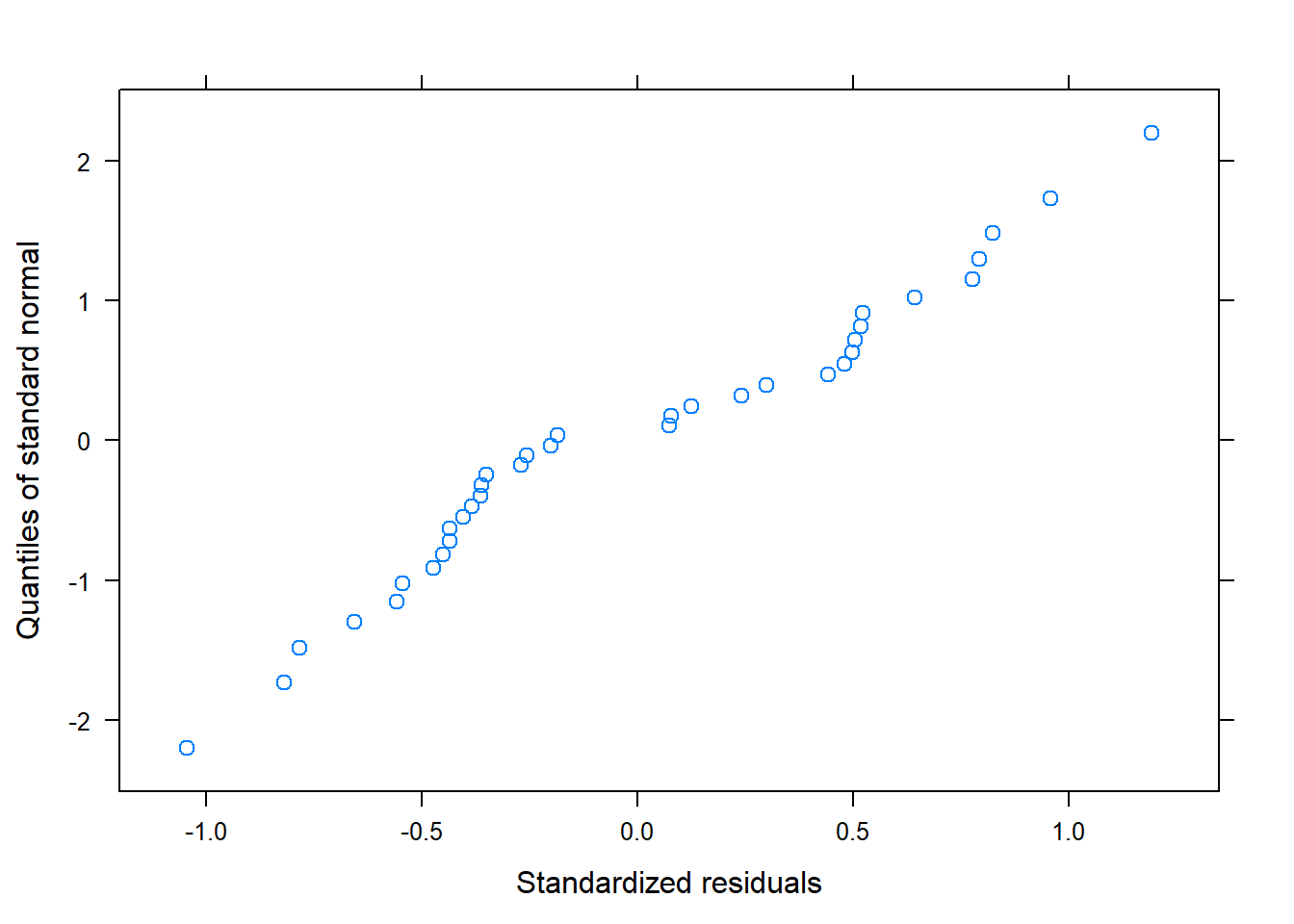
Según estos gra´ficos, diremos que sí se cumplen las premisas sobre los residuos.

Resultado

Por lo tanto el modelo final contendrá el tiempo, el tiempo al cuadrado, la contaste y los coeficientes aleatorios. Finalmente, los residuos se puede suponer independientes.

Observaciones

Con la función lme no se pueden introducir términos spline o smooth para estimar un efecto no paramétrico del tiempo.

4.4.2 Ejemplo 2

En la base de datos “Ejemplo_1W1B.csv” se tienen los datos de un estudio en el que participan 24 individuos randomizados en dos grupos de tratamiento (trat). Como en el anterior ejemplo, para cada invidivuo se miden los niveles a 1, 2 y 3 horas.

datos <- read.csv2("./datos/Ejemplo_1W1B.csv")
datos

   indiv trat tiempo medida indiv2
1      1    1      1   34.7      1
2      2    1      1   38.7      2
3      3    1      1   28.7      3
4      4    1      1   30.8      4
5      5    1      1   29.9      5
6      6    1      1   27.6      6
7      7    1      1   24.9      7
8      8    1      1   37.7      8
9      9    1      1   31.0      9
10    10    1      1   25.4     10
11    11    1      1   24.8     11
12    12    1      1   38.5     12
13     1    1      2   34.8      1
14     2    1      2   44.3      2
15     3    1      2   32.1      3
16     4    1      2   32.4      4
17     5    1      2   36.3      5
18     6    1      2   27.4      6
19     7    1      2   28.0      7
20     8    1      2   38.1      8
21     9    1      2   33.2      9
22    10    1      2   25.3     10
23    11    1      2   26.0     11
24    12    1      2   40.0     12
25     1    1      3   36.9      1
26     2    1      3   44.6      2
27     3    1      3   32.4      3
28     4    1      3   33.8      4
29     5    1      3   34.3      5
30     6    1      3   27.6      6
31     7    1      3   26.0      7
32     8    1      3   35.6      8
33     9    1      3   33.0      9
34    10    1      3   28.1     10
35    11    1      3   29.6     11
36    12    1      3   40.4     12
37     1    2      1   39.4     13
38     2    2      1   33.5     14
39     3    2      1   27.1     15
40     4    2      1   30.9     16
41     5    2      1   32.2     17
42     6    2      1   26.6     18
43     7    2      1   28.5     19
44     8    2      1   37.7     20
45     9    2      1   35.7     21
46    10    2      1   30.6     22
47    11    2      1   24.4     23
48    12    2      1   38.8     24
49     1    2      2   65.3     13
50     2    2      2   53.2     14
51     3    2      2   42.3     15
52     4    2      2   52.3     16
53     5    2      2   57.4     17
54     6    2      2   42.5     18
55     7    2      2   37.5     19
56     8    2      2   56.0     20
57     9    2      2   50.3     21
58    10    2      2   43.2     22
59    11    2      2   39.9     23
60    12    2      2   56.1     24
61     1    2      3   68.6     13
62     2    2      3   54.3     14
63     3    2      3   41.3     15
64     4    2      3   45.7     16
65     5    2      3   53.5     17
66     6    2      3   36.7     18
67     7    2      3   36.4     19
68     8    2      3   55.3     20
69     9    2      3   46.4     21
70    10    2      3   38.3     22
71    11    2      3   37.3     23
72    12    2      3   52.6     24

Fíjate que hay dos variables que codifican al individuo: la variable indiv va de 1 a 12 que son los individuos que hay dentro de cada grupo de tratamiento, mientras que indiv2 va de 1 a 24 que son el total de individuos.

4.4.2.1 Exploración de los datos

datos$trat <- factor(datos$trat)
p <- ggplot(data = datos, aes(x = tiempo, y = medida, group = indiv2))
p <- p + geom_line(col="grey") + stat_summary(aes(group = 1),
    geom = "line", fun = mean, size=2)
p + facet_grid( ~ trat)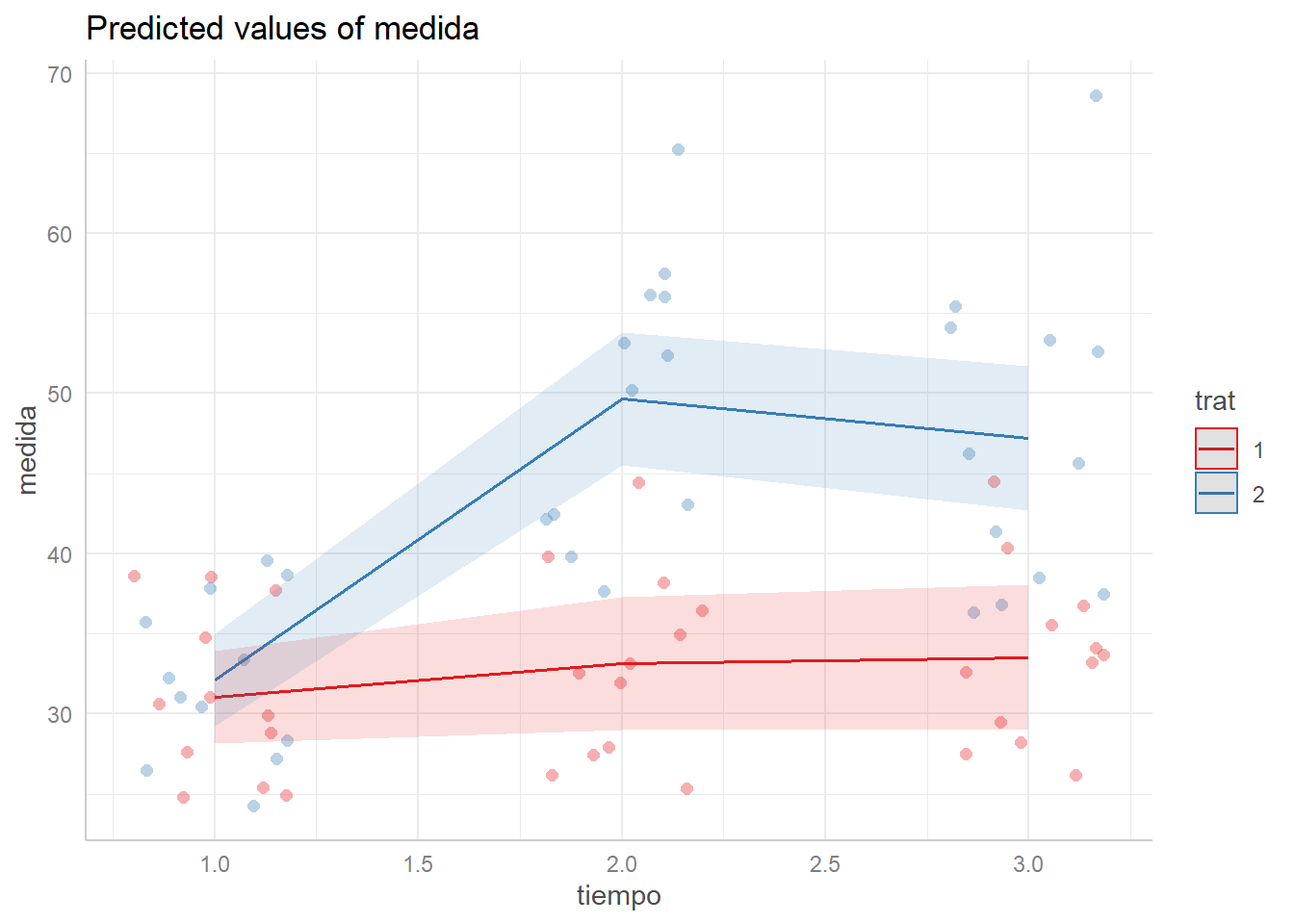

Para trat=1, la medida parece que no sube o sube muy poco. Mientras que para trat=2 sube mucho hasta la segunda medida y se estabiliza en la tercera medida. Por lo tanto, parece que sí hay una interacción entre el tiempo y el grupo de tratamiento.

4.4.2.2 Modelo de respuesta multivariante

Para analizar los datos mediante el modelo de respuesta multivariante, como antes hay que disponer los datos de forma horizontal.

datosh <- reshape(data=datos, 
              direction="wide", 
              v.names=c("medida"), 
              times=1:3, 
              timevar="tiempo", 
              idvar="indiv2")
datosh

   indiv trat indiv2 medida.1 medida.2 medida.3
1      1    1      1     34.7     34.8     36.9
2      2    1      2     38.7     44.3     44.6
3      3    1      3     28.7     32.1     32.4
4      4    1      4     30.8     32.4     33.8
5      5    1      5     29.9     36.3     34.3
6      6    1      6     27.6     27.4     27.6
7      7    1      7     24.9     28.0     26.0
8      8    1      8     37.7     38.1     35.6
9      9    1      9     31.0     33.2     33.0
10    10    1     10     25.4     25.3     28.1
11    11    1     11     24.8     26.0     29.6
12    12    1     12     38.5     40.0     40.4
37     1    2     13     39.4     65.3     68.6
38     2    2     14     33.5     53.2     54.3
39     3    2     15     27.1     42.3     41.3
40     4    2     16     30.9     52.3     45.7
41     5    2     17     32.2     57.4     53.5
42     6    2     18     26.6     42.5     36.7
43     7    2     19     28.5     37.5     36.4
44     8    2     20     37.7     56.0     55.3
45     9    2     21     35.7     50.3     46.4
46    10    2     22     30.6     43.2     38.3
47    11    2     23     24.4     39.9     37.3
48    12    2     24     38.8     56.1     52.6

respuesta <- as.matrix(datosh[,c("medida.1","medida.2","medida.3")])
modelo <- lm(respuesta ~ trat, data=datosh)
summary(modelo)

Response medida.1 :

Call:
lm(formula = medida.1 ~ trat, data = datosh)

Residuals:
    Min      1Q  Median      3Q     Max 
-7.7167 -3.9667 -0.7083  4.1271  7.6417 

Coefficients:
            Estimate Std. Error t value Pr(>|t|)    
(Intercept)   31.058      1.476  21.048 4.57e-16 ***
trat2          1.058      2.087   0.507    0.617    
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Residual standard error: 5.112 on 22 degrees of freedom
Multiple R-squared:  0.01156,   Adjusted R-squared:  -0.03337 
F-statistic: 0.2572 on 1 and 22 DF,  p-value: 0.6171


Response medida.2 :

Call:
lm(formula = medida.2 ~ trat, data = datosh)

Residuals:
     Min       1Q   Median       3Q      Max 
-12.1667  -6.6396   0.3375   5.2896  15.6333 

Coefficients:
            Estimate Std. Error t value Pr(>|t|)    
(Intercept)   33.158      2.113  15.692 1.98e-13 ***
trat2         16.508      2.988   5.524 1.50e-05 ***
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Residual standard error: 7.32 on 22 degrees of freedom
Multiple R-squared:  0.5811,    Adjusted R-squared:  0.5621 
F-statistic: 30.52 on 1 and 22 DF,  p-value: 1.495e-05


Response medida.3 :

Call:
lm(formula = medida.3 ~ trat, data = datosh)

Residuals:
     Min       1Q   Median       3Q      Max 
-10.8000  -5.9062  -0.6625   5.6250  21.4000 

Coefficients:
            Estimate Std. Error t value Pr(>|t|)    
(Intercept)   33.525      2.310  14.511 9.55e-13 ***
trat2         13.675      3.267   4.186 0.000384 ***
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Residual standard error: 8.003 on 22 degrees of freedom
Multiple R-squared:  0.4433,    Adjusted R-squared:  0.418 
F-statistic: 17.52 on 1 and 22 DF,  p-value: 0.0003835

modelo

Call:
lm(formula = respuesta ~ trat, data = datosh)

Coefficients:
             medida.1  medida.2  medida.3
(Intercept)  31.058    33.158    33.525  
trat2         1.058    16.508    13.675  

anova(modelo)

Analysis of Variance Table

            Df  Pillai approx F num Df den Df    Pr(>F)    
(Intercept)  1 0.97752  289.829      3     20 < 2.2e-16 ***
trat         1 0.84439   36.176      3     20 2.854e-08 ***
Residuals   22                                             
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

En este diseño aparece el efecto del tratamiento. Con la instrucción summary, contrasta si la media es diferente entre los dos grupos de tratamiento, y esto lo hace para cada momento por separado.

En la tabla ANOVA el p-valor del tratamiento corresponde al contraste global donde la $H_0$ plantea que las medias son iguales en ambos grupos y para todos los momentos. El término (intercept) de la tabla ANOVA contrasta la $H_0$ que las medias de los tres momentos son iguales a cero en el grupo control.

Observación

En ningún lugar se calcula el test sobre la interacción del tratamiento y el tiempo.

4.4.2.3 Suma de cuadrados

Para ajustar este modelo hay que usar los datos en disposición vertical. Como antes hay que convertir las variables tiempo, indiv2 y trat a factor.

library(ez)

datos.ez <- datos
datos.ez$tiempo <- factor(datos.ez$tiempo)
datos.ez$indiv2 <- factor(datos.ez$indiv2)
datos.ez$trat <- factor(datos.ez$trat)

ezANOVA(data=datos.ez, 
        dv=medida, 
        wid=indiv, 
        within=tiempo, 
        between=trat,
        detailed = TRUE)

$ANOVA
       Effect DFn DFd         SSn       SSd         F            p p<.05
1 (Intercept)   1  22 102808.4513 2849.9219 793.63083 9.363797e-19     *
2        trat   1  22   1952.0835 2849.9219  15.06913 8.040878e-04     *
3      tiempo   2  44   1397.0700  312.7422  98.27755 5.878117e-17     *
4 trat:tiempo   2  44    811.8211  312.7422  57.10794 5.921847e-13     *
        ges
1 0.9701554
2 0.3816578
3 0.3063929
4 0.2042582

$`Mauchly's Test for Sphericity`
       Effect         W           p p<.05
3      tiempo 0.5725954 0.002866835     *
4 trat:tiempo 0.5725954 0.002866835     *

$`Sphericity Corrections`
       Effect       GGe        p[GG] p[GG]<.05       HFe        p[HF] p[HF]<.05
3      tiempo 0.7005722 1.520842e-12         * 0.7336894 4.932994e-13         *
4 trat:tiempo 0.7005722 1.003472e-09         * 0.7336894 4.400536e-10         *

Vemos como se aplican las correcciones sólo en los términos “intra sujeto” que son el tiempo y la interacción grupo:tiempo, ya que el test de Mauchly es significativo (p-valor < 0.05). Una vez aplicados las correcciones sobre los grados de libertad, los p-valores cambian aunque las conclusiones son las mismas: tanto el efecto del tiempo como su interacción con el tratamiento son significativos.

ezPlot(data=datos.ez, 
       dv=medida, 
       wid=indiv, 
       within=tiempo, 
       between=trat,
       x=tiempo,
       split=trat)

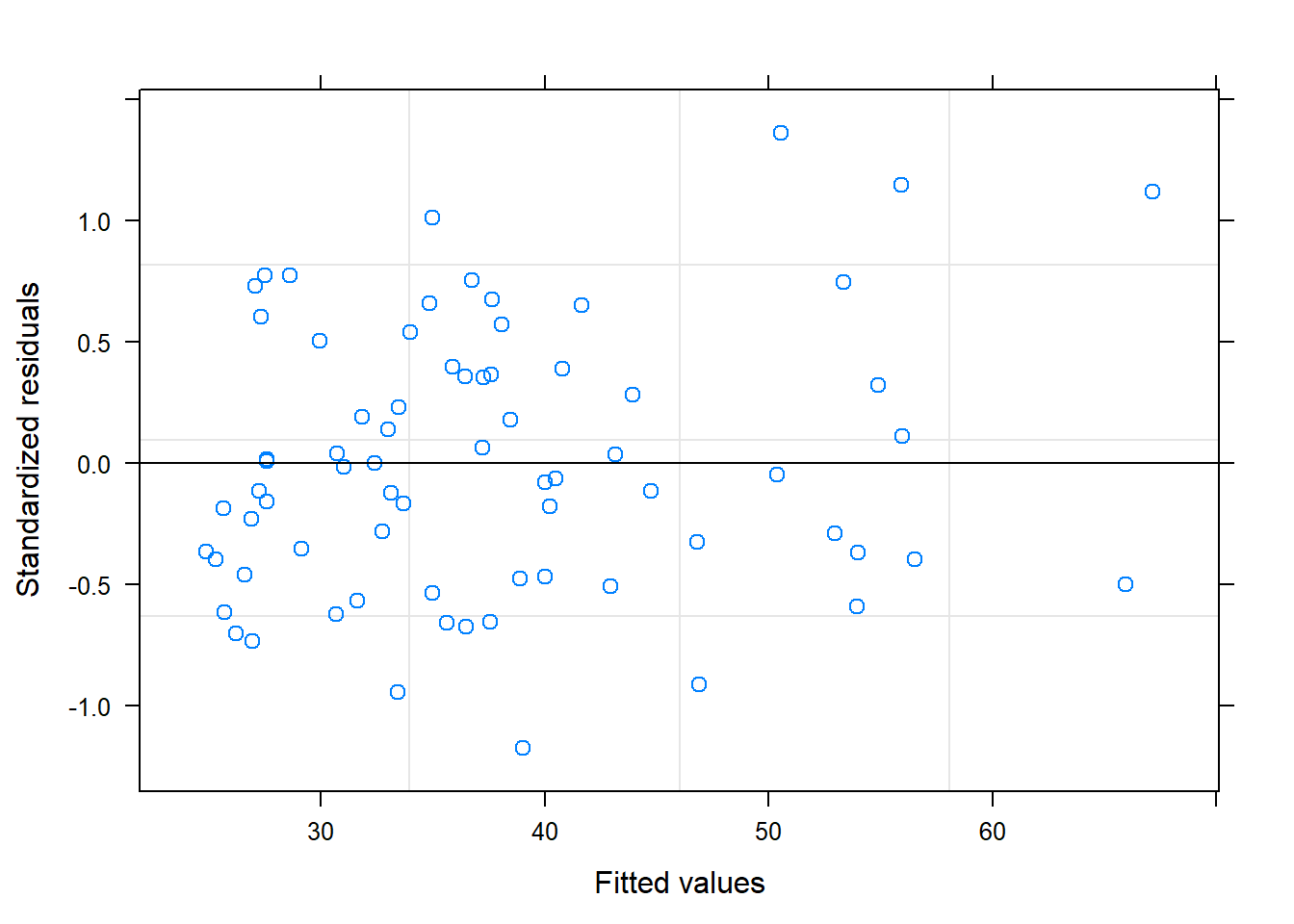
Las conclusiones con la tabla ANOVA corregida (tanto por GG como por HF), se ven claramente en el gráfico de interacción.

Nota: Es posible introducir más de un factor “entre sujeto”, especificando el argumento between=.(var1,var2) si se consideran dos factores entre sujetos, que deben estar cruzados.

4.4.2.4 Modelo lineal mixto

modelo <- lme(fixed = medida ~ poly(tiempo,2)*trat, 
              data=datos,
              random = ~ poly(tiempo,2) | indiv2,
              #correlation = corSymm()
              correlation = corAR1()
              )
summary(modelo)

Linear mixed-effects model fit by REML
 Data: datos 
      AIC      BIC   logLik
  386.914 417.5692 -179.457

Random effects:
 Formula: ~poly(tiempo, 2) | indiv2
 Structure: General positive-definite, Log-Cholesky parametrization
                 StdDev    Corr         
(Intercept)       6.528817 (Intr) p(,2)1
poly(tiempo, 2)1 15.016142  0.720       
poly(tiempo, 2)2  5.983554 -0.637 -0.653
Residual          1.290085              

Correlation Structure: AR(1)
 Formula: ~1 | indiv2 
 Parameter estimate(s):
         Phi 
5.459222e-05 
Fixed effects: medida ~ poly(tiempo, 2) * trat 
                           Value Std.Error DF    t-value p-value
(Intercept)             32.58056  1.896933 44  17.175384  0.0000
poly(tiempo, 2)1         8.54478  4.703086 44   1.816846  0.0761
poly(tiempo, 2)2        -3.46667  2.512364 44  -1.379842  0.1746
trat2                   10.41389  2.682669 22   3.881914  0.0008
poly(tiempo, 2)1:trat2  43.70542  6.651168 44   6.571089  0.0000
poly(tiempo, 2)2:trat2 -36.56667  3.553020 44 -10.291715  0.0000
 Correlation: 
                       (Intr) pl(,2)1 pl(,2)2 trat2  p(,2)1:
poly(tiempo, 2)1        0.659                               
poly(tiempo, 2)2       -0.435 -0.414                        
trat2                  -0.707 -0.466   0.308                
poly(tiempo, 2)1:trat2 -0.466 -0.707   0.293   0.659        
poly(tiempo, 2)2:trat2  0.308  0.293  -0.707  -0.435 -0.414 

Standardized Within-Group Residuals:
        Min          Q1         Med          Q3         Max 
-1.17636038 -0.41451565 -0.05512437  0.37021865  1.36156338 

Number of Observations: 72
Number of Groups: 24 

Nota: Si los individuos estuvieran anidados dentro de clusters, se especificaría en el argumento random = ~ 1 | indiv / clusters, donde “cluster” sería el nombre de la variable que codifica los clusters.

Observación Para que el modelo quede bien definido no es posible poner la interacción del tiempo y el tratamiento como coeficiente aleatorio. De esta manera se especifican como aleatorios la costante y los coeficientes del tiempo (lineal y cuadrático) para el grupo control.

Miramos si se puede simplificar la matriz de correlaciones de los efectos aleatorios:

modelo2 <- lme(fixed = medida ~ poly(tiempo,2)*trat, 
              data=datos,
              random = list(indiv2=pdDiag(~poly(tiempo,2))),
              #correlation = corSymm()
              correlation = corAR1()
              )
anova(modelo, modelo2)

        Model df      AIC      BIC    logLik   Test  L.Ratio p-value
modelo      1 14 386.9140 417.5692 -179.4570                        
modelo2     2 11 397.1845 421.2707 -187.5922 1 vs 2 16.27047   0.001

El test LRT es significativo (p-valor < 0.05). Por lo tanto nos quedamos con el modelo más complejo que supone que hay correlación entre los efectos aleatorios.

Seguidamente, miramos si se puede simplificar la matriz de correlaciones de los errores.

anova(modelo, update(modelo, correlation=NULL))

                                   Model df     AIC      BIC   logLik   Test
modelo                                 1 14 386.914 417.5692 -179.457       
update(modelo, correlation = NULL)     2 13 384.914 413.3795 -179.457 1 vs 2
                                        L.Ratio p-value
modelo                                                 
update(modelo, correlation = NULL) 1.169383e-08  0.9999

Sí que se puede suponer que hay indipendencia entre los residuos.

modelo <- update(modelo, correlation=NULL)

Por lo tanto el modelo final, que supone independencia entre residuos, tiene la siguiente estimación de los efectos fijos:

coef(summary(modelo))

                            Value Std.Error DF    t-value      p-value
(Intercept)             32.580556  1.896946 44  17.175271 3.966321e-21
poly(tiempo, 2)1         8.544784  4.703101 44   1.816840 7.605690e-02
poly(tiempo, 2)2        -3.466667  2.512343 44  -1.379854 1.746035e-01
trat2                   10.413889  2.682686 22   3.881888 8.041051e-04
poly(tiempo, 2)1:trat2  43.705415  6.651190 44   6.571067 4.875992e-08
poly(tiempo, 2)2:trat2 -36.566667  3.552990 44 -10.291803 2.730972e-13

Vemos como el efecto del tiempo para el grupo control no llega a ser significativo (p-valores >0.05) tanto para su componente lineal como cuadrático. Hay efecto del tratamiento en el momento basal (trat2).

Si quieremos ver el efecto del tiempo para el grupo 2, hay que cambiar su categoría de referencia.

datos$trat <- factor(datos$trat, levels=2:1)
coef(summary(update(modelo)))

                           Value Std.Error DF    t-value      p-value
(Intercept)             42.99444  1.896932 44  22.665259 6.756030e-26
poly(tiempo, 2)1        52.25020  4.703133 44  11.109658 2.358252e-14
poly(tiempo, 2)2       -40.03333  2.512374 44 -15.934465 6.870764e-20
trat1                  -10.41389  2.682666 22  -3.881917 8.040486e-04
poly(tiempo, 2)1:trat1 -43.70542  6.651235 44  -6.571023 4.876723e-08
poly(tiempo, 2)2:trat1  36.56667  3.553033 44  10.291676 2.732023e-13

Vemos que para el grupo 2 tanto la componente lineal como la cuadrática del tiempo son significativas.

Con la siguiente matriz de varianzas y covarianzas de los efectos aleatorios:

getVarCov(modelo)

Random effects variance covariance matrix
                 (Intercept) poly(tiempo, 2)1 poly(tiempo, 2)2
(Intercept)           42.626           70.565          -24.889
poly(tiempo, 2)1      70.565          225.490          -58.668
poly(tiempo, 2)2     -24.889          -58.668           35.800
  Standard Deviations: 6.5289 15.016 5.9833 

Y varianza de los residuos

sigma(modelo)^2

[1] 1.664249

Por último, validamos el modelo

par(mfrow=c(1,2))
plot(modelo)

qqnorm(modelo)

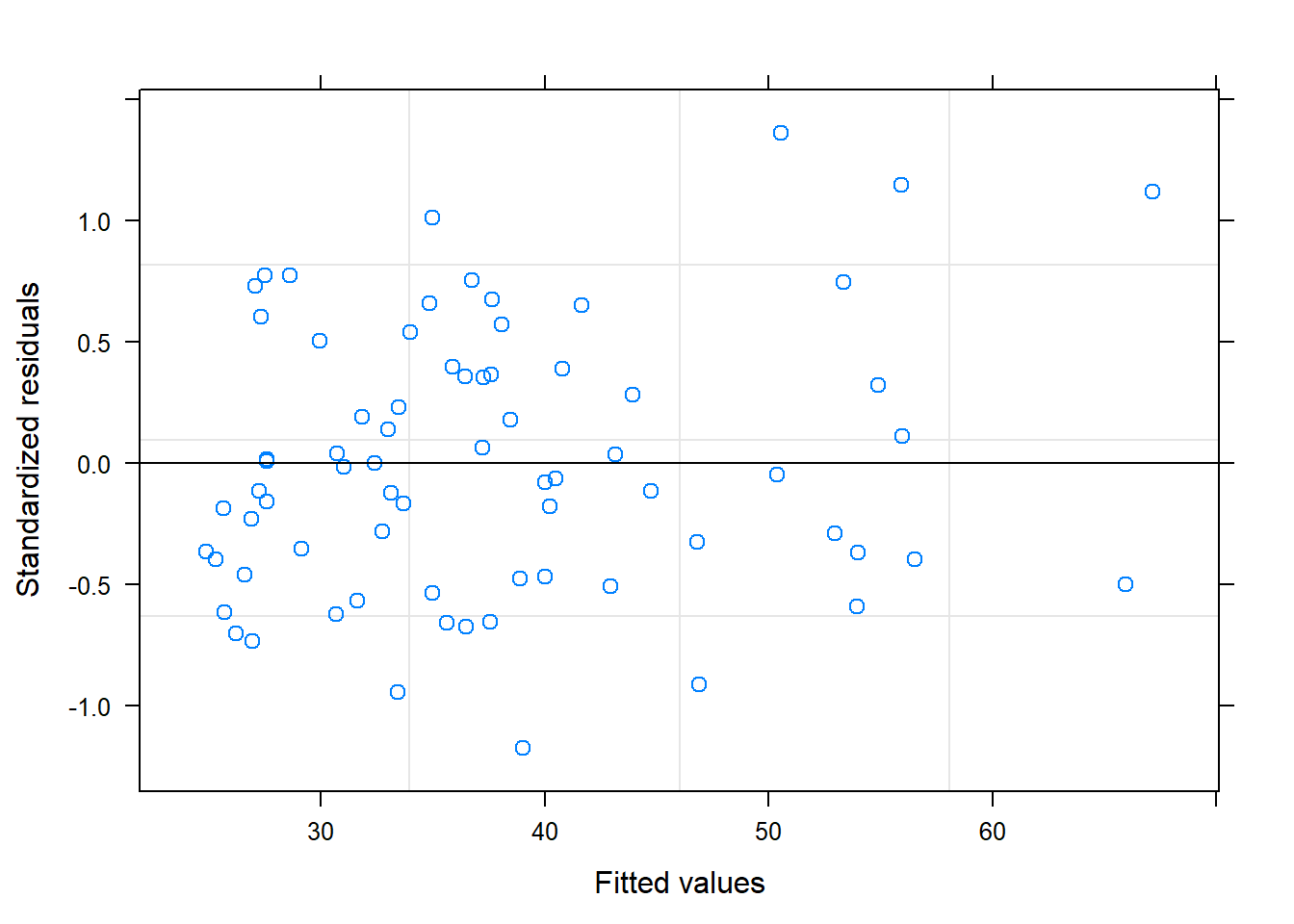
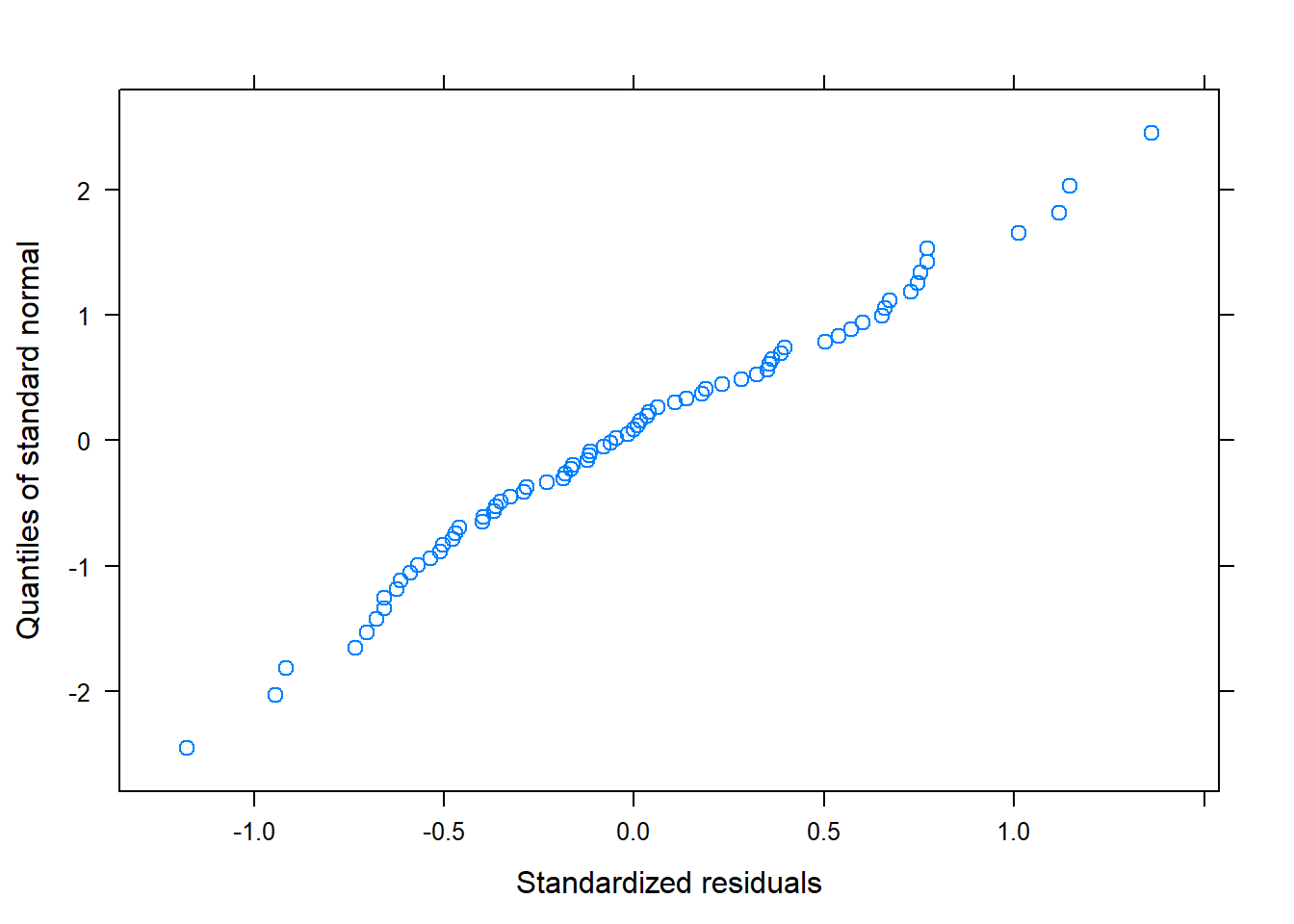
Según los gráficos, parece que sí que se cumplen las premisas sobre los residuos.

4.4.3 Ejemplo 3

En un estudio se quieren comparar el efecto de régimen de ejercicio sobre el sobrepeso. Para ello se reclutan 100 personas. A la mitad se le asigna el régimen y al resto se le hacen algunas recomendaciones (grupo control). Se mide el índice de masa corporal justo antes de empezar el estudio (momento basal), y a las 2, 4 y 6 semanas. Como la edad y el sexo son variables importantes para la variable importante también se registran.

Los datos los encontrarás en el fichero “imc.csv”

En este ejemplo vemos como algunos de los individuos nos falta alguna medida (a las 2, 4 o 6 semanas). Para ellos sólo usaremos la técnica de los LMM.

4.5 Ejercicios

4.5.1 Ejercicio 1

Los datos o2cons, disponibles en el paquete MANOVA.RM, contiene medidas sobre el consumo de oxígeno de los leucocitos (“O2”) de 144 individuos, 72 de ellos asignados al grupo control (“Group=P”) y el resto al grupo de tratamiento con Verum (Group=V). Además, para cada individuo se recoge si los estafilococos (“Staphylococci”) estaban activados o no (0/1). Para cada individuo se tomaron los niveles de oxígeno de los leucocitos después de 6, 12 y 18 minutos.

• Haz una pequeña descriptiva de los datos contenidos en esta base de datos

• Analiza la evolución del consumo de oxígeno del grupo de tratamiento (“Group=V”).

• Compara la evolución del consumo de O2 entre el grupo de intervención con el grupo de tratamiento.

library(MANOVA.RM)
data(o2cons)
# load("./datos/o2cons.rda")

?o2cons

4.5.2 Ejercicio 2

Analiza los datos Soybean disponibles en el paquete nlme.

data(Soybean)
# load("./datos/Soybean.rda")
?Soybean

######## scratch #############

data(package="nlme")

## contrastes polinómicos sobre el tiempo en modelos nlme

options(contrasts = c("contr.sum", "contr.poly"))
library(nlme)
model.lme <- lme(acc ~ cond*time, random = ~ 1 | PID, data = myData)

exactRLRT(m.slope, mA, m0)

anova(model.lme, type="marginal")

library(gmodels)
fit.contrast(model.lme, "time", t(contr.poly(4, c(1, 2, 3, 4))))


## correlation structure
with(datos, nlme::Structure(form  = ~ tiempo | indiv))
?corClasses

cs1 <- corAR1()
summary(cs1)
cs1ARMA <- corARMA(0.4, form = ~ 1 | Subject, q = 1)
cs1ARMA <- Initialize(cs1ARMA, data = Orthodont)
corMatrix(cs1ARMA)

cs1CompSymm <- corCompSymm(value = 0.3, form = ~ 1 | Subject)
cs2CompSymm <- corCompSymm(value = 0.3, form = ~ age | Subject)
cs1CompSymm <- Initialize(cs1CompSymm, data = Orthodont)
cs2CompSymm <- Initialize(cs2CompSymm, data = Orthodont)
corMatrix(cs1CompSymm)
corMatrix(cs2CompSymm)
Orthodont

cs1Symm <- corSymm(value =
        c(0.2, 0.1, -0.1, 0, 0.2, 0),
                   form = ~ 1 | Subject)
cs1Symm <- Initialize(cs1Symm, data = Orthodont)
corMatrix(cs1Symm)




################################################
################ comentaris ####################

## heterocedestitat segons una variable (ho explico que existeix però no ho tocarem)

nlme::lme(weights=varFun())


varPower
varExp
varFun ...


## validació (fet )

plot()
qqnorm()


## stepwise -> no ho faig. Prefereixo de treure els efectes fixes un a un a mà



## gràfic random effects (dic només com treure els efectes però ho comentaré només, no poso cap fórmula ni escric res més....)



## més exemples (dades simulades)



## mirar com posar referencies (per exemple pbkrtest)

---

1. pbkrtest↩︎