Capítulo 2 Laboratorios
library(stringr)
library(corrplot)## Warning: package 'corrplot' was built under R version 4.2.2## corrplot 0.92 loadedlibrary(readxl)
library(caret)## Warning: package 'caret' was built under R version 4.2.2## Carregando pacotes exigidos: ggplot2## Warning: package 'ggplot2' was built under R version 4.2.2## Carregando pacotes exigidos: latticelibrary(MASS)2.1 Laboratorio
2.1.1 BLOCO 1: R básico
- Calcule as seguintes expressoes no R:
- 12 + (16-7)x7-8/4
Resul = 12 + (16-7) * 7 - 9 / 4- Multiplique a sua idade por meses e salve o resultado em um objeto chamado idade_em_meses.
idade_em_meses = 49 * 12
print(idade_em_meses)## [1] 5882.1 - Em seguida, multiplique esse objeto por 30 e salve o resultado em um objeto chamado idade_em_dias.
idade_em_dias = idade_em_meses * 30- Guarde em um objeto chamado nome uma string contendo o seu nome completo
nome = "Josias Oliveira Lima"
nome = "Josias"
SobreNome = "Lima"
NomeCompleto <- str_c(nome," ",SobreNome)- Qual é a soma dos números de 101 a 1000?
sum( 101:1000 )## [1] 495450- Quantos algarismos possui o resultado do produto dos números de 1 a 12?
#Cria um objeto dianamico de n=12
for(coluna in 1:12)
{
x[[coluna]] <- c( coluna )
}
#lista Elementos do Vetor
print(x)## [1] 1.00 2.00 3.00 4.00 5.00 6.00 7.00 8.00 9.00 10.00 11.00 12.00
## [13] 46689.20 46804.83 48606.70 49447.08 50038.74 50216.60 53011.55 53643.98 51448.01 52368.13 55820.39 56039.98
## [25] 53509.42 53583.73 54402.65 57330.44 57655.82 55515.64 58403.14 58483.91 58528.00 58604.17 58772.98 58999.60
## [37] 59009.53 59134.94 59222.74 56681.77 56901.84 57867.57 61325.67 61382.59 59321.17 62999.41 93107.62 129919.40 #retorna o produto do Vetor
prod(x)## [1] 1.156442e+180- Use o vetor números abaixo para responder as questões seguintes:
numeros <- -4:26.1 - Escreva um código que devolva apenas valores positivos do vetor numeros.
numeros[numeros > 0]## [1] 1 26.2. - Escreva um código que de volta apenas os valores pares do vetor numeros.
numeros[numeros %% 2 == 0]## [1] -4 -2 0 26.3 - Filtre o vetor para que retorne apenas aqueles valores que, quando elevados a 2, são menores do que 4.
numeros[numeros^2 < 4]## [1] -1 0 1- Quais as diferenças entre NaN, NULL, NA e Inf? Digite expressões que retornem cada um desses valores.
NaN
numeros <- c( 0, NaN , "F", NaN , 3 )
sum(is.nan(numeros))## [1] 0Null
numeros <- c( NULL, 3 )
sum(is.null(numeros))## [1] 0NA
numeros <- c( NA, 2 )
sum(is.na(numeros))## [1] 1- Carregue o conjunto de dados airquality com o comando data(airquality) para responder às questões abaixo.
getwd()## [1] "C:/Users/Josias/Documents/IPT/BD/Cadernos_Josias"tabelaAir <- read.table("dados/airquality.csv" , sep=',', header=T)
#lista as 5 primeiras linhas da Tabelas
head(tabelaAir)## X Ozone Solar.R Wind Temp Month Day
## 1 2\t1 41 190 7.4 67 5 1
## 2 3\t2 36 118 8.0 72 5 2
## 3 4\t3 12 149 12.6 74 5 3
## 4 5\t4 18 313 11.5 62 5 4
## 5 6\t5 NA NA 14.3 56 5 5
## 6 7\t6 28 NA 14.9 66 5 6#lista as 5 ultimas linhas da tabelas
tail(tabelaAir)## X Ozone Solar.R Wind Temp Month Day
## 148 149\t148 14 20 16.6 63 9 25
## 149 150\t149 30 193 6.9 70 9 26
## 150 151\t150 NA 145 13.2 77 9 27
## 151 152\t151 14 191 14.3 75 9 28
## 152 153\t152 18 131 8.0 76 9 29
## 153 154\t153 20 223 11.5 68 9 30- Conte quantos NAs tem na coluna Solar.R.
sum(is.na(tabelaAir$Solar.R))## [1] 7- Filtre a tabela airquality com apenas linhas em que Solar.R é NA.
tabelaAir[is.na(tabelaAir$Solar.R),]## X Ozone Solar.R Wind Temp Month Day
## 5 6\t5 NA NA 14.3 56 5 5
## 6 7\t6 28 NA 14.9 66 5 6
## 11 12\t11 7 NA 6.9 74 5 11
## 27 28\t27 NA NA 8.0 57 5 27
## 96 97\t96 78 NA 6.9 86 8 4
## 97 98\t97 35 NA 7.4 85 8 5
## 98 99\t98 66 NA 4.6 87 8 6- Filtre a tabela airquality com apenas linhas em que Solar.R não é NA.
tabelaAir[!is.na(tabelaAir$Solar.R),]## X Ozone Solar.R Wind Temp Month Day
## 1 2\t1 41 190 7.4 67 5 1
## 2 3\t2 36 118 8.0 72 5 2
## 3 4\t3 12 149 12.6 74 5 3
## 4 5\t4 18 313 11.5 62 5 4
## 7 8\t7 23 299 8.6 65 5 7
## 8 9\t8 19 99 13.8 59 5 8
## 9 10\t9 8 19 20.1 61 5 9
## 10 11\t10 NA 194 8.6 69 5 10
## 12 13\t12 16 256 9.7 69 5 12
## 13 14\t13 11 290 9.2 66 5 13
## 14 15\t14 14 274 10.9 68 5 14
## 15 16\t15 18 65 13.2 58 5 15
## 16 17\t16 14 334 11.5 64 5 16
## 17 18\t17 34 307 12.0 66 5 17
## 18 19\t18 6 78 18.4 57 5 18
## 19 20\t19 30 322 11.5 68 5 19
## 20 21\t20 11 44 9.7 62 5 20
## 21 22\t21 1 8 9.7 59 5 21
## 22 23\t22 11 320 16.6 73 5 22
## 23 24\t23 4 25 9.7 61 5 23
## 24 25\t24 32 92 12.0 61 5 24
## 25 26\t25 NA 66 16.6 57 5 25
## 26 27\t26 NA 266 14.9 58 5 26
## 28 29\t28 23 13 12.0 67 5 28
## 29 30\t29 45 252 14.9 81 5 29
## 30 31\t30 115 223 5.7 79 5 30
## 31 32\t31 37 279 7.4 76 5 31
## 32 33\t32 NA 286 8.6 78 6 1
## 33 34\t33 NA 287 9.7 74 6 2
## 34 35\t34 NA 242 16.1 67 6 3
## 35 36\t35 NA 186 9.2 84 6 4
## 36 37\t36 NA 220 8.6 85 6 5
## 37 38\t37 NA 264 14.3 79 6 6
## 38 39\t38 29 127 9.7 82 6 7
## 39 40\t39 NA 273 6.9 87 6 8
## 40 41\t40 71 291 13.8 90 6 9
## 41 42\t41 39 323 11.5 87 6 10
## 42 43\t42 NA 259 10.9 93 6 11
## 43 44\t43 NA 250 9.2 92 6 12
## 44 45\t44 23 148 8.0 82 6 13
## 45 46\t45 NA 332 13.8 80 6 14
## 46 47\t46 NA 322 11.5 79 6 15
## 47 48\t47 21 191 14.9 77 6 16
## 48 49\t48 37 284 20.7 72 6 17
## 49 50\t49 20 37 9.2 65 6 18
## 50 51\t50 12 120 11.5 73 6 19
## 51 52\t51 13 137 10.3 76 6 20
## 52 53\t52 NA 150 6.3 77 6 21
## 53 54\t53 NA 59 1.7 76 6 22
## 54 55\t54 NA 91 4.6 76 6 23
## 55 56\t55 NA 250 6.3 76 6 24
## 56 57\t56 NA 135 8.0 75 6 25
## 57 58\t57 NA 127 8.0 78 6 26
## 58 59\t58 NA 47 10.3 73 6 27
## 59 60\t59 NA 98 11.5 80 6 28
## 60 61\t60 NA 31 14.9 77 6 29
## 61 62\t61 NA 138 8.0 83 6 30
## 62 63\t62 135 269 4.1 84 7 1
## 63 64\t63 49 248 9.2 85 7 2
## 64 65\t64 32 236 9.2 81 7 3
## 65 66\t65 NA 101 10.9 84 7 4
## 66 67\t66 64 175 4.6 83 7 5
## 67 68\t67 40 314 10.9 83 7 6
## 68 69\t68 77 276 5.1 88 7 7
## 69 70\t69 97 267 6.3 92 7 8
## 70 71\t70 97 272 5.7 92 7 9
## 71 72\t71 85 175 7.4 89 7 10
## 72 73\t72 NA 139 8.6 82 7 11
## 73 74\t73 10 264 14.3 73 7 12
## 74 75\t74 27 175 14.9 81 7 13
## 75 76\t75 NA 291 14.9 91 7 14
## 76 77\t76 7 48 14.3 80 7 15
## 77 78\t77 48 260 6.9 81 7 16
## 78 79\t78 35 274 10.3 82 7 17
## 79 80\t79 61 285 6.3 84 7 18
## 80 81\t80 79 187 5.1 87 7 19
## 81 82\t81 63 220 11.5 85 7 20
## 82 83\t82 16 7 6.9 74 7 21
## 83 84\t83 NA 258 9.7 81 7 22
## 84 85\t84 NA 295 11.5 82 7 23
## 85 86\t85 80 294 8.6 86 7 24
## 86 87\t86 108 223 8.0 85 7 25
## 87 88\t87 20 81 8.6 82 7 26
## 88 89\t88 52 82 12.0 86 7 27
## 89 90\t89 82 213 7.4 88 7 28
## 90 91\t90 50 275 7.4 86 7 29
## 91 92\t91 64 253 7.4 83 7 30
## 92 93\t92 59 254 9.2 81 7 31
## 93 94\t93 39 83 6.9 81 8 1
## 94 95\t94 9 24 13.8 81 8 2
## 95 96\t95 16 77 7.4 82 8 3
## 99 100\t99 122 255 4.0 89 8 7
## 100 101\t100 89 229 10.3 90 8 8
## 101 102\t101 110 207 8.0 90 8 9
## 102 103\t102 NA 222 8.6 92 8 10
## 103 104\t103 NA 137 11.5 86 8 11
## 104 105\t104 44 192 11.5 86 8 12
## 105 106\t105 28 273 11.5 82 8 13
## 106 107\t106 65 157 9.7 80 8 14
## 107 108\t107 NA 64 11.5 79 8 15
## 108 109\t108 22 71 10.3 77 8 16
## 109 110\t109 59 51 6.3 79 8 17
## 110 111\t110 23 115 7.4 76 8 18
## 111 112\t111 31 244 10.9 78 8 19
## 112 113\t112 44 190 10.3 78 8 20
## 113 114\t113 21 259 15.5 77 8 21
## 114 115\t114 9 36 14.3 72 8 22
## 115 116\t115 NA 255 12.6 75 8 23
## 116 117\t116 45 212 9.7 79 8 24
## 117 118\t117 168 238 3.4 81 8 25
## 118 119\t118 73 215 8.0 86 8 26
## 119 120\t119 NA 153 5.7 88 8 27
## 120 121\t120 76 203 9.7 97 8 28
## 121 122\t121 118 225 2.3 94 8 29
## 122 123\t122 84 237 6.3 96 8 30
## 123 124\t123 85 188 6.3 94 8 31
## 124 125\t124 96 167 6.9 91 9 1
## 125 126\t125 78 197 5.1 92 9 2
## 126 127\t126 73 183 2.8 93 9 3
## 127 128\t127 91 189 4.6 93 9 4
## 128 129\t128 47 95 7.4 87 9 5
## 129 130\t129 32 92 15.5 84 9 6
## 130 131\t130 20 252 10.9 80 9 7
## 131 132\t131 23 220 10.3 78 9 8
## 132 133\t132 21 230 10.9 75 9 9
## 133 134\t133 24 259 9.7 73 9 10
## 134 135\t134 44 236 14.9 81 9 11
## 135 136\t135 21 259 15.5 76 9 12
## 136 137\t136 28 238 6.3 77 9 13
## 137 138\t137 9 24 10.9 71 9 14
## 138 139\t138 13 112 11.5 71 9 15
## 139 140\t139 46 237 6.9 78 9 16
## 140 141\t140 18 224 13.8 67 9 17
## 141 142\t141 13 27 10.3 76 9 18
## 142 143\t142 24 238 10.3 68 9 19
## 143 144\t143 16 201 8.0 82 9 20
## 144 145\t144 13 238 12.6 64 9 21
## 145 146\t145 23 14 9.2 71 9 22
## 146 147\t146 36 139 10.3 81 9 23
## 147 148\t147 7 49 10.3 69 9 24
## 148 149\t148 14 20 16.6 63 9 25
## 149 150\t149 30 193 6.9 70 9 26
## [ reached 'max' / getOption("max.print") -- omitted 4 rows ]- Filtre a tabela airquality com apenas linhas em que Solar.R não é NA e Month é igual a 5.
tabelaAir[tabelaAir$Month == 5 & !is.na(tabelaAir$Solar.R), ]## X Ozone Solar.R Wind Temp Month Day
## 1 2\t1 41 190 7.4 67 5 1
## 2 3\t2 36 118 8.0 72 5 2
## 3 4\t3 12 149 12.6 74 5 3
## 4 5\t4 18 313 11.5 62 5 4
## 7 8\t7 23 299 8.6 65 5 7
## 8 9\t8 19 99 13.8 59 5 8
## 9 10\t9 8 19 20.1 61 5 9
## 10 11\t10 NA 194 8.6 69 5 10
## 12 13\t12 16 256 9.7 69 5 12
## 13 14\t13 11 290 9.2 66 5 13
## 14 15\t14 14 274 10.9 68 5 14
## 15 16\t15 18 65 13.2 58 5 15
## 16 17\t16 14 334 11.5 64 5 16
## 17 18\t17 34 307 12.0 66 5 17
## 18 19\t18 6 78 18.4 57 5 18
## 19 20\t19 30 322 11.5 68 5 19
## 20 21\t20 11 44 9.7 62 5 20
## 21 22\t21 1 8 9.7 59 5 21
## 22 23\t22 11 320 16.6 73 5 22
## 23 24\t23 4 25 9.7 61 5 23
## 24 25\t24 32 92 12.0 61 5 24
## 25 26\t25 NA 66 16.6 57 5 25
## 26 27\t26 NA 266 14.9 58 5 26
## 28 29\t28 23 13 12.0 67 5 28
## 29 30\t29 45 252 14.9 81 5 29
## 30 31\t30 115 223 5.7 79 5 30
## 31 32\t31 37 279 7.4 76 5 312.1.1.1 BLOCO 2: Análise descritiva de dados
- Carregue o conjunto de dados USArrests com o comando data(USArrests). Examine a sua documentação com help(USArrests) e responda as perguntas a seguir.
data <- USArrests- Qual o número médio e mediano de cada um dos crimes?
- Encontre a mediana e quartis para cada crime?
- Encontre o número máximo e mínimo para cada crime?
summary(data)## Murder Assault UrbanPop Rape
## Min. : 0.800 Min. : 45.0 Min. :32.00 Min. : 7.30
## 1st Qu.: 4.075 1st Qu.:109.0 1st Qu.:54.50 1st Qu.:15.07
## Median : 7.250 Median :159.0 Median :66.00 Median :20.10
## Mean : 7.788 Mean :170.8 Mean :65.54 Mean :21.23
## 3rd Qu.:11.250 3rd Qu.:249.0 3rd Qu.:77.75 3rd Qu.:26.18
## Max. :17.400 Max. :337.0 Max. :91.00 Max. :46.00- faça um gráfico adequado para o número de assassinatos (murder).
media = mean(data$Murder, na.rm = T)
media## [1] 7.788plot(data$Murder,xlab="", ylab = "", col = 3, pch = 17, lower.panel=NULL,main="Dispersão de Assassinatos tipo Murder")
abline(h = media)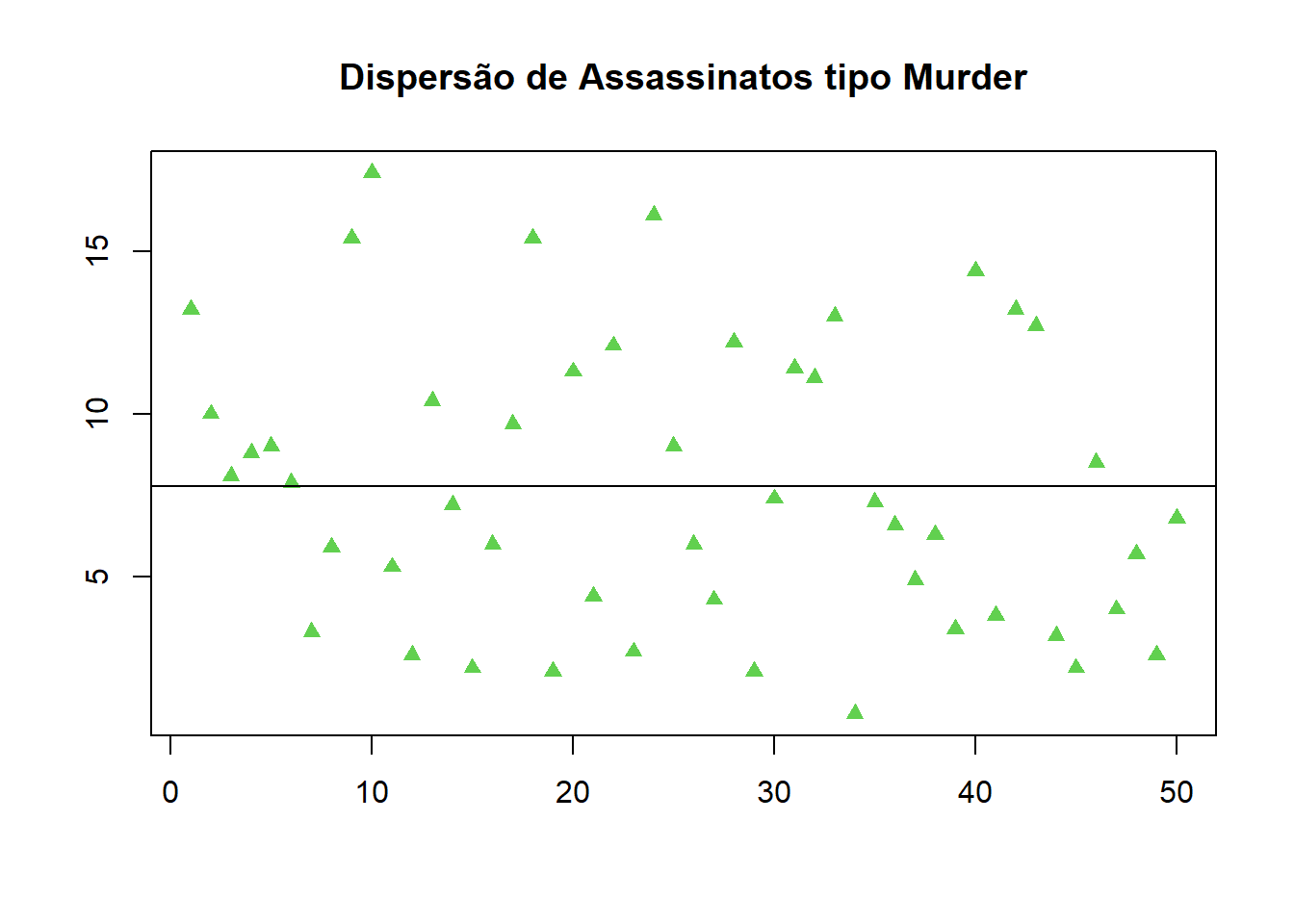
e) verifique se há correlação entre os diferentes tipos de crime.
corrplot(cor(data),method = "circle", type="upper", diag=FALSE,addCoef.col="black",tl.col="black")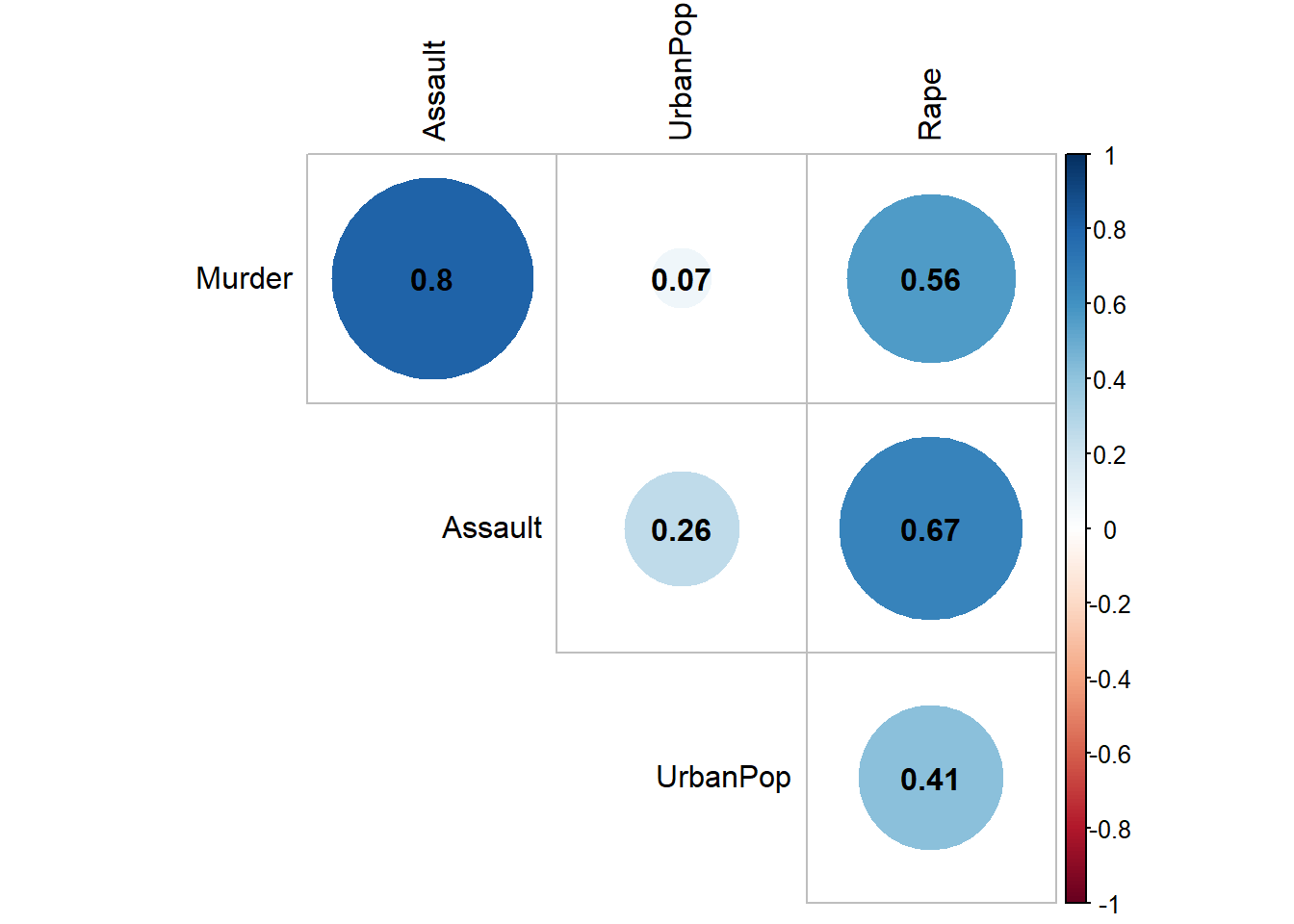
f) - Verifique se há correlação entre os crimes e a proporção de população urbana.
#Calcular o coeficiente de correlação de Pearson entre duas variaveis
cor ( data, data$UrbanPop, method = "pearson") ## [,1]
## Murder 0.06957262
## Assault 0.25887170
## UrbanPop 1.00000000
## Rape 0.41134124Referencia: ANÁLISE Multivariada - Trabalho 01. Disponível em: https://rpubs.com/viniciusrogerio/usarrests. Acesso em: 30 out. 2022.
# install.packages("readr")
imdb <- readr::read_rds("dados/imdb.rds")
imdb## # A tibble: 11,340 × 20
## id_fi…¹ titulo ano data_…² generos duracao pais idioma orcam…³ receita recei…⁴ nota_…⁵ num_a…⁶ direcao roteiro produ…⁷ elenco
## <chr> <chr> <dbl> <chr> <chr> <dbl> <chr> <chr> <dbl> <dbl> <dbl> <dbl> <dbl> <chr> <chr> <chr> <chr>
## 1 tt0092… Broad… 1987 1988-0… Comedy… 133 USA Engli… 2 e7 6.73e7 5.12e7 7.2 26257 James … James … Amerce… Willi…
## 2 tt0037… Murde… 1945 1945-0… Comedy… 91 USA Engli… NA NA NA 7.1 1639 George… Lou Br… Paramo… Fred …
## 3 tt0183… Me, M… 2000 2000-0… Comedy 116 USA Engli… 5.1e7 1.49e8 9.06e7 6.6 219069 Bobby … Peter … Twenti… Jim C…
## 4 tt0033… Never… 1941 1947-0… Comedy… 71 USA Engli… NA NA NA 7.2 2108 Edward… John T… Univer… W.C. …
## 5 tt0372… Adam … 2005 2007-0… Comedy… 99 USA Engli… NA 3.09e5 3.09e5 5.9 2953 Craig … Craig … Funny … Malco…
## 6 tt3703… Henry… 2015 2016-0… Drama 87 USA Engli… NA NA NA 6.1 2364 Stephe… Stephe… Chicag… Cole …
## 7 tt0093… No Wa… 1987 1987-1… Action… 114 USA Engli… 1.5e7 3.55e7 3.55e7 7.1 34513 Roger … Kennet… Orion … Kevin…
## 8 tt0494… Welco… 2008 2008-0… Comedy… 104 USA Engli… 3.5e7 4.37e7 4.24e7 5.5 13315 Malcol… Malcol… Univer… Marti…
## 9 tt0094… Some … 1987 1988-0… Drama,… 95 USA Engli… NA 1.86e7 1.86e7 7.1 27065 Howard… John H… Hughes… Eric …
## 10 tt1142… The F… 2008 2008-0… Drama 111 USA Engli… NA 3.71e7 3.71e7 5.7 6703 Tyler … Tyler … Louisi… Alfre…
## # … with 11,330 more rows, 3 more variables: descricao <chr>, num_criticas_publico <dbl>, num_criticas_critica <dbl>, and
## # abbreviated variable names ¹id_filme, ²data_lancamento, ³orcamento, ⁴receita_eua, ⁵nota_imdb, ⁶num_avaliacoes, ⁷producaoa). Crie um gráfico de dispersão da nota do imdb pelo orçamento.
plot(imdb$orcamento,xlab="", ylab = "", col = 3, pch = 17, lower.panel=NULL,main="Dispersão de Orcamneto")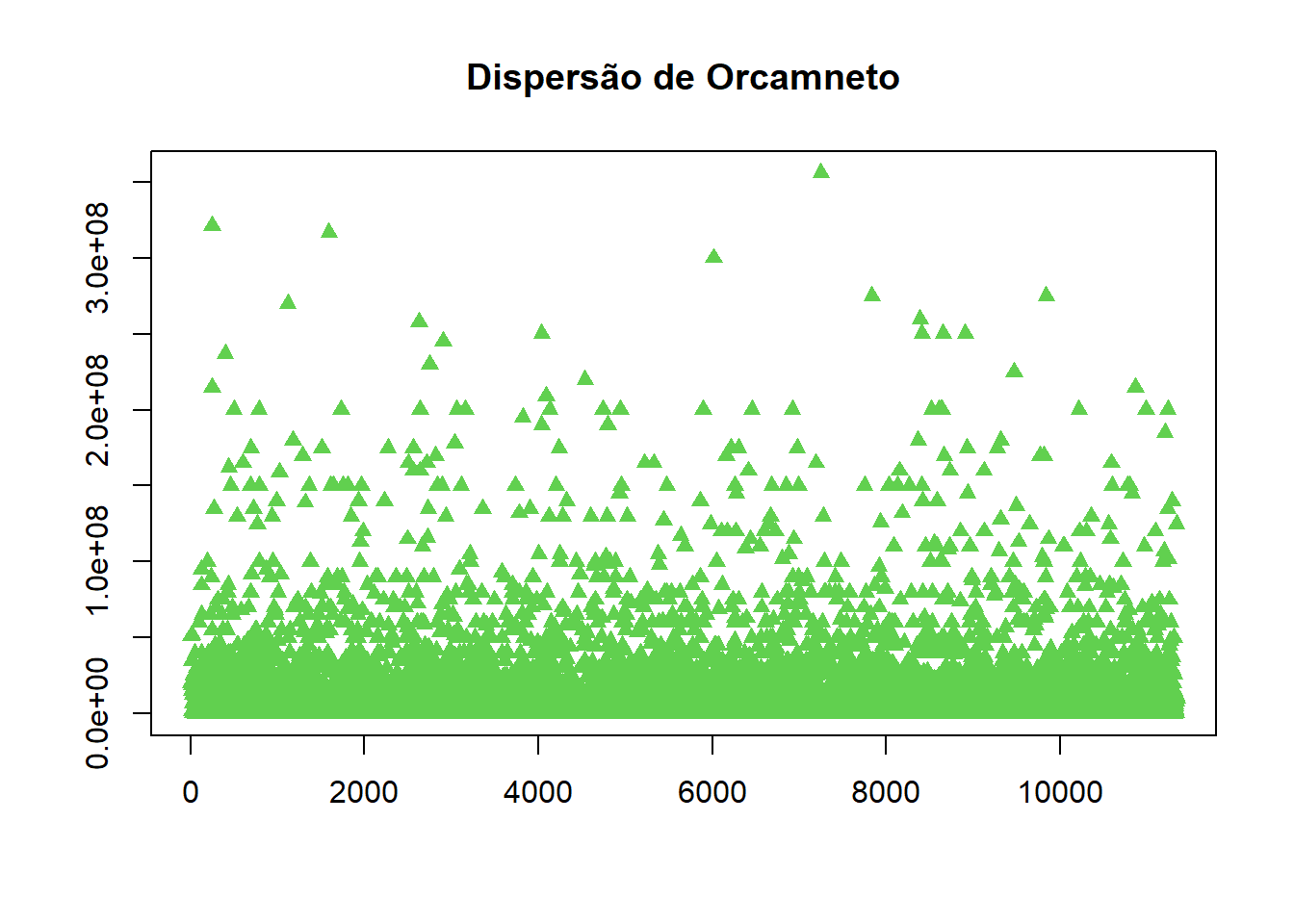
2.1.2 BLOCO 2: R básico
Carregar o conjunto de dados inibina
getwd()## [1] "C:/Users/Josias/Documents/IPT/BD/Cadernos_Josias"inibina <- read_excel("dados/inibina.xls")
nrow(inibina)## [1] 32sum()## [1] 0inibina$difinib = inibina$inibpos - inibina$inibpre
#agrupar as respostas e contador a qtde
inibina$resposta = as.factor(inibina$resposta)
plot(inibina$difinib ~ inibina$resposta, ylim = c(0,400))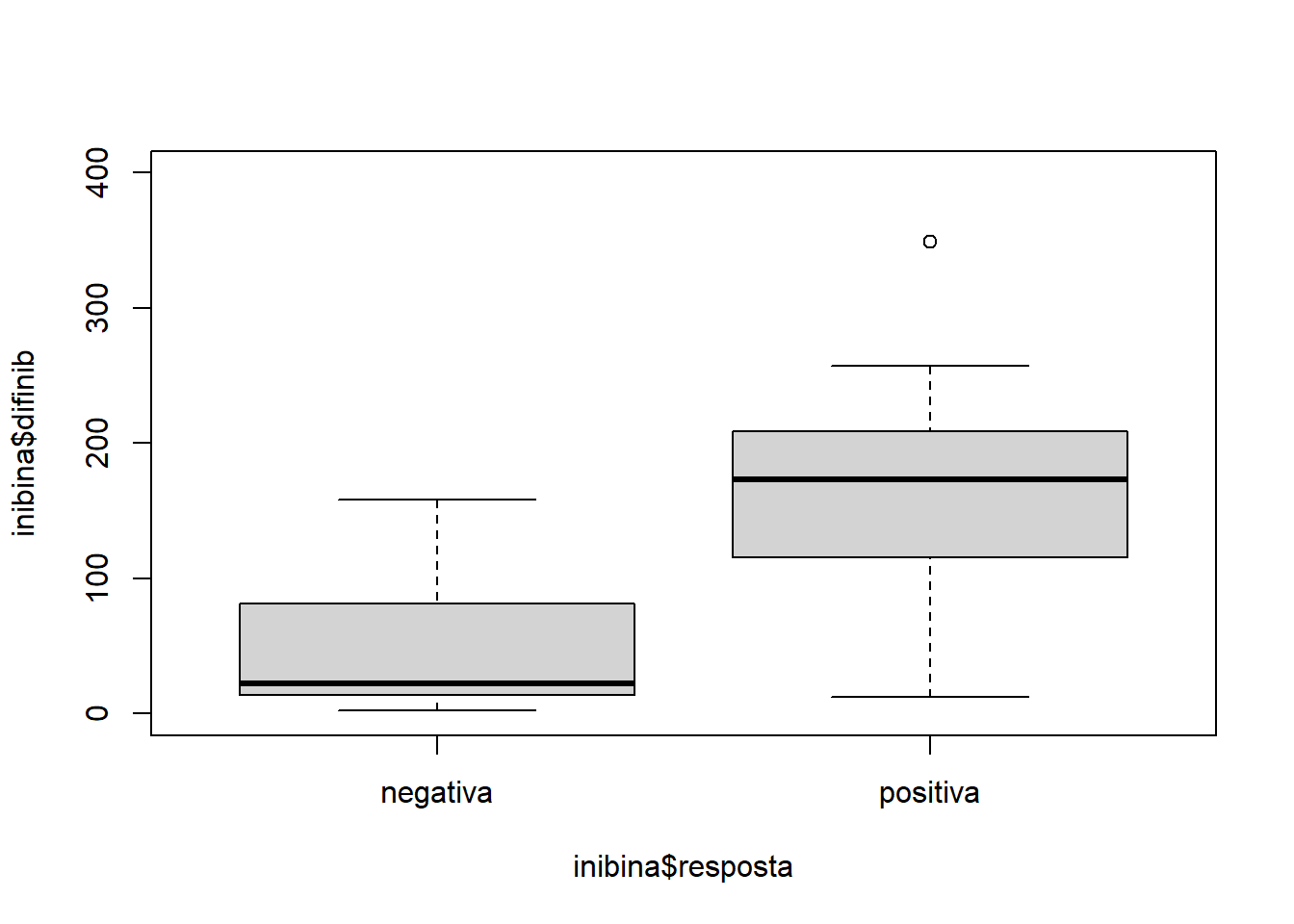
# Hmisc::describe(inibina)
summary(inibina)## ident resposta inibpre inibpos difinib
## Min. : 1.00 negativa:13 Min. : 3.02 Min. : 6.03 Min. : 2.48
## 1st Qu.: 8.75 positiva:19 1st Qu.: 52.40 1st Qu.: 120.97 1st Qu.: 24.22
## Median :16.50 Median :109.44 Median : 228.89 Median :121.18
## Mean :16.50 Mean :100.53 Mean : 240.80 Mean :140.27
## 3rd Qu.:24.25 3rd Qu.:148.93 3rd Qu.: 330.77 3rd Qu.:183.77
## Max. :32.00 Max. :186.38 Max. :1055.19 Max. :868.81sd( inibina$difinib )## [1] 159.2217modLogist01 = glm( resposta ~ difinib, family = binomial, data = inibina )
summary( modLogist01 )##
## Call:
## glm(formula = resposta ~ difinib, family = binomial, data = inibina)
##
## Deviance Residuals:
## Min 1Q Median 3Q Max
## -1.9770 -0.5594 0.1890 0.5589 2.0631
##
## Coefficients:
## Estimate Std. Error z value Pr(>|z|)
## (Intercept) -2.310455 0.947438 -2.439 0.01474 *
## difinib 0.025965 0.008561 3.033 0.00242 **
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## (Dispersion parameter for binomial family taken to be 1)
##
## Null deviance: 43.230 on 31 degrees of freedom
## Residual deviance: 24.758 on 30 degrees of freedom
## AIC: 28.758
##
## Number of Fisher Scoring iterations: 6#c. Ajuste um modelo de regressão logística aos dados. Qual é a acurácia do modelo em fazer classificação?
predito = predict.glm( modLogist01, type = "response")
classPred = ifelse(predito>0.5,"positiva", "negativa")
classPred = as.factor(classPred)
confusionMatrix(classPred, inibina$resposta, positive = "positiva" )## Confusion Matrix and Statistics
##
## Reference
## Prediction negativa positiva
## negativa 10 2
## positiva 3 17
##
## Accuracy : 0.8438
## 95% CI : (0.6721, 0.9472)
## No Information Rate : 0.5938
## P-Value [Acc > NIR] : 0.002273
##
## Kappa : 0.6721
##
## Mcnemar's Test P-Value : 1.000000
##
## Sensitivity : 0.8947
## Specificity : 0.7692
## Pos Pred Value : 0.8500
## Neg Pred Value : 0.8333
## Prevalence : 0.5938
## Detection Rate : 0.5312
## Detection Prevalence : 0.6250
## Balanced Accuracy : 0.8320
##
## 'Positive' Class : positiva
## #d.Use o classificador linear de Fisher para classificar a variável resposta de acordo com a variável preditora. Qual é a acurácia do classificador?
modFisher01 = lda( resposta ~ difinib, data = inibina, prior = c(0.5 , 0.5))
predito = predict(modFisher01)
confusionMatrix(classPred, inibina$resposta, positive = "positiva")## Confusion Matrix and Statistics
##
## Reference
## Prediction negativa positiva
## negativa 10 2
## positiva 3 17
##
## Accuracy : 0.8438
## 95% CI : (0.6721, 0.9472)
## No Information Rate : 0.5938
## P-Value [Acc > NIR] : 0.002273
##
## Kappa : 0.6721
##
## Mcnemar's Test P-Value : 1.000000
##
## Sensitivity : 0.8947
## Specificity : 0.7692
## Pos Pred Value : 0.8500
## Neg Pred Value : 0.8333
## Prevalence : 0.5938
## Detection Rate : 0.5312
## Detection Prevalence : 0.6250
## Balanced Accuracy : 0.8320
##
## 'Positive' Class : positiva
## #e. Use o classificador linear de Bayes para classificar a variável resposta de acordo com as variáveis explicativas. Utilize priori 0,65 e 0,35 para resposta negativa e positiva, respectivamente. Qual é a acurácia do classificador?
#Use o classificador knn para classificar a variável resposta de acordo com as variáveis preditoras. Utilize k = 1, 3, 5.
#library(iris)
#iris = tibble(iris)
#iris$ = iris[,1:4]